南京大学量子力学
量子力学最全名词解释及知识点整理

是三重简并的,对应于这些能级的态称为三重态( | 1,1⟩, | 1, − 1⟩, | 1,0⟩)
29. 正氦与仲氦p206
处于三重态的氦称为正氦,处于单态的氦称为仲氦,或者说基态的氦是仲氦
一些结论
1. 谐振子能量本征函数及其性质


为动量,λ为波⻓。
4. 态叠加原理(Superposition principle):p17
对 于 一 般 的 情 况 , 如 果 ψ1 和 ψ2 是 体 系 的 可 能 状 态 , 那 么 它 们 的 线 性 叠 加
ψ = c1ψ1 + c2ψ2也是这个体系的一个可能状态,其中c1和c2为复常数。
20. 偶极跃迁、偶极近似(Electric Dipole Approximation): p146
由于电磁波中电场对电子能量的影响远大于磁场,忽略光波中的磁场作用和原子的尺
寸,把电场近似地用Ex = E0 cos ωt(沿z轴传播的平面单色偏振光的电场)表示后得到的
结果,这样讨论的跃迁称为偶极跃迁,这种近似叫做偶极近似。
22. 简单塞曼效应、复杂塞曼效应(Zeeman e ect):p181
在外磁场较强的情况下,没有外磁场时的一条谱线在外磁场中将分裂为三条,这就是 简单塞曼效应。
在外磁场较弱时,电子自旋与轨道相互作用不能够忽略,光谱线分裂成偶数条,这称 为复杂塞曼效应。
23. 好量子数:p187
守恒量的特点:测量值的几率分布不随时间变化,守恒量的量子数称为好量子数。
•
谐振子能量的本征函数为:ψn(x)
=
Nne−
1 2
α2 x2Hn(α
量子力学习题集(NJU)

h ¯ k2
Note:
∫
∞
−∞
[ ( )] dx exp − α2 x2 + iβx + iγx2 =
(
π α2 + iγ
)1/2
−β 2 (α2 − iγ ) exp 4 (α4 + γ 2 )
[
]
4. 设粒子处于二维无限深势井中, 0, 0 ≤ x ≤ a, 0 ≤ y ≤ b; V (x) = ∞, 其它情况. 求粒子的能量本征值和本征函数,并讨论简并性。 参考答案:由于势阱无限深,在势阱外找到粒子的概率应该为零,因此势阱外的波函数为 ψ (x, y ) = 0. 在势井内部,定态薛定谔方程为 h ¯2 2 h ¯2 ∂2 ∂2 − ∇ ψ (x, y ) = − ( 2 + 2 )ψ (x, y ) = Eψ (x, y ). 2µ 2µ ∂x ∂y 这里,µ为粒子质量。做变量分离 ψ (x, y ) = f (x)g (y ), 我们有 其中,c > 0。 求解上面两个方程,我们有 f (x) = α eikx x + α e−ikx x , 1 2 g (y ) = β1 eiky y + β2 e−iky y ,
b
3
和
f (x) = A sin(k x), x g (y ) = B sin(ky y ). 进行归一化后,有 2 nπx mπx ψn,m (x, y ) = √ sin( ) sin( ). a b ab
而本征能量为 En,m = 当a = b时,则本征能量为 En,m =
2 2
4
h ¯ 2 π 2 n2 . 2ma2
于是, 1 ψ (x, 0) = √ [ψ1 (x) + eiϕ ψ2 (x)]. 2 (2) 1 h h ψ (x, t) = √ [ψ1 (x)e−iE1 t/¯ + eiϕ ψ2 (x)e−iE2 t/¯ ]. 2 |ψ (x, t)|2 = ψ ∗ (x, t)ψ (x, t) E1 − E2 1 2 2 (x) + ψ2 (x) + 2ψ1 (x)ψ2 (x) cos(ϕ + t)]. = [ψ1 2 h ¯ (3) ∫ ⟨x ˆ⟩ = 利用, ∫
量子力学基础知识

绪
新药的合成
天然药材
论
分离提取
结构测定
药理活性实验
分子设计合成
其中结构测定和分子设计必须具有扎实的结构化 学知识。
绪
四、主要参考书
论
1. 周公度等《结构化学习题解析(第4版)》,北京大学出版社,2008; 2. 麦松威等《高等无机结构化学(第2版)》,北京大学出版社,2006; 3. 李炳瑞《结构化学》,高等教育出版社,2
Wien(维恩) 曲线 验曲线比较吻合;在高频时,维
恩曲线较吻合。
实验曲线
0
但是在频率接近紫外光时,
理论计算值趋于无穷。
紫外
第一章
量子力学基础知识
Planck量子论
1. 黑体是由不同频率的谐振子组成; 2. 每个谐振子的能量总是某个最小能量单
位 ε的整数倍; E n n 1, 2, 3
4. 韦吉崇等《结构化学学习指导》,中国石化出版社,2010;
5. 林梦海等《结构化学》,科学出版社,2008; 6. 王军《结构化学》,科学出版社,2008; 7. 李奇《结构化学》,北京师范大学出版社,2008
绪
其它参考资料[ 强烈推荐]
所属领域:理论与计算化学
论
考研学校:南开大学、南京大学、吉林大学、厦门大学 精品课程:/course/jghx/jghx.htm
吻合的结果。
Planck能量量子化假设的提出,标志着量子理 论的诞生;
1918年,Planck获得的诺贝尔物理学奖。
第一章
量子力学基础知识
光 金属
电子
二、光电效应和光子学说
光电效应—光照射在金属表面 ,使金属发射出电子的现象。
光电子的产生与入射光的频率有关
南京大学物理考研专业与考试科目

看南大的吧,足够了,很全面物理学系(电话83596649)专业代码070201专业名称理论物理招生人数18研究方向01凝聚态理论与统计物理02计算物理03原子核理论与统计物理04量子场论与粒子物理05非线性物理和量子混沌考试科目①101政治②201英语一或202俄语③628量子力学④802普通物理一(含力学、热学、光学、电磁学)复试:统计物理参考书目《量子力学》(上册)蔡建华著,高等教育出版社;《量子力学》(上、下册)曾谨言著,科学出版社;《普通物理》(第一、二、三册)程守洙著,高等教育出版社;《热力学·统计物理》汪志诚著,高等教育出版社;《热力学与统计物理学》龚昌德著,人民教育出版社;《数学物理方法》梁昆淼等,高等教育出版社。
备注“物理学”为一级学科国家重点学科。
专业代码070202专业名称粒子物理与原子核物理招生人数8研究方向01穆斯堡尔谱学02核分析方法03核安全04核理论05应用中子物理06纳米技术和原子修饰07电子直线加速器研制与应用08宇宙学与超铉考试科目①101政治②201英语一或202俄语③629原子核物理④802普通物理一(含力学、热学、光学、电磁学)复试:量子力学参考书目《原子核物理》卢希庭著,原子能出版社;《普通物理》(第一、二、三册)程守洙著,高等教育出版社;《量子力学》(上、下册)曾谨言著,科学出版社;《近代物理学》王正行著,北京大学出版社;《原子核物理实验方法》(上册)复旦大学、清华大学、北京大学合著,原子能出版社。
备注“物理学”为一级学科国家重点学科。
专业代码070205专业名称凝聚态物理招生人数37研究方向01晶体生长、缺陷、物性02固体相变、光散射、内耗与超声衰减03光电功能晶体及其应用04铁电薄膜物理学与集成铁电学05衍射物理、同步辐射及应用06介电超晶格及应用、金属超晶格07磁学、磁性材料、磁光、磁电阻效应08纳米材料09低温物理、超导物理10太阳能光伏物理、能源与环境材料物理考试科目①101政治②201英语一或202俄语③628量子力学④802普通物理一(含力学、热学、光学、电磁学)复试:固体物理参考书目《固体物理学》黄昆、韩汝琦著,高等教育出版社;《量子力学》(上册)蔡建华著,高等教育出版社;《量子力学》(上,下册)曾谨言著,科学出版社;《普通物理》(第一、二、三册)程守洙著,高等教育出版社;《数学物理方法》梁昆淼著,高等教育出版社;《固体物理实验方法》王华馥著,高等教育出版社。
南京大学天文学系研究生培养方案草稿-南京大学研究生院

天文学一级学科(0704)研究生培养方案2006年5月修订一、培养目标1.具有扎实的数学、物理基础知识,较高的外语水平和熟练应用计算机的能力,具备一定的教学经验,毕业后能够适应在科研机构或高等院校从事科研和教学工作的需要。
2.硕士研究生要求掌握天文学的基础理论和基本观测事实,了解本专业某一前沿领域的发展方向和研究方法,具备一定的科研或应用能力。
3.博士研究生要求掌握坚实宽广的基础理论和系统深入的专业知识,对研究领域的现状、发展前景和存在问题有比较清晰的了解,能够独立地、创造性地开展科学研究工作。
三、学制硕士生学制为2.5年,博士生一般为3年,提前攻博生5年。
对部分研究生的弹性学制管理按照《南京大学研究生学籍管理规定》及其补充规定执行。
四、课程设置硕士研究生课程分为A、B、C、D四类,其中A类课程为全校公共课,B、C和D类课程分别为一级学科课程、二级学科(专业必修)课程和专业选修课程。
天文系研究生全部课程见下表。
五、培养方式1.对硕士研究生的培养以课程学习为主、学位论文为辅。
(1)硕士研究生须修满32学分,非本学科及同等学力入学者为36学分数的课程。
(2)除A类课程外,须至少修读2-3门B类课程(包括“天文文献阅读”课程)。
(3)天文系“戴文赛奖学金”将主要用于奖励课程学习成绩优秀的研究生。
2.对博士生的培养以学位论文为主、课程学习为辅。
(1)博士研究生在导师指导下须修读2-4门专业学位课程,其中导师讲授课程限1-2门。
(2)博士研究生在导师指导下选择学科前沿课题或有重要应用价值的课题进行研究。
在入学1-1.5年内在全系范围内作开题报告,在正式答辩前3个月内举行预答辩。
(3)为鼓励研究生在高水平的学术刊物上发表研究成果,对博士研究生科研成果的考核试行采用加权论文数的标准(试行期间学校原有考核标准继续有效)。
具体办法是,考虑不同学术期刊的影响因子和不同专业研究的特点,将天文学主要学术期刊(Nature、Science除外)分为三档,其中一档期刊包括ApJ, AJ, A&A, MNRAS, Solar Physics, PASP, PASJ, New Astronomy, ICARUS, Celest. Mech. Dyn. Astr., Earth, Moon & Planets等;二档期刊包括ApSS, Adv. Space Res., Science in China, Chinese Science Bulletin, Chinese Physics Letters,ChJAA等;三档期刊包括天文学报、天文学进展、空间科学学报、南京大学学报等。
报考2013年南京大学博士生名单
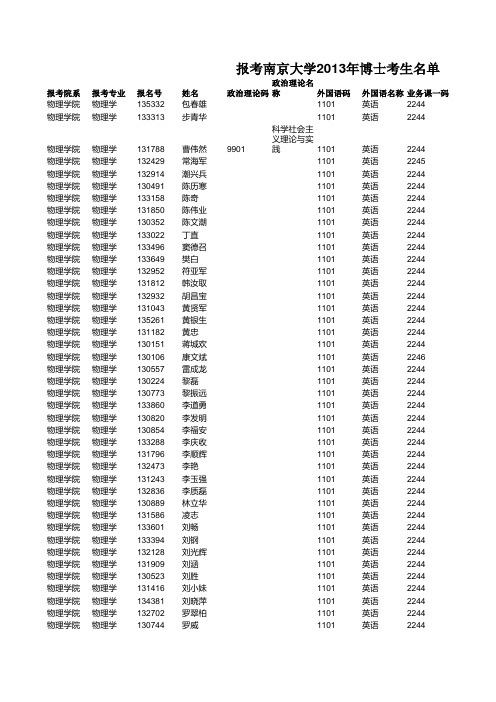
报考南京大学2013年博士考生名单报考院系报考专业报名号姓名政治理论码政治理论名称外国语码外国语名称业务课一码物理学院物理学135332包春雄1101英语2244物理学院物理学133313步青华1101英语2244物理学院物理学131788曹伟然9901科学社会主义理1101英语2244物理学院物理学132429常海军1101英语2245物理学院物理学132914潮兴兵1101英语2244物理学院物理学130491陈历寒1101英语2244物理学院物理学133158陈奇1101英语2244物理学院物理学131850陈伟业1101英语2244物理学院物理学130352陈文潮1101英语2244物理学院物理学133022丁直1101英语2244物理学院物理学133496窦德召1101英语2244物理学院物理学133649樊白1101英语2244物理学院物理学132952符亚军1101英语2244物理学院物理学131812韩汝取1101英语2244物理学院物理学132932胡昌宝1101英语2244物理学院物理学131043黄贤军1101英语2244物理学院物理学135261黄银生1101英语2244物理学院物理学131182黄忠1101英语2244物理学院物理学130151蒋城欢1101英语2244物理学院物理学130106康文斌1101英语2246物理学院物理学130557雷成龙1101英语2244物理学院物理学130224黎磊1101英语2244物理学院物理学130773黎振远1101英语2244物理学院物理学133860李道勇1101英语2244物理学院物理学130820李发明1101英语2244物理学院物理学130854李福安1101英语2244物理学院物理学133288李庆收1101英语2244物理学院物理学131796李顺辉1101英语2244物理学院物理学132473李艳1101英语2244物理学院物理学131243李玉强1101英语2244物理学院物理学132836李质磊1101英语2244物理学院物理学130889林立华1101英语2244物理学院物理学131586凌志1101英语2244物理学院物理学133601刘畅1101英语2244物理学院物理学133394刘钢1101英语2244物理学院物理学132128刘光辉1101英语2244物理学院物理学131909刘涵1101英语2244物理学院物理学130523刘胜1101英语2244物理学院物理学131416刘小妹1101英语2244物理学院物理学134381刘晓萍1101英语2244物理学院物理学132702罗翠柏1101英语2244物理学院物理学130744罗威1101英语2244物理学院物理学131735吕波1101英语2244物理学院物理学132526买力坦·开来木1101英语2244物理学院物理学130304毛伟锋1101英语2244物理学院物理学131456梅方1101英语2244物理学院物理学133485潘义明1101英语2244物理学院物理学131673乔川1101英语2244物理学院物理学134293沈辉1101英语2244物理学院物理学135251沈吉梅1101英语2244物理学院物理学130515沈乃丰1101英语2244物理学院物理学131546苏磊1101英语2244物理学院物理学132716涂宏庆1101英语2244物理学院物理学134960万志龙1101英语2244物理学院物理学133346王传聪1101英语2244物理学院物理学131866王道光1101英语2246物理学院物理学131875王辉1101英语2244物理学院物理学133236王鹏1101英语2244物理学院物理学131895王永龙1101英语2244物理学院物理学130480吴宏伟1101英语2244物理学院物理学134839吴建1101英语2244物理学院物理学133873吴鹏1101英语2244物理学院物理学135631吴闰生1101英语2244物理学院物理学131778吴兆峰1101英语2244物理学院物理学131878肖科文1101英语2244物理学院物理学133608徐超1101英语2244物理学院物理学132732徐海英1101英语2244物理学院物理学130240徐一飞1101英语2244物理学院物理学136022许瑞林1101英语2244物理学院物理学131250薛明明1101英语2244物理学院物理学132195杨斌1101英语2244物理学院物理学134680余幼胜1101英语2245物理学院物理学135470张法保1101英语2244物理学院物理学130699张恒1101英语2244物理学院物理学135957张红卫1101英语2244物理学院物理学131088张金锋1101英语2244物理学院物理学131985张丽1101英语2244物理学院物理学135843张茂书1101英语2244物理学院物理学131435张群永1101英语2244物理学院物理学130421张瑞芬1101英语2245物理学院物理学130381张新伟1101英语2244物理学院物理学131757张星1101英语2244物理学院物理学135635张耀1101英语2244物理学院物理学130296张渊1101英语2244物理学院物理学134827张者勇1101英语2244物理学院物理学132899赵杰1101英语2244物理学院物理学131588郑勇平1101英语2244物理学院物理学131661郑云龙1101英语2244物理学院物理学133741郑耘1101英语2244物理学院物理学134780周浩1101英语2244物理学院物理学130309朱庆利1101英语2244生名单业务课一名称业务课二码业务课二名称专项计划量子力学3357固体物理A量子力学3357固体物理A量子力学3361材料物理软物质物理3433统计物理量子力学3359光学概论B量子力学3433统计物理量子力学3359光学概论B量子力学3357固体物理A量子力学3357固体物理A量子力学3357固体物理A量子力学3359光学概论B量子力学3357固体物理A量子力学3357固体物理A量子力学3357固体物理A量子力学3359光学概论B量子力学3358量子场论量子力学3357固体物理A量子力学3357固体物理A量子力学3364原子物理生物物理3433统计物理量子力学3780铁磁学量子力学3357固体物理A量子力学3357固体物理A量子力学3780铁磁学量子力学3357固体物理A量子力学3780铁磁学量子力学3357固体物理A量子力学3357固体物理A量子力学3359光学概论B量子力学3359光学概论B对口支西量子力学3357固体物理A量子力学3780铁磁学量子力学3357固体物理A量子力学3357固体物理A量子力学3357固体物理A量子力学3357固体物理A量子力学3357固体物理A量子力学3357固体物理A量子力学3357固体物理A量子力学3357固体物理A量子力学3358量子场论量子力学3357固体物理A量子力学3359光学概论B量子力学3364原子物理少民计划量子力学3357固体物理A量子力学3357固体物理A量子力学3433统计物理量子力学3360原子核物理量子力学3357固体物理A量子力学3357固体物理A量子力学3364原子物理量子力学3780铁磁学量子力学3357固体物理A量子力学3357固体物理A量子力学3357固体物理A生物物理3433统计物理量子力学3357固体物理A量子力学3358量子场论量子力学3358量子场论量子力学3357固体物理A量子力学3357固体物理A量子力学3357固体物理A量子力学3357固体物理A量子力学3357固体物理A量子力学3359光学概论B量子力学3357固体物理A量子力学3357固体物理A量子力学3357固体物理A量子力学3357固体物理A量子力学3357固体物理A对口支西量子力学3358量子场论软物质物理3433统计物理量子力学3359光学概论B量子力学3358量子场论量子力学3357固体物理A量子力学3364原子物理量子力学3357固体物理A量子力学3357固体物理A量子力学3359光学概论B软物质物理3433统计物理量子力学3357固体物理A量子力学3357固体物理A少民计划量子力学3359光学概论B量子力学3357固体物理A量子力学3357固体物理A量子力学3357固体物理A量子力学3357固体物理A量子力学3358量子场论量子力学3357固体物理A量子力学3358量子场论量子力学3357固体物理A。
南京大学天文系课程介绍

天文与空间科学学院本科人才培养方案和指导性教学计划一、天文与空间科学学院概况南京大学天文与空间科学学院成立于2011年3月,其前身天文学系始建于1952年,是目前全国高校中历史最悠久、培养人才最多的天文学专业院系。
学院素以专业设置齐全、学历层次完备、师资力量雄厚、治学严谨而享有盛誉,在历届全国高校天文学科评比中均排名第一。
拥有为教学科研服务的中心实验室、太阳塔实验室、现代天文与天体物理教育部重点实验室和南京大学深空探测实验室等4个实验室。
目前拥有天文学国家一级重点学科(包括天体物理学、天体测量和天体力学2个国家二级重点学科),2个博士点和1个博士后流动站,今年新增空间科学与技术本科专业,培养具备扎实基础和实践技能,具有较强创新精神的空间科学与技术领域的高级专业人才,从事空间科学和深空探测等领域的工作。
??? 南京大学天文与空间科学学院拥有一支高水平的师资队伍。
现有教师约30名,包括4名中科院院士、2名长江学者、7名杰出青年科学基金获得者、1名国家百千万人才工程人选和5名教育部新(跨)世纪优秀人才支持计划入选者。
近年来,学院承担着多项国家自然科学基金项目和国家重点基础研究规划项目,科研成果显着,获多项国家级和省部级科研奖励。
学院与国内外多个科研和教学机构建立了密切的合作与人员交流联系和合作。
在南京大学“211”工程、“985”工程的重点支持下,学院正努力建设成为一个具有国际影响的天文学教学和科研中心。
2010年,南京大学与中科院紫金山天文台和中科院国家天文台南京天文光学技术研究所签订三方合作协议,共同在南京大学仙林校区建设“南京天文与空间科学技术园区”,即将开工建设的天文与空间科学学院办公大楼将坐落在该园区。
大楼总建筑面积达10000多平方米,将是一幢集科研、实验、教学、学术活动于一体的智能化建筑,将能够满足天文与空间科学学院未来20年在教学与科研方面的发展需要,并容纳多个研究中心,同时也是本学院教师与研究生科研、本科生实习的场所。
物理系研究生培养方案-南京大学研究生院

物理学院研究生培养方案研究生课程建设直接关系研究生基础知识的拓宽、解决实际问题能力的培养以及学位论文的质量。
因此,课程教学在实现研究生培养目标中占有重要地位。
硕士生研究生毕业的学分要求:本专业本科入学者32个学分,非本专业本科或同等学历入学者36个学分。
在培养方案中所列出的A是必修课;B类课程是重要的基础课程,每个硕士生必须至少选修2门B类课程;C类课程是各专业的学位课程,每个硕士生必须至少选修2门C类课程。
以下两门课D类课程,要求全系每个硕士生必须选修一到两门课,1)物理学进展;2)现代物理实验技术专题。
博士研究生除必须选修博士英语和现代科学技术革命与马克思主义两门公共课,还要求至少选修2门有关博士专业课程及专业英语。
凝聚态物理专业(070205)研究生培养方案-、培养目标培养我国建设需要,热爱祖国,思想先进,情操高尚,品德优良,具备严谨科学态度和优良学风,适应面向二十一世纪的德、智、体全面发展的凝聚态物理专业人才。
1.硕士学位掌握凝聚态物理的系统理论知识和基本实验技能,了解本领域研究动态,基本上能独立开展与本学科有关的研究和教学工作。
学位论文应具有一定的新颖性或应用背景.2.博士学位博士学位获得者应系统掌握凝聚态物理的基本理论,具有宽广和坚实的基础和基本实验操作技术,了解各自研究领域发展的历史现状和最新动态,能独立承担与各自研究领域有关的研究课题及基础教学工作。
学位论文要求具有重要的学术意义或应用价值。
并具有-定的创新性.论文在深度和广度两方面均需达到相应的要求.二、研究方向本专业分为两个培养方案。
凝聚态物理学培养方案(一)的研究方向:(1)晶体生长、缺陷、物性(2)固体相变、光散射、内耗与超声衰减(3)光电功能晶体及其应用(4)铁电、介电薄膜物理学与集成铁电学(5)衍射物理、同步辐射及应用(6)介电超晶格、金属超晶格及应用(7)磁学、磁性材料物理(8)自旋电子学(9)纳米材料科学与物理(10)超导电子学与物理(11)生物凝聚态物理(12)量子信息与量子计算(13)软凝聚态物理(14)表面、界面及相关物理(15)光电转换材料物理(16)强关联电子物理学(17)团簇结构与物理学凝聚态物理学培养方案(二)的研究方向:(1)纳米材料技术与应用(2)薄膜设计、生长、表征与器件(3)微波、光波吸收材料(4)稀土-过渡簇金属化合物的磁性及应用(5)半导体光伏材料与工艺(6)超导器件与新材料(7)清洁能源材料及器件(8)功能材料的设计与计算机模拟三、招生对象l.硕士研究生:符合报名资格,参加全国硕士研究生统一考试合格,再经面试合格者。
量子力学复习提纲

量子力学复习提纲一波函数一、波函数的意义及性质在量子力学理论体系中,体系的状态用波函数来描述,一般记为),(t rψ=ψ,其物理意义是玻恩的几率解释:在时刻t ,在),,(z y x 附近体积元dxdydz 内发现粒子(体系)的几率为dxdydz t r 2|),(|ψ。
对波函数,要认识一下几个问题: 1、关于波函数的归一化问题(1)几率描述中实质问题是相对几率,即要求任意两点的几率比值相同即可,因此),(t r ψ和),(t r Cψ描述的是同一个几率波。
这导致波函数总有一个不确定的常数因子。
(2)根据(1),我们一般要求波函数归一化,即选择常数C ,使1||2=ψ?τd C不过这样选择的常数C ,还有一个不确定的相因子,我们把满足这个条件的常数C ,叫归一化常数。
(3)由于我们关注的是相对几率,因此在某些情形下,我们也使用一些非归一化的波函数,如自由粒子平面波函数r p i e r=2/3)2(1)(πψ 粒子的位置本征函数)()(0r r r-=δψ2、波函数的标准化条件(1)既然波函数是几率波,因此要求波函数模方为有限,是必然的。
即=ψ2||有限值。
但实际上,只要波函数满足=ψτd 2||有限就可以了。
例如对粒子位置本征函数就是这样。
而这种放宽的条件会导致波函数在某点的值变为无穷大。
这也是允许的。
(2)波函数的连续性要根据定态薛定谔方程来确定。
)()()](2[222x E x x V dx d ψψμ=+- 因此,如果)(x V 是x 的连续函数,则)(x ψ和dxd ψ必为x 的连续函数。
如果><=ax V a x Vx V 21)(,其中21,V V 是常数,且)(12V V -有限,则波函数及其一阶导数连续。
证明:将薛定谔方程在a x =邻域积分,得0)(])([2)0()0(2l i m''=-?→?=--+?+-dx x E x V a a a a ψμψψεε所以,)('x ψ连续,从而)(x ψ也连续。
曾谨言《量子力学教程》(第3版)配套题库【名校考研真题-波函数与Schr

第 1 章 波函数与 Schrödinger 方程
一、选择题
1.光子和电子的波长都为 5.0 埃,光子的动量与电子的动量之比是多少?( )[中
南大学 2009 研]
A.1
B.3×1010
C.3.3×10-11
D.8.7×10-21
涉图像位置.C 项,电子能量增加并不会改变屏的特征光谱,不会变蓝.D 项,题中提到狭
2/7
圣才电子书 十万种考研考证电子书、题库视频学习平台
缝间距尺寸在德布罗意波长数量级,在电子能量变化不是很大时,电子波长应该仍与狭缝间 距相当,干涉图样不会消失.
4.题 2 中,如果两缝之间距离加倍,则干涉图样中相邻最大值之间距离( ).[中 南大学 2009 研]
A.干涉图样向装探测器的狭缝移动 B.干涉图样中相邻最大值之间距离改变 C.干涉图样பைடு நூலகம்失 D.干涉图样变弱
4/7
圣才电子书
【答案】C
十万种考研考证电子书、题库视频学习平台
【解析】由题意,通过该狭缝的电子位置将会由于测不准原理导致光子动量 P h 不
确定,以至于电子波长和频率会受到极大干扰,从狭缝射出的光波将不再是相干光,而干涉
2.试表述量子态的叠加原理并说明叠加系数是否依赖于时空变量及其理由.[南京大学 2009 研]
图 1-1
1/7
圣才电子书
A.向上移动距离 d
十万种考研考证电子书、题库视频学习平台
B.向下移动距离 d
C.向上移动距离 d/2
D.向下移动距离 d/2
【答案】B
【解析】分析未移动前位于屏幕正中间的点,令偏上的光线为 a,偏下的光线为 b,未
2005年硕士研究生入学考试及答案

目录1.05年北师大物理类各方向2.05年长光所3.05年东南大学4.05年中科大5.05年南京大学6.05年华中科大7.05年吉林大学(原子所)8.05年四川大学(原子与分子)9.05年北京理工10.05年河北理工11.05年长春理工北京师范大学2005年招收硕士研究生入学考试试题专业:物理类各专业科目代号:459研究方向:各方向考试科目:量子力学[注意]答案写在答题纸上,写在试题上无效。
1.(20分)一个电子被限制在一维谐振子势场中,活动范围求激发电子到第一激发态所需要的能量(用ev表示)(,,)提示:谐振子能量本征函数可以写成2.(30分)一个电子被限制在二维各向同性谐振子势场中(特征频率为)。
(1)写出其哈密顿量,利用一维谐振子能级公式找到此电子的能级公式和简并度。
(2)请推导电子的径向运动方程。
并讨论其在时的渐近解。
提示:极坐标下3.(50分)两个质量为的粒子,被禁闭在特征频率为的一维谐振子势场中,彼此无相互作用(此题中波函数无须写出具体形式):(1)如果两个粒子无自旋可分辨,写出系统的基态(两个都在自己的基态)和第一激发能级(即一个在基态,另一个在第一激发态)的波函数和能量(注意简并情形)。
(10分)(2)如果两个粒子是不可分辨的无自旋波色子,写出系统的基态和第一激发态的能量和波函数。
如果粒子间互作用势为,计算基态能级到一级微扰项。
(15分)(3分)如果两个粒子是不可分辨的自旋1/2粒子,写出基态能级和波函数(考虑自旋)。
如果粒子间互作用能为,计算基态能量。
(15分)(4)同(3),解除势阱,两个粒子以左一右飞出。
有两个探测器分别(同时)测量它们的y方向自旋角动量。
请问测量结果为两电子自旋反向的几率是多少?(10分)4.(30分)中心力场中电子自旋与轨道角动量存在耦合能。
总角动量,是的共同本征态。
现有一电子处于态,且。
(1)在一基近似下,可用代替,请问电子的能量与态差多少?(2)请计算该电子产生的平均磁矩,并由此计算在z方向均匀磁场B中电子的能量改变多少?(),当,,当,5.(20分)一个定域(空间位置不动)的电子(自旋1/2)处于z方向强磁场中。
量子力学考研真题与量子力学考点总结

量子力学考研真题与量子力学考点总结8粒子在势场V中运动并处于束缚定态中,试证明粒子所受势场作用力的平均值为零。
[中国科学院2006研]【解题的思路】直接利用势场中作用力的表达式,求解其平均值,然后利用与哈密顿量的对易关系就可得出结果。
【分析】在势场V中,粒子所受作用力为因此作用力F的平均值为得证。
【知识储备】①束缚态:在无穷远处,粒子的波函数为零的状态。
②即③在某一表象下,算符F ∧在ψ态中的平均值为29两个无相互作用的粒子置于一维无限深方势阱(0<x <a )中,对于以下两种情况,写出两粒子体系可具有的两个最低能量值,相应的简并度,以及上述能级对应的所有二粒子波函数:(1)两个自旋为1/2的可区分粒子; (2)两个自旋为1/2的全同粒子。
[中国科学院2007研]【解题的思路】对于可解模型一维无限深势阱,可以通过定态薛定谔方程来求解相应的本征波函数和本征值,由可区分粒子和全同粒子的性质,可以构造相应的两粒子波函数。
【分析】(1)对于一维无限深势阱中的单粒子,由定态薛定谔方程可得 波函数为本征能量为对于两个可区分粒子基态能量波函数因此,能级简并度为4。
第一激发态或者能量波函数因此,能级简并度为8。
(2)对于两个全同粒子,自旋1/2为费米子,则总波函数满足交换反对称关系。
基态能量波函数能级非简并。
第一激发态或者能量波函数能级简并度为4。
【知识储备】①一维无限深方势阱若势能满足在阱内(|x|<a),体系所满足的定态薛定谔方程是在阱外(|x|>a),定态薛定谔方程是体系的能量本征值本征函数②全同粒子a.全同粒子定义在量子力学中,把内禀属性(静质量、电荷、自旋等)相同的微观粒子称为全同粒子。
b.全同性原理全同性原理:由于全同粒子的不可区分性,使得由全同粒子所组成的体系中,两全同粒子相互代换不引起物理状态的改变。
描述全同粒子体系的波函数只能是对称的或反对称的,而且这种对称性不随时间改变。
c.两个电子的自旋函数若不考虑两电子自旋相互作用,两电子对称自旋波函数χS和反对称自旋波函数χA,分别写为【拓展发散】两个自旋为1的全同粒子,即玻色子,求解相应的波函数和能量,以及简并度。
北京大学南京大学量子力学考研试题题库

峪F黢 嘁ing
参 C)haptcΓ 1 0ri胥 :ins OfQuantum Physics
α1apter2 M【rtthcmatic1b()ls OfQ11ar、 tt1mλ4ec丨】anics Chaptcr3 POstulatcs OfQuantulvl人丌cchani(;s
C∷haptcr4 ()haptcr5
j的
本
^=o^不
征值 和本和f函
数
。
学 (b)在 宏农象巾,求 箅符
ε的铡i阵 表示 ,以 及 月的本 征竹 和l本 征 函数 。
)供ε 奋兀二砷 · ⑹ 求从 ⒔农象到 捻表象^的和幺i∷ 变换知阵。
(;罗
:(∶
彳a艹 £甫:口
″ι
w
厶 \ 丿
叫
+ d
n
` 丨
‘
\ ︑
R”
●夕
一b' 丶
0
d
丿
一 一
6,Ⅵ so″ 】而 ε 阝勿 切 /lT伤 nⅠ `卩 c犭 tRf/饣
ቤተ መጻሕፍቲ ባይዱ
J冫 幻 /s氵
)l飞 1nlC Ⅱ I。
PA· M· IⅡ rac
C,·
ρ .J· ∫·Sakur缸
sy11a笾冫us
考 7`3eP而
刀c洌es
q厂 Q溺 nFⅣ 饲
∧亻0c向 佣
泅
冫4th刚 itiOn
f‘
吹 ,
Ⅳ o初 mQ“ 溺/PrⅡ Jlf姒佗c九四崩 cs,Rc∽ scd Edi⒈ iOn 衤1.
王鸳?矿廴卩 嚅
。dFˇ 石 .
饣 马∷助赳 η
乙耕 ”:
·
爹 亻 鲁
汇总高校量子力学考研试题

汇总⾼校量⼦⼒学考研试题习题1⼀、填空题1.玻尔的量⼦化条件为。
2.德布罗意关系为。
3.⽤来解释光电效应的爱因斯坦公式为。
4.波函数的统计解释:_______________________________________________________________________________________________5.为归⼀化波函数,粒⼦在⽅向、⽴体⾓内出现的⼏率为,在半径为,厚度为的球壳内粒⼦出现的⼏率为。
6.波函数的标准条件为。
7.,为单位矩阵,则算符的本征值为__________。
8.⾃由粒⼦体系,__________守恒;中⼼⼒场中运动的粒⼦___________守恒。
9.⼒学量算符应满⾜的两个性质是。
10.厄密算符的本征函数具有。
11.设为归⼀化的动量表象下的波函数,则的物理意义为_______________________________________________。
12.______;_______;_________。
28.如两⼒学量算符有共同本征函数完全系,则___。
13.坐标和动量的测不准关系是____________________________。
14.在定态条件下,守恒的⼒学量是_______________________。
15.隧道效应是指__________________________________________。
16.量⼦⼒学中,原⼦的轨道半径实际是指____________________。
17.为氢原⼦的波函数,的取值范围分别为。
18.对氢原⼦,不考虑电⼦的⾃旋,能级的简并度为,考虑⾃旋但不考虑⾃旋与轨道⾓动量的耦合时,能级的简并度为,如再考虑⾃旋与轨道⾓动量的耦合,能级的简并度为。
19.设体系的状态波函数为,如在该状态下测量⼒学量有确定的值,则⼒学量算符与态⽮量的关系为__________。
20.⼒学量算符在态下的平均值可写为的条件为____________________________。
凝聚态物理与量子力学

!"#$%#&%$ ’())%* +,-&.!& (#$ /0(#)0’ ’%!,(#.!&
()*+ ,-./!
(! ("
()*+ 01.2342/5"
"!##$%, =,/($ ) "!##"&, =,/($ )
!"#$%&’"(& )* +,-./0. ,1$&/)($2 3$4)%$&)%- )* 5)2/6 5&$&" 7/0%).&%80&8%". ,1$(9/(: ;(/<"%./&- ,1$(9/(: !"#$%&’"(& )* +,-./0. ,1$(9/(: 1)%’$2 ;(/<"%./&-,1$(9/(:
凝聚态物理与量子力学 !
冯 端!
(! 南京大学物理系 ("
冯少彤"
南京 "!##$%) 南京 "!##"&)
固体微结构物理国家重点实验室
南京师范大学物理系
摘
要
文章扼要地回顾了量子力学在奠定凝聚态物理基础中所起的关键作用; 并讨论了当今凝聚态物理发展的 量子力学, 凝聚态物理
主要动向; 进而阐明了为何凝聚态物理, 不论在基础研究, 还是促进技术发展, 抑或推动学科交叉方面, 尚大有可为 ’ 关键词
物理
$
理论方法: 量子力学, 还是经典物理?
固体的能带理论是一种典型的凝聚态理论, 它
采用了量子力学的方法来处理电子系统的问题, 而 将离子 (或原子核) 看为经典粒子, 具有确切的位置, 形成周期势场 6 在这里不仅将两种粒子系统分别处 理, 而且采用了截然不同的理论方法, 需要适当的理
南京大学考研量子力学试题2001-2009

南京大学2001年硕士研究生入学考试试题———量子力学 专业: 理论物理、、凝聚态物理、光学等一、有一质量为μ的粒子处于长度为a 的一维无限深势阱中()⎩⎨⎧<<><∞=a x a x x x V 0,0;0,,在t=0时刻,粒子的状态由波函数()⎩⎨⎧<<-><=a x x a Ax a x x x 0),(;0,0ψ描述。
求: (20分) 1.归一化常数A; 2.粒子能量的平均值; 3.t=0时刻,粒子能量的几率分布; 4. 人艺t>0时刻的波函数的级数表达式。
提示:96145,3,14π=∑⋅⋅⋅=n n二、考虑势能为()⎩⎨⎧<>=0,00,0x x V x V 的一维系统,其中0V 为正常数。
若一能量为E 的粒子从-∞=x 处入射,其透射系数和反射系数各为多少?考虑E 的所有可能值。
(20分)三、有一质量为μ的粒子,在一维谐振子势场()2221x x V μω=中运动。
在动能μ22p T =的非相对论极限下,基态能ω 210=E ,基态波函数为()⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=ψ24102exp x x μωπμω。
考虑T 与p 的关系的相对论修正,计算基态能级的移动E ∆至21c 阶。
(c 为光速)(20分) 四、氯化钠晶体中有些负离子空穴,每个空穴束缚一个电子。
可将这些电子看成束缚在一个尺度为晶格常数的三维无限深势阱中。
晶体处于室温,试粗略地估计被这些电子强烈吸收的电磁波的最长的波长。
(20分) 提示:电子质量fm MeV c MeV mc ⋅≈=197,511.02 ,晶格常数01A a ≈ 五、考虑自旋 21=S 的系统, 1.求算符zy S B S A T ˆˆˆ+=的本征值和归一化本征波函数;(A 、B 为实常数) 2.若此时系统正处在T ˆ的某一个本征态上,求此时测量y S ˆ结果为⎪⎭⎫ ⎝⎛+2 的几率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
提示:电子质量,晶格常数
五、考虑自旋的系统,
1. 求算符的本征值和归一化本征波函数;(A、B为实常数)
3. t=0时刻,粒子能量的几率分布;
4. 人艺t>0时刻的波函数的级数表达式。
提示:
二、考虑势能为的一维系统,其中为正常数。若一能量为E的粒子从处入射,其透射系数和反射系数各为多少?考虑E的所有可能值。(20分)
三、有一质量为的粒子,在一维谐振子势场中运动。在动能的非相对论极限下,基态能,基态波函数为。考虑T与p的关系的相对论修正,计算基态能级的移动至阶。(c为光速)(20分)
2. 若此时系统正处在的某一个本征态上,求此时测量结果为的几率。(20分)
必须有所知,否则不如死。——罗曼·罗兰
必须有所知,否则不如死。——罗曼·罗兰
南京大学2001年硕士研究生入学考试试题---量子力学
专业: 理论物理、、凝聚态物理、光学等
一、有一质量为的粒子处于长度为a的一维无限深势阱中,在t=0时Байду номын сангаас,粒子的状态由波函数描述。求: (20分)
1. 归一化常数A;
2. 粒子能量的平均值;
