大学物理热力学
大学物理热力学PPT课件

02
对应态原理
不同物质在相同的对应状态下具有相同 的热力学性质。对应态参数包括对比压 强、对比体积和对比温度。
03
范德华方程与对应态 原理的应用
预测真实气体的性质,如液化温度、临 界参数等。
真实气体行为描述
压缩因子
描述真实气体与理想气体偏差程度的物理量,定义为Z = pV/nRT。对于理想气体,Z = 1;对于真实气体,Z ≠ 1。
细管电泳等。
固体熔化与升华过程分析
固体熔化
升华过程
熔化与升华的应用
固体在加热过程中,当温度达到 熔点时开始熔化,由固态转变为 液态。熔化过程中吸收热量,温 度保持不变。
某些物质在固态时可以直接升华 为气态,而无需经过液态阶段。 升华过程中也吸收热量,但温度 同样保持不变。
熔化与升华是物质相变的重要过 程,对于理解物质的热力学性质 和相变规律具有重要意义。同时, 在实际应用中也具有广泛用途, 如金属冶炼、材料制备等领域。
阿马伽分体积定律
混合气体的总体积等于各组分气体分体积之和,即V_total = V_1 + V_2 + ... + V_n。
理想气体混合物的性质
各组分气体遵守理想气体状态方程,且相互之间无化学反应。
范德华方程与对应态原理
01
范德华方程
对真实气体行为的描述,考虑了分子体 积和分子间相互作用力,形式为(p + a/V^2)(V - b) = RT,其中a、b为与物 质特性相关的常数。
维里方程
描述真实气体行为的另一种方程形式,考虑了高阶分子间 相互作用项,形式为pV = nRT(1 + B/V + C/V^2 + ...), 其中B、C等为维里系数。
大学物理第二十四讲 热力学第一定律、摩尔热容PPT课件

U
CV ,mT
i 2
RT
3104 J
2. Qp Cp,mT Cp,m (T2 T1) Cp,m (t2 t1)
t2
t1
Qp
Cp,m
t1
2Qp
(i 2)R
36C
t1 0C
19
例:热力学系统经历如图所示过程后回到初态a。设过 程 abc 中吸热600 J;过程 cda 向外放热450J,对外做 功-150J,求系统在 abc 过程中内能的增量及对外做功。
Please Criticize And Guide The Shortcomings
讲师:XXXXXX XX年XX月XX日
R(T2
T1)
o
VV
●等容过程中系统从外界吸收的热量全部转化为
系统的内能。
10
三、等压过程
dp 0
pV RT U i RT
2 Q U A
U
i 2
R(T2T1)ppA V2 V1
pdV
p(V2
V1 )
A
R(T2 T1)
o
V1
V2 V
Qp
U
A
i 2
R(T2
T1)
R(T2
T1)
Tb 2Ta Tc , Td Ta , Vc V3 4V1
所以
U
i 2
R(Td
Ta )
0
p
p2 a
Aab p2 (V2 V1) 2 p1V1 2 RTa
Abc
RTb
ln
Vc Vb
2 RTa
ln 2
p1
o V1
Acd p1(V2 V3 ) 2 p1V1 2 RTa
b 等温线
大学物理第8章:热力学基础

说明:A. 准静态过程为理想过程
弛豫时间 ( ):系统的平衡态被 破坏后再恢复到新的平衡态所需 要的时间。
气缸
B.一个热力学过程为准静态过程的必要条件为过程 所经历的时间大于驰豫时间 t 如:若气缸缸长 L 101 (m ),则 103 ~ 104 ( s ) 若活塞以每秒几十次的频率运动时, 每移动一次经 1 tt 时 t 10 ( s ) ,则满足 , C.准静态过程可以用宏观参量图给予表示
讨论: (1) n=0, 等压过程,Cp=CV+R ,过程方程: T/V=C4; (2) n=1, 等温过程,CT = , 过程方程: pV=C5; (3) n= , 等体过程, CV =iR/2 , 过程方程: p/T=C6; (4) n= , 绝热过程,CQ=0, 过程方程:
pV C1 , TV
RdT
由 pV=RT 于是得
C CV
pdV
pdV+Vdp=RdT
R pdV (1 ) Vdp 0 C CV dp R dV (1 ) 0 p C CV V
令
R 1 n —多方指数 C C V
21
dp dV n 0 p V
完成积分就得多方过程的过程方程:
V1
V2
i ( p2V2 p1V1 ) 2
只与始末状态有关
M i RT 2
( if
c const )
Q cM (T2 T1 )
与过程有关
特点
与过程有关
对微小过程:dQ=dE + dA
M i dQ RdT pdV 2
14
例题 8-2 如图所示,一定量气体经过程abc吸热 700J,问:经历过程abcda吸热是多少? 解 Q= E2-E1 + A i 过程abc : 700= Ec -Ea+ Aabc= ( pcVc paVa ) Aabc
大学物理中的热力学热能的转化与热力学定律

大学物理中的热力学热能的转化与热力学定律热力学是物理学中研究热能转化与热力学定律的一个重要分支。
热力学研究了热能与其他形式能量之间的转化关系,从而揭示了物质中热现象的本质规律和特性。
在大学物理学习中,了解热力学的基本原理对于理解能量转化和自然界中的热现象非常重要。
一、能量与热力学能量是物质存在时的基本属性,包括热能、机械能、化学能等形式。
热能指的是物质内部由分子振动和相对运动带来的能量。
热力学研究如何将热能转化为其他形式的能量,以及如何实现能量守恒。
二、热力学系统与热力学定律热力学中的系统指的是由一定数量物质和能量组成的系统,可以是封闭的、开放的或孤立的。
热力学定律是通过观察和研究系统中能量的转化和物质的变化得出的。
其中最重要的三条热力学定律分别是热力学第一定律、第二定律和第三定律。
三、热力学第一定律——能量守恒定律热力学第一定律表明能量在一个系统中是守恒的,能量可以转化为其他形式,但总量不变。
这意味着系统所吸收的热量与所做的功等于内能的变化。
即,ΔU = Q - W其中,ΔU表示内能的变化,Q表示系统吸收的热量,W表示系统对外界做的功。
四、热力学第二定律——熵增定律热力学第二定律是关于能量转化方向的定律。
它指出,孤立系统的熵增总是大于等于零,且在实际过程中熵增不会减小。
熵是描述能量分子混乱程度的物理量,熵增表示能量分子无序性的增加。
五、热力学第三定律——绝对零度定律热力学第三定律说明了在绝对零度下,系统的熵为零。
绝对零度是热力学温标的零点,相对于绝对零度,系统的热能全部被完全冻结,内能最小。
六、热力学中的热能转化在热力学中,热能可以通过热传导、热辐射和热对流等过程转化为其他形式的能量。
热传导是指通过物质内部的分子间碰撞,热能从高温区向低温区传递。
热辐射是指物质表面的热能通过辐射传递。
热对流是指通过液体或气体的传流而进行的热能转移过程。
七、热力学的应用热力学的研究在能源转换、工程设计、气候变化、环境保护等方面都有重要应用。
大学物理热学

ΔU=Q+W,其中ΔU表示系统内能的增量,Q表示外界对系统传递的热量,W表示外界对系统做的功。
热力学第二定律
内容
不可能把热从低温物体传到高温物体而不产生其他影响,或不可能从单一热源 取热使之完全转换为有用的功而不产生其他影响,或不可逆热力过程中熵的微 增量总是大于零。
表达式
对于可逆过程,有dS=(dQ/T);对于不可逆过程,有dS>(dQ/T),其中S表示熵, T表示热力学温度。
02
辐射传热特点
不需要介质,可在真空中传播;伴 随能量形式的转换;辐射强度与物
体温度的四次方成正比。
04
应用
太阳能利用、红外遥感测温、激光 器等。
复合传热过程分析
复合传热 分析方法 影响因素
应用
实际传热过程中往往同时存在热传导、对流和辐射三种传热方式。 根据具体传热条件,建立物理模型,综合运用热传导、对流和辐 射的传热规律进行分析计算。
02
理想气体性质及应用
理想气体状态方程
01
理想气体状态方程
pV = nRT,其中p为压强,V为 体积,n为物质的量,R为气体常 数,T为热力学温度。
02
理想气体状态方程 的适用条件
适用于稀薄气体,即气体分子间 距离较大,相互作用力可忽略不 计。
03
理想气体状态方程 的应用
可用于计算气体的压强、体积、 温度等物理量,以及进行气体状 态变化的分析。
热力学在其他领域应用
化学工业
制冷与空调
新能源领域
在化学工业中,热力学原理被广泛应用 于化学反应过程的分析和优化。通过热 力学计算和分析,可以确定化学反应的 条件、反应热、反应平衡常数等关键参 数,为化学工业的生产提供理论指导。
《大学物理》课件-热力学第一定律

21
例1 理想气体准静态等温膨胀做的功。并思考如何实现这 一准静态过程。
22
假设缸中由v mol气体,等温膨胀的温度为T,体积
变化为:
V1 →V2
则
V2
A=
V1
pdV
= V2RT
绝热壁
C
向真空中自由膨胀。测量 膨胀前后水温的变化。
气体
真空 水
实验结果:水温不变,
验证了理想气体的内能与体积无关。为什么?
dQ = 0,dA = 0 dE = 0 (V1 →V2 )
但水的热容比气体的大得多,焦耳实验中气体温度变化不 易测出。实验进一步改进。1852年焦耳和汤姆逊用节流方法重 新做了实验。
11
4.热力学第一定律 机械能守恒: Aex + Ain,n-cons = EB - EA 对保守系统: Aex = EB - EA = ΔE 质心参考系下:Aex = Ein,B - Ein,A
对单一组分的热力学系统(保守系统),外界对系统做 功可分为:①与系统的边界具有宏观位移相联系的宏观功; ②没有宏观位移的热传递型微观功。
Aex = A + Q 则机械能守恒在热力学系统的新形式: A + Q = ΔE
12
对于任何宏观系统的任何过程,系统从外界吸收的热
量等于系统内能的增量和系统对外做的功之和。
Q = E2-E1 + A
A = -A表示系统对外界做功。对初、末态为平衡态的无
限小过程
dQ = dE + dA
——涉及热现象的能量守恒定律的表述。 ——不需要能量输入而能继续做功的“第一类永动机”不 存在。
大学物理《热力学基础》

热力学第二定律的实验验证
卡诺循环实验
通过比较可逆卡诺循环和不可逆卡诺循环的效率, 证明了热力学第二定律的正确性。
焦耳实验
通测量热量和功之间的转换关系,证明了热力 学第二定律的正确性。
热辐射实验
通过测量不同温度下物体的辐射能,证明了熵增 加原理的正确性。
05 热力学的应用
热机效率的提高
热机效率的概念
热力学第二定律定义
熵增原理
热力学第二定律的本质
不可能把热从低温物体传到高温物体而不产 生其他影响;不可能从单一热源取热使之完 全转换为有用的功而不产生其他影响;不可 逆热力过程中熵的微增量总是大于零。
在封闭系统中,自发过程总是向着熵 增加的方向进行,即熵增加原理。
揭示了热量传递和做功过程的不可逆 性,是能量耗散和转化过程的宏观规 律。
通过学习热力学基础,学生可以了解热现象的本质和规律,掌握热力学的 分析方法,为后续的物理学习和实际应用打下基础。
热力学的重要性
热力学在能源、化工、材料 、环保等领域有广泛应用, 是解决实际问题的重要工具
。
热力学的基本原理和方法对 于理解其他物理分支(如电 磁学、光学)以及交叉学科 (如生物物理、地球物理)
热力学第二定律的应用
空调制冷原理
利用制冷剂在蒸发器中吸热蒸发而降低温度,再通过冷凝器放出热 量,使室内温度降低。
汽车发动机效率
汽车发动机效率不可能达到100%,因为发动机工作时会产生热量 损失,这些热量无法完全转化为机械功。
热机效率
热机效率不可能达到100%,因为燃料燃烧产生的热量不可能完全转 化为机械功,其中一部分热量会以热量的形式散失到环境中。
THANKS FOR WATCHING
大学物理~热力学基础

气体的内能
E i RT
2
(内能是态函数!)
气体的内能的增量
E i RT
2
二. 功
热量
P
S
dl
(1)功
计算系统在准静态膨胀过程中所作的功: dW F dl P S dl PdV
当活塞移动一段有限距离时
压强作功
W V2 P dV V1
V2
W PdV
热机发展简介
1698年萨维利和1705年纽可门先后发 明了蒸气机 ,当时蒸气机的效率极低 . 1765年瓦特进行了重大改进 ,大大提高了 效率 . 人们一直在为提高热机的效率而努 力,从理论上研究热机效率问题, 一方面 指明了提高效率的方向, 另一方面也推动 了热学理论的发展 .
各种热机的效率
大型柴油机效率
通过外界对系统作功的方法,提高系统的温 度,当系统的温度高于外界时,系统将当初所 吸的热量及由外界作功所转变的内能全部交还 给外界,系统恢复了原状。
外界呢?总能量没减少,但原来付出的机械能 变成了热能,外界没有恢复原状。所以
结论
热量从高温物体传到低温物 体的过程是不可逆的!
(3)气体的自由膨胀过程
dQ dE CV ( dT )V (dT )V
∵
1mol理想气体dE=
i 2
RdT
∴
Cv
=
i 2
R
(i为分子自由度)
所以,理想气体内能表达式又可写成
E CvT
2.定压摩尔热容量(Cp):
1mol气体在定压过程中吸收热量dQ与温度的变化dT之比
Cp
dQ ( dT )p
dE+PdV ( dT )p
大学热学物理知识点总结

大学热学物理知识点总结1.热力学基本定律热力学基本定律是热学物理的基础,它包括三个基本定律,分别是热力学第一定律、热力学第二定律和热力学第三定律。
(1)热力学第一定律热力学第一定律是能量守恒定律的热学表述,它规定了热力学系统能量的守恒性质。
简单地说,热力学第一定律表明了热力学系统能量的增减只与系统对外界做功和与外界热交换有关。
热力学第一定律的数学表达式为ΔU=Q-W,其中ΔU表示系统内能的增量,Q表示系统吸热的大小,W表示系统对外界所作的功。
由此可以看出,系统的内能变化量等于吸收热量减去做的功。
(2)热力学第二定律热力学第二定律是热力学系统不可逆性的表述,它规定了热力学系统内部的熵增原理,即系统的熵不会减小,而只会增加或保持不变。
简单地说,热力学第二定律表明了热力学系统内部的任何一种热力学过程都是不可逆的。
这意味着热力学系统永远无法使热量全部转化为功,总会有一部分热量被转化为无效热。
热力学第二定律还表明了热力学过程的方向性,即热量只能从高温物体传递到低温物体,而不能反向传递。
(3)热力学第三定律热力学第三定律规定了当温度趋于绝对零度时,任何物质的熵都将趋于一个有限值,这个有限值通常被定义为零。
简单地说,热力学第三定律表明了在绝对零度时,任何系统的熵都将趋于零。
热力学第三定律的提出对于热学物理的研究具有非常重要的意义,它为我们理解热学系统的性质提供了重要的基础。
2.热力学过程热力学过程是指热力学系统内部发生的一系列变化,包括各种状态参数的变化和热力学系统对外界的能量交换。
常见的热力学过程有等温过程、绝热过程、等容过程和等压过程等。
这些过程在日常生活以及工业生产中都有着广泛的应用。
(1)等温过程等温过程是指在恒定温度下进行的热力学过程。
在等温过程中,系统对外界做的功和吸收的热量之比是一个常数。
这意味着等温过程的压强和体积成反比,在P-V图上表现为一条双曲线。
常见的等温过程有等温膨胀和等温压缩等。
(2)绝热过程绝热过程是指在无热交换的情况下进行的热力学过程。
大学物理-热力学

存在温差而发生的能量传递 .
功与热量的异同 1)过程量:与过程有关;
T1 T2
T1 Q T2
2)等效性:改变系统热运动状态作用相同;
1卡 = 4.18 J , 1 J = 0.24 卡
3)功与热量的物理本质不同 .
功
宏观运动
分子热运动
热量
分子热运动
分子热运动
五、 内 能 (状态量)
物体内分子做无规运动的动能和势能的总和叫做 物体的内能。内能由系统的状态唯一地决定。内能的 改变量只由初末状态决定,和变化的具体过程无关。
p
A*
1
p
A*
1
2 *B
o
V
2 *B
o
V
理想气体内能 : 表征系统状态的单值函数 ,
理想气体 的内能仅是温度的函数 U U (T )
永 动 机 的 设 想 图
第一类永动机试图在不获 取能源的前提下使体系持续 地向外界输出能量。历史上 最著名的第一类永动机是法 国人亨内考在十三世纪提出 的“魔轮”,十五世纪,著 名学者达芬奇也曾经设计了 一个相同原理的类似装置, 1667年曾有人将达芬奇的设 计付诸实践,制造了一部直 径5米的庞大机械,但是这些 装置经过试验均以失败告终。
Cp,m CV ,m R
CV ,m
CV ,m
CV ,m
R 1
R
1
W 1 (T1 T2 ) 1 ( p1V1 p2V2 )
绝热过程方程的推导
dQ 0, dW dU pdV vCV ,mdT
pV vRT
pdV Vdp R pdV CV ,m
整理得
dp dV 0
pV
p
p2
2 T2
大学物理热力学基础

2.过程方程:
V T
=
const.
P
等压膨胀
1
2
3.过程曲线:
o V1
V2
V
2
4.能量转换关系: W = 1 P dV = P(V2 - V1)
Q PC P(T 2T 1) EC V(T 2T 1)
吸热一部分用于对外做功,其余用于增加系统内能。
14
实用文档
上页 下页 返回 退出
三.等温过程(isothermal process) P
1
1.特点: T = const.
等温膨胀
2.过程方程: P V = const.
2
3.过程曲线:
o V1
V2 V
4.能量转换关系: E = 0
Q= W
2
W = 1 P dV =
RT
2
1
dV V
W
RTl nV( 2 ) V1
P1V1
ln(V2 V1
)
P1V1
ln(P1 P2
)
系统吸热全部用来对外做功。
=
CP CV
=
i +2 i
>1
对单原子分子, i = 3, = 1.67 对双原子分子, i = 5, = 1.40 对多原子分子, i = 6, = 1.33 (以上均为刚性理想气体分子)
12
实用文档
上页 下页 返回 退出
§7.3 热力学第一定律对理想气体等值过程的应用
一.等容过程(isochoric process)
所以循环过程的效率为:
1Q2 17p2(V1V2)
Q1
5V`1(p1p2)
29
实用文档
上页 下页 返回 退出
大学物理热力学

02
数学表达式为:不可能通过有限个步骤将一个单一 热源的热量全部转化为机械功而不产生其他影响
04
此外,热力学第二定律还揭示了机械能与内能之间 的转化是不可逆的,即机械能可以完全转化为内能, 而内能不能完全转化为机械能而不产生其他影响
5
卡诺循环与卡 诺定理
卡诺循环与卡诺定理
01
02
卡诺循环是由法国物理学家 卡诺提出的一种理想化循环 过程,包括四个步骤:等温 膨胀、绝热膨胀、等温压缩 和绝热压缩
1
热力学的基本 概念
热力学的基本概念
热力学的基本概念包括系 统、状态、过程和循环等
系统是指研究对象的整体, 可以是气体、液体、固体
等
状态是指系统在某一时刻 的宏观物理量,如温度、
压力、体积等
过程是指系统状态的变化 历程,可以分为等温过程、
等压过程、绝热过程等
循环是指系统经过一系列 状态变化后又回到初始状
此外,热力学还在航天工 程、材料科学等领域得到
应用
11
热力学与其他 学科的联系
热力学与其他学科的联系
热力学与其他学科有着密切的 联系
例如,热力学与统计力学的关 系密切,统计力学从微观角度 研究物质的热力学性质,提供
了对热现象的微观描述
此外,热力学与电动力学也有 一定的联系,如电磁场的能量 和动量等物理量可以与热力学 中的熵和温度等概念相对应
12
未来展望
未来展望
随着科学技术的发展,热力学的研究和应用将 不断深入和扩展
例如,随着能源问题的日益严重,热力学在能 源利用和环境保护方面的应用将更加广泛;随 着纳米技术的发展,热力学在纳米材料和纳米 器件方面的应用将更加深入;随着气候变化和 环境问题的日益严重,热力学在地球科学和环 境科学方面的应用将更加重要
大学物理 热力学基础详解

§ 3 气体的摩尔热容量
热容量:
(简称热容) 表示升高1K所吸收的热量
dQ C dT
(JK-1)
摩尔热容Cm :当物质的量为1 mol 时的热容。 单位: (Jmol -1 K-1) 比热C比:当物质的量为 1 kg 时的热容。
C MC比
M C Cm M mol
单位: (J kg-1 K-1 )
(1)
理想气体状态方程 对其微分得:
M RdT PdV VdP M mol
M PV RT M mol
(2)
联立(1)、(2),得:
M PV const 将 与 PV RT 联立得: M mol
dP dV 0 P V
-1
PV const. ( 3)
(4)
V
T=const .
√ (C) -700J
(D) 1000J
1
e
c b
思路: Ta =Tb
Vb Va Vb Va
0 1 4 Eab 0
Va
V(10-3m3)
Qab Aab PdV
Vd
Eacbda 0
Qacbda Aacbda PdV PdV 500 - 1200( J )
-
P
-1
T =const . ( 5 )
(3)、(4)、(5)式称为绝热方程 (或泊松公式)。
注意:式中的各常数不相同!!!
绝热线比等温线陡 (1)、等温:PV=const
0 (2)、绝热: PV const
PA dp A点的斜率: dV VA a
PA dp A点的斜率: VA dV T
i2 Q A 2
大学物理 第21章 热力学第一定律
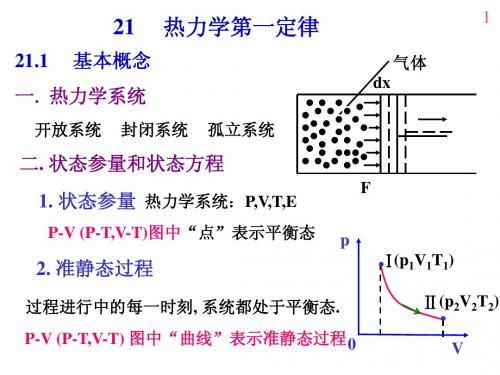
.Ⅰ(p V T )
1 1 1
Ⅱ(p2V2T2)
.
V
21.3 热力学第一定律
一. 功
系统对外做功(体积功) dx 气体 F
2
A Fdx PSdx PdV
A dA PdV
V1 V2
讨论:
1)A > 0 系统对外界做正功; A < 0 系统对外界做负功。 2)P-V 图上曲线下面积表示体积功大小。 3) 功是过程量。
CV (
定体摩尔热容量 CV , m
1 Q 摩尔热容量 C m dT
Q>0 Q<0
从外界吸收热量 系统向外界放热
dT dT 1 Q 1 dE ( )V ( ) dT dT
)V (
)V
三、内能
系统内所有粒子各种能量的总和。 热力学领域:系统内所有分子热运动动能和分子间 相互作用势能之和。 通常
绝热线比等温线陡
p1 p2 p2
0
等温线
( 1)
V
p nkT
{
等温: T不变,n
绝热: T ,n
p p
V1
V2
9
11
用比较曲线斜率的方法证明在p---V图上相交于任一点的理想 气体的绝热线比等温线陡。
证明:过p---V图上任一点(p,V)点,等温线的斜率为:
dp d C C pV p ( )T [ ( )]T 2 2 dV dV V V V V
4
E E (T ,V )
——内能是状态量。
理想气体内能:仅为分子热运动的各种动能之和。
——理想气体的内能是温度的单值函数。
M i E RT M mol 2
大学物理概论第4章-热力学student

dV
VA
等温方程: pV C2
Vdp pdV 0
A
等温
V
dp pA dV VA
结论:绝热线在A点的斜率大于等温线在A点的斜率。
例4 有8×10-3 kg氧气,体积为0.41×10-3 m3 ,温度
注意:功和热量都是过程 量,而内能是物态量,通 过做功或传递热量的过程 使系统的物态(内能)发 生变化。
热功当量:
1 cal = 4.186 J
焦耳用于测定热功当 量的实验装置。
4-2-2 热力学第一定律的数学描述
热力学第一定律: 包括热现象在内的能量守恒 定律。
Q (E2 E1) W
p4 p3 1atm
V4
V3 2
3.69 103 m3
T4
V4 V3
T3
450K
p/atm
3
2
1 V
V1 V4 V3
等体过程:
W1 0
Q1
E1
m M
5 2 R(T2
T1) 1248 J
等温过程: E2 0
Q2 W2
m M
RT2
ln
V3 V2
823 J
Q 表示系统吸收的热量,W 表示系统所做的功, E 表示系统内能的增量。
热力学第一定律微分式: dQ dE dW
符号规定:
1. 系统吸收热量Q为正,系统放热Q为负。 2. 系统对外做功W为正,外界对系统做功W为负。 3. 系统内能增加E为正,系统内能减少E为负。
第一类永动机: 不需要外界提供能量,但可以 连续不断地对外做功的机器。
不变,热量变为什么?氢的T,V各为多少?
大学物理下册第十一章 热力学基础

1. 定义:系统经历一系列变化后又回到初始状态的整 个过程。
准静态循环过程 ~ p-V图中的闭合曲线
p 正
O 2. 共同特征
E0
顺时针:正循环 逆
逆时针:逆循环 V
热力学第一定律: Q净 W净
3. 正循环及其效率
p
b
T1
a 净正正功 c
负功d功
W
O V1
V2
V
特征:
T2
Q净Q吸Q放
W净W对外 W外对系
第十一章 热力学基础
§11—1 内能 功 热量 一.热力学系统(系统)
需研究的对象——气、液、固,也称为工作物质。 以理想气体为系统,与之相互作用的环境称为外界。
二、内能
1.内能:大量分子的平均动能与分子间相互作用 的势能的总和.
实际气体:E=E (T,V )
对于理想气体,由于分子间无相互作用力,所以,理想气体
a. EM mCVT0
V2
m V 2
dV
b .
W p pdV
V1
M V 1
RT
V
m RT ln V 2 m RT ln p1
M
V1 M
p2
T Q
恒温热源 T
p
p1
(p1,V1,T)
P1V 1
ln
V2 V1
P2V 2
ln
V2 V1
P1V 1 ln
P1 P2
P2V 2 ln
P1 P2
(p2,V2,T)
PdVP1V1P2V2
1
系统要对外做功,必须以牺牲自身的内 能为代价.
p
4.P-V 图: 一条曲线.
绝热线比等温线陡.
绝热线 A
第11章 大学物理热力学基础

例: 一卡诺循环热机,高温热源的温度是400K,每一循 环从此热源吸进100J热量并向一低温热源放出80J热量。 求(1)这循环的热机的效率;(2)低温热源的温度。 解:(1)这循环的热机的效率为:
Q放 % Q吸
(2)设低温热源的温度T2,有
Q放 T % Q吸
(2)每一循环中外界必须作的功 Q吸 T2 w T1 T2 A
A 200J
22
§11.7 热力学第二定律的统计意义
一、热力学第二定律的微观解释
1、宏观状态与微观状态 宏观看:
左、右两部分各有多少粒子 而不去区分究竟是哪个粒子 微观上看: 具体哪个粒子在哪? 编号为 a b c d
左
宏观态
20世纪六七十年代以后,自从“大爆炸”宇宙模型 逐渐得到天体物理学界公认以来,“热寂”说这朵 漂浮在物理学上空的“乌云”逐渐云开雾散,人类 曾一度阴霾笼罩的心头终于迎来了一片朗朗晴空。
33
“大爆炸”宇宙模型
该理论认为,宇宙大约是在100—200亿年以前,从 高温高密的物质与能量的“大爆炸”而形成。随着 宇宙的不断膨胀,其中的温度不断降低,物质密度 也不断减小,逐渐衍生成众多的星系、星体、行星 等,直至出现生命。宇宙大爆炸理论是20世纪科学 研究的重大成就,是基于几十年的创新实验与理论 研究的结果。因而获得了科学界的公认,并成为现 代宇宙学的标准模型。
几率大的宏观态最易出现。 (平衡态)
1 4 6 4 1
1 4 6 4 1
在一孤立系统内,一切实际过程都是从概率小(微 观态小)的状态向概率大的宏观态(微观态多)进 行的 ——为热力学第二定律的统计意义
25
4. 热二律的微观解释 自发过程的方向性 如 自由膨胀
大学物理热力学知识点汇总

大学物理热力学知识点汇总热力学是大学物理中的一个重要部分,它研究的是热现象的规律以及与热相关的能量转化和传递。
以下将对大学物理热力学中的关键知识点进行汇总。
一、热力学系统和热力学平衡态热力学系统是指研究的对象,它可以是一个气体、液体或固体,也可以是由多个物体组成的系统。
而热力学平衡态则是指系统的宏观性质在长时间内不随时间变化的状态。
这包括热平衡(系统各部分温度相等)、力学平衡(系统各部分压力相等)、化学平衡(系统内各化学组分的浓度不再变化)。
二、热力学第零定律如果两个热力学系统中的每一个都与第三个热力学系统处于热平衡,那么这两个热力学系统也必定处于热平衡。
这个定律为我们定义了温度的概念,使我们能够通过比较不同系统之间的热平衡来测量温度。
三、热力学第一定律也被称为能量守恒定律,它表明一个热力学系统内能的增量等于外界向它传递的热量与外界对它所做的功之和。
用公式表示为:ΔU = Q + W。
其中,ΔU 是系统内能的变化,Q 是系统吸收的热量,W 是系统对外界所做的功。
在这个定律中,需要注意功的正负。
当系统对外做功时,W 为负;外界对系统做功时,W 为正。
同样,当系统吸收热量时,Q 为正;系统放出热量时,Q 为负。
四、等容过程等容过程是指系统的体积保持不变。
在等容过程中,系统不做功(W = 0),内能的变化等于吸收或放出的热量,即ΔU = Q。
五、等压过程等压过程中系统的压力保持不变。
此时,系统所做的功为 W =pΔV,内能的变化和吸收的热量的关系为ΔU =Q pΔV 。
六、等温过程等温过程中系统的温度保持不变。
在理想气体的等温过程中,内能不变(ΔU =0),系统吸收的热量等于对外界所做的功,即Q =W 。
七、绝热过程绝热过程是指系统与外界没有热量交换(Q =0)。
在绝热过程中,系统做功导致内能变化,即 W =ΔU 。
八、热力学第二定律它有多种表述方式,常见的有克劳修斯表述(热量不能自发地从低温物体传到高温物体)和开尔文表述(不可能从单一热源吸取热量,使之完全变为有用功而不产生其他影响)。
大学物理热力学的基本概念与热平衡定律解释

大学物理热力学的基本概念与热平衡定律解释热力学是研究物质的热现象与能量转化规律的学科,在自然科学中具有重要的地位。
热力学的研究对象包括热力学系统、热力学性质以及热力学定律等内容。
本文将介绍热力学的基本概念,并重点解释其中的热平衡定律。
一、热力学的基本概念1. 热力学系统:热力学系统是指研究对象,它可以是一个物体、一组物体或者一个空间范围内的物质。
热力学系统可以分为封闭系统、开放系统和孤立系统等不同类型。
2. 热力学性质:热力学性质是指描述热力学系统状态的物理量,如温度、压强、体积、内能等。
这些性质的变化可以通过热力学过程来描述,例如等温过程、绝热过程等。
3. 热力学定律:热力学定律是指总结和归纳得出的描述热力学现象和规律的定律,如热力学第一定律、热力学第二定律等。
二、热平衡定律的解释热平衡定律是热力学第零定律,它是热力学研究的基础。
热平衡定律的核心概念是热平衡,即两个物体之间不存在热量的净交换。
如果两个物体之间达到了热平衡,它们的温度是相等的。
反之,如果两个物体温度不相等,它们之间会发生热量的传递,直到达到热平衡为止。
热平衡定律可以用以下实例来解释。
假设有两个热力学系统A和B,它们之间没有物质交换,只能通过热交换来达到热平衡。
当A和B接触时,它们会发生热量的交换,直到两个系统的温度相等,称为热平衡状态。
在热平衡状态下,系统A和B的内能之和保持不变,即热平衡状态是一种稳定的状态。
根据热平衡定律,我们可以得出一个重要的推论:如果一个物体与另外两个物体都达到了热平衡,那么这两个物体之间也一定达到了热平衡。
这种传递性质使得热平衡成为一个具有普适性的概念,在热力学的研究中具有重要的应用。
总结起来,热力学的基本概念包括热力学系统、热力学性质和热力学定律。
热平衡定律是热力学研究的基石,它描述了热力学系统中热量传递的规律。
根据热平衡定律,我们可以判断系统是否处于热平衡状态,并通过热平衡状态来描述系统的特性。
热平衡定律的解释为我们理解和应用热力学提供了基础。
《大学物理》第九章 热力学基础 (2)

吸收热量
m M mol
CV T
m M mol
C p T
m RT ln V2
M mol
V1
或 m RT ln p1
M mol
p2
对外作功
0
pV
或 m RT M mol
m RT ln V2
M mol
V1
或 m RT ln p1
M mol
p2
内能增量
m M mol
CV T
m M mol
CV T
0
pV 常量
返回 退出
例9-2 设有氧气 8 g,体积为0.4110-3 m3 ,温度为 300 K。如氧气做绝热膨胀,膨胀后的体积为4.110-3 m3 。问:气体做功多少?氧气做等温膨胀,膨胀后 的体积也是4.110-3 m3 ,问这时气体做功多少?
解: m=0.008 kg M =0.032 kg T1=300 K
941 (J)
等温膨胀做功:
A
m M
RT1 ln
V2 V1
1 8.31 300 ln 10 4
1.44 103 (J)
返回 退出
作业 Page70 9-1 9-6
返回 退出
理想气体热力学过程的主要公式
过程 特征 过程方程
等体 V=常量 p 常量 T
等压 p=常量 V 常量 T
等温 T=常量 pV 常量
C
(3)比较各过程吸热多少?
D
解:(1) A A B A A C A A D
(2)等压过程 E A B 0
O V1
V2 V
等温过程 E A C 0 绝热过程 E A D A A D 0
(3) Q A B Q A C Q A D
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(C)
(D)
3、一容器内装有 N1 个单原子理想气体分子和 N 2 个刚性双原子理想气体分子,当该系统处 在温度为 T 的平衡态时,其内能为 (A) ( N1 + N 2 ) ç ç kt + (C) N1 [ (B) C ]
骣 3 ç 桫 2
5 ÷ kT ÷; 2 ÷
骣 1 3 5 ( N1 + N 2 ) ç kT + kT ÷ ÷ ç ç 桫 2 2 2 ÷
,两种气体分子 的速率 分布
填相同 或不相 同)(不相同 ,不 相同, 不相同 )
3、A、B、C 三个容器中皆装有理想气体,它们的分子数密度之比为 n A : n B : n C 4 : 2 : 1 ,
而分子的平均平 动动能之比为
A : B: C 1 : 2 : , 4则它们的压强之比
-21
1.04×10 )
-20
5、 (1)图(a)为同一温度下,不同的两种气体的速率分布曲线, ______曲线对应于摩尔质量较
2
大的气体.(2)图 (b)为不同温度下,同种气体 分子的速率分布曲线 . ______ 曲线对应于较 高的温度.(1, 2)
(三)难(综合题)
1、储存在体积为 4 cm 的中空钢筒里的氢气 的压强是 6 个大气压,在 1 个大气压时这些氢气能充
(A)等压过程; (C)等体过程;
3、两种不同的理想气体,若它们的最概然速率相等,则它们的 (A)平均速率相等,方均根速率相等; (C)平均速率不相等,方均根速率相等;
( B)平均速率相等,方均根速率不相等; (D)平均速率不相等,方均根速率不相等。
4、若在某个过程中,一定量的理想气体的内能 E 随压强 P 的变化 关系为一直线,如图( 4)所示(其延长线过 E-P 图的原点),则该 过程为 (A)等温过程; (C)绝热过程; [ D ]
PA:PB :PC
。 (1:1:1)
4、1mol 氧气(视为刚性双原子分子的理想气体)贮于一氧气瓶中,温度为 27℃,这瓶氧气 的内能为 分子的平均总动能为 兹曼常量 k=1.38×10 J·K )(6.23×10 ,
-23 -1 3
J;分子的平均平动动能为
-1 -1
J;
J。 (摩尔气体常量 R=8.31J·mol ·K ,坡尔 6.21×10 ,
v2
11、
v1
f (v)dv 表示的物理意义是
N ) N
------------------------------------- 。 (分布在任一有限速率范围 v1 v2 内的分子数 占总分子数的比率
12、在相同条件下,氧原子的平均动能是氧分子的平均动能的______倍.(
1 ) 2
(二)中(一般综合题) 1、如图 1 所示,两条曲线分别表示相同温度下,氢气和氧气分子的速率分布曲线,则 a 表 示▁▁▁▁气分子的速率分布曲线;b 表示▁▁▁气分子的速率 分布曲线。 (氧气,氢气) 2、若一瓶 氢气和 一瓶 氧气的 温度 、压 强、质量 均相同 ,则 它 们单位 体积 内的分 子数 均动能 ,单位体积内 气体 分子的 平 。(均 图1
(A) 1/6;
(B)12 倍;
(C ) 6 倍;
(D)15 倍。
2、若气体的温度降低,则 p 和 f ( p ) 为
[ A
]
(A)
p 变小而 f ( p ) 变大; p 和 f ( p ) 都变小;
(B)
p 变小而 f ( p ) 保持不变; p 保持不变而 f ( p ) 变小.
5、最概然速 率 V P 的物理 意义是 :在 一定温 度下 , V P 附近单 位速率 区间 内 的分子 数所 占的百 分比最 大; [ √ ]
6
6 、速 率 分 布 曲 线 上 有 一 个 最 大 值 , 与 这 个 最 大 值 相 应 的 速 率 V P 叫 做 平 均 速 率 ; [ × ] [ [ [ √ √ × ] ] ] √ ]
i i 2 KT , RT , KT ) 2 2 2 3 RT 代 表 的 物 理 意 义 3 、 对 于 单 原 子 分 子 理 想 气 体 , ① 2
为: ;②
3 R 代表的物理意义 2
为::
。( ①
3 RT 代表 1mol 单原子理 2
想气体 的内能 ,②
3 R 代表它的等体摩 尔热 容 ) 2
4、 自由度数为 i 的一定量的刚性分子理想气体,其体积为 V,压强为 p 时,其内能 E=_______. (
i PV ) 2
5 .两瓶不同种类的理想气体,它们温度相同,压强也相同,但体积不同,则它们分子的平 均平动动能-----,单位体积内分子的总平动动能-------。 (均填相同或 不相 同) (相 同, 相同) 6 .一定 量的某 种理 想气体 ,装在一 个密闭 的不 变形的 容器中 ,当气体 的温 度升高 时, 气体 分子 的平 均动 能 气体的 内能 ,气体分 子的 密度 ,气体的压 强 ,
3
1
______ kg mol ,由此确定它是______气.(32×10 kg.mol ,
-3 -1
1
氧)
10、 Nf (u )d u 表示的物理意义是 ------------------------------------ 。 (表示在 v 附近, v v dv 速率区间内的分子 数)
pV
MRT
(B) MKT
pV
(C)
KT
p
RT
p
12、一瓶氦气和一瓶氮气质量密度相同,分子平均平动动能相同,而且它们都处于平衡态, 则它们 [ C ]
(A)温度相同、压强相同; (B)温度、压强都不同;
4
(C)温度相同,但氦气的压强大于氮气的压强; (D)温度相同,但氦气的压强小于氮气的压强。
3kT 5 + N 2 kT ; 2 2
(D) N1
5 3 kT + N 2 kT 。 2 2
三、判断题 (一)易(基础题) 1、刚性多 原 子 分 子 共 有 6 个 自 由 度 ; 2、理想气体的温度越高,分子的数密度越大,其压强就越大; 3、理想气体的温度升高,分子的平均平动动能减小; 4、温度是表示大量分子平均平动动能大小的标志; [ [ [ [ √ √ × √ ] ] ] ]
(二)中(一般综合题) 1、两瓶不同类的理想气体,其分子平均平动动能相等,但分子数密度不相等,则 [ B ]
(A) 压强相等,温度相等;
(B) 温度相等,压强不相等;
(C) 压强相等,温度不相等;
(D) 方均根速率相等.
2、 一定质量的理想气体的内 E 随体积 V 的变化关系为一直线, 如图 ( 2 )所示 (其延长线过 E--V 图的原点) ,则此直线表示的过程为 [ A ] ( B)等温过程; (D) 绝热过程。 [ A 图(2) ]
3
(A) 分 子 平 均 速 率 相 同 ; (C) 内 能 相 等 ;
(B) 分 子 平 均 动 能 相 等 ; (D) 平 均 平 动 动 能 相 等 。 [ A ]
4.温度为 270C 的单原子理想气体的内能是 (A)全部分子的平动动能; (B)全部分子的平动动能与转动动能之和; (C)全部分子的平动动能与转动动能、振动动能之和; (D)全部分子的平动动能与分子相互作用势能之和。
A
]
(D)不能确定哪一种气体内能的增量大。
(A) 物体的温度越高,则热量愈多; (C) 物体的温度越高,则内能越小; 8、 一定质量的某理想气体按 (1)升高;
p =恒量的规律变化, 则理想气体的分子数密度 T
(3)不能确定; (4)降低。 [ B ]
(2)
]
(2)不变;
10、如果氢气和氦气的温度相同,摩尔数也相同,则
(B)等压过程; (D)等体过程。 图(4)
5、若氧分子[ O 2 ]气体离解为氧原子[O]气体后,其热力学温度提高一 倍,则氧原子的平均速率是氧分子的平均速率的 (A)4 倍; (B) 2 倍;
0 0
[
C
]
(C)2 倍;
(D)1 / 2 倍。
6、若室内生起炉子后温度从 15 C 升高到 27 C ,而室内气压不变,则此时室内的分子数减 少了 (A)0.5% ; (B)4% ; (C)9% ; [ (D)21% 。 B ]
图2
[
D
]
(C) 氧分子的质量比氢分子大,所以氢分子的速率一定比氧分子的速率大. (D) 氧分子的质量比氢分子大,所以氢分子的方均根速率一定比氧分子的方均根速率大. 2、速率分布函数 f ( )d 的物理意义为: (A)具有速率 的分子占总分子数的百分比; (B)具有速率 的分子数; (C)在速率 附近处于速率区间 d 内的分子数占总分子数的百分比; (D)速率分布在 附近的单位速率间隔中的分子数。 3 、 摩 尔 数 相 同 的 氦 (He) 和 氢 (H 2 ) , 其 压 强 和 分 子 数 密 度 相 同 , 则 它 们 的 [ D ] [ C ]
。 ( 均填增大、不 变或 减少 ) (增 大, 不变, 增大 , 增大) ,理想气体分子的平均平动动能与温度的关系
7、理想气体的压强公式为 为 。 (p
2 3 n k , k KT ) 3 2
8、有两瓶气体,一瓶是氧气,另一瓶是氢气(均视为刚性分子理想气体) ,若它们的压强、 体积、温度均相同,则氧气的内能是氢气的▁▁▁▁倍。 (1) 9、 一容器内贮有气体,其压强为 1atm,温度为 27ºC,密度为 1.3kg m ,则气体的摩尔质量为
05 章 一、填空题 (一)易(基础题) 1 、一定 质量的 气体 处于 平衡 态,则 气体 各部 分的 压强 各部分 的温度 ( 填相等或不相等 ) 。 ( 相 等 , 相等 ) ( 填相等或 不相等 ) ,
