陕西科技大学 过程装备与控制工程 课件 1机械设计(王宁侠)第3章
陕西科技大学过程装备与控制工程过程装备双语Chap.3-Piping and Vessels

Paddle and Figure Eight Blinds
Function:be used to shut off fluid in piping.
1. 2.
Type:
paddle blind
figure eight blind
flanges
Welded piping
Advantage:
1.
provide much more strength;
2.
3.
be notical services.
Note
In critical services——welded joints provide much more strength and less chance for leaks than do threaded joints; If piping is not critical——piping with threaded joints is generally much cheaper and easier to install than welded.
6. Cast iron piping
becomes brittle when it is exposed to fire and then sprayed with water ;
Would break under those condition. Not used in hazardous areas, nor is used to handle flammable materials.
Classification of pressure vessels
过程装备与控制工程第1章ppt课件

30
过程装备控制技术与应用 有自衡特性的单容对象
设水槽的横截面积为A,而A是个常数,则因为
V(A2-H 2)
所以
dV AdH dt (2-3)dt
调节阀的特性:在其它条件不变的情况下,通过调节阀 的流体流量与阀的开度以及阀前后的流体压降有关。
31
过程装备控制技术与应用
36
过程装备控制技术与应用
37
过程装备控制技术与应用
(2)双容液位对象(图2-5)
它有两个串联在一起的水槽,它们之间的连通管具有阻力, 因此两者的液位是不同的,来水qv1(系统输入)先进入水槽 1,然后再通过水槽2流出。水流入量qv1由阀1控制,流出量 qv2决定于阀2的开度(根据用户的需要改变),被控变量是 水槽2的液位h2 (系统输出) 。分析h2在阀1开度扰动下的动 态特性。根据物料平衡方程有:
回顾:《机械控制工程基础》§3.5 控制系统的动 态响应指标
20
过程装备控制技术与应用
偏差积分性能指标
误差: e(t)r(t)y(t) e(t)y( )y(t)
平方误差积分性能指标(ISE) 时间平方误差积分性能指标(ITSE) 绝对误差积分性能指标(IAE) 时间绝对误差积分性能指标(ITAE)
5
过程装备控制技术与应用
§1.1.2 过程装备控制的任务和要求
过程装备控制是针对过程装备的主要参数,即温度、 压力、流量、液位、成分和物性参数进行控制。 过程装备控制要求:安全性、经济性和 稳定性。 自动控制系统的要求:稳、准、快。
控制的任务:在了解、掌握工艺流程和生产过程的 静态和动态特性的基础上,根据上述三项要求,应 用理论对控制系统进行分析和综合,最后采用合适 的技术手段加以实现
陕西科技大学 过程装备与控制工程 课件 1机械设计(王宁侠)第1章

第1章 绪论 3. 可靠性设计 可靠性设计是以概率论和数理统计为理论基础,以失效分 析、失效预测及各种可靠性试验为依据,以保证产品的可靠性 为目标的一种现代设计方法。其主要特点是将传统设计中视为 单值而实际上具有多值性的设计变量(如载荷、材料性能和应
章)。
第1章 绪论 (2) 通用机械零部件设计(第5~18章)。 ① 传动零件:带传动、链传动、齿轮传动、蜗杆传动及 螺旋传动。 ② 轴系零部件:滑动轴承、滚动轴承、轴及联轴器、离 合器、制动器。
③ 联接零件:螺纹联接、铆接、焊接、粘接及轴毂联接。
④ 其他零部件:弹簧、机座与箱体。 (3) 总体构思与设计(结合课程设计进行)。
即可寻优求解。常用的优化算法有0.618法、Powell法、变尺度
法、惩罚函数法、基因算法等。采用优化设计方法可以在多变 量、多目标的条件下,获得高效率、高精度的设计结果,极大
地提高设计质量。
第1章 绪论
2. 计算机辅助设计 计算机辅助设计(CAD)是利用计算机运算快、计算准确、存储 量大、逻辑判断功能强等特点进行设计信息处理,并通过人机交互 作用完成设计工作的一种设计方法。它包括分析计算、自动绘图系 统和数据库三个方面。一个完整的机械产品CAD系统,应首先能够 确定机械结构的最佳参数和几何尺寸,这就要求具有进行机构运动 分析及综合、有限元分析和优化设计、可靠性设计等功能,然后能 够由分析计算结果自动显示和绘制机械的装配图和零件图,并可进 行动态修改。完善的数据库系统,可与计算机辅助制造、计算机辅 助监测、计算机管理自动化结合形成计算机集成制造系统 (CIMS), 综合进行市场预测、产品设计、生产计划、制造和销售等一系列工 作,实现人力、物力和时间等各种资源的有效利用,有效地促进现 代企业生产组织、管理和实现自动化,使企业总效益得到提高。
过程装备与控制工程专业PPT课件

• 080301机械制造工艺与设备;080302热加工工艺 及设备;080303铸造;080304塑性成形工艺及设备; 080305焊接工艺及设备;080306机械设计及制造; 080307化工设备与机械;080308船舶工程;080309汽 车与拖拉机;080310机车车辆工程;080311热力发动 机;080312流体传动及控制;080313流体机械及流体 工程;080314真空技术及设备;080315机械电子工程; 080316工业设计(注:可授工学或文学学士学位); 080317设备工程与管理
• 这样就在最大规模的专业调整中,保留了化机 专业的地位。把它拓宽为“过程装备与控制工 程”,为化工机械专业开辟了更加美好的前程。
• 化机专业为新中国的化工、石油化工和相关流 程工业的发展壮大建立了不可磨灭的功绩,今后 国家更需要大量过程装备方面的高级人才。
• 1993.7,国家教委高教司《普通高等学校本科专 业目录》。目录分设哲学、经济学、法学、教育学、 文学、历史学、理学、工学、农学、医学十大门类, 下设二级类71个,504种专业,比修订前的专业数减 少309种。工学门类下设二级类22个,181种专业;
• 本专业培养的质量总体来说比较好,能够满足过 程工业对人才的要求,成为企业的技术骨干。本专 业培养的学生,对于设计方面的能力较强,对于维 修、故障诊断方面的能力较弱;对于设备方面的能 力较强,对于控制方面的能力较弱;
“过程装备与控制工程”专业
人才培养规格
• 技术型人才:对以教学为主的院校,熟悉过程装 备及其控制的原理、操作、维修、管理,成为企业 设备动力部门的管理人才。
• 结构上本专业的学生要加强基础,加强“过 程原理与装备”、和“过程装备控制技术”课 程教育,突出“过程”,加强“控制”,丰富 “装备技术”。
陕西科技大学机电工程学院过程装备与控制工程过程装备制造与检测期末考试复习资料总结第二部分制造

第一节过程设备常用材料本节简述压力容器对材料性能的要求和常用材料的性能。
一.对材料性能的基本要求选择压力容器用材料应着重考虑:力学性能、工艺性能和耐腐蚀性能。
1. 材料的力学性能需要保证:强度指标、塑性指标和韧性指标。
⑴较高的强度强度指标是设计中决定许用应力[ζ]的重要依据。
常用的强度指标有抗拉强度ζb和屈服强度ζs。
高温下工作时,还要考虑蠕变极限和高温持久强度。
材料强度指标选取原则保证塑性指标及其他性能的要求下,尽量用强度指标高的材料,以减小容器的重量。
材料强度指标高,容器的厚度小、重量轻;但塑性、韧性一般都较差,焊接时易产生裂纹等缺陷。
⑵良好的塑性塑性指标主要包括伸长率δ、断面收缩率ψ和冷弯试验弯曲角α。
塑性指标选取原则:容器用钢材,要求具有较好的塑性。
因为塑性好的材料在破坏前一般都产生明显的塑性变形,不但容易发现,而且塑性变形可以松弛局部高应力,避免部件断裂。
标准对容器用钢材塑性的最基本要求:GB6654-86中规定,各钢种的延伸率δ5为(16~26)%;国际标准化组织(ISO)推荐规范中规定伸长率的下限值:碳钢及锰钢不小于16%;对合金钢不小于14%。
⑶较好的韧性虽然压力容器一般不受冲击载荷,但冲击值低、韧性差的材料,对缺口脆性比较敏感,特别是裂纹等缺陷。
所以用于制造压力容器承压部件的材料,要求具有较好的韧性。
2. 工艺性能材料的制造工艺性能差,不但难以加工制造,而且还容易在制造过程中产生各种缺陷。
工艺性能主要包括:冲压性能,焊接性能,热处理性能(1)良好的冲压加工性能:要求材料有良好的冲压加工性能。
否则冲压加工时,难变形,容易产生裂纹等缺陷。
塑性指标达到标准规定值的材料,都可以满足冲压工艺性能的要求;⑵较好的焊接性压力容器大多是焊接结构,制造材料的焊接性能至关重要。
焊接性差的材料,会在焊接接头内产生各种焊接缺陷,包括裂纹、未焊透等严重缺陷。
裂纹是最危险而一直被认为是不允许存在的缺陷。
所以在选用一种新材料焊制压力容器时,一般都要经过焊接性试验。
陕西科技大学机电工程学院过程装备与控制工程控制技术

第一章控制系统的基本概念1, 生产过程自动化系统包含如下四个部分的内容:自动检测系统(2)信号连锁系统(3)自动操纵系统(4)自动控制系统2,过程装备控制的任务和要求过程装备控制是工艺生产过程自动化的重要组成部分,它主要是针对过程装备的主要参数,即温度、压力、流量、液位(或物位)、成分和物性等参数进行控制。
工艺生产过程装备控制的要求是多方面的,最终可以归纳为三项要求:即安全性、经济性和稳定性。
3,控制系统的组成被控对象,测量元件和变送器,调节器:又称控制器,执行器4,控制系统的方框图 : 被控变量y ,给定值(或设定值)Ys ,测量值Ym,操纵变量(或控制变量)m ,干扰(或外界干扰)f ,偏差信号e ,控制信号u5,控制系统系统的分类按给定值的特点划分:定值控制系统,随动控制系统,程序控制系统按系统输出信号对操纵变量影响划分:闭环控制,开环控制按系统的复杂程度划分:简单控制系统,复杂控制系统按系统克服干扰的方法划分:反馈控制系统,前馈控制系统,前馈-反馈控制系统6,控制系统的过渡过程从被控对象受到干扰作用使被控变量偏离给定值时起,调节器开始发挥作用,使被控变量回复到给定值附近范围内。
然而这一回复并不是瞬间完成的,而是要经历一个过程,这个过程就是控制系统的过渡过程。
7,控制系统的过渡过程有发散振荡过程,等幅振荡过程,衰减振荡过程,非振荡的单调过程综上所述,一个自动控制系统的过渡过程,首先应是一个渐趋稳定的过程,这是满足输生产要求的基本保证;其次,在大多数场合下,应是一个衰减振荡的过程。
8,控制系统的性能指标一类是以系统受到单位阶跃输入作用后的响应曲线(又称为过渡过程曲线)的形式给出的,如最大偏差(或超调量)、衰减比、余差、回复时间等,称为过渡过程的质量指标;另一类是偏差积分性能指标,一般是希望输出与系统实际输出之间误差的某个函数的积分,常用的有平方误差积分指标(ISE)、时间乘平方误差的积分指标(ITSE)、绝对误差积分指标(IAE)以及时间乘绝对误差的积分指标(ITAE)等,这些值达到最小值的系统是某种意义下的最优系统。
陕西科技大学机电过控复习专刊第十二期第三部分

陕西科技大学期末考试复习题——第十二期第三篇(过程设备设计及制造检测公式集锦)陕西科技大学编机电过控系审第三篇 过程设备设计1,承受横向均布载荷的圆形薄板,其力学特征是什么?其承载能力低于薄壁壳体的承载能力的原因是什么? 答:受轴对称均布载荷薄圆板的应力有以下特点①板内为二向应力r σ、θσ。
平行于中面各层相互之间的正应力z σ及剪力r Q 引起的切应力τ均可予以忽略。
②正应力r σ、θσ沿板厚度呈直线分布,在板的上下表面有最大值,是纯弯曲应力。
③应力沿半径的分布与周边支承方式有关,工程实际中的圆板周边支承是介于两者之间的形式。
④薄板结构的最大弯曲应力max σ与()2t R 成正比,而薄壳的最大拉(压)应力max σ与t R 成正比,故在相同t R条件下,薄板的承载能力低于薄壳的承载能力。
2,试比较承受横向均布载荷作用的圆形薄板,在周边简支和固支情况下的最大弯曲应力和挠度的大小和位置。
答:1.挠度 周边固支和周边简支圆平板的最大挠度都在板中心。
周边固支时,最大挠度为 D pR wf '=644max周边简支时,最大挠度为D pR ws'++=64154maxμμ二者之比为μμ++=15max max fs w w 对于钢材,将3.0=μ代入上式得 08.43.013.05max max =++=fs w w这表明,周边简支板的最大挠度远大于周边固支板的挠度。
2.应力 周边固支圆平板中的最大正应力为支承处的径向应力,其值为()22max43t pR f r =σ 周边简支圆平板中的最大正应力为板中心处的径向应力,其值为()()22max833t pR s r μσ+=二者的比值为()()23maxmaxμσσ+=fr sr对于钢材,将3.0≈μ代入上式得()()65.123.3max max==fr sr σσ这表明周边简支板的最大正应力大于周边固支板的应力。
3,根据定义,用图标出计算厚度、设计厚度、名义厚度和最小厚度之间的关系;在上述厚度中,满足强度(刚度、稳定性)及使用寿命要求的最小厚度是哪一个?为什么?4,为什么GB150中规定内压圆筒厚度计算公式仅适用于设计压力[]φσtp 4.0≤?由圆筒的薄膜应力按最大拉应力准则导出的内压圆筒厚度计算公式为:[]ppR ti-=σδ22(1)按形状改变比能屈服失效判据计算出的内压厚壁筒体初始屈服压力与实测值较为吻合,因而与形状改变比能准则相对应的应力强度4eq σ能较好地反映厚壁筒体的实际应力水平。
陕西科技大学过程装备与控制工程过程装备与检测课程设计3.doc
高压氮气储罐的焊接工艺一,设计背景储罐作为储存设备,主要是指用于储存或盛装气体、液体、液化气体等介质的设备,在化工、石油、能源、轻工、环保、制药及食品等行业得到广泛应用,如本设计中的高压氮气储罐,储罐的结构形式主要有卧式储罐、立式储罐和球形储罐,,本设计中采用立式储罐。
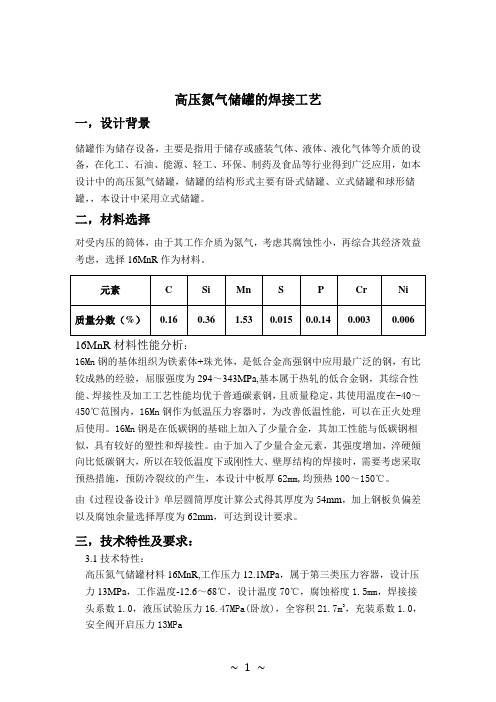
二,材料选择对受内压的筒体,由于其工作介质为氮气,考虑其腐蚀性小,再综合其经济效益考虑,选择16MnR作为材料。
16MnR材料性能分析:16Mn钢的基体组织为铁素体+珠光体,是低合金高强钢中应用最广泛的钢,有比较成熟的经验,屈服强度为294~343MPa,基本属于热轧的低合金钢,其综合性能、焊接性及加工工艺性能均优于普通碳素钢,且质量稳定,其使用温度在-40~450℃范围内,16Mn钢作为低温压力容器时,为改善低温性能,可以在正火处理后使用。
16Mn钢是在低碳钢的基础上加入了少量合金,其加工性能与低碳钢相似,具有较好的塑性和焊接性。
由于加入了少量合金元素,其强度增加,淬硬倾向比低碳钢大,所以在较低温度下或刚性大、壁厚结构的焊接时,需要考虑采取预热措施,预防冷裂纹的产生,本设计中板厚62mm,均预热100~150℃。
由《过程设备设计》单层圆筒厚度计算公式得其厚度为54mm,加上钢板负偏差以及腐蚀余量选择厚度为62mm,可达到设计要求。
三,技术特性及要求:3.1技术特性:高压氮气储罐材料16MnR,工作压力12.1MPa,属于第三类压力容器,设计压力13MPa,工作温度-12.6~68℃,设计温度70℃,腐蚀裕度1.5mm,焊接接头系数1.0,液压试验压力16.47MPa(卧放),全容积21.7m3,充装系数1.0,安全阀开启压力13MPa3.2技术要求:1)设备的施工与验收应符合《工程建设标准强制性条文》中的相关规定2)焊接采用电弧焊,焊条型号,低合金钢之间E5016,碳钢间E43033)焊接接头的形式及尺寸按图要求,角焊缝的焊脚高度为较薄件的厚度,法兰的焊接按相应的法兰标准规定,对接接头与角接接头需全焊透,接管焊缝成形表面均应圆滑过渡,不得有裂纹、咬边、及棱角.4)壳体钢板按GB6654-1996《压力容器钢板》及修改单中正火状态供货,且逐张进行超声检测,质量标准应不低于JB/T4730.3-2005中规定的II级,壳体的A类纵向焊接接头制备产品焊接试板,按《容规》第25条进行材料复验,坡口表面进行100%磁粉检测,并符合JB4730.4-2005中规定的I级5)塔体直线度允差25mm,安装垂直度允差为25mm6)裙座螺栓孔中心圆直径允差以及任意两孔弦长允差均为2mm7)壳体用钢板轧制,逐张进行-15℃夏比(V型缺口)冲击试验(横向),三个试样冲击平均值不得低于20J,允许其中一个试样冲击功小于平均值,但不得小于14J8)钢管应逐根按JB/T4730.3-2005中I级为合格9)裙座筒体与底封头的焊接接头必须采用全焊透连续焊,并进行磁粉检测,符合JB/T4730.4-2005中I级为合格10)设备压力试验合格后对全部焊缝按JB/T4730.4-2005进行磁粉检测,符合I级为合格,复验焊缝总长的20%11)热处理后,设备本体不得再行施焊四,焊接工艺设计4.1 焊缝编号及示意图4.2 接管与壳体,封头的焊接(1D,2D,3D)由GB150-1998《钢制压力容器》规定,接管,人孔,凸缘,补强圈等与壳体连的接头。
陕西科技大学过程装备与控制工程 机械设计课程设计2级齿轮减速器设计之轴及其轴承设计部分

d1=50mm d5=50mm
算,轴承7207C的寿命不满足减速器的预期寿命要 求,则改变直径系列,取7210C进行设计计算,由表 11-9得轴承内径d =50mm,外径D=90mm,宽度B = 20mm,定位轴肩直径da=57mm,外径定位直径 Da=83mm,对轴的力作用点与外圈大端面的距离 a3=19.4mm,故d1=50mm 通常一根轴上的两个轴承取相同的型号,则 d5=50mm (3)轴段②和轴段④的设计 轴段②上安 装齿轮3,轴段④上安装齿轮2,为便于齿轮的安装, d2和d4应分别略大于d1和d5,可初定d2=d4=52mm 齿轮2轮毂宽度范围为(1.2-1.5)d2=62.478mm,取其轮毂宽度与齿轮宽度b2=66mm相等,左端 采用轴肩定位,右端采用套筒固定。由于齿轮3的直 径比较小,采用实心式,取其轮毂宽度与齿轮宽度 b3=105mm相等,其右端采用轴肩定位,左端采用轴套 固定。为使套筒端面能够顶到齿轮端面,轴段②和轴 段④的长度应比相应齿轮的轮毂略短,故取 L2=102mm,L4=64mm (4)轴段③ 该段为中间轴上的两个齿轮提 供定位,其轴肩高度范围为(0.07-0.1)d2 = 3.645.2mm,取其高度为h=5mm,故d3=62mm 齿轮3左端面与箱体内壁距离与高速轴齿轮右端 面距箱体内壁距离均取Δ1=10㎜,齿轮2与齿轮3 的 距离初定为Δ3=10㎜,则箱体内壁之间的距离为 Bx=2Δ1+Δ3+b3+(b1+b2)/2 = [2×10+10+105+ (75+66)/2] ㎜=205.5㎜,取Δ3=10.5㎜,则箱体内壁 距离为Bx = 206㎜。齿轮2的右端面与箱体内壁的距 离Δ2=Δ1+(b1-b2)/2 = [10+(75-66)/2] ㎜ = 14.5㎜,则轴段③的长度为L3=Δ3=10.5㎜ (5)轴段①及轴段⑤的长度 该减速器齿轮 的圆周速度小于2m/s,故轴承采用脂润滑,需要用挡 油环阻止箱体内润滑油溅入轴承座,轴承内端面距箱 体内壁的距离取为Δ=12㎜,中间轴上两个齿轮的固 定均由挡油环完成,则轴段①的长度为 L1=B+Δ+Δ1+3㎜=(20+12+10+3) ㎜=45㎜
陕西科技大学机电工程学院过程装备与控制工程过程装备控制作用

陕西科技大学试题纸(A)课程过程控制技术及其应用班级学号姓名题号一二三四五六七八九十总分得分阅卷人一,填空题。
每空1分,共30分。
1,方框图由组成。
2,分程控制系统的目的是:。
3,自动调节系统常用的工程整定有。
4,调节系统中调节器正、反作用的确定依据是:。
5,比值控制系统有。
6,引用误差是指。
7,生产自动化控制系统包括。
8,控制通道和干扰通道分别是指。
9,压力计的选取原则是。
10,积分饱和的去除方法是。
11,控制对象的特性参数有。
12,液柱式压力计的工作原理是。
13,工业上常用控制规律有。
14,进行热电偶测量温度时,采用补偿导线的原因是,补偿导线的选用原则是。
热电偶温度计由组成。
15,温度变送器的功能作用是。
16,干扰是指、操作变量是.控制变量是指。
17,测量误差按性质可分为,,三大类。
18,复杂控制系统按照一定的分类方法被分为两大类,这两大类具体是指。
19,零点调整的含义是,零点迁移的两种具体形式包括。
20,动态前馈控制的设计思想是通过选择适当的控制器,使干扰信号经过控制器致被控量通道的动态特性完全复制对象通道的动态特性,并使它们符号(正、反),从而实现对干扰信号进行完全补偿的目标。
二,简答题。
每题5分,共30分。
1,什么是控制通道和扰动通道〔干扰通道)?对于不同的通道,对象的特性参数(K、T、τ)对控制有什么不同的影响?2,什么是前馈控制系统?它有什么特点?前馈控制的主要形式有哪几种?前馈控制与反馈控制的主要区别表现在哪些方面?工业上常用两者结合使用的系统,有什么好处?3,什么叫绝对误差、相对误差和引用误差?什么是仪表的精度和精度等级,怎样进行计算? 4,试简要分析本质安全防爆系统的防爆原理?如何进行防爆仪表铭牌的标注?5,试简述压差流量计和转子流量计的工作原理及其特点。
简要阐述两者之间的区别?6,用热电偶测温时,为什么要进行冷端温度补偿?其冷端温度补偿的方法有哪几种?三,分析题。
共20分1,什么是串级控制系统?串级控制系统的特点是什么?分析为什么串级调节系统的调节品质比单回路调节系统好?5分2,如图所示为一自力式贮槽水位控制系统。
过程装备控制技术及应用PPT教案

①简单控制系统
a.只有一个简单的反馈回路,又称为单回路控制系统。 b.单输入——单输出的线性控制系统。
第17页/共39页
18
②复杂控制系统 a. 系统中包含多个调节器,多个检测变送器或多个执行器。 b. 系统中存在有多个回路或者在系统中存在有多个输入信号
和多个输出信号。
夹 套 式 反 应 器
19
第18页/共39页
20
第19页/共39页
反馈控制系统
4.按系统克服干扰的方法划分 前馈控制系统
前馈-反馈控制系统
①反馈控制系统
f
扰动通道
x
e 调节器 p 调节阀 m
调节通道
y
被控对象
测量变送器 图1-5 反馈控制系统方框
21
第20页/共39页
22
②前馈控制系统
f
前馈补偿器
测量变送器
扰动通道
调节阀
m
y2
调节通道 y1
y
被控对象
图1-6 前馈控制系统方框图
第21页/共39页
f
③前馈-反馈控制系统
前馈补偿器 测量变送器
调节通道
x
调节器
调节阀
m
调节通道
y
被控对象
测量变送器
图1-7 前馈—反馈控制系统方框图
23
第22页/共39页
1.5 控制系统的过渡过程及其性能指标
控制系统的过渡过程
1.定义 从被控变量受到干扰作用使被控变量偏离给定值时起,
过程装备控制技术及应用
课程主要内容
典先
控 制 系 统 基 本 概 念
过 程 装 备 控 制 基 础
过 程 检 测 技 术
陕西科技大学机电工程学院过程装备与控制工程工业化学基础

第一章合成氨原料气的制备1.固体燃料气化:是指用氧或含氧气化剂对固体燃料(指煤和焦炭)进行热加工,使其转化为可燃性气体的过程,简称为“造气”。
气化所得到的可燃性气体称为煤气,进行气化反应的设备称为煤气发生炉。
2.煤气种类:空气煤气:是以空气作为气化剂所制得的煤气。
其成分主要为氮和二氧化碳。
水煤气:系以水蒸气为气化剂制得的煤气,主要成分为氢气和一氧化碳,两者含量之和可达到85%左右。
混合煤气:以空气相水蒸气同时作为气化剂所制得的煤气,其配比量以维持反应能够自热进行为原则。
半水煤气:以适量空气(或富氧空气)与水蒸气作为气化剂,所得气体的组成符合(co十H2)/N z=3.1—3.2(摩尔比)以能满足生产合成氨对氢氧比的要求。
3.间歇式制取半水煤气的工作循环(1)吹风阶段由煤气发生炉底部送入空气,提高燃料层温度,吹风气放空。
(2)上吹制气阶段水蒸气由炉底送入,经灰渣层预热、进入气化层进行气化反应,生成的煤气送入气柜。
随着反应的进行,燃料层下部温度下降,上部升高,造成煤气带走的显热增加。
因此,操作一段时间后需更换气流方向。
(3)下吹制气阶段水蒸气自上而下通过燃料层进行气化反应。
煤气由炉底引出,经回收热量后送入气柜。
由于煤气下行时经过灰渣层温度下降,从而减少了煤气带走的显热损失,燃料层温度均衡。
(4)二次上改阶段水蒸气自炉底送入,煤气炉底部的煤气排净,气作好安全准备。
目的是要将存在于为下一循环吹入空(5)空气吹净阶段目的是要回收存在于煤气炉上部及管道中残余的煤气,此部分吹风气亦应加以回收,作为半水煤气中N2的来源。
制气工艺条件:提高燃料层温度的方法,增加吹风速度,延长吹风时间(降低含CO量)5.烃类蒸气转化法是以气态烃和石脑油为原料生产合成氨最经济的方法。
具有不用氧气、投资省和能耗低的优点。
原理:烃类蒸气转化系将烃类与蒸汽的混合物流经管式炉管内催化剂床层,管外加燃料供热,使管内大部分烃类转化为H2、co和coB。
陕西科技大学 过程装备与控制工程 课件 1机械设计(王宁侠)第4章

边界摩擦类似两把刷子间的摩擦,其模型如图4-2(b)所示。吸
附在金属表面上多层分子边界膜的摩擦模型如图4-2(c)所示。 分子层距金属表面越远,吸附能力越弱,剪切强度越低,若干
层后就不再受约束。比较牢固地吸附在金属表面上的分子膜称
为边界膜,这种摩擦状态称为边界摩擦。边界膜按其形成机理 分为吸附膜和反应膜。
第4章 摩擦、 磨损及润滑概述
图 4-3 磨损过程
第4章 摩擦、 磨损及润滑概述 稳定磨损阶段内,摩擦条件相对稳定,零件在平稳而缓慢 的速度下磨损,磨损曲线的斜率近似为一常数,斜率越小,磨 损率越小。稳定磨损阶段的工作时间即为零件的使用寿命,磨 损率越小,零件的使用寿命越长。 经过稳定磨损阶段后,零件的表面遭到破坏,运动副中的
3. 疲劳磨损
在变接触应力的作用下,如果该应力超过材料相应的接触 疲劳极限,就会在摩擦副表面或表面以下一定深度处产生疲劳
裂纹。随着裂纹的扩展与相互连接,就会造成金属微粒从零件
工作表面上脱落,导致表面出现麻点状损伤现象,即形成疲劳 磨损(或称疲劳点蚀)。
第4章 摩擦、 磨损及润滑概述 为了提高零件表面的疲劳寿命,除应合理选择摩擦副材料 外,还应注意以下几点: (1) 合理选择零件接触面的表面粗糙度。一般情况下表面 粗糙度值越小,疲劳寿命越长。 (2) 合理选择润滑油的粘度。粘度低的润滑油易渗入裂缝,
第4章 摩擦、 磨损及润滑概述
图 4-1 滑动摩擦的分类
第4章 摩擦、 磨损及润滑概述 4.1.1 干摩擦 干摩擦是指摩擦表面之间无任何润滑剂或保护膜而直接接 触的纯净表面间的摩擦。在工程实际中,并不存在真正的干摩 擦,因为任何零件表面不仅会因氧化而形成氧化膜,而且或多 或少会被润滑剂所湿润,机械设计中,通常将未经人为润滑的
过程装备与控制技术课件

,
仪表的性能指标
2 变差(迟滞误差): 指在外界条件不变的情况下,用同一仪表对被测量在仪表全部 测量范围内进行正反行程测量时,被测量值正行和反行所得到 的两条特性曲线之间的最大偏差。
仪 表 的 指 示 值
反行程 最大绝对误差 正行程 被测变量
H max h 100% 满量程Ymax
稳定性 经济性 耐腐蚀 灵敏性 低能耗
准确性
测量及误差理论
(2)中间件(变送器或变换器)
★作用——
将传感器的输出信号进行变换,实现放大、远传、线性 化处理或转变成规定的统一信号,供给显示器等。
★要求——
能准确稳定地传输、放大和转换信号,且受外界其 他因素的干扰影响小,变换信号的误差小。
测量及误差理论
max 允 100% k % x上 x下
去掉%和±并与国家精度等级相比,取相等或高档的精度
仪表的性能指标
例:某反应器内的最高温度500℃。根据工艺要求,允许的最大绝 对误差不超过+7℃,试问应如何选择仪表的精度等级才能满足以 上要求? 解:根据工艺要求: 仪表的量程上限:X上=2 X
Max=
1000℃
仪表的允许引用误差为:
允
max 7 100% 100% 0.7% x上 x下 1000 0
去掉±、%,0.5<0.7<1.0,所以选精度等级0.5的仪表才能满 足工艺要求。精度等级1.0的仪表,其允许引用误差为±1.0%, 超过了工艺上允许的数值.
仪表的性能指标
仪表技术指标
仪表使用指标
仪表的性能指标
1.精确度: 是衡量仪表准确程度的一个品质指标。数值上等于在规 定的正常情况下,仪表所允许的引用误差。
陕西科技大学 过程装备与控制工程 课件 1机械设计(王宁侠)第2章

第2章 机械设计的基本要求和一般程序
2.1 机器的组成
2.2 机械设计的基本要求
2.3 机械设计的一般程序
2.4 机械零件的主要失效形式
2.5 机械零件应满足的基本要求
2.6 机械零件材料的选择原则
2.7 机械零件设计中的标准化
第2章 机械设计的基本要求和一般程序
据现有的技术、环境、经济、加工能力及时限等方面提出约束
条件,分析其实现的可能性,明确设计中的关键问题,拟定设 计任务书。设计任务书大体上应包括:机器的功能、技术经济
指标、制造技术关键、基本使用要求、特殊材料、必要的试验
项目、完成设计任务的预期期限及其他一些特殊要求等。此时, 这些要求及条件一般只能给出一个合理的范围,而不是准确的 数字。只有在充分调查研究和仔细分析的基础上,才能形成合 适可行的设计任务书。
第2章 机械设计的基本要求和一般程序
图 2-1 机器的组成
第2章 机械设计的基本要求和一般程序 1. 原动部分 原动部分是一台机器的心脏,它给机器提供运动和动力, 驱动整台机器完成预定功能。通常情况下,一台机器只有一个 原动部分(即动力源),复杂的机器也可能有好几个动力源。一 般来说,它们都是把其他形式的能量转换为可以利用的机械能。
代等。最后确定出功能参数,作为进一步设计的依据。在此过
程中,要处理好需要与可能、理想与现实、发展目标与当前目 标等之间可能产生的矛盾。
第2章 机械设计的基本要求和一般程序 2. 工作原理设计
1) 方案设计
工作原理是机器实现预期功能的依据,寻求方案时,可按 原动部分、传动部分和执行部分分别进行讨论。 (1) 执行部分方案设计。讨论机器的执行部分时,首先要 选择工作原理。工作原理不同,反映在生产方法不同,机器就 不同。例如,设计齿轮加工的机器时,其工作原理既可采用仿 型法(在普通铣床上即可完成),也可采用范成法。即使同一工 作原理,也可有多种不同的执行机构来实现,如滚齿机、插齿 机。因此,要设计更好、更新的机器就必须不断研究和发展新 的工作原理。根据不同的工作原理,可以拟定出多种不同的执 行机构的具体方案。设执行部分可有N1种方案。
陕西科技大学 过程装备与控制工程 课件 1机械设计(王宁侠)第3章解析

已知以上五个参数中的任意两个参数就可以确定出变应力 的类型和特征。几种典型的变应力的循环特性和应力特点如表 3-1所示。
第3章 机械零件的疲劳强度计算
当零件(例如弹簧)受变切应力作用时,以上概念仍然 适用,只需将公式中的σ改成τ即可。
第3章 机械零件的疲劳强度计算
3.2 材料的疲劳特性
3.2.1 材料的疲劳曲线 疲劳曲线是用一批标准试件进行疲劳实验得到的。以规定
相等而符号相反,即σmax=-σmin, 如图3-1(a)所示。例如,转动 的轴上作用一方向不变的径向力,则轴上各点的弯曲应力都属 于对称循环变应力。
第3章 机械零件的疲劳强度计算
2) 脉动循环变应力 脉动循环变应力中的σmin=0,如图3-1(b)所示。例如,齿
轮轮齿单侧工作时的齿根弯曲应力就属于脉动循环变应力。 3) 非对称循环变应力 非对称循环变应力中最大应力σmax和最小应力σmin的绝对
第3章 机械零件的疲劳强度计算 图 3-3 典型的疲劳曲线
第3章 机械零件的疲劳强度计算
1. 有限寿命区 曲线的BC段,随着循环次数的增加,使材料疲劳破坏的最大 应力不断下降。仔细检查试件在这一阶段的破坏断口状况,总能 见到材料已发生塑性变形的特征。C点相应的循环次数大约为 104(也有文献中认为约在105,现在工程实际上多以104为准)。这一 阶段的疲劳破坏,因为已伴随着材料的塑性变形,所以用应变-循 环次数来说明材料的行为更符合实际。因此,人们把这一阶段的 疲劳现象称为应变疲劳。由于应力循环次数相对很少,所以也叫 低周疲劳。有些机械零件在整个使用寿命期间应力变化次数只有 几百到几千次,但应力值较大,故其疲劳属于低周疲劳范畴。例 如飞机起落架、炮筒和压力容器等的疲劳均属于低周疲劳。但对 绝大多数通用零件来说,当其承受变应力作用时,其应力循环次 数一般都大于104,所以本章不讨论低周疲劳问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3章 机械零件的疲劳强度计算 当N≥104时,称为高周循环疲劳。图3-3中曲线CD代表有 限疲劳阶段。D点对应的疲劳极限ND称为循环基数,用N0表示。 在此范围内,试件经过一定次数的交变应力作用后会发生疲劳 破坏。曲线CD段上任何一点所代表的疲劳极限,称为有限寿 命疲劳极限。
第3章 机械零件的疲劳强度计算 2. 无限寿命区 当N≥N0时,疲劳曲线为水平线,对应于N0点的极限应力 σr称为持久疲劳极限,对称循环时用σ-1表示,脉动循环时用σ0 表示。 所谓“无限”寿命,是指零件承受的变应力水平低于或等
所示塑性材料的疲劳极限应力图近似呈抛物线,图3-4(b)所示 脆性材料的疲劳极限应力图呈直线。图3-4中, 横坐标σm为平 均应力,纵坐标σa为应力幅,曲线上A(0,σ-1)点的坐标表示出 对称循环应力的强度,
B(
0 0
应力的强度,C(σB,0)点的坐标表示出静应力的强度。
, 点的坐min m a
max min max
2 min 2
(3-1) (3-2)
m a
min r max
(3-3)
第3章 机械零件的疲劳强度计算 式中: σmax——循环中的最大应力; σmin——循环中的最小应力; σm——平均应力,为循环中应力不变部分,即静载分 量; σa——应力幅,为循环中应力变动部分,即动载分量;
m
m
(3-5)
kN
式中, kN——寿命系数。
N0 N
(3-6)
第3章 机械零件的疲劳强度计算 应当注意,材料的疲劳极限σr是在N=N0时求得的,当N >N0时,应取N=N0计算。各种金属材料的N0大致在106~
25×107之间,但通常材料的疲劳极限是在107(也有定为106或
5×106)循环次数下实验得来的,所以计算kN时取N0=107。对 于硬度低于350 HBS的钢, 若N>107,取N=N0=107, kN=1; 硬度高于350 HBS的钢,若N>25×107,取N=25×107。对于 有色金属也规定当N>25×107时,取N=25×107。
知的两点坐标 A 0, 1 及 D 0 , 0 求得 2 2K K 或
1e
1
K
ae e me
(3-11)
1 K ae me
(3-12)
第3章 机械零件的疲劳强度计算
max m a s 的变应力状况。
第3章 机械零件的疲劳强度计算
图 3-5 材料的疲劳极限应力图
第3章 机械零件的疲劳强度计算
于是,零件材料(试件)的极限应力曲线即为折线A′G′C。材
料中发生的应力如果处于OA′G′C区域以内,则表示不发生疲劳 破坏;如果发生在该区域以外,则表示一定要发生破坏;如正 图3-5中直线A′G′的方程可由已知两点坐标A′(0,σ-1)及 ( D
限平均应力;
ψσ——试件受循环弯曲应力时的材料常数,其值由试验
及下式决定:
2 1 0
0
(3-9)
根据试验,对于碳钢, ψσ≈0.1~0.2;对于合金钢,
ψσ≈0.2~0.3。
第3章 机械零件的疲劳强度计算
3.3 机械零件的疲劳强度计算
3.3.1 零件的极限应力图
由于零件几何形状、尺寸大小及加工质量等因素的影响,
第3章 机械零件的疲劳强度计算 对于非对称循环,Kσ是试件与零件极限应力幅的比值。于 是材料的极限应力图中的直线A′D′G′应按比例向下移,成为如 图3-6所示的直线ADG,而极限应力曲线的CG′部分,由于是按 照静应力的要求来考虑的,故不需进行修正。所以,零件的极
限应力曲线即由折线AGC表示。直线AG的方程,由已
第3章 机械零件的疲劳强度计算
图 3-3 典型的疲劳曲线
第3章 机械零件的疲劳强度计算
1. 有限寿命区 曲线的BC段,随着循环次数的增加,使材料疲劳破坏的最大 应力不断下降。仔细检查试件在这一阶段的破坏断口状况,总能 见到材料已发生塑性变形的特征。C点相应的循环次数大约为 104(也有文献中认为约在105,现在工程实际上多以104为准)。这一 阶段的疲劳破坏,因为已伴随着材料的塑性变形,所以用应变-循 环次数来说明材料的行为更符合实际。因此,人们把这一阶段的 疲劳现象称为应变疲劳。由于应力循环次数相对很少,所以也叫 低周疲劳。有些机械零件在整个使用寿命期间应力变化次数只有 几百到几千次,但应力值较大,故其疲劳属于低周疲劳范畴。例 如飞机起落架、炮筒和压力容器等的疲劳均属于低周疲劳。但对 绝大多数通用零件来说,当其承受变应力作用时,其应力循环次 数一般都大于104,所以本章不讨论低周疲劳问题。
r——循环特征(应力比),为最小应力与最大应力之比。
已知以上五个参数中的任意两个参数就可以确定出变应力 的类型和特征。几种典型的变应力的循环特性和应力特点如表
3-1所示。
第3章 机械零件的疲劳强度计算
当零件(例如弹簧)受变切应力作用时,以上概念仍然 适用,只需将公式中的σ改成τ即可。
第3章 机械零件的疲劳强度计算
N N0 C
m rN m r
式中: C、C′——实验常数;
m——随材料和应力状态而定的指数,如钢材弯曲疲劳
时m=9,钢材线接触疲劳时m=6。
第3章 机械零件的疲劳强度计算 若已知循环基数N0和疲劳极限σr、τr,则N次循环的疲劳极 限为
N0 rN r k N r N m N0 rN r k N r N
使得零件的疲劳极限要小于材料试件的疲劳极限。如零件的对 称循环弯曲疲劳极限以σ-1e表示,材料的对称循环弯曲疲劳极限
用σ-1表示,则在考虑了综合影响系数Kσ后三者关系为
1 K 1e 1 1e
K
(3-10)
这就是说,当已知Kσ及σ-1时,就可以不经试验而估算出零 件的对称循环弯曲疲劳极限σ-1e。
值不相等,如图3-1(c)所示。这种应力在一次循环中, σmax和
σmin可以具有相同的符号(正或负)或不同的符号。
第3章 机械零件的疲劳强度计算
图 3-1 几种典型的稳定循环变应力
第3章 机械零件的疲劳强度计算 2. 非稳定循环变应力 1) 规律性非稳定变应力 规律性非稳定变应力按一定规律周期性变化,且变化幅度 也按一定规律周期性变化,如图3-2(a)所示。例如专用机床的 主轴、高炉上料机构的零件等所受变应力属于此类。
好发生在折线A′G′C上,则表示工作应力状况正好达到极限状态。
0 0
2 , 2
求得,即
)
直线CG′的方程为
1 a m a m s
(3-7)
第3章 机械零件的疲劳强度计算
式中: a、 m ——试件受循环弯曲应力时的极限应力幅与极
第3章 机械零件的疲劳强度计算
图 3-4 疲劳极限应力图
第3章 机械零件的疲劳强度计算 工程上为计算方便,常将塑性材料疲劳极限应力图进行 简化,常用的一种简化疲劳极限应力图如图3-5所示。由于对 称循环变应力的平均应力σm=0,最大应力等于应力幅, 因此 对称循环疲劳极限在图3-5中以纵坐标轴上的A′点来表示。由 于脉动循环变应力的平均应力及应力幅均为
m a
0
2
第3章 机械零件的疲劳强度计算 因此脉动循环疲劳极限以原点O所作的45°射线上的D′点来表
示。连接A′、D′得直线A′D′。 由于这条直线与不同循环特性
时试验所求得的疲劳极限应力曲线非常接近,故用此直线代替 曲线是可以的,所以直线A′D′上任何一点都代表了一定循环特 性时的疲劳极限。横轴上任一点都代表应力幅等于零的应力, 即静应力。取C点的坐标值等于材料的屈服极限σS, 并自C点 作一直线与直线CO成45°的夹角,交A′D′的延长线于G′, 则 CG′上的任何一点均代表
图 3-6 零件的极限应力图
第3章 机械零件的疲劳强度计算 直线CG的方程为
式中:
ae me s ae
(3-13)
——零件受循环弯曲应力时的极限应力幅;
me——零件受循环弯曲应力时的极限平均应力;
ψσe——零件受循环弯曲应力时的材料常数。
第3章 机械零件的疲劳强度计算 ψσe可按下式计算:
σe
1 2 1 0 K K 0
(3-14)
式中,Kσ ——弯曲疲劳极限的综合影响系数。
第3章 机械零件的疲劳强度计算 Kσ可按下式计算:
件下,下同);
k 1 1 K 1 q
(3-15)
式中: kσ——零件的有效应力集中系数(脚标σ表示在正应力条
第3章 机械零件的疲劳强度计算
第3章 机械零件的疲劳强度计算
3.1 变应力的基本类型及特征参数
3.2 材料的疲劳特性
3.3 机械零件的疲劳强度计算
3.4 机械零件的接触强度
3.5 机械零件疲劳强度计算的相关系数
习题
第3章 机械零件的疲劳强度计算
3.1 变应力的基本类型及特征参数
3.1.1 变应力的基本类型
第3章 机械零件的疲劳强度计算
3.2.2 材料的极限应力线图
疲劳曲线一般是在对称循环变应力条件下得出的实验结果, 对于非对称循环变应力,不同的循环特征r对疲劳极限的影响也 不相同,其影响可以用疲劳极限应力图表示。 以σm和σa两参数确定不同循环特征r时的应力水平,根据实
验数据可以得到以σm-σa为坐标系的疲劳极限应力图。图3-4(a)
3.2 材料的疲劳特性
3.2.1 材料的疲劳曲线
疲劳曲线是用一批标准试件进行疲劳实验得到的。以规定
