七年级数学上册 4.3 角 4.3.3 余角和补角导学案(新版)新人教版
人教版数学七年级上册4.3.3余角与补角教案

-理解“互补”概念:学生可能难以理解互补的两角和为180°这一性质,需要通过直观的图形演示和实例说明。
-余角和补角的性质推导:推导同角(等角)的余角相等,互补的两角和为180°等性质,需要学生具备一定的逻辑推理能力。
-在复杂图形中识别和应用余角与补角:在实际问题中,学生可能难以在复杂的几何图形中识别出需求解的余角或补角。
还有一个值得注意的问题是,在总结回顾环节,部分学生表示对于某些知识点仍然存在疑问。我意识到,可能是在课堂中没有给予他们足够的提问机会,或者讲解得不够细致。因此,我打算在接下来的课程中,增加课堂互动环节,鼓励学生大胆提问,并及时给予解答。
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了余角与补角的基本概念、重要性和应用。同时,我们也通过实践活动和小组讨论加深了对余角与补角的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
4.通过实例和练习,让学生感受余角与补角在实际生活中的应用,提高学生的数学应用能力。
二、核心素养目标
1.培养学生几何直观和空间想象能力,通过余角与补角的学习,让学生能够直观感知几何图形的特征,形成空间想象力。
2.发展学生的逻辑推理能力,通过余角和补角的性质推导和应用,提高学生分析问题和解决问题的逻辑思维能力。
3.重点难点解析:在讲授过程中,我会特别强调余角和补角的概念,以及它们的应用。对于难点部分,如互补性质的推导,我会通过画图和具体例子来帮助大家理解。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与余角与补角相关的实际问题,如如何利用补角性质求解多边形内角和。
人教版七年级上册 4.3.3导学案(余角和补角)

§4.3.3余角和补角课时数:第55课时第4章班级姓名小组【学习目标】1、理解互为余角与互为补角的概念;2、掌握余角与补角的性质.【预习检测】一、知识储备:1.什么是直角?什么是平角?直角和平角的度数分别是多少?2. 如何进行两个角的与差的计算?二、问题导学:(阅读课本P137-138,回答下列问题)问题1.什么时候两个角互为余角?问题2. 什么时候两个角互为余角?问题3.如何计算一个角的余角和补角?问题4.余角和补角有什么性质?你能用几何语言表示这些性质吗?问题5.一个角的余角和补角有什么关系?三、自主反馈:1._____________的两个角互为余角,若∠1与∠2互余, 那么有:_____________________;_____________的两个角互为补角,若∠1与∠3互补,那么有:______ ___________.2.填空结论:∠α的余角是___________,∠α补角是__________,∠α的补角比它的余角大______.3.余角和补角的性质:(1)若∠1与∠2互余,∠1与∠3互余,那么有: ∠2_____∠3,用符号语言描述:∵∠1与∠2互余;即∠2=___-_____;∠1与∠3互余; 即∠3=___-_____;∴______________________________;(2)若∠1与∠2相等,∠1与∠3互补,∠2与∠4互补,那么有:∠3_____∠4; 用符号语言描述:∵__________________________________;___________________________________; ∴______________________________;总结:同角(等角)的补角_____:同角(等角)的___________.四、【合作探究】9. 如图,点A 、O 、E 在同一条直线上,射线OB 和射线OD 分别平分∠AOC 和∠EOC ,图中哪些角互为余角?图中与∠AOD 互补的角有哪些?五、【夯实积累】4. 已知∠α=35°,则∠α的余角是( ) A .35°B .55°C .65°D .145°5. 已知∠a =32°,则∠a 的补角为( ) A .58°B .68°C .148°D .168°6. 若∠α+∠β=90°,∠β+∠γ=90°,则∠α与∠γ的关系是( ) A .互余B .互补C .相等D .∠α=90°+∠γ7. 一个角是70°39′,它的余角是 °_____′,补角是 °_____′. 8. (1) ∠α与∠β互余,且∠α:∠β=5:4,求∠α与∠β的度数分别是多少?(2).一个角的补角是它的3倍,这个角是多少度? (3)一个角的余角比它的补角的21小200,求这个角的度数.六、归纳小结:1、余角和补角的定义和计算2、余角和补角的性质及几何语言表述【夯实积累】班级姓名小组1. ∠α=50°23′ , 则∠α的余角是__________;∠α的补角是_________.2.若∠1+∠2=90°,∠3+∠2=90°,∠1=40°,则∠3=______°, 依据是_________________.3. 已知∠1和∠2互余,∠2和∠3互补,若∠1=63°,则∠3=__________.4.将一副三角尺按不同位置摆放,在哪种摆放方式中∠a与∠B 互余的是______;∠a和∠B互补的是________;∠a与∠B相等的是________.5. 一个角比它的余角大25°,那么这个角的补角是()A.67.5°B. 22.5°C.57.5°D. 122.5°6.下列说法正确的是()A.90°的角是余角B.30°的角和60°的角是余角C.30°的角是90°的角的余角D.30°的角和60°的角互为余角7. 如果一个角的补角是120°,那么这个角的余角是()A.150°B.90° C.60° D.30°8. 已知∠α=300,∠α与∠β互补,∠α与∠γ互余,则∠β-∠γ的值等于()A.45° B.60° C.90° D.180°9.如图,已知直线AB,CD相交于点O,OE平分∠COB,若∠EOB=55°,则∠BOD的度数是()A.35°B.55°C.70°D.110°10. 如图,长方形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠BAF=60°,则∠DAE等于( )A.15°B.30°C.45°D.60°三、解答题:11.(1)若∠1=2∠2,且∠1+∠2=90°,求∠1和∠2的度数.DF CAEB(2)一个角的余角比它的补角的32还少40°,求这个角.。
2020七年级数学上册 4.3 角 4.3.3 余角和补角教案 (新版)新人教版

4.3.3 余角和补角
,讲述和余角补角有的概念和性质有关的知识,这些性质在学习对
掌握同角(等角)的余角相等,同角(等角)的补角相等,对顶角相等的
重点余角和补角的定义和性质
教学过程提要
学生要解决的问
,图中哪些角互为余
例1. 方位角的表达方式如图,(1)射线OA表示的方向为
巩固练习:
、互余:如果两个角的和是一个直角,那么这两个角叫做互为余角,其中一个角是另、互补:如果两个角的和是一个平角,那么这两个角叫做互为补角,其中一个角是另
P125 1。
七年级数学上册 4.3.3 余角和补角导学案1(新版)新人教版_2

余角(y úji ǎo)和补角 课题: 4.3.3 余角和补角(一) 序号:53学习目标:知识和技能:了解余角和补角的定义和性质,并能熟练应用2、过程和方法:掌握图形语言和文字语言的转化,3、情感、态度、价值观:通过联系实际,让学生在数学活动中发展合作交流的意识,培养数形结合的思想 学习重点:互余、互补等概念和性质学习难点:理解互余、互补等概念并熟练应用导学方法:课 时:1课时导学过程一、课前预习:预习课本,完成《导学案》教材导读二、课堂导学:1.情境导入:1.用量角器量出图中的两个角的度数,并求出这两个角的和.2.说出一副三角尺中各个角的度数.一幅三角板中,每一块都有一个角是900,且另外两角为300、600和450,450那么它们两者之间作何关系呢?2.出示任务,自主学习:认真自学课本P 137, 完成下面任务:1.思考:(1)如图1,已知∠1=62°,∠2=118°,那么 ∠1+∠2=(2)如图2,A 、O 、B 在同一直线上,∠1+∠2=2.你是怎样理解互为余角和互为补角的?并用几何语言表示。
3.互为余角或互为补角的两个角有怎样的关系?若一直任意一个角,那么他的余角和补角如何表示?3.合作探究:余角或补角都有角平分线吗?1 2 A O B图 2 1 2 图 1补角一定大于余角吗?3.《导学案》难点探究三、展示反馈学生口答,师生交流四、学习小结:1. 规定如果两个有的和等于900(直角),我们就说这两个角互为余角,即其中一个角是另一个角的余角.如果两个角的和等于1800(平角),就说这两个角互为补角(简称互补),其中的一个角是另一个角的补角.2.互为补角和互为余角的角主要反映角的数量关系,而不是角的位置关系.3.余角和补角的性质:同角(等角)的余角相等。
同角(等角)的补角相等。
五、达标检测:课本第138 页练习《导学案》自主测评课后练习:课本第139页习题43第7.11题;《导学案》基础反思、展题设计板书设计: 4.3.3 余角和补角1.余角和补角的定义2.余角和补角的性质课后反思:内容总结(1)余角和补角。
新人教版七年级上册数学导学案4.3.3余角和补角

新人教版七年级上册数学导教案: 4.3.3 余角和补角 (1)【学习目标】认识一个角的余角与补角,并能娴熟求出一个角的余角和补角。
【自主学习】(仔细察看,踊跃动脑,你会有新发现)1、在同一块三角板中的两个锐角之和等于度。
2、若∠ 1=60.5 ° , ∠ 2=29.5 °,则∠ 1+∠ 2=。
3、如图 1,∠ AOB=90°,那么∠ 1+∠ 2=。
概括 1: 余角的定义 :图 1假如个角的和等于,就说这个角互为,简称。
此中一个角是另一个角的。
几何表达:12图 24、若∠ 3=115°,∠ 4=65° , 则∠ 3+∠ 4=5、如图 3,已知点A、 O、 B 在向来线上,则∠ AOC+∠BOC=图 3概括 2:补角的定义:假如个角的和等于,就说这个角互为,简称。
此中一个角是另一个角的。
几何表达:43图 4【稳固新知】(活学活用,勇敢试试)例 1达成下表:30064030x(0x 90)的余角5300的补角720想想:同一个角的补角与它的余角之间有如何的数目关系?(余角和补角的性质之一)结论:同角的余角同角的补角例 2假如一个角的补角等于它的余角的 4 倍,那么求这个角的度数。
对应练习:6 、假如一个角的余角是它的 3 倍,那么求这个角是多少度?【当堂检测】1、52 ° 24′的余角是,补角是.2、假如∠ 1+∠ 2=90°∠ 1+∠ 3=90°,则2与 3 的关系是原因是;3、假如∠α的补角是 135°,则∠ α =____,∠α的余角是4、若一个角的余角等于它自己,则这个角的度数为_;,____;5、一个角为n( n<90°),则它的余角为,补角为;【讲堂小结】【拓展延长】6、如图 9,∠ AOC =∠ C OB = 90°,∠ DOE= 90°, A 、O、 B 三点在向来线上( 1)写出∠COE的余角,∠AOE的补角CDE( 2)找出图中一对相等的角,并说明原因A O B图 9。
新人教版七年级数学上册导学案-4.3.3余角和补角

4.3.3 余角和补角【学习目标】1.在具体的现实情境中,认识一个角的余角与补角,掌握余角和补角的性质.2.了解方位角,能确定具体物体的方位.3.进一步提高抽象概括能力,发展空间观念和知识运用能力,体会观察、归纳、推理对数学知识中获取数学猜想和论证的重要作用,能在独立思考和小组交流中获益.【学习重点】:认识角的互余、互补关系及其性质,确定方位【学习难点】:通过简单的推理,归纳出余角、补角的性质,能用规范的语言描述一、学前准备1.(1)在一副三角板中,每块都有一个角是90°,那么其余两个角的和是多少?(2)已知∠1=36°,∠2=54°,那么∠1+∠2=?2.提出问题.(1)观察方格如右图中的两个角,你能猜想∠1+∠2等于多少度?12(2)如果∠1=144°,∠2=36°,那么∠1+∠2=?二、探究活动(一).独立思考·解决问题1.余角与补角:一般地,如果两个角的和等于90°(直角),就说这两个角互为,即其中每一个角是另一个角的;类似地,如果两个角的和等于180°(平角),就说这两个角互为,即其中每一个角是另一个角的。
2.巩固反思.(1)填空:①47°18′的余角是______,补角是_______.②∠α(0°<∠α<90°)的余角是______,∠β(0°<β<180°)的补角是_______.(2)已知一个角是它补角的3倍,求这个角.(二).师生探究·合作交流1.例3.如图,∠1与∠2互补,∠3与∠4互补,如果∠1=∠3,那么∠2与∠4相等吗?为什么?2.余角与补角的性质.由上面可得到补角的一个性质:等角的补角;类似得到余角的性质:等角的余角 .练习:如图,∠EDC=∠CDF=90°,∠1=∠2.O BA(1)图中哪些角互为余角?哪些角互为补角?(2)∠ADC 与∠BDC 有什么关系?为什么?(3)∠ADF 与∠BDE 有什么关系?为什么?3.认识方位角.例4.如下图,货轮O 在航行过程中,发现灯塔A 在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上分别发现了客轮B 、货轮C 和海岛D .仿照表示灯塔方位的方法,画出客轮B 、货轮C 和海岛D 方向的射线.4.知识拓展:小宁从A 地向东北方向走62米到B 地,再从B 地向西走56米到C 地,这时她离A•地多少米?在A 地的北偏西多少度?画出图形(用1cm 表示10m ),然后用刻度尺和量角器进行测量.(精确到1m 、1°)三、学习体会1.本节课你有哪些收获?你还有哪些疑惑?2.预习时的疑难解决了吗?四、检测评估(一)填空题.1.52°24′的余角是_______,补角是________.2.如右图已知∠AOB ,在图中画出它的余角是_______,补角是_______.3.射线OA 方向是东北方向,射线OB 方向是北偏西60°,则∠AOB 度数是______.(二)选择题.4.一个角比它的余角大25°,那么这个角的补角是( ).A .67.5°B .22.5°C .57.5°D .122.5°5.和北偏西40°的射线OA 组成平角AOB 的射线OB 是( ).A .南偏东40°的射线B .南偏东50°的射线C .南偏东60°的射线D .东南方向的射线(三)解答题.6.如右图,E 、D 、F 在同一条直线上,∠CDE=90°,∠1=∠2.(1)哪些角互为余角?哪些角互为补角?(2)∠ADC 与∠BDC 有什么关系?为什么? (3)∠ADF 与∠BDE 有什么关系?为什么?7.已知:如下图,点A 、O 、B 在同一直线上,∠1与∠2互余,OE 、OF 分别是∠AOC 、∠AOD 的平分线,求∠EOF 的度数.五、拓展应用8.如下图,两辆汽车从A 点同时出发,一辆沿西北方向以30千米/时的速度行驶;•另一辆沿南偏东60°的方向以40千米/时的速度行驶,34小时后分别到达B 、C 两点,•如果图中1cm 代表10km ,那么试在图中画出B 、C 两点,并通过测量,说出此时两辆车的距离.D F 21E C BA。
七年级数学上册4.3角4.3.3余角和补角教案新版新人教版

第四章几何图形初步4.3 角4.3.3 余角和补角【知识与技能】(1)掌握余角、补角的概念,并能简单应用.(2)正确理解方位角,能画出方位角所表示方向的射线.【过程与方法】经历观察、操作、推理、交流等活动,发展学生的想象力,培养学生的推理能力和有条理的表达能力.【情感态度与价值观】培养学生简单的推理能力,渗透数形结合思想.余角和补角的概念及性质.运用余角和补角的性质.多媒体课件、量角器、三角尺纸板、一副三角尺cm情境:如图4-3.3-1(1),打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2.这个问题可以简单地表示为图4-3.3-1(2).其中∠EDC=90°,那么各个角与∠1有什么关系?学生进行小组合作探究.教师总结:有的角与∠1的和等于90°,如∠ADC;有的角与∠1的和等于180°,如∠ADF.今天我们来探究这些角之间的关系.一、思考探究,获取新知探究1:余角和补角的概念.教师提问:拿出准备好的三角尺纸板,将各个角剪下来,拼一拼,量一量,你能发现各个角之间有什么关系?学生自主探究、交流、讨论.教师总结:在一副三角尺中,每块都有一个角是90°,而其他两个角的和是90°.一般地,如果两个角的和等于90°(直角),就说这两个角互为余角,即其中一个角是另一个角的余角.上述问题中的∠1与∠ADC互为余角,即∠1是∠ADC的余角,∠ADC也是∠1的余角.类似地,如果两个角的和等于180°(平角),就说这两个角互为补角,即其中一个角是另一个角的补角.上述问题中的∠1与∠ADF互为补角,即∠1是∠ADF的补角,∠ADF也是∠1的补角.探究2:余角和补角的性质.教师提问:问题1:如果∠1与∠2互余,∠3与∠4互余,并且∠1=∠3,那么∠2与∠4相等吗?为什么?问题2:如果∠1与∠2互补,∠3与∠4互补,并且∠1=∠3,那么∠2与∠4相等吗?为什么?学生分组讨论,说出理由,最后师生共同归纳:余角和补角的性质:同角(等角)的余角相等;同角(等角)的补角相等.探究3:方位角.教师提问:如图4-3.3-2,请指出公园、医院、法院分别在学校的什么方向?学生讨论得出结论:公园在学校的南偏西75°方向上;医院在学校的北偏东30°方向上;法院在学校的南偏东45°(东南)方向上.教师总结:与方位角有关的说法,如正东、正南、正西、正北、东南、东北、西南、西北、北偏东多少度、北偏西多少度、南偏东多少度、南偏西多少度.二、典例精析,掌握新知本节课主要学习了余角、补角的概念,余角、补角的性质,方位角的表示.教材P139习题4.3第7,8题。
4.3.3余角和补角(1)-人教版七年级数学上册导学案

4.3.3余角和补角(1)备课时间: 授课时间: 授课班级: 学习目标:1、知识与技能:在具体的现实情境中,认识一个角的余角和补角.2、过程与方法:体会一个角的余角和补角的意义,经历探索性质的过程.3、情感态度与价值观:培养积极探索的精神.学习重点:正确求出一个角的余角和补角.学习难点:运用余角和补角的性质.学习方法:自主、合作、交流、展示.一、自主学习:1.思考:在一副三角板中同一块三角板的两个锐角和等于多少度?2.如图1,已知∠1=61°,∠2=29°,那么∠1+∠2= 。
3.如 图 2,已知点A 、O 、B 在一直线上 ,∠COD=90°,那么∠1+∠2= 。
4.互为余角的定义:思考:(1)如图3,已知∠1=62°,∠2=118°,那么 ∠1+∠2=(2)如图4,A 、O 、B 在同一直线上,∠1+∠2=5.互为补角的定义:问题1:以上定义中的“互为”是什么意思?问题2:若 ∠1+∠2 +∠3 =180° ,那么∠1、∠2、∠3互为补角吗?6.补角的性质:_______________________________余角的性质:_____________________________________2 图 1 90° 1 2 图 2 1 2 A O B 图 4 1 2 图3 C O DO E D C B A 二、合作探究、交流展示:例1:若一个角的补角等于它的余角4倍,求这个角的度数。
三、拓展延伸:例2:如图,∠AOC =∠COB =90°,∠DOE =90°,A 、O 、B 三点在一直线上(1)写出∠COE 的余角,∠AOE 的补角;(2)找出图中一对相等的角,并说明理由;四、课堂检测:1、一个角的余角比它的补角的31还少︒20,求这个角的度数。
2、若α∠和β∠互余,且α∠:β∠=7:2,求α∠、β∠的度数。
七年级(人教版)数学上册导学案:4.3.3余角和补角

科目数学班级学生姓名课题 4.3.3余角和补角课型新授课时 1 主备教师备课组长签字学习目标:通过预习课本及简单的推理认识一个角的余角和补角,掌握余角和补角的性质;并能理解方位角的意义,掌握方位角的判别与应用一、自主预习(一)余角和补角的概念1、如果____________________ 就说这两个角互为余角,简称为两个角____.其中一个角是另一个角的______.如图,∵ + =90°∴∠1与互余,∠1是的余角;的余角是∠22、如果____________________ 就说这两个角互为补角,简称为两个角____.其中一个角是另一个角的______.如图,已知点O是AB上一点:∵ + =180°∴∠AOC与互补,∠AOC是的补角,的补角是∠BOC.(二)余角和补角的性质1、70°的余角是_____,补角是_____;∠1的余角是______,补角是________2、∠1与∠2互补,∠3与∠4互补,如果∠1=∠3,那么∠2与∠4相等吗?为什么?理由:∵∠1+∠2= ∠3+∠4=∴∠2=180°- ∠4=180°- ,∵∠1=∠3∴180°-∠1=180°-∠3 即:∠ =∠3、∠1与∠2互补,∠3与∠4互补,如果∠1=∠3,那么∠2与∠4相等吗?为什么?归纳:补角的性质:___________________余角的性质:___________________(三)方位角画出下列方位角:(1)南偏东60°(2)北偏东30°(3)南偏西25°(4)西北方向二、合作探究1、若一个角的补角等于它的余角4倍,求这个角的度数。
2、如图.货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线。
新人教版七年级上册4.3.3 余角和补角导学案

新人教版七年级上册4.3.3 余角和补角导学案【学习目标】:1、认识一个角的余角和补角,并会求一个角的余角和补角;2、掌握余角和补角的性质,并能用它解决相关问题;3、认识并理解方位角,能画出方位角所表示方向的射线,并会在实际问题中应用它确定一个物体的位置,进一步体会数形结合的方法.【学习重点】:互余、互补的概念及其性质.【学习难点】:余角、补角的性质的应用.【教学过程】自主学习:1、如图1,∠1与∠2 的大小关系是;∠1与∠2 的数量关系是;若∠1=135°34′,则∠2= .2、如图2,∠3与∠4 的大小关系是;∠3与∠4 的数量关系是;若∠3=35°34′,则∠4= .新知探究:探究点一:余角与补角的概念1、观察一副三角尺,每块三角尺中,除直角外,其他两个锐角有什么关系?2、如图,已知∠BOD=90°,则∠BOC+∠COD= ;∠BOC+∠COA= .3、上题中,把∠BOC与∠COD叫做互为余角,∠BOC与∠COA叫做互为补角.归纳:如果两个角的,就说这两个角互为余角,即其中每一个角是另一个角的;如果两个角的,就说这两个角互为补角,即其中每一个角是另一个角的 .4、图中给出的各角中,哪些互为余角?哪些互为补角?探究点二:余角与补角的性质1、如果∠1+∠2=90°,∠1+∠3=90°,那么∠2和∠3的大小有什么关系?2、如果∠1+∠2=180°,∠1+∠3=180°,那么∠2和∠3的大小有什么关系?归纳:余角的性质:补角的性质:探究点三:方位角说明:一船常以正北、正南方向为基准,描述物体运动的方向.表示方向的角叫做方位角;方位角在航行、测绘等工作中经常用到.1、如图,在地理中规定上北,下南,左西,右东.如何作出北偏东60°的角?2、我们常说的西北方向指什么角?西南方向呢?在上图中作出这两个角.当堂训练1、①、已知∠1=200,∠2=300,∠3=600,∠4=1500,则∠2是___的余角,___是∠4的补角.②、如果∠α=39°31°,∠α的余角∠β =_____,∠α的补角=_____,∠α-∠β=_____.③、若∠1+∠2=90°,∠3+∠2=90°,∠1=40°,则∠3=______°,依据是______________.2、一个角的补角是130︒,则这个角是 ,它的余角是_____度. 温馨提示:若一角00(090)αα<<的补角为β,余角为γ,则βγ-= 。
七年级数学上册 4.3 角 4.3.3 余角和补角导学案新人教版

第四章几何图形初步4.3 角学习目标:1. 了解余角、补角的概念,掌握余角和补角的性质,并能利用余角、补角的知识解决相关问题.2. 了解方位角的概念,并能用方位角知识解决一些简单的实际问题.重点:了解余角、补角的概念及性质,了解方位角的概念和表达方式.难点:运用余角、补角和方位角的相关知识解题.一、知识链接如图①,在长方形中,∠1+∠2= °,∠3+∠4= °.图①二、新知预习1. 如果两个角的和等于90°(直角),就说这两个角互为______ (简称为两个角______ ).如图①,可以说∠1是∠2的余角,或∠2是∠1的余角,或∠1和∠2互余.2. 如果两个角的和等于180°(平角),就说这两个角互为______ (简称为两个角______).如图①,可以说∠3是∠4的补角,或∠4是∠3的补角,或∠3和∠4互补.三、自学自测1. 图中给出的各角,哪些互为余角?自主学习教学备注学生在课前完成自主学习部分配套PPT讲授1.情境引入(见幻灯片3)2. 图中给出的各角,哪些互为补角?四、我的疑惑__________________________________________________________________________________________________________________________________________________________________一、要点探究探究点1:有关余角和补角的计算例1 若一个角的补角等于它的余角的4 倍,求这个角的度数.方法总结:余补角问题中,若角之间有比较明显的倍分关系,可尝试将较小的角设为未知数,列方程解答.例2如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数.课堂探究教学备注配套PPT讲授2.探究点1新知讲授(见幻灯片4-12)观察与思考:∠α∠α的余角∠α的补角5°32°45°77°62°23′x°(0<x<90)观察可得结论:锐角的补角比它的余角大_____.针对训练1.如果∠a=36°,那么∠a的余角等于()A.54°B.64°C.144°D.134°2.如图,将一副直角三角板如图放置,若∠AOD=18°,则∠BOC的度数为_____.第2题图变式题图【变式题】一副三角板按如图方式摆放,且∠1的度数比∠2的度数大44°,则∠1=______.3.已知∠A与∠B互余,且∠A的度数比∠B度数的3倍还多30°,求∠B的度数.探究点2:余角和补角的性质思考:∠1 与∠2,∠3都互为补角,∠2 与∠3 的大小有什么关系?教学备注配套PPT讲授3.探究点2新知讲授(见幻灯片13-17)例3 如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.(1)∠AOD的余角是_______________,∠COD的余角是_________________;(2 )OE是∠BOC的平分线吗?请说明理由.针对训练如图,已知∠AOB=90°,∠AOC=∠BOD,则与∠AOC互余的角有__________________.探究点3:方位角八大方位正东:正南:正西:正北:西北方向:西南方向:东北方向:东南方向:例4如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上. 同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D. 仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.针对训练教学备注配套PPT讲授4.探究点3新知讲授(见幻灯片18-23)1. 如图,说出下列方位(1) 射线OA 表示的方向为.(2) 射线OB 表示的方向为.(3) 射线OC 表示的方向为. .(4) 射线OD 表示的方向为.2.费俊龙、聂海胜乘坐“神舟”六号遨游太空时,我国当时派出远望一号~四号船队,跟踪检测. 其中远望一、二号停在太平洋洋面上,某一时刻,分别测得神舟六号在北偏东60°和北偏东30°的方向,你能在下图中画出当时神舟六号所处的位置吗?二、课堂小结1.一个角的余角是它的2倍,这个角的度数是()A.30°B.45°C.60°D.75°当堂检测教学备注配套PPT讲授5.课堂小结2.下列说法正确的是()A.一个角的补角一定大于它本身B.一个角的余角一定小于它本身C.一个钝角减去一个锐角的差一定是一个锐角D.一个角的余角一定小于其补角3.已知∠A与∠B互余,∠B与∠C互补,若∠A=60°,则∠C的度数是_______.4.∠1与∠2 互余,∠1 = (6x + 8)°,∠2 = (4x-8)°,则∠1= ,∠2= .5. 请认真观察下图,回答下列问题:(1)图中有哪几对互余的角?(2) 图中哪几对角是相等的角(直角除外)?为什么?6 垃圾打捞船A和B都停驻在湖边观测湖面,从A船发现它的北偏东60°方向有白色漂浮物,同时,从B船也发现该白色漂浮物在它的北偏西30°方向.(1) 试在图中确定白色漂浮物C的位置;(2) 点C在点A的北偏东60°的方向上,那么点A在点C的________方向上.A. 南偏东30°B. 南偏西30°C. 南偏东60°D. 南偏西60°如有侵权请联系告知删除,感谢你们的配合!教学备注6.当堂检测(见幻灯片24-28)。
人教版七年级上册 4.3.3 余角和补角 导学案
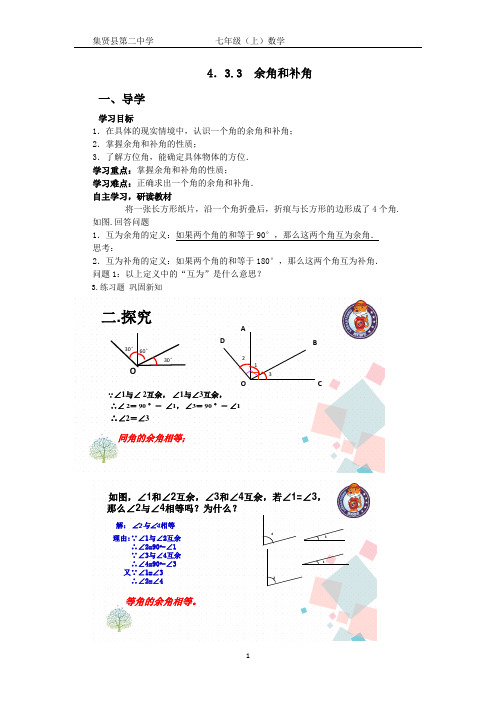
4.3.3 余角和补角一、导学学习目标1.在具体的现实情境中,认识一个角的余角和补角; 2.掌握余角和补角的性质;3.了解方位角,能确定具体物体的方位. 学习重点:掌握余角和补角的性质;学习难点:正确求出一个角的余角和补角. 自主学习,研读教材将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角. 如图.回答问题1.互为余角的定义:如果两个角的和等于90°,那么这两个角互为余角. 思考:2.互为补角的定义:如果两个角的和等于180°,那么这两个角互为补角. 问题1:以上定义中的“互为”是什么意思?3.练习题 巩固新知同角的余角相等;∵∠1与∠2互余,∠1与∠3互余,O60°30°BOCAD213∴∠2=90 °-∠1,∠3=90 °-∠1∴∠2=∠330°二.探究1243等角的余角相等。
理由:∵∠1与∠2互余∴∠2=90o -∠1∵∠3与∠4互余∴∠4=90o -∠3又∵∠1=∠3∴∠2=∠4解:∠2与∠4相等如图,∠1和∠2互余,∠3和∠4互余,若∠1=∠3,那么∠2与∠4相等吗?为什么?同理:同角或等角的补角相等 2. 你知道表示方向的一个成语吗?“四面”—东、南、西、北“八方”--东、南、西、北和东北、东南、西北、西南东西北南O正东:正南:正西:正北:西北方向:西南方向:东北方向:东南方向:射线OA ABCD45°EGFH45°八大方位45°45°射线OB 射线OC 射线OD射线OE 射线OF 射线OH 射线OG三.检测1.一个角是70°39′,求它的余角和补角。
2、∠A 的补角是它的3倍,∠A 是多少度?BAOC3、如图两堵墙围一个角∠AOB ,但人不能进入围墙,我们如何去测这个角的大小呢?四.拓展1、课堂小结2、强化训练(见课件题型)。
人教版-数学-七年级上册-人教版七上4.3.3 余角和补角 导学案

§4.3.3 余角和补角学习目标:1.了解余角和补角的概念,会求一个角的余角和补角.2.知道余角和补角的性质,并能用它解决相关问题.3.经历余角、补角性质的推导和应用过程,初步掌握图形语言与符号语言之间的相互转化,进一步提高识图能力,发展空间观念.4.通过互余、互补性质的学习过程,培养善于观察、独立思考、合作交流的良好学习习惯. 学习重点:余角和补角的概念及性质 学习难点:余角和补角的性质应用 学习过程:一、创设情景 明确目标比萨斜塔是世界著名建筑奇观,意大利的标志之一。
目前的倾斜约10%,即5.5度,偏离地基外沿2.3米,塔顶已南倾(即塔顶偏离垂直线)4.5米,每年倾斜约1毫米。
二、自主学习 指向目标 〖自学导读〗 (1)定义余角:如果两个角的和等于 ,就说这两个角...互为余角,简称互余,其中一个角是另一个角的 .思考:“互为”是什么意思?“互余”是几个角之间的关系? 几何语言: 因为∠1+∠2=___°,所以∠1和∠2互为余角 反之,因为∠1和∠2互为余角,所以∠1+∠2=___°(或∠1=__°-∠2) 补角:如果两个角的和等于 ,就说这两个角...互为补角,简称互补,其中一个角是另一个角的 . 几何语言: 因为∠1+∠2=___°,所以∠1和∠2互为补角反之,因为∠1和∠2互为补角,所以 (或∠1=___°-∠2) 思考:如何求一个角的余角或补角?(2)性质 注意:“同角”是指同一个角;“等角”是指相等的角。
条件 因为所以 结论(填“同”或“等”) ∠B 和∠C 都是∠A 的余角 ∠B =90°-∠A∠C =90°-∠A ∠B =∠C_____角的余角相等 ∠2是∠1的余角 ∠4是∠3的余角 ∠1与∠3相等 ∠2=90°-∠1 ∠4=90°-∠3∠1=∠3∠2=∠4_____角的余角相等 ∠B 和∠C 都是∠A 的补角 ∠B =180°-∠A ∠C =180°-∠A ∠B =∠C _____角的补角相等 ∠2是∠1的补角 ∠4是∠3的补角 ∠1与∠3相等 ∠2=180°-∠1 ∠4=180°-∠3∠1=∠3∠2=∠4_____角的补角相等〖自我评价〗1.一个角是35º,则它的余角是 º,它的补角是 º,它的补角比它的余角大 º.2.若∠A =79 º30′,则它的余角是 ,它的补角是 ,它的补角比它的余角大 º.213.若锐角∠A =x º,则它的余角是 º,它的补角是 º,它的补角比它的余角大 º.4.若∠A +∠B =90°,∠C +∠D =90°,且∠A =∠C ,则∠B 与∠D 的数量关系是_____,理由是______三、合作探究 达成目标 探究点一 余角和补角的概念例1.把下列表格补充完整。
七年级数学上册4.3角4.3.3余角和补角教案新人教版

4.3.3余角和补角三、精讲点拨、释疑解难例1、如图,点A ,O ,B 在同一条直线上,射线OD 和射线OE 分别平分∠AOC 和 ∠BOC ,图中哪些角互为余角?方法总结:本题考查了余角及角平分线的相关知识,利用了余角的性质,角平分线的性质进行计算,解决问题一定要结合图形认真分析,做到数形结合.例2、如图,货轮O 在航行过程中,发现灯塔A 在它南偏东60º的方向上,同时,在它北偏东40º、南偏西10º、西北(即北偏西45º)方向上又分别发现了客轮B,货轮C 和海岛D.仿照表示灯塔方位的方法,画出表示客轮B 、货轮C 和海岛D 方向的射线.分析画法:以点O 为顶点,表示正北方向的射线为角的一边,画40°的角,使它的另一边OB 落在东和北之间.射线OB 的方向就是北偏东40°,即客轮B 所在的方向.四、巩固训练、深化提高1、如果一个角的补角是120°,那么这个角的余角是( )A.150°B.90°C.60°D.30°2、下列关于余角、补角的说法:①一个角的补角一定比这 个角大;②两角互补,则两角中必有一个钝角;③∠α=90°-∠β,则 ∠α=90, ∠β互为余角;④∠α +∠β+∠γ=180°,则 ∠α ,∠β,∠γ互为补角。
其中正确的有___________。
(填上序号即可)3、一个角的补角是它的余角的4倍,求这个角的余角是多少度?分析:本题中存在等量关系,可列方程求解。
可以直接设未知数,也可以间接设未知数,列方程。
4、在海上有两艘军舰A 和B,测得A 在B 的北偏西 60°方向上,则由A 测得B 的方向是( )A.南偏东30°B.南偏东60°C.北偏西30°D.北偏西60°四、总结升华、反思提升本节课你有什么收获?还有什么困惑?【学生对本节课进行知识梳理,巩固教学目标。
七年级上册数学人教版小学《4.3.3 余角和补角》 名师教学-精品导学案

第四章几何图形初步§4.3.3 余角和补角第一课时学案一、课标对本课时的具体要求:理解余角、补角的概念,探索并掌握同角(等角)的余角相等,同角(等角)的补角相等的性质。
二、本课时的知识网络三、本课时的重点、难点【重点】认识角的互余、互补关系及其性质,【难点】通过简单的推理,归纳出余角、补角的性质,并能用规范的语言描述性质是难点。
四、学习目标1.在具体的现实情境中,认识一个角的余角和补角,2.掌握余角和补角的性质。
五、学习过程(一)多媒体出示活动指导,在明确的活动要求和问题引领下引导学生积极参与探讨和自主学习。
(5分钟)(学生根据要求,自读课本,完成学案所给的问题,在明确的引领下引导学生积极参与探讨和学习)(二)展示交流 探究新知(10分钟) 探究活动1:如图,是一个放在直线上的直角三角板,它的两个锐角∠CAB 与∠CBA 之间有什么关系?∠ABC 与∠CBD 有什么关系?答:两个锐角∠CAB 与∠CBA 的和等于 ,∠ABC 与∠CBD 的和等于 .2.互为余角的定义: 就说这两个角互为余角。
如图,若∠1=230,∠2=670,∠1与∠2互为 ;若∠AOB=900,∠3与∠4互为 。
3.互为补角的定义:如果两个角的和是180°(平角),那么这两个角叫做 ,其中一个角是另一个角的 。
如图,若∠5=230,∠6=1570,∠5与∠6互为 ;若∠AOB=1800,∠7与∠8互为 。
练习:填下列表:12 34A OB2143【设计意图】根据学生的情况,我主要采取自主探究、小组交流的方式学习余角和补角的概念,引导学生通过直观计算,总结规律,从而化抽象的概念为简明的关系,帮助学生正确理解并掌握。
(三)探讨释疑,突破难点(10分钟)探究活动3:如图:已知∠AOC ,利用三角板分别画它的余角和补角.(只要满足条件的角都可以) 问:从中发现了什么?结论: 。
结论:。
再问:如果两个角相等,那么它们的余角和补角有什么关系?如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?结论: 。
人教版数学七年级上册4.3.3《余角和补角》教案

(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“余角和补角在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解余角和补角的基本概念。余角是指两个角的和为90度,而补角是指两个角的和为180度。它们在几何学和日常生活中有着广泛的应用。
2.案例分析:接下来,我们来看一个具体的案例。假设我们有一个直角三角形,其中的一个角是30度,那么另一个锐角就是60度,它们互为余角。这个案例展示了余角在实际中的应用,以及它如何帮助我们解决问题。
-应用余角和补角解决实际问题。
二、核心素养目标
1.培养学生的逻辑推理能力,通过余角和补角的性质推导,使学生理解并掌握角度之间的关系;
2.提高学生的空间想象力和几何直观能力,通过绘制图形和实际操作,加深对余角和补角概念的理解;
3.培养学生的数据分析能力,使学生能够运用余角和补角进行角度计算,解决实际问题;
此外,在小组讨论环节,学生们表现出了很高的热情。他们围绕余角和补角在实际生活中的应用,提出了很多有趣的观点。但在引导讨论的过程中,我也发现有些学生的思考不够深入,容易停留在表面。为了提高他们的思考能力,我计划在以后的课堂中,多设置一些开放性和挑战性的问题,激发学生的思维。
实践活动方面,学生们通过分组讨论和实验操作,对余角和补角的性质有了更直观的认识。但在操作过程中,我也观察到有些学生动手能力较弱,对量角器等工具的使用不够熟练。因此,我打算在课后找时间,针对这部分学生进行单独辅导,提高他们的实际操作能力。
人教版七年级数学上册:4.3.3余角和补角(教案)

3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“余角和补角在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
1.提升学生逻辑推理能力,使其能运用余角和补角的性质进行角的转换和计算;
2.培养学生空间想象力和直观感知能力,通过实际问题的情境创设,让学生理解余角和补角在实际生活中的应用;
3.增强学生数学运算能力,使其熟练掌握互余两角和互补两角的计算方法,并能解决相关实际问题;
4.培养学生团队合作意识,通过小组讨论和互动,提高学生在解决问题时的沟通与协作能力;
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考,如“你们还能想到哪些生活中的例子可以用余角和补角来解释?”
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了余角和补角的基本概念、重要性和应用。通过实践活动和小组讨论,我们加深了对余角和补角的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
五、教学反思
在今天的教学过程中,我发现学生们对余角和补角的概念掌握得还算不错。他们在导入环节对日常生活中的角度问题表现出了浓厚的兴趣,这为后续的学习打下了一个良好的基础。但在实际操作和小组讨论中,我也注意到了一些问题。
d.应用:将余角和补角应用于几何图形的构造和计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章几何图形初步
4.3 角
学习目标:
1.
了解余角、补角的概念,掌握余角和补角的性质,并能利用余角、补角
的知识解决相关问题.
2. 了解方位角的概念,并能用方位角知识解决一些简单的实际问题.
重点:了解余角、补角的概念及性质,了解方位角的概念和表达方式.
难点:运用余角、补角和方位角的相关知识解题.
一、知识链接
如图①,在长方形中,∠1+∠2= °,
∠3+∠4= °.
图①
二、新知预习
1. 如果两个角的和等于90°(直角),就说这两个角互为______ (简称为两个角
______ ).
如图①,可以说∠1是∠2的余角,或∠2是∠1的余角,或∠1和∠2互余.
2. 如果两个角的和等于180°(平角),就说这两个角互为______ (简称为两个角
______).
如图①,可以说∠3是∠4的补角,或∠4是∠3的补角,或∠3和∠4互补.
三、自学自测
1. 图中给出的各角,哪些互为余角?
自主学习
教学备注
学生在课前
完成自主学
习部分
配套PPT讲
授
1.情境引入
(见幻灯片
3)
2. 图中给出的各角,哪些互为补角?
四、我的疑惑
_________________________________________________________________________________
_________________________________________________________________________________
一、要点探究
探究点1:有关余角和补角的计算
例1 若一个角的补角等于它的余角的 4 倍,求这个角的度数.
方法总结:余补角问题中,若角之间有比较明显的倍分关系,可尝试将较小的角设为未知数,
列方程解答.
例2如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分
线,若∠MON=40°,试求∠AOC与∠AOB的度数.
课堂探究
教学备注
配套PPT讲授
2.探究点1新
知讲授
(见幻灯片
4-12)
观察与思考:
∠α∠α的余
角
∠α的补
角
5°
32°
45°
77°
62°23′
x°(0<x<
90)
观察可得结论:
锐角的补角比它的余角大_____.
针对训练
1.如果∠a=36°,那么∠a的余角等于()
A.54° B.64° C.144° D.134°
2.如图,将一副直角三角板如图放置,若∠AOD=18°,则∠BOC的度数为_____.
第2题图变式题图
【变式题】一副三角板按如图方式摆放,且∠1的度数比∠2的度数大44°,则
∠1=______.
3.已知∠A与∠B互余,且∠A的度数比∠B度数的3倍还多30°,求∠B的度数.
探究点2:余角和补角的性质
思考:∠1 与∠2,∠3都互为补角,∠2 与∠3 的大小有什么关系?
教学备注
配套PPT讲授
3.探究点2新
知讲授
(见幻灯片
13-17)
例3 如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
(1)∠AOD的余角是_______________,∠COD的余角是_________________;
(2 )OE是∠BOC的平分线吗?请说明理由.
针对训练
如图,已知∠AOB=90°,∠AOC=∠BOD,则与∠AOC互余的角有__________________.
探究点3:方位角
八大方位
正东:
正南:
正西:
正北:
西北方向:
西南方向:
东北方向:
东南方向:
例4如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上. 同时,在它北偏东40
°,南偏西10°,西北 (即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D. 仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.
针对训练教学备注
配套PPT讲授
4.探究点3新知讲授
(见幻灯片18-23)
1. 如图,说出下列方位
(1) 射线 OA 表示的方向为 .
(2) 射线 OB 表示的方向为 .
(3) 射线 OC 表示的方向为 . .
(4) 射线 OD 表示的方向为 .
2.费俊龙、聂海胜乘坐“神舟”六号遨游太空时,我国当时派出远望一号~四号船队,
跟踪检测. 其中远望一、二号停在太平洋洋面上,某一时刻,分别测得神舟六号在北
偏东60°和北偏东30°的方向,你能在下图中画出当时神舟六号所处的位置吗?
二、课堂小结
1.一个角的余角是它的2倍,这个角的度数是()
A.30° B.45° C.60° D.75°
当堂检测
教学备注
配套PPT讲授
5.课堂小结
2.下列说法正确的是()
A.一个角的补角一定大于它本身
B.一个角的余角一定小于它本身
C.一个钝角减去一个锐角的差一定是一个锐角
D.一个角的余角一定小于其补角
3.已知∠A与∠B
互余,∠B与∠C互补,若∠A=60°,则∠C的度数是_______.
4.∠1与∠2 互余,∠1 = (6x + 8)°,∠2 = (4x-8)°,则∠1= ,∠2= .
5. 请认真观察下图,回答下列问题:
(1)图中有哪几对互余的角?
(2) 图中哪几对角是相等的角(直角除外)?为什么?
6 垃圾打捞船A和B都停驻在湖边观测湖面,从A船发现它的北偏东60°方向有白色
漂浮物,同时,从B船也发现该白色漂浮物在它的北偏西30°方向.
(1) 试在图中确定白色漂浮物C的位置;
(2) 点C在点A的北偏东60°的方向上,那么点A在点C的________方向上.
A. 南偏东30°
B. 南偏西30°
C. 南偏东60°
D. 南偏西60°
欢迎您的下载,资料仅供参考!
教学备注
6.当堂检测
(见幻灯片
24-28)。
