2018北京高三有机二模试卷
北京市朝阳区2018年5月高三二模理综(化学)试卷(含答案)

朝阳区2018年高三年级第二学期综合练习化学(二)2018.5.46.我国科技创新成果斐然,下列成果中以制备非金属单质为主要目的的是ABC D低温制备 H 2成功开采可燃冰 (CH 4·n H 2O )研制出 超高强钢合成全氮阴离子盐 (N 5)6(H 3O)3(NH 4)4Cl74A .氯离子的结构示意图:B .其溶液呈酸性的原因:NH 4Cl + H 2O ⇌ NH 3·H 2O +HClC .工业上“氮的固定”:NH 3 + HCl = NH 4ClD .比较微粒半径:N >Cl ->H8.下列变化中,未涉及...到电子转移的是 A .H 2C 2O 4使酸性KMnO 4溶液褪色 B .C 2H 5OH 使酸性K 2Cr 2O 7溶液变绿 C .CO 2使苯酚钠溶液变浑浊 D .H 2O 2使酸化的KI 溶液变黄 9.中国学者在水煤气变换[CO(g) + H 2O(g)CO 2(g) + H 2(g)ΔH ]中突破了低温下高转化率与高反应速率不能兼得的难题,该过程是基于双功能催化剂(能吸附不同粒子)催化实现的。
反应过程示意图如下:过程 I 过程 II 催化剂CH O下列说法正确的是A .过程Ⅰ、过程Ⅲ均为放热过程B .过程Ⅲ生成了具有极性共价键的H 2、CO 2C .使用催化剂降低了水煤气变换反应的ΔHD .图示过程中的H 2O 均参与了反应过程液态甲醇氢气催化剂10.一种长效、缓释阿司匹林(有机物L )的结构如下图所示:CH 2CH OnC O OCOCH 3下列分析不.正确..的是 A .有机物L 为高分子化合物 B .1 mol 有机物L 中含有2 mol 酯基C .有机物L 能发生加成、取代、氧化反应D .有机物L 在体内可缓慢水解,逐渐释放出OH COOH11.实验室模拟工业漂白液(有效成分为NaClO )脱除废水中氨氮(NH 3)的流程如下:提纯粗盐水精制盐水电解Cl 2吸收漂白液①②③④废水(含NH 3)NaCl下列分析正确的是A .①中采用蒸馏的方法精制粗盐水B .②中阳极的主要电极反应:4OH - - 4e - = 2H 2O + O 2↑C .③中制备漂白液的反应:Cl 2 + OH - = Cl - + HClOD .②、③、④中均发生了氧化还原反应 12.某小组比较Cl -、Br -、I - 的还原性,实验如下:实验1实验2实验3装置现象溶液颜色无明显变化;把蘸浓氨水的玻璃棒靠近试管口,产生白烟溶液变黄;把湿KI 淀粉试纸靠近试管口,变蓝 溶液变深紫色;经检验溶液含单质碘下列对实验的分析不合理...的是 A .实验1中,白烟是NH 4Cl B .根据实验1和实验2判断还原性:Br ->Cl - C .根据实验3判断还原性:I ->Br -D .上述实验利用了浓H 2SO 4的强氧化性、难挥发性等性质25.(17分)药物Q 适用于治疗高血压、心绞痛,可由有机物P 和L 制备。
2018年北京市房山区高考数学二模试卷(理科)

2018年北京市房山区高考数学二模试卷(理科)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 设集合A={x|x≤2},B={x|0<x<3},则A∪B=()A.{x|x≤2}B.{x|x<3}C.{x|2<x<3}D.{x|2≤x<3}2. 若复数iz=−1+i,则复数z在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限3. 执行如图的程序框图,输出的S值为()A.65B.64C.63D.334. 已知实数x,y满足{x+y−1≥0x≥0y≥0,则√x2+y2的取值范围是()A.(0, 1)B.(0, 1]C.[1, +∞)D.[√22,+∞)5. 已知函数f(x)的图象关于原点对称,且周期为4,若f(−1)=2,则f(2017)=()A.2B.0C.−2D.−46. 已知某几何体的三视图如图所示,则该几何体的最长棱为()A.4B.2√2C.√7D.27. △ABC 的三个内角分别为A ,B ,C ,则“B =π3”是“A ,B ,C 成等差数列”的( ) A.充分而不必要条件 B.必要而不充分条件 C.充要条件D.既不充分也不必要条件8. 定义:若存在常数k ,使得对定义域D 内的任意两个x 1,x 2(x 1≠x 2),均有|f(x 1)−f(x 2)|≤k|x 1−x 2|成立,则称函数f(x)在定义域D 上满足利普希茨条件.若函数f(x)=√x(x ≥1)满足利普希茨条件,则常数k 的最小值为( )A.4B.3C.1D.12二、填空题共6小题,每小题5分,共30分. 设双曲线x 2a 2−y 2b 2=1(a >0,b >0)的一条渐近线方程为x −2y =0,则该双曲线的离心率为________.若平面向量a →=(4,2),b →=(−2,m),且a →⊥(a →+b →),则实数m 的值为________.在(x +m)5的展开式中,含x 2项的系数为−10,则实数m 的值为________.设点A 是曲线{x =√3+cosθy =1+sinθ (θ是参数)上的点,则点A 到坐标原点的最大距离是________.能够说明“e x >x +1恒成立”是假命题的一个x 的值为________.已知函数f(x)=x|2x −a|−1.①当a =0时,不等式f(x)+1>0的解集为________;②若函数f(x)有三个不同的零点,则实数a 的取值范围是________.三、解答题共6小题,共80分.解答应写出文字说明、演算步骤或证明过程.已知函数f(x)=sinx −acosx 的一个零点是π4. (1)求实数a 的值;(2)设g(x)=f(x)⋅f(−x)+2√3sinxcosx ,若x ∈[0,π2],求g(x)的值域.1995年联合国教科文组织宣布每年的4月23日为世界读书日,主旨宣言为“希望散居在全球各地的人们,都能享受阅读带来的乐趣,都能尊重和感谢为人类文明作出巨大贡献的文学、文化、科学思想的大师们,都能保护知识产权.”为了解大学生课外阅读情况,现从某高校随机抽取100名学生,将他们一年课外阅读量(单位:本)的数据,分成7组[20, 30),[30, 40),…,[80, 90),并整理得到如下频率分布直方图:(Ⅰ)估计其阅读量小于60本的人数;(Ⅱ)已知阅读量在[20, 30),[30, 40),[40, 50)内的学生人数比为2:3:5.为了解学生阅读课外书的情况,现从阅读量在[20, 40)内的学生中随机选取3人进行调查座谈,用X表示所选学生阅读量在[20, 30)内的人数,求X的分布列和数学期望;(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替,试估计100名学生该年课外阅读量的平均数在第几组(只需写出结论).如图1,正六边形ABCDEF的边长为2,O为中心,G为AB的中点.现将四边形DEFC沿CF折起到四边形D1E1FC的位置,使得平面ABCF⊥平面D1E1FC,如图2.(Ⅰ)证明:D1F⊥平面E1OG;(Ⅱ)求二面角E1−OG−F的大小;(Ⅲ)在线段CD1上是否存在点H,使得BH // 平面E1OG?如果存在,求出D1HD1C的值;如果不存在,请说明理由.设函数f(x)=x(k−ln x),(k为常数),g(x)=1x −1xf(x).曲线y=f(x)在点(1,f(1))处的切线与x轴平行.(1)求k的值;(2)求g(x)的单调区间和最小值;(3)若g(x)−g(x)<1a对任意x>0恒成立,求实数a的取值范围.椭圆C:x2a2+y2b2=1(a>b>0)的离心率为12,O为坐标原点,F是椭圆C的右焦点,A为椭圆C上一点,且AF⊥x轴,△AFO的面积为34.(Ⅰ)求椭圆C的方程;(Ⅱ)过C上一点P(x0, y0)(y0≠0)的直线l:x0xa2+y0yb2=1与直线AF相交于点M,与直线x=4相交于点N.证明:当点P在C上移动时,|MF||NF|恒为定值,并求此定值.已知集合A=a1,a2,a3,…,a n,其中a i∈R(1≤i≤n, n>2),l(A)表示和a i+ a j(1≤i<j≤n)中所有不同值的个数.(Ⅰ)设集合P=2,4,6,8,Q=2,4,8,16,分别求l(P)和l(Q);(Ⅱ)若集合A=2,4,8,…,2n,求证:l(A)=n(n−1)2;(Ⅲ)l(A)是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由?参考答案与试题解析2018年北京市房山区高考数学二模试卷(理科)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.【答案】B【考点】并集及其运算【解析】根据并集的定义写出A∪B.【解答】集合A={x|x≤2},B={x|0<x<3},则A∪B={x|x<3}.2.【答案】A【考点】复数的运算【解析】把已知等式变形,利用复数代数形式的乘除运算化简,求出z的坐标得答案.【解答】由iz=−1+i,得z=−1+ii =(−1+i)(−i)−i2=1+i,∴复数z在复平面内对应的点的坐标为(1, 1),位于第一象限.3.【答案】C【考点】程序框图【解析】由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,可得答案.【解答】第一次执行循环体后,S=3,不满足退出循环的条件,n=2;第二次执行循环体后,S=7,不满足退出循环的条件,n=3;第三次执行循环体后,S=15,不满足退出循环的条件,n=4;第四次执行循环体后,S=31,不满足退出循环的条件,n=5;第五次执行循环体后,S=63,满足退出循环的条件,故输出的S=63,4.【答案】D【考点】简单线性规划【解析】先画出可行域,利用目标函数几何意义转化求解即可.【解答】实数x,y满足{x+y−1≥0 x≥0y≥0表示的可行域如图:√x2+y2的几何意义是可行域内的点与坐标原点的距离,可知P到原点的距离最小,即√2=√22.则√x2+y2的取值范围是:[√22, +∞).5.【答案】C【考点】函数奇偶性的性质【解析】由题意可得f(−x)=−f(x),f(x+4)=f(x),则f(2017)=f(1)=−f(−1),计算可得所求值.【解答】函数f(x)的图象关于原点对称,且周期为4,可得f(−x)=−f(x),f(x+4)=f(x),则f(2017)=f(504×4+1)=f(1)=−f(−1)=−2,故选:C.6.【答案】B【考点】由三视图还原实物图【解析】几何体为四棱锥,作出直观图,计算棱长即可得出答案.【解答】解:由三视图可知几何体为四棱锥S−ABCD,由侧视图可知棱锥底面ABCD是边长为2的正方形,顶点S在底面ABCD上的射影M为CD的中点,由主视图可知SM=√3,∴AM=√5,SA=√AM2+SM2=2√2.由对称性可知SB=SA=2√2.∴几何体最长的棱为2√2.故选B.7.【答案】C【考点】必要条件、充分条件与充要条件的判断【解析】A,B,C成等差数列⇔2B=A+C,A+B+C=π⇔B=π3,即可判断出结论.【解答】A,B,C成等差数列⇔2B=A+C,A+B+C=π⇔B=π3,∴ “B=π3”是“A,B,C成等差数列”的充要条件.8.【答案】D【考点】函数恒成立问题【解析】首先根据函数f(x)=√x(x≥1)满足利普希茨条件,得到k满足不等式k≥√x1−√x2x1−x2|=√x+√x ;然后由x1,x2∈[1, +∞)√x+√x的取值范围,而k√x+√x的最大值即可.【解答】由已知中中利普希茨条件的定义若函数f(x)=√x(x≥1)满足利普希茨条件,所以存在常数k,使得对定义域[1, +∞)内的任意两个x1,x2(x1≠x2),均有|f(x1)−f(x2)|≤k|x1−x2|成立,不妨设x1>x2,则k≥√x1−√x2x1−x2=√x+√x.而0<√x+√x <12,所以k的最小值为12.二、填空题共6小题,每小题5分,共30分.【答案】√52【考点】双曲线的离心率 【解析】根据题意,由双曲线的渐进性方程分析可得b a =12,即a =2b ,进而由双曲线的几何性质可得c =√a 2+b 2=√5b ,由双曲线的离心率公式计算可得答案. 【解答】 根据题意,双曲线x 2a2−y 2b 2=1(a >0,b >0)的渐进性方程为y =±ba x ,又由该双曲线的一条渐近线方程为x −2y =0,即y =12x , 则有ba =12,即a =2b , 则c =√a 2+b 2=√5b ,则该双曲线的离心率e =ca =√5b2b =√52;【答案】−6【考点】平面向量的坐标运算 【解析】可求出a →+b →=(2,m +2),根据a →⊥(a →+b →)便可得出a →⋅(a →+b →)=0,进行数量积的坐标运算即可求出m 的值. 【解答】a →+b →=(2,m +2);∵ a →⊥(a →+b →);∴ a →⋅(a →+b →)=(4,2)⋅(2,m +2)=8+2(m +2)=0;∴ m =−6. 【答案】 −1【考点】二项式定理的应用 【解析】 此题暂无解析 【解答】解:由二项展开式的通项可知,含x 2的项为C 53x 2m 3,则C 53m 3=−10, 解得m =−1. 故答案为:−1. 【答案】 3【考点】参数方程与普通方程的互化【解析】设A(√3+cosθ, 1+sinθ),原点O(0, 0),|AO|=√(√3+cosθ)2+(1+sinθ)2=√5+4sin(θ+π3),由此能求出点A到坐标原点取最大距离.【解答】∵点A是曲线{x=√3+cosθy=1+sinθ(θ是参数)上的点,∴设A(√3+cosθ, 1+sinθ),原点O(0, 0),|AO|=√(√3+cosθ)2+(1+sinθ)2=√3+2√3cosθ+cos2θ+1+2sinθ+sin2θ=√5+4sin(θ+π3),∴当sin(θ+π3)=1时,点A到坐标原点取最大距离(3)【答案】【考点】命题的真假判断与应用【解析】利用反例判断命题的真假即可.【解答】当x=0时,e x>x+1,不成立,【答案】(0, +∞),(2√2, +∞)【考点】函数零点的判定定理【解析】①把a=0代入函数解析式,可得不等式,对x分类求解得答案;②转化方程的根为两个函数的图象的交点,利用数形结合,通过函数的导数求解即可.【解答】①当a=0时,不等式f(x)+1>0⇔x|2x|−1+1>0,即2x|x|>0,若x<0,得−2x2>0,不合题意;若x=0,得0>0,不合题意;若x>0,得2x2>0,则x>(0)综上,当a=0时,不等式f(x)+1>0的解集为(0, +∞);②若函数f(x)有三个不同的零点,即方程x|2x−a|−1=0有3个不同根.即|2x−a|=1x有三个解,令y=|2x−a|,则y=1x {2x−a,x≥a2a−2x,x<a2,画出两个函数的图象,如图:x<a2,y=1x,由y′=−1x2=−2,解得x=√22,x=−√22(舍去),此时切点坐标(√22,√2),代入y=a−2x,可得a=2×√22+√2=2√2,函数f(x)=x|2x−a|−1有三个零点,则实数a的取值范围为(2√2, +∞).三、解答题共6小题,共80分.解答应写出文字说明、演算步骤或证明过程.【答案】(1)依题意,得f(π4)=0,即sinπ4−acosπ4=√22−√2a2=0,解得a=1.(2)由(1)得f(x)=sinx−cosx.g(x)=f(x)⋅f(−x)+2√3sinxcosx=(sinx−cosx)(−sinx−cosx)+√3sin2x =(cos2x−sin2x)+√3sin2x=cos2x+√3sin2x=2sin(2x+π6).由x∈[0,π2]得π6≤2x+π6≤7π6∴当2x+π6=π2即x=π6时,g(x)取得最大值2,当2x+π6=7π6即x=π2时,g(x)取得最小值−1.所以g(x)的值域是[−1, 2].【考点】三角函数的恒等变换及化简求值函数零点的判定定理【解析】(1)根据f(π4)=0计算a的值;(2)化简f(x)的解析式,再根据这些函数的单调性得出g(x)的最值即可.【解答】(1)依题意,得f(π4)=0,即sinπ4−acosπ4=√22−√2a2=0,解得a=1.(2)由(1)得f(x)=sinx−cosx.g(x)=f(x)⋅f(−x)+2√3sinxcosx=(sinx−cosx)(−sinx−cosx)+√3sin2x =(cos2x−sin2x)+√3sin2x=cos2x+√3sin2x=2sin(2x+π6).由x∈[0,π2]得π6≤2x+π6≤7π6∴当2x+π6=π2即x=π6时,g(x)取得最大值2,当2x+π6=7π6即x=π2时,g(x)取得最小值−1.所以g(x)的值域是[−1, 2].【答案】(Ⅰ)100−100×10×(0.04+0.02×2)=20(人)(Ⅱ)由已知条件可知:[20, 50)内人数为:100−100×10×(0.04+0.02+0.02+ 0.01)=10;[20, 30)人数为2人,[30, 40)人数为3人,[40, 50)人数为5人.X的可能取值为0,1,(2)P(X=0)=C33C20C53=110P(X=1)=C32C21C53=35P(X=2)=C31C22C53=310,所以X的分布列为EX=0×110+1×35+2×310=65.(Ⅲ)第五组.【考点】离散型随机变量的期望与方差【解析】(Ⅰ)利用100−100×10×(0.04+0.02×2)即可得出.(Ⅱ)由已知条件可知:[20, 50)内人数为:100−100×10×(0.04+0.02+0.02+ 0.01)=10;同理可得:[20, 30)人数为2人,[30, 40)人数为3人,[40, 50)人数为5人.X的可能取值为0,1,(2)利用超几何分布列及其数学期望计算公式可得.(Ⅲ)利用平均数的计算公式为:小矩形的面积乘以矩形底边中点的横坐标之和即可得出结论.【解答】(Ⅰ)100−100×10×(0.04+0.02×2)=20(人)(Ⅱ)由已知条件可知:[20, 50)内人数为:100−100×10×(0.04+0.02+0.02+ 0.01)=10;[20, 30)人数为2人,[30, 40)人数为3人,[40, 50)人数为5人.X的可能取值为0,1,(2)P(X=0)=C33C20C53=110P(X=1)=C32C21C53=35P(X=2)=C31C22C53=310,所以X的分布列为EX=0×110+1×35+2×310=65.(Ⅲ)第五组. 【答案】证明:(Ⅰ)图(1)中OG ⊥CF ,∴ 图(2)中,OG ⊥CF , 又面CD 1E 1F ⊥面ABCF ,面CD 1E 1F ∩面ABCF =CF ,∴ OG ⊥面CD 1E 1F ,∵ D 1F ⊂面CD 1E 1F ,∴ OG ⊥D 1F , 又O 为CF 的中点,∴ OF // =D 1E 1,又E 1D 1=E 1F , ∴ 四边形E 1D 1OF 为菱形,∴ D 1F ⊥OE 1 ∵ OG ∩OE 1=O ,∴ D 1F ⊥面E 1OG ………(2)取OF 的中点M ,连接E 1M ,MA ,以点M 为坐标原点, 建立空间直角坐标系M −xyz 如图所示. E 1(0,0,√3),O(0,1,0),G(√3,1,0),F(0,−1,0), ∴ OG →=(√3,0,0),OE 1→=(0,−1,√3), 设面OE 1G 的法向量为n →,∴ {n →⋅OG →=0n →⋅OE 1→=0⇒⇒{√3x =0−y +√3z =0⇒⇒{x =0y =√3z ,令z =1,则y =√3,∴ n →=(0,√3,1),设面FOG 的法向量为m →,则m →=(0,0,1), ∴ cos <m →,n →>=m →⋅n→|m →||n →|=12,∴ 二面角E 1−OG −F 的大小为π3.……… (Ⅲ)假设存在,设H(x, y, z),D 1HD1C=λ,λ∈[0,1],∴ D 1H →=λD 1C →D 1(0,2,√3),C(0,3,0),B(√3,2,0), ∴ D 1H →=(x,y −√2,z −√3),D 1C →=(0,1,−√3),∴ {x =0y −2=λz −√3=−λ√3∴ ∴ {x =0y =2+λz =√3−λ√3∴ ∴ H(0,2+λ,√3−λ√3)∴ BH →=(−√3,λ,√3−λ√3),∵ BH →⋅n →=0∴ √3λ+√3−√3λ=0∴ √3=0矛盾,∴ 在线段CD 1上不存在点H ,使得BH // 平面E 1OG .………【考点】二面角的平面角及求法【解析】(Ⅰ)推导出OG ⊥CF 则OG ⊥面CD 1E 1F ,从而OG ⊥D 1F ,再求出D 1F ⊥OE 1,由此能证明D 1F ⊥面E 1OG .(Ⅱ)取OF 的中点M ,连接E 1M ,MA ,以点M 为坐标原点,建立空间直角坐标系M −xyz ,利用向量法能求出二面角E 1−OG −F 的大小. (Ⅲ)假设存在,设H(x, y, z),D 1HD1C=λ,λ∈[0,1],利用向量法能求出在线段CD 1上不存在点H ,使得BH // 平面E 1OG . 【解答】证明:(Ⅰ)图(1)中OG ⊥CF ,∴ 图(2)中,OG ⊥CF , 又面CD 1E 1F ⊥面ABCF ,面CD 1E 1F ∩面ABCF =CF ,∴ OG ⊥面CD 1E 1F ,∵ D 1F ⊂面CD 1E 1F ,∴ OG ⊥D 1F , 又O 为CF 的中点,∴ OF // =D 1E 1,又E 1D 1=E 1F , ∴ 四边形E 1D 1OF 为菱形,∴ D 1F ⊥OE 1 ∵ OG ∩OE 1=O ,∴ D 1F ⊥面E 1OG ………(2)取OF 的中点M ,连接E 1M ,MA ,以点M 为坐标原点, 建立空间直角坐标系M −xyz 如图所示. E 1(0,0,√3),O(0,1,0),G(√3,1,0),F(0,−1,0), ∴ OG →=(√3,0,0),OE 1→=(0,−1,√3), 设面OE 1G 的法向量为n →,∴ {n →⋅OG →=0n →⋅OE 1→=0⇒⇒{√3x =0−y +√3z =0⇒⇒{x =0y =√3z ,令z =1,则y =√3,∴ n →=(0,√3,1),设面FOG 的法向量为m →,则m →=(0,0,1), ∴ cos <m →,n →>=m →⋅n→|m →||n →|=12,∴ 二面角E 1−OG −F 的大小为π3.……… (Ⅲ)假设存在,设H(x, y, z),D 1HD1C=λ,λ∈[0,1],∴ D 1H →=λD 1C →D 1(0,2,√3),C(0,3,0),B(√3,2,0), ∴ D 1H →=(x,y −√2,z −√3),D 1C →=(0,1,−√3),∴ {x =0y −2=λz −√3=−λ√3∴ ∴ {x =0y =2+λz =√3−λ√3∴ ∴ H(0,2+λ,√3−λ√3)∴ BH →=(−√3,λ,√3−λ√3),∵ BH →⋅n →=0∴ √3λ+√3−√3λ=0∴ √3=0矛盾,∴ 在线段CD 1上不存在点H ,使得BH // 平面E 1OG .………【答案】解:(1)因为f(x)=x(k−ln x),所以f′(x)=k−ln x−1,因为曲线y=f(x)在点(1,f(1))处的切线与x轴平行,所以f′(1)=0,所以k=1.(2)因为g(x)=1x −1xf(x)=1x−1+ln x,定义域为{x|x>0},所以g′(x)=−1x2+1 x =x−1x2,令g′(x)=0得x=1,当x变化时,g′(x)和g(x)的变化如下表x(0,1)1(1,+∞)g′(x)−0+g(x)↘0↗由上表可知,g(x)的单调递减区间为(0,1),单调递增区间为(1,+∞),最小值为g(1)= 0.(3)若g(a)−g(x)<1a 对任意x>0恒成立,则g(a)−g(x)min<1a,即lna<1,解得0<a<e.则实数a的取值范围为(0,e).【考点】利用导数研究曲线上某点切线方程【解析】【解答】解:(1)因为f(x)=x(k−ln x),所以f′(x)=k−ln x−1,因为曲线y=f(x)在点(1,f(1))处的切线与x轴平行,所以f′(1)=0,所以k=1.(2)因为g(x)=1x −1xf(x)=1x−1+ln x,定义域为{x|x>0},所以g′(x)=−1x2+1 x =x−1x2,令g′(x)=0得x=1,当x变化时,g′(x)和g(x)的变化如下表x(0,1)1(1,+∞)g′(x)−0+g(x)↘0↗由上表可知,g(x)的单调递减区间为(0,1),单调递增区间为(1,+∞),最小值为g(1)= 0.(3)若g(a)−g(x)<1a 对任意x >0恒成立,则g(a)−g(x)min <1a ,即lna <1,解得0<a <e .则实数a 的取值范围为(0,e). 【答案】(1)设F(c, 0),A(c, d),则c 2a 2+d 2b 2=1 又ca =12,∴ |d|=√32b ,∵ △AFO 的面积为34,∴ 12c|d|=12c ⋅√32b =34,bc =√3.由{a 2−b 2=c 2a =2cbc =√3 ,得{a =2b =√3c =1 ∴ C 的方程为x 24+y 23=1.(2)由(1)知直线l 的方程为x 0x 4+y 0y 3=1(y 0≠0),即y =12−3x 0x 4y 0(y 0≠0).∵ 直线AF 的方程为x =1,∴ 直线l 与AF 的交点为M(1,12−3x 04y 0),直线l 与直线x =4的交点为N(4, 3−3x 0), 则|MF|2|NF|2=(12−3x 04y 0)29+(3−3x 0y 0)2=(4−x 0)216y 02+16(1−x 0)2,又P(x 0, y 0)是C 上一点,则x 024+y 023=1.y 02=3−3x 024代入上式得:|MF|2|NF|2=(4−x 0)248−12x 02+16−32x0+16x 02=(4−x 0)24(x 02−8x 0+16)=14⋅(4−x 0)2(4−x 0)2=14,∴ |MF||NF|=12,为定值. 【考点】椭圆的离心率 【解析】(Ⅰ)设F(c, 0),A(c, d),代入可得c 2a 2+d 2b2=1.又c a =12,|d|=√32b ,根据△AFO 的面积为34,可得12c|d|=12c ⋅√32b =34,bc =√3.由{a 2−b 2=c 2a =2cbc =√3 ,解出即可得出. (Ⅱ)由(1)知直线l 的方程为x 0x 4+y 0y 3=1(y 0≠0),即y =12−3x 0x 4y 0(y 0≠0).由直线AF 的方程为x =1,可得直线l 与AF 的交点为M(1,12−3x 04y 0),直线l 与直线x =4的交点为N(4, 3−3x 0),可得:|MF|2|NF|2=(12−3x 04y 0)29+(3−3x 0y 0)2=(4−x 0)216y 02+16(1−x0)2,又P(x 0, y 0)是C 上一点,则x 024+y 023=1.y 02=3−3x 024,代入化简即可得出.【解答】(1)设F(c, 0),A(c, d),则c 2a 2+d 2b 2=1又ca =12,∴ |d|=√32b ,∵ △AFO 的面积为34,∴ 12c|d|=12c ⋅√32b =34,bc =√3.由{a 2−b 2=c 2a =2cbc =√3 ,得{a =2b =√3c =1 ∴ C 的方程为x 24+y 23=1.(2)由(1)知直线l 的方程为x 0x 4+y 0y 3=1(y 0≠0),即y =12−3x 0x 4y 0(y 0≠0).∵ 直线AF 的方程为x =1,∴ 直线l 与AF 的交点为M(1,12−3x 04y 0),直线l 与直线x =4的交点为N(4, 3−3x 0), 则|MF|2|NF|2=(12−3x 04y 0)29+(3−3x 0y 0)2=(4−x 0)216y 02+16(1−x0)2,又P(x 0, y 0)是C 上一点,则x 024+y 023=1.y 02=3−3x 024代入上式得:|MF|2|NF|=(4−x 0)248−12x 02+16−32x0+16x 02=(4−x 0)24(x 02−8x+16)=14⋅(4−x 0)2(4−x)=14,∴ |MF||NF|=12,为定值.【答案】(Ⅰ)根据题中的定义可知:由2+4=6,2+6=8,2+8=10,4+6=10,4+8=12,6+8=14,得l(P)=(5)由2+4=6,2+8=10,2+16=18,4+8=12,4+16=20,8+16=24,得l(Q)=(6)(Ⅱ)证明:因为a i +a j (1≤i <j ≤n)最多有C n 2=n(n−1)2个值,所以l(A)≤n(n−1)2.又集合A =2,4,8,,2n ,任取a i +a j ,a k +a l (1≤i <j ≤n, 1≤k <l ≤n), 当j ≠l 时,不妨设j <l ,则a i +a j <2a j =2j+1≤a l <a k +a l , 即a i +a j ≠a k +a l .当j =l ,i ≠k 时,a i +a j ≠a k +a l . 因此,当且仅当i =k ,j =l 时,a i +a j =a k +a l . 即所有a i +a j (1≤i <j ≤n)的值两两不同, 所以l(A)=n(n−1)2.(Ⅲ)l(A)存在最小值,且最小值为2n −(3)不妨设a 1<a 2<a 3<...<a n ,可得a 1+a 2<a 1+a 3<...<a 1+a n <a 2+a n <...<a n−1+a n ,所以a i +a j (1≤i <j ≤n)中至少有2n −3个不同的数,即l(A)≥2n −(3) 事实上,设a 1,a 2,a 3,,a n 成等差数列,考虑a i +a j (1≤i <j ≤n),根据等差数列的性质, 当i +j ≤n 时,a i +a j =a 1+a i+j−1; 当i +j >n 时,a i +a j =a i+j−n +a n ;因此每个和a i +a j (1≤i <j ≤n)等于a 1+a k (2≤k ≤n)中的一个, 或者等于a l +a n (2≤l ≤n −1)中的一个.所以对这样的A ,l(A)=2n −3,所以l(A)的最小值为2n −(3)【考点】 数列的应用计数原理的应用 【解析】(Ⅰ)直接利用定义把集合P =2,4,6,8,Q =2,4,8,16中的值代入即可求出l(P)和l(Q);(Ⅱ)先由a i +a j (1≤i <j ≤n)最多有C n 2=n(n−1)2个值,可得l(A)≤n(n−1)2;再利用定义推得所有a i +a j (1≤i <j ≤n)的值两两不同,即可证明结论.(Ⅲ)l(A)存在最小值,设a 1<a 2<<a n ,所以a 1+a 2<a 1+a 3<...<a 1+a n <a 2+a n <...<a n−1+a n .由此即可证明l(A)的最小值2n −(3) 【解答】(Ⅰ)根据题中的定义可知:由2+4=6,2+6=8,2+8=10,4+6=10,4+8=12,6+8=14,得l(P)=(5)由2+4=6,2+8=10,2+16=18,4+8=12,4+16=20,8+16=24,得l(Q)=(6)(Ⅱ)证明:因为a i +a j (1≤i <j ≤n)最多有C n 2=n(n−1)2个值,所以l(A)≤n(n−1)2.又集合A =2,4,8,,2n ,任取a i +a j ,a k +a l (1≤i <j ≤n, 1≤k <l ≤n), 当j ≠l 时,不妨设j <l ,则a i +a j <2a j =2j+1≤a l <a k +a l , 即a i +a j ≠a k +a l .当j =l ,i ≠k 时,a i +a j ≠a k +a l . 因此,当且仅当i =k ,j =l 时,a i +a j =a k +a l . 即所有a i +a j (1≤i <j ≤n)的值两两不同, 所以l(A)=n(n−1)2.(Ⅲ)l(A)存在最小值,且最小值为2n −(3)不妨设a 1<a 2<a 3<...<a n ,可得a 1+a 2<a 1+a 3<...<a 1+a n <a 2+a n <...<a n−1+a n ,所以a i +a j (1≤i <j ≤n)中至少有2n −3个不同的数,即l(A)≥2n −(3) 事实上,设a 1,a 2,a 3,,a n 成等差数列,考虑a i +a j (1≤i <j ≤n),根据等差数列的性质, 当i +j ≤n 时,a i +a j =a 1+a i+j−1; 当i +j >n 时,a i +a j =a i+j−n +a n ;因此每个和a i +a j (1≤i <j ≤n)等于a 1+a k (2≤k ≤n)中的一个, 或者等于a l +a n (2≤l ≤n −1)中的一个.所以对这样的A ,l(A)=2n −3,所以l(A)的最小值为2n −(3)。
【全国市级联考】北京市朝阳区2018届高三第二次综合练习(二模)理综化学试题(解析版)

北京市朝阳区2018年高三第二次综合练习(二模)理综化学试题1. 我国科技创新成果斐然,下列成果中以制备非金属单质为主要目的的是A. AB. BC. CD. D【答案】A【解析】A. 氢气是非金属单质,故A正确;B. 可燃冰(CH4·n H2O)不是非金属单质,故B错误;C. 高强钢属于金属的合金,不是非金属单质,故C错误;D. 全氮阴离子盐(N5)6(H3O)3(NH4)4Cl不是非金属单质,故D错误;故选A。
2. 下列关于NH4Cl的化学用语正确的是A. 氯离子的结构示意图:B. 其溶液呈酸性的原因:NH4Cl+H2O NH3·H2O+HClC. 工业上“氮的固定”:NH3 + HCl= NH4ClD. 比较微粒半径:N>Cl->H【答案】B【解析】A.Cl-的核电荷数为17,核外电子数为18,其结构示意图为,故A错误;B、NH4Cl溶液呈酸性的原因:NH4++H2O⇌NH3•H2O+H+,导致溶液中氢离子浓度大于氢氧根离子的浓度,溶液呈酸性,故B正确;C. NH3 + HCl = NH4Cl氮的化合物转化为氮的化合物,不属于“氮的固定”,故C错误;D. 氯离子有3个电子层,半径大于N原子的半径,故D错误;故选B。
3. 下列变化中,未涉及到电子转移的是A. H2C2O4使酸性KMnO4溶液褪色B. C2H5OH 使酸性K2Cr2O7溶液变绿C. CO2 使苯酚钠溶液变浑浊D. H2O2使酸化的KI 溶液变黄【答案】C点睛:本题考查了氧化还原反应的判断,氧化还原反应的本质是存在电子的转移,解答此类试题,要注意根据是否存在元素化合价的变化为依据进行判断。
4. 中国学者在水煤气变换[CO(g) +H2O(g)CO2(g) +H2(g) △H ]中突破了低温下高转化率与高反应速率不能兼得的难题,该过程是基于双功能催化剂( 能吸附不同粒子) 催化实现的。
反应过程示意图如下:下列说法正确的是A. 过程I、过程III均为放热过程B. 过程III生成了具有极性共价键的H2、CO2C. 使用催化剂降低了水煤气变换反应的△HD. 图示过程中的H2O均参与了反应过程【答案】D【解析】A. 根据反应过程示意图,过程Ⅰ中水分子中的化学键断裂的过程,为吸热过程,故A错误;B. 过程Ⅲ中CO、氢氧原子团和氢原子形成了二氧化碳、水、和氢气,H2中的化学键为非极性键,故B错误;C.催化剂不能改变反应的ΔH,故C错误;D. 根据反应过程示意图,过程Ⅰ中水分子中的化学键断裂,过程Ⅱ也是水分子中的化学键断裂的过程,过程Ⅲ中形成了水分子,因此H2O均参与了反应过程,故D正确;故选D。
北京市海淀区2018年高三二模化学试题

2018年海淀区高三二模理综化学部分1常温下某H2CO3溶液的pH约为5.5,c(CO32-)约为5×10-11mol/L,该溶液中浓度最低的离子是____。
(A)HCO3-(B)CO32-(C)H+(D)OH-2.下列变化过程不必利用催化剂的是____。
(A)NH3+O2→1.烧碱的古老制法可表示为Na2CO3+Ca(OH)2→CaCO3↓+2NaOH,那时还没有合成氨工业。
NO (B)CH4→CH3Cl (C)C6H6+H2→C6H12(D)C6H12O6→C2H5OH3.氢元素有三种同位素,各有各的丰度。
其中11H的丰度指的是____。
(A)自然界11H原子个数所占氢元素的百分数(B)自然界11H原子质量所占氢元素的百分数(C)11H在海水中所占氢元素的百分数(D)11H在单质氢中所占氢元素的百分数4.丙酸和甲酸乙酯是一对同分异构体,对这两种液体进行鉴别有多种方法。
下列方法中操作最不简便的一种是____。
(A)使用蒸馏水(B)使用NaHCO3溶液(C)使用新制Cu(OH)2(D)使用pH试纸5.下列变化过程中未必吸热的是____。
(A)电解质在熔融状态下电离(B)共价键断裂(C)原子失电子(D)溶解6.下列对应关系正确的是7.下列说法不正确...的是A.利用植物油的加成反应可以制得人造黄油B.75%的酒精可使蛋白质变性从而起到消毒作用C.纤维素在人体内可水解成葡萄糖,供人体组织的营养需要D .可用OH 3和HCHO 为原料合成]n OHCH 3CH 2H OH[8.下列有关NH 3的实验正确的是9.下列化学用语不能..正确解释相关事实的是 A .碱性氢氧燃料电池的正极反应:H 2 - 2e - + 2OH -=== 2H 2O B .用电子式表示NaCl 的形成过程:C .向含有Hg 2+的废水中加入Na 2S 可除去Hg 2+:Hg 2+ + S 2- === HgS ↓D .汽车尾气系统的催化转化器可降低NO 等的排放:2CO + 2NO === 2CO 2 +N 210.下列事实不能..用平衡移动原理解释的是 A. 钢铁在潮湿的空气中比在干燥空气中更容易生锈 B. 用加热蒸干AlCl 3溶液的方法不能制得无水AlCl 3C. 蒸馏水和0.1 mol •L -1 NaOH 溶液中的c (H +),前者大于后者D. 向含有少量Fe 3+的MgCl 2酸性溶液中加入MgCO 3,可将Fe 3+转化成Fe(OH)3除去11.下列事实不能说明元素的金属性或非金属性相对强弱的是 NH 3水Ca(OH)2和 NH 4Cl 固体催化剂12. 一定条件下,反应:6H 2 + 2CO 2C 2H 5OH + 3H 2O 的数据如下图所示。
2018北京东城高三二模语文试题及答案

2018北京东城高三二模语文试题及答案北京市东城区2017—2018学年度第二学期高三综合练习(二)语文 2018.5 本试卷共10页,150分。
考试时长150分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
一、本大题共8小题,共24分。
阅读下面的文字,回答1—8题。
材料一墨作为书写工具,同时也是重要的文化传承载体,已有几千年的历史。
殷商时代的甲骨文就以石墨、朱砂填色。
汉代纸料发明后,出现了一种以漆烟和松煤制成的丸状墨,这是日后用墨的滥觞.。
唐代是文化交流最广泛的朝代之一。
唐末奚超避乱至歙州,见此地多松且质优,新安江水质极佳,因此留在此地制墨。
因墨的主产区为歙州,故得名“歙墨”。
其后奚超之子改进捣烟、和胶的方法,制成了“拈来轻、嗅来馨、磨来清”“丰肌腻理、光泽如漆”的佳墨。
制墨工艺的改进,让书写更加流利,也加快了文化的传播速度。
宋室南渡后,宋墨的制作技艺臻.于成熟。
制墨业的繁荣表现在三个方面:第一,油烟墨的创立,开辟了中国制墨业的新领域。
千百年来,制墨主要以松烟为原料,由于长年累月取松烧烟,致使松树被砍伐殆.尽,新的制墨原料——桐油烟便应.运而生。
第二,制墨从业人员众多,名家辈出。
宋代制墨名家见诸史册的多达百余人,他们在选料、配方、烧制、用胶、捣杵等工艺方面,都有独到之处。
第三,达官贵人及文人墨客与制墨工匠切磋技艺,促进了制墨技艺的发展。
创造“瘦金体”书法的宋徽宗喜欢墨又懂制墨,他亲自实践,推动了制墨业的发展。
苏轼、陆游、黄庭坚等文人都有过参与制墨的经历。
宣和三年A.徽墨的发展经历了石墨、汉代丸状墨、唐代歙墨三个阶段B.唐墨以桐油烟为主要原料,墨色黑润,坚而有光,馨香浓郁C.清代徽墨墨雕题材丰富,一块徽墨的装饰图案汇集多种文化元素D.具有厚重历史文化的徽墨坚持创新,不断充实中国文化的内涵3.根据材料一,下列不属于...明代徽墨蓬勃发展原因的一项是(3分)A.新原料的应用B.新工艺的使用C.雕刻技术的进步D.文化人士的呼吁材料二作为传统工艺制品,徽墨因其装饰图案文化内容丰富,兼具实用与欣赏功能。
2018北京西城区高三数学(文)(二模)

( A)充分而不必要条件
(B)必要而不充分条件
( C)充分必要条件
(D)既不充分也不必要条件
7.设不等式组
x ≥ 1, x y ≥ 3, 表示的平面区域为 D .若直线 ax y 0 上存在区域 D 上的点, 2x y ≤ 5
则实数 a 的取值范围是
( A) [ 1 ,2] 2
(B) [ 1 ,3] 2
2018 北京西城区高三数
学(文)(二模)
第Ⅰ卷 (选择题 共 40 分)
2018.5
一、 选择题:本大题共 8 小题,每小题 5 分,共 40 分.在每小题列出的 四个选项中,选
出符合题目要求的一项.
1.若集合 A { x | 0 x 1} , B { x | x 2 2x 0} ,则下列结论中正确的是
中点. CD DA AF FE 2 , AB 4 . (Ⅰ)求证: DF // 平面 BCE ;
(Ⅱ)求证:平面 BCF 平面 GCE ; (Ⅲ)求多面体 AFEBCD 的体积.
19.(本小题满分 13 分)
3/9
已知函数 f ( x) ln x ax ,曲线 y f ( x) 在 x 1 处的切线经过点 (2, 1) . x
2/9
已知函数 f ( x)
cos2 x .
sin x cos x
(Ⅰ)求 f (x) 的定义域;
(Ⅱ)求 f (x) 的取值范围.
17.(本小题满分 13 分)
在某地区,某项职业的从业者共约 8.5 万人,其中约 3.4 万人患有某种职业病.为了解这种职业病与某项身体
指标(检测值为不超过 6 的正整数)间的关系,依据是否患有职业病,使用分层抽样的方法随机抽取了
1/9
( C) [1,2]
北京市各区2018届高三二模英语试卷-作文(含答案)

北京市海淀区2018届高三二模英语试卷作文第一节(15分)你班英语课上以“I Have A Dream”为题进行“说”的练习,请你写一份讲稿,内容包括:1.你的梦想是什么;2.你为何有此梦想;3.你如何实现梦想。
注意:1.词数不少于50;2.开头和结尾已给出,不计入总词数。
Hello, everybody! ___________________________________________________________________________________________________________________________________________________________ Thank you.第二节(20分)假设你是红星中学高三学生李华,请根据以下四幅图的先后顺序,用英语写一篇日记。
记述上周末你和你的英国朋友Jim用微信支付购物的过程。
注意:词数不少于60。
提示词:二维码QR code; 糖葫芦candy-coated haws(tanghulu)北京市海淀区2018届高三二模英语试卷参考作文第一节(15 分)One Possible VersionHello, everybody! I’m very glad to share my dream with you.I have a dream that one day I could be a pianist. I dream of playing a sweet tune for those who need music, bringing happiness to sorrowful souls and enthusiasm to weary spirits.I love music, and I love the feeling of playing music in front of the audience. Of all theins truments, the delicate yet powerful sound a piano makes impresses me most.It’s clear that I have a long way to go before I realize my dream. Therefore, I will practice every day as long as time permits and learn as many songs as I can. I will put my heart into my pursuit of music and never give up.I am confident that one day my dream will come true. Thank you.第二节(20分)One Possible VersionIt seems that everything in China is new to my British friend, Jim.Last weekend, when Jim and I were wand ering on the streets, enjoying the beautiful scenery and fresh air of spring, a candy-coated haws stand caught his attention. Having never tasted a candy-coated haw, he immediately went up to buy one.However, the vendor shook her head when seeing the 100-yuan note Jim handed over to her. She had no change! How disappointed Jim was! He was about to quit when I took out my cellphone, scanned the QR code on the stand and paid the vendor 5 yuan.Jim was surprised at what I had done. Then I explained to him that nowadays in China QR codes were everywhere, and we could pay with a cellphone for almost everything. “Wow!” Jim sai d, “The candy-coated haw tastes great, and the payment method seems even greater!”北京市西城区2018届高三二模英语试卷作文第一节(15分)假设你是红星中学校学生会主席李华。
2018北京高三有机二模试卷

海淀区二模25、(17分)芬太尼类似物J 具有镇痛作用。
它得合成方法如下:已知:(1)A 属于烯烃,A 得结构简式为 。
(2)①得化学方程式为 。
(3)②所属得反应类型为 反应。
(4)③得化学方程式为 。
(5)F 得结构简式为 。
(6)已知④有一定得反应限度,反应进行时加入吡啶(C 5H 5N ,一种有机碱)能提高J 得产率,原因就是 。
(7)写出满足下列条件得ClCH 2CH 2COOCH 3得同分异构体得结构简式: 。
a 、能与NaHCO 3反应b 、核磁共振氢谱只有两组峰(8)已知:(R 、R’为烃基)就是一种重要得化工中间体。
以环己醇()与乙醇为起始原料,结合已知信息选择必要得无机试剂,写出得合成路线。
(用结构简式表示有机物,用箭头表示转化关系,箭头上注明试剂与反应条件)朝阳二模25.(17分)药物Q 适用于治疗高血压、心绞痛,可由有机物P 与L 制备。
H 2NCO CH 2OCH 2CH OH CH 2NHCHCH 3CH 3(药物Q )(1)有机物P 得合成路线如下。
催化剂2AB3(有机物P )H 2NCHCH 3CH 3CH 3CH CH 2已知:RNH 2+R'C R''O 一定条件+R'C R''NRH 2O (R 、R ’、R ”代表烃基或氢)① A 得分子式为C 3H 8O ,其所含得官能团就是 。
② B 得核磁共振氢谱只有一个吸收峰,其结构简式就是 。
③ 由D 生成有机物P 得反应类型就是 。
(2)有机物L 得合成路线如下。
CH 3CHCH 22CH OHCHCOOH HO F有机物 LHCl已知:RNH 2+RNH CH 2CH 2OH O① 生成E 得化学方程式就是 。
②OH 与有机物M 发生加成反应, M 得结构简式为 。
③ F 含羧基,化合物N 就是 。
④ 生成有机物L 得化学方程式就是 。
(3)以O 为起始原料合成聚合物甲得路线如下:ONH 3一定条件HOOC COOH聚合物甲C 4H 11NO 2写出聚合物甲得结构简式: 。
北京市西城区2018届高三二模试题理科综合试卷(Word版-含答案)
西城区高三模拟测试理科综合2018.5本试卷共17页,共300分。
考试时长150分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题共120分)本部分共20小题,每小题6分,共120分。
在每小题列出的四个选项中,选出最符合题目要求的一项。
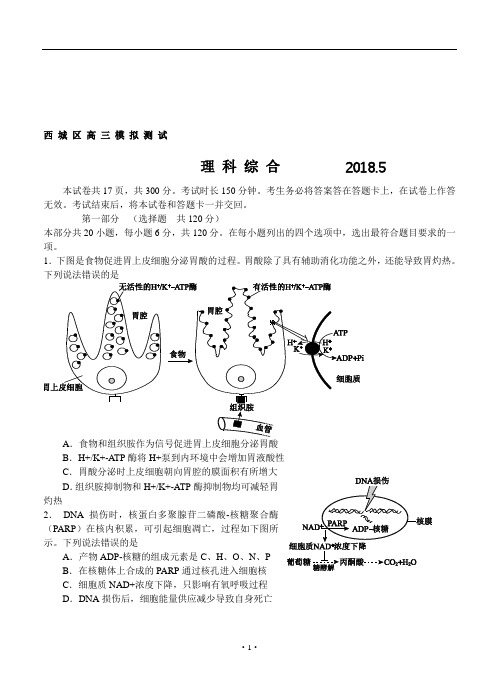
1.下图是食物促进胃上皮细胞分泌胃酸的过程。
胃酸除了具有辅助消化功能之外,还能导致胃灼热。
下列说法错误的是A.食物和组织胺作为信号促进胃上皮细胞分泌胃酸B.H+/K+-ATP酶将H+泵到内环境中会增加胃液酸性C.胃酸分泌时上皮细胞朝向胃腔的膜面积有所增大D.组织胺抑制物和H+/K+-ATP酶抑制物均可减轻胃灼热2.DNA损伤时,核蛋白多聚腺苷二磷酸-核糖聚合酶(PARP)在核内积累,可引起细胞凋亡,过程如下图所示。
下列说法错误的是A.产物ADP-核糖的组成元素是C、H、O、N、PB.在核糖体上合成的PARP通过核孔进入细胞核C.细胞质NAD+浓度下降,只影响有氧呼吸过程D.DNA损伤后,细胞能量供应减少导致自身死亡3.脱落酸(ABA)和赤霉素(GA)在种子萌发中起重要作用。
用35S-甲硫氨酸“饲喂”不同激素处理的大麦种子,提取蛋白质进行电泳,结果如右图。
下列说法错误的是A.在图中所示的蛋白质中,α-淀粉酶分子最大B.35S-甲硫氨酸是合成淀粉酶等蛋白质的原料C.ABA能拮抗GA诱导的α-淀粉酶合成D.GA通过抑制某些蛋白质合成抑制萌发4.栎树是某森林中主要的生产者,舞毒蛾啃食栎树。
栎树盛果期时丰富的果实会把白尾鹿吸引到森林中,鹿身上的扁虱会跳到森林地面产卵。
大量的栎树果实也吸引着白足鼠,扁虱卵孵化出的幼虫吸食白足鼠血和人血,同时会将白足鼠体内的螺旋菌传播给人类,使人类患上莱姆病。
下列相关分析错误的是A.扁虱与鼠、鹿、人之间的寄生关系导致螺旋菌传播到人B.舞毒蛾数量增加使栎树减产,人类患莱姆病的风险增加C.栎树盛果期时,该区域人类患上莱姆病的风险明显提高D.生物多样性是维持生态系统结构和功能稳态的必要条件5.利用竞争酶联免疫检测技术,检测抗虫棉中Bt抗虫蛋白表达量,原理如下图所示。
2018海淀区高三化学二模考试及答案

2018海淀区高三化学二模考试及答案————————————————————————————————作者:————————————————————————————————日期:海淀高三二模答题可能用到的相对原子质量:H 1 C 12 O 16 S 32 Pb 2076. 下列典籍记载的文字中,涉及置换反应的是A.以曾青(主要成分为硫酸铜)涂铁,铁赤色如铜(出自《抱朴子》)B.凡石灰(主要成分为碳酸钙),经火焚炼为用(出自《天工开物》)C.以毛袋漉去曲滓(酒糟),又以绢滤曲汁于瓮中(出自《齐民要术》)D.铅山县有苦泉(含硫酸铜),挹其水熬之,则成胆矾(出自《梦溪笔谈》)7. Lv (lì)是元素周期表第116号元素,Lv 的原子核外最外层电子数是6。
下列说法中,不正确...的是 A .Lv 的原子半径比S 的原子半径大 B .293116Lv 的原子核内有293个中子 C .Lv 位于元素周期表第七周期第ⅥA 族 D .290116Lv 、291116Lv 、292116Lv 互为同位素8. 下列解释工业生产或应用的化学用语中,不正确...的是A .氯碱工业中制备氯气:2NaCl(熔融)2Na + Cl 2↑ B .工业制硫酸的主要反应之一:2SO 2 + O 2 2SO 3C .氨氧化法制硝酸的主要反应之一:4NH 3 + 5O 24NO + 6H 2OD .利用铝热反应焊接铁轨:2Al + Fe 2O 3高温Al 2O 3 + 2Fe电解 催化剂△ 催化剂△9.三氟化氮(NF3)常用于微电子工业,可用以下反应制备:4NH3+ 3F2= NF3+ 3NH4F下列说法中,正确的是A.NF3的电子式为B.NH4F分子中仅含离子键C.在制备NF3的反应中,NH3表现出还原性D.在制备NF3的反应中,各物质均为共价化合物10.一种以石墨和过渡金属氧化物做电极材料、以固态有机高聚物做电解质溶剂的锂离子电池,其工作原理如图1所示,图2是合成有机高聚物的单体的结构简式。
2018届北京市朝阳区高三二模理数试题Word版含解析

2018届北京市朝阳区高三二模理数试题(考试时间120分钟满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分第一部分(选择题共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.+对应的点位于1.已知i为虚数单位,则复数z=i(12i)A.第一象限 B.第二象限 C.第三象限 D.第四象限【答案】B【解析】试题分析:因为,所以对应的点的坐标是,故选B.考点:1.复数的运算;2.复数在复平面内所对应的点.2.执行如图所示的程序框图,则输出的S值是A.23 B.31 C.32 D.63【答案】B【解析】第一次循环: ; 第二次循环:第三次循环:第四次循环:第五次循环:第六次循环:结束循环,输出选B.点睛:算法与流程图的考查,侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念,包括选择结构、循环结构、伪代码,其次要重视循环起点条件、循环次数、循环终止条件,更要通过循环规律,明确流程图研究的数学问题,是求和还是求项. 3.“0,0x y >>”是“2y xx y+≥”的 A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件 D .既不充分也不必要条件【答案】A 【解析】当时,由均值不等式成立。
但时,只需要,不能推出。
所以是充分而不必要条件。
选A.4.已知函数π()sin()(0)6f x x >=+ωω的最小正周期为4π,则A .函数()f x 的图象关于原点对称B .函数()f x 的图象关于直线π3x =对称 C .函数()f x 图象上的所有点向右平移π3个单位长度后,所得的图象关于原点对称D .函数()f x 在区间(0,π)上单调递增【答案】C 【解析】,所以不是奇函数, 图象不关于原点对称;时不是最值, 图象不关于直线对称; 所有点向右平移个单位长度后得为奇函数, 图象关于原点对称;因为,所以函数在区间上有增有减,综上选C.5.现将5张连号的电影票分给甲、乙等5个人,每人一张,且甲、乙分得的电影票连号,则共有不同分法的种数为A .12B . 24C .36D . 48 【答案】D【解析】甲、乙分得的电影票连号有种情况,其余三人有分法,所以共有,选D.点睛:求解排列、组合问题常用的解题方法:(1)元素相邻的排列问题——“捆邦法”;(2)元素相间的排列问题——“插空法”;(3)元素有顺序限制的排列问题——“除序法”;(4)带有“含”与“不含”“至多”“至少”的排列组合问题——间接法.6.某三棱锥的三视图如图所示,则该三棱锥最长的棱长为A. B. C. D.【答案】C【解析】三视图还原图形三棱锥,如下图:,所以最长边为,选C.7.已知函数log ,0,()3,40a x x f x x x >⎧⎪=⎨+-≤<⎪⎩(0a >且1)a ≠.若函数()f x 的图象上有且只有两个点关于y 轴对称,则a 的取值范围是A .(0,1)B .(1,4)C .(0,1)(1,)+∞UD .(0,1)(1,4)U 【答案】D 【解析】由题意得 与有且仅有一个交点,当时,有且仅有一个交点;当 时,需满足,因此的取值范围是,选D.点睛:涉及函数的零点问题、方程解的个数问题、函数图像交点个数问题,一般先通过导数研究函数的单调性、最大值、最小值、变化趋势等,再借助函数的大致图象判断零点、方程根、交点的情况,归根到底还是研究函数的性质,如单调性、极值,然后通过数形结合的思想找到解题的思路. 8.中国古代儒家要求学生掌握六种基本才艺:礼、乐、射、御、书、数,简称“六艺”.某 中学为弘扬“六艺”的传统文化,分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识的竞赛.现有甲、乙、丙三位选手进入了前三名的最后角逐.规定:每场 知识竞赛前三名的得分都分别为,,(,a b c a b c >>且,,)N a b c *∈;选手最后得分为各场得分之和.在六场比赛后,已知甲最后得分为26分,乙和丙最后得分都为11分,且乙在其中一场比赛中获得第一名,则下列说法正确的是A .每场比赛第一名得分a 为4B .甲可能有一场比赛获得第二名C .乙有四场比赛获得第三名D .丙可能有一场比赛获得第一名【答案】C【解析】若每场比赛第一名得分为4,则甲最后得分最高为,不合题意; 三人总分为,每场总分数为 分,所以,因此 甲比赛名次为5个第一,一个第三;而乙比赛名次有1个第一,所以丙没有一场比赛获得第一名,因此选C.即乙比赛名次为1个第一,4个第三,1个第二. 第二部分(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分. 9.双曲线22136x y -=的渐近线方程是 ,离心率是 . 【答案】 (1). (2).【解析】渐近线方程是 ,离心率为10.若平面向量(cos ,sin )a =θθ,(1,1)-b =,且a b ⊥,则sin 2θ的值是 .【答案】 【解析】由题意得11.等比数列{a n }的前n 项和为n S .已知142,2a a ==-,则{a n }的通项公式n a = , 9S = .【答案】 (1).(2). 2【解析】12.在极坐标系中,圆2cos ρθ=被直线1cos 2ρθ=所截得的弦长为 . 【答案】【解析】由题意得圆 ,直线 ,所以交点为 ,弦长为13.已知,x y 满足,4,2.y x x y x y k ≥⎧⎪+≤⎨⎪-≥⎩若2z x y =+有最大值8,则实数k 的值为 .【答案】【解析】由图知直线过A 点时取最大值8,由得 ,所以点睛:线性规划问题,首先明确可行域对应的是封闭区域还是开放区域、分界线是实线还是虚线,其次确定目标函数的几何意义,是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等等,最后结合图形确定目标函数最值取法、值域范围.14.已知两个集合,A B ,满足B A ⊆.若对任意的x A Î,存在,i j a a B Î()i j ≠,使得 12i j x a a λλ=+(12,{1,0,1}λλ?),则称B 为A 的一个基集.若 {1,2,3,4,5,6,7,8,9,10}A =,则其基集B 元素个数的最小值是 .【答案】4三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题满分13分)在△ABC 中, 角,,A B C 的对边分别为,,a b c ,且b c =,2sin B A .(Ⅰ)求cos B 的值;(Ⅱ)若2a =,求△ABC 的面积.【答案】(1)(2)16.(本小题满分13分)从某市的中学生中随机调查了部分男生,获得了他们的身高数据,整理得到如下频率分布直方图.(Ⅰ)求a的值;(Ⅱ)假设同组中的每个数据用该组区间的中点值代替,估计该市中学生中的全体男生的平均身高;(Ⅲ)从该市的中学生中随机抽取一名男生,根据直方图中的信息,估计其身高在180 cm 以上的概率.若从全市中学的男生(人数众多)中随机抽取3人,用X表示身高在180 cm以上的男生人数,求随机变量X的分布列和数学期望EX.【答案】(1)(2)(3)【解析】试题分析:(1)根据频率分布直方图中小长方形面积等于对应区间概率及所有小长方形面积之和为1得,解得.(2)根据平均数等于组中值与对应概率乘积的和得平均值,(3)先确定随机变量的取法:.再利用组合数求对应概率,列表可得分布列.最后根据数学期望公式求期望.试题解析:解:(Ⅰ)根据题意得:.解得.(Ⅱ)设样本中男生身高的平均值为,则.所以估计该市中学全体男生的平均身高为.(Ⅲ)从全市中学的男生中任意抽取一人,其身高在以上的概率约为.由已知得,随机变量的可能取值为.所以;;;.随机变量的分布列为因为~,所以.点睛:求解离散型随机变量的数学期望的一般步骤为:第一步是“判断取值”,即判断随机变量的所有可能取值,以及取每个值所表示的意义;第二步是“探求概率”,即利用排列组合、枚举法、概率公式(常见的有古典概型公式、几何概型公式、互斥事件的概率和公式、独立事件的概率积公式,以及对立事件的概率公式等),求出随机变量取每个值时的概率;第三步是“写分布列”,即按规范形式写出分布列,并注意用分布列的性质检验所求的分布列或某事件的概率是否正确;第四步是“求期望值”,一般利用离散型随机变量的数学期望的定义求期望的值,对于有些实际问题中的随机变量,如果能够断定它服从某常见的典型分布(如二项分布),则此随机变量的期望可直接利用这种典型分布的期望公式()求得.因此,应熟记常见的典型分布的期望公式,可加快解题速度.17.(本小题满分14分)如图1,在Rt △ABC 中,90C ∠=︒,4,2AC BC ==,D E ,分别为边,AC AB 的中点,点,F G 分别为线段,CD BE 的中点.将△ADE 沿DE 折起到△1A DE 的位置,使160A DC ∠=︒.点Q 为线段1A B 上的一点,如图2.(Ⅰ)求证:1A F BE ⊥;(Ⅱ)线段1A B 上是否存在点Q ,使得FQ 平面1A DE ?若存在,求出1AQ 的长,若不存在,请说明理由; (Ⅲ)当1134A Q AB =时,求直线GQ 与平面1A DE 所成角的大小. 【答案】(1)见解析(2)在线段上存在中点,使平面.且(3)图1图2BA 1FCED QG ABCDEFG【解析】试题分析:(1)先根据等腰三角形性质得.再由折叠中不变的垂直关系得,根据线面垂直判定定理得平面,即得.最后再根据线面垂直判定定理得平面,即得.(2)利用空间向量研究线面平行关系,即通过平面法向量与直线方向向量垂直进行研究,先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解出平面法向量,利用向量数量积求直线方向向量与法向量夹角,最后根据平面法向量与直线方向向量数量积为零列式求解参数.(3)利用空间向量求线面角,仍是先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解出平面法向量,利用向量数量积求直线方向向量与法向量夹角,最后根据线面角与向量夹角之间互余关系列式求线面角大小.试题解析:解:(Ⅰ)因为,所以△为等边三角形.又因为点为线段的中点,所以.由题可知,所以平面.因为平面,所以.又,所以平面.所以.(Ⅱ)由(Ⅰ)知平面,,如图建立空间直角坐标系,则,,,,,.设平面的一个法向量为,,,所以即令,所以,所以假设在线段上存在点,使平面.设,.又,所以.所以.则. 所以.解得,.则在线段上存在中点,使平面.且(Ⅲ)因为,又,所以.所以.又因为,所以.因为设直线与平面所成角为,则直线与平面所成角为.18.(本小题满分13分)已知椭圆W:22221x ya b+=(0)a b>>的上下顶点分别为,A B,且点B(0,1)-.12,F F分别为椭圆W的左、右焦点,且12120F BF∠=.(Ⅰ)求椭圆W的标准方程;(Ⅱ)点M是椭圆上异于A,B的任意一点,过点M作MN y⊥轴于N,E为线段MN 的中点.直线AE与直线1y=-交于点C,G为线段BC的中点,O为坐标原点.求OEG∠的大小.【答案】(1)(2)见解析【解析】试题分析:(1)由顶点坐标得再在中利用椭圆几何条件得.(2)利用向量数量积研究的大小.先设,则得.求出直线与直线交点,得.再根据向量数量积得,根据代入化简得,即得.试题解析:解:(Ⅰ)依题意,得.又,在中,,所以.所以椭圆的标准方程为.(Ⅱ)设,,则,.因为点在椭圆上,所以.即.又,所以直线的方程为.令,得.又,为线段的中点,所以.所以,.因为,所以..19.(本小题满分14分)已知函数2()e xf x x x =+-,2(),g x x ax b =++,a b ÎR . (Ⅰ)当1a =时,求函数()()()F x f x g x =-的单调区间;(Ⅱ)若曲线()y f x =在点(0,1)处的切线l 与曲线()y g x =切于点(1,)c ,求,,a b c 的值;(Ⅲ)若()()f x g x ≥恒成立,求a b +的最大值.【答案】(1)(2)【解析】试题分析:(1)先明确函数定义域,再求函数导数,根据导函数符号确定单调区间,(2)由导数几何意义得切线斜率为,则得,.即得(3)不等式恒成立问题,一般转化为对应函数最值问题:先利用导数研究函数最值:当时,在上单调递增. 仅当时满足条件,此时;当时,先减后增,,再变量分离转化为,最后利用导数研究函数最值,可得的最大值. 试题解析:解:(Ⅰ),则. 令得,所以在上单调递增. 令得,所以在上单调递减.(Ⅱ)因为,所以,所以的方程为.依题意,,.于是与抛物线切于点,由得.所以(Ⅲ)设,则恒成立.易得(1)当时,因为,所以此时在上单调递增.①若,则当时满足条件,此时;②若,取且此时,所以不恒成立.不满足条件;(2)当时,令,得由,得;由,得所以在上单调递减,在上单调递增.要使得“恒成立”,必须有“当时,”成立.所以.则令则令,得由,得;由,得所以在上单调递增,在上单调递减,所以,当时,从而,当时,的最大值为.综上,的最大值为.20.(本小题满分13分)各项均为非负整数的数列}{n a 同时满足下列条件: ①m a =1 ()N m ∈*;②1n a n ≤- (2)n ≥;③n 是12n a a a +++的因数(1n ≥).(Ⅰ)当5=m 时,写出数列}{n a 的前五项;(Ⅱ)若数列}{n a 的前三项互不相等,且3≥n 时,n a 为常数,求m 的值; (Ⅲ)求证:对任意正整数m ,存在正整数M ,使得n M ≥时,n a 为常数.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
海淀区二模25.(17分)芬太尼类似物J具有镇痛作用。
它的合成方法如下:已知:(1)A属于烯烃,A的结构简式为。
(2)①的化学方程式为。
(3)②所属的反应类型为反应。
(4)③的化学方程式为。
(5)F的结构简式为。
(6)已知④有一定的反应限度,反应进行时加入吡啶(C5H5N,一种有机碱)能提高J的产率,原因是。
(7)写出满足下列条件的ClCH2CH2COOCH3的同分异构体的结构简式:。
a.能与NaHCO3反应b.核磁共振氢谱只有两组峰(8)已知:(R、R’为烃基)是一种重要的化工中间体。
以环己醇()和乙醇为起始原料,结合已知信息选择必要的无机试剂,写出的合成路线。
(用结构简式表示有机物,用箭头表示转化关系,箭头上注明试剂和反应条件)二模25.(17分)药物Q 适用于治疗高血压、心绞痛,可由有机物P 和L 制备。
H 2NCO CH 2OCH 2CH OH CH 2NHCHCH 3CH 3(药物Q )(1)有机物P 的合成路线如下。
催化剂2A氧化B3一定条件(有机物P )H 2NCHCH 3CH 3CH 3CHCH 2已知:R NH 2+R'C R''O 一定条件+R'C R''NRH 2O (R 、R ’、R ”代表烃基或氢)① A 的分子式为C 3H 8O ,其所含的官能团是 。
② B 的核磁共振氢谱只有一个吸收峰,其结构简式是 。
③ 由D 生成有机物P 的反应类型是 。
(2)有机物L 的合成路线如下。
CH 3CHCH 22CH OHCHCOOH HO 催化剂F有机物 LAgHCl已知:RNH 2+RNH CH 2CH 2OH O① 生成E 的化学方程式是 。
② 与有机物M 发生加成反应, M 的结构简式为 。
③ F 含羧基,化合物N 是 。
④ 生成有机物L 的化学方程式是 。
(3)以为起始原料合成聚合物甲的路线如下:ONH 3一定条件HOOC COOH聚合物甲C 4H 11NO 2写出聚合物甲的结构简式: 。
海淀区二模25.(共17分,除特殊标注外,每空2分)(1)CH2=CH-CH3(2)(反应物产物写成2NH3\NH4Cl也给分)(3)取代(4)(5)(6)吡啶能与反应④的产物HCl发生中和反应,使平衡正向移动,提高J产率(7)(CH3)2CClCOOH(8)3分)二模25.(17分)(1)①羟基(或—OH)②③加成反应(或还原反应)(2)①50023222CH CH CH Cl CH CH CH Cl HCl=-+−−−→=-+℃②③3NH④CH2CH CH2O+CH2OHCOH2N CH2OCOH2N CH2CH CH2O+HCl(3)OCH2CH2NHCH2CH2O COCOOHnH顺义区25.(17分)香叶醇(D)是一种特殊的香料,也是一种重要的有机合成的原料。
由香叶醇合成功能高分子L的合成路线如下:已知:Ⅰ.(R代表烃基,X=Y代表C=C、C=O等不饱和键,可与其他基团相连)Ⅱ.1.A的名称是__________。
2.B的结构简式是__________。
3.D中官能团的名称是__________。
4.试剂a是__________。
5.由H得到I的反应类型是__________。
6.由E生成F的化学方程式是__________。
7.由I合成J需经历三步反应,其中第一步、第三步的化学方程式分别是顺义区25.(17分)(1)对二甲苯(1,4-二甲苯)2分(2)2分(3)碳碳双键、羟基2分(4)甲醇(CH3OH)2分(5)加成反应2分(6)2分(7)第一步:3分第三步:2分25.(17分)(1)丙烯(2分)(2)(2分)(3)acd (2分)(3分)(3分)25.(17分)EPR橡胶和PC塑料的合成路线如下:(1)A的名称是。
(2)C的结构简式。
(3)下列说确的是(选填字母)。
A. 反应Ⅱ的原子利用率为100%B. 反应Ⅲ为取代反应C. 1 mol E与足量金属Na 反应,最多可生成标准状况下22.4 L H2D. CH3OH在合成PC塑料的过程中可以循环利用(4)反应Ⅰ的化学方程式是_______________________________。
(5)反应Ⅳ的化学方程式是_______________________________。
(6)已知:以D和乙酸为起始原料合成无机试剂任选,写出合成路线(用结构简式表示有机物,用箭头表示转化关系,箭头上注明反应试剂和条件)。
东城25.(17分)合成药物中间体M的流程如下。
已知:(1)A的名称是________。
(2)B中含有的官能团是________。
(3)D的结构简式是________。
(4)反应①的化学方程式是________。
(5)反应②的反应类型是________。
(6)反应③的试剂和条件是________。
(7)由K生成L反应的化学方程式是________(8)写出中间产物的结构简式:中间产物Ⅰ ______ ,中间产物Ⅱ ______。
西城25.(17分)化合物N L的合成路线如下:1234请回答:(1)A的官能团名称是______。
(2)B不能发生银镜反应,A→B的化学方程式是______。
(3)C的结构简式是______。
(4)D→F的反应类型是______,F→G的化学方程式是______。
(5)J的结构简式是______。
(6)K含有六原子环结构,K→L的化学方程式是______。
(7)G和L经过3步反应合成N,路线如下:结合中间体L中间产物1:______,中间产物2:______。
东城25. (17分)(1)乙酸(2)氯原子羧基(3)HOOCCH2COOH(4)(5)氧化(6)浓HNO3和浓H2SO4、加热(7)(8)西城25.(17分,(1)1分,其他每空2分)(1)羟基(2)(3)(4)取代反应(或酯化反应)(5)(6)(7)25.苯巴比妥是一种巴比妥类药物,主要用于镇静、催眠,其合成路线如下(部分反应条件和试剂略):氧化氧化A 水溶液 D E已知: i. ii. iii.请回答下列问题:(1)B 的结构简式是 ,C 中含氧官能团的名称是 。
(2)E 与G 反应的反应类型是 。
(3)D + X→E + H 2O ,X 的结构简式是 。
(4)写出化合物I→苯巴比妥的化学方程式 。
(5)F 是一种二元羧酸,仅以乙烯为有机原料,选用必要的无机试剂合成F ,写出有关的化学方程式: 。
(6)已知:以丙二酸二乙酯和1,2-二溴乙烷为原料,合成对二甲酸环己烷(CHDA )的流程图如下,请写出中间产物的结构简式: 。
(CHDA丰台25.(17分)2005年诺贝尔化学奖授予了研究烯烃复分解反应的科学家,以表彰他们作出的卓越贡献。
烯烃复分解反应原理如下:试剂1试剂2 一定条件(苯巴比妥)CH 3CH 2OH 浓硫酸,△+ 中间 产物HI稀硫酸 ∆CH 2-COCB C 2H 5ONaF BrCH 2CH 2Br-CO 2G△现以烯烃C 5H 10为原料,合成有机物M 和N ,合成路线如下:OH CH 3多步反应 Br 2/CCl 4NaOH/H 2O △ 催化剂 A C 5H 10 B Br 2/CCl 4C D C 2H 2O 4 浓H 2SO 4/△MC 10H 16O 4(六元环酯)E F CH 3CH 2-C -COOH G C 5H 8O 2 (只有一个甲基) N C 13H 16O 2 X 浓硫酸/△(1)按系统命名法,有机物A 的名称是 。
(2)B 的结构简式是 。
(3)CD 的反应类型是 。
(4)写出D M 的化学方程式 。
(5)写出EF 合成路线(用结构简式表示有机物,用箭头表示转化关系,箭头上注明试剂和反应条件) 。
(6)已知X 的苯环上只有一个取代基,且取代基无甲基,则N 的结构简式为 。
(7)满足下列条件的X 的同分异构体共有 种,写出任意一种的结构简式 。
①遇FeCl 3溶液显紫色 ②苯环上的一氯取代物只有两种昌平25.(14分)(1) 醛基 (2)取代反应 (3)CH 3CH 2OH(4)(5)CH 2=CH 2 CH 2Br-CH 2Br (6) 2 + 2BrCH 2CH 2Br + 4C 2H 5ONa + 4C 2H 5OH + 4NaBr 丰台催化剂 C 2H 5CH=CHCH 3 + CH 2=CH 2C 2H 5CH=CH 2 + CH 2=CHCH 3NaOH, H 2O ∆ +一定条件+ 2C 2H 5OH∆Cu,O 2 ∆Br 2 CH 2OH-CH 2OH OHC-CHO HOOC-COOH ①Cu(OH)2, ②H +9.(17分)(1)苯甲醛(2)加成;酯化或取代(3)(4)(5)(6)(3分)9.(17分)化合物H是一种有机光电材料中间体。
实验室由芳香化合物A制备H的一种合成路线如下:已知:①2NaOH/H O32RCHO CH CHO RCH==CHCHO H O +−−−−→+△②(1)A 的化学名称是 。
(2)由C 生成D 和E 生成F 的反应类型分别是 、 。
(3)E 的结构简式为 。
(4)G 为甲苯的同分异构体,由F 生成H 的化学方程式为 。
(5)芳香化合物X 是F 的同分异构体,X 能与饱和碳酸氢钠溶液反应放出2CO ,其核磁共振氢谱显示有4种不同化学环境的氢,峰面积为6:2:1:1,写出2种符合要求的X 的结构简式 、 。
(6)写出用环戊烷和2-丁炔为原料制备化合物的合成路线 其他试剂任选)。
HOOCOH 2C25.(17分)可用作光电材料的功能高分子 M ( C CH n COOH)的单体K 的合成路线如下:(1)已知通过质谱仪测定的烃A的质荷比为106,A 的结构简式是。
(2)反应①的化学方程式是。
(3)反应②的反应类型是。
(4)反应②和③的目的是。
(5)C的同分异构体有多种,写出符合下列条件的所有同分异构体的结构简式:a.含有苯环结构b.属于醇类c.苯环上的核磁共振氢谱有3组峰。
(6)H 所含的官能团是。
(7)反应⑤中i的化学方程式是。
(8)写出以乙炔和甲醛为起始原料合成1,3-丁二烯的合成路线(无机试剂任选,用结构简式表示有机物,用箭头表示。
