6种粒子群算法程序
粒子群算法

粒子群算法1.粒子群算法简介1.1集群智能(Swarm Intelligence)Swarm可被描述为一些相互作用相邻的个体的集合体,蜂群、蚁群、鸟群都是Swarm 的典型例子。
鱼聚集成群可以有效地逃避捕食者,因为任何一只鱼发现异常都可以带动整个鱼群逃避。
蚂蚁成群则有利于寻找食物,因为任何一只蚂蚁发现食物都可以带领蚁群来共同搬运和进食。
一只蜜蜂或蚂蚁的能力非常有限,它几乎不可能独立存在于自然世界中,而多个蜜蜂或蚂蚁形成的Swarm则具有非常强的生存能力,且这种能力不是通过多个个体之间的能力简单叠加所获得的。
社会性动物群体所拥有的这种特性能够帮助个体很好的适应环境,个体所能获得的信息远比它通过自身感觉器官所取得的多,其根本原因在于个体之间存在着信息交互能力。
信息交互过程不仅仅在群体中传播信息,而且群内个体还能处理信息,并根据所获得的信息改变自身的一些行为模式和规范,这就使得群体涌现出一些单个个体不具备的能力和特性,尤其是对环境的适应能力。
这种对环境变化所具有适应的能力可以被认为是一种智能,称为集群智能(Swarm Intelligence)。
集群智能具有如下几个特点:1)群内个体具有执行简单的时间或空间上的评估和计算的能力。
2)群内个体能对环境(包括群内其他个体)的关键性因素的变化做出响应。
3)群内不同个体对环境中某一变化所表现出的响应行为具有多样性。
4)不是每次环境的变化都会导致整个群体的行为模式发生改变。
5)环境所发生的变化中,若出现群体值得付出代价的改变机遇,群体必须能够改变其行为模式。
1.2 粒子群算法介绍粒子群算法,也称粒子群优化算法(Particle Swarm Optimization),缩写为PSO,是根据集群智能Swarm Intelligence思想发展而来的一种算法,最早由Kennedy和Eberhart提出,该算法模拟了鸟群飞行觅食的行为,鸟之间通过集体的协作使群体达到最优目的。
粒子群优化算法 程序

粒子群优化算法程序粒子群优化算法(Particle Swarm Optimization, PSO)是一种基于群体智能的优化算法,它模拟了鸟群或鱼群等生物群体的行为,用于解决各种优化问题。
下面我将从程序实现的角度来介绍粒子群优化算法。
首先,粒子群优化算法的程序实现需要考虑以下几个关键步骤:1. 初始化粒子群,定义粒子的数量、搜索空间的范围、每个粒子的初始位置和速度等参数。
2. 计算适应度,根据问题的特定适应度函数,计算每个粒子的适应度值,以确定其在搜索空间中的位置。
3. 更新粒子的速度和位置,根据粒子的当前位置和速度,以及粒子群的最优位置,更新每个粒子的速度和位置。
4. 更新全局最优位置,根据所有粒子的适应度值,更新全局最优位置。
5. 终止条件,设置终止条件,如最大迭代次数或达到特定的适应度阈值。
基于以上步骤,可以编写粒子群优化算法的程序。
下面是一个简单的伪代码示例:python.# 初始化粒子群。
def initialize_particles(num_particles, search_space):particles = []for _ in range(num_particles):particle = {。
'position':generate_random_position(search_space),。
'velocity':generate_random_velocity(search_space),。
'best_position': None,。
'fitness': None.}。
particles.append(particle)。
return particles.# 计算适应度。
def calculate_fitness(particle):# 根据特定问题的适应度函数计算适应度值。
particle['fitness'] =evaluate_fitness(particle['position'])。
粒子群算法粒子群算法简介
粒子群算法(1)----粒子群算法简介二、粒子群算法的具体表述上面罗嗦了半天,那些都是科研工作者写论文的语气,不过,PSO的历史就像上面说的那样。
下面通俗的解释PSO算法。
PSO算法就是模拟一群鸟寻找食物的过程,每个鸟就是PSO中的粒子,也就是我们需要求解问题的可能解,这些鸟在寻找食物的过程中,不停改变自己在空中飞行的位置与速度。
大家也可以观察一下,鸟群在寻找食物的过程中,开始鸟群比较分散,逐渐这些鸟就会聚成一群,这个群忽高忽低、忽左忽右,直到最后找到食物。
这个过程我们转化为一个数学问题。
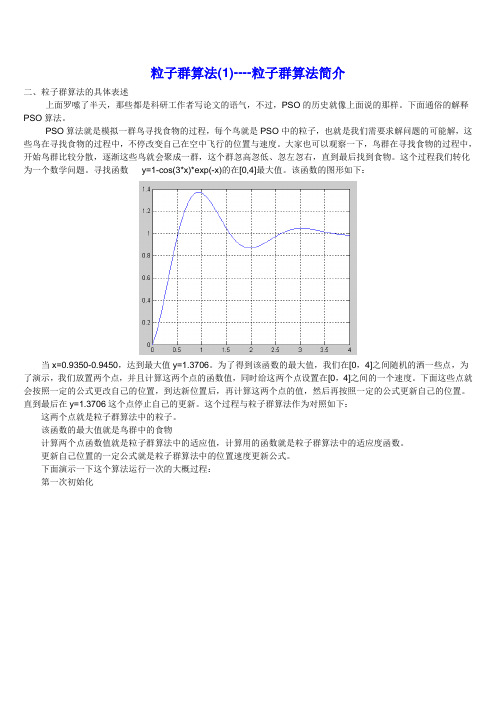
寻找函数y=1-cos(3*x)*exp(-x)的在[0,4]最大值。
该函数的图形如下:当x=0.9350-0.9450,达到最大值y=1.3706。
为了得到该函数的最大值,我们在[0,4]之间随机的洒一些点,为了演示,我们放置两个点,并且计算这两个点的函数值,同时给这两个点设置在[0,4]之间的一个速度。
下面这些点就会按照一定的公式更改自己的位置,到达新位置后,再计算这两个点的值,然后再按照一定的公式更新自己的位置。
直到最后在y=1.3706这个点停止自己的更新。
这个过程与粒子群算法作为对照如下:这两个点就是粒子群算法中的粒子。
该函数的最大值就是鸟群中的食物计算两个点函数值就是粒子群算法中的适应值,计算用的函数就是粒子群算法中的适应度函数。
更新自己位置的一定公式就是粒子群算法中的位置速度更新公式。
下面演示一下这个算法运行一次的大概过程:第一次初始化第一次更新位置第二次更新位置第21次更新最后的结果(30次迭代)最后所有的点都集中在最大值的地方。
粒子群算法(2)----标准的粒子群算法在上一节的叙述中,唯一没有给大家介绍的就是函数的这些随机的点(粒子)是如何运动的,只是说按照一定的公式更新。
这个公式就是粒子群算法中的位置速度更新公式。
下面就介绍这个公式是什么。
在上一节中我们求取函数y=1-cos(3*x)*exp(-x)的在[0,4]最大值。
粒子群算法文档【精品文档】(完整版)

§6.4 粒子群优化算法人们提出了群搜索概念,利用它们来解决现实中所遇到的优化问题,并取得了良好的效果.粒子群优化算法就是群体智能中的一种算法.粒子群算法是一种演化计算技术,是一种基于迭代的优化工具,系统初始化为一组随机解,通过迭代搜寻最优值,将鸟群运动模型中栖息地类比为所求问题空间中可能解的位置,利用个体间的传递,导致整个群体向可能解的方向移动,逐步发现较好解.6.4.1 基本粒子群算法粒子群算法,其核心思想是对生物社会性行为的模拟.最初粒子群算法是用来模拟鸟群捕食的过程,假设一群鸟在捕食,其中的一只发现了食物,则其他一些鸟会跟随这只鸟飞向食物处,而另一些会去寻找更好的食物源.在捕食的整个过程中,鸟会利用自身的经验和群体的信息来寻找食物.粒子群算法从鸟群的这种行为得到启示,并将其用于优化问题的求解.若把在某个区域范围内寻找某个函数最优值的问题看作鸟群觅食行为,区域中的每个点看作一只鸟,现把它叫粒子(particle).每个粒子都有自己的位置和速度,还有一个由目标函数决定的适应度值.但每次迭代也并不是完全随机的,如果找到了新的更好的解,将会以此为依据来寻找下一个解.图6.21给出了粒子运动的思路图.图6.21粒子运动的路线图下面给出粒子群算法的数学描述.假设搜索空间是D维的,群中的第i个粒子能用如下D维矢量所表示:12(,,,)i i i iD X x x x '=(6.43)每个粒子代表一个潜在的解,这个解有D 个维度.每个粒子对应着D 维搜索空间上的一个点.粒子群优化算法的目的是按照预定目标函数找到使得目标函数达到极值的最优点.第i 个粒子的速度或位置的变化能用如下的D 维向量表示:12(,,,)i i i iD V v v v '= (6.44)为了更准确地模拟鸟群,在粒子群优化中引入了两个重要的参量.一个是第i 个粒子曾经发现过的自身历史最优点(Personal best ,pbest),可以表示为:12(,,,)i i i iD P p p p '= (6.45)另一个是整个种群所找到的最优点(Global best ,gbest),可以表示为:12(,,,)g g g gD P p p p '= (6.46)PSO 初始化为一群随机粒子(随机解),然后通过迭代找到最优解.在每一次的迭代中,粒子通过跟踪两个“极值”(i P 和g P )来更新自己.在找到这两个最优值后,粒子通过下面的公式来更新自己的速度和位置:1122(1)()()(()())()(()())id id id id gd id v t wv t c r t p t x t c r t p t x t +=+-+-,(速度更新公式)(6.46)(1)()(1)id id id x t x t v t +=++(位置更新公式) (6.47)其中w 称之为惯性因子,在一般情况下,取1w =,1,2,,t G = 代表迭代序号,G 是预先给出的最大迭代数;1,2,,d D = , 1,2,,i N = ,N 是群的大小;1c 和2c 是正的常数,分别称为自身认知因子和社会认知因子,用来调整i P 和g P 的影响强度.1r 和2r 是区间[0,1]内的随机数.由(6.46)和(6.47)构成的粒子群优化称为原始型粒子群优化.从社会学的角度来看,公式(6.47)的第一部分称为记忆项,表示上次优化中的速度的影响;公式第二部分称为自身认知项,可以认为是当前位置与粒子自身最优位置之间的偏差,表示粒子的下一次运动中来源于自己经验的部分;公式的第三部分称为社会认知项,是一个从当前位置指向种群最佳位置的矢量,反映了群内粒子的协作和知识共享.可见,粒子就是通过自己的经验和同伴中最好的经验来决定下一步的运动.随着迭代进化的不断进行,粒子群逐渐聚集到最优点处,图6.22 给出了某个优化过程中粒子逐渐聚集的示意图.图6.22 粒子群在优化过程聚集示意图 综上所述,我们得到如下基本粒子群算法流程:(1) 设定参数,初始化粒子群,包括随机位置和速度;(2) 评价每个粒子的适应度;(3) 对每个粒子,将其当前适应值与其曾经访问过的最好位置pbest 作比较,如果当前值更好,则用当前位置更新pbest ;(4) 对每个粒子,将其当前适应值与种群最佳位置gbest 作比较,如果当前值更好,则用当前位置更新gbest ;(5) 根据速度和位置更新公式更新粒子;(6)若未满足结束条件则转第二步;否则停止迭代.迭代终止条件根据具体问题一般选为迭代至最大迭代次数或粒子群搜索到的最优位置满足预定的精度阈值.6.4.2 粒子群算法的轨迹分析1998年,Ozcan 在文献[13]中首先对粒子在一维空间的轨迹进行了讨论,并在1999年将粒子运动的轨迹分析推广到多维空间的情形,2002年,文献[14]从矩阵代数的观点讨论了粒子的轨迹问题,本节采用[15]中的差分方程思想分别讨论单个粒子在一维以及二维空间的轨迹问题。
粒子群算法程序(各段路的速度不同)(完整版)

1.用粒子群算法求解路径最短时的路径ticK=3;%车辆数D=200;%粒子群中粒子的个数Q=1000;%每辆车的容量w=0.729;%w为惯性因子c1=1.49445;%正常数,称为加速因子c2=1.49445;%正常数,称为加速因子Loop_max=50;%最大迭代次数%初始化城市坐标City=[18,54;22,60;58,69;71,71;83,46;91,38;24,42;18,40];n=size(City,1);%城市个数,包含中心仓库N=n-1;%发货点任务数for i=1:nfor j=1:nDistance(i,j)= sqrt((City(i,1)-City(j,1))^2+(City(i,2)-City(j,2))^2);%各城市节点之间的距离矩阵endendv=[20,20,20,21,21,19,20,20;20,20,19,20,19,21,20,21;20,19,20,20,20,20,21,20;21,20,20,19,20,21, 21,21;21,19,20,20,20,21,21,20;19,21,20,21,21,20,20,21;20,20,21,21,21,20,19,20;20,21,20,21,20, 21,20,20];for i=1:8for j=1:8if i==jv(i,j)=0;endendendg=[0, 890,140,280,330,210,410,570];%各发货点的货运量%初始化粒子群for i=1:Dfor j=1:NXv(i,j)=randi(K,1);%初始化粒子群中粒子的位置Vv(i,j)=randi(2*K-1,1)-K;%初始化粒子群中粒子的位置变化率Vr(i,j)=randi(2*N-1,1)-N;%初始化粒子群中离子的位置变化率Xvl(i,j)=Xv(i,j);%初始化粒子群中每个粒子的最优位置endendfor i=1:Da=randperm(N);for j=1:NXr(i,j)=a(j);%初始化粒子群中粒子的位置Xrl(i,j)=Xr(i,j);%初始化粒子群中每个粒子的最优位置endLg=100000;%初始化最优粒子对应的配送方案的总路径长度Xvg=ones(1,N);%粒子群中最优的粒子Xrg=ones(1,N);%粒子群中最优的粒子Loop=1;%迭代计数器while Loop<=Loop_max%循环终止条件%对粒子群中的每个粒子进行评价for i=1:Dk1=find(1==Xv(i,:));%找出第一辆车配送的城市编号nb1=size(k1,2);%计算第一辆车配送城市的个数if nb1>0%判断第一辆车配送城市个数是否大于0,如果大于0则a1=[Xr(i,k1(:))];%找出第一辆车配送城市顺序号b1=sort(a1);%对找出第一辆车的顺序号进行排序G1(i)=0;%初始化第一辆车的配送量k51=[];am=[];for j1=1:nb1am=find(b1(j1)==Xr(i,:));k51(j1)=intersect(k1,am);%计算第一辆车配送城市的顺序号G1(i)=G1(i)+g(k51(j1)+1);%计算第一辆车的配送量endk61=[];k61=[0,k51,0];%定义第一辆车的配送路径L1(i)=0;%初始化第一辆车的配送路径长度for k11=1:nb1+1L1(i)=L1(i)+Distance(k61(k11)+1,k61(k11+1)+1);%计算第一辆车的配送路径长度endelse%如果第一辆车配送的城市个数不大于0则G1(i)=0;%第一辆车的配送量设为0L1(i)=0;%第一辆车的配送路径长度设为0endk2=find(2==Xv(i,:));%找出第二辆车配送的城市编号nb2=size(k2,2);%计算第二辆车配送城市的个数if nb2>0%判断第二辆车配送城市个数是否大于0,如果大于0则a2=[Xr(i,k2(:))];%找出第二辆车配送城市的顺序号b2=sort(a2);%对找出的第二辆车的顺序号进行排序G2(i)=0;%初始化第二辆车的配送量k52=[];bm=[];for j2=1:nb2bm=find(b2(j2)==Xr(i,:));k52(j2)=intersect(k2,bm);%计算第二辆车配送城市的顺序号G2(i)=G2(i)+g(k52(j2)+1);%计算第二辆车的配送量k62=[];k62=[0,k52,0];%定义第二辆车的配送路径L2(i)=0;%初始化第二辆车的配送路径长度for k22=1:nb2+1L2(i)=L2(i)+Distance(k62(k22)+1,k62(k22+1)+1);%计算第二辆车的路径长度endelse%如果第二辆车配送的城市个数不大于0则G2(i)=0;%第二辆车的配送量设为0L2(i)=0;%第二辆车的配送路径长度设为0endk3=find(3==Xv(i,:));%找出第三辆车配送的城市编号nb3=size(k3,2);%计算第三辆车配送城市的个数if nb3>0%判断第三辆车配送城市个数是否大于0,如果大于0则a3=[Xr(i,k3(:))];%找出第三辆车配送城市的顺序号b3=sort(a3);%对找出的第三辆车的顺序号进行排序G3(i)=0;%初始化第三辆车的配送量k53=[];cm=[];for j3=1:nb3cm=find(b3(j3)==Xr(i,:));k53(j3)=intersect(k3,cm);%计算第三辆车配送城市的顺序号G3(i)=G3(i)+g(k53(j3)+1);%计算第三辆车的配送量endk63=[];k63=[0,k53,0];%定义第三辆车的配送路径L3(i)=0;%初始化第三辆车的配送路径长度for k33=1:nb3+1L3(i)=L3(i)+Distance(k63(k33)+1,k63(k33+1)+1);%计算第三辆车的路径长度endelse%如果第三辆车配送的城市个数不大于0则G3(i)=0;%第三辆车的配送量设为0L3(i)=0;%第三辆车的配送路径长度设为0endL(i)=0;%初始化每个粒子对应的配送方案总路径长度L(i)=L1(i)+L2(i)+L3(i);%计算每个粒子对应的配送方案总路径长度if L(i)<Lg&&G1(i)<Q&&G2(i)<Q&&G3(i)<Q%如果第i个粒子的总路径长度优于历史最优粒子并且满足车辆容量要求Xvg(:)=Xv(i,:);%将粒子i设为历史最优粒子Xrg(:)=Xr(i,:);%将粒子i设为历史最优粒子Lg=L(i);%将粒子i的总路径长度设为最优粒子对应的配送方案的总路径长度elseXvg(:)=Xvg(:);%最优粒子保持不变Xrg(:)=Xrg(:);%最优粒子保持不变Lg=Lg;%最优粒子所对应的配送方案的总路径长度也不变endLimin(i)=10000000;%初始化每个粒子代表的配送方案的历史最优总路径长度if L(i)<Limin(i)%如果本次循环得到的总路径长度优于粒子i历史最优总路径长度Limin(i)=L(i);%更新本次循环得到的总路径长度为粒子i的历史最优路径长度Xvl(i,:)=Xv(i,:);%更新本次得到的粒子i为i粒子的历史最优位置Xrl(i,:)=Xr(i,:); %更新本次得到的粒子i为i粒子的历史最优位置else%否则,保持粒子i的历史最优位置及历史最优路径长度不变Limin(i)=LL(i);Xvl(i,:)=Xv1(i,:);Xrl(i,:)=Xr1(i,:);endend%记录本次循环得到的所有粒子的位置for i=1:Dfor j=1:NXv1(i,j)=Xvl(i,j);%记录本次循环得到的所有粒子的位置Xr1(i,j)=Xrl(i,j);%记录本次循环得到的所有离子的位置endendLL(i)=0;%初始化每个粒子的历史最优路径总长度for i=1:DLL(i)=Limin(i);%对每个粒子的历史最优路径总长度进行赋值end%对粒子群中每个粒子进行迭代for i=1:Dfor j=1:NVv(i,j)=w*Vv(i,j)+c1*rand(1)*(Xvl(i,j)-Xv(i,j))+c2*rand(1)*(Xvg(1,j)-Xv(i,j));%计算位置变化率Vr(i,j)=w*Vr(i,j)+c1*rand(1)*(Xrl(i,j)-Xr(i,j))+c2*rand(1)*(Xrg(1,j)-Xr(i,j));%计算位置变化率%Vv(i,j)和Vr(i,j)进行上下限的限制if Vv(i,j)>K-1Vv(i,j)=K-1;elseif Vv(i,j)<1-KVv(i,j)=1-K;elseVv(i,j)=Vv(i,j);endendendfor i=1:Dfor j=1:NXv(i,j)=ceil(Xv(i,j)+Vv(i,j));%更新位置坐标%对Xv(i,j)进行上下限的限制if Xv(i,j)>KXv(i,j)=K;elseif Xv(i,j)<1Xv(i,j)=1;elseXv(i,j)=Xv(i,j);endXr(i,j)=Xr(i,j)+Vr(i,j);%更新位置坐标endendzx(Loop)=Lg;Loop=Loop+1;endXvg%输出粒子群中的最优粒子Xrg%输出粒子群中的最优粒子Lg%输出最优粒子所代表方案的总路径长度Loop%输出迭代的次数%计算最优粒子所代表的配送方案k1=find(1==Xvg(:));%找出第一辆车配送的城市编号k1=k1';nb1=size(k1,2);%计算第一辆车配送城市的个数if nb1>0%判断第一辆车配送城市个数是否大于0,如果大于0则a1=[Xrg(k1(:))];%找出第一辆车配送城市顺序号b1=sort(a1);%对找出第一辆车的顺序号进行排序G1=0;%初始化第一辆车的配送量k51=[];am=[];for j1=1:nb1am=find(b1(j1)==Xrg(:));k51(j1)=intersect(k1,am);%计算第一辆车配送城市的顺序号G1=G1+g(k51(j1)+1);%计算第一辆车的配送量endk61=[];k61=[0,k51,0];%定义第一辆车的配送路径L1=0;%初始化第一辆车的配送路径长度for k11=1:nb1+1L1=L1+Distance(k61(k11)+1,k61(k11+1)+1);%计算第一辆车的配送路径长度endelse%如果第一辆车配送的城市个数不大于0则G1=0;%第一辆车的配送量设为0L1=0;%第一辆车的配送路径长度设为0endk2=find(2==Xvg(:));%找出第二辆车配送的城市编号k2=k2';nb2=size(k2,2);%计算第二辆车配送城市的个数。
多目标粒子群算法流程

多目标粒子群算法流程
多目标粒子群算法是一种优化算法,用于解决多目标优化问题。
它的流程包括以下几个步骤:
1. 初始化:设置种群大小、粒子的初始位置和速度、惯性权重等参数。
2. 适应度计算:根据目标函数计算每个粒子的适应度值。
3. 个体历史最优更新:根据粒子的适应度值和历史最优位置,更新每个粒子的个体历史最优位置。
4. 群体历史最优更新:根据所有粒子的个体历史最优位置,更新全局历史最优位置。
5. 速度更新:根据个体历史最优位置和全局历史最优位置,以及惯性权重和加速系数,更新每个粒子的速度。
6. 位置更新:根据更新后的速度,更新每个粒子的位置。
7. 终止条件判断:如果达到指定的终止条件(如迭代次数、适应度值等),则算法停止。
8. 输出结果:输出最优解及其对应的适应度值。
多目标粒子群算法的优点是可以同时考虑多个目标函数,并找到它们之间的权衡点,从而得到更加全面和优秀的解。
- 1 -。
粒子群算法——精选推荐

粒⼦群算法粒⼦群算法粒⼦群算法,也称粒⼦群优化算法或鸟群觅⾷算法(Particle Swarm Optimization),缩写为 PSO,是近年来由J. Kennedy和R. C. Eberhart等开发的⼀种新的进化算法(Evolutionary Algorithm - EA)。
PSO 算法属于进化算法的⼀种,和模拟退⽕算法相似,它也是从随机解出发,通过迭代寻找最优解,它也是通过适应度来评价解的品质,但它⽐遗传算法规则更为简单,它没有遗传算法的“交叉”(Crossover)和“变异”(Mutation) 操作,它通过追随当前搜索到的最优值来寻找全局最优。
这种算法以其实现容易、精度⾼、收敛快等优点引起了学术界的重视,并且在解决实际问题中展⽰了其优越性。
粒⼦群算法是⼀种并⾏算法。
1算法介绍粒⼦群优化算法的基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。
PSO的优势在于简单容易实现并且没有许多参数的调节。
⽬前已被⼴泛应⽤于函数优化、神经⽹络训练、模糊系统控制以及其他遗传算法的应⽤领域。
1.1问题提出设想这样⼀个场景:⼀群鸟在随机的搜索⾷物。
在这个区域⾥只有⼀块⾷物,所有的鸟都不知道⾷物在哪。
但是它们知道⾃⼰当前的位置距离⾷物还有多远。
那么找到⾷物的最优策略是什么?最简单有效的就是搜寻⽬前离⾷物最近的鸟的周围区域。
1.2问题抽象鸟被抽象为没有质量和体积的微粒(点),并延伸到N维空间,粒⼦在N维空间的位置表⽰为⽮量X i=(x1,x2,…,x N),飞⾏速度表⽰为⽮量V i=(v1,v2,…,v N)。
每个粒⼦都有⼀个由⽬标函数决定的适应值(fitness value),并且知道⾃⼰到⽬前为⽌发现的最好位置(pbest)和现在的位置X i。
这个可以看作是粒⼦⾃⼰的飞⾏经验。
除此之外,每个粒⼦还知道到⽬前为⽌整个群体中所有粒⼦发现的最好位置(gbest)(gbest 是pbest中的最好值)。
粒子群算法步骤

粒子群算法(Particle Swarm Optimization,PSO)是一种基于群体智能的优化算法,用于解决优化问题。
下面是粒子群算法的一般步骤:1. 初始化参数:- 定义问题的适应度函数。
- 设置群体规模(粒子数量)和迭代次数。
- 随机初始化每个粒子的位置和速度。
- 设置每个粒子的个体最佳位置和整个群体的全局最佳位置。
2. 迭代优化:- 对于每个粒子:- 根据当前位置和速度更新粒子的新速度。
- 根据新速度更新粒子的新位置。
- 根据新位置计算适应度函数值。
- 更新粒子的个体最佳位置和整个群体的全局最佳位置。
- 结束条件判断:达到预设的迭代次数或满足特定的停止条件。
3. 输出结果:- 输出全局最佳位置对应的解作为优化问题的最优解。
在更新粒子的速度和位置时,通常使用以下公式:速度更新:v(t+1) = w * v(t) + c1 * r1 * (pbest - x(t)) + c2 * r2 * (gbest - x(t))位置更新:x(t+1) = x(t) + v(t+1)其中:- v(t) 是粒子在时间t 的速度。
- x(t) 是粒子在时间t 的位置。
- w 是惯性权重,用于平衡粒子的历史速度和当前速度的影响。
- c1 和c2 是加速因子,控制个体和全局最佳位置对粒子速度的影响。
- r1 和r2 是随机数,用于引入随机性。
- pbest 是粒子的个体最佳位置。
- gbest 是整个群体的全局最佳位置。
以上是粒子群算法的基本步骤,您可以根据具体的优化问题进行调整和扩展。
写出基本的粒子群算法,并用球形函数验证。

写出基本的粒子群算法,并用球形函数验证。
粒子群算法是一种经典的群体智能算法,通过模拟鸟群捕食过程中群体的协同行为,寻找最优解。
其基本思想是将问题的解看作空间中的一个粒子,并通过考虑粒子周围的信息和个体最优解来更新粒子的位置,以找到全局最优解。
本文将介绍基本的粒子群算法,并通过验证球形函数的方式对算法进行测试。
基本的粒子群算法的步骤如下:1.初始化粒子群:随机生成一定数量的粒子,并给每个粒子分配一个随机的初速度和位置。
同时,记录每个粒子的历史最优位置和历史最优适应度。
2.计算粒子的适应度:根据问题的适应度函数,计算每个粒子当前位置的适应度。
3.更新粒子的速度和位置:根据粒子的历史最优位置和全局最优位置来更新粒子的速度和位置。
设第i个粒子的当前速度为Vi,当前位置为Xi,历史最优位置为Pi,全局最优位置为Pg,学习因子为c1和c2,速度更新公式为:Vi(t+1) = w * Vi(t) + c1 * rand() * (Pi - Xi) + c2 * rand() * (Pg - Xi)位置更新公式为:Xi(t+1) = Xi(t) + Vi(t+1)其中,w为惯性因子,rand()为0到1的随机数。
4.更新粒子的历史最优位置:比较粒子当前位置的适应度与其历史最优适应度,如果当前适应度更优,则更新历史最优位置。
5.更新全局最优位置:将当前适应度最优的粒子位置作为全局最优位置。
6.终止条件判断:如果满足终止条件(如达到最大迭代次数或适应度满足要求),则停止算法;否则,回到步骤2。
接下来,我们使用球形函数作为问题的适应度函数对粒子群算法进行验证。
球形函数(Sphere Function)是优化问题中常用的测试函数之一,其计算公式为:f(x) = x1^2 + x2^2 + x3^2 + ... + xn^2其中,n为变量的维度。
首先,我们需要确定算法的参数,包括粒子数量、迭代次数、惯性因子w、学习因子c1和c2的取值等。
基本粒子群算法

基本粒子群算法1. 算法原理基本粒子群算法采用常数因子和及常惯性权重,粒子根据如下的公式来更新自己的速度和新的位置。
2. 算法步骤基本粒子群算法的基本步骤如下:(1)随机初始化种群中各微粒的位置和速度;(2)评价每个微粒的适应度,将当前各微子的位置和适应值存储在各微子的中,将所有的中适应最优个体的位置和适应值存储在中;(3)用下式更新粒子的速度和位移:(4)对每个微粒,将其适应值与其经历的最好位置作比较,如果较好,将其作为当前的最好位置;(5)比较当前所有和的值,更新;(6)若满足停止条件(通常为预设的运算精度或迭代次数),搜索停止,输出结果,否知返回(3)继续搜索。
3. 算法MATLAB实现在MATLAB中编程实现的基本粒子群算法优化函数为:。
功能:用基本粒子群算法求解无约束优化问题。
调用格式:其中,:待优化的目标函数;:粒子数目;:学习因子1;:学习因子2;:惯性权重;:最大迭代次数;:自变量的个数;:目标函数取最小值时的自变量值;:目标函数的最小值。
基本粒子群算法的MATLAB代码如下:function [xm,fv]=PSO(fitness,N,c1,c2,w,M,D)% fitness:待优化的目标函数;% N:粒子数目;% c1:学习因子1;% c2:学习因子2;% w:惯性权重;% M:最大迭代次数;% D:自变量的个数;% xm:目标函数取最小值时的自变量值;% fv:目标函数的最小值。
format long;for i=1:Nfor j=1:Dx(i,j)=randn; %随机初始化位置v(i,j)=randn; %随机初始化速度endendfor i=1:Np(i)=fitness(x(i,:));y(i,:)=x(i,:);endpg=x(N,:); %pg为全局最优for i=1:(N-1)if fitness(x(i,:))<fitness(pg)pg=x(i,:);endendfor t=1:Mfor i=1:N %速度、位移更新v(i,:)=w*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(pg-x(i,:)); x(i,:)=x(i,:)+v(i,:);if fitness(x(i,:))<p(i)p(i)=fitness(x(i,:));y(i,:)=x(i,:);endif p(i)<fitness(pg)pg=y(i,:);endendpbest(t)=fitness(pg);endxm=pg';fv=fitness(pg);例采用基本粒子群算法求取函数的最小值。
6种粒子群算法程序

6种粒子群算法程序程序1当c\\ = c i\ = 2 , c n = c22 = 1.5 , w = 1.2 oa)*主函数源程序(main.m)%------ 基本粒子群算法(particle swarm optimization)%------ 名称:基本粒子群算法%------ 初始格式化clear all; %清除所有变量C1C;%清屏format long; %将数据显示为长整形科学计数%……给定初始条条件............N=40; D=10; T=100; cl1=2;%3初始化群体个数%初始化群体维数%初始化群体最迭代次数%学习因子1c21=2;cl2=1.5;c22=1.5;w=L2; eps=10A(-6);%学习因子2%惯性权重%设置精度(在已知最小值的时候用)%……初始化种群个体(限定位置和速度)x=zeros(N,D);v=zeros(N,D); for i=l:Nfor j=l:Dx(lj)=randn; %随机初始化位置v(ij)=randn; %随机初始化速度end end%……显示群位置............... flgure(l)for j=l:Dif(rem(D,2)>0)subplot((D+l)/2,2J)elsesubplot(D/2,2,j)endplot(x(:,j);b*');grid on xlabelC 粒子■) ylabel(*初始位置J tlnfo=strcat(f第*har(j+48)J 维J;tlnfo=strcat(,M \cha r(floor(j/l 0)+48), char(rem(j,l 0)+48),'维');endtitle(tlnfo)end%-一-显示种群速度figure ⑵for j=l:Dif(rem(D^2)>0) subplot((D+l)/2,2J)elsesubplot(D/2,2J)endplot(x(:,j);b*');gricl on xlabelC 粒子') ylabel(,初始速度J tlnfo=strcatf 第,char(j+48),'维');if(j>9)tlnfo=strcat(* 第“har(floor(j/l())+48)9 char(rem(j,l 0)+48),'维);endtitle(tlnfo)endfigure ⑶%第一个图su bp lot( 1,2,1)%……初始化种群个体(在此限定速度和位置) .........xl=x;vl=v;%……初始化个体最优位置和最优值…pl=xl;pbestl=ones(NJ);for i=l:Npbestl (i)=fitness(x 1 (i,: ),D);end%……初始化全局最优位置和最优值 .........gl=l000*ones(l ,D);gbestl=1000;for i=l:Nlf(pbestl(i)<gbest 1)gl=pl(i,:);gbestl=pbestl(i);endendgbl=ones(l,T);%浸入主循环,按照公式依次迭代直到满足精度或者迭代次数…for i=l:Tfor J=1:NIf (fltness(xl(J,:),D)<pbestl(J))pl(J,:)=xl(|,:);pbestl (J)=fitness(x 1Q,: ),D);endlf(pbest 1 (])<gbest 1)gl=pl(j,:); gbestl=pbestl(J);endvl(j,:)=w*vl(J,:)+cll*rand*(pl(J,:)-xl(j,:))+c21*rand*(gl-xl(J,:));xl(J,:)=xl(J,:)+vl(j,:);endgbl(i)=gbestl;endplot(gbl)T empSt r=sprl ntf(• c 1 = %g ,c2=%g\cll,c21);title(TempStr);xiabelC迭代次数);ylabelC适应度值J;%第二个图subplot(l,2,2)%••…初始化种群个体(在此限定速度和位置) .........x2=x;v2=v;%••…初始化种群个体最有位置和最优解 .......p2=x2;pbest2=ones(N,l);for i=l:Npbest2(i)=fltness(x2(i,: ),D);end%••…初始化种全局最有位置和最优解……g2=1000*ones(l ,D);gbest2=1000;for i=X:Nif(pbest2(i)<gbest2)g2=p2(i,:);gbest2=pbest2(i);endendgb2=ones(l,T);%……浸入主循环,按照公式依次迭代直到满足精度或者迭代次数…for i=l:Tfor j=l:Nif (fitness(x2(J,:),D)<pbest2 ⑴)p2(J,:)=x2(j,:); pbest2(j)=fitness(x2(J,:),D);endif(pbest2(J)<gbest2)g2=p2(j,:);gbest2=pbest2(J);endV2(jv)=w*v2(j,:)+cl2*rand*(p2(j,:)-x2(j,:))+c22*rand*(g2-x2(j,:));x2(J,:)=x2(j,:)+v2(j,:);endgb2(i)=gbest2;endplot(gb2)TempStr=sprlntf(t cl= %g ,c2=%g\cl2,c22);title(TempStr);xiabclC迭代次数);ylabelC适应度值J;b)适应度函数%适应度函数(fitness.m)function result=fitness(x,D)sum=0;for i=l:Dsiim=sum+x(i)A2;endresult=sum;程序2当C11 =C2l =2 于C]2 =0,Cj2 = 2,w= 1.2 对比a)%主函数源程序(main.m)% ... 基本粒子群算法(particle swarm optimization)%……名称:基本粒子群算法%……初始格式化clear all; %清除所有变量clc; %清屏format long; %将数据显示为长整形科学计数cl2=0;c22=2;w=1.2; %惯性权重eps=10A(-6); %设置精度(在已知最小值的时候用) %……初始化种群个体(限定位置和速度) .........x=zeros(N,D);v=zeros(N,D);for i=l:Nfor j=l:Dx(lj)=randn; %随机初始化位置v(ij)=randn; %随机初始化速度endend%……显示群位置 ..............figure(l)for j=l:Dif(rem(D,2)>0)subplot((D+1 )/2,2 J)elsesubplot(D/2,2J)endplot(x(:J)/b*t);grid onxlabelC 粒子JylabelC初始位置JtInFo=strcatC 第’,char(j+48),1维f);if(j>9)tlnfo=strcat(f \char(floor(j/10)+48) t char(rem(j,10)+48),'维');endtitle(tlnfo)end%……显示种群速度flgure(2)for j=l:Dif(rem(D,2)>0)subplot((D+l)/2^2J)elsesubplot(D/2,2J)endplot(x(:J)/b*t);grid onxlabelC 粒子JylabelC初始速度Jtlnfo=strcat(v第,char(j+48),'维');if(j>9)tlnfo=strcat(,M t?char(floor(J/10)+48), char(rem(JJ0)+48)/ 维);encltitle(tlnfo)endfigure(3)%第一个图subplot(1^24)%……初始化种群个体(在此限定速度和位置)xl=x;vl=v;%……初始化个体最优位置和最优值…pl=xl;pbestl=ones(N,l);for i=l:Npbestl (i)=fitness(xl(i,:),D);end%……初始化全局最优位置和最优值 .........gl=l000*ones(l Q);gbestl=1000;for i=l:Nif(pbestl(i)<gbestl)gl=pl(i,:); gbestl=pbestl(i); endendgbl=ones(l,T);%••…浸入主循环,按照公式依次迭代直到满足精度或者迭代次数…for i=l:Tfor J=1:Nif (fitness(xl(J^:),D)<pbestl(J))pl(j,:)=xl(j,:);pbest 1 (J)=fitness(x 1 (J),D);endlf(pbestl (J )<gbest 1)gi=pia,:);gbestl=pbestl(j);endvl(J,:)=w*vl(J5:)+cll*ran(l*(pl(J,:)-xl(j,:))+c21*rand*(gl-xl(j,:));xl(j,:)=xl(J,:)+vl(j,:);endgbl(i)=gbestl;endplot(gbl)TempStr=sprlntf(,cl= %g 5c2=%g\cll,c21);title(TempStr);xlabef迭代次数);ylabelC适应度值J;%第二个图subplot( 1,2,2)%••…初始化种群个体(在此限定速度和位置) .........x2=x;v2=v;%-•…初始化种群个体最有位置和最优解 .......p2=x2;pbest2=ones(N,l);for i=l:Npbest2 ⑴=fltness(x2(i,:),D);end%-•…初始化种全局最有位置和最优解……g2=1000*ones(l Q);gbest2=1000;for i=l:Nif(pbest2(i)<gbest2)g2=p2(i,:); gbest2=pbest2(i);endendgb2=ones(l,T);%……浸入主循环,按照公式依次迭代宜到满足精度或者迭代次数…for i=l:Tfor j=l:Nif (fitness(x2(J,:),D)<pbest2(J))p2(j,:)=x2(j,:); pbest2(j)=fitness(x2(J,:),D);endif(pbest2(J)<gbest2)g2=p2(J,:); gbest2=pbest2(j);endv2Q,:)=w*v2(J,:)+cl2*rand*(p2(j,:)-x2(j,:))+c22*rand*(g2-x2(J,:));x2(J,:)=x2(j,:)+v2(j,:);endgb2(i)=gbest2;endplot(gb2)TempStr=sprlntf(,cl= %g ,c2=%f ,cl2,c22);title(TempStr);xlabef迭代次数);ylabelC适应度值J;b)适应度函数%适应度函数(fitness.ni)function result=fitness(x,D)sum=0;for i=l:Dsiim=sum+x(i)A2;end result=sum;程序3当 5 =c 2\ =2,闪=1.2于“2 = 2,C 22 =0,w = 1.2 对比a) %主函数源程序(main.m)% ... 基本粒子群算法(particle swarm optimization )%……名称:基本粒子群算法%……初始格式化clear all;clc;format long; %……给定初始条条件 ........... N=40;D=10;T=100; cl1=2;c21=2;cl2=2;%,初始化群体个数 %初始化群体维数 %初始化群体最迭代次数 %学习因子1 %学习因子2c22=0;w=L2; eps=10A (-6);%惯性权重 %设置精度(在已知最小值的时候用) %……初始化种群个体(限定位置和速度)x=zeros(N,D); v=zeros(N,D);for i=l:Nfor j=l:Dx(ij)=randn; %随机初始化位置 v(ij)=randn; %随机初始化速度 end end%……显示群位置 ..............flgure(l)for J=1:Dif(rem(D,2)>0)subplot((D+l)/2^2J)elsesubplot(D/2,2J)%清除所有变量 %清屏 %将数据显示为长整形科学计数plot(x(:J)/b*,);grid onxlabelC 粒子JylabelC初始位置Jtlnfo=strcat(f第;char(j+48),维J; if(j>9)tlnfo=strcat(,第;char(floor(j/10)+48), char(rem(ja0)+48);维J;encltitle(tlnfo)end%……显示种群速度flgure(2)for j=l:Dif(rem(D^2)>0)su bplot((D+1 )/2,2 J)elsesubplot(D/2,2J)endplot(x(: J;grid onxlabelC 粒子JylabelC初始速度') tInfo=strcatC 第,charQ+48),1维J; if(j>9)tlnfo=strcat(,第;chai*(floor(j/10)+48), char(rem(J40)+48)/ 维);end title(tlnfo)endflgure(3)%第一个图subplot(l929l)%……初始化种群个体(在此限定速度和位置) .........xl=x;vl=v;%……初始化个体最优位置和最优值…pl=xl;pbestl=ones(NJ);for i=l:Nend%……初始化全局最优位置和最优值 .........gl=l000*ones(l ,D);gbestl=1000;for i=l:Nlf(pbestl(i)<gbest 1)gl=pl(i,:);gbestl=pbestl(i);endendgbl=ones(l,T);%浸入主循环,按照公式依次迭代直到满足精度或者迭代次数…for i=l:Tfor J=1:NIf (fltness(xl(J,:),D)<pbestl(J))pl(J,:)=xl(|,:);pbestl (J)=fitness(x 1Q,: ),D);endlf(pbest 1 (])<gbest 1)gl=pl(j,:); gbestl=pbestl(J);endvl(j,:)=w*vl(J,:)+cll*rand*(pl(J,:)-xl(j,:))+c21*rand*(gl-xl(J,:));xl(J,:)=xl(J,:)+vl(j,:);endgbl(i)=gbestl;endplot(gbl)T empSt r=sprl ntf(• c 1 = %g ,c2=%g\cll,c21);title(TempStr);xiabelC迭代次数);ylabelC适应度值J;%第二个图subplot(l,2,2)%••…初始化种群个体(在此限定速度和位置) .........x2=x;v2=v;%••…初始化种群个体最有位置和最优解 .......p2=x2;pbest2=ones(N,l);for i=l:Npbest2(i)=fltness(x2(i,: ),D);end%••…初始化种全局最有位置和最优解……g2=1000*ones(l ,D);gbest2=1000;for i=X:Nif(pbest2(i)<gbest2)g2=p2(i,:);gbest2=pbest2(i);endendgb2=ones(l,T);%……浸入主循环,按照公式依次迭代直到满足精度或者迭代次数…for i=l:Tfor j=l:Nif (fitness(x2(J,:),D)<pbest2 ⑴)p2(J,:)=x2(j,:); pbest2(j)=fitness(x2(J,:),D);endif(pbest2(J)<gbest2)g2=p2(j,:);gbest2=pbest2(J);endv2(J,:)=w*v2(j,:)+cl2*rand*(p2(J,:)-x2(J,:))+c22*rand*(g2-x2(j,:));x2(J,:)=x2(j,:)+v2(j,:);endgb2(i)=gbest2;endplot(gb2)TempStr=sprlntf(f cl= %g ,c2=%g\cl2,c22);title(TempStr);xiabclC迭代次数);ylabelC适应度值J;b)适应度函数%适应度函数(fitness.m)function result=fitness(x,D)sum=0;for i=l:Dsiim=sum+x(i)A2;endresult=sum;程序4对c2, W2分别对其取值Cj =1.1, c2 =2, w, =1.2, w2 =1.5测试函数。
c语言实现的粒子群算法代码及解释

//粒子群PSO算法#include<stdio.h>#include<math.h>#include<time.h>#include<stdlib.h>#define PI 3.141592653589 /* */#define P_num 200 //粒子数目#define dim 50#define low -100 //搜索域范围#define high 100#define iter_num 1000#define V_max 20 //速度范围#define c1 2#define c2 2#define w 0.5#define alp 1double particle[P_num][dim]; //个体集合double particle_loc_best[P_num][dim]; //每个个体局部最优向量double particle_loc_fit[P_num]; //个体的局部最优适应度,有局部最优向量计算而来double particle_glo_best[dim]; //全局最优向量double gfit; //全局最优适应度,有全局最优向量计算而来double particle_v[P_num][dim]; //记录每个个体的当前代速度向量double particle_fit[P_num]; //记录每个粒子的当前代适应度double Sphere(double a[]){int i;double sum=0.0;for(i=0; i<dim; i++){sum+=a[i]*a[i];}return sum;}double Rosenbrock(double a[]){int i;double sum=0.0;for(i=0;i<dim-1; i++){sum+= 100*(a[i+1]-a[i]*a[i])*(a[i+1]-a[i]*a[i])+(a[i]-1)*(a[i]-1);return sum;}double Rastrigin(double a[]){int i;double sum=0.0;for(i=0;i<dim;i++){sum+=a[i]*a[i]-10.0*cos(2*PI*a[i])+10.0;}return sum;}double fitness(double a[]) //适应度函数{return Rastrigin(a);}void initial(){int i,j;for(i=0; i<P_num; i++) //随即生成粒子{for(j=0; j<dim; j++){particle[i][j] = low+(high-low)*1.0*rand()/RAND_MAX; //初始化群体particle_loc_best[i][j] = particle[i][j]; //将当前最优结果写入局部最优集合particle_v[i][j] = -V_max+2*V_max*1.0*rand()/RAND_MAX; //速度}}for(i=0; i<P_num; i++) //计算每个粒子的适应度{particle_fit[i] = fitness(particle[i]);particle_loc_fit[i] = particle_fit[i];}gfit = particle_loc_fit[0]; //找出全局最优j=0;for(i=1; i<P_num; i++){if(particle_loc_fit[i]<gfit){gfit = particle_loc_fit[i];j = i;}for(i=0; i<dim; i++) //更新全局最优向量{particle_glo_best[i] = particle_loc_best[j][i];}}void renew_particle(){int i,j;for(i=0; i<P_num; i++) //更新个体位置生成位置{for(j=0; j<dim; j++){particle[i][j] += alp*particle_v[i][j];if(particle[i][j] > high){parti cle[i][j] = high;}if(particle[i][j] < low){particle[i][j] = low;}}}}void renew_var(){int i, j;for(i=0; i<P_num; i++) //计算每个粒子的适应度{particle_fit[i] = fitness(particle[i]);if(particle_fit[i] < particle_loc_fit[i]) //更新个体局部最优值{particle_loc_fit[i] = particle_fit[i];for(j=0; j<dim; j++) // 更新局部最优向量{particle_loc_best[i][j] = particle[i][j];}}}for(i=0,j=-1; i<P_num; i++) //更新全局变量{if(particle_loc_fit[i]<gfit){gfit = particle_loc_fit[i];j = i;}}if(j != -1){for(i=0; i<dim; i++) //更新全局最优向量{particle_glo_best[i] = particle_loc_best[j][i];}}for(i=0; i<P_num; i++) //更新个体速度{for(j=0; j<dim; j++){particle_v[i][j]=w*particle_v[i][j]+c1*1.0*rand()/RAND_MAX*(particle_loc_best[i][j]-particle[i][j])+c2*1.0*rand()/RAND_MAX*(particle_glo_best[j]-particle[i][j]);if(particle_v[i][j] > V_max){particle_v[i][j] = V_max;}if(particle_v[i][j] < -V_max){particle_v[i][j] = -V_max;}}}}int main(){freopen("result.txt","a+",stdout);int i=0;srand((unsigned)time(NULL));initial();while(i < iter_num){renew_particle();renew_var();i++;}printf("粒子个数:%d\n",P_num);printf("维度为:%d\n",dim);printf("最优值为%.10lf\n", gfit);return 0; }。
粒子群算法matlab代码

一、粒子群主程序psize=20; %粒子个数的设置pd=12; %粒子的维数lz=zeros(psize,pd);for i=1:psize %随机生成粒子群,psize行pd列,pd维。
suiji=rand(1,pd);for j=1:pd/2if suiji(j)<0.5lz(i,j)=fix(unifrnd(0,100))*100;elselz(i,j)=fix(unifrnd(0,100)+1)*100;endendfor j=pd/2+1:1:pdif suiji(j)<0.5lz(i,j)=fix(unifrnd(0,45))/100;elselz(i,j)=fix(unifrnd(0,45)+1)/100;endendlz(i,1:pd/2)=sort(lz(i,1:pd/2));lz(i,pd/2+1:pd)=sort(lz(i,pd/2+1:pd));endlv=lz;goodvalue=lz; %每个粒子自己历史最好值初始化,psize行pd列。
vmax=20; %速度上限c1=2;c2=2; %学习因子w=0.729; %随机因子和惯性因子bestvalue=zeros(1,pd); %全局最好值初始化,1行pd列for j=1:pdbestvalue(1,j)=goodvalue(1,j);endfnew=zeros(1,psize);for j=1:psizefnew(j)=fpso(lz(1,:));endfold=fnew;flagstop=0; %终止标志k=0; %迭代次数记录f0=fpso(bestvalue); %适应值初始化while flagstop==0for i=1:psize %适应值比较,更新各自历史最好值(位置)fnew(i)=fpso(lz(i,:)); %记录每次每个粒子的适应值,便于以后设置终止条件if fnew(i)<fold(i)fold(i)=fnew(i); %fold记录每个粒子的最好历史值goodvalue(i,j)=lz(i,j);endendendfor i=1:psize%每个粒子历史最好值比较,更新全局最好值f1=fold(i);if f1<f0f0=f1;for j=1:pdbestvalue(1,j)=goodvalue(i,j);endendend%*********粒子趋一点终止条件*********%flagstop0=max(abs(fold)); %比较当次的所有粒子的适应值,flagstop1=min(abs(fold)); %若它们之间差别较小,则可以停止。
粒子群算法分类

粒子群算法分类目录粒子群算法分类 (1)一、经典的微粒群算法(PSO)简介 (1)二、经典的微粒群算法的运算过程 (2)三、两种基本的进化模型 (4)四、改进的微粒群算法 (5)五、流程及代码 (7)结论 (19)参考文献 (20)粒子群算法分类一、经典的微粒群算法(PSO)简介微粒群算法(Particle Swarm Optimization)是由美国社会心理学家James Kennedy和电气工程师Russell Eberhart在1995年共同提出的,是继蚁群算法之后的又一种新的群体智能算法,目前已成为进化算法的一个重要分支。
经典粒子群算法的基本思想是模拟鸟类群体行为,并利用了生物学家的生物群体模型,因为鸟类的生活使用了简单的规则:(1)飞离最近的个体;(2)飞向目标;(3)飞向群体的中心;来确定自己的飞行方向和飞行速度,并且成功的寻找到栖息地。
Heppner受鸟类的群体智能启发,建立了模型。
Eberhart和Kennedy对Heppner的模型进行了修正,同时引入了人类的个体学习和整体文化形成的模式,一方面个体向周围的优秀者的行为学习,另一方面个体不断总结自己的经验形成自己的知识库。
从而提出了微粒群算法(PSO)。
该算法由于运算速度快,局部搜索能力强,参数设置简单,近些年已收到学术界的广泛重视,现在微粒群算法在函数优化,神经网络训练,模式分类,模糊系统控制以及其他工程领域都得到了广泛的应用。
二、经典的微粒群算法的运算过程经典粒子群算法和其他的进化算法相似,也采用“群体”与“进化”的概念,同样是根据个体即微粒(particle )的适应度大小进行操作。
所不同的是,微粒群算法不像其他进化算法那样对个体使用进化算子,而是将每个个体看作是在N 维搜索空间中的一个无重量无体积的微粒,并在搜索空间中以一定的速度飞行。
该飞行速度是根据个体的飞行经验和群体的飞行经验来进行动态地调整。
Kennedy 和Eberhart 最早提出的PSO 算法的进化方程如下:其中:下标“i ”表示第i 个微粒,下标“j ”表示的是微粒i 的第j 维分量,t 表示第t 代,学习因子1C 和2C 为非负常数,1C 用来调节微粒向本身最好位置飞行的步长,2C 用来调节微粒向群体最好位置飞行的步长,通常1C 和2C 在[0,2]间取值。
粒子群算法分类

三.算法实现
①随机给出D维空间初始化粒子的速度和位置,并设定迭
代次数N;
②计算每个粒子在当前状态下的适应函数值 pi
;
③将②中计算的适应函数值 pi 与自身的优化解 pbesti 进行比较, 如果
pi pbesti
, 则用新的适
应函数值取代前一轮的优化解, 用新的粒子取代
前一轮粒子。即 pbesti
2. 种群规模N 3.适应度函数
1.学习因子
学习因子(也称加速度系数) 1和 c2分别调节粒 c 子向全局最优粒子和个体最优粒子方向飞行的最大步 长。若太小,则粒子可能远离目标区域;若太大则可 能导致粒子忽然向目标区域飞去或飞过目标区域。合 适的c1 和 c2可以加快收敛且不易陷入局部最优,目前
time=etime(clock,t0)
1.基本粒子群算法输出
2.改进后输出
3.比较
结论
通过粒子群算法能够很快的实现分类。而且通过惯 性权重的线性更新可以有效的防止局部最优。每种聚类 数目下的最优聚类可以根据输出的适应度fg判断,适应
度值越小越好,并且需多次运行判断。
参考文献
[1] 杨淑莹. 模式识别与智能计算[M].北京:电子工业出版
行移动,产生新的粒子,直到适应度不变。
流程图
开始 初始化 计算聚类中心和适应度 求取pid和pgd 更新惯性权重 更新粒子的速度和位置 以粒子位置为聚类中心重新聚类 N
达到终止条件 Y 输出结果
四.部分代码及仿真
clc; clear all; %sam=xlsread('.xls'); t0=clock;%开始计时 sam=[2793.36 1766.08 1207.88 245.75 3009.26 1803.14 1600.62 3373.67 1073.55 1895.18 3123.07 2248.4
粒子群算法的基本流程

粒子群算法的基本流程粒子群算法(Particle Swarm Optimization,PSO)是一种模拟鸟群觅食行为的优化算法,通过模拟鸟群中个体之间的协作和信息共享,寻找最优解。
它最早由美国社会心理学家Kennedy和Eberhart于1995年提出,被广泛应用于各个领域的优化问题。
粒子群算法的基本流程可以分为初始化、迭代更新和停止准则三个步骤。
1. 初始化在粒子群算法中,需要初始化一组粒子,每个粒子代表问题的一个解。
粒子的位置表示解的搜索空间中的一个点,粒子的速度表示解的搜索方向和速度。
初始化时,需要给每个粒子随机分配一个位置和速度,并记录每个粒子的历史最佳位置和全局最佳位置。
2. 迭代更新在每一次迭代中,需要更新每个粒子的位置和速度,以及更新每个粒子的历史最佳位置和全局最佳位置。
2.1 更新粒子的速度粒子的速度更新公式为:v(t+1) = w * v(t) + c1 * rand() * (pbest - x(t)) + c2 * rand() * (gbest - x(t))其中 v(t+1) 表示粒子在下一次迭代中的速度,v(t) 表示粒子当前的速度,w 是惯性权重,c1 和 c2 是加速因子,rand() 是一个介于0和1之间的随机数,pbest 表示粒子的历史最佳位置,gbest 表示全局最佳位置,x(t) 表示粒子当前的位置。
2.2 更新粒子的位置粒子的位置更新公式为:x(t+1) = x(t) + v(t+1)其中x(t+1) 表示粒子在下一次迭代中的位置,x(t) 表示粒子当前的位置,v(t+1) 表示粒子在下一次迭代中的速度。
2.3 更新粒子的历史最佳位置和全局最佳位置在每次迭代中,需要根据当前位置和历史最佳位置来更新粒子的历史最佳位置。
同时,需要根据所有粒子的历史最佳位置来更新全局最佳位置。
3. 停止准则迭代更新的过程会持续进行,直到满足停止准则为止。
常见的停止准则有达到最大迭代次数、目标函数值收敛等。
粒子群算法程序

粒子群算法程序function [m_pattern]=C_PSO(m_pattern,patternNum)disType=DisSelDlg();%获得距离计算型[centerNum iterNum]=InputClassDlg;%获得聚类中心数和最大迭代次数particleNum=200;%初始化粒子数%初始化中心和速度global Nwidth;for i=1:centerNumm_center(i).feature=zeros(Nwidth,Nwidth);m_center(i).patternNum=0;m_center(i).index=i;m_velocity(i).feature=zeros(Nwidth, Nwidth);for i=1:particleNumParticle(i).location=m_center;%粒子各中心Particle(i).velocity=m_velocity;%粒子各中心速度Particle(i).fitness=0;%适应度P_id(i).velocity=m_velocity;%粒子最优速度P_id(i).location=m_center;%粒子最优中心P_id(i).fitness=0;%粒子最优适应度endP_gd.location=m_center;%全局粒子最优中心P_gd.velocity=m_velocity;%全局粒子最优速度P_gd.fitness=0;%粒子全局最优适应度P_gd.string=zeros(1,patternNum);ptDitrib=zeros(particleNum,patternNum);%初始化粒子分布矩阵for i=1:particleNum %生产随机粒子分布矩阵ptDitrib(i,:)=randperm(patternNum);for j=1:patternNumif (ptDitrib(i,j)>centerNum)ptDitrib(i,j)=fix(rand*centerNum+1);endendend%生产初始粒子群for i=1:particleNumfor j=1:patternNumm_pattern(j).category=ptDitrib(i,j);endfor j=1:centerNumm_center(j)=CalCenter(m_center(j),m_pattern,patternNum);endParticle(i).location=m_center;end%初始化参数w_max=1;w_min=0;h1=2;h2=2;for iter=1:iterNum%计算粒子适应度for i=1:particleNumtemp=0;for j=1:patternNumtemp=temp+GetDistance(m_pattern(j),Particle(i).location(ptDitrib(i,j)),disType); endif (temp==0)%最优解,直接退出iter=iterNum+1;break;endParticle(i).fitness=1/temp;endif(iter>iterNum)break;endw=w_max-iter*(w_max-w_min)/iterNum;%更新权重系数for i=1:particleNum %更新P_id,P_gdif (Particle(i).fitness>P_id(i).fitness)P_id(i).fitness=Particle(i).fitness;P_id(i).location=Particle(i).location;P_id(i).velocity=Particle(i).velocity;if (Particle(i).fitness>P_gd(i).fitness)P_gd(i).fitness=Particle(i).fitness;P_gd(i).location=Particle(i).location;P_gd(i).velocity=Particle(i).velocity;P_gd.string=ptDitrib(i,:);endendend%更新粒子速度,位置for i=1:particleNumfor j=1:centerNumParticle(i).velocity(j).feature =...w*Particle(i).velocity(j).feature+h1*rand(Nwidth,Nwidth).*...(P_id(i).location(j).feature-Particle(i).location(j).feature)...+h2*rand(Nwidth, Nwidth).*(P_gd.location(j).feature...-Particle(i).location(j).feature);Particle(i).location(j).feature= Particle(i).location(j).feature...+ Particle(i).velocity(j).feature;endend%最近邻聚类for i=1:particleNumfor j=1:patternNummin=inf;for k=1:centerNumtempDis=GetDistance(m_pattern(j), Particle(i).location(k),disType);if(tempDis<min)min=tempDis;m_pattern(j).category=k;ptDitrib(i,j)=k;endendend%重新计算聚类中心for j=1:centerNumParticle(i).location(j)=CalCenter(Particle(i).location(j),m_pattern,patternNum); endendfor i=1:patternNumm_pattern(i).category=P_gd.string(1,i);endendend。
粒子群优化算法(详细易懂-很多例子)讲解学习

粒子群算法的构成要素 -停止准则
停止准则一般有如下两种: 最大迭代步数 可接受的满意解
v i k d = w v i k d - 1 c 1 r 1 ( p b e s t i d x i k d 1 ) c 2 r 2 ( g b e s t d x i k d 1 )
粒子速度更新公式包含三部分: 第一部分为粒子先前的速度 第二部分为“认知”部分,表示粒子本身的思考,可理解为 粒子i当前位置与自己最好位置之间的距离。 第三部分为“社会”部分,表示粒子间的信息共享与合作, 可理解为粒子i当前位置与群体最好位置之间的距离。
惯性因子
基本粒子群算法
失去对粒子本身
的速度的记忆
粒子群算法的构成要素-权重因子 权重因子:惯性因子 、学习因子
v i k d = w v i k d - 1 c 1 r 1 ( p b e s t i d x i k d 1 ) c 2 r 2 ( g b e s t d x i k d 1 )
Xik=Xik1+Vik1
V i =V i1,V i2,...,V iN X i= X i1,X i2,...,X iN
算法流程
1. Initial:
初始化粒子群体(群体规模为n),包括随机位置和速度。
2. Evaluation:
根据fitness function ,评价每个粒子的适应度。
3. Find the Pbest:
粒子群优化算法(PS0)
粒子群算法详解

粒子群算法详解
粒子群算法是一种群智能算法,常用于优化问题,如寻找函数的最小值或最大值等。
其基本原理是模拟鸟群或鱼群等生物集体行为,通过不断地调整每个粒子的位置和速度,最终找到最优解。
具体来说,粒子群算法由若干个粒子组成,每个粒子都有自己的位置和速度。
在每一次迭代中,每个粒子会根据自己的位置和速度进行更新,通过与其他粒子的交互来不断调整自己的位置和速度,以期望找到最优解。
具体而言,粒子群算法包括以下几个步骤:
1. 初始化粒子群:设置粒子群大小、每个粒子的位置和速度等参数。
2. 计算适应度函数:根据问题的具体情况,设计适应度函数,用于评估每个粒子的表现。
3. 更新粒子位置和速度:根据当前位置和速度,以及适应度函数的结果,更新每个粒子的位置和速度。
4. 更新全局最优解:根据适应度函数的结果,更新全局最优解。
5. 判断迭代终止条件:通过设定迭代次数或适应度函数的阈值等方式,判断是否需要继续迭代。
6. 输出结果:输出最优解或其他需要的结果。
总体来说,粒子群算法的优点是收敛速度快,易于实现和优化,适用于各种优化问题。
但其缺点是可能会陷入局部最优解,需要合理设置参数和调整算法,以克服这个问题。
粒子群算法ppt课件

粒子群算法Reynolds,Heppner,Grenader等发现,鸟群在行进过程中会突然同步地改变方向,散开或聚集。
一定有种潜在的规则在起作用,据此他们提出了对鸟群行为的模拟。
在他们的早期模型中,仅仅依赖个体间距的操作,即群体的同步是个体之间努力保持最优距离的结果。
1987年Reynolds对鸟群社会系统的仿真研究,一群鸟在空中飞行,每个鸟遵守以下三条规则:1)避免与相邻的鸟发生碰撞冲突;2)尽量与自己周围的鸟在速度上保持协调和一致;3)尽量试图向自己所认为的群体中靠近。
仅通过使用这三条规则,系统就出现非常逼真的群体聚集行为,鸟成群地在空中飞行,当遇到障碍时它们会分开绕行而过,随后又会重新形成群体。
作为CASKennedy和Eberhart在CAS中加入了一个特定点,定义为食物,鸟根据周围鸟的觅食行为来寻找食物。
他们的初衷是希望通过这种模型来模拟鸟群寻找食源的现象,然而实验结果却揭示这个仿真模型中蕴涵着很强的优化能力,尤其是在多维空间寻优中。
鸟群觅食行为Food Global BestSolutionPast BestSolution车辆路径问题构造一个2L维的空间对应有L个发货点任务的VRP问题,每个发货点任务对应两维:完成该任务车辆的编号k,该任务在k车行驶路径中的次序r为表达和计算方便,将每个粒子对应的2L维向量X分成两个L维向量:Xv(表示各任务对应的车辆)和Xr(表示各任务在对应的车辆路径中的执行次序)。
例如,设VRP问题中发货点任务数为7,车辆数为3,若某粒子的位置向量X为:发货点任务号: 1 2 3 4 5 6 7Xv : 1 2 2 2 2 3 3Xr : 1 4 3 1 2 2 1则该粒子对应解路径为:车1:0 → 1 → 0车2:0 → 4 →5 → 3→ 2→ 0车3:0 → 7→ 6→ 0粒子速度向量V与之对应表示为Vv和Vr。
该表示方法的最大优点是使每个发货点都得到车辆的配送服务,并限制每个发货点的需求仅能由某一车辆来完成,使解的可行化过程计算大大减少。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
gb1=ones(1,T); %----- 浸入主循环,按照公式依次迭代直到满足精度或者迭代次数 --for i=1:T
for j=1:N if (fitness(x1(j,:),D)<pbest1(j)) p1(j,:)=x1(j,:); pbest1(j)=fitness(x1(j,:),D); end if (pbest1(j)<gbest1) g1=p1(j,:); gbest1=pbest1(j); end
subplot((D+1)/2,2,j) else
subplot(D/2,2,j) end plot(x(:,j), 'b*' );grid on xlabel('粒子 ') ylabel('初始速度 ') tInfo=strcat('第,char(j+48),'维 '); if (j>9) tInfo=strcat( '第 ',char(floor(j/10)+48), char(rem(j,10)+48),'维); end title(tInfo) end figure(3) %第一个图 subplot(1,2,1)
figure(1)
for j=1:D
if (rem(D,2)>0)
subplot((D+1)/2,2,j) else
subplot(D/2,2,j) end plot(x(:,j), 'b*' );grid on xlabel('粒子 ') ylabel('初始位置 ') tInfo=strcat('第',char(j+48),'维 '); if (j>9) tInfo=strcat('第 ',char(floor(j/10)+48) , char(rem(j,10)+48),'维'); end title(tInபைடு நூலகம்o) end %------ 显示种群速度 figure(2) for j=1:D if (rem(D,2)>0)
end end gb2=ones(1,T); %------ 浸入主循环,按照公式依次迭代直到满足精度或者迭代次数 --for i=1:T
for j=1:N if (fitness(x2(j,:),D)<pbest2(j)) p2(j,:)=x2(j,:); pbest2(j)=fitness(x2(j,:),D); end if (pbest2(j)<gbest2) g2=p2(j,:);
end gb1(i)=gbest1; end
plot(gb1) TempStr=sprintf('c1= %g ,c2=%g',c11,c21); title(TempStr); xlabel('迭代次数 '); ylabel('适应度值 '); %第二个图 subplot(1,2,2) %----- 初始化种群个体(在此限定速度和位置) -----------x2=x; v2=v; %----- 初始化种群个体最有位置和 最优解 ----------p2=x2; pbest2=ones(N,1); for i=1:N
gbest2=1000; for i=1:N
if (pbest2(i)<gbest2) g2=p2(i,:); gbest2=pbest2(i);
end end gb2=ones(1,T); %------ 浸入主循环,按照公式依次迭代直到满足精度或者迭代次数 --for i=1:T
for j=1:N if (fitness(x2(j,:),D)<pbest2(j)) p2(j,:)=x2(j,:); pbest2(j)=fitness(x2(j,:),D); end if (pbest2(j)<gbest2) g2=p2(j,:); gbest2=pbest2(j); end
subplot(D/2,2,j) end plot(x(:,j), 'b*' );grid on xlabel('粒子 ') ylabel('初始速度 ') tInfo=strcat('第,char(j+48),'维 '); if (j>9) tInfo=strcat( '第 ',char(floor(j/10)+48), char(rem(j,10)+48),'维); end title(tInfo) end figure(3) %第一个图 subplot(1,2,1) %------ 初始化种群个体(在此限定速度和位置) -----------x1=x; v1=v; %------ 初始化个体最优位置和最优值 --p1=x1; pbest1=ones(N,1); for i=1:N pbest1(i)=fitness(x1(i,:),D); end %------ 初始化全局最优位置和最优值 --------------g1=1000*ones(1,D); gbest1=1000; for i=1:N if (pbest1(i)<gbest1)
pbest2(i)=fitness(x2(i,:),D); end %----- 初始化种全局最有位置和 最优解 -----g2=1000*ones(1,D); gbest2=1000; for i=1:N
if (pbest2(i)<gbest2) g2=p2(i,:); gbest2=pbest2(i);
程
序
1
当 c11 c21 2 , c12 c22 1.5 , w 1.2 。
a)% 主函数源程序()
%------ 基本粒子群算法 (particle swarm optimization)
%------ 名称: 基本粒子群算法
%------ 初始格式化
clear all;
%清除所有变量
clc;
%清屏
v1(j,:)=w*v1(j,:)+c11*rand*(p1(j,:)-x1(j,:))+c21*rand*(g1-x1(j,:)); x1(j,:)=x1(j,:)+v1(j,:);
end gb1(i)=gbest1; end plot(gb1) TempStr=sprintf('c1= %g ,c2=%g',c11,c21); title(TempStr); xlabel('迭代次数 '); ylabel('适应度值 '); %第二个图 subplot(1,2,2) %----- 初始化种群个体(在此限定速度和位置) -----------x2=x; v2=v; %----- 初始化种群个体最有位置和 最优解 ----------p2=x2; pbest2=ones(N,1); for i=1:N pbest2(i)=fitness(x2(i,:),D); end %----- 初始化种全局最有位置和 最优解 -----g2=1000*ones(1,D);
if (j>9)
tInfo=strcat('第 ',char(floor(j/10)+48) ,
char(rem(j,10)+48),'维'); end
title(tInfo)
end
%------ 显示种群速度 figure(2)
for j=1:D
if (rem(D,2)>0)
subplot((D+1)/2,2,j) else
gbest2=pbest2(j); end v2(j,:)=w*v2(j,:)+c12*rand*(p2(j,:)-x2(j,:))+c22*rand*(g2-x2(j,:)); x2(j,:)=x2(j,:)+v2(j,:); end gb2(i)=gbest2; end plot(gb2) TempStr=sprintf('c1= %g ,c2=%g',c12,c22); title(TempStr); xlabel('迭代次数 '); ylabel('适应度值 '); b)适应度函数 %适应度函数() function result=fitness(x,D) sum=0; for i=1:D sum=sum+x(i)^2; end result=sum; 程序 2
v2(j,:)=w*v2(j,:)+c12*rand*(p2(j,:)-x2(j,:))+c22*rand*(g2-x2(j,:)); x2(j,:)=x2(j,:)+v2(j,:);
end gb2(i)=gbest2; end plot(gb2) TempStr=sprintf('c1= %g ,c2=%g',c12,c22); title(TempStr); xlabel('迭代次数 '); ylabel('适应度值 '); b)适应度函数 %适应度函数() function result=fitness(x,D) sum=0; for i=1:D sum=sum+x(i)^2;
当 c11 c21 2 于 c12 0, c22 2, w 1.2 对比
a)%主函数源程序()
%------ 基本粒子群算法 (particle swarm optimization)
%------ 名称: 基本粒子群算法
%------ 初始格式化
clear all;
%清除所有变量
