理想气体状态方程专题训练
理想气体状态方程练习及答案

例1:如图所示,气缸A和容器B由一细管经阀门K相 连,A和B的壁都是透热的,A是放置在27℃、1atm 的空气中,B浸在127℃的恒温槽内.开始时,K是关 闭的,B内为真空,容积VB=10L,A内装有理想气体 ,体积VA=10L.假设气缸壁和活塞D之间无摩擦,细 管的容积可忽略不计,打开K,使气体由A流入B, 等到活塞D停止移动时,A内气体的体积将是多少? 答案:A内气体的体积将是2.5L
答案: ① p=1.43×105pa ,②fm=600N
例7:一个质量可不计的活塞将一定量的气体封闭在上端开口 的直圆柱形气缸内,活塞的面积为600cm3,活塞上堆放着铁砂, 如图所示。最初活塞搁置在气缸内壁的固定卡环上,气体柱的 高度为H0=20cm,温度为20℃,气体压强为1atm。 (不计活塞 与气缸之间的摩擦) ①现对气体缓缓加热,当气体温度升高到57℃时,活塞(及铁砂) 刚好开始离开卡环而上升,求铁砂的质量。 ②继续加热,当温度又升高多少时,气体柱高度H1长为30cm。 ③此后维持温度不变,逐渐取走铁砂,则直到铁砂全部取走 时,气柱长H2为多少?
答案: ①铁砂的质量为60kg。 ②温度为495K,又升高了165K。 ③H2为33cm。
例8: 、如图所示,气缸放置在水平平台上,活塞质量为 10kg,横截面积50cm2,厚度1cm,气缸全长21cm, 气缸质量20kg,大气压强为1×105Pa,当温度为7℃时, 活塞封闭的气柱长10cm,若将气缸倒过来放置时,活塞 下方的空气能通过平台上的缺口与大气相通 。g取10m/s2求: (1)气柱多长? (2)当温度多高时,活塞刚好接触平台? (3)当温度多高时,缸筒刚好对地面无压力。 (活塞摩擦不计)。
答案:(1)28cm(2)237℃
例5:如图所示,一个内径均匀的双U形曲管,用水银柱 将管的A部分封闭了一定质量的气体,当温度为T1 (K)时,空气柱A的长度为40 cm,右侧曲管的水银面 高度差为16 cm,当温度变为T2(K)时,量得曲管B处 的水银面比原来升高了10 cm,若外界大气压为76 cmHg,则T1: T2应为( ). A.2:1 B.3:1 C.4:1 D.3:2
理想气体状态方程应用练习题

理想气体状态方程应用练习题在学习物理学的过程中,理想气体状态方程是一个非常重要的知识点。
它不仅在理论研究中有着广泛的应用,在实际生活和工程领域也发挥着重要的作用。
接下来,让我们通过一些练习题来深入理解和掌握理想气体状态方程的应用。
一、基础练习题1、一密闭容器中装有一定质量的理想气体,在温度为 27℃时,压强为 10×10^5 Pa。
若将温度升高到 127℃,则容器内气体的压强变为多少?解:已知初始温度$T_1 = 27 + 273 = 300$ K,初始压强$P_1 =10×10^5$ Pa,最终温度$T_2 = 127 + 273 = 400$ K。
根据理想气体状态方程$P_1V_1/T_1 = P_2V_2/T_2$,由于容器密闭,体积不变,即$V_1 = V_2$。
所以$P_2 = P_1×T_2/T_1 =10×10^5×400/300 ≈ 133×10^5$ Pa2、一个容积为 20 L 的钢瓶中装有 150 atm 的氧气,若使用掉一半的氧气后,瓶内氧气的压强变为多少?温度不变。
解:初始压强$P_1 = 150$ atm,初始体积$V_1 = 20$ L,使用掉一半氧气后,剩余气体的物质的量为原来的一半。
因为温度不变,根据理想气体状态方程$P_1V_1 = P_2V_2$,体积不变,$V_1 = V_2$。
所以$P_2 = P_1/2 = 150/2 = 75$ atm二、综合练习题1、一定质量的理想气体,在压强不变的情况下,温度从 0℃升高到 100℃时,其体积增加了 1/3。
求原来气体的温度是多少?解:设原来气体的温度为$T_1$,最终温度$T_2 = 100 + 273 =373$ K。
根据理想气体状态方程$V_1/T_1 = V_2/T_2$,压强不变,$P_1 = P_2$。
已知体积增加了 1/3,即$V_2 = 4/3 V_1$。
理想气体的状态方程习题

理想气体状态方程习题1.如图所示,A、B两点代表一定质量理想气体的两个不同的状态,状态A的温度为T A,状态B的温度为T B。
由图可知A.T A =2T B B.T B =4T AC.T B =6T A D.T B =8T A2.一定质量理想气体A.先等压膨胀再等容降温,其温度必低于起始温度B.先等温膨胀再等压压缩,其体积必小于起始体积C.先等容升温再等压压缩,其温度有可能等于起始温度D.先等容加热再绝热压缩,其内能必大3.对于一定质量的理想气体,下述四个论述中正确的是A.当分子热运动变剧烈时,压强必变大B.当分子热运动变剧烈时,压强可以不变C.当分子间的平均距离变大时,压强必变小D.当分子间的平均距离变大时,压强必变大4.对一定质量的理想气体,下列状态变化中不可能的是A.使气体体积增大,同时温度降低、压强减小B.使气体温度升高,体积不变、压强减小C.使气体温度不变,而压强、体积同时增大D.使气体温度降低,压强减小、体积减小5.在下图中,不能反映理想气体经历了等温变化→等容变化→等压变化,又回到原来状态的图是6.如图所示,一定质量的理想气体,由状态A沿直线AB变化到B,在此过程中,气体分子的平均速率的变化情况是A.不断增大B.不断减小C.先减小后增大D.先增大后减小7.一定质量的某种气体自状态A经状态C变化到状态B,这一过程在V-T图上如图所示,则A.在过程AC中,气体的压强不断变大B.在过程CB中,气体的压强不断变小C.在状态A时,气体的压强最大D .在状态B 时,气体的压强最大8.如图所示,内壁光滑的气缸和活塞都是绝热的,缸内被封闭的理想气体原来体积为V ,压强为p ,若用力将活塞向右压,使封闭的气体体积变为V 2,缸内被封闭气体的 A .压强等于2p B .压强大于2p C .压强小于2p D .分子势能增大了9.甲、乙两个相同的密闭容器中分别装有等质量的同种气体,已知甲、乙容器中气体的压强分别为p 甲、p 乙,且p 甲<p 乙,则A .甲容器中气体的温度高于乙容器中气体的温度B .甲容器中气体的温度低于乙容器中气体的温度C .甲容器中气体分子的平均动能小于乙容器中气体分子的平均动能D .甲容器中气体分子的平均动能大于乙容器中气体分子的平均动能10.已知理想气体的内能与温度成正比.如图所示的实线为汽缸内一定质量的理想气体由状态1到状态2的变化曲线,则在整个过程中汽缸内气体的内能A .先增大后减小B .先减小后增大C .单调变化D .保持不变11.一定质量的气体做等压变化时,其V -t 图象如图所示,若保持气体质量不变,使气体的压强增大后,再让气体做等压变化,则其等压线与原来相比,下列可能正确的是A .等压线与t 轴之间夹角变大B .等压线与t 轴之间夹角不变C .等压线与t 轴交点的位置不变D .等压线与t 轴交点的位置一定改变12.如图所示为一定质量的理想气体沿着所示的方向发生状态变化的过程,则该气体压强变化是A .从状态c 到状态d ,压强减小B .从状态d 到状态a ,压强不变C .从状态a 到状态b ,压强增大D .从状态b 到状态c ,压强不变13.如图所示,一定质量的某种理想气体,由状态A 沿直线AB 变化到状态B ,A 、C 、B 三点所对应的热力学温度分别记为T A 、T C 、T B ,在此过程中,气体的温度之比T A ∶T B ∶T C 为A .1∶1∶1B .1∶2∶3C .3∶3∶4D .4∶4∶314.如图所示是一定质量的理想气体的p-V图线,若其状态由A→B→C→A,且A→B等容,B→C等压,C→A等温,则气体在ABC三个状态时A.单位体积内气体的分子数n a=n B=n CB.气体分子的平均速率v A>v B>v CC.气体分子在单位时间内对器壁的平均作用力F A>F B,F B=F CD.气体分子在单位时间内,对器壁单位面积碰撞的次数是N A>N B,N A>N C15.光滑绝热的活塞把密封的圆筒容器分成A、B两部分,这两部分充有温度相同的气体,平衡时V A∶V B=1∶2,现将A中气体加热到127 ℃,B中气体降低到27 ℃,待重新平衡后,这两部分气体体积的比V′A∶V′B为A.1∶1 B.2∶3 C.3∶4 D.2∶116.一个半径为0.1 cm的气泡,从18 m深的湖底上升.如果湖底水的温度是8 ℃,湖面的温度是24 ℃,湖面的大气压强是76 cmHg,那么气泡升至湖面时体积是多少?17.如图所示粗细均匀一端封闭一端开口的U形玻璃管,当t1=31℃,大气压强P0=76cmHg时,两管水银面相平,这时左管被封闭的气柱长L l= cm,则(1)当温度t2等于多少时,左管气柱长为9 cm?(2)当温度达到上问中的温度t2时,为使左管气柱长为8cm,应在右管中加人多长的水银柱?。
(完整版)理想气体状态方程专题训练
理想气体状态方程专题训练一、封闭气体压强计算1.在图中,各装置均静止,已知大气压强为P0 ,液体密度为ρ,求被封闭气体的压强p2.如图所示,一个横截面积为S的圆筒形容器竖直放置.金属圆板A的上表面是水平的,下表面是倾斜的,下表面与水平面的夹角为θ,圆板的质量为M.不计圆板与容器内壁之间的摩擦.若大气压强为p0,则求被圆板封闭在容器中的气体的压强p.3.如图所示,光滑水平面上放有一质量为M的汽缸,汽缸内放有一质量为m、可在气缸内无摩擦滑动的活塞,活塞面积为S,现用水平恒力F向右推汽缸,最后汽缸和活塞达到相对静止状态,求此时缸内封闭气体的压强P。
(已知外界大气压为P0)二、理想气体状态方程的基础应用4.一定质量的理想气体由状态A经过状态B变为状态C,其有关数据如p-T图象甲所示.若气体在状态A的温度为-73.15℃,在状态C的体积为0.6m3.求:(1)状态A的热力学温度;(2)说出A至C过程中气体的变化情形,并根据图象提供的信息,计算图中V A的值;(3)在图乙坐标系中,作出由状态A经过状态B变为状态C的V-T图象,并在图线相应位置上标出字母A、B、C.如果需要计算才能确定坐标值,请写出计算过程.三、单一封闭气体问题5.一足够长的粗细均匀的玻璃管开口向上竖直放置,管内由15cm长的水银柱封闭着50cm长的空气柱.若将管口向下竖直放置,空气柱长变为多少cm?(设外界大气压强为75cmHg,环境温度不变)6.在如图所示的气缸中封闭着温度为400K的空气,一重物用绳索经滑轮与缸中活塞相连接,重物和活塞均处于平衡状态,这时活塞离缸底的高度为10cm,如果缸内空气变为300K,问:(1)重物是上升还是下降?(2)这时重物将从原处移动多少厘米?(设活塞与气缸壁间无摩擦)7.如图所示,固定的绝热气缸内有一质量为m的“T”型绝热活塞(体积可忽略),距气缸底部h0处连接一U形管(管内气体的体积忽略不计).初始时,封闭气体温度为T0,活塞距离气缸底部为1.5h0,两边水银柱存在高度差.已知水银的密度为ρ,大气压强为p0,气缸横截面积为s,活塞竖直部分长为1.2h0,重力加速度为g.试问:(1)初始时,水银柱两液面高度差多大?(2)缓慢降低气缸内封闭气体的温度,当U形管两水银面相平时封闭气体的温度是多少?8.一汽缸竖直放在水平地面上,缸体质量M= 10kg,活塞质量M=4kg,活塞横截面积S=2×10-3 m2,活塞上面的汽缸内封闭了一定质量的理想气体,下面有气孔O与外界相通,大气压强p0=1.0×105Pa.活塞下面与劲度系数k = 2×103 N/m 的轻弹簧相连.当汽缸内气体温度为127℃时弹簧为自然长度,此时缸内气柱长度L1=20 cm,g取10m/s2,缸体始终竖直,活塞不漏气且与缸壁无摩擦.①当缸内气柱长度L2=24cm时,缸内气体温度为多少K?②缸内气体温度上升到T0以上,气体将做等压膨胀,则T0为多少K?四、多个相互关联的封闭气体问题9.如图,绝热气缸A与导热气缸B均固定于地面,由刚性杆连接的绝热活塞与两气缸间均为摩擦。
知识点:理想气体状态方程式(综合训练)

求:V0=? 解:空气的质量流量不变,则有
PV P0V0
T
T0
该风量换算为标准状态下风量为
V0
V
PT0 P0T
10200 869 273 760 (273 300)
5556.7
Nm3/h
知识点:理想气体状态方程式
3. 空气压缩机的贮气罐上的压力表读数为0.35MPa,温
度计读数为20℃。该贮气罐容积为2.8m3,求罐内空气质量。 已知大气压力755mmHg。若经过一段时间后,由于漏气使压 力表读数降低为0.305MPa,其余不变,求漏掉的空气质量。
已知:贮气罐初参数pe1=0.35MPa t1=20℃ V1=2.8m3 贮气罐终参数pe2=0.305MPa t2=20℃ V2= V1 大气 压pb=755mmHg
求:初参数下罐内空气质量m1=?、终参数下漏掉的空 气质量m1-m2=?
解:贮气罐初始绝对压力 p1= pb+pe1 =755×133.3+0.35×106=450641.5Pa
由理想气体状态方程,初参数下罐内空气质量
知识点:理想气体状态方程式
m1
p1V1 RT1
450641.5 2.8 287 (273 20)
15
kg
终参数下漏掉的空气质量
m1
m2
V1 RT1
( p1
p2 )
V1 RT1
( pe1
pe2 )
2.8 (0.35 0.305) 106 1.5 kg 287 293
高中物理理想气体的状态方程成长训练新人教选修

3 理想气体的状态方程主动成长夯基达标1.一定质量的理想气体,初始状态为p 、V 、T ,经过一系列状态变化后,压强仍为p ,则下列过程中可以实现的是( )A.先等温膨胀,再等容降温B.先等温压缩,再等容降温C.先等容升温,再等温压缩D.先等容降温,再等温压缩 解析:根据理想气体的状态方程C T PV =,若经过等温膨胀则T 不变V 增大,再经等容降温V 不变,T 减小,由C TPV =可知,V 增大,T 减小,P 一定变化.A 不正确.同理可以判断C 不正确,B 、D 正确. 答案:BD2.一定质量的理想气体经过一系列过程,如图8-3-3所示,下列说法中正确的是( )图8-3-3A.a→b 过程中,气体体积增大,压强减小B.b→c 过程中,气体压强不变,体积增大C.c→a 过程中,气体压强增大,体积变小D.c→a 过程中,气体内能增大,体积不变解析:a→b 过程中,T 不变,分子平均动能不变,p 减小,分子密集程度变小,气体体积变大,选项A 正确.b→c 过程中,压强不变,温度降低,分子平均动能变小,分子密集程度相应变大,故体积减小,选项B 错误.c→a 过程中,T 升高,内能增加,压强与温度成正比,体积不变,所以选项C 错误,选项D 正确. 答案:AD3.如图8-3-4所示,甲、乙、丙三根完全相同的玻璃管,一端封闭,管内各用相同长度的一段水银柱封闭了质量相等的空气,甲管竖直向下做自由落体运动,乙管竖直向上做加速度为g 的匀加速运动,丙管沿倾角为45°的光滑斜面下滑,若空气温度始终不变,当水银柱相对管壁静止时,甲、乙、丙三管内的空气柱长度l 甲、l 乙、l 丙的关系为( )图8-3-4A.l 乙=l 丙=l 甲B.l 乙<l 丙<l 甲C.l 乙>l 丙>l 甲D.l 乙<l 丙=l 甲解析:以水银柱为研究对象,甲受力如图4甲所示,产生向下a=g 的加速度,p 0S+mg-p 甲S=ma=mg,所以p 甲=p 0.乙受力如图4乙所示,产生竖直向上a=g 的加速度,p 乙S-mg-p 0S=ma=mg,p 乙S=2mg+p 0S =2ρShg+p 0S,p 乙=2ρgh+p 0.图4丙受力如图4丙所示,产生沿斜面向下的加速度a=gsin45°,沿斜面方向有p 0S-p 丙S+mgsinθ =ma=mgsin θ,p 丙=p 0.同质量气体,分子数目相同,温度相同,分子平均动能相等,压强大的只可能分子密集程度大,体积小,所以V 乙<V 丙=V 甲,故l 乙<l 丙=l 甲.答案:D4.如图8-3-5所示,导热汽缸开口向下,内有理想气体,缸内活塞可自由滑动且不漏气,活塞下挂一个砂桶,砂桶装满砂子时,活塞恰好静止,现在把砂桶底部钻一个小洞,细砂慢慢漏出,并缓慢降低汽缸外部环境温度,则( )图8-3-5A.气体压强增大,内能可能不变B.外界对气体做功,气体温度可能降低C.气体体积减小,压强增大,内能一定减小D.外界对气体做功,气体内能一定增加解析:要正确解答本题必须抓住几个关键的词语,“细砂慢慢漏出”、“缓慢降低”温度、“导热汽缸”所隐含的内容为:活塞受力平衡,内部气体压强增大)(0Smg p p -=;缸内气体温度逐渐降低,则气体内能减小.细砂慢慢漏出的过程中,由活塞的受力情况可知,缸内气体的压强逐渐增大,又因为内部气体温度随外界温度而降低,所以活塞将缓慢上升,其能量的转化情况是外界对气体做功,气体对外放热,气体内能减小,所以正确的选项为C.答案:C5.在冬季,装有半瓶热水的暖水瓶经过一个夜晚后,第二天拔瓶口的软木塞时觉得很紧,不易拔出来,其中主要原因是( )A.软木塞受潮膨胀B.瓶口因温度降低而收缩变小C.白天气温升高,大气压强变大D.瓶内气体因温度降低而压强减小解析:因为经过一夜,温度下降,分子平均动能变小,体积不变,分子密集程度不变,只有瓶内压强减小,外界压强不变,外界压强大于瓶内压强,故瓶塞被压紧.答案:D6.一定质量的理想气体( )A.先等压膨胀,再等容降温,其温度必低于起始温度B.先等温膨胀,再等压压缩,其体积必低于起始体积C.先等容升温,再等压压缩,其温度有可能等于起始温度D.先等容加热,再绝热压缩,其内能必大于起始内能解析:压强是由分子对器壁的频繁撞击引起的,微观上,分子平均动能和密集程度决定压强,等压膨胀,分子密集程度减小,必然分子平均动能增加,温度升高,再等容降温,最后的温度不一定低于起始温度,故A 选项错.先等温膨胀,体积变大,再等压压缩体积,最后体积不一定小于起始体积,故B 项错.先等容升温,再等压压缩,分子密集程度变大,分子平均动能减少,温度下降,其温度有可能大于、小于或等于起始温度,故C 项正确.从热力学第一定律知等容加热气体,是气体只吸收热量,内能增加再绝热压缩,是只对气体做功,内能一定增加,所以内能必大于起始内能,故D 项正确.答案:CD7.体积分别为30 L 和10 L 的两容器内,分别装有127℃,10 atm(106 Pa)的空气和真空,当把两者用细管连通后,气体的温度变成了47℃,则最终容器内气体的压强为____________. 解析:据222111T V P T V P =可得400403203010122112⨯⨯⨯==T V T V P P atm=6 atm 答案:6 atm8.如图所示绝热活塞将气缸分为两部分,起初两边均充有同温度的同种理想气体,平衡时V A ∶V B =2∶1,现将A 中气体温度升到127℃,B 气体温度降到-73℃,则平衡后左右两部分气体体积之比V′A ∶V′B =____________.解析:开始时两侧压强相同设为P 0,平衡后,两侧压强也相同,设为P.设V A =2V 0,V B =V 0,对A 有4002100'=A PV T V P ,对B 有400000'=B PV T V P 解得:V A ′∶V B ′=4∶1答案:4∶19.在湖面下50 m 深处,温度为7℃,体积为1 cm 3的气泡,升到湖面,温度为17℃,体积将变为多大?(p 0=10m 水柱)解析:在深处时p 1=p 0+h=(10+50) m=60 m 水柱V 1=1 cm 3T 1=(273+7) K=280 K在湖面时p 2=p 0=10 m 水柱V 2=?T 2=(273+17) K=290 K根据理想气体状态方程:222111T V p T V p = 得V 2=31221128010290160cm T p T V p ⨯⨯⨯==6.2 cm 3 答案:6.2 cm 310.放在光滑地面上的汽缸如图8-3-6所示,缸体质量为2 kg ,活塞质量为1 kg.静止时,活塞距离汽缸底面10 cm ,活塞面积为100 cm 2,外界大气压p 0为1×105 Pa.现用水平推力F 向左推活塞,活塞和汽缸以共同加速度向左加速运动,这时活塞和汽缸底的距离为8 cm,求水平推力F.(温度不变,下列因素不考虑:缸体厚度、空气阻力、活塞与汽缸间的摩擦)图8-3-6解析:本例气体系统处于力学非平衡状态,需要综合应用气体定律和牛顿运动定律解题.由于整个装置一起做加速运动,为了求F ,只要求出加速度即可.而求加速度最简便的方法是以缸体为研究对象,利用牛顿第二定律求解.装置静止时,汽缸内气体的压强为p 0,体积V 1=l 1S=1×10-3 m 3;设装置加速运动时气体的压强为p 2,体积V 2=l 2S=8×10-4 m 3,由玻意耳定律得:p 0V 1=p 2V 2 ①装置加速运动时,缸体受力情况如图所示,由牛顿第二定律得:p 2S-p 0S=Ma ②以整个装置为研究对象,则F=(M+m)a,解得F=(M+m)(p 0V 1S/V 2-p 0S)/M=375 N答案:375 N走近高考11.(2006上海高考,19A)一活塞将一定质量的理想气体封闭在水平固定放置的气缸内,开始时气体体积为V 0,温度为27℃.在活塞上施加压力,将气体体积压缩到2V 0/3,温度升高到57℃.设大气压强P 0=1.0×105Pa,活塞与气缸壁摩擦不计.(1)求此时气体的压强;(2)保持温度不变,缓慢减小施加在活塞上的压力使气体体积恢复到V 0,求此时气体的压强. 解析:(1)由气体状态方程知111000T V P T V P ,将P 0=1.0×105 Pa,T 0=300 K,T 1=330 K,V 1=320V 代入上式,解得P 1=1.65×105 Pa.(2)气体发生等温变化,据玻意耳定律有P 1V 1=P 2V 2,将V 2=V 1代入可得P 2=1.1×105 Pa.答案:(1)1.65×105 Pa (2)1.1×105 Pa12.(2004全国高考)一定质量的理想气体处于某一平衡状态,此时其压强为p 0,有人设计了四种途径,使气体经过每种途径后压强仍为p 0,这四种途径是:①先保持体积不变,降低压强,再保持温度不变,压缩体积②先保持体积不变,使气体升温,再保持温度不变,让体积膨胀③先保持温度不变,使体积膨胀,再保持体积不变,使气体升温④先保持温度不变,压缩气体,再保持体积不变,使气体降温则下列说法正确的是( )A.①②不可能B.③④不可能C.①③不可能D.①②③④都可能 解析:四种途径的变化过程中,均有可能使TPV 的值保持恒定,符合气体的性质规律,故D 项正确. 答案:D高考理综物理模拟试卷注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
专题14 理想气体状态方程

专题14 理想气体状态方程【母题题文】(2021·山东高考真题)血压仪由加压气囊、臂带,压强计等构成,如图所示。
加压气囊可将外界空气充入臂带,压强计示数为臂带内气体的压强高于大气压强的数值,充气前臂带内气体压强为大气压强,体积为V ;每次挤压气囊都能将360cm 的外界空气充入臂带中,经5次充气后,臂带内气体体积变为5V ,压强计示数为150mmHg 。
已知大气压强等于750mmHg ,气体温度不变。
忽略细管和压强计内的气体体积。
则V 等于( )A .330cmB .340cmC .350cmD .360cm 【母题题文】(2021·广东高考真题)在高空飞行的客机上某乘客喝完一瓶矿泉水后,把瓶盖拧紧。
下飞机后发现矿泉水瓶变瘪了,机场地面温度与高空客舱内温度相同。
由此可判断,高空客舱内的气体压强______(选填“大于”、“小于”或“等于”)机场地面大气压强:从高空客舱到机场地面,矿泉水瓶内气体的分子平均动能______(选填“变大”、“变小”或“不变”)。
【母题题文】(2021·湖南高考真题)小赞同学设计了一个用电子天平测量环境温度的实验装置,如图所示。
导热汽缸开口向上并固定在桌面上,用质量1600g m =、截面积220cm S =的活塞封闭一定质量的理想气体,活塞与汽缸壁间无摩擦。
一轻质直杆中心置于固定支点A 上,左端用不可伸长的细绳竖直悬挂活塞,右端用相同细绳竖直悬挂一个质量21200g m =的铁块,并将铁块放置到电子天平上。
当电子天平示数为600.0g 时,测得环境温度1300K T =。
设外界大气压强50 1.010Pa p =⨯,重力加速度210m/s g =。
(1)当电子天平示数为400.0g 时,环境温度2T 为多少?(2)该装置可测量的最高环境温度max T 为多少?一、单选题1.(2021·重庆市第三十七中学校高三月考)下列说法正确的是()A.花粉颗粒的布朗运动证明花粉分子在做永不停息的无规则运动B.气体很难被压缩证明气体分子间存在相互作用的斥力C.第二类永动机无法实现是因为违反了热力学第一定律D.液体由于表面张力呈收缩趋势是因为表层分子间距大于内部分子间距2.(2021·全国高三月考)下列说法错误的是()A.液晶显示器利用了液晶的光学性质具有各向异性的特点B.杯中的茶水慢慢冷却,该过程中有的水分子的运动速率反而增大了C.在南方的梅雨季节,湿衣服较不容易晾干,这是相对湿度较大的缘故D.空调可以把热量从温度较低的室内传递到温度较高的室外而不引起其他变化3.(2021·北京北理工附中)下列说法正确的是()A.布朗运动是悬浮在液体中,固体颗粒分子的无规则运动B.气体从外界吸收热量,气体的内能一定增大C.知道某物质的摩尔质量和密度可求出阿伏加德罗常数D.一定质量的气体,体积不变,温度越高,气体的压强就越大4.(2021·江苏高三月考)“用DIS研究在温度不变时,一定质量气体压强与体积关系”的实验装置如图所示。
气体定律的练习题

气体定律的练习题一、理想气体状态方程理想气体状态方程可表示为PV = nRT,其中P为气体的压力,V为气体的体积,n为气体的物质的量,R为气体常数,T为气体的绝对温度。
1. 一个容器中有2mol的氧气,该容器的体积为10L,温度为20°C。
计算氧气的压力。
解析:首先将温度转换为绝对温度,即20°C + 273.15 = 293.15 K。
代入理想气体状态方程中,得到P * 10 = 2 * 8.314 * 293.15,解得P ≈ 38.85 Pa。
2. 一瓶氮气的体积为5L,温度为25°C,物质的量为0.5mol。
求氮气的压力。
解析:将温度转换为绝对温度,即25°C + 273.15 = 298.15 K。
代入理想气体状态方程中,得到P * 5 = 0.5 * 8.314 * 298.15,解得P ≈ 81.86 Pa。
二、玻意耳-马略特定律根据玻意耳-马略特定律,当气体的物质的量和温度不变时,气体的压力与体积成反比。
3. 一气缸中的气体初始压力为2 atmos,体积为10L。
如果将气体的体积减小为5L,求气体的最终压力。
解析:根据玻意耳-马略特定律,初始压力P1 * 初始体积V1 = 终端压力P2 * 终端体积V2,代入已知条件,得到2 * 10 = P2 * 5,解得P2 = 4 atmos。
4. 一容器中的氧气体积为10L,压力为2 atm。
如果将氧气体积增大到20L,求氧气的最终压力。
解析:根据玻意耳-马略特定律,初始压力P1 * 初始体积V1 = 终端压力P2 * 终端体积V2,代入已知条件,得到2 * 10 = P2 * 20,解得P2 = 1 atm。
三、查理定律根据查理定律,当气体的压力和温度不变时,气体的体积与物质的量成正比。
5. 一个容器中含有3mol的气体,体积为12L。
如果将气体的物质的量增加到6mol,求气体的最终体积。
解析:根据查理定律,初始物质的量n1 / 初始体积V1 = 终端物质的量n2 / 终端体积V2,代入已知条件,得到3 / 12 = 6 / V2,解得V2 = 24L。
专题---理想气体状态方程计算题带答案

Word 资料理想气体状态方程计算题 1、如图所示,竖直放置的粗细均匀的 U 形管,右端封闭有一段空气柱,两管内水 银面高度差为h = 19 cm ,封闭端空气柱长度为 L i = 40 cm.为了使左、右两管中的 水银面相平,(设外界大气压强 p o = 76 cmHg ,空气柱温度保持不 变)试问: ①需从左管的开口端再缓慢注入高度多少的水银柱?此时封 闭端空气柱的长度是多少?②注入水银过程中,外界对封闭空气做 ________ (填“正功” “负功” 或“不做功”),气体将 _____ (填“吸热”或“放热”). 始温度为T °= 200 K ,外界大气压恒定不变为 p 0= 76 cmHg 。
现将玻璃管开口圭寸闭, 将系统温度升至 T = 400 K ,结果发现管中水银柱上升了 2 cm ,若空气可以看作理想气体,试求:①升温后玻璃管内封闭的上下两部分空气的压强分别为多少cmHg?②玻璃管总长为多少?5、如图所示为一简易火灾报警装置。
其原理是:竖直放置的试管中装有水银,当 温度升高时,水银柱上升,使电路导通,蜂鸣器发出报警的响声。
27 C 时,空气柱长度L i 为20cm ,水银上表面与导线下端的距离 L ?为10cm ,管内水银柱的高度 h 为8cm ,大气压强为75cm 水银柱高。
2、如图所示,U 形管右管横截面积为左管横截面积的 2倍,在左管内用水银封闭 一段长为26 cm 、温度为280 K 的空气柱,左、右两管水银面高度 差为36 cm ,外界大气压为76 cmHg 。
若给左管的封闭气体加热, 使管内气柱长度变为 30 cm ,则此时左管内气体的温度为多少?r26 r rn36 cdJdt-Jr —— (1 )当温度达到多少C 时,报警器会报警?(2)如果要使该装置在 87 C 时报警,则应该再往玻璃管 内注入多少cm 高的水银柱? ( 3)如果大气压增大,则该报警器的报警温度会受到怎样的影响?3、如图所示为一可以测量较高温度的装置,左、右两壁等长的 U 形管内盛有温度为0 C 的水银,左管上端开口,水银恰到管口,在封闭的右管上方有空气, 空气柱高h = 24 cm ,现在给空气柱加热,空气膨胀,挤出部分水银,当空气又 冷却到0 C 时,左边开口管内水银面下降了 H =5 空气被加热到的最高温度。
高中物理一轮复习理想气体状态方程专项训练-普通用卷
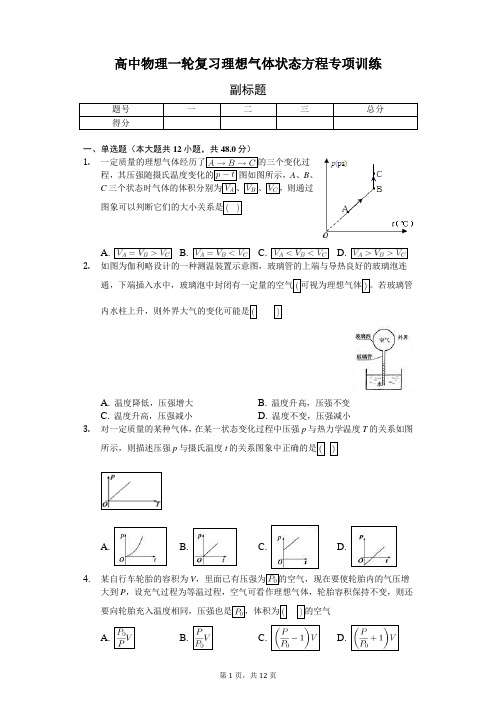
高中物理一轮复习理想气体状态方程专项训练副标题题号一二三总分得分一、单选题(本大题共12小题,共48.0分)1.一定质量的理想气体经历了的三个变化过程,其压强随摄氏温度变化的图如图所示,A、B、C三个状态时气体的体积分别为、、,则通过图象可以判断它们的大小关系是A. B. C. D.2.如图为伽利略设计的一种测温装置示意图,玻璃管的上端与导热良好的玻璃泡连通,下端插入水中,玻璃泡中封闭有一定量的空气可视为理想气体。
若玻璃管内水柱上升,则外界大气的变化可能是A. 温度降低,压强增大B. 温度升高,压强不变C. 温度升高,压强减小D. 温度不变,压强减小3.对一定质量的某种气体,在某一状态变化过程中压强p与热力学温度T的关系如图所示,则描述压强p与摄氏温度t的关系图象中正确的是A. B. C. D.4.某自行车轮胎的容积为V,里面已有压强为的空气,现在要使轮胎内的气压增大到P,设充气过程为等温过程,空气可看作理想气体,轮胎容积保持不变,则还要向轮胎充入温度相同,压强也是,体积为的空气A. B. C. D.5.如图,两端封闭的玻璃直管下方用一小段水银柱封闭了一定质量的理想气体,上方为真空.现在管的下方加热被封闭的气体,下图中不可能发生的变化过程是A. B.C. D.6.一定质量的理想气体,由状态沿直线AB变化到,如图所示,气体在A、B、C三个状态中的温度之比是A. 1:1:1B. 1:2:3C. 3:4:3D. 4:3:47.如图所示,一定质量的理想气体沿图线从状态a,经状态b变化到状态c,在整个过程中,其体积A. 逐渐增大B. 逐渐减小C. 先减小后增大D. 先增大后减小8.一定质量理想气体的状态变化如图所示,则该气体A. 状态b的压强大于状态c的压强B. 状态a的压强大于状态b的压强C. 从状态c到状态d,体积减小D. 从状态a到状态c,温度不变9.如图所示,一端开口一端封闭的长直玻璃管,灌满水银后,开口端向下竖直插入水银槽中,稳定后管内外水银面高度差为h,水银柱上端真空部分长度为L现将玻璃管竖直向上提一小段,且开口端仍在水银槽液面下方,则.A. h变大,L变大B. h变小,L变大C. h不变,L变大D. h变大,L不变10.如图所示,气缸上下两侧气体由绝热活塞隔开,活塞与气缸光滑接触。
理想气体状态方程练习

《气体》习题课学案专题一:三个实验定律和理想气体状态方程的应用例题1:如图所示,汽缸长为L =1 m ,固定在水平面上,汽缸中有横截面积为S =100 cm2的光滑活塞,活塞封闭了一定质量的理想气体,当温度为t =27 ℃,大气压强为p0=1×105Pa 时,气柱长度为l =90 cm ,汽缸和活塞的厚度均可忽略不计.求:(1)如果温度保持不变,将活塞缓慢拉至汽缸右端口,此时水平拉力F 的大小是多少?(2)如果汽缸内气体温度缓慢升高,使活塞移至汽缸右端口时,气体温度为多少摄氏度?总结方法:练习1.一定质量的气体,压强为3 atm ,保持温度不变,当压强减小了2 atm ,体积变化了4 L ,则该气体原来的体积为( )A.43 LB.2 LC.83L D.3 L 练习2:如图23所示,柱形容器内用不漏气的轻质绝热活塞封闭一定量的理想气体,容器外包裹保温材料.开始时活塞至容器底部的高度为H 1,容器内气体温度与外界温度相等为T 0,大气压强为P 0.在活塞上逐步加上多个砝码后,活塞下降到距容器底部H 2处,气体温度升高了ΔT , 此时气体压强是多少?(2)然后取走容器外的保温材料,活塞位置继续下降,最后静 止于距容器底部H 3处,求:气体最后的温度.图2-3专题二:相互关联的两部分气体的分析方法例题3:如图8-4所示,一个密闭的汽缸,被活塞分成体积相等的左、右两室,汽缸壁与活塞是不导热的;它们之间没有摩擦,两室中气体的初始体积均为V0、温度均为T0..现利用右室中的电热丝对右室加热一段时间,达到平衡后,左室的体积变为原来的3/4,气体的温度T1=300 K,求右室气体的温度.总结方法:练习:如图,绝热汽缸A与导热汽缸B均固定于地面,由刚性杆连接的绝热活塞与两汽缸间均无摩擦.两汽缸内装有处于平衡状态的理想气体,开始时体积均为V0、温度均为T0.缓慢加热A中气体,停止加热达到稳定后,A中气体压强为原来的1.2倍.设环境温度始终保持不变,求汽缸A中气体的体积V A和温度T A.专题三、变质量问题:例题4:氧气瓶的容积是40 L,其中氧气的压强是130 atm,规定瓶内氧气压强降到10 atm 时就要重新充氧,有一个车间,每天需要用1 atm的氧气400 L,这瓶氧气能用几天?假定温度不变.提示:总结方法:练习1.(2016·全国乙卷)一氧气瓶的容积为0.08 m3,开始时瓶中氧气的压强为20个大气压.某实验室每天消耗1个大气压的氧气0.36 m3.当氧气瓶中的压强降低到2个大气压时,需重新充气.若氧气的温度保持不变,求这瓶氧气重新充气前可供该实验室使用多少天.练习2.(变质量问题)某种喷雾器的贮液筒的总容积为7.5 L,如图所示,装入6 L的药液后再用密封盖将贮液筒密封,与贮液筒相连的活塞式打气筒每次能压入300 cm3,1 atm的空气,设整个过程温度保持不变,求:(1)要使贮气筒中空气的压强达到4 atm,打气筒应打压几次?(2)在贮气筒中空气的压强达到4 atm时,打开喷嘴使其喷雾,直到内外气体压强相等,这时筒内还剩多少药液?课后反思:。
理想气体状态方程专题训练

Part One
单击添加章节标题
Part Two
理想气体状态方程 的基本概念
理想气体状态方程的定义
理想气体:无黏 性、无分子间作 用力、忽略分子 体积的气体
理想气体状态方 程:PV=nRT, 其中P表示压强, V表示体积,n表 示摩尔数,R表 示气体常数,T 表示温度
理想气体状态方程 的练习题及解析
理想气体状态方程的基础练习题
● 题目:一个容积为20L的容器内,装有压强为100Pa的干燥空气。现将一束长度为10cm、直径为2cm的玻璃管开口端封闭,开口 端竖直插入水银槽中,使玻璃管内外的水银面一样高,若将容器内的空气温度升高到373K,求此时容器内空气的压强。
● (1)5min末A的物质的量浓度为 _______; ● (2)前5min内用B表示的化学反应速率v(B)为 _______; ● (3)前5min内A的转化率为 _______; ● (4)化学方程式中n的值 _______。
● 题目:在标准状况下,将氧气和二氧化氮按1:4的体积比充满干燥烧瓶,把烧瓶倒置于水中,瓶内液体逐渐上升,假设瓶内液体不 扩散,则最终烧瓶内溶液里溶质的物质的量浓度是 ( ) A. 1/28 mol/L B. 4/28 mol/L C. 1/39.2 mol/L D. 4/39.2 mol/L
添加标题
题目:一个容积为5L的容器内装有1大气压的空气,现将容器内的空气 温度升高到400K,求容器内气体的压强。
添加标题
题目:一个容积为3L的容器内装有1大气压的空气,现将容器内的空气 温度降低到270K,求容器内气体的压强。
理想气体状态方程的难题解析
不同气体混合物的处理
热力学练习题理想气体状态方程

热力学练习题理想气体状态方程热力学练习题 - 理想气体状态方程在热力学中,理想气体状态方程是描述气体基本性质的重要方程。
理解和应用该方程对于研究和解决与气体相关的问题具有重要的意义。
本文将通过一些练习题来巩固我们对理想气体状态方程的理解,并展示其应用。
练习题1:一个理想气体的压强为2.5 atm,体积为5 L,在温度为300 K下,求气体的物质的量。
解答1:根据理想气体状态方程可知,PV = nRT其中,P表示气体的压强,V表示气体的体积,n表示气体的物质的量,R表示理想气体常数,T表示热力学温度。
将已知数值代入方程,2.5 atm * 5 L = n * R * 300 K为了计算方便,我们将压强转化为国际单位制(SI)的单位 - 帕斯卡(Pa),1 atm = 101325 Pa。
则上述方程变为:(2.5 atm * 101325 Pa/atm) * 5 L = n * R * 300 K化简计算可得,n ≈ (2.5 * 101325 * 5) / (R * 300)根据理想气体状态方程中给出的气体常数的数值,替代R,并进行计算即可得到气体的物质的量。
练习题2:现有一定物质的理想气体,压强为3 atm,温度为400 K。
将气体的体积从V1缩小至V2后,新的压强为多少?解答2:根据理想气体状态方程可知,P1V1 = nRT1其中,P1表示气体的初始压强,V1表示气体的初始体积,n表示气体的物质的量,R表示理想气体常数,T1表示初始热力学温度。
当气体的体积从V1缩小至V2时,根据物态方程可知,P2V2 = nRT2其中,P2表示气体的新的压强,V2表示气体的新的体积,n表示气体的物质的量,R表示理想气体常数,T2表示气体的新的热力学温度。
将上述两个方程联立并消去物质的量n,可得新的压强P2的表达式为:P2 = (P1 * V1 * T2) / (V2 * T1)将已知数值代入方程,即可计算出气体的新的压强。
理想气体的状态方程4

高二物理理想气体状态方程练习【同步达纲练习】1.一定质量的理想气体,从初态(P1,V1,T1)变化到终态(P2,V2,T2),下列各量关系中不可能实现的应为( )A.P1>P2,V1>V2,T1>T2B.P1>P2,V1>V2,T1<T2C.P1<P2,V1>V2,T1<T2D.P1<P2,V1<V2,T1>T22.对一定质量的理想气体,在下列各种过程中,可能发生的过程是:( )A.气体膨胀对外做功,温度升高B.气体吸热,温度降低C.气体放热,压强增大D.气体放热,温度不变3.如图13.3-8所示,A、B两点表示一定质量的理想气体的两个状态,当气体自状态A变化到状态B 时( )A.体积必须变大B.有可能经过体积减小的过程C.外界必然对气体做正功D.气体必然从外界吸热4.如下图所示,能反映理想气体经历了等温变化等容变化等压变化,又回到原来状态的图是( )5.一汽泡以30m深的海底升到水面,设水底温度是4℃,水面温度是15℃,那么汽泡在水面的体积约是水底时( )A.3倍B.4倍C.5倍D.12倍6.如下图甲所示,P-T图上的图线abc表示一定质量的理想气体的状态变化过程,此过程在P-V图上(下图 (乙)所示)的图线应为( )甲乙7.一定量气体可经不同的过程以状态(P1、V1、T1)变到状态(P2、V2、T2),已知T2>T1.则在这些过程中( )A.气体一定都从外界吸收热量B.气体和外界交换的热量都是相等的C.外界对气体所做的功都是相等的D.气体内能间变化量都是相等的8.如下图所示,密封的圆柱形容器中盛有27℃,压强为1atm的空气,容器中间用两个绝热但能自由活动的活塞隔成体积相等的三个部分.将A部分加热到227℃,C部分加热到327℃,B部分温度不变.平衡后,A、B、C三部分体积之比为.9.如下图所示,A、B是两截面积相同的气缸,放在水平地面上,活塞可无摩擦地上、下移动.活塞上固定一细的刚性推杆,顶在一可绕水平固定轴O自由旋转的杠杆MN上,接触点光滑.活塞(连推杆)、杠杆的质量均可忽略,开始时,A和B中气体压强为P A=1.10×105Pa和P B=1.20×105Pa,体积均为V0=1.00L,温度均为T0=300K,杠杆处于水平位置,设大气压强始终P0=1.00×105Pa,当气缸B中气体的温度T B变为400K,体积V B=1.10L时,求气缸A中气体温度.【素质优化训练】1.如图所示,水平放置的密封气缸的活塞被很细的弹簧拉住,气缸内密封一定质量的气体.当缸内气体温度为27℃,弹簧的长度为30cm时,气缸内气体压强为缸外大气压的1.2倍.当缸内气体温度升高到127℃时,弹簧的长度为36cm.求弹簧的原长?(不计活塞与缸壁的摩擦)2.如图所示,在圆筒形真空容器内,弹簧下挂一重量可忽略的活塞.当弹簧自然伸长时,活塞刚好触及容器底部.如果活塞下充入一定质量的温度为T的某种气体,则气柱高度为h.问气体温度升高到T′时,气柱的高度h′是多少?(设活塞不漏气,且与器壁无摩擦)3.一个质量可不计的活塞将一定质量的理想气体封闭在上端开口的直立筒形气缸内,活塞上堆放着铁砂,如图所示,最初活塞搁置在气缸内壁的卡环上,气体柱的高度为H0,压强等于大气压强P0,现对气体缓慢加热,当气体温度升高了△T=60K时,活塞(及铁砂)开始离开卡环而上升,继续加热直到气柱高度为H1=1.5H0.此后在维持温度不变的条件下逐渐取走铁砂,直到铁砂全部取走时,气柱高度变为H2=1.8H0.求此时气体的温度.(不计活塞与气缸之间的摩擦)4.如图的容器内有少量红磷,充满氯气升温至400K,气体体积为1L.在恒温下充分反应.(1)写出可能发生的化学反应的化学方程式,并说明反应现象.(2)现测量容器内除存在氯气外,还有气态PCl 3和气态PCl 5,请写出这时容器中反应的化学方程式.(3)若容器内气体的体积已变为0.75L ,气态PCl 3和气态PCl 5的物质的量相等,求此时氯气的转化率.(4)若升温至800K ,氯气的转化率为45%,求这时容器中气体总体积.【生活实际运用】如下图所示,一圆柱形气缸直立在水平地面上,内有质量不计的可上下移动的活塞,在距缸底高为2H 0的缸口处有固定的卡环;使活塞不会从气缸中顶出,气缸壁和活塞都是不导热的,它们之间没有摩擦.活塞下方距缸底高为H 0处还有一固定的可导热的隔板,将容器分为A 、B 两部分,A 、B 中各封闭同种的理想气体,开始时A 、B 中气体的温度均为27℃,压强等于外界大气压强P 0,活塞距气缸底的高度为1.6H 0,现通过B 中的电热丝缓慢加热,试求:(1)当B 中气体的压强为1.5P 0时,活塞距缸底的高度是多少?(2)当A 中气体的压强为1.5P 0时,B 中气体的温度是多少?【知识验证实验】1.内容 实验室内备有米尺、天平、量筒、温度计、气压计等器材,需选取哪几件最必备的器材,测量哪几个数据,即可根据物理常数表和气体定律估算出教室内现有的空气分子数?2.提示 ①选取米尺、温度计、气压计三件器材②用米尺测出教室的长、宽、高,算出体积V ;用温度计测出室温,设为T ;用气压计测出大气压,设为P③对教室内质量为m 的空气变化到标准状态下有T PV =00'T V P (P 0=1atm,T 0=273K) ∴V ′=00TP P T V ④教室内空气分子数 N=0'V V N 0(V 0=22.4×10-3m 3,N 0=6.02×1023) =000V TP PV T N 0【知识探究学习】1.内容 如图所示,内径均匀的U 型细玻璃管一端开口,竖直放置,开口端与一个容积很大的贮气缸B 连通,封闭端由水银封闭一段空气A ,已知-23℃时空气柱A 长62cm ,右管水银面比左管水银面低40cm ,当气温上升到27℃时,水银面高度差变化4cm ,B 贮气缸左侧连接的细管的体积变化不计.(1)试论证当气温上升到27℃时,水银面高度差是增大4cm 还是减小4cn?(2)求-23℃时贮气缸B 中气体的压强.2.提示 (1)假设水银柱不动,由查理定律得11T P =22T P =T P △△ ∴△P=11T P △T 显然在△T 、T 1相同情况下,初始压强P 1越大,升高相同温度时,压强的增量越大,而初始状态时,P A <P B ,所以△P A <△P B ,则A 中水银上升,水银面高度差增大(2)设-23℃时,B 中气体压强为P B ,对A 中理想气体有A A A T L P ='''A A A T L P ,即25062)40(⨯-B P =30062)40'(⨯-B P ① 对B 中气体有250B P =300'B P ② 由①②得P B =140cmHg参考答案:【同步达纲练习】1.BD2.ABCD3.ABD (提示:连接OA 、OB 得到两条等容线,故有V B >V A ,A 项正确.由于没有限制自状态A 变化到状态B 的过程,所以可先减小气体的体积再增大气体的体积到B 状态,故B 项正确.因为气体体积增大,所以是气体对外做功,C 项错误.因为气体对外界做功,而气体的温度升高,内能增大,所以气体一定从外界吸热,D 项正确.)4.A5.B (提示:对气泡内的气体,在水底时有P 1=P 0+766.1310302⨯⨯P 0=4atm,T 1=277K ,在水面时P 2=1atm,T 2=288K,则111T V P =222T V P ,得12V V =4) 6.C (提示:由图 (甲)的P-T 图像可以看出,a →b 为等容升压,b →c 是等温降压,而在图中的四个图中能同时满足这一条件及先后顺序的只有C 图)7.D (提示:在P-V 图中,分别作两条与温度T 1、T 2对应的等温线t 1、t 2,如下图所示,设气体从状态A 经不同的过程AB 、AC 、AD 到达B 、C 、D 状态,(B 、C 、D 在温度为T 2的等温线上,A 在温度为T 1的等温线上)若由A →B ,从图中看出气体压缩,外界对气体做的功若大于气体内能的增加,则气体向外放热,所以A 项错误;若由A →D ,由图可见气体等压膨胀,气体内能增加的同时,还需对外做功,所以吸收的热量肯定比从A →c(A →c ,气体等容升压)多.因为从A →c 气体不对外做功,故B 、C 项也是错误的.理想气体的内能只与温度有关,气体从状态(P 1、V 1、T 1)不管经什么过程到状态(P 2、V 2、T 2)其温度的变化量相等,内能的变化量也相等,故D 项正确.)8.5∶3∶6 (提示:对A 中气体有3001V ⨯=500A V P ⨯,B 中气体3001V ⨯=300B V P ⨯,C 中气体3001V ⨯=600C V P ⨯) 9.设l 1、l 2是开始时,A 、B 推杆作用于杠杆的推力的力臂.由力矩平衡得(P A -P 0)l 1=(P B -P 0)l 2,∴l 1=2l 2 设V A 为末态气缸A 中气体的体积,由几何关系可知10l V V A -=20l V V B -,解得:V A =1.20升 设'B P 为末态气缸B 中的压强,由气态方程得10T V P B =BB B T V P ',解得P B ′=1.45×105Pa 设P A ′为末态气缸中压强,由力矩平衡得(P A ′-P 0)l 1=(P B ′-P 0)l 2,解得P A ′=1.23×105Pa设T A 为末态气缸A 的温度,由气态方程00T V P A =AA A T V P ',得T A =402.5k 【素质优化训练】1.21cm (提示:设弹簧原长为l ,活塞截面积为S ,弹簧劲度系数为k ,由题意得300302.10S P ⨯=40036S P •①,1.2P 0S=P 0S+k(0.3-l)②,PS=P 0S+k(0.36-l)③,由①②③得l)2.h ·T T ' (提示:设活塞截面积为S ,弹簧劲度系数为k ,由题意得:T Phs ='''T s h P ①,kh=PS ②,kh ′=P ′S ③,由①②③得h ′)3.540k (提示:设气体最初温度为T 0,则活塞刚离开卡环时温度为T 0+△T ,设气柱高为H 1时温度为T 1,高为H 2时温度为T 2.由等压升温过程得:T T H △+00=11T H ①,联系初态和终态的气态方程得:00T H =22T H ②,利用T 1=T 2由①②解得:T 2=)(12121H H H H H -△T ,代入数据得:T 2=540k.) 4.(1)2P+3Cl 2点燃2PCl 3;PCl 3+Cl 2=PCl 5 (2)PCl 3+Cl 2PCl 5+Q (3)设生成PCl 3的体积为V ,运用伏加德罗定律和原子守恒定律.求出反应中消耗Cl 2的体积为4V 1(1L-4V)+V+V=0.75L,V=0.125L ;Cl 2的转化率=LL 14125.0⨯×100%=50% (4)据题意,温度升高后,又有1L ×0.05=0.05L.Cl 2生成. PCl 3 + Cl 2 PCl 5升温后(0.125+0.05)L. (0.5+0.05)L (0.125-0.05)LV 总=(0.125+0.05)L+(0.5+0.05)L+(0.125-0.05)L=0.8L(末考虑温度对气体体积的影响) 没400K 时的压强、温度、气体体积为P 1、T 1、V 1、800K 时为P 2、T 2、V 2.根据气体定律知:111T V P =222T V P ,V 2=12111T P T V P ,因为P 1=P 2,12T T = 400800 =2,所以V 2=2V 1=0.8L ×2=1.6L. 【生活实际运用】(1)B 中气体做等容变化,由查理定律得'B B P P ='B B T T ,求得压强为1.5P 0时气体的温度T B ′=450K A 中气体做等压变化,由于隔板导热,A 、B 中气体温度相等,A 中气体温度也为450K ,对A 中气体有A A V V '=A A T T ',V A ′=A A T T 'V A =AB T T 'V A =0.9H 0S ,活塞距离缸底的高度为1.9H 0. (2)当A 中气体压强为 1.5P 0,活塞将顶在卡环处对A 中气体有AA A T V P =〃〃〃A A A T V P ,得T A ″=AA A A V P V P 〃〃T A =750K ,则B 中气体温度也为750K.。
理想气体状态方程练习题

理想气体状态方程练习题(一)1.关于理想气体,下列说法正确的是( )A.理想气体能严格遵守气体实验定律B.实际气体在温度不太高、压强不太大的情况下,可看成理想气体C.实际气体在温度不太低、压强不太大的情况下,可看成理想气体D.所有的实际气体任何情况下,都可以看成理想气体2.一定质量的理想气体,在某一平衡状态下的压强、体积和温度分别为p1、V1、T1,在另一平衡状态下的压强、体积和温度分别为p2、V2、T2,下列关系正确的是( )A.p1=p2,V1=2V2,T1=12T2 B.p1=p2,V1=12V2,T1=2T2C.p1=2p2,V1=2V2,T1=2T2 D.p1=2p2,V1=V2,T1=2T23.一定质量的理想气体,经历一膨胀过程,这一过程可以用下图上的直线ABC来表示,在A、B、C三个状态上,气体的温度T A、T B、T C相比较,大小关系为( )A.T B=T A=T CB.T A>T B>T CC.T B>T A=T CD.T B<T A=T C3.如图所示,一定质量的空气被水银封闭在静置于竖直平面的U形玻璃管内,右管上端开口且足够长,右管内水银面比左管内水银面高h,能使h变大的原因是A.环境温度升高B.大气压强升高C.沿管壁向右管内加水银D.U形玻璃管自由下落4 下图中A、B两点代表一定质量理想气体的两个不同的状态,状态A的温度为T A,状态B的温度为T B;由图可知( )A.T B=2T A B.T B=4T AC.T B=6T A D.T B=8T A5 有两个容积相等的容器,里面盛有同种气体,用一段水平玻璃管把它们连接起来。
在玻璃管的正中央有一段水银柱,当一个容器中气体的温度是0℃,另一个容器中气体的温度是20℃时,水银柱保持静止。
如果使两容器中气体的温度都升高10℃,管中的水银柱会不会移动?如果移动的话,向哪个方向移动?6一艘位于水面下200m 深处的潜水艇,艇上有一个容积为32m 的贮气筒,筒内贮有压缩空气,将筒内一部分空气压入水箱(水箱有排水孔和海水相连),排出海水310m ,此时筒内剩余气体的压强是95atm 。
理想气体的状态方程练习

理想气体状态方程检测1、如图8—24所示,粗细均匀一端封闭一端开口的U形玻璃管,当t1=310C,大气压强P0=76cmHg时,两管水银面相平,这时左管被封闭的气柱长L1=8cm,则(1)当温度t2多少时,左管气柱L2为9cm?(2)当温度达到上问中大的温度t2时,为使左管气柱长L为8cm,长的水银柱?图8—232、钢筒内装有3kg气体,当温度是-230C时,压强为4atm,如果用掉1kg后,温度升高到270C,求筒内气体的压强。
课后练习与提高1、对于理想气体下列哪些说法是不正确的()A、理想气体是严格遵守气体实验定律的气体模型B、理想气体的分子间没有分子力C、理想气体是一种理想模型,没有实际意义D、实际气体在温度不太低,压强不太大的情况下,可当成理想气体2、一定质量的理想气体,从状态P1、V1、T1变化到状态P2、V2、T2。
下述过程不可能的是()A、P2> P1,V2> V1,T2>T1B、P2> P1,V2> V1,T2<T1C、P2> P1,V2< V1,T2>T1D、P2> P1,V2< V1,T2<T13、密封的体积为2L的理想气体,压强为2atm,温度为270C。
加热后,压强和体积各增加20%,则它的最后温度是4、用活塞气筒向一个容积为V的容器内打气,每次能把体积为V0、压强为P0的空气打入容器内。
若容器内原有空气的压强为P0,打气过程中温度不变,则打了n次后容器内气体的压强为5、在温度为00C、压强为1.0×105Pa的状态下,1L空气的质量是1.29g,当温度为1000C、压强等于2.0×105Pa时。
1Kg空气的体积是多少?6、为了测定湖的深度,将一根试管开口向下缓缓压至湖底,测得进入管中的水的高度为管长的3/4,湖底水温为40C,湖面水温为100C,大气压强76cmHg。
求湖深多少?7、某房间的容积为20m3,在温度为170C,大气压强为74cmHg,室内空气质量为25Kg,则当温度升为270C,大气压强为76cmHg时,室内空气的质量为多少?参考答案[当堂达标]1、(1)78℃(2)11.75cm2、3.2atm[课后练习]1、A、C2、B3、432K4、P0(1+nV0/V)5、530L6、30.13m7、24.8Kg。
热力学练习题理想气体的状态方程

热力学练习题理想气体的状态方程热力学是研究能量转化和传递的学科,而理想气体的状态方程是热力学中一个重要的概念和计算工具。
理想气体是指在一定条件下呈现符合一定物理规律的气体,其中气体分子之间无相互作用力且体积可以忽略不计。
本文将通过几道练习题来解析理想气体的状态方程。
1. 练习题一一个摩尔的理想气体在体积为V、温度为T的条件下,其压强为P。
根据理想气体状态方程,求出该气体摩尔数n。
解答:根据理想气体状态方程 PV = nRT,其中R为气体常数。
将已知条件代入方程中,得到 P*V = n*R*T。
因此,该气体的摩尔数 n = (P*V) / (R*T)。
2. 练习题二一个体积为V的容器中有n1摩尔的理想气体,温度为T1。
若现在将该容器的体积变为原来的2倍,温度变为原来的1/2,求理想气体的摩尔数变化量Δn。
解答:根据理想气体状态方程的推导式 PV = nRT,可得 P*V = n*R*T。
将已知条件代入方程中,可以得到 P1*V1 = n1*R*T1。
又由于温度变为原来的1/2,即T2 = T1/2,而体积变为原来的2倍,即V2 = 2 * V1。
将新的温度和体积代入方程中,得到 P2*V2 = n2*R*T2。
将已知条件代入方程中,可以得到 P2*(2 * V1) = n2*R*(T1/2)。
将两个方程进行整合,并进行化简运算,可以得到Δn = n2 - n1 = -2 * n1。
因此,理想气体的摩尔数变化量Δn = -2 * n1。
3. 练习题三一个摩尔的理想气体在体积为V1、温度为T1的条件下,其压强为P1。
若将该气体的体积扩大一倍,温度升高50%,求新的压强P2。
解答:根据理想气体状态方程 PV = nRT,可以得到 P*V = n*R*T。
将已知条件代入方程中,可以得到 P1*V1 = n*R*T1。
若将该气体的体积扩大一倍,即V2 = 2*V1,温度升高50%,即T2 = 1.5*T1。
理想气体状态方程专题

理想气体状态方程一、基础知识回顾1、物质的量与微粒个数关系式2、摩尔质量、物质的量、物质质量关系式3、气体摩尔体积定义,单位,影响气体的体积的主要因素、、。
标况下气体体积大小主要取决于标况下气体体积与物质物质的量的关系4、巩固练习:(1)在反应X+2Y﹦R+2M中,已知R和M的摩尔质量之比为22:9,当1.6gX与Y完全反应后,生成4.4gR,则在此反应中Y和M的质量比为() A. 16:9 B. 23:9 C. 32:9 D. 46:9 (2)碳元素的相对原子质量为12,12C原子的质量为bg,A原子的质量为ag,阿伏加德罗常数为N A,则A的相对原子质量为() A. 12a/b B. aNa C. 12b/a D. 12aN A二、阿伏加德罗定律及其推论新知识要点1、阿伏加德罗定律:在相同、相同,相同的任何气体都含有数目的分子。
阿伏加德罗定律也适用于不反应的混合气体。
2、阿伏加德罗定律推论:使用气态方程PV=nRT有助于理解推论。
理想气体状态方程:PV=nRT(P—气体的压强,单位Pa;V—气体在给定条件下的体积,单位m3;T—绝对温度,单位K;n—物质的量,单位mol;R—摩尔气体常数,数值为8.314J·mol-1·K-1)。
根据气态状态方程PV=nRT,结合n=N/N A、n=m/M、V=m/ρ,阿伏加德罗定律有多个推论,下面重点练习四个重要推论:推论1 同温同压下,两气体的体积之比等于其之比,等于其之比。
用关系式表达即T、P相同。
例1、体积相同的容器,一个盛有一氧化氮,另一个盛有氮气和氧气,在同温同压下两容器内的气体一定具有相同的() A. 原子总数 B. 质子总数 C. 分子总数 D. 质量例2、化合物A是一种不稳定的物质,它的分子组成可用OxFy表示,10mLA气体能分解生成15mL O2和10mL F2(同温同压)。
A的化学式是________,推断的依据是_________ 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
理想气体状态方程专题训练
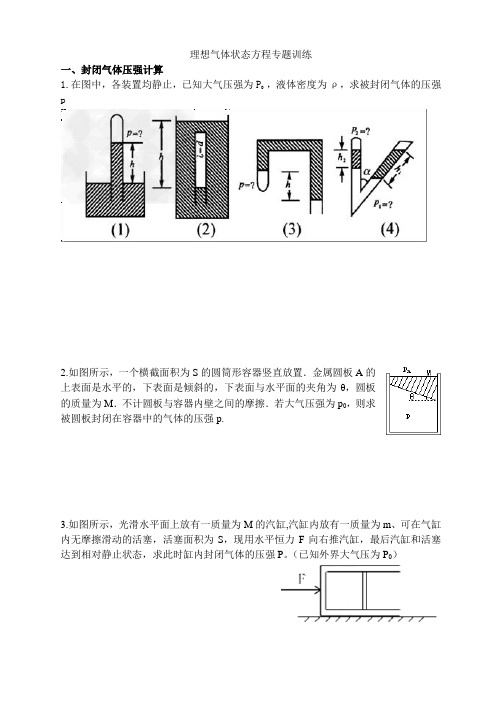
一、封闭气体压强计算
1.在图中,各装置均静止,已知大气压强为P0 ,液体密度为ρ,求被封闭气体的压强p
2.如图所示,一个横截面积为S的圆筒形容器竖直放置.金属圆板A的
上表面是水平的,下表面是倾斜的,下表面与水平面的夹角为θ,圆板
的质量为M.不计圆板与容器内壁之间的摩擦.若大气压强为p0,则求
被圆板封闭在容器中的气体的压强p.
3.如图所示,光滑水平面上放有一质量为M的汽缸,汽缸内放有一质量为m、可在气缸内无摩擦滑动的活塞,活塞面积为S,现用水平恒力F向右推汽缸,最后汽缸和活塞达到相对静止状态,求此时缸内封闭气体的压强P。
(已知外界大气压为P0)
二、理想气体状态方程的基础应用
4.一定质量的理想气体由状态A经过状态B变为状态C,其有关数据如p-T图象甲所示.若气体在状态A的温度为-73.15℃,在状态C的体积为0.6m3.求:
(1)状态A的热力学温度;
(2)说出A至C过程中气体的变化情形,并根据图象提供的信息,计算图中V A的值;(3)在图乙坐标系中,作出由状态A经过状态B变为状态C的V-T图象,并在图线相应位置上标出字母A、B、C.如果需要计算才能确定坐标值,请写出计算过程.
三、单一封闭气体问题
5.一足够长的粗细均匀的玻璃管开口向上竖直放置,管内由15cm长的水银柱
封闭着50cm长的空气柱.若将管口向下竖直放置,空气柱长变为多少cm?
(设外界大气压强为75cmHg,环境温度不变)
6.在如图所示的气缸中封闭着温度为400K的空气,一重物用绳索经
滑轮与缸中活塞相连接,重物和活塞均处于平衡状态,这时活塞离
缸底的高度为10cm,如果缸内空气变为300K,问:
(1)重物是上升还是下降?
(2)这时重物将从原处移动多少厘米?(设活塞与气缸壁间无摩擦)
7.如图所示,固定的绝热气缸内有一质量为m的“T”型绝热活塞(体积可忽略),距气缸底部h0处连接一U形管(管内气体的体积
忽略不计).初始时,封闭气体温度为T0,活
塞距离气缸底部为1.5h0,两边水银柱存在高
度差.已知水银的密度为ρ,大气压强为p0,
气缸横截面积为s,活塞竖直部分长为1.2h0,
重力加速度为g.试问:
(1)初始时,水银柱两液面高度差多大?
(2)缓慢降低气缸内封闭气体的温度,当U形管两水银面相平时封闭气体的温度是多少?
8.一汽缸竖直放在水平地面上,缸体质量M= 10kg,活塞质量M=4kg,活塞横截面积S=2×10-3 m2,活塞上面的汽缸内封闭了一定质量的理想气体,下面
有气孔O与外界相通,大气压强p0=1.0×105Pa.活塞下面与劲
度系数k = 2×103 N/m 的轻弹簧相连.当汽缸内气体温度为127℃
时弹簧为自然长度,此时缸内气柱长度L1=20 cm,g取10m/s2,缸
体始终竖直,活塞不漏气且与缸壁无摩擦.
①当缸内气柱长度L2=24cm时,缸内气体温度为多少K?
②缸内气体温度上升到T0以上,气体将做等压膨胀,则T0为多少
K?
四、多个相互关联的封闭气体问题
9.如图,绝热气缸A与导热气缸B均固定于地面,由刚性杆连接的绝热活塞与两气缸间均为摩擦。
两气缸内装有处于平衡状态的理想气体,开始时体积均为V0、温度均为T0。
缓慢加热A中气体,停止加热达到稳定后,A
中气体压强为原来的1.5倍。
设环境温度始终保持
不变,求气缸A中气体的体积V A和温度T A。
10.如图所示,有两个不计厚度的活塞M、N将两部分理想气体A、B封闭在竖直放置的绝热气缸内,温度均为27℃。
M活塞是导热的,N活塞是绝热的,均可沿气缸无摩擦地滑动,气缸底部有加热丝。
已知M活塞的质量m1=1kg,N
活塞的质量不计。
M、N活塞的横截面积均为S=2cm2,初始时M
活塞相对于底部的高度为h1=24cm,N活塞相对于底部的高度为
h2=12cm。
现将一质量为m2=1kg的小物体放在M活塞的上表面上,
活塞下降,稳定后B气体压强为P2。
已知大气压强为P0=1.0×
105Pa,取g=10m/s2。
(1)求稳定后B气体的压强P2;
(2)现通过加热丝对B气体进行缓慢加热,M、N活塞发生移动,
当M活塞距离底部的高度为h3=21.6cm时,停止加热。
求此时B气体的温度T2。
五、变质量问题
11.一个篮球的容积是2.5L,用打气筒给篮球打气时,每次把105Pa的空气打进去125cm3。
如果在打气前篮球里的空气压强也是105Pa,那么打30次以后篮球内的空气压强是多少Pa?(设在打气过程中气体温度不变)
12.用容积为V的活塞式抽气机对容积为V0的容器中的气
体抽气,如图所示。
设容器中原来气体压强为p0,抽气过
程中气体温度不变.求抽气机的活塞抽动n次后,容器中
剩余气体的压强p n为多大?。
