纯金属凝固部分课后习题

合集下载

金属学与热处理课后习题答案第三章

第三章二元合金的相结构与结晶3-1 在正温度梯度下，为什么纯金属凝固时不能呈树枝状生长，而固溶体合金却能呈树枝状成长？答：原因：在纯金属的凝固过程中，在正温度梯度下，固液界面呈平面状生长；当温度梯度为负时，则固液界面呈树枝状生长。

固溶体合金在正温度梯度下凝固时，固液界面能呈树枝状生长的原因是固溶体合金在凝固时，由于异分结晶现象，溶质组元必然会重新分布，导致在固液界面前沿形成溶质的浓度梯度，造成固液界面前沿一定范围内的液相其实际温度低于平衡结晶温度，出现了一个由于成分差别引起的过冷区域。

所以，对于固溶体合金，结晶除了受固液界面温度梯度影响，更主要受成分过冷的影响，从而使固溶体合金在正温度梯度下也能按树枝状生长。

3-2 何谓合金平衡相图，相图能给出任一条件下合金的显微组织吗？答：合金平衡相图是指在平衡条件下合金系中合金的状态与温度、成分间关系的图解，又称为状态图或平衡图。

由上述定义可以看出相图并不能给出任一条件下合金的显微组织，相图只能反映平衡条件下相的平衡。

3-3 有两个形状、尺寸均相同的Cu-Ni 合金铸件，其中一个铸件的W Ni =90%，另一个铸件的W Ni =50%，铸后自然冷却。

问凝固后哪一个铸件的偏析严重？为什么？找出消除偏析的措施。

答：W Ni =50%铸件凝固后偏析严重。

解答此题需找到Cu-Ni 合金的二元相图。

原因：固溶体合金结晶属于异分结晶，即所结晶出的固相化学成分与母相并不相同。

由Cu-Ni 合金相图可以看出W Ni =50%铸件的固相线和液相线之间的距离大于W Ni =90%铸件，也就是说W Ni =50%铸件溶质Ni 的k 0（溶质平衡分配系数）高，而且在相图中可以发现Cu-Ni 合金铸件Ni 的k 0是大于1，所以k 0越大，则代表先结晶出的固相成分与液相成分的差值越大，也就是偏析越严重。

消除措施：可以采用均匀化退火的方法，将铸件加热至低于固相线100-200℃的温度，进行长时间保温，使偏析元素充分扩散，可达到成分均匀化的目的。

纯金属的凝固习题与答案

纯金属的凝固习题与答案1 说明下列基本概念凝固、结晶、过冷、过冷度、结构起伏、能量起伏、均匀形核、非均匀形核、临界晶核半径、临界晶核形核功、形核率、生长线速度、光滑界面、粗糙界面、动态过冷度、柱状晶、等轴晶、树枝状晶、单晶、非晶态、微晶、液晶。

2 当球状晶核在液相中形成时，系统自由能的变化为σππ23344r G r G V +∆=∆，(1)求临界晶核半径c r ；(2)证明V V c c G A G c ∆-==∆231σ(c V 为临界晶核体积)；(3)说明上式的物理意义。

3 试比较均匀形核与非均匀形核的异同点，说明为什么非均匀形核往往比均匀形核更容易进行。

4 何谓动态过冷度?说明动态过冷度与晶体生长的关系。

在单晶制备时控制动态过冷度的意义？5 分析在负温度梯度下，液态金属结晶出树枝晶的过程。

6 在同样的负温度梯下，为什么Pb 结晶出树枝状晶而Si 的结晶界面却是平整的?7 实际生产中怎样控制铸件的晶粒大小?试举例说明。

8 何谓非晶态金属?简述几种制备非晶态金属的方法。

非晶态金属与晶态金属的结构和性能有什么不同。

9 何谓急冷凝固技术?在急冷条件下会得到哪些不同于一般晶体的组织、结构?能获得何种新材料?. 计算当压力增加到500×105Pa 时锡的熔点的变化，已知在105Pa 下,锡的熔点为505K ，熔化热7196J/mol ，摩尔质量为118.8×10-3kg/mol ，固体锡的体积质量7.30×103kg/m 3，熔化时的体积变化为+2.7%。

2. 考虑在一个大气压下液态铝的凝固，对于不同程度的过冷度，即：ΔT=1，10，100和200℃，计算： (a)临界晶核尺寸；(b)半径为r*的团簇个数；(c)从液态转变到固态时，单位体积的自由能变化ΔGv ； (d)从液态转变到固态时，临界尺寸r*处的自由能的变化 ΔGv 。

铝的熔点T m =993K ，单位体积熔化热ΔH f =1.836×109J/m 3，固液界面自由能γsc =93J/m 2，原子体积V 0=1.66×10-29m 3。

材料成形原理课后习题解答

材料成型原理第一章（第二章的内容）第一部分：液态金属凝固学答：（1）纯金属的液态结构是由原子集团、游离原子、空穴或裂纹组成。

原子集团的空穴或裂纹内分布着排列无规则的游离的原子，这样的结构处于瞬息万变的状态，液体内部存在着能量起伏。

（2）实际的液态合金是由各种成分的原子集团、游离原子、空穴、裂纹、杂质气泡组成的鱼目混珠的“混浊”液体，也就是说，实际的液态合金除了存在能量起伏外，还存在结构起伏。

答：液态金属的表面张力是界面张力的一个特例。

表面张力对应于液－气的交界面，而界面张力对应于固－液、液－气、固－固、固－气、液－液、气－气的交界面。

表面张力σ和界面张力ρ的关系如（1）ρ＝2σ/r,因表面张力而长生的曲面为球面时，r 为球面的半径；（2）ρ＝σ（1/r 1+1/r 2）,式中r 1、r 2分别为曲面的曲率半径。

附加压力是因为液面弯曲后由表面张力引起的。

答：液态金属的流动性和冲型能力都是影响成形产品质量的因素；不同点：流动性是确定条件下的冲型能力，它是液态金属本身的流动能力，由液态合金的成分、温度、杂质含量决定，与外界因素无关。

而冲型能力首先取决于流动性，同时又与铸件结构、浇注条件及铸型等条件有关。

提高液态金属的冲型能力的措施：（1）金属性质方面：①改善合金成分；②结晶潜热L 要大；③比热、密度、导热系大;④粘度、表面张力大。

（2）铸型性质方面：①蓄热系数大；②适当提高铸型温度；③提高透气性。

（3）浇注条件方面：①提高浇注温度；②提高浇注压力。

（4）铸件结构方面：①在保证质量的前提下尽可能减小铸件厚度；②降低结构复杂程度。

解：浇注模型如下：则产生机械粘砂的临界压力 ρ＝2σ/r显然 r ＝21×＝则 ρ＝410*5.05.1*2－＝6000Pa 不产生机械粘砂所允许的压头为H ＝ρ/（ρ液*g ）＝10*75006000＝解：由Stokes 公式上浮速度 92(2v )12r r r －＝r 为球形杂质半径，γ1为液态金属重度，γ2为杂质重度，η为液态金属粘度γ1＝g*ρ液＝10*7500＝75000γ2＝g 2*ρMnO ＝10*5400＝54000所以上浮速度 v ＝0049.0*95400075000(*10*1.0*223）－）（－＝s 解：（1）对于立方形晶核 △G 方＝－a 3△Gv+6a 2σ①令d △G 方/da ＝0 即－3a 2△Gv+12a σ＝0，则临界晶核尺寸a *＝4σ/△Gv ，得σ＝4*a △Gv ，代入① △G 方*＝－a *3△Gv ＋6 a *24*a △Gv ＝21 a *2△Gv 均质形核时a *和△G 方*关系式为：△G 方*＝21 a *3△Gv （2）对于球形晶核△G 球*＝－34πr *3△Gv+4πr *2σ 临界晶核半径r *＝2σ/△Gv ，则△G 球*＝32πr *3△Gv 所以△G 球*/△G 方*＝32πr *3△Gv/(21 a *3△Gv) 将r*＝2σ/△Gv ，a *＝4σ/△Gv 代入上式，得△G 球*/△G 方*＝π/6<1，即△G 球*<△G 方*所以球形晶核较立方形晶核更易形成3-7解： r 均*＝(2σLC /L)*(Tm/△T)＝319*6.618702731453*10*25.2*25）＋（－cm ＝*10－9m △G 均*＝316πσLC 3*Tm/（L 2*△T 2）＝316π*262345319*)10*6.61870(2731453*10*10*25.2(）＋（）－＝*10－17J 答：从理论上来说，如果界面与金属液是润湿得，则这样的界面就可以成为异质形核的基底，否则就不行。

第6章单组元相图及纯晶体的凝固笔记及课后习题详解 (已整理袁圆 2014.8.6)

第6章单组元相图及纯晶体的凝固6.1 复习笔记一、单元系相变的热力学及相平衡1．相平衡条件和相律组元：组成一个体系的基本单元，如单质（元素）和稳定化合物，称为组元。

相：体系中具有相同物理与化学性质的且与其他部分以界面分开的均匀部分，称为相。

相律：F=C－P+2；式中，F为体系的自由度数，它是指不影响体系平衡状态的独立可变参数（如温度、压力、浓度等）的数目；C为体系的组元数；P为相数。

常压下，F=C－P＋1。

2．单元系相图单元系相图是通过几何图像描述由单一组元构成的体系在不同温度和压条件下可能存在的相及多相的平衡。

图6-1 水的相图图6-2 Fe在温度下的同素异构转变上述相图中的曲线所表示的是两相平衡时温度和压力的定量关系，可由克劳修斯（Clausius）一克拉珀龙（Clapeyron）方程决定，即式中，为相变潜热；为摩尔体积变化；T是两相平衡温度。

有些物质在稳定相形成前，先行成自由能较稳定相高地亚稳定相。

二、纯晶体的凝固1．液态结构（1）液体中原子间的平均距离比固体中略大；（2）液体中原子的配位数比密排结构晶体的配位数减小；（3）液态结构的最重要特征是原子排列为长程无序，短程有序，存在结构起伏。

2．晶体凝固的热力学条件（6.1）式中，，是熔点T m与实际凝固温度T之差；L m是熔化热。

晶体凝固的热力学条件表明，实际凝固温度应低于熔点T m，即需要有过冷度△T。

3．形核晶体的凝固是通过形核与长大两个过程进行的，形核方式可以分为两类：均匀形核和非均匀形核。

（1）均匀形核①晶核形成时的能量变化和临界晶核新相晶核是在母相中均匀地生成的，即晶核由液相中的一些原子团直接形成，不受杂质粒子或外表面的影响假定晶胚为球形，半径为r，当过冷液中出现一个晶胚时，总的自由能变化：（6.2）由，可得晶核临界半径：（6.3）代入公式（1），可得：（6.4）由式可知，过冷度△T越大，临界半径则越小，则形核的几率越大，晶核数目增多。

第三章__纯金属的凝固答案

第三章纯金属的凝固本章主要内容：液态金属的结构；金属结晶过程：金属结晶的条件，过冷，热力学分析，结构条件晶核的形成：均匀形核：能量分析，临界晶核，形核功，形核率，非均匀形核：形核功，形核率晶体的长大：动态过冷度（晶体长大的条件），固液界面微观结构，晶体长大机制，晶体长大形态：温度梯度，平面长大，树枝状长大、结晶理论的应用实例：铸锭晶粒度的控制，单晶制备，定向凝固，非晶态金属一、填空1..在液态金属中进行均质形核时，需要__结构_起伏和____能量起伏。

1.金属凝固的必要条件是__________过冷度和能量起伏_____________。

2.细化铸锭晶粒的基本方法是：（1）___控制过冷度_，（2）___变质处理__，（3）____振动、搅拌等____。

5、形成临界晶核时体积自由能的减小只能补偿新增表面能的____2/3____。

6、液态金属均质形核时，体系自由能的变化包括（体积自由能）和（表面自由能）两部分，其中__表面_____自由能是形核的阻力，____体积___自由能是形核的动力；临界晶核半径r K与过冷度△T呈__反比_TLTrmm∆-=σ2_关系，临界形核功△G K等于____()223316TLTGmmk∆∙=∆σπ表面能的1/3___。

7 动态过冷度是______晶核长大时固液界面（前沿）的过冷度___。

8 在工厂生产条件下，过冷度增大，则临界晶核半径__减小___，金属结晶冷却速度越快，N/G比值___越大_____，晶粒越细_小。

9 制备单晶的基本原理是__保证一个晶核形成并长大__，主要方法有____尖端成核法和___垂直提拉法。

10. 获得非晶合金的基本方法是_____快速冷却___________。

11 铸锭典型的三层组织是______细晶粒区________, ___柱状晶区____, _____等轴晶区____。

12 纯金属凝固时，其临界晶核半径的大小、晶粒大小主要决定于_______过冷度_______________。

《金属学与热处理》第二版课后习题参考答案

金属学与热处理第一章习题1.作图表示出立方晶系（1 2 3）、（0 -1 -2）、（4 2 1）等晶面和[-1 0 2]、[-2 1 1]、[3 4 6] 等晶向3.某晶体的原子位于正方晶格的节点上，其晶格常数a=b≠c，c=2/3a。

今有一晶面在X、Y、Z坐标轴上的截距分别是5个原子间距，2个原子间距和3个原子间距，求该晶面的晶面参数。

解：设X方向的截距为5a，Y方向的截距为2a，则Z方向截距为3c=3X2a/3=2a，取截距的倒数，分别为1/5a，1/2a，1/2a化为最小简单整数分别为2,5,5故该晶面的晶面指数为（2 5 5）4.体心立方晶格的晶格常数为a，试求出（1 0 0）、（1 1 0）、（1 1 1）晶面的晶面间距，并指出面间距最大的晶面解：（1 0 0）面间距为a/2，（1 1 0）面间距为√2a/2，（1 1 1）面间距为√3a/3三个晶面晶面中面间距最大的晶面为（1 1 0）7.证明理想密排六方晶胞中的轴比c/a=1.633证明：理想密排六方晶格配位数为12，即晶胞上底面中心原子与其下面的3个位于晶胞内的原子相切，成正四面体，如图所示则OD=c/2，AB=BC=CA=CD=a因△ABC是等边三角形，所以有OC=2/3CE由于(BC)2=(CE)2+(BE)2则有(CD)2=(OC)2+(1/2c)2，即因此c/a=√8/3=1.6338.试证明面心立方晶格的八面体间隙半径为r=0.414R解：面心立方八面体间隙半径r=a/2-√2a/4=0.146a面心立方原子半径R=√2a/4，则a=4R/√2，代入上式有R=0.146X4R/√2=0.414R9.a）设有一刚球模型，球的直径不变，当由面心立方晶格转变为体心立方晶格时，试计算其体积膨胀。

b）经X射线测定，在912℃时γ-Fe的晶格常数为0.3633nm，α-Fe的晶格常数为0.2892nm，当由γ-Fe转化为α-Fe时，求其体积膨胀，并与a）比较，说明其差别的原因。

金属学与热处理课后习题答案第二章

第二章纯金属的结晶2-1 a）试证明均匀形核时，形成临界晶粒的△Gk与其体积V之间关系式为△Gk=V △Gv/2b）当非均匀形核形成球冠状晶核时，其△Gk与V之间的关系如何答：2-2 如果临界晶核是边长为a的正方体，试求出△Gk和a之间的关系。

为什么形成立方体晶核的△Gk比球形晶核要大。

答：2-3 为什么金属结晶时一定要由过冷度影响过冷度的因素是什么固态金属熔化时是否会出现过热为什么答：金属结晶时需过冷的原因：如图所示，液态金属和固态金属的吉布斯自由能随温度的增高而降低，由于液态金属原子排列混乱程度比固态高，也就是熵值比固态高，所以液相自由能下降的比固态快。

当两线相交于Tm温度时，即Gs=Gl，表示固相和液相具有相同的稳定性，可以同时存在。

所以如果液态金属要结晶，必须在Tm温度以下某一温度Tn，才能使Gs＜Gl，也就是在过冷的情况下才可自发地发生结晶。

把Tm-Tn的差值称为液态金属的过冷度影响过冷度的因素：金属材质不同，过冷度大小不同；金属纯度越高，则过冷度越大；当材质和纯度一定时，冷却速度越大，则过冷度越大，实际结晶温度越低。

固态金属熔化时是否会出现过热及原因：会。

原因：与液态金属结晶需要过冷的原因相似，只有在过热的情况下，Gl＜Gs，固态金属才会发生自发地熔化。

2-4 试比较均匀形核和非均匀形核的异同点。

答：相同点：1、形核驱动力都是体积自由能的下降，形核阻力都是表面能的增加。

2、具有相同的临界形核半径。

3、所需形核功都等于所增加表面能的1/3。

不同点：1、非均匀形核的△Gk小于等于均匀形核的△Gk，随晶核与基体的润湿角的变化而变化。

2、非均匀形核所需要的临界过冷度小于等于均匀形核的临界过冷度。

3、两者对形核率的影响因素不同。

非均匀形核的形核率除了受过冷度和温度的影响，还受固态杂质结构、数量、形貌及其他一些物理因素的影响。

2-5 说明晶体生长形状与温度梯度的关系。

答：液相中的温度梯度分为：正温度梯度：指液相中的温度随至固液界面距离的增加而提高的温度分布情况。

材料结构习题纯晶体凝固答案

《材料结构》习题：纯晶体的凝固1. 设均匀形核时其晶核为球形，试证明临界形核功ΔG c 与临界晶核体积V c 的关系为：12c c V G V G ∆=-∆ 2. 设非均匀形核时其晶核为球冠形，试证明临界形核功*c G ∆与临界晶核体积*c V 也存在上列关系式。

3. 当临界晶核为球形和小立方体形时，试分别求出各临界晶核中的原子数n 的表达式：n =f (ΔG V , σ,V)式中V 为每个原子的体积。

4. 试说明金属结晶时粗糙型液－固界面的微观结构特点，指出该界面在结晶过程中的作用。

5. 综述金属结晶的热力学条件、动力学条件、能量条件和结构条件。

6. 已知金的熔点Tm 为1063℃，熔化潜热Lm 为12.8kJ/mol ，密度为19.3g/cm3，摩尔质量为197g/mol 。

若液态金在1000℃均匀形核时的临界晶核半径r ＝43.3×10-10m ，试计算金的液固界面能σ和临界形核功。

7. 根据克拉珀龙方程可以推导出液－固或固－固相变温度与压力的关系式： T V T H P mm m ∆∆∆=∆ 式中，ΔH m 为相变潜热；T m 为相变温度；ΔV m 为摩尔体积变化。

试分别计算：(1) 已知α-F e →γ-Fe 在1大气压下T m ＝912℃，若外加压力增加到1000大气压时，转变温度应是多少（已知ΔH m ＝920.5J/mol ，α-F e 的密度为7.57g/cm 3，γ-Fe 的密度为7.63g/cm 3，Fe 的摩尔质量为55.85g/mol ）。

(2) 已知纯铁熔化时体积变化为膨胀3％，求10个大气压下的熔点（已知L m ＝15.2kJ/mol ，T m =1803K ，密度为7.6g/cm 3，摩尔质量为55.85g/mol ）。

习题答案1. 证明：设均匀形核时其球形晶核半径为r ，则32232344304802242143232V V V c Vc V c V c c V c c V c V G V G A r G r G r G rr G r G r G G r G r r G V G σππσππσσσπππ∆=∆+=∆+∂∆=⇒∆+∂∆∴=-=-∆∆∴∆=∆-=-∆=-∆令＝即2．证明：设非均匀形核时其球冠状晶核的曲率半径为r ，高为h ，则系统总表面自由能的增量ΔG S 为S L L W W LW LW G A A A A αααασσσσ∆==+-∑因为晶核周边表面张力应彼此平衡，则cos LW W L αασσσθ=+ 即cos W LW L αασσσθ-=-222(1cos )L A rh r αππθ==-222(sin )(1cos )W A r r απθπθ==-222S 232(1cos )(1cos )cos (23cos cos )L L L G r r r αααπθσπθσθπσθθ∆=---=-+ 球冠的体积 23311(3)(23cos cos )33V r h h r ππθθ=-=-+ 令31()(23cos cos )4f θθθ=-+ **3*24()4()3V S V L G V G G r G f r f απθπσθ∆=∆+∆=∆+则 **2**04()8()0c V c L G r G f r f rαπθπσθ∂∆=⇒∆+∂令＝ ****22L c c cL V r G r G αασσ∆∴=-=-∆ 即 ****3**2*3*424()()323c V cc V c c V r G G r G r f r G f ππθπθ⎛⎫∆∴∆=∆-=-∆ ⎪⎝⎭ **3***41()32c c c c V V r f G V G πθ=∴∆=-∆3．解: (1)当临界晶核为球形时，设其半径为r c ，则33333243233323c c c V Vc V r V r G G V n V G V σπσππσ=-∴==-∆∆∴==-∆(2)当晶核为正方形时，设其边长为a ，则326V V G V G A a G a σσ∆=∆+=∆+2403120c V c c VG a G a a r G σσ∂∆=⇒∆+=-∂∆令＝，即 333336464c c c V V V V a n V G V G σσ=∴==-=-∆∆4．答：金属结晶时粗糙型液－固界面的微观结构为粗糙界面。

金属凝固习题答案

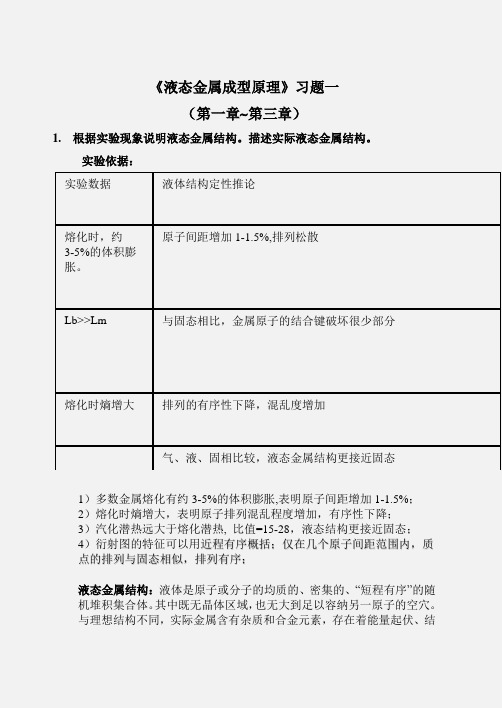
《液态金属成型原理》习题一（第一章第三章）1. 根据实验现象说明液态金属结构。

描述实际液态金属结构。

实验依据：1）多数金属熔化有约3-5%的体积膨胀,表明原子间距增加1-1.5%；2）熔化时熵增大，表明原子排列混乱程度增加，有序性下降；3）汽化潜热远大于熔化潜热, 比值=15-28，液态结构更接近固态；4）衍射图的特征可以用近程有序概括；仅在几个原子间距范围内，质点的排列与固态相似，排列有序；液态金属结构：液体是原子或分子的均质的、密集的、“短程有序”的随机堆积集合体。

其中既无晶体区域，也无大到足以容纳另一原子的空穴。

与理想结构不同，实际金属含有杂质和合金元素，存在着能量起伏、结实验数据液体结构定性推论熔化时，约3-5%的体积膨胀。

原子间距增加1-1.5%,排列松散Lb>>Lm 与固态相比，金属原子的结合键破坏很少部分熔化时熵增大排列的有序性下降，混乱度增加气、液、固相比较，液态金属结构更接近固态构起伏和成分起伏。

2.估计压力变化10kbar引起的铜的平衡熔点的变化。

已知液体铜的摩尔体积为8.0⨯10-6m3/mol，固态为7.6⨯10-6m3/mol，熔化潜热Lm=13.05kJ/mol，熔点为1085︒C。

41.56K3.推导凝固驱动力的计算公式，指出各符号的意义并说明凝固驱动力的本质。

本质：凝固驱动力是由过冷度提供的，过冷度越大，凝固驱动力越大。

4.在环境压力为100kPa下，在紧靠熔融金属的表面处形成一个直径为2μm的稳定气泡时，设气泡与液体金属的σ=0.84N/m，求气泡的内压力。

P=100kPa +( 2*0.84N/m)/(1*10-6m)=1780kPa5.如何区分固—液界面的微观结构？界面结构判据：Jackson因子α≤2，X=0.5时，∆G=min，粗糙界面；α≥3，X→ 0或1时，∆G=min，光滑界面；6.推导均质形核下临界晶核半径和临界形核功，并说明过冷度对二者的影响7.细化晶粒的目的？选择形核剂时的应遵循哪些原则？目的：增加晶粒数目，降低晶粒尺寸，增大晶界面积。

纯金属凝固部分课后习题

习题6-1 计算当压力增加到500×105Pa时锡的熔点变化，已知在105Pa下，锡的熔点为505K，熔化热为7196J/mol，摩尔质量为118.8×10-3kg/mol，固体锡的密度为7.30×103kg/m3，熔化时的体积变化为+2.7%。

6-2 根据下列条件建立单元系相图：①组元A在固态有两种结构A1和A2，且密度A2＞A1＞液体；②A1转变到A2的温度随压力增加而降低；③A1相在低温是稳定相；④固体在其本身的蒸气压1333Pa(10mmHg)下的熔点是8.2℃；⑤在1.013×105Pa(1个大气压)下沸点是90℃；⑥A1，A2和液体在1.013×106Pa(10个大气压)下及40℃时三相共存(假设升温相变△H＜0)。

6-3 考虑在1个大气压下液态铝的凝固，对于不同程度的过冷度，即△T=1，10，100和200℃，计算：①临界晶核尺寸；②半径为r*的晶核个数；③从液态转变到固态时，单位体积的自由能变化△GV；④从液态转变到固态时，临界尺寸r*处的自由能的变化△Gr*(形核功)。

铝的熔点Tm =993K，单位体积熔化热Lm=1.836×109J/m3，固液界面比表面能δ=93×10-3J/m2，原子体积V0=1.66×10-29m3。

6-4 ①已知液态纯镍在1.013×105Pa(1个大气压)，过冷度为319℃时发生均匀形核。

设临界晶核半径为1nm，纯镍的熔点为1726K，熔化热Lm=18075J/mol，摩尔体积V=6.6cm3/mol，计算纯镍的液一固界面能和临界形核功。

②若要在2045K发生均匀形核，须将大气压增加到多少?已知凝固时体积变化△V=-0.26cm3/mol(1J=9.87×106cm3·Pa)。

6-5 纯金属的均匀形核率可用下式表示：式中，A≈1035；；△G*为临界形核功；k为玻尔兹曼常数，其值为1.38×10-23J/K。

中南大学材料科学基础课后习题答案

中南大学材料科学基础课后习题答案(总12页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第一章原子排列与晶体结构1. [110]， (111)， ABCABC…，， 12 , 4 ， a r 42=； [111]， (110) , , 8 , 2 ， a r 43= ； ]0211[， (0001) ， ABAB ，， 12 ， 6 ， 2a r =。

2.， 4 ， 8 。

3.FCC ， BCC ，减少，降低，膨胀，收缩。

4.解答：见图1－1 5. 解答：设所决定的晶面为（hkl ），晶面指数与面上的直线[uvw]之间有hu+kv+lw=0，故有：h+k-l=0,2h-l=0。

可以求得（hkl ）＝（112）。

6 解答：Pb 为fcc 结构，原子半径R 与点阵常数a 的关系为a r 42=，故可求得a ＝×10-6mm 。

则（100）平面的面积S ＝a 2＝×0-12mm 2，每个（100）面上的原子个数为2。

所以1 mm 2上的原子个数s n 1=＝×1012。

第二章合金相结构一、填空1）提高，降低，变差，变大。

2）（1）晶体结构；（2）元素之间电负性差；（3）电子浓度；（4）元素之间尺寸差别3）存在溶质原子偏聚和短程有序。

4）置换固溶体和间隙固溶体。

5）提高，降低，降低。

6）溶质原子溶入点阵原子溶入溶剂点阵间隙中形成的固溶体，非金属原子与金属原子半径的比值大于时形成的复杂结构的化合物。

二、问答1、解答： -Fe 为bcc 结构，致密度虽然较小，但是它的间隙数目多且分散，间隙半径很小，四面体间隙半径为，即R ＝，八面体间隙半径为，即R ＝。

氢，氮，碳，硼由于与-Fe 的尺寸差别较大，在-Fe 中形成间隙固溶体，固溶度很小。

-Fe 的八面体间隙的[110]方向R= Ra ，间隙元素溶入时只引起一个方向上的点阵畸变，故多数处于-Fe 的八面体间隙中心。

纯金属的凝固习题与答案

3 试比较均匀形核与非均匀形核的异同点，说明为什么非均匀形核往往比均匀形核更容易进行。

4 何谓动态过冷度说明动态过冷度与晶体生长的关系。

在单晶制备时控制动态过冷度的意义5 分析在负温度梯度下，液态金属结晶出树枝晶的过程。

6 在同样的负温度梯下，为什么Pb 结晶出树枝状晶而Si 的结晶界面却是平整的7 实际生产中怎样控制铸件的晶粒大小试举例说明。

8 何谓非晶态金属简述几种制备非晶态金属的方法。

非晶态金属与晶态金属的结构和性能有什么不同。

9 何谓急冷凝固技术在急冷条件下会得到哪些不同于一般晶体的组织、结构能获得何种新材料. 计算当压力增加到500×105Pa 时锡的熔点的变化，已知在105Pa 下,锡的熔点为505K ，熔化热7196J/mol ，摩尔质量为×10-3kg/mol ，固体锡的体积质量×103kg/m 3，熔化时的体积变化为+%。

铝的熔点T m =993K ，单位体积熔化热ΔH f =×109J/m 3，固液界面自由能γsc =93J/m 2，原子体积V 0=×10-29m 3。

纯金属凝固部分课后习题

铝的熔点Tm =993K，单位体积熔化热Lm=1.836×109J/m3，固液界面比表面能δ=93×10-3J/m2，原子体积V0=1.66×10-29m3。

6-4 ①已知液态纯镍在1.013×105Pa(1个大气压)，过冷度为319℃时发生均匀形核。

设临界晶核半径为1nm，纯镍的熔点为1726K，熔化热Lm=18075J/mol，摩尔体积V=6.6cm3/mol，计算纯镍的液一固界面能和临界形核功。

②若要在2045K发生均匀形核，须将大气压增加到多少?已知凝固时体积变化△V=-0.26cm3/mol(1J=9.87×106cm3·Pa)。

6-5 纯金属的均匀形核率可用下式表示：式中，A≈1035；；△G*为临界形核功；k为玻尔兹曼常数，其值为1.38×10-23J/K。

中南大学材料科学基础课后习题

第一章原子排列与晶体结构1. fcc 结构的密排方向是，密排面是，密排面的堆垛顺序是，致密度为，配位数是 ,晶胞中原子数为，把原子视为刚性球时，原子的半径r与点阵常数a 的关系是；bcc 结构的密排方向是，密排面是 ,致密度为 ,配位数是 ,晶胞中原子数为，原子的半径r 与点阵常数a 的关系是；hcp 结构的密排方向是，密排面是，密排面的堆垛顺序是，致密度为，配位数是 ,，晶胞中原子数为，原子的半径r 与点阵常数a的关系是。

2. Al 的点阵常数为0.4049nm ，其结构原子体积是，每个晶胞中八面体间隙数为，四面体间隙数为。

3. 纯铁冷却时在912e 发生同素异晶转变是从结构转变为结构，配位数，致密度降低，晶体体积，原子半径发生。

4. 在面心立方晶胞中画出）（211晶面和]211[晶向，指出﹤110﹥中位于（111）平面上的方向。

在hcp 晶胞的（0001）面上标出）（0121晶面和]0121[晶向。

5. 求]111[和]120[两晶向所决定的晶面。

6 在铅的（100）平面上，1mm 2有多少原子？已知铅为fcc 面心立方结构，其原子半径R=0.175×10-6mm 。

第二章合金相结构一、填空1）随着溶质浓度的增大，单相固溶体合金的强度，塑性，导电性，形成间隙固溶体时，固溶体的点阵常数。

2）影响置换固溶体溶解度大小的主要因素是（1）；（2）；（3）；（4）和环境因素。

3）置换式固溶体的不均匀性主要表现为和。

4）按照溶质原子进入溶剂点阵的位置区分，固溶体可分为和。

5）无序固溶体转变为有序固溶体时，合金性能变化的一般规律是强度和硬度，塑性，导电性。

6）间隙固溶体是，间隙化合物是。

二、问答1、分析氢，氮，碳，硼在a-Fe 和g-Fe 中形成固溶体的类型，进入点阵中的位置和固溶度大小。

已知元素的原子半径如下：氢：0.046nm ，氮：0.071nm ，碳：0.077nm ，硼：0.091nm ，a-Fe ：0.124nm ，g-Fe ：0.126nm 。

纯金属的凝固答案

第三章纯金属的凝固本章主要内容:液态金属的结构；金属结晶过程：金属结晶的条件，过冷，热力学分析，结构条件晶核的形成：均匀形核：能量分析，临界晶核，形核功，形核率，非均匀形核：形核功，形核率晶体的长大：动态过冷度（晶体长大的条件），固液界面微观结构，晶体长大机制，晶体长大形态：温度梯度，平面长大，树枝状长大、结晶理论的应用实例：铸锭晶粒度的控制，单晶制备，定向凝固，非晶态金属一、填空仁在液态金属中进行均质形核时，需要结构起伏和_______ 能量起伏。

1. 金属凝固的必要条件是______________ 过冷度和能量起伏 _________________ 。

2. 细化铸锭晶粒的基本方法是：（1）—控制过冷度，（2）变质处理，（3）振动、搅拌等_______5、形成临界晶核时体积自由能的减小只能补偿新增表面能的____________ 2/3 ____ 。

6、液态金属均质形核时，体系自由能的变化包括（体积自由能）和（表面自由能）两部分，其中一表面 ____-2；九r = 自由能是形核的阻力，体积—自由能是形核的动力；临界晶核半径「K与过冷度厶T呈—反比_ L m.I T _关系，临界形核功△ G K等于—3（Lm也T）表面能的1/3—。

7动态过冷度是_________ 晶核长大时固液界面（前沿）的过冷度___。

8在工厂生产条件下，过冷度增大，则临界晶核半径—减小—，金属结晶冷却速度越快，N/G比值—越大_____________________ ，晶粒越纟旺_小。

9 制备单晶的基本原理是—保证一个晶核形成并长大一—，主要方法有_尖端成核法和—垂直提拉法。

10.获得非晶合金的基本方法是___________ 快速冷却 _____________ 。

11铸锭典型的三层组织是__________ 细晶粒区___________ ,—柱状晶区_______ , 等轴晶区_____ 。

12纯金属凝固时，其临界晶核半径的大小、晶粒大小主要决定于过冷度___________________ 。

纯金属凝固部分课后习题

金属学与热处理课后习题答案第三章

纯金属的凝固习题与答案

材料成形原理课后习题解答

第6章 单组元相图及纯晶体的凝固 笔记及课后习题详解 (已整理 袁圆 2014.8.6)

第三章__纯金属的凝固答案

《金属学与热处理》第二版课后习题参考答案

金属学与热处理课后习题答案第二章

材料结构习题纯晶体凝固答案

金属凝固习题答案

纯金属凝固部分课后习题

中南大学材料科学基础课后习题答案

纯金属的凝固习题与答案

纯金属凝固部分课后习题

中南大学 材料科学基础 课后习题

纯金属的凝固答案

第6章单组元相图及纯晶体的凝固笔记及课后习题详解 (已整理袁圆 2014.8.6)

中南大学材料科学基础课后习题