三年级奥数1-数数图形(1)
小学奥数-数数图形

例题:下面图形中有多少正方形?
难度: 适用范围:小学三年级及以上
题目解析:
采用分类数的方法,仔细数,不要遗漏。
题目
类数的方法,
首先确定正方形的类型,一共上面3种,分别数这3种 正方形的个数,按照一定的顺序数,仔细数☺。
3 × 6 = 18 (个) 5 × 2 = 10 (个)
4 × 1 = 4 (个) 合计:18 + 10 + 4 = 32(个)
题目解析:
难度: 适用范围:小学三年级及以上
A
E
F
G
B
J
M
I
D
C
题目
像 AFG一样的三角形有5个。 像 ABF一样的三角形有10个。 像 ABG一样的三角形有5个。 像 ABE一样的三角形有5个。 像 ACD一样的三角形有5个。
图中共有: 5+10+5+5+5+5=35(个) 三角形。
像 A MD一样的三角形有5个。
数数图形(五)
例题:数一数图中共有多少个三角形?
题目解析: 最小的小三角形有16个。
难度: 适用范围:小学三年级及以上
两个小三角形拼接成的三角形有10个。 图中共有
16 +10 + 8+ 2 =36(个)
题目
四个小三角形拼接成的三角形有8个。 三角形。
八个小三角形拼接成的三角形有2个。
数数图形(四)
数数图形(二)
例题:下面图形中有多少个三角形?
题目解析:
继续采用分类数的方法
小三角形共5个。
难度: 适用范围:小学三年级及以上
两个小三角形组成的三角形共6个。
题目
三年级奥数1-数数图形

第1讲 数数图形个数一、知识要点同学们,你想学会数图形的方法吗?要想不重复也不遗漏地数出线段、角、三角形、长方形……那就必须要有次序、有条理地数,从中发现规律,以便得到正确的结果。
要正确数出图形的个数,关键是要从基本图形入手。
首先要弄清图形中包含的基本图形是什么,有多少个,然后再数出由基本图形组成的新的图形,并求出它们的和。
二、精讲精练【例题1】数出下图中有多少条线段?【思路导航】方法一:我们可以采用以线段左端点分类数的方法。
以A 点为左端点的线段有:AB 、AC 、AD 3条;以B 点为左端点的线段有:BC 、BD 2条;以C 点为左端点的线段有:CD 1条。
所以,图中共有线段3+2+1=6(条)。
方法二:把图中线段 AB 、BC 、CD 看做基本线段来数,那么,由1条基本线段构成的线段有:AB 、BC 、CD 3条;由2条基本线段构成的线段有:AC 、BD 2条;由3条基本线段构成的线段有:AD 1条。
所以,图中一共有3+2+1=6(条)线段。
练习1:(1)数出下图中有多少条线段? (2)数出下图中有几个长方形?【例题2】数出图中有几个角?【思路导航】数角的个数可以采用与数线段相同的方法来数。
方法一:以OA 为一边的角有:∠AOB 、∠AOC 、∠AOD 3个;以OB 为一边的角还有: ∠BOC 、∠BOD 2个;以OC 为一边的角还有:∠COD 1个。
所以,图中共有角3+2+1=6(个)。
方法二:把图中∠AOB 、∠BOC 、∠COD 看做基本角来数,那么,由1个基本角构成的角有:∠AOB 、∠BOC 、∠COD 3个;由2个基本角构成的角有: ∠AOC 、∠BOD 2个;由3个基本角构成的角有:∠AOD 1个。
所以,图中一共有3+2+1=6(个)角。
DABCEA B CD ODC B A练习2:数出图中有几个角?(1) (2)【例题3】数出右图中共有多少个三角形?【思路导航】方法一:我们可以采用按边分类数的方法。
一起学奥数--数线段、数图形(三年级) PPT

风子编辑
第一课 数线段
教育目标
认识线段,并按一定的顺序数线段 找出数线段的规律
用数线段的方法,解决实际问题
教育重点
找出一定的规律,采用合适的方法,有次序、有条理的数出线段的 条数,不重复不遗漏。
教育难点
数线段方法在实际问题中的应用
线段:用直尺画线,把两点连接起来,就得到一条线段。连接线段的两 个点叫做线段的端点。
A
B
C
D
E
【分析】1)由题目可以知道,线段的基本单元为1,而基本单元为1的线段数 为4条;自左至右数由2、3、4个基本单元组成的线段,分别为3、2、1条。
动动手: p.84’ 随堂1
第二课 数图形
例1、下图中有多少个不同的三角形?
A
B
DE
C
【分析】1)一个顶点和这个顶点所对应的边被确定,则这个三角形就被确定 了。因此,公共点A所对应的线段数量,就是三角形的数量。
数线段是图形计数中最简单、最基本的问题,要准确的数出线段的 条数,必须做到有次序、有条理地进行计数。
数线段的方法
如下图线段,数一数共有几条?
A
B
C
D
E
方法一:用线段的左端点来分数 线段的方法。 以A为左端点的线段:4条 以B为左端点的线段:3条 以C为左端点的线段:2条 以D为左端点的线段:1条 合计:4+3+2+1=10条
循环赛也是数线段问题。 例:学校里组织乒乓球比赛,共有12个班级每班派出2名同学参加比 赛,要求每两位同学比赛一场且不得重复,问总共需要组织多少场比 赛?
【分析】首先确定人数,12个班级,每班2名,所以一共24名同学参加比赛。 要求每两位同学参加一次,且不重复,这与握手问题类似。我们可以对24名 同学编号后,进行复制,并站两排。 请同学们按握手问题分析过程 所以,总共需要组织比赛场次为:1+2+3+……+23=23×12=276场
最新三年级奥数(数图形)

学而优教育学科教师辅导讲义
(3)(4)
4.下图中各有多少个长方形?
(1) (2)
(3)
5.下图中有多少个正方形?
下列图形中各有多少条线段?下列图形中各有多少个三角形?
构建智慧课堂实施有效教学
孙桂芳
智慧与有效犹如一对双胞胎,是紧密相连的,智慧的课堂一定是有效的,而有效的课堂必定充满智慧。
一直以来,我校在教育局与东师大引领下积极探索构建智慧课堂的同时,努力实现有效教学。
新的课程理念认为,课堂教学不是简单的知识学习的过程,它是师生共同成长的生命历程,是不可重复的激情与智慧综合生成的过程。
让智慧打造高效课堂是时代的呼唤,是教学改革焕发生机与活力的最高境界。
一、让智慧呼唤灵感课堂
1、重视理论学习
学校积极推荐、印发相关学习材料,传递科研、课改等信息并按时组织教师学习。
将《新课程标准》、《开平区智慧课堂评价标准》、《税东中学智慧课堂评价标准》以及
税东中学智慧教学21条,全校教师皆已配备人手一份,也多次由周校长组织学习,并结合学校实际制订学校的的教学常规细则,让我们的教学有据可循,有理可依。
学科大组进行《课堂生成的智慧》相关理论学习,本学期至少两次,有组长搜集材料在统一的时间内组织学习。
学校还会对教师进行《教育的智慧与真情》等相关书籍的推荐,让全体教师都能了解深刻明白智慧课堂的内涵。
而实施前提是要求教师们做到四个千方百计:千方百计的调动学生的学习兴趣,千方百计的把学生的思维引向深入,千方百计的和生活实际相联系,千方百计的达成情感、态度、价值观。
小学三年级奥数_数图形个数

• 方法三:我们发现,要数出图中三角形的个数,只需 数出线段 AD中包含几条线段就可以了,即3+2+1=6( 个)。所以图中共有6个三角形。
练习3:
• 数出图中共有多少个三角形?
• (1)
A
B CD E F
• (2)
A
K GH I G B CD E F
A
B
• 【例题4】数出下图中有多少个长方形?
A
B
O
C
• (2)
A
B
O
C
D
E
P
• 【例题3】数出右图中共有多少个三角形?
AB C D
【思路导航】方法一:我们可以采用按边分类数的方法。 以PA为边的三角形有:△PAB、△PAC、△PAD、3个; 以PB为边的三角形还有:△PBC、△PBD 2个;以PC为 边的三角形还有:△PCD 1个。所以,图中共有三角形 3+2+1=6(个)。 方法二:把图中三角形 △PAB、△PBC、△PCD看做基 本三角形来数,那么,由1个基本三角形构成的三角形有: △PAB、△PBC、△PCD 3个;由2个基本三角形构成的 三角形有: △PAC、△PBD 2个;由3个基本三角形构成 的三角形有:△PAD 1个。所以,图中一共有3+2+1=6 (个)三角形。
方法二:把图中∠AOB、∠BOC、∠COD看做基本角来 数,那么,由1个基本角构成的角有:∠AOB、∠BOC、 ∠COD 3个;由2个基本角构成的角有: ∠AOC、∠BOD 2个;由3个基本角构成的角有:∠AOD 1个。所以,图 中一共有3+2+1=6(个)角。
练习2:
• 数出图中有几个角?
• (1)
(3+2+1)×(2+1)=18(个)
一起学奥数--数线段、数图形(三年级)ppt课件

动动手: p.79’ 随堂3
备注:数出来的线段是没有方向的,而车票从A站到B站,和从B站到A站是不一样 的,是有方向的
.
8
数线段案例
例3、如图,一条长为4的线段被等分为4份,端点及分点为(从左到右) A、B、C、D、E。这些点分别形成多少条长为1、2、3或4的线段?
.
6
数线段案例
例1、数出下图中共有多少条线段?(p.78’ 例1、2)
备注:引导小朋友来讲
动动手: p.78’ 随堂1;p.79’ 随堂2
.
7
数线段案例
例2、从A地到B地的列车,共经过10个车站(包括A、B在内),应当 准备多少种车票?
【分析】1)先看下车票样子,关注站名 2)有多少线段,即需要有多少个票价,
2)长方形的个数=长上的线段数×宽上的线段数
动动手: p.85 随堂2
.
14
例5、数一数下图中正方形的个数。
【分析】1)先按照普通的方法,找一定的规律数一数图中的正方形数量。自左 至右,自上至下,按1至多个基本单元组成正方形数数。9+4+1=14
2)大正方形的边上分别有3条线段,在分基本单元数正方形数量时,用心 去发现规律:9=3×3;4=2×2;1=1×1
备注:n×n个相同的正方形小格组成的大正方形的正方形数量为: n×n+(n-1)×(n-1)+……+1×1
动动手: p.86随堂3
.
15
例6、下图(1)中共有多少个三角形?下图(2)中有多少个正方形?
图(1)
图(2)
【分析】图(1)与(2)都是规则图形,针对该类图形,关键是找到分类的方 法。图(1)可以以最小三角形边长为基本单位,逐步增大边长,可以得到不同 分类的三角形数量。边长为1、2、3与4的三角形分别为16+7+3+1=27个。
3年级奥数 第1讲 数数图形

长方形总个数=10×3=#43;2+1=10,宽边线段:3+2+1=6
长方形总个数=10×6=60(个)
2.数出下图中有几个正方形?
有序的进行枚举,你发现了什么规律吗?
2.数出下图中有几个正方形?
有序的进行枚举,你发现了什么规律吗?
【答案】: 1个□组成:3×3=9(个) 4个□组成:2×2=4(个) 9个□组成:1×1=1(个) 一共有9+4+1=14(个)正方形
“数线段”的思路可以解答的 问题:两两组合的问题,比如 照照片,打电话,比赛场数 等……
注意:两个元素之间
不需要排序
1.三年级有6个班,如果每两个班要进行一次 拔河比赛,那么一共要组织多少场比赛?
2.有红、黄、蓝、白四个气球,如果选择其 中的两个气球扎成一束,那么共有多少种不 同的扎法?
★3.有1,2,3,4,5,6六个数字,这些数 字能组成多少个个位上的数字与十位上的数 字不同的两位数?
数一数,下图中有几条线段?
【思路导航】 方法二:把图中线段 AB、BC、CD、DE看做基本线段来数。(积木法)
数一数,下图中有几条线段?
【答案】:图中一共有10条线段。
线段的数法: 1.连线法 2.积木法 由n条基本线段组成的大线段, 线段总数为:1+2+3+…+n 注意:需满足例题样式哦
数出下图中有多少条线段? (1)
5.数正方形的方法: n×n个正方形组成的正方形总个数:1×1+2×2+3×3…+n×n
1.基本思路:有序+分类 2.基本题型:
①数线段、角、三角形 ②数正方形 3.常用方法: ①枚举法
要正确数出图形的个数, 关键是要从基本图形入手。 首先要弄清图形中包含的基 本图形是什么,有多少个; 其次再数出由基本图形组成 的新的图形;最后求出它们 的和。
三年级奥数第1讲——数数图形

举一反三
举一反三
举一反三 在下面线段上画上5个点,他会被分成几条线段?
举一反三
举一反三 数一数图中一共有几个角?
举一反三
【例三】
举一反三
举一反三
举一反三
举一反三
例题5 有10个小朋友,每2个人照一张合 影,一共要照多少张照片?
举一反三
1、三年级有六个班,如果每两个班要进行一次拔河 比赛,那么一共要组织多少场比赛?
举一反三
2、有红、黄、蓝、白四个气球,如果选择其中的两 个气球扎成一束,那么共有多少种不同的扎法?
举一反三
3、有1~6六个数字,这些数字能组成多少个个位上 的数字与十位上的数字不同的两位数?
随堂作业
随堂作业
随堂作业
随堂作业
随堂作业
ห้องสมุดไป่ตู้
小学三年级奥数-数图形个数

二、精讲精练
• 【例题1】数出下图中有多少条线段?
A B C D
【思路导航】方法一:我们可以采用以线段左端点分类 数的方法。以A点为左端点的线段有:AB、AC、AD 3 条;以B点为左端点的线段有:BC、BD 2条;以C点为 左端点的线段有:CD 1条。所以,图中共有线段 3+2+1=6(条)。 方法二:把图中线段 AB、BC、CD看做基本线段来数, 那么,由1条基本线段构成的线段有:AB、BC、CD 3条; 由2条基本线段构成的线段有:AC、BD 2条;由3条基本 线段构成的线段有:AD 1条。所以,图中一共有 3+2+1=6(条)线段。
• 方法三:我们发现,要数出图中三角形的个数,只需 数出线段 AD中包含几条线段就可以了,即3+2+1=6( 个)。所以图中共有6个三角形。
练习3:
• 数出图中共有多少个三角形? A • (1)
B C D
E
F
• ( 2)
A
GH I G B C D E
K
F
A
B
• 【例题4】数出下图中有多少个长方形?
练习1:
• (1)数出下图中有多少条线段?
Aபைடு நூலகம்B C D E
• (2)数出下图中有几个长方形?
A
• 【例题2】数出图中有几个角?
O
B C D
方法一:以OA为一边的角有:∠AOB、∠AOC、 ∠AOD 3个;以OB为一边的角还有: ∠BOC、∠BOD 2个;以OC为一边的角还有:∠COD 1 个。所以,图中共有角3+2+1=6(个)。 方法二:把图中∠AOB、∠BOC、∠COD看做基本角来 数,那么,由1个基本角构成的角有:∠AOB、∠BOC、 ∠COD 3个;由2个基本角构成的角有: ∠AOC、∠BOD 2个;由3个基本角构成的角有:∠AOD 1个。所以,图 中一共有3+2+1=6(个)角。
三年级奥数-1数数图形

拓展提升
5×4÷2=10个 10×2=20个
6×5÷2=15个 15×3=45个
5×4÷2=10种 答:售票员需要准备10种车票。
数长方形 数出下有几个长方形
A
B
D
C
数长方形 数出下图有几个长方形
A
B
D
C
数长方形的方法和数线段方法一样。长方形是由长和宽组成, 首先先数一数长CD边上线段数:4× 3 ÷ 2=6,再数宽AD边上 的线段数:3× 2 ÷ 2=3,最后长线段数×宽线段数=长方形数, 即:6×3=18个
下面图中有多少个角?
下面图中有多少个角?
5×4÷2=10个
7×6÷2=21个
数数三角形
数三角形
数三角形
方法一: 4+3+2+1=10个 方法二: 5×4÷2=10个
数三角形和数线段及数角的方法一样
方法一: 5+4+3+2+1=15个
方法二: 6×5÷2=15个
15个
21个
拓展提升
数出下列各图中有几个长方形?
课后作业:
1、数出下图有几个正方形?
2、有1~6六个数字,这些数 字能组成多少个个位上的 数字与十位上的数字不同 的两位数?
你学会了吗?
再见
10+9+8+7+6+5+4+3+2+1=55条 11×10÷2=55条
数角 探究下面图中有多少个角?再说说你的方法
探究下面图中有多少个角?再说说你的方法
想一想:数角的方法与数线段 的方法有什么联系?
数线段:线段总数=断点数×基本线段数÷ 2 数角:角总数=基本射线数×基本角数 ÷ 2
小学数学3年级培优奥数数数图形
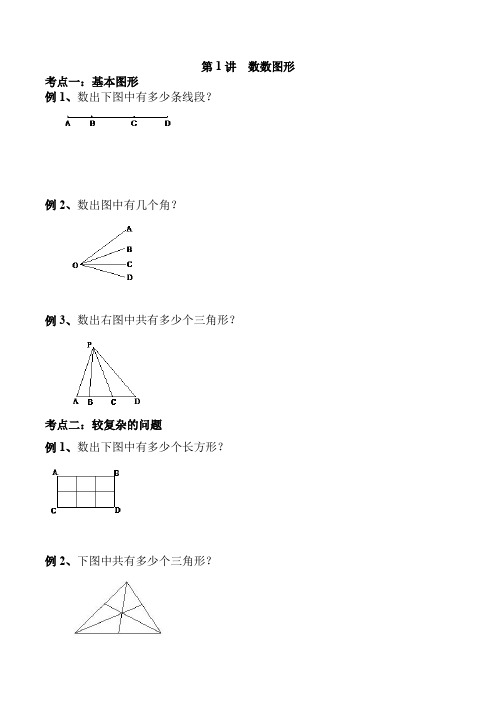
第1讲数数图形考点一:基本图形
例1、数出下图中有多少条线段?
例2、数出图中有几个角?
例3、数出右图中共有多少个三角形?
考点二:较复杂的问题
例1、数出下图中有多少个长方形?
例2、下图中共有多少个三角形?
例3、有5个同学,每两个人握手一次,一共要握手多少次?
例4、从广州到北京的某次快车中途要停靠8个大站,铁路局要为这次快车准备多少种不同车的车票?这些车票中有多少种不同的票价?
➢课堂狙击
1、数出下图中有多少条线段?
2、数出图中有几个角?
3、数出图中共有多少个三角形?
4、数出下图中有多少个长方形?
5、银海学校三年级有9个班,每两个班要比赛拔河一次,这样一共要拔河几次?
6、从上海到武汉的航运线途中,有9个停靠码头,航运公司要为这段航运线准
备多少种不同的船票?
➢课后反击
1、数出下图中有几个长方形?
2、数出图中有几个角?
3、数出图中共有多少个三角形?
4、数出下图中有多少个正方形?
5、数出下图中有多少个长方形?
6、有1,2,3,4,5,6,7,8等8个数字各用一次,能组成多少个不同的两位数?
7、从上海至青岛的某次直快列车,中途要停靠6个大站,这次列车有几种不同票价?
➢直击赛场
1、下边三个图中都有一些三角形,在图A中,有个;在图B中,有__ _个;在图C中,有______个。
(第一届小学“希望杯”全国数学邀请赛四年级
第1试)
2、数一数:图中共有________ 个正方形。
(第一届小学“希望杯”全国数学邀请赛四年级第2试)。
小学三年级奥数讲义全集

--小学三年级奥数讲义全集专题一数图形专题简析:先确定起始点或起始边,数出图形的数量,再依次以后一个点(或边)数出图形的数量。
最后求出它们的和。
例1、数出下面图中有多少条线段?思路:以A点为左端点的线段有:AB、AC、AD共3条;以B点为左端点的线段有:BC、BD共2条;以C点为左端点的线段有:CD共1条。
所以图中共有线段3+2+1=6条。
试一试1:数出下图中有( )条线段。
例2、数出下图中有几个角?思路:以AO为一边的角有:∠AOB、∠AOC、∠AOD三个;以BO为一边的角有:∠BOC、∠BOD 两个;以CO为一边的角有:∠COD一个。
所以图中共有3+2+1=6个角。
试一试2:数出下图中有()个角。
例3数出下面图中共有多少个三角形。
思路:数三角形的个数与数线段、数角的方法相同:以AB为边的三角形有:△ABC、△ABD、△AB E三个;以AC为边的三角形有:△ACD、△ACE 二个;以AD为边的三角形有:△ADE一个。
所以图中共有三角形3+2+1=6个。
试一试3:数出下面图中共有( )个三角形。
专题二:找规律专题简析:按照一定次序排列起来的一列数,叫做数列。
寻找数列的排列规律,除了从相邻两数的和、差考虑,有时还要从积、商考虑。
例1 在括号内填上合适的数。
(1):3、6、9、12、()、()(2):1、2、4、7、11、( )、( )(3): 2,6,18,54,( ),( )思路:第(1)小题:前一个数加上3就等于后一个数,相邻两个数的差都是3。
所以()里分别填15和18;(2)第(2)小题:相邻两个数的差依次是1,2,3,4……这样下一个数应为11增加5,所以应填16;再下一个数应比16大6,填22。
(3)第(3)小题:后一个数是前一个数的3倍,所以()里应分别填162和486。
试一试1:先找规律再填数。
(1)2,4,6,8,10,(),();(2)1,2,5,10,17,( ),( );(3)1,5,25,125,( ),( );例2先找出规律,再在括号里填上合适的数。
三年级奥数数数图形

学科教师辅导讲义知识梳理一、学会数图形同学们,你想学会数图形的方法吗?要想不重复也不遗漏地数出线段、角、三角形、长方形……那就必须要有次序、有条理地数,从中发现规律,以便得到正确的结果。
要正确数出图形的个数,关键是要从基本图形入手。
首先要弄清图形中包含的基本图形是什么,有多少个,然后再数出由基本图形组成的新的图形,并求出它们的和。
当我们识了线段、角、三角形、长方形等基本图形后,这些图形重重叠叠地交错在一起时就构成了复杂的几何图形。
要想准确地计数这类图形中所包含的某一种基本图形的个数,就需要仔细地观察,灵活地运用有关的知识和思考方法,掌握数图形的规律,才能获得正确的结果。
二、解题策略要准确、迅速地计数图形必须注意以下几点:1.弄清被数图形的特征和变化规律。
2.要按一定的顺序数,做到不重复,不遗漏。
典例分析考点一:基本图形例1、数出下图中有多少条线段?例2、数出图中有几个角?例3、数出右图中共有多少个三角形?考点二:较复杂的问题例1、数出下图中有多少个长方形?例2、下图中共有多少个三角形?例3、有5个同学,每两个人握手一次,一共要握手多少次?例4、从广州到北京的某次快车中途要停靠8个大站,铁路局要为这次快车准备多少种不同车的车票?这些车票中有多少种不同的票价?P(Practice-Oriented)——实战演练实战演练➢课堂狙击1、数出下图中有多少条线段?2、数出图中有几个角?3、数出图中共有多少个三角形?4、数出下图中有多少个长方形?5、银海学校三年级有9个班,每两个班要比赛拔河一次,这样一共要拔河几次?6、从上海到武汉的航运线途中,有9个停靠码头,航运公司要为这段航运线准备多少种不同的船票?➢课后反击1、数出下图中有几个长方形?2、数出图中有几个角?3、数出图中共有多少个三角形?4、数出下图中有多少个正方形?5、数出下图中有多少个长方形?6、有1,2,3,4,5,6,7,8等8个数字各用一次,能组成多少个不同的两位数?7、从上海至青岛的某次直快列车,中途要停靠6个大站,这次列车有几种不同票价?直击赛场1、下边三个图中都有一些三角形,在图A中,有个;在图B中,有__ _个;在图C中,有______个。
三年级奥数(数图形)
就读学校
二师小
年级
三
授课数
5
学员姓名
沈政翰
辅导科目
数学
学科教师
吴老师
课 题
第6讲数图形
授课日期
7-22
授课时段
8:30-10:00
教学目的
开发智力、启迪思维、培养观察能力和分析问题能力及逻辑推理能力。
教学内容
找规律是解决数学问题的一种重要手段。而发现规律既需要敏锐的观察力,又需要严密的逻辑推理能力。
例题与方法
例1.下图中有多少条线段?
例2. 下面图形中有几个角?
例3.下图中共有多少个三角形?
例4.右图中有多少个正方形?
例5.数一数图中共有多少个三角形?
练习与思考
1.下图中各有多少条线段?
(1)
(2)
(3)
2.下图中有多少个角?
3.下图中各有多少个三角形?
(1) (2)
(3) (4)
4.下图中各有多少个长方形?
(1) (2)
(3)
5.下图中有多少个正方形?
下列图形中各有多少条线段? 下列图形中各有多少个三角形?
晚饭过后,妈妈给小明出了一道“试眼力”的题目:数数窗户上一共有几个正方形。小明看,立刻回答:“窗户上有6个正方形。”妈妈笑了,爷爷在一旁也笑了,小明给弄了个“丈二和尚摸不着头脑”。小朋友,你知道小明的爷爷妈妈为什么笑吗?小明数昨难道不对吗?如果不对,那么窗户上窨有几个正方形呢?下面我们就一起来研究数图形的问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1讲 数数图形个数
一、知识要点
同学们,你想学会数图形的方法吗?要想不重复也不遗漏地数出线段、角、三角形、长方形……那就必须要有次序、有条理地数,从中发现规律,以便得到正确的结果。
要正确数出图形的个数,关键是要从基本图形入手。
首先要弄清图形中包含的基本图形是什么,有多少个,然后再数出由基本图形组成的新的图形,并求出它们的和。
二、精讲精练
【例题1】数出下图中有多少条线段?
【思路导航】方法一:我们可以采用以线段左端点分类数的方法。
以A 点为左端点的线段有:AB 、AC 、AD 3条;以B 点为左端点的线段有:BC 、BD 2条;以C 点为左端点的线段有:CD 1条。
所以,图中共有线段3+2+1=6(条)。
方法二:把图中线段 AB 、BC 、CD 看做基本线段来数,那么,由1条基本线段构成的线段有:AB 、BC 、CD 3条;由2条基本线段构成的线段有:AC 、BD 2条;由3条基本线段构成的线段有:AD 1条。
所以,图中一共有3+2+1=6(条)线段。
练习1:
(1)数出下图中有多少条线段? (2)数出下图中有几个长方形?
【例题2】数出图中有几个角?
【思路导航】数角的个数可以采用与数线段相同的方法来数。
方法一:以OA 为一边的角有:∠AOB 、∠AOC 、∠AOD 3个;以OB 为一边的角还有: ∠BOC 、∠BOD 2个;以OC 为一边的角还有:∠COD 1个。
所以,图中共有角3+2+1=6(个)。
方法二:把图中∠AOB 、∠BOC 、∠COD 看做基本角来数,那么,由1个基本角构成的角有:∠AOB 、∠BOC 、∠COD 3个;由2个基本角构成的角有: ∠AOC 、∠BOD 2个;由3个基本角构成的角有:∠AOD 1个。
所以,图中一共有3+2+1=6(个)角。
练习2:数出图中有几个角?
(1)
(2)
D
A
B
C
E
A B C D O
D
C B A A
【例题3】数出右图中共有多少个三角形?
【思路导航】方法一:我们可以采用按边分类数的方法。
以PA 为边的三角形有:△PAB 、△PAC 、△PAD 、3个;以PB 为边的三角形还有:△PBC 、△PBD 2个;以PC 为边的三角形还有:△PCD 1个。
所以,图中共有三角形3+2+1=6(个)。
方法二:把图中三角形 △PAB 、△PBC 、△PCD 看做基本三角形来数,那么,由1个基本三角形构成的三角形有:△PAB 、△PBC 、△PCD 3个;由2个基本三角形构成的三角形有: △PAC 、△PBD 2个;由3个基本三角形构成的三角形有:△PAD 1个。
所以,图中一共有3+2+1=6(个)三角形。
方法三:我们发现,要数出图中三角形的个数,只需数出线段 AD 中包含几条线段就可以了,即3+2+1=6(个)。
所以图中共有6个三角形。
练习3:数出图中共有多少个三角形?
(1) (2)
【例题4】数出下图中有多少个长方形?
【思路导航】数图中有多少个长方形和数三角形的方法一样,长方形是由长、宽两对线段围成,线段 CD 上有3+2+1=6(条)线段,其中每一条与AC 中一条线段对应,分别作为长方形的长和宽,这里共有6×1=6(个)长方形,而AC 上共有2+1=3(条)线段也就有6×3=18(个)长方形。
它的计算公式为:
长方形的总数=长边线段的总数×宽边线段的总数
(3+2+1)×(2+1)=18(个) 答:图中共有18个长方形。
练习4:
(1)数出下图中有多少个长方形? (2)数出下图中有多少个正方形?
P
C
B
K
G
I H G A
A
D
C
B
A
B
A
【例题5】有5个同学,每两个人握手一次,一共要握手多少次?
【思路导航】这道题可以用数线段的方法来解答。
根据题意,画出线段图,每一个端点代表一个同学。
从图上可以看出,第1个同学要与其余4个同学握手共握手4次;第2个同学还要与其余3个同学握手共握手3次,第3个同学要与其余2个同学握手共握手2次;第4个同学还要与最后1个同学握手共握手1次。
所以,一共要握手4+3+2+1=10(次)
练习5:
(1)银海学校三年级有9个班,每两个班要比赛拔河一次,这样一共要拔河几次? (2)有1,2,3,4,5,6,7,8等8个数字,能组成多少个不同的两位数?
5
4
3
2
1
第2讲寻找规律填空
一年有春夏秋冬四个季节,这四个季节按一定的顺序不断变化;在上楼的过程中,你可能会数台阶的级数,1、2、3……生活当中有很多有规律的数组合到一起,我们这次课,就是要仔细观察、分析一列数中已知数之间的关系,发现排列的规律,并根据这个规律填出所缺的数。
☆这可需要我们要长有一双像孙悟空那样的“火眼金睛”呀!
☆准备好了吗?让我们一起踏上发现之旅!
【基础知识】
1、数列:按一定次序排列的一列数就叫做数列。
2、项:数列中的每一个数都叫做这个数列的项。
第一个数叫做第1项,第二个数叫做第2项,……,
第n个数就叫做第n项。
3、有穷数列和无穷数列。
项数有限的数列称为有穷数列,项数无限的数列称为无穷数列。
4、观察小窍门:一般情况下我们需要仔细观察相邻的数之间的关系,但有时候可需要隔着来观察。
【例题1】观察下面的数列,说一说括号中应该填多少?
根据规律填数:
(1)2,4,6,8,(),……
(2)2,5,8,11,(),17,……
(3)25,20,15,10,()
习题:
(1)(),4,8,16,(),(),……
(2)1,3,9,27,(),243
(3)35,(),21,14,(),()
(4)64,32,16,8,(),2
【例题2】先找规律,再在括号里填上合适的数
(1)15,2,12,2,9,2,(),()
(2)21,4,18,5,15,6,(),()
(3)3,4,7,3,4,10,3,4,13,(),(),()
习题:
(1)2,1,4,1,6,1,(),()
(2)3,2,9,2,27,2,(),()
(3)18,3,15,4,12,5,(),()
(4)4,7,8,4,6,13,4,5,18,(),(),()
【例题3】先找规律,再在括号里填上合适的数
(1)2,5,14,41,( ) (2)252,124,60,28,( ) (3)1,2,5,13,34,( ) (4)1,4,9,16,25,36,( )
习题:
(1)2,3,5,9,17,( ),( ) (2)2,4,10,28,82,( ),( ) (3)5,9,6,10,7,( ) (4)6,12,20,30,42,( )
【例题4】根据前面图形里的数的排列规律,填入适当的数。
(1)
(3)
习题:找出排列规律,在空缺处填上适当的数。
(1) (3)
【例题5】按规律填数。
(1)187,286,385,( ),( )
(2)9
4
3
714
8
4
28
16
4
(2)4
8
927
6
8
28
7
(2)
练习5:根据规律,在空格内填数。
(1)198,297,396,( ),( ) (2) (3)。
