小学奥数 一年级奥数 图形的计数
(完整word版)一年级奥数【数一数】

第04讲数一数前两节课我们认识了许多几何图形,这节课我们在前面的基础上学习几何图形的计数问题。
通过本节课的学习,培养我们的空间想象能力,并且掌握图形计数的一些数学方法:分类法,归纳法等。
具体我们应该掌握以下问题:一、基本图形的识别二、点的计数问题三、线段的计数问题四、角的计数问题五、三角形的计数问题六、四边形的计数问题七、探索题目一、基本图形的识别例1 请观察下列图形,数一数,图中有几种图形,分别为什么图形?各有几个?解:上图中共有三种图形:三角形、矩形和圆,其中有6个三角形,4个长方形,4个圆。
例2 请观察下图中有几种角,并数一数它们分别有几个?解:上图中有三种角:锐角,直角和钝角,其中有3个锐角,2个直角,4个钝角。
[分析]这种类型的题目主要考察我们对于前两节课所学基本几何图形的识别问题。
而对于这几种图形的计数问题是比较简单的。
所以,能够熟练的识别几何图形是解决这类问题的关键。
二、点的计数问题例3 数一数,下图中共有多少点?解:1+3+6+9+12=31答:上题中共有31个点。
三、线段的计数问题例4 数一数,下图中共有几条线段?解:3+2+1=6答:上图中共有6条线段。
解:5+4+3+2+1=15答:上图中共有15条线段。
同学们,通过这两道题,我们能发现什么规律,考虑一下。
[分析]通过上面的两道例题,我们仔细分析,发现对于线段的计数问题是由规律可循的,即:如果图中有4个点,则线段的个数有:3+2+1;如果图中有6个点,则线段的个数有:5+4+3+2+1;。
那么,如果图中有10个点,那么线段的个数有多少个呢?所以,对于这类问题,我们主要是先找到点的个数,然后按照规律计算出线段的个数。
四、角的计数问题例6 数一数,下图中有几个锐角?解:3+2+1=6答:上图中共有6个锐角。
想一想:同学们,你们仔细看一下,仔细想一想,这道题有没有规律,这个规律和第三类问题的线段的计数问题的规律有相似之处吗?五、三角形的计数问题答:共有3+1个三角形。
小学奥数~平面图形计数-数正方形--不规则图形
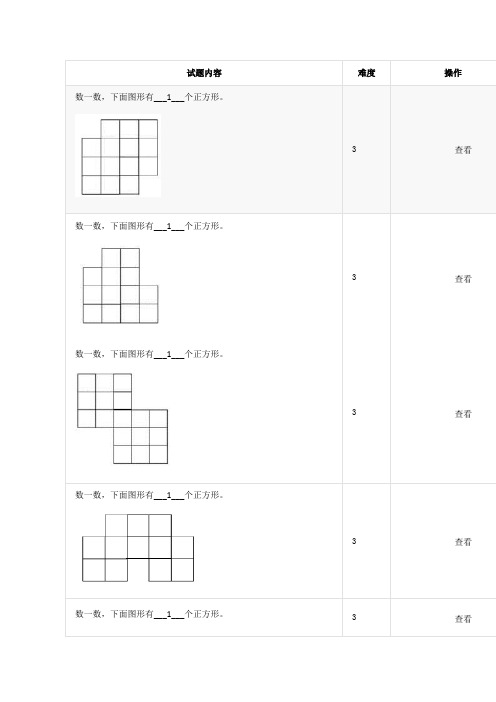
数一数,下面图形有___1___个正方形。
查看数一数,下面图形有___1___个正方形。
查看数一数,下面图形有___1___个正方形。
查看数一数,下面图形有___1___个正方形。
查看
查看
数一数,下面图形有___1___个正方形。
查看数一数,下面图形有___1___个正方形。
查看
查看
数一数,下面图形有___1___个正方形。
查看
数一数,下面图形有___1___个正方形。
查看
查看
数一数,下面图形有___1___个正方形。
查看数一数,下面图形有___1___个正方形。
查看数一数,下面图形有___1___个正方形。
查看
查看
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
一年级奥数-图形的计数

céngfǎ
层法
fāngfǎ yīcéngyīcéngshùqīngchǔ zuòhǎo jì suàn
方 法 :一hìguānjiàn
是关 键
qǐngláojì yìxiēchángyòngdejìsuànjiéguǒ ò
都 要 分 到 糖 ,但 分 到 的 糖 块 数 又
bùnéngyíyàngduō shuíhuìfēn jiéguǒxiǎohuǒbàn
不 能 一 样 多 , 谁 会 分 ?” 结 果 小 伙 伴
mendōubúhuìfēn wèishénmene rúguǒyàogòufēn
们 都 不 会 分 , 为 什 么 呢?如 果 要 够 分 ,
课 堂 小结
lì tǐ túxíngshùfāngkuài cóngshàngwǎngxiàfēn
1.立体 图 形 数 方 块 : 从 上 往 下 分
céngfǎ
层法
kǒujué shùtóudǐngjiālóushàng
口 诀:数 头 顶 加 楼 上
píngmiàntúxíng jì shùfǎ cóngshàngwǎngxiàfēn
有 一 天 小 猴 子 和 7 个 小 伙 伴 一起 出 去 玩 ,
xiǎohóuzináchūyībāotáng duìxiǎohuǒbànmenshuō
小 猴 子拿 出 一 包 糖 , 对 小 伙 伴 们 说 :
wǒmenláifēntángchība zhè lǐ miànyígòngyǒu kuài
“ 我 们 来 分 糖 吃 吧 , 这 里 面 一 共 有 35 块
táng xiànzàiwǒmenyígòngyǒu gèxiǎohuǒbàn měigè
小学奥数巧数图形大全
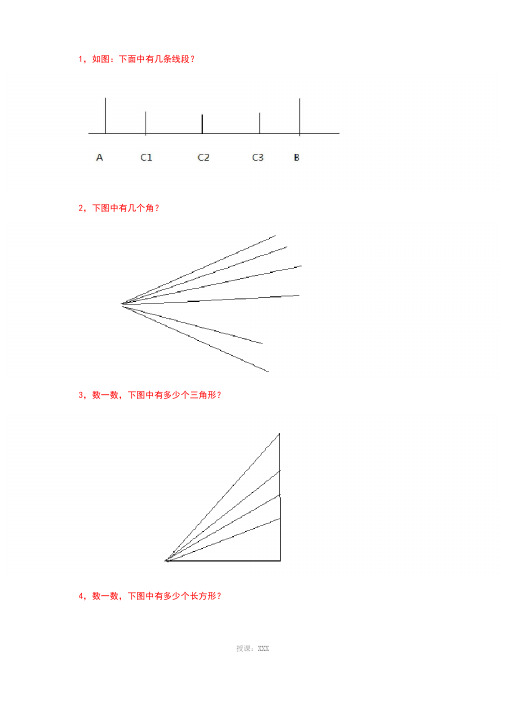
1,如图:下面中有几条线段?
2,下图中有几个角?
3,数一数,下图中有多少个三角形?4,数一数,下图中有多少个长方形?
1)
(2) 5,数一数,下图中有多少个正方形?
1,请同学们数出下列每条线上的线段的总条数。
(3) 2,如图:下面中有几条线段?
授课:XXX
5,数一数,下图中有多少个三角形?
如果横着再添一笔,共有多少个长方形?7,数一数,下图中有多少个三角形?
8,数一数,下图中有多少个长方形?
10,数一数,下图中有多少个三角形?
3,数一数,下图中各有多少个三角形?
A
4,数一数,下图中各有多少个三角形?
A
1
1
1
2
1
3
14
1
5
113 7,数一数,下图中有多少个长方形?
8,数一数,下图中有多少个长方形?
注:可编辑下载,若有不当之处,请指正,谢谢!)。
高思奥数一年级下册含答案第11讲 立体图形计数

第十一讲立体图形计数前续知识点:一年级第一讲;XX模块第X讲后续知识点:X年级第X讲;XX模块第X讲墨莫墨莫卡莉娅小高把相应的人物换成红字标明的人物.还记得我们都学习过哪些立体图形吗?正方体、长方体、圆柱体、球体……数不胜数.今天我们来学习一下立体图形的计数.在地球上,一个小正方体可以在没有任何支撑的情况下悬浮在空中吗?答案当然是不可以!聪明的你赶快来看一看,下面题目中的立体图形到底由几个小正方体组成的呢?例题1数一数,它们分别由几个小正方体组成?【提示】有没有看不见的正方体?练习1数一数,它们分别由几个小正方体组成?数正方体有许多方法,其中我们可以一层一层的分层数,试试看.例题2左边方框中的立体图形和右边哪个立体图形中的小正方体个数相同呢?【提示】数一数,分别有几个小正方体!练习2左边方框中的立体图形和右边哪个立体图形中的小正方体个数相同呢?分层数的方法不仅简单快捷,而且清晰明了,不容易数重数漏.结合找规律的方法,我们更能轻松数出立体图形的个数.例题3数一数,下面这个“宝塔”由多少个小正方体组成?A BC DA B【提示】找一找,每层之间有什么规律?练习3数一数,下面这个“楼梯”由多少个小正方体组成?例题4要想把下面左边的立体图形补全成为一个完整的大正方体,至少需要再加几个小正方体呢?【提示】左边的立体图形由几个小正方体组成的?右边的呢?练习4要想把下面左边的立体图形补全成为一个完整的大正方体,至少需要再加几个小正方体呢?例题5要想把下面的立体图形补全成为一个完整的大正方体,至少需要再加几个小正方体呢?【提示】补全后的大正方体是什么样的呢?例题6如图所示,将大正方体中的“L”形挖穿,你能数出现在这个立体图形有多少个小正方体吗?【提示】挖穿了几层?课外阅读长方体和正方体的故事长方体是一个聪明的小男孩儿,他生活在一个数学图形的古老部落.长老们说他们一直拥有自然女神的庇护,自然女神总是不定期地出现在他们部落,每一次,她都只见一个有缘人,如果这个有缘人能够通过她的考验,她就会满足这个有缘人的一个合理的愿望.有一天,长方体去小河边玩,已经有一些伙伴在河边嬉戏,有三角形,正方形,圆等等……长方体刚走到附近就听到三角形喊救命,原来是平行四边形掉到河里去,长方体奋不顾身地跳进了河里,拼死救人.最后长方体把平行四边形救出来了.大家都很感谢长方体.长方体坐在草原上看风景,自然女神出现了.自然女神说:“你已经通过了我的考验,告诉我,你有什么愿望?”长方体说:“我没有什么愿望.”自然女神说:“既然你不说,那我就自作主张替你做决定了.”自然女神知道长方体一个人玩,没有伙伴,就创造了正方体,正方体和长方体一样聪明,而且,正方体和长方体还十分相似,有许多共同的特点.长方体很喜欢这个新伙伴.长方体对自然女神说;“我很喜欢正方体,他有许多和我相似的地方,像我的影子,但又和我完全不一样,有自己的个性.”自然女神说:“你喜欢就好,其实,正方体是另一个特殊的你.比你自己还要特别的你.以后,你自然会明白的.”作业1. 数一数,它们分别由几个小正方体组成?2. 左边方框中的立体图形和右边哪个立体图形中的小正方体个数相同呢?3. 数一数,下面这个“楼梯”由多少个小正方体组成?C B4. 要想把下面左边的立体图形补全成为一个完整的大正方体,至少需要再加几个小正方体呢?5. 如图所示,将大正方体中的“T”字形挖穿,现在这个图形中有几个小正方体?第十一讲 立体图形计数1. 例题1答案:5;5;9;10详解:先数出能看到的正方体个数,再数出看不见的正方体个数,相加即可.2. 例题2答案:A详解:左边方框中的立体图形的小正方体个数为10个,A 的小正方体个数为10个,B 的小正方体个数为9个,C 的小正方体个数为8个,D 的小正方体的个数为11个.3. 例题3答案:35详解:每层的小正方体个数分别为1、3、6、10、15,加起来的和为35.规律是每层分别在上一层的基础上增加2、3、4、5个小正方体.4. 例题4答案:2;17详解:第一个图中完整的大正方体中的小正方体个数为8个,左边立体图形中的小正方体个数为6个,还需要862-=(个).第二个图中完整的大正方体中的小正方体个数为27个,左边立体图形中的小正方体个数为10个,还需要271017-=(个).5. 例题5答案:48详解:符合要求的完整的大正方体至少需要64个小正方体组成,现在有16个小正方体,还需要再加小正方体641648-=(个). 6. 例题6答案:52详解:完整的大正方体一共有1616161664+++=个)小正方体,“镂空”部分有333312+++= (个)小正方体,所以还剩下641252-= (个)小正方体.7. 练习1答案:5;4;6;8简答:第三个中有1个看不见的正方体,第四个中有3个看不见的正方体.8. 练习2答案:D简答:左边方框中的立体图形的小正方体的个数为7个,D 的小正方体的个数也为7个.9. 练习3答案:60简答:每层小正方体的个数分别为4、8、12、16、20,加起来的和为60.10. 练习4答案:3;13简答:第一个图中完整的大正方体中的小正方体个数为8个,左边立体图形中的小正方体个数为5个,还需要853-=(个).第二个图中完整的大正方体中的小正方体个数为27个,左边立体图形中的小正方体个数为4个,还需要271413-=(个).11. 作业1答案:6;8;9;10简答:观察这两层小正方体,分别数出每一层小正方体的个数,注意“看不见”的小正方体.也可分别数出每列的小正方体个数,加在一起即可.12. 作业2答案:A简答:左边方框中小正方体的个数是10个,而右边各立体图形的小正方体个数分别为:A .10个;B .13个;C .9个;D .9个.13. 作业3答案:20简答:从顶层开始数,最顶层为2个,第二层为4个,第三层为6个,第四层为8个,所以小正方体的个数为246820+++=(个).14. 作业4答案:9简答:左边的立体图形中小正方体的个数为36918++=(个),完整的大正方体中小正方体的个数为99927++=(个).还需要小正方体27189-=(个).15. 作业5答案:44简答:方法一:整个大正方体中小正方体的个数为1616161664+++=(个),“T ”字形中小正方体的个数为555520+++=(个)或4444420++++=(个),所以现在有小正方体642044-=(个). 方法二:每层剩下的小正方体有11个,共有4层,所以现在有小正方体:1111111144+++=(个).。
小学奥数 图形计数 知识点+例题+练习 (分类全面)

一、图形计数
要想不重复也不遗漏地数出线段、角、三角形、长方形……那就必须要有次序、有条理地数,从中发现规律,以便得到正确的结果。
要正确数出图形的个数,关键是要从基本图形入手。
首先要弄清图形中包含的基本图形是什么,有多少个,然后再数出由基本图形组成的新的图形,并求出它们的和。
例1、数出下图中有多少条线段?
巩固、数出下图中有几个长方形?
例2、数出图中有几个角?
D A B
C O
D C
B
A
巩固、数出图中有几个角?
例3、数出下图中共有多少个三角形?
巩固、数出图中共有多少个三角形?
例4、数出下图中有多少个长方形?
O C B A
P
C B A K G I H G F E A
D C B A
巩固、数出下图中有多少个正方形?
课后练习:
1、数出下图中有多少条线段?
2、数出图中有几个角?
E
A B C D E D
O
C B A
3、数出图中共有多少个三角形?
4、数出下图中有多少个长方形?
A
B A D
C B A。
小学一年级奥数题:图形计数练习题【五篇】

小学一年级奥数题:图形计数练习题【五篇】2.小敏到商店买文具用品。
她用所带钱的一半买了1支铅笔,剩下的一半买了1支圆珠笔,还剩下1元钱。
小敏原来有多少钱?3.有两篮苹果,第一篮25个,第二篮19个,从第一篮中拿几个放入第二篮,两篮的苹果数相等?4.小明从家到学校跑步来回要10分钟,如果去时步行,回来时跑步一共需要12分钟,那么小明来回都是步行需要几分钟?5.小红和小绿都有10块橡皮,小兰给小绿2块后,现在小绿比小兰多几块橡皮?【第二篇】1.有一本书,小华第一天看了2页,以后每一天都比前一天多看2页,第4天看了多少页?2.妈妈从家里到工厂要走3千米,一次,她上班走了2千米,又回家取一很重要工具,再到工厂。
这次妈妈上班一共走了多少千米?3.像18+81这样十位数字与个位数字顺序颠倒的一对两位数是好朋友,它们相加和是99,请问像这样的相加和是99的好朋友有几对?4.桌子上有三盘桃子,第一盘比第三盘多3只,第三盘比第二盘少5只。
问:哪盘桃子最少?5.13个小朋友玩"老鹰抓小鸡"的游戏,已经抓住了5只"小鸡",还有几只没抓住?6.修花坛要用94块砖,第一次搬来36块,第二次搬来38块,还要搬多少块?(用两种方法计算)7.海盗抓小孩去无人岛,一共抓了15个小孩,他让小孩排队报数,第一次把报单数的孩子都送去了无人岛,接着让剩下的孩子报数,又把报单数的孩子送去了无人岛,把其他孩子放回了家。
问强盗放多少个孩子回家?8.懒羊羊一次买来了30个苹果,它第一天吃了一些,第二天又吃了一些,这时还剩下12个苹果,懒羊羊两天一共吃了多少个苹果?9.5只兔子和4只猫一样重,那么一只兔重还是一只猫重?10.一只井底的蜗牛,白天能够爬2米,晚上下滑1米,已知井深5米,蜗牛多久能够爬到井外?【第三篇】1.小明把一根木棍锯成2段需要2分钟,那么依照这样的速度,把一根木棍据成3段需要多少分钟?2.一个猴子吃3个桃子多出一个,一个猴子吃4个桃子就少2个。
小学一年级奥数题及答案 - 认识图形题及答案
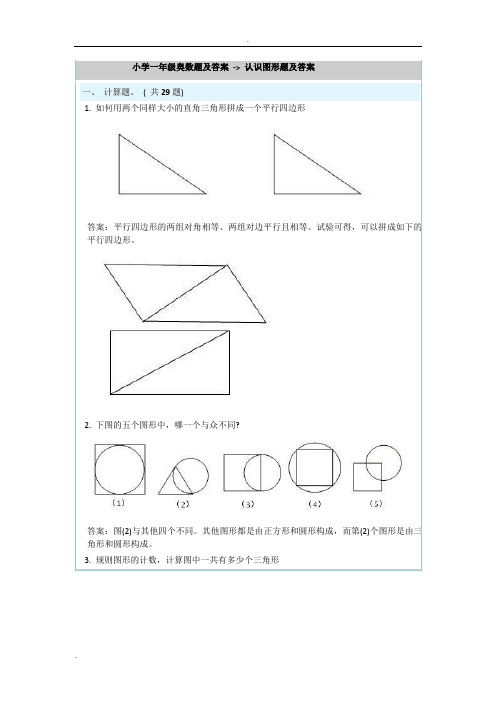
1. 如何用两个同样大小的直角三角形拼成一个平行四边形答案:平行四边形的两组对角相等、两组对边平行且相等。
试验可得,可以拼成如下的平行四边形。
2. 下图的五个图形中,哪一个与众不同?4. 一笔画就是笔不离纸,笔划不重复,一笔画出一个图形。
你能用一笔画出下面图形吗?答案:5. 数一数下列各图中有多少个三角形。
答案:分析总结:火柴棒类试题是最常见的看图类试题之一,通过移动一至三根火柴棒对之前的图案有小小的变化,成为另一个图案,这道试题是考察大家的应变能力。
7. 移动3根火柴棒,使桌子在两把椅子的中间.答案:答案:3根,具体操作如下:答案:10. 按图形变化的规律,在空格处应画什么样的图形?答案:11. 空白处应填什么样的图形?答案:答案:答案:答案:16.答案:17. 按照图形的变化规律,在“?”处画出相符的图形.答案:这组图形的变化只在于正方形中阴影部分的位置.通过观察,我们可以发现阴影部分是按照逆时针方向依次旋转得到的.所以“?”处的图形应为:18. 图中,哪个图形与众不同?19. 一单层砖墙下雨时塌了一处,请你数一数,需要多少块砖才能把墙补好?21. 把下面空白部分画完整。
答案:发现每一行都有这三个图形,只是位置发生了变化。
22. 下面的一组图形中,最后一个应画什么图案?答案:图形位置变化,并且是逆时针旋转着变化的答案:选1,5;选2,424. 细心观察下面这些图形,哪些图形能一笔画成,哪些图形不能?25. 下面五个图形,那个与其他四个不同?26. 在“?”处填入适当的数.27. 第一排和第二排的规律是一样的,根据这种规律把"?"补充完整.答案:根据上面的规律,第二排第三个图形应该是大三角形里面一个蓝色的小三角形.答案如图.28. 下图中的两个图形,有哪些相同点,有哪些不同点?请你仔细观察、分析。
29. 下面这面墙中间有个洞,需要用一些长方体砖补上,请选一个合适的图形把洞补上1. 根据下面各题图形之间的变化和排列规律,在方格中填上合适的图形。
奥数知识点 图形计数

巧数图形例1、数出下图中共有多少条线段。
分析与解:对于基础图形,用最小线段为单位,按序递增。
单拼:3(段),双拼:2(段),三拼:1(段)通过以上的计数方法可以发现:开小火车的方式解决。
最小线段(基础线段)的数量为火车头火车头为基础线段数3段:3+2+1=6(段)或者,线段个数=基础线段数×端点÷2(高阶)基础线段要求:手拉手,肩并肩对于相交的线段,分别计算各个方向,然后加总例2、数出下页左上图中锐角的个数。
分析与解:对于基础图形,可以使用开小火车的方式解决。
最小线段的数量为火车头。
或者,角的个数=最小角个数×(最小角个数+1)÷2又,角的个数=射线的个数×(射线个数-1)÷2例3、下列各图形中,三角形的个数各是多少?分析与解:对于基础图形,可以使用开小火车的方式解决,最小线段的数量为火车头。
所以,三角形个数=底边线段个数(每个底边基础线段构成一个基础三角形)或者,三角形的个数=最小三角形个数×(最小三角形个数+1)÷2(高阶)以上的内容基本是单层规整图形:数线段(数角,数三角形),解决方法:开小火车!对于多层规整的图形,应该以单层规整图形为基础,运用技术,算出多层规整图形的数量。
例4、下列图形中各有多少个三角形?分析与解:方法(1)使用分层计数法:图(1)图(2)上层:4+3+2+1=10(个)上层:4+3+2+1=10(个)下层: 0(个)中层: 0(个)上下层:4+3+2+1=10(个)下层: 0(个)上中层:4+3+2+1=10(个)中下层: 0(个)上中下层:4+3+2+1=10总数:10+0+10=20(个)总数:10+10+10=30(个)方法(2)公式法:第一层三角形的总数×层数公式法:第一层三角形的总数×层数图(1)图(2)第一层:4+3+2+1=10(个)第一层:4+3+2+1=10(个)层数: 2(层)层数: 3(层)总数:10×2=20(个)总数:10×3=30(个)例5、下列图形中各有多少个三角形?分层法:上层:4+3+2+1=10(个)下层: 4(个)(吹泡泡法)上下层:4+3+2+1=10(个)总数:10+4+10=24(个)小TIPS:吹泡泡法例6、右图中有多少个三角形?例7、右图中有多少个三角形?分析与解:对于不规则的图形,数之前,先将每个图形编号,编好后,先数单拼三角形1、4、3号,共3个。
高思奥数一年级下册含答案第11讲 立体图形计数

第十一讲立体图形计数前续知识点:一年级第一讲;XX模块第X讲后续知识点:X年级第X讲;XX模块第X讲墨莫墨莫卡莉娅小高把相应的人物换成红字标明的人物.还记得我们都学习过哪些立体图形吗?正方体、长方体、圆柱体、球体……数不胜数.今天我们来学习一下立体图形的计数.在地球上,一个小正方体可以在没有任何支撑的情况下悬浮在空中吗?答案当然是不可以!聪明的你赶快来看一看,下面题目中的立体图形到底由几个小正方体组成的呢?例题1数一数,它们分别由几个小正方体组成?【提示】有没有看不见的正方体?练习1数一数,它们分别由几个小正方体组成?数正方体有许多方法,其中我们可以一层一层的分层数,试试看.例题2左边方框中的立体图形和右边哪个立体图形中的小正方体个数相同呢?【提示】数一数,分别有几个小正方体!练习2左边方框中的立体图形和右边哪个立体图形中的小正方体个数相同呢?分层数的方法不仅简单快捷,而且清晰明了,不容易数重数漏.结合找规律的方法,我们更能轻松数出立体图形的个数.例题3数一数,下面这个“宝塔”由多少个小正方体组成?A BC DA B【提示】找一找,每层之间有什么规律?练习3数一数,下面这个“楼梯”由多少个小正方体组成?例题4要想把下面左边的立体图形补全成为一个完整的大正方体,至少需要再加几个小正方体呢?【提示】左边的立体图形由几个小正方体组成的?右边的呢?练习4要想把下面左边的立体图形补全成为一个完整的大正方体,至少需要再加几个小正方体呢?例题5要想把下面的立体图形补全成为一个完整的大正方体,至少需要再加几个小正方体呢?【提示】补全后的大正方体是什么样的呢?例题6如图所示,将大正方体中的“L”形挖穿,你能数出现在这个立体图形有多少个小正方体吗?【提示】挖穿了几层?课外阅读长方体和正方体的故事长方体是一个聪明的小男孩儿,他生活在一个数学图形的古老部落.长老们说他们一直拥有自然女神的庇护,自然女神总是不定期地出现在他们部落,每一次,她都只见一个有缘人,如果这个有缘人能够通过她的考验,她就会满足这个有缘人的一个合理的愿望.有一天,长方体去小河边玩,已经有一些伙伴在河边嬉戏,有三角形,正方形,圆等等……长方体刚走到附近就听到三角形喊救命,原来是平行四边形掉到河里去,长方体奋不顾身地跳进了河里,拼死救人.最后长方体把平行四边形救出来了.大家都很感谢长方体.长方体坐在草原上看风景,自然女神出现了.自然女神说:“你已经通过了我的考验,告诉我,你有什么愿望?”长方体说:“我没有什么愿望.”自然女神说:“既然你不说,那我就自作主张替你做决定了.”自然女神知道长方体一个人玩,没有伙伴,就创造了正方体,正方体和长方体一样聪明,而且,正方体和长方体还十分相似,有许多共同的特点.长方体很喜欢这个新伙伴.长方体对自然女神说;“我很喜欢正方体,他有许多和我相似的地方,像我的影子,但又和我完全不一样,有自己的个性.”自然女神说:“你喜欢就好,其实,正方体是另一个特殊的你.比你自己还要特别的你.以后,你自然会明白的.”作业1. 数一数,它们分别由几个小正方体组成?2. 左边方框中的立体图形和右边哪个立体图形中的小正方体个数相同呢?3. 数一数,下面这个“楼梯”由多少个小正方体组成?C B4. 要想把下面左边的立体图形补全成为一个完整的大正方体,至少需要再加几个小正方体呢?5. 如图所示,将大正方体中的“T”字形挖穿,现在这个图形中有几个小正方体?第十一讲 立体图形计数1. 例题1答案:5;5;9;10详解:先数出能看到的正方体个数,再数出看不见的正方体个数,相加即可.2. 例题2答案:A详解:左边方框中的立体图形的小正方体个数为10个,A 的小正方体个数为10个,B 的小正方体个数为9个,C 的小正方体个数为8个,D 的小正方体的个数为11个.3. 例题3答案:35详解:每层的小正方体个数分别为1、3、6、10、15,加起来的和为35.规律是每层分别在上一层的基础上增加2、3、4、5个小正方体.4. 例题4答案:2;17详解:第一个图中完整的大正方体中的小正方体个数为8个,左边立体图形中的小正方体个数为6个,还需要862-=(个).第二个图中完整的大正方体中的小正方体个数为27个,左边立体图形中的小正方体个数为10个,还需要271017-=(个).5. 例题5答案:48详解:符合要求的完整的大正方体至少需要64个小正方体组成,现在有16个小正方体,还需要再加小正方体641648-=(个). 6. 例题6答案:52详解:完整的大正方体一共有1616161664+++=个)小正方体,“镂空”部分有333312+++= (个)小正方体,所以还剩下641252-= (个)小正方体.7. 练习1答案:5;4;6;8简答:第三个中有1个看不见的正方体,第四个中有3个看不见的正方体.8. 练习2答案:D简答:左边方框中的立体图形的小正方体的个数为7个,D 的小正方体的个数也为7个.9. 练习3答案:60简答:每层小正方体的个数分别为4、8、12、16、20,加起来的和为60.10. 练习4答案:3;13简答:第一个图中完整的大正方体中的小正方体个数为8个,左边立体图形中的小正方体个数为5个,还需要853-=(个).第二个图中完整的大正方体中的小正方体个数为27个,左边立体图形中的小正方体个数为4个,还需要271413-=(个).11. 作业1答案:6;8;9;10简答:观察这两层小正方体,分别数出每一层小正方体的个数,注意“看不见”的小正方体.也可分别数出每列的小正方体个数,加在一起即可.12. 作业2答案:A简答:左边方框中小正方体的个数是10个,而右边各立体图形的小正方体个数分别为:A .10个;B .13个;C .9个;D .9个.13. 作业3答案:20简答:从顶层开始数,最顶层为2个,第二层为4个,第三层为6个,第四层为8个,所以小正方体的个数为246820+++=(个).14. 作业4答案:9简答:左边的立体图形中小正方体的个数为36918++=(个),完整的大正方体中小正方体的个数为99927++=(个).还需要小正方体27189-=(个).15. 作业5答案:44简答:方法一:整个大正方体中小正方体的个数为1616161664+++=(个),“T ”字形中小正方体的个数为555520+++=(个)或4444420++++=(个),所以现在有小正方体642044-=(个). 方法二:每层剩下的小正方体有11个,共有4层,所以现在有小正方体:1111111144+++=(个).。
小学奥数第五讲:图形的计数

小学奥林匹克数学第一集:第五讲:图形的计数一、数一数小朋友,你知道中有多少个三角形吗?我们可以这样想,图中的小三角形一共有4个,大三角形有1个,所以一共有5个三角形。
在数数时,要做到有次序,有条理,不遗漏也不重复,这样才能正确地数数。
例1:数一数下图各有几条线段?分析:我们可以照下面的方法数:解:共有线段4+3+2+1=10(条)例2:图中有多少个小正方体?分析:这个图形是由小正方体组成的。
可以采用数数的方法,按顺序数。
也可以根据图形的组成规律进行计算,如果每2个一摞,一共有4摞。
解:方法一:一个一个地数出8个正方体。
方法二:2×4=8(个)答:共有8个小正方体。
例3:将9个小正方体组成如图所示的“十”字形,再将表面涂成红色,然后将小正方体分开。
问(1)2面涂成红色的有几个?(2)4面涂成红色的有几个?(3)5面涂成红色的有几个?分析:整个图形表面涂成红色。
只有“粘在一起的”面没有涂色。
中间的一个小正方体2面涂色,四端的4个小正方体都是5面涂色,剩下的四个小正方体都是4面涂色。
解:(1)2面涂成红色的小正方体只有1个。
(2)4面涂成红色的小正方体有4个。
(3)5面涂成红色的小正方体有4个。
例4:亮亮从1写到100,他一共写了多少数字“1”?分析:在1到100这100个数中,“1”可能出现在个位、十位或百位上。
应分三种情况计数:“1”在个位上的数有:1、11、21、31、41、51、61、71、81、91共10个;“1”在十位上的数有:10、11、12、13、14、15、16、17、18、19共10个;“1”在百位上的数有:100 只有1个。
解:10+10+1=21(个)答:共写21个。
例5:27个小方块堆成一个正方体。
如果将表面涂成黄色,求:(1)3面涂成黄色的小方块有几块?(2)1面涂成黄色的小方块有几块?(3)2面涂成黄色的小方块有几块?分析:涂色的有26个小方块。
3面涂色的只有顶点上的8个小方块;1面涂色的只有六个面上中间的小方块;其余的必然是2面涂色的小方块。
小学一年级奥数 第十八讲 数图形(周四)

第十八讲数图形
周四
经典例题
数一数,右图中有多少个长方形?
名师导航:
将图中的各块编上号。
先数单个的长方形,,共有5个;接着数由两个长方形组成的大长方形,,共有2个;再数由三个长方形组成的大长方形,,共有2个;最后数由五个长方形组成的最大长方形,
,只有1个。
再把它们的个数加起来,就是总数。
详细解答:
一共有5+2+2+1=10(个)长方形。
温馨提示:
数长方形时,先数单个的长方形个数,再数由2个(或3个、4
个…)小长方形组成的长方形个数,再把各次数的个数相加就是长方形总数。
组合的长方形有时是横行的长方形组合,有时是竖行的长方形组合,数时要仔细辨清。
举一反三练习
1、数一数,下面每个图形里各有几个长方形?
(1)(2)
2、数一数,图中共有多少个长方形?
3、、数一数,下面每个图形里各有几个长方形?
(1)(2)。
奥数知识点 图形计数
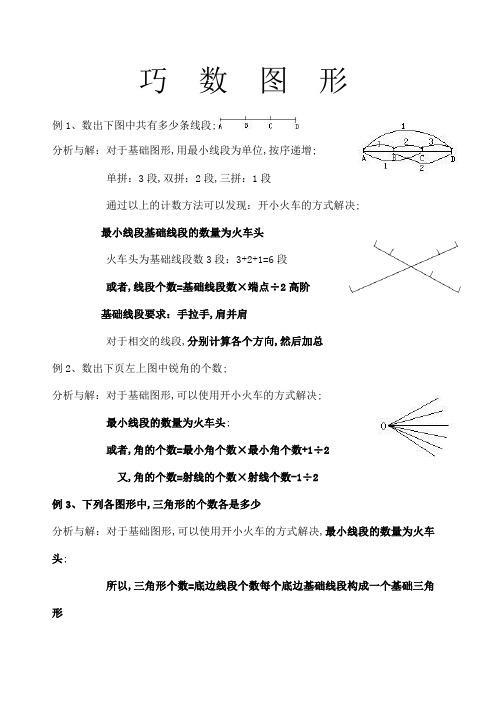
巧数图形例1、数出下图中共有多少条线段;分析与解:对于基础图形,用最小线段为单位,按序递增;单拼:3段,双拼:2段,三拼:1段通过以上的计数方法可以发现:开小火车的方式解决;最小线段基础线段的数量为火车头火车头为基础线段数3段:3+2+1=6段或者,线段个数=基础线段数×端点÷2高阶基础线段要求:手拉手,肩并肩对于相交的线段,分别计算各个方向,然后加总例2、数出下页左上图中锐角的个数;分析与解:对于基础图形,可以使用开小火车的方式解决;最小线段的数量为火车头;或者,角的个数=最小角个数×最小角个数+1÷2又,角的个数=射线的个数×射线个数-1÷2例3、下列各图形中,三角形的个数各是多少分析与解:对于基础图形,可以使用开小火车的方式解决,最小线段的数量为火车头;所以,三角形个数=底边线段个数每个底边基础线段构成一个基础三角形或者,三角形的个数=最小三角形个数×最小三角形个数+1÷2高阶以上的内容基本是单层规整图形:数线段数角,数三角形,解决方法:开小火车对于多层规整的图形,应该以单层规整图形为基础,运用技术,算出多层规整图形的数量;例4、下列图形中各有多少个三角形分析与解:方法1使用分层计数法:方法2公式法:第一层三角形的总数×层数例5、下列图形中各有多少个三角形小TIPS:吹泡泡法例6、右图中有多少个三角形例7、右图中有多少个三角形分析与解:对于不规则的图形,数之前,先将每个图形编号,编好后,先数单拼三角形1、4、3号,共3个;再数两个图形合成的双拼三角形,1+2号,2+3号,3+4号,4+1号,按顺序两个两个合并,共4个三角形;最后数由1+2+3+4号组成的四拼大三角形,有1个;所以3+4+1=8,共8个三角形;例8、下列各图形中,长方形的个数各是多少分析与解:对于单层基础图形,可以使用开小火车的方式解决;每个长方形相当于最小线段;所以数单层的基础长方形,就是数基础线段数;对于多层的长方形的个数=单层长方形的数量×层数个单层长方形的数量=长边上的线段数个,层数=宽边上线段的个数层例9、下列图形中,长方形的个数是多少个分析与解:对于基础图形,可以使用开小火车的方式解决;单层长方形的数量=长边线段数=4+3+2+1=10个,层数=宽边线段数=3+2+1=6层总数=4+3+2+1×3+2+1=60个例10、下列图形中,长方形的个数是多少个分析,先将<格1>与<格2>隐去,剩下的格3,就是一个多层规整长方形=10×6=60个格1带来的长方形=4个吹泡泡法格2带来的长方形=5个总数=60+4+5=69个例11、下列图形中,长方形的个数是多少个分析与解:了解正方形的构成特点:四边相等;方法1数格子:一格,四格,九格,十六格……方法2开小火车法:最小正方形的个数为“火车头”,后面的“车厢”中的每个乘数都减-1,直至出现1为止0乘任何数都等于0解:3×3+2×2+1×1=14个例12、下列图形中,正方形的个数是多少个分析与解:利用开小火车法:火车头为最小9正方形数量:6×5正方形个数=6×5+5×4+4×3+3×2+2×1=70个例13、数下列图形中共有21个三角形,一共需要多少个小棒:例10、在下图中,包含“”号的长方形和正方形共有多少个分析与解:对于不规整的图形,进行分类讨论;左图中,应先进行分类:正正方形与斜正方形正正方形=5+5=10个斜正方形= 5个总数=10+5=15个例11、如下图是由小立方体构成的塔,数一数有多少个小立方体分析与解:数立方体时,先从顶层数起;公式:本层可见数+上层数本题:1+3+1+5+4+7+9=30个例12、数一数,下列图形中有多少个长方形方法1:小讨厌法:不包含小讨厌的多层规整图形:10×6=60个小讨厌错误!+错误!+错误!:4+4+4=12,共:60+12=72个方法2:重叠法三年级:横:10×6=60个,竖:3×10=30个中重叠:3×6=18个,共:60+30-18=72个例13、数一数,第10个图形应该有多少圆圈组成通过观察可以发现如下的规律:1 2 3 (10)2 2+4+2 2+4+6+4+2 ……2+4+…+20…+4+22 8 18 (200)例13、数一数,第10个图形应该有多少条线段通过观察可以发现如下的规律:1 2 3 4 (10)1×2+2 3×2+3 6×2+4 10×2+5 55×2+1122=4 32=9 42=16 52=25 112=121 例14、数一数,下列图形中包含★长方形有多少个方法1勾对角线法:将★的左上角的点和右下角的点相连:通过加标字母A、B和a、b、c、d、e、f,帮助我们数图形:Aa、Ab、Ac、Ad、Ae、Af、Ba、Bb、Bc、Bd、Be、Bf、方法2公式法:经过★划十字线,左侧、右侧、上面、下面焦点数相乘:2×2×1×3=12个例15、数一数,下列图形中有多少条线段有多少个三角形1数线段:分方向:共:6×5+5=35条2数三角形:分方向中间五角星不用①③③④⑤:共10个三角形;仅使用①③③④⑤中一条:每一条有4个三角形,共4×5=20条使用①③③④⑤中的两条:共4个三角形;共:10+20+5=35个。
一年级奥数之图形的计数

图形的计数课kè前qián 活huó动dòng虎hǔ大dà王wáng 捉zhuō鼠shǔ大dà森sēn 林lín 里lǐ的de 老lǎo 鼠shǔ们men 正zhèng 在zài 搬bān 家jiā呢ne !不bú幸xìng 的de 是shì被bèi 森sēn 林lín 里lǐ的de 老虎lǎohǔ撞见zhuàngjiàn 了le ,老虎lǎohǔ这zhè回huí是shì大展dàzhǎn 拳脚quánjiǎo 呀ya !一会yīhuì就jiù抓zhuā了le 好hǎo 多duō只zhī老lǎo 鼠shǔ,高gāo 高gāo 兴xìng 兴xìng 的de 回huí到dào 了le 虎hǔ穴xué里lǐ,可kě是shì抓zhuā的de 老lǎo 鼠shǔ太tài 多duō了le ,虎hǔ大dà王wáng 数shù不bù清qīng 楚chǔ到dào 底dǐ有yǒu 几jǐ只zhī?就jiù找zhǎo 来lái 聪cōng 明míng 伶líng 俐lì的de 小xiǎo 青qīng 蛇shé给gěi 它tā数shù数shù,他tā则zé舒shū舒shū服fú服fú地dì躺tǎng 在zài 床chuáng 上shàng 吃chī方fāng 糕gāo 。
小xiǎo 青qīng 蛇shé认rèn 认rèn 真zhēn 真zhēn 地dì数shù了le 半bàn 天tiān ,然rán 后hòu 恭gōng 恭gōng 敬jìng 敬jìng 地dì说shuō:“尊zūn 敬jìng 的de 大dà王wáng ,您nín 只zhǐ需xū数shù一yí下xià你nǐ眼yǎn 前qián 的de 方fāng 糕gāo 就jiù知zhī道dào 您nín 一yí共gòng 抓zhuā了le 多duō少shǎo 只zhī老lǎo 鼠shǔ了le !”虎hǔ大dà王wáng 忙máng 说shuō:“这zhè些xiē方fāng 糕gāo 有yǒu 多duō少shǎo 块kuài ?我wǒ懒lǎn 得de 数shù了le 。
一年级奥数:《图形的计数》

一年级奥数:《图形的计数》《图形的计数》课前预热所属体系板块:第二级下图形的计数主要知识点:1)平面图形计数2)立体图形计数能力培养:计算能力、空间想象能力体系对接:第三级下飞速图形计数例题展示:数数看,下图一共有多少个小方块。
课前预热:简单复习各种平面图形,建立有序计数的能力。
《图形的计数》知识点精讲一、平面图形计数1、恰含法【例】下图有()个三角形。
【解析】恰恰包含1个三角形的有:3个恰恰包含2个三角形的有:2个恰恰包含3个三角形的有:1个一共有:3+2+1=6(个)2、分类法按大小、位置来分类【例】下图有()个正方形。
【解析】按大小来分类,小的正方形有:7个大的正方形有:4个一共有:7+4=11(个)二、立体图形计数分层数下层=上层+多出来的【例】下面的图形有()个方块堆成。
【解析】分层数。
从上往下数:第一层:1个第二层:2(多出来的)+1(上层)=3(个)第三层:1(多出来的)+3(上层)=4(个)一共有:1+3+4=8(个)三、空心图阵补全法数量=补完总数-补上的【例】数一数,下图中共有()颗星星。
【解析】补全:1+3+5+7+9+11+13=49(个)补:3+5=8(个)数量:49-8=41(个)四、至少……才够考虑最少情况【例】有一天,小猴和9个小伙伴一起玩。
小猴拿出一包糖,里面有54块。
小猴说:“咱们一共10个小伙伴,但分到的糖数量要不一样多,谁会分?”结果小伙伴们都无法分。
为什么?如果不能分,至少应该有多少块才够呢?【解析】1+2+3+4+5+6+7+8+9+10=55(块)答:所以不够分,至少要55块才够分。
《图形的计数》课后拓展练习1、下图中一共有多少个圆点。
2、下面一共有多少条线段。
3、下图是小明搭的积木,数一数一共有()个小正方体。
4、数一数,下面的“沙发”是由()块小方块搭成的。
【答案解析】1。
29个。
2。
6条。
3。
10个。
4。
20块。
奥数-05图形计数+答案

( )个
( )个
4
( )个
【例 7】
下图中各有多少个三角形?
分层法: 上 层: 下 层: 上下层: 总 数:
下图中,有多少个正方形?
解析:利用开小火车法: 火车头为最小正
5
练习一 下图中,有多少个正方形?
1、
2、
3、
( )个
( )个
( )个
【例 2】
下图形中,长方形有多少个? 解析,先将<格 1>与<格 2>隐去,剩下的
练习一
2
【例 2】 数出右图中共有多少条线段。 解析:(加法原理)从基本图形(只包含
最短线段)的个数出发,按序递增,依次数 出它们的个数,并求出它们的和是多少。最 小线段(基础线段)的数量为火车头,有 3
条,由两条基础线段拼成的线段有 2 条,由三条基础线段拼成的线段有 1 条,共有 3+2+1=6(条)。
练习七 下列图形中各有多少个三角形?
按分类加法原理
4+3+2+1=10(个) 4(个) 4+3+2+1=10(个) 10+4+10=24(个)
【例 8】 下图中有多少个三角形? 解析:假设每一个最小三角形的边长为 1。按边
的长度来分类计算三角形的个数。 边长为 1 的三角形,从上到下一层一层地数,有
一、图形计数方法——分类计数法
它是指先把所要计数的对象按性质、特点进行分类,统计出每一类的个数,再求 各类之和。分类计数的理论基础是“加法原理”。
运用加法原理的关键问题:确定分类的方法。 举例:下图中共有多少个图形? 可以分成圆、正方形、三角形和长方形 4 类,统计出各类的个数,再相加。也可 以按位置分上、中、下分别统计,再求和。
一年级奥数图形的计数
一年级奥数图形的计数下图所示的“塔”一年级奥数图形的计数
请你数一数,下图中共有多少个小叉子?
请你数一数,下图中共有多少个小叉子?
图形的计数(★★★)
(★★★)
(★★★★)
(★★★★)
(★★★★)
有一天王老师带着班上的10个小朋友去春游,王老师拿出一包糖,对同学们说:“我来给你们分糖吃吧,这里面一共有54块糖,现在我们一共有10个小朋友,每个都要分到糖,但分到的糖块数又不能一样多,谁会分?”结果小朋友们都不会分,为什么呢?如果要够分,最少要多少块糖呢?
(★★★★★)
时钟1点时敲一下,2点时敲两下,3点时敲三下,……,照这样敲下去,从1点开始时钟一共敲了28下时,时钟显示的是几点?当一共敲了78下时,时钟显示的是几点呢?
平时注意积累,记住一些有趣的和重要的运算结果,非常有助于我们计数。
比如,请同学们一定要记住下面几个自然数相加的结果。
(四1)图形的计数

图形的计数在解决图形的计数问题时,要根据图形的规律和特点选择适当的方法,常用的方法有:按规律顺序数和分类数两种。
例1、在下图中,如果线段 AB 上有99个点,那么图中共有多少条线段?99个点太多了,如果无法找到规律,可以从简单入手。
比如线段AB 上有一个点,那么有几条线段?线段AB 上如果有两个点,那么有几条线段?尝试两三次,就能找到规律。
解答请注意,这条线段上一共有101个点。
以 A 为左端点的线段有100条,以C 1为左端点的线段有99条,以C 2为左端点的线段有98条,……,以 C 99 为左端点的线段只有1条。
由此得到题图中共有线段的条数为100+99+98+…+3+2+1,即1+2+3+…+98+99+100。
得到的算式,如果按部就班地求和,计算是非常烦琐的。
那么有没有简便的算法呢?我们试一下配对求和,得到如下算式:(100+1)+(99+2)+(98+3)+…(51+50)=50×101=5050线段AB 上有99个点,再加上两个端点,总共有101个点,因此共有线段可以表示为101×100÷2=5050条。
如果线段上包括端点在内,共有十个点,那么总共有线段10×9÷2=45条。
想一想,如果一条线段上共有n 个点,那么这条线段上共有多少条线段呢?例2、如图,数一数图中共有多少个三角形?解答解这类问题和数线段问题有非常密切的联系。
AB B方法一,按规律数。
单个的基本三角形是4个,两个合一起的三角形有3个,三个合一起的三角形是2个,四个合在一起的大三角形是1个,共是4+3+2+1=10(个)。
方法二,按顺序数。
以AB为一边的4个,以AD为一边的3个,以AE为一边的2个,以AF为一边的1个。
所以,图中三角形的总数为4+3+2+1=10(个)。
这和线段 BC 上的线段总数为4+3+2+1=10(条)是完全一样的。
因此,对于这种图形,只要数出 BC 上共有多少条线段,那么, BC 上的线段总数就是所求的三角形个数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
bùnéngyíyàngduō shuíhuìfēn jiéguǒxiǎohuǒbàn
不 能 一 样 多 , 谁 会 分 ?” 结 果 小 伙 伴
mendōubúhuìfēn wèishénmene rúguǒyàogòufēn
们 都 不 会 分 , 为 什 么 呢?如 果 要 够 分 ,
“ 我 们 来 分 糖 吃 吧 , 这 里 面 一 共 有 35 块
táng xiànzàiwǒmenyígòngyǒu gèxiǎohuǒbàn měigè
糖 , 现 在 我 们 一 共 有 8个 小 伙 伴 ,每 个
dōuyàofēndàotáng dànfēndàodetángkuàishùyòu
túxíngde jì shù 图 形 的计 数
【例 1】(★★★)
shùyīshù xiàmianzhèduīmùtóuyígòngyǒuduōshǎo
数 一 数 ,下 面 这 堆 木 头 一 共 有 多 少
gēn
根?
【例 2】(★★★)
xiàtúsuǒshìde tǎ shìyóusìcéngméiyǒufèngxìdexiǎo
请 chāzi
叉 子?
【例 4】(★★★★)
qǐngnǐshùyīshù xiàtúzhōnggòngyǒuduōshǎogèxiǎo
请 你 数 一 数 ,下 图 中 共 有 多 少 个 小
chāzi
叉 子?
1
【例 5】(★★★★)
yǒuyītiānxiǎohóuzihé gèxiǎohuǒbànyìqǐchūqùwán
3. 请 牢 记一 些 常 用 的 计 算 结 果 哦!
2
课 堂 小结
lì tǐ túxíngshùfāngkuài cóngshàngwǎngxiàfēn
1.立体 图 形 数 方 块 : 从 上 往 下 分
céngfǎ
层法
kǒujué shùtóudǐngjiālóushàng
口 诀:数 头 顶 加 楼 上
píngmiàntúxíng jì shùfǎ cóngshàngwǎngxiàfēn
一 层 放 一 根 , 下 面 每 一 层 都 比它 上
miandeyīcéngyàoduōyīgēn xiǎngyīxiǎng zuìxiàmian
面 的 一 层 要 多 一 根 , 想 一 想 ,最 下 面
yīcéngfàngduōshǎogēnyuánmù
一 层 放 多 少 根 圆 木?
kètángxiǎojié
下 图 所 示 的“塔” 是 由 四 层 没 有 缝 隙的 小
lì fāngkuàilěichéng qiútǎzǒnggòngyǒuduōshǎokuài
立 方 块 垒 成 ,求 塔 总 共 有 多 少 块
xiǎo lì fāngkuài
小立 方 块?
【例 3】(★★★★)
qǐngnǐshùyīshù xiàtúzhōnggòngyǒuduōshǎogèxiǎo
有 一 天 小 猴 子 和 7 个 小 伙 伴 一起 出 去 玩 ,
xiǎohóuzináchūyībāotáng duìxiǎohuǒbànmenshuō
小 猴 子拿 出 一 包 糖 , 对 小 伙 伴 们 说 :
wǒmenláifēntángchība zhè lǐ miànyígòngyǒu kuài
2. 平 面 图 形 计 数 法 : 从 上 往 下 分
céngfǎ
层法
fāngfǎ yīcéngyīcéngshùqīngchǔ zuòhǎo jì suàn
方 法 :一 层 一 层 数 清 楚 , 做 好 计 算
shìguānjiàn
是关 键
qǐngláojì yìxiēchángyòngdejìsuànjiéguǒ ò
zuìshǎoyàoduōshǎokuàitángne
最 少 要 多 少 块 糖 呢?
【例 6】(★★★★★)
yǒu gēnyuánmù duīchéngbǎotǎxíng zuìshàngmian
有 55 根 圆 木 ,堆 成 宝 塔 形 ,最 上 面
yīcéngfàngyīgēn xiàmianměiyīcéngdōubǐtāshàng
