小学三年级奥数 巧数图形 知识点与习题
三年级奥数--第六讲--巧数图形(三)

新速度教育三年级奥数
第六讲——巧数图形(三)
1. 温故知新。
2. 无规则图形的数法:分类法。
从小到大,从左到右,从上到下数。
3. 请小朋友们数一数下列图形有多少个。
4. 巧数图形在实际生活中的应用。
5. 有10个小朋友,每2个人照一张合影,一共要照多少张照片? 思路导航:这道题可以用数线段的方法来解答。
6.分析:根据题意,画出线段图,每一个点代表一个小朋友:
从图上可以看出,第1个小朋友要与其余9个小朋友合影,要照9张照片;第2个小朋友还要与其余8个小朋友合影,再照8张照片……以此类推,第9个小朋友只要再与1个小朋友合影,再照1张照片。
所以,一共要照9+8+7+6+5+4+3+2+1=45张照片。
I H G
F E D C B
A
1098743
10.小朋友们,我们一起来练一练吧!!
1,三年级有6个班,每两个班要比赛拔河一次,这样一共要组织多少场比赛?
2,有红、黄、蓝、白四只气球,如果每两只气球扎成一束,共有多少种不同的扎法?
3,有1——6六个数字,能组成多少个不同的两位数?
4,数一数下图有多少个三角形。
三年级 数学奥数拓展培优 第3讲 巧数图形(学生版)
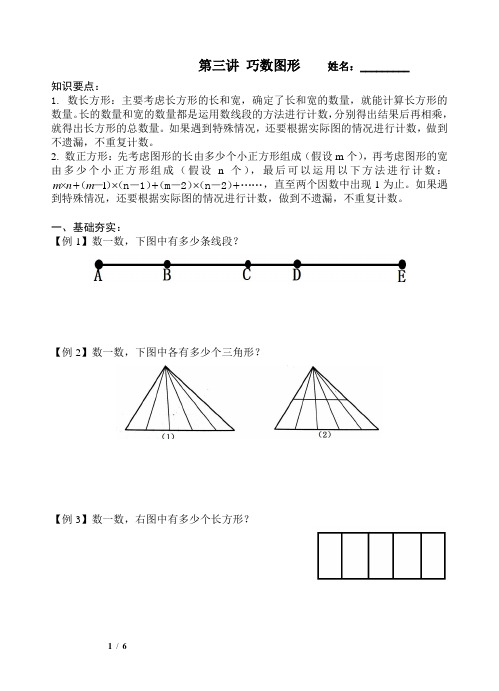
第三讲巧数图形姓名:_________
知识要点:
1. 数长方形:主要考虑长方形的长和宽,确定了长和宽的数量,就能计算长方形的数量。
长的数量和宽的数量都是运用数线段的方法进行计数,分别得出结果后再相乘,就得出长方形的总数量。
如果遇到特殊情况,还要根据实际图的情况进行计数,做到不遗漏,不重复计数。
2. 数正方形:先考虑图形的长由多少个小正方形组成(假设m个),再考虑图形的宽由多少个小正方形组成(假设n个),最后可以运用以下方法进行计数:(-)(n-1)(m-2)(n-2)……,直至两个因数中出现1为止。
如果遇+⨯+⨯+
×1
m n m
到特殊情况,还要根据实际图的情况进行计数,做到不遗漏,不重复计数。
一、基础夯实:
【例1】数一数,下图中有多少条线段?
【例2】数一数,下图中各有多少个三角形?
【例3】数一数,右图中有多少个长方形?
1/ 6。
小学三年级奥数第5讲 图形个数附答案解析

第5讲 图形个数一、知识要点小朋友,你想学会数图形的方法吗?要想不重复也不遗漏地数出线段、角、三角形……那就必须要有次序、有条理地数,从中发现规律,以便得到正确的结果。
要正确数出图形的个数,关键是要从基本图形入手。
首先要弄清图形中包含的基本图形是什么,有多少个,其次再数出由基本图形组成的新的图形,最后求出它们的和。
二、精讲精练【例题1】数一数,下图中有几条线段? 练习1:(1)数出下图中有多少条线段? (2)数出下图中有几个长方形?【例题2】数出图中有几个角?EABCDDABCODC BA练习2:数出图中有几个角?(1) (2)【例题3】数出下图中共有多少个三角形?练习3:数出图中共有多少个三角形?(1)(2)OCBA ED OC BA PDCBAFE AKG I H G A【例题4】数出下图中有多少个长方形? 练习4:(1)数出下图中有多少个长方形?(2)数出下图中有多少个正方形?【例题5】有5个同学,每两个人握手一次,一共要握手多少次? 练习5:(1)银海学校三年级有9个班,每两个班要比赛拔河一次,这样一共要拔河几次?DCBA DCBA(2)有1,2,3,4,5,6,7,8等8个数字,能组成多少个不同的两位数?三、课后作业1、数一数下图中各有多少条线段?(2)(3)2、数一数下图中有多少个锐角。
3、下列各图中各有多少个锐角?4、数一数下面图中各有多少个三角形。
5、数一数下面各图中分别有多少个长方形。
6、数一数,下面各图中分别有几个长方形?7、数一数下列各图中分别有多少个正方形?(每个小方格为边长是1的小正方形)第5讲图形个数答案解析一、知识要点同学们,你想学会数图形的方法吗?要想不重复也不遗漏地数出线段、角、三角形、长方形……那就必须要有次序、有条理地数,从中发现规律,以便得到正确的结果。
要正确数出图形的个数,关键是要从基本图形入手。
首先要弄清图形中包含的基本图形是什么,有多少个,然后再数出由基本图形组成的新的图形,并求出它们的和。
三年级奥数巧数图形

第2讲 巧数图形知识要点同学们,我们经常会遇到数图形的问题,对于较复杂的图形,经常会出现数重复或数漏掉的错误。
怎样才能不重复也不遗漏地数出图形的个数呢?这节课,我们将一起来寻找好的方法。
要正确数出图形的个数,关键是要从基本图形入手。
首先要弄清图形中包含的基本图形是什么,有多少个,然后再数出由基本图形组成的新的图形,并求出它们的和。
精典例题例1:数出下图中有多少条线段?模仿练习数一数,每种图形有多少个?有( )条线段 有( )个三角形有( )个角 有( )个长方形 有( )个正方形例2:数出图中共有多少个三角形?从短的线段入手,再两条两条拼接起来数,你发现规律了吗?EABCDODC B A FEDC B A模仿练习数一数,每幅图里有多少个三角形? (1) (2)有( )个三角形有( )个三角形例3:下面的图形中有多少个三角形?(第九届中国青少年数学论坛趣味数学解题技能展示大赛试题)模仿练习数一数,图中共有几个正方形?(2010武汉明心数学资优生水平测试题)精典例题例4:数出下图中有多少个长方形?多少个正方形?还能用刚才的方法来数吗?三角形很多,可以尝试按三角形的方向和大小尝试分类数。
KG I H G FEDC B A模仿练习1.数一数,图中有多少个长方形?2.数一数图中有多少个正方形?家庭作业1.数一数每幅图里面图形的个数(能计算的写出算式)。
(1) (2)前面学习的数长方形的方法还有用吗?怎么能用上呢?DCBA D CBA有( )条线段 有( )个角2.右图中有多少个三角形?3.图中有多少个长方形?(把你的想法分享给你的爸爸妈妈听,你能教会他们吗?分享后让爸爸妈妈给你打星,最多5颗星)4.数一数,右图中有多少个正方形?5.(20XX 年“陈省身杯”国际青少年数学邀请赛试题)。
巧数图形详细讲解小学三年级奥数(课堂PPT)

知识回顾 Knowledge Review
总共:10+10+4= 24 个
Page 19
拓展12:数出下图中所有三角形的个数。
(3+2+1)×55=25
5个 5个
小五边形外侧组合三角形有(3+2+1)×5-5=25个三角形。 以大五边形边为底边的等腰三角形有5个。 以小五边形顶角为顶角的等腰三角形有5个。
总共:25+5+5= 35 个。
Page 20
5个组合 1
总计
15
可见,整齐单排长方形个数的算法与线段计算相同。
Page 4
例3.数出图中共有多少三角形。
A
三角形个数: 4+3+2+1=10
1 2 34
B C DE F
数三角形有时也可以用数线段的方法;有的图形要用 编号数图形的方法,还有的图形先要分成几部分分别 去数,再考虑几部分拼合起来看看有没有产生新三角 形。
巧数图形
Page 1
白汀水
例1、数线段
31542
共5+4+3+2+1= 15条线段
Page 2
练习1、数线段
1 23 4
5
67
共 7+6+5+4+3+2+1=28 条线段
Page 3
例2、下面图中有几个长方形?
数一数:
总计: 5+4+3+2+1=15
单个
5
2个组合 4
3个组合 3
4个组合 2
Page 22
拓展15. 数一数,图中有多少个长方形?
三年级奥数--第五讲--巧数图形(二)
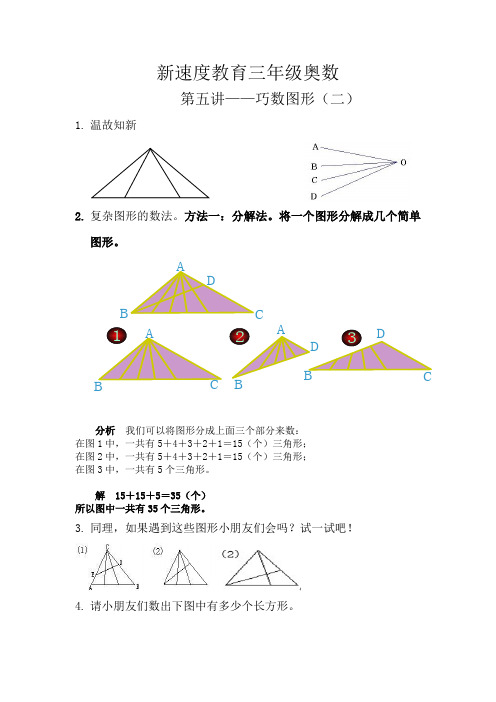
新速度教育三年级奥数
第五讲——巧数图形(二)
1. 温故知新
2. 复杂图形的数法。
方法一:分解法。
将一个图形分解成几个简单图形。
B C
分析 我们可以将图形分成上面三个部分来数:
在图1中,一共有5+4+3+2+1=15(个)三角形;
在图2中,一共有5+4+3+2+1=15(个)三角形;
在图3中,一共有5个三角形。
解 15+15+5=35(个)
所以图中一共有35个三角形。
3. 同理,如果遇到这些图形小朋友们会吗?试一试吧!
4. 请小朋友们数出下图中有多少个长方形。
分析:数图形中有多少个长方形和数三角形的方法一样,长方形是由长宽两对线段围成,线段CD 上有3+2+1=6条线段,其中每一条与AC 中一条线段对应,分别作为长方形的长和宽,这里共有6×1=6个长方形;而AC 上共2+1=3条线段也就有6×3=18个长方形。
它的计算公式为:
5. 方法二:长方形的总数=长边线段的总数×宽边线段的总数
6. 同理,如果遇到这些图形小朋友们会吗?试一试吧!
7. *请小朋友们数出下图中有多少个正方形。
分析:一个小正方形有9个,四个小正方形组成有4个,9个小正方形有1个,所以一共有1+4+9=15个
8.*方法三:公式法。
1*1+2*2+3*3+..+N*N=。
N 是一行正方形的个数。
9.练一练:
D B C
A。
小学三年级奥数第5讲 图形个数(含答案分析)

第5讲 图形个数一、知识要点小朋友,你想学会数图形的方法吗?要想不重复也不遗漏地数出线段、角、三角形……那就必须要有次序、有条理地数,从中发现规律,以便得到正确的结果。
要正确数出图形的个数,关键是要从基本图形入手。
首先要弄清图形中包含的基本图形是什么,有多少个,其次再数出由基本图形组成的新的图形,最后求出它们的和。
二、精讲精练【例题1】数一数,下图中有几条线段? 练习1:(1)数出下图中有多少条线段? (2)数出下图中有几个长方形?【例题2】数出图中有几个角?EABCDDABCODC BA练习2:数出图中有几个角?(1) (2)【例题3】数出下图中共有多少个三角形?练习3:数出图中共有多少个三角形?(1)(2)OCBA ED OC BA PDCBAFE AKG I H G A【例题4】数出下图中有多少个长方形? 练习4:(1)数出下图中有多少个长方形?(2)数出下图中有多少个正方形?【例题5】有5个同学,每两个人握手一次,一共要握手多少次? 练习5:(1)银海学校三年级有9个班,每两个班要比赛拔河一次,这样一共要拔河几次?DCBA DCBA(2)有1,2,3,4,5,6,7,8等8个数字,能组成多少个不同的两位数?三、课后作业1、数一数下图中各有多少条线段?(2)(3)2、数一数下图中有多少个锐角。
3、下列各图中各有多少个锐角?4、数一数下面图中各有多少个三角形。
5、数一数下面各图中分别有多少个长方形。
6、数一数,下面各图中分别有几个长方形?7、数一数下列各图中分别有多少个正方形?(每个小方格为边长是1的小正方形)第5讲 图形个数(答案)一、知识要点同学们,你想学会数图形的方法吗?要想不重复也不遗漏地数出线段、角、三角形、长方形……那就必须要有次序、有条理地数,从中发现规律,以便得到正确的结果。
要正确数出图形的个数,关键是要从基本图形入手。
首先要弄清图形中包含的基本图形是什么,有多少个,然后再数出由基本图形组成的新的图形,并求出它们的和。
小学三年级奥数-数图形个数

二、精讲精练
• 【例题1】数出下图中有多少条线段?
A B C D
【思路导航】方法一:我们可以采用以线段左端点分类 数的方法。以A点为左端点的线段有:AB、AC、AD 3 条;以B点为左端点的线段有:BC、BD 2条;以C点为 左端点的线段有:CD 1条。所以,图中共有线段 3+2+1=6(条)。 方法二:把图中线段 AB、BC、CD看做基本线段来数, 那么,由1条基本线段构成的线段有:AB、BC、CD 3条; 由2条基本线段构成的线段有:AC、BD 2条;由3条基本 线段构成的线段有:AD 1条。所以,图中一共有 3+2+1=6(条)线段。
• 方法三:我们发现,要数出图中三角形的个数,只需 数出线段 AD中包含几条线段就可以了,即3+2+1=6( 个)。所以图中共有6个三角形。
练习3:
• 数出图中共有多少个三角形? A • (1)
B C D
E
F
• ( 2)
A
GH I G B C D E
K
F
A
B
• 【例题4】数出下图中有多少个长方形?
练习1:
• (1)数出下图中有多少条线段?
Aபைடு நூலகம்B C D E
• (2)数出下图中有几个长方形?
A
• 【例题2】数出图中有几个角?
O
B C D
方法一:以OA为一边的角有:∠AOB、∠AOC、 ∠AOD 3个;以OB为一边的角还有: ∠BOC、∠BOD 2个;以OC为一边的角还有:∠COD 1 个。所以,图中共有角3+2+1=6(个)。 方法二:把图中∠AOB、∠BOC、∠COD看做基本角来 数,那么,由1个基本角构成的角有:∠AOB、∠BOC、 ∠COD 3个;由2个基本角构成的角有: ∠AOC、∠BOD 2个;由3个基本角构成的角有:∠AOD 1个。所以,图 中一共有3+2+1=6(个)角。
三年级奥数数图形

第1讲数图形
【知识要点】
线段:直线上两个点和它们之间的部分叫做线段,这两个点叫做线段的端点。
角:具有公共端点的两条射线组成的图形叫做角。
这个公共端点叫做角的顶点,这两条射线叫做角的两条边。
三角形:三角形是由同一平面内不在同一直线上的三条线段“首尾”顺次连接所组成的封闭图形。
长方形:四个角都是直角的四边形叫作矩形,又称长方形。
【经典例题】
【例1】数出下图中有多少条线段?
【练习1】数出下图中有多少条线段?
【例2】数出下图中有几个角?
【练习2】数出下图中有几个角?
【例3】数出下图中有几个三角形?
【练习3】数出下图中有几个三角形?
【例4】数出下图中有几个长方形?
【练习4】数出下图中有几个长方形?
【例5】有五名同学,每两名同学要握一次手,一共要握几次手?
【练习5】银海学校三年级有9个班,每两个班要比赛拔河一次,这样一共要拔河几次?
【例6】从广州到北京的某次快车中途要停靠8个大站,铁路局要为这次快车准备多少种不同车的车票?这些车票中有多少种不同的票价?
【练习6】从上海到武汉的航运线途中,有9个停靠码头,航运公司要为这段航运线准备多少种不同的船票?
【课堂练习】
1、数出下图中有多少条线段?
2、数出下图中有多少个角
3、数出下图各有多少个三角形?
4、下图中各有多少个长方形?
5、有1,2,3,4,5,6,7,8等8个数字各用一次,能组成多少个不同的两位数?
6、从上海至青岛的某次直快列车,中途要停靠6个大站,这次列车有几种不同票价?。
小学三年级奥数_巧数图形 _知识点与习题

例3下列图形中各有多少个三角形?分析与解:(1)只需分别求出以AB,ED为底边的三角形中各有多少个三角形。
以AB为底边的三角形ABC中,有三角形 1+2+3=6(个)。
以ED为底边的三角形CDE中,有三角形 1+2+3=6(个)。
所以共有三角形6+6=12(个)。
这是以底边为标准来分类计算的方法。
它的好处是可以借助“求底边线段数”而得出三角形的个数。
我们也可以以小块个数作为分类的标准来计算:图中共有6个小块。
由1个小块组成的三角形有3个; 由2个小块组成的三角形有5个; 由3个小块组成的三角形有1个; 由4个小块组成的三角形有2个; 由6个小块组成的三角形有1个。
所以,共有三角形 3+5+1+2+1=12(个)。
例4右图中有多少个三角形?解:假设每一个最小三角 形的边长为1。
按边的长度来分 类计算三角形的个数。
边长为1的三角形,从上到下一层一层地数,有 1+3+5+7=16(个); 边长为2的三角形(注意,有一个尖朝下的三角形)有1+2+3+1=7(个); 边长为3的三角形有1+2=3(个); 边长为4的三角形有1个。
所以,共有三角形 16+7+3+1=27(个)。
例6在下图中,包含“*”号的长方形和正方形共有多少个?解:按包含的小块分类计数。
包含1小块的有1个;包含2小块的有4个; 包含3小块的有4个;包含4小块的有7个; 包含5小块的有2个;包含6小块的有6个; 包含8小块的有4个;包含9小块的有3个; 包含10小块的有2个;包含12小块的有4个; 包含15小块的有2个。
所以共有 1+4+4+7+2+6+4+3+2+4+2=39(个)。
练习11 1.下列图形中各有多少条线段? 2.下列图形中各有多少个三角形? 3.下列图形中,各有多少个小于180°的角? 4.下列图形中各有多少个三角形? 5.下列图形中各有多少个长方形? 6.下列图形中,包含“*”号的三角形或长方形各有多少? 7.下列图形中,不含“*”号的三角形或长方形各有几个? 答案与提示 练习111.(1)28;(2)210。
三年级奥数专题-图形个数

三年级奥数专题-图形个数一、知识要点同学们,你想学会数图形的方法吗?要想不重复也不遗漏地数出线段、角、三角形、长方形……那就必须要有次序、有条理地数,从中发现规律,以便得到正确的结果.要正确数出图形的个数,关键是要从基本图形入手.首先要弄清图形中包含的基本图形是什么,有多少个,然后再数出由基本图形组成的新的图形,并求出它们的和. 二、精讲精练【例题1】数出下图中有多少条线段?【思路导航】方法一:我们可以采用以线段左端点分类数的方法.以A 点为左端点的线段有:AB 、AC 、AD 3条;以B 点为左端点的线段有:BC 、BD 2条;以C 点为左端点的线段有:CD 1条.所以,图中共有线段3+2+1=6(条).方法二:把图中线段 AB 、BC 、CD 看做基本线段来数,那么,由1条基本线段构成的线段有:AB 、BC 、CD 3条;由2条基本线段构成的线段有:AC 、BD 2条;由3条基本线段构成的线段有:AD 1条.所以,图中一共有3+2+1=6(条)线段.练习1:(1)数出下图中有多少条线段? (2)数出下图中有几个长方形?【例题2】数出图中有几个角?【思路导航】数角的个数可以采用与数线段相同的方法来数.方法一:以OA 为一边的角有:∠AOB 、∠AOC 、∠AOD 3个;以OB 为一边的角还有:∠BOC 、∠BOD 2个;以OC 为一边的角还有:∠COD 1个.所以,图中共有角3+2+1=6(个).方法二:把图中∠AOB 、∠BOC 、∠COD 看做基本角来数,那么,由1个基本角构成的角有:∠AOB 、∠BOC 、∠COD 3个;由2个基本角构成的角有: ∠AOC 、EA B C D DABCOD C B AOCBA∠BOD 2个;由3个基本角构成的角有:∠AOD 1个.所以,图中一共有3+2+1=6(个)角.练习2:数出图中有几个角? (1) (2)【例题3】数出右图中共有多少个三角形?【思路导航】方法一:我们可以采用按边分类数的方法.以PA 为边的三角形有:△PAB 、△PAC 、△PAD 、3个;以PB 为边的三角形还有:△PBC 、△PBD 2个;以PC 为边的三角形还有:△PCD 1个.所以,图中共有三角形3+2+1=6(个).方法二:把图中三角形 △PAB 、△PBC 、△PCD 看做基本三角形来数,那么,由1个基本三角形构成的三角形有:△PAB 、△PBC 、△PCD 3个;由2个基本三角形构成的三角形有: △PAC 、△PBD 2个;由3个基本三角形构成的三角形有:△PAD 1个.所以,图中一共有3+2+1=6(个)三角形.方法三:我们发现,要数出图中三角形的个数,只需数出线段 AD 中包含几条线段就可以了,即3+2+1=6(个).所以图中共有6个三角形.练习3:数出图中共有多少个三角形?(1) (2)【例题4】数出下图中有多少个长方形?【思路导航】数图中有多少个长方形和数三角形的方法一样,长方形是由长、宽两对线段围成,线段 CD 上有3+2+1=6(条)线段,其中每一条与AC 中一条线段对应,分别作为长方形的长和宽,这里共有6×1=6(个)长方形,而AC 上共有2+1=3(条)线段也就有6×3=18(个)长方形.它的计算公式为:长方形的总数=长边线段的总数×宽边线段的总数(3+2+1)×(2+1)=18(个) 答:图中共有18个长方形.O CBAAKGI H G D C B ADCBAPDC B A练习4:(1)数出下图中有多少个长方形? (2)数出下图中有多少个正方形?【例题5】有5个同学,每两个人握手一次,一共要握手多少次?【思路导航】这道题可以用数线段的方法来解答.根据题意,画出线段图,每一个端点代表一个同学. 从图上可以看出,第1个同学要与其余4个同学握手共握手4次;第2个同学还要与其余3个同学握手共握手3次,第3个同学要与其余2个同学握手共握手2次;第4个同学还要与最后1个同学握手共握手1次.所以,一共要握手4+3+2+1=10(次)练习5:(1)银海学校三年级有9个班,每两个班要比赛拔河一次,这样一共要拔河几次?(2)有1,2,3,4,5,6,7,8等8个数字,能组成多少个不同的两位数?DCBA54321。
巧数图形详解-小学奥数

4
24
12
24+16+12+4=56个
可看成由这个图形的3 个组合,单独一个有16 个三角形。
组合后增加8个三角形。
总共16×3+8=56
拓展9:下面图形中有多少个三角形?
拆走2条线后有3个三角形。 返回第1条线后增5个三角形。 返回第2条线后增8个三角形。
总共3+5+8=16个三角形。
个
设想大 长方形消失 则有15+10-1=24个
还原大长方形则增4
个
总共24+4总= 共282个8个
谢谢使用
6+5+4+3+2+1= 21个
练习2.数一数,下图中有多少个三角形?
12 3 4
1 234 5
(4+3+2+1)×2=20 个
(5+4+3+2+1)×3=45 个
例4.数一数,下图中有多少个角?
1
11
2
3
4
2
4+3+2+1=10 个
拓展1. 数一数,下图中有几个三角形?
拆除2条红线和蓝绿线后有三角 形 14个 2条红线返回后增加6个三角形
中横线移去后有18个三角形 中横线返回后增10个三角形 总共18+10=28(个)三角形
或12+6+8+2=28(个)三角形
5个组合
单个
3个组合 2个组合
拓展14. 数一数,图中有多少个长方形?
10
10
10
总共(4+3+2+1)×3=30 个
小学三年级奥数巧数图形知识点与习题教学内容

第11讲巧数图形数出某种图形的个数是一类有趣的图形问题。
由于图形千变万化,错综复杂,所以要想准确地数出其中包含的某种图形的个数,还真需要动点脑筋。
要想有条理、不重复、不遗漏地数出所要图形的个数,最常用的方法就是分类数。
例1数出下图中共有多少条线段。
分析与解:我们可以按照线段的左端点的位置分为A,B,C三类。
如下图所示,以A为左端点的线段有3条,以B为左端点的线段有2条,以C为左端点的线段有1条。
所以共有3+2+1=6(条)。
我们也可以按照一条线段是由几条小线段构成的来分类。
如下图所示,AB,BC,CD是最基本的小线段,由一条线段构成的线段有3条,由两条小线段构成的线段有2条,由三条小线段构成的线段有1条。
所以,共有3+2+1=6(条)。
由例1看出,数图形的分类方法可以不同,关键是分类要科学,所分的类型要包含所有的情况,并且相互不重叠,这样才能做到不重复、不遗漏。
例2 下列各图形中,三角形的个数各是多少?分析与解:因为底边上的任何一条线段都对应一个三角形(以顶点及这条线段的两个端点为顶点的三角形),所以各图中最大的三角形的底边所包含的线段的条数就是三角形的总个数。
由前面数线段的方法知,图(1)中有三角形1+2=3(个)。
图(2)中有三角形1+2+3=6(个)。
图(3)中有三角形1+2+3+4=10(个)。
图(4)中有三角形1+2+3+4+5=15(个)。
图(5)中有三角形1+2+3+4+5+6=21(个)。
例3下列图形中各有多少个三角形?分析与解:(1)只需分别求出以AB,ED为底边的三角形中各有多少个三角形。
以AB为底边的三角形ABC中,有三角形1+2+3=6(个)。
以ED为底边的三角形CDE中,有三角形1+2+3=6(个)。
所以共有三角形6+6=12(个)。
这是以底边为标准来分类计算的方法。
它的好处是可以借助“求底边线段数”而得出三角形的个数。
我们也可以以小块个数作为分类的标准来计算:图中共有6个小块。
小学三年级奥数专题一:数图形

小学三年级奥数专题一:数图形
专题简析:先确定起始点或起始边,数出图形的数量,再依次以后一个点(或边)数出图形的数量。
最后求出它们的和。
例1、数出下面图中有多少条线段?
思路:以A点为左端点的线段有:AB、AC、AD共3条;以B点为左端点的线段有:BC、BD共2条;以C点为左端点的线段有:CD共1条。
所以图中共有线段3+2+1=6条。
试一试1:数出下图中有( )条线段。
例2、数出下图中有几个角?
思路:以AO为一边的角有:∠AOB、∠AOC、∠AOD三个;以BO为一边的角有:∠BOC、∠BOD两个;以CO为一边的角有:∠COD一个。
所以图中共有3+2+1=6个角。
试一试2:数出下图中有()个角。
例3 数出下面图中共有多少个三角形。
思路:数三角形的个数与数线段、数角的方法相同:以AB为边的三角形有:△ABC、△ABD、△ABE三个;以AC为边的三角形有:△ACD、△ACE二个;以AD为边的三角形有:△ADE一个。
所以图中共有三角形3+2+1=6个。
试一试3:数出下面图中共有()个三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学三年级奥数巧数图形知识点与习题
数出某种图形的个数是一类有趣的图形问题.由于图形千变万化;错综复杂;所以要想准确地数出其中包含的某种图形的个数;还真需要动点脑筋.要想有条理、不重复、不遗漏地数出所要图形的个数;最常用的方法就是分类数.
例1数出下图中共有多少条线段.
分析与解:我们可以按照线段的左端点的位置分为A;B;C三类.如下图所示;以A为左端点的线段有3条;以B为左端点的线段有2条;以C为左端点的线段有1条.所以共有3+2+1=6(条).
我们也可以按照一条线段是由几条小线段构成的来分类.如下图所示;AB;BC;CD是最基本的小线段;由一条线段构成的线段有3条;由两条小线段构成的线段有2条;由三条小线段构成的线段有1条.
所以;共有3+2+1=6(条).
由例1看出;数图形的分类方法可以不同;关键是分类要科学;所分的类型要包含所有的情况;并且相互不重叠;这样才能做到不重复、不遗漏.
例2 下列各图形中;三角形的个数各是多少?
分析与解:因为底边上的任何一条线段都对应一个三角形(以顶点及这条线段的两个端点为顶点的三角形);所以各图中最大的三角形的底边所包含的线段的条数就是三角形的总个数.由前面数线段的方法知;
图(1)中有三角形1+2=3(个).
图(2)中有三角形1+2+3=6(个).
图(3)中有三角形1+2+3+4=10(个).
图(4)中有三角形1+2+3+4+5=15(个).
图(5)中有三角形
1+2+3+4+5+6=21(个).
例3下列图形中各有多少个三角形?
分析与解:(1)只需分别求出以AB;ED为底边的三角形中各有多少个三角形.
以AB为底边的三角形ABC中;有三角形
1+2+3=6(个).
以ED为底边的三角形CDE中;有三角形
1+2+3=6(个).
所以共有三角形6+6=12(个).
这是以底边为标准来分类计算的方法.它的好处是可以借助“求底边线段数”而得出三角形的个数.我们也可以以小块个数作为分类的标准来计算:图中共有6个小块.
由1个小块组成的三角形有3个;
由2个小块组成的三角形有5个;
由3个小块组成的三角形有1个;
由4个小块组成的三角形有2个;
由6个小块组成的三角形有1个.
所以;共有三角形
3+5+1+2+1=12(个).
(2)如果以底边来分类计算;各种情况较复杂;因此我们采用以“小块个数”为分类标准来计算:
由1个小块组成的三角形有4个;
由2个小块组成的三角形有6个;
由3个小块组成的三角形有2个;
由4个小块组成的三角形有2个;
由6个小块组成的三角形有1个.
所以;共有三角形
4+6+2+2+1=15(个).
例4右图中有多少个三角形?
解:假设每一个最小三角
形的边长为1.按边的长度来分
类计算三角形的个数.
边长为1的三角形;从上到下一层一层地数;有
1+3+5+7=16(个);
边长为2的三角形(注意;有一个尖朝下的三角形)有1+2+3+1=7(个);
边长为3的三角形有1+2=3(个);
边长为4的三角形有1个.
所以;共有三角形
16+7+3+1=27(个).
例5数出下页左上图中锐角的个数.
分析与解:在图中加一条虚线;如下页右上图.容
易发现;所要数的每个角都对应一个三角形(这个角与它所截的虚线段构成的三角形);这就回到例2;从而回到例1的问题;即所求锐角的个数;就等于从O点引出的6条射线将虚线截得的线段的条数.虚线上线段的条数有1+2+3+4+5=15(条).
所以图中共有15个锐角.
例6在下图中;包含“*”号的长方形和正方形共有多少个?
解:按包含的小块分类计数.
包含1小块的有1个;包含2小块的有4个;
包含3小块的有4个;包含4小块的有7个;
包含5小块的有2个;包含6小块的有6个;
包含8小块的有4个;包含9小块的有3个;
包含10小块的有2个;包含12小块的有4个;
包含15小块的有2个.
所以共有
1+4+4+7+2+6+4+3+2+4+2=39(个).
练习11
1.下列图形中各有多少条线段?
2.下列图形中各有多少个三角形?
3.下列图形中;各有多少个小于180°的角?
4.下列图形中各有多少个三角形?
5.下列图形中各有多少个长方形?
6.下列图形中;包含“*”号的三角形或长方形各有多少?
7.下列图形中;不含“*”号的三角形或长方形各有几个?
答案与提示练习11
1.(1)28;(2)210.
2.(1)36;(2)8.
3.(1)10;(2)15.
4.(1)9个;(2)16个;(3)21个.
5.(1)60个;(2)66个.
6.(1)12个;(2)32个.
7.(1)21个;(2)62个.
提示:4~7题均采用按所含小块的个数分类(见下表);表中空缺的为0.。
