小学三年级奥数-巧数图形

合集下载

三年级奥数--第六讲--巧数图形(三)

新速度教育三年级奥数
第六讲——巧数图形（三）
1. 温故知新。

2. 无规则图形的数法：分类法。

从小到大，从左到右，从上到下数。

3. 请小朋友们数一数下列图形有多少个。

4. 巧数图形在实际生活中的应用。

5. 有10个小朋友，每2个人照一张合影，一共要照多少张照片？思路导航：这道题可以用数线段的方法来解答。

6.分析：根据题意，画出线段图，每一个点代表一个小朋友：
从图上可以看出，第1个小朋友要与其余9个小朋友合影，要照9张照片；第2个小朋友还要与其余8个小朋友合影，再照8张照片……以此类推，第9个小朋友只要再与1个小朋友合影，再照1张照片。

所以，一共要照9＋8＋7＋6＋5＋4＋3＋2＋1=45张照片。

I H G
F E D C B
A
1098743
10．小朋友们，我们一起来练一练吧！！
1，三年级有6个班，每两个班要比赛拔河一次，这样一共要组织多少场比赛？
2，有红、黄、蓝、白四只气球，如果每两只气球扎成一束，共有多少种不同的扎法？
3，有1——6六个数字，能组成多少个不同的两位数？
4，数一数下图有多少个三角形。

巧数图形详细讲解小学三年级奥数(课堂PPT)

知识回顾 Knowledge Review
总共：10+10+4= 24 个
Page 19
拓展12：数出下图中所有三角形的个数。
(3+2+1)×55=25
5个 5个
小五边形外侧组合三角形有（3+2+1）×5-5=25个三角形。以大五边形边为底边的等腰三角形有5个。以小五边形顶角为顶角的等腰三角形有5个。
总共：25+5+5= 35 个。
Page 20
5个组合 1
总计
15
可见，整齐单排长方形个数的算法与线段计算相同。
Page 4
例3.数出图中共有多少三角形。
A
三角形个数： 4+3+2+1=10
1 2 34
B C DE F
数三角形有时也可以用数线段的方法；有的图形要用编号数图形的方法，还有的图形先要分成几部分分别去数，再考虑几部分拼合起来看看有没有产生新三角形。
巧数图形
Page 1
白汀水
例1、数线段
31542
共5+4+3+2+1= 15条线段
Page 2
练习1、数线段
1 23 4
5
67
共 7+6+5+4+3+2+1=28 条线段
Page 3
例2、下面图中有几个长方形?
数一数：
总计： 5+4+3+2+1=15
单个
5
2个组合 4
3个组合 3
4个组合 2
Page 22
拓展15. 数一数，图中有多少个长方形？

三年级上册奥数课件巧数图形2通用版(共36张ppt)

三年级上册奥数课件-巧数巧图数形图2形2通用通版用版（（共共 363张6张 pptpp）t）
三年级上册奥数课件-巧数巧图数形图2形2通用通版用版（（共共 363张6张 pptpp）t）
有多少个三角形呢？
练一练3
16个 7个
1个
3个
16＋7＋3＋1＝27（个）
三年级上册奥数课件-巧数巧图数形图2形2通用通版用版（（共共 363张6张 pptpp）t）
第一、二课最后复习
图形中的数学——巧数图形
1、基本技能：数线段的方法 2、知识转化：
3、知识拓展：
一共有多少条线段？
数线段复习
4条基本线段
4 + 3 + 2 + 1＝10（条）
先数基本线段，再从头到尾一直加到1。
一共有多少条线段呢？
4+3+2+1＝10条
6 + 10 ＝16条
第一、二课最后复习
有多少个正方形呢？
例二
9个
4个
能1不个能用数长方形的方法，
9＋来数4正＋方1形＝？14（个）
三年级上册奥数课件巧数图形2 通用版（共36张ppt）
三年级上册奥数课件-巧数巧图数形图2形2通用通版用版（（共共 363张6张 pptpp）t）
有多少个正方形呢？
练一练2
16个 9个
1个
4个
16+9+4+1＝30（个）
三年级上册奥数课件巧数图形2 通用版（共36张ppt）
分类法
三年级上册奥数课件巧数图形2 通用版（共36张ppt）
三年级上册奥数课件巧数图形2 通用版（共36张ppt）
怎样数正方形？
三年级上册奥数课件巧数图形2 通用版（共36张ppt）

巧数图形详解-小学奥数

题目三：数长方形
总结词
数长方形是巧数图形中的高级题目，主要考察学生的空间想象力和细致的观察能力。
详细描述
题目通常会给出一张由不同形状组成的图形，其中包含长方形。学生需要通过空间想象和细致的观察，数出长方形的数量。在数长方形的过程中，学生需要注意长方形的定义，即两组相对边等长。此外，学生还需要注意长方形可能存在不同的方向和旋转，确保
枚举法
总结词
逐一列举所有可能的情况，找出符合条件的结果。
详细描述
枚举法适用于图形数量较少、情况较为简单的问题。在解题时，需要逐一列举出所有可能的情况，并逐一检验是否符合题目要求。通过排除不符合条件的情况，最终找出符合条件的结果。
排除法
总结词
通过排除不符合条件的情况，逐步缩小范围，最终找出答案。
常见类型与实例
类型
常见的巧数图形题目包括数线段、数三角形、数正方形、数立方体等。
实例
如数线段，给定一条直线段，在直线段上任意取n个点，将线段分成n+1段，求这些小段的线段长度之和。
巧数图形的解题思路
观察
首先观察题目所给的图形，寻找其中的规律或
特征。
分析
分析图形的构成和数量关系，确定解进行逻辑推理，得出正确的答
案。
计算
进行必要的计算，得出最终答案。
02 巧数图形的解题技巧
观察法
总结词
通过细致观察图形特点，找出规律，解决问题。
详细描述
观察法是解决巧数图形问题的一种常用方法。在解题过程中，首先要仔细观察图形，注意图形的形状、大小、对称性等特征，以及各图形之间的相互关系。通过观察找出规律，从而解决问题。
详细描述
排除法是解决巧数图形问题的一种常用方法。在解题过程中，首先根据题目的要求和图形的特征，排除一些不可能的情况。然后逐步缩小范围，最终找出符合条件的结果。排除法可以有效地减少计算量，提高解题效率。

小学三年级奥数巧数图形知识点与习题

小学三年级奥数巧数图形知识点与习题数出某种图形的个数是一类有趣的图形问题.由于图形千变万化，错综复杂，所以要想准确地数出其中包含的某种图形的个数，还真需要动点脑筋.要想有条理、不重复、不遗漏地数出所要图形的个数，最常用的方法就是分类数.例1数出下图中共有多少条线段.分析与解：我们可以按照线段的左端点的位置分为A，B，C三类.如下图所示，以A为左端点的线段有3条，以B为左端点的线段有2条，以C为左端点的线段有1条.所以共有3＋2＋1＝6(条).我们也可以按照一条线段是由几条小线段构成的来分类.如下图所示，AB，BC，CD是最基本的小线段，由一条线段构成的线段有3条，由两条小线段构成的线段有2条，由三条小线段构成的线段有1条.所以，共有3＋2＋1＝6(条).由例1看出，数图形的分类方法可以不同，关键是分类要科学，所分的类型要包含所有的情况，并且相互不重叠，这样才能做到不重复、不遗漏.例2 下列各图形中，三角形的个数各是多少？分析与解：因为底边上的任何一条线段都对应一个三角形(以顶点及这条线段的两个端点为顶点的三角形)，所以各图中最大的三角形的底边所包含的线段的条数就是三角形的总个数.由前面数线段的方法知，图(1)中有三角形1＋2＝3(个).图(2)中有三角形1＋2＋3=6(个).图(3)中有三角形1＋2＋3＋4＝10(个).图(4)中有三角形1＋2＋3＋4＋5＝15(个).图(5)中有三角形1＋2＋3＋4＋5＋6=21(个).例3下列图形中各有多少个三角形？分析与解：(1)只需分别求出以AB，ED为底边的三角形中各有多少个三角形.以AB为底边的三角形ABC中，有三角形1＋2＋3＝6(个).以ED为底边的三角形CDE中，有三角形1＋2＋3＝6(个).所以共有三角形6＋6=12(个).这是以底边为标准来分类计算的方法.它的好处是可以借助“求底边线段数”而得出三角形的个数.我们也可以以小块个数作为分类的标准来计算：图中共有6个小块.由1个小块组成的三角形有3个；由2个小块组成的三角形有5个；由3个小块组成的三角形有1个；由4个小块组成的三角形有2个；由6个小块组成的三角形有1个.所以，共有三角形3＋5＋1＋2＋1＝12(个).(2)如果以底边来分类计算，各种情况较复杂，因此我们采用以“小块个数”为分类标准来计算：由1个小块组成的三角形有4个；由2个小块组成的三角形有6个；由3个小块组成的三角形有2个；由4个小块组成的三角形有2个；由6个小块组成的三角形有1个.所以，共有三角形4＋6＋2＋2＋1＝15(个).例4右图中有多少个三角形？解：假设每一个最小三角形的边长为1.按边的长度来分类计算三角形的个数.边长为1的三角形，从上到下一层一层地数，有1＋3＋5＋7=16(个)；边长为2的三角形(注意，有一个尖朝下的三角形)有1＋2＋3＋1=7(个)；边长为3的三角形有1＋2＝3(个)；边长为4的三角形有1个.所以，共有三角形16＋7＋3＋1＝27(个).例5数出下页左上图中锐角的个数.分析与解：在图中加一条虚线，如下页右上图.容易发现，所要数的每个角都对应一个三角形(这个角与它所截的虚线段构成的三角形)，这就回到例2，从而回到例1的问题，即所求锐角的个数，就等于从O点引出的6条射线将虚线截得的线段的条数.虚线上线段的条数有1+2+3+4+5=15(条).所以图中共有15个锐角.例6在下图中，包含“*”号的长方形和正方形共有多少个？解：按包含的小块分类计数.包含1小块的有1个；包含2小块的有4个；包含3小块的有4个；包含4小块的有7个；包含5小块的有2个；包含6小块的有6个；包含8小块的有4个；包含9小块的有3个；包含10小块的有2个；包含12小块的有4个；包含15小块的有2个.所以共有1＋4＋4＋7＋2＋6＋4＋3＋2＋4＋2=39(个).练习111.下列图形中各有多少条线段？2.下列图形中各有多少个三角形？3.下列图形中，各有多少个小于180°的角？4.下列图形中各有多少个三角形？5.下列图形中各有多少个长方形？6.下列图形中，包含“*”号的三角形或长方形各有多少？7.下列图形中，不含“*”号的三角形或长方形各有几个？答案与提示练习111.(1)28；(2)210.2.(1)36；(2)8.3.(1)10；(2)15.4.(1)9个；(2)16个；(3)21个.5.(1)60个；(2)66个.6.(1)12个；(2)32个.7.(1)21个；(2)62个.提示：4～7题均采用按所含小块的个数分类(见下表)，表中空缺的为0.。

巧数图形详细讲解小学三年级奥数课件

第24页/共35页
拓展18、下面图形中有多少个正方形，多少个三角形？
有1个正方形。8个三角形。有1正方形。8个三角形。
第25页/共35页
拓展19、下面二图形叠加后有多少个正方形，多少个三角
形？
+
二图形共有2个正方形，16个三角形
二图叠加后新增8个正方形，新增三角形：16+12=28个
二图叠加后总共有2+8=10个正方形，16+28=44个三角形。
个
设想大长方形消失则有15+10-1=24个
还原大长方形则增4
个
总共24+4总= 共282个8个
第32页/共35页
谢谢使用
第33页/共35页
知识回顾 Knowledge Review
第34页/共35页
感谢您的观看。
第35页/共35页
பைடு நூலகம்
练习1、数线段
1 23 4
5
67
共 7+6+5+4+3+2+1=28 条线段
第2页/共35页
• 例2、下面图中有几个长方形?
数一数：
总计： 5+4+3+2+1=15
单个
5
2个组合 4
3个组合 3
4个组合 2
5个组合 1
总计
15
可见，整齐单排长方形个数的算法与线段计算相同。
第3页/共35页
例3.数出图中共有多少三角形。
拆除2条红线和蓝绿线后有三角形 14个 2条红线返回后增加6个三角形
绿线返回后增加10个三角形
蓝线返回后增加14个三角形
还可以这样数：单个三角形 16个 2个三角形组合16个 4个三角形组合8个

第3讲--巧数图形--奥数个性化辅导(三年级)

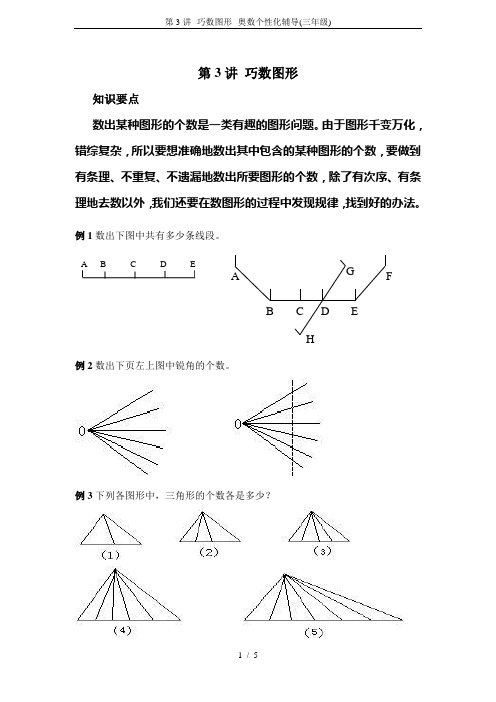
第3讲巧数图形
知识要点
数出某种图形的个数是一类有趣的图形问题。

由于图形千变万化，错综复杂，所以要想准确地数出其中包含的某种图形的个数，要做到有条理、不重复、不遗漏地数出所要图形的个数，除了有次序、有条理地去数以外，我们还要在数图形的过程中发现规律，找到好的办法。

例1数出下图中共有多少条线段。

例2数出下页左上图中锐角的个数。

例3下列各图形中，三角形的个数各是多少？
A
B
C D
E
F
G H A
B
C
D
E
例4下列图形中各有多少个三角形？
例5右图中有多少个三角形？
例6数一数下图中共有多少个正方形。

例7数一数下图中共有多少个长方形
练习
1、下列图形中各有多少条线段？
2、下列图形中，各有多少个小于180°的角？
3、下列图形中各有多少个三角形？
E
F
D A
B
C O
A B C D E F
A B C D E F
F G H
I
4、下图中各有多少个长方形？
(3)
5、下图中有多少个正方形？
拓展延伸
1、下列图形中，包含“*”号的正方形有多少？
3、右图中有多少个正方形？
4、数一数下图中有多少个平行四边形？
5、数一数下图中有多少个梯形？。

小学三年级奥数课件：巧数图形36页PPT

60、人民的幸福是至高无个的法。— —西塞罗
31、只有永远躺在泥坑里的人，才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭，生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍，级奥数课件：巧数图形
56、极端的法规，就是极端的不公。 ——西塞罗 57、法律一旦成为人们的需要，人们就不再配享受自由了。—— 毕达哥拉斯 58、法律规定的惩罚不是为了私人的利益，而是为了公共的利益；一部分靠有害的强制，一部分靠榜样的效力。 ——格老秀斯 59、假如没有法律他们会更快乐的话，那么法律作为一件无用之物自己就会消灭。— —洛克

三年级奥数巧数图形

第2讲巧数图形知识要点同学们，我们经常会遇到数图形的问题，对于较复杂的图形，经常会出现数重复或数漏掉的错误。

怎样才能不重复也不遗漏地数出图形的个数呢？这节课，我们将一起来寻找好的方法。

要正确数出图形的个数，关键是要从基本图形入手。

首先要弄清图形中包含的基本图形是什么，有多少个，然后再数出由基本图形组成的新的图形，并求出它们的和。

精典例题例1:数出下图中有多少条线段？模仿练习数一数，每种图形有多少个？有（）条线段有（）个三角形有（）个角有（）个长方形有（）个正方形例2:数出图中共有多少个三角形？从短的线段入手，再两条两条拼接起来数，你发现规律了吗？EABCDODC B A FEDC B A模仿练习数一数，每幅图里有多少个三角形？（1）（2）有（）个三角形有（）个三角形例3:下面的图形中有多少个三角形？（第九届中国青少年数学论坛趣味数学解题技能展示大赛试题）模仿练习数一数，图中共有几个正方形？（2010武汉明心数学资优生水平测试题）精典例题例4:数出下图中有多少个长方形？多少个正方形？还能用刚才的方法来数吗？三角形很多，可以尝试按三角形的方向和大小尝试分类数。

KG I H G FEDC B A模仿练习1.数一数，图中有多少个长方形？2.数一数图中有多少个正方形？家庭作业1.数一数每幅图里面图形的个数（能计算的写出算式）。

（1）（2）前面学习的数长方形的方法还有用吗？怎么能用上呢？DCBA D CBA有（）条线段有（）个角2.右图中有多少个三角形？3.图中有多少个长方形？（把你的想法分享给你的爸爸妈妈听，你能教会他们吗？分享后让爸爸妈妈给你打星，最多5颗星）4.数一数，右图中有多少个正方形？5.（20XX 年“陈省身杯”国际青少年数学邀请赛试题）。