第三章最小均方(LMS)算法
Lecture.LMS算法介绍

LMS算法介绍最小均方算法(Least Mean Square, LMS)是一种简单、应用为广泛的自适应滤波算法,是在维纳滤波理论上运用速下降法后的优化延伸,早是由Widrow 和Hoff 提出来的。
该算法不需要已知输入信号和期望信号的统计特征,“当前时刻”的权系数是通过“上一时刻”权系数再加上一个负均方误差梯度的比例项求得。
这种算法也被称为Widrow-Hoff LMS 算法,在自适应滤波器中得到广泛应用,其具有原理简单、参数少、收敛速度较快而且易于实现等优点。
1 最小均方误差以及均方误差曲面自适应滤波算法从某种角度也被称为性能表面搜索法,在性能曲面中,它是通过不断测量一个点是否接近目标值,来寻找优解的。
目前,使用为广泛的曲面函数之一是均方误差(MSE)函数,函数表达式如下:。
准则函数设计为求均方误差函数的小值,我们称之为小均方误差准则(MMSE),维纳滤波器就是基于这个准则推到出来的。
公式:,从上式可以看出均方误差与滤波器权向量是成二次函数关系,引入均方误差曲面来描述函数的映射关系,对应的权向量w的二次函数就是一个超抛物曲面。
2 LMS算法基本原理根据小均方误差准则以及均方误差曲面,自然的我们会想到沿每一时刻均方误差的陡下降在权向量面上的投影方向更新,也就是通过目标函数的反梯度向量来反复迭代更新。
由于均方误差性能曲面只有一个唯一的极小值,只要收敛步长选择恰当,不管初始权向量在哪,后都可以收敛到误差曲面的小点,或者是在它的一个邻域内。
这种沿目标函数梯度反方向来解决小化问题的方法,我们一般称为速下降法,表达式如下:,基于随机梯度算法的小均方自适应滤波算法的完整表达式如下:LMS 自适应算法是一种特殊的梯度估计,不必重复使用数据,也不必对相关矩阵和互相关矩阵进行运算,只需要在每次迭代时利用输入向量和期望响应,结构简单,易于实现。
虽然LMS 收敛速度较慢,但在解决许多实际中的信号处理问题,LMS 算法是仍然是好的选择。
最小均方误差算法

最小均方误差算法
最小均方误差算法(Least Mean Squares Algorithm,LMS算法)是一种常用的自适应滤波算法,主要用于信号处理、通信系统、控制系统等领域。
该算法的核心思想是通过不断调整滤波器系数,使得滤波器输出信号与期望信号之间的均方误差最小化。
LMS算法的基本原理是利用梯度下降法不断调整滤波器系数。
具体来说,假设滤波器的系数为w(n),期望输出信号为d(n),实际输出信号为y(n),则LMS 算法的更新公式为:
w(n+1) = w(n) + μe(n)x(n)
其中,μ为步长因子,e(n)为误差信号,即e(n) = d(n) - y(n),x(n)为输入信号。
LMS算法的优点是简单易实现,计算量较小,适用于实时处理。
但是,由于其采用的是梯度下降法,容易陷入局部最优解,收敛速度较慢,需要选择合适的步长因子和初始滤波器系数。
LMS算法的应用十分广泛,例如在通信系统中,可以用于自适应均衡、自适应滤波、自适应降噪等方面;在控制系统中,可以用于自适应控制、自适应识别等方面。
同时,LMS算法也是其他自适应滤波算法的基础,例如最小二乘算法、
递归最小二乘算法等。
总之,最小均方误差算法是一种重要的自适应滤波算法,具有广泛的应用前景和研究价值。
最小均方算法

第3章 最小均方算法3.1 引言最小均方(LMS ,least -mean -square)算法是一种搜索算法,它通过对目标函数进行适当的调整[1]—[2],简化了对梯度向量的计算。
由于其计算简单性,LMS 算法和其他与之相关的算法已经广泛应用于白适应滤波的各种应用中[3]-[7]。
为了确定保证稳定性的收敛因子范围,本章考察了LMS 算法的收敛特征。
研究表明,LMS 算法的收敛速度依赖于输入信号相关矩阵的特征值扩展[2]—[6]。
在本章中,讨论了LMS 算法的几个特性,包括在乎稳和非平稳环境下的失调[2]—[9]和跟踪性能[10]-[12]。
本章通过大量仿真举例对分析结果进行了证实。
在附录B 的B .1节中,通过对LMS 算法中的有限字长效应进行分析,对本章内容做了补充。
LMS 算法是自适应滤波理论中应用最广泛的算法,这有多方面的原因。
LMS 算法的主要特征包括低计算复杂度、在乎稳环境中的收敛性、其均值无俯地收敛到维纳解以及利用有限精度算法实现时的稳定特性等。
3.2 LMS 算法在第2章中,我们利用线性组合器实现自适应滤波器,并导出了其参数的最优解,这对应于多个输入信号的情形。
该解导致在估计参考信号以d()k 时的最小均方误差。
最优(维纳)解由下式给出:其中,R=E[()x ()]T x k k 且p=E[d()x()] k k ,假设d()k 和x()k 联合广义平稳过程。
如果可以得到矩阵R 和向量p 的较好估计,分别记为()R k ∧和()p k ∧,则可以利用如下最陡下降算法搜索式(3.1)的维纳解:w(+1)=w()-g ()w k k k μ∧w()(()()w())k p k R k k μ∧∧=-+2 (3.2) 其中,k =0,1,2,…,g ()w k ∧表示目标函数相对于滤波器系数的梯度向量估计值。
一种可能的解是通过利用R 和p 的瞬时估计值来估计梯度向量,即 10w R p -=(3.1)()x()x ()T R k k k ∧=()()x()p k d k k ∧= (3.3) 得到的梯度估计值为(3.4) 注意,如果目标函数用瞬时平方误差2()e k 而不是MSE 代替,则上面的梯度估计值代表了真实梯度向量,因为2010()()()()2()2()2()()()()T e k e k e k e k e k e k e k w w k w k w k ⎡⎤∂∂∂∂=⎢⎥∂∂∂∂⎣⎦ 2()x()e k k =-()w g k ∧= (3.5) 由于得到的梯度算法使平方误差的均值最小化.因此它被称为LMS 算法,其更新方程为 (1)()2()x()w k w k e k k μ+=+ (3.6) 其中,收敛因子μ应该在一个范围内取值,以保证收敛性。
最小均方算法

第3章 最小均方算法3.1 引言最小均方(LMS ,least -mean -square)算法是一种搜索算法,它通过对目标函数进行适当的调整[1]—[2],简化了对梯度向量的计算。
由于其计算简单性,LMS 算法和其他与之相关的算法已经广泛应用于白适应滤波的各种应用中[3]-[7]。
为了确定保证稳定性的收敛因子范围,本章考察了LMS 算法的收敛特征。
研究表明,LMS 算法的收敛速度依赖于输入信号相关矩阵的特征值扩展[2]—[6]。
在本章中,讨论了LMS 算法的几个特性,包括在乎稳和非平稳环境下的失调[2]—[9]和跟踪性能[10]-[12]。
本章通过大量仿真举例对分析结果进行了证实。
在附录B 的B .1节中,通过对LMS 算法中的有限字长效应进行分析,对本章内容做了补充。
LMS 算法是自适应滤波理论中应用最广泛的算法,这有多方面的原因。
LMS 算法的主要特征包括低计算复杂度、在乎稳环境中的收敛性、其均值无俯地收敛到维纳解以及利用有限精度算法实现时的稳定特性等。
3.2 LMS 算法在第2章中,我们利用线性组合器实现自适应滤波器,并导出了其参数的最优解,这对应于多个输入信号的情形。
该解导致在估计参考信号以d()k 时的最小均方误差。
最优(维纳)解由下式给出:其中,R=E[()x ()]T x k k 且p=E[d()x()] k k ,假设d()k 和x()k 联合广义平稳过程。
如果可以得到矩阵R 和向量p 的较好估计,分别记为()R k ∧和()p k ∧,则可以利用如下最陡下降算法搜索式(3.1)的维纳解:w(+1)=w()-g ()w k k k μ∧w()(()()w())k p k R k k μ∧∧=-+2 (3.2) 其中,k =0,1,2,…,g ()w k ∧表示目标函数相对于滤波器系数的梯度向量估计值。
一种可能的解是通过利用R 和p 的瞬时估计值来估计梯度向量,即 10w R p -=(3.1)()x()x ()T R k k k ∧=()()x()p k d k k ∧= (3.3) 得到的梯度估计值为(3.4) 注意,如果目标函数用瞬时平方误差2()e k 而不是MSE 代替,则上面的梯度估计值代表了真实梯度向量,因为2010()()()()2()2()2()()()()T e k e k e k e k e k e k e k w w k w k w k ⎡⎤∂∂∂∂=⎢⎥∂∂∂∂⎣⎦ 2()x()e k k =-()w g k ∧= (3.5) 由于得到的梯度算法使平方误差的均值最小化.因此它被称为LMS 算法,其更新方程为 (1)()2()x()w k w k e k k μ+=+ (3.6) 其中,收敛因子μ应该在一个范围内取值,以保证收敛性。
毕业设计(论文)-lms及rls自适应干扰抵消算法的比较[管理资料]
![毕业设计(论文)-lms及rls自适应干扰抵消算法的比较[管理资料]](https://img.taocdn.com/s3/m/e45ae55891c69ec3d5bbfd0a79563c1ec4dad715.png)
前言自适应信号处理的理论和技术经过40 多年的发展和完善,已逐渐成为人们常用的语音去噪技术。
我们知道, 在目前的移动通信领域中, 克服多径干扰, 提高通信质量是一个非常重要的问题, 特别是当信道特性不固定时, 这个问题就尤为突出, 而自适应滤波器的出现, 则完美的解决了这个问题。
另外语音识别技术很难从实验室走向真正应用很大程度上受制于应用环境下的噪声。
自适应滤波的原理就是利用前一时刻己获得的滤波参数等结果, 自动地调节现时刻的滤波参数, 从而达到最优化滤波。
自适应滤波具有很强的自学习、自跟踪能力, 适用于平稳和非平稳随机信号的检测和估计。
自适应滤波一般包括3个模块:滤波结构、性能判据和自适应算法。
其中, 自适应滤波算法一直是人们的研究热点, 包括线性自适应算法和非线性自适应算法, 非线性自适应算法具有更强的信号处理能力, 但计算比较复杂, 实际应用最多的仍然是线性自适应滤波算法。
线性自适应滤波算法的种类很多, 有RLS自适应滤波算法、LMS自适应滤波算法、变换域自适应滤波算法、仿射投影算法、共扼梯度算法等[1]。
其中最小均方(Least Mean Square,LMS)算法和递归最小二乘(Recursive Least Square,RLS)算法就是两种典型的自适应滤波算法, 它们都具有很高的工程应有价值。
本文正是想通过这一与我们生活相关的问题, 对简单的噪声进行消除, 更加深刻地了解这两种算法。
我们主要分析了下LMS算法和RLS算法的基本原理, 以及用程序实现了用两种算法自适应消除信号中的噪声。
通过对这两种典型自适应滤波算法的性能特点进行分析及仿真实现, 给出了这两种算法性能的综合评价。
1 绪论自适应噪声抵消( Adaptive Noise Cancelling, ANC) 技术是自适应信号处理的一个应用分支, 年提出, 经过三十多年的丰富和扩充, 现在已经应用到了很多领域, 比如车载免提通话设备, 房间或无线通讯中的回声抵消( AdaptiveEcho Cancelling, AEC) , 在母体上检测胎儿心音, 机载电子干扰机收发隔离等, 都是用自适应干扰抵消的办法消除混入接收信号中的其他声音信号。
matlab 最小均方误差(lms)算法

matlab 最小均方误差(lms)算法The least mean squares (LMS) algorithm in MATLAB is a widely used adaptive filter algorithm that aims to minimize the mean square error between the desired signal and the output of the filter. MATLAB provides convenient tools and functions for implementing and optimizing LMS algorithms, making it a popular choice for researchers and engineers working in signal processing and system identification.MATLAB中的最小均方误差(LMS)算法是一种广泛使用的自适应滤波器算法,旨在最小化期望信号与滤波器输出之间的均方误差。
MATLAB提供了方便的工具和函数,用于实现和优化LMS算法,使其成为信号处理和系统辨识领域的研究人员和工程师的首选。
One of the key advantages of using the LMS algorithm in MATLAB is its simplicity and efficiency. With just a few lines of code, users can implement an LMS filter and start optimizing it for their specific application. This ease of use makes MATLAB a popular choice for beginners and experts alike who are looking to quickly prototype and test adaptive filter solutions.在MATLAB中使用LMS算法的一个重要优势是其简单性和高效性。
神经网络与机器学习笔记—LMS(最小均方算法)和学习率退火
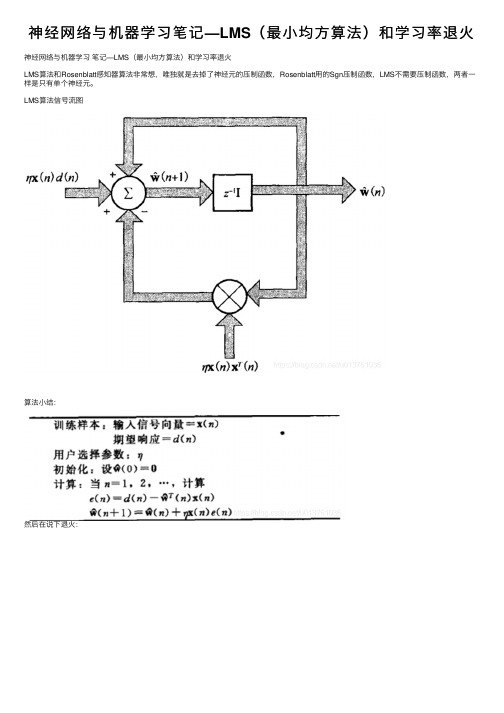
神经⽹络与机器学习笔记—LMS(最⼩均⽅算法)和学习率退⽕神经⽹络与机器学习笔记—LMS(最⼩均⽅算法)和学习率退⽕LMS算法和Rosenblatt感知器算法⾮常想,唯独就是去掉了神经元的压制函数,Rosenblatt⽤的Sgn压制函数,LMS不需要压制函数,两者⼀样是只有单个神经元。
LMS算法信号流图算法⼩结:然后在说下退⽕:#pragma once#include "stdafx.h"#include <string>#include <iostream>using namespace std;int gnM = 0; //训练集空间维度int gnN = 0; //突触权值个数double gdU0 = 0.1; //初始学习率参数,⽤于退⽕,前期可以较⼤double gdT = 1; //控制退⽕⽤的开始降温的时间点double gdN = 0; //当前⼯作时间(神经⽹络学习次数)//退⽕//U=U0/(1+(N/T))double GetNowU() {gdN++;//cout<< gdU0 / (1.0 + (gdN / gdT))<<endl;return gdU0 / (1.0 + (gdN / gdT));}void LMSInit(double *dX, const int &nM, double *dW, const int &nN, const double &dB, const double &dU0 ,const double &dT) { //dX 本次训练数据集//nM 训练集空间维度//dW 权值矩阵//nN 突触权值个数 LMS只有⼀个神经元,所以nM==nM//dB 偏置,正常这个是应该⾛退⽕动态调整的,以后再说,现在固定得了。
//dU0 初始学习率参数,⽤于退⽕,前期可以较⼤//dT控制退⽕⽤的开始降温的时间点if (nM > 0) {dX[0] = 1;//把偏置永远当成⼀个固定的突触}for (int i = 0; i <= nN; i++) {if (i == 0) {dW[i] = dB;//固定偏置}else {dW[i] = 0.0;}}gnM = nM, gnN = nN, gdU0 = dU0, gdT = dT;}double Sgn(double dNumber) {return dNumber > 0 ? +1.0 : -1.0;}//感知器收敛算法-学习void LMSStudy(const double *dX, const double dD, double *dW) {//dX 本次训练数据集//dD 本次训练数据集的期望值//dW 动态参数,突触权值double dY = 0;for (int i = 0; i <= gnM && i <= gnN; i++) {dY = dY + dX[i] * dW[i];}//dY = Sgn(dY); LMS这个地⽅不⽤了,Rosenblatt是需要的if (dD == dY) {return;//不需要进⾏学习调整突触权值}for (int i = 1; i <= gnM && i <= gnN; i++) {dW[i] = dW[i] + GetNowU() * (dD - dY) * dX[i];}}//感知器收敛算法-泛化double LMSGeneralization(const double *dX, const double *dW) { //dX 本次需要泛化的数据集//dW 已经学习好的突触权值//返回的是当前需要泛化的数据集的泛化结果(属于那个域的) double dY = 0;for (int i = 0; i <= gnM && i <= gnN; i++) {dY = dY + dX[i] * dW[i];}return Sgn(dY);}//双⽉分类模型,随机获取⼀组值/* ⾃⼰稍微改了下域1:上半个圆,假设圆⼼位坐标原点(0,0)(x - 0) * (x - 0) + (y - 0) * (y - 0) = 10 * 10x >= -10 && x <= 10y >= 0 && y <= 10域2:下半个圆,圆⼼坐标(10 ,-1)(x - 10) * (x - 10) + (y + 1) * (y + 1) = 10 * 10;x >= 0 && x <= 20y >= -11 && y <= -1*/const double gRegionA = 1.0; //双⽉上const double gRegionB = -1.0;//双⽉下void Bimonthly(double *dX, double *dY, double *dResult) {//dX 坐标x//dY 坐标y//dResult 属于哪个分类*dResult = rand() % 2 == 0 ? gRegionA : gRegionB;if (*dResult == gRegionA) {*dX = rand() % 20 - 10;//在区间内随机⼀个X*dY = sqrt(10 * 10 - (*dX) * (*dX));//求出Y}else {*dX = rand() % 20;*dY = sqrt(10 * 10 - (*dX - 10) * (*dX - 10)) - 1;*dY = *dY * -1;}}int main(){//system("color 0b");double dX[2 + 1], dD, dW[2 + 1]; //输⼊空间维度为3 平⾯坐标系+⼀个偏置double dB = 0;double dU0 = 0.1;double dT = 128; //128之后开始降温LMSInit(dX, 2, dW, 2, dB, dU0, dT);//初始化感知器double dBimonthlyX, dBimonthlyY, dBimonthlyResult;int nLearningTimes = 1024 * 10;//进⾏10K次学习for (int nLearning = 0; nLearning <= nLearningTimes; nLearning++) {Bimonthly(&dBimonthlyX, &dBimonthlyY, &dBimonthlyResult);//随机⽣成双⽉数据dX[1] = dBimonthlyX;dX[2] = dBimonthlyY;dD = dBimonthlyResult;LMSStudy(dX, dD, dW);//cout <<"Study:" << nLearning << " :X= " << dBimonthlyX << "Y= " << dBimonthlyY << " D=" << dBimonthlyResult<< "----W1= " << dW[1] << " W2= " << dW[2] << endl; }//进⾏LMS泛化能⼒测试测试数据量1Kint nGeneralizationTimes = 1 * 1024;int nGeneralizationYes = 0, nGeneralizationNo = 0;double dBlattGeneralizationSuccessRate = 0;for (int nLearning = 1; nLearning <= nGeneralizationTimes; nLearning++) {Bimonthly(&dBimonthlyX, &dBimonthlyY, &dBimonthlyResult);//随机⽣成双⽉数据dX[1] = dBimonthlyX;dX[2] = dBimonthlyY;//cout << "Generalization: " << dBimonthlyX << "," << dBimonthlyY;if (dBimonthlyResult == LMSGeneralization(dX, dW)) {nGeneralizationYes++;//cout << " Yes" << endl;}else {nGeneralizationNo++;//cout << " No" << endl;}}dBlattGeneralizationSuccessRate = nGeneralizationYes * 1.0 / (nGeneralizationNo + nGeneralizationYes) * 100;cout << "Study : " << nLearningTimes << " Generalization : " << nGeneralizationTimes << " SuccessRate:" << dBlattGeneralizationSuccessRate << "%" << endl; getchar();return 0;}执⾏结果:Study : 10240 Generalization : 1024 SuccessRate:96.6797%注意:相对于Rosenblatt算法,LMS如果直接把sgn去掉了可能出现泛化能⼒急剧下降的问题,我就是,直接变成50%了(和没学习⼀样),因为此时的学习率参数恒等于0.1有点⼤(为什么说0.1⼤,因为没有sgn了,算出的XW是⽐较⼤的,⽽这个时候我们训练数据集的期望结果,还是+1和-1)。
最小均方算法(lms)的原理

最小均方算法(lms)的原理
最小均方算法(LMS)是一种用于信号处理和自适应滤波的算法,它是一种迭代算法,
用于最小化预测误差的均方值。
在该算法中,滤波器的系数会根据输入信号实时地调整,
以使得滤波器的输出能够尽可能地接近期望输出。
LMS算法的核心理念是通过不断迭代,不断的调整滤波器的系数,使其能够最大限度
地降低误差。
该算法首先需要确定一组初始系数,并计算出当前的滤波器输出以及误差。
然后,根据误差的大小和方向来调整滤波器的系数,并重复这个过程,直到误差的均方值
达到最小。
这个过程的数学原理可以用一个简单的公式来表示:
w(n+1) = w(n) + µe(n)X(n)
其中, w(n)是当前滤波器的系数,µ是一个可调节的步长参数,e(n)是当前的误差,
X(n)是输入数据的向量。
在该算法中,步长参数µ的大小对LMS算法的性能有重要的影响。
如果其选择过大,
会导致算法不稳定,收敛到一个错误的值;而如果µ的值过小,则算法收敛速度慢。
此外,在使用LMS算法时,还需要进行一些预处理。
比如,在对输入信号进行滤波时,通常需要进行预加重处理,以便在高频段上增强信号的弱化部分。
同时,在为滤波器确定
初始系数时,还需要利用一些特定的算法来进行优化,以使得滤波器的性能能够得到进一
步的提升。
5.4最小均方算法

uv
uv
uv
w(n 1) w(n) 2e(n)x N (n)
问题:
能否由任意起始位置w(0)经迭代最终收敛到最优解w*
跟最速梯度法权向量的收敛性有何区别?
uvT uv Q e(n) d(n) w (n)xN (n)
uvT uv d(n) xN (n)w(n)
uv
uv
w(n 1) w(n) 2
页页
2 1(1 k22 ) 3 4 (1 k22 )
k2
[RX
(2)
1 i 1
a1 (i ) RX
(2
i)]/
1
1 3
则 2 3 4 (11 9) 2 3
2
k3 [RX (3) a2 (i)RX (3 i)] / 2
i 1
[ 1 4
a2 (1)RX
(2)
a2 (2)RX
(1)] /
c(2)
4.58
所以,ARMA(2,1)模型的系统函数为
1 0.57z1 H1(z) 1 2.93z1 2.59z2
X
第第
2. 已知平稳随机信号x(n)的自相关函数值:
1177 页页
R(0) 1, R(1) 0.5, R(2) 0.5, R(3) 0.25,
现用AR(3)模型估计它的功率谱,设模型参
i 1 p
1 ai zi
i 1
p
q
差分方程: x(n) ai x(n i) Gbi(n i)
i 1
i0
功率谱:
q
2
1 bie ji
Sx
(e
j
)
G 2
2
i 1 p
1 aie ji
i 1
LMS算法的简单研究

包括: (a)计算线性滤波器输出对输入信号的响应; (b)通过比较输出结果与期望响应产生估计误差。 2)自适应过程 根据估计误差自动调整滤波器参数。 下面简单简绍下 LMS 算法的基本步骤: 1、设置变量和参量: x(n)为输入向量,或称为训练样本 w(n)为权值向量 b(n)为偏差 d(n)为期望输出 y(n)为实际输出 u 为步长因子 n 为迭代次数 2、初始化,赋给 w(0)一个较小的随机非零值,令 n=0 ; 3、对于一组输入样本 x(n)和对应的期望输出 d,计算 e(n)=d(n)-x(n)w(n) w(n+1)=w(n)+ux(n)e(n) 4、判断是否满足条件,若满足算法结束,若否 n 增加 1,转入第 3 步继续执行。 由上边的权值系数更新过程可以看出,上 LMS 算法具有算法简单、每步迭代 计算量小、所需存储量小等特点,但是 LMS 算法的收敛速度一般较慢。另外 LMS 算法还有一些改进算法如归一化 LMS (NLMS)算法等。
随机性,因而实验中需进行多次 LMS 算法迭代,最后取平均。这里取实验次 数 M 为 80。 本实验将分四个步骤完成。 首先, 实验开始先定义参变量 M、 N 和 w=zeros(M,N,3,2)与 f=zeros(M,N,3,2), 括号里的 3 和 2 分别用来控制 3 种步长因子和 a 的两个不同参数。 然后,对不同的参数 a、不同的步长因子 u 和不同的试验次数 M 分别进行 N 次迭代来获得每个点的权值系数。 其次, 对于不同的参数 a 和步长因子分别计算它们的 M 次集平均权值特性和 均方误差特性。 最后, 分别绘出该一阶自适应预测器的权值和均方误差瞬时特性图与不同步 长因子下的学习曲线图。 本次实验的程序如下所示:
一、实验题目
For this computer experiment involving the LMS algorithm, use a first-order, autoregressive (AR) process to study the effects of ensemble averaging on the transient characteristics of the LMS algorithm for real data. Consider an AR process of order one, described by the difference equation
LMS算法-推导-应用-试验结果分析

μ的选择
对权系数向量更新公式(15)两边取数学期望,得
(17)
μ的选择
μ的选择
(18)
(19)
将式(19)代入式(18)后得:
(20)
μ的选择
(1)
(8-1-21a)
(8-1-21b) (8-1-21c) (8-1-21d)
(22)
μ的选择
或
(22)
LMS算法应用
LMS算法应用
LMS算法应用
MATLAB实验结果及分析
图4一阶自适应预测器的平方预测误差瞬时特性(u=0.05)
MATLAB实验结果及分析
由图4中所示的一阶自适应预测器的平方预测 误差瞬时特性曲线可以看出,LMS单一实现的 学习曲线呈现出严重的噪声存在形式,但经平 均处理以后得到了一条较稳定的曲线,即固定 u=0.05时的一阶自适应预测器的学习曲线。
自适应是指处理和分析过程中,根据处理数据的 数据特征自动调整处理方法、处理顺序、处理参 数、边界条件或约束条件,使其与所处理数据的 统计分布特征、结构特征相适应,以取得最佳的 处理效果 。
LMS算法推导:
LMS算法是自适应滤波器中常用的一种算法,与维纳 算法不同的是,其系统的系数随输入序列而改变。维 纳算法中截取输入序列自相关函数的一段构造系统的 最佳系数。而LMS算法则是对初始化的滤波器系数依 据最小均方误差准则进行不断修正来实现的。因此, 理论上讲LMS算法的性能在同等条件下要优于维纳算 法,但是LMS算法是在一个初始化值得基础上进行逐 步调整得到的,因此,在系统进入稳定之前有一个调 整的时间,这个时间受到算法步长因子u的控制,在一 定值范围内,增大u会减小调整时间,但超过这个值范 围时系统不再收敛,u的最大取值为R的迹。
lms算法公式

lms算法公式
最小均方算法(Least Mean Square, LMS)是一种最小化误差的算法。
在信号处理、系统辨识等许多领域中有广泛的应用。
现在,我们就详细描述一下LMS算法的公式。
LMS算法主要由两部分组成:滤波器和权值更新算法。
滤波器是用来滤除噪声,获取原始信号。
权值更新算法则是用来调整滤波器的系数,使得滤波器的输出越来越接近期望的结果。
这一过程可以用以下公式来描述:
假设n为时间下标,d(n)为期望的输出,x(n)为输入向量,其中包含了L个输入的样本x(n),x(n-1),…,x(n-L+1),w(n)是在时刻n的滤波器权重向量。
滤波器的输出为:
y(n)=w(n)T*x(n)
滤波器的误差为期望输出和滤波器实际输出之差,表示为:
e(n)=d(n)-y(n)
滤波器的权重更新可以通过以下公式进行:
w(n+1)=w(n)+μ*e(n)*x(n)
上述公式中,T代表转置,*代表点乘,μ为步长因子,用于调整滤波器权值更新的速度。
这就是LMS算法的基本公式。
在实际应用中,常常需要根据实际情况对步长因子μ进行调整,使得滤波器可以更快地达到最小均方误差,从而获得最佳的滤波效果。
lms算法基本思想及原理

lms算法基本思想及原理
一、最小均方算法(LMS)概述1959年,Widrow和Hoff在对自适应线性元素的方案一模式识别进行研究时,提出了最小均方算法(简称LMS算法)。
LMS算法是基于维纳滤波,然后借助于最速下降算法发展起来的。
通过维纳滤波所求解的维纳解,必须在已知输入信号与期望信号的先验统计信息,以及再对输入信号的自相关矩阵进行求逆运算的情况下才能得以确定。
因此,这个维纳解仅仅是理论上的一种最优解。
所以,又借助于最速下降算法,以递归的方式来逼近这个维纳解,从而避免了矩阵求逆运算,但仍然需要信号的先验信息,故而再使用瞬时误差的平方来代替均方误差,从而最终得出了LMS 算法。
因LMS算法具有计算复杂程度低、在信号为平稳信号的环境中的收敛性好、其期望值无偏地收敛到维纳解和利用有限精度实现算法时的稳定性等特性,使LMS算法成为自适应算法中稳定性最好、应用最广泛的算法。
下图是实现算法的一个矢量信号流程图:
图1 LMS算法矢量信号流程图
由图1我们可以知道,LMS算法主要包含两个过程:滤波处理和自适应调整。
一般情况下,LMS算法的具体流程为:
(1)确定参数:全局步长参数以及滤波器的抽头数(也可以称为滤波器阶数)
(2)对滤波器初始值的初始化
(3)算法运算过程:
滤波输出:y(n)=wT(n)x(n)
误差信号:e(n)=d(n)-y(n)
权系数更新:w(n+1)=w(n)+e(n)x(n)
二、性能分析在很大程度上,选取怎样的自适应算法决定着自适应滤波器是否具有好的性能。
因此,对应用最为广泛的算法算法进行性能分析则显得尤为重要。
平稳环境下算法的。
LMS算法的稳定性分析和算法收敛条件

LMS 算法的稳定性分析和算法收敛条件1最小均方法LMS 简介LMS (Least Mean Square )算法是Widrow 和Hoff 于1960年首次提出的,目前仍然是实际中使用的最广泛的一种算法。
LMS 算法是在最陡下降法的基础上实现的,它是维纳滤波和最速下降算法互相结合而生成的一种新的算法。
通过维纳滤波所求解的维纳解,.必须在已知输入信号与期望信号的先验统计信息,以及再对输入信号的自相关矩阵进行求逆运算的情况下才能得以确定。
因此,这个维纳解仅仅是理论上的一种最优解。
但是通过借助于最速下降算法,LMS 算法以递归的方式来逼近这个维纳解,从而避免了矩阵求逆运算。
2LMS 算法的导出在LMS 算法中用瞬时误差的平方来代替均方误差是LMS 算法最主要的思想,以瞬时误差信号平方的梯度作为均方误差函数梯度的估计。
在最陡下降法中其维纳解方程如下(1)()k k k μξ+=-∇w w (1-1) 其中ξk ∇为梯度矢量,此时的2[()]E e n ξ=, 此时取性能函数()n e 2=ξ来代替之前的性能函数,则新的维纳方程变为如下形式2(1)()()n n e n μ+=-∇w w (1-2) 同时又可以求得22()()()2()2()()e n e n e n e n e n n ∂∂∇===-∂∂x w w (1-3) 所以LMS 算法的权值更新方程可写成下式(1)()()()n n e n n μ+=+w w x (1-4) 为了了解LMS 算法与最速下降法所得到的权矢量之间的关系,需要重写LMS 算法的递推公式,因为)()()()(n w n x n d n e T -=代入LMS 算法的权值更新方程可得)())()()()(()()1(n x n w n x n d n u n w n w T -+=+ 即)()()())()(()1(n d n ux n w n x n ux I n w T +-=+对上式求均值,又因为w (n )和x (n )不相关,所以 )]()([)]([)])()([()]1([n d n x uE n w E n x n x uE I n w E T +-=+ (1-5)其中互相关矢量T L p p p n d n E ],...,,[)]()([121-==x p自相关矩阵()()T E n n ⎡⎤=⎣⎦R x x把P 和R 代入1-5式可得uP n w E uR I n w E +-=+)]([)()]1([ (1-6) 由式1-6可知LMS 算法的权矢量的平均值E[w(n)]的变化规律和最速下降法的权矢量w(n)完全一样。
最小均方(LMS)算法

第3章最小均方(LMS)算法最小均方算法即LMS算法是B.widrow和Hoff于1960年提出的:由于实现简单且对信号统计特性变化具有稳健件,LMS算法获得了极广泛的应用。
LMS算法是基于最小均方误差准则(MMSE)的维纳滤波器和最陡下降法提出的。
本章将进—步时论最小均方误差滤波器和针对这种滤波器的最陡下降法,并在此基础上详细讨论LMS算法。
LMS算法的缺点在于当输人信号的自相关关矩阵的特征值分散时,其收敛件变差。
为了克服这问题并进一步简化LMs算法,学者们进行广长期研究并提出了不少改进算法,本章将对这些算法进行讨论。
最小均方误差滤波器最小均方误差滤波器的推导第2章2.2节已对均于图1.2的最小均力误差滤波器作了概述。
本分将针对时域滤波情况进一步讨论最小均方误差滤波器。
为便于讨论,I.5国内外MIMO技术研究现状虽然MIMO无线通信技术源于天线分集技术与智能天线技术,但是MIMO系统在无需增加频谱与发射功率下就可以获得令人振奋的容量与可靠性提升,它引发了大量的理论研究与外场实验。
自从1995年Telatar推导出多天线高斯信道容量['6}, 1996年Foschini提出BLAST算法[72]与1998年Tarokh等提出空时编码[(4]以来,MIMO无线通信技术的研究如雨后春笋般涌现[(73-300]。
至2004年底,IEEE数据库收录该领域的研究论文己达数千篇(http://ieeexplore. ieee. org/},它们包含了MIMO无线通信技术的理论研究到实验验证以及商用化的各个方面。
目前,国际上很多科研院校与商业机构都争相对MIMO通信技术进行深入研究,MIMO技术正以前所未有的速度向前发展[85]。
这里列举一些国内外在研究MIMO 通信技术方面最具有代表性的机构与个人,以洞察MIMO技术的研究现状与发展动态。
A T&T Bell Lab是多天线技术研究的倡导者,其研究员I. E. Telatar ,G.J.Foschini、M.J.Gans,GD.Golden, R.A.V alenzuela, P.W.Wolniansky、D-S.Shiu,J.M.Kahn, J.Ling, J.C.Liberti,Jr.等长期从事MIMO技术研究[68,84],其第一个空时方案就是著名的BLAST结构[[74一,S,lzz],其开创性的研究包括【5,72-76,88】等]lproject/blastl] o J.H.Winters等还公布了一些研究与测试结果[ 19,64,96,180,279,282,283,285,286,306]。
NLMS,LMS算法介绍参考

CO N T E N T改进的LMS算法——NLMS算法LMS算法原理两种算法性能分析总结LMS(最小均方误差)算法是基于梯度的算法,应用准则是均方误差函数(MSE )最小化原则,它在迭代运算中不断地调整滤波器权系数,直到MSE 达到最小值为止。
设计自适应滤波器的最常用的结构就是横向滤波器结构,输出信号y n 为:y n =w T n ∗x n = i=0N−1w i n x(n −i)N 为滤波器阶数,w T n 为权系数的转置。
FIR 自适应滤波器输出的形式可以看做是x n 与w n 两个矩阵的卷积,误差信号为参考输入信号与实际输出信号的差值e n =d n −y n =d n −w T n ∗x(n)1LMS算法的基本思想是利用e n与x(n)的某种关系,来不断更新自适应滤波器的权系数,从而使均方误差达到最小值,达到最优滤波效果。
均方误差J n为:J n=E e2n=E[d2n−2d n w T n∗x n+w T n∗x n2]通过对J n求导来得到使取得最小值的滤波器权系数,得到使代价函数最小的滤波器系数值:w=R−1∗P其中P=E d n∗x n为输入信号和参考信号的互相关矩阵R=E[x n∗x T n]为输入信号的自相关矩阵将均方误差E e2n对各w i矢量求导,获得均方误差梯度∇n为:∇n=ðE[e2(n)]ðw i⋮ðE[e2(n)]ðw n1设w n +1表示n +1时刻的滤波器系数权矢量,根据最陡下降法,滤波器权系数递归迭代公式表示为:w n +1=w n +μx n ∗e(n)其中μ为自适应步长,用来控制滤波器算法收敛性和稳定性。
对于LMS 算法为了保证收敛,μ的取值范围为:0<μ<2λmax输入信号为加了高斯噪声后的随机信号,取μ=1,α=0.001,μ= 0.2得到两种算法的误差曲线如下图所示:下降曲线的斜率反应了算法的收敛速度,稳定后的误差反映了算法的精度。
LMSAlgorithm最小均方算法

LMSAlgorithm最小均方算法Machine Learning Basic Knowledge常用的数据挖掘机器学习知识(点)Basis(基础):MSE(MeanSquare Error?均方误差),LMS(Least MeanSquare?最小均方),LSM(Least Square Methods?最小二乘法),MLE(Maximum LikelihoodEstimation最大似然估计),QP(QuadraticProgramming?二次规划),?CP(ConditionalProbability条件概率),JP(Joint Probability?联合概率),MP(Marginal Probability边缘概率),Bayesian Formula(贝叶斯公式),L1 -L2Regularization(L1-L2正则,以及更多的,现在比较火的L2.5正则等),GD(Gradient Descent?梯度下降),SGD(Stochastic GradientDescent?随机梯度下降),Eigenvalue(特征值),Eigenvector(特征向量),QR-decomposition(QR分解),Quantile (分位数),Covariance(协方差矩阵)。
Common Distribution(常见分布):Discrete?Distribution(离散型分布):Bernoulli Distribution-Binomial(贝努利分步-二项分布),Negative?BinomialDistribution(负二项分布),Multinomial Distribution(多式分布),Geometric Distribution(几何分布),Hypergeometric Distribution(超几何分布),Poisson?Distribution?(泊松分布)ContinuousDistribution (连续型分布):Uniform Distribution(均匀分布),Normal Distribution-GaussianDistribution(正态分布-高斯分布),Exponential Distribution(指数分布),Lognormal Distribution(对数正态分布),Gamma Distribution(Gamma分布),Beta Distribution(Beta分布),Dirichlet Distribution(狄利克雷分布),Rayleigh Distribution(瑞利分布),Cauchy Distribution(柯西分布),Weibull Distribution (韦伯分布)Three Sampling Distribution(三大抽样分布):Chi-square Distribution(卡方分布),t-distribution(t-distribution),F-distribution(F-分布)Data Pre-processing(数据预处理):MissingValue Imputation(缺失值填充),Discretization(离散化),Mapping(映射),Normalization(归一化-标准化)。
最小均方算法lms的原理

最小均方算法lms的原理
LMS(Least Mean Squares)算法是一种常用的自适应滤波算法,常用于信号处理和通信领域。
LMS算法的原理如下:
1. 初始化权重向量w为一个随机向量。
2. 对于每个输入样本x(n),计算输出值y(n):y(n) = w^T * x(n),其中^T表示向量的转置。
3. 计算误差e(n):e(n) = d(n) - y(n),其中d(n)为期望输出。
4. 根据误差e(n)和输入样本x(n)更新权重向量w:w(n+1) = w(n) + μ* e(n) * x(n),其中μ为步长参数,控制权重的更新速度。
5. 重复步骤2至步骤4,直到达到指定的收敛条件或迭代次数。
LMS算法的基本思想是通过不断调整权重向量,使得输出值与期望输出之间的误差最小化。
通过迭代的方式,算法会逐渐收敛到最优解。
LMS算法的优点是计算简单且实时性好,适用于大规模实时系统。
然而,LMS 算法也存在一些缺点,例如对于高维数据和非线性问题效果较差,对输入信号的
统计特性要求较高。
因此,在实际应用中需要根据具体情况选择合适的自适应滤波算法。
第三章 最小均方(LMS)算法

2
w w E{e (n)}
2
w E{ d (n) } 2w Re{w rxd } w w R xx w
H H
2
2rxd 2R xx w 0
R xx w opt=rxd
(正规方程)
2
w opt=R r
H opt xd
-1 xx xd
H opt
min E{| d (n) | } 2 Re{w r } w R xx wopt
y(n) wi* x(n i 1)
i 1 M
w x(n) x (n)w
H T
*
e(n) d (n) y(n) d (n) w H x(n)
* rxx (i) E{x(n) x* (n i)} rxx (i) rxx (i)
rxd (i) E{x(n)d * (n i)}
x1 (n) 1 x (n) e j1 x( n) 2 j ( M 1)1 x ( n ) L e 1 e j 2 e j ( M 1)2 s1 (n) s ( n) e j L 2 e j ( M 1) L s L (n) 1
f f f T x f (x) x f ( x1 , x2 ,, x n ) [ , ,, ] x1 x2 x n
函数对于一维自变量x1的梯度
f ( x1 ) x1 f ( x1 ) x1
就是函数对x1的导数
对于复矢量x
xk xkr xkj [ x1 , ,xn ]T [ x1r , ,xnr ]T [ x1 j , ,xnj ]T x = xr + x j xr [ x1r , ,xnr ]T x j [ x1 j , ,xnj ]T
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E{| e(n) |2} E{e(n)e* (n)} E{| d (n) |2} w H rxd (w H rxd )* w H R xxw
E{| d (n) |2} 2 Re{w H rxd } w H R xxw
rxd (0)
rxd
E{x(n)d * (n)}
rxd (1)
x(n)
xT
(n)w*
i 1
e(n) d (n) y(n) d (n) w H x(n)
rxx (i) E{x(n)x* (n i)} rxx (i) rx*x (i) rxd (i) E{x(n)d * (n i)} rdx (i) rd*x (i)
f (w) E{| e(n) |2}
2 11
2 22
1
v'12
v'
2 2
1
(C1 / 1) (C2 / 2 )
1 均方误差椭圆
的长轴正比于
min
短轴正比于 1 max
§3.3 最陡下降法 3.3.1 最陡下降法的递推公式
=E{| d (n) |2} 2 Re{w H rxd } w H R xxw
w 2R xxw 2rxd
v(n) (I 2QΛQ1)n v(0) [Q(I 2Λ)Q1]n v(0)
正交原理
w=w E{| e2 (n) |} 0 e(n) d (n) w H x(n)
e er je j d dr jd j x xr jx j w w r jw j
| e |2 er2 e2j
[dr
(w
T r
x
r
wTj x
j
)]2
[d
j
(wTr x
j
wTj xr )]2
v w w opt = min+v H R xx v
R xxqi
iqi
i 1,2, , M
qiH q j
1 0
i j i j
q11 q1M
Q
q1 ,
,qM
qM1 qMM
Q H Q I, Q H Q1 Q H R xxQ Λ R xx QΛQH QΛQ1
Λ Diag(1, 2 , M ) =min vH QΛQH v
根据正交原理推正规方程
0 E{x(n)e*(n)} E{x(n)[d *(n) xH (n)wopt ]}
E{x(n)d *(n)} E{x(n)xH (n)}wopt
R xxw rxd
§3.2 关于均方误差性能函数的进一步讨论 3.2.1 均方误差性能函数的各种表达式
=min+(w wopt )H Rxx (w wopt )
w opt
R
r 1
xx xd
min
E{e2 (n)}min
E{d
2
(n)}
wH opt
rxd
w(n 1) w(n) w
w(n 1) w(n) [2R xxw(n) 2rxd ]
w(n 1) (I 2R xx )w(n) 2rxd
w(n 1) w opt (I 2R xx )[w(n) w opt ]
v' Q H v [v1 ', , vM ']T
v Qv'
min v'H Λv ' min M i vi' 2
i 1
qi ' QH qi [q1,L , qi ,L , qM ]H qi [0,L ,1,L 0]T
3.2.2 几何意义
w
w1 w2
w opt
wopt1 wopt 2
(正规方程) R xx w opt=rxd
wopt=R-xx1rxd
E{|
d
(n)
|2
}
wH opt
rxd
min
E{| d(n)
|2} 2 Re{woHptrxd }
wH opt
R
xx
wopt
E{|
d (n)
|2}
wH opt
R
w xx opt
正规方程的解
(1) 直接矩阵求逆算法(DMI算法)或采样矩阵求逆(SMI)算法。 (2) 最陡下降法(加权系数的递推)----最小均方算法即LMS算法 (3) Levinson-Durbin算法(加权系数的递推)利用矩阵的埃尔米特 和Toeplitz性质
v
w w opt
v1 v2
'
R xx
rxx (0)
rxx
(1)
rxx (1)
rxx (0) rxx (0) 0
图3.2 均方误差性能面
图3.3 等均方误差椭圆族
min vT R xx v C vT R xxv C1
v' v' C QT
R
xxQ
Λ
1
0
0
2
v'T Λv ' C1
第三章 最小均方(LMS)算法
§3.1 最小均方误差滤波器
图3.1 横式滤波器
w [w1 , w2 ,..., wM ]T
x(n) [x1(n), x2 (n),..., xM (n)]T [x(n), x(n 1))
M
wi* x(n i
1)
wH
3.3.2最陡下降法的性能分析
一、收敛性
w(n 1) w opt (I 2R xx )[w(n) w opt ]
v(n) w(n) w opt v(n 1) (I 2R xx )v(n) v(0) w(0) w opt v(n) (I 2R xx )n v(0) R xx QΛQH QΛQ1
v H R xxv E{v H x(n)x H (n)v} E{| x H (n)v |2} 0
(3)具有Toeplitz性质,即其任意对角线上的元素相等。
最佳解---维纳解
E{| d (n) |2} 2 Re{w H rxd } w H R xxw
f (w) E{| e(n) |2} w w E{e2 (n)} 0
rxd (1 M )
rxx (0)
R xx
E{x(n)x H (n)}
rxx (1)
(1)是埃米尔特矩阵
R
H xx
R xx
rxx (1 M )
rxx (1) rxx (0)
rxx (2 M )
rxx (M 1) rxx (M 2)
rxx (0)
(2)是正定的或半正定的。
w | e |2 wr | e |2 jw j | e |2 2xe*
w E{| e(n) |2} E{w | e(n) |2} E{2e* (n)x(n)} 0
E{x(n)e* (n)} 0 E{p(n)q* (n)} 0
E{x(n i)e* (n)} 0 i 0,1, , M 1
