农夫过河问题

合集下载

数据结构实验-农夫过河问题

农夫过河问题一、实验目的掌握广度优先搜索策略，并用队列求解农夫过河问题二、实验内容问题描述：一农夫带着一只狼，一只羊和一颗白菜，身处河的南岸，他要把这些东西全部运到北岸，遗憾的是他只有一只小船，小船只能容下他和一件物品。

这里只能是农夫来撑船，同时因为狼吃羊、羊吃白菜、所以农夫不能留下羊和狼或羊和白菜在河的一边，而自己离开；好在狼属肉食动物，不吃白菜。

农夫怎么才能把所有的东西安全运过河呢？实验要求如下：（1）设计物品位置的表示方法和安全判断算法；（2）设计队列的存储结构并实现队列的基本操作（建立空队列、判空、入队、出队、取对头元素），也可以使用STL中的队列进行代码的编写；（3）采用广度优先策略设计可行的过河算法；（4）输出要求：按照顺序输出一种可行的过河方案；提示：可以使用STL中的队列进行代码编写。

程序运行结果：二进制表示：1111011011100010101100011001，0000三、农夫过河算法流程⏹Step1：初始状态0000入队⏹Step2：当队列不空且没有到达结束状态1111时，循环以下操作：⏹队头状态出队⏹按照农夫一个人走、农夫分别带上三个物品走，循环以下操作：⏹农夫和物品如果在同一岸，则计算新的状态⏹如果新状态是安全的并且是没有处理过的，则更新path[ ]，并将新状态入队⏹当状态为1111时，逆向输出path[ ]数组附录一：STL中队列的使用注：队列，可直接用标准模板库（STL）中的队列。

需要#include<queue>STL中的queue，里面的一些成员函数如下（具体可以查找msdn，搜索queue class）：front：Returns a reference to the first element at the front of the queue.pop：Removes an element from the front of the queuepush：Adds an element to the back of the queueempty：Tests if the queue is empty三、实验代码FarmerRiver.H#ifndef FARMERRIVER_H#define FARMERRIVER_Hint FarmerOnRight(int status); //农夫，在北岸返回1，否则返回0int WorfOnRight(int status); //狼int CabbageOnRight(int status); //白菜int GoatOnRight(int status); //羊int IsSafe(int status); //判断状态是否安全，安全返回1，否则返回0void FarmerRiver();#endifSeqQueue.h#ifndef SEQQUEUE_H#define SEQQUEUE_Htypedef int DataType;struct Queue{int Max;int f;int r;DataType *elem;};typedef struct Queue *SeqQueue;SeqQueue SetNullQueue_seq(int m);int IsNullQueue_seq(SeqQueue squeue);void EnQueue_seq(SeqQueue squeue, DataType x);void DeQueue_seq(SeqQueue);DataType FrontQueue_seq(SeqQueue);#endifFarmerRiver.c#include <stdio.h>#include <stdlib.h>#include "SeqQueue.h"#include "FarmerRiver.h"int FarmerOnRight(int status) //判断当前状态下农夫是否在北岸{return (0!=(status & 0x08));}int WorfOnRight(int status){return (0!=(status & 0x04));}int CabbageOnRight(int status){return (0!=(status & 0x02));}int GoatOnRight(int status){return (0!=(status & 0x01));}int IsSafe(int status) //判断当前状态是否安全{if ((GoatOnRight(status)==CabbageOnRight(status)) &&(GoatOnRight(status)!=FarmerOnRight(status)))return (0); //羊吃白菜if ((GoatOnRight(status)==WorfOnRight(status)) && (GoatOnRight(status)!=FarmerOnRight(status))) return 0; //狼吃羊return 1; //其他状态是安全的}void FarmerRiver(){int i, movers, nowstatus, newstatus;int status[16]; //用于记录已考虑的状态路径SeqQueue moveTo;moveTo = SetNullQueue_seq(20); //创建空列队EnQueue_seq(moveTo, 0x00); //初始状态时所有物品在北岸，初始状态入队for (i=0; i<16; i++) //数组status初始化为-1{status[i] = -1;}status[0] = 0;//队列非空且没有到达结束状态while (!IsNullQueue_seq(moveTo) && (status[15]==-1)){nowstatus = FrontQueue_seq(moveTo); //取队头DeQueue_seq(moveTo);for (movers=1; movers<=8; movers<<=1)//考虑各种物品在同一侧if ((0!=(nowstatus & 0x08)) == (0!=(nowstatus & movers)))//农夫与移动的物品在同一侧{newstatus = nowstatus ^ (0x08 | movers); //计算新状态//如果新状态是安全的且之前没有出现过if (IsSafe(newstatus)&&(status[newstatus] == -1)){status[newstatus] = nowstatus; //记录新状态EnQueue_seq(moveTo, newstatus); //新状态入队}}}//输出经过的状态路径if (status[15]!=-1){printf("The reverse path is: \n");for (nowstatus=15; nowstatus>=0; nowstatus=status[nowstatus]){printf("The nowstatus is: %d\n", nowstatus);if (nowstatus == 0)return;}}elseprintf("No solution.\n");}Sequeue.c#include <stdio.h>#include <stdlib.h>#include "SeqQueue.h"SeqQueue SetNullQueue_seq(int m){SeqQueue squeue;squeue = (SeqQueue)malloc(sizeof(struct Queue));if (squeue==NULL){printf("Alloc failure\n");return NULL;}squeue->elem = (int *)malloc(sizeof(DataType) * m);if (squeue->elem!=NULL){squeue->Max = m;squeue->f = 0;squeue->r = 0;return squeue;}else free(squeue);}int IsNullQueue_seq(SeqQueue squeue){return (squeue->f==squeue->r);}void EnQueue_seq(SeqQueue squeue, DataType x) //入队{if ((squeue->r+1) % squeue->Max==squeue->f) //是否满printf("It is FULL Queue!");else{squeue->elem[squeue->r] = x;squeue->r = (squeue->r+1) % (squeue->Max);}}void DeQueue_seq(SeqQueue squeue) //出队{if (IsNullQueue_seq(squeue))printf("It is empty queue!\n");elsesqueue->f = (squeue->f+1) % (squeue->Max); }DataType FrontQueue_seq(SeqQueue squeue) //求队列元素{if (squeue->f==squeue->r)printf("It is empty queue!\n");elsereturn (squeue->elem[squeue->f]);}main.c#include <stdio.h>#include <stdlib.h>#include "FarmerRiver.h"int main(void){FarmerRiver();return 0;}实验结果：四、实验总结。

农夫过河问题(C++编写)

cout<<" **
------------------------
**\n";
cout<<" **
|
农夫过河问题
|
**\n";
cout<<" **
------------------------
**\n";
cout<<"
****************************************************************************\n";
1、问题描述
从前，一个农夫带着一只狼，一只羊和一棵白菜要河（注意该狼被农夫训服了，但还会吃羊）。他要将所有东西安全的带到河的对岸，不幸的是河边只有一条船，只能装下农夫和他的一样东西，并且农夫必须每次都随船过，因为只有他能撑船。在无人看管的情况下，狼要吃羊，羊要吃白菜，因此，农夫不能在河的某边岸上单独留下狼和羊，也不能单独留下羊和白菜。那么农夫如何才能使三样东西平安过河呢？
3）、如果上两个条件都不满，则可执行运输的动作，但每次都应考虑，该运输情况以前是否执行过（即两岸以及船上的东西以时四者各自的状态，并递归的进行下一次运载。
5、系统测试
6、经验总结
解决实际问题时，应先分析实际问题，找出实际问题的所有约束条件，然后对问题进行数学模型的抽象化，抓主要因素，省去一些不需要的因素，将其抽象为数学问题，然后再从整体上设计算法，搭建程序的框架，最后一步步完善细节，这样做，会使本来毫无头绪的问题变得清晰起来。
if (a[ferryTimes][i] == a[ferryTimes][3]) {

农夫过河问题趣味数学

农夫过河问题趣味数学
农夫过河问题的趣味数学如下：
从前，一个农夫带着一条狗、一只兔子和一棵青菜来到河边，他要把这三件东西带过河去。

河边仅有一只很小的旧船，农夫最多只能带其中的一样东西上船，否则就有沉船的危险。

刚开始，他带了青菜上船，回头一看，调皮的狗正在欺负胆小的兔子。

他连忙把青菜放在岸上，带着狗上了船，但贪嘴的兔子又要吃鲜嫩的青菜，农夫只好又回来。

他坐在岸边，看着这三件东西，静静地思索了一番，终于想出了一个渡河的办法。

第一步，农夫可以先带兔子到对岸，然后自己返回；第二步，带狗到对岸，但把兔子带回来；第三步，把兔子留下，带青菜到对岸，农夫自己返回；第四步，带兔子到对岸。

这样三件东西都完好地带过河去了。

题目流程农夫过河

题目流程农夫过河一、基础过河规则类题目（1 - 5题）题目1：农夫带着狼、羊和一筐白菜要过河。

只有一条小船，农夫每次只能带一样东西过河。

如果农夫不在，狼会吃羊，羊会吃白菜。

请问农夫怎样才能安全地把狼、羊和白菜都运到河对岸？解析：1. 农夫先把羊运到河对岸，然后农夫独自返回。

- 原因是狼不吃白菜，这样河这边留下狼和白菜是安全的。

2. 农夫再把狼运到河对岸，然后农夫带着羊返回。

- 因为如果不把羊带回来，狼会吃羊。

3. 农夫把白菜运到河对岸，然后农夫独自返回。

- 此时河对岸有狼和白菜，是安全的。

4. 最后农夫把羊运到河对岸。

题目2：农夫要带狐狸、鸡和一袋米过河。

船很小，农夫每次只能带一个东西过河。

如果农夫不在，狐狸会吃鸡，鸡会吃米。

农夫应该怎样安排过河顺序？解析：1. 农夫先把鸡运到河对岸，然后农夫独自返回。

- 这样河这边留下狐狸和米是安全的。

2. 农夫再把狐狸运到河对岸，然后农夫带着鸡返回。

- 防止狐狸吃鸡。

3. 农夫把米运到河对岸，然后农夫独自返回。

- 此时河对岸有狐狸和米，安全。

4. 最后农夫把鸡运到河对岸。

题目3：农夫带着狗、兔子和一篮胡萝卜过河。

船只能载农夫和一样东西。

若农夫不在，狗会咬兔子，兔子会吃胡萝卜。

怎样安全过河？解析：1. 农夫先带兔子过河，然后独自返回。

- 因为狗不吃胡萝卜，这样河这边狗和胡萝卜是安全的。

2. 农夫再带狗过河，然后带兔子返回。

- 避免狗咬兔子。

3. 农夫带胡萝卜过河，然后独自返回。

- 此时河对岸狗和胡萝卜安全。

4. 最后农夫带兔子过河。

题目4：有个农夫要带蛇、鼠和一袋谷子过河，船每次只能载农夫和一样东西。

农夫不在时，蛇会吃鼠，鼠会吃谷子。

如何安全渡河？解析：1. 农夫先带鼠过河，然后独自返回。

- 此时河这边蛇和谷子是安全的。

2. 农夫再带蛇过河，然后带鼠返回。

- 防止蛇吃鼠。

3. 农夫带谷子过河，然后独自返回。

- 河对岸蛇和谷子安全。

4. 最后农夫带鼠过河。

题目5：农夫带着猫、鱼和一盆花过河。

数据结构实验-农夫过河问题

这里只能是农夫来撑船，同时因为狼吃羊、羊吃白菜、所以农夫不能留下羊和狼或羊和白菜在河的一边，而自己离开；好在狼属肉食动物，不吃白菜。

需要#include<queue>STL中的queue，里面的一些成员函数如下（具体可以查找msdn，搜索queue class）：front：Returns a reference to the first element at the front of the queue.pop：Removes an element from the front of the queuepush：Adds an element to the back of the queueempty：Tests if the queue is empty三、实验代码FarmerRiver.H#ifndef FARMERRIVER_H#define FARMERRIVER_Hint FarmerOnRight(int status); //农夫，在北岸返回1，否则返回0int WorfOnRight(int status); //狼int CabbageOnRight(int status); //白菜int GoatOnRight(int status); //羊int IsSafe(int status); //判断状态是否安全，安全返回1，否则返回0void FarmerRiver();#endifSeqQueue.h#ifndef SEQQUEUE_H#define SEQQUEUE_Htypedef int DataType;struct Queue{int Max;int f;int r;DataType *elem;};typedef struct Queue *SeqQueue;SeqQueue SetNullQueue_seq(int m);int IsNullQueue_seq(SeqQueue squeue);void EnQueue_seq(SeqQueue squeue, DataType x);void DeQueue_seq(SeqQueue);DataType FrontQueue_seq(SeqQueue);#endifFarmerRiver.c#include <stdio.h>#include <stdlib.h>#include "SeqQueue.h"#include "FarmerRiver.h"int FarmerOnRight(int status) //判断当前状态下农夫是否在北岸{return (0!=(status & 0x08));}int WorfOnRight(int status){return (0!=(status & 0x04));}int CabbageOnRight(int status){return (0!=(status & 0x02));}int GoatOnRight(int status){return (0!=(status & 0x01));}int IsSafe(int status) //判断当前状态是否安全{if ((GoatOnRight(status)==CabbageOnRight(status)) && (GoatOnRight(status)!=FarmerOnRight(status)))return (0); //羊吃白菜if ((GoatOnRight(status)==WorfOnRight(status)) && (GoatOnRight(status)!=FarmerOnRight(status))) return 0; //狼吃羊return 1; //其他状态是安全的}void FarmerRiver(){int i, movers, nowstatus, newstatus;int status[16]; //用于记录已考虑的状态路径SeqQueue moveTo;moveTo = SetNullQueue_seq(20); //创建空列队EnQueue_seq(moveTo, 0x00); //初始状态时所有物品在北岸，初始状态入队for (i=0; i<16; i++) //数组status初始化为-1{status[i] = -1;}status[0] = 0;//队列非空且没有到达结束状态while (!IsNullQueue_seq(moveTo) && (status[15]==-1)){nowstatus = FrontQueue_seq(moveTo); //取队头DeQueue_seq(moveTo);for (movers=1; movers<=8; movers<<=1)//考虑各种物品在同一侧if ((0!=(nowstatus & 0x08)) == (0!=(nowstatus & movers)))//农夫与移动的物品在同一侧{newstatus = nowstatus ^ (0x08 | movers); //计算新状态//如果新状态是安全的且之前没有出现过if (IsSafe(newstatus)&&(status[newstatus] == -1)){status[newstatus] = nowstatus; //记录新状态EnQueue_seq(moveTo, newstatus); //新状态入队}}}//输出经过的状态路径if (status[15]!=-1){printf("The reverse path is: \n");for (nowstatus=15; nowstatus>=0; nowstatus=status[nowstatus]){printf("The nowstatus is: %d\n", nowstatus);if (nowstatus == 0)return;}}elseprintf("No solution.\n");}Sequeue.c#include <stdio.h>#include <stdlib.h>#include "SeqQueue.h"SeqQueue SetNullQueue_seq(int m){SeqQueue squeue;squeue = (SeqQueue)malloc(sizeof(struct Queue));if (squeue==NULL){printf("Alloc failure\n");return NULL;}squeue->elem = (int *)malloc(sizeof(DataType) * m);if (squeue->elem!=NULL){squeue->Max = m;squeue->f = 0;squeue->r = 0;return squeue;}else free(squeue);}int IsNullQueue_seq(SeqQueue squeue){return (squeue->f==squeue->r);}void EnQueue_seq(SeqQueue squeue, DataType x) //入队{if ((squeue->r+1) % squeue->Max==squeue->f) //是否满printf("It is FULL Queue!");else{squeue->elem[squeue->r] = x;squeue->r = (squeue->r+1) % (squeue->Max);}}void DeQueue_seq(SeqQueue squeue) //出队{if (IsNullQueue_seq(squeue))printf("It is empty queue!\n");elsesqueue->f = (squeue->f+1) % (squeue->Max); }DataType FrontQueue_seq(SeqQueue squeue) //求队列元素{if (squeue->f==squeue->r)printf("It is empty queue!\n");elsereturn (squeue->elem[squeue->f]);}main.c#include <stdio.h>#include <stdlib.h>#include "FarmerRiver.h"int main(void){FarmerRiver();return 0;}实验结果：四、实验总结。

农夫过河问题回溯法python实现

农夫过河问题是经典的逻辑谜题，在这个问题中，农夫需要把一只狼、一只羊和一棵白菜一起带过河。

然而，农夫只有一条小船，而且小船只能容纳农夫和另外一样东西。

而且，如果农夫不在场的话，狼会吃羊，羊会吃白菜。

所以农夫需要想办法把它们一一带过河，而且又不能让狼吃羊或者羊吃白菜。

这个问题看似简单，实际上需要一定的逻辑推理和计划安排才能成功通过。

回溯法是一种常用于解决这类问题的算法。

在计算机科学中，回溯法常常用于解决组合优化问题，它通过不断地尝试所有可能的步骤，直到找到解决方案为止。

在农夫过河问题中，回溯法可以帮助我们列举所有的可能方案，然后找出最优的解决方案。

下面我们将使用Python语言来实现农夫过河问题的回溯法解决方案。

1. 定义问题的状态空间在农夫过河问题中，我们可以定义每一种状态为(农夫位置, 狼位置, 羊位置, 白菜位置)。

其中，农夫位置、狼位置、羊位置和白菜位置均可取值为"左岸"或"右岸"。

(左岸, 左岸, 左岸, 左岸)代表所有的物品都在左岸，而农夫则准备过河。

2. 定义可行动作根据问题的描述，我们可以定义农夫可以采取的可行动作。

具体来说，农夫可以选择带一样东西过河，也可以选择不带东西过河。

我们可以定义可行动作为("不带东西过河"), ("狼过河"), ("羊过河"), ("白菜过河")。

3. 实现回溯法接下来，我们可以使用递归的方式来实现回溯法。

具体来说，我们可以定义一个递归函数backtrack(state, path)，其中state表示当前的状态，path表示从起始状态到当前状态的路径。

在递归函数中，我们首先判断是否已经找到了解决方案，如果是，则输出路径并返回；否则，我们尝试所有可行的动作，递归地调用backtrack函数，直到找到解决方案为止。

4. 完整代码实现下面是使用Python语言实现农夫过河问题的回溯法解决方案的完整代码：```pythondef is_valid(state):if state[1] == state[2] and state[0] != state[1]:return Falseif state[2] == state[3] and state[0] != state[2]:return Falsereturn Truedef backtrack(state, path):if state == ('右岸', '右岸', '右岸', '右岸'):print(path)returnactions = [(0, 0), (1, 0), (0, 1), (1, 1)]for i in range(4):new_state = tuple((state[j] if j < 3 else '左岸' if state[j] == '右岸' else '右岸') for j in range(4))if 0 in actions[i] and is_valid(new_state):backtrack(new_state, path + [(actions[i], new_state)])elif is_valid(new_state) and is_valid(tuple([new_state[j] if j != k else state[j] for j in range(4) for k in range(3, 4)])):backtrack(new_state, path + [(actions[i], new_state)])if __name__ == "__m本人n__":initial_state = ('左岸', '左岸', '左岸', '左岸')backtrack(initial_state, [])```在上面的代码中，我们首先定义了一个辅助函数is_valid，该函数用于判断当前状态是否合法。

农夫过河问题

农夫过河问题
一、先分析农夫过河的情景:1.他走到了小桥上,遇见了大象;2.他看见小桥很窄,不能通过大象,于是下来,又看见了小兔子;3.小兔子让他再回去把自己带来的萝卜给小猴子送去;4.他想了想,就决定去找乌龟帮忙。

二、农夫为什么要这样做?我们可以用图中所示的几种方法来解答:(1)如果你是农夫,你会怎么办呢?(2)我们在学习时也常常有这样的问题,面对某个复杂的问题,总是从多角度考虑它,然后得出最佳的解决方案。

比如我们要学好数学,需要同学之间互相讨论交流,取长补短,共同进步。

三、根据刚才提供的信息和已经确立的条件,你认为哪些条件更重要?请写出两点理由并说明原因。

四、结合生活实际谈谈应该怎样正确处理人与人之间的关系。

宽搜农夫过河问题

农夫过河问题宽搜（bfs）算法详解农夫过河问题（农夫、狼、羊和白菜的问题），描述如下：一个农夫，带着一只狼、一只羊、和一棵白菜，身处河的南岸，他要把这些东西全部运到北岸。

农夫的面前有一条小船，船小到只能容下他和一件物件。

另外，只能农夫会撑船。

又因为狼能吃羊，而羊爱吃白菜，所以农夫不能留下羊和白菜而自己离开，也不能留下狼和羊而自己离开。

但狼属于食肉动物，不吃白菜。

问农夫采取什么方案才能将所有的东西运过河？解题思路农夫过河问题的求解方法是使用广度优先搜索（BFS），即在搜索过程中总是最先搜索下面一步的所有可能状态，然后再进行考虑更后面的各种情况。

要实现广度优先搜索，一般采用队列结构。

把下一步所有可能达到的状态都列举出来，放在这个队列中，然后顺序取出来分别对其进行处理，处理过程中再把下一步的状态放在队列里。

在采用编程解决农夫过河的问题时，首先需要考虑以下几个问题：•程序中为了方便描述农夫过河过程中几个角色的位置（位于南岸还是北岸），最好的方法是用4 个二进制数，分别顺序表示农夫、狼、白菜和羊的位置。

在本节程序中，用二进制0 表示某角色在河的南岸，用 1 表示某角色在河的北岸。

例如，整数5（其二进制为0101），表示农夫和白菜在河的南岸，而狼和羊在北岸。

•为了方便获取各个角色当前所在的位置，程序中设置了如下 4 个函数。

其中，函数返回值为1，反之则表示角色在河的北岸：//表示农夫状态的函数，返回0 ，表示农夫在南岸，反之在北岸。

int farmer(int location){return(0!=(location & 0x08));}//表示狼的状态的函数，返回0 ，表示农夫在南岸，反之在北岸int wolf(int location){return(0!=(location & 0x04));}//表示白菜状态的函数，返回0 ，表示农夫在南岸，反之在北岸int cabbage(int location){return(0!=(location & 0x02));}//表示羊状态的函数，返回0 ，表示农夫在南岸，反之在北岸int goat(int location){return(0!=(location & 0x01));}其中，location 为当前4 种角色所处的状态，其值为0（0000）到15（1111）之间的数。

农夫过河问题

问题一：农夫，狐狸，鹅和麦粒过河问题。

他们都在河的左岸，现在要全部到对岸去，农夫有一条船，过河时，除农夫外，船上至多能载一样东西，狐狸要吃鹅，鹅要吃麦粒，除非农夫在那里。

规划出确保全部安全的过河方案。

解：用四元组（农夫，狐狸，鹅，麦粒）表示状态，其中每个元素都可为0或1。

0表示在左岸，用1表示在右岸。

用四元组(f、w、s、g)表示状态， f 代表农夫，w 代表狐狸，s 代表鹅，g 代表麦粒
初始状态S0:（0,0,0,0）目标状态：（1,1,1,1）
不合法状态有：（1,0,0，*），（1，*，0,0），（0,1,1，*），（0，*，1,1）
操作集F={p1,p2,p3,p4,q0,q1,q2,q3 }
首先分析如图所示：
操作符条件动作
p1 f=0，w=0f=1，w=1
s和g相异
p2 f=0，s=0 f=1，s=1
p3 f=0，g=0 f=1，g=1
w和s相异
q0 f=1 f=0
s和g相异
w和s相异
q1 f=1，w＝1f=0，w＝0
s和g相异
q2 f=1，s＝1 f=0，s＝0
q3 f=1，g＝1 f=0，g＝0
w和s相异
所以，方案有两种：
p2→ q0 → p3→ q2 → p2 → q0 → p2 p2→ q0 → p1→ q2 → p3→ q0→ p2。

农夫过河问题

农夫过河问题1. 题目描述：一个农夫带着一只狼，一只羊和一筐菜，欲从河的左岸坐船到右岸，由于船太小，农夫每次只能带一样东西过河，并且没有农夫看管的话，狼会吃掉羊，羊会吃菜。

设计一个方案，使农夫可以无损失的过河2. 题目分析：假设人、狼、菜、羊都在河岸a,要到b 河岸去。

题中的食物链关系为: 菜→羊→狼所以，第一次人只能带羊到b 河岸；回到a 时，人不能再将刚带过来的羊带回去，所以人是空手回到a 的；在a 河岸，人有两个选择选择一：（1）带狼到b,人再回到a 时，因为不能把狼和羊同时留下，所以只能带走羊；AA 羊 A B羊狼菜怎么办呢 B 羊 B 狼菜菜狼（2）再次回到a 后，人再到b 时，不能把羊和菜同时留下，所以只能带走菜；（3）再次回到a 时，因为狼和菜可以同时留下，所以优先选择空手过河；到a 后发现只剩下羊，所以带羊过河。

选择二：（1）带菜到b,人再回到a 时，因为不能把菜和羊同时留下，所以只能带走羊；（2）再次回到a 后，人再到b 时，不能把羊和狼同时留下，所以只能带走狼；狼羊羊 A菜 B 羊狼 A B 狼 AB 狼 AB 羊菜菜菜（3）再次回到a 时，因为狼和菜可以同时留下，所以优先选择空手过河；到a 后发现只剩下羊，所以带羊过河。

解：用四元组S 表示状态，即S ＝（L ，J ，M ，N ）其中L ：农夫 J ：狼 M ：羊 N ：菜用0表示在左岸岸，1表示在右岸，即S=（0，0，0，0）目标G ＝（1，1，1，1）定义操作符L （i ）表示农夫带东西到右岸：i=0 农夫自己到右岸；i=1 农夫带狼到右岸；i=2 农夫带羊到右岸；i=3 农夫带菜到右岸；定义操作符R （i ）表示农夫带东西到左岸：i=0 农夫自己到左岸；i=1 农夫带狼到左岸；i=2 农夫带羊到左岸；i=3 农夫带菜到左岸；约束状态如下：（1，0，0，1）狼、羊在左岸；（1，1，0，0）羊、菜在左岸；（0，1，1，0）狼、羊在右岸；（0，0，1，1）羊、菜在右岸；（1，0，0，0）狼、羊、菜在左岸；（0，1，1，1）狼、羊、菜在右岸；羊 A B狼菜。

农夫过河

数据结构课程设计《农夫过河》学院：软件学院班级：12软工移动2班姓名：学号：12151156711 问题描述农夫过河问题是指农夫带一只狼、一只羊和一棵白菜在河南岸, 需要安全运到北岸。

一条小船只能容下他和一件物品, 只有农夫能撑船，问农夫怎么能安全过河？狼吃羊, 羊吃白菜, 农夫不能将这两种或三种物品同时放在河的一侧, 因为没有农夫的照看, 狼就要吃羊, 而羊可能要吃白菜。

这类问题的实质是系统的状态问题, 要寻求的是从初始状态经一系列的安全状态到达系统的终止状态的一条路径。

2概要设计2.1 数据结构的设计农夫过河问题的模型化有一组状态( 如农夫和羊在南, 狼和白菜在北) ; 从一个状态可合法地转到另外几个状态( 如农夫自己过河或农夫带着羊过河) ; 有些状态不安全( 如农夫在北, 其他东西在南) ; 有一个初始状态( 都在南) ; 结束状态( 这里只有一个, 都在北) 。

问题表示: 需要表示问题中的状态, 农夫等位于南和北( 每个有两种可能) 。

可以采用位向量, 4 个二进制位的情况表示状态, 显而易见, 共24= 16种可能状态。

从高位到低位分别表示农夫、狼、白菜和羊。

0000( 整数0) 表示都在南岸, 目标状态1111( 即整数15) 表示都到了北岸。

有些状态0011,0101, 0111, 0001, 1100, 1001 是不允许出现的, 因为这些状态是不安全状态。

f( farmer) , w(wolf) , g(goat) , c( cabbage) 分别表示农夫自己、农夫携带狼、农夫携带羊、农夫携带菜过河。

现在的问题转化为: 找一条合法路径( 相邻状态之间的转移合法) , 从开始状态到某个结束状态, 途中不经过不安全状态。

2.2算法的设计求农夫、狼、白菜和羊的当前状态的函数为每一种状态做测试, 状态安全则返回0, 否则返回1。

安全性判断函数, 若状态安全则返回0int farmer(int location) //判断农夫位置对0做与运算，还是原来的数字，用来判断位置{return 0 != (location & 0x08);}int wolf(int location) //判断狼位置{return 0 != (location & 0x04);}int cabbage(int location) //判断白菜位置{return 0 != (location & 0x02);}int goat(int location) //判断羊的位置{return 0 !=(location & 0x01);}int safe(int location) // 若状态安全则返回 true{if ((goat(location) == cabbage(location)) && (goat(location) != farmer(location)) )return 0;if ((goat(location) == wolf(location)) && (goat(location) != farmer(location)))return 0;return 1; //其他状态是安全的借助于位向量和按位运算符, 很容易描述过河动作, 这种问题表示的设计使得程序的实现比较容易。

农夫过河问题的算法与实现汇总

农夫过河问题的算法与实现院（系）名称专业班级学号学生姓名指导教师年月日目录引言 (1)一.问题的描述 (2)二.需求分析 (3)三.概要设计 (4)3.1数据结构的设计 (4)3.2算法的设计 (5)3.3抽象数据类型的设计 (5)四.详细设计 (6)4.1算法的主要思想 (6)4.2主要功能函数设计 (7)4.3算法的实现 (7)五.代码实现 (10)六.测试与运行 (18)6.1测试工具 (18)6.2运行结果 (18)七.总结与体会 (19)八.参考文献 (20)农夫过河问题的算法与实现引言所谓农夫过河问题是指农夫带一只狼、一只羊和一棵白菜在河南岸, 需要安全运到北岸。

一条小船只能容下他和一件物品, 只有农夫能撑船。

问农夫怎么能安全过河, 当然狼吃羊, 羊吃白菜, 农夫不能将这两种或三种物品单独放在河的一侧, 因为没有农夫的照看, 狼就要吃羊, 而羊可能要吃白菜? 这类问题的实质是系统的状态问题, 要寻求的是从初始状态经一系列的安全状态到达系统的终止状态的一条路径.一.问题的描述任何的实际问题，都可以抽象成固定的数学模型，然后再根据模型解决问题。

这样就可以不考虑繁琐的实际过程，从而简化问题。

在我们的问题中，过河与没过河是两种不同的状态。

农夫、狼、羊和菜，分别处于这两种状态。

而，如果把他们看成一个系统，则农夫、狼、羊和菜的不同状态组合成系统的2的4次方种，即16种状态。

但在系统的16种状态中，有些不满足题给条件，应给予剔除。

剔除的判断条件：羊跟狼、菜状态相同，且不同于农夫的状态。

当我们挑选好一系列系统的合法状态后，我们的问题就清晰了很多。

我们不妨设，没过河状态为0，过河为1。

我们的问题就抽象为，系统从初始状态（0000），经过有限的合法状态，到达最终状态（1111）的过程。

系统不同的合法状态之间，可能，有的有路，有的则不能到达。

具体的判断条件是，农夫可以与一件物品同时边，或自己单独变。

根据这一个条件，我们可以抽象出一个图来：系统的每一种状态视为一个节点，满足条件的节点间有一条路。

农夫过河实验报告

农夫过河实验报告
实验报告：农夫过河
实验目的：
1. 了解农夫过河问题的规则和约束条件；
2. 分析农夫过河问题的求解思路；
3. 实现农夫过河问题的求解算法。

实验原理：
农夫过河问题是一种经典的逻辑推理问题，涉及农夫、狼、羊和菜四个角色过河的情景。

根据约束条件，农夫每次只能带一种物品过河，而且农夫不能将狼和羊、羊和菜同时留在岸边，否则会发生危险。

实验步骤：
1. 设计数据结构表示问题的状态，如使用二进制位表示农夫、狼、羊和菜的位置；
2. 使用递归算法实现问题的解法，通过深度优先搜索遍历所有可能的状态，并根据约束条件进行剪枝；
3. 运行程序，输出农夫过河的解答序列。

实验结果：
根据实验步骤中的算法和程序设计，成功地求解了农夫过河问题，并输出了正确的解答序列。

实验结果表明，农夫可以经过
一系列合法的操作，将狼、羊和菜都安全地带过河。

实验结论：
通过本次实验，我们深入理解了农夫过河问题的规则和约束条件，并成功地实现了问题的求解算法。

实验结果表明，农夫过河问题有多种可能的解法，但只有符合约束条件的解才是正确的解答。

这个经典的逻辑推理问题在计算机科学中具有重要的意义，可以用于教学和娱乐等领域。

农夫过河问题

课程设计题目：农夫过河一．问题描述一个农夫带着一只狼、一只羊和一箩白菜，身处河的南岸。

他要把这些东西全部运到北岸。

他面前只有一条小船，船只能容下他和一件物品，另外只有农夫才能撑船。

过河有以下规则：(1) 农夫一次最多能带一样东西(或者是狼、或者是羊、或者是白菜)过河；(2) 当农夫不在场是狼会吃羊；(3) 当农夫不在场是羊会吃掉白菜。

现在要求为农夫想一个方案，能将3 样东西顺利地带过河。

从出事状态开始，农夫将羊带过河，然后农夫将羊待会来也是符合规则的，然后农夫将羊带过河仍然是符合规则的，但是如此这般往返，搜索过程便进入了死循环，因此，在这里，采用改进的搜索算法进行搜索。

二．基本要求(1) 为农夫过河问题抽象数据类型，体会数据模型在问题求解中的重要性；(2) 要求利用数据结构的方法以及C + +的编程思想来完成问题的综合设计；(3) 在问题的设计中，使用深度优先遍历搜索方式，避免死循环状态；(4) 设计一个算法求解农夫过河问题，并输出过河方案；(5) 分析算法的时间复杂度。

三．概要设计(1) 数据结构的设计typedef struct // 图的顶点{int farmer; // 农夫int wolf; // 狼int sheep; // 羊int veget; // 白菜}Vertex;设计Vertex 结构体的目的是为了存储农夫、狼、羊、白菜的信息，因为在遍历图的时候，他们的位置信息会发生变化，例如1111 说明他们都在河的北岸，而0000 说明他们都在河的南岸。

t ypedef struct{int vertexNum; // 图的当前顶点数Vertex vertex[VertexNum]; // 顶点向量(代表顶点)bool Edge[VertexNum][VertexNum]; // 邻接矩阵 . 用于存储图中的边，其矩阵元素个数取决于顶点个数，与边数无关}AdjGraph; // 定义图的邻接矩阵存储结构存储图的方法是用邻接矩阵，所以设计一个简单的AdjGraph 结构体是为了储图的顶点数与边数，农夫过河问题我采用的是图的深度优先遍历思想。

农夫过河问题算法邻接矩阵

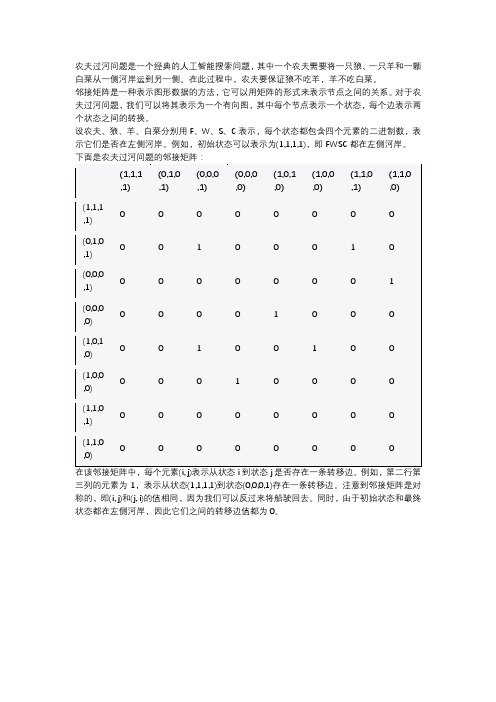
农夫过河问题是一个经典的人工智能搜索问题，其中一个农夫需要将一只狼、一只羊和一颗白菜从一侧河岸运到另一侧。

在此过程中，农夫要保证狼不吃羊，羊不吃白菜。

邻接矩阵是一种表示图形数据的方法，它可以用矩阵的形式来表示节点之间的关系。

对于农夫过河问题，我们可以将其表示为一个有向图，其中每个节点表示一个状态，每个边表示两个状态之间的转换。

设农夫、狼、羊、白菜分别用F、W、S、C表示，每个状态都包含四个元素的二进制数，表示它们是否在左侧河岸。

例如，初始状态可以表示为(1,1,1,1)，即FWSC都在左侧河岸。

下面是农夫过河问题的邻接矩阵：(1,1,1 ,1) (0,1,0,1)(0,0,0,1)(0,0,0,0)(1,0,1,0)(1,0,0,0)(1,1,0,1)(1,1,0,0)(1,1,1,1)0 0 0 0 0 0 0 0(0,1,0,1)0 0 1 0 0 0 1 0(0,0,0,1)0 0 0 0 0 0 0 1(0,0,0,0)0 0 0 0 1 0 0 0(1,0,1,0)0 0 1 0 0 1 0 0(1,0,0,0)0 0 0 1 0 0 0 0(1,1,0,1)0 0 0 0 0 0 0 0(1,1,0,0)0 0 0 0 0 0 0 0在该邻接矩阵中，每个元素(i, j)表示从状态i到状态j是否存在一条转移边。

例如，第二行第三列的元素为1，表示从状态(1,1,1,1)到状态(0,0,0,1)存在一条转移边。

注意到邻接矩阵是对称的，即(i, j)和(j, i)的值相同，因为我们可以反过来将船驶回去。

同时，由于初始状态和最终状态都在左侧河岸，因此它们之间的转移边值都为0。

农夫过河问题状态图及程序

农夫过河问题状态图及程序一、问题需求分析一个农夫带着一只狼、一只羊和一棵白菜，身处河的南岸。

他要把这些东西全部运到北岸。

问题是他面前只有一条小船，船小到只能容下他和一件物品，另外只有农夫能撑船。

另外，因为狼能吃羊，而羊爱吃白菜，所以农夫不能留下羊和白菜或者狼和羊单独在河的一边，自己离开。

请问农夫该采取什么方案才能将所有的东西运过河呢？二、算法选择求解这个问题的最简单的方法是一步一步进行试探，每一步都搜索所有可能的选择，对前一步合适的选择再考虑下一步的各种方案。

用计算机实现上述求解的搜索过程可以采用两种不同的策略：一种是广度优先(breadth_first) 搜索，另一种是深度优先(depth_first) 。

广度优先：u 广度优先的含义就是在搜索过程中总是首先搜索下面一步的所有可能状态，然后再进一步考虑更后面的各种情况。

u 要实现广度优先搜索，一般都采用队列作为辅助结构。

把下一步所有可能达到的状态都列举出来，放在这个队列中，然后顺序取出来分别进行处理，处理过程中把再下一步的状态放在队列里……。

u 由于队列的操作遵循先进先出的原则，在这个处理过程中，只有在前一步的所有情况都处理完后，才能开始后面一步各情况的处理。

三、算法的精化要模拟农夫过河问题，首先需要选择一个对问题中每个角色的位置进行描述的方法。

一个很方便的办法是用四位二进制数顺序分别表示农夫、狼、白菜和羊的位置。

例如用0表示农夫或者某东西在河的南岸，1表示在河的北岸。

因此整数5(其二进制表示为0101) 表示农夫和白菜在河的南岸，而狼和羊在北岸。

四、算法的实现完成了上面的准备工作，现在的问题变成：从初始状态二进制0000(全部在河的南岸) 出发，寻找一种全部由安全状态构成的状态序列，它以二进制1111(全部到达河的北岸) 为最终目标，并且在序列中的每一个状态都可以从前一状态通过农夫（可以带一样东西）划船过河的动作到达。

为避免不必要的瞎费功夫，要求在序列中不应该出现重复的状态。

农夫过河

程序设计报告题目：农夫过河专业：计算机科学与技术小组成员：班级:指导教师：日期：2014年12月25日成员分工：农夫过河【摘要】农夫问题即一个农民带着一只狼、一只羊和一棵白菜，身处河的南岸,他需要把这些东西全部运到河的北岸。

而他只有一条小船，且这只小船小到只能容下他和一件物品,另外只有农民能撑船。

农夫不能留下狼和羊自己离开，也不能留下白菜和羊自己离开,更不能留下狼，羊和白菜而独自离开，因为没有农夫的照看,狼就要吃掉羊,而羊又要吃掉白菜。

好在狼是是肉动物，它不吃白菜，问农夫应该采取什么方案才能将所有的东西安全地从河的南岸运到北岸？这类农夫问题是一个传统的数据结构问题,利用基于队列的图的广度优先搜索求解农夫过河问题是一个易于理解、切实可行的方案,具有一定的推广价值。

关键字：农夫过河问题;队列;广度优先搜索一、实验内容概述(设计任务与技术要求)农民过河问题是指农民需要带一只狼、一只羊和一棵白菜到河的南岸去,需要安全运到北岸。

而一条小船只能容下他和一件物品,只有农民能撑船。

问农民怎么能安全过河,问题中需要涉及到狼会吃羊,羊会吃白菜,所以农民不能将这两种或三种物品单独放在河的一侧,因为没有农民的照看,狼就要吃掉羊,而羊可能又要吃掉白菜。

这类问题的实质是系统的状态问题,要寻求的是从初始状态经一系列的安全状态到达系统的终止状态的一条路径。

根据实际情况，对此问题分析可以得到不同的特征：1,是农民和羊在河的南岸，狼和白菜在河的北岸；2,是从一个状态可转到另外一个状态，而不违反狼吃羊，羊吃草的规则（例如农民自己过河或者农民带着羊过河）；3,是有些状态是不安全的（例如农民一人在北岸，而其他的东西都在南岸）；4,是初始状态是农民，羊，狼，白菜都在河的南岸和结束状态是农民，羊，狼，白菜都在河的北岸。

实现农夫过河问题，则需要找到一条合法的路径（相邻状态之间的转移合法），从开始状态到某个结束状态，路途中不能经过不安全的状态。

十个有趣的智力小测试

十个有趣的智力小测试一、智力小测试1：农夫过河有一个农夫带着一只狼、一只羊和一棵白菜要过河。

但是船很小，每次只能带一样东西过河。

如果农夫不在，狼会吃羊，羊会吃白菜。

那农夫要怎么才能把狼、羊和白菜都安全运到河对岸呢？这题主要是考验逻辑思维能力啦。

其实答案是这样的，农夫先把羊运到河对岸，然后农夫自己返回。

接着农夫把狼运到河对岸，但是这时候不能把羊单独留下，所以要把羊再带回来。

然后把白菜运到河对岸，农夫再自己返回。

最后把羊运到河对岸就好啦。

这就像我们生活中安排事情的先后顺序一样，要考虑到不同事物之间的相互关系呢。

二、智力小测试2：水壶装水有两个水壶，一个能装5升水，一个能装3升水，旁边有个无限量的水源，怎么用这两个水壶量出4升水呢？这个题很有趣哦。

我们可以先把3升的水壶装满水，倒入5升的水壶中。

然后再把3升的水壶装满水，继续倒入5升的水壶直到5升的水壶满了，这时候3升的水壶里还剩1升水。

把5升水壶里的水倒掉，把3升水壶里剩下的1升水倒入5升水壶。

再把3升水壶装满水倒入5升水壶，这样5升水壶里就有4升水啦。

这就好比我们在做资源分配的时候，要巧妙地利用有限的资源来达到目的呢。

三、智力小测试3：称乒乓球有12个乒乓球，其中有一个重量和其他的不一样（不知道是轻是重），用一个没有砝码的天平称三次，找出这个不一样的乒乓球。

这题有点烧脑呢。

我们把12个球平均分成三组，每组4个。

第一次称其中两组，如果天平平衡，那不一样的球就在没称的那组里。

如果不平衡，就记住哪边重哪边轻。

然后从有问题的那组里拿两个球和正常组的两个球称第二次，如果平衡，不一样的球就在剩下的两个里，如果不平衡，就根据之前记住的轻重情况判断不一样的球在这两个里还是另外两个里。

第三次称就可以确定不一样的球了。

这就像我们在排查问题的时候，要逐步缩小范围呢。

四、智力小测试4：青蛙跳井一口井深10米，一只青蛙在井底，它每次能跳3米，但每次跳完后会滑下2米，这只青蛙需要跳几次才能跳出井口呢？这青蛙有点调皮呢。

农夫过河问题算法设计与实现

农夫过河问题算法设计与实现咱来唠唠农夫过河这个有趣的问题。

一、问题描述农夫要带着一只狼、一只羊和一棵白菜过河。

但是呢，船很小，每次农夫只能带一样东西过河。

而且啊，如果农夫不在，狼会吃羊，羊会吃白菜，这可就麻烦大了。

二、算法设计思路1. 初始状态- 河这边有农夫、狼、羊和白菜，河对岸啥都没有。

2. 第一步很关键- 农夫肯定不能先带狼或者白菜，为啥呢？因为如果先带狼过去，把羊和白菜留在这边，羊就会吃白菜；要是先带白菜过去，狼就会吃羊。

所以农夫得先带羊过河。

- 然后农夫自己返回。

这时候河这边有狼和白菜，河对岸有羊。

3. 第二步- 农夫再带狼或者白菜过河。

假设农夫带狼过河吧。

- 但是农夫不能把羊单独留在对岸啊，所以农夫得把羊再带回来。

这时候河这边有羊和白菜，河对岸有狼。

4. 第三步- 农夫把羊放下，带白菜过河。

- 然后农夫自己返回。

这时候河这边有羊，河对岸有狼和白菜。

5. 最后一步- 农夫再带羊过河，这样就都安全地到对岸啦。

三、算法实现（用简单的文字描述过程）1. 开始：- 农夫在起始岸，物品（狼、羊、白菜）也在起始岸，对岸为空。

2. 第一次过河：- 农夫带羊过河，此时起始岸有狼和白菜，对岸有羊和农夫。

- 农夫独自返回起始岸，此时起始岸有农夫、狼、白菜，对岸有羊。

3. 第二次过河：- 农夫带狼过河，此时起始岸有白菜，对岸有狼、羊和农夫。

- 农夫带羊返回起始岸，此时起始岸有农夫、羊、白菜，对岸有狼。

4. 第三次过河：- 农夫带白菜过河，此时起始岸有羊，对岸有狼、白菜和农夫。

- 农夫独自返回起始岸，此时起始岸有农夫、羊，对岸有狼、白菜。

5. 第四次过河：- 农夫带羊过河，此时起始岸为空，对岸有农夫、狼、羊、白菜，大功告成！你看，这样一步一步的，就像走迷宫一样，按照规则走，就能让农夫带着他的东西安全过河啦。

农夫过河问题

数据结构实验-农夫过河问题

农夫过河问题(C++编写)

农夫过河问题趣味数学

题目 流程农夫过河

数据结构实验-农夫过河问题

农夫过河问题回溯法python实现

农夫过河问题

宽搜农夫过河问题

农夫过河问题

农夫过河问题

农夫过河

农夫过河问题的算法与实现汇总

农夫过河 实验报告

农夫过河问题

农夫过河问题算法邻接矩阵

农夫过河问题状态图及程序

农夫过河

十个有趣的智力小测试

农夫过河问题算法设计与实现

题目流程农夫过河

农夫过河实验报告