正余弦定理、三角形的一些公式

合集下载

正弦定理和余弦定理公式

正弦定理和余弦定理公式正弦定理是指在一个三角形ABC中，三角形的任意一个角a、b、c的正弦与相对应的边的比例相等，即：sin(a)/a = sin(b)/b = sin(c)/c其中a、b、c分别表示三角形的三个边长，A、B、C分别表示对应的角度。

根据正弦定理公式，我们可以推导出以下两个关系式：a/sin(A) = b/sin(B) = c/sin(C)A = arcsin(a/b*sin(B)) = arcsin(a/c*sin(C))B = arcsin(b/a*sin(A)) = arcsin(b/c*sin(C))C = arcsin(c/a*sin(A)) = arcsin(c/b*sin(B))这些关系式可以帮助我们在已知三角形的两个角度和一个边长的情况下，求解出其他未知的边长和角度。

正弦定理的应用：-在解决三角形边长和角度的问题时，特别是当已知一个角度和两个边长时，可以利用正弦定理来求解其他未知量。

-在几何学中，可以利用正弦定理来计算两个不相邻边的夹角。

余弦定理是用来计算一个三角形的任意一个角的余弦值的平方与其余两边长度的关系。

在一个三角形ABC中，余弦定理可以表达如下：c^2 = a^2 + b^2 - 2ab*cos(C)b^2 = a^2 + c^2 - 2ac*cos(B)a^2 = b^2 + c^2 - 2bc*cos(A)其中a、b、c分别表示三角形的三个边长，A、B、C分别表示对应的角度。

根据余弦定理公式，我们可以推导出以下两个关系式：cos(A) = (b^2 + c^2 - a^2) / 2bccos(B) = (a^2 + c^2 - b^2) / 2accos(C) = (a^2 + b^2 - c^2) / 2ab这些关系式可以帮助我们在已知三角形的三个边长的情况下，求解出三个角度的余弦值。

余弦定理的应用：-在解决三角形边长和角度的问题时，特别是当已知三个边长时，可以利用余弦定理来求解其他未知量。

正余弦定理、三角形的一些公式

正弦定理：在一个三角形中，各边和它所对角的正弦的比相等，即sin A sin B sinC 2R （R为外接圆的半径）变形有: a 2Rsin A b 2Rs inB c 2Rs inC三角形的面积公式:SABC s"A島sin Bb2Rs"C 2R1 1absinC acsin B2 21bcsin A2余弦定理：三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍。

即变形有:cosA22bccosA b■ 2 2 2b c a2bccosB2accosB2 2 ■ 2a c b2aca2b22abcosC2 ■ 2 2 a b c cosC -2ab判断三角形的形状:2 a2 a2 a b2b2b22 c2 c2 , 2c ,bABC为钝角三角形ABC为直角角三角形2a2 2c ,c a2b2,ABC为锐角三角形三角形中有:ABC中 (1) sin(A⑵若A、B)B、si nCC成等差数列,cos(A两角和差的正余弦公式及两角和差正切公式sin sin cos cos sin cos( cos cos sin sin tantan tan二倍角公式:半角公式: sin 2tan 2tan tan2sin cos2 tan1 tan2aB） cosC ta n（A B）a、b、c成等比数列，则该三角ta nC形为正三角形sincostancos2 cos21 2si n222cos字〈正员磅所在的象限炖件（正负涉在刚沁）sin coscos costan tancos sinsin sin1 tan tansin 2现货原油R6008mxehUmG。

余弦定理公式大全

正弦、余弦定理解斜三角形建构知识结构1．三角形基本公式：（1）内角和定理：A+B+C=180°，sin(A+B)=sinC, cos(A+B)= -cosC,cos2C =sin 2B A +, sin 2C =cos 2B A + （2）面积公式：S=21absinC=21bcsinA=21casinBS= pr =))()((c p b p a p p --- (其中p=2cb a ++, r 为内切圆半径)（3）射影定理：a = b cos C + c cos B ；b = a cos C + c cos A ；c = a cos B + b cos A 2．正弦定理：2sin sin sin a b cR A B C===外证明：由三角形面积111sin sin sin 222S ab C bc A ac B ===得sin sin sin a b c A B C==画出三角形的外接圆及直径易得：2sin sin sin a b cR A B C===3．余弦定理：a 2=b 2+c 2-2bccosA , 222cos 2b c aA bc+-=；证明：如图ΔABC 中，sin ,cos ,cos CH b A AH b A BH c b A ===-22222222sin (cos )2cos a CH BH b A c b A b c bc A=+=+-=+-当A 、B 是钝角时，类似可证。

正弦、余弦定理可用向量方法证明。

要掌握正弦定理、余弦定理及其变形，结合三角公式，能解有关三角形中的问题． 4．利用正弦定理，可以解决以下两类问题：（1）已知两角和任一边，求其他两边和一角；（2）已知两边和其中一边的对角，求另一边的对角；有三种情况：bsinA<a<b 时有两解；a=bsinA 或a=b 时有解；a<bsinA 时无解。

5．利用余弦定理，可以解决以下两类问题：（1）已知三边，求三角；（2）已知两边和它们的夹角，求第三边和其他两角。

三角函数诱导公式正弦定理余弦定理基本公式

三角函数诱导公式正弦定理余弦定理基本公式1.三角函数诱导公式：正弦诱导公式：sin(a ± b) = sin(a)cos(b) ± cos(a)sin(b)余弦诱导公式：cos(a ± b) = cos(a)cos(b) ∓ sin(a)sin(b)正切诱导公式：tan(a ± b) = (tan(a) ± tan(b))/(1 ∓ tan(a)tan(b))这些诱导公式可以用来简化计算，将三角函数的运算转化为其他三角函数的运算，从而简化复杂的计算过程。

2.正弦定理：正弦定理用于求解具有三个边的三角形的角度。

根据正弦定理，三角形的三个边的比例等于其对应角度的正弦值的比例。

正弦定理的公式如下：a/sin(A) = b/sin(B) = c/sin(C)其中，a、b、c为三角形的三个边的长度，A、B、C为对应的三个角的度数。

正弦定理可以通过三边求角、两边一角求边等问题中使用。

3.余弦定理：余弦定理用于求解具有三个边或两边一角的三角形的边长。

根据余弦定理，三角形的一个边的平方等于另外两边的平方的和减去这两边长度的乘积与这两边所夹角的余弦值的两倍的乘积。

余弦定理的公式如下：c² = a² + b² - 2abcos(C)其中，a、b、c为三角形的三个边的长度，C为夹在a、b之间的角的度数。

余弦定理可以通过三边求角、两边一角求边等问题中使用。

4.基本三角函数公式：基本三角函数公式包括正弦、余弦、正切的定义和性质。

正弦公式：sin(a) = opposite/hypotenuse = a/c余弦公式：cos(a) = adjacent/hypotenuse = b/c正切公式：tan(a) = opposite/adjacent = a/b其中，a、b为直角三角形的两个直角边的长度，c为斜边的长度。

这些基本公式在解决直角三角形问题中非常常用。

立体几何三角函数计算公式

立体几何三角函数计算公式在立体几何中，三角函数是非常重要的工具，它们可以帮助我们计算各种三维空间中的角度、距离和其他属性。

本文将介绍一些常见的立体几何三角函数计算公式，并讨论它们的应用。

1. 余弦定理。

在立体几何中，余弦定理是一个非常有用的公式，它可以帮助我们计算三角形的边长。

余弦定理的公式如下：c^2 = a^2 + b^2 2ab cos(C)。

其中，a、b、c 分别表示三角形的三条边，C 表示夹在边 a 和 b 之间的角度。

利用余弦定理，我们可以计算出任意三角形的边长，从而更好地理解三维空间中的形状和结构。

2. 正弦定理。

正弦定理是另一个常见的三角函数计算公式，它可以帮助我们计算三角形的边长和角度。

正弦定理的公式如下：a/sin(A) = b/sin(B) = c/sin(C)。

其中，a、b、c 分别表示三角形的三条边，A、B、C 分别表示对应的角度。

利用正弦定理，我们可以计算出任意三角形的边长和角度，从而更好地理解三维空间中的形状和结构。

3. 三角函数的性质。

除了上述的定理之外，三角函数还有一些重要的性质，这些性质在立体几何的计算中也非常有用。

其中，最重要的性质包括：三角函数的周期性，正弦函数和余弦函数的周期都是 2π，而正切函数的周期是π。

三角函数的奇偶性，正弦函数是奇函数，余弦函数是偶函数，而正切函数则是奇函数。

三角函数的单调性，在特定的定义域内，三角函数都有自己的单调性，这可以帮助我们更好地理解它们的变化规律。

利用这些性质，我们可以更好地理解和运用三角函数，从而更好地解决立体几何中的各种问题。

4. 三角函数的应用。

在立体几何中，三角函数有着广泛的应用。

例如，在计算三维空间中的角度和距离时，我们经常会用到正弦、余弦和正切函数。

另外，在计算三角形的面积和体积时，三角函数也可以发挥重要的作用。

此外，三角函数还可以帮助我们计算各种立体图形的表面积和体积，从而更好地理解它们的性质和结构。

总之，立体几何三角函数计算公式是非常重要的工具，它们可以帮助我们更好地理解和运用三维空间中的角度、距离和其他属性。

直角三角形的正弦定理与余弦定理

直角三角形的正弦定理与余弦定理直角三角形是指其中一个角度为90度的三角形。

在直角三角形中，有两个特殊的角度，一个是直角角度，即90度角；另一个角度则是锐角或钝角。

正弦定理和余弦定理是用于计算三角形中任意一边和角度之间的关系的数学定理。

在直角三角形中，正弦定理和余弦定理可以简化为更常用的形式。

1. 正弦定理：正弦定理表示三角形的边与其对应的角度之间的关系。

对于任意三角形ABC，其中C为直角角度，a、b、c分别为对应的边长。

正弦定理的公式表达为：sin(A) / a = sin(B) / b = sin(C) / c其中sin(A)表示角A的正弦值，同理sin(B)和sin(C)表示角B和角C的正弦值。

根据正弦定理，我们可以计算直角三角形中任意一边的长度。

2. 余弦定理：余弦定理表示三角形的边与其对应的角度之间的关系。

对于任意三角形ABC，其中C为直角角度，a、b、c分别为对应的边长。

余弦定理的公式表达为：c^2 = a^2 + b^2 - 2ab * cos(C)其中cos(C)表示角C的余弦值。

根据余弦定理，我们可以计算直角三角形中任意一边的长度。

通过正弦定理和余弦定理，我们可以解决一些与直角三角形相关的计算问题，比如已知两边长度和一个角度，求解其他角度或边长。

举个例子，如果我们已知一个直角三角形的直角边长为3，斜边长为5，我们可以通过计算求得另一直角边的长度。

首先，我们可以使用正弦定理计算斜边对应的角度sin(C) = c / a = 5 / 3，通过反正弦函数求得角C的值为35.26度。

然后，我们可以使用余弦定理计算另一直角边的长度c^2 = a^2 + b^2 - 2ab * cos(C)，代入已知的值计算得到c^2 = 9 + b^2 - 2 * 3b * cos(35.26)，进一步简化为b^2 - 6b * cos(35.26) + 4 = 0。

然后解一元二次方程得到b的值，从而求得另一直角边的长度。

任意三角形三角函数公式

任意三角形三角函数公式一、正弦定理正弦定理是三角形中的重要定理之一，它描述了三角形的边长和角度之间的关系。

在任意三角形ABC中，我们可以用正弦定理来表示三角形的边长和角度之间的关系。

正弦定理的数学表达式为：a/sinA = b/sinB = c/sinC其中a、b、c分别表示三角形ABC的三边的长度，A、B、C表示对应的角度。

通过正弦定理，我们可以计算出三角形中任意一个角的正弦值，从而进一步计算出三角形的边长。

二、余弦定理余弦定理是三角形中的另一个重要定理，它描述了三角形的边长和角度之间的关系。

在任意三角形ABC中，我们可以用余弦定理来表示三角形的边长和角度之间的关系。

余弦定理的数学表达式为：c^2 = a^2 + b^2 - 2abcosC其中a、b、c分别表示三角形ABC的三边的长度，C表示对应的角度。

通过余弦定理，我们可以计算出三角形中任意一个角的余弦值，从而进一步计算出三角形的边长。

三、正切定理正切定理是三角形中的另一个重要定理，它描述了三角形的边长和角度之间的关系。

在任意三角形ABC中，我们可以用正切定理来表示三角形的边长和角度之间的关系。

正切定理的数学表达式为：tanA = a/b其中a、b分别表示三角形ABC的两边的长度，A表示对应的角度。

通过正切定理，我们可以计算出三角形中任意一个角的正切值，从而进一步计算出三角形的边长。

正弦定理、余弦定理和正切定理是三角形中常用的三角函数公式。

它们描述了三角形中边长和角度之间的关系，可以方便地计算三角形的边长和角度。

在实际应用中，这些三角函数公式被广泛运用于测量、导航、建筑等领域。

通过测量三角形的边长和角度，我们可以确定物体的位置、测量距离、计算高度等。

这些三角函数公式为我们提供了一个强大的工具，帮助我们解决实际问题。

正弦定理、余弦定理和正切定理是解决三角形问题的重要工具。

它们通过三角函数的关系，将三角形的边长和角度联系起来，为我们提供了便捷的计算方法。

三角函数公式万能公式

三角函数公式万能公式三角函数有六个主要的函数，分别是正弦函数（sin）、余弦函数（cos）、正切函数（tan）、余切函数（cot）、正割函数（sec）和余割函数（csc）。

这些函数之间存在着一系列的关系和公式。

1.万能公式之正弦定理：正弦定理用于计算非直角三角形的边与角之间的关系。

假设ABC是一个非直角三角形，a、b、c分别为边BC、AC、AB的长度，α、β、γ分别为对应边的对角。

则正弦定理可以表示为：sinα/a = sinβ/b = sinγ/c根据这个公式，我们可以通过已知的边长和角度来计算三角形中的其他边长和角度。

2.万能公式之余弦定理：余弦定理用于计算非直角三角形的边和角之间的关系。

假设ABC是一个非直角三角形，a、b、c分别为边BC、AC和AB的长度，α、β、γ分别为对应边的对角。

则余弦定理可以表示为：c^2 = a^2 + b^2 - 2ab*cosγ根据这个公式，我们可以通过已知的边长和角度来计算三角形中的其他边长和角度。

3.万能公式之正切定理：正切函数用于计算直角三角形的边与角之间的关系。

在一个直角三角形ABC中，A为直角，a、b、c分别为边BC、AC和AB的长度，α、β、γ分别为其他两个角。

则正切定理可以表示为：tanα = a/b这个公式可以帮助我们通过已知的边长和角度来计算三角形中的其他边长和角度。

4.万能公式之勾股定理：勾股定理用于计算直角三角形中的边之间的关系。

假设ABC是一个直角三角形，A为直角，a、b、c分别为边BC、AC和AB的长度。

勾股定理可以表示为：c^2=a^2+b^2根据这个公式，我们可以通过已知的边长来计算直角三角形中的其他边长。

5.万能公式之三角恒等式：三角函数还有许多重要的恒等式，这些恒等式为计算和简化三角函数的值提供了便利。

其中一些常见的三角恒等式包括：sin^2θ + cos^2θ = 11 + tan^2θ = sec^2θ1 + cot^2θ = csc^2θsin2θ = 2sinθcosθcos2θ = cos^2θ - sin^2θtan2θ = (2tanθ) / (1 - tan^2θ)这些恒等式可以用来简化复杂的三角函数表达式，以及推导其他三角函数的值和关系。

三角形公式大全

三角形面积公式：三角形的面积等于底边乘以高再除以2，即S=（1/2）bh，其中b是底边长，h是高。

直角三角形勾股定理：直角三角形的两条直角边的平方和等于斜边的平方，即a²+b²=c²，其中a、b是直角边，c是斜边。

三角形余弦定理：三角形中任意一边的平方等于另外两边平方和减去这两边的乘积与这两边对应角的余弦值的积的两倍，即c²=a²+b²-2ab cos C，其中a、b为已知边，c为未知边，C为已知夹角。

三角形正弦定理：三角形中任意一条边的长度与这条边对应的角的正弦值成比例，即a/sin A = b/sin B = c/sin C，其中a、b、c分别为三角形的边长，A、B、C分别为对应的角度。

三角形余弦定理的变形：可以通过将余弦定理公式变形得到另外两个公式：a²=b²+c²-2bc cos A，b²=a²+c²-2ac cos B。

海伦公式：已知三角形的三边长a、b、c，可以通过海伦公式求出三角形面积，即S=√[s（s-a）（s-b）（s-c）]，其中s=（a+b+c）/2为三角形半周长。

内心公式：三角形内心到三边的距离分别为r₁、r₂、r₃，三角形的面积为S，则有S=r₁s=r₂s=r₃s，其中s=（a+b+c）/2为半周长。

外心公式：三角形外接圆半径R等于三边长度的乘积除以4倍三角形面积，即R=abc/4S。

这些公式可以帮助我们计算三角形的各种属性，如面积、边长、角度等。

三角形的余弦定理与正弦定理

三角形的余弦定理与正弦定理三角形是几何学中最基本的形状之一。

在研究三角形的性质和特征时，余弦定理和正弦定理起到了重要的作用。

它们是利用三角形的边长和角度之间的关系来解决各种三角形问题的工具。

本文将详细介绍三角形的余弦定理与正弦定理的定义、公式推导和应用。

一、余弦定理余弦定理是描述三角形边长与角度关系的定理。

对于任意三角形ABC，假设a、b、c分别表示BC、AC和AB的边长，而∠A、∠B和∠C分别表示三角形的内角A、B和C，则余弦定理可以表示为以下公式：c² = a² + b² - 2ab·cosCb² = a² + c² - 2ac·cosBa² = b² + c² - 2bc·cosA其中，cosA、cosB和cosC分别表示角A、B和C的余弦值。

推导过程：我们可以通过向三角形ABC引入高，再利用勾股定理和直角三角形的性质推导余弦定理。

设三角形ABC的高为h，起点为顶点A，终点为D，连接BD和CD，如图所示。

[图示]由于三角形ADC为直角三角形，根据勾股定理，我们可以得到：AC² = AD² + CD² ------ (1)在三角形ABD中，我们可以应用勾股定理得到：AB² = AD² + BD² ------ (2)注意到BD = BC - CD，将其代入式(2)，我们可以得到：AB² = AD² + (BC - CD)²= AD² + BC² + CD² - 2BC·CD ------ (3)由于三角形ABC为平面图形，AD ⊥ BC，所以∠ADC = ∠C。

根据余弦定理，我们可以得到：CD² = AC² + AD² - 2AC·AD·cosC ------ (4)将式(1)代入式(4)，我们可以得到：CD² = (AD² + CD²) + AD² - 2√(AD² + CD²)√AD·cosC= 2AD² + CD² - 2AD·CD·cosC将式(4)代入式(3)，我们可以得到：AB² = 2AD² + BC² - 2BC·CD + 2AD² - 2√(AD² + CD²)√AD·cosC= 4AD² + BC² - 2BC·CD - 2√(AD² + CD²)√AD·cosC= 4AD² + BC² - 2BC·CD - 2AC·AD·cosC由于三角形为平面图形，所以CD = BC·cosA，代入上式得：AB² = 4AD² + BC² - 2BC²·cosA - 2AC·AD·cosC= 4AD² + BC² - 2BC²·cosA - 2AC²·cosC= 4AD² + BC² - 2AC²·cosC - 2BC²·cosA由几何性质可知，4AD² = c²，所以：c² = a² + b² - 2ab·cosC ------ (5)同理，可以推导出余弦定理的其他两个公式。

正余弦定理公式

正余弦定理公式
正余弦定理是一种几何定理，它可以用来解决三角形的角度和边长之间的关系。

它最初由古希腊数学家和哲学家尼古拉斯·斯卡拉特斯（Nicolas Scarf）发现，并于十六世纪被瓦特里克（Watirik）提出。

正余弦定理是三角形中最重要的定理之一，它可以用来求解三角形的角度和边长之间的关系，从而为三角形的解决提供帮助。

正余弦定理有以下公式：
a^2=b^2+c^2-2bc*cosA
b^2=a^2+c^2-2ac*cosB
c^2=a^2+b^2-2ab*cosC
公式中，a，b，c分别表示三角形的三条边，A，B，C表示三角形的三个内角。

正余弦定理的用途极其广泛，它可以用来求解三角形的角度和边长之间的关系，这可以用来解决一些涉及三角形的问题。

例如，如果已知三角形的三条边，可以使用正余弦定理来求解三角形的三个内角；如果已知三角形的三个内角，可以使用正余弦定理来求解三角形的三条边。

正余弦定理还可以用来解决三角形的面积、外角和其他一些问题。

正余弦定理的应用非常广泛，它不仅在几何方面有着重要的作用，而且在物理、化学、天文、地理等许多学科中也有着重要的作用。

正余弦定理的发现和应用为这些学科的发展做出了重要贡献，使许多复杂的问题得到解决，为研究三角形提供了帮助，为科学技术的进步做出了重要贡献。

正余弦定理公式大全

正余弦定理公式大全正弦定理和余弦定理是解三角形问题时常用到的两个重要定理，它们可以帮助我们求解三角形的边长和角度，解决各种实际问题。

下面我们将详细介绍正弦定理和余弦定理的公式及应用。

首先，我们来看正弦定理。

对于任意三角形ABC，其三条边分别为a，b，c，对应的角分别为A，B，C。

正弦定理可以表示为：a/sinA = b/sinB = c/sinC。

其中，a/sinA = b/sinB = c/sinC这个比值关系被称为正弦定理的比值形式。

正弦定理告诉我们，一个三角形的每条边与其对立角的正弦值之比是相等的。

这个定理可以帮助我们求解三角形的边长和角度，应用非常广泛。

接下来，我们来看余弦定理。

对于任意三角形ABC，其三条边分别为a，b，c，对应的角分别为A，B，C。

余弦定理可以表示为：a^2 = b^2 + c^2 2bccosA。

b^2 = a^2 + c^2 2accosB。

c^2 = a^2 + b^2 2abcosC。

余弦定理告诉我们，一个三角形的每条边的平方与其余两条边的平方之差与对应的角的余弦值之积是相等的。

这个定理同样可以帮助我们求解三角形的边长和角度，解决各种实际问题。

在实际问题中，我们可以根据具体情况选择使用正弦定理或余弦定理来求解三角形的边长和角度。

在使用正弦定理和余弦定理时，我们需要注意角度的单位，通常情况下我们使用弧度制来计算。

在求解问题时，我们可以根据已知条件，利用正弦定理和余弦定理建立方程，然后求解方程，得到未知量的值。

在使用正弦定理和余弦定理时，我们需要注意角度的对应关系，确保计算结果的准确性。

总之，正弦定理和余弦定理是解三角形问题时常用到的两个重要定理，它们可以帮助我们求解三角形的边长和角度，解决各种实际问题。

希望本文介绍的正弦定理和余弦定理的公式及应用对您有所帮助。

余弦定理与正弦定理

余弦定理与正弦定理余弦定理和正弦定理是解决三角形中边长和角度之间关系的重要定理。

它们在三角学中有着广泛的应用，能够帮助我们计算未知边长或角度。

本文将介绍余弦定理和正弦定理的定义、公式以及应用，并探讨它们的区别和联系。

一、余弦定理的定义和公式余弦定理是在三角形中，通过已知边长和夹角计算其他边长的定理。

它的定义如下：在三角形ABC中，设三条边分别为a、b、c，对应的夹角分别为A、B、C，则余弦定理的公式为：c² = a² + b² - 2abcosC其中，c为三角形对应于角C的边长，a和b为与角C相邻的两条边长，cosC为角C的余弦值。

二、正弦定理的定义和公式正弦定理是在三角形中，通过已知两个角度和一个边长计算其他边长的定理。

它的定义如下：在三角形ABC中，设三条边分别为a、b、c，对应的夹角分别为A、B、C，则正弦定理的公式为：a/sinA = b/sinB = c/sinC其中，a、b、c为三角形的边长，A、B、C为对应的角度。

三、余弦定理和正弦定理的应用1. 通过余弦定理计算未知边长或角度：- 已知两边长和夹角：可以使用余弦定理计算第三条边长，或者计算其他两个角度。

- 已知三边长：可以使用余弦定理计算其中一个角度。

2. 通过正弦定理计算未知边长或角度：- 已知两角度和一个边长：可以使用正弦定理计算其他两条边长。

- 已知一个角度和两边长：可以使用正弦定理计算另外两个角度。

四、余弦定理与正弦定理的区别和联系余弦定理和正弦定理在解决三角形问题时具有不同的应用场景。

余弦定理适用于已知边长和夹角的情况，可以求解缺失的边长或角度。

而正弦定理适用于已知两个角度和一个边长的情况，同样可以求解其他边长或角度。

此外，两个定理之间也存在一定的联系。

通过余弦定理可以推导出正弦定理，而正弦定理也可以推导出余弦定理。

在解决问题时，可以根据具体情况选择使用其中一个定理进行计算。

总结：余弦定理和正弦定理是解决三角形中边长和角度之间关系的重要定理。

正弦余弦正切关系公式

正弦余弦正切关系公式正弦余弦正切关系公式_____________________________在数学中，正弦余弦正切关系公式是指三角函数的关系，这三个函数之间有着密切的联系，也叫作余弦定理或者余弦公式。

正弦余弦正切关系公式是数学中最基本的定理之一，它可以帮助我们计算出三角函数和三角形之间的关系。

一、正弦余弦正切关系1.正弦定理：正弦定理指的是一个三角形的两个直角边的长度和对边的长度之间的关系。

它表示对边的长度和两个直角边的长度成正比，即：a/sinA=b/sinB=c/sinC。

2.余弦定理：余弦定理也叫作余弦公式，它指的是一个三角形的三条边之间的关系。

它表明了三条边之间的关系，即：a^2=b^2+c^2-2bc*cosA，b^2=a^2+c^2-2ac*cosB，c^2=a^2+b^2-2ab*cosC。

3.正切定理：正切定理是指一个三角形的对边和两个直角边之间的关系，即：tanA=a/b,tanB=b/c,tanC=c/a。

二、推导过程以上面三条定理都可以通过推导求出，下面就以求出余弦定理为例，来说明推导过程。

1.假设有一个三角形ABC，其中AB=a,BC=b,CA=c。

2.根据余弦定理，可以得出A=cosA=(b^2+c^2-a^2)/2bc。

3.将A代入余弦函数，即得到cosA=(b^2+c^2-a^2)/2bc。

4.将上面得到的等式乘以2bc,即得到b^2+c^2-a^2=2bc*cosA。

5.将上面得到的等式再乘以-1,即得到a^2=b^2+c^2-2bc*cosA,这就是余弦定理。

三、应用场景正弦余弦正切关系公式在数学中有着广泛的应用。

它可以用来计算三角函数和三角形之间的关系，也可以用来求解一些复杂的问题。

此外，它还可以用来解决物理方面的问题，比如流体力学、电磁学以及重力加速度等问题。

四、总结总之，正弦余弦正切关系公式是数学中最基本的定理之一，它可以帮助我们求出三角函数和三角形之间的关系，也可以用来解决物理方面的问题。

正余弦定理三角形一些公式

1 / 1 正弦定理：在一个三角形中，各边和它所对角的正弦的比相等，即 R c C R b B R a A C R c B R b AR a R R Cc B b A a 2sin 2sin 2sin sin 2sin 2sin 2)(2sin sin sin =========变形有：为外接圆的半径三角形的面积公式：A bcB acC ab S ABC sin 21sin 21sin 21===∆余弦定理：三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍。

即ab c b a C ac b c a B bca cb A C ab b ac B ac c a b Abc c b a 2cos 2cos 2cos cos 2cos 2cos 2222222222222222222-+=-+=-+=-+=-+=-+=变形有：判断三角形的形状：为锐角三角形，为直角角三角形为钝角三角形ABC b a c c a b c b a ABC c b a ABC c b a ∆+<+<+<∆+=∆+>222222222222222,,三角形中有：形为正三角形成等比数列，则该三角、、成等差数列，、、）若（）（中c b a C B A CB AC B A C B A ABC 2tan )tan(cos )cos(sin )sin(1-=+-=+=+∆两角和差的正余弦公式及两角和差正切公式 ()βαβαβαsin cos cos sin sin -=- ()βαβαβαsin cos cos sin sin +=+cos()cos cos sin sin αβαβαβ-=+ ()cos cos cos sin sin αβαβαβ+=-()βαβαβαtan tan 1tan tan tan +-=- ()tan tan tan 1tan tan αβαβαβ++=- 二倍角公式： ααααββααααα22222tan 1tan 22tan 1cos 2sin 21sin cos 2cos cos sin 22sin -=-=-=-==半角公式：。

几何中的正弦定理与余弦定理

几何中的正弦定理与余弦定理几何学是一门研究空间和形状的学科，其中涉及到许多重要的定理和公式。

正弦定理和余弦定理是几何学中两个基础而重要的定理，它们在解决三角形的边长和角度方面起着至关重要的作用。

一、正弦定理正弦定理是指在一个任意三角形中，三条边与其对应的角之间的关系。

根据正弦定理，我们可以得到以下公式：a/sin A = b/sin B = c/sin C其中，a、b和c分别代表三角形的三条边的长度，A、B和C分别代表三角形的三个对应角的度数。

通过正弦定理，我们可以求解一个未知边长或未知角度，只需知道其他两条边长或角度即可。

例如，当我们知道三角形的两条边长a和b，以及它们夹角C的度数，我们可以利用正弦定理计算第三条边c的长度：c = (sin C * a) / sin B通过正弦定理，我们可以方便地解决一些与三角形相关的几何问题，比如寻找缺失的边长或角度。

二、余弦定理余弦定理是描述一个三角形中的边长和角度之间的关系。

与正弦定理类似，余弦定理也是解决三角形问题的重要工具。

根据余弦定理，我们可以得到以下公式：c^2 = a^2 + b^2 - 2abcos C其中，a、b和c分别代表三角形的三条边的长度，C代表三角形的夹角的度数。

通过余弦定理，我们可以求解一个未知边长或未知角度，只需知道其他两条边长或角度即可。

例如，当我们知道三角形的两条边长a和b，以及它们夹角C的度数，我们可以利用余弦定理计算第三条边c的长度：c = √(a^2 + b^2 - 2abcos C)除了求解边长，余弦定理也可以用来求解角度。

例如，当我们已知三角形的三条边长a、b和c时，我们可以利用余弦定理求解夹角A的余弦值：cos A = (b^2 + c^2 - a^2) / 2bc通过计算余弦值的反函数，我们可以得到夹角A的度数。

综上所述，正弦定理和余弦定理是解决几何学中三角形问题的重要工具。

它们可以帮助我们计算未知的边长和角度，解决各种与三角形相关的几何问题。

(完整版)正弦定理、余弦定理知识点

正弦定理、余弦定理讲师：王光明【基础知识点】1. 三角形常用公式：A ＋B ＋C ＝π；S ＝ab sin C ＝bc sin A ＝＝ca sin B ；2121212．三角形中的边角不等关系: A>B a>b,a+b>c,a-b<c ；；⇔3．【正弦定理】：＝＝＝2R （外接圆直径）；A a sin B b sin Ccsin 正弦定理的变式：； a ∶b ∶c ＝sin A ∶sin B ∶sin C ．⎪⎩⎪⎨⎧===C R c B R b AR a sin 2sin 2sin 24．正弦定理应用范围： ①已知两角和任一边，求其他两边及一角． ②已知两边和其中一边对角，求另一边的对角．③几何作图时，存在多种情况．如已知a 、b 及A ，求作三角形时，要分类讨论，确定解的个数．已知两边和其中一边的对角解三角形，有如下的情况：(1)A 为锐角AABa=bsin A bsin A<a<b a b ≥ 一解两解一解(2)A 为锐角或钝角当时有一解.a>b 5．【余弦定理】　a 2=b 2+c 2-2bccosA ．c 2=a 2+b 2-2abcosC ．b 2=a 2+c 2-2accosB ．若用三边表示角，余弦定理可以写为、6．余弦定理应用范围：（1）已知三角形的三条边长，可求出三个内角；（2）已知三角形的两边及夹角，可求出第三边．【习题知识点】知识点1　运用判断三角形形状例题1在△ABC 中已知acosB=bcosA,试判断△ABC 的形状.【分析】利用正弦定理或余弦定理判断三角形形状,可以将三角形中的边用角表示,也可将角用边来表示．从中找到三角形中的边角关系，判断出三角形的形状.【解析】解法1：由扩充的正弦定理：代入已知式2RsinAcosB=2RsinBcosAsinAcosB-cosAsinB=0 ， sin(A-B)=0A-B=0 ∴A=B 即△ABC 为等腰三角形解法2:由余弦定理: 22222222bc a c b b ac b c a a -+⋅=-+⋅ 22b a = ∴ b a =即△ABC 为等腰三角形.知识点2 运用正、余弦定理解三角形解三角形问题中正、余弦定理的选择:(1)在下述情况下应首先使用余弦定理: ①已知三条边(边边边),求三个角;②已知两边和它们的夹角(边角边),求其它一边和两角;(2)在下述情况下应首先使用正弦定理:①已知两边和一边的对角(边边角),求其它一边和两角;②已知两角和任一边(角角边、角边角),求其它两边和一角.例题2　在△ABC 中，已知，，B=45︒ 求A 、C 及c .3=a 2=b 【分析】在解斜三角形应用过程中，注意要灵活地选择正弦定和余弦定理，解得其它的边和角【解析】解法1：由正弦定理得：23245sin 3sin sin === b B a A ∵B=45︒<90︒ 即b <a ∴A=60︒或120︒当A=60︒时C=75︒ 22645sin 75sin 2sin sin +===BCb c当A=120︒时C=15︒ 22645sin 15sin 2sin sin -===B C b c 解法2：设c =x 由余弦定理将已知条件代入，整理：解之：B ac c a b cos 2222-+=0162=+-x x 226±=x 当时从而A=60︒ ，C=75︒226+=c 2)13(231226223)226(22cos 22221=++=+⋅⋅-++=-+=bc a c b A 当时同理可求得：A=120︒ C=15︒.226-=c 知识点3 解决与三角形在关的证明、计算问题例题3 已知A 、B 、C 为锐角，tanA=1，tanB=2，tanC=3，求A+B+C 的值．　【分析】本题是要求角，要求角先要求出这个角的某一个三角函数值，再根据角的范围确定角．本题应先求出A+B 和C 的正切值，再一次运用两角和的正切公式求出A+B+C ．【解析】 A B C 、、为锐角∴<++<0270°°A B C 又，，由公式可得tan tan A B ==12tan()tan tan tan tan A B A B A B +=+-⋅=+-=-112123[]tan()tan ()A B C A B C ++=++=++-+⋅tan()tan tan()tan A B C A B C 1 =-+--⨯33133() =0所以A+B+C=π知识点4 求三角形的面积例题4 △ABC 中，D 在边BC 上，且BD ＝2，DC ＝1，∠B ＝60o ，∠ADC ＝150o ，求AC 的长及△ABC 的面积．【解析】在△ABC 中，∠BAD ＝150o －60o ＝90o ，∴AD ＝2sin60o ＝3．A在△ACD 中，AD 2＝(3)2＋12－2×3×1×cos150o ＝7，∴AC ＝7． ∴AB ＝2cos60o ＝1．S △ABC ＝21×1×3×sin60o ＝343．知识点4 解决实际为题例题4 如图，海中有一小岛，周围3.8海里内有暗礁。

正弦定理余弦定理

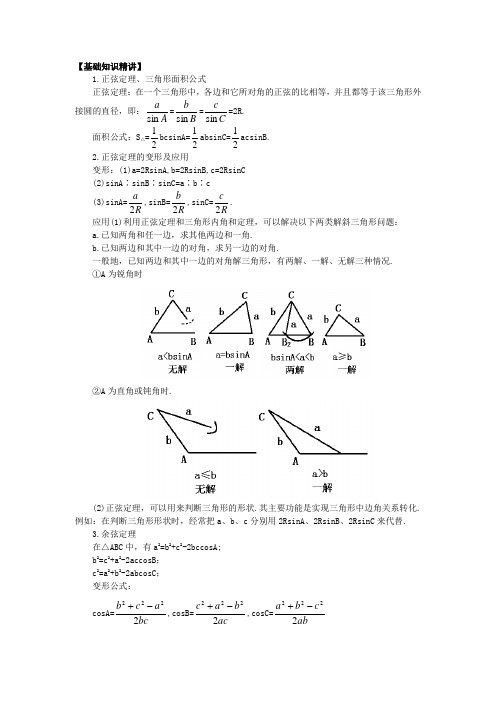
【基础知识精讲】1.正弦定理、三角形面积公式正弦定理：在一个三角形中，各边和它所对角的正弦的比相等，并且都等于该三角形外接圆的直径，即：A a sin =B b sin =C csin =2R. 面积公式：S △=21bcsinA=21absinC=21acsinB.2.正弦定理的变形及应用变形：(1)a=2RsinA,b=2RsinB,c=2RsinC (2)sinA ∶sinB ∶sinC=a ∶b ∶c (3)sinA=R a 2,sinB=R b 2,sinC=Rc 2. 应用(1)利用正弦定理和三角形内角和定理，可以解决以下两类解斜三角形问题：a.已知两角和任一边，求其他两边和一角.b.已知两边和其中一边的对角，求另一边的对角.一般地，已知两边和其中一边的对角解三角形，有两解、一解、无解三种情况. ①A 为锐角时②A 为直角或钝角时.(2)正弦定理，可以用来判断三角形的形状.其主要功能是实现三角形中边角关系转化.例如：在判断三角形形状时，经常把a 、b 、c 分别用2RsinA 、2RsinB 、2RsinC 来代替.3.余弦定理在△ABC 中，有a 2=b 2+c 2-2bccosA; b 2=c 2+a 2-2accosB ； c 2=a 2+b 2-2abcosC ；变形公式：cosA=bc a c b 2222-+,cosB=ac b a c 2222-+,cosC=abc b a 2222-+在三角形中，我们把三条边(a 、b 、c)和三个内角(A 、B 、C)称为六个基本元素，只要已知其中的三个元素(至少一个是边)，便可以求出其余的三个未知元素(可能有两解、一解、无解)，这个过程叫做解三角形，余弦定理的主要作用是解斜三角形.4.解三角形问题时，须注意的三角关系式：A+B+C=π 0＜A ，B ，C ＜πsin2B A +=sin 2C -π=cos 2Csin(A+B)=sinC特别地，在锐角三角形中，sinA ＜cosB,sinB ＜cosC,sinC ＜cosA.【重点难点解析】掌握正、余弦定理，并学会用其余弦定理解三角形.例1 在△ABC 中，已知A ＞B ＞C ，且A=2C,b=4,a+c=8，求a 、c 的长.解：由正弦定理A a sin =C c sin 及A=2C 得C a 2sin =C c sin ,即C C a cos sin 2=Ccsin , ∴cosC=ca 2. 由已知a+c=8=2b 及余弦定理，得cosC=abcb a 2222-+=)()2(222c a a c c a a +-++ =)(4))(35(c a a c a c a ++-=a ca 435-.∴ca 2=a ca 435-，整理得(2a-3c)(a-c)=0∴a ≠c,∴2a=3c. ∵a+c=8,∴a=524,c=516. 例2 在△ABC 中，如果lga-lgc=lgsinB=-lg 2，且B 为锐角，试判断此三角形的形状.解：∵lga-lgc=lgsinB=-lg 2,∴sinB=22 又∵0°＜B ＜90°，∴B=45° 由lga-lgc=-lg 2,得c a = 22. 由正弦定理得c A sin sin = 22.即2sin(135°-C)= 2sinC即2［sin135°cosC-cos135°sinC ］=2sinC.∴cosC=0,得C=90° 又∵A=45°,∴B=45°从而△ABC 是等腰直角三角形.例3 如图已知：平行四边形两邻边长为a 和b(a ＜b)，两对角线的一个交角为θ(0°＜θ＜90°)，求该平行四边形的面积.分析：由于已知了平行四边形相邻两边长和对角线的一个交角，再考虑到平行四边形的面积是△AOB 的四倍，因此只要求OA ·OB ·sin θ即可.解：设平行四边形ABCD 的对角线AC 与BD 相交于O.AB=a,BC=b,∠AOB=θ，又设OA=x,OB=y.在△AOB 中，应用余弦定理可得： a 2=x 2+y 2-2xycos θ ① 在△BOC 中，应用余弦定理可得： b 2=x 2+y 2-2xycos(180°-θ) ② 由②-①得： b 2-a 2=4xycos θ∵0°＜θ＜90°，∴xy=θcos 422a b - (b ＞a)∴S □=4S △AOB =2xysin θ=222b a -tan θ例4 在△ABC 中，已知4sinBsinC=1,b 2+c 2-a 2=bc,且B ＞C ，求A 、B 、C.分析：由于题设条件b 2+c 2-a 2=bc 十分特殊，将它与余弦定理对照可得A=60°,这样B+C=120°，于是再利用条件4sinBsinC=1，可求得B 与C.解：由余弦定理cosA=bca c a 2222-+=bc bc 2=21.又∵0°＜A ＜180°∴A=60°∴B+C=120°,又由于4sinBsinC=1 ∴4sinBsin(120°-B)=1 ∴4sinB(23cosB+21sinB)=1∴3sin2B+2sin 2B=1 ∴3sin2B=cos2B∴tan2B=33,∴2B=30°或2B=210°由于B+C=120°,且B ＞C ，60°＜B ＜120° ∴2B=210°,∴B=105°,从而C=15° ∴A=60°,B=105°,C=15°例5 已知△ABC 中，a ，b ，c 为角A ，B ，C 的对边，且a+c=2b ，A-C=3π,求sinB 的值. 解法一：由正弦定理和已知条件a+c=2b ，得sinA+sinC=2sinB ，由和差化积公式得 2sin2C A +·cos 2CA -=2sinB 由A+B+C=π，得 sin2C A +=cos 2B 又A-C=3π,得 23cos 2B =sinB∴23cos 2B =2sin 2B ·cos 2B又∵0＜2B ＜2π,cos 2B≠0 ∴sin2B =43 从而cos2B =2sin 12B -=413 ∴sinB=23·413 =839. 解法二：由正弦定理和已知条件a+c=2b ，得sinA+sinC=2sinB∵A-C=3π,A+B+C=π 两式相减可得B=32π-2C∴sin(3π+C)+sinC=2sinB 得sin 3πcosC+cos 3πsinC+sinC=2sinB∴23cosC+23sinC=2sinB即3cos(3π-C)=2sinB ∴3cos 2B =4sin 2B ·cos 2B∵0＜B ＜π,∴cos 2B≠0∴sin2B =43 cos2B =2sin 12B -=413 ∴sinB=23·cosB=839【难题巧解点拔】例1 △ABC 中，若a=5,b=4,cos(A-B)=3231，求AB. 分析：很明显，只要求cosC 的值，应用余弦定理即可求出AB. 解法一：由已知条件a=5,b=4b a b a -+=B A B A sin sin sin sin -+=2sin2cos 2cos2sinB A B A BA B A -+-+=9，①由已知cos(A-B)= 3231,根据半角公式有sin2B A +=2)cos(1B A --=81,cos 2B A -=2)cos(1B A -+=863代入①式得tg2B A +=639∵tg 2B A +=ctg 2C , ∴tg2C = 963,根据万能公式cosC=81∴c 2=a 2+b 2-2abcosC=36,AB=c=6解法二：∵A ＞B ，如图，作∠BAD=∠B,∴AD=BD∠CAD=∠A-∠B 令AD=BD=y,CD=x,由余弦定理cos(A-B)=boyx y b 2222-+= 3231,x=a-y,∴yy 8910-= 3231,y=4,x=1 △CAD 中再由余弦定理cosC=81,∴c=6 评析：上述解法反映边向角的转化，也可由角向边转化直接求出边.例2 半圆O 的直径为2，A 为直径延长线上的一点，且OA=2，B 为半圆周上任意一点以AB 为边向形外作等边三角形ABC(如图)，问B 点在什么位置时，边形OACB 的面积最大，并求出这个最大面积.解：设∠AOB=x ，则 S △AOB =21·2·1·sinx=sinx, AB 2=OA 2+OB 2-2·OA ·OB ·cosx=5-4cosx. S △ABC =43AB 2=43 (5-4cosx)= 45-3cosx ∴S OACB =S △AOB +S △ABC=sinx-3cosx+435 =2sin(x-3π)+435 ∵0＜x ＜π,-3π＜x-3π＜32π ∴x-3π=2π时，∴即x=65π时,S OACB 有最大值2+435(平方单位) 例3 已知△ABC 中，AB=AC=a,∠BAC=φ，等边三角形PQR 的三边分别通过A ，B ，C 三点.试求△PQR 的面积的最大值.分析：先依题意画出图形(如图).因为变动三角形PQR 为正三角形，它的面积S=43PQ 2，问题可转化为求边长PQ 的最大值.为此需要建立PQ 的函数式，这又必须选取适当的量作为自变量.观察图形可以发现，PQ 的位置是随着∠PAB 的大小变化而变化的.不妨就以∠PAB 为自变量.以下的程序就是应用三角形的边角关系，求出以∠PAB 的三角函数表示PQ 的解析式，最后求它的最大值.解：设∠PAB=x,那么∠PBA=120°-x,∠QAC=180°-x-φ，∠QCA=x+φ-60°.在△PAB 中，∵)120sin(x PA-︒=︒60sin AB ，∴PA=32a sin(120°-x),在△AQC 中，)60sin(︒-Φ+x AQ=︒60sin AC∴AQ=32a sin(x+φ-60°)∴PQ=PA+AQ=32a ［sin(120°-x)+sin(x+φ-60°)=34a sin(2Φ+30°)cos(90°-2Φ-x). 因为其中a,2Φ+30°都是常量，所以当90°-2Φ-x=0即x=90°-2Φ时，取得 (PQ)max =34a sin(2Φ+30°) 同时也就取得了 (S △)max =43 (PQ)2max=334a 2sin 2(2Φ+30°)例4 在△ABC 中，已知A=2C ，求证：3b ＜c-a ＜2b.证明：在△ABC 中，由A=2C ，得C=2A ，∴B=π-3A,∴0＜A ＜3πb ac - =B A C sin sin sin -=)sin(sin sin C A A C +-=2cos2sin 2sin2cos 2C A C A A C A C ++-+ =23sin 2sin A =2sin 2cos 2sin 42sin2A A A A -=12cos 412-A =1cos 21+A .∵0＜A ＜3π，∴21＜cosA ＜1，即2＜2cosA+1＜3∴31＜b a c -＜21,故3b ＜c-a ＜2b.评析：解本题的关键是利用正弦定理及三角公式将b a c -转化为1cos 21+A ，结合角A的取值范围推得结论.【课本难题解答】课本第132页，习题5.9第8题：｜F ｜≈132N ，β≈38° 第9题两条对角线的长分别是415cm 和43cm,面积是48cm 2.【命题趋势分析】本节主要考查：1.根据已知条件，求三角形的末知元素，或判断三角形的形状. 2.运用正、余弦定理及关系式A+B+C=π解决三角形中的计算和证明问题. 3.利用所学的三角知识解决与三角形有关的三角函数问题和简单的实际问题. 根据考试的方向，可以预见，利用正、余弦定理解斜三角形问题将会与三角函数、数列、方程、向量等知识相结合，尤其是与生活、生产、科学实验实际相结合，考查综合运用数学知识的能力.【典型热点考题】例1 在△ABC 中，a ，b ，c 分别是角A 、B 、C 的对边，设a+c=b ，A-C=3π，求sinB 的值.解：根据正弦定理和已知可得：sinA+sinC=2sinB,A+B+C=π 则2sin2C A +·cos 2CA -=2sinB.又A-C=3π,sin 2C A -=cos 2B∴2cos 2B cos 6π=2sinB=4sin 2B cos 2B又∵0＜2B ＜2π∴sin2B =43 cos2B =2sin 12B -= 413 ∴sinB=2·413·43=839例2 若△ABC 的三个内角A 、B 、C 成等差数列，且最大边为最小边的2倍，则三内角之比为 .解：设三角形三内角从小到大依次为B-d,B,B+d, 则B-d+B+B+d=180°∴B=60° 设最小边为x ，则最大边为2x,从而)60sin(d x -︒=)60sin(2d x +︒⇒tand=33,d=30° 所以三内角分别为A=30°,B=60°,C=90°,得三内角之比为1∶2∶3. ∴应填1∶2∶3.例3 在△ABC 中，A 、B 、C 三顶点所对边分别为a,b,c ，试证明b 2=c 2+a 2-2accosB.证明：因为=+则有：2=·=(+)·(+)=2+2+2·=AB 2+BC 2+2｜AB ｜·｜BC ｜cos(180°-B)=c 2+a 2-2accosB 所以b 2=c 2+a 2-2ac ·cosB例4 求sin 220°+cos 280°+3sin20cos80°的值.解：设△ABC 中的A=10°,B=20°,C=150°对应边分别为a,b,c. △ABC 的外接圆半径为2R ，则由正弦定理得： a=2Rsin10°,b=2Rsin20°,c=2Rsin150° 由余弦定理，得：(2Rsin150°)2=(2Rsin10°)2+(2Rsin20°)2-2(2Rsin10°)(2Rsin20°)cos150°即：sin 2150°=sin 210°+sin 220°+3sin10°sin20°则：cos 280°+sin 220°+3sin20°cos80°=41 说明：本题采用了构造法，题中余弦变正弦之后，注意到3=-2cos(180°-10°-20°).【同步达纲练习】一、选择题1.在△ABC 中，已知a=52,c=10,A=30°，则B 等于( ) A.105°B.60°C.15°D.105°或15°2.在△ABC 中，若b=22,a=2，且三角形有解，则A 的取值范围是( ) A.0°＜A ＜30° B.0°＜A ≤45° A.0°＜A ＜90°D.30°＜A ＜60° 3.在△ABC 中，若2cos A a =2cos B b =2cosC c，则△ABC 的形状是( )A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形4.在△ABC 中，若a=2,b=22,c=6+2，则∠A 的度数是( )A.30°B.45°C.60°D.75°5.设m 、m+1、m+2是钝角三角形的三边长，则实数m 的取值范围是( ) A.0＜m ＜3 B.1＜m ＜3 C.3＜m ＜4 D.4＜m ＜66.在△ABC 中，已知sinA ∶sinB ∶sinC=3∶5∶7,则此三角形的最大内角的度数等于( )A.75°B.120°C.135°D.150°7.△ABC 中，若c=ab b a ++22，则角C 的度数是( ) A.60°B.120°C.60°或120°D.45°8.在△ABC 中，若A=60°,b=16,且此三角形的面积S=2203，则a 的值是( ) A. 2400B.25C.55D.499.在△ABC 中，若acosA=bcosB,则△ABC 是( )A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰三角形或直角三角10.在钝角三角形ABC 中，三边长是连续自然数，则这样的三角形( ) A.不存在 B.有无数多个 C.仅有一个 D.仅有两个二、填空题1.在△ABC 中，A=120°,B=30°,a=8,则c= .2.在△ABC 中，已知a=32,cosC=31,S △ABC =43，则b= . 3.已知锐角三角形边长分别为2、3、x ，则x 的取值范围是 . 4.在△ABC 中，A=60°,b ∶c=8∶5,其内切圆关径r=23,则a= ，b= ,c= .5.在△ABC 中，A=60°,b=1,面积为3，则CB A cb a sin sin sin ++++= .6.在△ABC 中，已知A 、B 、C 成等差数列，且边b=2，则外接圆半径R= .三、解答题1.设三角形三边长分别为15，19，23，现将三边长各缩短x 后，围成一个钝角三角形，求x 的取值范围.2.在△ABC 中，已知它的三边a ，b ，c 成等比数列，试证明：tan 2A tan 2C ≥31.3.已知在△ABC 中，c=22,a ＞b,C=4π,tanA ·tanB=6,试求a,b 以及此三角形的面积.【素质优化训练】1.在△ABC 中，已知a-b=4,a+c=2b ，且最大角为120°，求△ABC 的三边长.2.如图，在60°的∠XAY 内部有一点P ，P 到边AX 的距离是PC=2，P 到边AY 的距离是PB=11，求点P 到顶点A 的距离.3.在△ABC 中，若C=3B ，求bc的取值范围.4.已知△ABC 是钝角三角形，∠B ＞90°,a=2x-5,b=x+1,c=4,求x 的取值范围.5.在△ABC 中，已知cos 2B+cos 2C=1+cos 2A,且sinA=2sinBcosC,cosC=sinB ，求证：b=c 且A=90°.6.在△ABC 中，a,b,c 分别是角A 、B 、C 的对边，若a 2+c 2=2001c 2,求BA Ccot cot cot +的值.【生活实际运用】某人在塔的正东方沿南60°西的道路前进40米后，望见塔在东北方向上，若沿途测得塔的最大仰角为30°，求塔高.解：如图，由题设条件知： ∠CAB=∠1=90°-60°=30°∠ABC=45°-∠1=45°-30°=15° ∴∠ACB=180°-∠BAC-∠ABC =180°-30°-15°=135° 又∵AB=40米.在△ABC 中，由正弦定理知：︒15sin AC =︒135sin 40∴AC=︒︒135sin 15sin 40=402sin(45°-30°)=402 (sin45°cos30°-cos45°sin30°) =402 (22·23-22·21)=20(3-1)在图中，过C 作AB 的垂线，设垂足为E ，则沿AB 测得塔的最大仰角就是∠CED ，∴∠CED=30°.在Rt △ACE 中，EC=AC ·sinBAC=AC ·sin30°=20·(3-1)·21=10(3-1) 在Rt △DCE 中，塔高CD=CE ·tan ∠CED=10(3-1)·tan30°=3)33(10- (米).【知识验证实验】外国船只除特许者外，不得进入离我国海岸线d 海里以内的海域.设B 和C 是我国的两个设在海边的观测站，B 与C 之间的距离为m 海里，海岸线是过B 、C 的直线.一外国船在A 点处，现测得∠ABC=α、∠ACB=β.试求α、β满足什么关系时，就应向示经特许的外国船只A 发出警告?解：如图所示，作AD ⊥BC ，垂足为D ，在△ABC 中，∠BAC=180°-(α+β)∴sin ∠BAC=sin(α+β).由正弦定理得：βsin AB =)sin(βα+BC ,αsin AC =)sin(βα+BC. ∵BC=m ，故有： AB=)sin(sin βαβ+m ,AC=)sin(sin βαα+m由于S △ABC =21BC ·AD=21 m ·AD 且S △ABC =21AB ·AC ·sin(α+β). 所以21)sin(sin βαα+m ·)sin(sin βαβ+m ·sin(α+β)= 21mAD.从而有：AD=)sin(sin sin βαβα+m因此，当AD ≤d,即)sin(sin sin βαβα+m ≤d 时，就应向外国船只A 发出警发.【知识探究学习】如图，在四边形ABCD 中，BC=m,DC=2m,四个内角A 、B 、C 、D 之比为3∶7∶4∶10,试求△ABD 的面积.解：由于四个内角A 、B 、C 、D 比为3∶7∶4∶10，所以可设它们的大小依次为：3x 、7x 、4x 、10x.由四边形的内角和为360°，所以有：3x+7x+4x+10x=360°，可求得：x=15°. 在△BCD 中，由余弦定理得； BD 2 =BC 2+DC 2-2BC ·DC ·cosC.=m 2+(2m)2-2·m ·(2m)cos60° =3m 2∴BD=3m.这时，在△BCD 中，BD 2+BC 2=DC 2,所以△BCD 是直角三角形，DC 是斜边. ∴∠CDB=30°,∠ADB=120°. 在△ABD 中，由正弦定理得：AB=A ADB BD sin sin ∠∙=︒︒45sin 120sin 3m =223m,另外∠ABD=105°-90°=15°,BD=3m.所以S △ADB =21AB ·BD ·sin15°=21·223m ·3m ·sin15° =8239-m 2.参考答案【同步达纲练习】一、1.D 2.B 3.B 4.A 5.B 6.B 7.B 8.C 9.D 10.C二、1.338 2.213 3.(5，13) 4.14，10，16 5. 338 6. 332 三、1.3＜x ＜112.提示可证：a+c ≥2b ，再得sinA+sinC ≥2sinB ，和差化积可得结论3.a=5106,b=558,S △=524【素质优化训练】1.a=14,b=10,c=62.143.1＜b c＜3 4. 310＜x ＜4 5.可求出B=C=45° 6.1000。

正余弦定理三角形的一些公式

正余弦定理三角形的一些公式
正弦定理是三角形的重要定理之一，它表示在任意三角形ABC中，三个角的正弦之比等于对应的边长之比。

具体表达式为：
sin(A)/a = sin(B)/b = sin(C)/c
其中A、B、C为三角形的三个角度，a、b、c为对应的边长。

余弦定理是三角形的另一个重要定理，它表示在任意三角形ABC中，任意一边的平方等于其余两边平方之和减去这两边长度的两倍乘以它们的夹角的余弦值。

具体表达式为：
c² = a² + b² - 2abcosC
其中a、b、c为三角形的边长，C为对应的夹角。

此外，三角形还有许多其他的重要公式，如海伦公式、正弦面积公式等。

海伦公式是用来计算三角形面积的公式，它表示在已知三角形的三个边长a、b、c的情况下，可以通过以下公式计算三角形的面积S：S=√[s(s-a)(s-b)(s-c)]
其中s为半周长，即s=(a+b+c)/2
正弦面积公式是另一种计算三角形面积的公式，它表示在已知三角形的一个角度和对应的边长的情况下，可以通过以下公式计算三角形的面积S：
S = (1/2)absinC
其中a、b为已知的两个边长，C为已知的一个角度。

此外，还有一些与三角形有关的等式公式。

例如，三角形内角和为180度，即A＋B＋C＝180度；三角形的外角和等于360度，即α＋β＋γ＝360度。

以上是关于正余弦定理和三角形的一些公式。

这些公式在解决各种三角形问题时非常重要，能够帮助我们计算三角形的各种属性和关系。

正余弦定理、三角形的一些公式

正弦定理和余弦定理公式

正余弦定理、三角形的一些公式

余弦定理公式大全

三角函数诱导公式正弦定理余弦定理基本公式

立体几何三角函数计算公式

直角三角形的正弦定理与余弦定理

任意三角形三角函数公式

三角函数公式万能公式

三角形公式大全

三角形的余弦定理与正弦定理

正余弦定理公式

正余弦定理公式大全

余弦定理与正弦定理

正弦余弦正切关系公式

正余弦定理三角形一些公式

几何中的正弦定理与余弦定理

(完整版)正弦定理、余弦定理知识点

正弦定理 余弦定理

正余弦定理三角形的一些公式

正弦定理余弦定理