小学奥数几何篇 五大模型——等积变换和共角定理(附答案)
五年级奥数.几何.五大模型(C级).学生版

一、等积模型DC BA①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; ③夹在一组平行线之间的等积变形,如右图ACDBCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.二、共角定理(鸟头定理)两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.:():()ABC ADE S S AB AC AD AE =⨯⨯△△(1)(2)知识框架五大模型(二)(3)(4)三、蝴蝶定理任意四边形中的比例关系(“蝴蝶定理”):①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.S 4S 3S 2S 1O DCBA梯形中比例关系(“梯形蝴蝶定理”): ①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.A BCDO ba S 3S 2S 1S 4四、相似模型(一)金字塔模型 (二) 沙漏模型GF E ABCD AB CDEF G①AD AE DE AFAB AC BC AG===; ②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方; ⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半. 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.五、共边定理(燕尾定理)有一条公共边的三角形叫做共边三角形。
小学奥数几何五大模型.pdf
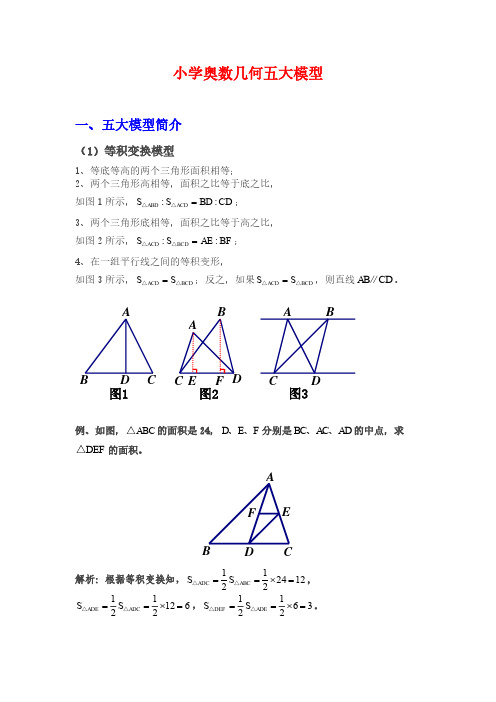
(4)相似模型
1、相似三角形:形状相同、大小不相等的两个三角形相似;
2、寻找相似模型的大前提是平行线:平行于三角形一边的直线和其他两边或两边延长线相交,所构成的三角形与原三角形相似。
3、相似三角形性质:
①相似三角形的一切对应线段(对应高、对应边)的比等于相似比;
②相似三角形周长的比等于相似比;
③相似三角形面积的比等于相似比的平方。
相似模型大致分为金字塔模型、沙漏模型这两大类,注意这两大类中都含有DE BC ∥。
(一)金字塔模型 (二) 沙漏模型
结论:因为DE BC ∥,所以ADE ABC △∽△,则
①AD AE DE
==;②22::ADE ABC S S AD AB =△△。
②::ABO BCO S S AE EC =△△;
E
D C B
A E D
C
B A
③::ACO BCO S S AF FB =△△。
二、五大模型经典例题详解 (1)等积变换模型
例1、图中的E F G 、、分别是正方形ABCD 三条边的三等分点,如果正方形的边长是12,那么阴影部分的面积是多少?
G
F
E D C
B
A。
小学奥数几何五大模型
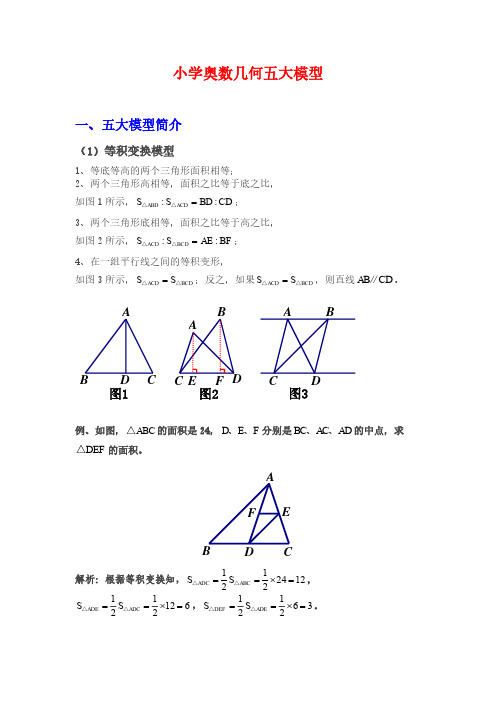
(4)相似模型1、相似三角形:形状相同、大小不相等的两个三角形相似;2、寻找相似模型的大前提是平行线:平行于三角形一边的直线和其他两边或两边延长线相交,所构成的三角形与原三角形相似。
3、相似三角形性质:①相似三角形的一切对应线段(对应高、对应边)的比等于相似比;②相似三角形周长的比等于相似比;③相似三角形面积的比等于相似比的平方。
相似模型大致分为金字塔模型、沙漏模型这两大类,注意这两大类中都含有DE BC ∥。
(一)金字塔模型 (二) 沙漏模型结论:因为DE BC ∥,所以ADE ABC △∽△,则①AD AE DE==;②22::ADE ABC S S AD AB =△△。
②::ABO BCO S S AE EC =△△;ED C BA E DCB A③::ACO BCO S S AF FB =△△。
二、五大模型经典例题详解 (1)等积变换模型例1、图中的E F G 、、分别是正方形ABCD 三条边的三等分点,如果正方形的边长是12,那么阴影部分的面积是多少?GFE D CBA解析:把另外三个三等分点标出之后,正方形的3条边AB BC CD 、、就被分成了相等的三段。
把点H 和这些分点、正方形的顶点连接,这样就把整个正方形分割成了9个形状各不相同的三角形,同时我们把空白部分的6个三角形按顺时针标记1~6。
这9个三角形的底边都是正方形边长的三分之一;阴影部分被分割成了其中的3个三角形。
根据等积变换模型可知,CD 边上的阴影三角形的面积与第1、2个三角形相等;BC 边上的阴影三角形与第3、4个三角形相等;AB 边上的阴影三角形与第5、6个三角形相等。
因此,阴影面积是空白面积的二分之一,是正方形面积的三分之一,即:12×12÷3=48。
例2、如图所示,Q E P M 、、、分别为直角梯形ABCD 两边AB CD 、上的点,且DQ CP ME 、、彼此平行,已知5753AD BC AE EB ====、、、,求阴影部分三角形PQM 的面积。
小学奥数之几何五大模型
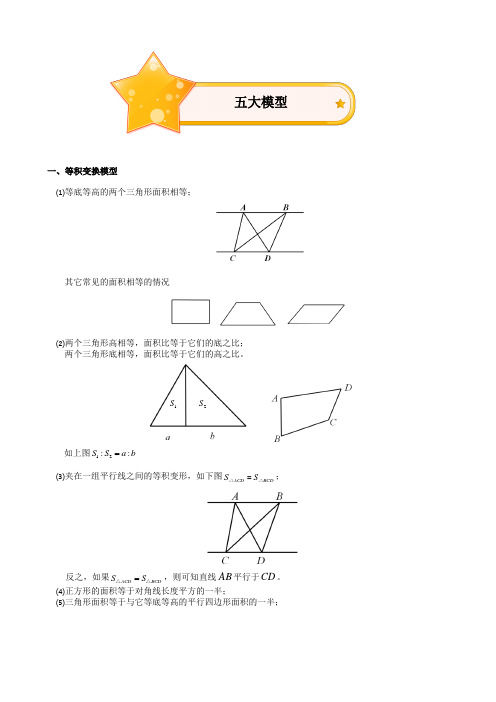
一、等积变换模型⑴等底等高的两个三角形面积相等;其它常见的面积相等的情况⑵两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比。
如上图12::S S a b =⑶夹在一组平行线之间的等积变形,如下图ACD BCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD 。
⑷正方形的面积等于对角线长度平方的一半;⑸三角形面积等于与它等底等高的平行四边形面积的一半;五大模型1S 2S二、鸟头定理(共角定理)模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图,在ABC △中,,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上,E 在AC 上(如图2),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△图1 图2三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”):①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
梯形中比例关系(“梯形蝴蝶定理”)①2213::S S a b =②221324::::::S S S S a b ab ab =; ③梯形S 的对应份数为()2a b +。
四、相似模型相似三角形性质:金字塔模型 沙漏模型 ①AD AE DE AFAB AC BC AG===; ②22::ADE ABC S S AF AG =△△。
所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方。
【精品】五年级下册数学竞赛试题- 14讲 图形-五大模型 全国通用(含答案)
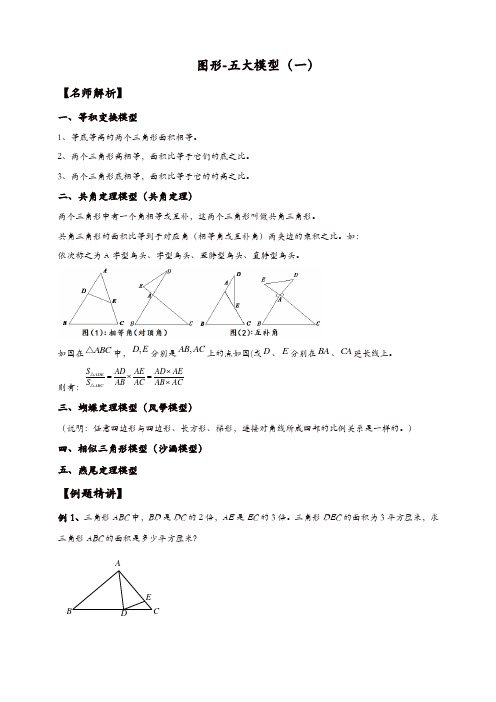
图形-五大模型(一)【名师解析】一、等积变换模型1、等底等高的两个三角形面积相等。
2、两个三角形高相等,面积比等于它们的底之比。
3、两个三角形底相等,面积比等于它的的高之比。
二、共角定理模型(共角定理)两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等到于对应角(相等角或互补角)两夹边的乘积之比。
如: 依次称之为A 字型鸟头、字型鸟头、歪脖型鸟头、直脖型鸟头。
如图在ABC △中,,D E 分别是,AB AC 上的点如图(或D 、E 分别在BA 、CA 延长线上。
则有:ADE ABC S AD AE AD AES AB AC AB AC⨯=⨯=⨯△△三、蝴蝶定理模型(风筝模型)(说明:任意四边形与四边形、长方形、梯形,连接对角线所成四部的比例关系是一样的。
)四、相似三角形模型(沙漏模型) 五、燕尾定理模型【例题精讲】例1、三角形ABC 中,BD 是DC 的2倍,AE 是EC 的3倍。
三角形DEC 的面积为3平方厘米,求三角形ABC 的面积是多少平方厘米?EADCB练习、在下图中,已知CF=2DF ,DE=EA ,△BCF 的面积为2,四边形BFDE 的面积为4,求△ABE 的面积。
FEDC BA例2、(1)在下图中,2AB BD AC CE ==,,如果29ADE S cm D =,求ABC S D ?EDC B A练习、如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.D EABC例3、正方形ABCD 边长为6 厘米,BC CF AC AE 3131==,.三角形DEF 的面积为多少平方厘米?BD练习、如图,1ABC S =△,5BC BD =,4AC EC =,DG GS SE ==,AF FG =.求FGSS.SGF E DCBA例4、一个长方形,被两条直线分成四个长方形,其中三个的面积是20亩、25亩和30亩.问另一个长方形的面积是多少亩?练习、下图中,长方形被两条直线分成四个小长方形,其中三个的面积分别是12平方米、8平方米、20平方米,求另一个(图中阴影都分)例5、如图,22S =,34S =,求梯形的面积?练习5、如下图,梯形ABCD 的AB 平行于CD ,对角线AC ,BD 交于O ,已知AOB △与BOC△的面积分别为25 平方厘米与35平方厘米,那么梯形ABCD 的面积是________平方厘米.3525OABCD例六、如图,长方形ABCD 的面积是2平方厘米,2EC DE =,F 是DG 的中点.阴影部分的面积是多少平方厘米?练习、ABCD 是边长为12厘米的正方形,E 、F 分别是AB 、BC 边的中点,AF 与CE 交于G ,则四边形AGCD 的面积是_________平方厘米.GABCDFE【选讲】△ABC 中,D 、E 分别是边AB 、AC 上的点,BE 、CD 相交于点F ,1016BDF CEF S S ∆∆==,,,20BCF S ∆=,求△ABC 面积。
几何之五大模型

几何之五大模型在小学奥数知识体系中,几何五大模型是几何专题中非常重要的一块知识点,方法性很强,掌握了几何的五大模型,对于我们解决组合型直图形或者非规则图形是非常有帮助的,所以几何五大模型在小学几何体系中的重中之重!几何五大模型的难点在于我们要在掌握各个模型适用的题型、相应的方法、公式的基础上学会灵活运用,还有就是有时要根据题意同时运用多种模型,从而更好的解决问题!PS:对于不同题型均会有例题讲解分析以及精选练习题,以供大家有针对性学习巩固,相信大家对于应用题的攻克将不在话下!一、五大模型简介(1)等积变换模型1、等底等高的两个三角形面积相等;2、两个三角形高相等,面积之比等于底之比,如图①所示,S1:S2=a:b;3、两个三角形底相等,面积在之比等于高之比,如图②所示,S1:S2=a:b;4、在一组平行线之间的等积变形,如图③所示,S△ACD=S△BCD;反之,如果S△ACD=S△BCD,则可知直线AB平行于CD。
例、如图,三角形ABC的面积是24,D、E、F分别是BC、AC、AD的中点,求三角形DEF的面积。
(2)鸟头(共角)定理模型1、两个三角形中有一个角相等或互补,这两个三角形叫共角三角形;2、共角三角形的面积之比等于对应角(相等角或互补角)两夹边的乘积之比。
如图下图三角形ABC中,D、E分别是AB、AC上或AB、AC延长线上的点则有:S△ABC:S△ADE=(AB×AC):(AD×AE)我们现在以互补为例来简单证明一下共角定理!如图连接BE,根据等积变化模型知S△ADE:S△ABE=AD:ABS△ABE:S△CBE=AE:CE所以S△ABE:S△ABC=S△ABE:(S△ABE+S△CBE)=AE:AC因此S△ADE:S△ABC =(S△ADE:S△ABE)×(S△ABE:S△ABC)=(AD:AB)×(AE:AC)。
例、如图在ΔABC中,D在BA的延长线上,E在AC上,且AB:AD=5:2,AE:EC=3:2,△ADE的面积为12平方厘米,求ΔABC的面积。
小升初数学几何五大模型-纯wordA4幅面小边距适合打印编辑-

小学奥数几何五大模型一、五大模型简介(1)等积变换模型1、等底等高的两个三角形面积相等;2、两个三角形高相等,面积之比等于底之比,如图①所示,S1:S2=a:b;3、两个三角形底相等,面积在之比等于高之比,如图②所示,S1:S2=a:b;4、在一组平行线之间的等积变形,如图③AB//CD则S△ACD=S△BCD;反之, S△ACD=S△BCD,则直线AB//CD。
例、如图,三角形ABC的面积是24,D、E、F分别是BC、AC、AD的中点,求三角形DEF 的面积。
(2)鸟头(共角)定理模型1、两个三角形中有一个角相等或互补,这两个三角形叫共角三角形;2、共角三角形的面积之比等于对应角(相等角或互补角)两夹边的乘积之比。
如图下图三角形ABC中,D、E分别是AB、AC上或AB、AC延长线上的点S△ABC:S△ADE=(AB×AC):(AD×AE)我们现在以互补为例来简单证明一下共角定理!如图连接BE,根据等积变化模型知,S△ADE:S△ABE=AD:AB、S△ABE:S△CBE=AE:CE,所以S△ABE:S△ABC=S△ABE:(S△ABE+S△CBE)=AE:AC,因此S△ADE:S△ABC=(S△ADE:S△ABE)×(S△ABE:S△ABC)=(AD:AB)×(AE:AC)。
例、如图在ΔABC中,D在BA的延长线上,E在AC上,且AB:AD=5:2,AE:EC=3:2,△ADE的面积为12平方厘米,求ΔABC的面积。
(3)蝴蝶模型1、梯形中比例关系(“梯形蝴蝶定理”)例、如图,梯形ABCD,AB与CD平行,对角线AC、BD交于点O,已知△AOB、△BOC 的面积分别为25平方厘米、35平方厘米,求梯形ABCD的面积。
、任意四边形中的比例关系(“蝴蝶定理”):例、如图,四边形ABCD的对角线AC、BD 交于点O,如果三角形ABD的面积等于三角形BCD面积的1/3,且AO=2、DO=3,求CO的长度是DO长度的几倍。
五年级下册数学竞赛试题---14讲-图形-五大模型----全国通用(含答案)

五年下册奥数试题-图形-五大模型(一)姓名 得分【名师解析】一、等积变换模型1、等底等高的两个三角形面积相等。
2、两个三角形高相等,面积比等于它们的底之比。
3、两个三角形底相等,面积比等于它的的高之比。
二、共角定理模型(共角定理)两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等到于对应角(相等角或互补角)两夹边的乘积之比。
如: 依次称之为A 字型鸟头、X 字型鸟头、歪脖型鸟头、直脖型鸟头。
如图在ABC △中,,D E 分别是,AB AC 上的点如图(或D 、E 分别在BA 、CA 延长线上。
则有:ADE ABC S AD AE AD AE S AB AC AB AC ⨯=⨯=⨯△△三、蝴蝶定理模型(风筝模型)(说明:任意四边形与四边形、长方形、梯形,连接对角线所成四部的比例关系是一样的。
)四、相似三角形模型(沙漏模型)五、燕尾定理模型【例题精讲】例1、三角形ABC 中,BD 是DC 的2倍,AE 是EC 的3倍。
三角形DEC 的面积为3平方厘米,求三角形ABC 的面积是多少平方厘米?EAD C B练习、在下图中,已知CF=2DF ,DE=EA ,△BCF 的面积为2,四边形BFDE 的面积为4,求△ABE 的面积。
FE DCB A例2、(1)在下图中,2AB BD AC CE ,,如果29ADE S cm ,求ABC S ?E D C BA练习、如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.DEAB C例3、正方形ABCD 边长为6 厘米,BC CF AC AE 3131==,.三角形DEF 的面积为多少平方厘米?BD练习、如图,1ABC S =△,5BC BD =,4AC EC =,DG GS SE ==,AF FG =.求FGS S .SGFE D CB A例4、一个长方形,被两条直线分成四个长方形,其中三个的面积是20亩、25亩和30亩.问另一个长方形的面积是多少亩?练习、下图中,长方形被两条直线分成四个小长方形,其中三个的面积分别是12平方米、8平方米、20平方米,求另一个(图中阴影都分)长方形的面积。
五年级奥数几何专项六 五大模型(二)

一、等积模型①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比;③夹在一组平行线之间的等积变形,如右图ACDBCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.二、共角定理(鸟头定理)两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.DC BA知识框架五大模型(一) 五大模型(二):():()ABC ADE S S AB AC AD AE =⨯⨯△△三、蝴蝶定理任意四边形中的比例关系(“蝴蝶定理”): ①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.梯形中比例关系(“梯形蝴蝶定理”):①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.(1)(2)(3)(4)S 4S 3S 2S 1O DCBA A BCD O ba S 3S 2S 1S 4四、相似模型(一)金字塔模型 (二) 沙漏模型①AD AE DE AFAB AC BC AG ===; ②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方; ⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半. 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.五、共边定理(燕尾定理)有一条公共边的三角形叫做共边三角形。
小学奥数必学几何五大模型及例题解析

小学奥数必学几何五大模型及例题解析一、等积变换模型——很重要,小学常考⑴等底等高的两个三角形面积相等;⑵两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比。
如下图右图12::S S a b =⑶夹在一组平行线之间的等积变形,如下图ACDBCD S S =△△;反之,如果ACDBCD S S =△△,则可知直线AB 平行于CD 。
⑷正方形的面积等于对角线长度平方的一半;⑸三角形面积等于与它等底等高的平行四边形面积的一半;经典例题:1S 2S 解析:连接CE ,如图。
AE=3AB,所以S △AEC =3S △ABC=3 所以 S △BCE =2又因为:BD=2BC,所以S △BDE =2 S △BCE =4点评:此题就是三角形等积变换模型的直接应用二、鸟头定理(共角定理)模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图,在ABC △中,,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上,E 在AC 上(如图2),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△图1 图2此模型的结论可以用将来初中学到的正弦定理进行证明!因为S △ABC =AB ×ACsinA ,S △ADE =AD ×AEsinA所以:S △ABC :S △ADE= (AB ×ACsinA ):(AD ×AEsinA )=(AB ×AC ):(AD ×AE )经典例题:S △ADF :S △ABC=(AD ×AF ):(AB ×AC )=(2BD ×AF ):(3BD ×4AF )=1:6 S △BDE :S △ABC=(BD ×BE ):(AB ×BC )=(BD ×BE ):(3BD ×2BE )=1:6 S △CEF :S △ABC=(CE ×CF ):(CB ×CA )=(CE ×3AF ):(2CE ×4AF )=3:8 1-1/6-1/6-3/8=7/24 S △ABC =7÷7/24=24(平方厘米).点评:本题直接用到鸟头模型,先分别求出三个角上的三个三角形占S △ABC 的比例,再求出S △DEF 占S △ABC 的比例,就能直接求出S △ABC 的面积。
小学数学五大经典几何图形模型及解题思路精讲

小学数学五大经典几何图形模型及解题思路精讲1、等积变换模型(1)等底等高的两个三角形面积相等;(2)两个三角形高相等,面积之比等于底之比;(3)两个三角形底相等,面积在之比等于高之比;(4)在一组平行线之间的等积变形。
【例题】如图,三角形A B C的面积是24,D、E、F分别是B C、A C、A D的中点,求三角形DE F的面积。
2、鸟头(共角)定理模型(1)两个三角形中有一个角相等或互补,这两个三角形叫共角三角形;(2)共角三角形的面积之比等于对应角(相等角或互补角)两夹边的乘积之比。
【例题】如图在△A B C中,D在B A的延长线上,E在AC上,且A B:A D=5:2,AE:E C=3:2,△A D E的面积为12平方厘米,求△ABC的面积。
3、蝴蝶模型(1)梯形中比例关系(“梯形蝴蝶定理”)①S2=S4(因为S△ABC= S△DBC,所以S△ABC-S△OBC= S△DBC-S△OBC)S1:S3=a2:b2②S1:S3:S2:S4= a2:b2:ab:ab③梯形S的对应份数为(a+b)2。
(2)任意四边形中的比例关系(“蝴蝶定理”)①S1:S2=S4:S3或者S1×S3=S4×S2;②AO:OC=(S1+S2):(S4+S3)蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径,通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
【例题】如图,己知正方形AB C D的边长为10厘米,E为AD的中点,F为CE的中点,G为B F的中点,求三角形BD G的面积。
4、相似模型(1)相似三角形:形状相同,大小不相等的两个三角形相似。
(2)寻找相似模型的大前提是平行线:平行于三角形一边的直线和其他两边或两边延长线相交,所构成的三角形与原三角形相似。
(3)相似三角形性质①相似三角形的一切对应线段(对应高、对应边)的比等于相似比;②相似三角形周长的比等于相似比;③相似三角形面积的比等于相似比的平方。
小学数学五大几何模型总结

五大模型(二)知识框架一、等积模型DC BA①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; ③夹在一组平行线之间的等积变形,如右图ACDBCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.二、共角定理(鸟头定理)两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.:():()ABC ADE S S AB AC AD AE =⨯⨯△△(1)(2)(3)(4)三、蝴蝶定理任意四边形中的比例关系(“蝴蝶定理”):①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.S 4S 3S 2S 1O DC BA梯形中比例关系(“梯形蝴蝶定理”): ①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.A B C DO ba S 3S 2S 1S 4四、相似模型(一)金字塔模型 (二) 沙漏模型GF E AB CD ABCDEF G①AD AE DE AFAB AC BC AG===; ②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方; ⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半. 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.五、共边定理(燕尾定理)有一条公共边的三角形叫做共边三角形。
小高奥数几何-三角形五大模型及例题解析

三角形五大模型【专题知识点概述】本讲复习以前所学过的有关平面几何方面的知识,旨在提高学生对该部分知识的综合运用能力。
重点模型重温一、等积模型①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如右图12::S S a b =③夹在一组平行线之间的等积变形,如右图ACD BCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形);⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.二、等分点结论(“鸟头定理”)如图,三角形AED 占三角形ABC 面积的23×14=16DCBAbas 2s1三、任意四边形中的比例关系 (“蝴蝶定理”)① S 1︰S 2=S 4︰S 3 或者S 1×S 3=S 2×S 4 ② ②AO ︰OC=(S 1+S 2)︰(S 4+S 3)梯形中比例关系(“梯形蝴蝶定理”)① S 1︰S 3=a 2︰b 2②S 1︰S 3︰S 2︰S 4= a 2︰b 2︰ab ︰ab ; ③S 的对应份数为(a+b )2模型四:相似三角形性质如何判断相似(1)相似的基本概念:两个三角形对应边城比例,对应角相等。
(2)判断相似的方法:①两个三角形若有两个角对应相等则这两个三角形相似;②两个三角形若有两条边对应成比例,且这两组对应边所夹的角相等则两个三角形相似。
hh H cb a CB Aac b HC BA①a b c hA B C H=== ; ② S 1︰S 2=a 2︰A 2模型五:燕尾定理S 4S 3s 2s 1O DCBA S 4S 3s 2s 1baS △ABG :S △AGC =S △BGE :S △GEC =BE :EC ;S △BGA :S △BGC =S △AGF :S △GFC =AF :FC ; S △AGC :S △BCG =S △ADG :S △DGB =AD :DB ;【重点难点解析】1. 模型一与其他知识混杂的各种复杂变形2. 在纷繁复杂的图形中如何辨识“鸟头”【竞赛考点挖掘】1. 三角形面积等高成比2. “鸟头定理”3. “蝴蝶定理”【习题精讲】【例1】(难度等级 ※)如图,长方形ABCD 的面积是56平方厘米,点E 、F 、G 分别是长方形ABCD 边上的中点,H 为AD 边上的任意一点,求阴影部分的面积.【例2】(难度等级 ※)如右图,ABFE 和CDEF 都是矩形,AB 的长是4厘米,BC 的长是3厘米,那么图中阴影部分的面积是____平方厘米.G HFE DCBA【例3】(难度等级 ※)如图,在三角形ABC 中,BC=8 厘米,AD=6厘米,E 、F 分别为AB 和AC 的中点,那么三角形EBF 的面积是多少平方厘米?【例4】(难度等级 ※※※)如图,在面积为1的三角形ABC 中,DC=3BD,F 是AD 的中点,延长CF 交AB 边于E,求三角形AEF 和三角形CDF 的面积之和。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等积变换与共角定理
我们的目标:掌握三角形等积变换与共角定理的基本模型;学会构造出模型进行解题三角形等积变换模型
(1)等底等高的两个三角形面积相等;
(2)两个三角形高相等,面积比等于底之比;如左图1 2 : :S S a b
(3)两个三角形底相等,面积比等于高之比;
在一组平行线之间的等积变形,如右图;
S△ACD=S△BCD;
共角定理
两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形.
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.
如下两图
例1. 如图三角形ABC的面积为1,其中AE=3AB,BD=2BC,三角形BDE的面积是多少?
例2. 如图,三角形ABC的面积是24,D、E分别是BC、AC和AD的中点,求三角形DEF的面积。
例3.如图,在角MON的两边上分别有A、C、E及B、D、F六个点,并且△
OAB、△ABC、△BCD、△CDE 、△DEF 的面积都等于1,则△DCF的面积等于
例4.E、M分别为直角梯形ABCD两边的点,且DQ、CP、ME彼此平行,若AD=5,BC=7,AE=5,EB=3.求阴影部分的面积
例5.如图,已知CD=5,DE=7,EF=15,FG=6,线段AB将图形分成两部分,左边部分面积是38,右边部分是65,那么三角形ADG的面积是
例6. 如图,正方形的边长为10,四边形EFGH的面积为5,那么阴影部分的面积是
例7. 已知正方形的边长为10,EC=3,BF=2,则S
=
四边形ABCD
例8.如图,平行四边形ABCD,BE=AB,CF=2BC,DG=3DC,HA=4AD,平行四边形ABCD的面积是2,求平行四边形ABCD与四边形EFGH的面积比。
例9. 已知△DEF的面积为7平方厘米,BE=CE,AD=2BD,CF=3AF,求△ABC的面积
等积变换与共角定理习题
1. 如图,在长方形ABCD中,Y是BD的中点,Z是DY的中点,如果AB=24厘米,BC=8厘米,求三角形ZCY的面积
2. 如图,点D、E、F在线段CG上,已知CD=2厘米,DE=8厘米,EF=20厘米,FG=4厘米,AB将整个图形分成上下两部分,下边部分面积是67平方厘米,上边部分是166平方厘米,则三角形ADG的面积是多少平方厘米?
3. 如图,阴影部分四边形的外界图形是边长为12厘米的正方形,则阴影部分四边形的面积是多少平方厘米?
4. 如图,四边形EFGH的面积是66平方米,EA=AB,CB=BF,DC=CG,HD=DA,求四边形ABCD 的面积。
5. 如图,在△ABC中,延长AB至D,是BD=AB,延长BC至E,使CE=1
BC,F是AC的中点,
6. 如图,S△ABC=1,BC=5BD,AC=4EC,DG=GS=SE,AF=FG,求S△FGS
7. 如图,正方形ABCD的边长为6,AE=1.5,CF=2,长方形EFG和的面积为
8. 如图,已知三角形ABC面积为1,延长AB至D,使CE=2BC;延长CA至F,使AF=3AC,求三角形DEF的面积。
