计量经济学 多元线性回归分析;eviews6操作
计量经济学EVIEWS软件学习

实验一Eviews的基本操作与一元线性回归模型的最小二乘估计实验目的:1、熟悉Eviews的窗口与界面2、掌握Eviews的命令与菜单的操作3、掌握用Eviews估计与检验一元线性回归模型实验内容:1、启动Eviews双击Eviews图标,出现Eviews窗口,它由以下部分组成:标题栏“Eviews”、主菜单“File,Edit,…,Help”、命令窗口(空白处)和工作区域。
命令窗口工作区域图1-12、产生文件Eviews的操作在工作文件中进行,故首先要有工作文件,然后进行数据输入、分析等等操作。
(1)读已存在文件:File→Open→Workfile。
(2)新建文件:File→New→Workfile,出现对话框“工作文件范围”,选取或填上数据类型、起止时间。
OK后,得到一个无名字的工作文件,其中有:时间范围、当前工作文件样本范围、filter 、默认方程、系数向量C、序列RESID。
在主菜单上依次点击File/New/Workfile,即选择新建对象的类型为工作文件,将弹出一个对话框(如图所示),由用户选择数据的时间频率(frequency)、起始期和终止期。
图1-2工作文件对话框其中, Annual——年度 Monthly——月度Semi-annual——半年 Weekly——周Quarterly——季度 Daily——日Undated or irregular——非时序数据选择时间频率为Annual(年度),再分别点击起始期栏(Start date)和终止期栏(End date),输入相应的日前1985和1998。
然后点击OK按钮,将在EViews 软件的主显示窗口显示相应的工作文件窗口(如图所示)。
图1-3工作文件窗口工作文件窗口是EViews的子窗口,工作文件一开始其中就包含了两个对象,一个是系数向量C(保存估计系数用),另一个是残差序列RESID(实际值与拟合值之差)。
(3)命令方式新建文件在EViews软件的命令窗口中直接键入CREATE命令,也可以建立工作文件。
计量经济学计量经济学教学案例

计量经济学教学案例案例一 简单线性回归模型一、主题与背景用真实数据进行简单线性回归分析,应用Eviews6.0分析软件进行操作,与课本内容相对应,分析模型的截距、斜率以及可决系数,引导学生熟悉Eviews6.0的基本操作,能够解读分析报告,并尝试进行被解释变量的预测,体会变量测度单位的改变和函数形式变化给OLS 估计结果和统计特征的影响。
二、情景描述对于由CEO 构成的总体,令y 代表年薪(salary),单位为千美元。
令x 表示某个CEO 所在公司在过去三年的平均股本回报率(roe ,股本回报率定义为净收入占普通股价的百分比)。
为研究该公司业绩指标和CEO 薪水之间的关系,可以定义以下模型:Salary=0β+1βroe + u . 斜率参数1β衡量当股本回报率增长一个单位(一个百分点)时CEO 年薪的变化量,由于更高的股本回报率预示更高的CEO 年薪,所以,1β>0。
三、教学过程设计(一)数据说明数据集CEOSAL1.RAW 包含1990年209位CEO 的相关信息,该数据来自《商业周刊》(5/6/91),该样本中CEO 年薪的平均值为$1,281,120,最低值和最高值分别为$223,000和$14,822,000,1988、1989和1990年的平均股本回报率是17.18%。
(二)操作建议1:在 eviews6.0命令输入窗口定义变量:data salary roe2、用 edit+/- 编辑数据3、描述统计分析过程:view---descriptive stats---common sample4、画散点图:Scat roe salary5、在eviews6.0命令输入窗口运行简单线性回归 Ls salary c roe6、用resids 观测残差7、产生新序列:S eries lsalary =log(salary)8、改变函数形式:Ls lsalary c lsales9、改变变量测度单位:Ls salary*1000 c roe四、教学研究(一)案例结论1、回归结果估计出的回归线为:salˆary = 963.191 + 18.501 roe(1)截距和斜率保留了3位小数,回归结果显示,如果股本回报率为0,年薪的预测值为截距963.191千美元,可以把年薪的预测变化看做股本回报率变化的函数:∆salˆary = 18.501 (∆roe),这意味着当股本回报率增加1个百分点,即∆roe =1,则年薪的预测变化就是18.5千美元,在线性方程中,估计的变化与初始年薪无关。
运用EVIEWS建立多元线性回归并进行相关检验

运用EVIEWS 建立多元线性回归并进行相关检验姓名:jelly一、输入数据某社区家庭对某种消费品的消费需要调查二、根据数据画出散点图从上面两散点图可以看出此社区家庭对某商品的消费支出与家庭月收入、商品的价格大致呈线性关系且随着家庭收入和户主受教育年数的逐渐增大对此商品的消费支出也呈逐渐增大的趋势。
三、样本相关阵从样本相关阵可以看出,某商品的消费支出与家庭月收入、商品的价格的相关系数高达0.965046和0.752695 ,说明某商品的消费支出与家庭月收入、商品的价格有显著的线性关序号 商品 价格X1 家庭月 收入X2 对某商品的消费支出Y 1 23.56 7620 591.9 2 24.44 9120 654.5 3 32.07 10670 623.6 4 32.46 11160 647 5 31.15 11900 674 6 34.14 12920 644.4 7 35.3 14340 680 8 38.7 15960 724 9 39.63 18000 757.1 10 46.68 19300 706.8系,可以考虑建立二元线性回归模型。
四、对数据进行普通最小二乘估计,OLS 表如下五、写出估计方程12626.50939.7905700.28618i Y X X ∧=-+(40.13010) (3.197843) (0.05838)t=(15.611195) (-3.061617) (4.902030)20.902218R = 2R =0.874281 六、随机干扰项2'1e e n k σ∧=--'''''ˆˆˆˆˆ()()()()e e Y YY Y Y X Y X Y Y Y X βββ=--=--=-=2116.85 所以22116.85ˆ302.411021σ==-- 由OLS 表得20.902218R = 2R =0.874281 七、由OLS 可得 F=32.29 0.05(2,7) 4.74F =因为32.29>4.74,所以方程的总体线性性显著成立由OLS 表可得 C 的t 值为15.61 X1的t 值为-3.06 X2的值为4.90 0.025(7) 2.365t =所以常输项,X1和X2的总体参数都显著的异于零将数据分别代入以下三个式子:0ˆ00.025ˆt S ββ±⨯ 1ˆ10.025ˆt S ββ±⨯ 2ˆ20.025ˆt S ββ±⨯ 可得参数95%的置信区间分别为(531.62,724.40) -17.35,-2.22) (0.014,0.042)八、X1=35 X2=20000将X1,X2代人方程可得Y 为856.20Y 的均值0ˆY S =37.05 0.025(7) 2.365t = 所以Y 的均值在95%的置信区间为(768.58,943.82)Y 的个值0ˆY S =40.93 0.025(7) 2.365t =所以Y 的个值在95%的置信区间为(759.41,952.99)第二个实验输入数据,对其进行回归分析输出OLS 表由表可得方程为ˆln 101540.609ln 0.361ln Y K L =++ (1.59)(3.45) (1.79)2R =0.8099 2R =0.7963 F=59.660.05(2,28)F =3.34 0.025(28)t =2.048 0.01(28)t =1.701所以lnK 与lnL 联合起来对lnY 有显著的线性影响在5%的显著性水平下,lnK 的参数通过了检验但lnL 的参数未通过t 检验,如果设定显著性水平为10%,lnL 与lnK 都通过检验。
计量经济学Eview分析教程

第一部分Eviews基本操作第一章预备知识一、什么是Eviews(全称Econometric Views)Eviews 软件是QMS(Quantitative Micro Software)公司开发的基于Windows平台下的应用软件,其前身是DOS操作系统下的TSP软件,最新版本是Eviews6.0。
该软件是由经济学家开发,主要应用在经济学领域,可用于回归分析与预测(regression and forecasting)、时间序列(Time series)以及横截面数据(cross-sectional data )分析。
与其他统计软件(如EXCEL、SAS、SPSS)相比,Eviews功能优势是回归分析与预测。
二、Eviews工作特点初学者需牢记以下两点。
一、Eviews软件对对象(objects)的具体操作是在Workfile 中进行,也就是说,如果想用Eviews进行具体的操作,必须先新建一个或打开一个已经存在在硬盘(或软盘)上的Workfile,在此Workfile中进行输入数据、建造模型等操作;二、Eviews处理的对象及运行结果都称之为objects,如序列(sereis)方程(equations)、模型(models)、系数(coefficients)等objects。
objects可以不同形式浏览(views),比如表格(spreadsheet)、图(graph)、描述统计(descriptive statistics)等,但这些浏览(views)不是独立的objects,他们随原变量序列(views)的改变而改变。
如果想将某个浏览(views)转换成一个独立的objects,可使用freeze 按钮将该views“冻结”,从而形成一个独立的objects,然后可对其进行编辑或存储。
三、一个作示例在这里,我们通过一个简单的回归分析例子来显示一个Eviews过程,不对Eviews的功能展开讨论,目的是使读者先对Eviews有个概括了解。
计量经济学 多元线性回归分析;eviews6操作ppt课件

CONSP
GDPP
CONSP
1978
395.8
675.1
1990
797.1
1979
437.0
716.9
1991
861.4
1980
464.1
763.7
1992
966.6
1981
501.9
792.4
1993
1048.6
1982
533.5
851.1
1994
1108.7
1983
572.8
931.4
1995
1213.1
根据最小二乘原理,参数估计值应该是下列方程组的解
ˆ 1
Q
0
ˆ 2 Q
0
ˆ k
Q
0
n
n
其中 Q ei2 (Yi Yˆi)2
i1
i1
n
2
Yiˆ1ˆ2X2i ˆkXki
i1
完整版PPT课件
11
于是得到关于待估参数估计值的正规方程组:
ˆ1 ˆ2 X 2i ˆk X ki ˆ1 ˆ2 X 2i ˆk X ki
Sample: 1978 2000 Included observations: 23
Coefficient Std. Error t-Statistic Prob.
C
201.1228 14.88892 13.50822
0
X
0.386173 0.007224 53.45683
0
R-squared Adjusted R-squared
或 1
n
x2 ji1 n
(XjiXj)2 Q j
1 xx Q n
Eviews6.0线性回归

R2 k1
F1R2Tk
在原假设为误差正态分布下,统计量服从 F(k – 1 , T – k) 分布。
25
F统计量下的P值,即Prob(F-statistic), 是F检验的边际显 著性水平。如果P值小于所检验的边际显著水平,比如说 0.05,则拒绝所有系数都为零的原假设。注意F检验是一个 联合检验,即使所有的t统计量都是不显著的,F统计量也可 能是高度显著的。
变量名下;如果是使用公式法来说明方程,EViews会列出实际 系数 c(1), c(2), c(3) 等等。
对于所考虑的简单线性模型,系数是在其他变量保持不变
的情况下自变量对因变量的边际收益。系数 c 是回归中的常数 或者截距---它是当其他所有自变量都为零时预测的基本水平。 其他系数可以理解为假设所有其它变量都不变,相应的自变量
ARCH方法。 EViews计算R2 的公式为:
R21 uˆuˆ
, uˆyXb
(yy)(yy)
其中,uˆ是残差,y 是因变量的均值。
19
(2) R2 调整 使用R2 作为衡量工具存在的一个问题,即在增加新的自变 量时R2 不会减少。在极端的情况下,如果把样本观测值都作R 2为 自变量,总能得到R2 为1。
s uˆuˆ/(Tk)
(4)残差平方和 残差平方和可以用于很多统计计算中,为了方便,现在将 它单独列出:
T
uˆuˆ (yt Xtb)2 t1 21
(5) 对数似然函数值 EViews可以作出根据系数的估计值得到的对数似然函数 值(假设误差为正态分布)。似然比检验可通过观察方程严 格形式和不严格形式的对数似然值之间的差异来进行。 对数似然计算如下:
要求掌握多元线性回归分析的eviews操作及相应的统计分析;掌握

上机练习3要求:掌握多元线性回归分析的eviews操作及相应的统计分析;掌握偏相关系数和弹性系数计算以及多参数假设检验。
一、根据ex43的数据,建立简单消费函数模型,假定消费量仅依赖于同期可支配个人收入。
即为第一次上机作业ex32的例子,求出求出边际消费倾向的 95% 置信区间,检验该模型中正态分布的假设是否成立。
建立简单储蓄函数模型,假定储蓄是同期可支配收入的函数。
分析两个模型系数之间的关系。
可以发现:两个方程密切相关,两个斜率系数之和等于1。
另外,两个模型的回归平方和、回归标准误差以及残差均相等。
个人消费:GC储蓄:GS=GYD-GC可支配个人收入:GYD单位:十亿美元二、下表给出美国1980~1996年间城市劳动力参与率、失业率和平均小时工资的数据:年 劳动力参与率 失业率平均小时工资年 劳动力参与率失业率平均小时工资1980 63.8 7.1 7.78 198966.5 5.3 7.64 1981 63.9 7.6 7.69 199066.5 5.6 7.52 1982 64 9.7 7.68 199166.2 6.8 7.45 1983 64 9.6 7.79 199266.4 7.5 7.41 1984 64.4 7.5 7.8 199366.3 6.9 7.39 1985 64.8 7.2 7.77 199466.6 6.1 7.4 1986 65.3 7 7.81 199566.6 5.6 7.4 1987 65.6 6.2 7.73 199666.8 5.4 7.43 1988 65.9 5.5 7.69由此考虑问题:经济形势会影响人们进入劳动力市场的决定吗?这里用失业率来度量经济形势,用劳动力参与率度量劳动力的参与。
建立劳动力参与率对失业率和平均小时工资的二元回归方程。
(1)检验系数和方程的显著性;(2)系数的符号与你希望的一致吗?说出系数的经济含义; (3)以此例为例说明,二元回归可用两个一元回归来做。
eviews6.0实际操作:多重共线性

案例1:经济理论指出,家庭消费支出(Y )不仅取决于可支配收入(X 1),还决定于个人财富(X 2),即可设定如下回归模型:01122i i i i Y X X u βββ=+++操作:对以上数据利用最小二乘法进行回归分析,分析:(1) 样本可决系数为96%,表示收入和财富可以解释消费支出总变动的96%; (2) F 统计量为88.84,对应的p 值为0.000011,小于0.05,表明方程总体线性显著,或者解释变量中至少有一个是对被解释变量有显著影响;(3) 两变量的t 统计量对应的p 值均大于0.05,表明两解释变量对被解释变量的影响是不显著的,与F 统计量所得到的结果矛盾; (4) 财富变量的系数符号与实际情况不符;综合(2)、(3)、(4)表明可能存在严重的多重共线性。
通过计算两解释变量之间的相关系数为0.9986,高于样本可决系数96%。
表明收入和财富之间高度相关,使得无法分辨二者对被解释变量的贡献。
相关系数:125()()i i j j X X X X X X r --=∑(5) 因此该回归结果不可靠,可以考虑只作消费支出对收入或财富的一元线性回归模型来替代二元回归模型。
案例2:天津市1974—1987年粮食需求的相关数据:Y=粮食销售量(万吨/年);X1=市常住人口(万人);X2=人均收入(元/年);X3=肉销售量(万吨/年);X4=假定粮食需求函数:01122334455t t t t t t tY X X X X X u ββββββ=++++++(1)普通最小二乘法估计此模型,运行结果:得到回归模型:12345ˆ 3.490.130.07 2.67 3.45 4.49Y X X X X X =-++++- (-0.12)( 2.12) (1.94) (2.13) (1.41) (-2.03)R 2=0.97 F=52.53 T=14(2)多重共线性判定:模型可能存在多重共线性。
计量经济学eviews操作

计量经济学实验指导系部:基础部专业:计算与信息科学教师:仓定帮I.实验一多元线性回归模型 (3)II.实验二异方差的检验与处理 (16)III.实验三序列相关的检验与处理 (24)IV.实验四多重共线性的检验与处理 (32)V.实验五虚拟变量模型 (39)VI.实验六分布滞后模型 (45)VII.实验七联立方程模型 (51)VIII.实验八时间序列模型分析 (58)IX.实验九V AR模型的建立与分析 (77)A. ADF检验 (78)B. VAR模型的建立 (79)C. 协整检验 (80)D. GRANGER因果检验 (81)E. 脉冲响应分析 (81)实验内容注:必做实验课堂时间完成,选做实验由学生课后选择时间完成。
每次实验后学生上交实验分析结果。
I.实验一多元线性回归模型【实验目的】通过本实验,了解Eviews软件,熟悉软件建立工作文件,文件窗口操作,数据输入与处理等基本操作。
掌握多元线性回归模型的估计方法,学会用Eiews 软件进行多元回归分析。
通过本实验使得学生能够根据所学知识,对实际经济问题进行分析,建立计量模型,利用Eiews软件进行数据分析,并能够对输出结果进行解释说明。
【实验内容及步骤】本实验选用美国金属行业主要的27家企业相关数据,如下表,其中被解释变量Y表示产出,解释变量L表示劳动力投入,K表示资本投入。
试建立三者之间的回归关系。
7 2427.89 452 3069.91 21 5159.31 835 5206.368 4257.46 714 5585.01 22 3378.4 284 3288.729 1625.19 320 1618.75 23 592.85 150 357.3210 1272.05 253 1562.08 24 1601.98 259 2031.9311 1004.45 236 662.04 25 2065.85 497 2492.9812 598.87 140 875.37 26 2293.87 275 1711.7413 853.1 154 1696.98 27 745.67 134 768.5914 1165.63 240 1078.79【实验内容及步骤】1.数据的输入STEP1:双击桌面上Eviews快捷图标,打开Eviews,如图1.图1STEP2:点击Eviews主画面顶部按钮file/new/Workfile ,如图2,弹出workfile create对话框如图3。
计量经济学软件EViews的使用简介

SHOW(打开对象窗口) (打开对象窗口) 格式: 格式: SHOW 对象名 CLOSE (关闭对象窗口) 关闭对象窗口) 格式: 格式: CLOSE 对象名
(4)估计方法命令
• LS普通最小二乘法 LS普通最小二乘法 格式: 格式: LS 被解释变量 • TSLS二阶段最小二乘法 TSLS二阶段最小二乘法
(2)工作文件(Workfile) )工作文件( )
在启动软件包以后,必须在内存RAM中建立工作文件,工作方作中 中建立工作文件, 在启动软件包以后,必须在内存 中建立工作文件 可以包括的对象有序列、 方程、图形、系统、模型及系数向量等。 可以包括的对象有序列、组、方程、图形、系统、模型及系数向量等。
计量经济学软件EViews的使用简介 的使用简介 计量经济学软件
• 一、EViews的基本概念 的基本概念
• 二、 EViews的使用简介 的使用简介
1、创建工作文件 、 2、输入与编辑数据 、 3、图形分析 、 4、用OLS估计模型中的求知参数 、 估计模型中的求知参数 5、模型检验 、 6、预测 、
格式: 格式: GENR
数据序列对象表达式 SERIES(创建数据序列对象)。 SERIES不需要赋值。 不需要赋值。 (创建数据序列对象)。 不需要赋值 格式: 格式: SERIES 数据序列名
EQUATION(创建估计式对象) (创建估计式对象) 格式: 格式: EQUATION 估计式对象
EQUATION 估计式对象 及估计表达式
(6)剪切板 ) 先使用主菜单上的Edit Copy,再使用 先使用主菜单上的 ,再使用Edit Paste 将保存在剪切板上的内容粘贴到其他地方。 将保存在剪切板上的内容粘贴到其他地方。 (7)窗口间切换 ) (8)数据文件(Data bank) )数据文件( ) 2、方程、指数平滑、标签、程序、残差、t统计量 、方程、指数平滑、标签、程序、残差、 统计量 (1)方程 方程(Equation) 方程 新建方程方法一: 新建方程方法一:New Object Equation后打开一个对 后打开一个对 话框,然后列出包含在方程里的变量名, 话框,然后列出包含在方程里的变量名,因变量之后排 列回归解释变量。例如,设定一个y关于 关于x和截距进行归 列回归解释变量。例如,设定一个 关于 和截距进行归 的线性消费的例子如下: 的线性消费的例子如下:y c x 新建方程方法二:例如:道格拉斯生产函数: 新建方程方法二:例如:道格拉斯生产函数: Y=c(1)*(L^c(2))*(k^c(3))
计量经济学eviews操作步骤

计量经济学eviews操作步骤嘿,朋友们!今天咱就来聊聊计量经济学 eviews 的操作步骤。
这玩意儿啊,就像是打开经济学奥秘大门的一把钥匙呢!
首先,你得把 eviews 这个软件给装上吧。
就跟你要出门得先穿好鞋一样,这可是基础中的基础呀。
装好了之后,打开软件,那界面就展现在你眼前啦。
就好像进入了一个神秘的数字世界。
接下来,你得把你要用的数据给弄进去呀。
这就好比做饭得先有食材呀,没数据你可玩不转呢。
把数据整整齐齐地放进去,就跟给它们排好队似的。
然后呢,就是各种分析啦。
什么回归分析呀,什么统计检验呀。
这就像给数据做各种体检,看看它们是不是健康,有没有啥问题。
你得仔细盯着那些结果,就像医生看检查报告一样认真。
比如说回归分析吧,你得选好自变量和因变量,就像给它们配对似的。
然后看着软件给你算出一堆数字和图表,你得能看懂呀,这可需要点本事呢。
还有啊,统计检验也很重要呢。
就像给数据做质量检测,看看合不合格。
要是不合格,那你就得重新琢磨琢磨啦。
在操作的过程中,可别马虎呀!就跟走路一样,一步一步都得走稳了。
要是不小心弄错了,那可就麻烦啦。
哎呀,这计量经济学 eviews 操作步骤其实说起来也不难,但就是得细心、耐心。
你想想,要是你盖房子,那每一块砖不都得放好呀,这eviews 操作也是一样的道理。
总之呢,多练习,多琢磨,你肯定能掌握好这门技术。
到时候,你
就能在经济学的世界里畅游啦,就像鱼儿在大海里自由自在地游一样!加油吧,朋友们!相信你们一定可以的!。
eviews做回归分析报告

eviews做回归分析报告回归分析是一种常见的统计分析方法,可用于研究变量之间的关系以及预测未来的趋势。
EViews作为一款专业的经济计量软件,提供了强大的回归分析功能,能够帮助研究人员进行回归模型的构建和分析。
首先,我们需要明确回归模型的基本概念。
回归模型用于描述一个或多个自变量与因变量之间的关系。
在EViews中,我们可以通过以下步骤进行回归分析。
1. 数据准备在进行回归分析之前,首先需要准备好需要分析的数据。
在EViews中,数据可以以多种格式导入,如Excel、CSV等。
确保数据的准确性和完整性很重要,因为数据质量会直接影响回归分析的结果。
2. 构建回归模型在EViews中,可以通过菜单栏上的“Proc”选项选择“Estimate”来构建回归模型。
在打开的窗口中,我们可以选择自变量和因变量,并设定模型的形式。
例如,如果我们想建立一个线性回归模型,可以选择“OLS”作为估计方法,并指定自变量和因变量的名称。
3. 模型诊断构建回归模型后,需要进行模型诊断以评估模型的拟合优度和假设检验等指标。
EViews提供了多种模型诊断方法,如残差分析、多重共线性检验和异方差性检验等。
通过这些方法,我们可以评估回归模型的合理性,并对模型进行进一步改进。
4. 结果解释在进行回归分析后,EViews会生成一个回归结果报告,其中包含了模型的参数估计、显著性检验和拟合优度等指标。
对于参数估计,我们可以通过解释估计系数的符号和大小来说明自变量与因变量之间的关系。
同时,我们也需要关注显著性检验的结果,以确定模型的统计显著性。
5. 结果导出和呈现最后,我们可以将回归结果导出为表格或图表的形式,以便更好地呈现和解释结果。
在EViews中,我们可以使用菜单栏上的“View”选项选择“Coefficients”或“Residuals”来查看具体的回归系数或残差。
回归分析是一种常用的统计方法,可以帮助研究人员深入理解变量之间的关系,并进行未来的趋势预测。
计量经济学实验操作指导(完整版)--李子奈

计量经济学试验 (完整版)——李子奈目录实验一一元线性回归一实验目的:掌握一元线性回归的估计与应用,熟悉EViews的基本操作。
二实验要求:应用教材P61第12题做一元线性回归分析并做预测。
三实验原理:普通最小二乘法。
四预备知识:最小二乘法的原理、t检验、拟合优度检验、点预测和区间预测。
五实验内容:第2章练习12下表是中国2007年各地区税收Y和国内生产总值GDP 的统计资料。
单位:亿元安徽401.9 7364.2 甘肃142.1 2702.4 福建594.0 9249.1 青海43.3 783.6 江西281.9 5500.3 宁夏58.8 889.2 山东1308.4 25965.9 新疆220.6 3523.2 河南625.0 15012.5(1)作出散点图,建立税收随国内生产总值GDP变化的一元线性回归方程,并解释斜率的经济意义;(2)对所建立的回归方程进行检验;(3)若2008年某地区国内生产总值为8500亿元,求该地区税收收入的预测值及预测区间。
六实验步骤1.建立工作文件并录入数据:(1)双击桌面快速启动图标,启动Microsoft Office Excel, 如图1,将题目的数据输入到excel表格中并保存。
(2)双击桌面快速启动图标,启动EViews6程序。
(3)点击File/New/ Workfile…,弹出Workfile Create对话框。
在Workfile Create对话框左侧Workfile structuretype栏中选择Unstructured/Undated选项,在右侧DataRange中填入样本个数31.在右下方输入Workfile的名称P53.如图2所示。
图 1 图 2(4)下面录入数据,点击File/Import/Read Text-Lotus-Excel...选中第(1)步保存的excel表格,弹出Excel Spreadsheet Import对话框,在Upper-left data cell栏输入数据的起始单元格B2,在Excel 5+sheet name栏中输入数据所在的工作表sheet1,在Names for series or Number if named in file栏中输入变量名Y GDP,如图3所示,点击OK,得到如图4所示界面。
Eviews6.0面板数据操作指南
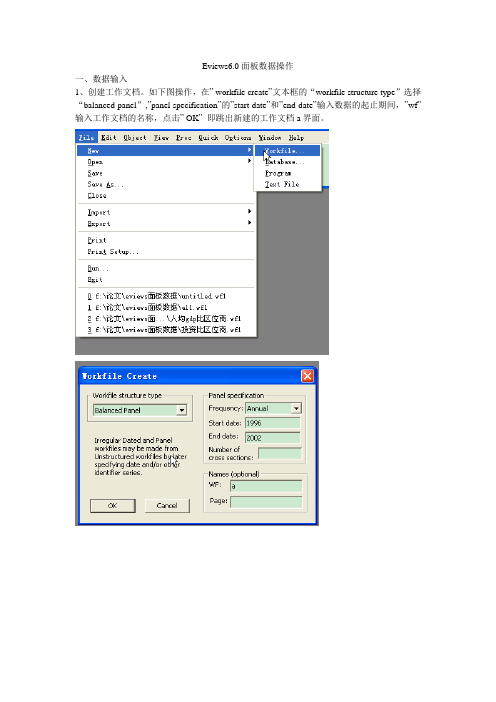
Eviews6.0面板数据操作一、数据输入1、创建工作文档。
如下图操作,在” workfile create”文本框的“workfile structure type”选择“balanced panel”,”panel specification”的”start date”和”end date”输入数据的起止期间,”wf”输入工作文档的名称,点击” OK”即跳出新建的工作文档a界面。
2、创建新对象。
操作如下图。
在”new object”文本框的”type of object”选择”pool”,”name for object ”输入新对象的名称。
创建成功后的界面如下面第3张图所示。
3、输入数据。
双击”workfile”界面的,跳出”pool”界面,输入个体。
一般输入方式为如下:若上海输入_sh,北京输入_bj,…。
个体输入完成后,点击该界面的键,在跳出的”series list”输入变量名称,注意变量后要加问号。
格式如下:y? x?。
点击”OK”后,跳出数据输入界面,如下面第4张图所示。
在这个界面上点击键,即可以输入或者从EXCEL处复制数据。
在输入数据后,记得保存数据。
保存操作如下:在跳出的“workfile save”文本框选择“ok”即可,则自动保存到我的文档。
然后在“workfile”界面如下会显示保存路径:d:\my documents\a.wf1。
若要保存到自己选择的路径下面,则在保存时选择“save as”,在跳出的文本框里选择自己要保存的路径以及命名文件名称。
4、单位根检验。
一般回归前要检验面板数据是否存在单位根,以检验数据的平稳性,避免伪回归,或虚假回归,确保估计的有效性。
单位根检验时要分变量检验。
(补充:网上对面板数据的单位根检验和协整检验存在不同意见,一般认为时间区间较小的面板数据无需进行这两个检验。
)(1)生成数据组。
如下图操作。
点击”make group”后在跳出的”series list”里输入要单位根检验的变量,完成后就会跳出如下图3所示的组数据。
计量经济学实验一 计量经济学软件EViews

实验一计量经济学软件EViews一、计量经济学软件EViews的使用实验目的:熟悉EViews软件的基本使用功能。
实验要求:快速熟悉描述统计和线性回归分析。
实验原理:软件使用。
实验数据:1978-2005年广东省消费和国内生产总值统计数据。
实验步骤:(一)启动EViews软件进入Windows以后,双击桌面EViews6图标启动EViews,进入EViews窗口。
EViews的四种工作方式:(1)鼠标图形导向方式;(2)简单命令方式;(3)命令参数方式(1与2相结合);(4)程序(采用EViews命令编制程序)运行方式。
(二)创建工作文件假定我们要研究广东省消费水平与国内生产总值(支出法)之间的关系,收集了1978—2005年28年的样本资料(表1-1),消费额记作XF(亿元),国内生产总值记作GDP(亿元)。
根据资料建立消费函数。
进入EViews后的第一件工作,通常应由创建工作文件开始。
只有建立(新建或调入原有)工作文件,EViews才允许用户输入,开始进行数据处理。
建立工作文件的方法是点击File/New/Workfile。
选择新建对象的类型为工作文件。
选择数据类型和起止日期,并在对话框中提供必要的信息:适当的时间频率(年、季度、月度、周、日);最早日期和最晚日期。
开始日期是项目中计划的最早的日期;结束日期是项目计划的最晚日期,以后还可以对这些设置进行修改。
非时间序列提供最大观察个数。
建立工作文件对话框如图1-2所示,按OK确认,得新建工作文件窗口(图1-3)。
表1-1图1-2工作文件窗口是EViews的子窗口。
它也有标题栏、控制栏、控制按钮。
标题栏指明窗口的类型是Workfile、工作文件名和存储路径。
标题栏下是工作文件窗口的工具条。
工具条上是一些按钮。
图1-3View —观察按钮;Proc —过程按钮;Save —保存工作文件;Show —显示序列数据;Fetch —读取序列;Store —存储序列;Delete —删除对象;Genr —生成新的序列;Sample —设置观察值的样本区间。
计量经济学多重共线性的诊断及处理Eviews
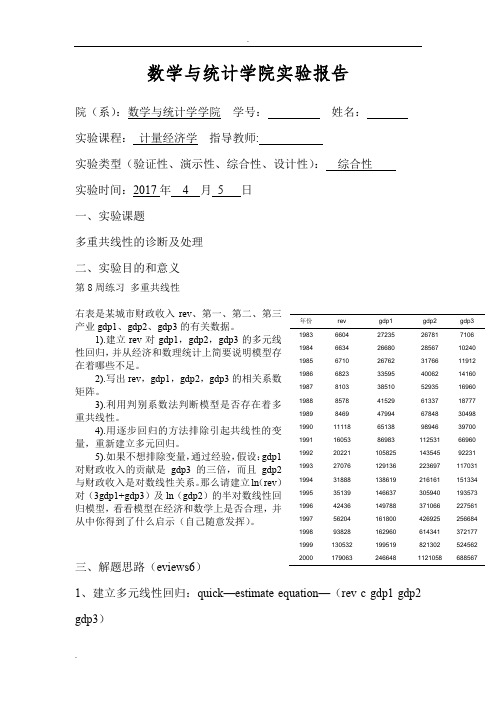
数学与统计学院实验报告院(系):数学与统计学学院 学号: 姓名: 实验课程: 计量经济学 指导教师:实验类型(验证性、演示性、综合性、设计性): 综合性 实验时间:2017年 4 月 5 日 一、实验课题多重共线性的诊断及处理 二、实验目的和意义第8周练习 多重共线性右表是某城市财政收入rev 、第一、第二、第三产业gdp1、gdp2、gdp3的有关数据。
1).建立rev 对gdp1,gdp2,gdp3的多元线性回归,并从经济和数理统计上简要说明模型存在着哪些不足。
2).写出rev ,gdp1,gdp2,gdp3的相关系数矩阵。
3).利用判别系数法判断模型是否存在着多重共线性。
4).用逐步回归的方法排除引起共线性的变量,重新建立多元回归。
5).如果不想排除变量,通过经验,假设:gdp1对财政收入的贡献是 gdp3的三倍,而且gdp2与财政收入是对数线性关系。
那么请建立ln (rev )对(3gdp1+gdp3)及ln (gdp2)的半对数线性回归模型,看看模型在经济和数学上是否合理,并从中你得到了什么启示(自己随意发挥)。
三、解题思路(eviews6)1、建立多元线性回归:quick —estimate equation —(rev c gdp1 gdp2 gdp3)年份 rev gdp1 gdp2 gdp3 1983 6604 27235 26781 7106 1984 6634 26680 28567 10240 1985 6710 26762 31766 11912 1986 6823 33595 40062 14160 1987 8103 38510 52935 16960 1988 8578 41529 61337 18777 1989 8469 47994 67848 30498 1990 11118 65138 98946 39700 1991 16053 86983 112531 66960 1992 20221 105825 143545 92231 1993 27076 129136 223697 117031 1994 31888 138619 216161 151334 1995 35139 146637 305940 193573 1996 42436 149788 371066 227561 1997 56204 161800 426925 256684 1998 93828 162960 614341 372177 1999 130532 199519 821302 524562 200017906324664811210586885672、建立相关系数矩阵:quick--group statistic--correlation--rev gdp1 gdp2 gdp3)3、判定系数法:利用一解释变量由其他解释变量变出模型一::quick—estimate equation—(gdp1 c gdp2 gdp3)模型二::quick—estimate equation—(gdp2 c gdp1 gdp3)模型三::quick—estimate equation—(gdp3 c gdp1gdp2)4、逐步回归:quick—estimate equation—method:stepwise—rev c- gdp1 gdp2 gdp35、建立对数线性关系:quick—estimate equation—LOG(REV) C3*GDP1+GDP3 LOG(GDP2)四、实验过程记录与结果1、建立多元回归方程:模型:REV = 7726.69598122 - 0.180508326923*GDP1 + 0.0759120320555*GDP2 + 0.185205459439*GDP3通过多元回归模型可见,该模型通过假设检验,但是两个解释变量的效果并不好(p>0.05);第二点是GDP1表示第一产业,不存在负值,所以不满足经济条件2、相关系数矩阵:(3、判定系数法:(利用一解释变量由其他解释变量变出,检验拟合优度)由系数判定法,可以看出三个模型都显著性成立,即任意一个解释变量都能由其他解释变量线性变出,所以可以得出该模型存在多重共线性。
实验4:计量经济学实验【多元线性回归及非线性回归模型的线性化】

二、学习的基本内容(重点)
1、多元线性回归模型的基本理论和方法; 2、多元线性回归模型的有关检验(统计 检验); 3、看懂Eviews软件的回归分析结果; 4、采用合适的形式报告有关结果; 5、经典线性回归模型的扩展——多元非 线性回归模型的线性化处理。
三、知识点回顾
1、多元线性回归模型的概念
与一元线性回归模型类似,对多元线性回归模型 Y X X X 有以下几个基本假设,如果实 际模型满足这些假设,则 OLS 就是最优的估计方法; (1) 解释变量 X 1 , X 2 , , X k 是非随机的或固定的,且相互之间 互不相关(无多重共线性),随机干扰项 i 是随机变量; (2)随机干扰项 i 具有 0 均值,同方差及不序列相关性,即
ˆ 1 ˆ ˆ k
0
( k 1) 1
三、知识点回顾
2、多元线性回归模型的四种重要关系式 (4)样本回归模型:
样本回归函数的随机形式表示为:
ˆ ˆ ˆ ˆ ˆ Yi Yi e i 0 1 X 1 i 2 X 2 i k X ki e i
三、知识点回顾
2、多元线性回归模型的四种重要关系式 (2)总体回归函数(方程)
上述多元回归模型中的确定性部分(趋势部分)
E (Y | X 1 i , X 2 i , X ki ) 0 1 X 1 i 2 X 2 i k X ki
此式揭示了所考察总体被解释变量与解释变量之间的平均变 化规律,即解释变量取固定值时,被解释变量Y 的平均响 应; 多元回归斜率系数的含义:表示在保持回归方程中其他解释 变量不变时,所考察的解释变量每增加一个单位,将导致被 解释变量Y的均值的变化量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i E(i )
E
X 1i i
X
1i E(i
)
0
X Ki i X Ki E(i )
假设6,向量 有一多维正态分布,即
μ~ N(0, 2I)
同一元回归一样,多元回归还具有如下两个重要假设: 假设7,样本容量趋于无穷时,各解释变量的方差趋于有界常数,即n∞时,
yi ˆ1x1i ˆ2 x2i ˆk xki ei
其矩阵形式为
i=1,2…n
y xβˆ e
其中 :
y1
x11 x21 xk1
1
n
x
2 ji
1 n
( X ji X j )2 Q j
或
1 xx Q n
其中:Q为一非奇异固定矩阵,矩阵x是由各解释变量的离差为元素组成 的nk阶矩阵
x11 xk1 x
x1n xkn
假设8,回归模型的设定是正确的。
§3.2 多元线性回归模型的估计
估计方法:OLS、ML或者MM 一、普通最小二乘估计 *二、最大或然估计 *三、矩估计 四、参数估计量的性质 五、样本容量问题 六、估计实例
ˆ1 ˆ2 X 2i ˆk X ki Yi X ki
解该k个方程组成的线性代数 方程组,即可以得到 k个 待估参数的估计值
正规方程组的矩阵形式
n
X 1i
X 1i
X
2 1i
X ki
X ki X 1i
X X 1i
X
ki
X
2 ki
ki
ˆ 0 ˆ1
ˆ k
第三章 经典单方程计量经济 学模型:多元回归
多元线性回归模型 多元线性回归模型的参数估计 多元线性回归模型的统计检验 多元线性回归模型的预测 回归模型的其他形式 回归模型的参数约束
§3.1 多元线性回归模型
一、多元线性回归模型 二、多元线性回归模型的基本假定
一、多元线性回归模型
多元线性回归模型:表现在线性回归模型中的解 释变量有多个。
Cov(i , j ) E(i j ) 0
i j i, j 1,2, , n
假设5,解释变量与随机项不相关
Cov( X ji , i ) 0
j 1,2 , k
假设6,随机项满足正态分布
i ~ N (0, 2 )
上述假设的矩阵符号表示 式:
假设1,nk矩阵X是非随机的,且X的秩=k,即X满秩。
Yˆ Xβˆ
或
Y Xβˆ e
其中:
ˆ1
ˆ
ˆ2
ˆk
e1
e
e2 en
二、多元线性回归模型的基本假定
假设1,解释变量是非随机的或固定的,且各 X之间互不相关(无多重共线性)。
假设2,3,4,随机误差项具有零均值、同方差 及不序列相关性
E(i ) 0
Var(i ) E(i2 ) 2
样本回归函数:用来估计总体回归函数
Yˆi ˆ1 ˆ2 X2i ˆ3 X3i ˆk Xki
其随机表示式:
Yi ˆ1 ˆ2 X2i ˆ3 X3i ˆk Xki ei
ei称为残差或剩余项(residuals),可看成是
总体回归函数中随机扰动项i的近似替代。
样本回归函数的矩阵表达:
也被称为总体回归函数的随机表达形式。它 的 非随机表达式为:
E(Yi | X 2i , X 3i , X ki ) 1 2 X 2i 3 X 3i k X ki
方程表示:各变量X值固定时Y的平均响应。
j也被称为偏回归系数,表示在其他解释变
量保持不变的情况下,Xj每变化1个单位时,Y 的均值E(Y)的变化;
或者说j给出了Xj的单位变化对Y均值的“直
接”或“净”(不含其他变量)影响。
总体回归模型n个随机方程的矩阵表达式为 Y Xβ μ
其中
Y1 1 1 X21 L
其中:Y
Y2
2
X
1
X 22
L
M M M
Yn
k
1 X2n L
X k1 u1
Xk2
U
u2
M
X
kn
un
假设2,3,4
E (μ)
E
1
E(1
)
0
n E( n )
E (μμ )
E
1
1
n
n
E
12
n
1
1 n
2 n
var(1 )
cov(
n
,
1
)
cov(1, n ) 2
var( n )
0
0 2I
2
假设5,E(X’ )=0,即
ˆ1
Q0
ˆ2
ˆk
Q
Q
0 0
其中
n
n
Q ei2 (Yi Yˆi ) 2
i 1
i 1
n
2
Yi ˆ1 ˆ2 X 2i ˆk X ki
i1
于是得到关于待估参数估计值的正规方程组:
ˆ1 ˆ2 X 2i ˆk X ki Yi ˆ1 ˆ2 X 2i ˆk X ki Yi X1i
一、普通最小二乘估计
对于随机抽取的n组观测值 (Yi , X ji ), i 1,2, , n, j 0,1,2, k
如果样本函数的参数估计值已经得到,则有:
Yˆi ˆ1 ˆ2 X 2i ˆ3 X3i ˆk X kiFra biblioteki=1,2…n
根据最小二乘原理,参数估计值应该是下列方程组的解
一般表现形式:
模型:Yt 1 2t X 2t L k X kt ut
t=1,2…,n
其中:k-1为解释变量的X数目,j称为回归参数
(regression coefficient)。
习惯上:把常数项看成为一虚变量的系数,该 虚变量的样本观测值始终取1。这样:
模型中解释变量的数目为(k)
模型:Yt 1 2t X 2t L k X kt ut
1 X 11 X k1
1 X 12 Xk2
1 Y1
X 1n Y2
X kn
Yn
即
(XX)βˆ XY 由于X’X满秩,故有
βˆ (XX)1 XY
将上述过程用矩阵表示如下:
即求解方程组:
βˆ (Y
Xβˆ )(Y
Xβˆ )
0
βˆ (YY βˆ XY YXβˆ βˆ XXβˆ ) 0
XY XXβˆ 0
得到:XY XXβˆ 于是: βˆ (XX)1 XY
⃟正规方程组 的另一种写法
对于正规方程组
XY XXβˆ
XXβˆ Xe XXβˆ
于是
Xe 0
(*)
或
ei 0
(**)
X ji ei 0
i
(*)或(**)是多元线性回归模型正规方程组的另一种写法
⃟样本回归函数的离差形式
