南邮信号与系统答案第6章

合集下载

南邮信号与系统课后答案精选精品PPT课件

如图所示，试求该系统的零状态响应。
xk
hk
4
3 2
4
2 1
-2 -1 0 1 2 3 k
-2
-1 0 1 2 3 4 k
-1
解： xk 4, 2,3,2 hk 4,,1,2,1
4 2 3 2 4 1 2 1
4 2 3 2 8 4 6 4 4 2 3 2 16 8 12 8 16 12 22 5 2 7 2
k
1
uk
4 3
1k 1
8 3
0.5k 1 u k
2 3
1k 2
4 3
0.5k 2
k 1
k 1
2 3
1k
2
4 3
0.5k 2
4 3
1k
1
8 3
0.5k 1
uk
2 3
1k
1 3
0.5k
4 3
1k
4 3
0.5k
uk
21k 0.5k uk
2-25 计算下列卷积
2 2 e3tut
hh00
1 0 2 1
c1c1 0.02.55cc22
0 1
c1
c2
2
3 4
3
h0
k
2 3
1k
4 3
0.5k
uk
1
hk h0 k 2 2h0 k 1
2 3
1k 2
4 3
0.5k 2
uk
1
2
2 3
1k 1
4 3
0.5k 1 u k
2 3
1k 2
4 3
0.5k 2
第二章信号与系统的时域分析
作业
1

信号与系统第六章习题答案

z z −3 = z −1 z −1
， ε [n − 8] ↔ z
−8
z z −7 = z −1 z −1
再根据 z 变换的线性，则有：
Z [ε [n] − 2ε [n − 4] + ε [n − 8]] =
n
z 2 z −3 z − 7 z − 2 z −3 + z −7 − + = z −1 z −1 z −1 z −1
z z ，有 F1 ( z ) = z−a z +1
n
（4）令 f 1 [n] = (− 1) ε [n] ⋅ ，则根据 a nε [n ] ↔ 所以根据 z 变换的微分性质，有：
f [n] = (− 1) nε [n]⋅ = nf 1 [n]
F (z ) = − z
（5） nε [n] ↔
d z F1 (z ) = − dz ( z + 1)2
F (z) F (z) 为有理分式，则可将展开成部分分式，再乘以 z ，再利用常 z z
j π 4 −j π 4
n
n
对该级数，当 e
z
−1
< 1且 e
z
−1
< 1 ，即 z > 1 时，级数收敛，并有
1 F (z ) = × 2
1 1 − e 4 z −1
j π
1 + × 2
1 1− e
−j π 4
z −1
1 z z = + π π j −j 2 z−e 4 z−e 4

n ∞ ∞ 1 n ∞ 1 n 1 −1 n n −n F ( z ) = Z + 3 ε [n] = ∑ + 3 ε [n ]z = ∑ z + ∑ 3 z −1 n= 0 n= 0 2 2 2 n=0

信号与系统课后答案第六章作业答案

⋅
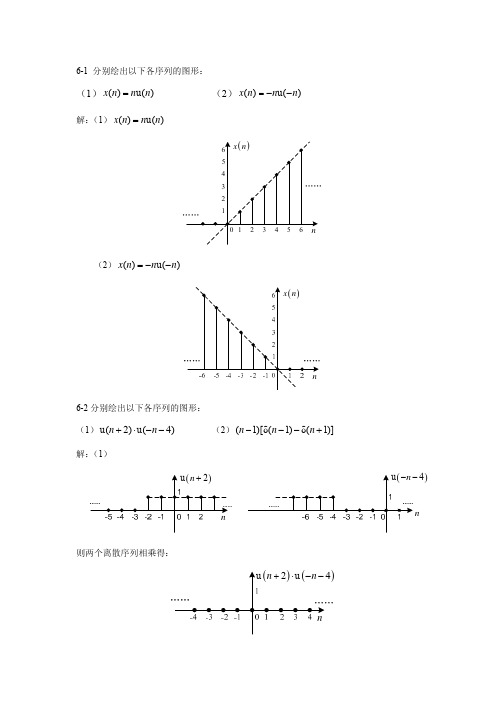
2⎤⎥⎦
⋅
u
(n
−
3)
=
2⋅
( −1)n
⎡2 ⎢⎣ k =0
( −1)− k
⎤ ⎥⎦
⋅
u
(n
−
3)
∑ y
f
(3)
=
2
⋅
(
−1)3
⎡ ⎢⎣
k
2 =0
(
−1)−k
⎤ ⎥⎦
=
2
⋅
( −1)
⋅
(1
−1
+
1)
=
−2
∑ y
f
(4)
=
2
⋅
(
−1)4
⎡ ⎢⎣
k
2 =0
(
−1)−k⎤ ⎥⎦=2⋅(1)
⋅
(1
−1
+
1)
-1
对应时刻点相乘后累加得 y(1) = 4 。由于 f1(n) 和 f2 (n) 为有限序列，故该题可采用数乘法进行计算：
11112 2 2 2 ↑ 1 1 1 1 −1 −1 −1 ↑
−1 −1 −1 −1 − 2 − 2 −2 −2 −1 −1 −1 −1 − 2 − 2 −2 −2 −1 −1 −1 −1 − 2 − 2 −2 −2
u
(
n
+
4)
（4）利用卷积的性质（ f (n) *δ(n − m) = f (n − m) ）可得：
nu(n) * δ(n + 3) = nu(n) n=n+3 = (n + 3) u(n + 3)
6-7 如题图 6-4 所示，如果 y(n) = f1(n) * f2 (n) ，则试求 y(−2)、y(0)、y(1) 的值。

信号与系统第三版第六章习题答案

1
2 t 2
cos
2 2
t ]u (t )
6.13 一个因果LTI系统的频率响应为：
5 jw 7 H ( jw) ( jw 4)[( jw) 2 jw 1]
(a) 求该系统的冲激响应
(b) 试确定由一阶系统和二阶系统构成的串联型结构 (c)试确定由一阶系统和二阶系统构成的串联型结构解:(a) 5 jw 7 1 jw 2
I 2 (w) 2 jw H ( jw) E (w) 8 jw 3
(b) 对H(jw)作反傅立叶变换可得h(t)
2 jw 1 H ( jw) 8 jw 3 4
h(t ) F 1{H ( jw)}
3 32 3 jw 8 3t 1 3 8 (t ) e u (t ) 4 32
(b) 对H(jw)作反傅立叶变换可得h(t)
3 3 3( jw 3) 2 H ( jw) 2 ( jw 2)( jw 4) ( jw 2) jw 4
3 2t h(t ) F {H ( jw)} (e e 4t )u (t ) 2 (c) 3( jw 3) 3 jw 9 Y ( w) H ( jw) 2 ( jw 2)( jw 4) ( jw) 6 jw 8 X ( w)
1 X ( w) ( jw 2) 2
Y (w) H ( jw) X (w)
2 Y ( w) 3 ( jw 2) ( jw 4)
1 1 4 2 3 ( jw 2) ( jw 2) ( jw 2) ( jw 4) 1 4 1 2
1 2t 1 2t 1 2 2t 1 4t y (t ) F {Y ( w)} ( e te t e e )u (t ) 4 2 2 4 2 2 ( jw ) 2 (c) H ( jw) ( jw) 2 2 jw 1

信号与系统第6章习题解答

d ( z 1) 2 X ( z ) z n 1 ] dz z 1 zn z 1 ( z 2) 2
z 1
d zn nz n1 )] z 1 [ ( dz z 2 z2 x(n) (2 n n 1)u (n)
( n 1)u (n)
⑵ X ( z)
X 1 ( z)
n
1 ( 2 ) u (n)z
n

n
1 ( ) n z n n 0 2
1 1 1 2z

2z 2z 1
1 1, 2z
z 1/ 2
3
1 1 1 x 2 n u n 10 2 2 2
m

z zm
z n
z a
a n
Z Z 1 a n u (n 1) Z a
6-7 （1）， X (z)
1 0.5 z 1 1 0.5 z 1
z 0.5
5
X ( z)
1 0.5 z 1 X 1 ( z) X 2 ( z) 1 (0.5 z 1 ) 1 (0.5 z 1 )
x 2 (n) 5 3 n u ( n 1) x(n) x1 n x 2 n 5u (n) 5 3 n u ( n 1)
3、留数法：因为 1<lzl<3，故是双边序列，需要分别考虑 n 0和n 0 的情况。
z 1 ，右边序列， n 0 ，在此逆时针围线内 X z z n1 有一阶极点 z=1，
1
1 1 z 2

1 1 1 2z
,
z 1, 2
1 1 2z

南邮信与系统课后答案

(3)Hz2z32zz11
解：
Hz的极点z1为 1，z2
1 2
即在单位圆上有z1 单1极，点且 z2 12位于单位圆内
因此系统为临界稳定。
5-17 对下列差分方程描系述统的画出模拟图。
( 1 ) y k 5 y k 1 6 y k 2 x k 3 x k 2
解： 1 由零极点图可得：
H
z
H
0
z
z
1 z
1
2
lim h k 1 h
k
3
由终值定理知：
h lim z 1 H z 1
z1
3
即
lim z
z1
1H
0
z
z
1 z
1
1 3
2
解得
:H
0
1 2
1z
H z 2 z 1 z 1
2
2 由 H z 可写出系统的差分方程
k0
yk
y zs k
y zi k
1 2
2 3
1k
1 3
2k ,
k0
5-11 某离散系统得模图拟5图1所如示。
Y ( s)
X (s)
z 1
z 1
3 4
1 8
求：1 求H z
Yz ； X z
2 单位函数响应hk；
3 写出系统的差分方程；
4 求系统的单位阶跃响应gk 。
解： 1 对加法器列方程得：
为：
yk 2 1 yk 1 1 yk 1 xk 1
2
2
2
对齐次方程 y k 2 1 y k 1 1 y k 0 进行 Z 变换：
2
2

信号与系统第二版课后答案

信号与系统第二版课后答案《信号与系统》（第二版）课后习题解析燕庆明主编高等教育出版社目录第1章习题解析 2 第2章习题解析 5 第3章习题解析15 第4章习题解析22 第5章习题解析30 第6章习题解析40 第7章习题解析48 第8章习题解析54第1章习题解析1-1 题1-1图示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？c d题1-1图解 a 、 c 、 d 为连续信号； b 为离散信号； d 为周期信号；其余为非周期信号； a 、 b 、 c 为有始（因果）信号。

1-2 给定题1-2图示信号f t ，试画出下列信号的波形。

[提示：f 2t 表示将f t 波形压缩，f 表示将f t 波形展宽。

]a 2 f t 2b f 2tc fd f t +1题1-2图解以上各函数的波形如图p1-2所示。

图p1-21-3 如图1-3图示，R、L、C元件可以看成以电流为输入，电压为响应的简单线性系统SR、SL、SC，试写出各系统响应电压与激励电流函数关系的表达式。

题1-3图解各系统响应与输入的关系可分别表示为；；1-4 如题1-4图示系统由加法器、积分器和放大量为a的放大器三个子系统组成，系统属于何种联接形式？试写出该系统的微分方程。

题1-4图解系统为反馈联接形式。

设加法器的输出为x t ，由于且故有即1-5 已知某系统的输入 f t 与输出y t 的关系为y t | f t |，试判定该系统是否为线性时不变系统？解设T为系统的运算子，则可以表示为：不失一般性，设f t f1 t + f2 t ，则；故有显然即不满足可加性，故为非线性时不变系统。

1-6 判断下列方程所表示的系统的性质。

1 23 4解 1 线性； 2 线性时不变； 3 线性时变； 4 非线性时不变。

1-7 试证明方程所描述的系统为线性系统。

式中a为常量。

证明不失一般性，设输入有两个分量，且则有相加得即可见即满足可加性，齐次性是显然的。

信号与系统课后习题答案

f 2 (−1) (t) =
δ (t − 2) − δ (t − 3)
*
t ε e(−t+1) (t + 1)dt
−∞
= [δ (t − 2) − δ (t − 3)]* (1 − e−(t+1) )ε (t + 1)
= (1 − e−(t−2+1) )ε (t − 2 + 1) − (1 − e−(t−3+1) )ε (t − 3 + 1)
) − iL (t) − uC (t) R1
R2
状态方程为：
⎪⎪⎧u&C (t) ⎨
=
f (t) R1C
−
uC (t) R1C
−
iL (t) C
⎪⎪⎩i&L
(t)
=
uC
(t)
− R2iL L
(t)
1．17 写出题图 1．8 系统的输入输出方程。
解：（b）系统框图等价为：
⎧x′′(t) = f (t) − 3x′(t) − 2 y(t)
x2(0-)＝1 时，y2(t)＝4e-t-2e-3t，t≥0 则 x1(0-)＝5，x2(0-)＝3 时，系统的零输入响应： yx(t)＝y(t)＝5y1(t)＋3y2(t)＝22e-t 十 9e-3t，t≥0
1．22 在题 1.21 的基础上，若还已知 f(t)＝ε(t)，x1(0-)＝0，x2(0-)＝0 时，有 y(t)＝2+e-t+2e-3t，t≥0 试求当 f(t)＝3ε(t)，x1(0-)＝2，x2(0-)＝5 时的系统响应 y(t)。解：记，f(t)＝ε(t)，x1(0-)＝0，x2(0-)＝0 时，系统响应 yf(t)＝y(t)＝2+e-t+2e-3t，t≥0 则当 f(t)＝3ε(t)，x1(0-)＝2，x2(0-)＝5 时的系统全响应 y(t)为： y(t)＝3yf(t)＋2y1(t)＋5y2(t)

南邮电磁场第6章习题解答

第6章习题解答6.1 已知空气中存在电磁波的电场强度为 ()80cos 6π102πy E e E t z =⨯+V /m试问：此波是否为均匀平面波？传播方向是什么？求此波的频率、波长、相速以及对应的磁场强度H 。

解：均匀平面波是指在与电磁波传播方向相垂直的无限大平面上场强幅度、相位和方向均相同的电磁波。

电场强度瞬时式可以写成复矢量j 0ekzy E e E -=。

该式的电场幅度为0E ，相位和方向均不变，且0z E e ⋅=⇒z E e ⊥，此波为均匀平面波。

传播方向为沿着z -方向。

由时间相位86π10t t ω=⨯ ⇒ 86π10ω=⨯ 波的频率Hz 1038⨯=f 波数2πk = 波长2π 1 m k λ== 相速p 310 m/s v kω==⨯ 由于是均匀平面波，因此磁场为j 0w w1() e kz z x E H e E e Z Z -=-⨯= 6.2 有一频率为600MHz 的均匀平面波在无界理想介质(r r 4,1εμ==)中沿x +方向传播。

已知电场只有y 分量，初相位为零，且010t t ==s 时，1x =m 处的电场强度值为800kV/m 。

试写出E 和H 的瞬时表达式。

解：根据题意，角频率812π10ω=⨯，r r 0028πk cωωεμεμεμ====，因此 80cos(12π108π)y E e E t x =⨯-由s 10=t ，m 1=x 处的电场强度值为kV /m 800，可以得到kV/m 8000=E8800cos(12π108π) kV/m y E e t x =⨯-根据电场的瞬时表达式可以写出电场的复矢量为j8π800e kV/m x y E e -=波阻抗为()0r w r 060π ΩZ μμμεεε===。

因此磁场强度复矢量为 j8πw 140() e kA/m 3πxx z H e E e Z -=⨯= 因此，磁场的瞬时表达式为840cos(12π108π)3πzH e t x =⨯- 6.3 在无界理想介质中，均匀平面波的电场强度为 ()80sin 2π102πx E e E t z =⨯-V /m已知介质的r 1μ=，试求其r ε，并写出H 的表达式。

第6章北邮信号与系统课后习题解答

a
,
z a
H (z) [h(n)] [ (n 2)] z2, z 0
Y (z)
X
(z)
H (z)
z
z a
z2 ,
z a
由于 z a ，可知 y(n) 是右边序列，因此由位移特性知
y(n) an2u(n 2)
（3）
X
(z)
[ x(n)]
[anu(n)]zz 源自a,H (z)
[h(n)]
1
2
所以
X (z)
z
z
1 2
z
z
2
（1）当
z
2 时为右边序列，
x(n)
1 n 2
2n
u(n)
（2）当
z
0.5 为左边序列，
x(n) 2n
1 2
n
u
(n
1)
（3）当 0.5
z
2 时为双边序列，
x(n)
1 2
n
u
(n)
2n
u(n
1)
6-10 解：
（1）
X
(z)
[ x(n)]
z
z
1 2
z
1 3
z
3
1 2
z
2
1 3
7
得：
X (z)
3z
z
1 2
2z
z
1 3
，收敛域为： 1 3
z
1 2
所以：
x(n)
2
1 3
n
u(n)
3
1 2
n
u
(
n
1)
（6）由题：
X (z) z

（南京邮电大学）DSP习题答案汇总~~

（南京邮电⼤学）DSP习题答案汇总~~第⼀章习题1.1 在⼀间暗室⾥通过⼀个闪光频率为8Hz 的闪光灯观察⼀个以6Hz 为频率旋转的转轮。

求转轮表现出的转速并判断观察者对转轮旋转⽅向的判断正误。

若闪光灯频率变为12Hz ，16Hz 或24Hz ，重复上述问题。

本题涉及了转轮的问题，⽤到了公式)mod(s a f f f =，当a f 和f 符号相同时，观察者能观察到正确的转动⽅向；当a f 和f 符号相反时，观察者观察到的是错误的转动⽅向；否则，观察者不能辨别转轮的⽅向。

参考课本28页例题1.4.10。

1.2 对模拟信号x(t)=10sin(2πt)+10sin(8πt)+5sin(12πt) （其中t 以秒为单位）进⾏采样，采样频率s f =5Hz ，求x(t)的重建信号)(t x a 的表达式；证明两个信号具有相同的采样值，即)()(nT x nT x a =。

若采样率s f =10Hz ，重复上述问题。

本题通过证明说明了当a f1.3 以3Hz 的频率对信号x(t)=cos(5πt)+4sin(2πt)sin(3πt)进⾏抽样（其中t 以毫秒为单位）。

求（1）x(t)的重建信号)(t x a ；（2）写出重建信号是)(t x a ，但⼜不同于x(t)的另外两个信号x 1(t)和x 2(t)。

⽤到了公式)mod(s a f f f =，参见课本19页例1.4.7。

1.9 Consider the following sound wave, where t is in millisecond: x(t )=sin(10πt )+sin(20πt )+sin(60πt )+sin(90πt )This signal is prefiltered by an analog antialiasing prefilter H (f ) and then sampled at audio rate of 40kHz.The resulting samples are immediately reconstructed using an ideal reconstructor. Determine the output ya(t ) of the reconstructor in the following cases and compare it with the audible part of x(t ):a. When there is no prefilter ,that is, H(f )≡1.b. When H(f ) is an ideal prefilter with cutoff of 20kHz.c. When H(f ) is a practical prefilter that has a flat passband up to 20kHz and attenuates at arate of 48db?ocate beyond 20kHz.(You may ignore the effects of the phase response of the filter.)1.11 Give Eq.(1.5.4), prove the inverse DTFT property (1.5.5),that is,)(f X ∧=∞-∞=∑n x(nT)ejfTnπ-2 => x(nT)=-221fs fs sf )(f X ∧ejfTnπ2df1.12 Consider a pure sinusoid of frequency f 0 , x (t )=cos(2πf 0t ). Show that the spectrum of the sampled sinusoid x (n T) is : )(f X ∧=)]()([2100s s m mf f f mf f f T ++δ+--δ∑∞-∞=第⼆章习题2．1考虑⼀个3⽐特长的双极性⼆进制补码的逐次逼近A/D 转换器，其中满量程幅度为R ＝16V 。

南京邮电学院《信号与系统》信号3.7-9,11

yzi (t) 7e2t 5e3t
全响应为y(t) yzs (t) yzi (t)
7e2t 5e3t [ 1 et e2t 1 e3t ] (t)
ቤተ መጻሕፍቲ ባይዱ
2
2
例：已知系统的传递函数H () 1 ,输入激励为 j 2
x(t) (t), 试求系统的零状态响应
解：X () () 1 j
3.7 相关函数和谱密度 (只讲3.7.1)
T
周期信号 fT (t) 的平均功率为
P
1 T
2 T
f
2 T
(t
)dt
2
平均功率也可以在频域内获得，称为帕什瓦
尔定理：
P Fn 2
n
描述平均功率随频率的分布情况。
Fn 2 ~ n 0 称为功率信号的功率谱。
非周期信号有 f (t)
1.能量信号：有能量谱密度；
了一个信号）二. 信号作用于线性系统时，频域求解其零状
态响应；直观了解输入、输出信号频谱和
系统的频率特性。
讨论信号作用于线性系统时在频域中求解零状态响应的方法，又称频域分析法。
频域分析法的理论基础是时域卷积定理。一. 系统函数 H()的意义
由线性时不变系统的数学模型
an y (n) (t) an1 y (n1) (t) a1 y'(t) a0 y(t) bm x(m) (t) bm1x(m1) (t) b1x'(t) b0 x(t)
虚指数信号之和，即单元信号是 e jt ，先求
取各个单元信号作用于系统的响应，再叠加。
实际上，电路分析中的相量法，仅仅是 e jt
取为常数，又取其实部时的情况。
或者说，相量法是频域分析法中单一频率的特例。（这也解释了虚指函数的实际意义）

南京邮电学院《信号与系统》信号3.6

冲激强度为指数形式傅里叶级数的复系数Fn乘以2
例：求 cos 0t的频谱密度函数
解：cos 0 t
1 (e j0t 2
e j0t )
F ()
( )
1 F1 F1 2
0
0
频谱密度为位于
和
0
处的冲激，冲激强度为
0
1 2
2
cos0t [ ( 0 ) ( 0 )]
4单位冲激序列T (t)
n
1e T
jn0t
1 T
e jn0t
n
T
(t)
2
T
(
n
n0 )
0 0
( )
f (t)
F ( )
(1)
( 0 )
0 T 2T t
0 020
2 傅里叶系数与傅里叶变换非周期信号的频谱密度F ( )与相应的周期信号的傅里叶复系数Fn之间的关系
F ( ) TlimTFn n0 F ( )
T (t)是以T为周期的单位冲激信号，T (t) (t nT ) n
展开为指数形式傅氏级数
T (t) Fne jn0t n
式中，Fn
1 T
T
2 T
T
(t
)e
jn0t
dt
2
T
(t)在( T 2
,
T 2
)之间为（t
),
Fn
1 T
T
2
T 2
(t)e jn0t dt
1 T
T
(t)
解： (t) () 1 j
由对称性
( )
求 ()
1
[(t)
1]
2
j(t)
() 1 (t) 1

信号与系统第1至8章习题参考解答

《信号与系统》第1~8章习题参考解答第一章 (2)第二章 (13)第三章 (22)第四章 (35)第五章 (48)第六章（无） (56)第七章 (57)第八章 (65)第一章1-4 对于例1-1所示信号，由f (t )求f (−3t − 2)，但改变运算顺序，先求f (3t )或先求f (−t )，讨论所得结果是否与原例之结果一致。

解：(1). 例1-1的方法： f (t )→ f (t − 2)→ f (3t − 2)→ f (−3t − 2) (2). 方法二：f (t )→ f (3t )→ 2[3()]3f t − →f (−3t − 2) (3). 方法三：f (t )→f (−t ) →[(2)]f t −+ →f (−3t − 2)方法三：1-5 已知()f t ，为求0()f t at −应按下列哪种运算求得正确结果（式中0t ，a 都为正值）？（1）()f at −左移0t （2）()f at 右移0t （3）()f at 左移0t a （4）()f at −右移0ta解：（4）()f at −右移t a：故（4）运算可以得到正确结果。

注：1-4、1-5 题考察信号时域运算：1-4 题说明采用不同的运算次序可以得到一致的结果； 1-5 题提醒所有的运算是针对自变量t 进行的。

如果先进行尺度变换或者反转变换，再进行移位变换，一定要注意移位量和移位的方向。

1-9 粗略绘出下列各函数式的波形图：（1）()(2)()t f t e u t −=− （2）2()(36)()t t f t e e u t −−=+ （3）3()(55)()t t f t e e u t −−=−（4）()cos(10)[(1)(2)]t f t e t u t u t π−=−−− 解：（1）()(2)()tf t e u t −=−（2）2()(36)()ttf t e eu t −−=+（3）3()(55)()ttf t e eu t −−=−（4）()cos(10)[(1)(2)]tf t e t u t u t π−=−−−1-12 绘出下列各时间函数的波形图，注意它们的区别：（1）[()(1)]−−；t u t u t（2）(1)�；t u t−（3）[()(1)](1)−−+−；t u t u t u t（4）(1)(1)−−；t u t（5）(1)[()(1)]−−−−；t u t u t（6）[(2)(3)]−−−；t u t u t（7）(2)[(2)(3)]t u t u t−−−−。

南邮信号与系统课后答案第三章

3-14
如题图 3 14 所示信号 f t F ，在不求出前提下，求
1
F 的
f t
(1) F 0 F 0
-1
0
1
t
解： F 0 F 0

f t e
j t
dt
0

f t dt
f 1 t
1
(a)
2 5
0
-1
2 5
t
2 2 解： f 1 t cos 10 t u t u t cos 10 tg 4 t 5 5 5 2 f t g 4 t Sa F 5 5 5 4 f 1 t 1 2
y 1 t
H 2
cos 2 t
4 5
sin 2 t cos 2 t 127
4 5 Ae
j

另解：
1 j2 1 j2
j
e
j 127

y t A cos 2 t cos 2 t 127

1 10
g 10 t Sa 5 1 10 5
1 10 , A 10
Sa 5 t 2
g 10
对称性
u 5 u 5

g 10

5
3-8
已知 f t F ，求下列函数的傅里叶
2 j
F e
2 j
t ( 6 ) t 2 f 2

南邮信号与系统文字概念题集锦(借鉴相关)

文字概念题集锦第一章：1. 按时间函数的可积分性，信号可以分为功率信号、能量信号、非功非能信号。

一个信号不可能同时既是功率信号，又是能量信号。

一般说来周期信号都是功率信号；2. 信号的特性可以从两方面来描述，即时间特性和频率特性。

3.按函数时间取值的连续性，确定信号可以分为连续时间信号和离散时间信号。

连续信号在不连续点处的导数为冲激信号。

4.信号的计算包括信号的相加和相乘，信号的导数与积分，信号的时移和折叠及信号的尺度变换。

5.信号有哪些分类？答：确定信号和随机信号，连续信号和离散信号，周期信号和非周期信号，能量信号和功率信号。

6.如果信号不仅在时间取值是离散的，在幅度取值上是量化的，称此信号为数字信号。

7.系统的定义：系统是由若干个相互作用和相互依赖的事物组合而成的具有特定功能的整体。

8. 输入和输出均为连续时间信号的系统称为连续时间系统.9. 请具体描述线性系统具备的三个条件。

答：分解性：指全响应可以分为零输入响应和零状态响应相加；零状态线性：指系统有多个输入时，零状态响应对每个输入都呈线性；零输入线性：指系统有多个初始状态时，零输入响应对每个初始状态都呈线性。

10、所谓线性特性是指齐次性和叠加性。

11、连续系统的模拟一般需要加法器、标量乘法器和积分器。

12、线性系统具有分解特性、零状态线性、零输入线性13、简述线性系统的判断条件。

答；线性系统要满足齐次特性和叠加特性。

14、简述时不变系统的判断条件。

答；输入信号延迟t0时刻作用到系统，若输出信号也延迟t0时刻，则该系统为时不变系统。

15、因果系统是响应不会超前激励的系统，非因果系统是响应领先于激励的系统，是一种非真实系统。

16.简述因果系统的定义。

答：响应不超前于激励的系统称为因果系统17、简述连续信号和离散信号的概念，并从日常生活中举一两个连续信号和离散信号的例子。

答：在整个时间轴上有定义的信号称为连续信号，在某个具体时刻有定义的信号称为离散信号。

南京邮电大学信号与系统习题2

2
t
t

( c ) 当 2 t 3时, y (t ) （ 2)d 2
1
2 1
0 1 2
2
( d ) 当 3 t 4时,
t 2
2 1 0 1 2
(e) 当 t 4时, y (t ) 0
ZB

《信号与系统》SIGNALS AND SYSTEMS
t
2 1 0 1 2

(b) 当 1 t 2时, y (t ) （ 2)d 2
1

t
x( ) h( ) (t ) x( ) h( ) (t ) x( ) h( ) (t ) x x x
2 2 2 t 2 1
0 1 2
2

2 1
0
2

(a ) 当 t 1时, y (t ) 0
(b) 当 1 t 2时, y ( t ) （ 2 t ) d 2
h(t ) x( ) h( ) 2 t
2 1
0
t 1
h(t ) x( ) h( ) 2 t
2
h(t ) x( ) h( ) 2 t
e e

(5) et (t ) * cost (t )
2t t
e e

2 ( t )
d e
2t

t
t
e 2t (e t 0) e
t
e d

t
e(t ) cosd (t ) et
t
0

e cosd (t )
《信号与系统》SIGNALS AND SYSTEMS 3

信号与系统第6章课后习题答案

z -1 (6) F ( z ) = (1 - 6 z -1 ) 2 分子分母同乘z 2得： z F ( z) = ( z - 6)2 根据z变换z域微分特性 dF ( z ) nf (n) « - z dz z -a az n × a nU (n) « - z ( ) ' = - z[ ] = z-a ( z - a) 2 ( z - a) 2 1 \ Z -1[ F ( z )] = × n × 6n U (n) 6
（3）
4 z ( z + 2) 4 z 2 + 8z 4 + 8 z -1 Y ( z) Q H ( z) = = 2 = = ( z + 3)( z + 1) z + 4 z + 3 1 + 4 z -1 + 3z -2 X ( z )
\ Y ( z ) + 4 z -1Y ( z ) + 3 z -2Y ( z ) = 4 X ( z ) + 8 z -1 X ( z ) 系统差分方程为： y (n) + 4 y (n - 1) + 3 y (n - 2) = 4 x( n) + 8 x( n - 1)
解：
np p + )U (n) 2 4
(2) f (n) = 0.5n U (n) + d (n - 2) 0.5n U (n) « z z - 0.5
d ( n) « 1
Q f ( n ± m) « z ± m F ( z ) \ d (n - 2) « z -2 综上，根据z变换的线性性质： 0.5n U (n) + d (n - 2) « z + z -2 z - 0.5
Þ
F ( ) =

南京邮电学院《信号与系统》第二次习题课

Fn
S a(n )
10
A F()
包络线是一取样函数，
其图形如左
2 2
零交点位置 2 , 4
即当 nk(k1,2,3 ) 时，频谱的幅值为0。
10
此时
n 1,2 0,3 0, 0
频率 n 0 f5 K 0 ,1 H K 0Z ,1 H 0K 5Z H 0 Z 所以不能选出50 KHz，100 KHz频率分量。
2. Fn ~n0 是偶函数； Fn~n0 是奇函数。
3. 偶函数；奇函数，奇虚函数和偶谐函数的特点。
4. 单边频谱、双边频谱会画。实偶函数的频谱是实偶函数；
实奇函数的频谱是虚奇函数。 5. 周期信号的功率谱 Fn 2 ~n0
平均功率: P T 1 T 2 T 2f2(t)dt, P n F n2A 0 22 1n 1A n 2
再均移位 5.7、放大 5 倍，即可。
（四）非周期能量信号的能量谱密度：
F() 2 ~
非周期能量信号的能量：
E f2(t)d t, E 1F ()2d
2
信号的脉冲宽度和频带宽度
单个矩形脉冲： t2
（五）系统不失真传输的条件：
时域表示：
y(t)K x(ttd)
频域表示： H () H ( ( )) K td
f4(t)
-1 0 1 t -2
f3(t)f1( t)
F1()
R 1()j1 I()
f4(t) f1 ( t)
F1()
R 1()j1 I()
f5(t) 2
f5 (t) f1 (t) f1 ( t)
-1 0 1 t -2
F 1()F 1( )
2j I1()
3 f6(t) -1 0 1