南邮信号与系统课后答案第二章
南邮信号与系统课后答案精选精品PPT课件

如图所示,试求该系统的零状态响应。
xk
hk
4
3 2
4
2 1
-2 -1 0 1 2 3 k
-2
-1 0 1 2 3 4 k
-1
解: xk 4, 2,3,2 hk 4,,1,2,1
4 2 3 2 4 1 2 1
4 2 3 2 8 4 6 4 4 2 3 2 16 8 12 8 16 12 22 5 2 7 2
k
1
uk
4 3
1k 1
8 3
0.5k 1 u k
2 3
1k 2
4 3
0.5k 2
k 1
k 1
2 3
1k
2
4 3
0.5k 2
4 3
1k
1
8 3
0.5k 1
uk
2 3
1k
1 3
0.5k
4 3
1k
4 3
0.5k
uk
21k 0.5k uk
2-25 计算下列卷积
2 2 e3tut
hh00
1 0 2 1
c1c1 0.02.55cc22
0 1
c1
c2
2
3 4
3
h0
k
2 3
1k
4 3
0.5k
uk
1
hk h0 k 2 2h0 k 1
2 3
1k 2
4 3
0.5k 2
uk
1
2
2 3
1k 1
4 3
0.5k 1 u k
2 3
1k 2
4 3
0.5k 2
第二章 信号与系统的时域分析
作业
1
南京邮电学院《信号与系统》第一次习题课

此时F1() 与F2(t-)无重叠, F1(t) *F2(t) =0;
b.当-1≤t-0.5(头部进入)并且t-3.5<-1(尾部
没有进入)时,即 -0.5≤t<2.5,如图④
图④ F2(t-)
F1()
此时
-3.5+t -1 0 -0.5+t
t 0.5
y(t) 1
F10 ( )F 2[(t 1) (t 1)]
-1 0 1 tt
F2(t) 3
01 4 t
F2 (t)
(t 1)[ (t 1) (t 4)]
F3(t) 2 24
0
t
-2
F3(t) 2t[(t) (t 1)] 2(t 2)[(t 1) (t 3)] 2(t 4)[(t 3) (t 4)]
四、已知函数的波形如图所示:
f1(t) 1
0 123
f2(t)
(1)
(1)
1
t
t
-0.5 (1)
1.5
求: (a) f 1(t) f 2(t)
f3(t)
(1)
(1)
-1 0 1
t
(b) f 1(t) f 3(t) f 3(t)
(c) {[ f 1(t) f 3(t)][(t 1) (t 3)]} f 3(t)
c.当t-3.5≥-1(尾部进入)并且t-0.5<3(头部 没有出来)时,即 2.5≤t<3.5,如图⑤
图⑤
F2(t-) F1()
-1 –3.5+t-0.5+t 3
此时
t 0.5
y(t) t3.5 F10 ( )F20 (t )d
d.当t-3.5<3(尾部没有出来),t-0.5≥3(头 部已出来)时,即 3.5≤t<6.5,如图⑥
《信号与系统》第二章习题解答

yt xt ht
(b) If d y t dctontains only three
value of a?
discontinuities,what is the
Solution :
yt
a
0 a 1 1+a t
5
Chapter 2
Problems Solution
2.11 Let xt ut 3 ut 5 ht e3tut
a
u0 tcostdt
cost
1
t0
b
5
0
sin2t t 3dt 0
c
5
5
u1 1
cos2
d
1 t
6 4
u1tcos2 1tdt
1cos2t 0 t 0
8
Chapter 2
Problems Solution
2.22a
xt ht
e e
tut
信号与系统 第二章习题 王老师经典解法(青岛大学)小白发布
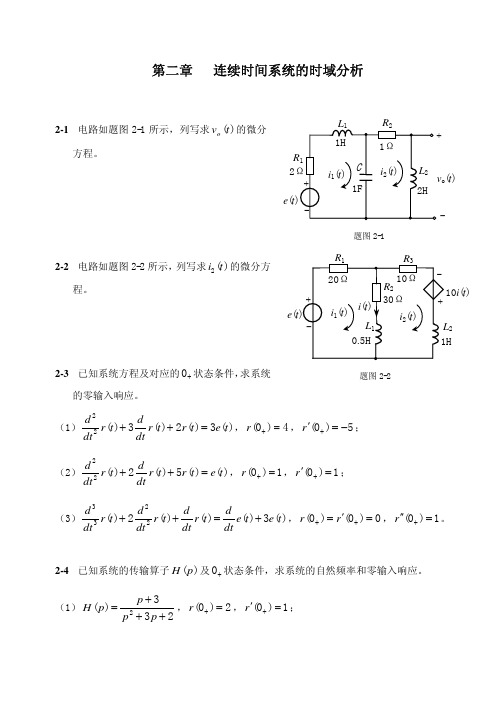
2-16 已知 f1 (t ) =
画出下列各卷积的波形。 (1) s1 (t ) = f1 (t ) ∗ f 2 (t ) ; (2) s2 (t ) = f1 (t ) ∗ f 2 (t ) ∗ f 2 (t ) ; (3) s3 (t ) = f1 (t ) ∗ f 3 (t ) 。
2-17 求题图 2-17 所示电路在 e(t ) = (1 + 2e
第二章
连续时间系统的时域分析
2-1 电路如题图 2-1 所示,列写求 vo (t ) 的微分 方程。
L1 1H R1 2Ω + e(t) i 1 (t )
R2 1Ω + L2 2H 题图 2-1
C
1F
i 2 (t )
vo(t)
2-2 电路如题图 2-2 所示, 列写求 i2 (t ) 的微分方 程。
题图 2-18
−2 t
− 1)U (t ) , 试利用卷积的性质求题
1 0 -1
e2(t)=tU(t) 1 t 0
e3(t)
t 0 1
2-19 一线性时不变的连续时间系统,其初始状态一定,当输入 e1 (t ) = δ (t ) 时,其全响应
r1 (t ) = −3e − tU (t ) ; 当 输 入 e2 (t ) = U (t ) 时 , 其 全 响 应 r2 (t ) = (1 − 5e − t )U (t ) 。 求 当 输 入 e(t ) = tU (t ) 时的全响应。
2-14 计算卷积 f (t ) = f 1 (t ) ∗ f 2 (t ) ,其中 f1 (t ) = sgn(t − 1) , f 2 (t ) = e 2-15 求下列卷积 (1) f1 (t ) = e
南京邮电学院《信号与系统》第二次习题课PPT课件

数F3()。
18
解:(1)对于f1(t),求其导数f1’(t)
f1(t) 1
f1(t) ()S( a 2)•ej 2ejT
0
1 Tt
f1’(t)
Sa()•ej2 ejT
1
T
f1(t)F1()
2
j
0 1 (1) t
19
由图可看出
f2(t)f1( tT)
f1(t)
F 2 () F 1 ()• e j T
35
(五(1 ))求[下( 列 信5 号) 的傅( 氏 反5 变)换• ]co s
5
解:由公式 ( t 5 ) ( t 5 ) 1 0 S a 5
由对称性 1 0 S a 5 t 2 ( 5 ) ( 5 )
由公式 co s 5 5 tS a5 t ( ( 5 )5 ) ( ( 55 ) ) (t 5)(t 5) 2cos5 36
周期矩形脉冲:幅高A,周期 T,脉宽
Fn
A
T
Sa(n0)
2
…
-2T
f(t)
A
-T
-/2 /2
T
…
2T
4
(二)非周期信号
1. 傅里叶变换 正反变换的定义式;
2. 频谱密度F()的物理意义;
3. 周期信号fT (t) 的复系数 Fn 与非周期信号 f (t ) 的频谱密度F()的关系;
F ()
cost[(t1)(t1)] 则
2 fa(t)
1
fa ( t) fa 0 ( t 2 ) fa 0 ( t) fa 0 ( t 2 )
(t 1 ) (t 1 ) 1 •2 S( a •2 ) 2 S( a )
fa0(t) S( a 2) 2 S( a 2)
南邮信号与系统课后答案第二章 ppt课件

xk
yk
h1k
h3 k
h2k
解: hkkh1kh2kh3kh3kh1kh3kh2kh3k
1kukuk1kukk11kuk
2
2
2
2kuk22kuk2k1uk12uk2k1uk1
2k2uk12k1uk12k22k1uk1
1 k 2
4 3
0.5k 2
k 1
k 1
2 3
1k 2
4 3
0.5k 2
4 3
1k 1
8 3
0
.5
k
1
u
k
2 3
1k
1 3
0.5k
4 3
1k
4 3
0.5k
u k
2 1k 0.5k uk
2-25 计算下列卷积
2 2e3tut
解原 : 式 e3tut2e3tut2ut
1 uk 1 1 uk 3
n 1
n 1
kuk 1 k 2uk 3
k k 1 k 2 uk 3 k 2uk 3
k k 1 k k 2 2uk 3
k k 1 k k 2 2uk 3
k 1
k2
k 1 2 k 2 2uk 3
k 1 2uk 2
(1)yk10.5ykxk1,xk1kuk
3
解: 设h0k 10.5h0k k
特征方程: 0.5 0 特征根: 0.5
h0k c10.5k uk 1
h011 0.5c1 c2 h0k20.5kuk1
h k h 0 k 1 2 0 . 5 k 1 u k 0 . 5 k u k
ykxkh k 1 kuk0 .5 kuk
3
k
信号与系统第二章习题与答案

第二章习题与答案1.求以下序列的z 变换并画出零极点图和收敛域。
分析:Z 变换概念∑∞-∞=-==n nzn x z X n x Z )()()]([,n 的取值是)(n x 的有值范围。
Z 变换的收敛域 是知足∞<=∑∞-∞=-M zn x n n)(的z 值范围。
解:(1) 由Z 变换的概念可知:∞====<<<<z z az a z az a z a az ,0 1, 11,1 零点为:极点为:即:且收敛域:)(21)()2(n u n x n⎪⎭⎫⎝⎛=)1(21)()3(--⎪⎭⎫⎝⎛-=n u n x n)1(,1)()4(≥=n nn x 为常数)00(0,)sin()()5(ωω≥=n n n n x 10,)()cos()()6(0<<+=r n u n Ar n x n Φω)1||()()1(<=a an x nnn nzaz X -∞-∞=⋅=∑)(nn n nn n z a za-∞=---∞=-∑∑+=1nn n nn n z a z a -∞=∞=∑∑+=01))(1()1()1)(1(1111212a z az a z a az az a za az az ---=---=-+-=-解:(2) 由z 变换的概念可知:n n nz n u z X -∞-∞=∑=)()21()( ∑∞=-=0)21(n n n z 12111--=z 211121><⋅z z 即:收敛域: 0 21==z z 零点为:极点为:解:(3)nn n z n u z X -∞-∞=∑---=)1()21()(∑--∞=--=1)21(n n n z∑∞=-=12n n n z zz212--= 12111--=z 21 12 <<z z 即:收敛域:0 21 ==z z 零点为:极点为: 解: (4) ∑-⋅∞==11)(n nz n z X∑∞--=-=•••11)(1)(n n z n n dz z dX 21)(11z z z n n -=-=∑∞=-- ,1||>z。
信号与系统课后答案 第2章 习题解

第2章 习 题2-1 求下列齐次微分方程在给定起始状态条件下的零输入响应(1)0)(2)(3)(22=++t y t y dt d t y dt d ;给定:2)0(,3)0(==--y dt dy ; (2)0)(4)(22=+t y t y dt d ;给定:1)0(,1)0(==--y dtd y ;(3)0)(2)(2)(22=++t y t y dt d t y dt d ;给定:2)0(,1)0(==--y dt dy ; (4)0)()(2)(22=++t y t y dt d t y dt d ;给定:2)0(,1)0(==--y dtdy ; (5)0)()(2)(2233=++t y dt d t y dt d t y dt d ;给定:2)0(,1)0(,1)0(22===---y dt d y dt d y 。
(6)0)(4)(22=+t y dt d t y dt d ;给定:2)0(,1)0(==--y dtdy 。
解:(1)微分方程的特征方程为:2320λλ++=,解得特征根:121, 2.λλ=-=- 因此该方程的齐次解为:2()t th y t Ae Be --=+.由(0)3,(0)2dy y dt--==得:3,2 2.A B A B +=--=解得:8, 5.A B ==- 所以此齐次方程的零输入响应为:2()85tty t e e--=-.(2)微分方程的特征方程为:240λ+=,解得特征根:1,22i λ=±.因此该方程的齐次解为:()cos(2)sin(2)h y t A t B t =+.由(0)1,(0)1d y y dx --==得:1A =,21B =,解得:11,2A B ==. 所以此齐次方程的零输入响应为:1()cos(2)sin(2)2y t t t =+.(3)微分方程的特征方程为:2220λλ++=,解得特征根:1,21i λ=-± 因此该方程的齐次解为:()(cos()sin())th y t e A t B t -=+.由(0)1,(0)2dy y dx--==得:1,2,A B A =-= 解得:1,3A B ==.所以齐次方程的零输入响应为:()(cos()3sin())ty t e t t -=+.(4)微分方程的特征方程为:2210λλ++=,解得二重根:1,21λ=-.因此该方程的齐次解为:()()th y t At B e -=+. 由(0)1,(0)2dy y dx--==得:1,2,B A B =-=解得:3, 1.A B == 所以该方程的零输入响应为:()(31)ty t t e -=+.(5)微分方程的特征方程为:3220λλλ++=,解得特征根: 1,21λ=-,30λ=. 因此该方程的齐次解为:()()th y t A Bt C e -=++.由22(0)1,(0)1,(0)2d d y y y dx dt---===得:1,1,22A C B C C B +=-=-=. 解得:5,3,4A B C ==-=-.所以方程的零输入响应为:()5(34)ty t t e -=-+.(6)微分方程的特征方程为:240λλ+=,解得特征根:120,4λλ==-. 因此该方程的齐次解为:4()th y t A Be -=+.由(0)1,(0)2d y y dx --==得:1,42A B B +=-=.解得:31,22A B ==-. 所以此齐次方程的零输入响应为:431()22ty t e -=-.2-2 已知系统的微分方程和激励信号,求系统的零状态响应。
2信号与系统-每章课后答案第二章作业PPT课件

21.11.2020
7
2.7 写出下列信பைடு நூலகம்的波形图。
(a)f(t)u(4t2)
( b ) f( t ) ( t 2 ) 3 ( t 2 ) 2 ( t )
(c) f (t) (34t) 1 (t - 3)
-4 4
1(t - 3)
44
21.11.2020
8
2.8 设 f (t) 在 t 0 及 t 8 时 f(t), 0 , f(0 )且 4 ;已知 f(t)f(2t) 的波形如图所示,试确定 f (t) 的波形。
请对以下连续时间系统确定哪些性质成立、哪些不成立,
并陈述你的理由。下列中 y(t) 和 x (t ) 分别记作系统的输出和
输入。
(a)y(t) dx(t) dt
时不变、线性、因果、 稳定
( b) y(t)co3t)sx((t) 时变、线性、因果、稳 定
(c)y(t) 2t x()d
(d)y(t) x(t ) 3
的波形。
21.11.2020
6
2.6 写出信号 f1(t) 和 f2 (t) 的表达式。
f1(t)u(t)u(t2) f 2 ( t ) - u ( t 1 ) ( t 1 ) u ( t 1 ) ( t 1 ) u ( t 1 ) 2 u ( t 1 ) u ( t 2 )
- 0(t)3(t)d t-3
(3)4(t-5)(t)dt4(t5 )22(t)d t4(-1 -)4
-3
2
-3
( 4)(t2t2)(2t)dt(t2t2)1(t)d t121
-
-
2
2
(5)t (t2)(t2)dt4t (t2)d t4u(t2)
信号与系统第二章答案

f (n ) x (n ) y ( n) ,欲使 f (n ) 是周期的,必须有 N 0 kN1 mN 2
(h)
(i)
(j)
x (n ) 2 cos( n / 4) sin( n / 8) 2 sin( n / 2 / 6) x (t ) 2 cos(3t / 4) ,周期信号, T
2 3
。
解:(a)
(b)
x (n ) cos(8 n / 7 2) ,周期信号, Q 0 x (t ) e j ( t 1) ,周期信号, T 2 。
(c)
(a)
h (t 3)
(b)
h (1 2t )
(3) 根据图 P2.1(a) 和(b) 所示的
x (t ) 和 h (t ) ,画出下列各信号的波形图,并加以标注。
(b)
(a)
x(t )h(t )
x(1 t )h(t 1)
(c)
t x (2 )h (t 4) 2
图 P2.1 解:(1) 各信号波形如下图所示:
(d)
x (n ) e j (n / 8 )
(e)
x (n ) (n 3m ) (n 1 3m)
m 0
(f)
x (t ) cos 2 t u (t ) x (t ) Ev cos 2 t u (t )
(g)
x (n ) cos( n / 4) cos( n / 4) x (t ) Ev cos(2 t / 4) u (t )
(b) 不正确。设
x (n ) g (n ) h (n ) ,其中 g ( n) sin
n ,对所有 n , 4
信号与系统第二版课后答案

信号与系统第二版课后答案《信号与系统》(第二版)课后习题解析燕庆明主编高等教育出版社目录第1章习题解析 2 第2章习题解析 5 第3章习题解析15 第4章习题解析22 第5章习题解析30 第6章习题解析40 第7章习题解析48 第8章习题解析54第1章习题解析1-1 题1-1图示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号?c d题1-1图解 a 、 c 、 d 为连续信号; b 为离散信号; d 为周期信号;其余为非周期信号; a 、 b 、 c 为有始(因果)信号。
1-2 给定题1-2图示信号f t ,试画出下列信号的波形。
[提示:f 2t 表示将f t 波形压缩,f 表示将f t 波形展宽。
]a 2 f t 2b f 2tc fd f t +1题1-2图解以上各函数的波形如图p1-2所示。
图p1-21-3 如图1-3图示,R、L、C元件可以看成以电流为输入,电压为响应的简单线性系统SR、SL、SC,试写出各系统响应电压与激励电流函数关系的表达式。
题1-3图解各系统响应与输入的关系可分别表示为;;1-4 如题1-4图示系统由加法器、积分器和放大量为a的放大器三个子系统组成,系统属于何种联接形式?试写出该系统的微分方程。
题1-4图解系统为反馈联接形式。
设加法器的输出为x t ,由于且故有即1-5 已知某系统的输入 f t 与输出y t 的关系为y t | f t |,试判定该系统是否为线性时不变系统?解设T为系统的运算子,则可以表示为:不失一般性,设f t f1 t + f2 t ,则;故有显然即不满足可加性,故为非线性时不变系统。
1-6 判断下列方程所表示的系统的性质。
1 23 4解 1 线性; 2 线性时不变; 3 线性时变; 4 非线性时不变。
1-7 试证明方程所描述的系统为线性系统。
式中a为常量。
证明不失一般性,设输入有两个分量,且则有相加得即可见即满足可加性,齐次性是显然的。
信息论第二章答案(南邮研究生作业).doc

2-1 同时掷两个正常的骰子,也就是各面呈现的概率都是1/6,求:(1)“3和5同时出现”这事件的自信息量。
(2)“两个1同时出现”这事件的自信息量。
(3)两个点数的各种组合(无序对)的熵或平均信息量。
(4)两个点数之和(即2,3,…,12构成的子集)的熵。
(5)两个点数中至少有一个是1的自信息。
解:(1)bitx p x I x p i i i 170.4181log )(log )(18161616161)(=-=-==⨯+⨯=(2)bit x p x I x p i i i 170.5361log)(log )(3616161)(=-=-==⨯=(3)两个点数的排列如下: 11 12 13 14 15 16 21 22 23 24 25 26 31 32 33 34 35 36 41 42 43 44 45 46 51 52 53 54 55 56 61 62 63 64 65 66共有21种组合:其中11,22,33,44,55,66的概率是3616161=⨯ 其他15个组合的概率是18161612=⨯⨯symbol bit x p x p X H ii i / 337.4181log 18115361log 3616)(log )()(=⎪⎭⎫ ⎝⎛⨯+⨯-=-=∑(4)参考上面的两个点数的排列,可以得出两个点数求和的概率分布如下:symbolbit x p x p X H X P X ii i / 274.3 61log 61365log 365291log 912121log 1212181log 1812361log 3612 )(log )()(36112181111211091936586173656915121418133612)(=⎪⎭⎫ ⎝⎛+⨯+⨯+⨯+⨯+⨯-=-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎥⎦⎤⎢⎣⎡∑(5)bitx p x I x p i i i 710.13611log )(log )(3611116161)(=-=-==⨯⨯=2-2 设有一离散无记忆信源,其概率空间为[]⎥⎦⎤⎢⎣⎡=====8/14/14/18/332104321x x x x P X(1) 求每个符号的自信息量;(2) 若信源发出一消息符号序列为(202 120 130 213 001 203 210 110 321 010 021 032 011 223 210),求该消息序列的自信息量及平均每个符号携带的信息量。
信号与系统课后答案2
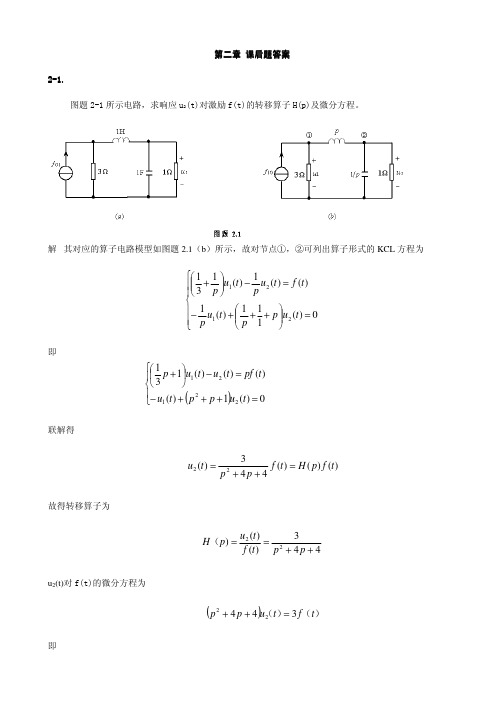
A1e −2t
+
2 A2e−8t
故有
uc (0+ ) = A1 + A2 = 6
i(0+ )
=
1 2
A1
+
2 A2
=
0
联解得 A1-=8,A2=-2。故得
uc (t) = 8e−2t − 2e−8t V t ≥ 0
又得
i(t) = −C duc = 4e−2t − 4e−8t A t ≥ 0 dt
1 1
+
p u2 (t)
=
0
即
1 3
p
+ 1u1 (t )
− u2 (t)
=
pf
(t)
( ) − u1(t) + p2 + p +1 u2 (t) = 0
联解得
u2 (t) =
p2
3 + 4p + 4
f (t) =
H ( p) f (t)
故得转移算子为
H(p) =
u2 (t) f (t)
=
p2
3 + 4p + 4
f1(t −1) − f1(t − 2) + f1(t − 3)
y2(t)的波形如图题 2.10(d)所示 2-11.
d f (t)
试证明线性时不变系统的微分性质与积分性质,即若激励 f(t)产生的响应为 y(t),则激励 dt
产生
∫ ∫ d
的响应为 dt
y(t)
(微分性质),激励
t −∞
f (τ )dτ
故得
3 3
进一步又可求得 uc(t)为
uc
(t )
信号与系统第二章习题答案

(− 3C1 + 3C2 )δ (t ) + (C1 + C2 )δ ' (t ) − (− 2C1 + C 2 )δ (t ) = δ (t )
h (t ) = C1e −2t + C2 e t ε (t )
对上式求一阶、二阶导数,得
(
)
h ' (t ) = − 2C1e −2t + C 2e t ε (t ) + C1e −2t + C2 e t δ (t )
(
)
(
t
)
h '' (t ) = 4C1e −2 t + C2 e t ε (t ) + − 2C1e −2t + C 2e t δ (t ) + − 2C1e − 2t
d 2e (t ) d 2i1 (t ) di1 (t ) di 2 (t ) = 4 + 6 + 2 dt 2 dt 2 dt dt
将⑴式、⑸式代入⑽式中,得到:
⑾
对⑾式求导,得到:
⑿
再将⑴式代入⑿式中,得到 i1 (t ) 的微分方程为:
64
d 2e (t ) d 2i1 (t ) di1 (t ) = 4 + 6 + 4i1 (t ) dt 2 dt 2 dt
⑼
再将⑴式代入⑼式中,得到 i 2 (t ) 的微分方程为:
2
d 2i 2 (t ) di 2 (t ) de(t ) + 3 + 2i 2 (t ) = 2 dt dt dt
⑽
对⑹式求一阶导,得到:
di (t ) di (t ) du (t ) de(t ) = 4 1 +2 2 + c dt dt dt dt di (t ) de(t ) = 4 1 + 6i1 (t ) + 2i2 (t ) dt dt
信号与系统的课后答案

(1)
(2) 利用(1)的结果,证明阶跃响应
证(1)因为
y(t)=f(t)h(t)
由微分性质,有
y(t)=f(t)h(t)
再由积分性质,有
(2)因为
s(t)=(t)h(t)
由(1)的结果,得
3-1求题3-1图所示周期信号的三角形式的傅里叶级数表示式。
题3-1图
解对于周期锯齿波信号,在周期( 0,T)内可表示为
3-5试求下列信号的频谱函数。
(1)
(2)
解(1)
(2)
3-6对于如题3-6图所示的三角波信号,试证明其频谱函数为
题3-6图
证因为
(
0,|t| >
则
3-7试求信号f(t) = 1 + 2cost+ 3cos3t的傅里叶变换。
解因为
12()
2cost2[(1)+(+ 1)]
3cos3t3[(3)+(+ 3)]
(t+ 3 ) *(t5 )=
也可以利用迟延性质计算该卷积。因为
(t) *(t)=t(t)
f1(tt1) *f2(tt2)=f(tt1t2)
故对本题,有
(t+ 3 ) *(t5 )=(t+ 35)(t+ 35)=(t2)(t2)
两种方法结果一致。
(c)tet(t) *(t)= [tet(t)]= (ettet)(t)
故其变换
式中,F()为f(t)的频谱。x(t)的频谱图如图p4-7所示。
图p4-7
4-8题4-8图所示(a)和(b)分别为单边带通信中幅度调制与解调系统。已知输入f(t)的频谱和频率特性H1()、H2()如图所示,试画出x(t)和y(t)的频谱图。
信号与系统第二版课后答案

所以三角级数为
3-2求周期冲激序列信号
的指数形式的傅里叶级数表示式,它是否具有收敛性?
解冲激串信号的复系数为
所以
因Fn为常数,故无收敛性。
3-3设有周期方波信号f(t),其脉冲宽度= 1ms,问该信号的频带宽度(带宽)为多少?若压缩为0.2ms,其带宽又为多少?
解对方波信号,其带宽为 Hz,
当1= 1ms时,则
(2)
(3)
(4)
解(1)t(t1 )=(t1 )
(2)
(3)
(4)
2-6设有题2-6图示信号f(t),对(a)写出f(t)的表达式,对(b)写出f(t)的表达式,并分别画出它们的波形。
题2-6图
解(a)
f(t) =(t2 ),t= 2
2(t4 ),t= 4
(b)f(t) =2(t)2(t1)2(t3)+ 2(t4)
图p2-6
2-7如题2-7图一阶系统,对(a)求冲激响应i和uL,对(b)求冲激响应uC和iC,并画出它们的波形。
题2-7图
解由图(a)有
即
当uS(t) =(t),则冲激响应
则电压冲激响应
对于图(b)RC电路,有方程
即
当iS=(t)时,则
同时,电流
2-8设有一阶系统方程
试求其冲激响应h(t)和阶跃响应s(t)。
故对应的变换
所以
5-4用部分分式法求下列象函数的拉氏反变换。
(1)
(2)
(3)
(4)
解(1)
故有
所以
(2)
可得
又
可得
B= 0,C= 1
所以
证明不失一般性,设输入有两个分量,且
则有
相加得
信号与系统理论及应用 习题 - 第2章-作业参考答案

=
1 2
������2
=
2������ 6������
=
1 3
∴T = 1 ������0 = 2������ x(t) = cos(4πt + 5) − sin(6πt − 2)
= 1 (������������(4������������+5) + ������−������(4������������+5)) − 1 (������������(6������������−2) − ������−������(6������������−2))
=
������ 2
−
2
������−3
=
2
−
������ 2
(a)振幅谱
(b)相位谱
2.3 已知周期信号 x(t)的傅立叶级数展开式系数 Xk 如图所示分布,求 x(t)的表达式。
解:
5 4 3
Xk
5
4
3
-3 -2 -1 1 2 3 (k 0 )
题 2.3 图
∞
x(t) = ∑ ������������������������������������0������
������������
������������
由对称性得:
2 ↔ 2������������������������(−������)
������������
∴1
������
↔
������������������������������(−������)
=
{−������������������������,,
=
8 ������������0
[1
南京邮电大学信号与系统习题2

t
t
( c ) 当 2 t 3时, y (t ) ( 2)d 2
1
2 1
0 1 2
2
( d ) 当 3 t 4时,
t 2
2 1 0 1 2
(e) 当 t 4时, y (t ) 0
ZB
《信号与系统》SIGNALS AND SYSTEMS
t
2 1 0 1 2
(b) 当 1 t 2时, y (t ) ( 2)d 2
1
t
x( ) h( ) (t ) x( ) h( ) (t ) x( ) h( ) (t ) x x x
2 2 2 t 2 1
0 1 2
2
2 1
0
2
(a ) 当 t 1时, y (t ) 0
(b) 当 1 t 2时, y ( t ) ( 2 t ) d 2
h(t ) x( ) h( ) 2 t
2 1
0
t 1
h(t ) x( ) h( ) 2 t
2
h(t ) x( ) h( ) 2 t
e e
(5) et (t ) * cost (t )
2t t
e e
2 ( t )
d e
2t
t
t
e 2t (e t 0) e
t
e d
t
e(t ) cosd (t ) et
t
0
e cosd (t )
《信号与系统》SIGNALS AND SYSTEMS 3
信号与系统第2章答案

0 t 1时,
( 2).1 t 2时,
h(t ) h(t 1) h(t 2) h(t ) h(t 1) 1
h(t ) 1 h(t 1) 1 (t 1) 2 t (3).2 t 3时, h(t ) h(t 1) h(t 2) 1
解: (a) 特征方程为 λ2+3λ+2=0 得 λ1=-2, λ2=-1。
(f). (D2+2D+2)y(t)=Dx(t)
则 h(t)= (c1eλ1 t+ c2eλ2t)u(t)=( c1e- 2 t+ c2e-t)u(t) h`(t)= (c1+ c2)δ(t)+(-2c1e- 2 t-c2e-t)u(t) h``(t)= (c1+ c2)δ`(t)+(-2c1-c2) δ(t)+ (4c1e- 2 t+c2e-t)u(t)
E 4
e
3 ( t T ) 8
]u (t T )
e
u (t T )
2.22 某LTI系统的输入信号x(t)和其零状态响应yx(t)的 波形如图P2.22所示。(a)求该系囊统的冲激响应 h(t),(b)用积分器,加法器和延时器(T=1s)构成该系统。 解: (a)
0
x(t ) (t ) (t 1) (t 2) t, 0 t 1 y x (t ) 1, 1 t 3 4 t , 3 t 4 x(t ) h(t ) (t ) (t 1) (t 2) h(t ) y x (t ) t, 0 t 1 h(t ) h(t 1) h(t 2) 1, 1 t 3 4 t , 3 t 4
