第三章 自动机基础(1)
第三章有穷自动机

例:将图示的DFA M最小化。
a
b
6
4
a
a
a
b
a
1
ab
5a
7
b3
b
b
2 b
1、将M状态分为两个子集: P0=({1,2,3,4},{5,6,7})
2、{1,2,3,4}读入a后划为: P1=({1,2},{3,4},{5,6,7})
3、进一步划分: P2=({1,2},{3},{4},{5,6,7})
对M的状态集S进行划分的步骤:
①把S的终态与非终态分开,分成两个子集, 形成基本划分,属于这两个不同子集的 状态是可区别的。
②假定某个时候已含m个子集,记={I(1) , I(2) , …,I(m) }且属于不同子集的状态是可 区别的,再检查中的每个I能否进一步划 分,对于某个I(i) ,令I(i) ={S1,S2,…,Sk}, 若存在一个输入字符使得move(I(i) ,a)不包 含在现行的某一子集I(i)中,则将I(i)一分 为二。
若M的某些结既是初态结,又是终态结,
或者存在一条从某个初态结到某个终态结 的道路,则空字可为M所接受。
例: NFA M=({0,1,2,3,4},{a,b},f,{0},{2,4})
f(0,a)={0,3} f(2,b)={2} f(0,b)={0,1}
f(3,a)={4} f(1,b)={2} f(4,a)={4}
M’=(K, ,f,S,Z)
一个含有m个状态和n个输入字符的NFA 可表示为一张状态转换图,该图含有m个 状态结,每个结可射出若干条 箭弧与别的 结点相连接,每条弧用*中的一个字(不 一定要不同的字,且可以为空字)作标记 (称输入字),整个图至少含有一个初态 结以及若干个终态结。
自动机安全操作规程(三篇)

自动机安全操作规程1. 介绍自动机是一种能够自主执行特定功能的机械设备,广泛应用于生产、制造和工业领域。
为了确保自动机的安全操作,特制定以下规程,以供参考和遵守。
2. 操作前的准备2.1 在进行任何操作前,必须先对自动机进行一次全面的检查,确保其运行状态良好且不会产生危险。
2.2 确定自动机的工作环境是否符合安全要求,包括清洁、无积水、无杂物等。
3. 人员要求3.1 进行自动机操作的人员必须经过相应的培训,了解其工作原理、操作规程、安全注意事项等。
3.2 操作人员必须年满18岁,并具备良好的体力和心理素质,能够承受工作压力和应对紧急情况。
4. 个人防护装备4.1 在进行自动机操作时,必须佩戴符合国家标准要求的个人防护装备,包括安全帽、护目镜、耳塞、手套、防护服等。
4.2 需要特殊防护的操作,如涉及化学物品、高温、高压等,应根据具体情况选用相应的个人防护装备。
5. 操作注意事项5.1 在进行自动机操作前,必须切断电源或其他能源,确保设备处于停止状态。
5.2 操作人员禁止穿着长发、宽松衣物、珠宝等容易纠缠到设备的物品。
5.3 操作人员不得在设备运行过程中站立或靠近工作区域,以免发生意外伤害。
5.4 在操作过程中,应密切观察设备运行情况,发现异常或故障立即停止操作,并报告相关人员进行检修。
6. 废弃物处理6.1 所有生产过程中产生的废弃物必须按照规定进行分类、清理和处理。
6.2 严禁将废弃物随意丢弃或倾倒在非指定区域或非指定容器中。
7. 紧急情况处理7.1 在紧急情况下,如设备故障、短路、泄漏等,操作人员必须立即停止操作,切断电源,并呼叫相应的紧急维修人员进行处理。
7.2 在紧急情况下,如火灾、爆炸等,操作人员应迅速撤离现场,并按照应急预案进行应对。
8. 日常维护8.1 定期对自动机进行维护保养,包括清洁、润滑、更换磨损部件等。
8.2 定期检查设备各项安全装置的功能是否正常,如安全门、急停按钮、漏电保护等。
编译原理第三章 自动机基础(1)

接受空串的 FA的典型特征!
Ⅱ.第二条通路:FA2
+ ① => ①
∴ L(FA1)={ abnc| n≥0 }
b + ① => ④
bb + ① => ④ => ④
…
因而
∴ L(FA2)={ bn| n≥0 }
∴ L(FA)={abnc, bn| n≥0}
3.2.3 有限自动机的两种表现形式
【例3.6】有限自动机 :FA=( Q,∑,S,F, ) 其中: Q={1,2,3,4},∑={a,b,c}, S={1,2}, F={3,4}
9.
={abn|n≥0}
10.7. L((a|b)*)= (L(a|b))*={a,b}*
11. 即:由a,b组成的所有符号串(包括空串)集合。
➢基本图形库
=+>
.=+>
=.+ℓ>
=+ℓ>
A
P: E T
F
T | E +T | E -T F | T *F | T /F i|( E )
=>*, =>+ , =>.* , =>.+ , =>l* , =>l+ , =>.l+ ,=>.l*
如 右图有限自动机:
则 L(FA)的 识别过程如下所
+- ①
a b
b ②
c
b
③-
示:
④-
※ L(FA)的生成(或识别)过程示例:
Ⅰ.第一条通路:FA1 ac
+ ① => ② => ③
+- ①
编译原理第三章_有穷自动机

例 过河问题 分析(续)
初始状态:MWGC-φ;终止状态:φ-MWGC。 g
MWGC-φ
WC-MG
问题:
6
例 过河问题 状态转换图
起始 g
MWGC-φ g
g φ-MWGC
g
7
WC-MG
m
m MWC-G
w
w
c
C-MWG
c W-MGC
g
g
MGC-W c
MG-WC
w
m
c G-MWC
m
gg MWG-C
+dd. ddd;
输入符号串
数字 数字
SB
.
数字
+
A
H
-.
数字
.G
接收:若扫描完输入串, 且在一个终止状态上结 束。
数字 阻塞:若扫描结束但未 停止在终止状态上;或 者为能扫描完输入串 (如遇不合法符号)。
不完全描述:某些状态 对于某些输入符号不存 在转换。
练习:+34.567 .123 3.4.5
w
有穷自动机(FA)
数字系统:可以从一个状态移动到另一个状态;每次 状态转换,都上由当前状态及一组输入符号确定的;可以 输出某些离散的值集。
FA:一个状态集合;状态间的转换规则;通过读头来 扫描的一个输入符号串。
读头:从左到右扫描符号串。移动(扫描)是由状态 转换规则来决定的。
8
读头
一个FA的例子
(3)运行: 串f(,Q,且t1tt21)∈= Σf(,f(Qt1,t2t1∈), Σt2*),其中Q∈K, t1t2为输入字符
17
例3
题:试证abba可为例1的DFA M所识别(所接受)。
第1讲-确定的有限自动机

对于Σ*中的任何字符串α,若DFA M中存在一条从 初态结点到某一终态结点的路,且这条路上所有弧的标
记连接成的字符串等于α,则称α可以被DFA M所接受 (识别)。
若M的初态结点同时又是终态结点,则空串ε可被 M所接受(识别)。
若α∈Σ*,f(S, α)=P,其中S为DFA M的初始状 态,P∈Z,Z为终态集,则称字符串α可以被DFA M 所接受(识别) 。
DFA M= ({S,U,V,Q}, {a,b}, f,S,{Q})
事实上,状态转换图是有限自动机的一种表示形式,假定DFA M 含有m个状态,n个输入字符,那么这个状态转换图含有m个状态 (结点),每个结点最多有n个弧射出,整个图含有唯一一个初态 结点(冠以“⇒” )和若干个终态结点(用双圈表示),若有f(ki,a)=kj (ki∈K,kj∈K,a∈Σ),则从状态结点ki到状态结点kj画标记为a的弧。
(4) S0∈S,是唯一的初始状态;
(5) F ⊆ S,是终止状态集合。
编 译 技术
chapter3 词法分析——有限自动机
例:为下图所示的状态图构造确定的有限自动机。
f(S,a)=U f(S,b)=V f(V,a)=U f(V,b)=Q f(U,a)=Q f(U,b)=V f(Q,a)=Q f(Q,b)=Q
编 译 技术
chapter3 词法分析——有限自动机
一个DFA还可以用一个矩阵(状态矩阵)表示: 矩阵的行表示状态,列表示输入字符,矩阵元素表示 相应状态行和输入字符列下的新状态。
例:上例的DFA的矩阵表示如下:
字符
状态
a
S
U
U
Q
V
U
Q
Q
b
V0 V0 Q0 Q1
自动机原理

自动机原理自动机是计算机科学中的一个重要概念,它是一种抽象的数学模型,用于描述具有特定行为模式的系统。
自动机理论在计算理论、人工智能、编程语言设计等领域都有着广泛的应用。
本文将介绍自动机的基本原理,包括自动机的定义、分类、特性以及应用。
自动机是一种抽象的数学模型,用于描述系统的行为。
它由一组状态、一组输入符号和状态转移函数组成。
在任何时刻,自动机都处于其中一个状态,并根据输入符号和状态转移函数进行状态转移。
自动机可以分为有限自动机和无限自动机两种类型。
有限自动机在有限状态集合上运行,而无限自动机则在无限状态集合上运行。
有限自动机包括确定性有限自动机(DFA)和非确定性有限自动机(NFA)。
确定性有限自动机是一种特殊的有限自动机,它对于每个输入符号都有唯一的状态转移。
非确定性有限自动机在某些情况下可以有多个状态转移。
无限自动机则包括图灵机和线性有界自动机等类型。
自动机具有以下特性,确定性、完备性、最小性和等价性。
确定性是指对于任何输入符号,自动机都有唯一的状态转移。
完备性是指自动机能够处理所有可能的输入序列。
最小性是指自动机的状态数目是最小的。
等价性是指两个自动机能够接受相同的语言。
自动机理论在计算理论、人工智能、编程语言设计等领域都有着广泛的应用。
在计算理论中,自动机被用来描述计算模型的行为。
在人工智能领域,自动机被用来建模智能系统的行为。
在编程语言设计中,自动机被用来设计词法分析器和语法分析器。
总之,自动机是计算机科学中的一个重要概念,它是一种抽象的数学模型,用于描述具有特定行为模式的系统。
自动机理论在计算理论、人工智能、编程语言设计等领域都有着广泛的应用。
希望本文能够帮助读者更好地理解自动机的基本原理和应用。
第三章 形式语言与自动机

NLPR
E ⇒ E + T ⇒ E + T*F ⇒ E + T*a ⇒ E + F*a ⇒ E + a*a ⇒ T +a*a ⇒ F + a*a ⇒ a + a*a
NLPR, CASIA 2006-3-8
(最右推导)
宗成庆:《自然语言理解》讲义
3.2 形式语言
句型与句子
NLPR
一些特殊类型的符号串为文法 G=(N, Σ, P, S) 的 句子形式(句型): (1) S 是一个句子形式; (2) 如果 αβγ 是一个句子形式,且 β → δ 是 P 的 产生式,则 αδγ 也是一个句子形式; 文法 G 的不含非终结符的句子形式称为 G 生成的 句子。由文法 G 生成的语言,记作 L(G),指 G 生成 ⇒ 的所有句子的集合。即:L(G) = {x | x ∈ Σ, S ∗ x } G
NLPR, CASIA
2006-3-8
宗成庆:《自然语言理解》讲义
3.2 形式语言
例 3.1:G = ({E, T, F}, {a, +, *, (, )}, P, E) P: E→E+T|T F → (E) | a 字符串 a+a*a 的两种推导过程: E ⇒ E + T ⇒ T + T ⇒ F + T ⇒ a + T ⇒ a + T*F ⇒ a + F*F ⇒ a + a*F ⇒ a + a*a (最左推导) T → T*F | F
NLPR, CASIA 2006-3-8 宗成庆:《自然语言理解》讲义
3.1 几个基本概念
字符串 (string)
NLPR
字符串定义:假定 Σ 是字符的有限集合,它的每一个 元素称之为字符。由 Σ 中字符相连而成的有限序列被 称之为Σ 上的字符串(或称符号串,或称链)。 特殊 地,不包括任何字符的字符串称为空串,记作 ε。 符号串的长度:符号串中符号的个数。符号串x的长 度用|x|表示。 |ε| = 0。 包括空串的 Σ 上字符串的全体记为 Σ*。
编译原理2.2 自动机理论

A=(aA|dA)|(a|d)
A=a|d
将它化为正规文法 变成A→
A=(a|d)A|(a|d)
A=(a|d)*(a|d)
(a|d)A|(a|d)
再根据上述 规则2转换 x=y= (a|d)
19
将A代入S=aA|a得到如下: S=a( (a|d)*(a|d)) |a =a(a|d)+|a
=a((a|d)+|)= a(a|d)+
含义:当前状态为 Ki,输入字符a, 转换为Kj状态
DFA映射的唯一性和初态的唯一性
22
DFA等价表示法:
DFA形式定义=状态转换图=状态矩阵
1、单词的构成规则用状态转换图表示
方法如下: 初始态用 “-”或“”表示;
终态点用 “+” 或“” 表示;
若f(Ki ,a)= Kj ,则从状态点Ki 到Kj画弧,标
“” 都是左结合的
9
讨论下面两个例子 例1 令={l,d},则上的正规式 r=l(ld)定义 的正规集为: {l,ll,ld,ldd,„„},其中l 代表字母,d代表数字,正规式 即是 字母 (字母|数字) ,它表示的正规集中的每个 元素的模式是“字母打头的字母数字串”, 就是Pascal和多数程序设计语言允许的标 识符的词法规则.
对于Σ*中的任何字符串t,若存在一条初态到 某一终态的路,且这条路上所有弧的标记符连接成 的字符串等于t,则称t可为DFA M所接受。 若M的初态同时又是终态,则空字可为M所接 受。
33
4、接受(识别)的理解:
① 设QK,函数f(Q,)=Q,则输入字符串是 空串,并停留在原状态上。
② 输入字符串t(t表示成Tt1形式,TΣ,t1 Σ*),在DFA M上运行的定义为:f(Q,Tt1) =f(f(Q,T),t1),其中QK。
3 FA 语言与自动机导论

A
i FA M
B
状态 A i B d F
FA f (A, i) = B f (B, i) = B f (B, d) = B (B为终止状态)
RG AiB BiB BdB Bε
B
B
B
1
状态转换矩阵
11
FA的状态转换图
状态转换图显示了一个由状态、转换组成的状态 机。
有限自动机的状态转换图说明系统的动态视图。 状态图强调一个对象按事件次序发生的行为。
22
例3.3扩:接受语言{x000 | x {0,1}*} ∪{x001 | x {0,1}*}的 FA
解:该语言定义的句子以000或001结尾。设q0为DFA的开 始状态,用q1记住结尾串中的第一个0;用q2记住在q1之 后紧接着又读到的一个0;用q3记住在q2后紧接着又读到 的一个0,用q4记住在q2后紧接着又读到的一个1,识别 该语言的FA如下图(3-5):
则 A也作为终止状态
13
3.2 有穷状态自动机
主要内容:
1、DFA的形式化定义
2、DFA的仿真算法(伪代码描述)
14
一.有穷自动机的形式化定义
1. 确定的有穷自动机DFA
一个确定的有穷自动机DFAM是一个五元组(5-tuple): M=(K,Σ, δ ,q0,F) 其中:K:状态的非空有穷集 Σ:有穷输入字母表 δ:K× Σ到K的一个映射(是单值函数)
q0∈K 是开始状态
F K 是终止状态集
15
例3-2:构造一个DFA,识别语言{x000y | x,y {0,1}*} 解:该语言定义的句子都会有三个连续的0。设q0为DFA 的开始状态,用q1记住子串“000”的第一个0;用q2记住 在q1之后紧接着又读到的一个0,这可能是子串“000”的 第2个0;用q3记住在q2后紧接着又读到的一个0,发现子 串“000”即识别结束。识别该语言的确定的有穷状态自 动机如下图:
chapter 3-有穷状态自动机

1 0 q1 1 q2 0
0 1 q3
0,1
q4
第三章、有穷状态自动机
例2、假设字母表为{0,1},构造一个识别含有001子串的所有 字符串的DFA的状态图。
1 0 q1 1 q2 0
0 1 q3
0,1
q4
第三章、有穷状态自动机
关键问题:DFA与NFA等价吗?
第三章、有穷状态自动机
第三章、有穷状态自动机
NFA与DFA的等价性
NFA与DFA等价是指两种模型识别相同的语言类(正则语言)。 对于任意给定的DFA,存在一个NFA与之等价; 对于任意给定的NFA,存在一个DFA与之等价。 DFA本身就是一种NFA,所以,要证明DFA与NFA等价,只需证明 对于任意给定的NFA,存在一个DFA与之等价。 下面根据给定的NFA构造一个DFA: 这里M2=(Q2,Σ,δ,q0,F ),Q2 =P(Q),
第三章、有穷状态自动机
δ1
q01 q1 q2
0 1
q1 q2 q1
0 q02 q3 q4
q01 q1 Q2
1 q3 q4 q5
δ2
q02 q3 q4
q5
q5
q5
第三章、有穷状态自动机
下面构造M= (Q,Σ,δ,q,F), (1)Q={(r1,r2) ∣ r1∈Q1且r2∈Q2}; (2)Σ= {0,1}; (3)转移函数 δ((r1,r2) ,a)= δ (δ1 (r1,a) ,δ 2(r2,a)), 如下页表所示; (4)q0=(q01,q02)是M的起始状态; (5)F={(q2,q02),(q2,q3),(q2,q4),(q2,q5),(q01,q4), (q1,q4)}。
自动机与形式语言第三章epsilon-NFA

2019/10/20
8
ε-NFA状态的闭包
• ε-CLOSURE(q)= 从状态q出发,跟随ε标
记的弧所能到达的状态的集合。 ε
• 例: ε-CLOSURE(A)= {A};
ε-CLOSURE(E)= {B, C, D, E}.
1
1
1B
C
D
A εε 0
• 状态集合的闭包ε-CLOSURE(P) 0
DFA NFA ε-NFA RE RG
正则语言 (RL)
2019/10/20
1
3.4 带空移动的有穷状态自动机
• 接受语言{0n1m2k|n,m,k≥0}的NFA
2019/10/20
2
3.4 带空移动的有穷状态自动机
• 允许带ε 输入的状态跳转 • 这些状态跳转可以同时进行,无需输入字
E
F
0
= 集合P中所有元素的ε闭包的集合
例: ε-CLOSURE({A,E})= {A,B,C,D,E};
9
3.4 带空移动的有穷状态自动机
⑴ ε -CLOSURE(q)={p|从q到p有一条标记为ε 的路}。
(2) CLOSURE (P) CLOSURE ( p)
pP
2019/10/20
13
3.4 带空移动的有穷状态自动机
• 对任意(P,a)∈2 Q×∑。
(5) (P, a) (q, a)
qP
(6)ˆ(P, w) ˆ(q, w)
qP
2019/10/20
14
3.4 带空移动的有穷状态自动机
• 在ε -NFA中,对任意a∈∑,q∈Q,
ˆ(q, a) (q, a)
D
形式语言与自动机_课件_陈有祺第03章 有穷自动机

从定义3.7可知,在δ(q0,x)的众多状态中,只要有一个状态属于 终结状态集F,则x就被该NFA M接受。如对例3.4中的NFA,字 符串01001是被接受的,因为δ(q0 ,01001)={q0,q1,q4} ,而 q0∈F。但字符串010是不被接受的,因为δ(q0 ,010)={q0,q3} ,其中没有一个状态在F中。
从给定集合构造接受该集合的FA
实现上述思路的FA M1如图所示
初始状态标记为“1”,表示要么还没有读入符号,要么刚读过符号1。对 于“0”状态遇1,“01” 状态遇0,“010”状态再遇0或1的情况,上 面已经做了解释。其他情况是:“0”状态遇0,此时应当保持在“0”状 态,意味着刚读过的符号是0;再有“01”状态遇1,表示这次的期望“ 半途而废”,只能从头再来,所以转回到“1”状态。
形式语言与自动机
第三章 有穷自动机
非形式化描述 有穷自动机的基本定义 非确定的有穷自动机 具有ε转移的有穷自动机 有穷自动机的应用 具有输出的有穷自动机
有穷状态系统
指针式钟表共有12*60*60个状态
围棋共有3361个状态
电梯的控制结构
某些电子产品中的开关电路,具有n个门的开关网络有 2n种状态
分析:x∈L当且仅当把x看成二进制数时,x模5与0同余。换句话说,x 要能被5整除。例如,0,101,1010,1111等都能被5整除,而10, 11,100,110等都不能被5整除。
当二进制数x的位数向右不断增加时,它的值(换算成十进制)的增加很 有规律:x0的值等于2x,x1的值等于2x+1。
词法分析与有限状态自动机

2011-1-5
华东师大计算机科学技术系
6
FA的形式描述 的形式描述
1. 对q, q1 ∈Q a ∈VT δ(q,a)={q1}的含义为:当 的含义为: 的含义为 前状态为q,若输入头所指符号为a, 前状态为 ,若输入头所指符号为 ,则转向下一 状态q 输入头右移。 状态 1,输入头右移。 2. ∵ δ是Q×VT × 2Q上的一个单射 一般地δ ∴一般地δ(q,a)={q1,q2,……qn} qi ∈Q i=1,2,…n 因此称FA M为不确定的 ,记为 为不确定的 因此称 为不确定的FA,记为NFA。 。 Q,即对任何 ∈Q,ai∈ 3. 若映射δ是Q×VT 若映射δ ,即对任何q∈ , × VT,δ(q,ai)至多只有一个元素 ,称FA M是确 至多只有一个元素q’ 至多只有一个元素 是确 定性的FA,记为DFA。 定性的 ,记为 。
2011-1-5 华东师大计算机科学技术系 15
FA的确定化 的确定化
• 定义 :对FA M与FA M’,若L(M)=L(M’)则 定义3: 与 , 则 等价。 称M与M’等价。 与 等价 • 3.1.4 FA的确定化 的确定化 • 定理 定理3.1 对任一给定的 对任一给定的NFA M存在一个 存在一个DFA M’ 存在一个 使L(M)=L(M’)。 。 • 分析: 分析: 由定理3.1 L(DFA) ⊇ L(NFA) 由定理 由FA的定义 L(DFA) ⊆ L(NFA) 的定义 L(DFA) = L(NFA) 得到
第三章 词法分析与有限状态自动机
• 词法分析程序的主要功能是识别单词,这将涉及 词法分析程序的主要功能是识别单词, 3型文法、正则表达式和有限状态自动机。本章 型文法、 型文法 正则表达式和有限状态自动机。 将讨论这三者间的关系。 将讨论这三者间的关系。 • 3.1 有限状态自动机(Finite-state Automate 有限状态自动机 machine FA)
第3章有穷自动机(胡)

(4) (a | b)* 是正规式 , 则相应正规集为 L((a | b)*)=(L(a | b))*= { a, b }*={ε,a,b,ab,ba, …} (5) ba* 是正规式 , 则相应正规集为 L(ba*)=L(b)L(a*)={b,ba,baa,baaa,…} (6) (a | b)*(aa | bb ) (a | b)*是正规式 , 则相应正规集为 L((a | b)*(aa | bb ) (a | b)*) =L((a | b)*)L(aa | bb ) L((a | b)*) ={a,b}*{aa,bb}{a,b}*
注意: 1)对于 关键字、运算符和界符 种别码是一字一 符。可以完全代表它自己。也就不用写自身值。 2)对于标识符和常数就必须依赖自身值来区分。 标识符自身值是它自己的字符串。 常数自身值是常数本身的二进制数值。 我们可以用指向标识符表或常数表的入口指针作 为它们的自身值
下表是简单语言单词符号的内部表示:
3.4 有穷自动机
自动机是一种能进行运算并实现自我控制的装置,
计算机就是一部自动机。自动机是描述符号串处理的强
有力的工具。因而自动机成为研究词法分析器的重要基
础。在识别功能上与正规文法类和正规表达式等价。 下面介绍有关有穷自动机的基本概念和理论以及正 规文法、正规表达式与有穷自动机之间的相互关系。
例题1 (右线性) 给定文法G[Z]: Z→0A A→0A|0B B→1A| ε 解:首先改为正规方程组: Z=0A A=0A+0B B=1A+ε 联立求解:3)代入2) A = 0A+01A+0 = (0+01)A+0 其次应用求解规则得 A =(0+01)*0 代入1)中 Z = 0 (0+ 01)*0 正规式为 = 0 ( 0 | 01 )* 0
编译原理课件第3章有穷自动机

确定性有穷自动机 (DFA)
1
定义
DFA 是有穷自动机的一种,用于表示确定性状态自动机,它从一个状态转移到 另一个状态,每次只读入一个输入字符。
2
应用
在编译原理的词法分析中,DFA 可帮助语法分析器DFA 可以使用状态表或状态图来实现。
非确定性有穷自动机 (NFA)
定义
NFA 是有穷自动机的一种,其中一个状态可以 有多个后继状态,并且可以从一个状态转移到 多个状态。
应用
在词法分析中,NFA 可以解决正则表达式匹配 问题,同时也被用于编程语言中的语法分析。
有穷自动机的应用
词法分析
在编写编译器时,有穷自动机可以用来进行词法分析,从而将源程序转换成更易于处理和理 解的单词串。
计算理论
有穷自动机是计算理论中的重要概念,被广泛应用于机器学习、人工智能和计算机科学的许 多领域。
有穷自动机
编译原理课件第3章介绍有穷自动机,这是一种数学模型,用于描述自动的计 算过程。有穷自动机是编译原理中非常重要的概念。
有穷自动机概述
1 定义
有限状态机,又称有穷状态自动机。它是一个表示有限个特定状态及在这些状态之间的 转移和动作等行为的数学模型。
2 应用
有穷自动机在计算机科学中很有用,例如编写正则表达式、词法分析和语法分析。
状态图
有穷自动机可以使用状态图来表示,通常包括起始状态、接受状态、状态转移和输入字母表。
有穷自动机的分类
有限状态自动机
这是大多数情况下使用的模型,用于表示有穷状 态自动机,由确定性自动机和非确定性自动机两 种类型。
无限状态自动机
用于表示无限状态自动机,由部分确定性自动机 和无限确定性自动机两种类型。
有穷自动机的定义
形式语言与自动机理论--第三章参考答案
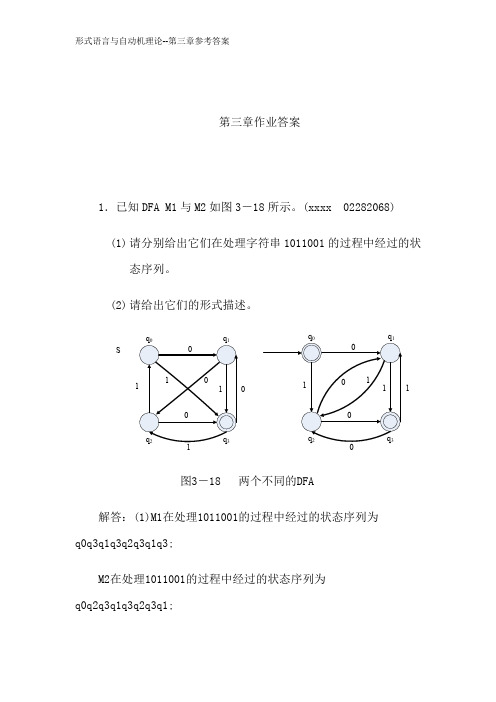
第三章作业答案1.已知DFA M1与M2如图3-18所示。
(xxxx 02282068) (1) 请分别给出它们在处理字符串1011001的过程中经过的状态序列。
(2) 请给出它们的形式描述。
Sq q1q q图3-18 两个不同的DFA解答:(1)M1在处理1011001的过程中经过的状态序列为q0q3q1q3q2q3q1q3;M2在处理1011001的过程中经过的状态序列为q0q2q3q1q3q2q3q1;(2)考虑到用形式语言表示,用自然语言似乎不是那么容易,所以用图上作业法把它们用正则表达式来描述:M1: [01+(00+1)(11+0)][11+(10+0)(11+0)]* M2: (01+1+000){(01)*+[(001+11)(01+1+000)]*} *******************************************************************************2.构造下列语言的DFA( xx02282085 ) (1){0,1}*,1(2){0,1}+,1(3){x|x{0,1}+且x 中不含00的串}(设置一个陷阱状态,一旦发现有00的子串,就进入陷阱状态)(4){ x|x{0,1}*且x中不含00的串}(可接受空字符串,所以初始状态也是接受状态)(5){x|x{0,1}+且x中含形如10110的子串}(6){x|x{0,1}+且x中不含形如10110的子串}(设置一个陷阱状态,一旦发现有00的子串,就进入陷阱状态)(7){x|x{0,1}+且当把x看成二进制时,x模5和3同余,要求当x为0时,|x|=1,且x0时,x的首字符为1 }1.以0开头的串不被接受,故设置陷阱状态,当DFA在启动状态读入的符号为0,则进入陷阱状态2.设置7个状态:开始状态qs,q0:除以5余0的等价类,q1:除以5余1的等价类,q2:除以5余2的等价类,q3:除以5余3的等价类,q4:除以5余4的等价类,接受状态qt3.状态转移表为(8){x|x{0,1}+且x的第十个字符为1}(设置一个陷阱状态,一旦发现x的第十个字符为0,进入陷阱状态)(9){x|x{0,1}+且x以0开头以1结尾}(设置陷阱状态,当第一个字符为1时,进入陷阱状态)(10){x|x{0,1}+且xxx至少含有两个1}(11){x|x{0,1}+且如果x以1结尾,则它的xx为偶数;如果x以0结尾,则它的xx为奇数}可将{0,1}+的字符串分为4个等价类。
自动机课程要点

本课程知识要点第一章:基础知识基本概念:集合、关系、函数、字符、串、语言第二章:FA要点:DFA·,NFA,DFA与NFA的等价性;带ε-NFA作业或练习题:Example 2.2、Example 2.3;Example 2.4;Exercise 2.2.4Example 2.7;Example 2.8;Exercise 2.3.1;Exercise 2.5.1;2.2.1(a);2.2.2;2.3.4(a);2.4.1(a)并编程实现第三章:RERE的构造,与自动机的转化;代数定律作业或练习题:Example 3.2,Example 3.5, Theorem 3.7, Theorem 3.11第四章:RE性质泵引理,封闭性作业或练习题:Example 4.3, Exercise 4.1.1, Exercise 4.1.2,Analyze the time complexity of conversion among representations of Languages第五章:CFG/CFLCFG,语法分析树作业或练习题:Example 5.2, Exercise 5.1.1 a) and b), 5.1.2(a), Exercise 5.1.7, 5.2.1Theorem 5.14, Theorem 5.18第六章:PDAPDA定义及描述,PDA语言(以空栈和终结状态方式接受),PDA与CFG的转化作业或练习题:Example 6.3, Example 6.10, Exercise 6.2.1 a), 6.2.2 a), 6.2.4,6.2.8, 6.3.1, 6.3.3, 6.3.6第七章:CFL性质乔姆斯基范式,泵引理,封闭性作业或练习题:Exercise 7.1.2, Exercise 7.2.1,Theorem 7.17第八章:TMTM的定义与描述,TM语言,TM停机作业或练习题:Example 8.2, Exercise 8.2.2 a)实验:编写至少2个程序,语言不限,实现(但不限于这2个):1)NFA到DFA的转换;2)CFG到PDA的转换;调研:Try to learn RE in Java, C++ or C#, and try to do some test and write a paper about these RE最终成绩认定:实验源程序和实验报告占30%,平时占10%,期末卷面成绩占60%,课堂参讲+5分。
自动机-第3章

k k-1 k-1 k-1 k-1 在定理的证明中,R ij = R ij +R ik (R kk )* R kj k 全部R ij 计算过程是
初始化 for(i = 0;i <= n;i + + )
0 for(i = 0; j <= n; j + + ) 构造R ij k 生成全部R ij
for(k = 1; k <= n; k + + ) for(i = 0;i <= n;i + + )
§1.正则表达式:例
• 01反复出现0或多次的所有0,1串。 (01)* • 以0开头,其后跟随0或多个1所有串。 01* • 以00或11开始的所有0,1串。 (00+11)(0*+1*)* • 以00或11结尾的所有0,1串。 (0*1*)*(00+11) • 倒数第4个符号是1的所有0,1串。 (0*1*)*1(0+1) (0+1) (0+1)
• 从DFA到RE.
q1 Q1 s Q2 q2 R22 R11 +Q1S*P1 R12+ Q1S*P2 S P2 R12 T p2 (R+SU*T)*SU* R11 P1 p1 R R21 S U
q1
p1
R
q2
R21+ Q2S*P1 R22+Q2S*P2
R* p2
例
ADF→RE
0,1 1 A B 0,1 C 0,1 D
k-1 R ik k-1 R kk
R k-1 kk
R k-1 kj
k k-1 因此,这时R ij = R ik (R k-1 )* R k-1 kk kj k k-1 k-1 将1,合起来,则有R ij = R ij +R ik (R k-1 )* R k-1。最后R = 2 kk kj NhomakorabeaU
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
+- ①
a b
b ②
c
b
③-
【图符说明】:
FA3:
④-
•{1,2,3,4} — 状态集;
其中: +(开始状态); -(结束状态)
•{a,b,c} — 字母表;
•δ(1,a)=2 – 变换 ( 或 ① a ② );… ( 表示1状态遇符号a变到2状态,…);
【运行机制】:
一个 FA,若存在一条从某开始状态 i 到某结束 状态 j 的通路,且这条通路上所有边的标记连成的 符号串为,则 就是一个句子;所有这样的 的集 合,就是该 FA 表示的语言。
※ 设 val(e),L(e) 分别表示正规式 e 的值和语言,
则:
L(e)={ x| x=val(e)}
即 正规式表示的语言是该正规式所有值的集合(正规集)。
※ 正规式表示正规语言示例:
【例】:
⑴ e1= a*b+
展开:
L(e1)= { ambn| m≥0 ,n≥1 } ,
= { b,ab,bb,aaa,aab,aba,abb,… }
【例3.3】 L2 ={(ab)n| n≥1 } , 正规语言 ? ∵ 可由正规文法定义:
G2(S): S -> aA ; A -> bB ; B -> aA|
∴ L2 是正规语言。
【例3.4】 L3 ={anbn| n≥0 } , 正规语言 ? ∵ 不能由正规文法定义(正规文法无法描述a和b数量
上相等!): ∴ L3 不是正规语言!
【定义】 正规语言是指由正规文法定义的语言; 程序设计语言中的单词,大都属于此种语言。
▪正规文法是指仅有三种形式的产生式:
⑴ A -> aB ⑵ A -> a ⑶ A ->
▪正规语言有三种等价的表示方法: ⑴ 正规文法 ⑵ 正规式 ⑶ 有限自动机
【例3.1】 G(Z):A ->aA|
正规文法
∵ A=> ;
Q(有限状态集); ∑(字母表); S(开始状态集,S Q); F(结束状态集,F Q );
i,j∈Q, a∈∑+{};
:变换(二元函数):
【含义】
(i,a)=j 或 i a j
状态 i 遇符号 a,变换为状态 j
3.2.2 有限自动机怎样描述语言
令 L(FA)为自动机FA所描述的正规语言;则
• 产生式形式为:A -> ⑷ 3 型语言 由 3型文法定义
又称 正规文法/ 语言 !
• 产生式形式为:A->aB , A->a , A->
【注】 四类语言为 包含关系,且有 L0 ⊃L1 ⊃ L2 ⊃ L3; 编译处理中,主要应用后两种文法!
第 3 章 自动机基础
自动机 — 是一种语言模型,是语言的一种识别 工具,其中的
⑵ e2=(ab)+
L(e2) = {(ab)n| n≥1 } , = { ab,abab,ababab,abababab,… }
⑶ e3= ab*c|b*
L(e3) = { abnc, bn | n≥0 },
= { ac,abc,abbc,abbbc,…; ε,b,bb,bbb,…}
3.1.2 正规语言的有限自动机表示法:
A=>aA=>aaA=>aaaA=>…=>an ,n≥0
∴ L(G)={ an | n≥0 }
正规语言
※ 正规语言判定示例:
【例3.2】 L1 ={ ambn| m≥0 ,n≥1 } , 正规语言 ? ∵ 可由正规文法定义:
G1(S): S -> aS|bA ; A -> bA|
∴ L1 是正规语言。
L1= { ambn| m≥0 ,n≥1 } , FA1:
L2= {(ab)n| n≥1 } , FA2:
L3= { abnc ,bn|n≥0 },
a
b
+① b ②-
+① a
②b
③-
a
FA3:
+- ①
a b
b ②
c
b
③-
④-
※ 初看起来,有限自动机是带标记的有向图!
※有限自动机表示法说明:
L3= { abnc ,bn|n≥0 }
2.7 形式语言的分类问题
形式语言分为四类,由文法产生式的形式不同而区别,令:
A,B ∈VN,a∈VT,(x yαβ)∈(VN+VT)* ⑴ 0 型语言 由 0型文法定义
又称 无限制文法/ 语言 !
• 产生式形式为: -> ⑵ 1 型语言 由 1型文法定义
又称 上下文有关文法/ 语言 !
• 产生式形式为:xAy -> xy 又称 上下文无关文法/ ⑶ 2 型语言 由 2型文法定义 语言 !
有限自动机(finite automata)FA 被用来处理 正规语言,后者是编译程序设计中词法 分析的对象。
【内容提要】
3.1 正规语言及其描述方法 3.2 有限自动机的定义与分类 3.3 有限自动机的等价变换1,2 3.4 有限状态自动机的实现问题 3.5 正规语言描述方法间的相互转换
3.1 正规语言及其描述方法
※ 正规语言的三种表示法综合示例:
【例3.5】 L ={ abnc, bn| n≥0 },∑= {a,b,c};
1. 正规文法描述:
G(S): S-> aA|bB| ,A -> bA|c ,B -> bB|
2. 正规式描述: e = ab*c|b*
3. 有限自动机描述: 表示可接受 FA:
+- ①
3.1.1 正规语言的正规式表示法
※ 正规式 是指由字母表中的符号,通过以下 三种运算(也可以使用圆括号)连接起来构成的表达式
e : 连接 ( .) 或( | ) 闭包( +,* )
例:
正规式 ab.cde ab|cde
a+ a*
正规式的 值 abcde ab , cde a ,aa ,aaa ,… ,an ,… ε , a , aa , aaa , … , an , …
L(FA)={
x|
i
x =>
j
,
x∈∑*
,i∈S,j∈F
}
含义是: 即:
设 x=a1 a2…an , ai∈∑+{}
则有
i
a1
=>
i1
a2
=>
i2
…
an
=&g状态 i 到某结束状态 j 的 连续变换,且每次变换(=>)的边标记连成的符号串恰 好为 x ;称x为FA接受,否则拒绝。
a b
b ②
c
b
③-
空串!
④-
【注】 凡是能由上述三种方法表示的语言,一定 是正规语言;反之,凡是不能由上述三种方法表示 的语言,一定不是正规语言。
3.2 有限自动机的定义和分类
3.2.1 有限自动机的定义
【定义】 有限自动机是一种数学模型,用于描述正 规语言,可定义为五元组: FA=( Q,∑,S,F, ) 其中:
