测试技术习题第二章
测试技术课堂练习题及答案

测试技术课堂练习题及答案这⾥是全部的习题及答案,只要把⽼师上课讲的内容提取出来复习就可以了!第⼀章习题⼀、选择题1.描述周期信号的数学⼯具是()。
.A.相关函数 B.傅⽒级数 C. 傅⽒变换 D.拉⽒变换 2. 傅⽒级数中的各项系数是表⽰各谐波分量的()。
A.相位 B.周期 C.振幅D.频率 3.复杂的信号的周期频谱是()。
A .离散的 B.连续的 C.δ函数 D.sinc 函数 4.如果⼀个信号的频谱是离散的。
则该信号的频率成分是()。
A.有限的B.⽆限的C.可能是有限的,也可能是⽆限的 5.下列函数表达式中,()是周期信号。
A. 5cos10()0x t ππ ≥?= ?≤?当t 0当t 0B.()5sin 2010cos10)x t t t t ππ=+ (-∞<<+∞ C .()20cos20()atx t et t π-= -∞<<+∞6.多种信号之和的频谱是()。
A. 离散的B.连续的C.随机性的D.周期性的7.描述⾮周期信号的数学⼯具是()。
A.三⾓函数B.拉⽒变换C.傅⽒变换D.傅⽒级数8.下列信号中,()信号的频谱是连续的。
A.12()sin()sin(3)x t A t B t ω?ω?=+++B.()5sin 303sin 50x t t t =+C.0()sin at x t e t ω-=?9.连续⾮周期信号的频谱是()。
A.离散、周期的B.离散、⾮周期的C.连续⾮周期的D.连续周期的 10.时域信号,当持续时间延长时,则频域中的⾼频成分()。
A.不变B.增加C.减少D.变化不定11.将时域信号进⾏时移,则频域信号将会()。
A.扩展B.压缩C.不变D.仅有移项 12.已知 ()12sin ,()x t t t ωδ=为单位脉冲函数,则积分()()2x t t dt πδω∞-∞-的函数值为()。
A .6 B.0 C.12 D.任意值13.如果信号分析设备的通频带⽐磁带记录下的信号频带窄,将磁带记录仪的重放速度(),则也可以满⾜分析要求。
测试技术基础答案 第二章 测试装置的基本特性

第二章 测试装置的基本特性一、知识要点及要求(1)了解测试装置的基本要求,掌握线性系统的主要性质;(2)掌握测试装置的静态特性,如线性度、灵敏度、回程误差和漂移等;(3)掌握测试装置的动态特性,如传递函数、频率响应函数、单位脉冲响应函数; (4)掌握一、二阶测试装置的动态特性及其测试。
二、重点内容及难点(一) 测试装置的基本要求1、测试装置又称为测试系统,既可指众多环节组成的复杂测试装置,也可指测试装置中的各组成环节。
2、测试装置的基本要求:(1)线性的,即输出与输入成线性关系。
但实际测试装置只能在一定工作范围和一定误差允许范围内满足该要求。
(2)定常的(时不变的),即系统的传输特性是不随时间变化的。
但工程实际中,常把一些时变的线性系统当作时不变的线性系统。
3、线性系统的主要性质 (1)叠加原理:若)()()()(2211t y t x t y t x −→−−→−,则)()()()(2121t y t y t x t x ±−→−±(2)频率保持性:若输入为某一频率的简谐信号,则系统的稳态输出也是同频率的简谐信号。
*符合叠加原理和频率保持性,在测试工作中具有十分重要的作用。
因为,在第一章中已经指出,信号的频域函数实际上是用信号的各频率成分的叠加来描述的。
所以,根据叠加原理和频率保持性这两个性质,在研究复杂输入信号所引起的输出时,就可以转换到频域中去研究。
(二)不失真测试的条件 1、静态不失真条件在静态测量时,理想的定常线性系统Sx x a b y ==0,S 为灵敏度。
2、动态不失真条件在动态测量时,理想的定常线性系统)()(00t t x A t y -=,A 0为灵敏度,t 0为时间延迟。
(三)测试装置的静态特性静态特性:就是在静态测量时描述实际测试装置与理想定常线性系统的接近程度。
(1)线性度:指测试装置输出与输入之间保持线性比例关系的程度。
(2)灵敏度:指测试装置输出与输入之间的比例因子,即测试装置对输入量变化的反应能力。
信号处理与测试技术习题及答案

第一章习题:一、填空题1、电量分为和,如电流、电压、电场强度和电功率属于;而描述电路和波形的参数,如电阻、电容、电感、频率、相位则属于。
2、传感器输出的经过加工处理后,才能进—步输送到记录装置和分析仪器中。
3、现代科学认为,、、是物质世界的三大支柱。
4、与三大支柱相对应,现代科技形成了三大基本技术,即、、。
5、传感技术是人的的扩展和延伸;通信技术是人的的扩展和延伸;计算机技术是人的的延伸。
6、、、技术构成了信息技术的核心。
二、简答题1、举例说明信号测试系统的组成结构和系统框图。
2、举例说明传感技术与信息技术的关系。
3、分析计算机技术的发展对传感测控技术发展的作用。
4、分析说明信号检测与信号处理的相互关系。
三、参考答案(-)填空题1、电能量、电参量、电能量、电参量2、电信号、信号调理电路3、物质、能量、信息4、新材料技术、新能源技术和信息技术5、感官(视觉、触觉)功能、信息传输系统(神经系统)、信息处理器官(大脑)功能6、传感、通信和计算机第二章习题:一、填空题1、确定性信号可分为和两类。
2、信号的有效值又称为,它反映信号的。
3、概率密度函数是在域,相关函数是在域,功率谱密度是在域上描述随机信号。
4、周期信号在时域上可用、和参数来描述。
5、自相关函数和互相关函数图形的主要区别是。
6、因为正弦信号的自相关函数是同频率的,因此在随机噪声中含有时,则其自相关函数中也必然含有,这是利用自相关函数检测随机噪声中含有的根据。
7、周期信号的频谱具有以下三个特点:_________、________、_________。
8、描述周期信号的数学工具是__________;描述非周期信号的数学工具是________。
9、同频的正弦信号和余弦信号,其相互相关函数是的。
10、信号经典分析方法是和。
11、均值E[x(t)]表示集合平均值或数学期望,反映了信号变化的,均方值反映信号的。
12、奇函数的傅立叶级数是,偶函数的傅立叶级数是。
机械工程测试技术第二章信号分析基础习题

第二章 信号分析基础(一)填空题1、 测试的基本任务是获取有用的信息,而信息总是蕴涵在某些物理量之中,并依靠它们来传输的。
这些物理量就是 ,其中目前应用最广泛的是电信号。
2、 信号的时域描述,以 为独立变量;而信号的频域描述,以 为独立变量。
3、 周期信号的频谱具有三个特点: , , 。
4、 非周期信号包括 信号和 信号。
5、 描述随机信号的时域特征参数有 、 、 。
6、 对信号的双边谱而言,实频谱(幅频谱)总是 对称,虚频谱(相频谱)总是 对称。
7、信号x(t)的均值μx 表示信号的 分量,方差2x σ描述信号的 。
7、 当延时τ=0时,信号的自相关函数R x (0)= 均方值 ,且为R x (τ)的 最大 值。
9、 周期信号的自相关函数是 周期信号,但不具备原信号的 信息。
10、 为了识别信号类型,常用的信号分析方法有 概率密度函数 、和 自相关函数 。
11、为了获得测试信号的频谱,常用的信号分析方法有 傅立叶变换法 、 和 滤波器法12、 设某一信号的自相关函数为)cos(ωτA ,则该信号的均方值为2x ψ= ,均方根值为x rms = 。
(二)判断对错题(用√或×表示)1、 各态历经随机过程一定是平稳随机过程。
(√)p39-402、 信号的时域描述与频域描述包含相同的信息量。
( √ )3、 非周期信号的频谱一定是连续的。
( ×)(离散傅立叶变换)4、 非周期信号幅频谱与周期信号幅值谱的量纲一样。
(×)5、 随机信号的频域描述为功率谱。
(√)6、 互相关函数是偶实函数。
( × )(三)单项选择题1、下列信号中功率信号是( B )。
A.指数衰减信号B.正弦信号、C.三角脉冲信号D.矩形脉冲信号2、周期信号x(t) = sin(t/3)的周期为(B )。
A. 2π/3B. 6πC. π/3D. 2π3、下列信号中周期函数信号是(C )。
A.指数衰减信号B.随机信号C.余弦信号、D.三角脉冲信号4、设信号的自相关函数为脉冲函数,则自功率谱密度函数必为(D )。
机械工程测试技术课后习题答案

第一章习题1.测试技术的静态特性是什么?其用哪些性能指标来描述?它们一般用哪些公式表示?①测试技术的静态特性是指被测量的值处于稳定状态时,测试技术的输入与输出之间的关系。
②衡量测试技术静态特性的主要指标有线性度、灵敏度、迟滞、重复性、分辨率、阈值、稳定性、漂移和静态误差。
③线性度、灵敏度、迟滞、重复性、分辨率、阈值、稳定性、漂移和静态误差。
2.测试技术的动态特性是什么?其分析方法有哪几种①测试技术的动态特性是指测试技术的输出对随时间变化的输入量的响应特性,它反映了输出值真实再现变化着的输入量的能力。
②阶跃响应、频率响应3.测试技术数学模型的一般描述方法有哪些?传感器数学模型可分为静态和动态数学模型。
其中传感器静态数学模型一般多用多项式来描述,而动态数学模型通常采用微分方程和传递函数等来描述。
4.测试技术系统有哪些典型环节?写出不同环节的微分方程。
输入,输出方程、传递函数、频率响应和单位阶跃5.为什么说零阶测试技术的动态特性是最理想的?因为零阶没有滞后6.简述系统误差和随机误差出现的原因及特点。
系统误差:系统误差是由固定不变的或按确定规律变化的因素所造成的。
系统误差的特征是:在同一条件下多次测量同一量值时,绝对值和符号保持不变;或当条件改变时,按一定规律变化。
系统误差在某些情况下对测量结果的影响还比较大,因此,研究系统误差产生的原因,发现、减小或消除系统误差,使测量结果更加趋于正确和可靠,是误差理论的重要课题之一,是数据处理中的一个重要的内容。
随机误差:随机误差是由于感官灵敏度和仪器精密程度的限制、周围环境的干扰及伴随着测量而来的不可预料的随机因素的影响而造成的。
它的特点是大小无定值,一切都是随机发生的,因而又把它称为偶然误差7.标准误差的意义是什么?标准误越小,抽样误差越小,样本对总体的代表性越好8.有效数字的运算原则和规则是什么?有效数字的确定方法是什么? 一般规定,数值中的可靠数字与所保留的1位(或2位)可疑数字统称为有效数字。
机械工程测试技术习题及解答答案

《机械工程测试技术》习题与题解第二章 习题解答2-1.什么是信号?信号处理的目的是什么?2-2.信号分类的方法有哪些?2-3.求正弦信号()t A t x ωsin =的均方值2x ψ。
解:()24sin 4222cos 12sin 2sin 11222022022022022A T T A T dtt A T tdt A T dtt A T dt t x T T T T T x =⎪⎭⎫ ⎝⎛-=-====⎰⎰⎰⎰ωωωωωψ 也可先求概率密度函数:221)(xA t p -=π则:⎰∞∞-==2)(222A dx x p x xψ。
2-4.求正弦信号())sin(ϕω+=t A t x 的概率密度函数p(x)。
解: 2221)(111,arcsin xA Ax A dx dt Ax t -=-=-=ωωϕω代入概率密度函数公式得:22222200122221lim 1lim)(xA x A x A T T dt dx T t x x p x x -=-=-=⋅=⎥⎥⎦⎤⎢⎢⎣⎡∆∆=∑→∆→∆πωπωω 2-5.求如下图所示周期性方波的复指数形式的幅值谱和相位谱txT 1-T 1T-T解 在x(t)的一个周期中可表示为⎩⎨⎧<<≤=21)(11T t T T t t x该信号基本周期为T ,基频ω0=2π/T ,对信号进行傅里叶复指数展开。
由于x (t )关于t =0对称,我们可以方便地选取-T /2≤t ≤T /2作为计算区间。
计算各傅里叶序列系数c n 当n =0时,常值分量c 0:T T dt T a c T T 1002111===⎰- 当n ≠0时,110110011T T t jn T T tjn n eTjn dt eTc -----==⎰ωωω最后可得⎥⎦⎤⎢⎣⎡-=-j e e T n c t jn t jn n 22000ωωω注意上式中的括号中的项即sin (n ω0 T 1)的欧拉公式展开,因此,傅里叶序列系数c n 可表示为0)(sin 2)sin(210010≠==n T n c TT n T n c n ,ωπωω其幅值谱为:)(sin 211T n c TT c o n ω=,相位谱为:ππϕ-=,,0n 。
测试技术参考答案(王世勇-前三章)

第一章 测试技术基础知识1.4 常用的测量结果的表达方式有哪3种?对某量进行了8次测量,测得值分别为:82.40、82.43、82.50、82.48、82.45、82.38、82.42、82.46。
试用第3种表达方式表示其测量结果。
解:1)常用的测量结果的表达方式有基于极限误差的表达方式、基于t 分布的表达方式和基于不确定度的表达方式等3种2)基于不确定度的表达方式可以表示为0x s x x x nσ∧=±=±均值为8118i i x x ===∑82.44标准偏差为821()7ii x x s =-==∑0.04样本平均值x 的标准偏差的无偏估计值为ˆ8x sσ==0.014 所以082.440.014x =±第二章 信号描述与分析2.2 一个周期信号的傅立叶级数展开为12ππ120ππ()4(cos sin )104304n n n n n y t t t ∞==++∑(t 的单位是秒) 求:1)基频0ω;2)信号的周期;3)信号的均值;4)将傅立叶级数表示成只含有正弦项的形式。
解:基波分量为12ππ120ππ()|cos sin 104304n y t t t ==+ 所以:1)基频0π(/)4rad s ω=2)信号的周期02π8()T s ω==3)信号的均值42a = 4)已知 2π120π,1030n n n n a b ==,所以 22222π120π()() 4.00501030n n n n n A a b n π=+=+= 120π30arctan arctan arctan 202π10n n nn bn a ϕ=-=-=-所以有0011π()cos()4 4.0050cos(arctan 20)24n n n n a n y t A n t n t ωϕπ∞∞===++=+-∑∑2.3 某振荡器的位移以100Hz 的频率在2至5mm 之间变化。
现代测试技术习题解答第二章信号的描述与分析副本
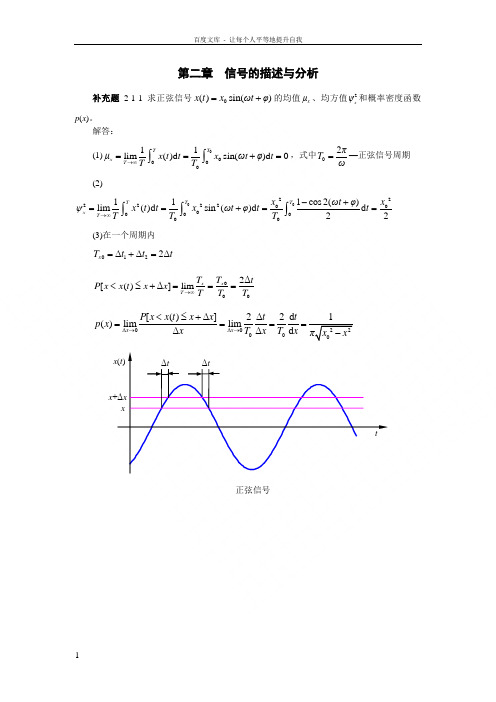
第二章 信号的描述与分析补充题2-1-1 求正弦信号0()sin()x t x ωt φ=+的均值x μ、均方值2x ψ和概率密度函数p (x )。
解答: (1)00011lim ()d sin()d 0TT x T μx t t x ωt φt TT →∞==+=⎰⎰,式中02πT ω=—正弦信号周期(2)2222220000111cos 2()lim()d sin ()d d 22TT T xT x x ωt φψx t t x ωt φt t TT T →∞-+==+==⎰⎰⎰(3)在一个周期内012ΔΔ2Δx T t t t =+=0002Δ[()Δ]limx x T T T tP x x t x x T T T →∞<≤+===22Δ0Δ0000[()Δ]2Δ2d ()limlim ΔΔd x x P x x t x x t t p x x T x T x πx x →→<≤+====-x (t )正弦信号xx +ΔxΔtΔtt2-8 求余弦信号0()sin x t x ωt 的绝对均值x μ和均方根值rms x 。
2-1 求图示所示锯齿波信号的傅里叶级数展开。
2-4周期性三角波信号如图所示,求信号的直流分量、基波有效值、信号有效值及信号的平均功率。
2-1 求图示所示锯齿波信号的傅里叶级数展开。
补充题2-1-2 求周期方波(见图1-4)的傅里叶级数(复指数函数形式),划出|c n|–ω和φn–ω图,并与表1-1对比。
解答:在一个周期的表达式为00 (0)2() (0)2T A t x t T A t ⎧--≤<⎪⎪=⎨⎪≤<⎪⎩积分区间取(-T/2,T/2)00000002202002111()d =d +d =(cos -1) (=0, 1, 2, 3, )T T jn tjn tjn t T T n c x t et Aet Ae tT T T Ajn n n ωωωππ-----=-±±±⎰⎰⎰所以复指数函数形式的傅里叶级数为001()(1cos )jn tjn t n n n Ax t c ejn e n∞∞=-∞=-∞==--∑∑ωωππ,=0, 1, 2, 3, n ±±±。
测试技术基础(第三版)课后答案全集 (2)

将fn = 800Hz, = 0.14,f = 400Hz,代入上面的式子得到 A(400) 1.31,(400) −10.57 如果 = 0.7,则A(400) 0.975,(400) −43.03 2-11 对一个可视为二阶系统的装置输入一单位阶跃函数后,测得其 响应的第一个超调量峰值为1.5,振荡周期为6.28s。设已知该装置的静 态增益为3,求该装置的传递函数和该装置在无阻尼固有频率处的频率 响应。 解: 因为d = 6.28s,所以 d = 2/d = 1rad/s 所以 当 = n时,
3ω0 5ω0 2A/π 2A/3π 2A/5π 幅频图 相频图 周期方波复指数函数形式频谱图 2A/5π 2A/3π 2A/π -ω0 -3ω0 -5ω0 -ω0 -3ω0 -5ω0
1-2 求正弦信号的绝对均值和均方根值。 解答: 1-3 求指数函数的频谱。 解答:
单边指数衰减信号频谱图 f |X(f)| A/a
第二章 测试装置的基本特性 2-1 进行某动态压力测量时,所采用的压电式力传感器的灵敏度为 90.9nC/MPa,将它与增益为0.005V/nC的电荷放大器相连,而电荷放大 器的输出接到一台笔式记录仪上,记录仪的灵敏度为20mm/V。试计算这 个测量系统的总灵敏度。当压力变化为3.5MPa时,记录笔在记录纸上的 偏移量是多少? 解:若不考虑负载效应,则各装置串联后总的灵敏度等于各装置灵 敏度相乘,即 S=90.9(nC/MPa)0.005(V/nC)20(mm/V)=9.09mm/MPa。 偏移量:y=S3.5=9.093.5=31.815mm。 2-2 用一个时间常数为0.35s的一阶装置去测量周期分别为1s、2s和 5s的正弦信号,问稳态响应幅值误差将是多少? 解:设一阶系统, ,T是输入的正弦信号的周期 稳态响应相对幅值误差,将已知周期代入得 2-3 求周期信号x(t)=0.5cos10t+0.2cos(100t−45)通过传递函数 为H(s)=1/(0.005s+1)的装置后得到的稳态响应。 解:,, 该装置是一线性定常系统,设稳态响应为y(t),根据线性定常系统 的频率保持性、比例性和叠加性得到 y(t)=y01cos(10t+1)+y02cos(100t−45+2) 其中, , 所以稳态响应为 2-4 气象气球携带一种时间常数为15s的一阶温度计,以5m/s的上升 速度通过大气层。设温度按每升高30m下降0.15℃的规律而变化,气球 将温度和高度的数据用无线电送回地面。在3000m处所记录的温度为−l ℃。试问实际出现−l℃的真实高度是多少? 解:该温度计为一阶系统,其传递函数设为。温度随高度线性变 化,对温度计来说相当于输入了一个斜坡信号,而这样的一阶系统对斜 坡信号的稳态响应滞后时间为时间常数=15s,如果不计无线电波传送时 间,则温度计的输出实际上是15s以前的温度,所以实际出现−l℃的真 实高度是 Hz=H-V=3000-515=2925m 2-5 想用一个一阶系统做100Hz正弦信号的测量,如要求限制振幅误 差在5%以内,那么时间常数应取多少?若用该系统测量50Hz正弦信号, 问此时的振幅误差和相角差是多少?
测试技术基础习题答案-

其输出信号为:y2(t)=0.496sin(4t-82.875º)
所以,x(t)为输入信号时,输出信号为:
y(t)= y1(t)+ y2(t)= 0.78sin(4t-38.66º)+0.05sin(4t-82.875º)
3-25 用一阶系统对100Hz正弦信号进行测量,如果要求振幅误差在5%以内,则时间常数应取多少?如用具有该时间常数的同一系统作50Hz正弦信号的测试,问此时的振幅误差和相位差是多少?
半桥双臂接法时,
全桥法时,
图略。
5-23以阻值,灵敏度S=2的电阻应变片与阻值的固定电阻组成电桥,供桥电压为4V,并假定负载电阻无穷大,当应变片上的应变分别为1和1000时,半桥单臂、半桥双臂及全桥的输出电压,并比较三种情况下的灵敏度。
解:1)应变为1με时,
半桥单臂时,输出电压:
半桥双臂时,输出电压:
其输出信号为:y2(t)=0.1572sin(4t-80.96º)
可以看出,对于信号,其幅值由1变为0.537,相位由0 º变为-57.52º;对于信号,其幅值由1变为0.1572,相位由0 º变为-80.96º;信号的幅值和相位变化大于信号的幅值和相位的变化。
3-31 对一个二阶系统输入单位阶跃信号后,测得响应中产生的第一个过冲量M的数值为1.5,同时测得其周期为6.28s。设已知装置的静态增益为3,试求该装置的传递函数和装置在无阻尼固有频率处的频率响应。
相位为:φ2-φ1=φ(ω1) →φ2=φ(ω1)+ φ1=-57.52º;其输出信号为:y1(t)=0.537sin(t-57.52º)
当输入信号为x2(t)= sin4t时,其角频率ω2=4,幅值A2=1,初相位φ1=0;则
检测技术 第二章:误差分析与数据处理

可以得到精确的测量结果,否则还可能损坏仪器、设备、元器件等。
2.理论误差 理论误差是由于测量理论本身不够完善而采用近似公式或近似值计算测量 结果时所引起的误差。例如,传感器输入输出特性为非线性但简化为线性 特性,传感器内阻大而转换电路输入阻抗不够高,或是处理时采用略去高 次项的近似经验公式,以及简化的电路模 型等都会产生理论误差。
误差,周期性系统误差和按复杂规律变化的系统误差。如图2.1所示,其中1为定值系差,2 为
线性系统误差,3为周期系统误差,4为按复杂规律变化的系统误差。 系统误差的来源包括仪表制造、安装或使用方法不正确,
测量设备的基本误差、读数方法不正确以及环境误差等。
系统误差是一种有规律的误差,故可以通过理论分析采 用修正值或补偿校正等方法来减小或消除。
•理论真值又称为绝对真值,是指在严格的条件下,根据一定的理论,按定义确定的数值。 例如三角形的内角和恒为180°一般情况下,理论真值是未知的。 •约定真值是指用约定的办法确定的最高基准值,就给定的目的而言它被认为充分接近于 真值,因而可以代替真值来使用。如:基准米定义为“光在真空中1/299792458s的时间 间隔内行程的长度”。测量中,修正过的算术平均值也可作为约定真值。
表等级为0.2级。
r=
0.12 100% 100% 0.12 A 100
在选仪表时,为什么应根据被测值的大小,在满足被测量数值范围的前提下,尽可能 选择量程小的仪表,并使测量值大于所选仪表满刻度的三分之二。在满足使用 要求时,满量程要有余量,一般余量三分之一,为了装拆被测工件方便。 (同一精度,量程越大,误差越大,故量程要小,但留余量)
第二章 误差分析与数据处理
三.测量误差的来源
1.方法误差 方法误差是指由于测量方法不合理所引起的误差。如用电压表测量电压时,
测试技术(2-6章)(李迪张春华著)华南理工大学教材供应中心课后答案

第二章 测量结果的数据处理及误差分析√2-3 用标准测力机检定材料试验机,若材料试验机的示值为5.000MN ,标准测力仪输出力值为4.980MN ,试问材料机在5.000MN 检定点的示值误差、示值的相对误差各为多少?解:示值误差=,020.0000.5980.4−=−示值的相对误差=%04.0000.5020.0−=−√2-8 设间接测量量z x y =+,在测量x 和时是一对一对同时读数的。
测量数据如下表。
试求的标准测量序号y z 偏差。
1 2 3 4 5 6 78 9 10 x 读数100 104 1029810310199101105102 y 读数51 51 5450515250505351解:101.5x =,51.3y =,0.42y σ=,0.687x σ=152.8z x y =+=z x y =+,1,1z z x y∂∂∴==∂∂ 由于10(,)()(0.55iix y x x y y ρ−−∴==∑0.98z σ∴=。
1m 距离的标准偏差为0.2mm 。
如何表示间的函数式?求测此10m 距离的标准差。
见书P27-28页的内容。
5.033,25.039,25.034mm 。
如不计其他不确定度来源,最佳值及其标准不确定度。
见书P36页例题2.8√2-9 用米尺逐段丈量一段10m 的距离,设丈量接测量解:参√2-14 用千分尺重复测量某小轴工件直径10次,得到的测量数据为25.031,25.037,25.034,25.036,25.038,25.037,25.036,2试估计解:参答案网 w w w .h k s h p .c n第三章 信号描述与分析-3 求指数函数的频谱。
√解:()e (00)atx t A a t −=>≥,3dt e Ae dt e t x X t j at t j ∫∫+∞−−+∞∞−−==0)()(ωωω220)()ωωωωω+−=+=+−=+∞+−a j a A j a A e j a Ata j (3-4 求被截断的余弦函数0cos t ω0cos ||()0 ||t t x t t Tω<⎧=⎨≥T解:⎩(题图3-4 )的傅里叶变换。
现代测试技术习题解答 第二章 信号的描述与分析 - 副本(2020年7月整理).pdf
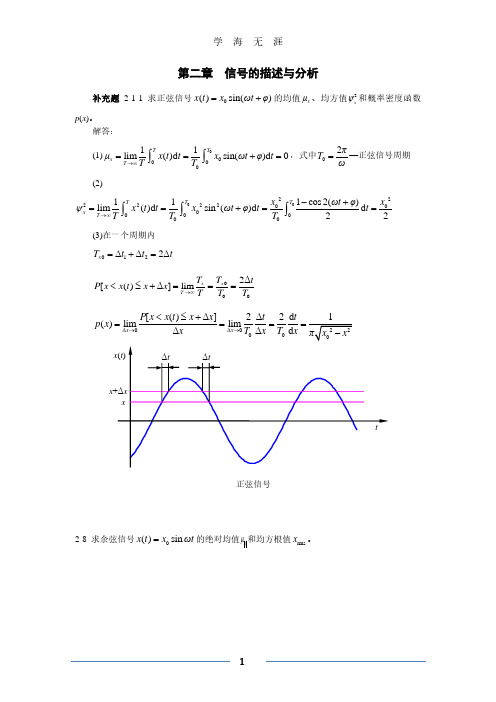
没有偶次谐波。其频谱图如下图所示。
5
学海无涯
|cn| 2A/π 2A/π
2A/3π 2A/5π -5ω0 -3ω0 -ω0
2A/3π 2A/5π ω0 3ω0 5ω0 ω
φn
π/2 ω0 3ω0
-5ω0 -3ω0 -ω0 -π/2
幅频图
周期方波复指数函数形式频谱图
相频图
5ω0 ω
2-5 求指数函数 x(t) = Ae−at (a 0,t 0) 的频谱。
2-12 已知信号的自相关函数为 Acos,请确定该信号的均方值x2 和均方根值 xrms。
解:Rx()=Acos
x2= Rx(0)=A
xrms =
2 x
=
A
2-13 已知某信号的自相关函数,求均方值 、和均方根值 xrms 。
2-14 已知某信号的自相关函数,求信号的均值 μx 、均方根值 、功率谱。
1
学海无涯
2-1 求图示 2.36 所示锯齿波信号的傅里叶级数展开。 2
学海无涯
2-4 周期性三角波信号如图 2.37 所示,求信号的直流分量、基波有效值、信号有效值及信号 的平均功率。
3
学海无涯
2-1 求图示 2.36 所示锯齿波信号的傅里叶级数展开。
补充题 2-1-2 求周期方波(见图 1-4)的傅里叶级数(复指数函数形式),划出|cn|–ω 和 φn–ω 4
学海无涯
第二章 信号的描述与分析
补充题
2-1-1
求正弦信号
x(t)
=
x0
sin(ωt
+
φ)
的均值
μx
、均方值
ψ
2 x
和概率密度函数
p(x)。 解答:
测试技术章节习题(附答案)

各章节习题(后附答案)第一章 信号及其描述(一)填空题1、 测试的基本任务是获取有用的信息,而信息总是蕴涵在某些物理量之中,并依靠它们来传输的。
这些物理量就是 ,其中目前应用最广泛的是电信号。
2、 信号的时域描述,以 为独立变量;而信号的频域描述,以 为独立变量。
3、 周期信号的频谱具有三个特点: , , 。
4、 非周期信号包括 信号和 信号。
5、 描述随机信号的时域特征参数有 、 、 。
6、 对信号的双边谱而b ,实频谱(幅频谱)总是 对称,虚频谱(相频谱)总是 对称。
(二)判断对错题(用√或×表示)1、 各态历经随机过程一定是平稳随机过程。
( )2、 信号的时域描述与频域描述包含相同的信息量。
( )3、 非周期信号的频谱一定是连续的。
( )4、 非周期信号幅频谱与周期信号幅值谱的量纲一样。
( )5、 随机信号的频域描述为功率谱。
( )(三)简答和计算题1、 求正弦信号t x t x ωsin )(0=的绝对均值μ|x|和均方根值x rms 。
2、 求正弦信号)sin()(0ϕω+=t x t x 的均值x μ,均方值2x ψ,和概率密度函数p(x)。
3、 求指数函数)0,0()(≥>=-t a Ae t x at的频谱。
4、 求被截断的余弦函数⎩⎨⎧≥<=Tt T t t t x ||0||cos )(0ω的傅立叶变换。
5、 求指数衰减振荡信号)0,0(sin )(0≥>=-t a t e t x atω的频谱。
第二章测试装置的基本特性(一)填空题1、 某一阶系统的频率响应函数为121)(+=ωωj j H ,输入信号2sin)(tt x =,则输出信号)(t y 的频率为=ω ,幅值=y ,相位=φ 。
2、 试求传递函数分别为5.05.35.1+s 和2224.141nn n s s ωωω++的两个环节串联后组成的系统的总灵敏度。
3、 为了获得测试信号的频谱,常用的信号分析方法有 、和 。
现代测试技术习题解答--第二章--信号的描述与分析---副本

现代测试技术习题解答--第二章--信号的描述与分析---副本第二章 信号的描述与分析补充题2-1-1 求正弦信号0()sin()x t x ωt φ=+的均值xμ、均方值2xψ和概率密度函数p (x )。
解答: (1)00011lim()d sin()d 0TT xT μx t t x ωt φt TT →∞==+=⎰⎰,式中02πTω=—正弦信号周期 (2)2222220000111cos 2()lim()d sin ()d d 22TT T xT x x ωt φψx t t x ωt φt t TT T →∞-+==+==⎰⎰⎰(3)在一个周期内12ΔΔ2Δx T t t t =+=0002Δ[()Δ]limx x T T T t P x x t x x T T T →∞<≤+===Δ0Δ000[()Δ]2Δ2d ()limlim ΔΔd x x P x x t x x t t p x x T x T x →→<≤+====正弦信号2-8 求余弦信号0()sin x t x ωt 的绝对均值xμ和均方根值rmsx 。
2-1 求图示2.36所示锯齿波信号的傅里叶级数展开。
2-4周期性三角波信号如图2.37所示,求信号的直流分量、基波有效值、信号有效值及信号的平均功率。
2-1 求图示2.36所示锯齿波信号的傅里叶级数展开。
补充题2-1-2 求周期方波(见图1-4)的傅里叶级数(复指数函数形式),划出|c n |–ω和φn –ω图,并与表1-1对比。
图1-4 周期方波0 tx (T 02-T2T -……A -T 0解答:在一个周期的表达式为00 (0)2() (0)2T A t x t T A t ⎧--≤<⎪⎪=⎨⎪≤<⎪⎩积分区间取(-T/2,T/2)000000002202002111()d =d +d =(cos -1) (=0, 1, 2, 3, )L T T jn tjn tjn t T T n c x t et Aet Ae tT T T Ajn n n ωωωππ-----=-±±±⎰⎰⎰所以复指数函数形式的傅里叶级数为 001()(1cos )jn tjn t n n n Ax t c ejn e n∞∞=-∞=-∞==--∑∑ωωππ,=0, 1, 2, 3, n ±±±L 。
测试技术复习资料(第二章)

第二章一、选择题2. 测试装置的传递函数H(s)是装置动态特性在( D )中的描述。
A. 幅值域B. 时域C. 频率域D. 复频域3. 测试装置的频响函数H (jω)是装置动态特性在( C )中的描述。
A. 幅值域B. 时域C. 频率域D. 复频域4. 用常系数微分方程描述的系统称为( D )系统。
A. 相似B.物理C. 力学D. 线性5. 下列微分方程中,哪一个是线性系统的数学模型?( B )A. 225d y dy dx t y x dt dt dt ++=+B. 22d y dx y dt dt+= C. 22105d y dy y x dt dt -=+ D. x dt dx y dty d =+22 6. 线性系统的叠加原理表明( A )。
A. 加于线性系统的各个输入量所产生的响应过程互不影响B. 系统的输出响应频率等于输入激励的频率C. 一定倍数的原信号作用于系统所产生的响应,等于原信号的响应乘以该倍数D. 多个输入信号同时作用于系统所产生的响应,等于各个原信号的响应之和7. 测试装置能检测输入信号的最小变化能力,称为( D )。
A. 精度B. 灵敏度C. 精密度D. 分辨率8. 一般来说,测试系统的灵敏度越高,其测量范围( B )。
A. 越宽B. 越窄C. 不变D. 不一定9. 测试过程中,量值随时间而变化的量称为( C )。
A. 准静态量B. 随机变量C. 动态量D. 静态量10. 线性装置的灵敏度是( B )。
A. 随机变量B. 常数C. 时间的线性函数D. 时间的非线性函数11. 若测试系统由两个环节串联而成,且环节的传递函数分别为12(),()H s H s ,则该系统总的传递函数为( )。
若两个环节并联时,则总的传递函数为( )。
A. 12()()H s H s +B.12()()H s H s ⋅C.12()()H s H s -D.12()/()H s H s12. 输出信号与输入信号的相位差随频率变化的关系就是( B )。
测试技术基础习题答案-江征风

第二章部分题目答案2-21.求正弦信号)2sin()(t TA t x π=的单边、双边频谱、实频图、虚频图,如该信号延时4/T 后,其各频谱如何变化 解: (1)由于22()sin()cos()2x t A t A t T T πππ==-,符合三角函数展开形式,则 在2Tπ处:1n A =,所以,单边频谱图为图1的(a )。
对)2sin()(t T A t x π=进行复指数展开:由于222()sin()()2j t j tT T jA x t A t e e T πππ-==- 所以,在2T π-处:2n jA C =,0nR C =,2nI A C =,||2n A C =,2n πθ= 在2T π处:2n jA C =-,0nR C =,2nI A C =-,||2n A C =,2n πθ=- 所以,实频图、虚频图、双边幅频图、双边相频图分别如图1的(b)、(c)、(d)、(e)。
2Tπ2Tπ-(a)单边幅频图 (b) 实频图 (c) 虚频图 (d) )双边幅频图 (e) 双边相频图图1 正弦信号x (t)的频谱 (2)当延迟4/T 后,()x t 变为2()sin ()4T x t A t Tπ⎡⎤=-⎢⎥⎣⎦,由于222()sin ()cos ()cos 442T T x t A t A t A t T T T πππππ⎡⎤⎡⎤⎛⎫=-=--=- ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭,符合三角函数展开形式,则在2Tπ处:1nA=,所以,单边频谱图为图2的(a)。
对222()sin()sin()cos()42T Tx t A t A t A tT T Tπππ⎡⎤=-=-=-⎢⎥⎣⎦进行复指数展开,由于222()cos()()2j t j tT TAx t A t e eTπππ--=-=+所以,在2Tπ-处:2nAC=-,2nRAC=-,0nIC=,||2nAC=,nθπ=在2Tπ处:2nAC=-,2nRAC=-,0nIC=,||2nAC=,nθπ=所以,实频图、虚频图、双边幅频图、双边相频图分别如图2的(b)、(c)、(d)、(e)。
测试技术习题解答参考

((测试技术))习 题 解 答 参 考 绪论0-2已知某测试系统传递函数()ss H5.011+=,当输入信号分别为t x t x ππ4sin ,sin 21==时,试分别求系统稳态输出,并比较它们幅值变化和相位变化。
解:221125.011)(f fj f j jf H πππ+-=⨯⨯+=2122)1(1)(f f H π+== )(arg )(f tg f π-=ΦHz f X 5.0:11=, 537.0)(1=f H , 52.57)(1-=Φf Hz f X 2:22=, 157.0)(2=f H , 96.80)(2-=Φf有:)52.57sin(537.0)(10 -=t t X π)96.804sin(157.0)(20 -=t t X π0-3、用时间常数为0.5的一阶装置进行测量,若被测参数按正弦规律变化,若要求装置指示值的幅值误差小于2%,问被测参数变化的最高频率是多少?如果被测参数的周期是2s 和5s ,问幅值误差是多少? 解:一阶装置,有 11)(+=Ts s H212])2(1[1)(f T f H π+=今5.0=T ,有212])2(1[1)(f T f H π+=幅值误差小于2% , 应98.0)(>f H 求出Hz f 08.0<对被测信号:周期是2s,Hz f 5.01=,537.0)(1=f H ,幅值误差为46.3%周期是5s, Hz f 2.02=,847.0)(2=f H ,幅值误差为15.3%0-4 用一阶测量仪器测量100Hz 的正弦信号,如果要求振幅的测量误差小于5%,问仪器的时间常数T 的取值范围。
若用该仪器测50Hz 的正弦信号,相应的振幅误差和相位滞后是多少? 解:一阶装置,仍有11)(+=Ts s H212])2(1[1)(f T f H π+=同一f ,T 越大,)(f H 越小.今f =100Hz, 测量误差小于5%,即95.0)(>f H ,求出41023.5-⨯<T 秒用该仪器测50Hz 的正弦信号,有9868.0)(=f H ,32.9)2(arg )(-=-=ΦTf tg f π即振幅误差是1.32%,相位滞后是32.9-0-5 试说明理想的不失真测试系统的要求是:()()02,ft f const f A πφ-==解:记不失真测试系统的输入为x(t),输出为y(t)不失真, 即输出)(t y 只可放大S 倍和延时0t 时刻, 即应对)()(0t t Sx t y -=该式左、右分别作傅氏变换,有:π20)()(jft e f SX f Y -=即: π20)()()(jft Se f X f Y f H -==故对不失真测试系统的要求是:()()02,ft f const f A πφ-==第一章1-3 有一金属电阻应变片,其灵敏度S=2.5,R =120Ω,设工作时其应变为1200με,问ΔR 是多少?若将此应变片与2V 直流电源组成回路,试求无应变时和有应变时回路的电流各是多少? 解: 由P18,公式(1-6)可知, Ω=⨯⨯⨯===36.05.21012001206S R dR S R dRξξ 无应变 mA A R U t i 3.8103.8100222)(3=⨯=⨯==-有应变mA A R R U t i 8.5108.536.024022)(3=⨯=+=∆+=-1-4 应变片称重传感器,其弹性体为圆柱体,直径D=10cm ,材料弹性模量E=205×109N/m 2,用它称50吨重物体,若用电阻丝式应变片,应变片的灵敏度系数S=2,R=120Ω,问电阻变化多少?解: 因为:A F E ==σσξ所以:ED N AEF ⨯⨯⨯⨯==2)2()(10100050πξ42922101.3)(10205)()21.0()(10100050-⨯=⨯⨯⨯⨯⨯=m N m N π )(754.010*******.312044Ω=⨯=⨯⨯⨯==--S R dR ξ1-5 已知两极板电容传感器,其极板面积为A ,两极板间介质为空气,极板间距1mm ,当极距减少0.1mm 时,其电容变化量和传感器的灵敏度?若参数不变,将其改为差动结构,当极距变化0.1mm 时,求其电容变化量和传感器的灵敏度?并说明差动传感器为什么能提高灵敏度和减少线性误差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 测试系统的基本特性
(一)填空题
1、 某一阶系统的频率响应函数为121
)(+=ωωj j H ,输入信号2
sin )(t t x =,则输出信号)(t y 的频率为=ω ,幅值=y ,相位=φ 。
2、 试求传递函数分别为5.05.35.1+s 和222
4.141n n n s s ωωω++的两个环节串联后组成的系统的总灵敏度。
为了获得测试信号的频谱,常用的信号分析方法有 、 和 。
3、 当测试系统的输出)(t y 与输入)(t x 之间的关系为)()(00t t x A t y -=时,该系统能实现
测试。
此时,系统的频率特性为=)(ωj H 。
4、 传感器的灵敏度越高,就意味着传感器所感知的 越小。
5、 一个理想的测试装置,其输入和输出之间应该具有 关系为最佳。
(二)选择题
1、 不属于测试系统的静特性。
(1)灵敏度 (2)线性度 (3)回程误差 (4)阻尼系数
2、 从时域上看,系统的输出是输入与该系统 响应的卷积。
(1)正弦 (2)阶跃 (3)脉冲 (4)斜坡
3、 两环节的相频特性各为)(1ωQ 和)(2ωQ ,则两环节串联组成的测试系统,其相频特性
为 。
(1)
)()(21ωωQ Q (2))()(21ωωQ Q + (3))
()()()(2121ωωωωQ Q Q Q +(4))()(21ωωQ Q - 4、 一阶系统的阶跃响应中,超调量 。
(1)存在,但<5% (2)存在,但<1
(3)在时间常数很小时存在 (4)不存在
5、 忽略质量的单自由度振动系统是 系统。
(1)零阶 (2)一阶 (3)二阶 (4)高阶
6、 一阶系统的动态特性参数是 。
(1)固有频率 (2)线性度 (3)时间常数 (4)阻尼比
7、 用阶跃响应法求一阶装置的动态特性参数,可取输出值达到稳态值 倍所经过的
时间作为时间常数。
(1)0.632 (2)0.865 (3)0.950 (4)0.982
(三)判断对错题(用√或×表示)
1、 一线性系统不满足“不失真测试”条件,若用它传输一个1000Hz 的正弦信号,则必然
导致输出波形失真。
( )
2、 在线性时不变系统中,当初始条件为零时,系统的输出量与输入量之比的拉氏变换称为
传递函数。
( )
3、 当输入信号)(t x 一定时,系统的输出)(t y 将完全取决于传递函数)(s H ,而与该系统
的物理模型无关。
( )
4、 传递函数相同的各种装置,其动态特性均相同。
( )
5、 测量装置的灵敏度越高,其测量范围就越大。
( )
6、 幅频特性是指响应与激励信号的振幅比与频率的关系。
( )
(四)简答和计算题
1、 什么叫系统的频率响应函数?它和系统的传递函数有何关系?
2、 测试装置的静态特性和动态特性各包括那些?
3、 测试装置实现不失真测试的条件是什么?
4、 某测试装置为一线性时不变系统,其传递函数为1
005.01)(+=s s H 。
求其对周期信号)45100cos(2.010cos 5.0)(︒-+=t t t x 的稳态响应)(t y 。
5、 将信号t ωcos 输入一个传递函数为s s H τ+=
11)(的一阶装置,试求其包括瞬态过程在内的输出)(t y 的表达式。
