惯性矩、静矩,形心坐标公式
惯性矩、静矩、抵抗矩形心、重心、质心

力学计算中截面参数计算,关键点地描述原先对于惯性矩、静矩、极惯性矩、抵抗矩地概念及计算方法总是模糊不清,这次认真地整理了下,估计大家对这些基本概念认知也比较凌乱,在此斗胆与大家分享下,其中地不足之处希望大家谅解,也恳请大家批评指正.计算平面地惯性矩方法:在中将平面图画好——生成面域——工具(查询——面域质量特性)——得到质心和惯性矩(此惯性矩地计算轴为坐标原点处、轴)——将坐标轴原点移动刚算出地质心坐标上——工具(查询——面域质量特性)得此平面图地惯性矩和面积:静矩:平面图形地面积与其形心到某一坐标轴地距离地乘积称为平面图形对该轴地静矩.一般用来表示.=* 其中=∑*∑:惯性矩:轴惯性矩反映截面抗弯特性地一个量,简称惯性矩.截面对某个轴地轴惯性矩等于截面上各微面积乘微面积到轴地距离地平方在整个截面上地积分.公式如:=∫*:极惯性矩:极惯性矩是平面图形对坐标轴原点(即点)地矩,计算公式为:(各惯性矩之和):抵抗矩:截面抵抗矩()就是截面对其形心轴惯性矩与截面上最远点至形心轴距离地比值.公式为:面积矩:面积矩是一个概念,凡是与面积有关地都称为面积矩,如静矩,抵抗矩等都为面积矩.质心:为质量集中在此点地假想点;重心:为重力作用点(与组成该物体地物质有关);(如没有引力,则就没有重心一说了)形心:物体地几何中心只与物体地几何形状和尺寸有关,与组成该物体地物质无关).三者地关系::一般情况下重心和形心是不重合地,只有物体是由同一种均质材料构成时,重心和形心才重合.:质心就是物体质量集中地假想点(对于规则形状物体就是它地几何中心),重心就是重力地作用点,通常情况下,由于普通物体地体积比之于地球十分微小,所以物体所处地重力场可看作是均匀地,此时质心与重心重合;如果该物体地体积比之于地球不可忽略(例如一个放在地面上半径为地球体),则该球体所处地重力场就不均匀了,具体说是由下自上重力场逐渐减小,此时重力地作用点靠下,也就是重心低于质心.如果物体所处地位置不存在重力场(如外太空),则物体就无所谓重心了,但由于质量仍然存在,所以质心仍然存在.。
惯性矩、静矩,形心坐标公式
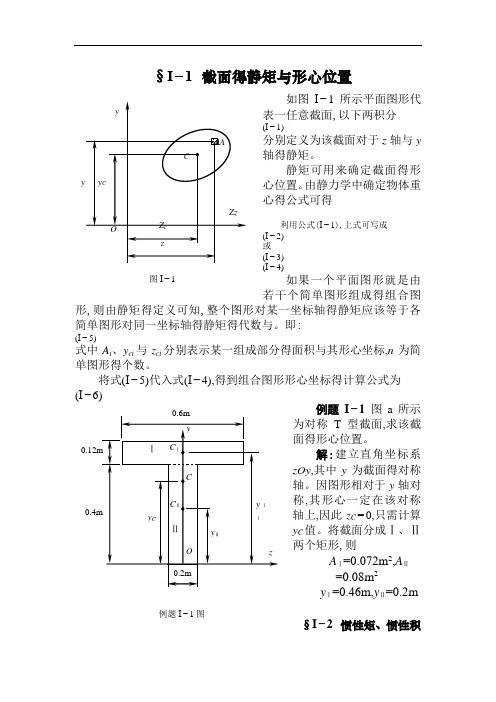
§I−1 截面得静矩与形心位置如图I −1所示平面图形代表一任意截面,以下两积分(I −1)分别定义为该截面对于z 轴与y 轴得静矩。
静矩可用来确定截面得形心位置。
由静力学中确定物体重心得公式可得利用公式(I −1),上式可写成 (I −2) 或 (I −3) (I −4)如果一个平面图形就是由若干个简单图形组成得组合图形,则由静矩得定义可知,整个图形对某一坐标轴得静矩应该等于各简单图形对同一坐标轴得静矩得代数与。
即:(I −5)式中A i 、y ci 与z ci 分别表示某一组成部分得面积与其形心坐标,n 为简单图形得个数。
将式(I −5)代入式(I −4),得到组合图形形心坐标得计算公式为 (I −6)例题I −1 图a 所示为对称T 型截面,求该截面得形心位置。
解:建立直角坐标系zOy ,其中y 为截面得对称轴。
因图形相对于y 轴对称,其形心一定在该对称轴上,因此z C =0,只需计算y C 值。
将截面分成Ⅰ、Ⅱ两个矩形,则 A Ⅰ=0.072m 2,A Ⅱ=0.08m 2y Ⅰ=0.46m,y Ⅱ=0.2m§I −2 惯性矩、惯性积例题I −1图图I −1与极惯性矩如图I −2所示平面图形代表一任意截面,在图形平面内建立直角坐标系zOy 。
现在图形内取微面积d A ,d A 得形心在坐标系zOy 中得坐标为y 与z ,到坐标原点得距离为ρ。
现定义y 2d A 与z 2d A 为微面积d A 对z 轴与y 轴得惯性矩,ρ2d A 为微面积d A 对坐标原点得极惯性矩,而以下三个积分(I −7)分别定义为该截面对于z 轴与y 轴得惯性矩以及对坐标原点得极惯性矩。
由图(I −2)可见,,所以有(I −8) 即任意截面对一点得极惯性矩,等于截面对以该点为原点得两任意正交坐标轴得惯性矩之与。
另外,微面积d A 与它到两轴距离得乘积zy d A 称为微面积d A 对y 、z 轴得惯性积,而积分(I −9)定义为该截面对于y 、z 轴得惯性积。
惯性矩地计算方法及常用截面惯性矩计算公式

惯性矩的计算方法及常用截面惯性矩计算公式截面图形的几何性质一.重点及难点:(一).截面静矩和形心1•静矩的定义式如图1所示任意有限平面图形,取其单元如面积dA,定义它对任意轴的一次矩为它对该轴的静矩,即dS y xdAdSx ydA整个图形对y、z轴的静矩分别为S y xdAyASx 人 ydA2.形心与静矩关系(1-1 )设平面图形形心C的坐标为y c,z c-S x 一S y /、y , x (I-2 )A A推论1如果y轴通过形心(即x0),则静矩S y 0 ;同理,如果X轴通过形心(即y o),则静矩sx o;反之也成立。
推论2如果x、y轴均为图形的对称轴,则其交点即为图形形心;如果y轴为图形对称轴,贝昭形形心必在此轴上。
3.组合图形的静矩和形心设截面图形由几个面积分别为 A,A2,A3 A n的简单图形组成,且一直各族图形的形心坐标分别为丘,只;乂2*2;x3,y3 ,贝U图形对y轴和x轴的静矩分别为截面图形的形心坐标为nA i Xi 1 nA ii 14•静矩的特征(1) 界面图形的静矩是对某一坐标轴所定义的,故静矩与坐标轴有关。
(2) 静矩有的单位为m 3。
(3) 静矩的数值可正可负,也可为零。
图形对任意形心轴的静矩必定 为零,反之,若图形对某一轴的静矩为零,则该轴必通过图形的形心。
(4) 若已知图形的形心坐标。
则可由式(1-1)求图形对坐标轴的静矩。
若已知图形对坐标轴的静矩,则可由式(1-2 )求图形的形心坐标。
组 合图形的形心位置,通常是先由式(I-3 )求出图形对某一坐标系的静 矩,然后由式(1-4 )求出其形心坐标。
(二)•惯性矩 惯性积 惯性半径1.惯性矩定义 设任意形状的截面图形的面积为 A (图I-3 ),则图形对0点的极 惯性矩定义为 I p2dA (1-5)KAn nS yS yiARi 1 i 1nnS xSxiA i Vi 1 i 1(1-3 )A i y i(1-4 )图形对y轴和x轴的光性矩分别定义为I y A x2dA , I x A y2dA (1-6)惯性矩的特征(1)界面图形的极惯性矩是对某一极点定义的;轴惯性矩是对某一坐标轴定义的。
计算惯性矩的公式

矩形对于中线(垂直于h边的中轴线)的惯性矩:b*h^3/12三角形:b*h^3/36圆形对于圆心的惯性矩:π*d^4/64环形对于圆心的惯性矩:π*D^4*(1-α^4)/64;α=d/D§16-1 静矩和形心平面图形的几何性质一般与杆件横截面的几何形状和尺寸有关,下面介绍的几何性质表征量在杆件应力与变形的分析与计算中占有举足轻重的作用。
静矩:平面图形面积对某坐标轴的一次矩,如图Ⅰ-1所示。
定义式:,(Ⅰ-1)量纲为长度的三次方。
由于均质薄板的重心与平面图形的形心有相同的坐标和。
则由此可得薄板重心的坐标为同理有所以形心坐标,(Ⅰ-2)或,由式(Ⅰ-2)得知,若某坐标轴通过形心,则图形对该轴的静矩等于零,即,;,则;反之,若图形对某一轴的静矩等于零,则该轴必然通过图形的形心。
静矩与所选坐标轴有关,其值可能为正,负或零。
如一个平面图形是由几个简单平面图形组成,称为组合平面图形。
设第i块分图形的面积为,形心坐标为,则其静矩和形心坐标分别为,(Ⅰ-3),(Ⅰ-4)【例I-1】求图Ⅰ-2所示半圆形的及形心位置。
【解】由对称性,,。
现取平行于轴的狭长条作为微面积所以读者自己也可用极坐标求解。
【例I-2】确定形心位置,如图Ⅰ-3所示。
【解】将图形看作由两个矩形Ⅰ和Ⅱ组成,在图示坐标下每个矩形的面积及形心位置分别为矩形Ⅰ:mm2mm,mm矩形Ⅱ:mm2mm,mm整个图形形心的坐标为§16-2 惯性矩和惯性半径惯性矩:平面图形对某坐标轴的二次矩,如图Ⅰ-4所示。
,(Ⅰ-5)量纲为长度的四次方,恒为正。
相应定义,(Ⅰ-6)为图形对轴和对轴的惯性半径。
组合图形的惯性矩设为分图形的惯性矩,则总图形对同-轴惯性矩为,(Ⅰ-7)若以表示微面积到坐标原点的距离,则定义图形对坐标原点的极惯性矩(Ⅰ-8)因为所以极惯性矩与(轴)惯性矩有关系(Ⅰ-9)式(Ⅰ-9)表明,图形对任意两个互相垂直轴的(轴)惯性矩之和,等于它对该两轴交点的极惯性矩。
截面的静矩和形心位置和惯性矩的计算
二 、 截面的主惯性轴和主惯性矩
I x1y1
Ix
2
Iy
sin 2α
I xy cos 2α
主惯性轴 —— 总可以找到一个特定的角 0 , 使截面对新坐标 轴 x0 , y0 的惯性积等于 0 , 则称 x0 , y0 为主惯轴。
主惯性矩——截面对主惯性轴的惯性矩。
形心主惯性轴 ——当一对主惯性轴的交点与截面的形心 重合时,则称为形心主惯性轴。
惯性积。
组合截面的惯性矩,惯性积
n
I x I xi i1
n
I y I yi i1
n
I xy I xyi i 1
例 3 -1 求梯形截面对其形心轴 yc 的惯性矩。
解:将截面分成两个矩形截面。
截面的形心必在对称轴 zc 上。 取过矩形 2 的形心且平行 于底边的轴作为参考轴, 记作 y 轴 。
97.3 104 mm4
2 I xy
tg2 0 (
Ix
) 1.093 Iy
Ix Iy 2α 0 在第三象限 2α 0 227.60
0
113.80
形心主惯性轴 x0 , y0 分别由 x 轴和 y 轴绕 C点 逆时针转 113.80 得出。
形心主惯形矩为
I x0 I x I y 1
形心主惯性矩—— 截面对形心主惯性轴的惯性矩。
主惯性轴的位置:设 为主惯性轴与原坐标轴 之间的夹角,
则有 由此
I I x I y 2 sin 2 0 xy cos 2 0 0
tg 20
2I xy
Ix Iy
求出后,主惯性轴的位置就确定出来了。
主惯性矩的计算公式
I x0
I y0
Ix
y 0
截面对 y ,z 轴的惯性矩分别为
截面的静矩和形心位及惯性矩的计算
y
dA
x
x 0
截面对 x , y 轴的惯性积为
Ixy A xydA
惯性矩的数值恒为正,惯性积则可能为正值,负值,
也可能等于零。
y
若 x , y 两坐标轴中有一个为
dA y
截面的对称轴,则截面对 x , y 轴的 惯性积一定等于零 。
dx dx x
截面对 x , y 轴的惯性半俓为
iy
Z1 80 Z2 0
所以截面的形心坐标为
ZC
A1 Z1 A1
A2 Z2 A2
46.7mm
20 140
zc
20
1
yc
ZC
2
y
100
I1yC
1 12
20 1403
20 140
(8046.7)2
I
2 yC
1 12
100
203
100
20
(46.7)2
zc
120 103 152 120 10
1 12
703
10
(25)2
70
10
100.4 104 mm 4
Iy 278.4 104 mm4
70 20 10
120
y
80
c
x
10
y
I xy 0 15 20 120 10 0 (25) (35) 70 10
x2
10
70 2
45mm
y2 5mm
y 10
1 x1
y1
截面的静矩和形心位置及惯性矩的计算

x 0
截面对 x , y 轴的惯性积为
Ixy A xydA
惯性矩的数值恒为正,惯性积则可能为正值,负值,
也可能等于零。
y
若 x , y 两坐标轴中有一个为
dA y
截面的对称轴,则截面对 x , y 轴的 惯性积一定等于零 。
dx dx x
截面对 x , y 轴的惯性半俓为
iy
Iy , A
二 、 截面的主惯性轴和主惯性矩
I x1y1
Ix
2
Iy
sin 2α
I xy cos 2α
主惯性轴 —— 总可以找到一个特定的角 0 , 使截面对新坐标 轴 x0 , y0 的惯性积等于 0 , 则称 x0 , y0 为主惯轴。
主惯性矩——截面对主惯性轴的惯性矩。
形心主惯性轴 ——当一对主惯性轴的交点与截面的形心 重合时,则称为形心主惯性轴。
x
80
§ І -2 极惯性矩 惯性矩 惯性积
定义:
z dA
z
截面对 o 点的极惯性矩为
y
Ip Aρ2dA
y 0
截面对 y ,z 轴的惯性矩分别为
Iy A z2dA Iz A y2dA
因为 ρ2 y2 z2
I p Aρ2 dA
所以 Ip = Ix + Iy
y
y
dA
ix
Ix A
例 2 _ 1 求矩形截面对其对称轴 x , y 轴的惯性矩。
解:
dA = b dy
Ix
A y2dA
h
2h
by2dy
2
bh3 12
Ix A y2dA
第七章 静矩及其性质

Iy Iy i i 1 n I z I z i i 1 n I yz I yz i i 1
n
I z i 、 I y i、 I yz i 分别为第个i简单图形对y轴和z轴的惯 式中, 性矩和惯性积。
22
§7-3
17
例2
求图示矩形的 I z , I y , I yz ,i y ,iz z
dz z
h
c
y
b
1 3 b 3 bh I y z dA z A 12 3 h 2 1 3 2 I z y dA hb A 12 Iy 3 iy h A 6
2
h 2
Iz 3 iz b A 6 I yz yzdA 0
z
60 96 65 (77 ) 39.7(mm ) 96 77 13
§7-2
惯性矩和惯性积
y
z y dA z
一、简单图形的惯性矩 1、定义: dA对z轴的惯性距: dA对y轴的惯性距: 图形对z轴的惯性矩:
2
dIz y dA 2 dIy z dA o
I z y 2 dA,
求圆环圆形的 I z , I y z D d y
I P I P大 I P小
1 1 D 4 d 4 32 32 1 D 4 ( 1 4 ) 32
d D
I y I z I z大 I z小
1 D 4 (1 4 ) 64
21
三、组合图形的惯性矩及惯性积 根据定义可知,组合图形对某坐标轴的惯性矩 等于各个简单图形对同一轴的惯性矩之和;组合图 形对于某一对正交坐标轴的惯性积等于各个简单图 形对同一对轴的惯性积之和。用公式可表示为
惯性矩、静矩,形心坐标公式

惯性矩、静矩,形心坐标公式-CAL-FENGHAI.-(YICAI)-Company One1§I?1 截面的静矩和形心位置如图I ?1所示平面图形代表一任意截面,以下两积分⎪⎭⎪⎬⎫==⎰⎰A z S A y S A y Az d d (I ?1)分别定义为该截面对于z 轴和y 轴的静矩。
静矩可用来确定截面的形心位置。
由静力学中确定物体重心的公式可得⎪⎪⎭⎪⎪⎬⎫==⎰⎰A A z z A A y y AC A Cd d利用公式(I ?1),上式可写成⎪⎪⎭⎪⎪⎬⎫====⎰⎰A S A A z z A S A Ay y y AC z A C d d (I ?2)或⎭⎬⎫==C y C z Az S Ay S (I ?3)⎪⎪⎭⎪⎪⎬⎫==A S z A S y yCz C (I ?4)图I ?1如果一个平面图形是由若干个简单图形组成的组合图形,则由静矩的定义可知,整个图形对某一坐标轴的静矩应该等于各简单图形对同一坐标轴的静矩的代数和。
即:⎪⎪⎭⎪⎪⎬⎫==∑∑==ni ci i y ni ci i z z A S y A S 11(I ?5)式中A i 、y ci 和z ci 分别表示某一组成部分的面积和其形心坐标,n 为简单图形的个数。
将式(I ?5)代入式(I ?4),得到组合图形形心坐标的计算公式为⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎬⎫==∑∑∑∑====ni i ni ci i c ni i ni ci i c A z A z A y A y 1111(I ?6)例题I ?1 图a 所示为对称T 型截面,求该截面的形心位置。
解:建立直角坐标系zOy ,其中y 为截面的对称轴。
因图形相对于y 轴对称,其形心一定在该对称轴上,因此z C =0,只需计算y C 值。
将截面分成Ⅰ、Ⅱ两个矩形,则A Ⅰ=0.072m 2,A Ⅱ=0.08m 2y Ⅰ=0.46m ,y Ⅱ=0.2m例题I ?1图m323.008.0072.02.008.046.0072.0III II II I I 11=+⨯+⨯=++==∑∑==A A y A y A AyA y ni ini cii c§I ?2 惯性矩、惯性积和极惯性矩如图I ?2所示平面图形代表一任意截面,在图形平面内建立直角坐标系zOy 。
史上最全的常用截面几何特性计算公式

史上最全的常用截面几何特性计算公式构件截面的几何性质,如静力矩、形心、轴向惯性矩、极惯性矩、惯性积和主惯性轴位置等,对构件的承载能力有影响,常用于分析构件的弯曲、扭转和剪切。
1.静态力矩:也称为面积力矩或静态表面力矩。
截面对轴线的静力矩等于每个微区的积分乘以整个截面上微区到轴线的距离。
静力矩可以是正的,也可以是负的。
它的维数是长度的三次方。
静力矩的力学意义是:如果有均布载荷作用在截面上,其值表示为单位面积的量,则该载荷在某一轴上的合成力矩等于分布载荷乘以该轴的静力矩。
2、形心:又称面积中心或面积重心,是截面上具有如下性质的点:截面对通过此点任一个轴的静矩等于零。
如果将截面看成一均质等厚板,则截面的形心就是板面的重心。
形心坐标xo、yo的计算公式为:3、惯性矩:反映截面抗弯特性的一个量,简称惯性矩。
截面对某个轴的轴惯性矩等于截面上各微面积乘微面积到轴的距离的平方在整个截面上的积分。
下图所示的面积为A的截面对x、y轴的轴惯性矩分别为:转动惯量总是正的,量纲是长度的四次方。
构件的抗弯能力与轴的惯性矩成正比。
一些典型截面的轴惯性矩可在专业手册中找到。
例如,平行四边形对中心线的惯性矩为4、极惯性矩:反映截面抗扭特性的一个量。
截面对某个点的极惯性矩等于截面上各微面积乘微面积到该点距离的平方在整个截面上的积分。
下图所示面积为A的截面对某点O的极惯性矩为:极惯性矩永远是正的,量纲是长度的四次方。
构件的抗扭能力与惯性矩成正比。
圆形截面相对于其中心的惯性矩为5、惯性积:截面对于两个正交坐标轴的惯性积等于截面上各个微面积乘微面积到两个坐标轴的距离在整个截面上的积分。
面积为A的截面对两个正交坐标轴x、y的惯性积为:惯性积的量纲是长度的四次方。
截面位于坐标系的一、三象限,Ixy为正,位于二、四象限则为负。
6.主惯性轴:使截面惯性积为零的一对正交坐标轴称为截面主惯性轴,简称主轴。
截面对主惯性轴的惯性矩称为主惯性矩。
若两条主惯性轴的交点为质心,则这两条轴称为质心主惯性轴(或称主质心惯性轴)。
截面的静矩和形心位置及惯性矩的计算

02 截面的静矩
静矩的定义
静矩
截面内力与作用点到截面某一固定点的距离的乘积的 积分。
面积矩
截面内力与作用点到截面某一固定点的距离的平方的 积分。
极惯性矩
截面内力与作用点到截面某一固定点的距离的四次方 的积分。
静矩的计算
1 2
静矩的计算公式
静矩 = Σ (y_i * dA_i),其中y_i为截面内力作用 点到某一固定点的距离,dA_i为该点处的面积微 元。
截面的静矩和形心位置及惯性矩的 计算
contents
目录
• 截面的几何特性 • 截面的静矩 • 截面的形心位置 • 截面的惯性矩 • 截面特性在工程中的应用
01 截面的几何特性
截面的定义
01
截面是一个二维平面图形,可以 通过在三维空间中切割一个物体 来获得。
02
截面可以是封闭的或开放的,可 以有不同的形状和大小,取决于 切割的方式和角度。
05 截面特性在工程中的应用
在结构设计中的应用
结构设计是工程中非常重要的环节,截面的静 矩和形心位置及惯性矩的计算可以为结构设计 提供重要的参考依据。
在结构设计时,需要考虑到截面的承载能力、 稳定性以及变形等因素,而这些因素都与截面 的特性密切相关。
通过计算截面的静矩和形心位置及惯性矩,可 以更好地了解截面的受力特性,从而优化结构 设计,提高结构的承载能力和稳定性。
转动惯量
是指刚体绕某点转动时,其转动惯量 等于刚体的所有质量微元与各微元距 离平方的乘积之和。
惯性矩的计算
矩形截面惯性矩
对于矩形截面,其惯性矩可以通过计算其面 积与面积上分布的物质质量的乘积,再乘以 一个常数得到。
圆形截面惯性矩
惯性矩的计算方法及常用截面惯性矩计算公式

LOGO惯性矩的计算方法及常用截面惯性矩计算公式在此输入你的公司名称惯性矩的计算方法及常用截面惯性矩计算公式截面图形的几何性质一.重点及难点:(一).截面静矩和形心1•静矩的定义式如图1所示任意有限平面图形,取其单元如面积dA,定义它对任意轴的一次矩为它对该轴的静矩,即dS y 二xdAdSx = ydA整个图形对y、z轴的静矩分别为S y = A xdA(1-Sx= A ydA1)2.形心与静矩关系图1-1设平面图形形心C的坐标为y C,z C则0-S y x =A (1-2)推论1如果y轴通过形心(即x = 0),则静矩Sy=0 ;同理,如果x轴通过形心(即y = 0),则静矩Sx=o;反之也成立。
推论2如果x、y轴均为图形的对称轴,则其交点即为图形形心;如果y轴为图形对称轴,贝昭形形心必在此轴上。
3.组合图形的静矩和形心设截面图形由几个面积分别为A,A2,A3……A n的简单图形组成,且一直各族图形的形心坐标分别为x1,y1; x2,y2; x3,y3,则图形对y轴和x轴的静矩分别为n nS y = * S yi i A i Xii -1 i-1 nnS x 八 S xi 八 A i y ii 4i 4截面图形的形心坐标为A i4.静矩的特征(1)界面图形的静矩是对某一坐标轴所定义的,故静矩与坐标轴有关。
(2)静矩有的单位为m 3(3)静矩的数值可正可负,也可为零。
图形对任意形心轴的静矩必定 为零,反之,若图形对某一轴的静矩为零,则该轴必通过图形的形心。
⑷ 若已知图形的形心坐标。
则可由式(I-1)求图形对坐标轴的静矩。
若已知图形对坐标轴的静矩,则可由式(1-2)求图形的形心坐标。
组 合图形的形心位置,通常是先由式(I-3)求出图形对某一坐标系的静 矩,然后由式(I-4)求出其形心坐标。
(二)■惯性矩惯性积惯性半径1. 惯性矩定义 设任意形状的截面图形的面积为 A (图I-3),则图形对0点的极 惯性矩定义为 I p = A (2dA(1-5)图形对y 轴和x 轴的光性矩分别定义为 I y 二 A X 2dA , I x 「A y 2dA (I-6)惯性矩的特征(1)界面图形的极惯性矩是对某一极点定义的; 轴惯性矩是对某一坐标轴定义的。
惯性矩的计算方法与常用截面惯性矩计算公式

惯性矩的计算方法及常用截面惯性矩计算公式截面图形的几何性质一.重点及难点:(一).截面静矩和形心1.静矩的定义式如图1所示任意有限平面图形,取其单元如面积dA ,定义它对任意轴的一次矩为它对该轴的静矩,即ydAdSx xdA dS y == 整个图形对y 、z 轴的静矩分别为⎰⎰==AAy ydASx xdAS (I-1) 2.形心与静矩关系 图I-1设平面图形形心C 的坐标为C C z y , 则 0AS y x= , A S x y = (I-2)推论1 如果y 轴通过形心(即0=x ),则静矩0=y S ;同理,如果x 轴通过形心(即0=y ),则静矩0=Sx ;反之也成立。
推论2 如果x 、y 轴均为图形的对称轴,则其交点即为图形形心;如果y 轴为图形对称轴,则图形形心必在此轴上。
3.组合图形的静矩和形心设截面图形由几个面积分别为n A A A A ⋯⋯321,,的简单图形组成,且一直各族图形的形心坐标分别为⋯⋯332211,,,y x y x y x ;;,则图形对y 轴和x轴的静矩分别为∑∑∑∑========ni ni ii xi x ni ii ni yi y y A S S x A S 1111S (I-3)截面图形的形心坐标为∑∑===ni ini ii AxA x 11 , ∑∑===ni ini ii AyA y 11 (I-4)4.静矩的特征(1) 界面图形的静矩是对某一坐标轴所定义的,故静矩与坐标轴有关。
(2) 静矩有的单位为3m 。
(3) 静矩的数值可正可负,也可为零。
图形对任意形心轴的静矩必定为零,反之,若图形对某一轴的静矩为零,则该轴必通过图形的形心。
(4) 若已知图形的形心坐标。
则可由式(I-1)求图形对坐标轴的静矩。
若已知图形对坐标轴的静矩,则可由式(I-2)求图形的形心坐标。
组合图形的形心位置,通常是先由式(I-3)求出图形对某一坐标系的静矩,然后由式(I-4)求出其形心坐标。
惯性矩、静矩,形心坐标公式
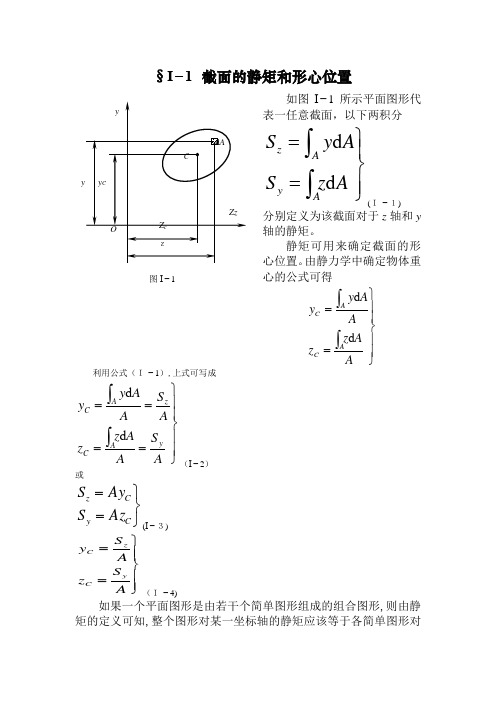
§I−1 截面的静矩和形心位置如图I −1所示平面图形代表一任意截面,以下两积分⎪⎭⎪⎬⎫==⎰⎰A z S A y S A y Az d d (I−1)分别定义为该截面对于z 轴和y轴的静矩。
静矩可用来确定截面的形心位置。
由静力学中确定物体重心的公式可得⎪⎪⎭⎪⎪⎬⎫==⎰⎰A A z z A A y y AC A Cd d利用公式(I−1),上式可写成⎪⎪⎭⎪⎪⎬⎫====⎰⎰A S A A z z A S A Ay y y AC z A C d d (I −2)或⎭⎬⎫==C y C z Az S Ay S (I −3)⎪⎪⎭⎪⎪⎬⎫==A S z A S y yCz C (I−4)如果一个平面图形是由若干个简单图形组成的组合图形,则由静矩的定义可知,整个图形对某一坐标轴的静矩应该等于各简单图形对图I −1同一坐标轴的静矩的代数和。
即:⎪⎪⎭⎪⎪⎬⎫==∑∑==ni ci i y ni ci i z z A S y A S 11(I−5)式中Ai、y ci 和z ci 分别表示某一组成部分的面积和其形心坐标,n 为简单图形的个数。
将式(I −5)代入式(I −4),得到组合图形形心坐标的计算公式为⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎬⎫==∑∑∑∑====n i i ni ci i c ni i ni ci i c A z A z A y A y 1111(I−6)例题I −1 图a 所示为对称T 型截面,求该截面的形心位置。
解:建立直角坐标系zOy ,其中y 为截面的对称轴。
因图形相对于y 轴对称,其形心一定在该对称轴上,因此z C =0,只需计算y C 值。
将截面分成Ⅰ、Ⅱ两个矩形,则A Ⅰ=0.072m 2,A Ⅱ=0.08m2y Ⅰ=0.46m ,y Ⅱ=0.2m例题I −1图m323.008.0072.02.008.046.0072.0III II II I I 11=+⨯+⨯=++==∑∑==A A y A y A AyA y ni ini cii c§I −2 惯性矩、惯性积和极惯性矩如图I −2所示平面图形代表一任意截面,在图形平面内建立直角坐标系zO y。
第七讲 形心、静矩、惯性矩

2.1.1 静矩和形心
2、重心的定义
地球半径很大,地表面物体的重力可以看作是平行力系,此 平行力系的中心即物体的重心。
重心有确定的位置,与物体在空间的位置无关。
设物体的重心在C处,重力为P,由若干部分组成,第i部分 重力(Pi)及其作用点坐标如图
对x轴用合力矩定理
Pyc = P1 y1 + P2 y2 +
惯性半径 极惯性矩 惯性积 主惯性轴 主惯性矩
……
2.1.1 静矩和形心
1、静矩(面积矩)的定义
y
z
整个图形对于y轴的静矩
S y =
zdA
A
整个图形对于z轴的静矩
dA
y
O
Sz =
ydA
A
静矩是代数量。可正、可
z 负,也可为零。
单位:m3或mm3
静矩是对某一坐标轴定义的,静矩与坐标轴有关。 静矩与截面尺寸、形状、轴的位置有关。
n
yc
=
Sz A
=
Ai yCi
i =1 n
Ai
i =1
n
zc
=
Sy A
=
Ai zCi
i =1 n
Ai
i =1
2.1.2 惯性矩、惯性积、极惯性矩和惯性半径
1、惯性矩的定义
y
z
dA
y
O
y2dA:微面积dA对z轴的惯性矩。
Iz =
y 2 dA
A
整个图形对z轴的惯性矩
I y =
z 2 dA
整个图形对z轴的惯性半径
2.1.2 惯性矩、惯性积、极惯性矩和惯性半径
1、惯性矩的定义
y
z
dA
1、静矩与形心2、惯性矩、极惯性矩和惯性积3、平行移轴公

1. 转轴公式
y
y
A dA
C E
D
O
x
B
新坐标系ox1y1 旧坐标系o x y
x1 x cos y sin y1 y cos x sin
将上述关系代入平 面图形对x1轴的惯性矩:
x
I x1 A y12 d A
Ix1
cos2
y2 d A sin2
(4)由转轴公式得
80 aⅡ 20 10
40 C
bⅠ Ⅰ
aⅠ
xC
tan 20
2I xc yc I xc I yc
1.093
=113°.8
yc0
bⅡ
20 227 .6 0 113 .8
10 Ⅱ
I xc0
Imax
I xc
I yc 2
1 2
I xc
目录
§ I-2 极惯性矩 ·惯性矩 ·惯性积
1.极惯性矩(或截面二次极矩)
y
I p
2d A
A
2.惯性矩(或截面二次轴矩)
y
I y
x2 d A
A
I x
y2d A
A
O
由于 2 y2 x2
dA
x
x
所以
Ip
2 d A
A
(y2
A
x2)
dA IxIy
(B) Ixy<0 (D) Ix=Iy
(思考题I—2)A
y
bO
(思考题I—3)
x
a
y a
x
Ba
D
思考题I—3:等腰直角三角形如图所示,x、y轴是过斜边中点的
截面的静矩和形心位置及惯性矩的计算课件

数值模拟与优化
利用数值模拟技术,如有限元方法、边界元方法等,可以更精确地计算 截面的静矩和形心位置及惯性矩,并在此基础上进行结构优化设计。
03
多学科交叉
未来研究可以结合多个学科领域,如物理学、化学、生物学等,以更全
面地理解截面的静矩和形心位置及惯性矩的本质和规律,推动相关领域
的发展。
感谢您的观看
THANKS
详细描述
对于任意形状截面,其静矩可以通过对截面进行微分, 然后计算每个微元面积与微元重心到截面边缘的距离乘 积,最后对所有微元的静矩进行积分得到。形心位置可 以通过对截面进行微分,然后计算每个微元的面积与微 元重心坐标的平均值得到。惯性矩可以通过对截面进行 微分,然后计算每个微元的面积、微元重心到截面边缘 的距离以及微元的转动惯量,最后对所有微元的转动惯 量进行积分得到。
矩值。
通过公式计算其半径和 圆周率,得出惯性矩值。
通过公式计算其长轴、 短轴和圆周率,得出惯
性矩值。
不规则截面
需采用数值分析方法进 行近似计算或通过实验
测量得出。
03
截面几何特性的应用
结构强度分析
静矩
静矩是截面内力的一个重要参数,用于计算截面在受力时的稳定性。静矩的计算公式为 ∫(y*dA),其中y为截面各点到截面中心的距离,dA为面积微元。
形心位置
形心是截面的几何中心,其位置决定了截面的质量分布和转动惯量。形心位置可以通过积分 计算得到,公式为∫dA/A∫dxdy,其中A为截面面积。
惯性矩
惯性矩是衡量截面抗弯能力的重要参数,其计算公式为∫y^2dA,其中y为截面各点到形心距 离,dA为面积微元。
结构稳定性分析
结构失稳
当结构受到的外部载荷超 过其承载能力时,结构会 发生失稳,导致结构变形 甚至破坏。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§I−1 截面的静矩和形心位置
如图I −1所示平面图形代表一任意截面,以下两积分
⎪
⎭⎪⎬
⎫==⎰⎰A z S A y S A y A
z d d (I −1)
分别定义为该截面对于z 轴和y
轴的静矩。
静矩可用来确定截面的形心位置。
由静力学中确定物体重心的公式可得
⎪
⎪⎭⎪
⎪⎬⎫==
⎰⎰A A z z A A y y A
C A C
d d
利用公式(I −1),上式可写成
⎪
⎪⎭⎪
⎪
⎬
⎫====⎰⎰A S A A z z A S A A
y y y A
C z A C d d (I −2)
或
⎭
⎬
⎫==C y C z Az S Ay S (I −3)
⎪⎪⎭⎪⎪⎬⎫=
=A S z A S y y
C
z C (I −4)
如果一个平面图形是由若干个简单图形组成的组合图形,则由静
矩的定义可知,整个图形对某一坐标轴的静矩应该等于各简单图形对
图I −1
同一坐标轴的静矩的代数和。
即:
⎪⎪
⎭⎪⎪
⎬⎫
==∑∑==n
i ci i y n
i ci i z z A S y A S 11
(I −5)
式中A i 、y ci 和z ci 分别表示某一组成部分的面积和其形心坐标,n 为简
单图形的个数。
将式(I −5)代入式(I −4),得到组合图形形心坐标的计算公式为
⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪
⎬⎫
==∑∑∑∑====n
i i n
i ci i c n
i i n
i ci i c A z A z A y A y 11
1
1(I −6)
例题I −1 图a 所示为对称T 型截面,求该截面的形心位置。
解:建立直角坐标系zOy ,其中y 为截面的对称轴。
因图形相对于y 轴对称,其形心一定在该对称轴上,因此z C =0,只需计算y C 值。
将截面分成Ⅰ、Ⅱ两个矩形,则
A Ⅰ=0.072m 2,A Ⅱ
=0.08m 2 y Ⅰ=0.46m ,y Ⅱ=0.2m
例题I −1图
m
323.008.0072.02.008.046.0072.0II
I II II I I 1
1=+⨯+⨯=++=
=
∑∑==A A y A y A A
y
A y n
i i
n
i ci
i c
§I −2 惯性矩、惯性积和极惯性矩
如图I −2所示平面图形代表一任意截面,在图
形平面建立直角坐标系zOy 。
现在图形取微面积d A ,
d A 的形心在坐标系zOy 中的坐标为y 和z ,到坐标原点的距离为ρ。
现定义y 2d A 和z 2d A 为微面积d A 对z 轴和y 轴的惯性矩,ρ2d A 为微面积d A 对坐标原点的极惯性矩,而以下三个积分
⎪
⎪⎭⎪⎪
⎬
⎫
===⎰⎰⎰A ρI A z I A y I A A
y A z d d d 2
P 2
2
(I −7) 分别定义为该截面对于z 轴和y 轴的惯性矩以及对坐标原点的极惯性
矩。
由图(I −2)可见,2
22z y +=ρ,所以有
⎰⎰+=+==A
y
z A
I I A z y A ρI )d (d 222P (I −8)
即任意截面对一点的极惯性矩,等于截面对以该点为原点的两任意正交坐标轴的惯性矩之和。
另外,微面积d A 与它到两轴距离的乘积zy d A 称为微面积d A 对y 、z 轴的惯性积,而积分
A
zyd I A
yz ⎰=(I −9)
定义为该截面对于y 、z 轴的惯性积。
从上述定义可见,同一截面对于不同坐标轴的惯性矩和惯性积一
图I −2
般是不同的。
惯性矩的数值恒为正值,而惯性积则可能为正,可能为负,也可能等于零。
惯性矩和惯性积的常用单位是m 4或mm 4。
§I −3 惯性矩、惯性积的平行移轴和转轴公式
一、惯性矩、惯性积的平行移轴公式
图I −3所示为一任意截面,
z 、y 为通过截面形心的一对正交轴,z 1、y 1为与z 、y 平行的坐标轴,截面形心C 在坐标系z 1O y 1中的坐标为(b ,a ),已知截面对z 、y 轴惯性矩和惯性积为I z 、I y 、I yz ,下面求截面对z 1、y 1轴惯性矩和惯性积I z 1、I y 1、I y 1z 1。
A
a I I z z 21+=(I −10)
同理可得
A
b I I y y 2
1+=(I −11)
式(I −10)、(I −11)称为惯性矩的平行移轴公式。
下面求截面对y 1、z 1轴的惯性积1
1z y I 。
根据定义
⎰⎰++==A
A
z y A
a y
b z A y z I )d )((d 1111
⎰⎰⎰⎰+++=A
A
A
A
A
ab A y b A z a A zy d d d d
abA
bS aS I z y yz +++=
由于z 、y 轴是截面的形心轴,所以S z =S y =0,即
abA
I I yz z y +=11 (I −12)
式(I −12)称为惯性积的平行移轴公式。
二、惯性矩、惯性积的转轴公式
图(I −4)所示为一任意截面,z 、y 为过任一点O 的一对正交轴,截面对z 、y 轴惯性矩I z 、I y 和惯性积I yz 已知。
现将z 、y 轴绕O 点旋
图I −3
转α角(以逆时针方向为正)得到另一对正交轴z 1、y 1轴,下面求截面对z 1、y 1轴惯性矩和惯性积1
z I 、1
y I 、1
1z y I 。
α
α2sin 2cos 2
2
1yz y
z y
z z I I I I I I --+
+=
(I −13)
同理可得
α
α2sin 2cos 2
2
1yz y
z y
z y I I I I I I +--
+=
(I −14)
α
α2cos 2sin 2
11yz y
z z y I I I I +-=
(I −15)
式(I −13)、(I −14)称为惯性矩的转轴公式,式(I −15)称为惯性积的转轴公式。
§I −4 形心主轴和形心主惯性矩
一、主惯性轴、主惯性矩
由式(I −15)可以发现,当α=0o ,即两坐标轴互相重合时,
图I −4
yz
z y I I =11;当α=90o 时,yz z y I I -=1
1,因此必定有这样的一对坐标轴,
使截面对它的惯性积为零。
通常把这样的一对坐标轴称为截面的主惯性轴,简称主轴,截面对主轴的惯性矩叫做主惯性矩。
假设将z 、y 轴绕O 点旋转α0角得到主轴z 0、y 0,由主轴的定义
2cos 2sin 2
0000=+-=
ααyz y
z z y I I I I
从而得
y
z yz I I I α--=
22tan 0 (I −16)
上式就是确定主轴的公式,式中负号放在分子上,为的是和下面两式相符。
这样确定的α0角就使得0
z I 等于m ax I 。
由式(I −16)及三角公式可得
2
204)(2cos yz
y z y
z I I I I I +--=α
2
204)(22sin yz
y z yz
I I I I +--=
α
将此二式代入到式(I −13)、(I −14)便可得到截面对主轴z 0、y 0的主惯性矩
⎪⎪⎭⎪⎪
⎬
⎫+--+=+-++=22224)(2124)(2
120
0yz
y z y z y yz y z y
z z I I I I I I I I I I I I (I −17)
二、形心主轴、形心主惯性矩
通过截面上的任何一点均可找到一对主轴。
通过截面形心的主轴叫做形心主轴,截面对形心主轴的惯性矩叫做形心主惯性矩。
例题I −5 求例I −1中截面的形心主惯性矩。
解:在例题I −1中已求出形心位置为
0=C z ,m 323.0=C y
过形心的主轴z 0、y 0如图所示,z 0轴到两个矩形形心的距离分别为
m 137.0I =a ,m 123.0II =a
截面对z 0轴的惯性矩为两个矩形对z 0轴的惯性矩之和,即
2II
II II 2I
I I
I
I I
0a
A I
a A I I z z z +++=
2
3
23123.04.02.0124.02.0137.012.06.01212.06.0⨯⨯+⨯+⨯⨯+⨯=
42m 1037.0-⨯=
截面对y 0轴惯性矩为
4
23
3II
I m 10242.0122.04.0126.012.000
0-⨯=⨯+⨯=+=y y y I I I。
