常用截面惯性矩计算公式
截面几何特性怎么计算公式

截面几何特性怎么计算公式截面几何特性的计算公式。
截面几何特性是指在工程学和物理学中,用来描述截面形状和尺寸的一些参数,这些参数对于材料的强度、刚度和形变等性能具有重要的影响。
在工程设计和分析中,我们经常需要计算截面的一些特性,比如面积、惯性矩、截面模量等。
下面我们将介绍一些常见的截面几何特性的计算公式。
1. 面积。
截面的面积是描述截面大小的一个重要参数,通常用A表示,其计算公式为:A = ∫y dA。
其中y是截面某一点到参考轴的距离,dA表示微元面积。
对于简单几何形状的截面,可以直接通过几何关系计算出面积,比如矩形的面积为长乘以宽,圆形的面积为πr^2。
2. 惯性矩。
截面的惯性矩描述了截面对于转动的惯性,通常用I表示,其计算公式为:I = ∫y^2 dA。
对于简单几何形状的截面,可以通过几何关系计算出惯性矩,比如矩形的惯性矩为bh^3/12,圆形的惯性矩为πr^4/4。
3. 截面模量。
截面模量描述了截面对拉伸和压缩的抵抗能力,通常用S表示,其计算公式为:S = I/c。
其中c为截面到参考轴的距离。
对于简单几何形状的截面,可以通过几何关系计算出截面模量,比如矩形的截面模量为bh^2/6,圆形的截面模量为πr^3/4。
4. 弯曲模量。
截面的弯曲模量描述了截面对弯曲的抵抗能力,通常用W表示,其计算公式为:W = S/y_max。
其中y_max为截面到参考轴的最大距离。
对于简单几何形状的截面,可以通过几何关系计算出弯曲模量,比如矩形的弯曲模量为bh^2/4,圆形的弯曲模量为πr^3/2。
5. 截面形心。
截面的形心描述了截面的几何中心,通常用x_bar和y_bar表示,其计算公式为:x_bar = ∫x dA / A。
y_bar = ∫y dA / A。
对于简单几何形状的截面,可以通过几何关系计算出形心的坐标,比如矩形的形心坐标为(b/2, h/2),圆形的形心坐标为(0, 0)。
以上是一些常见的截面几何特性的计算公式,这些参数对于工程设计和分析具有重要的意义。
常用截面惯性矩计算公式

常用截面惯性矩计算公式截面的惯性矩是描述截面抵抗弯曲的特性之一,也称为截面二阶矩。
它是通过计算截面各点到其中一轴线的距离的二次方与其对应的面积乘积之和来获得。
常用的截面惯性矩计算公式如下:1.矩形截面的惯性矩公式:对于矩形截面,惯性矩可以通过以下公式进行计算:I=(b*h^3)/12其中,I为惯性矩,b为矩形宽度,h为矩形高度。
2.圆形截面的惯性矩公式:对于圆形截面,惯性矩可以通过以下公式进行计算:I=(π*R^4)/4其中,I为惯性矩,R为圆的半径。
3.I型截面的惯性矩公式:对于I型截面(又称为双T型截面或工字型截面),惯性矩可以通过以下公式进行计算:I = bw * hw^3 / 12 + hf * tf^3 / 12 + 2 * tf * hf * (hw / 2 + tf / 2)^2其中,I为惯性矩,bw为上翼板的宽度,hw为上翼板的高度,hf为下翼板的高度,tf为翼板的厚度。
4.H型截面的惯性矩公式:对于H型截面,惯性矩可以通过以下公式进行计算:I = [bw * (hw^3 - tw1 ^3) / 12] + [hf * (tf^3 - tw2^3) / 12] + 2 * tw1 * hw^3 / 12 + 2 * tw2 * tf^3 / 12 + 2 * hf * (hw / 2 + tf / 2)^2其中,I为惯性矩,bw为上翼板的宽度,hw为上翼板的高度,hf为下翼板的高度,tf为翼板的厚度,tw1为上翼板的厚度,tw2为下翼板的厚度。
5.T型截面的惯性矩公式:对于T型截面,惯性矩可以通过以下公式进行计算:I = [bw * hw^3 / 12] + [tf * hf^3 / 12] + tw * hw * (hw / 2 + tf)^2其中,I为惯性矩,bw为翼板的宽度,hw为翼板的高度,hf为梁的高度,tf为梁的厚度,tw为翼板的厚度。
这些公式是根据不同截面形状和尺寸推导出来的,可以用于计算截面的惯性矩。
常见截面的惯性矩和抗弯截面系数

常见截面惯性矩和抗弯截面系数自动计算 简介本文档主要介绍:工程常见截面的截面惯性矩、抗弯截面系数,主要包括矩形、矩形管、圆形、圆管、椭圆、椭圆管、六边形、花键的截面惯性矩、抗弯截面系数公式及公式自动求值方法。
理论依据根据材料力学,抗弯截面系数W X 与截面惯性矩I X 的关系公式如下: 的距离离中性为,其中轴X最远点截面上W max maxy y I X X 。
下面一一列出前述各形状截面的公式和wxMaxima 计算机自动求值算式。
矩形矩形截面如下图所示。
平行于X 轴的矩形边长为b ,平行于Y 轴的矩形边长为h ,矩形截面相对于X 轴的截面惯性矩公式为:123bh I X = 其相对于X 轴的抗弯截面系数公式为:6212W 23max bh h bh y I X X === 下面为wxMaxima 计算机自动求值算式,将下面的内容复制进wxMaxima 软件的空白区域,将数值修改为与工程实际情况相符合的数值,然后点击菜单栏的“单元”→“对单元进行求值”,即可得到想要的结果:/*矩形的截面惯性矩和抗弯截面系数计算*//*设置软件输出结果为数值*/if numer#false then numer:true else numer:true;b:38;h:130;Ix:1/12*b*h^3;Wx:1/6*b*h^2;/*作用在截面上的弯矩*/M:109874;/*弯矩在截面上产生的应力*/σ:M/Wx;矩形管矩形管截面如下图所示。
平行于X 轴的内部矩形边长为b ,平行于Y 轴的内部矩形边长为h ,平行于X 轴的外部矩形边长为B ,平行于Y 轴的外地部矩形边长为H ,矩形管截面相对于X 轴的截面惯性矩公式为:1212-123333bh BH bh BH I X -== 其相对于X 轴的抗弯截面系数公式为:hbh BH h bh BH y I X X 6212W 3333max -=-== /*矩形管的截面惯性矩和抗弯截面系数计算*//*设置软件输出结果为数值*/if numer#false then numer:true else numer:true;b:38;h:130;Ix:(B*H^3-b*h^3)/12;Wx:(B*H^3-b*h^3)/6/H;/*作用在截面上的弯矩*/M:109874;/*弯矩在截面上产生的应力*/σ:M/Wx;圆形圆形截面如下图所示。
惯性矩、静矩、截面抵抗矩计算

惯性矩和对Y轴的惯性矩。
y
解:
100
1)求出A1和A2分别对自身形心 2
轴的惯性矩
0
I x1
b1h13 12
100 203 12
66.67 103
100
A1 •Ⅱ•ຫໍສະໝຸດ A2Ⅰx1
xc a2 30 x
Ix2
b2h23 12
20 100 3 12
16.67 105
2 0
2)求对整个截面形心X轴的惯性矩
截面对x轴的惯性矩:
I x y2dA
量纲:L4 y
A
截面对y轴的惯性矩: I y x2dA
A
注意:
1)同一截面对不同的轴惯性 矩不同;
2)惯性矩永远为正值;
x
dA
y r
x
3)惯性矩的单位为m4;
2、惯性半径(回转半径)
截面对x轴的惯性半径: ix I x / A 截面对y轴的惯性半径: iy I y / A
二、常见截面的惯性矩和惯性半径
形心轴:通过截面形心的坐标轴 ➢ 矩形截面对于其对称轴(即形心轴)x,y的惯性矩。
y
对x轴的惯性矩
x
Ix
1 12
bh3
h 对y轴的惯性矩:
b
Iy
1 12
hb3
➢ 矩形截面对于其对称轴(即形心轴)x,y的惯性半径。
y
对x轴的惯性半径
x
h
ix
Ix A
1/12bh3 h
截面的几何性质
知识点:截面惯性矩和静矩的计算 一、截面惯性矩的定义及计算 二、常见截面的惯性矩和惯性半径 三、组合截面的概念 四、惯性矩的平行移轴公式 五、静矩的概念及公式 六、常见截面的静矩
常用截面几何特性计算公式

常用截面几何特性计算公式截面几何特性是指用于描述一个截面的形状和大小的参数,常用的包括面积、惯性矩、截面模量、截面半径等。
这些参数在工程中非常重要,因为它们能够直接影响截面的受力性能。
下面将介绍一些常用的截面几何特性计算公式。
1.截面面积计算公式:截面面积是指截面内部所有点的面积总和。
对于一些常见的截面形状,可以使用以下公式进行计算:-矩形截面面积:A=b*h,其中b为矩形的宽度,h为矩形的高度。
-圆形截面面积:A=π*r^2,其中r为圆的半径。
-等边三角形截面面积:A=(s^2*√3)/4,其中s为三角形的边长。
-梯形截面面积:A=(a+b)*h/2,其中a和b为梯形的上底和下底长度,h为梯形的高度。
2.截面惯性矩计算公式:惯性矩是描述截面抵御扭转和弯曲的能力的参数。
对于一些常见的截面形状,可以使用以下公式进行计算:-矩形截面惯性矩:I=(b*h^3)/12,其中b为矩形的宽度,h为矩形的高度。
-圆形截面惯性矩:I=π*r^4/4,其中r为圆的半径。
-等边三角形截面惯性矩:I=(s^4*√3)/64,其中s为三角形的边长。
-梯形截面惯性矩:I=[(b1*h1^3)+(b2*h2^3)]/12,其中b1和b2为梯形的上底和下底长度,h1和h2为梯形的高度。
3.截面模量计算公式:截面模量是描述截面抵御弯曲的能力的参数。
对于一些常见的截面形状,可以使用以下公式进行计算:-矩形截面模量:S=(b*h^2)/6,其中b为矩形的宽度,h为矩形的高度。
-圆形截面模量:S=π*r^3/3,其中r为圆的半径。
-等边三角形截面模量:S=(s^3*√3)/36,其中s为三角形的边长。
-梯形截面模量:S=[(b1*h1^2)+(b2*h2^2)]/6,其中b1和b2为梯形的上底和下底长度,h1和h2为梯形的高度。
4.截面半径计算公式:截面半径是描述截面的曲率半径的参数,通常用于弯曲性能的评估。
-矩形截面半径:r=h/2,其中h为矩形的高度。
惯性矩总结(含常用惯性矩公式)

惯性矩就是一个物理量,通常被用作描述一个物体抵抗扭动,扭转得能力。
惯性矩得国际单位为(m^4)。
工程构件典型截面几何性质得计算2、1面积矩1.面积矩得定义图2-2、1任意截面得几何图形如图2-31所示为一任意截面得几何图形(以下简称图形)。
定义:积分与分别定义为该图形对z轴与y轴得面积矩或静矩,用符号S z与S y,来表示,如式(2—2、1)(2—2、1)面积矩得数值可正、可负,也可为零。
面积矩得量纲就是长度得三次方,其常用单位为m3或mm3。
2.面积矩与形心平面图形得形心坐标公式如式(2—2、2)(2—2、2)或改写成,如式(2—2、3)(2—2、3)面积矩得几何意义:图形得形心相对于指定得坐标轴之间距离得远近程度。
图形形心相对于某一坐标距离愈远,对该轴得面积矩绝对值愈大。
图形对通过其形心得轴得面积矩等于零;反之,图形对某一轴得面积矩等于零,该轴一定通过图形形心。
3.组合截面面积矩与形心得计算组合截面对某一轴得面积矩等于其各简单图形对该轴面积矩得代数与。
如式(2—2、4)(2—2、4)式中,A与y i、z i分别代表各简单图形得面积与形心坐标。
组合平面图形得形心位置由式(2—2、5)确定。
(2—2、5)2、2极惯性矩、惯性矩与惯性积1.极惯性矩任意平面图形如图2-31所示,其面积为A。
定义:积分称为图形对O点得极惯性矩,用符号I P,表示,如式(2—2、6)(2—2、6)极惯性矩就是相对于指定得点而言得,即同一图形对不同得点得极惯性矩一般就是不同得。
极惯性矩恒为正,其量纲就是长度得4次方,常用单位为m4或mm4。
(1)圆截面对其圆心得极惯性矩,如式(2—7)(2—2、7)(2)对于外径为D、内径为d得空心圆截面对圆心得极惯性矩,如式(2—2、8)(2—2、8)式中,d/D为空心圆截面内、外径得比值。
2.惯性矩在如图6-1所示中,定义积分,如式(2—2、9)(2—2、9)称为图形对z轴与y轴得惯性矩。
常用截面惯性矩计算公式_百度文库

常用截面惯性矩计算公式_百度文库截面惯性矩是描述截面形状对于抗弯刚度的影响的一个物理量,常用截面惯性矩计算公式有以下几种:
1.矩形截面惯性矩计算公式:
矩形截面的惯性矩计算公式为I=b*h^3/12,其中b为矩形截面的宽度,h为矩形截面的高度。
2.圆形截面惯性矩计算公式:
圆形截面的惯性矩计算公式为I=π*d^4/64,其中d为圆形截面的直径。
3.正方形截面惯性矩计算公式:
正方形截面的惯性矩计算公式为I=a^4/12,其中a为正方形截面的边长。
4.等边三角形截面惯性矩计算公式:
等边三角形截面的惯性矩计算公式为I=a^4/80.9,其中a为等边三角形截面的边长。
5.环形截面惯性矩计算公式:
环形截面的惯性矩计算公式为I=π*(D^4-d^4)/64,其中D为大圆直径,d为小圆直径。
6.T形截面惯性矩计算公式:
T形截面的惯性矩计算公式稍复杂,可以分解为矩形和矩形之和。
可以分别计算底座和翼板的惯性矩,然后相加。
7.I形截面惯性矩计算公式:
I形截面的惯性矩计算公式也稍复杂,可以分解为矩形和矩形之和,也可以通过几何分解法计算。
以上是常见的几种截面形状的惯性矩计算公式,不同形状的截面有不同的计算方法。
通过计算截面惯性矩,可以评估截面的抗弯刚度性能,并在设计工程结构时进行应用。
常用截面惯性矩与截面系数的计算
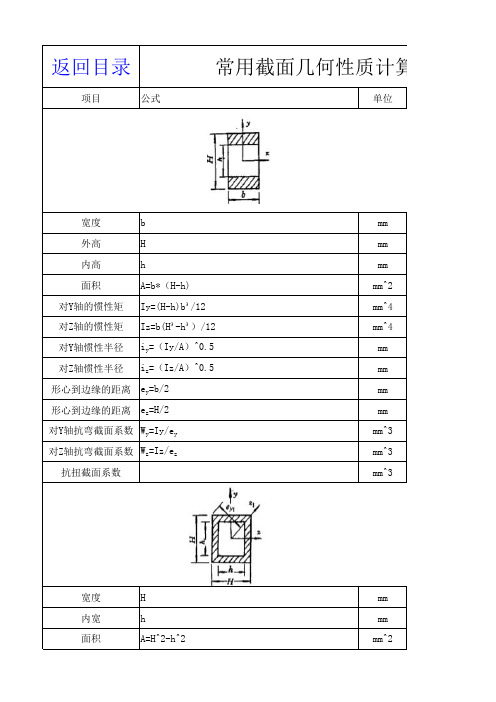
常用截面几何性质计算返回目录项目公式单位宽度b mm外高H mm内高h mm面积A=b*(H-h)mm^2对Y轴的惯性矩Iy=(H-h)b³/12mm^4对Z轴的惯性矩Iz=b(H³-h³)/12mm^4对Y轴惯性半径i y=(Iy/A)^0.5mm对Z轴惯性半径i z=(Iz/A)^0.5mm形心到边缘的距离e y=b/2mm形心到边缘的距离e z=H/2mm对Y轴抗弯截面系数W y=Iy/e y mm^3对Z轴抗弯截面系数W z=Iz/e z mm^3抗扭截面系数mm^3宽度H mm内宽h mm面积A=H^2-h^2mm^2对Y轴的惯性矩Iy=(H^4-h^4)/12mm^4对Z轴的惯性矩Iz=(H^4-h^4)/12mm^4对Y轴惯性半径i y=(Iy/A)^0.5mm 对Z轴惯性半径i z=(Iz/A)^0.5mm 形心到边缘的距离e y=H/2mm 形心到边缘的距离e z=H/2mm 形心到边缘的距离e z1=0.707*H mm 对Y轴抗弯截面系数W y=Iy/e y mm^3对Z轴抗弯截面系数W z=Iz/e z mm^3对Z轴抗弯截面系数W z1=Iz/e z mm^3抗扭截面系数mm^3宽度a mm直径d mm面积A=a^2-Pi*d^2/4mm^2对Y轴的惯性矩Iy=a^4/12-Pi*d^4/64mm^4对Z轴的惯性矩Iz=a^4/12-Pi*d^4/64mm^4对Y轴惯性半径i=(Iy/A)^0.5mm 对Z轴惯性半径i=(Iz/A)^0.5mm 形心到边缘的距离e y=a/2mm 形心到边缘的距离e z=a/2mm 对Y轴抗弯截面系数W y=Iy/e y mm^3对Z轴抗弯截面系数W z=Iz/e z mm^3抗扭截面系数mm^3a=0,三角形顶宽a mm底宽b mm高h mm面积A=h*(a+b)/2mm^2对Y轴的惯性矩mm^4对Z轴的惯性矩Iz=h^3*(a^2+4*a*b+b^2)/36/(a+b)mm^4对Y轴惯性半径mm 对Z轴惯性半径iz=(Iz/A)^0.5mm 形心到边缘的距离e y1=h*(2*a+b)/(a+b)/3mm 形心到边缘的距离e y2=h*(a+2*b)/(a+b)/3mm 对底边抗弯截面系数W z1=Iz/e y1mm^3对顶边抗弯截面系数W z2=Iz/e y2mm^3抗扭截面系数mm^3正多边形边数n边长a mm 外接圆半径R=a/2/sin(180°/n)mm 内接圆半径r=a/2/sin(180°/n)mm 面积A=n*R^2*sin(2*Pi/n)/2mm^2惯性矩I=A*(6*R^2-a^2)/24mm^4对Y轴惯性半径i=(I/A)^0.5mm形心到底边的距离e y=r mm 形心到顶边的距离e y1=R mm 对底边抗弯截面系数W z=I/R/cos(Pi/n)mm^3对顶点抗弯截面系数W z1=I/R mm^3抗扭截面系数mm^3宽度a mm直径d mm面积A=a^2-Pi*d^2/4mm^2对Y轴的惯性矩Iy=a^4/12-Pi*d^4/64mm^4对Z轴的惯性矩Iz=a^4/12-Pi*d^4/64mm^4对Y轴惯性半径i=(Iy/A)^0.5mm 对Z轴惯性半径i=(Iz/A)^0.5mm 形心到边缘的距离e y=a/2mm 形心到边缘的距离e z=a/2mm 对Y轴抗弯截面系数W y=Iy/e y mm^3对Z轴抗弯截面系数W z=Iz/e z mm^3抗扭截面系数mm^3外径D mm内径d mm面积A=Pi*(D^2-d^2)/4mm^2惯性矩I=Pi*(D^4-d^4)/64mm^4惯性半径i=(Iz/A)^0.5mm 形心到边缘的距离e=D/2mm 抗弯截面系数W=I/e mm^3抗扭截面系数Wt=Pi*D^3(1-(d/D)^4)/16mm^3外径D mm内径d mm面积A=Pi*(D^2-d^2)/8mm^2对Y轴的惯性矩Iy=Pi*(D^4-d^4)/128mm^4对Z轴的惯性矩Iz=0.00686*(D^4-d^4)-0.0177*D^2*d^2*(D-d)/(D+d mm^4对Y轴惯性半径i y=(Iy/A)^0.5mm 对Z轴惯性半径i z=(Iz/A)^0.5mm 形心到边缘的距离e y=2*(D^2+D*d+d^2)/3*Pi*(D+d)mm 形心到边缘的距离e z=D/2mm 对Y轴抗弯截面系数W y=Pi*D^3*(1-d^4/D^4)/64mm^3对顶点的抗弯截面系数W z=Iz/(D/2-e y)mm^3对底边的抗弯截面系数W z1=Iz/e y mm^3抗扭截面系数mm^3直径d mm宽度b mm深度t mm面积A=Pi*d^2/4-b*t mm^2对Y轴的惯性矩Iy=Pi*d^4/64-t*b^3/12mm^4对Z轴的惯性矩Iz=Pi*d^4/64-b*t*(d-t)^2/4mm^4对Y轴惯性半径i y=(Iy/A)^0.5mm 对Z轴惯性半径i z=(Iz/A)^0.5mm 形心到边缘的距离e y=d/2mm 形心到边缘的距离e z=d/2mm 对Y轴抗弯截面系数W y=Iy/e y mm^3对Z轴抗弯截面系数W z=Iz/e z mm^3抗扭截面系数mm^3直径d mm宽度b mm深度t mm面积A=Pi*d^2/4-2*b*t mm^2对Y轴的惯性矩Iy=Pi*d^4/64-t*b^3/6mm^4对Z轴的惯性矩Iz=Pi*d^4/64-b*t*(d-t)^2/2mm^4对Y轴惯性半径i y=(Iy/A)^0.5mm 对Z轴惯性半径i z=(Iz/A)^0.5mm 形心到边缘的距离e y=d/2mm 形心到边缘的距离e z=d/2mm 对Y轴抗弯截面系数W y=Iy/e y mm^3对Z轴抗弯截面系数W z=Iz/e z mm^3抗扭截面系数mm^3直径d mm支架d1mm面积A=Pi*d^2/4-d1*d mm^2对Y轴的惯性矩Iy=Pi*d^4*(1-1.69*d1/d)/64mm^4对Z轴的惯性矩Iz=Pi*d^4*(1-1.69*d1^3/d^3)/64mm^4对Y轴惯性半径i y=(Iy/A)^0.5mm 对Z轴惯性半径i z=(Iz/A)^0.5mm 形心到边缘的距离e y=d/2mm 形心到边缘的距离e z=d/2mm 对Y轴抗弯截面系数W y=Iy/e y mm^3对Z轴抗弯截面系数W z=Iz/e z mm^3抗扭截面系数mm^3宽度B mm宽度b mm高度H mm高度h mm面积A=B*H+b*h mm^2对Z轴的惯性矩Iz=(B*H^3+b*h^3)/12mm^4对Z轴惯性半径i z=(Iz/A)^0.5mm 形心到边缘的距离e z=H/2mm 对Z轴抗弯截面系数W z=Iz/e z mm^3抗扭截面系数mm^3宽度B mm宽度a mm高度H mm高度d mm面积A=B*H+b*h mm^2对Z轴的惯性矩Iz=mm^4对Z轴惯性半径i z=(Iz/A)^0.5mm 形心到边缘的距离e y=d/2mm 形心到边缘的距离e z=d/2mm 对Y轴抗弯截面系数W y=Iy/e y mm^3对Z轴抗弯截面系数W z=Iz/e z mm^3抗扭截面系数mm^3宽度B mm宽度a mm205214 4533.375 7642.7109384.6026074495.9760858861010 453.3375 764.271093810102020。
常用截面惯性矩的计算

』
s
I---Bd-blF+04
•
3
符号意义及单位g Ir一一惯性炬 (cm竹 B一一拥图所示 (cm) ←一如图所示 (cm) ←一童心 s 到捆应边的距离 (cm) e;-一童心 S 到相应边的距离 (cm) ←斗日 图所示 (cm)
←一拥图所示 (cm)
b/ l • b/ l
,
aH2+bd2 e1=2(d+bd)
Hale Waihona Puke U-x ('i织锐纺织 工
/ dJF
y
tiT 龟) lIr
;rd'"
/_ =
• 64
符号意义及单位 :
IX 截面对 x 轴的惯性短 (crn斗
d 截面直径 (crn)
|引
飞 x 0(
3
z
龟t l
I x_=
1l(D 4 _ d 4 ) 64
符号意义及单位=
IX 截面时 x 轴的惯性短 (cnr)
D 大径 ( cm)
t :.
~ 唱=
,
『 、.
bI B
-,,,‘ x
BH in -O '2 -
、‘d
叫
·EA& ,
符号意义及单位: If-J惯性矩 (cm竹 B一一细图所示 (cm) b一一在日图所示 (cm) H一一夜日困所示 (cm) h一一在日图所示 (cm )
z
b/ 2
b
q
:r -
8 /21 比 11 8/2
1•.--BH312+bd
符号意义及单位z J"一惯性短 ( cm4 ) B一一细图所示 (cm) b一一在日图所示 (cm) H一一夜日图所示 (cm) h一__J如图所示 (cm)
常用截面惯性矩计算公式_百度文库
新闻网页贴吧知道音乐图片视频地图百科文库
百度文库专业资料工程科技机械/仪表
限时!免财富值下载
常用截面惯性矩计算公式83689人阅读全部DOC PPT TXT PDF XLS
搜索文档帮助
二级(456)|||私信(0)|下载客户端|百度首页
leeming168个人中心
限时!免财富值下载到手机
2/31 财富值
你可能喜欢
剪力弯矩计算公式刘鸿文版材料力学课件...简支梁挠度计算公式材料力学习题集Excel使用技巧大...工字钢槽钢H型钢截面各类梁反力剪力弯矩挠度计算公式一览表11页5财富值
各类梁支反力剪力弯矩挠度计算公式一览表11页免费
梁反力剪力弯矩挠度计算公式11页免费
剪力弯矩计算公式11页2财富值
剪力弯矩计算公式11页免费
更多与“剪力弯矩计算公式”相关的文档>>
©2013 Baidu使用百度前必读 | 文库协议。
截面惯性矩(材料力学)(仅供借鉴)

6
例1:求图示T形截面的形心及对z轴的静矩 y
1.求形心
100
知A=A1+A2 yC1=60 yC2=0
20
n Ai yCi
选坐标轴z1作为参考轴
yC i1 Ai
yC
20100 60 100 20 2
30mm
100
2、求静矩
•
•Ⅰ
•
ⅡyC1
zC
z1
B•
方法1) Sz yC
y
I yz yzdA
A
3.说明: h
1)同一图形对不同轴的惯性积不同; A1 A2
z
2)惯性积可正,可负,可为零。
b
b
3)惯性积的单位:m4
4.结论:
当坐标系的两轴中的任一轴为图形的对称轴时,图形 对此轴的惯性积为零,反之,若图形对坐标系的惯性 积为零时,此坐标轴中必一有类参一考 轴为图形的对称轴。 11
一类参考
43
拉(压)杆横截面上的应力
σ= FN MPa
A
F
mn
F
FN 表示横截面轴力(N)
mn
A 表示横截面面积(mm2)
F
FN
一类参考ቤተ መጻሕፍቲ ባይዱ
44
——横截面上的应力
一类参考
45
截面上的应力
例题3-2
A 1
45°
C
2
FN1
y
FN 2 45° B
F
图示结构,试求杆件AB、CB的
应力。已知 F=20kN;斜杆AB为直
900多年来历经数次地震不倒,现存唯一木塔
一类参考
20
古代建筑结构
2200年以前建造的都江堰安澜索桥
(完整版)惯性矩的计算方法及常用截面惯性矩计算公式

(完整版)惯性矩的计算⽅法及常⽤截⾯惯性矩计算公式惯性矩的计算⽅法及常⽤截⾯惯性矩计算公式截⾯图形的⼏何性质⼀.重点及难点:(⼀).截⾯静矩和形⼼1.静矩的定义式如图1所⽰任意有限平⾯图形,取其单元如⾯积dA ,定义它对任意轴的⼀次矩为它对该轴的静矩,即ydA dSx xdAdS y == 整个图形对y 、z 轴的静矩分别为 ??==A Ay ydA Sx xdA S (I-1) 2.形⼼与静矩关系图I-1 设平⾯图形形⼼C 的坐标为C C z y , 则 0 AS y x = , A S x y = (I-2)推论1 如果y 轴通过形⼼(即0=x ),则静矩0=y S ;同理,如果x 轴通过形⼼(即0=y ),则静矩0=Sx ;反之也成⽴。
推论2 如果x 、y 轴均为图形的对称轴,则其交点即为图形形⼼;如果y 轴为图形对称轴,则图形形⼼必在此轴上。
3.组合图形的静矩和形⼼设截⾯图形由⼏个⾯积分别为n A A A A ??321,,的简单图形组成,且⼀直各族图形的形⼼坐标分别为??332211,,,y x y x y x ;;,则图形对y 轴和x 轴的静矩分别为∑∑∑∑========n i n i ii xi x n i ii n i yi y y A S S x A S 1111S (I-3)截⾯图形的形⼼坐标为∑∑===n i i n i i iAx A x 11, ∑∑===n i in i i i A y A y 11 (I-4) 4.静矩的特征(1) 界⾯图形的静矩是对某⼀坐标轴所定义的,故静矩与坐标轴有关。
(2) 静矩有的单位为3m 。
(3) 静矩的数值可正可负,也可为零。
图形对任意形⼼轴的静矩必定为零,反之,若图形对某⼀轴的静矩为零,则该轴必通过图形的形⼼。
(4) 若已知图形的形⼼坐标。
则可由式(I-1)求图形对坐标轴的静矩。
若已知图形对坐标轴的静矩,则可由式(I-2)求图形的形⼼坐标。
矩形截面惯性矩计算公式

一.矩形截面惯性矩计算公式
截面惯性矩公式,矩形:b*h^3/12、三角形:b*h^3/36、圆形:π*d^4/64 、环形:π*D^4*(1-α^4)/64;α=d/D 。
截面惯性矩指截面各微元面积与各微元至截面上某一指定轴线距离二次方乘积的积分。
截面惯性矩是衡量截面抗弯能力的一个几何参数。
任意截面图形内取微面积dA与其搭配z轴的距离y的平方的乘积y²dA定义为微面积对z轴的惯性矩,在整个图形范围内的积分则称为此截面对z轴的惯性矩Iz。
相关信息:
矩形惯性矩是利用定积分进行求解的,与高中的知识无关,运用的是大学微积分的知识。
惯性矩定义即:面积元素dA与其至z轴或y轴距离平方的乘积y²dA或z²dA,分别称为该面积元素对于z轴或y轴的惯性矩或截面二次轴矩。
惯性矩的数值恒大于零。
常用截面几何特性计算公式

常用截面几何特性计算公式截面几何特性是指用来描述截面形状和大小的一些参数,可以用来进行结构设计和分析。
常用的截面几何特性包括面积、周长、惯性矩、截面模量等。
下面将详细介绍常用的截面几何特性计算公式。
1.面积(A):截面的面积是指该截面所围成的平面区域的大小,用来描述截面的大小。
常见的截面面积计算公式有:-矩形截面:A=b*h,其中b为矩形的宽度,h为矩形的高度。
-圆形截面:A=π*r^2,其中π约等于3.14,r为圆的半径。
-梯形截面:A=(a+b)*h/2,其中a和b为梯形的上底和下底长度,h为梯形的高度。
2.周长(P):截面的周长是指该截面围成的边界线的总长度,用来描述截面的形状。
常见的截面周长计算公式有:-矩形截面:P=2*(b+h),其中b为矩形的宽度,h为矩形的高度。
-圆形截面:P=2*π*r,其中π约等于3.14,r为圆的半径。
-梯形截面:P=a+b+2*L,其中a和b为梯形的上底和下底长度,L为梯形的斜边长度。
3.惯性矩(I):惯性矩是描述截面抵抗弯曲或扭转作用的能力,常用于计算截面的弯矩和扭矩。
惯性矩有I_x和I_y两个方向,分别表示关于x轴和y轴的惯性矩。
常见的截面惯性矩计算公式有:-矩形截面:I_x=(b*h^3)/12,I_y=(h*b^3)/12,其中b为矩形的宽度,h为矩形的高度。
-圆形截面:I_x=I_y=(π*r^4)/4,其中π约等于3.14,r为圆的半径。
-梯形截面:I_x=(b*h^3)/36*(3*a+b),I_y=(h*b^3)/36*(a+3*b),其中a和b为梯形的上底和下底长度,h为梯形的高度。
4.截面模量(W):截面模量是一种描述截面承受弯曲时变形能力的特性,常用于计算截面的弯曲应力和挠度。
截面模量有W_x和W_y两个方向,分别表示关于x轴和y轴的截面模量。
-矩形截面:W_x=(b*h^2)/6,W_y=(h*b^2)/6,其中b为矩形的宽度,h为矩形的高度。
