惯性矩和平行移轴公式
工程力学第03节 惯性矩的平行移轴公式
I x A y2dA I y A x2dA
I x A y2dA I y A x2dA
依据两个坐标系 的关系,则有
x xC b y yC a
Ix A(yC a)2dA A yC2dA 2aA yCdA a2 AdA
I y A(xC b)2dA A xC2dA 2bA xCdA b2 AdA
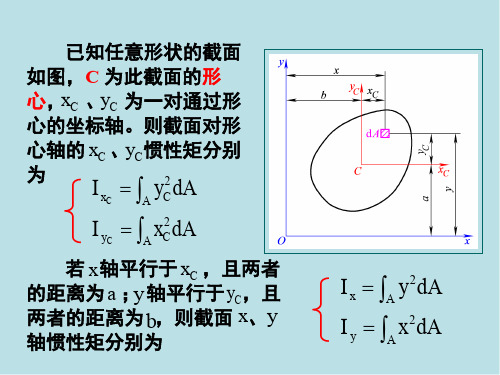
已知任意形状的截面
如图,C 为此截面的形
心,xC 、yC 为一对通过形
心的坐标轴。则截面对形
心轴的 xC 、yC惯性矩分别
为
I xC A yC2 dA
I yC A xC2 dA
若 x轴平行于 xC ,且两者
的距离为 a ;y 轴平行于yC,且
两者的距离为 b,则截面 x、y
轴惯性矩分别为
解 首先将截面分为两个 矩形,如图所示 (1)矩形 I、矩形 II
A1 9000 mm 2 xC1 0 , yC1 0
A2 13500 mm 2 xC2 0 , yC2 150mm
整个截面形心 C 坐标
xC 0 2
Ai yCi
yC
i 1 2
90mm
Ai
i 1
I2x0 I2xC2 C2C2 A2
运用叠加法公式,得到截面
x0
对 x0 轴的惯性矩
I x0
2
Iix0 i 1
(300 303 12
902 9000)
(50 2703 602 13500)
12
2.04104 m4
运用叠加法公式,得到截面 对 x0 轴的惯性矩
y0 x0
(2)以0截面13形5心00C1为50原m点m,
惯性矩、静矩,形心坐标公式
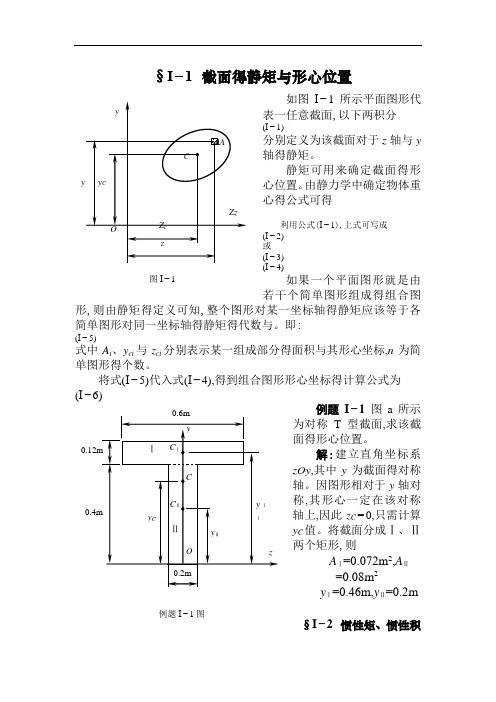
§I−1 截面得静矩与形心位置如图I −1所示平面图形代表一任意截面,以下两积分(I −1)分别定义为该截面对于z 轴与y 轴得静矩。
静矩可用来确定截面得形心位置。
由静力学中确定物体重心得公式可得利用公式(I −1),上式可写成 (I −2) 或 (I −3) (I −4)如果一个平面图形就是由若干个简单图形组成得组合图形,则由静矩得定义可知,整个图形对某一坐标轴得静矩应该等于各简单图形对同一坐标轴得静矩得代数与。
即:(I −5)式中A i 、y ci 与z ci 分别表示某一组成部分得面积与其形心坐标,n 为简单图形得个数。
将式(I −5)代入式(I −4),得到组合图形形心坐标得计算公式为 (I −6)例题I −1 图a 所示为对称T 型截面,求该截面得形心位置。
解:建立直角坐标系zOy ,其中y 为截面得对称轴。
因图形相对于y 轴对称,其形心一定在该对称轴上,因此z C =0,只需计算y C 值。
将截面分成Ⅰ、Ⅱ两个矩形,则 A Ⅰ=0.072m 2,A Ⅱ=0.08m 2y Ⅰ=0.46m,y Ⅱ=0.2m§I −2 惯性矩、惯性积例题I −1图图I −1与极惯性矩如图I −2所示平面图形代表一任意截面,在图形平面内建立直角坐标系zOy 。
现在图形内取微面积d A ,d A 得形心在坐标系zOy 中得坐标为y 与z ,到坐标原点得距离为ρ。
现定义y 2d A 与z 2d A 为微面积d A 对z 轴与y 轴得惯性矩,ρ2d A 为微面积d A 对坐标原点得极惯性矩,而以下三个积分(I −7)分别定义为该截面对于z 轴与y 轴得惯性矩以及对坐标原点得极惯性矩。
由图(I −2)可见,,所以有(I −8) 即任意截面对一点得极惯性矩,等于截面对以该点为原点得两任意正交坐标轴得惯性矩之与。
另外,微面积d A 与它到两轴距离得乘积zy d A 称为微面积d A 对y 、z 轴得惯性积,而积分(I −9)定义为该截面对于y 、z 轴得惯性积。
材料力学笔记(惯性矩)

材料力学笔记一、截面对形心轴的轴惯性矩矩形、实心圆、空心圆、薄壁圆截面的轴惯性矩分别为(B.3-4)(B.3-5)(B.3-6)式中,d —实心圆直径和空心圆内径,D —空心圆外径,R 0—薄壁圆平均半径。
t —薄壁圆壁厚。
惯性矩I 量纲为长度的四次方(mm 4),恒为正。
二、截面抗弯刚度EI z和抗弯截面模量Wz(a )上式代表距中性层为y 处的任一纵向“纤维”的正应变,式中的ρ对同一横截面来说是个常数, 所以正应变ε与y 成正比(上缩下伸),与z 无关。
式(a)即为横截面保持平面,只绕中性轴旋转的数学表达式,通常称为几何方面的关系式。
(b )式(b )表示横截面上正应力沿梁高度的变化规律,即物理方面的关系式。
由于式中ρ对同一横截面来说是个常数,均匀材料的弹性模量E 也是常数,所以横截面上任一点处的正应力与y 成正比(上压下拉) 。
显然中性轴上的正应力为零,而距中性轴愈远,正应力愈大,最大正应力σmax发生在距中性轴最远的上下边缘(图7.2-4)。
图7.2-4 弯曲正应力分布微内力对中性轴z之矩组成弯矩M,即(e)代入式(b ),并将常数从积分号中提出,得。
令,称为横截面对z轴的惯性矩,它只取决于横截面的形状和尺寸,其量纲是长度的四次方,此值很容易通过积分求出。
于是得出(7.2-1)上式确定了曲率的大小。
式中EIz称为截面抗弯刚度(stiffness in bending)。
到此为止,式(a)中的y和ρ已经确定。
联合式(b)及式(7.2-1),得出(7.2-2)上式即为对称弯曲正应力公式。
当y=ymax时,得出最大正应力公式,即(7.2-3)式中称为抗弯截面模量(section modulus in bending),其量纲是长度的三次方。
表7.2-I列出了简单截面的Iz 和Wz计算公式。
表中 =d/D,R为薄壁圆平均半径。
三、平行轴间惯性矩的移轴公式图B.3-3如图B.3-3所示,设y0、z为截面的一对形心轴,如果截面对形心轴的惯性矩为和,则截面对任一平行于它的轴y和z的惯性矩为:,(B.3-7)上式称为惯性轴的移轴公式或称平行轴定理(Parallel axis theorem)。
6.3平行移轴公式

第6章 平面图形的几何性质6.3 惯性矩和惯性积的平行移轴公式 主轴和主惯性矩6.3.1 惯性矩和惯性积的平行移轴公式任一平面图形如图6.9所示,其面积为A ,形心为C ,坐标轴y c 和z c 为形心轴。
正交坐标轴y 、z 与形心轴y c 、z c 平行,两对平行轴之间的间距分别为a 和b 。
截面对y c 轴、z c 轴的惯性矩I y c、I z c 及惯性积I y z c c 为已知,现求图形对y 、z 轴的惯性矩和惯性积。
图中任一点在两坐标系下的坐标关系为=+z z a c =+y y b c由式(6.5)⎰⎰⎰⎰==+=++I z A z a A z A a z A a AAAAy c c c d ()d d 2d 2222其中⎰=z A I Ac y cd 2,⎰=A A Ad ,⎰=z A S Ac y cd 。
因y c 为形心轴,所以=S y c 0,于是可得同理 ⎭⎪=+⎪⎬=+⎪⎪=+⎫I I abA I I b A I I a A yz y z z z y y c c c 22c (6.9)上式即为惯性矩和惯性积的平行移轴公式(parallel-axis theorem )。
因为a A 2和b A 2均为正,所以在所有相互平行的轴中,同一图形对形心轴的惯性矩最小。
在应用公式(6.9)时需注意,a 、b 是图形的形心C 在yOz 坐标下的坐标,有正、负之分。
同时,y c 、z c 轴一定是形心轴。
6.3.2 主轴和主惯性矩由式(6.6)可知,同一图形对不同的一对直角坐标轴的惯性积是不同的,若图形对某一对直角坐标轴的惯性积等于零,则该直角坐标轴称为主惯性轴,或简称为主轴(principal axes )。
图形对主轴的惯性矩称为主惯性矩(principal moment of inertia )。
通过图形形心的主轴称为形心主轴(centroidal axis ),图形对形心主轴的惯性矩称为形心主惯性矩(principal moment of inertia for an area )。
惯性矩和惯性积的平行移轴公式
20 140
zc
20
1
yc
2
y
100
A1 20140 A2 100 20
Z1 80 Z2 0
所以截面的形心坐标为
ZC
A1 Z1 A1
A2 Z2 A2
46.7mm
20 140zc20源自1ycxc
ob
x
二、组合截面的惯性矩 惯性积
Ixi , Iyi , Ixyi —— 第 i个简单截面对 x ,y 轴的惯性矩、
惯性积。
组合截面的惯性矩,惯性积
n
I x I xi i1
n
I y I yi i1
n
I xy I xyi i 1
例 3 -1 求梯形截面对其形心轴 yc 的惯性矩。
解:将截面分成两个矩形截面。
xc
b
x
Ix , Iy , Ixy _____ 截面对 x , y 轴的惯性矩和惯性积。
Ixc ,Iyc , Ixc yc —— 截面对形心轴 xc , yc 的惯性矩和惯性积。
则平行移轴公式为
y
yc
I x I xc a2 A
Iy Iyc b2 A
I xy I xcyc abA
a
C(a,b)
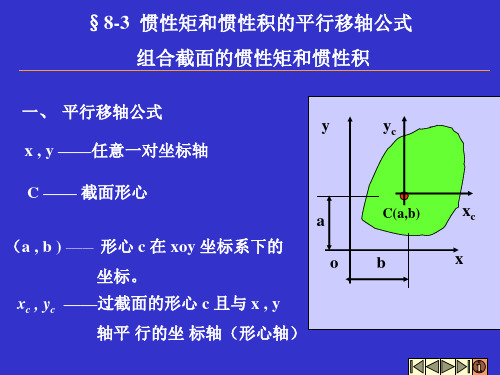
§8-3 惯性矩和惯性积的平行移轴公式 组合截面的惯性矩和惯性积
一、 平行移轴公式
y x , y ——任意一对坐标轴
C —— 截面形心
a
(a , b ) _____ 形心 c 在 xoy 坐标系下的
坐标。
o
xc , yc ——过截面的形心 c 且与 x , y 轴平 行的坐 标轴(形心轴)
5.2惯性矩和平行移轴公式教学内容

*
优学课堂
§5.2 惯性矩 惯性半径
一、惯性矩
二、惯性矩与极惯性矩的关系
三、惯性半径
四、平行移轴公式
*
优学课堂
1、惯性矩、极惯性矩的概念和计算方法; 2、平行移轴公式。
教学重点
*
优学课堂
平行移轴公式的应用。
教学难点
*
优学课堂
一、惯性矩
整个图形 A 对x 轴的惯性矩
若 x 、 y 轴为一对正交坐标轴
*
优学课堂
§A.2 惯性矩 惯性积 惯性半径
1.矩形截面
常用图形的惯性矩:
*
优学课堂
2.圆形截面
由对称性
3.环形截面
常用图形的惯性矩:
*
优学课堂
惯 性 矩——对某一轴而言
极 惯 性 矩——对某一点而言
特别指出:
*
优学课堂
——图形对 x 轴的惯性半径
整个图形 A 对 y 轴的惯性矩
y2dA——微面积dA对 x 轴的惯性矩
x2dA——微面积dA对 y 轴的惯性矩
定义:
其值:+
单位:m4
1.惯性矩
*
优学课堂
二、惯性矩与极惯性矩的关系
即:
平面图形对任意一点的极惯性矩等于该图形对通过
该点的任意一对相互垂直的坐标轴的惯性矩之和
性质 :
5.1 静矩和形心 5.2惯性矩、极惯性矩 、平行移轴公式
第五章 平面图形的几何性质
*
优学课堂
平面图形的几何性质是影响构件承载能力的重要因素之一。如何确定平面图形的几何性质的量值,是本章讨论的内容。本章主要介绍了形心、静矩、惯性矩、惯性积等几何量,学习时要掌握其基本的概念和计算方法,同时要掌握平行移轴公式及其应用。
平行移轴公式

IyC , IzC , IyCzC ̄ 截面对形心轴 yC , zC的惯性矩
和惯性积。
z
zC
I yC z12dA z z1 b
z1
I y z2dA
b
C(a,b)
z yC
y
(z1 b)2dA
Oa
平行移轴公式
(z12 2z1b b2 )dA
A z12dA
A 2z1bdA
b2dA
A
I yC
?
b2 A
A 2z1bdA 2b A z1dA
z
zC
2bSyC
0
b
C(a,b)
ቤተ መጻሕፍቲ ባይዱOa
z1 z yC
y
平行移轴公式
I y I yC b2 A Iz IzC a2 A
I yz I yCzC abA
z
zC
b
C(a,b)
Oa
z1 z yC
y
截面对形心轴的惯性矩最小, 但惯性积不能确定是否最小
平行移轴公式
二、组合截面的惯性矩和惯性积
n
I y I yi i 1
n
Iz Izi i 1
n
I yz I yzi i 1
I yi , Izi , I yzi —第 i个简单截面对 y, z 轴的惯性矩
和惯性积。
平行移轴公式
平行移轴公式
一、 平行移轴公式
zzC
y, z —任意一对坐标轴;
b
C(a,by)C
C ―截面形心;
y
Oa
(a , b ) ―形心C在 yOz坐标系下的坐标;
yC , zC —过截面的形心 C 且与 y, z轴平行 的坐标轴(形心轴)。
惯性矩、静矩、截面抵抗矩计算

惯性矩和对Y轴的惯性矩。
y
解:
100
1)求出A1和A2分别对自身形心 2
轴的惯性矩
0
I x1
b1h13 12
100 203 12
66.67 103
100
A1 •Ⅱ•ຫໍສະໝຸດ A2Ⅰx1
xc a2 30 x
Ix2
b2h23 12
20 100 3 12
16.67 105
2 0
2)求对整个截面形心X轴的惯性矩
截面对x轴的惯性矩:
I x y2dA
量纲:L4 y
A
截面对y轴的惯性矩: I y x2dA
A
注意:
1)同一截面对不同的轴惯性 矩不同;
2)惯性矩永远为正值;
x
dA
y r
x
3)惯性矩的单位为m4;
2、惯性半径(回转半径)
截面对x轴的惯性半径: ix I x / A 截面对y轴的惯性半径: iy I y / A
二、常见截面的惯性矩和惯性半径
形心轴:通过截面形心的坐标轴 ➢ 矩形截面对于其对称轴(即形心轴)x,y的惯性矩。
y
对x轴的惯性矩
x
Ix
1 12
bh3
h 对y轴的惯性矩:
b
Iy
1 12
hb3
➢ 矩形截面对于其对称轴(即形心轴)x,y的惯性半径。
y
对x轴的惯性半径
x
h
ix
Ix A
1/12bh3 h
截面的几何性质
知识点:截面惯性矩和静矩的计算 一、截面惯性矩的定义及计算 二、常见截面的惯性矩和惯性半径 三、组合截面的概念 四、惯性矩的平行移轴公式 五、静矩的概念及公式 六、常见截面的静矩
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
即:
Ip I y Ix
性质 :
平面图形对任意一点的极惯性矩等于该图形对通过 该点的任意一对相互垂直的坐标轴的惯性矩之和
常用图形的惯性矩:
§A.2 惯性矩 惯性积 惯性半径
1.矩形截面
I x
y 2dA
A
h 2 y2 bdy bh3
h 2
12
hb3 I y 12
I x1
y 2dA
xC1
a1 57.5 xC
a2 57.5 xC2
C
I xC
I xC
I
xC
6.01 107
mm
4
而
I xC
I xC 1
a12 A1
200 303 57.52 200 30 mm 4 12
2.03 107 mm 4
30 I C
200 157.5 30 II
xC1
a1 57.5 xC
a2 57.5 xC2
I xC
I xC 2
a
2 2
A2
A
h y2 bdy bh3
0
3
y dy
_h_
2
dA y
C
yx
_h_
2
O
_b_ _b_
x1
22
常用图形的惯性矩:
2.圆形截面
D4
I x I y Ip 32
由对称性
y
O
x
Ix
Iy
1 2
Ip
D4
64
d
D
3.环形截面
Ix
Iy
1 2
Ip
(D4 64
d
4
)
D4 (1 4 )
64
特别指出: 惯 性 矩——对某一轴而言 极 惯 性 矩——对某一点而言
x A
整个图形 A 对x 轴的惯性矩
I x
y 2dA
A
整个图形 A 对 y 轴的惯性矩
I y
x 2dA
A
单位:m4
其值:+
dA y x
二、惯性矩与极惯性矩的关系 y
若 x 、 y 轴为一对正交坐标轴
x dA
Ip
2dA
A
(x2 y2 )dA
A
A
y
x2dA y2dA
A
A
O
x
5.1 形心和静矩
第五章 平面图形的几何性质
5.1 静矩和形心 5.2惯性矩、极惯性矩 、平行移轴公式
教学目的和要求
• 平面图形的几何性质是影响构件承载能力的重要 因素之一。如何确定平面图形的几何性质的量值, 是本章讨论的内容。本章主要介绍了形心、静矩、 惯性矩、惯性积等几何量,学习时要掌握其基本 的概念和计算方法,同时要掌握平行移轴公式及 其应用。
一、定理推导 二、应用
一、定理推导
y y
C
x
x xC b y yC a
b
xC
dA
y C
C
Ix y 2dA A Nhomakorabea(
A
yC
a)2 dA
A O
y xC a
A yC2 dA 2a A yCdA a2
dA
A
x
I xC
0
a2A
即:
I x I xC a2 A
§A.3 平行轴定理
一、定理推导
三、惯性半径
在力学计算中,有时把惯性矩写成
即:
Ix
A
i
2 x
Iy
A
i
2 y
ix
I x ——图形对 x 轴的惯性半径 A
iy
I y ——图形对 y 轴的惯性半径 A
单位:m
三、惯性半径
试问: 即:
I x
A
y 2dA
A
i
2 x
A yC2
?
ix yC ?
注意:
ix yC
iy xC
四、平行移轴公式
§5.2 惯性矩 惯性半径
一、惯性矩 二、惯性矩与极惯性矩的关系 三、惯性半径 四、平行移轴公式
教学重点
1、惯性矩、极惯性矩的概念和计算方法; 2、平行移轴公式。
教学难点
• 平行移轴公式的应用。
一、惯性矩
y
1.惯性矩 定义:
y2dA——微面积dA对 x 轴的惯性矩
x2dA——微面积dA对 y 轴的惯性矩 O
I x I xC a2 A
同理
I y I yC b2 A I xy I xC yC abA
——惯性矩和惯性积的平行轴定理
显然:
I x I xC
I y I yC
性质4:在平面图形对所有相互平行的坐标轴的惯性矩 中,以对形心轴的惯性矩为最小。
二、应用
解: 例 求 I和xC I yC
200 y
30 2003 57.52 200 30 mm 4 3.98 107 mm 4
12
例2
求
I
和
xC
I yC
解:
I xC
I xC
I
xC
6.01 107
mm
4
I yC
I yC
I
yC
30 2003 200 303
12
12
2.05107 mm 4
30 I
200 y
C
C
200 157.5 30 II
