材料力学大作业03。
哈工大材料力学上机大作业(VB编)
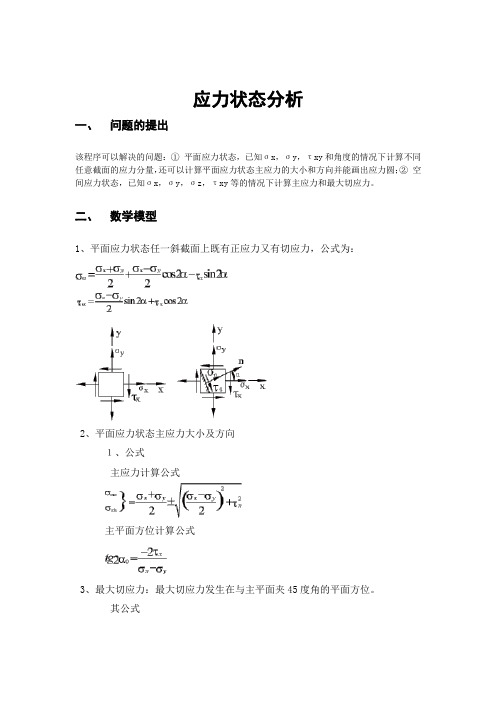
应力状态分析一、问题的提出该程序可以解决的问题:①平面应力状态,已知σx,σy,τxy和角度的情况下计算不同任意截面的应力分量,还可以计算平面应力状态主应力的大小和方向并能画出应力圆;②空间应力状态,已知σx,σy,σz,τxy等的情况下计算主应力和最大切应力。
二、数学模型1、平面应力状态任一斜截面上既有正应力又有切应力,公式为:2、平面应力状态主应力大小及方向1、公式主应力计算公式主平面方位计算公式3、最大切应力:最大切应力发生在与主平面夹45度角的平面方位。
其公式4、应力圆应力圆原理:圆心:半径:5、三向应力状态三向应力计算公式:特征方程:222222x y x y xy αασσσσσττ+-⎛⎫⎛⎫-+=+ ⎪ ⎪⎝⎭⎝⎭2x y a σσ+=222x y xy R σστ-⎛⎫=+ ⎪⎝⎭三个不变量三、程序流程图㈠ 平面应力计算 打开界面选择平面应力计算 出现数据输入对话框 输入σx ,σy ,τxy 和角度 点击计算 可计算出任意截面的应力分量以及三个主应力和最大切应力 记录数据点击清除可进行重复计算㈡ 空间应力状态计算打开界面选择空间应力状态计算 出现数据输入对话框输入σx ,σy ,σz ,τxy ,τyz ,τxz 点击计算 得出结果可计算出三个主应力及最大切应力 记录数据点击清除可以重复计算四、程序说明本程序分为平面应力状态与空间应力状态,点击相应主菜单进行相应的计算。
平面应力状态:本程序能进行多次重复输入与计算根据提示输入数据进行计算输入X ,Y ,XY 方向上的应力值及X'转动的角度值,点击"计算"按扭,进行数值计算。
1x y z I σσσ=++2x yx y zy z xz xy y yz z zx x I στστσττστστσ=++3x yx zx xy y zy xz yz zI στττστττσ=可画出与数据相对应的应力圆空间应力状态:本程序能进行多次重复输入与计算根据提示输入数据进行计算输入X,Y,Z,XY,YZ,ZY方向上的应力值,点击"计算"按扭,可以计算出三个主应力及最大切应力。
材料力学第三章答案

材料力学第三章答案材料力学第三章答案【篇一:材料力学习题册答案-第3章扭转】是非判断题二、选择题0 b 2t?d316?1?? ? b wp??d316?1?? ?2c wp??d316?1?? ? d w3p??d316?1?? ?46.对于受扭的圆轴,关于如下结论:①最大剪应力只出现在横截面上;②在横截面上和包含杆件的纵向截面上均无正应力;③圆轴内最大拉应力的值和最大剪应力的值相等。
现有四种答案,正确的是( a )a ②③对b①③对c①②对d 全对7.扭转切应力公式?mnp?i?适用于(d)杆件。
pa 任意杆件;b 任意实心杆件;c 任意材料的圆截面;d 线弹性材料的圆截面。
9.若将受扭实心圆轴的直径增加一倍,则其刚度是原来的( d a 2倍; b 4倍; c 8倍; d 16倍。
三、计算题1.试用截面法求出图示圆轴各段内的扭矩t,并作扭矩图2.图示圆轴上作用有四个外力偶矩me1 =1kn/m, me2 =0.6kn/m,)me3= me4 =0.2kn/m, ⑴试画出该轴的扭矩图;⑵若me1与me2的作用位置互换,扭矩图有何变化?(1)(2)解:me1与me2的作用位置互换后,最大扭矩变小。
3.如图所示的空心圆轴,外径d=100㎜,内径d=80㎜,m=6kn/m,m=4kn/m.请绘出轴的扭矩图,并求出最大剪应力解:扭矩图如上,则轴面极惯性矩id4?d4)(1004?804)(10?3)4p=?(32??32?5.8?10?6m4㎜,l=500tr4?103?50?103ip5.8?104.图示圆形截面轴的抗扭刚度为g ip,每段长1m,试画出其扭矩图并计算出圆轴两端的相对扭转角。
ab+ad=cdab=t1l?90?gipgipad=bc=t2l100gipgipcd=t3l40gipgip?90?100?4050?gipgip【篇二:《材料力学》第3章扭转习题解】[习题3-1] 一传动轴作匀速转动,转速n?200r/min,轴上装有五个轮子,主动轮ii输入的功率为60kw,从动轮,i,iii,iv,v依次输出18kw,12kw,22kw和8kw。
材料力学大作业

梁的强度计算(材料力学大作业)
姓名:
班级:
学号:
题目:
2014年4月
梁的强度计算
一、说明
本作业的目的在于对梁的强度计算作一全面训练。
包括内力图、截面选择及主应力校核等,对弯曲应力及应力状态等基本概念也将作进一步的巩固。
二、已知条件
图号,数据号。
梁的许用应力[σ]=140Mpa。
三、要求
1.作剪力图和弯矩图;
2.根据正应力强度条件选定工字钢的型号;
3.画出危险截面处正应力及切应力的分布图;
4.画出指定截面m-n(内力分量较大的一侧)上1、2、3、4及5点处的应力状态,用应力圆求其主应力的大小及方向(主平面的方位在单元体上表示),并画出该截面上最大主应力的分布图;
5.用第三或第四强度理论对梁进行全面校核。
四、作业内容及要求
1.计算说明书一份;
2.图一份,包括:
(1)剪力图和弯矩图;
(2)危险截面处正应力及切应力的分布图;
(3)指定截面上1-5点处的应力状态,应力圆及最大主应力的分布图。
3.计算过程及相关图均要求A4幅面,封面用统一格式。
五、图及数据
图:
作业说明:
每个班分4个组,每组又分为三个小组。
每组做一个图号的题,而其中三个小组各采用三组数据中的其中一组。
即全班共有12种题。
要求统一封面,均用A4纸。
(为节约计,用纸可以班统一购买)。
作业于5月23日交系办公室闫老师(或马老师)代收。
材料力学上机大作业

2013年材力上机大作业应力状态分题目要求:输入:1.平面应力状态输入:(σx、σy、τxy);某截面方位角α2.空间应力状态输入:(σx、σy、σz、τxy、τyz、τxz)输出:1.输出主应力(σ1、σ2、σ3)2.最大剪应力(τmax=τ13=(σ1—σ3)/2)3.如为平面应力状态则需输出方位角α斜截面上的应力σa、τa及主方向角αa4.画出应力圆示意图二、程序原文:#include<stdio.h>#include <math.h>void Erxiang(float xigemaX,float xigemaY,float taoxy,float aerfa); /*二向应力求解函数*/void Sanxiang(float xigemaX,float xigemaY,float xigemaZ,float taoxy,float taoxz,float taoyz);/*三向应力求解函数*/void main(){int a;/*状态标志量,用以进行二向应力与三向应力问题的选择*/float xigemaX,xigemaY,xigemaZ,taoxy,taoxz,taoyz,aerfa;/*各应力及α*/printf("Select items from 2 or 3\n");/*选择二向应力问题或三向应力问题,键入2或3,以回车结束*/scanf("%d",&a);if(a==2)/*键入2后执行二向应力求解过程*/{printf("xigemaX:");/*屏幕提示输入*/scanf("%f",&xigemaX);/*键入已知数值,以回车结束,下同*/printf("xigemaY:");scanf("%f",&xigemaY);printf("taoxy:");scanf("%f",&taoxy);printf("aerfa:");scanf("%f",&aerfa);Erxiang(xigemaX,xigemaY,taoxy,aerfa);}else/*键入3后执行三向应力求解过程*/{printf("xigemaX:");scanf("%f",&xigemaX);printf("xigemaY:");scanf("%f",&xigemaY);printf("xigemaZ:");scanf("%f",&xigemaZ);printf("taoxy:");scanf("%f",&taoxy);printf("taoxz:");scanf("%f",&taoxz);printf("taoyz:");scanf("%f",&taoyz);Sanxiang(xigemaX,xigemaY,xigemaZ,taoxy,taoxz,taoyz);}}void Erxiang(float xigemaX,float xigemaY,float taoxy,float aerfa)/*二向应力求解函数*/{float aerfa2,a;/*aerfa2为所求主应力角*/float xigema1,xigema2,xigema3,xigemaaerfa,taoaerfa;/*分别为三个主应力与α方向上的正应力与切应力*/xigema1=(xigemaX+xigemaY)/2+sqrt(taoxy*taoxy+((xigemaX-xigemaY)/2)*((xigemaX-xigema Y)/2));xigema2=(xigemaX+xigemaY)/2-sqrt(taoxy*taoxy+((xigemaX-xigemaY)/2)*((xigemaX-xigema Y)/2));a=2*taoxy/(xigemaX-xigemaY);aerfa=(aerfa/180)*3.141592657;/*角度转化为弧度*/aerfa2=atan(a)/2;xigemaaerfa=(xigemaX+xigemaY)/2+(xigemaX-xigemaY)*cos(2*aerfa)/2+taoxy*sin(2*aerfa);taoaerfa=-(xigemaX-xigemaY)*sin(2*aerfa)/2+taoxy*cos(2*aerfa);aerfa2=aerfa2/3.141592657*180;if(xigema2>=0)/*进行主应力的大小排序与各解的输出*/{printf("xigema1=%f,xigema2=%f,xigema3=0\n",xigema1,xigema2);/*输出主应力*/printf("aerfa1=%f,aerfa2=%f\n",aerfa2,aerfa2+90);/*输出主应力角*/printf("xigemaaerfa=%f,taoaerfa=%f\n",xigemaaerfa,taoaerfa);/*输出α方向上的应力*/}else if(xigema1<=0){printf("xigema1=0,xigema2=%f,xigema3=%f\n",xigema1,xigema2);printf("aerfa1=%f,aerfa2=%f\n",aerfa2,aerfa2+90);printf("xigemaaerfa=%f,taoaerfa=%f\n",xigemaaerfa,taoaerfa);}else{printf("xigema1=%f,xigema2=0,xigema3=%f\n",xigema1,xigema2);printf("aerfa1=%f,aerfa2=%f\n",aerfa2,aerfa2+90);printf("xigemaaerfa=%f,taoaerfa=%f\n",xigemaaerfa,taoaerfa);}}void Sanxiang(float xigemaX,float xigemaY,float xigemaZ,float taoxy,float taoxz,float taoyz)/*三向应力求解函数*/{float a,b,c,d,deta,k,t,xita,xigema1,xigema2,xigema3;/*定义一元三次方程相关系数与三个主应力*/float yoona;a=1;b=-(xigemaX+xigemaY+xigemaZ);c=(xigemaX*xigemaY-taoxy*taoxy+xigemaY*xigemaZ-taoyz*taoyz+xigemaZ*xigemaX-taoxz*t aoxz);d=-(xigemaX*xigemaY*xigemaZ+taoxy*taoyz*taoxz+taoxz*taoxy+taoyz-xigemaX*taoyz*taoyz-taoxy*taoxy*xigemaZ-xigemaY*taoxz*taoxz);deta=b*b-4*a*c;k=b/a;t=(2*a*b-3*a*b)/(2*pow(a,3/2));xita=acos(t);if(deta>0)/*主应力求解过程*/{printf("error!!");}else if(deta==0){xigema1=-b/a+k;xigema2=-k/2;xigema3=xigema2;}else;{xigema1=(-b-2*pow(a,1/2)*cos(xita/3))/(3*a);xigema2=(-b+pow(a,1/2)*(cos(xita/3)+pow(3,1/2)*sin(xita/3)))/(3*a);xigema3=(-b+pow(a,1/2)*(cos(xita/3)-pow(3,1/2)*sin(xita/3)))/(3*a);}if(xigema1<xigema2)/*主应力大小排序*/{yoona=xigema1;xigema1=xigema2;xigema2=yoona;}else;if(xigema2<xigema3){yoona=xigema3;xigema3=xigema2;xigema2=yoona;}else;if(xigema1<xigema2){yoona=xigema2;xigema2=xigema1;xigema1=yoona;}else;printf("xigema1=%f,xigema2=%f,xigema3=%f\n",xigema1,xigema2,xigema3);/*输出结果*/ }三、运行范例:应力状态选择,输入2代表平面应力状态,3代表空间应力状态;选择平面应力状态,输入应力σx=40Mpa,σy=-20Mpa,τxy=40Mpa,α=30º;输出结果,σ1=60Mpa,σ2=0;σ3=—40Mpa,σa=59.641014Mpa,τ—5.980763Mpa;。
北航材料力学模拟题三
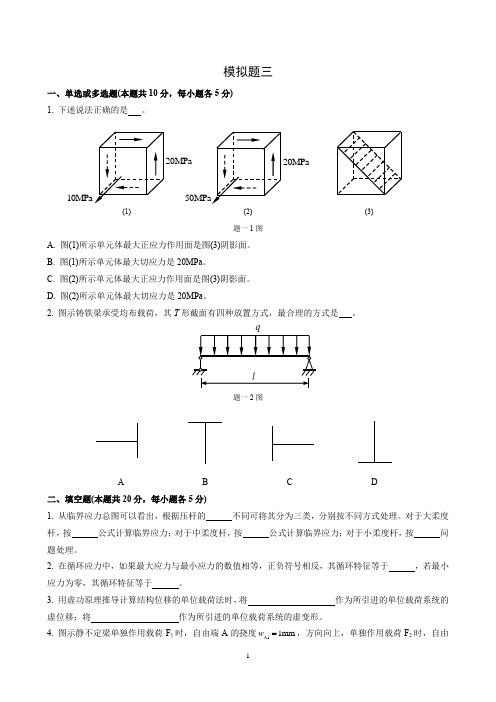
模拟题三一、单选或多选题(本题共10分,每小题各5分) 1. 下述说法正确的是 。
(1) (2) (3)题一1图A. 图(1)所示单元体最大正应力作用面是图(3)阴影面。
B. 图(1)所示单元体最大切应力是20MPa 。
C. 图(2)所示单元体最大正应力作用面是图(3)阴影面。
D. 图(2)所示单元体最大切应力是20MPa 。
2. 图示铸铁梁承受均布载荷,其T 形截面有四种放置方式,最合理的方式是 。
题一2图A B C D二、填空题(本题共20分,每小题各5分)1. 从临界应力总图可以看出,根据压杆的 不同可将其分为三类,分别按不同方式处理。
对于大柔度杆,按 公式计算临界应力;对于中柔度杆,按 公式计算临界应力;对于小柔度杆,按 问题处理。
2. 在循环应力中,如果最大应力与最小应力的数值相等,正负符号相反,其循环特征等于 ,若最小应力为零,其循环特征等于 。
3. 用虚功原理推导计算结构位移的单位载荷法时,将 作为所引进的单位载荷系统的虚位移;将 作为所引进的单位载荷系统的虚变形。
4. 图示静不定梁单独作用载荷F 1时,自由端A 的挠度Α11mm w ,方向向上,单独作用载荷F 2时,自由20MPa20MPaq端A 的挠度Α22mm w =-,方向向下。
若两载荷同时作用,则自由端A 的挠度A w = ,方向向 。
题二4图三、(本题15分)一均质杆重W ,长l ,横截面积A ,材料弹性模量为E 。
在轴线上距顶端3l 的C 点受到向上的轴向外力2F W =作用而匀加速上升,试计算杆的总伸长。
题三图四、(本题15分)图示两端固定圆截面轴,承受集度为m 的均布扭力偶与矩为M 的集中扭力偶作用,2M ma =,轴的直径为d 。
试求最大扭转切应力。
题四图五、(本题15分) 作梁的剪力和弯矩图题五图ACBA2qaqa2图示简支木梁长l =1m ,承受均布载荷q =5kN/m 。
梁截面为矩形,从圆木截面截取。
木材许用正应力[]σ=10MPa 。
材料力学大作业

《材料力学》大作业班级:理科12-1班题目:古代寓言“七根筷子”说的是,7根筷子分开来时每一根很容易被折断,可一旦绑在一起,就很难轻易将它们折断,体现了团结的力量。
请从材料力学角度分析,折断7根筷子所用的力量是折断1根筷子的多少倍?设筷子是一个直径为D 的圆截面杆。
要求:1.每班分成2个小组,分工合作,完成本次大作业(注明小组成员姓名、学号)。
2.需给出相应的力学模型、求解过程、结果讨论等。
一、假设7筷子大小、材料均相同,形状为圆台状,长度为l =30mm ,圆的半径分别为D ,许用拉应力等于许用压应力为[]σ,各个筷子之间没有相对滑动(即摩擦力视为无穷大),因为用手折断筷子时力主要集中在手的两端,所以模型可简化为图(1)。
(1)先求一根筷子折断时的力1F 长度单位为图(1)在距离为x 处的弯矩M Fx =-(00.005x ≤≤),0.005M F =(0.0050.025x ≤≤),()0.0050.025M F F x =+-(0.0250.03x ≤≤),对中性轴的惯性矩464z D I π=,其弯矩图如图(2)所以危险截面在x=0.005-0.025m 处,此处的应力40.32z M FI Dσπ==,当折断筷子时[]σσ≥即[]410.32D F F πσ=≥。
(2)求七根筷子并排折断时的力2F七根筷子并排,排列方式如下图(3)所示图(3)其每根受力方式如图(1)所示,但筷子的受力力F 均匀分布在7跟筷子上,即每根筷子受力为17F ,每根筷子的弯矩图如图(2)所示,由弯矩图可知其危险截面在x=0.005-0.025mm 处。
7根筷子的弯矩为0.005M F =。
由图(4)七根筷子并排的截面可得对中性轴的惯性矩4764z D I π=图(4)危险截面处的应力40.327z M F I Dσπ==,当折断筷子时[]σσ≥,即[]42170.32D F F πσ=≥。
结果讨论:[][]4214170.3270.32D FD F πσπσ==,折断时所需力为折断一根筷子的7倍。
材料力学第3章扭转习题及答案

材料力学第3章扭转习题及答案第三章扭转一、判断题1.杆件受扭时,横截面上的最大切应力发生在距截面形心最远处。
(× ) 2.薄壁圆管和空心圆管的扭转切应力公式完全一样。
(× )3.圆杆扭转变形实质上是剪切变形。
(√ )4.非圆截面杆不能应用圆截面杆扭转切应力公式,是因为非圆截面杆扭转时“平截面假设”不能成立。
(√ )5.材料相同的圆杆,它们的剪切强度条件和扭转强度条件中,许用应力的意义相同,数值相等。
(× ) 6.切应力互等定理,仅适用于纯剪切情况。
(× ) 7.受扭杆件的扭矩,仅与杆件受到的转矩(外力偶矩)有关,而与杆件的材料及其横截面的大小、形状无关。
( √ ) 8.受扭圆轴在横截面上和包含轴的纵向截面上均无正应力。
(√ ) 9.受扭圆轴的最大切应力只出现在横截面上。
(× ) 10.因木材沿纤维方向的抗剪能力差,故若受扭木质圆杆的轴线与木材纤维方向平行,当扭矩达到某一极限值时,圆杆将沿轴线方向出现裂纹。
(√ )二、填空题1.一级减速箱中的齿轮直径大小不等,在满足相同的强度条件下,高速齿轮轴的直径要比低速齿轮轴的直径(小)。
2.当实心圆轴的直径增加1培时,其抗扭强度增加到原来的( 8 )倍,抗扭刚度增加到原来的( 16 )倍。
3.直径D=50mm 的圆轴,受扭矩T=2.15kn.m ,该圆轴横截面上距离圆心10mm 处的剪应力τ=(35.0 MPa ),最大剪应力τmax=(87.6 MPa )。
4.一根空心轴的内外径分别为d ,D ,当D=2d 时,其抗扭截面模量为(33256153215D d ππ或)。
5.直径和长度均相等的两根轴,在相同的扭矩作用下,而材料不同,它们的τmax 是(相)同的,扭转角φ是(不)同的。
6.等截面圆轴扭转时的单位长度相对扭转角为θ,若圆轴直径增大一倍,则单位长度扭转角将变为(16θ)。
三、选择题1.内、外径之比为α的空心圆轴,扭转时轴内的最大切应力为τ ,这时横截面上内边缘的切应力为( B )。
材料力学习题的答案解析
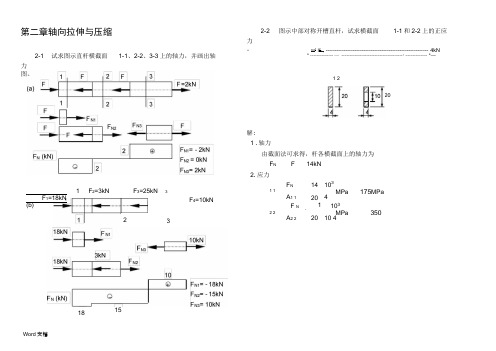
第二章轴向拉伸与压缩2-1 试求图示直杆横截面1-1、2-2、3-3上的轴力,并画出轴力图。
F1=18kN (b)F3=25kN 3力。
解:2-2 图示中部对称开槽直杆,试求横截面1-1和2-2上的正应1 .轴力M1I2- , --------------------------------------------------------- 4kN* -------------- —------------------------------------- r .------------- *—1 2201 F2=3kNF4=10kN2 31518F N F14kN2.应力F N141031 1MPa175MPaA1 1204F N141032 2MPa350A2 22010 4由截面法可求得,杆各横截面上的轴力为2-3 图示桅杆起重机,起重杆 AB 的横截面是外径为 20mm 、 径为18 mm 的圆环,钢丝绳 BC 的横截面面积为 BC 横截面上的应力。
AB 和钢丝绳 o 10mm 2。
试求起重杆解:1 .轴力 取节点 F x 0 :B 为研究对象,受力如图所示, F NBC F NAB cos30 F cos 45 2-4 图示由铜和钢两种材料组成的等直杆,铜和钢的弹性模量分别为 E 1100 GPa 和 E 2210 GPa 。
若杆的总伸长为A l 0.126mm ,试求载荷F 和杆横截面上的应力。
2铜1钢/ /F140 . -400600解:1•横截面上的应力由题意有I 1Fh FI 2 l 2E 1AE 2A由此得到杆横截面上的应力为l h I 2 E 1 E 2 h E 1l 2E 20.126 600 400 100 103 210 103 MPa 15.9MPaF y 0 : 由此解得: 2 .应力 起重杆横截面上的应力为F NABABF NAB sin 30 F sin 45 F NAB 2.83kN , 2.83 103 A AB ____ 2。
材料力学习题解答[第三章]汇总
![材料力学习题解答[第三章]汇总](https://img.taocdn.com/s3/m/89b5e7a868dc5022aaea998fcc22bcd126ff4236.png)
材料⼒学习题解答[第三章]汇总3-1求图中所⽰杆各个横截⾯上的应⼒,已知横截⾯⾯积A=400mm 2。
解a):MPaMPa1004001040050400102033231=?==-=?-=σσσ题3-1a)图解b):MPa MPaMPa2540010105050400102032231=?=-=-=?-=右左σσσ MPa MPa 125400105025333=?==右左σσ题3-1b)图3-2图中为变截⾯杆,如果横截⾯⾯积A 1=200mm 2,A 2=300mm 2,A 3=400mm 2,求杆内各横截⾯上的应⼒。
解a ):MPaMPa MPa10040010407.663001020502001010333231=?=-=?-==?=σσσ题3-2a)图解b):MPaMPa 7540033321-=?-==?==σσσ题3-2b)图30kN3-3 图⽰杆系结构中,各杆横截⾯⾯积相等,即A=30cm 2,载荷F=200kN 。
试求各杆横截⾯上的应⼒。
解:(1)约束反⼒:kNF F kN F F kN F F AXAY Dy 2001504315043======(2)各杆轴⼒)(250150200)(150)(200)(1502222压压拉拉kN F F F kN F F kN F F kN F F NCD NAC NAC D NCD AX NAC AY NAB =+=+======= 题3-3图(3)各杆的正应⼒)(3.8330010250,)(5030010150)(7.6630010200,)(50300101503333压压拉拉MPa MPa MPa MPa AC CDAC AB -=?-=-=?-==?==?=σσσσ 3-4钢杆CD 直径为20mm ,⽤来拉住刚性梁AB 。
已知F=10kN ,求钢杆横截⾯上的正应⼒。
解:)(7.112204104.3544.3545cos 1)5.11(232拉MPa d F kNF F NCD CD oNCD =??===?+=ππσ题3-4图3-5图⽰结构中,1、2两杆的横截⾯直径分别为10mm 和20mm ,试求两杆内的应⼒。
材料力学习题及答案
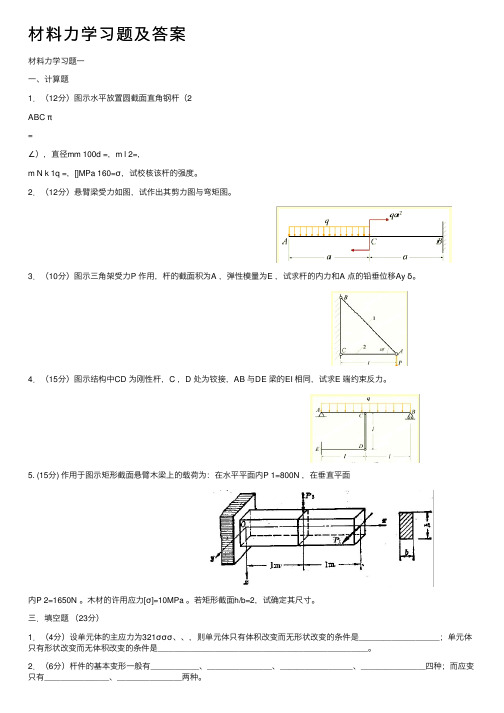
材料⼒学习题及答案材料⼒学习题⼀⼀、计算题1.(12分)图⽰⽔平放置圆截⾯直⾓钢杆(2ABC π=∠),直径mm 100d =,m l 2=,m N k 1q =,[]MPa 160=σ,试校核该杆的强度。
2.(12分)悬臂梁受⼒如图,试作出其剪⼒图与弯矩图。
3.(10分)图⽰三⾓架受⼒P 作⽤,杆的截⾯积为A ,弹性模量为E ,试求杆的内⼒和A 点的铅垂位移Ay δ。
4.(15分)图⽰结构中CD 为刚性杆,C ,D 处为铰接,AB 与DE 梁的EI 相同,试求E 端约束反⼒。
5. (15分) 作⽤于图⽰矩形截⾯悬臂⽊梁上的载荷为:在⽔平平⾯内P 1=800N ,在垂直平⾯内P 2=1650N 。
⽊材的许⽤应⼒[σ]=10MPa 。
若矩形截⾯h/b=2,试确定其尺⼨。
三.填空题(23分)1.(4分)设单元体的主应⼒为321σσσ、、,则单元体只有体积改变⽽⽆形状改变的条件是__________;单元体只有形状改变⽽⽆体积改变的条件是__________________________。
2.(6分)杆件的基本变形⼀般有______、________、_________、________四种;⽽应变只有________、________两种。
3.(6分)影响实际构件持久极限的因素通常有_________、_________、_________,它们分别⽤__________、_____________、______________来加以修正。
4.(5分)平⾯弯曲的定义为______________________________________。
5.(2分)低碳钢圆截⾯试件受扭时,沿____________截⾯破坏;铸铁圆截⾯试件受扭时,沿____________⾯破坏。
四、选择题(共2题,9分)2.(5分)图⽰四根压杆的材料与横截⾯均相同,试判断哪⼀根最容易失稳。
答案:()材料⼒学习题⼆⼆、选择题:(每⼩题3分,共24分)1、危险截⾯是______所在的截⾯。
材料力学大作业
1.躲避防患:有“伤口”(即使很小)的单股绳不要使用。远离已有小裂缝的玻璃、陶瓷制品等,以防它们”突然崩溃”溅出碎片伤人。在刮大风的时候,不要站在大的玻璃窗下。不要购买那些某处曲率大的产品。
2.分散应力:玻璃有小裂缝,能止住裂缝继续变长吗?答案是可以的,裂缝的末尾打一个适当大小的圆孔来分散应力即可止住其继续变长。使用同样原理的例子还有比如,修补车胎的师傅,会把车胎裂口的两端剪成圆形后再修补。
3.逐渐变温:冬天把烫开水冲入普通玻璃保温瓶时,应先把温度较低的温、热水倒进去预热,倒出之后,再进一步预热。多次预热后再冲入开水。同理,在夏天把诸如雪糕等低温物体放进普通玻璃桶时,应逐渐降温。
4.减小曲率:在制作各种拉力工具时,拉脚的拐弯处应设圆角,这并不是为了美观,这是为了避免应力集中。应用同样方法的还有在有凹洞的物品表面涂油漆或胶水填补凹洞。
图2
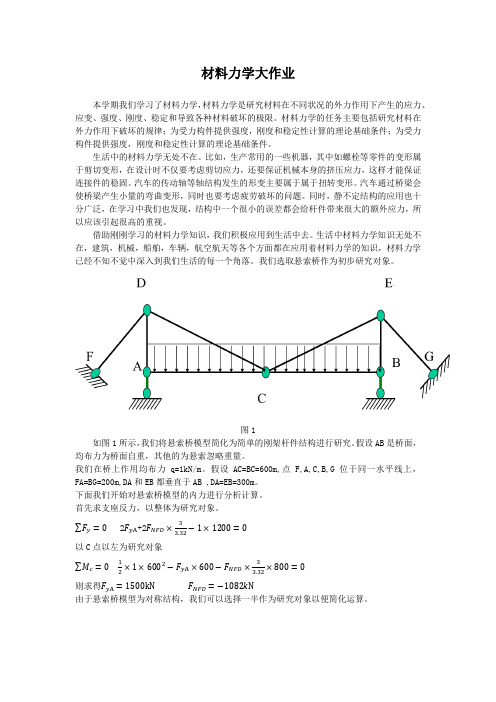
选取左半边结构如图2所示,由于此结构为正对称结构,所以C节点暴漏出内力为轴力和弯矩(剪力在正对称结构中等于0)。我们对A点用节点法可得A处没有水平,只有竖向分力。所以C点暴漏出的轴力等于0,由于C节点是铰接,所以C节点的弯矩也等于0,所以取左半边结构后,可简化为图3所示结构。
图3
取节点D求DC杆内力。
则
图4
取I—I截面如图4,取左部分为研究对象如图5。
图5
则
下面求AC杆的弯矩和剪力。
如此一来这题我们就做完了,接下来我们只需画出悬索桥模型的内力图即可,鉴于内力图太大,就不粘贴到此文章当中。由内力图我们可以看出,悬索部分均没有剪力和弯矩,只有轴力,而桥面部分则正好相反,没有轴力,只有剪力和弯矩。这样一来,我们就可以确定桥面上弯矩最大处在A点左边300m和B点右边300m处, 。这样我们就可以针对此最大弯矩对桥面进行加固,以使桥面能承受大于 的弯矩。由轴力图我们可以看出DA和EB悬索承受最大的轴力,这样我们就需要在这2根杆上进行加固,使它至少能承受1200kN的力,否则他就会断裂,甚至造成桥的坍塌。
材料力学作业及答案

【A】
【B】
【C】
【D】 解:正确答案为【D】; 【A】 分离体上不能带有支座,因为支座处的支反力要影响分离体的平衡(如下图所示),
因此必须将支座去除,用相应的支反力取而代之; 【B】 用截面法计算轴力时,不要在集中力作用点上取截面,因为此处的受力比较复杂,
为了保险起见,建议大家用 的公式来计算线应变。从这个公式可以看出,当材料相同的时, E
线应变的变化规律与正应力的变化规律相同,正应力发生变化的截面上,线应变也将发生变化。
三、图示立柱由横截面面积分别为 A 和 2A 的 AB 和 BC 段组成,已知材料的容重为 ,弹性模量为 E,则
解:正确答案为【A】。 [B]问题出在分子上的 3,在用胡克定律计算变形时分子上要用轴力,而不能用杆件上作用的外力。 [C]这是一个常见的错误,很多同学会仿照对变形进行分段累加的算法来计算线应变,要注意变形有累 加意义,即一段杆件的总的变形量等于每个分段变形量的代数和;但是线应变指的是在一个很小的范围 内杆件的变形程度,可以简单地将线应变理解成是属于某个截面的。当一段杆件受力均匀时,这段杆件 各个横截面上的线应变都是相等的,你可以笼统地说这段杆件的线应变是多少,但是当两段杆件的轴力 不同时,只能说两段杆件的线应变个各是多少,而不能把两段杆件的线应变加起来。不要说是两段杆件 的线应变,即便是把两个截面不同的线应变加起来都没有任何力学意义。就像汽车在公路上行驶,在第 一段上是一个速度,在第二段上是另一个速度,显然把这两个速度加起来是没有什么意义的。 [D]当两段杆件的变形程度不同时,不能像本选项那样将两段杆件连在一起,一次性计算线应变,必须 是各算各的。
在材料力学中采用“突变”的形式来处理。在这种处理方式下,这个截面上的轴力 是不确定的,在材料力学中绘制出来的集中力作用截面附近的轴力图,如下图所示, 此时只需要求出集中力作用截面左右两条线代表的轴力值即可,因此,应该在集中 力作用截面的左右两侧取计算截面。,而不要把计算截面取在集中力的作用截面上。
重视《材料力学》大作业 提高学生的综合能力

学习研究方法对解决 工程实际问题有 很大 帮助。另外 , 材 料力学》 《 课 () 2 按照学 习基础的好坏 分组。这种分组方 法适合于绘图部分较 程的内容与工程实际结合的十分密切 , 既具有 理论 性 , 它 又有一定的实 少 , 计算过程较长 , 计算工作 量大 , 各组计算 难度差别 大的情况。当教
用性。因此 , 工科类各专业学生知识结构和 能力结构 来看 , 从 它处在关 师所给条件不一样 时, 例如 : 大作业题型不一样 , 而造成难度 差异较大 。 键位置 , 起着基础知识 向专业知识过渡 的桥梁作 用。它 是从抽 象的思 或者是所给数据不 同造成 计算工作量 , 度等方面 不同。都可以采用 难 维方式向解决工程 实际问题的思维 方式转变 的重要环 节。事实证 明, 这种方法 , 这种方法的 目的, 就是针对不 同的学生层次 , 分配不 同的 目 对本课程学习的好坏将对学 生学习专业 知识 , 提高解决 生产实 际问题 标和任务 , 以使各层次的学生都能完成基本任务 , 达到甚至超越教学的 的能力与水平都有重大影响。 基本要求。这种分组方法一般 以 5—8人 为宜。能够独立 完成任务的 问题 的 提 出 人也不多 , 相互帮助 , 优劣互补也是完成 目标 的主要方法。这种 分组 方
书本知识通过 加工处 理升华 后 , 为自 己所掌 握的知 识的 重要环 节。 信 , 变 各方面都很优秀的 领导者。就像一个 班就必须有 班长一样 。这种 因此 , 在布置大作业时要注意以下几个问题 : 分组方法重点培养的是集 体主义精神 , 团队精神。一个好 的团队必须 1 合 理 选 题 、 有一个好的领导者。常言道 “ 火车跑得快 , 全靠车头带 。 所 以, 在分 组
一
材料力学作业1

材料力学大作业01思考题:(大作业中会有第三章学完再做)作业题 01什么是材料的强度,举例说明,不可和导学资料举例一致。
答:材料的强度就是指构件或零部件抵抗破坏的能力。
如:北京怀柔白河桥被货车压塌。
什么是材料的刚度,举例说明,不可和导学资料举例一致。
答:刚度是构件或零部件具有的抵抗弹性变形的能力。
如行李箱不易变形。
强度越大,刚度越大,对不对,为什么?答:强度越大,刚度越大,这不一定。
刚度K=EI,E是材料的性质,I是材料结构的性质,所以K的大小不仅与E材料本身的性质有关,还与I材料结构的性质有关。
例如:钢铁的强度要比塑料的强度大,但是一个薄铁片比一个大的塑料块更容易折弯。
刚度越大,强度越大,对不对,为什么?答:刚度越大,强度越大,也不对。
例如:建造钢结构房屋,在外力作用下,弹性变形或位移超过工程允许范围就容易造成坍塌事故。
什么是建筑结构的稳定性,举例说明,不可和导学资料举例一致。
答:稳定性是保持原来状态的能力,建筑结构稳定性指的是建筑中的各组成结构之间不容易出现键的断裂。
例如:三角架支好后,在外力作用下仍然能保持原样。
强度越大,稳定性越好,对不对,为什么?刚度越大,稳定性越好对不对,为什么?答:强度越大,稳定性越好,是不对的。
因为稳定性是结构保持原有平衡形态的能力,钢铁的强度高,但做成细长的条状也是很容易被折弯,保持不了原来的平衡形态。
刚度越大,稳定性越好,也是不对的。
稳定性有时候与刚度有关,有时候与刚度无关。
同样材质的物体,方形结构要比圆形结构的稳定性更好。
作业题 02外力引起内力,应力是内力的集度,应力应变的关系叫本构关系。
那么请问:应变的正负号在《材料力学》中是如何规定的。
应力的正负号在《材料力学》中是如何规定的,为什么这么规定。
内力的正负号在《材料力学》中是如何规定的,为什么这么规定。
外力的正负号在《材料力学》中是如何规定的。
答:正应力受拉为正,剪应力顺时针为正。
应变的正负号是拉应变为正,剪应变以“剪应力顺时针为正”相对应来规定正负。
材料力学大三
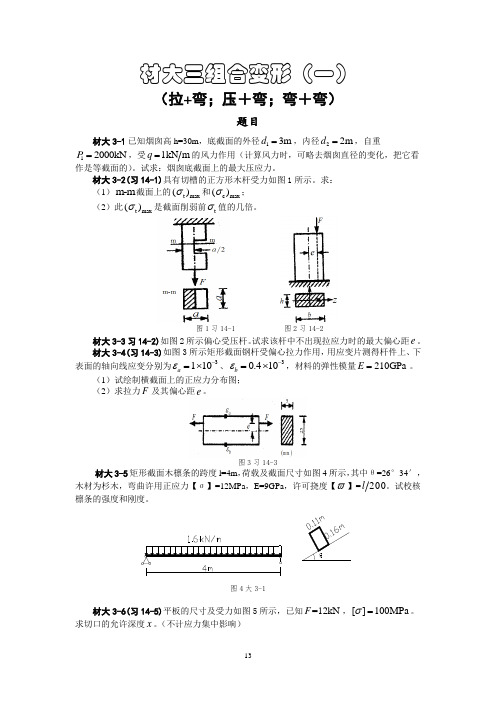
材大三组合变形(一)(拉+弯;压+弯;弯+弯)题目材大3-1已知烟囱高h=30m ,底截面的外径13m d =,内径22m d =,自重12000kN P =,受1kN m q =的风力作用(计算风力时,可略去烟囱直径的变化,把它看作是等截面的)。
试求:烟囱底截面上的最大压应力。
材大3-2(习14-1)具有切槽的正方形木杆受力如图1所示。
求: (1)m-m 截面上的t max ()σ和c max ()σ;(2)此t max ()σ是截面削弱前t σ值的几倍。
图1习14-1 图2习14-2材大3-3习14-2)如图2所示偏心受压杆。
试求该杆中不出现拉应力时的最大偏心距e 。
材大3-4(习14-3)如图3所示矩形截面钢杆受偏心拉力作用,用应变片测得杆件上、下表面的轴向线应变分别为3110a ε-=⨯、30.410b ε-=⨯,材料的弹性模量210GPa E =。
(1)试绘制横截面上的正应力分布图; (2)求拉力F 及其偏心距e 。
图3习14-3材大3-5矩形截面木檩条的跨度l=4m ,荷载及截面尺寸如图4所示,其中θ=26°34′,木材为杉木,弯曲许用正应力【σ】=12MPa ,E=9GPa ,许可挠度【ϖ】=200l 。
试校核檩条的强度和刚度。
图4大3-1材大3-6(习14-5)平板的尺寸及受力如图5所示,已知=12kN F ,[]100MPa σ=。
求切口的允许深度x 。
(不计应力集中影响)MPa WMA F N c 72.0212.0508.0max =+=+=σ图5习14-5 图6习14-4材大3-7(习14-4)托架如图6所示,已知AB 为矩形截面梁,宽度=20mm b ,高度=40mm h ,杆CD 为圆管,其外径=30mm D ,内径=24mm d ,材料的[]=160MPa σ。
若不考虑CD 杆的稳定问题,试按强度要求计算结构的许可载荷[]q 。
答案材大3-1烟囱产生压弯组合变形,在底截面上的轴力和弯矩分别为:N 12000kN F P =-=-2211130450kN m22M qh ==⨯⨯=⋅ 故烟囱底截面上的最大压应力为:()3N 1222000100.508MPa 324F A σπ⨯===-()3244450100.212MPa 3-216432M W σπ⨯===⨯材大3-2(1)t,max 28F a σ=,c,max 24Fa σ-=; (2)t,max t8σσ=。
材料力学作业参考题解课件

总结词:掌握扭转的基本概念、 应力分布、变形特点以及强度条 件。
扭转是材料力学中另一种常见的 受力形式,主要研究圆轴在扭矩 作用下的应力、应变和变形。
强度条件是判断圆轴是否发生扭 转变破坏的标准,包括最大工作 扭矩和许用扭矩等。
04
材料力学应用实例
桥梁结构分析
总结词
桥梁结构分析是材料力学应用的重要领域之 一,涉及桥梁的稳定性、强度和刚度等方面 的分析。
详细描述
在建筑结构分析中,需要考虑建筑物的梁、柱、板等构件的承载能力和变形,以及地震 等自然灾害的影响。通过材料力学的基本原理和方法,可以评估建筑物的结构安全性和
可靠性,为建筑物的优化设计提供依据。
汽车结构分析
要点一
总结词
汽车结构分析是材料力学应用的又一重要领域,涉及汽车 的结构设计、碰撞安全和轻量化等方面的分析。
弯曲是材料力学中又一重要的受 力形式,主要研究梁在弯矩作用 下的应力、应变和变形。
弯曲时,梁内部的应力分布与变 形特点是关键,需要理解弯曲正 应力和弯曲剪切应力的概念。
强度条件是判断梁是否发生弯曲 破坏的标准,包括最大工作弯曲 正应力和许用弯曲正应力等。
扭转
详细描述
扭转时,圆轴内部的应力分布与 变形特点是关键,需要理解剪切 应力和剪切应变的概念。
强度条件是判断杆件是否发生破坏的标 准,包括最大工作应力、许用应力和安 全系数等。
拉伸和压缩时,杆件内部的应力分布与 变形特点是关键,需要理解轴向拉压应 力、轴向应变和横向应变的概念。
详细描述
拉伸和压缩是材料力学中最基本的受力 形式,主要研究杆件在拉力或压力作用 下的应力、应变和变形。
剪切
总结词:掌握剪切的基本 概念、应力分布、变形特 点以及强度条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料力学大作业03
1.压杆稳定是不是就是偏心受压(压弯组合),不是的话,它和大偏心受压,小偏心受压有什么区别。
答:压杆稳定是指当受拉杆件的应力达到屈服极限或强度极限时,将引起塑性变形或断裂。
长度较小的受压短柱也有类似的现象,例如低碳碳钢短柱被压扁,铸铁短柱被压碎。
这些都是由于强度不足引起的失效。
大偏心受压的破坏就是受拉破坏,小偏心就是受压破坏。
大小偏心受压破坏原因就是,大偏心由于压力偏离构件轴心比小偏心要远,受压产生的弯矩比较大,构件就相当于是受弯破坏的。
小偏心的偏心距比较小,距离轴心近(可以就理解为压力作用在轴心上),构件就是受压破坏的。
2.简述圣维南原理及其应用。
答:圣维南原理是弹性力学的基础性原理,其内容是:分布于弹性体上一小块面积(或体积)内的荷载所引起的物体中的应力,在离荷载作用区稍远的地方,基本上只同荷载的合力和合力矩有关;荷载的具体分布只影响荷载作用区附近的应力分布。
还有一种等价的提法:如果作用在弹性体某一小块面积(或体积)上的荷载的合力和合力矩都等于零,则在远离荷载作用区的地方,应力就小得几乎等于零。
圣维南原理在实用上和理论上都有重要意义。
在解决具体问题时,如果只关心远离荷载处的应力,就可视计算或实验的方便,改变荷载的分布情况,不过须保持它们的合力和合力矩等于原先给定的值。
圣维南原理是定性地说明弹性力学中一大批局部效应的第一个原理。
3.简述应力集中及其应用。
答:应力集中:应力集中是指结构或构件的局部区域的最大应力值比平均应力值高的现象。
应用:自行车内胎被刺破后,可用橡胶补块补块一般剪成圆形或椭圆形,而非正方形,且补的边缘剪成斜茬形下面(与内胎粘合面)宽,补块的边缘剪成斜茬形使整个内胎平滑降低应力集中应数,避免在运动中由于应力集中出现补快脱落的情况。
4.简述塑性材料低碳钢受力变形的几个阶段,及其表现。
答:(1)弹性阶段:这一阶段试样的变形完全是弹性的,全部写出荷载后,试样将恢复其原长。
此阶段内可以测定材料的弹性模量E。
(2)屈服阶段bc:试样的伸长量急剧地增加,而万能试验机上的荷载读数却在很小范围内波动。
如果略去这种荷载读数的微小波动不计,这一阶段在拉伸图上可用水平线段来表示。
若试样经过抛光,则在试样表面将看到大约与轴线成45°方向的条纹,称为滑移线。
(3)强化阶段ce 试样经过屈服阶段后,若要使其继续伸长,由于材料在塑性变形过程中不断强化,故试样中抗力不断增长。
(4)颈缩阶段和断裂ef:试样伸长到一定程度后,荷载读数反而逐渐降低。
此时可以看到试样某一段内横截面面积显著地收缩,出现“颈缩”的现象,一直到试样被拉断。
