材料力学大作业-组合截面几何性质计算

材料力学截面几何特性

= 144 ×10 4 mm 4 + 1200mm 2 × (20mm) 2 + 0.58 ×10 mm + 700mm × (35mm)
4 4 2 2
= 278.33mm
4
I xC yC = A1 xc1 yc1 + A2 xc 2 yc 2
= 1200mm × (15mm) × (20mm)
2
A
ρ
= ∫ ( yC + b) 2 dA
A 2 = ∫ ( yC + 2byC + b 2 )dA A
= I xC + 2bS xC + b 2 A
I x = I xC + 2bS xC + b 2 A
因为C为形心因为为形心
S xC = AyC = 0
Ix = IxC + b2 A
同理: 同理:
+ 700mm × (25mm) × (35mm)
2
= 97.25 ×10 4 mm 4
(2)计算主轴位置
tan 2α 0 =
2 I xy Ix Iy
2 × 97.25 ×10 4 mm 4 = 100.33 ×10 4 mm 4 278.33 ×10 4 mm 4 = 1.093
α 0 = 113.80
I x1 = ∫ y12 dA
α
= ∫ ( x sin α + y cos α ) dA
2
= I x cos 2 α 2 I xy sin α cos α + I y sin 2 α
I x1 = I x cos 2 α 2 I xy sin α cos α + I y sin 2 α
I x1 = Ix + Iy 2 + Ix Iy 2 cos 2α I xy sin 2α

材料力学截面的几何性质

附
录
附录Ⅰ
§Ⅰ-1 §Ⅰ-2 §Ⅰ-3 §Ⅰ-4
截面的几何性质
截面的静矩和形心位置惯性矩、惯性积和惯性半径平行移轴公式转轴公式主惯性矩
静矩与形心
一、静矩的定义(与力矩类似)（也称面积矩或一次矩）截面对z轴的静矩： y 截面对y轴的静矩：
Sz Sy
dS
A A
z

ydA
A
3
z 100
I
C
CI
a1 a2
I y I yI I yII 443 10 768 10
4
4
y
1211 104 mm 4
由于z轴是对称轴，故图形对两轴的惯性积为
140 103.3
CII
II
y
I yz 0
20
I z y 2 dA 2h y 2 bdy
3
附
录
组合截面形心
组合截面：如果截面的图形是由几个简单图形(如矩形、圆形等）组成的，这种截面称为组合截面。组合截面对X、Y轴静矩的计算：
S x Ai yci Ayc
i
n
S y Ai xci Axc
i
n
Ai——任一简单图形的面积； xci，yci——任一简单图形的形心坐标； n——全部简单图形的个数。确定组合截面形心位置的公式：
C H/2
X
1 h 1 h yc 1 y1 ( y1 ) ( y1 ) 2 2 2 2
h 1 h S x Ayc 1 b( y 1 ) ( y 1 ) 2 2 2
b
b 2 2 (h 4y1 ) 8
例2、图形对 x 轴的静矩为

材料力学—截面几何性质

主轴:满足惯性积为零的坐标轴
主惯性矩:对主轴的惯性矩
主形心轴与主形心惯性矩
I y
Iy
Iz
I y Iz cos2
I
2
2
z
I yz sin2
主形心轴主形心轴
Cy0z0－形心直角坐标系 Oyz－任意直角坐标系
二者平行
第六章弯曲应力
二、惯性积的平行移轴定理
I yz
yzdA
A
y a y0 , z b z0
I yz Aa y0 b z0 dA
I y0z0 A y0 z0dA, A y0dA 0, A z0dA 0
I yz I y0z0 Aab
1
1
yc1 A1 yc2 A2 yc3 A3
n
n
yc
Sz A
Si
i 1
A
i 1
yci Ai A
Sz
S(整) z
S(孔) z
y
c
S(整) z
A( 整 )
S(孔) z
A(孔)
负面积法
第六章弯曲应力
例：确定下图所示截面的形心位置
50
50
A1
z
60
A2
10
解：将截面分为两部分，利用组合截面的公式：
第六章弯曲应力
A-4 转轴公式与惯性矩
一、转轴公式 y1 ycos zsin z1 zcos ysin
I y1z1 A( ycos zsin )(zcos ysin )dA
：始边y轴，为正
I y1z1
Iy
2
Iz
sin2
I yzcos2
I y1 I y Iz I y Iz cos2

(材料力学)截面几何性质习题及参考答案

截面几何性质作业专业班级姓名学号1. 判断题（1）任意平面图形至少有1对形心主惯性轴，等边三角形有3对形心主惯性轴。

（ × ）（2）平面图形的几何性质中，静矩和惯性矩的值可正、可负、可为零。

（ × ）（3）平面图形中，使静矩为零的轴必为对称轴。

（ × ） 2. 选择题（1）若截面图形有对称轴，则该图形对其对称轴的（ A ）。

A. 静矩为零，惯性矩不为零B. 静矩和惯性矩均不为零C. 静矩和惯性矩均为零D. 静矩不为零，惯性矩为零（2）设图形具有三个以上（含三个）对称轴时，对某一形心轴的惯性矩I 1 ，对某一对正交形心轴的惯性积为I 2。

则当形心轴绕形心旋转时（ A ）。

A. I 1值不变，I 2恒等于零B. I 1 值不变，I 2不恒等于零C. I 1值变化，I 2恒等于零D. I 1值变化，I 2不恒等于零（3）任意图形的面积为A ，x C 轴通过形心C ，x 1轴和x C 轴平行，并相距a ，已知图形对x 1轴的惯性矩是I 1，则对x C 轴的惯性矩为（ A ）。

A. 21xC I I Aa =-B. 0xC I =C. 21xC I I Aa =+D. 1xC I I Aa =+C x 1（4）图示等底等高的矩形和平行四边形，对其形心轴y 的惯性矩I a 和I b 满足（ A ）。

A. I a = I bB. I a > I bC. I a < I bD. 不能确定（a ）（b ）（5）设矩形对其对称轴z 的惯性矩为I ，当其长宽比保持不变，面积增加1倍时，该矩形对其对称轴z 的惯性矩将变为（ A ）。

A. 4IB. 2IC. 8ID. 16I（6）图示任意形状图形，形心轴z 将图形分为两部分，则一定成立的是（ A ）。

A. S z 1 + S z 2 = 0B. I z 1 = I z 2C. A 1 = A 2D. S z 1 = S z 2（7）图形对通过某点的所有轴的惯性矩中，图形对主惯性轴的惯性矩一定（ A ）。

截面几何特性怎么计算公式

截面几何特性怎么计算公式截面几何特性的计算公式。

截面几何特性是指在工程学和物理学中，用来描述截面形状和尺寸的一些参数，这些参数对于材料的强度、刚度和形变等性能具有重要的影响。

在工程设计和分析中，我们经常需要计算截面的一些特性，比如面积、惯性矩、截面模量等。

下面我们将介绍一些常见的截面几何特性的计算公式。

1. 面积。

截面的面积是描述截面大小的一个重要参数，通常用A表示，其计算公式为：A = ∫y dA。

其中y是截面某一点到参考轴的距离，dA表示微元面积。

对于简单几何形状的截面，可以直接通过几何关系计算出面积，比如矩形的面积为长乘以宽，圆形的面积为πr^2。

2. 惯性矩。

截面的惯性矩描述了截面对于转动的惯性，通常用I表示，其计算公式为：I = ∫y^2 dA。

对于简单几何形状的截面，可以通过几何关系计算出惯性矩，比如矩形的惯性矩为bh^3/12，圆形的惯性矩为πr^4/4。

3. 截面模量。

截面模量描述了截面对拉伸和压缩的抵抗能力，通常用S表示，其计算公式为：S = I/c。

其中c为截面到参考轴的距离。

对于简单几何形状的截面，可以通过几何关系计算出截面模量，比如矩形的截面模量为bh^2/6，圆形的截面模量为πr^3/4。

4. 弯曲模量。

截面的弯曲模量描述了截面对弯曲的抵抗能力，通常用W表示，其计算公式为：W = S/y_max。

其中y_max为截面到参考轴的最大距离。

对于简单几何形状的截面，可以通过几何关系计算出弯曲模量，比如矩形的弯曲模量为bh^2/4，圆形的弯曲模量为πr^3/2。

5. 截面形心。

截面的形心描述了截面的几何中心，通常用x_bar和y_bar表示，其计算公式为：x_bar = ∫x dA / A。

y_bar = ∫y dA / A。

对于简单几何形状的截面，可以通过几何关系计算出形心的坐标，比如矩形的形心坐标为(b/2, h/2)，圆形的形心坐标为(0, 0)。

以上是一些常见的截面几何特性的计算公式，这些参数对于工程设计和分析具有重要的意义。

截面几何性质 (材料力学)

Ⅱ
O xⅡ 80
10
120
x1 5mm 2
y1
2
60mm
x
矩形II A2 10 70 700mm2
x2 10 70 45mm 2
y2

10 2

5mm
代入组合截面的形心坐标公式
2
Ai xi
x

i 1 2
Ai
i 1
2
Ai yi
y

i 1 2
Ai
n
Ai xi
x

i 1 n
Ai
i 1
n
Ai yi
y

i 1 n
Ai
i 1
（注：被“减去”部分图形的面积应代入负值）
例试计算图示三角形截面对于与其底边重合的x轴
的静矩。
y
dy
h
b (y )
y
O
b
x
解：取平行于x轴的狭长条，易求 b( y) b (h y)
h
因此 d A b (h y) d y 所以对x轴的静矩为
S x
h yd A
A
h b (h y) y d y bh2
0h
6
例：试计算图示截面形心C的位置。
y
10
Ⅰ
xⅠ
C (y ,x )
解：将截面分为1、2两个矩形。
建立坐标系如图示。
各矩形的面积和形心坐标如下：矩形I
A1 10120 1200mm2
120 y1 y
Ⅱ
10
同理，有：
Ix Ixc a2 A I y I yc b2 A

材料力学第四章截面的几何性质

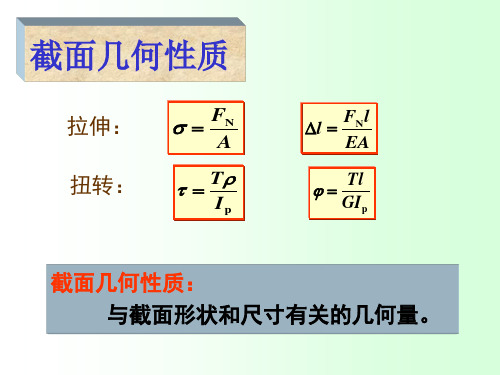
I y A z 2dA I z A y2dA
n
I y
I yi
i 1
n
I z
I zi
i 1
n
I p
I pi
i 1
z
I p A2dA
y
A1 A2
…
dA
An
z
y o
【例题 4】试计算图示圆环对其形心轴的惯性矩和极惯性矩。
z
Iy
Iz
D4 64
d 4 64
y
C
D4 d 4
I p 32 32
0 23.7 0 23.7 90
zo z zc
1 cm
Iyc = 279 cm4
Izc = 100 cm4
Iyczc = -97 cm4
yo
12 cm
0
yc
c
o
8 cm
1 cm y
Imax
m in
I yc
I zc 2
I yc
2
I zc
2
I2 yc zc
Iyc = 279 cm4 Izc = 100 cm4 Iyczc = -97 cm4
0
o
y1
u
y
证明：设通过截面 O 点的y、z 轴为主轴，u、v 为另一对主轴，其中o不是 /2 的整数倍，由转轴公式：
I uv
Iy
Iz 2
sin 20
I yz cos 20
0
而：I yz 0 sin 20 0 I y Iz
从而：
I y1z1
Iy
2
Iz
sin
2
I yz
cos 2
0
故过Ｏ点的任何一对正交轴都是主轴，定理得证。

组合截面计算

钢铝组合截面杆件的设计闭思廉李硕龚沁华深圳中航幕墙工程有限公司深圳市皇城广场1804室 518045摘要钢铝组合截面是工程中经常应用的一种截面形式。

本文对钢铝组合截面的截面特性计算以及截面验算进行简略的介绍。

关键词钢铝组合截面，钢铝叠合截面一．引言在幕墙支承结构和铝合金门窗骨架设计中，为了节省铝合金用量、降低成本，往往采用钢、铝组合截面的杆件，外露部分采用铝合金型材，隐蔽部分亦即主要受力部分采用钢型材，这样，即达到了外表美观靓丽、截面小巧而承载能力高、造价又低廉的目的。

另外，在幕墙加固工程中，钢铝组合截面也时有应用。

钢、铝组合截面的形式，一般常用的不外乎如图 1所示的两种。

其中 a所示的是将钢型材川入铝合金型材的腔内；而 b所示是钢、铝合金型材并列，二者截面一般有一个共同的对称轴。

钢、铝型材的组合方式，又可分为叠合式和组合式两种。

所谓叠合式，即钢、铝型材之间不加连接，仅仅从构造上能保证二者同时受力即可；而组合式和叠合式不同，它是在钢、铝型材之间用物理的或化学的方法将二者紧密相连的组合形式。

由于这两种截面的组合方式不同，所以在受力后的表现也不同，设计计算方法也完全不同，下面分别予以介绍。

图 1二．叠合式截面杆件的设计如图 2所示叠合式截面杆，当其在横向力作用下受弯时，杆件将发生弯曲变形。

由于钢、铝型材之间不加连接，因此，在二者接触面间无任何约束（忽略摩擦），当杆件发生弯曲变形时，在接触面间，二者会产生相互错动，受荷前在同一竖向截面内的abcd亦不在同一截面了，可见，此时的受弯杆件，已不符合“平截面的假定”条件，因此，二者已不能按一体进行计算了。

考虑到钢、铝型材受荷后，截面未脱开，二者有着共同的边界约束条件，在正常受力情况下，变形在弹性范围内，因此二者各自沿自身截面中和轴产生挠曲，且，二者产生的挠度相等。

所以：g l q q = gxg lx l I E I E 亦即，二者分配的荷载与其刚度成正比，于是有： q l =gxg lx l lxl I E I E I E q+；q g =gx g lx l gx g I E I E I E q +若以内力的形式来表达，亦可写成如下的形式： M l =gxg lx l lxl I E I E I E M+；M g =gx g lx l gx g I E I E I E M +N l =gg l l ll A E A E A E N+；N g =g g l l g g A E A E A E N +其中：M ， N-----总弯矩，总轴力M l ，N l -----铝合金型材分配的弯矩，轴力 M g ，N g -----钢型材分配的弯矩，轴力A l ，A g -----铝合金型材截面面积，钢型材截面面积据此即可对叠合式截面杆件进行设计了。

材料力学截面的几何性质

O1 O 2
O
x
O3
x 1
C
课堂练习
I.
&
任意图形，若对某一对正交坐标轴的惯性积为零，则这一对坐标轴一定是该图形的（）。
B
A. 形心轴； B. 主轴 C. 主形心轴 D. 对称轴在图示开口薄壁截面图形中，当（为一对主轴。
y
）时，y-z轴始终保持
A. y轴不动，x轴平移； B. x轴不动，y轴平移； C. x轴不动，y轴任意移动；
y b C 1x C 2x O a x
æ 1 öæ 2 ö æ 1 öæ h ö = ç bh ÷ç h ÷ + ç ah ÷ç ÷ è 2 øè 3 ø è 2 øè 3 ø
h 2 = (a + 2 b ) 6
形心位置
h
x = 0
h 2 (a + 2 b ) h a + 2 b S x y = = பைடு நூலகம்· = 6 A h 3 a + b (a + b ) 2
主惯性矩:
图形对主轴的惯性矩,称主惯性矩
形心主轴:
过形心的主轴称为形心主轴
形心主矩:
图形对形心主轴的惯性矩称为形心主矩
课堂练习
I.
&
在下列关于平面图形的结论中，（
）是错误的。
A.图形的对称轴必定通过形心； B.图形两个对称轴的交点必为形心； C.图形对对称轴的静矩为零； D.使静矩为零的轴必为对称轴。在平面图形的几何性质中，（
y
dA y
ü2、惯性矩和极惯矩永远为正，
惯性积可能为正、为负、为零。
x 1
ü3、任何平面图形对于通过其形

材料力学第9章截面的几何性质

3.86 108 mm4
I zC ,2 =I zC ,1 3.86 108 mm4
I zC ,3 =I zC3 A3 ( yC yC3 )2
= 350 503 mm4 350 50 (228.76 355)2 mm4 12
2.83108 mm4
y C3 y C1 y C y C2
2 2 2 22 2
+b( h y) ( y + 1 ( h y)
2
22
B
(H 2
ቤተ መጻሕፍቲ ባይዱ h2)
b
h2 (
y2)
8
24
H
H
2
2
B
B
2
2
2
h
b
C
z
y
A2
2
h
y
A1
C2(zC2, yC2) C1(zC1, yC1)
第9章截面的几何性质
9.1 静矩 9.2 惯性矩、惯性积和极惯性矩 9.3 转轴公式、主惯性轴和主惯性矩
228.76mm
y
C1
y
C3
y
C2
y
O A1 C1
A3 C3 y
z
A2 C2
9.2 惯性矩、惯性积和极惯性矩
（2）计算对形心轴的惯性矩
I zC =I zC ,1 I zC ,2 I zC ,3
I zC ,1=I zC1 A1( yC yC1)2
= 75 3803 mm4 75 380 (228.76 190)2 mm4 12
S
z
z y
3、惯性半径
I y Aiy2 I z A iz2
iy
Iy A
iz
Iz A

材料力学附录Ⅰ截面的几何性质

材料力学附录Ⅰ截面的几何性质随着材料科学的不断发展，材料力学成为研究材料内部结构和力学行为的重要学科之一。

在材料力学中，研究截面的几何性质是必不可少的一部分。

本文将着重介绍截面几何性质的相关知识，探讨其在材料力学中的应用。

一、截面的定义截面是指在任意平面上与某个物体相交的部分，一般用于描述杆件、梁、板等结构物体的断面形态。

材料力学中，截面的几何参数是研究杆件、梁、板等结构物体受力行为的重要基础。

二、常见截面形状和特征常见的截面形状包括矩形、圆形、三角形、梯形、T形等。

其几何参数如截面面积、惯性矩、位置矩、受压、受弯等，均是描述结构物体受力行为的重要指标。

对于矩形截面来说，其惯性矩最大的方向是短边方向，即截面中心距离短边较远的一侧。

圆形截面的惯性矩与位置矩均与截面对称轴有关。

对于三角形截面来说，其惯性矩与位置矩也是与截面对称轴有关的，而梯形截面和T形截面的惯性矩和位置矩则需要具体计算得出。

三、截面的常见计算公式在计算截面的几何性质时，需要用到一些公式。

以下是一些常见的公式：1、截面面积截面面积是截面内部曲线及其间距离所组成的面积。

不同截面形状的截面面积计算公式如下：矩形截面：A = bh圆形截面：A = πr²三角形截面：A = 1/2bh梯形截面：A = 1/2(a+b)hT形截面：A = (bh₁+ (b₂-h₂)h₂/2)2、截面惯性矩截面惯性矩是描述结构物体受弯作用时截面抵抗弯曲的能力的重要参数，其计算公式如下：Ixx = ∫(y²)dAIyy = ∫(x²)dA其中，x，y分别表示离截面中心最远的两侧点的坐标，dA表示一个面积微元。

3、位置矩位置矩是描述结构物体受纵向荷载作用时截面的抵抗能力的参数，其计算公式如下：Qx = ∫(y)dAQy = ∫(x)dA其中，x，y分别表示离截面中心最远的两侧点的坐标，dA表示一个面积微元。

四、截面几何性质在材料力学中的应用截面几何性质在材料力学中具有广泛的应用。

截面几何性质材料力学

4）静矩为0的轴为截面的形心轴。
例求图示T形截面的形心位置。
100 A1 A1
解：建立参考坐标系。
n
20
z z'
yC
Ai yCi
i 1 n
Ai
A1 yC1 A2 yC2 A1 A2
100
i 1
A2
A2 y A3 20
100 2010 100 20 70
z"
100 20 100 20
= 40 mm
128
d4
18
Iy
z0 z1 A1 z
A2 C
y1
C’ o y
A3
3）解法三
I z I z1
I z0
I z01 I z0 2 I z0 3
d 4
128
d4
I z0 2 I y 128
d4
I z0 2 128 I y
Iz
I z1
I z0 2
OC 2
d2
16
d 4 d 4
128
d 4
128
d4
18
Iy
z
z0
C o
z1
y1 y
2）解法二
I z1 I y1 I z0 I y
I z0 I z1 I y1 I y 2I z1 I y
2 d 4
256
Iy
d 4
128
Iy
Iz
I z0
OC2
d2
16
d 4
128
Iy
(
2 2d )2 d 2 3 16
d 4
3. 在一组平行轴系中对形心轴的惯性矩最小；
4. a、b代表形心C在yoz座标系中的坐标，可正可负。

《材料力学》附录I 截面的几何性质习题解

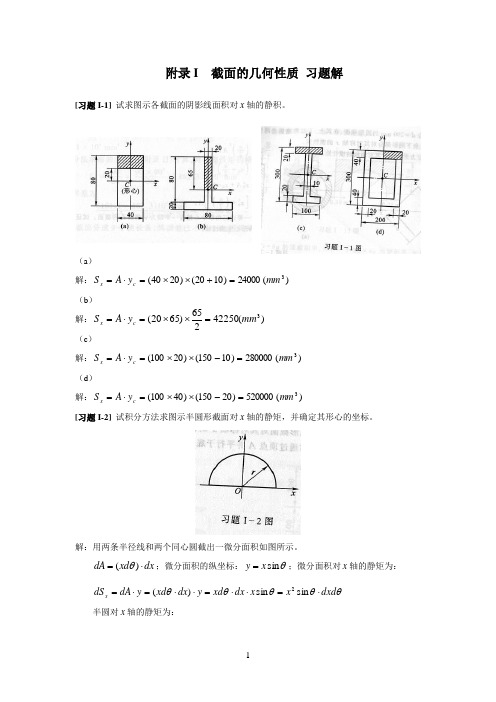
附录I 截面的几何性质习题解[习题I-1] 试求图示各截面的阴影线面积对x 轴的静积。

（a ）解：)(24000)1020()2040(3mm y A S c x =+⨯⨯=⋅=（b ）解：)(42250265)6520(3mm y A S c x =⨯⨯=⋅= （c ）解：)(280000)10150()20100(3mm y A S c x =-⨯⨯=⋅=（d ）解：)(520000)20150()40100(3mm y A S c x =-⨯⨯=⋅=[习题I-2] 试积分方法求图示半圆形截面对x 轴的静矩，并确定其形心的坐标。

解：用两条半径线和两个同心圆截出一微分面积如图所示。

dx xd dA ⋅=)(θ；微分面积的纵坐标：θsin x y =；微分面积对x 轴的静矩为： θθθθθdxd x x dx xd y dx xd y dA dS x ⋅=⋅⋅=⋅⋅=⋅=sin sin )(2半圆对x 轴的静矩为：32)]0cos (cos [3]cos []3[sin 33003002r r x d dx x S r rx =--⋅=-⋅=⋅=⎰⎰πθθθππ因为c x y A S ⋅=，所以c y r r ⋅⋅=232132π π34ry c = [习题I-3] 试确定图示各图形的形心位置。

（a ）解：解：[习题I-4] 试求图示四分之一圆形截面对于x 轴和y 轴的惯性矩x I 、y I 和惯性积xy I 。

解：用两条半径线和两个同心圆截出一微分面积如图所示。

dx xd dA ⋅=)(θ；微分面积的纵坐标：θsin x y =；微分面积对x 轴的惯性矩为： θθθθθdxd x dx xd x dx xd y dA y dI x ⋅=⋅⋅=⋅==232222sin sin )(四分之一圆对x 轴的惯性矩为： ⎰⎰⎰-⋅==2/0042/02322c o s 1]4[s i n ππθθθθd x d dx x I r rx)]2(2cos 21[2142/02/04θθθππd d r ⎰⎰-⋅= }]2[sin 212{82/04πθπ-=r 164r ⋅=π由圆的对称性可知，四分之一圆对y 轴的惯性矩为：164r I I x y ⋅==π微分面积对x 轴、y 轴的惯性积为：xydA dI xy =8)42(21]42[21)(21444042222022r r r x x r dx x r x ydx xdx I r rx r rxy =-=-=-==⎰⎰⎰- [习题I-5] 图示直径为mm d 200=的圆形截面，在其上、下对称地切去两个高为mm 20=δ的弓形，试用积分法求余下阴影部分对其对称轴x 的惯性矩。

材料力学大作业-组合截面几何性质计算

Harbin Institute of Technology材料力学电算大作业课程名称：材料力学设计题目：组合截面几何性质计算作者院系：作者班级：作者姓名：作者学号：指导教师：完成时间：一、软件主要功能X4，X5，X6分别是n1个圆形截面，n2个圆环形截面，n3个矩形截面的形心位置X与面积的乘积Y4，Y5，Y6分别是n1个圆形截面，n2个圆环形截面，n3个矩形截面的形心位置Y与面积的乘积Xc,Yc是总截面的形心坐标Ix1,Ix2,Ix3分别是n1个圆形截面，n2个圆环形截面，n3个矩形截面对通过形心且与x轴平行的轴的惯性矩Iy1,Iy2,Iy3分别是n1个圆形截面，n2个圆环形截面，n3个矩形截面对通过形心且与y轴平行的轴的惯性矩Ixy1,Ixy2,Ixy3分别是n1个圆形截面，n2个圆环形截面，n3个矩形截面对通过形心且与x,y轴平行的两轴的惯性积a是通过形心的主轴与x轴的夹角Imax,Imin分别是截面对形心主轴的主惯性矩软件截图：二、程序源代码Dim n1 As DoubleDim d1(10) As DoubleDim X1(10) As DoubleDim Y1(10) As DoubleDim n2 As DoubleDim d2(10) As DoubleDim d3(10) As DoubleDim X2(10) As DoubleDim Y2(10) As DoubleDim n3 As DoubleDim h(10) As DoubleDim d(10) As DoubleDim X3(10) As DoubleDim Y3(10) As DoubleDim S1 As Double, S2 As Double, S3 As DoubleDim X4 As Double, Y4 As Double, X5 As Double, Y5 As Double, X6 As Double, Y6 As DoubleDim Xc As Double, Yc As DoubleDim Ix1 As Double, Iy1 As Double, Ix2 As Double, Iy2 As Double, Ix3 As Double, Iy3 As Double, Imax As Double, Imin As DoubleDim Ixy1 As Double, Ixy2 As Double, Ixy3 As DoubleDim a As DoublePrivate Sub Text1_Change()n1 = Val(Text1.Text)For i = 1 To n1d1(i) = Val(InputBox("输入第" & (i) & "个圆的直径"))X1(i) = Val(InputBox("输入第" & (i) & "个圆的圆心的x坐标值")) Y1(i) = Val(InputBox("输入第" & (i) & "个圆的圆心的y坐标值")) Next iFor i = 1 To n1S1 = S1 + 3.14159 * d1(i) * d1(i) / 4X4 = X4 + X1(i) * 3.14159 * d1(i) * d1(i) / 4Y4 = Y4 + Y1(i) * 3.14159 * d1(i) * d1(i) / 4Next iEnd SubPrivate Sub Text2_Change()n2 = Val(Text2.Text)For i = 1 To n2d2(i) = Val(InputBox("输入第" & (i) & "个圆环的外径"))d3(i) = Val(InputBox("输入第" & (i) & "个圆环的内径"))X2(i) = Val(InputBox("输入第" & (i) & "个圆的圆心的x坐标值")) Y2(i) = Val(InputBox("输入第" & (i) & "个圆的圆心的y坐标值")) Next iFor i = 1 To n2S2 = S2 + 3.14159 * (d2(i) * d2(i) - d3(i) * d3(i)) / 4X5 = X5 + X2(i) * 3.14159 * (d2(i) * d2(i) - d3(i) * d3(i)) / 4Y5 = Y5 + Y2(i) * 3.14159 * (d2(i) * d2(i) - d3(i) * d3(i)) / 4Next iEnd SubPrivate Sub Text3_Change()n3 = Val(Text3.Text)For i = 1 To n3h(i) = Val(InputBox("输入第" & (i) & "个矩形的高"))d(i) = Val(InputBox("输入第" & (i) & "个矩形的宽"))X3(i) = Val(InputBox("输入第" & (i) & "个矩形形心的x坐标值")) Y3(i) = Val(InputBox("输入第" & (i) & "个矩形形心的y坐标值")) Next iFor i = 1 To n3S3 = S3 + h(i) * d(i)X6 = X6 + X3(i) * h(i) * d(i)Y6 = Y6 + Y3(i) * h(i) * d(i)Next iEnd SubPrivate Sub Command1_Click()Xc = (X4 + X5 + X6) / (S1 + S2 + S3)Yc = (Y4 + Y5 + Y6) / (S1 + S2 + S3)Text4 = XcText5 = YcEnd SubPrivate Sub Command2_Click()Picture1.BackColor = vbWhitePicture1.Scale (-Max - 10, Max + 10)-(Max + 10, -Max - 10)Picture1.Line (0, Max + 10)-(0, -Max - 10)Picture1.Line (Max + 10, 0)-(-Max - 10, 0)Picture1.FillStyle = 0For i = 1 To n1 Step 1Picture1.FillColor = vbBluePicture1.Circle (X1(i), Y1(i)), d1(i) / 2, vbRedNext iFor i = 1 To n2 Step 1Picture1.FillColor = vbGreenPicture1.Circle (X2(i), Y2(i)), d2(i) / 2, vbRedPicture1.FillColor = vbWhitePicture1.Circle (X2(i), Y2(i)), d3(i) / 2, vbRedNext iFor i = 1 To n3 Step 1Picture1.FillColor = vbRedPicture1.Line (X3(i) - d(i) / 2, Y3(i) - h(i) / 2)-(X3(i) + d(i) / 2, Y3(i) + h(i) / 2), vbRed, BFNext iEnd SubPrivate Sub Command3_Click()For i = 1 To n1Ix1 = Ix1 + 3.14159 * d1(i) * d1(i) * d1(i) * d1(i) / 64 + (Y1(i) -Yc) * (Y1(i) - Yc) * 3.14159 * d1(i) * d1(i) / 4Iy1 = Iy1 + 3.14159 * d1(i) * d1(i) * d1(i) * d1(i) / 64 + (X1(i) - Xc) * (X1(i) - Xc) * 3.14159 * d1(i) * d1(i) / 4Ixy1 = Ixy1 + (X1(i) - Xc) * (Y1(i) - Yc) * 3.14159 * d1(i) * d1(i) / 4Next iFor i = 1 To n2Ix2 = Ix2 + 3.14159 * (d2(i) * d2(i) * d2(i) * d2(i) - d3(i) * d3(i) * d3(i) * d3(i)) / 64 + (Y2(i) - Yc) * (Y2(i) - Yc) * 3.14159 * (d2(i) * d2(i) - d3(i) * d3(i)) / 4Iy2 = Iy2 + 3.14159 * (d2(i) * d2(i) * d2(i) * d2(i) - d3(i) * d3(i) * d3(i) * d3(i)) / 64 + (X2(i) - Xc) * (X2(i) - Xc) * 3.14159 * (d2(i) * d2(i) - d3(i) * d3(i)) / 4Ixy2 = Ixy2 + (X2(i) - Xc) * (Y2(i) - Yc) * 3.14159 * (d2(i) * d2(i) - d3(i) * d3(i)) / 4Next iFor i = 1 To n3Ix3 = Ix3 + h(i) * h(i) * h(i) * d(i) / 12 + (Y3(i) - Yc) * (Y3(i) - Yc) * h(i) * d(i)Iy3 = Iy3 + d(i) * d(i) * d(i) * h(i) / 12 + (X3(i) - Xc) * (X3(i) - Xc) * h(i) * d(i)Ixy3 = Ixy3 + (X3(i) - Xc) * (Y3(i) - Yc) * h(i) * d(i)Next iImax = (Ix1 + Ix2 + Ix3 + Iy1 + Iy2 + Iy3) / 2 + Sqr((Ix1 + Ix2 + Ix3 - Iy1 - Iy2 - Iy3) * (Ix1 + Ix2 + Ix3 - Iy1 - Iy2 - Iy3) / 4 + (Ixy1 + Ixy2 + Ixy3) * (Ixy1 + Ixy2 + Ixy3))Imin = (Ix1 + Ix2 + Ix3 + Iy1 + Iy2 + Iy3) / 2 - Sqr((Ix1 + Ix2 + Ix3 - Iy1 - Iy2 - Iy3) * (Ix1 + Ix2 + Ix3 - Iy1 - Iy2 - Iy3) / 4 + (Ixy1 + Ixy2 + Ixy3) * (Ixy1 + Ixy2 + Ixy3))Text6 = ImaxText7 = IminIf Ix <> Iy Thena = Math.Atn(-2 * (Ixy1 + Ixy2 + Ixy3) / (Ix1 + Ix2 + Ix3 - Iy1 - Iy2 - Iy3)) / 2Picture1.Line (Xc, Yc)-(Xc + 20, Yc + 20 * Tan(a)), vbGreenPicture1.Line (Xc, Yc)-(Xc - 20 * Tan(a), Yc + 20), vbGreenElsePicture1.Line (Xc, Yc)-(Xc, Yc + 20), vbGreenPicture1.Line (Xc, Yc)-(Xc + 20, Yc), vbGreenEnd IfEnd Sub程序见/share/link?shareid=734076929&uk=100682977 三、例题的计算结果数据已知一工字型钢如图所示上下两矩形一样，宽是1，高是0.4，中间的矩形宽是0.4，高是2 求形心及主惯性矩解：Xc=0.5 Yc=1.4Ix1= 0.58 Iy1=0.0333Ix2= 0.267 Iy2=0.0107Ix3= 0.58 Iy3=0.0333Ixy1= Ixy2= Ixy3=0夹角a=0°Ix总= Ix1+ Ix2+ Ix3=1.427Iy总= Iy1+ Iy2+ Iy3=0.0773Imax=1.427Imin=0.0773计算结果如图：。

【工程力学】截面几何性质【工程类精品资料】

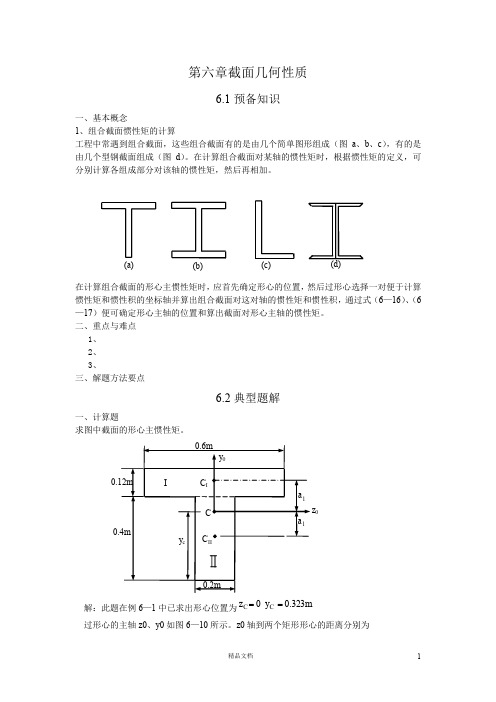
第六章截面几何性质6.1预备知识一、基本概念1、组合截面惯性矩的计算工程中常遇到组合截面，这些组合截面有的是由几个简单图形组成（图a 、b 、c ），有的是由几个型钢截面组成（图d ）。

在计算组合截面对某轴的惯性矩时，根据惯性矩的定义，可分别计算各组成部分对该轴的惯性矩，然后再相加。

在计算组合截面的形心主惯性矩时，应首先确定形心的位置，然后过形心选择一对便于计算惯性矩和惯性积的坐标轴并算出组合截面对这对轴的惯性矩和惯性积，通过式（6—16）、（6—17）便可确定形心主轴的位置和算出截面对形心主轴的惯性矩。

二、重点与难点 1、 2、 3、三、解题方法要点6.2典型题解一、计算题求图中截面的形心主惯性矩。

解：此题在例6—1中已求出形心位置为0=C z m y C 323.0=过形心的主轴z0、y0如图6—10所示。

z0轴到两个矩形形心的距离分别为z 0(b) (c)(d)(a)m a I 137.0=m a II 123.0=截面对z 0轴的惯性矩为两个矩形面积对轴的惯性矩之和，即424232301037.0123.04.02.0124.02.0137.012.06.01212.06.02m m A I A I I IIa II II zCII IaI I zCI z -⋅⨯=⎪⎪⎭⎫ ⎝⎛⨯⨯+⨯+⨯⨯+⨯=+++= 截面对y 0轴的惯性矩为4243300010242.0)122.04.0126.012.0(m m I I I IIy Iy y -⨯=⨯+⨯+=二、计算题求图所示箱形截面对其对称轴z 的惯性矩Iz 。

解：可将箱形看作由大矩形减去小矩形组合而成，大、小矩形都关于z 轴对称，所以121233bh BH I I I z z z -=＝－小大三、计算题试求图中所示截面图形对形心轴的惯性矩。

解：此图形为矩形截面中挖去—圆形截面，计算时可把圆形看成负的面积。

c点为图形的箱形截面c1形心，选y c ，z 轴为参考坐标轴，由于y c 为组合图形的对称轴，所以有0=z 。

材料力学大作业-组合截面几何性质计算

材料力学 截面几何特性

材料力学 截面的几何性质

材料力学—截面几何性质

(材料力学)截面几何性质习题及参考答案

截面几何特性怎么计算公式

截面几何性质 (材料力学)

材料力学第四章截面的几何性质

组合截面计算

材料力学 截面的几何性质

材料力学 第9章 截面的几何性质

材料力学 附录Ⅰ截面的几何性质

截面几何性质材料力学

《材料力学》附录I 截面的几何性质 习题解

材料力学大作业-组合截面几何性质计算

【工程力学】截面几何性质【工程类精品资料】

材料力学截面几何特性

材料力学截面的几何性质

材料力学截面的几何性质

材料力学第9章截面的几何性质

材料力学附录Ⅰ截面的几何性质

《材料力学》附录I 截面的几何性质习题解