L形截面—截面几何性质计算
第三章 截面几何特征

(2)求形心:
yc
A y
i 1 n i
n
i
A
i 1
A 600 30 300 5 Ⅰy CⅠ A Ⅱ y cⅡ 21.67m m A A 600 300 Ⅰ Ⅱ
i
zc
A z
i 1 n i
n
i
A
i 1
A 600 5 300 25 Ⅰz CⅠ A Ⅱ z cⅡ 11.67m m A A 600 300 Ⅰ Ⅱ
第三章 截面的几何性质
一、 截面的形心和静矩
1、 截面的静矩
静矩是对一定轴而言的,同一截面对不 同坐标轴的静矩是不同的。静矩可能为正 值或负值,也可能为0,其常用单位是m3 或mm3。
* SZ ydA A
S* y zdA
A
组合截面的静矩等于各组成部分对于该轴静矩代数和
S Z Ai yi
IZ
因为
2 2 y dA ( y a ) dA c
A
A
2 2 y dA 2 a y dA a c c dA
A
A
A
A
y c2 dA 为截面形心轴惯性矩
y c dA
A
为截面对形心轴的静矩,其值为零
I Z I zc a 2 A
故上式简化为
I y I yc b 2 A I yz I yczc abA
A
惯性矩恒为正值,其常用的单位是m4和mm4
矩形截面
bh3 IZ 12
hb3 Iy 12
圆形截面
IZ I y
D4
64
第三章 截面的几何性质
第七章 截面的几何性质

A 120 ×10 × 60 + 70 ×10 × 5 = = 39.7mm 120 ×10 + 70 ×10
yc =
Sy
5
§7-2 惯性矩、惯性积与极惯性 惯性矩、
一、惯性矩
Iz = ∫ y dA
2 A
I y = ∫ z dA
2 A
工程中常把惯性矩表示为平面图形的面积与某一长度平方的乘积, 即
I y = A iy
主惯性轴和主惯性矩
一、主惯性轴和主惯性矩 (1)主惯性轴 主惯性轴 当平面图形对某一对正交坐标轴z0 、
y0的惯性积 Iz0y0=0时,则坐标轴 z0 、y0称为主惯性轴。 因此,具有一个或两个对称轴的正交坐标轴一定是 平面图形的主惯性轴。 (2)主惯性矩 平面图形对任一主惯性轴的惯性矩称为 主惯性矩 主惯性矩。
例 计算图所示阴影部分截面的形心主惯性矩Iz。
解:1)求形心位置 由于y 轴为对称轴,故形心必在 此轴上,建立yoz′坐标系,故zc′=0 。将阴影部分截面看成是矩形Ⅰ 减去圆形Ⅱ而得到,故其形心的yc 坐标为:
15
ΣAi y ci yc = =( A
600 × 1000 × 500 − 600 × 1000 −
2
I z = Aiz
2
6
i y 、i z
分别称为平面图形对y轴和z轴的惯性半径
二、惯性积
I zy = ∫ A zydA
若截面具有一根对称轴,则该 截面对于包括此对称轴在内的 二正交坐标轴的惯性积一定等 于零。
I zy = 0
7
三、极惯性矩
Ip =
2
∫A
ρ dA
2
2 2
Qρ = z + y
立体几何中的截面(解析版)
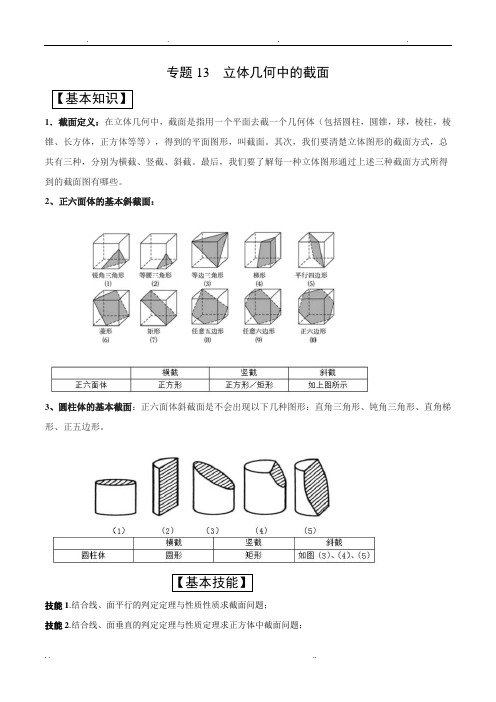
专题13 立体几何中的截面【基本知识】1.截面定义:在立体几何中,截面是指用一个平面去截一个几何体(包括圆柱,圆锥,球,棱柱,棱锥、长方体,正方体等等),得到的平面图形,叫截面。
其次,我们要清楚立体图形的截面方式,总共有三种,分别为横截、竖截、斜截。
最后,我们要了解每一种立体图形通过上述三种截面方式所得到的截面图有哪些。
2、正六面体的基本斜截面:3、圆柱体的基本截面:正六面体斜截面是不会出现以下几种图形:直角三角形、钝角三角形、直角梯形、正五边形。
【基本技能】技能1.结合线、面平行的判定定理与性质性质求截面问题;技能2.结合线、面垂直的判定定理与性质定理求正方体中截面问题;技能3.猜想法求最值问题:要灵活运用一些特殊图形与几何体的特征,“动中找静”:如正三角形、正六边形、正三棱锥等;技能4.建立函数模型求最值问题:①设元②建立二次函数模型③求最值。
例1 一个正方体接于一个球,过这个球的球心作一平面,则截面图形不可能...是( )分析 考虑过球心的平面在转动过中,平面在球的接正方体上截得的截面不可能是大圆的接正方形,故选D 。
例2 如图,在透明的塑料制成的长方体ABCD-A 1B 1C 1D 1容器灌进一些水,固定容器底面一边BC 于地面上,再将容器倾斜,随着倾斜程度的不同,有下列四个命题:① 水的部分始终呈棱柱状; ② 水面EFGH 的面积不改变; ③ 棱A 1D 1始终与水面EFGH 平行;④ 当容器倾斜到如图5(2)时,BE·BF 是定值; 其中正确的命题序号是______________分析 当长方体容器绕BC 边转动时,盛水部分的几何体始终满足棱柱定义,故①正确;在转动过程中EH//FG ,但EH 与FG 的距离EF 在变,所以水面EFGH 的面积在改变,故②错误;在转动过程中,始终有BC//FG//A 1D 1,所以A 1D 1//面EFGH ,③正确;当容器转动到水部分呈直三棱柱时如图5(2),因为BC BF BE V ⋅⋅=21水是定值,又BC 是定值,所以BE·BF 是定值,即④正确。
材料力学 截面的几何性质

1、矩形截面 h
Iz
y2dA
A
2 h
y 2bdy
h
2
dy y
b y 3 2 1 bh3 3 h 12
2
同理
Iy
z2dA 1
A
12
hb3
b h z
y
26
2、实心圆截面
y
已知
IP
A2dA
D 4 32
D
z
则 I P A2 d A A y 2 d A A z 2 d I A z I y
A
Iz Iy
此式说明了极惯性矩与轴惯性矩之间的关系。
z
y
o
A dA
z
y
惯性积
定义
Iyz
yzdA
A
z y
A dA
为图形对y、z轴的惯性积 。
z
o
y
惯性积的数值可正,可负,也可为零。惯性积的量纲是[长 度]4 ,常用单位为m4和mm4。
定理:若有一个轴是图形的对称轴,则图形对这对轴 的惯性积必然为零。
4.3 形心主惯性轴和形心主惯性矩
若主惯性轴通过形心,则该轴称为形心主惯性轴(principal centroidal axis)。
图形对形心主惯性轴的惯性矩称为形心主惯性矩。 由于图形对于对称轴的惯性积等于零,而对称轴又过形心,所以,图形 的对称轴就是形心主惯性轴。
形心主惯性轴的特点可归纳为以下几点: ⑴形心主惯性轴是通过形心,由角定向的一对互 相垂直的坐标轴。
32
32
圆环形对y(或z)轴的惯性矩为
IyIz1 2Ip6 D4414
由于y轴为对称轴,故
Iyz 0
z
y
d D
ansys apdl l型梁截面类型

一、概述ANSYS APDL(ANSYS Parametric Design Language)是一种强大的有限元分析软件,常用于工程领域进行结构、流体、热力、电磁等多物理场耦合分析。
在结构分析中,L型梁截面类型是一种常见的横截面形状,具有较好的承载能力和刚度。
本文将讨论在ANSYS APDL中如何使用L型梁截面类型进行结构分析。
二、L型梁截面类型的定义1. L型梁截面的特点L型梁截面通常由一块主梁和一块翼板组成,形状类似英文字母“L”。
主梁的截面通常为矩形或者工字形,翼板则位于主梁的一侧,用于增加截面面积和提高截面的抗弯能力。
L型梁截面在工程实践中被广泛应用,例如建筑结构、桥梁、机械设备等领域。
2. L型梁截面类型的参数在ANSYS APDL中,可以通过定义L型梁截面类型的参数来描述其几何形状和材料性质。
常见的参数包括主梁的宽度和高度、翼板的宽度和高度、横向剪切连接的刚度等。
这些参数将直接影响到L型梁截面的受力性能,因此在进行结构分析时需要对其进行合理的设定。
三、在ANSYS APDL中创建L型梁截面类型1. 参数化定义在ANSYS APDL中,可以通过PARAM命令来定义L型梁截面类型的参数。
通过参数化定义,可以方便地对梁截面进行调整,使其适应不同的工程需求。
可以定义主梁的宽度为W,高度为H,翼板的宽度为B,高度为D,从而形成一个L型梁截面类型的参数化模型。
2. 几何建模通过ANSYS APDL的几何建模功能,可以根据上述参数化定义创建具体的L型梁截面模型。
可以采用命令行方式进行建模,也可以通过预定义的几何图形进行快速建模。
在建模过程中,需要注意模型的对称性和材料性质的设置,以保证分析结果的准确性。
3. 材料属性定义在进行结构分析之前,需要对L型梁截面的材料属性进行定义。
可以通过MATERIAL命令来指定材料类型、弹性模量、泊松比、屈服强度等参数。
这些材料属性将直接影响到梁截面的受力性能,因此需要根据实际情况进行合理的设定。
材料力学截面的几何性质课件

目录
• 截面的基本性质 • 截面的二次矩 • 截面的抗弯截面系数 • 截面的抗扭截面系数 • 材料力学截面的应用
01 截面的基本性质
截面的面积
面积
截面面积是二维平面图形被截后,与 原图形相比增加的面积。对于矩形、 圆形、三角形等简单形状,截面面积 可以通过几何公式直接计算。
的刚度和稳定性。
截面惯性矩
截面惯性矩是衡量截面抗弯刚度 的指标,对于承受弯矩的构件, 选择具有较大惯性矩的截面可以
减少挠度和转角。
截面抵抗矩
截面抵抗矩是衡量截面抗剪切能 力的指标,对于承受剪力的构件 ,选择具有较大抵抗矩的截面可
以增加构件的承载能力。
工程设计中的应用
桥梁设计
在桥梁设计中,需要考虑梁的截面尺寸、材料类型和截面形式等 因素,以确保桥梁具有足够的强度和刚、单位等因素,以确保数 据处理结果的准确性和可靠性。
1.谢谢聆 听
根据微面积和其对应的主 轴方向余弦,计算出截面 二次矩。
主轴的确定
根据计算出的惯性矩,找 出三个主轴的方向余弦和 角度。
实例分析
圆截面
圆截面的二次矩为常数, 且各主轴与截面垂直,说 明圆截面在弯曲时没有翘 曲的趋势。
矩形截面
矩形截面的二次矩与宽度 的平方成正比,说明矩形 截面有较好的抗弯能力。
工字形截面
工字形截面的二次矩比同 样面积的矩形截面小,但 抗弯能力仍高于同样重量 的实心杆件。
03 截面的抗弯截面系数
定义与性质
01
抗弯截面系数是截面对其轴线的惯性矩除以截面的面积 得到的数值,用来度量截面在弯矩作用下抵抗变形的能 力。
02
不同形状的截面有不同的抗弯截面系数,如圆截面为1 ,矩形截面为1.13,工字形截面为1.44等。
立体几何中的截面(解析版)

专题13 立体几何中的截面【基本知识】1.截面定义:在立体几何中,截面是指用一个平面去截一个几何体(包括圆柱,圆锥,球,棱柱,棱锥、长方体,正方体等等),得到的平面图形,叫截面。
其次,我们要清楚立体图形的截面方式,总共有三种,分别为横截、竖截、斜截。
最后,我们要了解每一种立体图形通过上述三种截面方式所得到的截面图有哪些。
2、正六面体的基本斜截面:3、圆柱体的基本截面:正六面体斜截面是不会出现以下几种图形:直角三角形、钝角三角形、直角梯形、正五边形。
【基本技能】技能1.结合线、面平行的判定定理与性质性质求截面问题;技能2.结合线、面垂直的判定定理与性质定理求正方体中截面问题;技能3.猜想法求最值问题:要灵活运用一些特殊图形与几何体的特征,“动中找静”:如正三角形、正六边形、正三棱锥等;技能4.建立函数模型求最值问题:①设元②建立二次函数模型③求最值。
例1 一个正方体内接于一个球,过这个球的球心作一平面,则截面图形不可能...是()分析考虑过球心的平面在转动过中,平面在球的内接正方体上截得的截面不可能是大圆的内接正方形,故选D。
例2 如图,在透明的塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜程度的不同,有下列四个命题:①水的部分始终呈棱柱状;②水面EFGH的面积不改变;③棱A1D1始终与水面EFGH平行;④当容器倾斜到如图5(2)时,BE·BF是定值;其中正确的命题序号是______________分析当长方体容器绕BC边转动时,盛水部分的几何体始终满足棱柱定义,故①正确;在转动过程中EH//FG,但EH与FG的距离EF在变,所以水面EFGH的面积在改变,故②错误;在转动过程中,始终有BC//FG//A1D1,所以A1D1//面EFGH,③正确;当容器转动到水部分呈直三棱柱时如图5(2),因为BCBFBEV⋅⋅=21水是定值,又BC是定值,所以BE·BF是定值,即④正确。
强基专题--立体几何中的截面问题

强基专题3 立体几何中的截面问题
[跟进训练]
1.(2021·重庆模拟)在三棱锥 P-ABC 中,PA,PB,PC 两两垂直,
PA=3,PB=4,PC=5,点 E 为线段 PC 的中点,过点 E 作该三棱
锥外接球的截面,则所得截面圆的面积不可能为( )
A.6π
B.8π
C.10π
D.12π
1234 5
(2)当π2<θ<π时,0<α<θ<π,此时sin θ<1,sin α可以取到最 大值1,
此时过圆锥母线的截面面积最大,最大值为S=12l2.
1234 5
强基专题3 立体几何中的截面问题
综上所述,过圆锥母线的截面面积的最大值与轴截面顶角θ的范 围有关,
当0<θ≤π2时,轴截面面积最大,最大值为S=12l2sin θ. 当π2<θ<π时,过圆锥母线的截面面积最大,最大值为S=12l2.
同理 FG∥EH,所以四边形 EFGH 为平行四边形,又 AD⊥BC, 所以四边形 EFGH 为矩形.
1234 5
强基专题3 立体几何中的截面问题
由相似三角形的性质得BECF=AACF,FACC=AFDG, 所以BECF+FAGD=AACF+FACC,BC=AD=2, 所以 EF+FG=2,所以四边形 EFGH 的周长为定值 4,S 四边形 EFGH =EF×FG≤EF+2 FG2=1, 所以四边形 EFGH 的面积有最大值 1.故选 B.]
1 2
l2sin θ.截面VCD的面积S′=12l2sin α.在△V强基专题3 立体几何中的截面问题
(1)当0<θ≤π2时,0<α<θ≤π2,sin α<sin θ⇒S′<S,此时过圆 锥母线的截面面积最大为轴截面面积S=12l2sin θ.
截面形状及相应面积的求法 (1)结合线、面平行的判定定理与性质定理求截面问题; (2)结合线、面垂直的判定定理与性质定理求正方体中截面问题; (3)猜想法求最值问题:“要灵活运用一些特殊图形与几何体的 特征,“动中找静”,如正三角形、正六边形、正三棱锥等; (4)建立函数模型求最值问题:①设元;②建立二次函数模型; ③求最值.
人教A版高考总复习一轮文科数学精品课件 第8章立体几何 指点迷津(八) 空间几何体的截面问题 (2)

所以截面面积为
+
S= 2
·h=
2+2 2
2
×
3 2
2
=
2 2
)
2
9
.故选
2
B.
=
9
2
=
3 2
,
2
本 课 结 束
是棱C1C的中点,则过线段AG且平行于平面A1EF的截面图形为(
A.矩形
B.三角形
C.正方形
D.等腰梯形
)
答案:D
解析:取BC的中点H,连接AH,GH,由题意得GH∥EF,AH∥A1F,
又GH⊄平面A1EF,EF⊂平面A1EF,
∴GH∥平面A1EF,同理AH∥平面A1EF,
又GH∩AH=H,GH,AH⊂平面AHG,
α∥平面A1BC1或者α与平面A1BC,BC,CC1,C1D1,D1A1,A1A的中点为E,F,G,H,K,L,易证点
E,F,G,H,K,L共面.则正六边形EFGHKL平行于平面A1BC1.
由 KH
1
A1C1,得
2
KH=
2
,
2
正六边形 EFGHKL 的面积
第八章
指点迷津(八) 空间几何体的截面问题
空间几何体的截面问题
用平面去截一个几何体,所截出的面叫做截面.我们可以想象,类似于用刀
去切(截)几何体,把几何体分成两部分,刀在几何体上留下的痕迹就是截面
的形状,截面是一个平面图形.空间几何体的截面问题涉及平面的基本事实、
空间线面的位置关系、点线共面、线共点等问题,综合性较强,对直观想象
和逻辑推理的数学素养有着较高的要求.
高考数学复习考点题型专题讲解18 几何体的截面或交线

高考数学复习考点题型专题讲解专题18 几何体的截面或交线1.空间几何体截面的作图主要原理:两个基本事实及两个性质.两个基本事实为:(1)如果两个不重合的平面有一个公共点,那么它们相交于过此点的一条直线;(2)如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内. 两个性质为:(1)如果一条直线平行于一个平面,经过这条直线的平面与这个平面相交,那么这条直线就和交线平行;(2)如果两个平面平行,第三个平面和它们相交,那么两条交线平行.2.立体几何中的截面类型(1)平面截球:圆面(见专题17).(2)平面截正方体:三角形、四边形、五边形、六边形.(3)平面截圆柱曲面:圆、椭圆、矩形.(4)平面截圆锥曲面:椭圆、双曲线、抛物线.类型一截面的作法空间几何体的截面作图主要作法:(1)直接法;(2)平行线法;(3)延长法;(4)辅助平面法.例1 已知正方体A1B1C1D1-ABCD,E,F,H分别是A1B1,B1C1,AD的中点,试过三点E,F,H作截面.解如图,连接EF,并且延长,与D1A1,D1C1的延长线分别交于N,R两点,连接NH并延长分别交AA1和D1D的延长线于S,T,连接TR分别交CD,CC1于M,G,顺次连接点E,F,G,M,H,S,E,则六边形EFGMHS就是所作截面.训练1 如图,在正方体ABCD-A1B1C1D1中,E,F,G分别在AB,BC,DD1上,求作过E,F,G三点的截面.解作法:①在底面AC内,过E,F作直线EF,分别与DA,DC的延长线交于L,M.②在侧面A1D内,连接LG交AA1于K.③在侧面D1C内,连接GM交CC1于H.④连接KE,FH,则五边形EFHGK即为所求的截面.类型二截面形状的判断首先根据条件作出相应的截面图形,再结合线面的位置关系的判定与性质加以分析,得到截面图形所满足的特征性质,确定其形状.例2 如图,在正方体ABCD-A1B1C1D1中,点E,F分别是棱B1B,B1C1的中点,点G是棱C 1C的中点,则过线段AG且平行于平面A1EF的截面图形为( )A.矩形B.三角形C.正方形D.等腰梯形答案 D解析取BC的中点H,连接AH,GH,AD1,D1G,由题意得GH∥EF,AH∥A1F,又GH⊄平面A1EF,EF⊂平面A1EF,所以GH∥平面A1EF,同理AH∥平面A1EF,又GH∩AH=H,GH,AH⊂平面AHGD1,所以平面AHGD1∥平面A1EF.故过线段AG 且与平面A 1EF 平行的截面图形为四边形AHGD 1,显然为等腰梯形. 训练2(多选)(2022·苏北四市调研)已知正方体ABCD -A 1B 1C 1D 1的棱长为a ,点E ,F ,G 分别为棱AB ,AA 1,C 1D 1的中点.下列结论中正确是( )A.过E ,F ,G 三点作正方体的截面,所得截面为正六边形B.B 1D 1∥平面EFGC.BD 1⊥平面ACB 1D.异面直线EF 与BD 1所成角的正切值为22答案 ACD解析 对于A ,因为E ,F ,G 为棱AB ,AA 1,C 1D 1的中点,设A 1D 1的中点为M ,BC 的中点为N ,CC 1的中点为P ,连接点M ,F ,E ,N ,P ,G 可得截面为正六边形,所以A 正确; 对于B ,通过以DA 为x 轴,DC 为y 轴,DD 1为z 轴建立空间直角坐标系,求出B 1D 1→,平面EFG 法向量n 1,可推出B 1D 1→·n 1≠0,故B 1D 1与平面EFG 不平行,所以B 错误; 对于C ,同上建系,求出BD 1→,平面ACB 1的法向量n 2,可推得BD 1→=λn 2,所以BD 1⊥平面ACB 1,所以C 正确;对于D ,同上建系,求出EF →,BD 1→,设夹角为θ, 则cos θ=|EF →·BD 1→||EF →|·|BD 1→|,由sin 2θ+cos 2θ=1,tan θ=sin θcos θ,得tan θ=22,所以D 正确.类型三截面图形面积或周长的计算求截面图形的面积的前提是确定截面的形状,转化为平面图形求解.例3 (1)(2022·济南模拟)已知正四面体ABCD的棱长为2,平面α与棱AB,CD均平行,则α截此正四面体所得截面面积的最大值为( )A.1B.2C.3D.2(2)在三棱锥P-ABC中,PB=6,AC=3,G为△PAC的重心,过点G作三棱锥的一个截面,使截面平行于直线PB和AC.则截面的周长为________.答案(1)A (2)8解析(1)如图,设E为棱BC上任一点,且BE→=λBC→,λ∈(0,1),过E作EF∥AB交AC于F,作EN∥CD交BD于N,过F作FM∥CD交AD于M,连接MN,则四边形EFMN即平面α截四面体ABCD所得的截面,所以EFAB=ECBC=1-λ,所以EF=2(1-λ),同理可得EN=2λ. 又四面体ABCD为正四面体,所以AB⊥CD,所以EF⊥EN,截面EFMN为矩形,且EN+EF=2,则矩形EFMN 的面积S =EF ·EN ≤⎝⎛⎭⎪⎫EF +EN 22=1, 当且仅当EF =EN =1,即λ=12时,“=”成立,故选A.(2)过点G 作EF ∥AC 分别交PA ,PC 于点E ,F ,过E ,F 分别作EN ∥PB ,FM ∥PB ,分别交AB ,BC 于点N ,M ,连接MN ,∴四边形EFMN 是平行四边形,∴EF 3=23,即EF =MN =2, FM PB =FM 6=13,即FM =EN =2, ∴截面的周长为2×4=8.训练3 如图,在棱长为1的正方体ABCD -A 1B 1C 1D 1中,M ,N 分别是A 1D 1,A 1B 1的中点,过直线BD 的平面α∥平面AMN ,则平面α截该正方体所得截面的面积为( )A.2B.98C.3D.62答案 B解析 如图1,分别取B 1C 1,C 1D 1的中点E ,F ,连接EF ,BE ,DF ,B 1D 1,ME , 易知EF ∥B 1D 1∥BD ∥MN ,AB ∥ME ,AB =EM , 所以四边形ABEM 为平行四边形, 则AM ∥BE ,又BD 和BE 为平面BDFE 内的两条相交直线,所以平面AMN ∥平面BDFE ,即平面BDFE 为平面α,BD =2,EF =12B 1D 1=22,得四边形BDFE 为等腰梯形,DF =BE =52,在等腰梯形BDFE (如图2)中,过E ,F 作BD 的垂线,垂足分别为G ,H ,则四边形EFGH 为矩形, ∴其高FG =DF 2-DG 2=54-18=324, 故所得截面的面积为12×⎝ ⎛⎭⎪⎫22+2×324=98.一、基本技能练1.过一个圆锥的侧面一点(不是母线的端点)作圆锥的截面,则截面与该圆锥侧面的交线可以是图形①圆;②椭圆;③抛物线的一部分;④双曲线的一部分中的( )A.①②③④B.①③④C.①②D.①②④答案 A解析根据截面与圆锥的位置关系,所得的图形如图所示,故截面与该圆锥侧面的交线可以是图形①圆;②椭圆;③抛物线的一部分;④双曲线的一部分.2.如图是正方体或四面体,P,Q,R,S分别是所在棱的中点,则这四个点不共面的一个图是( )答案 D解析对于A,PS∥QR,故P,Q,R,S四点共面;同理,B、C图中四点也共面;D中四点不共面.3.如图,长方体ABCD-A′B′C′D′中被截去一小部分,其中EH∥A′D′.剩下的几何体是( )A.棱台B.四棱柱C.五棱柱D.六棱柱答案 C解析∵EH∥A′D′,EH∥平面BCC′B′,∴EH∥GF,又平面ABB′A′∥平面DCC′D′,∴EF∥GH,四边形EFGH为平行四边形.故剩下的几何体为五棱柱.4.在正方体ABCD-A1B1C1D1中,M,N分别是棱DD1和BB1上的点,MD=13DD1,NB=13BB1,那么正方体的过M,N,C1的截面图形是( )A.三角形B.四边形C.五边形D.六边形答案 C解析正方体ABCD-A1B1C1D1中,M、N分别是棱DD1和BB1上的点,MD=13DD1,NB=13BB1,延长C1M交CD的延长线于P,延长C1N交CB的延长线于Q,连接PQ交AD于E,AB于F,连接NF,ME,则正方体的过M,N,C1的截面图形是五边形.故选C.5.在棱长为a的正方体ABCD-A1B1C1D1中,点E,F,G分别为棱AB,CC1,C1D1的中点,则该正方体被过E,F,G三点的平面截得的截面面积为( )A.34a2B.32a2C.334a2D.332a2答案 C解析作出过E,F,G三点的截面,如图,由图可知,截面为正六边形,且边长为22a,所以截面面积S=6×12×32×⎝⎛⎭⎪⎫22a2=334a2,故选C.6.若平面α截三棱锥所得截面为平行四边形,则该三棱锥中与平面α平行的棱有( )A.0条B.1条C.2条D.1条或2条答案 C解析如图所示,平面α即平面EFGH,则四边形EFGH为平行四边形,则EF∥GH.∵EF⊄平面BCD,GH⊂平面BCD,∴EF∥平面BCD.又∵EF⊂平面ACD,平面BCD∩平面ACD=CD,∴EF∥CD.又EF⊂平面EFGH,CD⊄平面EFGH.∴CD∥平面EFGH,同理,AB∥平面EFGH.所以与平面α(平面EFGH)平行的棱有2条.7.(2022·重庆诊断)在棱长为4的正方体ABCD-A1B1C1D1中,点M为B1C1的中点,过点D 作平面α使α⊥BM,则平面α截正方体所得截面的面积为( )A.42B.4 5C.85D.16 2答案 C解析分别取AA1,BB1的中点E,N,连接DE,CN,EN,则EN∥DC,EN=DC,所以四边形ENCD是平行四边形,由于△B1BM≌△BCN,所以∠MBB1+∠BNC=90°,所以BM⊥CN,又因为DC⊥BM,DC∩CN=C,所以BM⊥平面ENCD,所以平面ENCD即为平面α,又CN=25,所以截面的面积为25×4=8 5.8.(2022·南通调研)已知正方体ABCD-A1B1C1D1的棱长为2,M为CC1的中点,若AM⊥平面α,且B∈平面α,则平面α截正方体所得截面的周长为( )A.32+25B.4+4 2C.22+25D.6 2答案 A解析正方体ABCD-A1B1C1D1中,BD⊥AC,所以BD⊥AM(三垂线定理),如图,取BB1中点N,A1B1中点E,连接MN,AN,BE,可知BE⊥AN,所以BE⊥AM(三垂线定理),所以AM⊥平面DBE,取A1D1中点F,则α即为截面BEFD,易求周长为32+2 5.9.(多选)如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,过对角线BD1的一个平面交棱AA1于点E,交棱CC1于点F,得四边形BFD1E,在以下结论中,正确的是( )A.四边形BFD1E有可能是梯形B.四边形BFD1E在底面ABCD内的投影一定是正方形C.四边形BFD1E有可能垂直于平面BB1D1DD.四边形BFD1E面积的最小值为6 2答案BCD解析对于选项A,过BD1,作平面与正方体ABCD-A1B1C1D1的截面为四边形BFD1E,如图所示,因为平面ABB1A1∥平面DCC1D1,且平面BFD1E∩平面ABB1A1=BE,平面BFD1E∩平面DCC1D1=D1F,所以BE∥D1F,同理D1E∥BF.故四边形BFD1E为平行四边形,因此A错误;对于选项B,四边形BFD1E在底面ABCD内的投影一定是正方形ABCD,因此B正确;对于选项C,当点E,F分别为AA1,CC1的中点时,EF⊥平面BB1D1D,又EF⊂平面BFD1E,则平面BFD1E⊥平面BB1D1D,因此C正确;对于选项D,当F点到线段BD1的距离最小时,平行四边形BFD1E的面积最小,此时点E,F分别为AA1,CC1的中点,此时最小值为12×2×3=62,因此D 正确.故选BCD.10.(多选)(2022·石家庄模拟)在正方体ABCD -A 1B 1C 1D 1中,P 是面对角线BD 上的动点,Q 是棱C 1D 1的中点,用过A 1,P ,Q 三点的平面截正方体ABCD -A 1B 1C 1D 1,则所得截面多边形可能是( )A.三角形B.四边形C.五边形D.六边形 答案 ABC解析 如图①,当点P 与点D 重合时,截面多边形是三角形,选项A 满足题意;图①图②如图②,取棱CD 的中点Q 1,连接QQ 1和AQ 1, 因为Q 是棱C 1D 1的中点,所以QQ1∥DD1∥AA1,将点P移动到平面AA1QQ1与BD交点处,此时截面多边形是四边形,选项B满足题意;图③如图③,令点P距离点B较近,此时截面多边形是五边形,选项C满足题意;易知点P无论如何移动,截面与平面ABCD的交线都平行于A1Q,所以这条交线只能与正方形ABCD的边AB,AD之一有交点(顶点A除外),则截面不可能与正方形ABB1A1和正方形ADD1A1都有交线(棱AA1除外),所以截面不可能与正方体的六个面都有交线,则截面多边形不能是六边形,所以选项D不满足题意.故选ABC.11.如图是长方体被一平面所截得的几何体,四边形EFGH为截面,则四边形EFGH的形状为________.答案平行四边形解析∵平面ABFE∥平面DCGH,又平面EFGH∩平面ABFE=EF,平面EFGH∩平面DCGH=HG,∴EF∥HG.同理EH∥FG,∴四边形EFGH是平行四边形.12.(2022·衡水模拟)在棱长为1的正方体ABCD-A1B1C1D1中,E为棱CD的中点,过B,E,D的截面与棱A1B1交于F,则截面BED1F分别在平面A1B1C1D1和平面ABB1A1上的正投影1的面积之和为________.答案 1解析因为平面BED1F∩平面ABCD=BE,平面BED1F∩平面A1B1C1D1=D1F,平面A1B1C1D1∥平面ABCD,所以BE∥D1F,同理D1E∥BF,所以截面BED1F是平行四边形,所以BE=D1F,所以A1F=CE,从而B1F=DE,截面BED1F在平面A1B1C1D1上的正投影是以B1F为底,该底对应的高为1的平行四边形,在平面ABB1A1上的正投影是以A1F为底,该底上的高为1的平行四边形,因此两个投影的面积和S=(CE+DE)×1=1为定值.二、创新拓展练13.(2022·浙江五校联考)如图,正三棱柱ABC-A1B1C1的高为4,底面边长为43,D是B1C1的中点,P是线段A1D上的动点,过BC作截面α⊥AP于点E,则三棱锥P-BCE体积的最小值为( )A.3B.2 3C.43D.12答案 C解析如图,取BC的中点F,连接FD,FA,FE,FP,过点E作EH⊥AF于点H,则BC⊥平面AFDA1,所以BC⊥EH,AF∩BC=F,所以EH⊥平面ABC.因为AF=6,且V P-ABC=13×123×4=163=V P-EBC+V E-ABC,所以当三棱锥E-ABC体积最大时,三棱锥P-BCE体积最小.因为AE⊥EF,所以AE2+EF2=AF2=36≥2AE·EF,所以AE·EF≤18.设三棱锥E-ABC的高为h,由AE·EF=AF·h,得h=AE·EFAF≤3,因为V E-ABC=13×S△ABC×h=43h,所以(V E-ABC)max=123,所以(V P-EBC)min=43,故选C.14.(多选)如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题中正确的是( )A.当0<CQ<12时,S为四边形B.当CQ=12时,S为等腰梯形C.当CQ=34时,S与C1D1的交点R满足C1R=13D.当34<CQ<1时,S为六边形答案ABC解析如图1,当Q为CC1的中点,即CQ=12时,PQ∥BC1且PQ=12BC1,图1 又AD1綊BC1,故PQ ∥AD 1且PQ =12AD 1,PA =D 1Q ,故截面APQD 1为等腰梯形,故B 正确;当0<CQ <12时,只需在DD 1上取点M 使PQ ∥AM ,即可得截面APQM 为四边形,故A 正确;当CQ =34时,延长AP ,DC 交于M ,连接QM ,直线QM 与C 1D 1交于点R ,如图2,因CQ =34,则C 1Q =14,CS =1,又C 1R CM =C 1Q QC ,故C 1R =13,选项C 正确;图2当34<CQ <1时,S 为五边形,D 错误. 15.(多选)(2022·烟台调研)如图,在长方体ABCD -A 1B 1C 1D 1中,AB =BC =1,AA 1=2,M 为AA 1的中点,过B 1M 作长方体的截面α交棱CC 1于点N ,则下列说法正确的是( )A.截面α可能为五边形B.存在点N ,使得BN ⊥截面αC.若截面α为平行四边形,则1≤CN ≤2D.当点N与点C重合时,截面面积为36 4答案ACD解析选项A,设P为CC1的中点,当N在PC1之间时,截面α为平行四边形NQMB1,当N在PC之间时,截面α为五边形N1Q1GMB1,其中NQ∥B1M,N1Q1∥B1M,故选项A,C正确;若BN⊥截面α,则BN⊥B1M,这显然是不成立的,因为如果成立,可以推出B1M⊥平面BB1C1C,显然错误,故选项B错误;当点N与点C重合时,截面为梯形CGMB1,易知G为AD的中点.易求CG=GM=52,MC=3,MB1=2,B1C=5,所以CM⊥B1M,△CGM为等腰三角形,故S=S△CGM+S△CMB1=12×3×22+12×3×2=364,故选项D正确.故选ACD.16.(多选)(2022·南京师大附中模拟)如图,圆柱的底面半径和高均为1,线段AB是圆柱下底面的直径,点O是下底面的圆心.线段EF是圆柱的一条母线,且EO⊥AB.已知平面α经过A,B,F三点,将平面α截这个圆柱所得到的较小部分称为“马蹄体”.记平面α与圆柱侧面的交线为曲线C,则( )A.曲线C是椭圆的一部分B.曲线C是抛物线的一部分C.二面角F-AB-E的大小为π4D.马蹄体的体积为V满足13<V<π4答案ACD解析将相同的圆柱按如图方式拼接在一起,将两个球放入圆柱内,使每一个球既与圆柱相切,又与曲线C所在平面相切,球与曲线C的切点为Q,R,取曲线C上一点P,过P点的圆柱母线与两球交于M,N两点,由于PM,PR同是下面球的切线,PN,PQ同是上面球的切线,可得PM=PR,PN=RQ,则PR+PQ=PM+PN=MN>QR,由椭圆定义知:曲线C是椭圆的一部分,A正确;B错误;连接OF,由EO⊥AB,EF⊥AB,知AB⊥平面EOF,故OF⊥AB,则∠FOE为二面角F-AB-E的平面角,又OE=EF=1,则∠FOE=π4,C正确;由补成的几何体知马蹄体的体积为V小于圆柱体的14,即为V<π4,又V F-AEB=13×12×2×1×1=13,所以V>13,所以13<V<π4,D正确.故选ACD.17.(2022·广州模拟)四棱锥P-ABCD各顶点都在球心为O的球面上,且PA⊥平面ABCD,底面ABCD为矩形,PA=AB=2,AD=4,设E,F分别是PB,BC的中点,则球O被平面AEF所截得的截面面积为________.答案14π3解析由题可知PC的中点即为球心O,故球的半径R=12+12+22=6,设球心O到平面AEF的距离为d,截面圆的半径为r.由题意可知球心O到平面AEF的距离等于点B到平面AEF的距离,在三棱锥B-AEF中,由等体积法可得d=23 3,故r2=R2-d2=143,故截面面积S=πr2=14π3.18.(2022·武汉三模)已知正方体ABCD-A1B1C1D1的棱长为1,点P在线段CB1上,若平面α经过点A,C1,P,则它截正方体ABCD-A1B1C1D1所得的截面的周长最小值为________.答案2 5解析当点P靠近点C或与点C重合时,A,C1,P三点确定的平面α如图①所示,图①因为平面ADD1A1∥BCC1B1,所以AE∥QC1,同理AQ∥EC1,所以四边形AEC1Q是平行四边形,即为所求的截面,设D1E=x(0≤x≤1),则A1E=1-x,所以AQ=EC1=x2+1,QC1=AE=(1-x)2+1,AQ+AE=x2+1+(1-x)2+1=(x-0)2+(0-1)2+(x-1)2+(0-1)2,可以看作R(x,0)到M(0,1)和N(1,1)距离之和的最小值,M(0,1)关于x轴的对称点为M′(0,-1),连接M′N,其长度即AQ+AE的最小值,由勾股定理得|M′N|=5,所以周长的最小值为2 5.图②当点P靠近点B1或与点B1重合时,A,C,P三点确定的平面α如图②所示,因为平面ADD1A1∥BCC1B1,1所以AE∥QC1,同理AQ∥EC1,所以四边形AEC1Q是平行四边形,即为所求的截面,同理,所求周长的最小值为2 5.综上所述,周长的最小值为2 5.。
L形截面性质计算

L形截面性质计算L形截面是一种常见的结构形状,具有较好的抗弯强度和刚度。
在进行L形截面性质计算时,需要考虑截面的几何形状和材料性质。
下面将介绍L形截面的性质计算方法及相关参数。
首先,我们需要确定L形截面的几何形状参数,包括L形截面的宽度(b1、b2)、高度(h)和厚度(t1、t2)。
这些参数可以通过实际测量或技术图纸获得。
接下来,我们需要计算L形截面的面积(A)、截面惯性矩(I)、截面模量(S)、抗弯强度(W)等参数。
1.L形截面的面积(A)可以通过宽度和高度计算得到,即A=b1*t1+b2*t22.L形截面的截面惯性矩(I)是衡量截面抗弯刚度的重要参数。
对于L形截面而言,有两个主轴,我们可以分别计算关于两个主轴的截面惯性矩。
设L形截面的横向主轴为x轴,纵向主轴为y轴,截面惯性矩可分为Ix和Iy。
-Ix=b1*t1^3/12+A*(h/2)^2-Iy=b2*t2^3/12+A*(h/2)^23.L形截面的截面模量(S)是一个衡量截面抗弯强度的参数,表示材料受力时截面形状承受的变形程度。
计算公式为S=Ix/y,其中y为截面形心到纵向最外边缘(L形截面纵向边缘)的距离,为h/24. L形截面的抗弯强度(W)是指截面在外力作用下抵抗弯曲的能力。
对于简支梁而言,其抗弯强度可通过计算最大弯矩(Mmax)来确定。
对于L形截面而言,横向主轴上的最大弯矩即为最大弯矩,公式为 Mmax =W/y,其中W为抗弯截面模量。
以上是L形截面的几何性质计算方法,接下来将介绍关于L形截面材料性质的参数计算。
1.L形截面的面积折减系数:由于截面形状的不规则,L形截面在受弯时会发生应力集中。
为了更加准确地反映材料的抗弯性能,需要考虑截面的减效系数。
其计算公式为C=0.75+(h/2t1)*(0.55-0.19t1/h),其中h 和t1分别为L形截面的高度和厚度。
2.L形截面材料的屈服强度:L形截面的屈服强度可以根据材料的抗拉强度(σt)和折减系数(C)计算得到,公式为Fy=σt*C,其中Fy为L形截面的屈服强度。
立体几何中的截面(解析版)
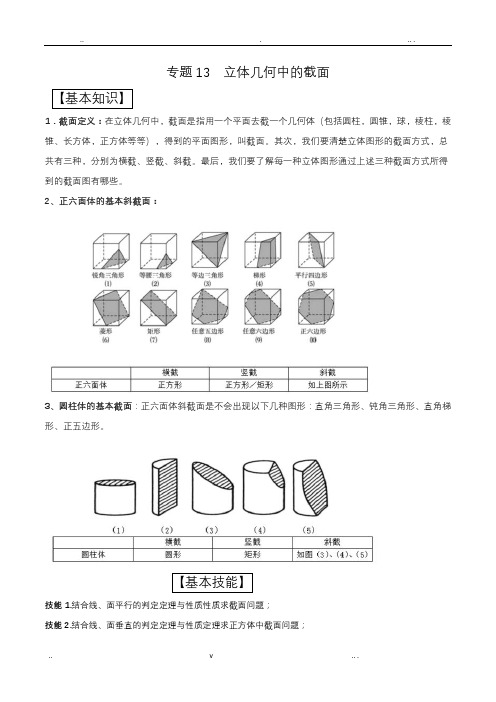
专题13 立体几何中的截面【基本知识】1.截面定义:在立体几何中,截面是指用一个平面去截一个几何体(包括圆柱,圆锥,球,棱柱,棱锥、长方体,正方体等等),得到的平面图形,叫截面。
其次,我们要清楚立体图形的截面方式,总共有三种,分别为横截、竖截、斜截。
最后,我们要了解每一种立体图形通过上述三种截面方式所得到的截面图有哪些。
2、正六面体的基本斜截面:3、圆柱体的基本截面:正六面体斜截面是不会出现以下几种图形:直角三角形、钝角三角形、直角梯形、正五边形。
【基本技能】技能1.结合线、面平行的判定定理与性质性质求截面问题;技能2.结合线、面垂直的判定定理与性质定理求正方体中截面问题;技能3.猜想法求最值问题:要灵活运用一些特殊图形与几何体的特征,“动中找静”:如正三角形、正六边形、正三棱锥等;技能4.建立函数模型求最值问题:①设元②建立二次函数模型③求最值。
例1 一个正方体内接于一个球,过这个球的球心作一平面,则截面图形不可能...是()分析考虑过球心的平面在转动过中,平面在球的内接正方体上截得的截面不可能是大圆的内接正方形,故选D。
例2 如图,在透明的塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜程度的不同,有下列四个命题:①水的部分始终呈棱柱状;②水面EFGH的面积不改变;③棱A1D1始终与水面EFGH平行;④当容器倾斜到如图5(2)时,BE·BF是定值;其中正确的命题序号是______________分析当长方体容器绕BC边转动时,盛水部分的几何体始终满足棱柱定义,故①正确;在转动过程中EH//FG,但EH与FG的距离EF在变,所以水面EFGH的面积在改变,故②错误;在转动过程中,始终有BC//FG//A1D1,所以A1D1//面EFGH,③正确;当容器转动到水部分呈直三棱柱时如图5(2),因为BCBFBEV⋅⋅=21水是定值,又BC是定值,所以BE·BF是定值,即④正确。
立体几何中的截面问题

立体几何中的截面问题一.基本原理:过正方体(长方体)上三点做截面.1.三点中有两点共面例1.如图,在正方体ABCD-A 1B 1C 1D 1中,E,F,G 分别在AB,BC,DD 1上,求作过E,F,G 三点的截面.思路:当三点中有两点共面时,做截面的思路就是先找共面两点所在直线与该平面所有的棱交点,而这些交点由同时在另外一个平面中,即该截面和正方体某个侧面的交点,这样利用公理1,逐次相连找到所有的交点,即可得到截面.解析:作法:①.由于F E ,共面,在底面AC 内,过F E ,作直线EF ,与DA 于L ,显然,此时L 即在侧面D A 1内,又在欲求截面内,而该截面与侧面D A 1又交于点G ,根据公理1,截面与侧面D A 1交于L .同理,过F E ,作直线EF 与DC 的延长线交于M ,此时M 即在侧面1DC 内,又在欲求截面内,根据公理1,截面与侧面1DC 交于M .②在侧面D A 1内,连接LG 交1AA 于K .③在侧面1DC 内,连接GM 交1CC 于H .④连接FH KE ,.则五边形EFHGK EFHGK 即为所求的截面.练习1.(三点两两共面)P,Q,R 三点分别在直四棱柱AC 1的棱BB 1,CC 1和DD 1上,试画出过P,Q,R 三点的截面作法.解析:作法:(1)连接QP,QR 并延长,分别交CB,CD 的延长线于E,F.(2)连接EF 交AB 于T,交AD 于S.(3)连接RS,TP.则五边形PQRST 即为所求截面.例2.(三点所在的棱两两异面)如图,长方体1111D C B A ABCD -中,R Q P ,,分别为111,,CC AB D A 上三点,求过这三点的截面.分析:此题的难点在于R Q P ,,三点均不在同一个侧面(底面)中,这样我们就暂时无法通过侧面(底面)中连线与棱的交点来找到截面的边界点,于是需要先做出一个平面来,让上面三点RQ P ,,中有两点共面,这就转化成例1的情形,从而解决问题.解:如图,作1//BB QE 交11B A 与E ,则1,RC QE 确定一个平面,转化为例1的情形.连接QR EC ,1,交于点F ;连接PF 交1111,B A D C 延长线于H G ,;连接HQ 交11,BB AA 延长线于J I ,;连接JR 交BC 于K .则KRGPIQK 为所作截面.例3.利用平行关系确定截面在三棱锥A BCD -中,AB CD a ==,截面MNPQ 与AB ,CD 都平行,则截面MNPQ 的周长等于()A.2a B.4a C.a D.无法确定解析:设AM k CM=,因为//AB 平面MNPQ ,平面ABC 平面MNPQ MN =,AB Ì平面ABC ,所以//MN AB ,同理可得//PQ AB ,//MQ CD ,//NP CD ,故四边形MNPQ 为平行四边形,所以11MN PQ AB AB k ==+,1MQ NP k CD CD k ==+.因为AB CD a ==,所以1a MN PQ k==+,1ak MQ NP k ==+,所以四边形MNPQ 的周长为2211a ak MN PQ MQ NP a k k ⎛⎫+++=+= ⎪++⎝⎭.故选:A.二.截面的的画法小结1.确定截面的主要依据有(1)平面的四个公理及推论.(2)直线和平面平行的判定和性质.(3)两个平面平行的性质.2.作截面的几种方法(1)直接法:有两点在几何体的同一个面上,连接该两点即为几何体与截面的交线,找截面实际就是找交线的过程。
41-截面的几何参数解析

yC
i1 2
Ai
i1
0 2 7 0 1 0 3 5 0 1 0 3 1 5 0 1 0 3
将组合图形分解为若干简单图形,并确定组合图形的形心位 置。
以形心为坐标原点,设Oyz坐标系,y、z 轴 一般与简单图 形的形心主轴平行。确定简 单图形对自身形心轴的惯性矩,利 用移轴 定理(必要时用转轴定理)确定各个简单 图形对y、z轴 的惯性矩和惯性积,相加(空洞时则减)后便得到整个图形的 Iy、Iz 和Iyz。
A
例1:试求匀质槽形钢板的
形心。
y
A
y
y
解:由对称性可知 xc 0
o
A 1 A 2 1 3 0 0 3c 02 m 0y1=y2=15cm
A3102020c0m 2 y35cm
3
yc
i1
3
A
i y ci Ai
3001522005=12.5cm 3002200
i1
30cm
10cm x
(2)负面积法 解:由对称性可知
❖3、截面对形心轴的静矩为零
❖4、若截面对某轴的静矩为零,则该轴必为形心轴
例3 求图示阴影部分的面积对y轴的静矩。
h
2
a
y
h 2
b
解: S y
b(ha) 2
(
h 2
2
a)
a
b h2
a2
2 4
§4.2 惯性矩、极惯性矩、惯性积
一、极惯性矩:是面积对极点的二次矩。
y
I
2dA
A
——图形对 O 点的极惯性矩
I I b2A
y1
yc
I I a2A
z1
zc
几何体截面归类十四种(解析版)

几何体截面归类十四种1.目录重难点题型归纳⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1【题型一】截面做法基础1:平行线法⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1【题型二】截面做法基础2:相交线法⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5【题型三】截面形状判定⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9【题型四】求截面周长⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯11【题型五】求截面面积⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯14【题型六】截面分两部分体积⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯16【题型七】与线、面平行的截面⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯19【题型八】与直线、平面垂直的截面⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯21【题型九】外接球截面⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯23【题型十】内切球截面⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯25【题型十一】“动点”型截面⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯28【题型十二】截面与角度⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯34【题型十三】与截面有关的最值⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯36【题型十四】截面综合应用⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯39好题演练⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯42 1.重难点题型归纳重难点题型归纳题型一:截面做法基础1:平行线法【典例分析】1已知正方体ABCD -A 1B 1C 1D 1的体积为1,点M 在线段BC 上(点M 异于B 、C 两点),点N 在CC 1上满足CN =C 1N ,若平面AMN 截正方体ABCD -A 1B 1C 1D 1所得的截面为五边形,则线段BM 的取值范围是( )A.0,12B.12,1C.13,1D.12,13【答案】B【分析】由正方体的性质及面面平行的性质分析截面与上底面A 1B 1C 1D 1的两条边A 1D 1和C 1D 1有交点,然后作出截面AMNTS ,由相似形得出A 1S =2CM =2(1-BM ),从而可得BM 的范围.【详解】因为截面过A 点,那么它只能与正方体的过点A 的三个面中两个面有交线,因此截面的边只能在正方体ABCD -A 1B 1C 1D 1的两个侧面ABB 1A 1和侧面ADD 1A 1的其中一个上(已经有一条边是AM ),从而截面必与上底面A 1B 1C 1D 1有交线,由面面平行的性质定理知这个交线与直线AM 平行,如下图,在B 1C 1上取点P ,使得B 1P =BM ,连接PM 可得平行四边形BMPB 1,则PM ⎳BB 1且PM =BB 1,而BB 1与AA 1平行且相等,得PM ⎳AA 1且PM =AA 1,从而AMPA 1是平行四边形,所以A 1P ⎳AM ,在A 1D 1上取A 1Q =C 1P 得平行四边形A 1PC 1Q ,因此有A 1P ⎳C 1Q ,如下图,截面是五边形AMNTS ,由面面平行的性质定理得AS ⎳MN ,因为两个角∠A 1AS 和∠MNC 的两边分别平行,且它们都是锐角,所以∠A 1AS =∠CNM ,而∠AA 1S =∠NCM =90°,所以△AA 1S ∼△NCM ,所以AA 1NC =A 1S CM,CN =C 1N ,因此有CN =12CC 1=12AA 1,所以A 1S =2CM ,所以A 1S =2CM =2(1-BM ),0<2(1-BM )<1,12<BM <1,故选:B .方法归纳【技法指引】】基础模型:如下图E 、F 是几等分点,不影响作图。
《材料力学》i截面的几何性质习题解

附录I 截面的几何性质 习题解[习题I-1] 试求图示各截面的阴影线面积对x 轴的静积。
(a )解:)(24000)1020()2040(3mm y A S c x =+⨯⨯=⋅=(b )解:)(42250265)6520(3mm y A S c x =⨯⨯=⋅= *(c )解:)(280000)10150()20100(3mm y A S c x =-⨯⨯=⋅=(d )解:)(520000)20150()40100(3mm y A S c x =-⨯⨯=⋅=[习题I-2] 试积分方法求图示半圆形截面对x 轴的静矩,并确定其形心的坐标。
解:用两条半径线和两个同心圆截出一微分面积如图所示。
dx xd dA ⋅=)(θ;微分面积的纵坐标:θsin x y =;微分面积对x 轴的静矩为: θθθθθdxd x x dx xd y dx xd y dA dS x ⋅=⋅⋅=⋅⋅=⋅=sin sin )(2半圆对x 轴的静矩为: .32)]0cos (cos [3]cos []3[sin 33003002r r x d dx x S r rx =--⋅=-⋅=⋅=⎰⎰πθθθππ因为c x y A S ⋅=,所以c y r r ⋅⋅=232132π π34ry c = [习题I-3] 试确定图示各图形的形心位置。
(a ) 解:习题I-3(a): 求门形截面的形心位置矩形 Li 'Bi Ai Yci AiYci Yc 离顶边上 400 20 8000 &160 1280000 左 150 20 3000 75 225000 .右150 20 3000 75 225000 !140001730000Ai=Li*BiYc=∑AiYci/∑Ai?(b)解: 习题I-3(b): 求L 形截面的形心位置矩形 Li Bi Ai Yci —AiYciYc Xci AiXci Xc 下1601016005(800080128000左 90 10 900 55 。
截面几何性质

a b b C. Iy ≺ Iy, x ≻ Ix; Ia y
b b D Iy ≺ Iy, x ≺ Ix。 . a Ia y
o
x
o
x
(a)
(b)
C
课堂练习
I.
图示半圆形,若圆心位于坐标原点,则(
y
2R
R
O
C. Iy ≻ Ix;
B
R
x
课堂练习
I.
图示任意形状截面,若Oxy轴为一对主形心轴,则 ( )不是一对主轴。
A O ; . xy
y1
y
B. O xy; 1 1
C. O x1y1 ; 2
D O x1y。 . 3
O1 O2
O
O3
x
x1
C
课堂练习
I.
任意图形,若对某一对正交坐标轴的惯性积为零, 则这一对坐标轴一定是该图形的( )。
xy
∫
A
∫
A
5、组合图形对某一点的极惯性矩或对某一轴的惯性矩、惯性积 、组合图形对某一点的极惯性矩或对某一轴的惯性矩、 dA x x n n n n
y
y
2
∫ (− xy )dA = 0
A 2
dA
I P = ∑ I Pi
i =1
I x = ∑ I xi
i =1
I y = ∑ I yi
i =1
I xy = ∑ I xyi
D
课堂练习
I. 图示任意形状截面,它的一个形心轴zc把截面分成 Ⅰ和Ⅱ两部分,在以下各式中,( )一定成立。
A I +I .
《立体几何》微专题3 空间中的截面

《立体几何》微专题3 空间中的截面一、内容解析在立体几何中,截面是指用一个平面去截一个几何体(如圆柱、圆锥、球、棱柱、棱锥、长方体等)所得的平面图形.高考中涉及空间几何体截面的地方较多,如:判断截面图形的形状,判断截面与其他直线(平面)的位置关系,计算截面的边长、周长和面积(或者求相关几何体的表面积、体积)等.在破解较复杂的综合问题的过程中,要把握好“定位”、“定形”、“定量”这三个环节.首先,由已知条件作出截面与空间几何体的交线;其次,根据线面位置关系相关定理确定截面的基本特征;再次,运用平面几何的有关知识计算截面的边长、周长、面积等.其中,作出空间几何体的截面图形是解决问题的关键.现将空间几何体中截面作图的主要原理(三个公理+两个定理)梳理如下:1.三个公理ABPPA唯一的注:平面的三公理说明了三个问题:(1)平面是平的,平面是无限延展的;(2)要确定两平面交线,可以找两个两平面的交点;(3)确定一个平面的4种方法.【应用举例】如图所示,G是正方体ABCD-A1B1C1D1的棱DD1延长线上的一点,E,F是棱AB,BC的中点.试分别画出过下列各点、直线的平面与正方体表面的交线.(1)过点G及AC;(2)过三点E,F,D1.【分析】我们可以将截面与空间几何体表面的交集(交线)叫做截线,将截面与空间几何体的棱的交集(交点)叫做截点.本题的关键在于确定截点,有了位于多面体同一表面上的两个截点即可连接成截线,从而得到截面.【作法】(1)连接GA交A1D1于点M,连接GC交C1D1于点N;连接MN,AC,则MA,CN,MN,AC为所求平面与正方体表面的交线.如图①所示.(2)连接EF交DC的延长线于点P,交DA的延长线于点Q;连接D1P交CC1于点M,连接D1Q交AA1于点N;连接MF,NE,则D1M,MF,FE,EN,ND1为所求平面与正方体表面的交线.如图②所示.2.两个定理则过这条直线的任一平面与此平面的交【应用举例】(1)在三棱锥P-ABC中,G为△PAC的重心,过点G作三棱锥的截面α,使其平行于PB 和AC,请画出截面α与三棱锥表面的交线.【分析】若截面α与PB和AC平行,则交线分别与PB和AC中的一条平行.【作法】如图,过G作EF∥AC,分别交PA,PC于点E,F,过点F作FM∥PB交BC于点M,过点E作EN∥PB交AB于点N,连接MN,可知EN∥FM,所以E、F、M、N四点共面,且MN∥AC∥EF,EN∥PB∥FM,则EF,FM,MN,EN即为截面α与三棱锥表面的交线.(2)如图,一个四面体木块ABCD,在△ABC的面内有一点P,过点P作一个截面α,使其垂直于直线AD,请画出截面α与四面体表面的交线.【分析】若截面α与AD垂直,则交线与AD垂直.由于在平面ABD和平面ACD内垂直于AD的直线有无数条,故根据面面平行的性质定理,可采用平移法,先作出AD的一个垂面,再平移至点P.【作法】如图,在AD上任取异于A,D的一点Q,过点Q分别在平面ABD和平面ACD 内作QR⊥AD,QS⊥AD,分别交AB,AC于R,S两点.连接RS,过点P在平面ABC内作EF∥RS交AB,AC于E,F两点.过F在平面ACD内作FG∥SQ交AD于G,连接EG,可先证明平面QRS∥平面EFG,再由面面平行的性质定理证明RQ∥EG,从而可证直线AD垂直于平面EFG,则EF,FG,GE即为截面α与四面体表面的交线.【注】截面问题中与平行有关的定理不仅可以用于在截面作图的过程中确定截面的交线,还可以判断截面图形的形状.有关线面、面面垂直的定理在解题时主要用于确定截面的位置关系,故不再专门列出.通过上述分析,可以将空间几何体中截面作图方法小结如下:① 若已知两点在同一平面内,只要连接这两点,就可以得到截面与多面体的一个面的截线; ② 若面上只有一个已知点,应设法在同一平面内再找出第二个确定的点; ③ 若已知两个点分别在两个相邻的面上,应找出这两个平面的交线与截面的交点; ④ 若所做截面要求与多面体的某一条棱平行,则由一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行的性质,可得截面与平面的交线; ⑤ 若两平行平面中的一个平面与截面有交线,另一个面上只有一个已知点,则由平行平面与第三个平面相交,那么它们的交线互相平行的性质,可得截面与平面的交线; ⑥ 若有一个点在面上而不在棱上,则可通过作辅助平面转化为棱上的点的问题;同理,若已知点在体内,则可通过辅助平面使它转化为面上的点,再转化为棱上的点的问题来解决.下面以正方体为例,列举其基本斜截面图形如下(横截面和竖截面均为正方形): ① 三角形(锐角三角形) (等腰三角形) (等边三角形)注:可以分别用反证法和余弦定理证明,不可能出现直角三角形和钝角三角形截面. ② 四边形(梯形) (平行四边形) (菱形) (矩形) 注:可以用反证法证明,不可能出现直角梯形截面. ③ 五边形1A1A1A1A1A1A1A(普通五边形)注:可以用反证法证明,不可能出现正五边形截面. ④ 六边形(普通六边形) (正六边形)其他空间多面体和旋转体的截面也可以类似作出,并进行分类研究. 二、典型例题题型一、判断截面图形的形状例1 过正方体ABCD -A 1B 1C 1D 1的棱AB ,BC 的中点E ,F 作一个截面使截面与底面所成的角为45o ,则此截面的形状为( )A .三角形或五边形B .三角形或六边形C .六边形D .三角形 【分析】此题中可以直接去找与底面成45o 角的截面,也可以找一些特殊位置的截面,通过计算其与底面所成角得出所求截面的相对位置,体现了运动变化的动态探究. 【答案】B 【解析】如图,显然,本题中的截面有两个,其中一个与线段B 1B 相交,截面为三角形,故只需判断另一个截面的位置和形状.111A1A A连接BD 交EF 于G ,设上下底面中心分别为O 1,O ,设过点D 1的截面与底面的所成角为α,易得tan α=tan ∠D 1GD =223<1, 故α<45o ;设过棱A 1C 1的截面与底面的所成角为β,易得tan β=tan ∠O 1GO =22>1,故α>45o , 故所求截面应与A 1D 1,C 1D 1都相交(不过其端点),为六边形. 故选B .【注】若截面与棱D 1D 相交,则截面为五边形;若截面与棱A 1D 1,C 1D 1都相交(不过其端点),则截面为六边形;若截面与棱A 1B 1,B 1C 1都相交(不过点B 1),则截面为四边形.题型二、判断截面与其他直线(平面)的位置关系例2 如图,在下列三个正方体ABCD -A 1B 1C 1D 1中,E ,F ,G 均为所在棱的中点,过E ,F ,G 作正方体的截面.在各正方体中,直线BD 1与平面EFG 的位置关系描述正确的是( )① ② ③ A . BD 1∥平面EFG 的有且只有①;BD 1⊥平面EFG 的有且只有② B . BD 1∥平面EFG 的有且只有②;BD 1⊥平面EFG 的有且只有① C . BD 1∥平面EFG 的有且只有①;BD 1⊥平面EFG 的有且只有②③ D . BD 1∥平面EFG 的有且只有②;BD 1⊥平面EFG 的有且只有③【分析】无论是线面位置关系,还是面面位置关系,归根结底都应转化为对线线位置关系的探求.在判断截面与其他直线(平面)的位置关系的问题中,可以借助截面图形中现有的直线探寻位置关系,也可以将截面进行延展,作出与空间几何体的交线,通过交线(也可以是截面中的其他直线)探寻位置关系. 【答案】C【解析】若从图①研究起,取A 1D 1中点H ,通过截面EFHG 与对角面BDD 1B 1平行,可得BD 1∥面EFG ,从而排除B ,D 选项;1A1A1A若从图②研究起,可通过证明BD 1⊥EF ,BD 1⊥EG ,得证BD 1⊥平面EFG ,从而排除B ,D 选项;对比A ,C 选项,只需考查图③对应的结论:取AA 1中点M ,连EM ,FM ,仿图②,可证BD 1⊥平面EFM ,故BD 1⊥EF ;类似可证得BD 1⊥GF (BD 1⊥EG ) .从而BD 1⊥平面EFG ,排除A . 故选C .题型三、计算截面的面积和周长例3 有一正三棱柱(底面为正三角形的直棱柱)木料ABC -A 1B 1C 1,各棱长都为2.已知O 1,O 2分别为上,下底面的中心,M 为O 1O 2的中点,过A ,B ,M 三点的截面把该木料截成两部分,则截面面积为( )A . 7B . 1639C . 3194D . 2【分析】本题中构造截面并发现截面的特征是解决问题的关键,而构造截面的过程需运用面面平行的性质定理. 【答案】 B【解析】如图,在正三棱柱ABC -A 1B 1C 1中,各棱长都为2,M 为O 1O 2的中点, 由面面平行的性质定理,可知过A ,B ,M 三点的截面为等腰梯形ABEF , 则EF =13A 1B 1=23,梯形的高为PD =22+(233)2=433,则截面面积为S =12×(23+2)×433=1639. 故选B .例4 已知正方体ABCD -A 1B 1C 1D 1的棱长为2,M 为CC 1的中点,若AM ⊥平面α,且B ∈平面α,则平面α截正方体所得截面的周长为( )1AA . 32+2 5B . 4+4 2C . 22+2 5D . 6 2【分析】本题中构造与AM 垂直的截面是解决问题的关键,而构造截面的过程需运用线面垂直的判定定理(定义)和面面平行的性质定理. 【答案】A【解析】如图,取BB 1中点N ,A 1B 1中点E ,连接MN ,AN ,BE ,可证AM ⊥面DBE , 由面面平行的性质定理可知截面α与正方体的上下底面的交线平行.由E 为A 1B 1中点可取A 1D 1中点F ,则α即为截面BEFD ,易求周长为32+25,故选A .三、反馈练习A 组(一)单选题:1.截一个几何体,所得各截面都是圆面,则这个几何体一定是( )A. 圆柱B. 圆锥C. 球D. 圆台【答案】C【解析】A.圆柱的轴截面是一个矩形,此选项错误; B.圆锥的轴截面是一个三角形,此选项错误; C.球的截面是一个圆面,此选项正确; D.圆台的轴截面一个梯形,此选项错误. 故选C .2.如图,在四棱锥P -ABCD 中,AD 与BC 相交.若平面α截此四棱锥得到的截面是一个平行四边形,则这样的平面α的个数是( )A .不存在B .恰有1个C .恰有5个D .有无数个1A【答案】D【解析】 在平面ABCD 中作直线MN ∥AB ,交AD 、BC 于点M 、N ,在平面PAB 中作EF ∥AB ,交PA 、PB 于点E 、F ,使MN =EF ,由线面平行的性质定理可知四边形EFNM 为平行四边形,这样的平行四边形显然可以做无数个,且平行四边形所在平面即为所求的平面α. 故选D .(二)多选题:3. (多选题)过正方体中心的截面图形可以是( )A .三角形B .四边形C .五边形D .六边形 【答案】BD【解析】过正方体中心的截面图形至少与正方体的四个面相交,所以不可能是三角形.又因为截面是五边形时不过正方体的中心.过正方体一面上相邻两边的中点及正方体的中心的截面形状为正六边形. 故答案为BD .4.(多选题)用一个平面截正四面体,下列结论中正确的是( ) A .正四面体的截面不可能是正方形; B .正四面体的截面可能是等腰梯形; C .正四面体的截面可能是直角三角形;D .若正四面体的截面是三角形,一定是等腰三角形. 【答案】BC【解析】利用正四面体的性质,分析4个选项,取正四面体各条棱的中点连接而成的截面图形是正方形,故选项A 错误;当截面只与正四面体对棱中的一条平行时,截面为等腰梯形,故选项B 正确;对于选项C 、D ,正四面体的截面可以是三角形,但不一定为等腰三角形,A如下图,过点A 作AO ⊥平面BCD ,要构造截面直角三角形APQ ,只需先在底面BCD 内构造直角三角形OPQ ,故选项C 正确,选项D 错误,故答案为BC .(三)填空题:5.过正方体ABCD -A 1B 1C 1D 1的顶点A 1,C 1,B 的平面与底面ABCD 所在的平面的交线为l ,则l 与A 1C 1的位置关系是________. 【答案】平行【解析】由于平面ABCD ∥平面A 1B 1C 1D 1,平面A 1B 1C 1D 1∩平面A 1C 1B =A 1C 1,平面ABCD ∩平面A 1C 1B =l ,所以l ∥A 1C 1.6.在棱长为1的正方体ABCD -A 1B 1C 1D 1中,平面α与正方体每条棱所成的角均相等,则平面α截正方体所形成的三角形截面中,截面面积的最大值为_____________;平面α与正方体每条棱所成的角的正弦值为_____________. 【答案】32,33 【解析】如图,在正方体ABCD -A 1B 1C 1D 1中,与A 1B 1,A 1D 1, A 1A 平行的直线各有4条, ∵A 1B 1=A 1D 1=A 1A ,∴三棱锥A 1-AB 1D 1是正三棱锥,∴A 1B 1,A 1D 1,A 1A 与平面AB 1D 1所成角相等,∴与正方体的12条棱所在直线所成角均相等的一个平面α是平面A 1BD 1(或平面AB 1C 或平面ACD 1),且截面面积最大,1A由棱长为1,故AB 1=2,再由三角形AB 1D 1为正三角形,其面积为34×(2)2=32,故答案为32. 由顶点A 1到平面AB 1D 1的距离为体对角线的13,则平面α与正方体每条棱所成的角的正弦值为33a a =33.(四)解答题:7.如图所示,在正方体ABCD −A 1B 1C 1D 1中,试作出过AC 且与直线D 1B 平行的截面,并说明理由.【解答】如图,连接DB 交AC 于点O ,取D 1D 的中点M ,连接MA ,MC ,MO ,则截面MAC 即为所求作的截面.证明:∵MO 为△D 1DB 的中位线,∴D 1B ∥MO .∵D 1B ⊄平面MAC ,MO ⊂平面MAC ,∴D 1B ∥平面MAC ,则截面MAC 为过AC 且与直线D 1B 平行的截面.8.下图表示以AB =4,BC =3的矩形ABCD 为底面的长方体被一平面斜截所得的几何体,其中四边形EFGH 为截面.已知AE =5,BF =8,CG =12,1A A1A(1)截面四边形EFGH 是否为菱形?证明你的结论;(2) 求DH 的长. 【解答】(1)截面EFGH 为菱形.证明如下:∵平面ABFE ∥平面DCGH ,且平面EFGH 分别截平面ABFE 与平面DCGH 得直线EF 与直线GH ,∴EF ∥GH .同理,FG ∥EH ,∴四边形EFGH 为平行四边形.又∵EF 2=AB 2+(BF -AE )2=25,FG 2=BC 2+(CG -BF )2=25,∴EF =FG =5, ∴四边形EFGH 为菱形.(2) ∵几何体是长方体被一平面斜截所得的,∴AE +CG =BF +DH ,将AE =5,BF =8,CG =12代入得,DH 的长为9.B 组填空题:9.各面均为等边三角形的四面体ABCD 的外接球的表面积为12π,过棱AB 作球的截面,则截面面积的最小值为________. 【答案】2π【解析】根据题意,球的半径为3,面积最小的截面是以AB 为直径的截面,将四面体ABCD 放置于正方体中,可得正方体的外接球就是四面体ABCD 的外接球,设AB =a ,则△ABC 的外接圆半径为32a ×23=33a ,可求得三棱锥的高为a 2-13a 2=63a 2,则63a -32+33a 2=32,解得a =2,进而截面面积的最小值为π×22=2π.故答案为2π.10.如图,已知球O 是棱长为1的正方体ABCD -A 1B 1C 1D 1的内切球,则平面ACD 1截球O 的截面面积为________.AE【答案】π6 【解析】根据题意知,平面ACD 1是边长为2的正三角形,且球与以点D 为公共点的三个面的切点恰为三角形ACD 1三边的中点,故所求截面的面积是该正三角形的内切圆的面积,则由上图得,△ACD 1内切圆的半径是22×tan30o =66, 则所求的截面圆的面积是π×(66)2=π6.故答案为66.11. 如图,正方体ABCD -A 1B 1C 1D 1的棱长为a ,动点P 在对角线BD 1上,过点P 作垂直于BD 1的平面γ,记这样得到的截面多边形(含三角形)的周长为y ,设BP=x ,则当x ∈[33a ,233 a ]时,函数y=f (x )的值域为________.【答案】{32a } 【解析】1AA1A如图,当x ∈[33a ,233 a ]时,截面多边形为六边形HIJKLM , 设11111B I HIA CBC λ==,则11111C I IJ B C B C λ==-,故HI+IJ=2a 为定值,从而截面多边形(含三角形)的周长为32a .12.如图,在四面体ABCD 中,AB =CD =2,AC =BD =3,AD =BC =5,E ,F 分别是AD ,BC 的中点.若用一个与直线EF 垂直,且与四面体的每个面都相交的平面α去截该四面体,由此得到一个多边形截面,则该多边形截面面积的最大值为________.【答案】62 【解析】将四面体补成长、宽、高分别为3,2,1的长方体,如图,∵EF ⊥α,∴截面为平行四边形MNKL ,可得KL +KN =5,G 1A ABGHDA设异面直线BC 与AD 所成的角为θ,则sin θ=sin ∠HFB =sin ∠LKN ,可得sin θ=265, S MNKL =NK ·KL sin ∠NKL ≤62(NK +KL 2)2=62,当且仅当KL =KN 时取等号,故该多边形截面面积的最大值为62.四、真题再现1. (2015全国2文 19)如图,长方体ABCD -A 1B 1C 1D 1中,AB =16,BC =10,AA 1=8,点E ,F 分别在A 1B 1,D 1C 1上,A 1E =D 1F =4.过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.(Ⅰ)在图中画出这个正方形(不必说明画法和理由); (Ⅱ)求平面α把该长方体分成的两部分体积的比值. 【解答】(Ⅰ)交线围成的正方形EHGF 如图:(Ⅱ)作EM ⊥AB ,垂足为M ,则AM =A 1E =4,EB 1=12,EM =AA 1=8.因为EHGF 为正方形,所以EH =EF =BC =10.于是MH =EH 2-EM 2=6,AH =10,HB =6. 因为长方形被平面α分成两个高为10的直棱柱,所以其体积的比值为97(79也正确).2. (2016年全国1文 11)平面α过正方体ABCD -A 1B 1C 1D 1的顶点A ,α∥平面CB 1D 1,α∩平面ABCD =m ,α∩平面ABB 1A 1=n ,则m ,n 所成角的正弦值为A .32 B .22 C .33 D .13【答案】A1A AAA 1【解析】因为过点A 的平面α与平面CB 1D 1平行,平面ABCD ∥平面A 1B 1C 1D 1,所以m ∥B 1D 1∥BD ,又A 1B ∥平面CB 1D 1,所以n ∥A 1B ,则BD 与A 1B 所成的角为所求角,所以m ,n 所成角的正弦值为32,选A .3. (2018全国1理 12)已知正方体的棱长为1,每条棱所在直线与平面α所成的角相等,则α截此正方体所得截面面积的最大值为A .334B .233C .324D .32【答案】A【解析】记该正方体为ABCD -A'B'C'D',正方体的每条棱所在直线与平面α所成的角都相等,即共点的三条棱A'A ,A'B',A'D'与平面α所成的角都相等,如图,连接AB',AD',B'D',因为三棱锥A'-AB'D'是正三棱锥,所以A'A ,A'B',A'D'与平面AB'D'所成的角都相等,分别取C'D',B'C',BB',AB ,AD ,DD'的中点E ,F ,G ,H ,I ,J ,连接EF ,FG .GH ,IH ,IJ ,IE ,易得E ,F ,G ,H ,I ,J 六点共面,平面EFGHIJ 与平面AB'D'平行,且截正方体所得截面的面积最大,又EF =FG =GH =IH =IJ =JE =22,所以该正六边形的面积为6×34×(23)2=334,所以α截此正方体所得截面面积的最大值为334,故选A .4.(2019全国2文 16)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.(本题第一空2分,第二空3分.)【答案】26,2-1.【解析】如图,依题意知,题中的半正多面体的上、下、左、右、前、后6个面都在正方体的表面上,且该半正多面体的表面由18个正方形,8个正三角形组成,故该半正多面体共有18+8=26个面,或者逐层计算得8+8+8+2=26个面.关注到该半正多面体的俯视图(或水平截面、竖直截面)的轮廓是一个正八边形,设该半正多面体的棱长为x,则x+22x+22x=1,解得x=2-1.。
截面几何性质-L形截面

b= t= h= tw= A= S= SS= y= yy= x= xx= Ix= ix= Iy= iy= Wx= Wxx= Wy= Wyy= γ = G= 200 16 300 20 8880 9.2304E+05 8.2400E+04 1.0395E+02 1.9605E+02 9.2793E+00 1.9072E+02 8.4299E+07 9.7433E+01 4.3424E+07 9.7433E+01 8.1099E+05 4.2998E+05 4.6797E+06 2.2768E+05 78.5 0.6971 弱肢宽 b (mm) 弱肢厚 t (mm) 强肢高(包括弱肢厚) h (mm) 腹板厚 tw (mm) 截面面积 A (mm) (mm3) 截面对弱肢边缘轴的面积矩 S=∑Ai*yi (mm3) 截面对强肢边缘轴的面积矩 SS=∑Ai*xi 形心主轴x到弱肢边缘的距离 y=S/A (mm) 形心主轴x到强肢下边缘的距离 yy=h-y (mm) 形心主轴y到强肢边缘的距离 x=SS/A (mm) 形心主轴y到弱肢下边缘的距离 xx=b-x (mm) (mm4) 惯性矩 Ix=∑(Ix1+Ai*yi^2) 回转半径 ix=sqrt(Ix/A) (mm) (mm4) 惯性矩 Iy=∑(Iy1+Ai*xi^2) 回转半径 iy=sqrt(Iy/A) (mm) (mm3) 截面抵抗矩 Wx=Ix/y (mm3) 截面抵抗矩 Wxx=Ix/(h-y) (mm3) 截面抵抗矩 Wy=Iy/x (mm3) 截面抵抗矩 Wyy=Iy/(b-x) (kN/m3) 材料重度 γ (钢材为78.5kN/m3) (kN/m) 每延米自重 技术学院覃智斌编制整理,目的是为了便于 在电脑上用Excel和在PDA上用Pocket Excel进行简单的结构手算,程序 根据新规范编制,如有什么疑问请联系我,以便立刻修正! 2。程序中黄底红字的部分需要使用者根据实际情况输入,黑色的部分 请不要随便更改,除非你发现有错误! email:qinzhibin0654@ OICQ:595519509
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
b= t= h= tw= A= S= SS= y= yy= x= xx= Ix= ix= Iy= iy= Wx= Wxx= Wy= Wyy= γ = G= 200 16 300 20 8880 9.2304E+05 8.2400E+04 1.0395E+02 1.9605E+02 9.2793E+00 1.9072E+02 8.4299E+07 9.7433E+01 4.3424E+07 9.7433E+01 8.1099E+05 4.2998E+05 4.6797E+06 2.2768E+05 78.5 0.6971 弱肢宽 b (mm) 弱肢厚 t (mm) 强肢高(包括弱肢厚) h (mm) 腹板厚 tw (mm) 截面面积 A (mm) (mm3) 截面对弱肢边缘轴的面积矩 S=∑Ai*yi (mm3) 截面对强肢边缘轴的面积矩 SS=∑Ai*xi 形心主轴x到弱肢边缘的距离 y=S/A (mm) 形心主轴x到强肢下边缘的距离 yy=h-y (mm) 形心主轴y到强肢边缘的距离 x=SS/A (mm) 形心主轴y到弱肢下边缘的距离 xx=b-x (mm) (mm4) 惯性矩 Ix=∑(Ix1+Ai*yi^2) 回转半径 ix=sqrt(Ix/A) (mm) (mm4) 惯性矩 Iy=∑(Iy1+Ai*xi^2) 回转半径 iy=sqrt(Iy/A) (mm) (mm3) 截面抵抗矩 Wx=Ix/y (mm3) 截面抵抗矩 Wxx=Ix/(h-y) (mm3) 截面抵抗矩 Wy=Iy/x (mm3) 截面抵抗矩 Wyy=Iy/(b-x) (kN/m3) 材料重度 γ (钢材为78.5kN/m3) (kN/m) 每延米自重 G=Aγ
声明: 1。本程序编制的目的是为了便于在电脑上用Excel和在PDA上用Pocket Excel进行简单的结构手算,程序根据新规范编制,如有什么疑问请联 系我,以便立刻修正! 2。程序中黄底红字的部分需要使用者根据实际情况输入,黑色的部分 请不要随便更改,除
