基于MATLAB的曲柄摇杆机构优化设计说明
matlab四连杆优化设计

机械优化设计在matlab中的应用东南大学机械工程学院**一优化设计目的:在生活和工作中,人们对于同一个问题往往会提出多个解决方案,并通过各方面的论证从中提取最佳方案。
最优化方法就是专门研究如何从多个方案中科学合理地提取出最佳方案的科学。
由于优化问题无所不在,目前最优化方法的应用和研究已经深入到了生产和科研的各个领域,如土木工程、机械工程、化学工程、运输调度、生产控制、经济规划、经济管理等,并取得了显著的经济效益和社会效益。
二优化设计步骤:1. 机械优化设计的全过程一般可以分为如下几个步骤:1)建立优化设计的数学模型;2)选择适当的优化方法;3)编写计算机程序;4)准备必要的初始数据并伤及计算;5)对计算机求得的结果进行必要的分析。
其中建立优化设计数学模型是首要的和关键的一步,它是取得正确结果的前提。
优化方法的选取取决于数学模型的特点,例如优化问题规模的大小,目标函数和约束函数的性态以及计算精度等。
在比较各种可供选用的优化方法时,需要考虑的一个重要因素是计算机执行这些程序所花费的时间和费用,也即计算效率。
2. 建立数学模型的基本原则与步骤①设计变量的确定;设计变量是指在优化设计的过程中,不断进行修改,调整,一直处于变化的参数称为设计变量。
设计变量的全体实际上是一组变量,可用一个列向量表示:②目标函数的建立;选择目标函数是整个优化设计过程中最重要的决策之一。
当对某以设计性能有特定的要求,而这个要求有很难满足时,则针对这一性能进行优化会得到满意的效果。
目标函数是设计变量的函数,是一项设计所追求的指标的数学反映,因此它能够用来评价设计的优劣。
目标函数的一般表达式为:f (X )= I (勺卞比衍产斗一話J ,要根据实际的设计要求来设计目标函数。
在可行域中,任意设计点满足全部约束条件,称为可行解,但不是最优解,而优化设 计就是要求出目标函数在可行域的最优解。
二实例分析(机械优化设计P241页例8-5)设计一曲柄摇杆机构如图,要求:曲柄11从曲萨笄叭产%+ 9"时・操秆】3的转角屐佳再現巳知的运动规律:2X ((p-<p 0) ft 2壮=%+亦且已知分析:1) 设计变量的确定决定机构尺寸的各杆长度,以及当摇杆按已知运动规律开始运行时,曲柄所载的位置角应列为设计变量,即:JI. . ,srTX= “勺勺勺牝=I 】S h »屮oI = 1 考虑到机构的杆长按比例变化时,不会改变其运动规律,因此在计算时常取,而其他杆长则按比例取为 L 的倍数。
基于MATLAB优化工具箱的平面连杆机构的设计

2. 29384450528368 % 最优点 fva l= 0. 00316609088036 % 最优值 ex itflag= 5 % 收敛情况
ou tp u t= itera t ion s: 23 % 迭代次数
完成以上 3 个M 文件后, 在M A TLAB 命令窗口 键入m ub iao, 得到如下结果: Op ti m iza t ion term ina ted: m agn itude of d irect iona l deriva t ive in sea rch d irect ion less than 23 op t ion s. To lFun and m ax i m um con st ra in t vio la t ion is . To lCon. less than op t ion s
F (x ) =
∑ (7
i= 0
i
- 7 si )
2
按图 2, 式中 7i= 70+ 7
si
整理得约束条件
g 3 (x ) = 1 g 5 (x ) = 6 g 6 (x ) = x 1 x1 ≤ 0 x2 ≤0 g 4 (x ) = 1 - x 2 ≤ 0 x1 x2 -
2 2 (Υ Υ i o ) ( i = 0, 1, 2, …, n ) 3Π
2 2 (Υ - Υ 0) 3Π
7 = 7 0+ 于许用值 [ Χ]= 45° 。
并要求在给定的运动范围内, 机构的最小传动角不小
2. 1 建立连杆机构设计的优化数学模型 2. 1. 1 确定设计变量
) , 女, 陕西礼泉人, 现任西安工业大学机电工程学院助教, 从事机械设计方面的教学和研究工作。
基于matlab的连杆机构设计

基于matlab的连杆机构设计————————————————————————————————作者: ————————————————————————————————日期:目录1平面连杆机构的运动分析 (1)1.2 机构的工作原理 (1)1.3机构的数学模型的建立 (1)1.3.1建立机构的闭环矢量位置方程...................................................11.3.2求解方法.....................................................................22基于MATLAB程序设计 (4)2.1 程序流程图 (4)2.2 M文件编写 (6)2.3程序运行结果输出 (7)3 基于MATLAB图形界面设计 (11)3.1界面设计……………………………………………………………………………………………113.2代码设计……………………………………………………………………………………………124 小结 (17)参考文献 (18)1平面连杆机构的运动分析1.1 机构运动分析的任务、目的和方法曲柄摇杆机构是平面连杆机构中最基本的由转动副组成的四杆机构,它可以用来实现转动和摆动之间运动形式的转换或传递动力。
对四杆机构进行运动分析的意义是:在机构尺寸参数已知的情况下,假定主动件(曲柄)做匀速转动,撇开力的作用,仅从运动几何关系上分析从动件(连杆、摇杆)的角位移、角速度、角加速度等运动参数的变化情况。
还可以根据机构闭环矢量方程计算从动件的位移偏差。
上述这些内容,无论是设计新的机械,还是为了了解现有机械的运动性能,都是十分必要的,而且它还是研究机械运动性能和动力性能提供必要的依据。
机构运动分析的方法很多,主要有图解法和解析法。
当需要简捷直观地了解机构的某个或某几个位置的运动特性时,采用图解法比较方便,而且精度也能满足实际问题的要求。
基于MATLAB的曲柄摇杆串RRP型Ⅱ级杆组平面六杆机构的运动分析

加速度的运动规律线图。
关键词:六杆机构;运动分析;MA,IIAB 中图分类号:7I玛91文献标志码:A文章编号:1003—0794(2008)02.0073.03
Kinematical Analysis of Plane Crank Jigging Rod Connect to RRP
ⅡLevel of Group Mechanism Using MATLAB
分析。曲柄1转动角度叭连杆2转动角度臼及摇 常数,对式(2)求时间导数,得到连杆2的角速度09,:
万方数据
一73—
.巡:垫№:兰 .基主丛坚幽塑些煎鲎堑童婴型壁堡盘堑垩亘盔堑垫煎笪重塾坌堑==堑塑墓:簦 箜罂鲞箜兰塑一
及摇杆3角速度∞,,方程式如下
lor i=l:72
8iconsL
8
。二L【一 -一L2:2Csoins 0 LL3,3Csions艿艿艿].儿f叫三i1】J=【‘cL止oLll cos三∞ 】。Jc… 6,
针对常用的一种平面六杆机构为了了解其各个构件在不同时刻的运动参数以及运动曲线本文通过在二维直角坐标系中建立其位置速度加速度复数位置方程借助强大的matlab软件求解方程并利用c语言编程实现时域内各个构件的瞬时参数的数值求解及可视化并将数据导入excel中进行参数曲线绘制即可很形象的得到各个构件的运动参数变化规律及相关的临界状态从而使该机构的运动分析变得简单精确为机构的动力学分析提供了基础
基于MATLAB的双曲柄五杆移栽机构运动学仿真及优化设计

基于MATLAB的双曲柄五杆移栽机构运动学仿真及优化设计作者:程志广李健来源:《科技视界》2018年第12期【摘要】本文建立了双曲柄五杆机构的数学模型,运用多目标优化函数对双曲柄五杆机构进行优化设计,采用MATLAB进行编程计算,得到了栽植点速度加速度、曲柄半径、机架杆长度、主副曲柄相位角差等主要结构参数之间的变化关系,并获得一组最优解。
从而为后期机构的研制、秧苗移栽直立度和薄膜刮伤试验提供了理论依据。
【关键词】钵苗移栽;多目标优化;运动学仿真中图分类号: S223 文献标识码: A 文章编号: 2095-2457(2018)12-0072-002DOI:10.19694/ki.issn2095-2457.2018.12.0310 引言移栽技术在提高作物生长的抗灾抗逆能力、保证作物稳产增产和提高产品品质等方面起着很大作用。
然而进行膜上移栽作业时存在栽植器鸭嘴末端容易刮伤地膜、直立度低等问题,影响了移栽技术在农业生产中的广泛应用[1-2]。
故本文以平面多杆机构鸭嘴式栽植器为例对一种双曲柄五杆移栽机构进行优化设计和仿真分析,从而为实际机构的试验研制提供理论支撑。
1 双曲柄五杆移栽机构运动学模型及工作原理双曲柄五杆移栽机构示意图如图1所示,该移栽机构由双曲柄五杆机构及鸭嘴器组成,机构自由度为2。
其中机架为OE,曲柄OB、ED为输入构件,输出构件为连杆CD,鸭嘴器Lf 固定在CD一端。
移栽进行时曲柄OB、ED以相同角速度同向匀速运动。
当鸭嘴器在最高位置时钵苗落入鸭嘴中进行喂苗。
当鸭嘴到达最低位置时,鸭嘴器在凸轮控制系统作用下张开。
钵苗落入打好的穴口中,完成一次栽植过程。
图1 双曲柄五杆栽植机构示意图2 双曲柄五杆栽植机构运动学模型建立如图1所示,以O为原点建立直角坐标系,各杆角位移以X轴正方向为基准,逆时针为正,机组前进方向为X轴负方向[3]。
设机构中各杆件OB、AB、AD、DE、AC、OE、CF 长度分别为L0、L1、L2、L3、L4、L5,鸭嘴器长度为Lf,两曲柄初始相位角分别为ψ0、ψ3,连杆DE、CF角位移分别为ψ2、ψ4。
曲柄连杆机构matlab课程设计

曲柄连杆机构matlab课程设计一、课程目标知识目标:1. 理解曲柄连杆机构的基本原理与运动特性;2. 掌握利用MATLAB软件进行曲柄连杆机构的运动仿真与分析;3. 学会结合实际工程案例,运用所学知识解决曲柄连杆机构的相关问题。
技能目标:1. 能够运用MATLAB软件构建曲柄连杆机构的模型;2. 能够对曲柄连杆机构进行运动分析,并绘制出相应的运动轨迹图;3. 能够根据分析结果,优化曲柄连杆机构的结构参数。
情感态度价值观目标:1. 培养学生对机械原理及MATLAB软件的兴趣,激发学习热情;2. 培养学生严谨的科学态度,注重理论与实践相结合;3. 增强学生的团队协作意识,提高沟通与表达能力。
本课程针对高年级学生,结合学科特点,注重理论知识与实践技能的结合。
通过本课程的学习,使学生能够掌握曲柄连杆机构的基本原理,运用MATLAB软件进行运动仿真与分析,培养解决实际工程问题的能力。
同时,课程强调团队合作,提升学生的综合素质,为将来的学术研究和职业发展打下坚实基础。
二、教学内容1. 曲柄连杆机构基本原理:介绍曲柄连杆机构的类型、特点及其在工程中的应用,重点讲解其运动学及动力学原理。
教材章节:第二章 曲柄连杆机构2. MATLAB软件操作:讲解MATLAB软件的基本操作,包括界面、常用命令、数据类型等,为后续运动仿真打下基础。
教材章节:第一章 MATLAB基础3. 曲柄连杆机构建模与仿真:教授如何使用MATLAB软件构建曲柄连杆机构的模型,进行运动仿真,分析运动特性。
教材章节:第三章 曲柄连杆机构建模与仿真4. 结构参数优化:介绍曲柄连杆机构结构参数对运动性能的影响,教授如何运用MATLAB软件进行参数优化。
教材章节:第四章 曲柄连杆机构优化设计5. 实际工程案例:分析典型曲柄连杆机构在实际工程中的应用,结合MATLAB软件进行案例分析,提高学生解决实际问题的能力。
教材章节:第五章 曲柄连杆机构工程应用案例教学内容安排与进度:共分为五个阶段,每个阶段2学时,共计10学时。
基于Matlab的曲柄摇杆机构参数化设计

小车前轮为转向轮,后轮为驱动轮,假设小车为一个其在固定驱动力作用下做周期运动,如图从图2可以发现,其轨迹近似为正弦曲线,小车能够通过方向控制机构-曲柄摇杆机构控制前轮周期性转向,从而绕过图中方格交点位置的障碍物。
障碍物之间的间距就可以进行优化了。
从小车简图中可以发现,核心的机构就是一个曲柄摇杆机构,小车底盘与立柱组成曲柄长度与连杆长度可以调节,它们决定了摇杆也就是前轮的摆角。
前轮为转向轮,控制整个小车的运动轨迹,所以需要对这个曲柄摇杆机构进行建模,通质点运动规律。
假设为;。
如何确定质点运动轨迹呢?自行车,若自行车前进方向不变,二者轨迹(即车轮与地面接触点的轨迹)自行车前进时前轮左右摆动,前轮可左右左转角度为正,内,后轮在t 时刻的位置用置表示。
自行车后轮旋转线速度为定值,考虑几种情况:——————————————————基金项目:天津市自然科学基金项目(18JCQNJC75200);天津市图1小车简图图2小车运动轨迹图3小车简图控制轮R基座连杆曲柄后轮R1转角前后轮中心距L才能用点,向,有关。
这样得到一个几何位置关系:其中L表示前后轮之间的距离,这是由自行车决定的,令表示后轮与前轮的方则有姿势关系:表示后轮在s时,前轮的偏转角,左转为式(2)两方程就能决定车轮的运动轨迹。
用角度表示方向,β(s)表示后轮的角度,θ(s)表示前轮相则前轮角度β+θ,基本微分方程:后轮速度前轮速度,为单位向量其中,)再求导,得即求得至此可得轮转角,W=W1/(2.52·R1),控制轮转3参数化设计根据求得的参数表达式,编写程序,用Matlab通过运行程序,可以绘制出小车运动轨迹图形,结合实际运动情况,综合考虑振幅的大小选择300-400mm,幅过大,可以有效躲避中间的障碍物,但能量相同的情况下,绕过的障碍物就会减少。
同理,振幅减小,绕过障碍物会增加,但会更容易撞到障碍物,所以也要结合实际经验合理优化。
仿真运动轨迹如图5所示。
基于MATLAB的优化设计

基于MATLAB的优化设计基于MATLAB 的曲柄摇杆机构优化设计1. 问题的提出根据机械的用途和性能要求的不同,对连杆机构设计的要求是多种多样的,但这些设计要求可归纳为以下三种问题:(1)满足预定的运动规律要求;(2)满足预定的连杆位置要求;(3)满足预定的轨迹要求。
在在第一个问题里按照期望函数设计的思想,要求曲柄摇杆机构的曲柄与摇杆转角之间按照()f φ?=(称为期望函数)的关系实现运动,由于机构的待定参数较少,故一般不能准确实现该期望函数,设实际的函数为()F φ?=(称为再现函数),而再现函数一般是与期望函数不一致的,因此在设计时应使机构再现函数()F φ?=尽可能逼近所要求的期望函数()f φ?=。
这时需按机械优化设计方法来设计曲柄连杆,建立优化数学模型,研究并提出其优化求解算法,并应用于优化模型的求解,求解得到更优的设计参数。
2. 曲柄摇杆机构的设计在图 1 所示的曲柄摇杆机构中,1l 、2l 、3l 、 4l 分别是曲柄AB 、连杆BC 、摇杆CD 和机架AD 的长度。
这里规定0?为摇杆在右极限位置0φ时的曲柄起始位置角,它们由1l 、2l 、3l 和4l 确定。
图1 曲柄摇杆机构简图设计时,可在给定最大和最小传动角的前提下,当曲柄从0?转到090??+时,要求摇杆的输出角最优地实现一个给定的运动规律()f ?。
这里假设要求:()()20023E f φ?φ??π==+- (1)对于这样的设计问题,可以取机构的期望输出角()E f φ?=和实际输出角()F φ?=的平方误差之和作为目标函数,使得它的值达到最小。
2.1 设计变量的确定决定机构尺寸的各杆长度1l 、2l 、3l 和4l ,以及当摇杆按已知运动规律开始运行时,曲柄所处的位置角0?应列为设计变量,即: []12340Tx l l l l ?= (2)考虑到机构的杆长按比例变化时,不会改变其运动规律,通常设定曲柄长度1l =1.0,在这里可给定4l =5.0,其他杆长则按比例取为1l 的倍数。
优化设计:曲柄摇杆机构

曲柄摇杆机构摇杆输出角的优化设计姓名:朱朝钰班级:机械本143学号:2014211212指导老师:马齐江二0一七年四月目录一、问题描述 (3)二、优化分析 (3)1.约束提取 (3)2.目标函数 (4)3.标准形式 (5)三、优化求解 (6)四、结论 (7)一、问题描述作业:设计曲柄摇杆机构。
要求:曲柄从0ϕ转到20πϕ+时,摇杆的输出角最优地实现一个给定的运动规律;()()πϕϕψϕψ3200-+==--f 曲柄与机架共线位置时的转角满足:︒≥︒≤45,135min max γγ图1二、优化分析1.约束提取a.杆长条件:最长杆与最短杆之和小于等于其他两杆之和{}0,,m ax 21432432≤+---l l l l l l lb.曲柄机构存在条件:任意三杆长之和必须大于另一杆长{}0,,,m ax 214324321<----l l l l l l l lc.曲柄摇杆条件:曲柄最短10132≤-≤-l ld.传动角⎪⎪⎩⎪⎪⎨⎧︒≤-+=+-+=︒≥-+=--+=1352362)(arccos 452162)(arccos322322322142322max 322322322142322min l l l l l l l l l l r l l l l l l l l l l r 2.目标函数首先根据已知的运动规律与机构实际运动规律之间的最小偏差指标来建立目标函数:21)(min ∑=-⎪⎭⎫⎝⎛-=ni i i x F ψψ设置初始位置如下图图2其中:⎩⎨⎧︒=︒=→⎭⎬⎫==090350032ϕψl l 对于任意位置,如下图所示图3根据几何关系可得出一下公式:ii i ii i i i i i l l l ϕϕβϕϕαπϕαβπψcos 1026cos 5arccoscos 10262cos 1026arccos0;32223--=--+-=≤≤--= 3.标准形式目标函数:21)(min ∑=-⎪⎭⎫⎝⎛-=ni i i x F ψψ约束条件:{}{}⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧≤---=≤--+=≤---=≤---=≤-=≤-=====0414.1360414.116065,,,1max 2045,,max 2010151..32232263223225323243232332214211l l l l g l l l l g l l l l g l l l l g l g l g l h l h t s三、优化求解根据以上条件,使用Excel进行优化分析,得知结果如下。
MATLAB的曲柄滑块和四杆机构的综合设计说明

《计算机仿真技术》课程设计报告姓名:叶 / 浦合昀学号: 4/ 7专业班级:机械卓越141 指导教师:孝保2015年 6月目录1.仿真问题描述.........................................................................2.仿真问题数学模型.....................................................................3.Matlab实现方法 ......................................................................4.Matlab代码 ..........................................................................5.仿真结论.............................................................................6.遇到的问题和解决的方式...............................................................7.课程学习意见与建议...................................................................1.仿真问题描述已知机架AD 长为L1,曲柄AB 长为L2,连杆BC 长L3,另一机架长CD 长为L4,与AB 杆相连的是一滑块E 。
BE 杆长为L5,设计一个四杆加滑块的机构,其中L1-L5杆长可变。
并且可以通过输入的杆长,来判别,该机构到底可不可行。
L3L4 L2 L5L12.仿真问题数学模型(1)四杆机构的设计:在用矢量法建立机构的位置方程时,需将构件用矢量来表示,并作出机构的封闭矢量多边形。
基于MATLAB的同步带传动优化设计
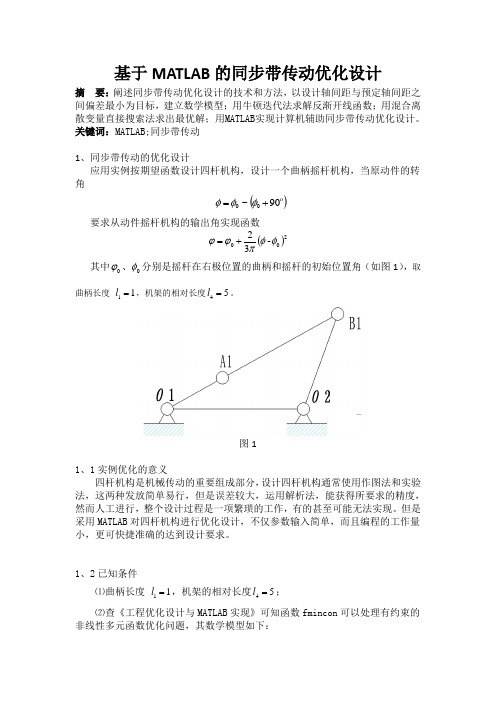
基于MATLAB 的同步带传动优化设计摘 要:阐述同步带传动优化设计的技术和方法,以设计轴间距与预定轴间距之间偏差最小为目标,建立数学模型;用牛顿迭代法求解反渐开线函数;用混合离散变量直接搜索法求出最优解;用MATLAB 实现计算机辅助同步带传动优化设计。
关键词:MATLAB;同步带传动1、同步带传动的优化设计应用实例按期望函数设计四杆机构,设计一个曲柄摇杆机构,当原动件的转角()90~00+=φφφ要求从动件摇杆机构的输出角实现函数()200-32φφπϕϕ+= 其中0ϕ、0φ分别是摇杆在右极位置的曲柄和摇杆的初始位置角(如图1),取曲柄长度 11=l ,机架的相对长度54=l 。
图11、1实例优化的意义四杆机构是机械传动的重要组成部分,设计四杆机构通常使用作图法和实验法,这两种发放简单易行,但是误差较大,运用解析法,能获得所要求的精度,然而人工进行,整个设计过程是一项繁琐的工作,有的甚至可能无法实现。
但是采用MATLAB 对四杆机构进行优化设计,不仅参数输入简单,而且编程的工作量小,更可快捷准确的达到设计要求。
1、2已知条件⑴曲柄长度 11=l ,机架的相对长度54=l ;⑵查《工程优化设计与MATLAB 实现》可知函数fmincon 可以处理有约束的非线性多元函数优化问题,其数学模型如下:)(min x f..t s ()0≤x C ()0=x C eq b Ax ≤ eq eq b x A = b b u x l ≤≤其中,b b eq u l b b x ,,,,为向量,eq A A ,为矩阵;()()x C x C eq ,是返回的函数向量;()x f 为目标函数。
()()()x C x C x f eq ,,可以是非线性函数。
Fmincon 函数调用格式为:[x,fval]=fmincon(FUN,X0,A,B,Aeq,Beq,lb,ub,NONLCON,OPTIONS)其中:NONLCON 是用户定义的非线性约束函数,用来计算非线性不等式约束()0≤x C 和非线性等式()0=x C eq 在x 处的值。
基于matlab的4连杆机构设计

基于matlab的4连杆机构设计第一篇:基于matlab的4连杆机构设计目录1平面连杆机构的运动分析 (1)1.2 机构的工作原理................................................................................................1 1.3 机构的数学模型的建立.......................................................................................1 1.3.1建立机构的闭环矢量位置方程...................................................1 1.3.2求解方法.....................................................................2 2 基于MATLAB程序设计..........................................................................................4 2.1 程序流程图 (4)2.2 M文件编写 (6)2.3 程序运行结果输出.............................................................................................7 3 基于MATLAB图形界面设计....................................................................................11 3.1界面设计 (11)3.2代码设计 (12)4 小结 (17)参考文献………………………………………………………………………………………………18平面连杆机构的运动分析1.1 机构运动分析的任务、目的和方法曲柄摇杆机构是平面连杆机构中最基本的由转动副组成的四杆机构,它可以用来实现转动和摆动之间运动形式的转换或传递动力。
基于Matlab的四杆机构优化设计简介

·制造业信息化·Vol.22.,200922009机电产品开发与创新Development &Innovation of M achinery &E lectrical P roducts3,No.1Jan .,2010第23卷第1期2010年1月收稿日期:2009-11-06作者简介:李建霞,女,河南信阳人,教授。
主要从事计算机辅助设计教学与研究工作。
已发表核心期刊论文20余篇;王良才,男,山东济南人,副教授。
主要从事机械设计教学与研究工作。
已发表核心期刊论文10余篇。
0引言Matlab 语言是一种非常强大的工程计算语言,提供了非常丰富的Matlab 优化工具箱。
其优化工具箱有许多常用的优化算法,广泛应用于线性规划、二次规划、非线性优化、最小二乘法问题、非线性方程求解、多目标决策等问题,其函数表达简洁,优化算法选择灵活,参数设置自由,相比于其它很多成熟的优化程序具有明显的优越性。
机械优化设计是在现代机械设计理论发展基础上产生的一种新的设计方法,在机械零部件设计中取得了广泛的应用。
机械优化设计是在进行某种机械产品设计时,根据规定的约束条件,优选设计参数,使某项或几项设计指标获得最优值。
在进行优化设计时,首先要建立工程设计问题的数学模型,然后按照数学模型的特点选择优化方法及其计算程序,求得最优设计方案。
1四杆机构优化设计的数学模型四杆机构是机械传动的重要组成部分。
设计四杆机构通常使用作图法与实验法,这两种方法简单易行,但误差较大,运用解析法,能获得所要求的精度,然而用人工进行,整个设计过程是一项繁琐、冗长的工作,甚至可能无法实现。
采用Matlab 优化工具箱对四杆机构进行优化设计,不仅参数输入简单,而且编程工作量小,可更快捷准确地达到设计要求。
四杆机构种类很多,这里只以曲柄摇杆机构为例说明四杆机构优化设计方法。
Matlab 优化工具箱是一套功能强大的工程计算软件,集数值计算、符号运算、可视化建模、仿真和图形处理等多种功能于一体,被广泛应用于机械设计、自动控制和数理统计等工程领域。
基于MATLAB的曲柄摇杆机构的机械优化设计

基于MATLAB的曲柄摇杆机构的机械优化设计以曲柄摇杆机构为例,建立了运动分析数学模型。
以曲柄摇杆机构对应位置实际输出值与期望函数值的平方偏差之和的最小值作为实际目标进行优化。
应用MATLAB软件进行了优化设计和仿真分析,为机构优化设计提供了一种高效、直观的仿真手段,提高了对平面四连杆机构的分析设计能力。
标签:MATLAB;曲柄摇杆机构;优化设计前言平面四连杆机构虽然结构简单,但能有效地实现给定的运动规律或运动轨迹,很好地完成预定的动作,因而在工程实践中得到了广泛应用[1]。
传统的设计方法主要是图解法或分析法,对连杆机构设计,无论设计精度还是设计效率都相对低下,不能满足现代机械高速高精度的要求。
随着计算机技术的不断发展,为机构运用运动仿真实现优化设计提供了有效的手段。
MATLAB是一套功能强大的科学计算软件[2],被广泛应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。
其具有强大的数值计算能力和高效的工具箱函数,高效求解复杂庞大的实际工程问题,并可以根据需要,实现计算结果的可视化效果。
首先构建四连杆机构的数学模型,再利用MATLAB 软件强大的数值计算能力和高效的工具箱函数,以某规定期望函数的平面四连杆机构(机构运动简图如图1 所示)为例进行优化设计并进行了仿真计算,实现了机构运动仿真的可视化。
1 曲柄摇杆机构的数学模型1.1 设计变量机构的基本变量为各杆杆长及曲柄转角,根据曲柄摇杆机构各杆长度间的关系,独立的杆长变量有三个,分别为L2,L3,L4取杆长L1=1。
故曲柄摇杆机构的设计变量可以表示为:1.2 目标函数1.3 约束条件该机构的约束条件有两个方面:一是最小传动角约束条件[3];二是保证四杆机构满足曲柄存在的条件。
(1)最小传动角约束或对应的约束函数为:(2)曲柄存在的条件按曲柄存在条件,由机械原理可知:2 结果比较文章的算例是四连杆机构的一个经典案例,常被研究四连杆机构的学者进行引用,但是很多人研究的都是已知曲柄和机架的参数优化设计,而把机架也作为未知量求解的程序较少,也就是研究的多是两参数的问题,一般把曲柄设置为1,机架设置为5,然后编程进行优化,结果如表1。
基于VB与Matlab的曲柄摇杆机构设计

基于VB与Matlab的曲柄摇杆机构设计
唐昌松
【期刊名称】《现代机械》
【年(卷),期】2010(000)002
【摘要】本文分析了基于VB与Matlab的接口编程技术进行曲柄摇杆机构设计的方法,介绍了VB调用Matlab的实现方法.其充分发挥了VB在开发友好用户界面的简单易用及Matlab的科学计算功能强大的优势,此方法可推广到其它设计研究中.【总页数】2页(P37-38)
【作者】唐昌松
【作者单位】徐州工业职业技术学院,江苏,徐州,221140
【正文语种】中文
【中图分类】TH112
【相关文献】
1.基于MATLAB的曲柄摇杆机构的机械优化设计 [J], 朱艳华;周春梅
2.基于MATLAB的曲柄摇杆机构优化设计 [J], 李莹莹;游敏;徐建军
3.基于Matlab优化工具箱函数的已知连杆长度及其两相对位置尺寸的曲柄摇杆机构优化设计 [J], 金慧
4.基于Matlab的曲柄摇杆机构参数化设计 [J], 李世文;王力强;潘鑫;谭积明;翰林;李国和
5.基于Matlab的曲柄摇杆机构参数化设计 [J], 李世文;王力强;潘鑫;谭积明;翰林;李国和
因版权原因,仅展示原文概要,查看原文内容请购买。
优化设计-曲柄摇杆机构优化设计

优化设计-曲柄摇杆机构优化设计
[文档标题]
[摘要]
本文档旨在对曲柄摇杆机构进行优化设计,提高其性能和效率。
文档详细介绍了曲柄摇杆机构的原理和结构,分析了优化设计的必要性和目标,展示了具体的优化方案和实施过程。
通过本文档的阅读,读者将对曲柄摇杆机构的优化设计有一个深入的了解,并能够根据实际需求进行相应的设计和改进。
[目录]
1.引言
1.1 研究背景
1.2 研究目的
1.3 研究内容
2.曲柄摇杆机构原理和结构
2.1 曲柄摇杆机构的定义
2.2 曲柄摇杆机构的工作原理
2.3 曲柄摇杆机构的结构组成
3.优化设计的必要性
3.1 现有曲柄摇杆机构存在的问题
3.2 优化设计的目标
4.优化设计方案
4.1 参数分析和优化目标的确定
4.2 设计方案的制定
4.3 仿真分析和评估
5.优化设计的实施过程
5.1 实施步骤和流程
5.2 设计实验和数据分析
5.3 结果和效果评估
6.结论
6.1 实施结果总结
6.2 存在的问题和进一步改进方向[附件]
- 附件1:曲柄摇杆机构优化设计报告- 附件2:仿真分析数据表格
- 附件3:设计实验原始数据
[法律名词及注释]
1.专利法:指国家对某项新的技术或技术方案所给予的一种专
门的权利保护。
2.商标法:指用于表示特定商品来源的某种标志的法律规定和
制度。
3.著作权法:指对于某种独立的创作作品,其作者取得的权利。
4.侵权:指在未取得相应权利人同意的情况下,侵犯他人在专利、商标、著作权等方面的合法权益的行为。
[全文结束]。
基于Matlab优化工具箱函数的已知连杆长度及其两相对位置尺寸的曲柄摇杆机构优化设计

基于Matlab优化工具箱函数的已知连杆长度及其两相对位置尺寸的曲柄摇杆机构优化设计金慧【期刊名称】《浙江万里学院学报》【年(卷),期】2012(025)005【摘要】The target function was formulated by complex number vector method,the constraint condition of the winch and rocker machine was analyzed,and the design of the winch and rocker machine was optimized by using the Optimization Function of Optimization Toolbox of Matlab.%文章利用复数矢量法建立了曲柄摇杆机构的优化设计目标函数,分析了曲柄摇杆机构存在的约束条件,并利用MATLAB工具箱优化函数对已知连杆长度及其两相对位置尺寸的曲柄摇杆机构进行了优化设计。
【总页数】4页(P80-83)【作者】金慧【作者单位】浙江万里学院,浙江宁波315100【正文语种】中文【中图分类】TH112【相关文献】1.基于MATLAB优化工具箱的平面连杆机构的设计 [J], 王文娟2.基于改进遗传算法的曲柄摇杆机构再现已知运动规律的优化设计 [J], 张进华;张鄂3.基于MATLAB的曲柄摇杆机构优化设计 [J], 李莹莹;游敏;徐建军4.用遗传算法设计已知连杆长及两运动位置的曲柄摇杆机构 [J], 林和德5.基于MATLAB优化工具箱的提升机构优化设计 [J], 张其龙;王科社;刘晓川;赵伟茗因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程作业曲柄摇杆优化设计姓名:XX学号:XXXXX班级:XXXXX XX大学机械与动力学院目录1摘要2问题研究2.1问题重述2.2问题分析3数学模型的建立3.1设计变量的确定3.2目标函数的建立3.3约束条件的确定3.4标准数学模型4使用MATLAB编程求解4.1调用功能函数4.2首先编写目标函数M 文件4.3编写非线性约束函数M 文件4.4编写非线性约束函数M 文件confun.m4.5运行结果5结果分析6结论推广7过程反思8个人小结9参考文献1摘要: 为分析机构能够满足给定的运动规律和运动空间的要求,运用Matlab 22.10(32πψψ+=式中0ϕ和0ψ得小于45=≥][min γγ1可空间,可以适当预选机架杆的长度,现取l 4 =5。
2.2 问题分析设计时,可在给定最大和最小传动角的前提下,当曲柄从0ϕ转到090ϕ︒+时,要求摇杆的输出角最优地实现一个给定的运动规律()f ϕ。
这里假设要求:()()20023E f φϕφϕϕπ==+- (1)图1 曲柄摇杆机构简图对于这样的设计问题,可以取机构的期望输出角()E f φϕ=和实际输出角()F φϕ=的平方误差之和作为目标函数,使得它的值达到最小。
在图 1 所示的曲柄摇杆机构中,1l 、2l 、3l 、 4l 分别是曲柄AB 、连杆BC 、摇杆CD 和机架AD 的长度。
这里规定0ϕ为摇杆在右极限位置0φ时的曲柄起始位置角,它们由1l 、2l 、3l 和4l 确定。
3数学模型的建立 3.1 设计变量的确定决定机构尺寸的各杆长度1l 、2l 、3l 和4l ,以及当摇杆按已知运动规律开始运行时,曲柄所处的位置角0ϕ应列为设计变量,所有设计变量有:[][]1234512340TTx x x x x x l l l l ϕ== (2)考虑到机构的杆长按比例变化时,不会改变其运动规律,通常设定曲柄长度1l =1.0,在这里可给定4l =5.0,其他杆长则按比例取为1l 的倍数。
若取曲柄的初始位置角为极位角,则ϕ及相应的摇杆l 位置角φ均为杆长的函数,其关系式为:()()()()2222212432301242125arccos 2101l l l l l l l l l l ϕ⎡⎤⎡⎤++-+-+==⎢⎥⎢⎥++⎢⎥⎢⎥⎣⎦⎣⎦ (3)()()222221243230343125arccos 210l l l l l l l l l φ⎡⎤⎡⎤+--+--==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦(4)因此,只有2l 、3l 为独立变量,则设计变量为[][]1223T Tx x x l l ==。
3.2 目标函数的建立目标函数可根据已知-的运动规律与机构实际运动规律之间的偏差最小为指标来建立,即:()()21mi n mE i i i f x φφ==-→∑ (5)式中,Ei φ-期望输出角; m-输出角的等分数;i φ-实际输出角,由图 1 可知:图2 曲柄摇杆机构的运动学关系()()02i i i i i i i παβϕπφπαβπϕπ--≤≤⎧⎪=⎨-+≤≤⎪⎩ (6) 式中,222222322132arccos arccos 22i i i i i r l l r x x rl r x α⎛⎫⎛⎫+-+-== ⎪ ⎪⎝⎭⎝⎭ (7)222241424arccos arccos 210i i i i i r l l r rl r β⎛⎫⎛⎫+-+== ⎪ ⎪⎝⎭⎝⎭(8)i r == (9)3.3 约束条件 曲柄存在条件:12131423;,l l l l l l l l ≤≤+≤+ ()()24133412,l l l l l l l l ≤-+≤-+ 曲柄与机架共线位置时的传动角(连杆BC 和摇杆CD 之间的夹角): 最小传动角min min 45r BCD ︒=∠≥ 最大传动角max max 135r BCD ︒=∠≤ 由上面的分析可以算出:()222222234112min231216arccos 4522l l l l x x r l l x x ︒⎡⎤+--⎡⎤+-⎢⎥==≥⎢⎥⎢⎥⎣⎦⎣⎦ (10)()222222234112max231236arccos 13522l l l l x x r l l x x ︒⎡⎤+-+⎡⎤+-⎢⎥==≤⎢⎥⎢⎥⎣⎦⎣⎦ (11)3.4 标准数学模型通过上面的分析后,将输入角分成 30 等分(m=30),经过转化为标准形式得到曲柄摇杆机构优化设计标准数学模型为:()()21min mEi i i f x φφ==-→∑[][]2312TTx l l x x ==()()()()()()()112231241252122612122271212101060..40401.41436036 1.4140g x x g x x g x x x s t g x x x g x x x g x x x x x g x x x x x =-≤⎧⎪=-≤⎪⎪=--≤⎪=--≤⎨⎪=--≤⎪=+--≤⎪⎪=---≤⎩ (12) 机械优化设计中的问题,大多数属于约束优化问题,此为非线性约束优化问题,运用 MATLAB 优化工具箱的命令函数 fmincon 来处理有约束的非线性多元函数最小化优化问题。
4使用MATLAB 编程求解4.1 本问题属于一般非线性规划问题,其标准型为:min ()f x,,()0..()0,AX b Aeq X beq C X s t Ceq X vlb X vub ≤∙=≤⎧⎨=≤≤⎩ (13)调用MATLAB 软件优化工具箱中非线性规划求解函数fmincon 来求解。
其命令的基本格式为: [函数] fmincon [格式]x = fmincon(fun,x0,A,b) x = fmincon(fun,x0,A,b,Aeq,beq) x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub) x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon) x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options) [x,fval] = fmincon(…) [x,fval,exitflag] = fmincon(…) [x,fval,exitflag,output] = fmincon(…) [x,fval,exitflag,output,lambda] = fmincon(…) [x,fval,exitflag,output,lambda,grad] = fmincon(…) [x,fval,exitflag,out put,lambda,grad,hessian] = fmincon(…) [说明]fun 是目标函数options 设置优化选项参数fval 返回目标函数在最优解x点的函数值exitflag 返回算法的终止标志output 返回优化算法信息的一个数据结构grad 返回目标函数在最优解x点的梯度hessian 返回目标函数在最游解x点Hessian矩阵值编写程序求解4.2首先编写目标函数M 文件fun1.mfunction f=fun1(x)s=30;qb=1;jj=5;fx=0;ci0=acos(((qb+x(1))^2-x(2)^2+jj^2)/(2*(qb+x(1))*jj));%曲柄初始角fa0=acos(((qb+x(1))^2-x(2)^2-jj^2)/(2*x(2)*jj));%摇杆初始角for i=1:sci=ci0+(pi*i)/(2*s);fai(i)=fa0+(2*(ci-ci0)^2)/(3*pi);ri=sqrt(qb^2+jj^2-2*qb*jj*cos(ci));alfi=acos(((ri^2+x(2)^2)-x(1)^2)/(2*ri*x(2)));bati=acos((ri^2+jj^2-qb^2)/(2*ri*jj));if ci>0 && ci<=pipsi(i)=pi-alfi-bati;elseif ci>pi && ci<=2*pipsi(i)=pi-alfi+bati;endfx=fx+(fai(i)-psi(i))^2;endf=fx;i=1:1:30;plot(i,fai(i),i,psi(i),'--'); %画曲线图legend('期望曲线','实际曲线'); %标注曲线图对应名称4.3编写非线性约束函数M 文件confun.mfunction [c,ceq]=confun(x)qb=1;jj=5;m=45*pi/180;n=135*pi/180;c(1)=x(1)^2+x(2)^2-2*x(1)*x(2)*cos(m)-(jj-qb)^2;%重合时最小传动角的非线性约束条件c(2)=-x(1)^2-x(2)^2+2*x(1)*x(2)*cos(n)+(jj+qb)^2;%共线时最小传动角的非线性约束条件ceq=[];4.4在MATLAB 命令窗口调用优化程序x0=[6;6];lb=[1;1];ub=[];a=[-1 0;0 -1;-1 -1;1 -1; -1 1];b=[-1;-1;-6;4;4];options=optimset('LargeScale','off','display','iter');[x,fval,exitflag]=fmincon(@fun1,x0,a,b,[],[],lb,ub,@confun,options);4.5运行结果x =[4.1285 2.3226]fval =0.0076图3 输出角期望曲线与在MATLAB结果下的实际曲线对比图图4 传动角与曲柄输入角变化关系图5结果分析通过Matlab工具箱的优化求解,我们得到了最终的曲柄摇杆机构的最优杆长条件,即L2=4.1285,L3=2.3226。
从运行结果上面来看,得到的数据还是比较理想的,在输出角期望曲线与在MATLAB结果下的实际曲线对比图(图3)中,我们可以清楚地看到,期望曲线与实际曲线的拟合程度比较好。
在传动角6结论推广由于在本问题当中,曲柄长度L1和机架长度L4是预先取的L1=1,L4=5,我们通过对L2和L3的优化设计,最终得到了L2=4.1285,L3=2.3226,如果把1看作是单位长度,那么我们最终求解出来的其实是曲柄摇杆机构符合已知运动轨迹的杆长比例。
只要曲柄摇杆机构的四杆长度按照这个比例,即L1:L2:L3:L4=1:4.1285:2.3226:5,那么我们得到的曲柄摇杆机构的运动轨迹都是比较理想的。
