杨氏双缝干涉条纹的特点共65页文档
合集下载
相干光杨氏双缝干涉
S
W
实验装置：
M1
d S1
x o
虚光源 S1、S2
S2
M2
W'
L S1S2 平行于WW ' d L
屏幕上O点在两个虚光源连线的垂直平分线上，屏幕
上明暗条纹中心对O点的偏离x为：
x k L
d
明条纹中心的位置
k 0,1,2
x 2k 1 L
2d
暗条纹中心的位置
18
第19页/共21页
二、 洛埃镜实验
解：由明纹公式：
xk
kD
d
两条 4 级明纹的距离为：
x 2kD
d
4
o I
4
x
2 4
632 .8 10 9 500 1.2 10 3
10 3
2.1 10 3 m
15
第16页/共21页
例2：白色平行光垂直入射到间距为 d=0.25mm 的双缝 上，距缝 50cm 处放置屏幕，分别求第一级和第五级明 纹彩色带的宽度。（设白光的波长范围是从400.0nm 到 760.0nm）。
第20页/共21页
n1 n1 n2
n2
19
谢谢您的观看！
20
第21页/共21页
飞速的发展，形成了非线性光学等现代光学。
1
第2页/共21页
相干光
一、光波
红外光：λ>760nm
可见光：400nm与760nm之间
紫外光：λ<400nm 光的颜色：
单色光——只含单一波长的光：激光
复色光——不同波长单色光的混合：白光
二、光矢量
光是电磁波，它具有相互垂直的电场强度矢量和磁 场强度矢量。
通常电场强度E的振动称为光振动，
普通物理学 §12-3 双缝干涉
附加了半个波长的波程差，称为半波损失.
上页 下页 返回 退出
思考：
明条纹
k
暗条纹
d
o D
光密介质 半波损失
1 ( k ) 2
练习卷 3174
上页 下页 返回 退出
(1)两相邻明纹（或暗纹）间距
D x 10 12mm d
D d
(2)
(3) 不变
上页 下页 返回 退出
上页 下页 返回 退出
（2）将双缝干涉装置由空气中放入水中时，屏上的 干涉条纹有何变化？ 两相邻明纹（或暗纹）间距
D D x n d d n
实验装置放入水中后条纹间距变小
上页 下页 返回 退出
（3）若S1、S2两条缝的宽度不等，条纹有何变化？ 两条缝的宽度不等，使两光束的强度不等；原 极小处的强度不再为零，条纹的可见度变差。
k=1.1
这一结果表明：在中央白色明纹两侧， 只有第一 级彩色光谱是清晰可辨的。
上页 下页 返回 退出
波源
d
o D
思考题：
中央明纹向何方向移动？条纹间距如何变化
上页 下页 返回 退出
1 2
o D
零级 明纹
波程差＝0
1 2
零级 明纹
波程差＝0
o D
上页 下页 返回 退出
D
上页 下页 返回 退出
上页 下页 返回 退出
§12-3 双缝干涉
一、杨氏双缝实验
杨（T.Young）在1801年首先用实验方法研究光的干涉
上页 下页 返回 退出
相干光的获得：分波阵面法
x
r
1
x
p
r
· x
第二节双缝干涉
光程: 在传播时间相同或相位改变相同的条件下,把光在介质 中传播的路程折合为光在真空中传播的相应路程,光程等于介 质折射率乘以光在介质中传播的路程.
2. 光程差
两束相干光,分别在两介质中传播后p点相遇,其相位差为
∆φ
=
2π r2 λ2
−
2π r1 λ1
=
2πn2 r2 λ0
−
2πn1 r1 λ0
=
2π λ0
传播的路径x 应为
x = ct = c r = nr
u
在介质中相应的相位改变为
∆φ = 2π r λ
在改变相同相位的条件下,光波在不同介质中传播的路程是 不同的.
∆φ = 2π r = 2π x λ λ0
x = λ 0r = nr λ
上式说明在相位变化相同的条件下,光在介质中传播的路程r
可折合为光在真空中传播的路程 nr.
= 0,1,2,3.........) I (k = 0,1,2,3.........)
=
4I1 I=
0
加强 减弱
两束不相干的光波在空间相遇其光强为 I = I1 + I2 ,没有干涉项. 四. 光波的半波损失
光波传播遇两个不同的介质,介质的疏密由两个介质的折射率 决定,光疏介质,折射率n相对小;光密介质,折射率n相对大. 光由光疏介质→光密介质→光疏介质,有半波损失,此时有位 相的突变. 五. 光程 光程差
解：无云母片， r1 = r2 δ =0
s1
r1
加上云母片，
s2
r2
P0
δ =[(r1 − e)⋅1+ ne− r2 ⋅1] = (n −1)e r1 = r2
p0处为第七级明纹
δ = 7λ = (n −1)e e = 7λ = 6.6 ×10−6 m
§11.2 杨氏双缝干涉解析
作者：杨茂田 Chapter 11. 光学
§11. 2 杨氏双缝干涉
一、观测屏上的光强分布
p点光振动方程：
p
x o
D
E1p A10 cos ( t 2 r1 ) E2p A20 cos ( t 2 r2 )
S1
d
S2
r1 r2
Ep Ap cos( t )
作者：杨茂田 Chapter 11. 光学
§11. 2 杨氏双缝干涉
观测屏上光强曲线(按位置分布)：
Ip
4I0
5 2
- 2
3 2
-
2
3 2
2
x D
5 2
d
2
关于中央明纹对称！ 相邻两条明(暗)纹间距：
x xk 1 xk D d
作者：杨茂田 Chapter 11. 光学
2 ( r2 r1 )
作者：杨茂田 Chapter 11. 光学
§11. 2 杨氏双缝干涉
2 2 光强：Ip Ap , , I1 A10
2 I 2 A20
Ip I1 I 2 2 I1 I 2 cos ( )
设 x << D ( 旁轴条件 )
S1
d
r1 r2
2 ( r2 r1 ) 2
( δ 为光程差 ) 明纹 暗纹
2k 2
Ip Ipmax 干涉加强
( 2k 1) I p Ipmin 干涉减弱 2
作者：杨茂田 Chapter 11. 光学
§11. 2 杨氏双缝干涉
观测屏上光强分布曲线：
大学物理-杨氏双缝干涉
杨氏双缝干涉条纹的讨论
d' k 明纹 d k 0 , 1 , 2 , x d' ( 2k 1) 暗纹 d 2
白光照射时，出现彩色条纹
(P99)
二、三级间开始有重叠
k 3
k 2
k 1
k 1
k2
k 3
相邻两条明纹(或暗纹)间距
d' x d
总结: 真空中杨氏双缝干涉实验
2
1
B
2
C
h
A
作AB BC, 则A、B为同相点(A、B在同一波面上) 光线1 A C 光线2 B C
波程差 AC BC
2
入射波1自空气（光疏媒质）射入 湖水（光密媒质），反射波AC有 半波损失
二、半波损失（书P101 理解掌握）
设媒质1、2的折射率分别为n1、n2，若 n1>n2，则
2) 零级明纹（k = 0）对应 = 0
k
干涉加强明纹
(P98)
d
s1
r1
r2
d'
B
s
x
o
o
s2
k=0 k=0
r
x
d' k d
明纹位置
4)零级暗纹,第一条暗纹
Ex:书P167：11-8
d' ( 2k 1) 暗纹位置 d 2 3) x是可测量量(大量)
k 0,1,2,
Chap 11 (波动)光学
可见光波长范围 : 400 ~ 760 nm (P82) 11-1 相干光 一 光是一种电磁波（横波 P94）
1、普通光源发光特点(书 P95 )：
波动光学第1讲——光的干涉 杨氏双缝干涉.ppt
三棱镜 滤光片 激光器件
三. 光的相干性
光的干涉现象：
当两列相干光相遇时,在相遇空间出现明暗稳定 分布的现象
1、原子的发光机理
E
0
E 3
1.5eV
E 2
3.4eV
E 1
13.6eV
波列
E
E 3
波列长L =
E
c (E E )/h
2
2
1
E
1
● ●
●
●
0 1.5eV 3.4eV
d
(n 1)d 3.5
S1
r1
d 3.5
n 1
a
S2
r2 D
o
3.5 632 .8 10 9 1.4 1
5.5 10 -6 m
作 业 题：习题16.12、16.14、16.15； 预习内容：§16.4-16.5 复习内容： 本讲
2、相干光的获得
利用普通光源获得相干光的方法的基本原理是把由 光源同一点发出的光设法分成两部分，然后再使这两部分
叠加起来。
分波阵面法
在同一波面上两固定点光源，发出的光 产生干涉的方法为分波面法。如杨氏双 缝干涉实验（图1）
分振幅法
一束光线经过介质薄膜的反射与折射， 形成的两束光线产生干涉的方法为分振 幅法。如薄膜干涉（图2）。
讨论
以中央明条纹为中心、两侧对称分布的、 平行等距的明暗相间的直条纹
三．菲涅耳双棱镜干涉
P
S： 线光源 B： 障碍物
B
P： 屏
S
:M1、M2：平面镜
A： 镜交线 镜面夹角
S1M21
S2
A M2
O
r : S与A距离
三. 光的相干性
光的干涉现象：
当两列相干光相遇时,在相遇空间出现明暗稳定 分布的现象
1、原子的发光机理
E
0
E 3
1.5eV
E 2
3.4eV
E 1
13.6eV
波列
E
E 3
波列长L =
E
c (E E )/h
2
2
1
E
1
● ●
●
●
0 1.5eV 3.4eV
d
(n 1)d 3.5
S1
r1
d 3.5
n 1
a
S2
r2 D
o
3.5 632 .8 10 9 1.4 1
5.5 10 -6 m
作 业 题：习题16.12、16.14、16.15； 预习内容：§16.4-16.5 复习内容： 本讲
2、相干光的获得
利用普通光源获得相干光的方法的基本原理是把由 光源同一点发出的光设法分成两部分，然后再使这两部分
叠加起来。
分波阵面法
在同一波面上两固定点光源，发出的光 产生干涉的方法为分波面法。如杨氏双 缝干涉实验（图1）
分振幅法
一束光线经过介质薄膜的反射与折射， 形成的两束光线产生干涉的方法为分振 幅法。如薄膜干涉（图2）。
讨论
以中央明条纹为中心、两侧对称分布的、 平行等距的明暗相间的直条纹
三．菲涅耳双棱镜干涉
P
S： 线光源 B： 障碍物
B
P： 屏
S
:M1、M2：平面镜
A： 镜交线 镜面夹角
S1M21
S2
A M2
O
r : S与A距离
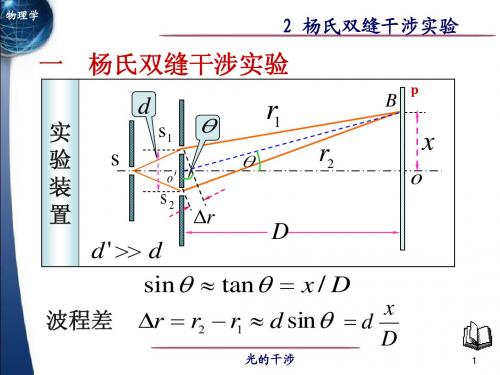
第2节 杨氏双缝干涉实验
r1
r2
D
加强
B
p
x
o
s2
r
x r d D
(2k 1) 减弱 2
光的干涉
k
k 0,1,2,
2
物理学
2 杨氏双缝干涉实验
d
s1
r1
r2
D
明纹 暗纹
光的干涉
B
p
s
x
o
o
s2
r
D k d x D (2k 1) d 2
k 0,1,2,
'
光的干涉
5
物理学
2 杨氏双缝干涉实验
(2) 、d ' 一定时,条纹间距 d 与 x 的关系如何？
光的干涉
6
物理学
2 杨氏双缝干涉实验
二 缝宽对干涉条纹的影响 空间相干性
实验观察到，随缝宽的增大，干涉 条纹变模糊，最后消失．
空间相干性
光的干涉
7
物理学
2 杨氏双缝干涉实验
三
劳埃德镜
P'
P
s1
物理学
2 杨氏双缝干涉实验
一
实 验 装 置
杨氏双缝干涉实验
d
s1
r1
r2
D
B
p
s
x
o
o
s2
r
d ' d sin tan x / D
波程差
x r r2 r1 d sin d D
光的干涉
1
物理学
2 杨氏双缝干涉实验
d
实 s 验 装 置
s1
o
杨氏双缝干涉(精)
1、杨氏双缝干涉（1）杨氏简介托马斯·杨（Thomas Young），英国物理学家、医师、考古学家，波动光学的伟大奠基人，在光学、生理光学、材料力学等方面都有重要的贡献。
●波动光学——双缝干涉十八世纪前后，牛顿的“光的微粒说”在光学研究中占统治地位。
杨氏在德国留学期间便对光的微粒说提出了怀疑。
他在哥丁根的博士论文中提出了关于声和光都是波动，不同颜色的光和不同频率的声都是一样的观点。
他认为，正如惠更斯以前所说的那样，光是一种波动。
1801年，杨氏出版了《声和光的实验和探索概要》一书，系统地论述了光的波动观点，向牛顿提出了挑战。
杨氏认为，解释强光和弱光的传播速度一样，用波动说比用微粒说更有效。
他还证明了惠更斯在冰洲石中所看到的双折射现象是正确的。
为了证实光的波动说的正确性，托马斯·杨用非常巧妙的方法得到了两个相干光源，并进行了著名的光的干涉实验。
他最初的实验方法是用强光照射小孔，以孔作为点光源，发出球面波，在离开小孔一定距离的地方放置另外两个小孔，它们把前一小孔发出的球面波分离成两个很小的部分作为相干光源。
于是在这两个小孔发出的光波相遇区域产生了干涉现象，在双孔后面的屏幕上得到了干涉图样。
●生理光学——三原色原理托马斯·杨在生理光学方面也有深入的研究。
他的光学理论研究也是从这里开始的。
他把光学理论应用于医学之中，奠定了生理光学的基础。
他提出了眼睛观察不同距离的物体是靠改变眼球水晶体的曲度来调节的观点，这是最早的眼睛光学原理的解释。
他还提出了人们对颜色的辨别是由于视网膜上有几种不同的结构，分别感受红、绿、蓝光线的假设，以此可以说明色盲的成因。
他还建立了三原色原理，认为一切色彩都是有红、绿、蓝三种原色按不同的比例混合而成的。
这一原理已成为现代颜色理论的基础。
●材料力学——杨氏模量托马斯·杨在材料力学方面最早提出弹性模量的概念，并认为剪应力也是一种弹性形变。
后来以他的名字命名了弹性模量，称为杨氏模量。
杨氏双缝干涉实验
1.菲涅耳双面镜
P
M1
sL
s1
d
s2
o
M2
D
2.劳埃德镜
P'
P
s1
d
s2
ML
D
当P移动到P/时屏与反射镜M接触,由于半波损失,接触处为暗纹。
d
x
D2
k
加
强
明纹公式x （k - 1）D
2d
总结杨氏双缝干涉
d
x DBiblioteka k加强 明纹公式x k D d 条纹间距 x D
d
2a
x D
2
k
加
强 明纹公式x （k - 1）D 2 2a
分波面与分振幅
一、 杨氏双缝干涉
1、 杨氏双缝干涉实验装置
双缝
红光 观察屏 入射
白光 入射
s
s1
2ao
s2
2a
r1 r2
D
D 2a
D
Bp
x
o
x
2、干涉条纹
r2 r1 r
s 2asin
D 2a
s1
2a
o
r1
r2
p
x
o
sin tan x / D
2a tan 2a x
s 2 r
光程差
2a
x D
k
干涉加强
2、干涉条纹
明纹公式 x k D
2a
暗纹公式 x (2k 1) D
4a
k 0,1,2,
3 干涉条纹形状及间距
明纹条件 暗纹条件
x k D
x
2a (2k 1)
D
4a
k 0,1,2,
相邻两条明纹或暗纹的距离：
§11.2 杨氏双缝干涉
D xk ( 2k 1) d 2 x sin tg D
r2 r1 d x D
S1
d
x
r1
p
r2
o
x o
S2
D
2k
2
明纹
2
( 2k 1)
暗纹
作者：杨茂田 Chapter 11. 光的干涉与衍射
§11. 2 杨氏双缝干涉
S2
作者：杨茂田 Chapter 11. 光的干涉与衍射
§11. 2 杨氏双缝干涉
一、观测屏上的光强分布
p点光振动方程：
p
E1p A10 cos ( t E2p A20 cos ( t
2
2
r1 )
S1
r1 r2
x o
d
r2 )
S2
D
Ep Ap cos( t )
2 ( r2 r1 ) 2
( δ 为光程差 ) 干涉加强 干涉减弱 明纹 暗纹
2k
2
I p I pmax
( 2k 1)
2
I p I pmin
作者：杨茂田 Chapter 11. 光的干涉与衍射
§11. 2 杨氏双缝干涉
观测屏上光强分布曲线：
2 2 2
2
( r2 r1 )
作者：杨茂田 Chapter 11. 光的干涉与衍射
§11. 2 杨氏双缝干涉
2
光强：Ip
Ap ,
2
I1 A10 ,
2
I 2 A20
r2 r1 d x D
S1
d
x
r1
p
r2
o
x o
S2
D
2k
2
明纹
2
( 2k 1)
暗纹
作者：杨茂田 Chapter 11. 光的干涉与衍射
§11. 2 杨氏双缝干涉
S2
作者：杨茂田 Chapter 11. 光的干涉与衍射
§11. 2 杨氏双缝干涉
一、观测屏上的光强分布
p点光振动方程：
p
E1p A10 cos ( t E2p A20 cos ( t
2
2
r1 )
S1
r1 r2
x o
d
r2 )
S2
D
Ep Ap cos( t )
2 ( r2 r1 ) 2
( δ 为光程差 ) 干涉加强 干涉减弱 明纹 暗纹
2k
2
I p I pmax
( 2k 1)
2
I p I pmin
作者：杨茂田 Chapter 11. 光的干涉与衍射
§11. 2 杨氏双缝干涉
观测屏上光强分布曲线：
2 2 2
2
( r2 r1 )
作者：杨茂田 Chapter 11. 光的干涉与衍射
§11. 2 杨氏双缝干涉
2
光强：Ip
Ap ,
2
I1 A10 ,
2
I 2 A20
11-2 双缝实验
红光光强分布图
D x d
I
4I 0
波 长 不 同 条 纹 间 距 不 同
D D 4 1 2 1 d d
紫光光强分布图
0
D 2 1 d
D 4 1 d
x
I 4I 0
D D 4 2 2 2 d d
0
D D 2 2 4 2 d d
第十一章 光学
x
11-2-1 用白光光源进行双缝干涉实验，求清晰可辨光谱的级次。
1
频率
v0 v0
波长 0
0 / n
波速 c
u c/n
介质中 n (n 1)
(4)狭缝S向下移动；
中心上移，间距不变
D 条纹间距：x d
(5)双缝向下移动；
中心下移，间距不变 狭缝
双缝
11-2-3 以单色光照射到相距为0.2mm的双缝上，双缝与屏幕的垂直距离为1m。 求(1)从第一明条纹到同侧的第四级明纹间的距离为7.5mm，求单色光的波长； (2)若入射光的波长为600nm，中央明纹中心距离最邻近的暗纹中心的距离 是多少？
11-2 杨氏双缝干涉(Young‘s Double-slit Interference Experiment)
杨氏双缝干涉实验图示
双缝 单缝
S1 S2
屏
暗条纹 明条纹 暗条纹
S
明条纹 暗条纹 明条纹 暗条纹
明 暗 相 间 等 间 距 的 条 纹
第十一章 光学
10-3 波的干涉 (Interference of Waves)
明条纹中心位置
D xk k , k 0, 1, 2, d d x14 D 500nm x14 x4 x1 k4 k1 D k4 k1 d
D x d
I
4I 0
波 长 不 同 条 纹 间 距 不 同
D D 4 1 2 1 d d
紫光光强分布图
0
D 2 1 d
D 4 1 d
x
I 4I 0
D D 4 2 2 2 d d
0
D D 2 2 4 2 d d
第十一章 光学
x
11-2-1 用白光光源进行双缝干涉实验，求清晰可辨光谱的级次。
1
频率
v0 v0
波长 0
0 / n
波速 c
u c/n
介质中 n (n 1)
(4)狭缝S向下移动；
中心上移，间距不变
D 条纹间距：x d
(5)双缝向下移动；
中心下移，间距不变 狭缝
双缝
11-2-3 以单色光照射到相距为0.2mm的双缝上，双缝与屏幕的垂直距离为1m。 求(1)从第一明条纹到同侧的第四级明纹间的距离为7.5mm，求单色光的波长； (2)若入射光的波长为600nm，中央明纹中心距离最邻近的暗纹中心的距离 是多少？
11-2 杨氏双缝干涉(Young‘s Double-slit Interference Experiment)
杨氏双缝干涉实验图示
双缝 单缝
S1 S2
屏
暗条纹 明条纹 暗条纹
S
明条纹 暗条纹 明条纹 暗条纹
明 暗 相 间 等 间 距 的 条 纹
第十一章 光学
10-3 波的干涉 (Interference of Waves)
明条纹中心位置
D xk k , k 0, 1, 2, d d x14 D 500nm x14 x4 x1 k4 k1 D k4 k1 d
杨氏双缝(修改好)
r1 r2
*
Pபைடு நூலகம்
E = E + E + 2E10E20 cos ∆ϕ
2 2 10 2 20
I = I1 + I2 + 2 I1I2 cos ∆ϕ
I=
∫ (I τ
0
1
τ
1
+ I2 + 2 I1I2 cos ∆ϕ )dt
= I1 + I2 + 2 I1I2 ⋅
∫ cos ∆ϕdt τ
0
1
τ
I = I1 + I2 + 2 I1I2 ⋅
a、非相干叠加 、
∫ cos ∆ϕdt τ
0
1
τ
独立光源的两束光或同一光源的不同部位所发出 独立光源的两束光或同一光源的不同部位所发出 的光的位相差“瞬息万变” 的光的位相差“瞬息万变”
τ
∫ cos ∆ϕdt = 0 τ
0
1
I = I1 + I2
叠加后光强等与两光束单独照射时的光强之和， 叠加后光强等与两光束单独照射时的光强之和， 无干涉现象
λ
S d
S1
S2
r1 r2
p
δ = r2 − r 1
r1
2=D2+(x-d/2)2
x o
D
r22=D2+(x+d/2)2
r22- r12=2xd
(r2- r1)( r2+r1)=2xd
D >> d
r2+r1≈2D
x ∴δ = d ⋅ D
2、杨氏干涉条纹
（1）明纹：干涉加强 明纹：
δ = ± kλ
D x = ±k λ d
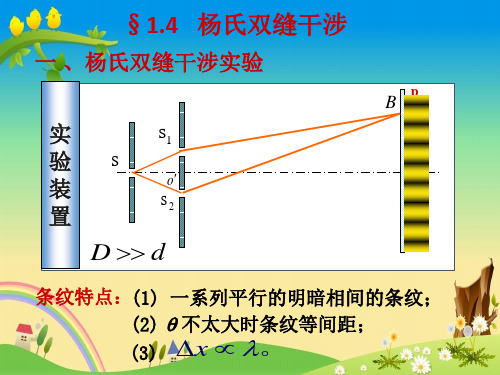
【大学物理】第四讲 双缝干涉
s2
r
D
D d
Bp
x
o
通常D x sin tan x / D
光程差
x
r r2 r1 d sin
d D
d
s1
r1
s
r2
o
s2
r
D
Bp
x
o
x
k D
d
D (2k 1)
明纹中心 k 0,1,2,
暗纹中心
d
2
明、暗条纹中心位置
k D
x
d
D (2k 1)
d
2
明纹中心 k 0,1,2,
x
D d
n
D d
n
n水> n空气
x水 x空气
结论：实验装置放入水中后条纹间距变小。
例题1-1 在杨氏双缝干涉实验中，用波
长=589.3 nm的纳灯作光源，屏幕距双缝
的距离D=1m，问：
(1)当双缝间距2mm 和10 mm时，两相邻 明条纹中心间距是多少？
(2)如肉眼仅能分辨两条纹的间距为0.15 mm ，现用肉眼观察干涉条纹，问双缝的最 大间距是多少？
折射波无半波损失。
Δx14
D d
x4
kλ ,
x1
k
0,
D d
k4
1,
2,
k1
λ d x14 500 nm
D k4 k1
(2) x’
1 2
D λ 1.5 d
mm
例题1-2 当双缝干涉装置的一条狭缝后面盖 上折射率为 n 1.58的云母片时，观察到屏幕 上干涉条纹移动了9个条纹间距，已知波长 ，求云 5母50片nm的厚度。
述内容有
r
D
D d
Bp
x
o
通常D x sin tan x / D
光程差
x
r r2 r1 d sin
d D
d
s1
r1
s
r2
o
s2
r
D
Bp
x
o
x
k D
d
D (2k 1)
明纹中心 k 0,1,2,
暗纹中心
d
2
明、暗条纹中心位置
k D
x
d
D (2k 1)
d
2
明纹中心 k 0,1,2,
x
D d
n
D d
n
n水> n空气
x水 x空气
结论：实验装置放入水中后条纹间距变小。
例题1-1 在杨氏双缝干涉实验中，用波
长=589.3 nm的纳灯作光源，屏幕距双缝
的距离D=1m，问：
(1)当双缝间距2mm 和10 mm时，两相邻 明条纹中心间距是多少？
(2)如肉眼仅能分辨两条纹的间距为0.15 mm ，现用肉眼观察干涉条纹，问双缝的最 大间距是多少？
折射波无半波损失。
Δx14
D d
x4
kλ ,
x1
k
0,
D d
k4
1,
2,
k1
λ d x14 500 nm
D k4 k1
(2) x’
1 2
D λ 1.5 d
mm
例题1-2 当双缝干涉装置的一条狭缝后面盖 上折射率为 n 1.58的云母片时，观察到屏幕 上干涉条纹移动了9个条纹间距，已知波长 ，求云 5母50片nm的厚度。
述内容有
杨氏双缝
决定干涉条纹衬比度的因素： 决定干涉条纹衬比度的因素： 1)振幅比 振幅相差越大，衬比度越差。 振幅比 振幅相差越大，衬比度越差。 2)光源的宽度 光源宽度越大，衬比度越差。 光源的宽度 光源宽度越大，衬比度越差。 3)光源的单色性 光源单色性越差，衬比度越差。 光源的单色性 光源单色性越差，衬比度越差。
λ ─真空中波长 真空中波长
光在介质中传播路程长为d时 光在介质中传播路程长为 时，产生的相位改变 为： d ∆ϕ = ϕ b − ϕ a = 2π n a λ b λn · ·
n
λ n ─介质中波长 介质中波长
d
介质
λn λ 结论：经过相同的距离，产生的相位差不同。 结论：经过相同的距离，产生的相位差不同。
定义光程 ：介质折射率n和光在介质中传播的 定义光程 L：介质折射率 和光在介质中传播的 距离d的乘积 的乘积nd 距离 的乘积 。即： L = nd 光程是光的等效真空路程， 光程是光的等效真空路程，在相位改变相同或 传播时间相等的条件下， 传播时间相等的条件下，光在介质中传播的路 程d 等效于光在真空中传播的路程nd 。 等效于光在真空中传播的路程 光程差： 光程差： δ = ∆L = L2 − L1
由同方向同频率振动的合成规律
2 A 2 = A12 + A2 + 2 A1 A2 cos ∆ϕ ,
得屏上某点光强
I = I 1 + I 2 + 2 I 1 I 2 cos ∆ϕ ,
衬比度：表示条纹的明显程度。 衬比度：表示条纹的明显程度。
I max − I min V= I max + I min
2 ∆ϕ I = 4 I1 cos 2 I I1 = I 2
§3.1 杨氏双缝干涉
杨氏双缝干涉条纹的特点PPT65页
23、一切节省，归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰，决心到最后会全部推倒。——莎士比亚
25、学习是劳动，是充满思想的劳动。——乌申斯基
谢谢！
杨氏双缝干涉条纹的特点
46、法律有权打破平静。——马·格林 47、在一千磅法律里，没有一盎司仁 爱。— —英国
48、法ቤተ መጻሕፍቲ ባይዱ一多，公正就少。——托·富 勒 49、犯罪总是以惩罚相补偿；只有处 罚才能 使犯罪 得到偿 还。— —达雷 尔
50、弱者比强者更能得到法律的保护 。—— 威·厄尔
21、要知道对好事的称颂过于夸大，也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤，荒于嬉；行成于思，毁于随。——韩愈
25、学习是劳动，是充满思想的劳动。——乌申斯基
谢谢！
杨氏双缝干涉条纹的特点
46、法律有权打破平静。——马·格林 47、在一千磅法律里，没有一盎司仁 爱。— —英国
48、法ቤተ መጻሕፍቲ ባይዱ一多，公正就少。——托·富 勒 49、犯罪总是以惩罚相补偿；只有处 罚才能 使犯罪 得到偿 还。— —达雷 尔
50、弱者比强者更能得到法律的保护 。—— 威·厄尔
21、要知道对好事的称颂过于夸大，也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤，荒于嬉；行成于思，毁于随。——韩愈
§112 杨氏双缝干涉.
1)
2
关于中央明纹对称！
S1
do
S2
x
r1
p
r2 x
o
D
相邻两条明(暗)纹间距：
x
xk1 xk
D d
Chapter 11. 光学
作者：杨茂田§11. 2 杨氏双缝干涉
观测屏上光强曲线(按位置分布)：
Ip 4I0
P. 13 /25 .
- 2 -
5 2
3 2
2
2
x
D d
3 5
22
2
P. 24 /25 .
1. 干涉规律：
2k
明纹
r2 r1
2
(2k 1)
暗纹
(
k 0, 1,
2, )
2
2.
相邻明纹(暗纹)间距：x
D d
3. 双缝干涉条纹特点 : 平行、等间距、等亮度的条纹！
4. 条纹位置分布：
( 请看录像 )
306 Chapter 11. 光学
作者：杨茂田§11. 2 杨氏双缝干涉
p
设 x << D ( 旁轴条件 )
S1
r1 r2
x
d
o
I1 I2 I0
Ip
4I0
cos2(
2
)
S2
D
2
(r2
r1 )
Ipmin 0 Ip Ipmax 4I0 与p点位置有关！
Chapter 11. 光学
作者：杨茂田§11. 2 杨氏双缝干涉
P. 6 /25 .
2k
Ip Ipmax 干涉加强
Chapter 11. 光学
作者：杨茂田§11. 2 杨氏双缝干涉
2杨氏双缝干涉解析
[2( k 1 ) 1 ]D (2 k 1 )D D x 2a 2a a
可以看出相邻明纹与相邻暗纹的间距都相 同，所以条纹明暗相间平行等距。
§2.相干光源 / 六、讨论
4.条纹间距与各量之间的关系
x
D
a
a. S
x
S1 a
S2
r1 r2
D
P x O
I
屏
干 涉 条 纹 光 强 分 布
§2.相干光源 / 一、杨氏双缝干涉
二.两条光线的光程差
S 1S 2 R OPQ ，
x S 1R D
S
点 光 源
单 缝
S1 a Q r 2 R S2
双 缝
r1
P x o
I D
屏
§2.相干光源 / 二、两条光线的光程差
x S 1R D
S 2S 1 R 很小, S 1 R a ，
o
I
§2.相干光源 / 六、讨论
x
S1 a
S2
x
D
a
r1 r2
D
S
P x O
o
I
§2.相干光源 / 六、讨论
b. a x
x
D
a
S
S1 a
S2
r1 r2
D
P x O
o I
§2.相干光源 / 六、讨论
a x
x
D
a
S
S1 a
S2
r1 r2
六、讨论
1.明纹位置
k D xk a k=0时： x 0 0
明 纹
O
0
I
零级明纹位 于屏幕中央，只 有一条。
可以看出相邻明纹与相邻暗纹的间距都相 同，所以条纹明暗相间平行等距。
§2.相干光源 / 六、讨论
4.条纹间距与各量之间的关系
x
D
a
a. S
x
S1 a
S2
r1 r2
D
P x O
I
屏
干 涉 条 纹 光 强 分 布
§2.相干光源 / 一、杨氏双缝干涉
二.两条光线的光程差
S 1S 2 R OPQ ，
x S 1R D
S
点 光 源
单 缝
S1 a Q r 2 R S2
双 缝
r1
P x o
I D
屏
§2.相干光源 / 二、两条光线的光程差
x S 1R D
S 2S 1 R 很小, S 1 R a ，
o
I
§2.相干光源 / 六、讨论
x
S1 a
S2
x
D
a
r1 r2
D
S
P x O
o
I
§2.相干光源 / 六、讨论
b. a x
x
D
a
S
S1 a
S2
r1 r2
D
P x O
o I
§2.相干光源 / 六、讨论
a x
x
D
a
S
S1 a
S2
r1 r2
六、讨论
1.明纹位置
k D xk a k=0时： x 0 0
明 纹
O
0
I
零级明纹位 于屏幕中央，只 有一条。
8.3杨氏双缝干涉000
透射波没有半波损失
入射波 n1
反射波
n2
透射波
上页
下页
例1 双缝干涉实验中，用钠光灯作单色光源，其波长为 589.3 nm，屏与双缝的距离 D=600 mm
求 (1) d =1.0 mm 和 d =10 mm，两种情况相邻明条纹 间距分别为多大？(2) 若相邻条纹的最小分辨距离 为 0.065 mm，能分清干涉条纹的双缝间距 d 最大 是多少？
解 (1) 明纹间距分别为
x D 600 5.893104 0.35mm
d
1.0
x D 600 5.893104 0.035mm
d
10
(2) 双缝间距 d 为
d D 600 5.893104 5.4mm
x
0.065
上页
下页
例2 用白光作光源观察杨氏双缝干涉。设缝间距为d ，
缝面与屏距离为 D。
(2k 1) ,
2
x( 2k 1)
(2k 1) D 2d
条纹间距：x D
d
由上式可以看出
①. △x与缝间距d成反比；
②. 白光入射时：
颜色的次序
上页
下页
x
二. 洛埃镜实验
S•
•O
O
S •
xd
D2
接触处, 屏上O 点出现暗条纹
半波损失
n1 n2 有半波损失 n1 n2 无半波损失
§8.3 杨氏双缝干涉
一.杨氏双缝干涉
实位置 明条纹位置 明条纹位置
上页
下页
理论分析
单色光入射
r1 P ·x
r2
x
d
0
D
d >> ，D >> d （d 10 -4m， D m）
入射波 n1
反射波
n2
透射波
上页
下页
例1 双缝干涉实验中，用钠光灯作单色光源，其波长为 589.3 nm，屏与双缝的距离 D=600 mm
求 (1) d =1.0 mm 和 d =10 mm，两种情况相邻明条纹 间距分别为多大？(2) 若相邻条纹的最小分辨距离 为 0.065 mm，能分清干涉条纹的双缝间距 d 最大 是多少？
解 (1) 明纹间距分别为
x D 600 5.893104 0.35mm
d
1.0
x D 600 5.893104 0.035mm
d
10
(2) 双缝间距 d 为
d D 600 5.893104 5.4mm
x
0.065
上页
下页
例2 用白光作光源观察杨氏双缝干涉。设缝间距为d ，
缝面与屏距离为 D。
(2k 1) ,
2
x( 2k 1)
(2k 1) D 2d
条纹间距：x D
d
由上式可以看出
①. △x与缝间距d成反比；
②. 白光入射时：
颜色的次序
上页
下页
x
二. 洛埃镜实验
S•
•O
O
S •
xd
D2
接触处, 屏上O 点出现暗条纹
半波损失
n1 n2 有半波损失 n1 n2 无半波损失
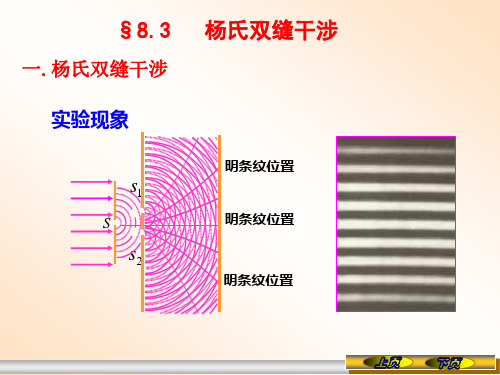
§8.3 杨氏双缝干涉
一.杨氏双缝干涉
实位置 明条纹位置 明条纹位置
上页
下页
理论分析
单色光入射
r1 P ·x
r2
x
d
0
D
d >> ，D >> d （d 10 -4m， D m）