机械优化设计期末作业——最小体积二级圆柱齿轮减速器的最优设计
二级圆柱齿轮减速器设计方案
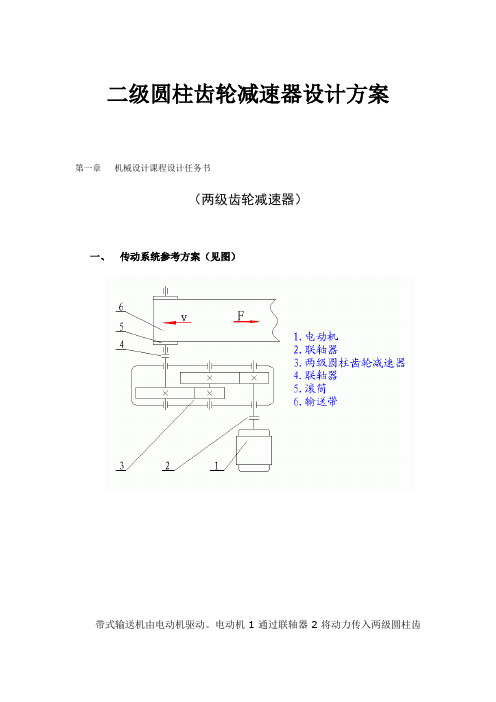
二级圆柱齿轮减速器设计方案第一章机械设计课程设计任务书(两级齿轮减速器)一、传动系统参考方案(见图)带式输送机由电动机驱动。
电动机1通过联轴器2将动力传入两级圆柱齿轮减速器3,再通过联轴器4将动力传至输送机卷筒5,带动输送带6工作。
二、原始数据(将与组号对应的原始数据填入以下空格中)输送带有效拉力F= 3500 N;输送带工作速度v= 0.85 m/s (允许误差±5%);输送机滚筒直径d= 400 mm;减速器设计寿命为5年。
三、工作条件两班制,常温下连续工作;空载起动,工作载荷平稳;三相交流电源,电压为380/220伏。
第二章设计计算说明书一.选择电机1.选择电动机的类型和结构型式根据工作条件,本设计方案中选用Y系列三相笼型异步电动机。
2.选择电动机额定功率对于不变载荷下长期连续运行的机械,要求。
为所选电动机额定功率,为根据工作要求所需的电动机功率。
1)确定式中:F——运输带拉力,N;v——运输带线速度,m/s。
2)确定式中:——带传动效率,—一对齿轮传动效率,—一对滚动轴承效率,——弹性联轴器效率,——卷筒效率,3)计算1.确定电动机转速式中:n——滚筒轴转速,r/min;D——滚筒直径,mm;v——运输带线速度,m/s。
式中:——电动机可选转速范围;—一,转动装置总传动比的合理范围;—一带转动和耳机援助齿轮减速器的传动比合理范围。
普通V带传动,;二级圆柱齿轮减速器,;n——滚筒轴转速。
根据和从设计手册中选择电动机型号,有关性能参数及尺寸如下表二.确定传动装置总传动比和各级传动比的分配1.确定总传动比式中:—一电动机满载转速, r/min。
2.各级传动比分配其中,,、分别为减速器高速级和低速级传动比。
1)带传动比为避免大带轮半径过大导致与底座相碰,。
2)各级齿轮传动比、为使两级齿轮传动中的大齿轮直径相近,浸油深度接近相等则三.计算各轴转速、功率和转矩(运动和动力参数)按照转速从高到低将减速器三根轴依次定为Ⅰ轴、Ⅱ轴和Ⅲ轴。
机械设计课程设计:二级圆锥-圆柱齿轮减速器设计
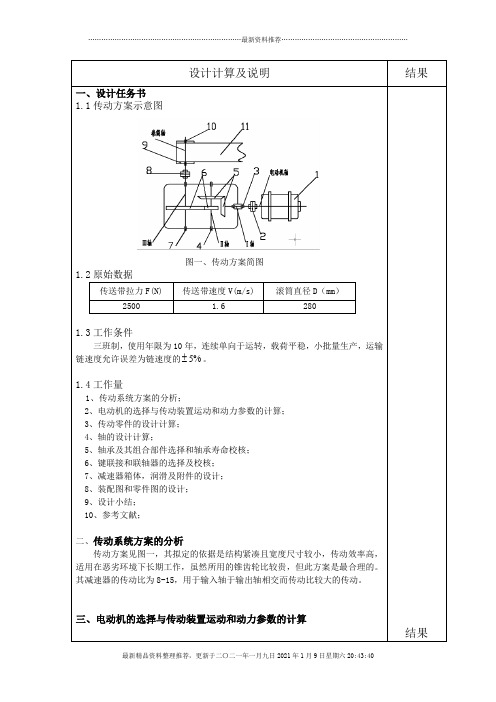
设计计算及说明结果一、设计任务书1.1传动方案示意图图一、传动方案简图1.2原始数据传送带拉力F(N) 传送带速度V(m/s) 滚筒直径D(mm)2500 1.6 2801.3工作条件三班制,使用年限为10年,连续单向于运转,载荷平稳,小批量生产,运输链速度允许误差为链速度的%5。
1.4工作量1、传动系统方案的分析;2、电动机的选择与传动装置运动和动力参数的计算;3、传动零件的设计计算;4、轴的设计计算;5、轴承及其组合部件选择和轴承寿命校核;6、键联接和联轴器的选择及校核;7、减速器箱体,润滑及附件的设计;8、装配图和零件图的设计;9、设计小结;10、参考文献;二、传动系统方案的分析传动方案见图一,其拟定的依据是结构紧凑且宽度尺寸较小,传动效率高,适用在恶劣环境下长期工作,虽然所用的锥齿轮比较贵,但此方案是最合理的。
其减速器的传动比为8-15,用于输入轴于输出轴相交而传动比较大的传动。
三、电动机的选择与传动装置运动和动力参数的计算结果a(第八版)》表15-3,取0112A =,得 设计计算及说明结果35.1996095.4112n P A d 33I I 0min ===mm 输入轴的最小直径为安装联轴器的直径12d ,为了使所选的轴直径12d 与联轴器的孔径相适应,故需同时选取联轴器型号。
联轴器的计算转矩2ca A T K T =,查《机械设计(第八版)》表14-1,由于转矩变化很小,故取 1.3A K =,则 2ca A T K T ==1.3X49.24=64012N.Mm查《机械设计课程设计》表14-4,选Lx3型弹性柱销联轴器其工称转矩为1250N.m ,而电动机轴的直径为38mm 所以联轴器的孔径不能太小。
取12d =30mm ,半联轴器长度L=82mm ,半联轴器与轴配合的毂孔长度为60mm 。
4、轴的结构设计(1)拟定轴上零件的装配方案(见图五)图五、输入轴轴上零件的装配(2)根据轴向定位的要求确定轴的各段直径和长度1) 为了满足半联轴器的轴向定位,12段轴右端需制出一轴肩,故取23段的直径mm 37d 23=。
【毕业设计】-二级直齿圆柱齿轮减速器的设计(含全套CAD图纸)

【毕业设计】-二级直齿圆柱齿轮减速器的设计(含全套CAD图纸)xxxx大学毕业设计说明书学生姓名:学号:学院:专业:题目:二级直齿圆柱齿轮减速器的设计指导教师:职称:职称:20** 年12 月5 日目录1引言. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12传动装置总体设计. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 2. 0 设计任务书. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 2. 1 确定传动方案. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 2. 2 电动机的选择. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62. 2. 1 电动机的容量选择. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62. 2. 2 电动机转速的选择. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72. 2. 3 电动机型号的确定. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82. 2. 4 传动比的分配. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82. 2. 5 传动系统的运动和动力参数计算. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 3传动零件的设计计算. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103. 1 高速级齿轮的参数计算. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103. 1. 1 材料选择及热处理. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103. 1. 2 齿根弯曲疲劳强度设计. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103. 2 低速级齿轮的计算. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 134轴及轴承装置的设计计算. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 164. 1 轴的设计. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 164. 1. 1 中间轴的设计. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 174. 1. 2 输入轴的设计. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 184. 1. 3 输出轴的设计. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 194. 2 轴的校核. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 214. 2. 1 输入轴的校核. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 214. 2. 2 中间轴的校核. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 264. 2. 3 输出轴的校核. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 294. 3 轴承的寿命计算. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 304. 3. 1 7006C 型轴承的校核. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 304. 3. 2 7013C 型轴承的校核. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 314. 3. 3 7008C 型轴承的校核. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32结论. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34致谢. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35参考文献. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 361 引言齿轮传动是现代机械中应用最广的一种传动形式。
机械设计课程设计_二级展开式圆柱齿轮减速器(含全套图纸)

课程设计报告二级展开式圆柱齿轮减速器姓名:学院:专业:年级:学号:指导教师:2006年6月29日一.设计题目设计一用于卷扬机传动装置中的两级圆柱齿轮减速器。
轻微震动,单向运转,在室内常温下长期连续工作。
卷筒直径D=500mm,运输带的有效拉力F=10000N, 卷筒效率5η=0.96,运输带速度0.3/v m s=,电源380V,三相交流.二.传动装置总体设计:1. 组成:传动装置由电机、减速器、工作机组成。
2. 特点:齿轮相对于轴承不对称分布,故沿轴向载荷分布不均匀,要求轴有较大的刚度。
3. 确定传动方案:考虑到电机转速高,传动功率大,将V带设置在高速级。
其传动方案如下:三.选择电动机1.选择电动机类型:按工作要求和条件,选用三相笼型异步电动机,封闭型结果,电压380V,Y 型。
2.选择电动机的容量电动机所需的功率为:WdaPP=η KW1000WFVP= KW所以1000daFVP=η KW由电动机到运输带的传动总功率为1a422345η=η•η•η•η•η1η—带传动效率:0.962η—每对轴承的传动效率:0.99 3η—圆柱齿轮的传动效率:0.96 4η—联轴器的传动效率:0.99 5η—卷筒的传动效率:0.96则:4210.960.990.960.990.960.79a 422345η=η•η•η•η•η=⨯⨯⨯⨯= 所以 94650.33.8100010000.81d a FV p η=⨯==⨯KW3.确定电动机转速 卷筒的工作转速为6010006010000.311.46500V n D ⨯⨯⨯===∏∏⨯r/min查指导书第7页表1:取V 带传动的传动比2i =~4带;二级圆柱齿轮减速器传动比840i =~减速器,所以总传动比合理范围为16160i =~总,故电动机转速的可选范围是:n n i =⨯=(16~160)⨯11.46=183~1834总卷筒电机r/min符合这一范围的同步转速有750、1000和1500r/min 。
二级圆柱直齿齿轮减速器设计

二级圆柱齿轮减速器的设计班级: 11 机械电子工程姓名:张群学号: 2011100619指导老师:沈智罗沛兰日期: 2013 年12月24日目录一、设计任务书··········································3二、传动方案的分析与拟定································4 三、电动机的选择计算····································5 四、传动装置的运动及动力参数的选择和计算················6 五、传动齿轮的设计计算··································7 六、轴的设计计算······································10七、滚动轴承的选择和计算· ·····························15八、键联接选择和计算· ································16九、联轴器的选择·····································17十、减速器箱体的设计· ·································17十一、减速器附件的选择与设计· ·························18十二、减速器的润滑方式和密封类型的选择·················20十三 . 设计小结··········································21十四 . 参考资料··········································22一、设计任务书I 、课程设计 ( 论文 ) 题目:带式输送传动装置(二级圆柱齿轮减速器)的设计II、课程设计 ( 论文 ) 使用的原始资料 ( 数据 ) 及设计技术要求:1、设计题目:要求:拟定传动关系:由电动机、 V 带、减速器、联轴器、工作机构成。
设计题目二级直齿圆柱齿轮减速器

设计题目:二级直齿圆柱齿轮减速器1. 要求:拟定传动关系:由电动机、V带、减速器、联轴器、工作机构成。
2. 工作条件:双班工作,有轻微振动,小批量生产,单向传动,使用5年,运输带允许误差5%3. 知条件:运输带卷筒转速19r/min ,减速箱输出轴功率P二4.25马力,传动装置总体设计:1. 组成:传动装置由电机、减速器、工作机组成。
2. 特点:齿轮相对于轴承不对称分布,故沿轴向载荷分布不均匀,要求轴有较大的刚度。
3. 确定传动方案:考虑到电机转速高,传动功率大,将V带设置在高速级。
其传动方案如下:三、选择电机1 . 计算电机所需功率P d:查手册第3页表1-7 :1—带传动效率:0.962 —每对轴承传动效率:0.993 —圆柱齿轮的传动效率:0.964 —联轴器的传动效率:0.9935 —卷筒的传动效率:0.96说明:—电机至工作机之间的传动装置的总效率:•4• 3 * 5P wP-P 4 5 P」一=3.6732确定电机转速:查指导书第7页表1:取V带传动比i=2 4二级圆柱齿轮减速器传动比i=8 40所以电动机转速的可选范围是:n电机二n卷筒i总二19 2[4 ^40 =304 3040/min符合这一范围的转速有:750、1000、1500、3000根据电动机所需功率和转速查手册第155页表12-1有4种适用的电动机型号,因此有4种传动比方案如下:综合考虑电动机和传动装置的尺寸、重量、和带传动、减速器的传动比,可见第3种方案比较合适,因此选用电动机型号为Y132M1 -6,其主要参数如下:额定功率kW满载转速同步转速质量A D E F G H L AB4 960 1000 73 216 38 80 10 33 132 515 280四确定传动装置的总传动比和分配传动比:总传动比:n 960i 总50.53n卷筒19分配传动比:取i带二3.05则“》50.53/3.0516.49b二1.31.52取^ = 1.32经计算i2 二3.56"二4.56注:因为材料选择45#调质,查课本225页表14-1得匚B=650MPa,查课本231页表14-3得许用弯曲应力l-」b l-60MPa,贝V:3 142 103357.5mm0.1「J 0.1 60考虑到键槽的影响,取 d =1.05 57.5 = 60.3mm因为d5 =80mm d,所以该轴是安全的。
课程设计 二级直齿圆柱齿轮减速器设计

目录一、传动方案分析 (2)二、选择电动机 (3)三、计算总传动比及分配各级的传动比 (4)四、计算传动装置的运动和动力参数 (6)五、V带传动设计计算 (6)六、直齿圆柱齿轮传动设计计算 (8)七、轴的结构设计计算及校核 (13)八、滚动轴承的选择及校核计算 (18)九、联轴器的选择计算 (18)十、键联接的选择及校核计算 (18)十一、润滑方式 (18)十二、参考文献 (18)十三、设计小结 (19)一、 传动方案分析机械设计课程设计题目:设计两级圆柱齿轮减速器减速器工作条件:此减速器用于热处理车间两件清洗传送带的减速,此设备两班制工作,工作期限十年,户内使用。
传送方案如下图所示:已知工作条件:鼓轮直径 : 370mm ,传送带运行速度 : 1.25m/s ,传送带从动轴所需扭矩 : 850N ·m为了估计传动装置的总传动比范围,以便选择合适的传动机构和拟定传动方案,可先由已知条件计算鼓轮的转速,即:m i n/6537025.1100060100060r Dvn w ≈⨯⨯⨯=⨯=ππ二、 选择电动机1、电动机类型选择根据电源及工作机工作条件,选用卧式封闭型Y (IP44)系列三相交流异步电动机。
2、电动机功率的选择 1)、工作机所需功率kw Tn p w w 8.59550658509550≈⨯==2)、电动机输出功率为dpwdp P η=传动装置的总效率5453221ηηηηηη=式中54321\\\\ηηηηη为从动机至工作机之间的个传动机构和轴承的效率。
查《机械设计课程设计》表2-4得:V 带传动效率1η=0.96,圆柱齿轮传动效率为2η=0.97,滚动轴承效率3η=0.99,弹性联轴器传动效率4η=0.99, 平带传动效率96.05=η。
则:82.096.099.099.097.096.0525453221≈⨯⨯⨯⨯==ηηηηηη故 kw p p wd 07.782.08.5≈==η根据电动机输出功率kw p d 07.7=,查表选择电动机的额定功率kw p ed 5.7=3)、电动机转速的选择为了便于选择电动机转速,先推算电动机转速的可选范围。
二级斜齿圆柱齿轮减速器设计书

二级斜齿圆柱齿轮减速器设计书一. 课程设计书设计课题:设计一用于带式运输机上的两级展开式圆柱齿轮减速器.运输机连续单向运转,载荷变化不大,空载起动,滚筒效率为0.96(包括滚筒与轴承的损失效率),减速器小批量生产,使用期限8年(300天/年),两班制工作,运输容许速度误差为5%,车间有三相交流,电压380/220V原始数据:表A二. 设计要求1.减速器装配图一张(A0或A1)。
2.零件工作图1~3张。
3.设计说明书1份。
三. 设计步骤1. 传动装置总体设计方案2. 电动机的选择3. 确定传动装置的总传动比和分配传动比4. 计算传动装置的运动和动力参数5. 设计V带和带轮6. 齿轮的设计7. 滚动轴承和传动轴的设计8. 键联接设计9. 箱体结构设计10. 润滑密封设计 11. 联轴器设计1.传动装置总体设计方案:1. 组成:传动装置由电机、减速器、工作机组成。
2. 特点:齿轮相对于轴承不对称分布,故沿轴向载荷分布不均匀, 要求轴有较大的刚度。
3. 确定传动方案:考虑到电机转速高,传动功率大,将V 带设置在高速级。
其传动方案如下:图一:(传动装置总体设计图)2.电动机的选择工作机有效功率:P =FV/1000=7000×1.1/1000=7.7kw总效率: η=η1×η1×η2×η2×η2×η3×η3×η4查表9.1(《机械设计课程设计》第三版 哈尔滨工业大学出版社 王连明 宋宝玉 主编)注:设计书中后面所要查表的数据都来自此书,不再加以说明。
如有数据来自其他书,设计书中会有说明。
η1(联轴器)=0.99 η2(轴承)=0.98 η3(齿轮)=0.98 η4(滚筒效率)=0.96 η=0.99×0.99×0.98×0.98×0.98×0.98×0.98×0.96=0.85电动机所需工作功率为: P =P/η=7.7/0.85=9.06kW卷筒转速: n =D π60v 1000⨯=40014.3 1.1601000⨯⨯⨯≈53r/min ,经查表按推荐的传动比合理范围,二级圆柱斜齿轮减速器传动比i =8~40。
二级圆柱齿轮减速器设计

摘要本设计是关与二级圆柱齿轮的结构设计和注意问题.根据对减速器的计算来拟订减速器的传动方案.通过计算来选择合适的电动机,以及传动系统的运动和动力参数计算.较重要的是齿轮的设计和轴的设计,这些在正文中会详细。
通过二级圆柱齿轮的结构设计,使我更好的了解二级圆柱齿轮减速器在齿轮的热处理,材料的选择,齿面,齿根的强度校核等参数的运用。
还有轴的热处理,材料的选择,以及轴的受力分析等。
关键字:电动机;齿轮;低速级直齿圆柱齿轮;轴;滚动轴承;键联结;联轴器;箱体;AbstractT h i s d e s i g n i s s h u t a n d s e c o n d a r y c yl i n d r i c a l g e a r s s t r u c t u r e d e s i g n a n d a t t e n t i o n p r o b l e m s.A c c o r d i n g t o t h e c a l c u l a t i o n o f r e d u c e r g e a r r e d u c e r t o d r a f t t h e t r a n s m i s s i o n s c h e m e T h r o u g h t h e c a l c u l a t i o n o f t h e m o t o r t o c h o o s e a p p r o p r i a t e a n d t r a n s m i s s i o n s ys t e m o f s p o r t a n d d yn a m i c p a r a m e t e r c a l c u l a t i o n.M o r e i m p o r t a n t l y g e a r d e s i g n a n d a x i a l d e s i g n, w h i c h w i l l b e d e t a i l e d i n t h e t e x t.T h r o u g h t h e s e c o n d a r y c yl i n d r i c a l g e a r s s t r u c t u r a l d e s i g n,m a k e m e b e t t e r u n d e r s t a n d i n g o f s e c o n d a r y c yl i n d r i c a l g e a r r e d u c e r g e a r h e a t t r e a t m e n t,i n t h e c h o i c e o f m a t e r i a l s,t h e t o o t h s u r f a c e r o o t t h e u s e o f p a r a m e t e r s s u c h a s s t r e n g t h c h e c k.A n d s h a f t h e a t t r e a t m e n t,c h o i c e o f m a t e r i a l s,a n d a x l e f o r c e a n a l ys i s,e t c.K e y w o r d s:m o t o r;G e a r;Lo w l e v e l;s p u r g e a r s A x i s;R o l l i n g b e a r i n g;K e y b o n d;C o u p l i n g;C a b i n e t;目录第一章绪论 (1)1.1本设计的目的及意义 (1)1.2减速器的发展状况 (1)1.3减速器的发展趋势 (2)1.4研究内容 (2)第二章传动方案的拟定 (3)2.1电动机的选择 (3)2.1.1电动机容量的选择。
机械设计课程设计二级圆柱齿轮减速器的设计

机械设计课程设计二级圆柱齿轮减速器的设计机械设计课程设二级圆柱齿轮减速器的设计目录1.题目 (1)2.传动方案的分析 (2)3.电动机选择,传动系统运动和动力参数计算 (2)4.传动零件的设计计算 (5)5.轴的设计计算 (16)6.轴承的选择和校核 (26)7.键联接的选择和校核 (27)8.联轴器的选择 (28)9.减速器的润滑、密封和润滑牌号的选择 (28)10.减速器箱体设计及附件的选择和说明 (29)11.设计总结 (31)12.参考文献 (31)题目:设计一带式输送机使用的V带传动或链传动及直齿圆柱齿轮减速器。
设计参数如下表所示。
1、基本数据数据编号QB-5运输带工作拉力F/N2000运输带工作速度1.4v/(m/s)卷筒直径D/mm340滚筒效率η0.962.工作情况两班制,连续单向运转,载荷平稳;3.工作环境室内,灰尘较大,环境最高温度35度左右。
4.工作寿命15年,每年300个工作日,每日工作16小时5.制作条件及生产批量: 一般机械厂制造,可加工7~8级齿轮;加工条件:小批量生产。
生产30台6.部件:1.电动机,2.V带传动或链传动,3.减速器,4.联轴器,5.输送带6.输送带鼓轮7.工作条件:连续单向运转,工作时有轻微振动,室内工作;运输带速度允许误差±5%;两班制工作,3年大修,使用期限15年。
(卷筒支承及卷筒与运输带间的摩擦影响在运输带工作拉力F中已考虑。
)8.设计工作量:1、减速器装配图1张(A0或sA1);2、零件图1~3张;3、设计说明书一份。
§2传动方案的分析1—电动机,2—弹性联轴器,3—两级圆柱齿轮减速器,4—高速级齿轮,5—低速级齿轮6—刚性联轴器7—卷筒方案分析:由计算(下页)可知电机的转速的范围为:674.410~3372.04r/min 由经济上考虑可选择常用电机为1500r/min .功率为4kw.又可知总传动比为17.082.如果用带传动,刚减速器的传动比为5—10,用二级圆柱齿轮减速器则传动比太小,而用一级则有点过大,从而齿轮过大,箱体就随着大.因而不用带传动直接用联轴器,因有轻微振动,因而用弹性联轴器与电机相连.两级展开式圆柱齿轮减速器的特点及应用:结构简单,但齿轮相对于轴承的位置不对称,因此要求轴有较大的刚度。
二级圆柱齿轮减速器毕业设计

济源职业技术学院毕业设计题目二级圆柱齿轮减速器的设计系别机电系专业机电一体化技术班级机电0711班姓名学号07011121指导教师日期2009年12月设计任务书设计题目:二级圆柱齿轮减速器设计要求:运输带拉力 F = 2400 N运输带速度 V = 1.8m/s卷筒直径 D = 260 mm滚筒及运输带效率η=0.96 。
要求电动机长期连续运转,载荷不变或很少变化。
电动机的额定功率Ped稍大于电动机工作功率Pd。
工作时,载荷有轻微冲击。
室内工作,水份和灰份为正常状态,产品生产批量为成批生产,允许总速比误差为±4%,要求齿轮使用寿命为8年,传动比准确,有足够大的强度,两班工作制,轴承使用寿命不小于25000小时,要求轴有较大刚度,试设计二级圆柱齿轮减速器。
设计进度要求:第一周:熟悉题目,收集资料,理解题目,借取一些工具书。
第二周:完成减速器的设计及整理计算的数据,为下步图形的绘制做准备。
第三周:完成了减速器的设计及整理计算的数据。
第四周:按照上一阶段所计算的数据,完成Solidworks装配体和CAD零部件的的绘制。
第五周:根据设计和图形绘制过程中的心得体会撰写论文,完成了论文的撰写。
第六周:修改、打印论文,完成。
指导教师(签名):齿轮传动是现代机械中应用最广的一种传动形式。
它的主要优点是:①瞬时传动比恒定、工作平稳、传动准确可靠,可传递空间任意两轴之间的运动和动力;②适用的功率和速度范围广;③传动效率高,η=0.92-0.98;④工作可靠、使用寿命长;⑤外轮廓尺寸小、结构紧凑。
由齿轮、轴、轴承及箱体组成的齿轮减速器,用于原动机和工作机或执行机构之间,起匹配转速和传递转矩的作用。
齿轮减速器的特点是效率高、寿命长、维护简便,因而应用极为广泛。
齿轮减速器按减速齿轮的级数可分为单级、二级、三级和多级减速器几种;按轴在空间的相互配置方式可分为立式和卧式减速器两种;按运动简图的特点可分为展开式、同轴式和分流式减速器等。
【精品】二级圆柱齿轮减速器的优化设计——最终版

二级圆柱齿轮减速器的优化设计——最终版学士学位论文二级圆柱齿轮减速器的优化设计摘要本文主要阐述了二级圆柱齿轮减速器的一般设计和优化设计过程,通过对比可知优化设计的优点,在现代机械化大生产过程中所显现的优越性、经济性,对于解放设计人员的劳动重复性,给予设计人员的新的设计思路和设计理念,使之在设计过程中以更多的创造性劳动,减少其重复性劳动。
二级圆柱齿轮减速器的优化设计主要是在满足其各零件的强度和刚度的条件下对其体积进行优化设计,这主要是因为,二级圆柱齿轮减速器的效率和其它的设计要素一般是比较高的,没有必要在对其进行优化,影响它性能、质量、成本的主要方面主要体现在强度要求和质量体积要求。
本文主要介绍了二级圆柱齿轮减速器的优化过程,建立其数学模型,目标函数,约束条件,并编写其通用的优化设计程序。
优化设计程序的建立使得减速器的设计计算更为简单,只要设计人员根据程序的提示要求,输入各个设计参数就可以得到满足要求的各种减速器的性能、结构尺寸。
这对于二级圆柱齿轮减速器的系列化设计生产具有重大意义。
关键词:圆柱齿轮减速器,数学建模,优化设计目录摘要 (1)目录 (1)第一章概述 (2)1.1机械优化设计与减速器设计现状 (2)1.2课题的主要任务 (2)1.3课题的任务分析 (3)第二章二级圆柱齿轮减速器的一般设计过程 (4)2.1传动装置运动和参数的确定 (4)2.1.1 设计参数 (4)2.1.2 基本运动参数的确定 (4)2.2齿轮设计部分 (5)2.2.1 第一级齿轮 (5)2.2.2 第二级齿轮 (9)2.3轴设计部分 (12)2.3.1 轴1 (12)2.3.2 轴2 (15)2.3.3 轴3 (21)第三章二级圆柱齿轮减速器的优化设计 (24)3.1减速器的数学模型 (24)3.2计算传动装置的运动和动力参数 (29)3.3减速器常规参数的设定 (30)3.4约束条件的确定 (30)第四章减速器优化设计中的几个重要问题 (40)4.1数学模型的尺度变换 (40)4.2数据表和线图的处理 (41)4.3最优化方法的选择 (41)4.4编写和调试程序的一些注意点 (44)结论 (45)参考文献 (46)致谢 (47)附录:程序源代码 (48)第一章概述1.1 机械优化设计与减速器设计现状机械优化设计是在电子计算机广泛应用的基础上发展起来的一门先进技术。
两级同轴式圆柱齿轮减速器的设计

两级同轴式圆柱齿轮减速器的设计摘要:本篇论文主要以“两级同轴式圆柱齿轮减速器的设计”为论题,研究减速器设计及过程中需要注意的问题。
由于减速器应用广泛,与生活息息相关,因此研究减速器的设计具有重要意义,为此写下了这篇论文。
两级同轴式圆柱齿轮减速器的设计通常包括以下内容:决定传动装置的总体设计方案;选择电动机;计算传动装置的运动和动力参数;传动零件、轴的设计计算;轴承、连接键、润滑密封和联轴器的选择及计算等。
顺泽公司 .关键词:减速器;设计方法一、减速器设计的一般资料减速器的种类很多,设计减速器前必须要先对减速器有一些基本的了解,了解减速器的一般资料有助于我们更好的发现其优点和缺点,只有这样我们才能设计出实用的减速器,下面的一些设计减速器须知的必要依据。
(一)常用减速器的分类、型式及其应用范围减速器的类型很多,不同类型的减速器有不同的特点,设计减速器时,首先应该根据各类减速器的特点选择一种进行设计。
各类减速器的形式、特点及应用见表本次论文设计我选择设计其中的两级同轴式圆柱齿轮减速器进行设计,两级同轴式圆柱齿轮减速器,两级同轴式圆柱齿轮减速器应用广泛,优点和缺点明显,具有代表性。
(二)关于减速机的构造(1)传动零件及其支撑减速机传动零件包括轴、齿轮、带轮、蜗杆等,其中,齿轮、带轮、蜗杆、蜗轮安装在轴上,而轴则通过滚动轴承由箱体上的轴承孔、轴承盖加以固定和调整。
轴承盖是固定和调整轴承的零件,其具体尺寸依轴承和轴承孔的结构尺寸而定,设计时可以可以参考相关的推荐尺寸确定。
(2)箱体结构减速机的箱体一般由铸铁材料铸造而成,分为上箱体和下箱体。
箱体上设有定位销孔以安装定位;设有螺栓孔以安装连接上下箱体的螺栓;设有地脚螺钉孔以将箱体安装在地基上。
为了提高轴承座的支撑刚度,通常在上下箱体的轴承座孔上下与箱体的连接处设有加强肋。
(三)减速机主要零件的配合减速器主要零件的配合见表3-1表3-1减速器主要零件配合(四)减速器附件减速机附件及其功用如下:①窥视孔和视孔盖:为了便于检查向内传动零件的齿合情况以及将润滑油注入箱体内,在减速机机体的箱盖顶部设有窥视孔。
二级斜齿圆柱齿轮减速器优化设计

二级斜齿圆柱齿轮减速机优化设计1. 题目二级斜齿圆柱齿轮减速机。
高速轴输入功率R=6.2kW ,高速轴转速n 1=1450r/min ,总传动比i Σ=31.5,齿轮的齿宽系数Φa =0.4;齿轮材料和热处理;大齿轮45号钢正火硬度为187~207HBS ,小齿轮45号钢调质硬度为228~255HBS 。
总工作时间不小于10年。
要求按照总中心距最小确定总体方案中的主要参数。
2.已知条件已知高速轴输入功率R=6.2kW ,高速轴转速n 1=1450r/min ,总传动比i Σ=31.5,齿轮的齿宽系数Φa =0.4。
3.建立优化模型3.1问题分析及设计变量的确定由已知条件求在满足使用要求的情况下,使减速机的总中心距最小,二级减速机的总中心距为:()()11123212112cos n n m z i m z i a a a β∑+++=+=其中1n m 、2n m 分别为高速级和低速级齿轮副的模数,1z 、3z分别为高速级和低速级小齿轮齿数,1i 、2i分别为高速级和低速级传动比,β为齿轮副螺旋角。
所以与总中心距a ∑相关的独立参数为:1n m 、2n m 、1z 、3z 、1i (2131.5i i =)、β。
则设计变量可取为:x=[1n m 2n m 1z 3z 1i β]T =[1x 2x 3x 4x 5x 6x ]T 3.2目标函数为()()()135********.52cos f x x x x x x x x =+++⎡⎤⎣⎦为了减速机能平稳运转,所以必须满足以下条件:12131253.56142216227815n n m m z z i β≤≤≤≤≤≤≤≤≤≤≤≤、、、5.8、3.3约束条件的建立3.3.1线性不等式约束条件()1120g x x =-≤ ()2150g x x =-≤ ()323.50g x x =-≤ ()4260g x x =-≤ ()53140g x x =-≤ ()63220g x x =-≤ ()74160g x x =-≤ ()84220g x x =-≤ ()955.80g x x =-≤ ()10570g x x =-≤ ()11680g x x =-≤ ()126150g x x =-≤3.3.2非线性不等式约束条件1)齿轮的接触应力不得大于许用应力值,得[]11H H σσ=≤[]22H H σσ=≤即[][]2331113121123323232222cos 08925cos 08925H n H n m z i K T mz i K Tαασϕβσϕβ-≥⨯-≥⨯2)齿轮的弯曲应力不得大于许用弯曲应力值,得[][]1111112121221.5F F n F F F K T bd m Y Y Y σσσσσ=≤=≤即[]()[]()132211111123222111111cos 031cos 03F n F n Y i m z K T Y i m z K T αασϕβσϕβ+-≥+-≥和[]()[]()332232232243224223221cos 031cos 03F n F n Y i m z K T Y i m z K T αασϕβσϕβ+-≥+-≥其中齿形系数的计算如下:21112222233324440.1690.0066660.00008540.1690.0066660.00008540.1690.0066660.00008540.1690.0066660.0000854Y z z Y z z Y z zY z z =+-=+-=+-=+-3)高速级齿轮和低速级齿轮不得发生干涉,得:()()232111112cos 0n n n m z i E m m z i β+-+-≥E 为低速轴轴线与高速级大齿轮齿顶圆之间的距离,单位为mm 。
最小体积二级圆柱齿轮减速器的优化设计

最小体积二级圆柱齿轮减速器的优化设计班级:机制072 学号: 姓名:输入功率(P=31kw )一.建立数学模型该减速器的总中心距计算式为)]1()1([cos 2123211121i Z m i Z m a a a n n +++=+=∑β1.选取设计变量由涉及的独立参数,取T T n n x x x x x x i Z Z m m X ],,,,,[],,,,,[65432113121==β2.建立目标函数)cos 2/()]/5.311()1([)(6542531x x x x x x x X f +++=)1(])(1)(1)(1[)()()(1721)(=+⋅⋅⋅⋅⋅⋅+++=k k r X g X g X g r X f X F 3.确定约束条件(1)确定上、下限从传递功率于转速可估计85.31≤≤n m 标准值(3.5,4,5,6,7,8)105.32≤≤n m 标准值(4,5,6,8,10)综合考虑传动平稳等等各种因素,取:78.522141≤≤≤≤i Z 15822163≤≤≤≤βZ由此建立12个不等式约束条件式08)(08.5)(016)(014)(04)(05.3)(6115947352311≥-=≥-=≥-=≥-=≥-=≥-=x X g x X g x X g x X g x X g x X g 015)(07)(022)(022)(010)(08)(61251048362412≥-=≥-=≥-=≥-=≥-=≥-=x X g x X g x X g x X g x X g x X g(2)按齿面接触强度公式23/],[)1(925mm N bi KT i a H iH σσ≤+=得到高速级和低速级齿面接触强度条件分别为0cos )925(8][3112131312≥-βϕσT K i Z m an H [1]0cos )925(8][3222233322≥-βϕσT K i Z m an H [2](3)按轮齿弯曲强度计算公式[][]22211221111111/,/,5.1mm N y y mm N y m bd T K F F F F n F σσσσσ≤=≤=得到高速级和低速级大小齿轮的弯曲强度条件分别为0cos )1(3][2213111111≥-+βϕσZ m i T K y n a F [3]0cos )1(3][2213111122≥-+βϕσZ m i T K y n a F [4]0cos )1(3][2233222233≥-+βϕσZ m i T K y n a F [5]0cos )1(3][2233222244≥-+βϕσZ m i T K y n a F [6](4)按高速级大齿轮与低速轴不干涉相碰条件02/22≥--de E a得 0)(cos 2)1(1111232≥-+-+i Z m m E i Z m n n n β [7]对式[1]至式[7]代入有关数据:m mE y y y y K K m mN i T m m N n P T m m N m m N m m N F F F F H 50302.0,256.0,302.0,248.0204.1,225.1210760,2107609550/6.410][][,/0.445][][/5.896][432121121112422312=======⋅=⋅=======σσσσσ(注:查相关《机械设计手册》,得相关公式:许用接触应力 i i b d F Z Z Z Z K K K K Z t B E H H H V A H 11+⋅=εαββσ许用弯曲应力 αββεαασF F V A S F nt F K K K K Y Y Y Y bm F =21311)1(2000HP a a a t i KT i A a a b d T F σϕϕ+=== 因螺旋角、材料、要求等与例题相同,各类系数(如K ,y,E之类)与例题相同;因材料与例题选取相同,则a A 、HP σ等参数相同。
最小体积圆柱齿轮减速器的优化设计

最小体积圆柱齿轮减速器的优化设计淮南职业技术学院(安徽!"!##$)郭益友【摘要】将多目标优化方法应用于单级斜齿圆柱齿轮减速器的设计,可得到整体优化的结构设计方案,使齿轮传动在满足承载能力、强度、使用寿命的条件下,结构最紧凑,重量最轻。
【关键词】减速器优化设计中心距一、前言我国通用圆柱齿轮减速器虽已有标准系列,但并不是最优的。
而用机械优化设计的方法,将工程实际问题转化为优化设计的数字模型,然后根据数学模型的特性,选择适当的优化设计计算方法及其程序,通过计算机求得最优解,从而在短时间得到最佳设计结果。
二、建立目标函数球磨机单级斜齿圆柱齿轮减速器传动的原始数据及设计要求:小齿轮传递额定功能!!"#$%&,转速"’!()*+/,-.,传动比#!)#’’,单向运转满载)$***/。
传动误差不超过0$1。
小齿轮用2*3+钢调质,硬度42’!456789;大齿轮用2$钢正火,硬度’64!4’(789。
要求在满足刚度、强度和寿命等条件下,使体积最小。
减速器优化的目标很多,但最小的体积可以节约材料,降低成本,满足许多特殊场合要求。
因此,将齿轮减速器的体积最小作为优化目标函数,要求结构最紧凑,重量最轻,也就是说减速器中总中心距最小,因此以中心距$为目标函数,有%(:)!$!&.’(’’;’4)4<=>!!’4<=>!&.’’’(’;#)(’)三、确定设计变量计算中心距的独立参数有:&.’、’’、#、!,故取设计变量为(![&.’、)’、#、!]*[(’、(4、()、(2]*(4)四、确定约束条件!"确定设计变量的上下限’#4!&.’!)#2;’2!)’!6*4!#!$;5?!!!’$?(换算成弧度)由此建立不等式约束条件+’(()!(’@’#4"*;+4(()!)#2@(’"*。
+)(()!(4@’2"*;+2(()!6*@(4"*。
二级直齿圆柱齿轮减速器优化设计

c(7)=x(5)-0.2
c(8)=x(6)-0.2
c(9)=1200-x(5)*x(3)
c(10)=1560-x(6)*x(4)
c(11)=x(9)-25
c(12)=35-x(9)
c(13)=x(10)-30
c(14)=40-x(10)
c(15)=x(7)-x(1)-0.5*x(10)-40
c(28)=55-sqrt((67*10^8*x(8))/(x(6)^2*x(4)^2)+20*10^8*1.75^2)/0.1*x(12)^3
c(22)=249.71-(2*1.3*16.55*10^4)/(x(2)*x(13)*x(6)^2*(0.2824+0.0003539x(14)-0.0000854x(14)^2))
c(23)=0.003*x(7)-(588.8*x(7)^3)/(3014*x(3)*x(5)*x(9)^4)
c(24)=0.003x(8)-(984.32*x(8)^3)/(2833*x(6)*x(3)*x(11)^4)
一级减速:
二级减速:
(10)主动轴的弯曲强度条件:
式中: ——轴上的扭矩, ;
——轴上的弯矩, , ;
——考虑扭矩和弯矩的作用性质差异的系数,取 ;
——轴的许用弯曲应力, ;
——轴的抗弯剖面系数,对实心轴
(11)仿照前面的处理方法可得从动轴弯曲强度条件:
2.
1、采用MATLAB工具箱进行优化
首先在当前MATLAB的工作目录下建立目标函数文件myfun.m文件:
式中:
——载荷系数,取 =1.3;
——小齿轮传递转矩;
——齿轮许用接触应力,现按原材料及原设计数据,取 =885 ;
惩罚函数法二级圆柱齿轮减速器的优化设计

惩罚函数法二级圆柱齿轮减速器的优化设计1序言1.1选题的依据及意义齿轮减速器是原动机和工作机之间的独立的闭式传动装置,用来降低转速和增大转矩,以满足工作需要,在某些场合也用来增速,称为增速器。
其特点是减速电机和大型减速机的结合。
无须联轴器和适配器,结构紧凑。
负载分布在行星齿轮上,因而承载能力比一般斜齿轮减速机高。
满足小空间高扭矩输出的需要。
广泛应用于大型矿山,钢铁,化工,港口,环保等领域。
与K、R系列组合能得到更大速比。
圆柱齿轮传动与普通定轴齿轮传动相比较,具有质量小、体积小、传动比大、承载能力大以及传动平稳和传动效率高等优点,这些已被我国越来越多的机械工程技术人员所了解和重视。
由于在各种类型的圆柱齿轮传动中均有效的利用了功率分流性和输入、输出的同轴性以及合理地采用了内啮合,才使得其具有了上述的许多独特的优点。
圆柱齿轮传动不仅适用于高速、大功率而且可用于低速、大转矩的机械传动装置上。
它可以用作减速、增速和变速传动,运动的合成和分解,以及其特殊的应用中;这些功用对于现代机械传动发展有着重要意义。
因此,圆柱齿轮传动在起重运输、工程机械、冶金矿山、石油化工、建筑机械、轻工纺织、医疗器械、仪器仪表、汽车、船舶、兵器、和航空航天等工业部门均获得了广泛的应用。
对这种减速器进行优化设计,必将获得可观的经济效益。
+QQ1162401387获取CAD,SW,PROE等格式图纸选做这个毕业设计,一方面对于减速器的内部结构和工作原理也有一定的了解和基础,其次通过对圆柱齿轮减速器这一毕业课题设计可以巩固我大学4年来所学的专业知识,对于我也是一种检验。
可以全面检验我大学所学的知识是否全面,是否能灵活运用到实际生活工作中。
在做的过程中我还可以不断学习和拓宽视野和思路,做到理论与实际相结合的运用。
最重要的是对于即将离校走向社会的我是一种挑战,培养我独立思考,树立全局观念,为以后的我奠定坚实的基础。
1.2研究概况及发展趋势随着时代进步,科技与时俱进,对于齿轮的传动越来越多的科技因素在起着主导地位。
二级圆柱齿轮减速器机械设计设计

二级圆柱齿轮减速器计算说明书学院:专业:班级:目录 (2)一、设计数据及要求 (2)二、确定各轴功率、转矩及电机型号 (3)I.工作机有效功率 (3)2•查各零件传动效率值 (4)3•电动机输出功率 (4)4.工作机转速 (4)5•选择电动机 (4)6•理论总传动比 (4)7•传动比分配 (5)&各轴转速 (5)9•各轴输入功率: (5)10•电机输岀转矩: (5)II.各轴的转矩 (5)12 .误差 (6)三、选择齿轮材料,热处理方式和精度等级 (6)四、齿轮传动设计与校核计算 (6)(二)、低速级 (16)五、初算轴径 (17)六、校核轴的强度和轴承寿命: (18)(―)、中间轴 (18)(二).............................................................. 、输入轴23(三) .............................................................. 、输出轴27七、滚动轴承的校核计算 (32)八、平键联接的选用和计算 (37)九、选择联轴器 (39)十、润滑方式 (39)十一、设计总结 (40)十二、参考文献 (41)一、设计数据及要求1 •设计题目设讣一链板式输送机传动装琵两班制工作,连续单向运转,轻微振动,使用年限5年, 单件生产,输送带允许误差为土%5。
2 •原始数据链条曳引力F= 5200N 链条速度v= 0.3m/s 链条节距A 125mm链轮齿数Z=63 •方案图1 -电动机2, 4-联轴器3 -减速器5-链板6-开式齿轮传动链板式输送机传动装置二、确定各轴功率、转矩及电机型号1 •工作机有效功率/>=F-V =5200 X O.3=1.56K W2 •查各零件传动效率值联轴器(弹性)〃严0.99,轴承;/2 = 0.99 ,齿轮= 0.97 链轮久=°・%故:工〃 =z/12••弘=0.992 x0.995 x 0.973 x 0.96 = 0.81663•电动机输出功率4•工作机转速60xl000v _ 60x1000x0.3链轮转速=24r/minZt125x6电动机转速的可选范用:n rf=n M,.f = 24x(24〜120) = 576〜2880〃min5•选择电动机选电动机型号为Y112M—6,同步转速940r/miiK满载转速1000r/min,额左功率2.2Kw 电动机外形尺寸132475x(135/2 + 210)x315216X140 1238 X 8010X86•理论总传动比7•传动比分配取开式齿轮传动比心=3,又i t =L4i u故i } = 4.28 , i n = 3.058•各轴转速n = i d = 940 r/niin吩铲謹E.63〃讪9•各轴输入功率:P 、=Pd •小= L9\ x 0.99x0.97 = l ・83Kw Pu =7 •弘=1.83 x 0.99 x 0.97 = l ・76KwP m = P\{・ J]2 • “3 = 1.76 x 0.99 x 0.97 = 1.69 Kw P* =召][• a = 1.69 x 0.97 = 1.52 Kw = />|(= 1.52 x0.99 = l.51Kw940^24= 39.17 h 3.05=72.01 r/nin72.01=24/7 niin10 •电机输出转矩:7; = 9.55 xl06x^- = 9.55 xl03x —= 19.40/V ・md n d940笛•各轴的转矩T\=TdF、= 19.40 x 0.99 x 0.97 = 18・63N ・m7], =7;■ ;;2• “3 • /[ = 18.63 x 0.99 x0.97 x 4.28=76.60/V • m几I =刁1 * 〃2 * “3 ■心I=76.60 x 0.99 x 0.97 x3.05 = 224.32N • m7]v =心•帀=224.32 x 0.99 = 222.08N•加T..{ = 7;• % •必=222.08 x 0.97 x 0.99 = 213.26N • m12 •误差三、选择齿轮材料,热处理方式和精度等级考虑到齿轮所传递的功率不大,故小齿轮选用45#钢,表而淬火,齿而硬度为40〜55HRC,齿轮均为硬齿而。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最小体积二级圆柱齿轮减速器的最优设计如图所示的二级斜圆柱齿轮减速器,高速轴输入功率P1 = 5.0kw,高速轴转速n1 = 1940rpm,总传动比iΣ= 31.5,此轮的齿宽系数ψa= 0.4;齿轮材料和热处理大齿轮45号钢正火HB = 187~207,小齿轮45号钢调质HB = 228~255.总工作时间不少于10年。
要求按总中心距aΣ最小来确定总体方案中的各个主要参数。
减速器的总中心距计算公式为aΣ= a1 + a2 = 12cosβ[m n1Z1(1+i1) + m n2Z3(1 + i2)]式中m n1,m n2——高速级与低速级的齿轮法面模数,mmi1,i2——高速级与低速级传动比Z1,Z3——高速级与低速级小齿轮齿数β——齿轮的螺旋角1. 选取设计变量计算总中心距涉及的独立参数有,故取X = [m n1,m n2,Z1,Z3,i1,β]T = [x1,x2,x3,x4,x5,x6]T2. 建立目标函数f(X) = [x1x3 (1+x5) + x2x4 (1 + 31.5/ x5)]/(2cos x6)3. 确定约束条件(1)确定约束条件的上下界限从传递功率与转速可估计2≤m n1≤7 标准值(2,2.5,3,4,5)2≤m n2≤9 标准值(3.5,4,5,6)综合考虑传动平稳、轴向力不可太大,能满足短期过载,高速级与低速级大齿轮浸油深度大致相近,轴齿轮的分度圆尺寸不能太小等因素,取:16≤Z1≤2418≤Z3≤245.8≤i1≤780≤β≤150由此建立12个不等式约束条件式g1(X) = x1– 2 ≥0g2(X) = 7 –x1≥0g3(X) = x2– 4.5≥0g4(X) = 9 –x2≥0g5(X) = x3– 16≥0g6(X) = 24 –x3≥0g7(X) = x4– 18≥0g8(X) = 24 –x4≥0g9(X) = x5– 5.8≥0g10(X) = 7 –x5≥0g11(X) = x6–0.1396≥0g12(X) = 0.2618 –x6≥0(已将角度化成弧度)(2)按齿面接触强度公式δH = 925a()i + 13KT1bi≤ [δH],N/mm2得到高速级和低速级齿面接触强度条件分别为[δH]2m n13Z13i1ψa8(925)2K1T1– cos3β≥0 ①[δH]2m n23Z33i2ψa8(925)2K2T2– cos3β≥0 ②式中,[δH]——许用接触应力,MpaT1,T2——分别为高速轴I和中间轴II的转矩,N·mmK1,K2——分别为高速级和低速级载荷系数.(3)按轮齿弯曲强度计算公式δF1 = 1.5 K1T1bd1 m n1y1≤ [δF]1,N·mm2δF2 = δF1 y1y2≤ [δF]2,N·mm2得到高速级和低速级大小齿轮的弯曲强度条件分别为[δF]1ψa y13 K1T1(1 + i1) m n13Z12– cos2β≥0 ③[δF]2ψa y23 K1T1(1 + i1) m n13Z12– cos2β≥0 ④和[δF]3ψa y33 K2T2(1 + i2) m n23Z32– cos2β≥0 ⑤[δF]4ψa y43 K2T2(1 + i2) m n23Z32– cos2β≥0⑥其中[δF]1,[δF]2,[δF]3,[δF]4——分别为齿轮1,2,3,4的许用弯曲应力,N/mm2;y1,y2,y3,y4——分别为齿轮1,2,3,4的齿形系数.(4)按高速级大齿轮与低速轴不干涉相碰的条件a2–E– de2/2≥0得m n2Z3(1 + i2) – 2 cosβ(E + m n1) –m n1Z1i1≥0 ⑦式中E——低速轴轴线与高速级大齿轮齿顶圆之间的距离,mm;de2——高速级大齿轮齿的齿顶圆直径,mm.对式①至⑦代入有关数据:[δH] = 518.75 N·mm2[δF]1= [δF]3= 153.5 N·mm,[δF]2= [δF]4= 141.6 N·mm2T1 =29638 N·mm,T2 = 28749i1 N·mmK1 = 1.225,K2 = 1.204y1=0.248,y2=0.302,y3=0.256,y4=0.302E = 50mm得g13(X) = 4.331×10-7x13x33x5– cos3x6≥0g14(X) = 1.431×10-5x23x43–x5cos3x6≥0g15(X) = 1.398×10-4(1 + x5)x13x32– cos2x6≥0g18(X) = 1.570×10-4(1 + x5)x13x32– cos2x6≥0g16(X) = 1.514×10-4(31.5 + x5)x23x42–x52cos2x6≥0g19(X) = 1.647×10-4(31.5 + x5)x23x42–x52cos2x6≥0g17(X) = x2x4 (31.5 + x5) – 2x5cos x6 (x1+50) –x1x3x52≥0g18(X)、g19(X)和g15(X)、g16(X)相比为明显的消极约束,可省略。
共取g1(X)至g17(X)的17个约束条件。
4. 选用合适的算法求解这一约束问题采用复合形法求解。
在进行优化的过程中,6个变量都是作为连续变量处理的,因为齿轮的齿数应为整数,模数应取标准模数,所以最后对结果进行适当调整。
Private Sub Command1_Click()N = 6: E = 0.01Dim X(13, 6), F(13), A(6), B(6)For j = 1 To 6A(j) = InputBox(A(j), "输入估计边界的下界")B(j) = InputBox(B(j), "输入估计边界的上界")Next j180: For I = 1 To 12190: GoSub 730If AA = 0 Then GoTo 190Next II0 = 1: I1 = 1: I2 = 1: K = 0240: For I = 1 To 12If F(I) > F(I0) Then I1 = I0: I0 = I: GoTo 280If F(I) > F(I1) Then I1 = IIf F(I) < F(I2) Then I2 = I280: Next IK = K + 1: R = 0For j = 1 To 6R = R + (X(I0, j) - X(I2, j)) ^ 2Next jIf Sqr(R) < E Then ZZ = 0: GoTo 670340: For j = 1 To 6X(0, j) = 0For I = 1 To 12X(0, j) = X(0, j) + X(I, j)Next IX(0, j) = (X(0, j) - X(I0, j)) / 11Next jI = 0GoSub 760If AA = 1 Then GoTo 480For j = 1 To 6A(j) = X(I2, j): B(j) = X(0, j): X(1, j) = X(I2, j)Next jGoTo 180480: H = 1.3: I = 13490: For j = 1 To 6X(13, j) = X(0, j) + H * (X(0, j) - X(10, j))Next jGoSub 760H = H / 2If AA = 0 Then GoTo 490If F(13) >= F(I1) Then GoTo 610For j = 1 To 6X(I0, j) = X(13, j)Next jF(I0) = F(13)GoTo 240610: If H > E Then GoTo 490730: For j = 1 To 6X(I, j) = A(j) + Rnd(1) * (B(j) - A(j))Next j760: AA = 0g1 = X(I, 1) - 2g2 = 7 - X(I, 1)g3 = X(I, 2) - 4.5g4 = 9 - X(I, 2)g5 = X(I, 3) - 16g6 = 24 - X(I, 3)g7 = X(I, 4) - 18g8 = 24 - X(I, 4)g9 = X(I, 5) - 5.8g10 = 7 - X(I, 5)g11 = X(I, 6) - 0.1396g12 = 0.2618 - X(I, 6)g13 = 4.331 * 10 ^ -7 * X(I, 1) ^ 3 * X(I, 3) ^ 3 * X(I, 5) - Cos(X(I, 6)) ^ 3g13 = 1.431 * 10 ^ -5 * X(I, 2) ^ 3 * X(I, 4) ^ 3 - X(I, 5) * Cos(X(I, 6)) ^ 3g15 = 1.398 * 10 ^ -4 * (1 + X(I, 5)) * X(I, 1) ^ 3 * X(I, 3) ^ 2 - Cos(X(I, 6)) ^ 2g16 = 1.514 * 10 ^ -4 * (31.5 + X(I, 5)) * X(I, 2) ^ 3 * X(I, 4) ^ 2 - X(I, 5) ^ 2 * Cos(X(I, 6)) ^ 2 g17 = X(I, 2) * X(I, 4) * (31.5 + X(I, 5)) - 2 * X(I, 5) * Cos(X(I, 6)) * (X(I, 1) + 50) - X(I, 1) * X(I, 3) * X(I, 5) ^ 2If g1 >= 0 And g2 >= 0 And g3 >= 0 And g4 >= 0 And g5 >= 0 And g6 >= 0 And g7 >= 0 And g8 >= 0 And g9 >= 0 And g10 >= 0 And g11 >= 0 And g12 >= 0 And g13 >= 0 And g14 >= 0 And g15 >= 0 And g16 >= 0 And g17 >= 0 Then GoTo 800Return800: AA = 1F(I) = (X(I, 1) * X(I, 3) * (1 + X(I, 5)) + X(I, 2) * X(I, 4) * (1 + 31.5 / X(I, 5))) / (2 * Cos(X(I, 6))) ReturnFor j = 1 To 6C = X(I0, j): X(I0, j) = X(I1, j): X(I1, j) = CNext jC = F(I0): F(I0) = F(I1): F(I1) = C: ZZ = 1670: PrintFor j = 1 To 6Print "x*("; j; ")="; X(I2, j)Next jPrint K; "F*="; F(I2)If ZZ = 1 Then GoTo 340End Sub运算结果如下:齿数取整数,模数取标准模数,取m n1=2,m n2=6,取Z1=18,Z3=20,i1=6.24,β=0.1928756rad,则i2=5.05,Z2=98,Z4=94,螺旋角β=1103' 3.45''。
