机械原理PPT
合集下载
机械原理(全套15PPT课件)
按形状分为盘形、圆柱形、平板型等；按从动件类型分为尖底、滚子、平底等
从动件的常用运动规律
等速运动规律
从动件匀速运动，产生刚性冲击
等加速等减速运动规律
从动件分段匀变速运动，产生柔性冲击
简谐运动规律（余弦加速度运动规律）
从动件按余弦规律加速运动，无冲击
正弦加速度运动规律
从动件按正弦规律加速运动，无冲击
平面四杆机构的设计
按照给定的连杆位置设计四杆机构
按照给定的运动轨迹设计四杆机构
作图法、解析法
作图法、解析法
按照给定的急回特性设计四杆机构
按照给定的传动角设计四杆机构
作图法、解析法
作图法、解析法
05 凸轮机构及其设 计
凸轮机构的应用和分类
凸轮机构的应用
自动机械、操纵控制、传动装置等
凸轮机构的分类
重要性
机械原理是机械工程学科的基础 ，对于理解和分析机械系统的运 动、力和能量传递过程具有重要 意义。
机械原理的研究对象和内容
研究对象
机械系统，包括机构、传动、控制等 方面。
研究内容
机构的结构分析、运动分析、力分析 、动力学分析、优化设计等。
机械原理的发展历程和趋势
发展历程
从简单机械到复杂机械系统，从经验设计到基于科学计算的设计。
机械原理(全套15PPT课件)
contents
目录
• 机械原理概述 • 机构的结构分析 • 平面机构的运动分析 • 平面连杆机构及其设计 • 凸轮机构及其设计 • 齿轮机构及其设计
01 机械原理概述
机械原理的定义与重要性
定义
机械原理是研究机械系统中力的 传递、转换和效应的基本规律和 原理的学科。
具有急回特性、死点位置、压力角和 传动角等特性，这些特性对机构的运 动性能和动力性能有重要影响。
从动件的常用运动规律
等速运动规律
从动件匀速运动，产生刚性冲击
等加速等减速运动规律
从动件分段匀变速运动，产生柔性冲击
简谐运动规律（余弦加速度运动规律）
从动件按余弦规律加速运动，无冲击
正弦加速度运动规律
从动件按正弦规律加速运动，无冲击
平面四杆机构的设计
按照给定的连杆位置设计四杆机构
按照给定的运动轨迹设计四杆机构
作图法、解析法
作图法、解析法
按照给定的急回特性设计四杆机构
按照给定的传动角设计四杆机构
作图法、解析法
作图法、解析法
05 凸轮机构及其设 计
凸轮机构的应用和分类
凸轮机构的应用
自动机械、操纵控制、传动装置等
凸轮机构的分类
重要性
机械原理是机械工程学科的基础 ，对于理解和分析机械系统的运 动、力和能量传递过程具有重要 意义。
机械原理的研究对象和内容
研究对象
机械系统，包括机构、传动、控制等 方面。
研究内容
机构的结构分析、运动分析、力分析 、动力学分析、优化设计等。
机械原理的发展历程和趋势
发展历程
从简单机械到复杂机械系统，从经验设计到基于科学计算的设计。
机械原理(全套15PPT课件)
contents
目录
• 机械原理概述 • 机构的结构分析 • 平面机构的运动分析 • 平面连杆机构及其设计 • 凸轮机构及其设计 • 齿轮机构及其设计
01 机械原理概述
机械原理的定义与重要性
定义
机械原理是研究机械系统中力的 传递、转换和效应的基本规律和 原理的学科。
具有急回特性、死点位置、压力角和 传动角等特性，这些特性对机构的运 动性能和动力性能有重要影响。
机械原理齿轮机构及其设计PPT
α
5、基圆 rb
s = e = p/2
6、齿顶高 ha
O
7、齿根高 hf
8、全齿高 h h = ha + hf
9、压力角 α
一、齿轮各部分名称
ακ
1、齿数 z
2、模数 m (非常主要旳概念) 以齿轮分度圆为计算各部分尺寸基准
齿数 z ×齿距 p = 分度圆周长 πd
分度圆直径d = z × p / π
一对齿轮作无侧隙啮合传动时，共存在四个基本原因：
两个几何原因，即一对共轭旳渐开线齿廓 给定其中任何三个原因， 两个运动原因，即两轮旳角速度 ω0 和ω 就能取得第四个原因
刀具齿廓拟定，强制刀具与轮坯以定传动比 i = ω0/ω运动
刀具旳齿廓（一种几何原因）就必然在轮坯上切削（包络）出轮 坯旳齿廓（另一种几何素）。
连续传动旳条件为：B1B2 ≥ Pb
可表达为：重叠度ε a = B1B2 / Pb≥ 1
ε a 分析：重叠度旳大小表白同步参加啮合轮齿啮合对数旳平均值
ε a = 1 时，一直只有一对轮齿啮合，确保最低连续传动； ε a < 1 时，齿轮传动部分时间不连续； ε a > 1 时，部分时间单齿啮合，部分时间双齿啮合。
pb
2
B1B2
B1P + PB2
ω2
ε = pb = πmcosα
ε=
1 （z1（tan α a1 – tanα ’) + z2（tan α a2 – tanα ’））
2π
由上式可知，重叠度 ε 与齿数 z 正有关，z 越大ε 越高；
啮合角 α’ 越大，重叠度 ε 越小。与模数m无关。
四、原则中心距 a 与实际中心距 a’
机械原理图PPT(44张)
将死的野狗没有人爱
31
飞机的星形发动机
将死的野狗没有人爱
32
缝纫机
将死的野狗没有人爱
33
舰炮弹药装填系统
将死的野狗没有人爱
34
汽车等速万向节
将死的野狗没有人爱
35
V 型发动机 ——汽缸排列在成一定 角度的两个平面上，V6发动机
将死的野狗没有人爱
36
直列式发动机——它的汽缸肩并肩地排 成一排，L4发动机，一般的车都用
42
拉链工作原理
将死的野狗没有人爱
43
无管虹吸原理
将死的野狗没有人爱
44
•
1．从人人自畏、噤若寒蝉的“文革十 年”到 新时期 艺术家 心情畅 达、创 作自由 ，其差 别有如 天壤， 主要是 因为当 代艺术 批评的 失语与 批评家 的缺席 。
•
2．在中国历史上，不乏艺术家特立独 行的故 事，也 不乏统 治者铲 除异端 的故事 ，这些 与艺术 家创作 中重大 主题表 现不够 、历史 进程描 述不力 的缺陷 有很大 关系。
将死的野狗没有人爱
16
让人发狂的异型齿轮机构，你能想 象其中的三维啮合和运行状态吗
将死的野狗没有人爱
17
除了8
数一数，这是多少缸、多少气门的 发动机
将死的野狗没有人爱
19
德国人菲加士·汪克尔在上世纪初 发明的转子发动机
将死的野狗没有人爱
20
•
. 人类在发展基因工程作物时没有充 分考虑 对人体 和环境 可能产 生的长 期影响 ，此方 面研究 有很大 的欠缺 。
•
6．这篇文章围绕一个“乐”字，先叙 事后议 论，语 言如行 云流水 ，洋洋 洒洒， 收纵自 如，得 心应手 ，颇有 大家风 范。
机械原理图ppt课件(44张)
•
3朗读是加深记忆的有效方法，但并不 是唯一 的方法 。记忆 规律， 还有许 多未解 之谜， 有待我 们继续 探索和 发现。
•
4．草书特点是结构简省，笔画连绵； 楷书由 隶书逐 渐演变 而来， 更趋简 化，字 形由扁 改方， 平正而 不呆， 齐整而 不拘。
•
5．行书是在隶书的基础上发展起源的 ，介于 楷书、 草书之 间的一 种字体 ，是为 了弥补 楷书的 书写速 度太慢 和草书 的难于 辨认而 产生的 。
将死的野狗没有人爱
6
全自动小型冲锋枪的上弹、击发、 退壳机构，看三分钟，才有完整
连续的印象
将死的野狗没有人爱
7
特殊的减速传动机构，有没有参 考性？
将死的野狗没有人爱
8
中学生用乐高积木营造的自动化 世界
将死的野狗没有人爱
9
周期性滑轨拨叉机构，巧妙而常 用的机械结构
将死的野狗没有人爱
10
细密的小型金属锁链就是这样高 速形成的
将死的野狗没有人爱
11
最清晰、完整的自动枪械（机枪） 上弹、击发、退壳机构
将死的野狗没有人爱
12
扭簧摆动机构，工程师既熟悉又 陌生的机构
将死的野狗没有人爱
13
连续摆、滑机构
将死的野狗没有人爱
14
这一定是中国保定出品的机械手， 保定府才玩铁球嘛
将死的野狗没有人爱
15
鲁班自制飞鸟，骑乘游九州，不 是传说哦
•
6.会赏析其语言，如从遣词、用句、 修辞等 方面揣 摩、推 敲、理 解作者 炼字达 意的技 巧；
•
7.从作家作品的语言风格的比较中， 从用韵 、节奏 、音调 三个方 面去品 味其语 言的音 乐美、 节奏美 、韵律 美。
机械原理ppt课件完整版
齿轮传动的设计步骤
包括选择齿轮类型、确定齿轮模 数、齿数、压力角等参数，进行 齿轮强度校核等。
齿轮传动的应用
广泛应用于各种机械设备中，如 汽车、机床、工程机械等。
链传动的设计与分析
链传动的类型
包括滚子链传动、齿形链传动等。
链传动的设计步骤
包括选择链条类型、确定链条节距、链轮齿 数等参数，进行链条强度校核等。
定义与研究对象
机械系统动力学是研究机械系统在力作用下的运动规律及其与力的相互关系的学科。它主要 关注机械系统在外力作用下的运动状态，如速度、加速度、位移等的变化规律。
基本术语与概念
包括力、质量、加速度、动量、动能、势能等，这些术语和概念是描述机械系统运动状态的 基础。
动力学原理
牛顿运动定律、动量定理、动能定理等是机械系统动力学的基本原理，它们揭示了机械系统 运动的基本规律。
命和可靠性。
检测装备
包括测量仪器、检测设备等，用 于对加工过程中的产品精度和质 量进行检测和控制，确保产品符
合设计要求。
先进制造技术与装备简介
数控技术
机器人技术
通过计算机编程控制机床等加工装备，实现 自动化、高精度和高效率的加工过程。
应用机器人进行自动化生产，提高生产效率 和产品质量，降低劳动强度和生产成本。
2023
PART 03
机械传动与驱动
REPORTING
机械传动的类型和特点
摩擦传动
螺旋传动
利用摩擦力传递动力和运动的传动方 式，如带传动、摩擦轮传动等。其特 点是结构简单、成本低廉，但传动效 率较低且易磨损。
利用螺旋副传递动力和运动的传动方 式，如螺旋千斤顶、螺旋压力机等。 其特点是结构简单、自锁性好，但传 动效率较低。
《机械原理自由度》课件
机械故障诊断
通过运动分析诊断机械故障的原因 和位置。
控制系统设计
利用运动分析结果设计控制系统的 参数和策略。
机构运动分析的实例
平面四杆机构的运动分析
01
通过解析法计算平面四杆机构的自由度，并分析其运动特性。
凸轮机构的运动分析
02
利用实验法测量凸轮机构的位移、速度和加速度，分析其运动
规律。
机器人臂关节的运动分析
03
通过数值法模拟机器人臂关节的运动行为，优化关节的设计参
数。
04
机构动力学分析
机构动力学的基本概念
机构动力学是研究机 械系统中机构运动及 其与力的关系的学科 。
机构动力学的基本概 念包括力、力矩、加 速度、速度和位移等 。
它涉及到系统的平衡 、运动规律、动态响 应等方面的内容。
机构动力学分析的Байду номын сангаас法
空间机构自由度计算
总结词
空间机构自由度计算是机械原理中一个复杂的概念，它涉及到机构在空间中的 运动自由度数。
详细描述
空间机构的自由度计算公式为F=6n-(3PL + Ph)，其中n为活动构件数，PL为低 副数，Ph为高副数。与平面机构不同，空间机构需要考虑三个方向的自由度， 因此计算更为复杂。
特殊机构自由度计算
通过建立平面连杆机构的运动学和动力学模型，分析其运动规律 和动态响应。
凸轮机构的动力学分析
研究凸轮机构的动态行为，包括从动件的运动规律和受力情况等。
齿轮机构的动力学分析
分析齿轮机构的动态特性，如振动、冲击和噪声等，以提高齿轮传 动的平稳性和可靠性。
05
机构优化设计
机构优化设计的目标和方法
目标
《机械原理》ppt课件
01机械原理概述Chapter机械原理的定义与重要性定义重要性机械原理的研究对象和内容研究对象主要研究各种机构（如连杆机构、凸轮机构、齿轮机构等）和机器（如内燃机、电动机、机床等）的工作原理、运动特性、力学性能以及设计计算方法等。
研究内容包括机构的组成原理、运动学分析、动力学分析、机械效率与自锁、机器的平衡与调速等。
机械原理的发展历程和趋势发展历程发展趋势02机构的结构分析与设计Chapter机构的基本概念和分类机构定义由刚性构件通过运动副连接而成的系统，用于传递运动和力。
机构分类根据运动特性可分为连杆机构、凸轮机构、齿轮机构等。
运动副类型包括低副（转动副、移动副）和高副（点接触、线接触）。
结构分析通过自由度计算、运动链分析等方法，确定机构的组成、运动特性和约束条件。
综合方法基于功能需求，选择合适的机构类型，进行组合、变异和演化，设计出满足特定要求的机构。
创新设计运用创新思维和现代设计方法，如拓扑优化、仿生学等，进行机构创新设计。
机构的结构分析和综合方法机构设计的原则和方法设计原则设计方法案例分析03机械传动与驱动Chapter机械传动的类型和特点摩擦传动啮合传动利用齿轮、链轮等啮合元件传递动力和运动。
具有传动效率高、工作可靠、使用寿命长等优点，但需要较高的制造精度和安装精度。
齿轮类型选择齿轮参数设计强度校核030201齿轮传动的设计与分析链传动和带传动的设计与分析链传动设计带传动设计强度校核液压与气压传动的设计与分析液压传动设计01气压传动设计02控制与调节0304机械系统动力学与振动Chapter机械系统动力学的基本概念和方法动力学基本概念动力学建模方法动力学分析方法机械系统的振动分析和控制振动基本概念振动分析方法振动控制策略机械系统动力学优化设计方法优化设计基本概念动力学优化设计方法优化设计实例分析05机械制造工艺与装备Chapter机械制造工艺的基本概念和流程机械制造工艺的基本概念机械制造工艺的流程机械制造装备的分类和特点机械制造装备的分类机械制造装备的特点先进制造技术是指基于先进制造理论、技术和方法的总称，包括计算机辅助设计（CAD ）、计算机辅助制造（CAM ）、计算机辅助工艺规划（CAPP ）、数控技术（NC ）、柔性制造系统（FMS ）等。
机械原理(全套154页PPT课件)
接触，且易于制造，易于保证所要求的制造精度 3）能够实现多种运动轨迹曲线和运动规律，工程
上常用来作为直接完成某种轨迹要求的执行机构。
4）可实现远距离传递的操纵机构。
不足之处： 1）不易于传递高速运动。 2）可能产生较大的运动累积误差。 3）平面连杆机构的设计较为繁难。
§2-1 平面四杆机构的基本形式、演变
构件和零件 构件 机器中的独立运动单元 • 零件 机器中的制造单元
机架（固定构件）
构件分成以下几种
主动件
活动构件
从动件
其中，运动规律已知的活动构件称为原动件，
输出运动或动力的从动件称为输出件。
由若干零件组成 的构件——连杆
1--连杆体 2--螺栓 3--螺母 4--连杆盖
1
2 3
4
二、运动副及其分类
n –活动构件数；Pl –低副数；Ph –高副数
n = 3, Pl= 4 F = 3×3–2×4 = 1
n = 4, Pl = 5 F = 3×4–2×5 = 2
平面机构具有确定运动的条件是：
１）机构自由 度数 F≥1。 2） 原动件数目等于机构自由度数F.
三、计算机构自由度时应注意的几种情况
1) 正确确定运动副的数目 由三个或三个以上构件组成的轴线重
如转动副、移动副。
2）高副：点或线接触的运动副。 如齿轮副、凸轮副。
也可将运动副分为平面运动副和空间运动副。
1）平面运动副：组成运动副两构件间作相对平 面运动，如转动副、移动副、凸轮副、齿轮副。
2）空间运动副：组成运动副两构件间作相对空 间运动。如螺旋副，球面副。
第一章
平面机构具有确定 运动的条件
构件运动，即对整个机构运动无关的自由度。
上常用来作为直接完成某种轨迹要求的执行机构。
4）可实现远距离传递的操纵机构。
不足之处： 1）不易于传递高速运动。 2）可能产生较大的运动累积误差。 3）平面连杆机构的设计较为繁难。
§2-1 平面四杆机构的基本形式、演变
构件和零件 构件 机器中的独立运动单元 • 零件 机器中的制造单元
机架（固定构件）
构件分成以下几种
主动件
活动构件
从动件
其中，运动规律已知的活动构件称为原动件，
输出运动或动力的从动件称为输出件。
由若干零件组成 的构件——连杆
1--连杆体 2--螺栓 3--螺母 4--连杆盖
1
2 3
4
二、运动副及其分类
n –活动构件数；Pl –低副数；Ph –高副数
n = 3, Pl= 4 F = 3×3–2×4 = 1
n = 4, Pl = 5 F = 3×4–2×5 = 2
平面机构具有确定运动的条件是：
１）机构自由 度数 F≥1。 2） 原动件数目等于机构自由度数F.
三、计算机构自由度时应注意的几种情况
1) 正确确定运动副的数目 由三个或三个以上构件组成的轴线重
如转动副、移动副。
2）高副：点或线接触的运动副。 如齿轮副、凸轮副。
也可将运动副分为平面运动副和空间运动副。
1）平面运动副：组成运动副两构件间作相对平 面运动，如转动副、移动副、凸轮副、齿轮副。
2）空间运动副：组成运动副两构件间作相对空 间运动。如螺旋副，球面副。
第一章
平面机构具有确定 运动的条件
构件运动，即对整个机构运动无关的自由度。
机械原理瞬心及位置确定讲课ppt
2 P23
C
3
4
D
P34
瞬心P13、P24的位置需用三心定理确又与P23、P34 在同一直
P12
12
P23
线上 故两直线P12P14 和P23P34的 P14 交点就是P24。
3
4
P34
P13
➢同理，两直线P12P14 和P23P34的交点就是P24 。
❖两构件组成纯滚动高副 接触点就是其瞬心
❖ 两构件组成滚动兼滑动高副 瞬心在接触点处两高副元素的 公法线上。
位例置：确定—图—示铰②链借四助杆三机心构定的理瞬确心定
❖三心定理：
作平面运动的三个构件的三个
瞬心位于同一直线上。
B
P12
1
A P14
❖ 瞬心P12、P23、P34、P14的位置可
直观地确定，标在图中。
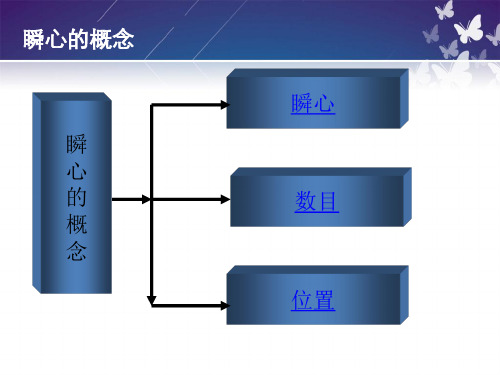
瞬心的概念
瞬 心 的 概 念
瞬心 数目 位置
瞬心
瞬心就是两构件上瞬时速度相同的重合点（即 等速重合点）。
数目
位置确定—— ① 由瞬心定义确定
❖两构件组成转动副 转动副的中心就是其瞬心;
❖两构件组成移动副 其瞬心在垂直于导路 方向的无穷远处；
构件1、2之间用 P12表示
位置确定—— ① 由瞬心定义确定
机械原理完整ppt课件
微器等。
04 连杆机构与凸轮机构
连杆机构的基本形式和设计方法
连杆机构的基本形式
包括曲柄摇杆机构、双曲柄机构、双摇杆机构等，每种形式都有其特定的运动特 性和应用场合。
连杆机构的设计方法
根据给定的运动规律和设计要求，选择合适的连杆机构形式，并通过几何关系、 运动学分析和动力学计算等方法，确定机构的尺寸、运动参数和动力参数。
机械原理完整ppt课 件
目录
CONTENTS
• 机械原理概述 • 机构的结构分析与设计 • 机械传动与驱动 • 连杆机构与凸轮机构 • 间歇运动机构与组合机构 • 机械系统动力学与平衡 • 现代设计方法在机械原理中的应用
01 机械原理概述
机械原理的定义与重要性
定义
机械原理是研究机械系统运动、 力和能量转换规律的科学。
01
链传动应用
适用于机床、起重机械、农业机械等需要较大传动比和较高效率的场合
。
02
带传动应用
广泛应用于轻工、纺织、化工等行业的传动系统中，如缝纫机、皮带运
输机等。
03
螺旋传动应用
常用于机床进给机构、千斤顶、螺旋压力机等需要直线运动或升降运动
的场合。同时，在精密仪器和微调装置中也有广泛应用，如精密螺旋测
中的重要性。
优化设计的数学模型
02
讲解优化设计的数学模型，包括设计变量、目标函数和约束条
件等要素的定义和表示方法。
优化算法与实例分析
03
介绍常用的优化算法，如梯度下降法、遗传算法等，并通过实
例分析展示如何在机械设计中应用这些算法进行优化。
可靠性设计在机械原理中的应用
可靠性设计的基本概念
介绍可靠性设计的定义、目的和意义，阐述可靠性设计在机械设计中的重要性。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2
D
2
p'(a') d'
3
c'
1
A
1
x
6
C
x
n2' b'
n t a C a B a CB a CB
方向： 沿xx 大小： ? √ √ C→ B 22lAB ⊥CB ?
用加速度影像法求出d'点 作Δb'c'd' ~ ΔBCD aD= μa p'd'
t aCB n 'c ' a 2 2 l BC l BC
课堂练习
图示机构,已知各构件尺寸和ω1，用瞬心法求v5 解题思路：
1
求３ 求v5
C D
3
E
4
A
1 2
ω1
5 6
F
利用P13
利用P35
B
机械原理 —— 平面机构的运动分析
P15
求P13
求P35
P56→∞
求P15
v5 v P15 1 P16 P15 l
P35
E P 34
3 4
1 AP13 3 DP13
2 P13 vP13 B 1 AP
1 P13P14L = 3 P13P34 L
4
P34
D
P13 P14 3 1 逆时针 P13 P34
机械原理 —— 平面机构的运动分析
3 平面高副机构
3 2 1 1 1 2 3
P23
vP12 P12 P23
P13
P12 vP12
P23
P13
取μa= aB/ p'b'作加速度图 aC= μa p'c'
逆时针
⊥CB ?
p(a) d
c
取μv= υB/ pb作速度图 υC= μυ pc 3）求υD ：
方向： 大小：
b
v D v B v DB v C v DC
? ?
⊥BA ⊥DB √
Δbcd ~ ΔBCD
故d点也可用速度影像法求出
√
?
√
⊥DC ?
机械原理 —— 平面机构的运动分析
机械原理 —— 平面机构的运动分析
一、速度瞬心Instant Center
《理论力学》：当任一刚体相对于另一 刚体作平面运动时，在任一瞬时，都可 以认为它们是绕某一点作相对转动，该 点称为瞬时相对回转中心。 (Ａ 瞬时相对回转中心的位置? P12 既然P12是瞬时相对回转中心,则该 瞬时两构件在P12的相对速度为 零，或者说绝对速度相等,所以, P12为两构件该瞬时的等速重合点 速度瞬心:两构件瞬时等速重合点 相对速度为零，绝对速度相等 瞬心：相对瞬心、绝对瞬心 瞬心：
（1）取l , 作机构运动简图 （2）速度分析
解:
B D ω1 A
1
求解顺序： 1）求υB ： υB= ω1lAB ，方向⊥AB向右下 2）求υC ：
方向： 沿xx 大小： ? ⊥BA 1lAB
v B v C v D、 2
aB
vB
2
x
6
3
C
x
v C v B v CB
2
,Ａ １) ２
υＡ２Ａ１
(B
２ ,B １)
υ B２B１
P12
1
机械原理 —— 平面机构的运动分析
三、瞬心位置的确定
(1) 由瞬心定义确定
通过运动副直接相联的构件——显瞬心
n
P12
P12 纯滚动
P12
滚＋滑
C 2
P23
P12 B
1
3
P12 P12
机械原理 —— 平面机构的运动分析
瞬心位置的确定
1 P12 P12 2 P23 P12
v 2 v P 12 1 P13 P12 L 向上
机械原理 —— 平面机构的运动分析
例3 已知：铰链四杆机构各杆的长度。
求：机构的传动比 i=2/4 解：1. 取l 作机构运动简图 2. 求瞬心数目：N=4(4-1)/2=6 3. 求瞬心p24 要点： 取含2、4构件的三构件组两次确定p24 1-2-4构件组、 2-3-4构件组 同理得p13 vp24 v p p 12 24 2 3.求2 /4 p 24 v p 24 p14 p 24 4
例1
图示机构,已知各构件尺寸和1(顺时针），求vC 、vD和2
求解顺序：
v B v C v D、 2
ω1 A
1
B D aB vB
2
解： (续) υC （1）取l ，作机构运动简图； （2）速度分析 1）求υB 2）求υC 3）求υD 4）求ω2
vCB v bc 2 lBC lBC
t aCB
t aC
C B 1 1 A 1 2
n aCB n aC 3
B→A ⊥AB
C→B
⊥CB
?
①从p’点(极点)开始，作p’n1’∥BA ( anB ), 继续作n1’b’⊥BA ( atB ) ②过加速度图上b’点作b’n2’∥CB ( anCB ), 继续作n2’c’⊥CB ( atCB ) ③过加速度图上p’点作p’n3’∥CD ( anC ), 继续作n3’c’⊥CD ( atC ) ； 两线相交点c点即为所求。
逆时针方向
x
6
3
C
x
p(a) d
c
b
机械原理 —— 平面机构的运动分析
同一构件上两点间的加速度关系
1. 速度分析 2. 加速度分析
p(a) d b
例2 图示机构,已知各构件尺寸和aB，求aC 、aD和2
求解顺序： a B aC a D、 2
B
c
2
aB vB
解法二： 1 取μl作机构运动简图 2 求绝对瞬心P13 取含1、3构件的三构件组两次确定p13 1-2-3构件组、 1-3-4构件组 3 求2 /4
P13 P34
４ ２
３
P23 ２
１
4 P14
vP 23 3 P23 P 13 2 P 23 P 12 v P 34 3 P34 P13 4 P34 P14
P12
P23 P12 2 P34 P13 l v P 34 P23 P13 P P P P 4 2 23 12 34 13 P34 P14 l P34 P14 l P23 P13 P34 P14
2 ...... 4
机械原理 —— 平面机构的运动分析
v5 v P 35 3 DP35
P56→∞
D
P16
1 2
A ω1
5
P13 C
P23
P36
F P45
6
P12
B
机械原理 —— 平面机构的运动分析
3-3 用矢量方程图解法作机构的运动分析
一、针对的工程问题 二、矢量方程图解法原理 三、同一构件上两点间的速度和加速度关系 四、两构件重合点间的速度和加速度关系 五、小结
C→B
2 2 BC
⊥CB
?
取加速度比例尺a作加速度多边形图，可求出aC
机械原理 —— 平面机构的运动分析
加速度多边形的作法： n t n t n t aC aC aC a B a B aCB aCB
方向： ? 大小： ?
C→D ⊥CD
2 3 lCD ? 2 12 l AB 1 l AB 2 l BC
2 p14 p 24 i 4 p12 p 24
p24
分析：
显瞬心：p12, p23, p34, p14 隐含的瞬心：p13, p24
p13 p34
４ ２
３
p23 ２
１
4 p14
p12
机械原理 —— 平面机构的运动分析
例3 已知：铰链四杆机构各杆的长度。
求：机构的传动比 i=2/4
速度大小 图示线段长度
B 1 1 A 4 c D 方向： ⊥CD 大小： ? ⊥BA 1lAB C ⊥CB ?
μυ=
υCB
2
②从p点（极点）开始，作pb⊥BA， pb表示υB， pb =υB/ μυ ③过速度图上b点作bc⊥CB ， 过速度图上p点作pc⊥CD ； 两线相交点c点即为所求。 ④量得线段pc的长度，则υC= μv pc υC方向为p →c,即⊥CD 解:（续） 求：3= vC/lCD ，顺时针方向 (4)求2：2=vCB/lBC=μvbc/ lBC ， 逆时针方向
E
4
B D(D4,D5) 1
1 5
1
A
aB
vB
2 3
x
6
C
x
F
机械原理 —— 平面机构的运动分析
1. 速度分析
引例 图示铰链四杆机构,已知各构件尺寸和1 ，求3和2
解:
1 取l作机构运动简图； 2 速度分析 求解顺序：vB→ vC → 3、2 (1) 求vB ： vB= ω1·lAB ，方向:⊥AB向右下 (2) 求vC ：
t aB
a
n B
4
D
p’
aC an B
c’
anC aB
n3’
解:（续） 求：3= atC/lCD ，逆时针方向 (4)求2：2=atCB/lBC 逆时针方向
aCB
n1’ n2’
atB
anCB
b’
机械原理 —— 平面机构的运动分析
例1 图示机构,已知各构件尺寸和1(顺时针），求vC 、vD和2
υC
3
υB
υC