小学六年级奥数- 面积计算(一)
图形面积(六年级奥数题及答案)

1、有10张扑克牌,点数分别为1,2,3,…,9,10。
从中任意取出若干张牌,为了使其中必有几张牌的点数之和等于1 5,问最少要取多少张牌?
2、在三角形ABC中,点E是BC边上的中点,点F是中线A E上的点,其中AE=3AF,并且延长BF与AC相交于D,如下图所示。
若三角形ABC的面积为48,请问三角形AFD的面积为多少?
点击下一页查看答案
1.有10张扑克牌,点数分别为1,2,3,…,9,10。
从中任意取出若干张牌,为了使其中必有几张牌的点数之和等于15,问最少要取多少张牌?
解答:若只取5张牌,有可能不满足条件,例如1,2,8,9,10。
因此,最少取的张数不小于6。
下面证明6可以满足条件。
可以将5-10分成3组:{5,10},{6,9},{7,8},每组至多选一个
则若在1,2,3,4中任意选三个数,它们的和一定在上面三组数中,即6个数必有若干个之和为15。
2.在三角形ABC中,点E是BC边上的中点,点F是中线AE上的点,其中AE=3AF,并且延长BF与AC相交于D,如下图所示。
若三角形ABC的面积为48,请问三角形AFD的面积为多少?。
奥数圆面积计算六年级上册培优

奥数组合图形面积计算1:求出阴影部分的面积(单位:厘米)6×6×3.14×41 =9×3.14=28.26(平方厘米)2、求下面图形的阴影部分面积单位:厘米(1)6×6÷2=18(平方厘米)( 2)6×6=36(平方厘米)3、求出阴影部分的面积(单位:厘米)4×4×3.14×41-4×4÷2+4×2÷2 =12.56-8+4=8.56(平方厘米)4、求下列图形的阴影部分的面积(单位厘米)(1) 4×2=8(平方厘米) (2) 4×4÷2=8(平方厘米)5、两圆半径都是1厘米,且图中两个阴影部分的面积相等。
求长方形ABO 1O 的面积。
3.14×12×41×2=1.57(平方厘米) 6、圆的周长为12.56厘米,AC 两点把圆周分成相等的两段弧,阴影部分(1)的面积与阴影部分(2)的面积相等,求平行四边形ABCD 的面积。
12.56÷3.14=4(厘米) 22×3.14=12.56(平方厘米)7、直径BC=8厘米,AB=AC ,D 为AC 的中点,求阴影部分的面积。
8×4÷2÷2=8(平方厘米)3.14×42×41-4×4÷2=12.56-8=4.56(平方厘米) 8+4.56=12.56(平方厘米)8、求阴影部分的面积。
(单位:厘米)。
CD:DF=FE:EBD F ×FE=CD ×EB=6×4=24(平方厘米)9、求四边形ABCD 的面积。
(单位:厘米)7×7÷2-3×3÷2=24.5-4.5=20(平方厘米)10、BE 长5厘米,长方形AEFD面积是38平方厘米。
六年级奥数专题圆的面积
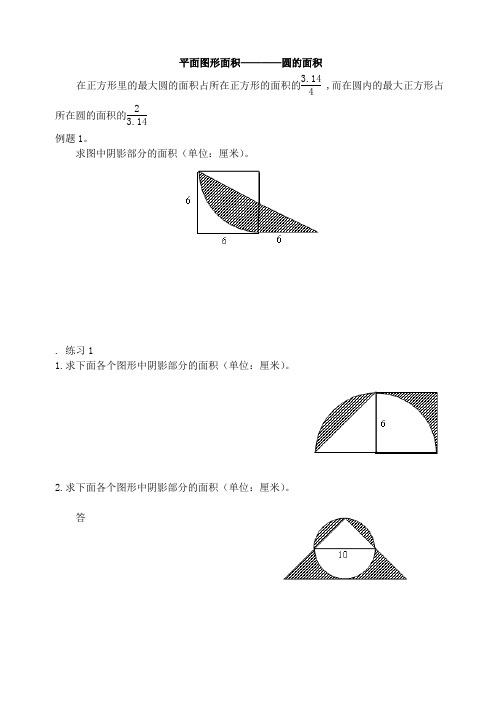
平面图形面积————圆的面积在正方形里的最大圆的面积占所在正方形的面积的3.144 ,而在圆内的最大正方形占所在圆的面积的23.14例题1。
求图中阴影部分的面积(单位:厘米)。
. 练习11.求下面各个图形中阴影部分的面积(单位:厘米)。
2.求下面各个图形中阴影部分的面积(单位:厘米)。
答1、计算下面图形中阴影部分的面积(单位:厘米,正方形边长4)。
答2、计算下面图形中阴影部分的面积(单位:厘米,正方形边长4)。
答1 2. 练习41、如图所示,三角形ABC是直角三角形,AC长4厘米,BC长2厘米。
以AC、BC为直径画半圆,两个半圆的交点在AB边上。
求图中阴影部分的面积。
答例题5。
在图中,正方形的边长是10厘米,求图中阴影部分的面积。
.1、求下面各图形中阴影部分的面积(单位:厘米)。
答2、求右面各图形中阴影部分的面积(单位:厘米)。
答3、求右面各图形中阴影部分的面积(单位:厘米)。
答.例题6。
在图的扇形中,正方形的面积是30平方厘米。
求阴影部分的面积。
练习61、如图所示,平行四边形的面积是100平方厘米,求阴影部分的面积。
答圆的面积与组合圆积专题训练一、填空题1.算出下面圆内正方形的面积为 .2.右下图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是平方厘米.3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是 厘米.(保留两位小数)5.左下图三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. AB 长40厘米, BC 长 厘米6.如右下图,阴影部分的面积为2平方厘米,7.157平方厘米,这个扇形的圆心角是 .度。
8.图中扇形的半径OA=OB=6厘米.45=∠AOB , AC 垂直OB 于C,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.在右图中(单位:厘米),两个阴影部分面积的和是 平方厘米.10.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大 平方厘米.11.左下图在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取3.14,结果精确到1平方厘米)12.右上图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).13.如左下图所示,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π14.如右下图,151=∠的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是 .15. 如左下图已知:ABCD 是正方形, ED=DA=AF=2厘米,阴影部分的面积是 .16.右下图中,扇形BAC 的面积是半圆ADB 的面积的311倍,那么,CAB 是 度.。
小学六年级奥数第27讲 表面积与体积(一)(含答案分析)

第27讲表面积与体积(一)一、知识要点小学阶段所学的立体图形主要有四种长方体、正方体、圆柱体和圆锥体。
从平面图形到立体图形是认识上的一个飞跃,需要有更高水平的空间想象能力。
因此,要牢固掌握这些几何图形的特征和有关的计算方法,能将公式作适当的变形,养成“数、形”结合的好习惯,解题时要认真细致观察,合理大胆想象,正确灵活地计算。
在解答立体图形的表面积问题时,要注意以下几点:(1)充分利用正方体六个面的面积都相等,每个面都是正方形的特点。
(2)把一个立体图形切成两部分,新增加的表面积等于切面面积的两倍。
反之,把两个立体图形粘合到一起,减少的表面积等于粘合面积的两倍。
(3)若把几个长方体拼成一个表面积最大的长方体,应把它们最小的面拼合起来。
若把几个长方体拼成一个表面积最小的长方体,应把它们最大的面拼合起来。
二、精讲精练【例题1】从一个棱长10厘米的正方体木块上挖去一个长10厘米、宽2厘米、高2厘米的小长方体,剩下部分的表面积是多少?这是一道开放题,方法有多种:①按图27-1所示,沿着一条棱挖,剩下部分的表面积为592平方厘米。
图27--1②按图27-2所示,在某个面挖,剩下部分的表面积为632平方厘米。
图27--2③按图27-3所示,挖通某两个对面,剩下部分的表面积为672平方厘米。
图27--3练习1:1、从一个长10厘米、宽6厘米、高5厘米的长方体木块上挖去一个棱长2厘米的小正方体,剩下部分的表面积是多少?2、把一个长为12分米,宽为6分米,高为9分米的长方体木块锯成两个想同的小厂房体木块,这两个小长方体的表面积之和,比原来长方体的表面积增加了多少平方分米?3、在一个棱长是4厘米的立方体上挖一个棱长是1厘米的小正方体后,表面积会发生怎样的变化?图27—4【例题2】把19个棱长为3厘米的正方体重叠起来,如图27-4所示,拼成一个立体图形,求这个立体图形的表面积。
要求这个复杂形体的表面积,必须从整体入手,从上、左、前三个方向观察,每个方向上的小正方体各面就组合成了如下图形(如图27-5所示)。
(完整版)六年级奥数练习(阴影面积)1
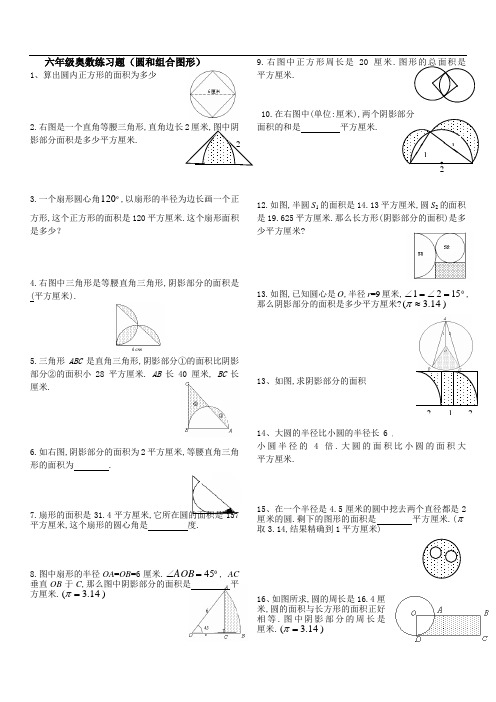
六年级奥数练习题(圆和组合图形)1、算出圆内正方形的面积为多少 2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是多少平方厘米. 3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是多少? 4.右图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).5.三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. AB 长40厘米, BC 长厘米.6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积为 .7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC垂直OB 于C ,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是平方厘米. 10.在右图中(单位:厘米),两个阴影部分 面积的和是 平方厘米.12.如图,半圆S 1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O ,半径r =9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米?)14.3(≈π13、如图,求阴影部分的面积 .14、大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面平方厘米.15、在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取3.14,结果精确到1平方厘米)16、如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是厘米.)14.3(=π2 1 2112217.下图中正方形部分是一个水池,其余部分是草坪,已知正方形的面积是300平方米,草坪的面积是多少平方米?17、已知:ABC D 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .18、如图:阴影部分的面积是多少?四分之一大圆的半径为r .(计算时圆周率取722)19、已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.20.如图{图在下面}两个连在一起的轮轴,已知小轮的半径是3分米,当这个小轮转3圈时,大轮正好转一圈,21.3只蜜蜂分别沿着阴影部分的边缘飞1次,那只蜜蜂飞过的路线最长?(3个正方形的边长都为4m )23.将半径分别是3厘米和2厘米的两个半圆如图放置,求阴影部分的周长24.求阴影部分的面积25.一个圆环外直径是内直径的二分之三倍,圆环面积150cm ,求外圆的面积26.一个长方形的面积是20平方厘米,如果在这个长方形里画一个最大的半圆形,这个半圆形是多少平方厘米?因为这个半圆的直径是长方形的长,半径是宽,说明长方形的长是宽的2倍。
小学奥数蓝色面积练习题

小学奥数蓝色面积练习题一、基础面积计算1. 一个长方形的长是10厘米,宽是5厘米,求这个长方形的面积。
2. 一个正方形的边长是8厘米,求这个正方形的面积。
3. 一个三角形的底是12厘米,高是6厘米,求这个三角形的面积。
4. 一个圆的半径是4厘米,求这个圆的面积。
二、组合图形面积计算5. 有一块长方形土地,长是20米,宽是15米,中间有一个边长为5米的正方形花坛,求土地的种植面积。
6. 一个长方形和正方形的组合图形,长方形的长是10厘米,宽是6厘米,正方形的边长是4厘米,求组合图形的面积。
7. 一个三角形和一个梯形的组合图形,三角形的底是8厘米,高是6厘米,梯形的上底是5厘米,下底是10厘米,高是4厘米,求组合图形的面积。
三、面积问题应用8. 一个长方形游泳池的长是50米,宽是25米,要在游泳池四周铺上宽度为2米的蓝色地砖,求铺地砖的面积。
9. 一个花园的形状是半圆形,直径为30米,要在花园的边界上种一圈蓝色小花,求种花所需的面积。
10. 一个正方形广场的边长是40米,要在广场中央画一个边长为20米的蓝色大方块,求蓝色大方块以外的面积。
四、面积比较与推理11. 两个长方形,长分别为15厘米和12厘米,宽分别为10厘米和8厘米,哪个长方形的面积更大?12. 两个圆,半径分别为6厘米和8厘米,哪个圆的面积更大?13. 一个三角形和一个等底等高的平行四边形,三角形的底是10厘米,高是6厘米,求平行四边形的面积。
五、趣味面积题14. 一块蓝色正方形地毯,边长为9厘米,将其剪成四个相同的小正方形,求每个小正方形的面积。
15. 一个蓝色长方形纸片,长是18厘米,宽是12厘米,将其剪成三个相同的小长方形,求每个小长方形的面积。
16. 有一块蓝色土地,形状为直角梯形,上底是6米,下底是10米,高是4米,求土地的面积。
六、等面积问题17. 有两个相同面积的长方形,一个长方形的长是16厘米,宽是4厘米,求另一个长方形的宽,如果它的长是8厘米。
【强烈推荐】六年级奥数练习(阴影面积)1

六年级奥数练习(阴影面积)11、算出圆内正方形的面积为多少 2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是多少平方厘米. 3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是多少?4.右图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).5.三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. AB 长40厘米, BC 长 厘米.6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积为 .7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC 垂直OB 于C ,那么图中阴影部分的面积是 平方厘米.)14.3(=π 9.右图中正方形周长是20厘米.图形的总面积是平方厘米.10.在右图中(单位:厘米),两个阴影部分面积的和是 平方厘米. 12.如图,半圆S 1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O ,半径r =9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米?)14.3(≈π13、如图,求阴影部分的面积 . 14、大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大 平方厘米. 15、在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取3.14,结果精确到1平方厘米)16、如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π17.下图中正方形部分是一个水池,其余部分是草坪,已知正方形的面积是300平方米,草坪的面积是多少平方米?17、已知:ABC D 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .18、如图:阴影部分的面积是多少?四分之一大圆的半径为r .(计算时圆周率取722)19、已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积.20.如图{图在下面}两个连在一起的轮轴,已知小轮的半径是3分米,当这个小轮转3圈时,大轮正好转一圈,21.3只蜜蜂分别沿着阴影部分的边缘飞1次,那只蜜蜂飞过的路线最长?(3个正方形的边长都为4m )23.将半径分别是3厘米和2厘米的两个半圆如图放置,求阴影部分的周长24.求阴影部分的面积25.一个圆环外直径是内直径的二分之三倍,圆环面积150cm ,求外圆的面积26.一个长方形的面积是20平方厘米,如果在这个长方形里画一个最大的半圆形,这个半圆形是多少平方厘米?因为这个半圆的直径是长方形的长,半径是宽,说明长方形的长是宽的2倍。
举一反三--六年级奥数面积计算(1)

组合图形的面积(1)
13、图中BO=2DO,阴影部分 的面积是4平方厘米,求梯形 ABCD的面积是多少平方厘米?
14、如图,正方形ABCD的边长 是12厘米,CE=4厘米。求阴影 部分的面积。
组合图形的面积(1)
15、图中三角形ABC的面积是 36平方厘米,AC长8厘米,DE 长3厘米,求阴影部分的面积 (ADFC不是正方形)。 16、有两种自然的放法将正 方形内接于等腰直角三角形。 已知等腰直角三角形的面积 是36平方厘米,两个正方形 的面积分别是多少?
六年奥数——举一反三 面积计算(一)
组合图形的面积(1)
1、已知右面的两个正方形边长 分别为6分米和4分米,求图中阴 影部分的面积。
2、如图,这个长方形的长是9厘 米,宽是8厘米,A和B是宽的中 点,求长方形内阴影部分的面积。
组合图形的面积(1)
3、右图是两个相同的直角三 角形叠在一起,求阴影部分的 面积。(单位:厘米)
4、如图,长方形长18厘米, 宽12厘米,AE、AF两条线段 把长方形面积三等分,求三 角形AEF的面积。
组合图形的面积(1)
5、如图,三角形ABC的面积是 24平方厘米,且DC=2AD,E、 F分别是AF、BC的中点,那么 阴影部分的面积是多少?
6、如图,三角形ABC的面积是 90平方厘米,EF平行于BC, AB=3AE,那么三角形甲、乙、 丙的面积各是多少平方厘米?
组合图形的面积(1)
7、在等腰梯形ABCD中,AD=12 厘米,高DF=10厘米。三角形 CDE的面积是12平方厘米。求梯 形面积。
8、如图,三角形EDF的面积比三 角形ABE的面积大6平方厘米,已 知长方形ABDC的长和宽分别为6 厘米、4厘米,DF的长多少厘米?
六年级奥数专题圆的面积

平面图形面积————圆的面积在正方形里的最大圆的面积占所在正方形的面积的3.144 ,而在圆内的最大正方形占所在圆的面积的23.14例题1。
求图中阴影部分的面积(单位:厘米)。
. 练习11.求下面各个图形中阴影部分的面积(单位:厘米)。
2.求下面各个图形中阴影部分的面积(单位:厘米)。
答1、计算下面图形中阴影部分的面积(单位:厘米,正方形边长4)。
答2、计算下面图形中阴影部分的面积(单位:厘米,正方形边长4)。
答1 2. 练习41、如图所示,三角形ABC是直角三角形,AC长4厘米,BC长2厘米。
以AC、BC为直径画半圆,两个半圆的交点在AB边上。
求图中阴影部分的面积。
答例题5。
在图中,正方形的边长是10厘米,求图中阴影部分的面积。
.1、求下面各图形中阴影部分的面积(单位:厘米)。
答2、求右面各图形中阴影部分的面积(单位:厘米)。
答3、求右面各图形中阴影部分的面积(单位:厘米)。
答.例题6。
在图的扇形中,正方形的面积是30平方厘米。
求阴影部分的面积。
练习61、如图所示,平行四边形的面积是100平方厘米,求阴影部分的面积。
答圆的面积与组合圆积专题训练一、填空题1.算出下面圆内正方形的面积为 .2.右下图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是平方厘米.3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是 厘米.(保留两位小数)5.左下图三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. AB 长40厘米, BC 长 厘米6.如右下图,阴影部分的面积为2平方厘米,7.157平方厘米,这个扇形的圆心角是 .度。
8.图中扇形的半径OA=OB=6厘米.45=∠AOB , AC 垂直OB 于C,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.在右图中(单位:厘米),两个阴影部分面积的和是 平方厘米.10.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大 平方厘米.11.左下图在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取3.14,结果精确到1平方厘米)12.右上图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).13.如左下图所示,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π14.如右下图,151=∠的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是 .15. 如左下图已知:ABCD 是正方形, ED=DA=AF=2厘米,阴影部分的面积是 .16.右下图中,扇形BAC 的面积是半圆ADB 的面积的311倍,那么,CAB 是 度.。
六年级上册奥数题圆的面积

小学六年级奥数教材课程圆的周长和面积一条线段绕着它固定的一端在平面内旋转一周,它的另一端在平面内画出一条封闭的曲线,这条封闭的曲线就是圆。
画圆时,固定的一点叫做圆心,从圆心到圆上任意一点的线段叫做圆的半径,在同一个圆中,所有的半径都相等。
通过圆心,并且两端在圆上的线段叫做直径。
在同一个圆中,所有的直径都相等,且等于半径的2倍。
圆心决定圆的位置,半径决定圆的大小。
任意一个圆,它的周长除以直径的商总是一个固定的数,这个数叫圆周率。
如果用C 表示圆周的长度,d 表示这个圆的直径,r 表示它的半径,π表示圆周率,就有C dπ=或2C r。
π是一个无限不循环小数,π=3.14159265358979323846…。
圆的周长:C=2πr 或C=πd,圆的面积:S=πr 2。
圆的周长和面积计算的基本方法是仔细观察,发现特点,找出内在的联系,常常通过对图形的割补、旋转、平移、等积变形等方法加以解决。
需要精巧的构思和恰当的设计,把形象思维和抽象思维结合起来。
(本讲π均取 3.14)例1、上海外滩海关大钟钟面的直径是5.8米,钟面的面积是多少平方米?时针长2.7米,时针绕一圈时针尖端走过途径的长度是多少米?(得数保留一位小数)分析与解法:钟面的直径是5.8米这个条件是直接的,时针长指的是半径。
解:钟面的面积是:3.14×(5.8×2)2≈26.4(平方米)。
时针绕一圈时针尖端走过途径的长度是:2×3.14×2.7≈17.0(米)。
例2、如图所示,试比较大圆的面积与阴影部分的面积、大圆的周长与阴影部分的周长。
图图(1)分析与解法:本题有两问,一是比较阴影部分面积与大圆的面积;二是比较阴影部分周长与大圆的周长。
为了考虑问题方便,我们把图经过割补成图(1),在图(1)中更容易看出大圆与小圆阴影部分的关系。
学习目标总结重点AOB解:先比较大圆面积与阴影部分的面积。
设大圆半径为r,则小圆半径为r,大圆面积为S 1=πr 2。
六年级奥数-面积计算

面积计算(一)专题简析:计算平面图形的面积时,有些问题乍一看,在已知条件与所求问题之间找不到任何联系,会使你感到无从下手。
这时,如果我们能认真观察图形,分析、研究已知条件,并加以深化,再运用我们已有的基本几何知识,适当添加辅助线,搭一座连通已知条件与所求问题的小“桥”,就会使你顺利达到目的。
有些平面图形的面积计算必须借助于图形本身的特征,添加一些辅助线,运用平移旋转、剪拼组合等方法,对图形进行恰当合理的变形,再经过分析推导,方能寻求出解题的途径。
例题1。
已知图18-1中,三角形ABC 的面积为8平方厘米,AE =ED ,BD=23 BC ,求阴影部分的面积。
【思路导航】阴影部分为两个三角形,但三角形AEF 的面积无法直接计算。
由于AE=ED,连接DF ,可知S △AEF =S △EDF (等底等高),采用移补的方法,将所求阴影部分转化为求三角形BDF 的面积。
因为BD=23 BC ,所以S △BDF =2S △DCF 。
又因为AE =ED ,所以S △ABF =S △BDF =2S △DCF 。
因此,S △ABC =5 S △DCF 。
由于S △ABC =8平方厘米,所以S △DCF =8÷5=1.6(平方厘米),则阴影部分的面积为1.6×2=3.2(平方厘米)。
练习11、 如图18-2所示,AE =ED ,BC=3BD ,S △ABC =30平方厘米。
求阴影部分的面积。
2、 如图18-3所示,AE=ED ,DC =13 BD ,S △ABC =21平方厘米。
求阴影部分的面积。
3、 如图18-4所示,DE =12AE ,BD =2DC ,S △EBD =5平方厘米。
求三角形ABC 的面积。
AB CFD E18-2ABCFE D18-1 ABCFED 18-3CB D EF 18-4例题2。
两条对角线把梯形ABCD 分割成四个三角形,如图18-5所示,已知两个三角形的面积,求另两个三角形的面积各是多少?【思路导航】已知S △BOC 是S △DOC 的2倍,且高相等,可知:BO =2DO ;从S △ABD 与S △ACD相等(等底等高)可知:S △ABO 等于6,而△ABO 与△AOD 的高相等,底是△AOD 的2倍。
举一反三六年级奥数面积计算1

1、已知右面的两个正方形边长 分别为6分米和4分米,求图中阴 影部分的面积。
2、如图,这个长方形的长是9厘 米,宽是8厘米,A和B是宽的中 点,求长方形内阴影部分的面积。
组合图形的面积(1)
3、右图是两个相同的直角三 角形叠在一起,求阴影部分的 面积。(单位:厘米)
4、如图,长方形长18厘米, 宽12厘米,AE、AF两条线段 把长方形面积三等分,求三 角形AEF的面积。
Hale Waihona Puke 组合图形的面积(1)11、图中ABCD是正方形,BE=EC, AB=12厘米,阴影面积是多少?
12、如图,边长为10和15的两个 正方体并放在一起,求三角形 ABC(阴影部分)的面积。
组合图形的面积(1)
13、图中BO=2DO,阴影部分 的面积是4平方厘米,求梯形 ABCD的面积是多少平方厘米?
8、如图,三角形EDF的面积比三 角形ABE的面积大6平方厘米,已 知长方形ABDC的长和宽分别为6厘 米、4厘米,DF的长多少厘米?
组合图形的面积(1)
9、如图,长方形的长12厘米, 宽8厘米,A、B两点是长方形 长和宽的中点,那么阴影部 分的面积是多少?
10、如图,平行四边形ABCD中, E、F分别是AC、BC的三等分点, 平行四边形面积为54平方厘米, 求三角形BEF的面积。
14、如图,正方形ABCD的边长 是12厘米,CE=4厘米。求阴影 部分的面积。
组合图形的面积(1)
15、图中三角形ABC的面积是 36平方厘米,AC长8厘米,DE 长3厘米,求阴影部分的面积 (ADFC不是正方形)。
16、有两种自然的放法将正 方形内接于等腰直角三角形。 已知等腰直角三角形的面积 是36平方厘米,两个正方形 的面积分别是多少?
六年级奥数-椭圆部分面积

六年级奥数-椭圆部分面积
引言
本文档将介绍六年级奥数中椭圆部分面积的相关知识和计算方法。
椭圆的定义
椭圆是平面上一条固定点到平面上任意一点的距离之和等于常数的点的轨迹。
椭圆由两个焦点(F1和F2)和一条连接它们的直线(主轴)组成。
主轴的两端点称为椭圆的顶点。
椭圆的中点称为椭圆的中心。
椭圆的部分面积
椭圆的部分面积是指在椭圆内部取一段弧所围成的面积。
分别用S表示椭圆的面积,S1表示扇形面积,S2表示三角形面积,则椭圆的部分面积等于S1减去S2。
椭圆部分面积的计算公式
假设椭圆的长轴为a,短轴为b,椭圆的角度为θ(θ范围在0至360度),则椭圆部分面积的计算公式为:
S = π * a * b * θ / 360 - 1/2 * a * b * sin(θ)
实例演示
例如,给定一个椭圆,其长轴为10,短轴为6,所需计算的部分面积的角度为60度。
代入公式,可得:
S = π * 10 * 6 * 60 / 360 - 1/2 * 10 * 6 * sin(60) = 15π - 60√3
结论
本文档介绍了六年级奥数中椭圆部分面积的定义和计算方法。
通过使用相关公式和实例演示,可以有效地计算椭圆的部分面积。
参考资料
无。
六年级奥数第27讲 表面积与体积(一)

第27讲表面积与体积(一)一、知识要点小学阶段所学的立体图形主要有四种长方体、正方体、圆柱体和圆锥体.从平面图形到立体图形是认识上的一个飞跃,需要有更高水平的空间想象能力.因此,要牢固掌握这些几何图形的特征和有关的计算方法,能将公式作适当的变形,养成“数、形”结合的好习惯,解题时要认真细致观察,合理大胆想象,正确灵活地计算.在解答立体图形的表面积问题时,要注意以下几点:(1)充分利用正方体六个面的面积都相等,每个面都是正方形的特点.(2)把一个立体图形切成两部分,新增加的表面积等于切面面积的两倍.反之,把两个立体图形粘合到一起,减少的表面积等于粘合面积的两倍.(3)若把几个长方体拼成一个表面积最大的长方体,应把它们最小的面拼合起来.若把几个长方体拼成一个表面积最小的长方体,应把它们最大的面拼合起来.二、精讲精练【例题1】从一个棱长10厘米的正方体木块上挖去一个长10厘米、宽2厘米、高2厘米的小长方体,剩下部分的表面积是多少?这是一道开放题,方法有多种:①按图27-1所示,沿着一条棱挖,剩下部分的表面积为592平方厘米.图27--1②按图27-2所示,在某个面挖,剩下部分的表面积为632平方厘米.图27--2③按图27-3所示,挖通某两个对面,剩下部分的表面积为672平方厘米.图27--3练习1:1、从一个长10厘米、宽6厘米、高5厘米的长方体木块上挖去一个棱长2厘米的小正方体,剩下部分的表面积是多少?2、把一个长为12分米,宽为6分米,高为9分米的长方体木块锯成两个想同的小厂房体木块,这两个小长方体的表面积之和,比原来长方体的表面积增加了多少平方分米?3、在一个棱长是4厘米的立方体上挖一个棱长是1厘米的小正方体后,表面积会发生怎样的变化?图27—4【例题2】把19个棱长为3厘米的正方体重叠起来,如图27-4所示,拼成一个立体图形,求这个立体图形的表面积.要求这个复杂形体的表面积,必须从整体入手,从上、左、前三个方向观察,每个方向上的小正方体各面就组合成了如下图形(如图27-5所示).图27—5从前往后看从左往右看从上往下看而从另外三个方向上看到的面积与以上三个方向的面积是相等的.整个立体图形的表面积可采用(S 上+S 左+S 前)×2来计算.(3×3×9+3×3×8+3×3×10)×2=(81+72+90)×2=243×2=486(平方厘米)答:这个立体图形的表面积是486平方厘米.练习2:1、用棱长是1厘米的立方体拼成图27-6所示的立体图形.求这个立体图形的表面积.图27—62、一堆积木(如图27-7所示),是由16块棱长是2厘米的小正方体堆成的.它们的表面积是多少平方厘米?图27-73、一个正方体的表面积是384平方厘米,把这个正方体平均分割成64个相等的小正方体.每个小正方体的表面积是多少平方厘米?【例题3】把两个长、宽、高分别是9厘米、7厘米、4厘米的相同长方体,拼成一个大长方体,这个大长方体的表面积最少是多少平方厘米?把两个相同的大长方体拼成一个大厂房体,需要把两个相同面拼合,所得大厂房体的表面积就减少了两个拼合面的面积.要使大长方体的表面积最小,就必须使两个拼合面的面积最大,即减少两个9×7的面.(9×9+9×4+7×4)×2×2—9×7×2=(63+36+28)×4—126=508—126=382(平方厘米)答:这个大厂房体的表面积最少是382平方厘米.练习3:1、把底面积为20平方厘米的两个相等的正方体拼成一个长方体,长方体的表面积是多少?2、将一个表面积为30平方厘米的正方体等分成两个长方体,再将这两个长方体拼成一个大长方体.求大长方体的表面积是多少.3、用6块(如图27-8所示)长方体木块拼成一个大长方体,有许多种做法,其中表面积最小的是多少平方厘米?3厘米1厘米2厘米图27-8【例题4】一个长方体,如果长增加2厘米,则体积增加40立方厘米;如果宽增加3厘米,则体积增加90立方厘米;如果高增加4厘米,则体积增加96立方里,求原长方体的表面积.我们知道:体积=长×宽×高;由长增加2厘米,体积增加40立方厘米,可知宽×高=40÷2=20(平方厘米);由宽增加3厘米,体积增加90立方厘米,可知长×高=90÷3=30(平方厘米);由高增加4厘米,体积增加96立方厘米,可知长×宽=96÷4=24(平方厘米).而长方体的表面积=(长×宽+长×高+宽×高)×2=(20+30+24)×2=148(平方厘米).即40÷2=20(平方厘米)90÷3=30(平方厘米)96÷4=24(平方厘米)(30+20+24)×2=74×2=148(平方厘米)答:原长方体的表面积是148平方厘米.1、一个长方体,如果长减少2厘米,则体积减少48立方厘米;如果宽增加5厘米,则体积增加65立方厘米;如果高增加4厘米,则体积增加96立方厘米.原来厂房体的表面积是多少平方厘米?2、一个厂房体木块,从下部和上部分别截去高为3厘米和2厘米的长方体后,便成为一个正方体,其表面积减少了120平方厘米.原来厂房体的体积是多少立方厘米?3、有一个厂房体如下图所示,它的正面和上面的面积之和是209.如果它的长、宽、高都是质数,这个长方体的体积是多少?高宽长图27-9【例题5】如图27-10所示,将高都是1米,底面半径分别为1.5米、1米和0.5米的三个圆柱组成一个物体.求这个物体的表面积.如果分别求出三个圆柱的表面积,再减去重叠部分的面积,这样计算比较麻烦.实际上三个向上的面的面积和恰好是大圆柱的一个底面积.这样,这个物体的表面积就等于一个大圆柱的表面积加上中、小圆柱的侧面积.3.14×1.5×1.5×2+2×3.14×1.5×1+2×3.14×1×1+2×3.14×0.5×1=3.14×(4.5+3+2+1)=3.14×10.5=32.97(平方米)答:这个物体的表面积是32.97平方米.1、一个棱长为40厘米的正方体零件(如图27-11所示)的上、下两个面上,各有一个直径为4厘米的圆孔,孔深为10厘米.求这个零件的表面积.2、用铁皮做一个如图27-12所示的工件(单位:厘米),需用铁皮多少平方厘米?3、如图27-13所示,在一个立方体的两对侧面的中心各打通一个长方体的洞,在上、下侧面的中心打通一个圆柱形的洞.已知立方体棱长为10厘米,侧面上的洞口是边长为4厘米的正方形,上、下侧面的洞口是直径为4厘米的圆,求该立方体的表面积和体积(π取3.14).。
举一反三- 六年级奥数 -第18讲 面积计算(一)

第18讲面积计算(一)一、知识要点计算平面图形的面积时,有些问题乍一看,在已知条件与所求问题之间找不到任何联系,会使你感到无从下手。
这时,如果我们能认真观察图形,分析、研究已知条件,并加以深化,再运用我们已有的基本几何知识,适当添加辅助线,搭一座连通已知条件与所求问题的小“桥”,就会使你顺利达到目的。
有些平面图形的面积计算必须借助于图形本身的特征,添加一些辅助线,运用平移旋转、剪拼组合等方法,对图形进行恰当合理的变形,再经过分析推导,方能寻求出解题的途径。
二、精讲精练【例题1】已知如图,三角形ABC的面积为8平方厘米,AE=ED,BD=2/3BC,求阴影部分的面积。
练习1:1、如图,AE=ED,BC=3BD,S△ABC=30平方厘米。
求阴影部分的面积。
2、如图所示,AE=ED,DC=1/3BD,S△ABC=21平方厘米。
求阴影部分的面积。
3、如图所示,DE=1/2AE,BD=2DC,S△EBD=5平方厘米。
求三角形ABC的面积。
【例题2】两条对角线把梯形ABCD分割成四个三角形,如图所示,已知两个三角形的面积,求另两个三角形的面积各是多少?练习2:1、两条对角线把梯形ABCD分割成四个三角形,(如图所示),已知两个三角形的面积,求另两个三角形的面积是多少?2、已知AO=1/3OC,求梯形ABCD的面积(如图所示)。
【例题3】四边形ABCD的对角线BD被E、F两点三等分,且四边形AECF的面积为15平方厘米。
求四边形ABCD的面积(如图所示)。
练习3:1、四边形ABCD的对角线BD被E、F、G三点四等分,且四边形AECG的面积为15平方厘米。
求四边形ABCD的面积(如图)。
2、如图所示,求阴影部分的面积(ABCD为正方形)。
【例题4】如图所示,BO=2DO,阴影部分的面积是4平方厘米。
那么,梯形ABCD的面积是多少平方厘米?练习4:1、如图所示,阴影部分面积是4平方厘米,OC=2AO。
求梯形面积。
小学奥数:基本图形的面积计算.专项练习及答案解析

小学数学平面图形计算公式:1 、正方形:周长=边长×4;面积=边长×边长2 、正方体:表面积=棱长×棱长×6;体积=棱长×棱长×棱长3 、长方形:周长=(长+宽)×2;面积=长×宽4 、长方体:表面积(长×宽+长×高+宽×高)×2;体积=长×宽×高5、三角形:面积=底×高÷26 平行四边形:面积=底×高7 梯形:面积=(上底+下底)×高÷2模块一、基本公式的应用【例 1】如图,两个正方形边长分别是5厘米和4厘米,图中阴影部分为重叠部分。
则两个正方形的空白部分的面积相差多少平方厘米?【考点】基本图形的面积计算【难度】2星【题型】解答【关键词】华杯赛,五年级,决赛,第9题,10分【解析】5×5-4×4=9(平方厘米),两个正方形的空白部分的面积相差9平方厘米。
【答案】9平方厘米【巩固】如图12,边长为4cm的正方形将边长为3cm的正方形遮住了一部分,则空白部分的面积的差等于2cm。
【考点】基本图形的面积计算【难度】2星【题型】填空【关键词】希望杯,4年级,初赛,19题【解析】空白部分的面积差等于两个正方形的面积差,即⨯-⨯=44337(平方厘米)。
【答案】7平方厘米【例 2】在一个正方形水池的四周,环绕着一条宽2米的路(如图),这条路的面积是120平方米,那么水池的面积是______ 平方米。
水池例题精讲知识点拨4-2-1.基本图形的面积计算【考点】基本图形的面积计算【难度】2星【题型】填空【关键词】希望杯,4年级,初赛,19题【解析】四个边角的面积和为2×2×4=16,则水池的边长为:104÷2÷4=13,所以水池的面积是:13×13=169平方米。
六年级奥数-15图形面积(一)

面积计算(一)1.学会用割补、拼接、等面积变换等基本技巧计算平面图形面积2.了解平面几何六大模型3.熟悉圆与扇形的面积求法1.计算平面图形面积的技巧:割补拼接、等面积变换、和差法、转化法2.几何六大模型:等积变换、鸟头模型、蝴蝶模型、相似模型、燕尾模型、一半模型3.圆形与扇形的面积公式。
☞考点说明:研究的是怎样把一个三角形内部两个成燕子尾巴关系的三角形(其实两个三角形的关系是共边)面积的比转化成线段长度之间的比1.燕尾模型:一个三角形内部,内部某个点与三个顶点分别相连后,会形成左、右、下三个燕尾三角形,并会形成(左、右)(左、下)(右、下)三组燕尾。
2.燕尾定理(1)S△ABG:S△ACG=S△BGE:S△CGE=BE:CE(2)S△BGA:S△BGC=S△GAF:S△GCF=AF:CF(3)S△AGC:S△BGC=S△AGD:S△BGD=AD:BD3.证明燕尾定理例:如右图,D是BC上任意一点,请你说明:1423:::S S S S BD DC==类型一、几何六大模型——燕尾模型S 3S 1S 4S 2E D C B A【解析】三角形BED 与三角形CED 同高,分别以BD 、DC 为底,所以有14::S S BD DC =;三角形ABE 与三角形EBD 同高,12::S S ED EA =;三角形ACE 与三角形CED 同高,43::S S ED EA =,所以1423::S S S S =;综上可得,1423:::S S S S BD DC ==.例1.已知在下面两幅图中,三角形ABD 的面积都是15,三角形ACD 的面积都是20,三角形CDE 的面积都是8,求三角形BDE 的面积.练习1.如图,已知三角形ABD 的面积是35平方厘米,三角形ACD 的面积是25平方厘米,三角形BCD 的面积是24平方厘米.求三角形CDE 的面积是多少?燕尾定理结合分比定理、风筝模型等解题例2.如图,三角形ABC 的面积是1,E 是AC 的中点,点D 在BC 上,且:1:2BD DC =,AD 与BE 交于点F .则四边形DFEC 的面积等于.练习2.如图,已知BD DC =,2EC AE =,三角形ABC 的面积是30,求阴影部分面积.题目条件比较少,那么创造条件——做辅助线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学奥数 举一反三
(六年级)
第18讲 面积计算(一) 一、知识要点 计算平面图形的面积时,有些问题乍一看,在已知条 件与所求问题之间找不到任何联系,会使你感到无从下手。 这时,如果我们能认真观察图形,分析、研究已知条件, 并加以深化,再运用我们已有的基本几何知识,适当添加 辅助线,搭一座连通已知条件与所求问题的小“桥”,就 会使你顺利达到目的。有些平面图形的面积计算必须借助 于图形本身的特征,添加一些辅助线,运用平移旋转、剪 拼组合等方法,对图形进行恰当合理的变形,再经过分析 推导,才能寻求出解题的途径。
因为S△ABD与S△ACD等底等高 因为S△BOC是S△DOC的2倍 所以S△ABO=6 所以△ABO是△AOD的2倍
所以△AOD=6÷2=3。
答:△AOD的面积是3。
二、精讲精练
练习2: 1.两条对角线把梯形ABCD分割成四个三角形,(如图所示),已知 两个三角形的面积,求另两个三角形的面积是多少?
二、精讲精练
练习5: 1.如图所示,长方形ABCD的面积是20平方厘米,三角形ADF的面积为5平方 厘米,三角形ABE的面积为7平方厘米,求三角形AEF的面积。
二、精讲精练
练习5: 2.如图所示,长方形ABCD的面积为20平方厘米,S△ABE=4平方厘米, S△AFD=6平方厘米,求三角形AEF的面积。
二、精讲精练
练习1:
1.如图,AE=ED,BC=3BD,S△ABC=30平方厘米。 求阴影部分的面积。
二、精讲精练练习1:Fra bibliotek2.如图所示,AE=ED,DC=1/3BD,S△ABC=21平方 厘米。求阴影部分的面积。
二、精讲精练
练习3:
2.如图所示,AE=ED,DC=1/3BD,S△ABC=21平方 厘米。求阴影部分的面积。
二、精讲精练
练习3: 1.四边形ABCD的对角线BD被E、F、G三点四等分,且 四边形AECG的面积为15平方厘米。求四边形ABCD的面 积(如图)。
二、精讲精练
练习3: 2.已知四边形ABCD的对角线被E、F、G三点四等分,且 阴影部分面积为15平方厘米。求四边形ABCD的面积(如 图所示)。 。
二、精讲精练
练习5: 3.如图所示,长方形ABCD的面积为24平方厘米,三角形ABE、AFD的面积 均为4平方厘米,求三角形AEF的面积。
谢谢观看
S梯形ABCD=12+4+2=18(平方厘米) 答:梯形ABCD的面积是18平方厘米。
二、精讲精练
练习4: 1.如图所示,阴影部分面积是4平方厘米,OC=2AO。求梯形面积。
二、精讲精练
练习4: 2.已知OC=2AO,S△BOC=14平方厘米。求梯形的面积(如图所 示)。
二、精讲精练
练习4: 3.已知S△AOB=6平方厘米。OC=3AO,求梯形的面积(如图所 示)。
二、精讲精练
练习1:
3.如图所示,DE=1/2AE,BD=2DC,S△EBD=5平方 厘米。求三角形ABC的面积。
二、精讲精练
【例题2】两条对角线把梯形ABCD分割成四个三角形,如图所示,已 知两个三角形的面积,求另两个三角形的面积各是多少?
【思路导航】已知S△BOC是S△DOC的2倍,且高相等,可知:BO= 2DO;从S△ABD与S△ACD相等(等底等高)可知:S△ABO等于6, 而△ABO与△AOD的高相等,底是△AOD的2倍。所以△AOD的面积 为6÷2=3。
二、精讲精练
练习3: 3.如图所示,求阴影部分的面积(ABCD为正方形)。
二、精讲精练
【例题4】如图所示,BO=2DO,阴影部分的面积是4平方厘米。那么, 梯形ABCD的面积是多少平方厘米?
【思路导航】因为BO=2DO,取BO中点E,连接AE。根据三角形等 底等高面积相等的性质,可知S△DBC=S△CDA;S△COB= S△DOA=4,类推可得每个三角形的面积。所以, S△CDO=4÷2=2(平方厘米) S△DAB=4×3=12平方厘米
二、精讲精练
练习2: 2.已知AO=1/3OC,求梯形ABCD的面积(如图所示)。
二、精讲精练
练习2: 3.已知三角形AOB的面积为15平方厘米,线段OB的长度为OD的3倍。 求梯形ABCD的面积。(如图所示)。
二、精讲精练
【例题3】四边形ABCD的对角线BD被E、F两点三等分,且四边形 AECF的面积为15平方厘米。求四边形ABCD的面积(如图所 示)。
二、精讲精练
【例题5】如图所示,长方形ADEF的面积是16,三角形ADB的面积是3,三角 形ACF的面积是4,求三角形ABC的面积。
【思路导航】连接AE。仔细观察添加辅助线AE后,使问题可有如下解法。
由图上看出:三角形ADE的面积等于长方形面积的一半(16÷2)=8。用8减 去3得到三角形ABE的面积为5。同理,用8减去4得到三角形AEC的面积也为4。 因此可知三角形AEC与三角形ACF等底等高,C为EF的中点,而三角形ABE与 三角形BEC等底,高是三角形BEC的2倍,三角形BEC的面积为5÷2=2.5,所 以,三角形ABC的面积为16-3-4-2.5=6.5。
二、精讲精练 【例题1】已知如图,三角形ABC的面积为8平方厘米,AE =ED,BD=2/3BC,求阴影部分的面积。 【思路导航】阴影部分为两个三角形,但三角形AEF的面 积无法直接计算。由于AE=ED,连接DF,可知 S△AEF=S△EDF(等底等高),采用移补的方法,将所 求阴影部分转化为求三角形BDF的面积。 因为BD=2/3BC,所以S△BDF=2S△DCF。又因为AE= ED,所以S△ABF=S△BDF=2S△DCF。 因此,S△ABC=5 S△DCF。由于S△ABC=8平方厘米, 所以S△DCF=8÷5=1.6(平方厘米),则阴影部分的面 积为1.6×2=3.2(平方厘米)。
