八年级上学期数学压轴题复习学生
2021-2022学年沪科版八年级数学第一学期期末复习压轴题专题训练(附答案)

2021-2022学年沪科版八年级数学第一学期期末复习压轴题专题训练(附答案)1.如图,点C在线段AB上,DA⊥AB,EB⊥AB,FC⊥AB,且DA=BC,EB=AC,FC=AB,∠AFB=51°,则∠DFE=.2.某经销商从市场得知如下信息:A品牌计算器B品牌计算器进价(元/台)700100售价(元/台)900160他计划用4万元资金一次性购进这两种品牌计算器共100台,设该经销商购进A品牌计算器x台,这两种品牌计算器全部销售完后获得利润为y元.(1)求y与x之间的函数关系式;(2)若要求全部销售完后获得的利润不少于1.26万元,该经销商有哪几种进货方案?(3)选择哪种进货方案,该经销商可获利最大?最大利润是多少元?3.上周六上午8点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离y (千米)与他们路途所用的时间x(时)之间的函数图象,请根据以上信息,解答下列问题:(1)求直线AB所对应的函数关系式;(2)已知小颖一家出服务区后,行驶30分钟时,距姥姥家还有80千米,问小颖一家当天几点到达姥姥家?4.阅读下列一段文字,然后回答下列问题.已知在平面内两点P1(x1,y1)、P2(x2,y2),其两点间的距离,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.(1)已知A(2,4)、B(﹣3,﹣8),试求A、B两点间的距离;(2)已知A、B在平行于y轴的直线上,点A的纵坐标为4,点B的纵坐标为﹣1,试求A、B两点间的距离;(3)已知一个三角形各顶点坐标为D(1,6)、E(﹣2,2)、F(4,2),你能判定此三角形的形状吗?说明理由;(4)在(3)的条件下,平面直角坐标系中,在x轴上找一点P,使PD+PF的长度最短,求出点P的坐标以及PD+PF的最短长度.5.如图信息,L1为走私船,L2为我公安快艇,航行时路程与时间的函数图象,问(1)在刚出发时我公安快艇距走私船多少海里?(2)计算走私船与公安快艇的速度分别是多少?(3)写出L1,L2的解析式(4)问6分钟时两艇相距几海里.(5)猜想,公安快艇能否追上走私船,若能追上,那么在几分钟追上?6.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.(1)填空:折线OABC表示赛跑过程中的路程与时间的关系,线段OD表示赛跑过程中的路程与时间的关系.赛跑的全程是米.(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?(3)乌龟从出发到追上兔子用了多少分钟?(4)兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟?7.如图1,∠MON=90°,点A、B分别在OM、ON上运动(不与点O重合).(1)若BC是∠ABN的平分线,BC的反方向延长线与∠BAO的平分线交于点D.①若∠BAO=60°,则∠D=°.②猜想:∠D的度数是否随A,B的移动发生变化?并说明理由.(2)若∠ABC=∠ABN,∠BAD=∠BAO,则∠D=°.(3)若将“∠MON=90°”改为“∠MON=α(0°<α<180°)”,∠ABC=∠ABN,∠BAD=∠BAO,其余条件不变,则∠D=°(用含α、n的代数式表示)8.已知,如图,在△ABC中,∠A=∠ABC,直线EF分别交△ABC的边AB,AC和CB的延长线于点D,E,F.(1)求证:∠F+∠FEC=2∠A;(2)过B点作BM∥AC交FD于点M,试探究∠MBC与∠F+∠FEC的数量关系,并证明你的结论.9.图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:;(2)仔细观察,在图2中“8字形”的个数:个;(3)图2中,当∠D=50度,∠B=40度时,求∠P的度数.(4)图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.(直接写出结果,不必证明).10.好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决.如图,在△ABC中,∠BAC=50°,点I是两角B、C平分线的交点.问题(1):填空:∠BIC=°.问题(2):若点D是两条外角平分线的交点;填空:∠BDC=°.问题(3):若点E是内角∠ABC、外角∠ACG的平分线的交点,试探索:∠BEC与∠BAC 的数量关系,并说明理由.问题(4):在问题(3)的条件下,当∠ACB等于多少度时,CE∥AB.11.如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在线段AB上以1cm/s 的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为xcm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.12.在Rt△ABC中,BC=AC,∠ACB=90°,点D为射线AB上一点,连接CD,过点C 作线段CD的垂线l,在直线l上,分别在点C的两侧截取与线段CD相等的线段CE和CF,连接AE、BF.(1)当点D在线段AB上时(点D不与点A、B重合),如图1①请你将图形补充完整;②线段BF、AD所在直线的位置关系为,线段BF、AD的数量关系为;(2)当点D在线段AB的延长线上时,如图2①请你将图形补充完整;②在(1)中②问的结论是否仍然成立?如果成立请进行证明,如果不成立,请说明理由.13.如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连接EG、EF.(1)求证:BG=CF;(2)请你判断BE+CF与EF的大小关系,并说明理由.14.如图,在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD.AG.(1)求证:AD=AG;(2)AD与AG的位置关系如何.15.已知Rt△ABC≌Rt△ADE,其中∠ACB=∠AED=90°.(1)将这两个三角形按图①方式摆放,使点E落在AB上,DE的延长线交BC于点F.求证:BF+EF=DE;(2)改变△ADE的位置,使DE交BC的延长线于点F(如图②),则(1)中的结论还成立吗?若成立,加以证明;若不成立,写出此时BF、EF与DE之间的等量关系,并说明理由.16.Rt△ABC中,∠ABC=90°,在直线AB上取一点M,使AM=BC,过点A作AE⊥AB且AE=BM,连接EC,再过点A作AN∥EC,交直线CM、CB于点F、N.(1)如图1,若点M在线段AB边上时,求∠AFM的度数;(2)如图2,若点M在线段BA的延长线上时,且∠CMB=15°,求∠AFM的度数.17.如图(1),在等边△ABC的顶点B、C处各有一只蜗牛,它们同时出发分别以每分钟1个单位的速度由B向C和由C向A爬行,其中一只蜗牛爬到终点s时,另一只也停止运动,经过t分钟后,它们分别爬行到D,P处,请问:(1)在爬行过程中,BD和AP始终相等吗?为什么?(2)问蜗牛在爬行过程中BD与AP所成的∠DQA大小有无变化?请证明你的结论.(3)若蜗牛沿着BC和CA的延长线爬行,BD与AP交于点Q,其他条件不变,如图(2)所示,蜗牛爬行过程中的∠DQA大小变化了吗?若无变化,请证明.若有变化,请直接写出∠DQA的度数.18.如图,在Rt△ABC中,∠ACB=90°,∠A=22.5°,斜边AB的垂直平分线交AC于点D,点F在AC上,点E在BC的延长线上,CE=CF,连接BF,DE.线段DE和BF 在数量和位置上有什么关系?并说明理由.19.如图,已知点O是∠APB内的一点,M,N分别是点O关于P A、PB的对称点,连接MN,与P A、PB分别相交于点E、F,已知MN=6cm.(1)求△OEF的周长;(2)连接PM、PN,若∠APB=a,求∠MPN(用含a的代数式表示);(3)当∠a=30°,判定△PMN的形状,并说明理由.20.直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.21.(1)如图(1),在△ABC中,∠A=62°,∠ABD=20°,∠ACD=35°,求∠BDC的度数.(2)图(1)所示的图形中,有像我们常见的学习用品﹣﹣圆规.我们不妨把这样图形叫做“规形图”,观察“规形图”图(2),试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由.(3)请你直接利用以上结论,解决以下三个问题:①如图(3),把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=50°,则∠ABX+∠ACX=°.②如图(4)DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数.22.如图,在△ABC中,∠ABC,∠ACB的角平分线相交于点O.(1)若∠A=50°,求∠BOC的度数;(2)设∠A的度数为n°(n为已知数),求∠BOC的度数;(3)当∠A为多少度时,∠BOC=3∠A?参考答案1.解:连接BD、AE,∵DA⊥AB,FC⊥AB,∴∠DAB=∠BCF=90°,在△DAB和△BCF中,,∴△DAB≌△BCF(SAS),∴BD=BF,∠ADB=∠ABF,∴∠BDF=∠BFD,∵∠DAB=90°,∴∠ADB+∠DBA=90°,∴∠DBF=∠ABD+∠ABF=90°,∴∠BFD=∠BDF=45°,同理∠AFE=45°,∴∠DFE=45°+45°﹣51°=39°,故答案为:39°.2.解:(1)y=(900﹣700)x+(160﹣100)×(100﹣x)=140x+6000,其中700x+100(100﹣x)≤40000,得x≤50,即y=140x+6000,(0<x≤50);(2)令y≥12600,则140x+6000≥12600,∴x≥47,又∵x≤50,∴47≤x≤50∴经销商有以下三种进货方案:方案A品牌(台)B品牌(台)①4852②4951③5050(3)∵y=140x+6000,140>0,∴y随x的增大而增大,∴x=50时,y取得最大值,又∵140×50+6000=13000,∴选择方案③进货时,经销商可获利最大,最大利润是13000元.3.解:(1)设直线AB所对应的函数关系式为y=kx+b,把(0,320)和(2,120)代入y=kx+b得:,解得:,∴直线AB所对应的函数关系式为:y=﹣100x+320;(2)设直线CD所对应的函数关系式为y=mx+n,把(2.5,120)和(3,80)代入y=mx+n得:,解得:,∴直线CD所对应的函数关系式为y=﹣80x+320,当y=0时,x=4,∴小颖一家当天12点到达姥姥家.4.解:(1)∵A(2,4)、B(﹣3,﹣8),∴AB==13;(2)∵A、B在平行于y轴的直线上,点A的纵坐标为4,点B的纵坐标为﹣1,∴AB=|4﹣(﹣1)|=5;(3)△DEF为等腰三角形,理由为:∵D(1,6)、E(﹣2,2)、F(4,2),∴DE==5,DF==5,EF==6,即DE=DF,则△DEF为等腰三角形;(4)做出F关于x轴的对称点F′,连接DF′,与x轴交于点P,此时DP+PF最短,设直线DF′解析式为y=kx+b,将D(1,6),F′(4,﹣2)代入得:,解得:,∴直线DF′解析式为y=﹣x+,令y=0,得:x=,即P(,0),∵PF=PF′,∴PD+PF=DP+PF′=DF′==,则PD+PF的长度最短时点P的坐标为(,0),此时PD+PF的最短长度为.5.解:(1)在刚出发时我公安快艇距走私船5海里.(2)公安快艇是4分钟6海里,走私船是每分钟=1海里;公安快艇的速度是=海里.(3)设L1:y1=k1x+b过(0,5)和(4,9)点解得∴y1=x+5设L2:y2=k2x过(4,6)点∴y2=x(4)当x=6时,y1=11,y2=9;11﹣9=26分钟时相距2海里.(5)y1=y2x+5=xx=1010分钟时相遇.6.解:(1)∵乌龟是一直跑的而兔子中间有休息的时刻;∴折线OABC表示赛跑过程中兔子的路程与时间的关系;线段OD表示赛跑过程中乌龟的路程与时间的关系;由图象可知:赛跑的路程为1500米;故答案为:兔子、乌龟、1500;(2)结合图象得出:兔子在起初每分钟跑700米.1500÷30=50(米)乌龟每分钟爬50米.(3)700÷50=14(分钟)乌龟用了14分钟追上了正在睡觉的兔子.(4)∵48千米=48000米∴48000÷60=800(米/分)(1500﹣700)÷800=1(分钟)30+0.5﹣1×2=28.5(分钟)兔子中间停下睡觉用了28.5分钟.7.解:(1)①∵∠BAO=60°、∠MON=90°,∴∠ABN=150°,∵BC平分∠ABN、AD平分∠BAO,∴∠CBA=∠ABN=75°,∠BAD=∠BAO=30°,∴∠D=∠CBA﹣∠BAD=45°,故答案为:45;②∠D的度数不变.理由是:设∠BAD=α,∵AD平分∠BAO,∴∠BAO=2α,∵∠AOB=90°,∴∠ABN=∠AOB+∠BAO=90°+2α,∵BC平分∠ABN,∴∠ABC=45°+α,∴∠D=∠ABC﹣∠BAD=45°+α﹣α=45°;(2)设∠BAD=α,∵∠BAD=∠BAO,∴∠BAO=3α,∵∠AOB=90°,∴∠ABN=∠AOB+∠BAO=90°+3α,∵∠ABC=∠ABN,∴∠ABC=30°+α,∴∠D=∠ABC﹣∠BAD=30°+α﹣α=30°,故答案为:30;(3)设∠BAD=β,∵∠BAD=∠BAO,∴∠BAO=nβ,∵∠AOB=α°,∴∠ABN=∠AOB+∠BAO=α+nβ,∵∠ABC=∠ABN,∴∠ABC=+β,∴∠D=∠ABC﹣∠BAD=+β﹣β=,故答案为:.8.(1)证明:∵∠FEC=∠A+∠ADE,∠F+∠BDF=∠ABC,∴∠F+∠FEC=∠F+∠A+∠ADE,∵∠ADE=∠BDF,∴∠F+∠FEC=∠A+∠ABC,∵∠A=∠ABC,∴∠F+∠FEC=∠A+∠ABC=2∠A.(2)∠MBC=∠F+∠FEC.证明:∵BM∥AC,∴∠MBA=∠A,、∵∠A=∠ABC,∴∠MBC=∠MBA+∠ABC=2∠A,又∵∠F+∠FEC=2∠A,∴∠MBC=∠F+∠FEC.9.解:(1)∵∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°,∠AOD=∠BOC,∴∠A+∠D=∠C+∠B,故答案为:∠A+∠D=∠C+∠B;(2)①线段AB、CD相交于点O,形成“8字形”;②线段AN、CM相交于点O,形成“8字形”;③线段AB、CP相交于点N,形成“8字形”;④线段AB、CM相交于点O,形成“8字形”;⑤线段AP、CD相交于点M,形成“8字形”;⑥线段AN、CD相交于点O,形成“8字形”;故“8字形”共有6个,故答案为:6;(3)∠DAP+∠D=∠P+∠DCP,①∠PCB+∠B=∠P AB+∠P,②∵∠DAB和∠BCD的平分线AP和CP相交于点P,∴∠DAP=∠P AB,∠DCP=∠PCB,①+②得:∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠P AB+∠P,即2∠P=∠D+∠B,又∵∠D=50度,∠B=40度,∴2∠P=50°+40°,∴∠P=45°;(4)关系:2∠P=∠D+∠B.∠D+∠1=∠P+∠3①∠B+∠4=∠P+∠2②①+②得:∠D+∠1+∠4+∠B=∠P+∠3+∠2+∠P,∵∠DAB和∠DCB的平分线AP和CP相交于点P,∴∠1=∠2,∠3=∠4∴2∠P=∠D+∠B.10.解:(1)∵点I是两角B、C平分线的交点,∴∠BIC=180°﹣(∠IBC+∠ICB)=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=90+∠BAC=115°;(2)∵BE、BD分别为∠ABC的内角、外角平分线,∴∠DBI=90°,同理∠DCI=90°,在四边形CDBI中,∠BDC=180°﹣∠BIC=90°﹣∠BAC=65°;(3)∠BEC=∠BAC.证明:在△BDE中,∠DBI=90°,∴∠BEC=90°﹣∠BDC=90°﹣(90°﹣∠BAC)=∠BAC;(4)当∠ACB等于80°时,CE∥AB.理由如下:∵CE∥AB,∴∠ACE=∠A=50°,∵CE是∠ACG的平分线,∴∠ACG=2∠ACE=100°,∴∠ABC=∠ACG﹣∠BAC=100°﹣50°=50°,∴∠ACB=180°﹣∠BAC﹣∠ABC=80°.11.解:(1)当t=1时,AP=BQ=1,BP=AC=3,又∠A=∠B=90°,在△ACP和△BPQ中,,∴△ACP≌△BPQ(SAS).∴∠ACP=∠BPQ,∴∠APC+∠BPQ=∠APC+∠ACP=90°.∴∠CPQ=90°,即线段PC与线段PQ垂直.(2)存在,理由:①若△ACP≌△BPQ,则AC=BP,AP=BQ,则,解得;②若△ACP≌△BQP,则AC=BQ,AP=BP,则,解得:;综上所述,存在或,使得△ACP与△BPQ全等.12.解:(1)①见图1所示.②证明:∵CD⊥EF,∴∠DCF=90°,∵∠ACB=90°,∴∠ACD=∠BCF∵BC=AC,CD=CF,∴△ACD≌△BCF,∴AD=BF,∠BAC=∠FBC,∴∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°,即BF⊥AD.故答案为:垂直、相等.(2)①见图2所示.②成立.理由如下:证明:∵CD⊥EF,∴∠DCF=90°,∵∠ACB=90°,∴∠DCF+∠BCD=∠ACB+∠BCD,即∠ACD=∠BCF,∵BC=AC,CD=CF,∴△ACD≌△BCF,∴AD=BF,∠BAC=∠FBC,∴∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°,即BF⊥AD.13.解:(1)证明:∵BG∥AC,∵D为BC的中点,∴BD=CD又∵∠BDG=∠CDF,在△BGD与△CFD中,∵∴△BGD≌△CFD(ASA).∴BG=CF.(2)BE+CF>EF.∵△BGD≌△CFD,∴GD=FD,BG=CF.又∵DE⊥FG,∴EG=EF(垂直平分线到线段端点的距离相等).∴在△EBG中,BE+BG>EG,即BE+CF>EF.14.(1)证明:∵BE、CF分别是AC、AB两边上的高,∴∠AFC=∠BFC=∠BEC=∠BEA=90°∴∠BAC+∠ACF=90°,∠BAC+∠ABE=90°,∠G+∠GAF=90°,∴∠ABE=∠ACF.在△ABD和△GCA中,,∴△ABD≌△GCA(SAS),∴AD=GA,(2)结论:AG⊥AD.理由:∵△ABD≌△GCA(SAS),∴∠BAD=∠G,∴∠BAD+∠GAF=90°,∴AG⊥AD.15.证明:(1)如图①,连接AF,∵Rt△ABC≌Rt△ADE,∴AC=AE,BC=DE,∵∠ACB=∠AEF=90°,AF=AF,∴Rt△ACF≌Rt△AEF,∴CF=EF,∴BF+EF=BF+CF=BC,∴BF+EF=DE;(2)如图②,(1)中的结论不成立,有DE=BF﹣EF,理由是:连接AF,∵Rt△ABC≌Rt△ADE,∴AC=AE,BC=DE,∵∠E=∠ACF=90°,AF=AF,∴Rt△ACF≌Rt△AEF,∴CF=EF,∴DE=BC=BF﹣FC=BF﹣EF,即DE=BF﹣EF.16.解:(1)连接EM.∵AE⊥AB,∴∠EAM=∠B=90°.在△AEM与△BMC中,,∴△AEM≌△BMC(SAS).∴∠AEM=∠BMC,EM=MC.∵∠AEM+∠AME=90°,∴∠BMC+∠AME=90.∴∠EMC=90°.∴△EMC是等腰直角三角形.∴∠MCE=45°∵AN∥CE,∴∠AFM=∠MCE=45°;解:(2)如图2,连接ME.同(1)△AEM≌△BMC(SAS),则EM=MC,∠MEA=∠CMB=15°.又∵∠MEA+∠EMA=90°,∴∠EMC=60°,∴△EMC是等边三角形,∴∠ECM=60°,∵AN∥CE∴∠AFM+∠ECM=180°,∴∠AFM=120°.17.解:(1)在爬行过程中,BD和AP始终相等,理由是:∵△ABC是等边三角形,∴∠CAB=∠C=∠ABP=60°,AB=BC,在△BDC和△APB中,,∴△BDC≌△APB(SAS),∴BD=AP.(2)蜗牛在爬行过程中BD与AP所成的∠DQA大小无变化,理由:∵△BDC≌△APB,∴∠CBD=∠BAP,∴∠DQA=∠DBA+∠BAP=∠DBA+∠CBD=∠ABC=60°,即蜗牛在爬行过程中BD与AP所成的∠DQA大小无变化,始终是60°.(3)蜗牛爬行过程中的∠DQA大小无变化,理由是:根据题意得:BP=CD,∵BC=AC,∴CP=AD,∵△ABC是等边三角形,∴AC=AB,∠CAB=∠ACB=60°,∵∠ACP+∠ACB=180°,∠DAB+∠CAB=180°,∴∠ACP=∠BAD,在△ABD和△ACP中,,∴△ABD≌△ACP(SAS),∴∠CAP=∠ABD,∴∠AQD=∠ABD+∠BAQ=∠CAP+∠QAB=180°﹣∠CAB=180°﹣60°=120°,即蜗牛爬行过程中的∠DQA无变化,等于120°.18.解:DE=BF,DE⊥BF.理由如下:连接BD,延长BF交DE于点G.∵点D在线段AB的垂直平分线上,∴AD=BD,∴∠ABD=∠A=22.5°.在Rt△ABC中,∵∠ACB=90°,∠A=22.5°,∴∠ABC=67.5°,∴∠CBD=∠ABC﹣∠ABD=45°,∴△BCD为等腰直角三角形,∴BC=DC.在△ECD和△FCB中,,∴Rt△ECD≌Rt△FCB(SAS),∴DE=BF,∠CED=∠CFB.∵∠CFB+∠CBF=90°,∴∠CED+∠CBF=90°,∴∠EGB=90°,即DE⊥BF.19.解:(1)∵M,N分别是点O关于P A、PB的对称点,∴EM=EO,FN=FO,∴△OEF的周长=OE+OF+EF=ME+EF+FN=MN=6cm;(2)连接OP,∵M,N分别是点O关于P A、PB的对称点,∴∠MP A=∠OP A,∠NPB=∠OPB,∴∠MPN=2∠APB=2a;(3)∵∠a=30°,∴∠MPN=60°,∵M,N分别是点O关于P A、PB的对称点,∴PM=PO,PN=PO,∴PM=PN,∴△PMN是等边三角形.20.解:(1)∠AEB的大小不变.如图1,∵直线MN与直线PQ垂直相交于O,∴∠AOB=90°,∴∠OAB+∠OBA=90°,∵AE、BE分别是∠BAO和∠ABO角的平分线,∴∠BAE=∠OAB,∠ABE=∠ABO,∴∠BAE+∠ABE=(∠OAB+∠ABO)=45°,∴△ABE中,∠AEB=180°﹣45°=135°;(2)∠CED的大小不变.如图2,延长AD、BC交于点F.∵直线MN与直线PQ垂直相交于O,∴∠AOB=90°,∴∠OAB+∠OBA=90°,∴∠P AB+∠MBA=270°,∵AD、BC分别是∠BAP和∠ABM的角平分线,∴∠BAD=∠BAP,∠ABC=∠ABM,∴∠BAD+∠ABC=(∠P AB+∠ABM)=135°,∴∠F=45°,∴∠FDC+∠FCD=135°,∴∠CDA+∠DCB=225°,∵DE、CE分别是∠ADC和∠BCD的角平分线,∴∠CDE+∠DCE=112.5°,∴△CDE中,∠E=180°﹣112.5°=67.5°.21.解:(1)在△ABC中,∵∠A+∠ABC+∠ACB=180°,∴∠ABC+∠ACB=180°﹣62°=118°,∵∠ABD=20°,∠ACD=35°,∴∠DBC+∠DCB=118°﹣20°﹣35°=63°∴∠BDC=180°﹣(∠DBC+∠DCB)=117°;(2)∠BDC=∠A+∠B+∠C.理由:连接BC在△ABC中,∵∠A+∠ABD+∠DBC+∠ACD+∠BCD=180°,∴∠A+∠ABD+∠ACD=180°﹣∠DBC﹣∠BCD,在△DBC中,∵∠BDC+∠DBC+∠BCD=180°,∴∠BDC=180°﹣∠DBC﹣∠BCD,∴∠BDC=∠A+∠B+∠C;(3)①∵△XBC中,∠X=90°,∴∠XBC+∠XCB=90°,∵△ABC中,∠A=50°,∴∠ABC+∠ACB=130°,∴∠ABX+∠ACX=130°﹣90°=40°.故答案为:40;②∵∠DAE=50°,∠DBE=130°,∴∠ADB+∠AEB=80°,∵DC平分∠ADB,EC平分∠AEB,∴∠ADC=∠ADB,∠AEC=∠AEB,∴∠ADC+∠AEC=(∠ADB+∠AEB)=40°,∴∠DCE=∠A+∠ADC+∠AEC=50°+40°=90°.22.解:(1)∵∠A=50°,∴∠ABC+∠ACB=180°﹣∠A=180°﹣50°=130°,∵∠ABC,∠ACB的角平分线相交于点O,∴∠OBC=∠ABC,∠OCB=∠ACB,∴∠OBC+∠OCB=(∠ABC+∠ACB)=×130°=65°,∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣65°=115°;(2)∵∠A=n°,∴∠ABC+∠ACB=180°﹣∠A=180°﹣n°,∵∠ABC,∠ACB的角平分线相交于点O,∴∠OBC=∠ABC,∠OCB=∠ACB,∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°﹣n°)=90°﹣n°,∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(90°﹣n°)=90°+n°;(3)∵∠BOC=3∠A,∴90°+∠A=3∠A,∴∠A=36°.。
八年级数学上册 压轴题 期末复习试卷测试卷(含答案解析)

八年级数学上册 压轴题 期末复习试卷测试卷(含答案解析)一、压轴题1.在平面直角坐标系中,点A 、B 在坐标轴上,其中A(0,a)、B(b ,0)满足:222110a b a b --++-=.(1)直接写出A 、B 两点的坐标;(2)将线段AB 平移到CD ,点A 的对应点为C(-3,m),如图(1)所示.若S ΔABC =16,求点D 的坐标;(3)平移线段AB 到CD ,若点C 、D 也在坐标轴上,如图(2)所示,P 为线段AB 上一动点(不与A 、B 重合),连接OP ,PE 平分∠OPB ,交x 轴于点M ,且满足∠BCE=2∠ECD . 求证:∠BCD=3(∠CEP-∠OPE).2.如图,以直角三角形AOC 的直角顶点O 为原点,以OC ,OA 所在直线为轴和轴建立平面直角坐标系,点A (0,a ),C (b ,0)满足a 6b 80-+-=. (1)a = ;b = ;直角三角形AOC 的面积为 .(2)已知坐标轴上有两动点P ,Q 同时出发,P 点从C 点出发以每秒2个单位长度的速度向点O 匀速移动,Q 点从O 点出发以每秒1个单位长度的速度向点A 匀速移动,点P 到达O 点整个运动随之结束.AC 的中点D 的坐标是(4,3),设运动时间为t 秒.问:是否存在这样的t ,使得△ODP 与△ODQ 的面积相等?若存在,请求出t 的值;若不存在,请说明理由.(3)在(2)的条件下,若∠DOC =∠D CO ,点G 是第二象限中一点,并且y 轴平分∠GOD .点E 是线段OA 上一动点,连接接CE 交OD 于点H ,当点E 在线段OA 上运动的过程中,探究∠GOD ,∠OHC ,∠ACE 之间的数量关系,并证明你的结论(三角形的内角和为180).3.如图1所示,直线:5L y mx m =+与x 轴负半轴,y 轴正半轴分别交于A 、B 两点.(1)当OA OB =时,求点A 坐标及直线L 的解析式.(2)在(1)的条件下,如图2所示,设Q 为AB 延长线上一点,作直线OQ ,过A 、B 两点分别作AM OQ ⊥于M ,BN OQ ⊥于N ,若17AM =,求BN 的长. (3)当m 取不同的值时,点B 在y 轴正半轴上运动,分别以OB 、AB 为边,点B 为直角顶点在第一、二象限内作等腰直角OBF ∆和等腰直角ABE ∆,连接EF 交y 轴于P 点,如图3.问:当点B 在y 轴正半轴上运动时,试猜想PB 的长是否为定值?若是,请求出其值;若不是,说明理由.4.(1)探索发现:如图1,已知Rt △ABC 中,∠ACB =90°,AC =BC ,直线l 过点C ,过点A 作AD ⊥l ,过点B 作BE ⊥l ,垂足分别为D 、E .求证:AD =CE ,CD =BE . (2)迁移应用:如图2,将一块等腰直角的三角板MON 放在平面直角坐标系内,三角板的一个锐角的顶点与坐标原点O 重合,另两个顶点均落在第一象限内,已知点M 的坐标为(1,3),求点N 的坐标.(3)拓展应用:如图3,在平面直角坐标系内,已知直线y =﹣3x+3与y 轴交于点P ,与x 轴交于点Q ,将直线PQ 绕P 点沿逆时针方向旋转45°后,所得的直线交x 轴于点R .求点R 的坐标.5.如图(1),AB =4cm ,AC ⊥AB ,BD ⊥AB ,AC =BD =3cm .点 P 在线段 AB 上以 1/cm s 的速度由点 A 向点 B 运动,同时,点 Q 在线段 BD 上由点 B 向点 D 运动.它们运动的时间为 t (s ).(1)若点 Q 的运动速度与点 P 的运动速度相等,当t =1 时,△ACP 与△BPQ 是否全等,请说明理由, 并判断此时线段 PC 和线段 PQ 的位置关系;(2)如图(2),将图(1)中的“AC ⊥AB ,BD ⊥AB”为改“∠CAB =∠DBA =60°”,其他条件不变.设点 Q 的运动速度为x /cm s ,是否存在实数x ,使得△ACP 与△BPQ 全等?若存在,求出相应的x 、t 的值;若不存在,请说明理由.6.直角三角形ABC中,∠ACB=90°,直线l过点C.(1)当AC=BC时,如图①,分别过点A、B作AD⊥l于点D,BE⊥l于点E.求证:△ACD≌△CBE.(2)当AC=8,BC=6时,如图②,点B与点F关于直线l对称,连接BF,CF,动点M从点A出发,以每秒1个单位长度的速度沿AC边向终点C运动,同时动点N从点F出发,以每秒3个单位的速度沿F→C→B→C→F向终点F运动,点M、N到达相应的终点时停止运动,过点M作MD⊥l于点D,过点N作NE⊥l于点E,设运动时间为t秒.①CM=,当N在F→C路径上时,CN=.(用含t的代数式表示)②直接写出当△MDC与△CEN全等时t的值.∆中,线段AM为BC边上的中线.动点D在直线AM上时,以7.如图,在等边ABCCD为一边在CD的下方作等边CDE∆,连结BE.∠的度数;(1)求CAM∆≅∆;(2)若点D在线段AM上时,求证:ADC BEC∠是否(3)当动点D在直线AM上时,设直线BE与直线AM的交点为O,试判断AOB为定值?并说明理由.8.如图所示,在平面直角坐标系xOy 中,已知点A 的坐标(3,2)-,过A 点作AB x ⊥轴,垂足为点B ,过点(2,0)C 作直线l x ⊥轴,点P 从点B 出发在x 轴上沿着轴的正方向运动.(1)当点P 运动到点O 处,过点P 作AP 的垂线交直线l 于点D ,证明AP DP =,并求此时点D 的坐标;(2)点Q 是直线l 上的动点,问是否存在点P ,使得以P C Q 、、为顶点的三角形和ABP ∆全等,若存在求点P 的坐标以及此时对应的点Q 的坐标,若不存在,请说明理由.9.如图,在平面直角坐标系中,直线334y x =-+分别交,x y 轴于A B ,两点,C 为线段AB 的中点,(,0)D t 是线段OA 上一动点(不与A 点重合),射线//BF x 轴,延长DC交BF 于点E . (1)求证:AD BE =;(2)连接BD ,记BDE 的面积为S ,求S 关于t 的函数关系式;(3)是否存在t 的值,使得BDE 是以BD 为腰的等腰三角形?若存在,求出所有符合条件的t 的值;若不存在,请说明理由.10.阅读下列材料,并按要求解答.(模型建立)如图①,等腰直角三角形ABC 中,∠ACB =90°,CB =CA ,直线ED 经过点C ,过A 作AD ⊥ED 于点D ,过B 作BE ⊥ED 于点E .求证:△BEC ≌△CDA . (模型应用)应用1:如图②,在四边形ABCD 中,∠ADC =90°,AD =6,CD =8,BC =10,AB 2=200.求线段BD 的长.应用2:如图 ③,在平面直角坐标系中,纸片△OPQ 为等腰直角三角形,QO =QP ,P (4,m ),点Q 始终在直线OP 的上方.(1)折叠纸片,使得点P与点O重合,折痕所在的直线l过点Q且与线段OP交于点M,当m=2时,求Q点的坐标和直线l与x轴的交点坐标;(2)若无论m取何值,点Q总在某条确定的直线上,请直接写出这条直线的解析式.11.如图,A,B是直线y=x+4与坐标轴的交点,直线y=-2x+b过点B,与x轴交于点C.(1)求A,B,C三点的坐标;(2)点D是折线A—B—C上一动点.①当点D是AB的中点时,在x轴上找一点E,使ED+EB的和最小,用直尺和圆规画出点E 的位置(保留作图痕迹,不要求写作法和证明),并求E点的坐标.②是否存在点D,使△ACD为直角三角形,若存在,直接写出D点的坐标;若不存在,请说明理由△和ACF,连接12.如图,以ABC的边AB和AC,向外作等腰直角三角形ABEEF,AD是ABC的高,延长DA交EF于点G,过点F作DG的垂线交DG于点H.(1)求证:FHA ADC ≌△△; (2)求证:点G 是EF 的中点.【参考答案】***试卷处理标记,请不要删除一、压轴题1.(1)A (0,3),B (4,0);(2)D (1,-265);(3)见解析 【解析】 【分析】(1)根据非负数的性质求解;(2)如图1中,设直线CD 交y 轴于E .首先求出点E 的坐标,再求出直线CD 的解析式以及点C 坐标,利用平移的性质得到点D 坐标;(3)如图2中,延长AB 交CE 的延长线于M .利用平行线的性质以及三角形的外角的性质求证; 【详解】(1)∵222110a b a b --++-=, ∴220,2110a b a b --=+-=,∴2202110a b a b --=⎧⎨+-=⎩ ,∴34a b =⎧⎨=⎩,∴A (0,3),B (4,0);(2)如图1中,设直线CD 交y 轴于E .∵CD//AB , ∴S △ACB =S △ABE ,∴12AE×BO=16, ∴12×AE×4=16, ∴AE=8, ∴E (0,-5),设直线AB 的解析式为y=kx+b ,将点A (0,3),(4,0)代入解析式中得:343k b ⎧=-⎪⎨⎪=⎩ , ∴直线AB 的解析式为y=334x -+, ∵AB//CD ,∴直线CD 的解析式为y=34x c -+, 又∵点E (0,-5)在直线CD 上,∴c=5,即直线CD 的解析式为y=354x --, 又∵点C (-3,m )在直线CD 上,∴m=115, ∴C (-3,115), ∵点A (0,3)平移后的对应点为C (-3, 115), ∴直线AB 向下平移了265个单位,向左平移了3个单位, 又∵B (4,0)的对应点为点D ,∴点D 的坐标为(1,-265); (3)如图2中,延长AB 交CE 的延长线于点M .∵AM ∥CD , ∴∠DCM=∠M , ∵∠BCE=2∠ECD , ∴∠BCD=3∠DCM=3∠M ,∵∠M=∠PEC-∠MPE ,∠MPE=∠OPE , ∴∠BCD=3(∠CEP-∠OPE ). 【点睛】考查了非负数的性质、平行线的性质、三角形的外角的性质、一次函数的应用等知识,解题关键是灵活运用所学知识解决问题,学会添加常用辅助线,利用平行线的性质解决问题.2.(1)6;8;24;(2)存在 2.4t =时,使得△ODP 与△ODQ 的面积相等;(3)∠GOD+∠ACE=∠OHC ,见解析 【解析】 【分析】(1)利用非负性即可求出a ,b 即可得出结论,即可求出△ABC 的面积; (2)先表示出OQ ,OP ,利用那个面积相等,建立方程求解即可得出结论; (3)先判断出∠OAC=∠AOD ,进而判断出OG ∥AC ,即可判断出∠FHC=∠ACE ,同理∠FHO=∠GOD ,即可得出结论. 【详解】解:(1) 解:(1)∵b 80-=,∴a-6=0,b-8=0, ∴a=6,b=8,∴A (0,6),C (8,0); ∴S △ABC=6×8÷2=24,故答案为(0,6),(8,0); 6;8;24 (2) ∵114222ODQ D S OQ x t t ∆=⋅=⋅⋅= 11(82)312322ODP D S OP y t t ∆=⋅=⋅-⋅=- 由2123t t =-时, 2.4t =∴存在 2.4t =时,使得△ODP 与△ODQ 的面积相等 (3) )∴2∠GOA+∠ACE=∠OHC ,理由如下: ∵x 轴⊥y 轴,∴∠AOC=∠DOC+∠AOD=90° ∴∠OAC+∠ACO=90° 又∵∠DOC=∠DCO ∴∠OAC=∠AOD ∵y 轴平分∠GOD ∴∠GOA=∠AOD ∴∠GOA=∠OAC ∴OG ∥AC ,如图,过点H 作HF ∥OG 交x 轴于F , ∴HF ∥AC ∴∠FHC=∠ACE 同理∠FHO=∠GOD , ∵OG ∥FH , ∴∠GOD=∠FHO ,∴∠GOD+∠ACE=∠FHO+∠FHC 即∠GOD+∠ACE=∠OHC , ∴2∠GOA+∠ACE=∠OHC . ∴∠GOD+∠ACE=∠OHC .【点睛】此题是三角形综合题,主要考查了非负性的性质,三角形的面积公式,角平分线的定义,平行线的性质,正确作出辅助线是解本题的关键. 3.(1)5y x =+;(2)223)PB 的长为定值52【解析】 【分析】(1)先求出A 、B 两点坐标,求出OA 与OB ,由OA= OB ,求出m 即可;(2)用勾股定理求AB ,再证AMO OBN ∆≅∆,BN=OM ,由勾股定理求OM 即可; (3)先确定答案定值,如图引辅助线EG ⊥y 轴于G ,先证AOB EBG ∆≅∆,求BG 再证BFP GEP ∆≅∆,可确定BP 的定值即可.【详解】(1)对于直线:5L y mx m =+. 当0y =时,5x =-. 当0x =时,5y m =.()5,0A ∴-,()0,5B m .OA OB =.55m ∴=. 解得1m =.∴直线L 的解析式为5y x =+.(2)5OA =,17AM =∴由勾股定理,2222OM OA AM =-=.180AOM AOB BON∠+∠+∠=︒.90AOB∠=︒.90AOM BON∴∠+∠=︒.90AOM OAM∠+∠=︒.BON OAM∴∠=∠.在AMO∆与OBN∆中,90BON OAMAMO BNOOA OB∠=∠⎧⎪∠=∠=︒⎨⎪=⎩.()AMO OBN AAS∴∆≅∆.22BN OM∴==..(3)如图所示:过点E作EG y⊥轴于G点.AEB∆为等腰直角三角形,AB EB∴=90ABO EBG∠+∠=︒.EG BG⊥,90GEB EBG∴∠+∠=︒.ABO GEB∴∠=∠.AOB EBG∴∆≅∆.5BG AO∴==,OB EG=OBF∆为等腰直角三角形,OB BF∴=BF EG∴=.BFP GEP∴∆≅∆.1522BP GP BG∴===.【点睛】本题考查求解析式,线段的长,判断定值问题,关键是掌握求坐标,利用条件OA= OB,求OM,用勾股定理求AB,再证AMO OBN∆≅∆,构造AOB EBG∆≅∆,求BG,再证BFP GEP∆≅∆.4.(1)见解析(2)(4,2)(3)(6,0)【解析】【分析】(1)先判断出∠ACB=∠ADC,再判断出∠CAD=∠BCE,进而判断出△ACD≌△CBE,即可得出结论;(2)先判断出MF=NG,OF=MG,进而得出MF=1,OF=3,即可求出FG=MF+MG=1+3=4,即可得出结论;(3)先求出OP=3,由y=0得x=1,进而得出Q(1,0),OQ=1,再判断出PQ=SQ,即可判断出OH=4,SH=0Q=1,进而求出直线PR的解析式,即可得出结论.【详解】证明:∵∠ACB=90°,AD⊥l∴∠ACB=∠ADC∵∠ACE=∠ADC+∠CAD,∠ACE=∠ACB+∠BCE∴∠CAD=∠BCE,∵∠ADC=∠CEB=90°,AC=BC∴△ACD≌△CBE,∴AD=CE,CD=BE,(2)解:如图2,过点M作MF⊥y轴,垂足为F,过点N作NG⊥MF,交FM的延长线于G,由已知得OM=ON,且∠OMN=90°∴由(1)得MF=NG,OF=MG,∵M(1,3)∴MF=1,OF=3∴MG=3,NG=1∴FG=MF+MG=1+3=4,∴OF﹣NG=3﹣1=2,∴点N的坐标为(4,2),(3)如图3,过点Q作QS⊥PQ,交PR于S,过点S作SH⊥x轴于H,对于直线y=﹣3x+3,由x=0得y=3∴P(0,3),∴OP=3由y=0得x=1,∴Q(1,0),OQ=1,∵∠QPR=45°∴∠PSQ=45°=∠QPS∴PQ=SQ∴由(1)得SH=OQ,QH=OP∴OH=OQ+QH=OQ+OP=3+1=4,SH=OQ=1∴S(4,1),设直线PR为y=kx+b,则341bk b=⎧⎨+=⎩,解得1k2b3⎧=-⎪⎨⎪=⎩∴直线PR为y=﹣12x+3由y=0得,x=6∴R(6,0).【点睛】本题是一次函数综合题,主要考查了待定系数法,全等三角形的判定和性质,构造出全等三角形是解本题的关键.5.(1)全等,垂直,理由详见解析;(2)存在,11tx=⎧⎨=⎩或232tx=⎧⎪⎨=⎪⎩【解析】【分析】(1)在t =1的条件下,找出条件判定△ACP和△BPQ全等,再根据全等三角形的性质和直角三角形的两个锐角互余的性质,可证∠CPQ= 90°,即可判断线段 PC 和线段 PQ 的位置关系;(2)本题主要在动点的条件下,分情况讨论,利用三角形全等时对应边相等的性质进行解答即可.【详解】(1)当t=1时,AP= BQ=1, BP= AC=3,又∠A=∠B= 90°,在△ACP和△BPQ中,{AP BQ A B AC BP=∠=∠=∴△ACP≌△BPQ(SAS).∴∠ACP=∠BPQ ,∴∠APC+∠BPQ=∠APC+∠ACP = 90*.∴∠CPQ= 90°,即线段PC 与线段PQ 垂直;(2)①若△ACP ≌△BPQ ,则AC= BP ,AP= BQ ,34t t xt =-⎧⎨=⎩解得11t x =⎧⎨=⎩; ②若△ACP ≌△BQP ,则AC= BQ ,AP= BP ,34xt t t =⎧⎨=-⎩解得:232t x =⎧⎪⎨=⎪⎩ 综上所述,存在11t x =⎧⎨=⎩或232t x =⎧⎪⎨=⎪⎩使得△ACP 与△BPQ 全等. 【点睛】本题主要考查三角形全等与动点问题,熟练掌握三角形全等的性质与判定定理,是解决本题的关键.6.(1)证明见解析;(2)①CM =8t -,CN =63t -;②t =3.5或5或6.5.【解析】【分析】(1)根据垂直的定义得到∠DAC=∠ECB ,利用AAS 定理证明△ACD ≌△CBE ;(2)①由折叠的性质可得出答案;②动点N 沿F→C 路径运动,点N 沿C→B 路径运动,点N 沿B→C 路径运动,点N 沿C→F 路径运动四种情况,根据全等三角形的判定定理列式计算.【详解】(1)∵AD ⊥直线l ,BE ⊥直线l ,∴∠DAC+∠ACD=90°,∵∠ACB=90°,∴∠BCE+∠ACD=90°,∴∠DAC=∠ECB ,在△ACD 和△CBE 中,ADC CEB DAC ECB CA CB ∠∠⎧⎪∠∠⎨⎪⎩===,∴△ACD ≌△CBE (AAS );(2)①由题意得,AM=t ,FN=3t ,则CM=8-t ,由折叠的性质可知,CF=CB=6,∴CN=6-3t ;故答案为:8-t ;6-3t ;②由折叠的性质可知,∠BCE=∠FCE ,∵∠MCD+∠CMD=90°,∠MCD+∠BCE=90°,∴∠NCE=∠CMD ,∴当CM=CN 时,△MDC 与△CEN 全等,当点N 沿F→C 路径运动时,8-t=6-3t ,解得,t=-1(不合题意),当点N 沿C→B 路径运动时,CN=3t-6,则8-t=3t-6,解得,t=3.5,当点N 沿B→C 路径运动时,由题意得,8-t=18-3t ,解得,t=5,当点N 沿C→F 路径运动时,由题意得,8-t=3t-18,解得,t=6.5,综上所述,当t=3.5秒或5秒或6.5秒时,△MDC 与△CEN 全等.【点睛】本题考查了折叠的性质,全等三角形的判定和性质,掌握全等三角形的判定定理和性质定理,灵活运用分情况讨论思想是解题的关键.7.(1)30°;(2)证明见解析;(3)AOB ∠是定值,60AOB ∠=︒.【解析】【分析】(1)根据等边三角形的性质可以直接得出结论;(2)根据等边三角形的性质就可以得出AC AC =,DC EC =,,60ACB DCE ∠=∠=︒,由等式的性质就可以BCE ACD ∠=∠,根据SAS 就可以得出ADC BEC ∆≅∆;(3)分情况讨论:当点D 在线段AM 上时,如图1,由(2)可知ACD BCE ≅∆∆,就可以求出结论;当点D 在线段AM 的延长线上时,如图2,可以得出ACD BCE ≅∆∆而有30CBE CAD ∠=∠=︒而得出结论;当点D 在线段MA 的延长线上时,如图3,通过得出ACD BCE ≅∆∆同样可以得出结论.【详解】(1)ABC ∆是等边三角形,60BAC ∴∠=︒.线段AM 为BC 边上的中线,12CAM BAC ∴∠=∠, 30CAM ∴∠=︒.(2)ABC ∆与DEC ∆都是等边三角形,AC BC ∴=,CD CE =,60ACB DCE ∠=∠=︒,ACD DCB DCB BCE ∴∠+∠=∠+∠,ACD BCE ∠∠∴=.在ADC ∆和BEC ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩,()ACD BCE SAS ∴∆≅∆;(3)AOB ∠是定值,60AOB ∠=︒,理由如下:①当点D 在线段AM 上时,如图1,由(2)可知ACD BCE ≅∆∆,则30CBE CAD ∠=∠=︒,又60ABC ∠=︒,603090CBE ABC ∴∠+∠=︒+︒=︒,ABC ∆是等边三角形,线段AM 为BC 边上的中线AM ∴平分BAC ∠,即11603022BAM BAC ∠=∠=⨯︒=︒ 903060BOA ∴∠=︒-︒=︒.②当点D 在线段AM 的延长线上时,如图2,ABC ∆与DEC ∆都是等边三角形,AC BC ∴=,CD CE =,60ACB DCE ∠=∠=︒,ACB DCB DCB DCE ∴∠+∠=∠+∠,ACD BCE ∠∠∴=,在ACD ∆和BCE ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩,()ACD BCE SAS ∴∆≅∆,30CBE CAD ∴∠=∠=︒,同理可得:30BAM ∠=︒,903060BOA ∴∠=︒-︒=︒.③当点D在线段MA的延长线上时,ABC∆与DEC∆都是等边三角形,AC BC∴=,CD CE=,60ACB DCE∠=∠=︒,60ACD ACE BCE ACE∴∠+∠=∠+∠=︒,ACD BCE∠∠∴=,在ACD∆和BCE∆中AC BCACD BCECD CE=⎧⎪∠=∠⎨⎪=⎩,()ACD BCE SAS∴∆≅∆,CBE CAD∴∠=∠,同理可得:30CAM∠=︒150CBE CAD∴∠=∠=︒30CBO∴∠=︒,∵30BAM∠=︒,903060BOA∴∠=︒-︒=︒.综上,当动点D在直线AM上时,AOB∠是定值,60AOB∠=︒.【点睛】此题考查等边三角形的性质,全等三角形的判定及性质,等边三角形三线合一的性质,解题中注意分类讨论的思想解题.8.(1)证明见解析;(2,3)D;(2)存在,(0,0)P,(2,3)Q或(0,0)P,(2,3)Q-或(4,0)P,(2,7)Q或(4,0)P,(2,7)Q-或1(,0)2P-,(2,2)Q-或1(,0)2P-,(2,2)Q-.【解析】【分析】(1)通过全等三角形的判定定理ASA证得△ABP≌△PCD,由全等三角形的对应边相等证得AP=DP,DC=PB=3,易得点D的坐标;(2)设P (a ,0),Q (2,b ).需要分类讨论:①AB =PC ,BP =CQ ;②AB =CQ ,BP =PC .结合两点间的距离公式列出方程组,通过解方程组求得a 、b 的值,得解.【详解】(1)AP PD ⊥90APB DPC ∴∠+∠=AB x ⊥轴90A APB ∴∠+∠=A DPC ∴∠=∠在ABP ∆和PCD ∆中A DPC AB PCABP PCD ∠=∠⎧⎪=⎨⎪∠=∠⎩()ABP PCD ASA ∴∆≅∆AP DP ∴=,3DC PB ==(2,3)D ∴(2)设(,0)P a ,(2,)Q b①AB PC =,BP CQ =223a a b ⎧-=⎪⎨+=⎪⎩,解得03a b =⎧⎨=±⎩或47a b =⎧⎨=±⎩ (0,0)P ∴,(2,3)Q 或(0,0)P ,(2,3)Q -或(4,0)P ,(2,7)Q 或(4,0)P ,(2,7)Q - ②AB CQ =,BP PC =,322a a b +=-⎧⎨=⎩,解得122a b ⎧=⎪⎨⎪=±⎩ 1(,0)2P ∴-,(2,2)Q -或1(,0)2P -,(2,2)Q - 综上:(0,0)P ,(2,3)Q 或(0,0)P ,(2,3)Q -或(4,0)P ,(2,7)Q 或(4,0)P ,(2,7)Q -或1(,0)2P -,(2,2)Q -或1(,0)2P -,(2,2)Q - 【点睛】 考查了三角形综合题.涉及到了全等三角形的判定与性质,两点间的距离公式,一元一次绝对值方程组的解法等知识点.解答(2)题时,由于没有指明全等三角形的对应边(角),所以需要分类讨论,以防漏解.9.(1)详见解析;(2)36(04)2BDE t t S -+≤<=;(3)存在,当78t =或43时,使得BDE 是以BD 为腰的等腰三角形.【解析】【分析】 (1)先判断出EBC DAC ∠=∠,CEB CDA ∠=∠,再判断出BC AC =,进而判断出△BCE ≌△ACD ,即可得出结论;(2)先确定出点A ,B 坐标,再表示出AD ,即可得出结论;(3)分两种情况:当BD BE =时,利用勾股定理建立方程2223(4)t t +=-,即可得出结论;当BD DE =时,先判断出Rt △OBD ≌Rt △MED ,得出DM OD t ==,再用OM BE =建立方程求解即可得出结论.【详解】解:(1)证明:射线//BF x 轴,EBC DAC ∴∠=∠,CEB CDA ∠=∠,又C 为线段AB 的中点,BC AC ∴=,在△BCE 和△ACD 中, CEB CDA EBC DAC BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BCE ≌△ACD (AAS ),BE AD ∴=;(2)解:在直线334y x =-+中, 令0x =,则3y =,令0y =,则4x =,A ∴点坐标为(4,0),B 点坐标为(0,3),D 点坐标为(,0)t ,4AD t BE ∴=-=,113(4)36(04)222BDE ABD B S S AD y t t t ∴==⋅=-⨯=-+<;(3)当BD BE =时,在Rt OBD ∆中,90BOD ∠=︒,由勾股定理得:222OB OD DB +=,即2223(4)t t +=-解得:78t =; 当BD DE =时,过点E 作EM x ⊥轴于M ,90BOD EMD ∴∠=∠=︒,//BF OA ,OB ME ∴=在Rt △OBD 和Rt △MED 中,==BD DE OB ME⎧⎨⎩, ∴Rt △OBD ≌Rt △MED (HL ),OD DM t ∴==,由OM BE =得:24t t =- 解得:43t =, 综上所述,当78t =或43时,使得△BDE 是以BD 为腰的等腰三角形.【点睛】本题是一次函数综合题,主要考查了平行线的性质,全等三角形的判定和性质,勾股定理,用方程的思想解决问题是解本题的关键.10.模型建立:见解析;应用1:652:(1)Q (1,3),交点坐标为(52,0);(2)y =﹣x+4【解析】【分析】根据AAS 证明△BEC ≌△CDA ,即可;应用1:连接AC ,过点B 作BH ⊥DC ,交DC 的延长线于点H ,易证△ADC ≌△CHB ,结合勾股定理,即可求解;应用2:(1)过点P 作PN ⊥x 轴于点N ,过点Q 作QK ⊥y 轴于点K ,直线KQ 和直线NP 相交于点H ,易得:△OKQ ≌△QHP ,设H (4,y ),列出方程,求出y 的值,进而求出Q (1,3),再根据中点坐标公式,得P(4,2),即可得到直线l 的函数解析式,进而求出直线l 与x 轴的交点坐标;(2)设Q (x ,y ),由△OKQ ≌△QHP ,KQ =x ,OK =HQ =y ,可得:y =﹣x +4,进而即可得到结论.【详解】如图①,∵AD⊥ED,BE⊥ED,∠ACB=90°,∴∠ADC=∠BEC=90°,∴∠ACD+∠DAC=∠ACD+∠BCE=90°,∴∠DAC=∠BCE,∵AC=BC,∴△BEC≌△CDA(AAS);应用1:如图②,连接AC,过点B作BH⊥DC,交DC的延长线于点H,∵∠ADC=90°,AD=6,CD=8,∴AC=10,∵BC=10,AB2=200,∴AC2+BC2=AB2,∴∠ACB=90°,∵∠ADC=∠BHC=∠ACB=90°,∴∠ACD=∠CBH,∵AC=BC=10,∴△ADC≌△CHB(AAS),∴CH=AD=6,BH=CD=8,∴DH=6+8=14,∵BH⊥DC,∴BD=应用2:(1)如图③,过点P作PN⊥x轴于点N,过点Q作QK⊥y轴于点K,直线KQ和直线NP相交于点H,由题意易:△OKQ≌△QHP(AAS),设H(4,y),那么KQ=PH=y﹣m=y﹣2,OK=QH=4﹣KQ=6﹣y,又∵OK=y,∴6﹣y=y,y=3,∴Q(1,3),∵折叠纸片,使得点P与点O重合,折痕所在的直线l过点Q且与线段OP交于点M,∴点M是OP的中点,∵P(4,2),∴M(2,1),设直线Q M的函数表达式为:y=kx+b,把Q(1,3),M(2,1),代入上式得:213k bk b+=⎧⎨+=⎩,解得:25kb=-⎧⎨=⎩∴直线l的函数表达式为:y=﹣2x+5,∴该直线l与x轴的交点坐标为(52,0);(2)∵△OKQ≌△QHP,∴QK=PH,OK=HQ,设Q (x ,y ),∴KQ =x ,OK =HQ =y ,∴x +y =KQ +HQ =4,∴y =﹣x +4,∴无论m 取何值,点Q 总在某条确定的直线上,这条直线的解析式为:y =﹣x +4, 故答案为:y =﹣x +4.【点睛】本题主要考查三角形全等的判定和性质定理,勾股定理,一次函数的图象和性质,掌握“一线三垂直”模型,待定系数法是解题的关键.11.(1)A(-4,0) ;B(0,4);C(2,0);(2)①点E 的位置见解析,E (43-,0);②D 点的坐标为(-1,3)或(45,125) 【解析】【分析】(1)先利用一次函数图象上点的坐标特点求得点A 、B 的坐标;然后把B 点坐标代入y=−2x +b 求出b 的值,确定此函数解析式,然后再求C 点坐标;(2)①根据轴对称—最短路径问题画出点E 的位置,由待定系数法确定直线DB 1的解析式为y=−3x−4,易得点E 的坐标;②分两种情况:当点D 在AB 上时,当点D 在BC 上时.当点D 在AB 上时,由等腰直角三角形的性质求得D 点的坐标为(−1,3);当点D 在BC 上时,设AD 交y 轴于点F ,证△AOF 与△BOC 全等,得OF=2,点F 的坐标为(0,2),求得直线AD 的解析式为122y x =+,与y=−2x +4组成方程组,求得交点D 的坐标为(45,125). 【详解】 (1)在y=x +4中,令x =0,得y=4,令y =0,得x=-4,∴A(-4,0) ,B(0,4)把B(0,4)代入y=-2x+b ,得b =4,∴直线BC 为:y=-2x+4在y=-2x +4中,令y =0,得x=2,∴C 点的坐标为(2,0);(2)①如图∵点D是AB的中点∴D(-2,2)点B关于x轴的对称点B1的坐标为(0,-4),设直线DB1的解析式为y kx b=+,把D(-2,2),B1(0,-4)代入,得224k bb-+=⎧⎨=-⎩,解得k=-3,b=-4,∴该直线为:y=-3x-4,令y=0,得x=43 -,∴E点的坐标为(43-,0).②存在,D点的坐标为(-1,3)或(45,125).当点D在AB上时,∵OA=OB=4,∴∠BAC=45°,∴△ACD是以∠ADC为直角的等腰直角三角形,∴点D的横坐标为421 2,当x=-1时,y=x+4=3,∴D点的坐标为(-1,3);当点D在BC上时,如图,设AD交y轴于点F.∵∠FAO+∠AFO=∠CBO+∠BFD,∠AFO=∠BFD,∴∠FAO=∠CBO ,又∵AO=BO ,∠AOF=∠BOC ,∴△AOF ≌△BOC (ASA )∴OF=OC=2,∴点F 的坐标为(0,2),设直线AD 的解析式为y mx n =+,将A (-4,0)与F (0,2)代入得402m n n -+=⎧⎨=⎩, 解得1,22m n ==, ∴122y x =+, 联立12224y x y x ⎧=+⎪⎨⎪=-+⎩,解得:45125x y ⎧=⎪⎪⎨⎪=⎪⎩, ∴D 的坐标为(45,125). 综上所述:D 点的坐标为(-1,3)或(45,125) 【点睛】本题是一次函数的综合题,难度适中,考查了利用待定系数法求一次函数的解析式、轴对称的最短路径问题、直角三角形问题,第(2)②题采用了分类讨论的思想,与三角形全等结合,解题的关键是灵活运用一次函数的图象与性质以及全等的知识.12.(1)证明见解析;(2)证明见解析.【解析】【分析】(1)先利用同角的余角相等得到一对角相等,再由一对直角相等,且AF AC =,利用AAS 得到AFH CAD ∆≅∆;(2)由(1)利用全等三角形对应边相等得到FH AD =,再EK AD ⊥,交DG 延长线于点K ,同理可得到AD EK =,等量代换得到FK EH =,再由一对直角相等且对顶角相等,利用AAS 得到FHG EKG ≅△△,利用全等三角形对应边相等即可得证.【详解】证明:(1) ∵FH AG ⊥,90AEH EAH ∴∠+∠=︒,90FAC ∠=︒,90FAH CAD ∴∠+∠=︒,AFH CAD ∴∠=∠,在AFH ∆和CAD ∆中,90AHF ADCAFH CADAF AC∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,()AFH CAD AAS∴∆≅∆,(2)由(1)得AFH CAD∆≅∆,FH AD∴=,作FK AG⊥,交AG延长线于点K,如图;同理得到AEK ABD∆≅∆,EK AD∴=,FH EK∴=,在EKG∆和FHG∆中,90EKG FHGEGK FGHEK FH∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,()EKG FHG AAS∴∆≅∆,EG FG∴=.即点G是EF的中点.【点睛】此题考查了全等三角形的判定与性质,熟练掌握K字形全等进行证明是解本题的关键.。
八年级上册数学压轴题精选

八年级上册数学压轴题精选一、整数运算1. 求解下列算式:(1)$(-5) \times (-8) = ?$(2)$7 \div (-3) = ?$二、分数运算1. 求解下列算式:(1)$\frac{2}{3} + \frac{1}{4} = ?$(2)$\frac{5}{6} - \frac{1}{3} = ?$三、代数式化简1. 将下列代数式化简为最简形式:(1)$2x - (3x + 4) =$?(2)$\frac{3}{4}(x-1) - \frac{1}{2}(2x-3) =$?四、方程解求1. 求解下列一元一次方程:(1)$2x + 5 = 13$(2)$\frac{3x}{2} - 1 = 7$五、图形计算1. 计算下列图形的周长和面积:(1)矩形的长为5cm,宽为3cm。
(2)正方形的边长为8cm。
六、比例与相似1. 求解下列比例:(1)$\frac{4}{5} = \frac{12}{x}$ (2)$\frac{2}{3} = \frac{x}{9}$ 七、平面几何1. 判断下列命题的真假:(1)直角三角形的两条直角边的平方和等于斜边的平方。
(2)等腰三角形的两条底边相等。
八、统计与概率1. 求解下列问题:(1)一筐中有红球12个,蓝球18个,随机摸出一个求红球的概率。
(2)甲、乙两个班级的学生人数分别是45人和50人,从两个班级任意抽取一个学生,求乙班学生被抽中的概率。
以上是八年级上册数学压轴题精选。
通过掌握这些题目类型,学生们可以对课本中重要的数学知识点进行巩固和提升。
希望同学们能够通过认真解答这些题目,提高自己的数学水平。
八年级数学上册期末压轴20题(解析版)

八年级上册数学压轴题专题练习(解析版)一、压轴题1.如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点 P在线段 AB上以1cm/s的速度由点 A向点 B运动,同时,点 Q在线段 BD上由点 B向点 D运动.它们运动的时间为t(s).(1)若点 Q的运动速度与点 P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段 PC和线段 PQ的位置关系;(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点 Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.2.在Rt ABC中,∠ACB=90︒,∠A=30︒,BD是ABC的角平分线,DE⊥AB于点E.(1)如图1,连接EC,求证:EBC是等边三角形;(2)如图2,点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM下方作∠BMG=60︒,MG交DE延长线于点G.求证:AD=DG+MD;(3)如图3,点N是线段AD上的点,以BN为一边,在BN的下方作∠BNG=60︒,NG交DE延长线于点G.直接写出ND,DG与AD数量之间的关系.3.在《经典几何图形的研究与变式》一课中,庞老师出示了一个问题:“如图1,等腰直角三角形的三个顶点分别落在三条等距的平行线l1,l2,l3上,∠BAC=90︒,且每两条平行线之间的距离为1,求AB的长度”.在研究这道题的解法和变式的过程中,同学们提出了很多想法:(1)小明说:我只需要过B、C向l1作垂线,就能利用全等三角形的知识求出AB的长.(2)小林说:“我们可以改变ABC的形状.如图2,AB=AC,∠BAC=120︒,且每两条平行线之间的距离为1,求AB的长.”(3)小谢说:“我们除了改变ABC的形状,还能改变平行线之间的距离.如图3,等边三角形ABC三个顶点分别落在三条平行线l1,l2,l3上,且l1与l2之间的距离为1,l2与l3之间的距离为2,求AB的长、”请你根据3位同学的提示,分别求出三种情况下AB的长度.4.在ABC中,AB=AC,D是直线AB上一点,E在直线BC上,且DE=DC.(1)如图1,当D在AB上,E在CB延长线上时,求证:∠EDB=∠ACD;(2)如图2,当ABC为等边三角形时,D是BA的延长线上一点,E在BC上时,作EF//AC,求证:BE=AD;(3)在(2)的条件下,∠ABC的平分线BF交CD于点F,连AF,过A点作AH⊥CD于点H,当∠EDC=30︒,CF=6时,求DH的长度.5.(阅读材科)小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的项角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小明发现若∠BAC=∠DAE,AB=AC,AD=AE,则△ABD≌△ACE.(材料理解)(1)在图1中证明小明的发现.(深入探究)(2)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:①BD=EC;②∠BOC=60°;③∠AOE=60°;④EO=CO,其中正确的有.(将所有正确的序号填在横线上).(延伸应用)(3)如图3,AB=BC,∠ABC=∠BDC=60°,试探究∠A与∠C的数量关系.6.阅读下面材料,完成(1)-(3)题.数学课上,老师出示了这样一道题:如图1,已知等腰△ABC中,AB=AC,AD为BC边上的中线,以AB为边向AB左侧作等边△ABE,直线CE与直线AD交于点F.请探究线段EF、AF、DF之间的数量关系,并证明.同学们经过思考后,交流了自已的想法:小明:“通过观察和度量,发现∠DFC的度数可以求出来.”小强:“通过观察和度量,发现线段DF和CF之间存在某种数量关系.”小伟:“通过做辅助线构造全等三角形,就可以将问题解决.”......老师:“若以AB为边向AB右侧作等边△ABE,其它条件均不改变,请在图2中补全图形,探究线段EF、AF、DF三者的数量关系,并证明你的结论.”(1)求∠DFC的度数;(2)在图1中探究线段EF、AF、DF之间的数量关系,并证明;(3)在图2中补全图形,探究线段EF、AF、DF之间的数量关系,并证明.7.(1)填空①把一张长方形的纸片按如图①所示的方式折叠,EM,FM为折痕,折叠后的C点落在B 1M或B1M的延长线上,那么EMF的度数是________;②把一张长方形的纸片按如图②所示的方式折叠,B点与M点重合,EM,FM为折痕,折叠后的C点落在A1M或A1M的延长线上,那么EMF的度数是_______.(2)解答:①把一张长方形的纸片按如图③所示的方式折叠,EM,FM为折痕,折叠后的C点落在B1M或B1M的延长线上左侧,且EMF80,求C1MB1的度数;②把一张长方形的纸片按如图④所示的方式折叠,B点与M点重合,EM,FM为折痕,折叠后的C点落在A1M或A1M的延长线右侧,且EMF60,求C1MA1的度数.(3)探究:把一张四边形的纸片按如图⑤所示的方式折叠,EB,FB为折痕,设ABC,EBF,A1BC1,求,,之间的数量关系.8.已知ABC和ADE都是等腰三角形,AB AC,AD AE,DAE BAC.(初步感知)(1)特殊情形:如图①,若点D,E分别在边AB,AC上,则DB__________EC.(填>、<或=)(2)发现证明:如图②,将图①中的ADE绕点A旋转,当点D在ABC外部,点E 在ABC内部时,求证:DB EC.(深入研究)(3)如图③,ABC和ADE都是等边三角形,点C,E,D在同一条直线上,则∠CDB的度数为__________;线段CE,BD之间的数量关系为__________.(4)如图④,ABC和ADE都是等腰直角三角形,∠BAC=∠DAE=90︒,点C、D、E在同一直线上,AM为ADE中DE边上的高,则∠CDB的度数为__________;线段AM,BD,CD之间的数量关系为__________.(拓展提升)(5)如图⑤,ABC和ADE都是等腰直角三角形,∠BAC=∠DAE=90︒,将ADE绕点A逆时针旋转,连结BE、CD.当AB=5,AD=2时,在旋转过程中,△ABE与ADC的面积和的最大值为__________.9.直角三角形ABC中,∠ACB=90︒,直线l过点C.(1)当AC=BC时,如图1,分别过点A和B作AD⊥直线l于点D,BE⊥直线l于点E,ACD与△CBE是否全等,并说明理由;(2)当AC=8cm,BC=6cm时,如图2,点B与点F关于直线l对称,连接BF、CF,点M是AC上一点,点N是CF上一点,分别过点M、N作MD⊥直线l于点D,NE⊥直线l于点E,点M从A点出发,以每秒1cm的速度沿A→C路径运动,终点为C,点N从点F出发,以每秒3cm的速度沿F→C→B→C→F路径运动,终点为F,点M,N同时开始运动,各自达到相应的终点时停止运动,设运动时间为t秒,当△CMN为等腰直角三角形时,求t的值.10.已知:ABC中,过B点作BE⊥AD,∠ACB=90︒,AC=BC.(1)如图1,点D在BC的延长线上,连AD,作BE⊥AD于E,交AC于点F.求证:AD=BF;(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC 于F,连DE,问BD与CF有何数量关系,并加以证明;(3)如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC=3MC,请直接写出DB的值.BC11.(1)在等边三角形ABC中,①如图①,D,E分别是边AC,AB上的点且AE=CD,BD与EC交于点F,则∠BFE的度数是度;②如图②,D,E分别是边AC,BA延长线上的点且AE=CD,BD与EC的延长线交于点F,此时∠BFE的度数是度;(2)如图③,在△ABC中,AC=BC,∠ACB是锐角,点O是AC边的垂直平分线与BC的交点,点D,E分别在AC,OA的延长线上,AE=CD,BD与EC的延长线交于点F,若∠ACB=α,求∠BFE的大小.(用含α的代数式表示).12.已知ABC,P是平面内任意一点(A、B、C、P中任意三点都不在同一直线上).连接 PB、PC,设∠PBA=s°,∠PCA=t°,∠BPC=x°,∠BAC=y°.(1)如图,当点 P在ABC内时,①若 y=70,s=10,t=20,则 x=;②探究 s、t、x、y之间的数量关系,并证明你得到的结论.(2)当点 P在ABC外时,直接写出 s、t、x、y之间所有可能的数量关系,并画出相应的图形.13.Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.(1)若点P在线段AB上,如图(1)所示,且∠α=60°,则∠1+∠2=;(2)若点P在线段AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为;(3)若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由;(4)若点P运动到△ABC形外,如图(4)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.14.探索发现:11111111 =1-;=-;=-……1⨯222⨯3233⨯434根据你发现的规律,回答下列问题:(1)11=,=;n⨯(n+1)4⨯5111⋅+++1⨯22⨯33⨯4+1n⨯(n+1)(2)利用你发现的规律计算:(3)利用规律解方程:111112x-1 ++++=x(x+1)(x+1)(x+2)(x+2)(x+3)(x+3)(x+4)(x+4)(x+5)x(x+5) 15.数学活动课上,老师出了这样一个题目:“已知:MF⊥NF于F,点A、C分别在NF和MF上,作线段AB和CD(如图1),使∠FAB-∠MCD=90︒.求证:AB//CD”.(1)聪聪同学给出一种证明问题的辅助线:如图2,过A作AG//FM,交CD于G.请你根据聪聪同学提供的辅助线(或自己添加其它辅助线),给出问题的证明.(2)若点E在直线CD下方,且知∠BED=30︒,直接写出∠ABE和∠CDE之间的数量关系.16.现给出一个结论:直角三角形斜边的中线等于斜边的一半;该结论是正确的,用图形语言可以表示为:如图1在∆ABC中,∠C=90︒,若点D为AB的中点,则CD=请结合上述结论解决如下问题:1AB.2已知,点P是射线BA上一动点(不与A,B重合)分别过点A,B向直线CP作垂线,垂足分别为E,F,其中Q为AB的中点(1)如图2,当点P与点Q重合时,AE与BF的位置关系____________;QE与QF的数量关系是__________(2)如图3,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明.(3)如图4,当点P在线段BA的延长线上时,此时(2)中的结论是否成立?请画出图形并写出主要证明思路.17.在△ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.(1)如图,当点D在BC延长线上移动时,若∠BAC=40°,则∠ACE=,∠DCE=,BC、DC、CE之间的数量关系为;(2)设∠BAC=α,∠DCE=β.①当点D在BC延长线上移动时,α与β之间有什么数量关系?请说明理由;②当点D在直线BC上(不与B,C两点重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.(3)当CE∥AB时,若△ABD中最小角为15°,试探究∠ACB的度数(直接写出结果,无需写出求解过程).18.阅读材料并完成习题:在数学中,我们会用“截长补短”的方法来构造全等三角形解决问题.请看这个例题:如图1,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若AC=2cm,求四边形ABCD的面积.解:延长线段CB到E,使得BE=CD,连接AE,我们可以证明△BAE≌△DAC,根据全等三角形的性质得AE=AC=2,∠EAB=∠CAD,则∠EAC=∠EAB+∠BAC=∠DAC+∠BAC=∠BAD=90°,得S四边形ABCD =S△ABC+S△ADC=S△ABC+S△ABE=S△AEC,这样,四边形ABCD的面积就转化为等腰直角三角形EAC面积.(1)根据上面的思路,我们可以求得四边形ABCD的面积为 cm2.(2)请你用上面学到的方法完成下面的习题.如图2,已知FG=FN=HM=GH+MN=2cm,∠G=∠N=90°,求五边形FGHMN的面积.19.(1)如图1,ABC和DCE都是等边三角形,且B,C,D三点在一条直线上,连接AD,BE相交于点P,求证:BE=AD.(2)如图2,在BCD中,若∠BCD<120︒,分别以BC,CD和BD为边在BCD外部作等边ABC,等边△CDE,等边BDF,连接AD、BE、CF恰交于点P.①求证:AD=BE=CF;②如图2,在(2)的条件下,试猜想PB,PC,PD与BE存在怎样的数量关系,并说明理由.20.阅读并填空:如图,ABC是等腰三角形,AB=AC,D是边AC延长线上的一点,E在边AB上且联接DE交BC于O,如果OE OD,那么CD=BE,为什么?解:过点E作EF AC交BC于F所以∠ACB=∠EFB(两直线平行,同位角相等)∠D=∠OEF(________)在OCD与△OFE中⎧∠COD=∠FOE(________)⎪⎨OD=OE⎪∠D=∠OEF⎩所以△OCD≌△OFE,(________)所以CD=FE(________)因为AB=AC(已知)所以∠ACB=∠B(________)所以∠EFB=∠B(等量代换)所以BE=FE(________)所以CD=BE【参考答案】***试卷处理标记,请不要删除一、压轴题⎧t=2⎧t=1⎪1.(1)全等,垂直,理由详见解析;(2)存在,⎨或⎨3x=1x=⎩⎪2⎩【解析】【分析】(1)在t =1的条件下,找出条件判定△ACP和△BPQ全等,再根据全等三角形的性质和直角三角形的两个锐角互余的性质,可证∠CPQ= 90°,即可判断线段 PC和线段 PQ的位置关系;(2)本题主要在动点的条件下,分情况讨论,利用三角形全等时对应边相等的性质进行解答即可.【详解】(1)当t=1时,AP= BQ=1, BP= AC=3,又∠A=∠B= 90°,在△ACP和△BPQ中,AP=BQ{∠A=∠BAC=BP∴△ACP≌△BPQ(SAS).∴∠ACP=∠BPQ ,∴∠APC+∠BPQ=∠APC+∠ACP = 90*.∴∠CPQ= 90°,即线段PC与线段PQ垂直;(2)①若△ACP ≌△BPQ ,则AC= BP ,AP= BQ ,⎧3=4-t ⎨t =xt⎩解得⎨⎧t =1;x =1⎩②若△ACP ≌△BQP ,则AC= BQ ,AP= BP ,⎧3=xt ⎨t =4-t⎩⎧t =2⎪解得:⎨3x =⎪⎩2⎧t =2⎧t =1⎪综上所述,存在⎨或⎨3使得△ACP 与△BPQ 全等.x =1x =⎩⎪⎩2【点睛】本题主要考查三角形全等与动点问题,熟练掌握三角形全等的性质与判定定理,是解决本题的关键.2.(1)证明见解析;(2)证明见解析;(3)结论:AD =DG -ND ,证明见解析.【解析】【分析】(1)先根据直角三角形的性质得出∠ABC =60︒,再根据角平分线的性质可得CD =ED ,然后根据三角形的判定定理与性质可得BC =BE ,最后根据等边三角形的判定即可得证;(2)如图(见解析),延长ED 使得DF =MD ,连接MF ,先根据直角三角形的性质、等边三角形的判定得出∆MDF 是等边三角形,再根据等边三角形的性质、角的和差得出∠F =∠MDB ,MF =MD ,∠FMG =∠DMB ,然后根据三角形全等的判定与性质、等量代换即可得证;(3)如图(见解析),参照题(2),先证∆HDN 是等边三角形,再根据等边三角形的性质、角的和差得出∠H =∠NDG ,NH =ND ,∠HNB =∠DNG ,然后根据三角形全等的判定与性质、等量代换即可得证.【详解】(1)∠ACB =90︒,∠A =30︒∴∠ABC =90︒-∠A =60︒BD 是∠ABC 的角平分线,DE ⊥AB∴CD =ED⎧CD=ED在∆BCD和∆BED中,⎨BD=BD⎩∴∆BCD≅∆BED(HL)∴BC=BE∴∆EBC是等边三角形;(2)如图,延长ED使得DF=MD,连接MF∠ACB=90︒,∠A=30︒,BD是∠ABC的角平分线,DE⊥AB∴∠ADE=∠BDE=60︒,AD=BD∴∠MDF=∠ADE=60︒,∠MDB=180︒-∠ADE-∠BDE=60︒∴∆MDF是等边三角形∴MF=DM,∠F=∠DMF=60︒∠BMG=60︒∴∠DMF+∠DMG=∠BMG+∠DMG,即∠FMG=∠DMB⎧∠F=∠MDB=60︒⎪在∆FMG和∆DMB中,⎨MF=MD⎪∠FMG=∠DMB⎩∴∆FMG≅∆DMB(ASA)∴GF=BD,即DF+DG=BD∴AD=DF+DG=MD+DG即AD=DG+MD;(3)结论:AD=DG-ND,证明过程如下:如图,延长BD使得DH=ND,连接NH由(2)可知,∠ADE=60︒,∠HDN=180︒-∠ADE-∠BDE=60︒,AD=BD ∴∆HDN是等边三角形∴NH=ND,∠H=∠HND=60︒∠BNG=60︒∴∠HND+∠BND=∠BNG+∠BND,即∠HNB=∠DNG⎧∠H=∠NDG=60︒⎪在∆HNB和∆DNG中,⎨NH=ND⎪∠HNB=∠DNG⎩∴∆HNB≅∆DNG(ASA)∴HB =DG ,即DH +BD =DG∴ND +AD =DG即AD =DG -ND .【点睛】本题考查了直角三角形的性质、等边三角形的判定与性质、三角形全等的判定定理与性质等知识点,较难的是题(2)和(3),通过作辅助线,构造一个等边三角形是解题关键.3.(1)5;(2)【解析】【分析】(1)分别过点B ,C 向l 1作垂线,交l 1于M ,N 两点,证明△ABM ≌△CAN ,得到AM=CN ,AN=BM ,即可得出AB ;(2)分别过点B ,C 向l 1作垂线,交l 1于点P ,Q 两点,在l 1上取M ,N 使∠AMB=∠CNA=120°,证明△AMB ≌△CAN ,得到CN=AM ,再通过△PBM 和△QCN 算出PM 和NQ 的值,得到AP ,最后在△APB 中,利用勾股定理算出AB 的长;(3)在l 3上找M 和N ,使得∠BNC=∠AMC=60°,过B 作l 3的垂线,交l 3于点P ,过A 作l 3的垂线,交l 3于点Q ,证明△BCN ≌△CAM ,得到CN=AM ,在△BPN 和△AQM 中利用勾股定理算出NP 和AM ,从而得到PC ,结合BP 算出BC 的长,即为AB.【详解】解:(1)如图,分别过点B ,C 向l 1作垂线,交l 1于M ,N 两点,由题意可得:∠BAC=90°,∵∠NAC+∠MAB=90°,∠NAC+∠NCA=90°,∴∠MAB=∠NCA ,在△ABM 和△CAN 中,221221;(3)33⎧∠AMB =∠CNA ⎪⎨∠MAB =∠NCA ,⎪AB =AC ⎩∴△ABM ≌△CAN (AAS ),∴AM=CN=2,AN=BM=1,∴AB=22+12=5;(2)分别过点B,C向l1作垂线,交l1于P,Q两点,在l1上取M,N使∠AMB=∠CNA=120°,∵∠BAC=120°,∴∠MAB+∠NAC=60°,∵∠ABM+∠MAB=60°,∴∠ABM=∠NAC,在△AMB和△CNA中,⎧∠AMB=∠CNA⎪⎨∠ABM=∠NAC,⎪AB=AC⎩∴△AMB≌△CNA(AAS),∴CN=AM,∵∠AMB=∠ANC=120°,∴∠PMB=∠QNC=60°,∴PM=11 BM,NQ=NC,22∵PB=1,CQ=2,设PM=a,NQ=b,∴a2+12=4a2,b2+22=4b2,解得:a=323,b=,332⎛23⎫43=∴CN=AM=22+ ,⎪3⎪3⎝⎭∴AB=AP2+BP2=(AM+PM)2+BP2=221;3(3)如图,在l3上找M和N,使得∠BNC=∠AMC=60°,过B作l3的垂线,交于点P,过A作l3的垂线,交于点Q,∵△ABC是等边三角形,∴BC=AC,∠ACB=60°,∴∠BCN+∠ACM=120°,∵∠BCN+∠NBC=120°,∴∠NBC=∠ACM,在△BCN和△CAM中,⎧∠BNC=∠CMA⎪⎨∠NBC=∠MAC,⎪BC=AC⎩∴△BCN≌△CAM(AAS),∴CN=AM,BN=CM,∵∠PBN=90°-60°=30°,BP=2,∴BN=2NP,在△BPN中,BP2+NP2=BN2,即22+NP2=4NP2,解得:NP=23,3∵∠AMC=60°,AQ=3,∴∠MAQ=30°,∴AM=2QM,在△AQM中,AQ2+QM2=AM2,即32+QM2=4QM2,解得:QM=3,∴AM=23=CN,∴PC=CN-NP=AM-NP=在△BPC中,BP2+CP2=BC2,43,3⎛43⎫221即BC=BP2+CP2=22+ ,=⎪3⎪3⎝⎭2∴AB=BC=221.3【点睛】本题考查了全等三角形的判定和性质,平行线之间的距离,等腰三角形的性质,等边三角形的性质以及勾股定理,解题的关键是利用平行线构造全等三角形,再利用全等三角形的性质以及勾股定理求解.4.(1)见解析;(2)见解析;(3)3【解析】【分析】(1)根据等腰三角形的性质和外角的性质即可得到结论;(2)过E作EF∥AC交AB于F,根据已知条件得到△ABC是等边三角形,推出△BEF是等边三角形,得到BE=EF,∠BFE=60°,根据全等三角形的性质即可得到结论;(3)连接AF,证明△ABF≌△CBF,得AF=CF,再证明DH=AH=【详解】解:(1)∵AB=AC,∴∠ABC=∠ACB,∵DE=DC,∴∠E=∠DCE,∴∠ABC-∠E=∠ACB-∠DCB,即∠EDB=∠ACD;(2)∵△ABC是等边三角形,∴∠B=60°,∴△BEF是等边三角形,∴BE=EF,∠BFE=60°,∴∠DFE=120°,∴∠DFE=∠CAD,在△DEF与△CAD中,1CF=3.2⎧∠EDF=∠DCA⎪⎨∠DFE=∠CAD,⎪DE=CD⎩∴△DEF≌△CAD(AAS),∴EF=AD,∴AD=BE;(3)连接AF,如图3所示:∵DE=DC,∠EDC=30°,∴∠DEC=∠DCE=75°,∴∠ACF=75°-60°=15°,∵BF平分∠ABC,∴∠ABF=∠CBF,在△ABF和△CBF中,⎧AB=BC⎪⎨∠ABF=∠CBF,⎪BF=BF⎩△ABF≌△CBF(SAS),∴AF=CF,∴∠FAC=∠ACF=15°,∴∠AFH=15°+15°=30°,∵AH⊥CD,∴AH=11AF=CF=3,22∵∠DEC=∠ABC+∠BDE,∴∠BDE=75°-60°=15°,∴∠ADH=15°+30°=45°,∴∠DAH=∠ADH=45°,∴DH=AH=3.【点睛】本题考查了全等三角形的判定与性质,等腰三角形和直角三角形的性质,三角形的外角的性质,等边三角形的判定和性质,证明三角形全等是解决问题的关键.5.(1)证明见解析;(2)①②③;(3)∠A+∠C=180°.【解析】【分析】(1)利用等式的性质得出∠BAD=∠CAE,即可得出结论;(2)同(1)的方法判断出△ABD≌△ACE,得出BD=CE,再利用对顶角和三角形的内角和定理判断出∠BOC=60°,再判断出△BCF≌△ACO,得出∠AOC=120°,进而得出∠AOE=60°,再判断出BF<CF,进而判断出∠OBC>30°,即可得出结论;(3)先判断出△BDP是等边三角形,得出BD=BP,∠DBP=60°,进而判断出△ABD≌△CBP (SAS),即可得出结论.【详解】(1)证明:∵∠BAC=∠DAE,∴∠BAC+∠CAD=∠DAE+∠CAD,∴∠BAD=∠CAE,在△ABD和△ACE中,⎧AB=AC⎪⎨∠BAD=∠CAE,⎪AD=AE⎩∴△ABD≌△ACE;(2)如图2,∵△ABC和△ADE是等边三角形,∴AB=AC,AD=AE,∠BAC=∠DAE=60°,∴∠BAD=∠CAE,在△ABD和△ACE中,⎧AB=AC⎪⎨∠BAD=∠CAE,⎪AD=AE⎩∴△ABD≌△ACE,∴BD=CE,①正确,∠ADB=∠AEC,记AD与CE的交点为G,∵∠AGE=∠DGO,∴180°-∠ADB-∠DGO=180°-∠AEC-∠AGE,∴∠DOE=∠DAE=60°,∴∠BOC=60°,②正确,在OB上取一点F,使OF=OC,∴△OCF是等边三角形,∴CF=OC,∠OFC=∠OCF=60°=∠ACB,∴∠BCF=∠ACO,∵AB=AC,∴△BCF≌△ACO(SAS),∴∠AOC=∠BFC=180°-∠OFC=120°,∴∠AOE=180°-∠AOC=60°,③正确,连接AF,要使OC=OE,则有OC=∵BD=CE,∴CF=OF=1 CE,21BD,2∴OF=BF+OD,∴BF<CF,∴∠OBC>∠BCF,∵∠OBC+∠BCF=∠OFC=60°,∴∠OBC>30°,而没办法判断∠OBC大于30度,所以,④不一定正确,即:正确的有①②③,故答案为①②③;(3)如图3,延长DC至P,使DP=DB,∵∠BDC=60°,∴△BDP是等边三角形,∴BD=BP,∠DBP=60°,∵∠BAC=60°=∠DBP,∴∠ABD=∠CBP,∵AB=CB,∴△ABD≌△CBP(SAS),∴∠BCP=∠A,∵∠BCD+∠BCP=180°,∴∠A+∠BCD=180°.【点睛】此题考查三角形综合题,等腰三角形的性质,等边三角形的性质,全等三角形的判定和性质,构造等边三角形是解题的关键.6.(1)60°;(2)EF=AF+FC,证明见解析;(3)AF=EF+2DF,证明见解析.【解析】【分析】(1)可设∠BAD=∠CAD=α,∠AEC=∠ACE=β,在△ACE中,根据三角形内角和可得2α+60+2β=180°,从而有α+β=60°,即可得出∠DFC的度数;(2)在EC上截取EG=CF,连接AG,证明△AEG≌△ACF,然后再证明△AFG为等边三角形,从而可得出EF=EG+GF=AF+FC;(3)在AF上截取AG=EF,连接BG,BF,证明方法类似(2),先证明△ABG≌△EBF,再证明△BFG为等边三角形,最后可得出结论.【详解】解:(1)∵AB=AC,AD为BC边上的中线,∴可设∠BAD=∠CAD=α,又△ABE为等边三角形,∴AE=AB=AC,∠EAB=60°,∴可设∠AEC=∠ACE=β,在△ACE中,2α+60°+2β=180°,∴α+β=60°,∴∠DFC=α+β=60°;(2)EF=AF+FC,证明如下:∵AB=AC,AD为BC边上的中线,∴AD⊥BC,∴∠FDC=90°,∵∠CFD=60°,则∠DCF=30°,∴CF=2DF,在EC上截取EG=CF,连接AG,又AE=AC,∴∠AEG=∠ACF,∴△AEG≌△ACF(SAS),∴∠EAG=∠CAF,AG=AF,又∠CAF=∠BAD,∴∠EAG=∠BAD,∴∠GAF=∠BAD+∠BAG=∠EAG+∠BAG=∠60°,∴△AFG为等边三角形,∴EF=EG+GF=AF+FC,即EF=AF+FC;(3)补全图形如图所示,结论:AF=EF+2DF.证明如下:同(1)可设∠BAD=∠CAD=α,∠ACE=∠AEC=β,∴∠CAE=180°-2β,∴∠BAE=2α+180°-2β=60°,∴β-α=60°,∴∠AFC=β-α=60°,又△ABE为等边三角形,∴∠ABE=∠AFC=60°,∴由8字图可得:∠BAD=∠BEF,在AF上截取AG=EF,连接BG,BF,又AB=BE ,∴△ABG ≌△EBF (SAS ),∴BG =BF ,又AF 垂直平分BC ,∴BF=CF ,∴∠BFA=∠AFC=60°,∴△BFG 为等边三角形,∴BG=BF ,又BC ⊥FG ,∴FG=BF=2DF ,∴AF =AG +GF =BF +EF =2DF +EF .【点睛】本题考查了全等三角形的判定和性质、等边三角形的性质、等腰三角形的性质等知识,解决问题的关键是常用辅助线构造全等三角形,属于中考常考题型.7.90︒,45︒;20︒,30︒;a +γ=2β,a -γ=2β.【解析】【分析】(1)①如图①知∠EMC 1=11∠BMC 1,∠C 1MF =∠C 1MC 得22∠EMF =1(∠BMC 1+∠C 1MC )可求出解.2111∠ABC 1,∠C 1BF =∠C 1BC 得∠EBF =(∠ABC 1+∠C 1BC )可222②由图②知∠EBA 1=求出解.(2)①由图③折叠知∠CMF =∠FMC 1,∠BME =∠EMB 1,可推出(∠BMC -∠EMF )-∠EMF =∠C 1MB 1,即可求出解.②由图④中折叠知∠CMF =∠C 1MF ,∠ABE =∠A 1BE ,可推出290︒-60︒+∠A 1MC 1=90︒,即可求出解.(3)如图⑤-1、⑤-2中分别由折叠可知,a -β=β-γ、a -β=β+γ,即可求得()a +γ=2β、a -γ=2β.【详解】解:(1)①如图①中,11∠EMC 1=∠BMC 1,∠C 1MF =∠C 1MC ,22∴∠EMF =∠EMC 1+∠C 1MF =故答案为90︒.②如图②中,11(∠BMC 1+∠C 1MC )=⨯180︒=90︒,2211∠EBA 1=∠ABC 1,∠C 1BF =∠C 1BC ,22∴∠EBF =∠EBC 1+∠C 1BF =故答案为45︒.(2)①如图③中由折叠可知,11(∠ABC 1+∠C 1BC )=⨯90︒=45︒,22∠CMF =∠FMC 1,∠BME =∠EMB 1,∠C 1MF +∠EMB 1-∠EMF =∠C 1MB 1,∴∠CMF +∠BME -∠EMF =∠C 1MB 1,∴(∠BMC -∠EMF )-∠EMF =∠C 1MB 1,∴180︒-80︒=∠C 1MB 1=20︒;②如图④中根据折叠可知,∠CMF =∠C 1MF ,∠ABE =∠A 1BE ,︒2∠CMF +2∠ABE +∠AMC =90,11︒∴2(∠CMF +∠ABE )+∠AMC 11=90,(∴2(90∴290︒-∠EMF +∠A 1MC 1=90︒,︒)-60︒+∠A 1MC 1=90︒,)︒∴∠AMC =30;11(3)如图⑤-1中,由折叠可知,a -β=β-γ,∴a +γ=2β;如图⑤-2中,由折叠可知,a -β=β+γ,∴a -γ=2β.【点睛】本题考查了图形的变换中折叠属全等变换,图形的角度及边长不变及一些角度的计算问题,突出考查学生的观察能力、思维能力以及动手操作能力,本题是代数、几何知识的综合运用典型题目.8.(1)=;(2)证明见解析;(3)60°,BD=CE;(4)90°,AM+BD=CM ;(5)7【解析】【分析】(1)由DE ∥BC ,得到DB EC =,结合AB=AC ,得到DB=EC ;AB AC(2)由旋转得到的结论判断出△DAB≌△EAC,得到DB=CE;(3)根据等边三角形的性质和全等三角形的判定定理证明△DAB≌△EAC,根据全等三角形的性质求出结论;(4)根据全等三角形的判定和性质和等腰直角三角形的性质即可得到结论;(5)根据旋转的过程中△ADE的面积始终保持不变,而在旋转的过程中,△ADC的AC始终保持不变,即可.【详解】[初步感知](1)∵DE∥BC,∴DB EC=,AB AC∵AB=AC,∴DB=EC,故答案为:=,(2)成立.理由:由旋转性质可知∠DAB=∠EAC,在△DAB和△EAC中⎧AD=AE⎪⎨∠DAB=∠EAC,⎪AB=AC⎩∴△DAB≌△EAC(SAS),∴DB=CE;[深入探究](3)如图③,设AB,CD交于O,∵△ABC和△ADE都是等边三角形,∴AD=AE,AB=AC,∠DAE=∠BAC=60°,∴∠DAB=∠EAC,在△DAB和△EAC中⎧AD=AE⎪⎨∠DAB=∠EAC,⎪AB=AC⎩∴△DAB≌△EAC(SAS),∴DB=CE,∠ABD=∠ACE,∵∠BOD=∠AOC,∴∠BDC=∠BAC=60°;(4)∵△DAE 是等腰直角三角形,∴∠AED=45°,∴∠AEC=135°,在△DAB 和△EAC 中⎧AD =AE⎪⎨∠DAB =∠EAC,⎪AB =AC⎩∴△DAB ≌△EAC (SAS ),∴∠ADB=∠AEC=135°,BD=CE ,∵∠ADE=45°,∴∠BDC=∠ADB-∠ADE=90°,∵△ADE 都是等腰直角三角形,AM 为△ADE 中DE 边上的高,∴AM=EM=MD ,∴AM+BD=CM ;故答案为:90°,AM+BD=CM ;【拓展提升】(5)如图,由旋转可知,在旋转的过程中△ADE 的面积始终保持不变,△ADE 与△ADC 面积的和达到最大,∴△ADC 面积最大,∵在旋转的过程中,AC 始终保持不变,∴要△ADC 面积最大,∴点D 到AC 的距离最大,∴DA ⊥AC ,∴△ADE 与△ADC 面积的和达到的最大为2+故答案为7.【点睛】此题是几何变换综合题,主要考查了旋转和全等三角形的性质和判定,旋转过程中面积变化分析,解本题的关键是三角形全等的判定.9.(1)全等,理由见解析;(2)t=3.5秒或5秒1×AC×AD=5+2=7,2【解析】【分析】(1)根据垂直的定义得到∠DAC=∠ECB ,利用AAS 定理证明△ACD ≌△CBE ;(2)分点F 沿C→B 路径运动和点F 沿B→C 路径运动两种情况,根据等腰三角形的定义列出算式,计算即可;【详解】解:(1)△ACD 与△CBE 全等.理由如下:∵AD ⊥直线l ,∴∠DAC+∠ACD=90°,∵∠ACB=90°,∴∠BCE+∠ACD=90°,∴∠DAC=∠ECB ,在△ACD 和△CBE 中,⎧∠ADC =∠CEB⎪⎨∠DAC =∠ECB,⎪CA =CB⎩∴△ACD ≌△CBE (AAS );(2)由题意得,AM=t ,FN=3t ,则CM=8-t ,由折叠的性质可知,CF=CB=6,∴CN=6-3t ,点N 在BC 上时,△CMN 为等腰直角三角形,当点N 沿C→B 路径运动时,由题意得,8-t=3t-6,解得,t=3.5,当点N 沿B→C 路径运动时,由题意得,8-t=18-3t ,解得,t=5,综上所述,当t=3.5秒或5秒时,△CMN 为等腰直角三角形;【点睛】本题考查的是全等三角形的判定和性质,掌握全等三角形的判定定理和性质定理,灵活运用分情况讨论思想是解题的关键.10.(1)见详解,(2)BD =2CF ,证明见详解,(3)【解析】【分析】(1)欲证明BF =AD ,只要证明∆BCF ≅∆ACD 即可;(2)结论:BD =2CF .如图2中,作EH ⊥AC 于H .只要证明∆ACD ≅∆EHA ,推出CD =AH ,EH =AC =BC ,由∆EHF ≅∆BCF ,推出CH 2.3=CF 即可解决问题;(3)利用(2)中结论即可解决问题;【详解】(1)证明:如图1中,BE⊥AD于E,∴∠AEF=∠BCF=90︒,∠AFE=∠CFB,∴∠DAC=∠CBF,BC=AC,∴∆BCF≅∆ACD(AAS),∴BF=AD.(2)结论:BD=2CF.理由:如图2中,作EH⊥AC于H.∠AHE=∠ACD=∠DAE=90︒,∴∠DAC+∠ADC=90︒,∠DAC+∠EAH=90︒,∴∠ADC=∠EAH,AD=AE,∴∆ACD≅∆EHA,∴CD=AH,EH=AC=BC,CB=CA,∴BD=CH,∠EHF=∠BCF=90︒,∠EFH=∠BFC,EH=BC,∴∆EHF≅∆BCF,∴FH=FC,∴BD=CH=2CF.(3)如图3中,作EH⊥AC于交AC延长线于H.∠AHE=∠ACD=∠DAE=90︒,∴∠DAC+∠ADC=90︒,∠DAC+∠EAH=90︒,∴∠ADC=∠EAH,AD=AE,∴∆ACD≅∆EHA,∴CD=AH,EH=AC=BC,CB=CA,∴BD=CH,∠EHM=∠BCM=90︒,∠EMH=∠BMC,EH=BC,∴∆EHM≅∆BCM,∴MH=MC,∴BD=CH=2CM.AC=3CM,设CM=a,则AC=CB=3a,BD=2a,∴DB2a2==.BC3a3【点睛】本题考查三角形综合题、全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.另外对于类似连续几步的综合题,一般前一步为后一步提供解题的条件或方法.11.(1)①60°;②60°;(2)∠BFE =α.【解析】【分析】(1)①先证明△ACE≌△CBD得到∠ACE=∠CBD,再由三角形外角和定理可得∠BFE=∠CBD+∠BCF;②先证明△ACE≌△CBD得∠ACE=∠CBD=∠DCF,再由三角形外角和定理可得∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA;(2)证明△AEC≌△CDB得到∠E=∠D,则∠BFE=∠D+∠DCF=∠E+∠ECA=∠OAC=α.【详解】(1)如图①中,∵△ABC是等边三角形,∴AC=CB,∠A=∠BCD=60°,∵AE=CD,∴△ACE≌△CBD,∴∠ACE=∠CBD,∴∠BFE=∠CBD+∠BCF=∠ACE+∠BCF=∠BCA=60°.故答案为60.(2)如图②中,∵△ABC是等边三角形,∴AC=CB,∠A=∠BCD=60°,∴∠CAE=∠BCD=′120°∵AE=CD,∴△ACE≌△CBD,∴∠ACE=∠CBD=∠DCF,∴∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA=60°.故答案为60.(3)如图③中,∵点O是AC边的垂直平分线与BC的交点,∴OC=OA,∴∠EAC=∠DCB=α,∵AC=BC,AE=CD,∴△AEC≌△CDB,∴∠E=∠D,∴∠BFE=∠D+∠DCF=∠E+∠ECA=∠OAC=α.【点睛】本题综合考查了三角形全等以及三角形外角和定理.12.(1)①100;②x=y+s+t;(2)见详解.【解析】【分析】(1)①利用三角形的内角和定理即可解决问题;②结论:x=y+s+t.利用三角形内角和定理即可证明;(2)分6种情形分别求解即可解决问题.【详解】解:(1)①∵∠BAC=70°,∴∠ABC+∠ACB=110°,∵∠PBA=10°,∠PCA=20°,∴∠PBC+∠PCB=80°,∴∠BPC=100°,∴x=100,故答案为:100.②结论:x=y+s+t.理由:∵∠A+∠ABC+∠ACB=∠A+∠PBA+∠PCA+∠PBC+∠PCB=180°,∠PBC+∠PCB+∠BPC=180°,∴∠A+∠PBA+∠PCA=∠BPC,∴x=y+s+t.(2)s、t、x、y之间所有可能的数量关系:如图1:s+x=t+y;如图2:s+y=t+x;如图3:y=x+s+t;如图4:x+y+s+t=360°;如图5:t=s+x+y;如图6:s=t+x+y;【点睛】本题考查三角形的内角和定理,三角形的外角的性质等知识,解题的关键是学会用分类讨论的思想思考问题.13.(1)150°;(2)∠1+∠2=90°+α;(3)∠1=90°+∠2+α,理由详见解析;(4)∠2=90°+∠1-α,理由详见解析【解析】【分析】(1)先用平角的得出,∠CDP=180°-∠1,∠CEP=180°-∠2,最后用四边形的内角和即可;(2)同(1)方法即可;(3)利用平角的定义和三角形的内角和即可得出结论;(4)利用三角形的内角和和外角的性质即可得出结论.【详解】解:(1)∵∠1+∠CDP=180°,∴∠CDP=180°-∠1,同理:∠CEP=180°-∠2,根据四边形的内角和定理得,∠CDP+∠DPE+∠CEP+∠C=360°,∵∠C=90°,∴180°-∠1+α+180°-∠2+90°=360°,∴∠1+∠2=90°+α=90°+60°=150°,故答案为:150;(2)∵∠1+∠CDP=180°,∴∠CDP=180°-∠1,同理:∠CEP=180°-∠2,根据四边形的内角和定理得,∠CDP+∠DPE+∠CEP+∠C=360°,∵∠C=90°,∴180°-∠1+α+180°-∠2+90°=360°,∴∠1+∠2=90°+α,故答案为:∠1+∠2=90°+α;(3)∠1=90°+∠2+∠α.理由如下:如图3,设DP与BE的交点为F,∵∠2+∠α=∠DFE,∠DFE+∠C=∠1,∴∠1=∠C+∠2+∠α=90°+∠2+∠α.(4)∠2=90°+∠1-∠α,理由如下:如图4,设PE 与AC 的交点为G ,∵∠PGD =∠EGC ,∴∠α+180°-∠1=∠C +180°-∠2,∴∠2=90°+∠1-∠α.故答案为∠2=90°+∠1-∠α.【点睛】此题是三角形综合题,主要考查了四边形的内角和,三角形的内角和,三角形的外角的性质,平角的定义,解本题的关键是将∠1,∠2,α转化到一个三角形或四边形中,是一道比较简单的中考常考题.14.(1)【解析】【分析】(1)根据简单的分式可得,相邻两个数的积的倒数等于它们的倒数之差,即可得到和1111n -,-;(2);(3)见解析.45n n +1n +114⨯51n ⨯(n +1)(2)根据(1)规律将乘法写成减法的形式,可以观察出前一项的减数等于后一项的被减数,因此可得它们的和.(3)首先利用(2)的和的结果将左边化简,再利用分式方程的解法求解即可.【详解】111111=-=-,解:(1);n (n +1)n n +14⨯545故答案为1111-,-45n n +111111+-+-+22334+111n -=1-= ;n n +1n +1n +1(2)原式=1-1111-+-+(3)已知等式整理得:x x +1x +1x +2112x -1-=所以,原方程即:,x x +5x (x +5)方程的两边同乘x (x +5),得:x +5﹣x =2x ﹣1,解得:x =3,检验:把x =3代入x (x +5)=24≠0,∴原方程的解为:x =3.【点睛】+112x -1-=x +4x +5x (x +5)本题主要考查学生的归纳总结能力,关键在于根据简单的数的运算寻找规律,是考试的热点.15.(1)见解析;(2)∠ABE -∠CDE =30︒【解析】(1)根据聪聪提供的辅助线作法进行证明,先由平行线的性质得:∠AGC=∠MCD,∠F+∠GAF=90︒,再证明∠MCD=∠BAG,可得结论;(2)根据平行线的性质和三角形的外角性质可得结论.【详解】解:(1)证明:如图2,过A作AG//FM,交CD于G,∴∠AGC=∠MCD,∠F+∠GAF=90︒,FN⊥FM,∴∠F=90︒,∴∠GAF=90︒,∠FAB-∠MCD=90︒,∴∠FAB-∠GAF=∠MCD=∠BAG,∴AB//CD;(2)解:∠ABE-∠CDE=30︒,理由如下:如图3,AB//CD,∴∠BPD=∠ABE,∠BPD=∠CDE+∠BED,∠BED=30︒,∴∠BPD-∠CDE=30︒,∴∠ABE-∠CDE=30︒.。
初二数学全等三角形压轴题

人教版数学八年级上册第十二章全等三角形压轴题训练1.已知,是等腰直角三角形,,点在轴负半轴上,直角顶点在轴上,点在轴左侧.如图,若的坐标是,点的坐标是,求点的坐标;如图,若点的坐标为,与轴交于点,求线段的长;如图,若轴恰好平分,与轴交于点,过点作轴于点,则、、间有怎样的数量关系?并说明理由.2.如图,在平面直角坐标系中,直线分别交轴、轴于、两点,且,满足,且,是常数.直线平分,交轴于点.若的中点为,连接交于,求证:;如图,过点作,垂足为,猜想与间的数量关系,并证明你的猜想;如图,在轴上有一个动点在点的右侧,连接,并作等腰,其中,连接并延长交轴于点,当点在运动时,的长是否发生改变?若改变,请求出它的变化范围;若不变,求出它的长度.3.如图,点,分别在直线,上,,顶点在点右侧的两边分别交线段于,直线于,,,交直线于点.若平分,求证:;已知的平分线与的平分线交于点请把图形补完整,并证明:.4.解答下列问题:如图,,射线在这个角的内部,点、分别在的边、上,且,于点,于点求证:如图,点、分别在的边、上,点、都在内部的射线上,、分别是、的外角已知,且求证:如图,在中,,点在边上,,点、在线段上,若的面积为,求与的面积之和.5.在平面直角坐标系中,直线与两坐标轴分别交于点与点,以为边作直角三角形,并且.如图,若点在第三象限,请构造全等,求出点的坐标;若点不在第三象限,请直接写出所有满足条件的点的坐标;在的条件下,过点作交轴于点,求证:.6.已知,点在上以的速度由点向点运动,同时点在上由点向点运动.它们运动的时间为.如图,,,若点的运动速度与点的运动速度相等,当时,与是否全等,请说明理由,并判断此时线段和线段的位置关系;如图,将图中的“,”为改“”,其他条件不变.设点的运动速度为,是否存在实数,使得与全等?若存在,求出相应的、的值;若不存在,请说明理由.7.如图,点,将一个的角尺的直角顶点放在点处,角尺的两边分别交轴、轴正半轴于,即,求证:平分;作的平分线交于点,过点作轴于,求的值;把角尺绕点旋转时,的值是否会发生变化?若发生变化请说明理由;若不变请求出这个值.8.画,并画的平分线.图图图将一块足够大的三角尺的直角顶点落在射线的任意一点上,并使三角尺的一条直角边与垂直,垂足为点,另一条直角边与交于点如图证明:;把三角尺绕点旋转,三角尺的两条直角边分别交、于点、如图,与相等吗?请直接写出结论:_____填,,;若点在的反向延长线上,其他条件不变如图,与相等吗?若相等请进行证明,若不相等请说明理由.9.如图,,点是的中点,直线于点,点在直线上,直线点以每秒个单位长度的速度,从点沿路径向终点运动,运动时间设为秒.如图,当时,作直线于点,此时与全等吗请说明理由.如图,当点在上时,作于点,于点.是否存在或与全等的时刻若存在,求出的值若不存在,请说明理由.连接,当时,求的长.10.如图,已知在四边形中,,点、分别是边、上的点,连接、、,.直接写出、、三者之间的数量关系____________________;若,猜想线段、、三者之间有怎样的数量关系?并加以证明;如图,若点、分别是、延长线上的点,且,其它条件不变时,猜想线段、、三者之间有怎样的数量关系?并加以证明.11.如图:在四边形中,,,,,分别是,上的点,且探究图中线段,,之间的数量关系。
八上数学几何压轴题30道

八上数学几何压轴题30道当提到数学几何的压轴题,我们通常指的是那些考察学生对几何知识和解题能力的较难题目。
以下是30道八年级数学几何的压轴题示例:1. 计算一个正方形的对角线长度。
2. 证明三角形内角和为180度。
3. 判断一个四边形是否为平行四边形,并解释你的答案。
4. 计算一个圆的周长和面积。
5. 证明垂直平分线定理。
6. 证明等腰三角形的性质。
7. 计算一个梯形的面积。
8. 证明两条平行线被一条横截线所切割,对应角相等。
9. 计算一个正五边形的内角和外角。
10. 证明直角三角形的斜边长度与直角边长度的关系。
11. 解释相似三角形的性质。
12. 计算一个圆锥的体积。
13. 证明圆的直径与周长的关系。
14. 解释正交投影的原理。
15. 证明圆的切线与半径的垂直关系。
16. 计算一个正多边形的内角和外角。
17. 证明平行线的性质。
18. 解释三视图的绘制方法。
19. 计算一个球的表面积和体积。
20. 证明圆柱的体积公式。
21. 解释平行四边形的性质。
22. 计算一个椎体的体积。
23. 证明同位角与内错角的关系。
24. 解释棱台的性质。
25. 计算一个多面体的表面积和体积。
26. 证明圆锥的侧面积公式。
27. 解释圆的切线定理。
28. 计算一个圆环的面积。
29. 证明立体图形的展开图与表面积的关系。
30. 解释圆锥的性质。
以上是30道八年级数学几何的压轴题示例,这些题目涵盖了几何知识的各个方面,旨在考察学生的几何分析和解决问题的能力。
希望这些题目能够帮助你更好地理解数学几何的知识。
北师大版八年级上专题复习:压轴题

初二数学专题训练(1)—压轴题班级: 姓名: 座号:1.已知∠MAN,AC平分∠MAN.(1)在图1中,若∠MAN=120°,∠ABC=∠ADC=90°,求证:AB+AD=AC;(2)在图2中,若∠MAN=120°,∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.2.如图,已知在△ABC中,AB=AC,∠A=120°,DF垂直平分AB交AB于F,交BC于D.求证:BD=1DC2.3.等边△ABC边长为8,D为AB边上一动点,过点D作DE⊥BC于点E,过点E作EF⊥AC于点F.(1)若AD=2,求AF的长;(2)求当AD取何值时,DE=EF.4.已知△ABC为边长为10的等边三角形,D是BC边上一动点:①如图1,点E 在AC 上,且BD=CE,BE 交AD 于F,当D 点滑动时,∠AFE 的大小是否变化?若不变,请求出其度数.②如图2,过点D 作∠ADG=60°与∠ACB 的外角平分线交于G,当点D 在BC 上滑动时,有下列两个结论:①DC+CG 的值为定值;②DG-CD 的值为定值.其中有且只有一个是正确的,请你选择正确的结论加以证明并求出其值.5.如图,在平面直角坐标系中,直线AB 交x 轴于点A(a,0),交y 轴于点B(0,b),且a、b6.如图1,在Rt△ACB 中,∠ACB=90°,∠ABC=30°AC=1点D 为AC 上一动点,连接BD,以BD 为边作等边△BDE,EA 的延长线交BC 的延长线于F,设CD=n,(1)当n=1时,则AF=____________;(2)当0<n<1时,如图2,在BA 上截取BH=AD,连接EH,求证:△AEH 为等边三角形.7.如图,在平面直角坐标系xoy 中,直线AP 交x 轴于点P(p,0),交y 轴于点A(0,a),且a、b 2(p 1)0+=.(1)求直线AP 的解析式;(2)如图1,点P 关于y 轴的对称点为Q,R(0,2),点S 在直线AQ 上,且SR=SA,求直线RS 的解析式和点S 的坐标;(3)如图2,点B(-2,b)为直线AP 上一点,以AB 为斜边作等腰直角三角形ABC,点C 在第一象限,D 为线段OP 上一动点,连接DC,以DC 为直角边,点D 为直角顶点作等腰三角形DCE,EF⊥x 轴,F 为垂足,下列结论:①2DP+EF 的值不变;②AO EF 2DP-的值不变;其中只有一个结论正确,请你选择出正确的结论,并求出其定值.8.如图,点A、C 分别在一个含45°的直角三角板HBE 的两条直角边BH 和BE 上,且BA=BC,过点C 作BE 的垂线CD,过E 点作EF 上AE 交∠DCE 的角平分线于F 点,交HE 于P.(1)试判断△PCE 的形状,并请说明理由;(2)若∠HAE=120°,AB=3,求EF 的长.9.如左图:直线y=kx+4k(k≠0)交x 轴于点A,交y 轴于点C,点M(2,m)为直线AC 上一点,过点M 的直线BD 交x 轴于点B,交y 轴于点D.(1)求OC OA的值(用含有k 的式子表示). (2)若S △BOM =3S △DOM ,且k 为方程(k+7)(k+5)-(k+6)(k+5)=92的根,求直线BD 的解析式. (3)如右图,在(2)的条件下,P 为线段OD 之间的动点(点P 不与点O 和点D 重合),OE 上AP 于E,DF 上AP 于F,下列两个结论:①AE OE DF +中哪一个结论是正确的,并说明理由并求出其值.10.已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点,(1)如图,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形; (2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?证明你的结论.11.两个等腰直角△ABC和等腰直角△DCE如图1摆放,其中D点在AB上,连接BE.(1)则BEAD=_________,∠CBE=________度;(2)当把△DEF绕点C旋转到如图2所示的位置时(D点在BC上),连接AD并延长交BE于点F,连接FC,则BEAD_________,∠CFE=_________度;(3)把△DEC绕点C旋转到如图3所示的位置时,请求出∠CFE的度数__________.。
人教版八年级数学上学期期末压轴精选30题(解析版)

人教版八年级数学上学期期末压轴精选30题考试范围:全册的内容,共30小题. 八年级期中)ABC 中,120,点D9060 90或60 D 90或120【答案】D 【分析】ADC △为直角三角形分两种情况讨论一是当AD BC ⊥时,的度数;二是D 的度数即可.时,AD C ' 为直角三角形,AB AC =120=,30C ∴∠=AD B D AC ''∴∠+∠=综上所述120=︒ 或90故选:D【点睛】本题考查了等腰三角形的性质,三角形外角定义,直角三角形等知识,熟悉掌握有关知识是解题4得到相应的规律,根据规律再进行计算即可.1112x =-+x ,A.6B.7C.8D.9若ABC的三边则ABC.直角三角形.等腰三角形或直角三角形20=,从而可得【详解】解:ABC∆的三边22+-=b c22=,b c是等腰直角三角形.【点睛】本题主要考查等腰直角三角形,非负数性质,解答的关键是对相应的知识的掌握与运用.90C +∠60时,AF ABC S ab =其中正确的个数是(A .0个B .1个C .2个D .3个证得HBO EBO ≌,得到再证得HAO FAO ≌,得到∴BF 是ABC ∠的角平分线,和EBO 中,EBO ,∴()SAS HBO EBO ≌60BOH BOE ∠=∠=︒在HAO和FAO中,HAO FAOAO AOAOH AOF∠=∠=∠=∠,∴()ASAHAO FAO≌AF AH=,AB BH AH BE=+=故②正确;作OH AC⊥于H,OM∴BAC∠和ABC∠的平分线相交于点O,ABCS=③正确.故选:C【点睛】本题主要考查了三角形内角和定理,三角形外角的性质,三角形全等的性质和判定,正确作出辅助线证得HBO EBO≌,得到重庆市第七中学校八年级阶段练习)都用右边的整式减去左边的整式,所得之差写在这两个整式之间,可以产生一个新整式串:这称为第一次操作;将第一次操作后的整式串按上述方式再做一次操作,以此类推.通过下列实际操作,第二次操作后整式串为:x解:第一次操作后的整式串为:x<,329x∴<,即2∴-,3(9)0x即第二次操作后,当|第三次操作后整式串为第四次操作后整式串为3,个,故③的说法错误,不符合题意;第一次操作后所有整式的和为若ABC的边∆的值,作图后由AOD形一边边长大于另两边之差,小于它们之和,即可得中线长m的取值范围.20)===,DO CO ∠=∠, AO BOAOD BOC【答案】36︒##36度个1A BC 中,个12A A D ;在边2A D ,按此方法继续下去,第n 个等腰三角形的底角度数是1n -在1A BC 中,)202︒÷=1DA ,12802=⨯︒,【答案】②④##④②【详解】∠∴90BAC ︒∠=,AB AC =,∴45B C ∠==︒∠,在BED 和△BED △≌△ED FD =;②正确;BED △≌△Rt ABC 中,=90,AB =45,过点过点C 作CF 垂足是ABD ≌△10=ADE S ,=4CEF S 则=24ABC S .【答案】①②③【分析】先根据垂直定义和等角的余角相等证得BAD CAF ∠=∠,B ACF ∠=∠,再利用ASA 可判断①正确;再证明ADE AFE △≌△可判断②正确;利用全等三角形的面积相等可判断③正确;根据全等三角形的性质和三角形的三边关系可判断④错误.【详解】解:在Rt ABC 中,=90BAC ∠,=AB AC ,45B ACB ∴∠=∠=,90BAD DAC ∠+∠=,AF AD ⊥,90CAF DAC ∴∠+∠=︒,BAD CAF ∴∠=∠,CF BC ⊥,9045ACF ACB ∴∠=︒-∠=,则B ACF ∠=∠,在ABD △和ACF △中,BAD CAF AB ACB ACF ∠=∠⎧⎪=⎨⎪∠=∠⎩()ABD ACF ASA ∴≌,故①正确;AD AF ∴=,45DAE ∠=,AF AD ⊥,9045FAE DAE DAE ∴∠=-∠==∠,在ADE 和AFE △中,AD AF DAE FAE AE AE =⎧⎪∠=∠⎨⎪=⎩()ADE AFE SAS ∴≌,∴=DE EF ,故②正确;∴ADE AFE △≌△,ABD ACF ≌△△,ABD ACF SS ∴=,ADE AFE S S =,BD CF =,DE EF =, ABC ABD ADE AEC SS S S ∴=++ ACF ADE AEC S S S =++ADE AFE CEF S S S ++ADE CEF S S +104⨯+24,故③正确;CEF 中,CF CE +BD CE ∴+故④错误,综上,正确的是故答案为:【点睛】本题考查等腰三角形的性质、全等三角形的判定与性质、三角形的三边关系、等角的余角相等等(1)图2中的阴影部分的边长为___________;,在等腰直角ABC 中,是ABC 内一点,连接CE 交于点(1)如图1,求BFC ∠的度数;证得ABD ACE ≅,得出)设AC 交EG 于点H 45AED ACG ︒==∠,推出2BAD CGD α==∠,则BAD ,得出KAG ∠=∠证得AKG ADG ≅,得出180BKG AKG ︒+∠=,得出,得出GB GK DG ==,推出BDG EDF α=∠=,即可得出结论所示:∴AE AD ⊥,∴BAD CAE∠=∠,在ABD△和ACE△中,AB ACBAD CAEAD AE⎧⎪∠∠⎨⎪⎩===,∴(SAS)ABD ACE≅,∴ABD ACF∠=∠,∴AHB FHC∠=∠,∴90BFC BAC︒∠=∠=;(2)设AC交EG于点H,在AB上截取AK AD=,连接KG,如图2所示:∴,90AD AE DAE︒=∠=∴45,AED ACG︒∠==∠∴,AHE GHC∠=∠∴,EAC CGE∠=∠由(1)知:,BAD CAE∠=∠∴,BAD CGD∠=∠设2,BAD a CGD∠==∠∴2,EAC BAD a∠=∠=∴1802,BGD a︒∠=-∴180,BAD BGD︒∠+∠=∴180,ABG ADG︒∠+∠=∴AG平分,BAD∠∴,KAG DAG a∠=∠=在AKG△和ADG△中,,AK ADKAG DAGAG AG=⎧⎪∠=∠⎨⎪=⎩∴(SAS),AKG ADG≅13的解为_____;_____的解为八年级期末)已知,在等边ABC中,(1)如图1,求AFD∠的度数;10AF,求BCD ,从而得到∴ABC 为等边三角形,60C ∠=︒,在ABE 和△中,AB BC ABE BCD BE CD =∠=∠=)SAS ABE △≌△,BAE CBD ∠=∠AFD ∠=∠∴AMB ABM ∠=∠,∴AB AM =,∴AH BD ⊥,∴10MH BH ==,∴51015FM FH HM =+=+=.【点睛】本题考查等边三角形的性质、全等三角形的判定与性质、等腰三角形的性质、含30︒的直角三角形的性质,熟练掌握等边三角形的性质和等腰三角形的性质,证明三角形全等是解题的关键.21.(2022·四川省内江市第二中学八年级期中)阅读材料利用公式法,可以将一些形如()20ax bx c a ++≠的多项式变形为()2a x m n ++的形式,我们把这样的变形方法叫做多项式()20ax bx c a ++≠的配方法,运用多项式的配方法及平方差公式能对一些多项式进行因式分解例如245x x +-2224225x x =++--()()()()()229232351x x x x x =+-=+++-=+- 根据以上材料,解答下列问题.(1)分解因式(利用公式法):228x x +-;(2)已知ABC 的三边长a ,b ,c ,且满足221012610a b a b +--+=,求ABC 的最大边c 的取值范围.(3)已知2261P x y x =-+-,22413Q x y =++,试比较P ,Q 的大小.【答案】(1)()()42x x +-(2)611c ≤<(3)P Q <【分析】(1)仿照题意进行求解即可;(2)利用完全平方公式将所给式子变形为()()22560a b -+-=进而求出a 、b 的值,再根据三角形三边的关系求解即可;(3)利用作差法求出()()2232P Q x y -=---+,据此即可得到答案.【详解】(1)解:228x x +- 2222118x x =++--()219x =+- ()()1313x x =+++-()()42x x =+-;(2)解:∴221012610a b a b +--+=,∴22221051260a a b b -++-+=,∴()()22560a b -+-=,∴()()225060a b -≥-≥,,∴()()22560a b -=-=,∴5060a b -=-=,,∴56a b ==,,∴b a c a b -<<+,∴111c <<,∴c 是最大边,∴611c ≤<;(3)解:∴2261P x y x =-+-,22413Q x y =++,∴222612413P Q x y x x y -=-+----,226414x x y y =-+---2269441x x y y =-+----- ()()22321x y =---+-, ∴()()223020x y -≥+≥,,∴()()22320x y ---+≤,()()223210x y ---+-< ∴0P Q -<,∴P Q <.【点睛】本题主要考查了因式分解的应用,三角形三边的关系,平方的非负性,熟知完全平方公式是解题的关键.22.(2022·福建·莆田锦江中学八年级期中)如图,AB AD ⊥,且AB AD =,AC AE ⊥,且AC AE =(1)如图1,连接DC 、BE ,求证:DC BE =;(2)如图2,求证:ABC ADE S S ∆∆=(3)如图3,GF 经过A 点与DE 交于G 点,且GF BC ⊥于F 点.求证:G 为DE 的中点.【答案】(1)见解析;(2)见解析;(3)见解析.【分析】(1)根据垂直可得90BAE CAE ==︒∠∠,得出DAC BAE ∠=∠,根据全等三角形的判定证明DAC BAE ≅,可得答案;(2)作EM AD ⊥交DA 的延长线于M ,作CN AB ⊥,进而可得CAN MAE =∠∠,根据全等三角形的判定证明ACN AEM ≅,进而得出CN EM =,根据三角形的面积公式可得;(3)作DM AG ⊥交AG 的延长线于M ,作EN AG ⊥,先证明C NAE =∠∠,再证FCA NAE ≅,得出AF NE =;再证明BAF ADM ≅,得出AF DM =,进而得出DM NE =,再证明DMG ENG ≅,即可得出答案.【详解】(1)∴AB AD ⊥,AC AE ⊥,∴90BAE CAE ==︒∠∠∴BAD BAC BAC CAE +=+∠∠∠∠∴DAC BAE ∠=∠在DAC △和BAE 中,AD AB DAC BAE AC AE =⎧⎪∠=∠⎨⎪=⎩∴DAC BAE ≅∴DC BE =(2)作EM AD ⊥交DA 的延长线于M ,作CN AB ⊥∴90EMD CNA ==︒∠∠∴90MAN CAE ==︒∠∠∴MAN CAM CAE CAM -=-∠∠∠∠∴CAN MAE =∠∠在ACN △和AEM △中,∴ACN AEM ≅CN EM =AB AD =,1122AB CN AD ⨯⨯=⨯ABC ADE S S ∆∆=(3)作DM AG ⊥交AG 的延长线于M ,作EN AG ⊥在CAF 和NEA 中,90CFA ENA C NAE AC AE ∠=∠=︒∠=∠=∴FCA NAE ≅∴AF NE =BAF B BAF +=∠∠∠B DAM ∠=∠在BAF △和ADM △90BFA DMA B DAM ∠=∠=⎧⎪∠=∠⎨∴BAF ADM ≅AF DM =DM NE =在DMG 和ENG △中,DMG ENG DGM NGE DM NE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴DMG ENG ≅∴DG EG =∴G 为DE 的中点.【点睛】本题考查全等三角形的判定与性质,直角三角形的两个锐角互余,正确作辅助线证明三角形全等是解题的关键.23.(2022·山东淄博·八年级期中)阅读下列材料:常用的分解因式方法有提公因式、公式法等.但有的多项式只用上述方法就无法分解,如22424x y x y -+-,细心观察这个式子会发现前两项符合平方差公式,后两项可提取公因式,分解过程为:22424x y x y -+-()()22424x y x y =-+-分组()()()2222x y x y x y =-++-组内分解因式 ()()222x y x y =-++整体思想提公因式这种分解因式的方法叫分组分解法,利用这种方法解决下列问题:(1)分解因式:22993x x y y -+-;(2)已知ABC 的三边a b c 、、满足220a b ac bc --+=,判断ABC 的形状并说明理由.【答案】(1)()()x y x y -+-333(2)ABC 为等腰三角形;理由见解析【分析】(1)先用平方差公式与提公因式法分组分解,然后根据整体思想提公因式即可;(2)将220a b ac bc --+=通过因式分解化为()()0a b a b c -+-=;由三角形的三边关系可知0a b c +->;所以0a b -=,即a b =,从而得出结论;【详解】(1)解:22993x x y y -+-()()22993x y x y =---()()()3333x y x y x y =-+--()()333x y x y =-+-(2)解:依据分组分解法,得()()220a b ac bc ---=()()()0a b a b c a b -+--=()()0a b a b c -+-=根据三角形三边关系,易得0a b c +->∴0a b -=∴a b =∴ABC 为等腰三角形【点睛】本题考查了因式分解、等腰三角形的判定;熟练掌握因式分解的方法是解题的关键. 24.(2022·浙江·八年级专题练习)(1)阅读理解:如图1,在ABC 中,若10AB =,6AC =.求BC 边上的中线AD 的取值范围.解决此问题可以用如下方法:延长AD 到点E ,使DE AD =,再连接BE (或将ACD 绕着点D 逆时针旋转180︒得到EBD △),把AB ,AC ,2AD 集中在ABE 中,利用三角形三边的关系即可判断中线AD 的取值范围是______;(2)问题解决:如图2,在ABC 中,D 是BC 边上的中点,DE DF ⊥于点D ,DE 交AB 于点E ,DF 交AC 于点F ,连接EF ,求证:BE CF EF +>;(3)问题拓展:如图3,在四边形ABCD 中,180B D ∠+∠=︒,CB CD =,140BCD ∠=︒,以C 为顶点作一个70︒角,角的两边分别交AB ,AD 于E ,F 两点,连接EF ,探索线段BE ,DF ,EF 之间的数量关系,并加以证明.【答案】(1)28AD <<;(2)见解析;(3)BE DF EF +=,证明见解析【分析】(1)延长AD 至E ,使DE AD =,连接BE ,证明SAS BDE CDA ≌(),根据三角形三边关系即可求解;(2)延长FD 至点M ,使DM DF =,连接BM ,EM ,同(1)得,(SAS)BMD CFD ∆≌,证明(SAS)EDM EDF ≌在BME ∆中,由三角形的三边关系得BE BM EM +>,即可得证;(3)延长AB 至点N ,使BN DF =,连接CN ,证明(SAS)NBC FDC ≌,(SAS)NCE FCE ≌,根据求的三角形的性质即可得证.【详解】(1)解:延长AD 至E ,使DE AD =,连接BE ,如图①所示:∴AD 是BC 边上的中线,∴BD CD =,在BDE △和CDA 中,BD CD BDE CDA DE AD =⎧⎪∠=∠⎨⎪=⎩∴SAS BDE CDA ≌(), ∴6BE AC ==,在ABE 中,由三角形的三边关系得:AB BE AE AB BE -<<+,∴106106AE -<<+,即416AE <<,∴28AD <<;故答案为:28AD <<;(2)证明:延长FD 至点M ,使DM DF =,连接BM ,EM ,如图所示同(1)得,(SAS)BMD CFD ∆≌,BM CF ∴=DE DF ⊥,DM DF =,DE DE =(SAS)EDM EDF ∴≌,EM EF ∴=在BME ∆中,由三角形的三边关系得BE BM EM +>,BE CF EF ∴+>(3)BE DF EF +=证明如下:延长AB 至点N ,使BN DF =,连接CN ,如图所示180ABC D ∠+∠=︒,180NBC ABC ∠+∠=︒NBC D ∴∠=∠在NBC 和FDC △中,BN DF NBC D BC DC =⎧⎪∠=∠⎨⎪=⎩,(SAS)NBC FDC ∴≌CN CF ∴=,NCB FCD ∠=∠140BCD ∠=︒,70ECF ∠=︒70BCE FCD ∴∠+∠=︒,70ECN ECF ∴∠=︒=∠(SAS)NCE FCE∴≌EN EF∴=.BE BN EN+=,BE DF EF∴+=【点睛】本题考查全等三角形的判定及性质、三角形三边关系、角的和差等,解答此题的关键是作出辅助对于任意2x与一个分式51x的和的形式.拆分成一个整式与一个分式(分子为整数)的和的形式;的值为整数,直接写出满足条件的整数对于任意整数(1)(2)证明:90ABC =QEA =∠=BAP APB ∠+∠中,证明:ΔPAB ≅,ACB ∆为等腰三角形,AB CB ∴=,QE CB ∴=,在ΔQEM CBM ∆中,QME QEM QE CB ∠=⎧⎪∠=⎨⎪=⎩QA AP ⊥,HA AC ⊥,AP PD ⊥,QAH ∴∠QAH ∴∠PAQ ∆为等腰直角三角形,AQ AP ∴=在AQH ∆和AQH AQ APQAH ∠⎧⎪=⎨⎪∠⎩HA AC ⊥HAF ∴∠在AHF ∆AH AD HAF AF AF =⎧⎪∠=⎨⎪=⎩ΔAHF ∴≌m n 的正方形.(1)请用两种不同的方法求图2中阴影部分的面积.【点睛】本题主要考查完全平方差公式和完全平方和公式的联系,会用代数式表示图形面积是解决问题的关键;两数的完全平方和比它们的完全平方差多了两数积的4倍,该结论经常用到.28.(2022·广东·江门市新会尚雅学校八年级阶段练习)(1)如图1,已知,在ABC 中,10AB AC ==,BD 平分ABC ∠,CD 平分ACB ∠,过点D 作EF BC ∥,分别交AB 、AC 于E 、F 两点,则图中共有________个等腰三角形:EF 与BE 、CF 之间的数量关系是________,AEF △的周长是________.(2)如图2,若将(1)中“ABC 中,10AB AC ==”改为“若ABC 为不等边三角形,8AB =,10AC =”其余条件不变,则图中共有________个等腰三角形;EF 与BE 、CF 之间的数量关系是什么?证明你的结论,并求出AEF △的周长.(3)已知:如图3,D 在ABC 外,AB AC >,且BD 平分ABC ∠,CD 平分ABC 的外角ACG ∠,过点D 作DE BC ∥,分别交AB 、AC 于E 、F 两点,则EF 与BE 、CF 之间又有何数量关系呢?写出结论并证明.【答案】(1)5,EF BE CF =+,20(2)2,EF BE CF =+,证明见详解,18(3)EF BE CF =-,证明见详解【分析】(1)根据角平分线的定义可得,EBD CBD FCD BCD ∠=∠∠=∠,再根据平行线的性质,“两直线平行,同位角相等”、“两直线平行,内错角相等”可知DB DC =,AEF ABC AFE ACB ∠=∠∠=∠,,EDB CBD FDC BCD ∠=∠∠=∠,即可求出AEF AFE ∠=∠,,EBD EDB FDC FCD ∠=∠∠=∠,根据“等角对等边”可知,,BE DE CF DF AE AF ===,即可确定等腰三角形的数量,EF 与BE 、CF 之间的数量关系以及AEF △的周长;(2)若ABC 为不等边三角形,根据角平分线的定义可知,EBD CBD FCD BCD ∠=∠∠=∠,再结合平线性的性质“两直线平行,内错角相等”可知,EDB CBD FDC BCD ∠=∠∠=∠,即可推导,EBD EDB FDC FCD ∠=∠∠=∠,然后根据“等角对等边”即可证明,BE DE CF DF ==,然后解答即可;(3)根据角平分线的定义可知,EBD CBD FCD GCD ∠=∠∠=∠,再结合平线性的性质“两直线平行,内错角相等”可知,EDB CBD FDC GCD ∠=∠∠=∠,即可推导,EBD EDB FDC FCD ∠=∠∠=∠,然后根据“等角对等边”即可证明,BE DE CF DF ==,即可证明EF 与BE 、CF 之间的数量关系.【详解】解:(1)∴AB AC =,∴A ABC CB =∠∠,∴BD 平分ABC ∠,CD 平分ACB ∠,∴,EBD CBD FCD BCD ∠=∠∠=∠,∴DBC DCB ∠=∠,∴DB DC =,∴EF BC ∥,∴,AEF ABC AFE ACB ∠=∠∠=∠,,EDB CBD FDC BCD ∠=∠∠=∠,∴AEF AFE ∠=∠,,EBD EDB FDC FCD ∠=∠∠=∠,∴,,BE DE CF DF AE AF ===,∴等腰三角形有,,,,ABC AEF DEB DFC DBC ,共计5个,∴EF DE DF BE CF =+=+,即EF BE CF =+,∴AEF △的周长AE EF AF =++AE DE DF AF =+++AE BE CF AF =+++AB AC =+1010=+20=,故答案为:5,EF BE CF =+,20;(2)若ABC 为不等边三角形,∴BD 平分ABC ∠,CD 平分ACB ∠,∴,EBD CBD FCD BCD ∠=∠∠=∠,∴EF BC ∥,∴,EDB CBD FDC BCD ∠=∠∠=∠,∴,EBD EDB FDC FCD ∠=∠∠=∠,∴,BE DE CF DF ==,∴等腰三角形有,DEB DFC ,共计2个,故答案为:2;∴,BE DE CF DF ==,∴EF DE DF BE CF =+=+,即EF BE CF =+;∴AEF △的周长AE EF AF =++AE DE DF AF =+++AE BE CF AF =+++AB AC =+810=+18=;(3)EF 与BE 、CF 之间的数量关系为:EF BE CF =-,证明:∴BD 平分ABC ∠,CD 平分ACG ∠,∴,EBD CBD FCD GCD ∠=∠∠=∠,∴EF BC ∥,∴,EDB CBD FDC GCD ∠=∠∠=∠,∴,EBD EDB FDC FCD ∠=∠∠=∠,∴,BE DE CF DF ==,∴EF DE DF BE CF =-=-,即EF 与BE 、CF 之间的数量关系为EF BE CF =-.【点睛】本题主要考查了等腰三角形的判定与性质、平行线的性质、角平分线的定义等知识,熟练掌握等腰三角形的判定与性质是解题关键.29.(2022·重庆市第一一〇中学校九年级开学考试)“数形结合百般好”.在代数式的学习过程中我们可以结合图形理解相关公式的产生,如图1所示的正方形,我们可以利用两种不同的方法计算它的面积,从而得到完全平方公式:()222+2a b a ab b +=+.请结合以上知识,解答下列问题:(1)写出图2所示的长方形所表示的数学等式 ;(2)根据图3得到的结论,解决下列问题:若8a b c ++=,19ab ac bc ++=,求代数式222a b c ++的值;(3)小明同学用图4中x 张边长为a 的正方形纸片,y 张边长为b 的正方形纸片,z 张边长分别为a ,b 的长方形纸片拼出一个面积为()()2365a b a b ++的长方形,求代数式x y z ++的值.【答案】(1)()()22232a b a b a ab b ++=++(2)26(3)55【分析】(1)根据表示图形面积的两种方法即可得到答案;(2)由题意得到大正方形的面积=()2a b c ++,各个小图形面积之和=222222a b c ab ac bc +++++,利用面积相等和已知条件即可求解;(3)大长方形的面积为()()222365122815a b a b a ab b ++=++,小图形的面积分别为22,,a b ab ,进一步即可得到答案. 【详解】(1)拼成的大长方形面积之和()()2a b a b =++,各个小图形面积之和2232a ab b =++,∴图2所表示的数学等式是()()22232a b a b a ab b ++=++.故答案为:()()22232a b a b a ab b ++=++.(2)图(3)中大正方形的面积=()2a b c ++,各个小图形面积之和=222222a b c ab ac bc +++++,∴()2222222a b c a b c ab ac bc ++=+++++.∴8a b c ++=,19ab ac bc ++=.∴()222222228a b c a b c ab ac bc ++=+++++=,即()222264a b c ab ac bc +++++=,∴()2226426421926a b c ab ac bc ++=-++=-⨯=.(3)大长方形的面积为:()()2222236512101815122815a b a b a ab ab b a ab b ++=+++=++, ∴小图形的面积分别为22,,a b ab ,∴12,15,28x y z ===.∴12152855x y z ++=++=.【点睛】本题考查多项式乘多项式的计算,整体代入思想,数形结合思想,能够通过几何图形找到代数之间的等量关系是解决此类题型的关键.30.(2022·全国·八年级专题练习)认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.(1)探究1:如图1,在ABC 中,O 是ABC ∠与ACB ∠的平分线BO 和CO 的交点,试分析BOC ∠与A ∠有怎样的关系?请说明理由.(2)探究2:如图2中,O 是ABC ∠与外角ACD ∠的平分线BO 和CO 的交点,试分析BOC ∠与A ∠有怎样的关系?请说明理由.(3)探究3:如图3中,O 是外角DBC ∠与外角ECB ∠的平分线BO 和CO 的交点,则BOC ∠与A ∠有怎样的关系?(直接写出结论)∴BO 和CO 分别是ABC ∠和ACD ∠的角平分线,是ABC 的一个外角,(12ACD A =∠是BOC 的一个外角,1212BOC =∠-∠=∠12BOC A =∠; )解:∴O 是外角1OBC CBD =∠在BOC 中,180BOC =(11802-∠︒(11801802︒-1在BOC 中,5)解:∴BCD CDE ∠+∠CP DP ,分别平分PCD PDC ∠+∠在PCD 中,()()1801801808595CPD PCD PDC PCD PDC ︒︒︒︒︒∠=-∠+∠=-∠+∠=-=.【点睛】本题主要考查了三角形外角的性质与三角形内角和定理,多边形内角和定理,熟练掌握三角形外角的性质与三角形内角和定理,多边形内角和定理,利用类比思想解答是解题的关键.。
人教版八年级数学上册期末专题复习:几何压轴题强化训练试题(含答案)

人教版八年级数学上册期末专题复习:几何压轴题强化训练试题1、如图,AB>AC,∠BAC的平分线与BC边的中垂线GD相交于点D,过点D作DE⊥AB于点E,DF⊥AC于点F,求证:BE=CF.2、如图,△ABC中,∠ACB=90°,AC=BC,将△ABC绕点C逆时针旋转角α.(0°<α<90°)得到△A1B1C1,连接BB1.设CB1交AB于D,A1B1分别交AB、AC于E、F.(1)在图中不再添加其它任何线段的情况下,请你找出一对全等的三角形,并加以说明(△ABC与△A1B1C1全等除外);(2)当△BB1D是等腰三角形时,求α.3、如图,在△ABC中,∠BAC=120°,AD,BE分别为△ABC的角平分线,连结DE.(1)求证:点E到DA,DC的距离相等;(2)求∠DEB的度数.4、在△ABC中,∠ACB=90°,AC=BC,直线,MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.(1)当直线MN绕点C旋转到如图1的位置时,求证:DE=AD+BE;(2)当直线MN绕点C旋转到如图2的位置时,求证:DE=AD﹣BE;(3)当直线MN绕点C旋转到如图3的位置时,线段DE、AD、BE之间又有什么样的数量关系?请你直接写出这个数量关系,不要证明.5、概念学习:规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.理解概念(1)如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB,请写出图中两对“等角三角形”.概念应用(2)如图2,在△ABC中,CD为角平分线,∠A=40°,∠B=60°.求证:CD为△ABC的等角分割线.(3)在△ABC中,∠A=42°,CD是△ABC的等角分割线,直接写出∠ACB的度数.6、如图,∠ABC=∠BAD=90°,点E,F分别是AC,BC的中点。
人教版八年级数学上册期中考试压轴题专题复习题(含答案)

人教版八年级数学上册期中考试压轴题专题复习题1、在△ABC中,AB=BC,△ABC≌△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点,观察并猜想线段EA1与FC有怎样的数量关系?并证明你的结论.2、两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.求证:(1)△ABE≌△ACD;(2)DC⊥BE.3、如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.(1)若∠C=40°,求∠BAD的度数;(2)若AC=5,DC=4,求△ABC的周长.4、如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;(2)若B、C在DE的两侧(如图所示),其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.5、如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.(1)求∠CBE的度数;(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.6、如图,△ABC为等腰直角三角形,点D是边BC上一动点,以AD为直角边作等腰直角△ADE,分别过A、E点向BC边作垂线,垂足分别为F、G.连接BE.(1)证明:BG=FD;(2)求∠ABE的度数.7、如图,正方形ABCD的对角线交于点O,点E、F分别在AB、BC上(AE<BE),且∠EOF=90°,OE、DA的延长线交于点M,OF、AB的延长线交于点N,连接MN.(1)求证:OM=ON.(2)若正方形ABCD的边长为4,E为OM的中点,求MN的长.8、如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.(1)点D在边AB上时,证明:AB=FA+BD;(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请画出图形并直接写出正确结论.9、如图,△ABC中,∠ACB=90°,AC=BC,将△ABC绕点C逆时针旋转角α.(0°<α<90°)得到△A1B1C1,连接BB1.设CB1交AB于D,A1B1分别交AB、AC于E、F.(1)在图中不再添加其它任何线段的情况下,请你找出一对全等的三角形,并加以说明(△ABC 与△A1B1C1全等除外);(2)当△BB1D是等腰三角形时,求α.10、CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:①如图1,若∠BCA=90°,∠α=90°,则BE CF;(填“>”,“<”或“=”);EF,BE,AF三条线段的数量关系是:.②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件,使①中的两个结论仍然成立,并证明两个结论成立.(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想并证明.11、在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧..作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.(1)如图1,当点D在线段BC上,如果∠BAC=90º,则∠BCE= º.(2)设∠BAC=α,∠BCE=β.①如图2,当点D在线段BC上移动,则α、β之间有怎样的数量关系?请说明理由;②当点D在直线BC上移动,则α、β之间有怎样的数量关系?请画出图形,并直接写出你的结论.12、在△ABC中,∠C>∠B,AE平分∠BAC,F为射线AE上一点(不与点E重合),且FD⊥BC 于D;(1)如果点F与点A重合,且∠C=50°,∠B=30°,如图1,求∠EFD的度数;(2)如果点F在线段AE上(不与点A重合),如图2,问∠EFD与∠C﹣∠B有怎样的数量关系?并说明理由.(3)如果点F在△ABC外部,如图3,此时∠EFD与∠C﹣∠B的数量关系是否会发生变化?请说明理由.13、如图,△ABC是等边三角形,AB=6,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.(1)当∠BQD=30°时,求AP的长;(2)证明:在运动过程中,点D是线段PQ的中点;(3)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.14、问题背景:如图1:在四边形ABC 中,AB=AD,∠BAD=120∘,∠B=∠ADC=90∘.E,F 分别是BC,CD 上的点。
八年级数学上册期末压轴100题:第十一章20题(含答案)

6.①③④
【分析】
利用高线和同角的余角相等,三角形内角和定理即可证明①,再利用等量代换即可得到③
④均是正确的,②缺少条件无法证明.
【详解】
(1)求∠E的度数.
(2)点P为直线AC上的一个动点,过点P作PF∥AE,且PF=AE,连DF.
①如图2,当点P在点C的右侧,且∠PFD=25°时,判断DE与DF的位置关系,并说明理由.
②在整个运动中,是否存在点P,使得∠PFD=2∠EDF?若存在,请求出∠PFD的度数,若不存在,请说明理由.
18.如图1,点E是直线AB,CD内部一点,AB//CD,连接EA,ED.
8.31
【分析】
直线a,b交于点A,与边框的交点分别为B,C,由对顶角的性质可求解∠ABC和∠ACB的度数,再根据三角形的内角和定理可求解.
【详解】
解:直线a,b∠交于点A,与边框的交点分别为B,C,如图,
∵∠1=71°,∠2=78°,
∴∠ABC=∠1=71°,∠ACB=∠2=78°,
∵∠A+∠ABC+∠ACB=180°,
(4)如图(4),直线 平分 的外角 , 平分 的外角 ,猜想 与 、 的数量关系是________.
13.同学们以“一块直角三角板和一把直尺”开展数学活动,提出了很多数学问题,请你解答:
(1)如图1,∠α和∠β具有怎样的数量关系?请说明理由;
(2)如图2,∠DFC的平分线与∠EGC的平分线相交于点Q,求∠FQG的大小;
(3)如图3,若将(2)中的“点E在射线OC上”改为“点E在射线OD上”,其他条件不变,直接写出∠EGF的度数(用含有a的代数式表示)
八年级上册上海数学压轴题 期末复习试卷测试卷(解析版)
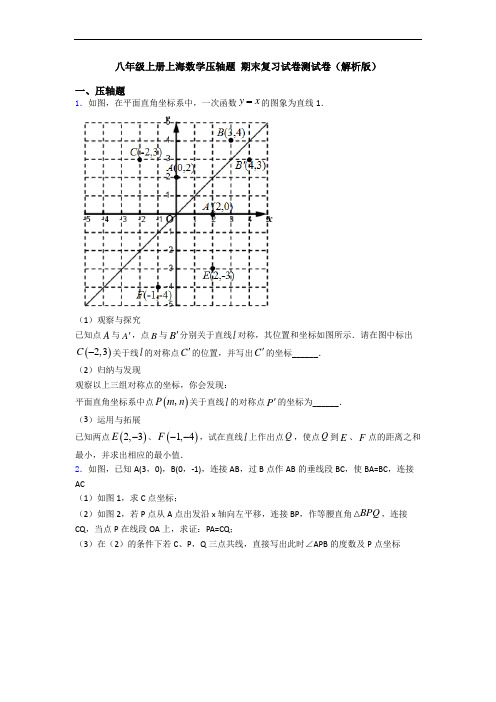
八年级上册上海数学压轴题 期末复习试卷测试卷(解析版)一、压轴题1.如图,在平面直角坐标系中,一次函数y x =的图象为直线1.(1)观察与探究已知点A 与A ',点B 与B '分别关于直线l 对称,其位置和坐标如图所示.请在图中标出()2,3C -关于线l 的对称点C '的位置,并写出C '的坐标______.(2)归纳与发现观察以上三组对称点的坐标,你会发现:平面直角坐标系中点()P m n ,关于直线l 的对称点P '的坐标为______. (3)运用与拓展已知两点()2,3E -、()1,4F --,试在直线l 上作出点Q ,使点Q 到E 、F 点的距离之和最小,并求出相应的最小值.2.如图,已知A(3,0),B(0,-1),连接AB ,过B 点作AB 的垂线段BC ,使BA=BC ,连接AC(1)如图1,求C 点坐标;(2)如图2,若P 点从A 点出发沿x 轴向左平移,连接BP ,作等腰直角BPQ ,连接CQ ,当点P 在线段OA 上,求证:PA=CQ ;(3)在(2)的条件下若C 、P ,Q 三点共线,直接写出此时∠APB 的度数及P 点坐标3.如图①,在ABC ∆中,12AB =cm ,20BC =cm ,过点C 作射线//CD AB .点M 从点B 出发,以3 cm/s 的速度沿BC 匀速移动;点N 从点C 出发,以a cm/s 的速度沿CD 匀速移动.点M 、N 同时出发,当点M 到达点C 时,点M 、N 同时停止移动.连接AM 、MN ,设移动时间为t (s).(1)点M 、N 从移动开始到停止,所用时间为 s ; (2)当ABM ∆与MCN ∆全等时,①若点M 、N 的移动速度相同,求t 的值; ②若点M 、N 的移动速度不同,求a 的值;(3)如图②,当点M 、N 开始移动时,点P 同时从点A 出发,以2 cm/s 的速度沿AB 向点B 匀速移动,到达点B 后立刻以原速度沿BA 返回.当点M 到达点C 时,点M 、N 、P 同时停止移动.在移动的过程中,是否存在PBM ∆与MCN ∆全等的情形?若存在,求出t 的值;若不存在,说明理由.4.已知在△ABC 中,AB =AC ,∠BAC =α,直线l 经过点A (不经过点B 或点C ),点C 关于直线l 的对称点为点D ,连接BD ,CD .(1)如图1,①求证:点B ,C ,D 在以点A 为圆心,AB 为半径的圆上; ②直接写出∠BDC 的度数(用含α的式子表示)为 ;(2)如图2,当α=60°时,过点D 作BD 的垂线与直线l 交于点E ,求证:AE =BD ; (3)如图3,当α=90°时,记直线l 与CD 的交点为F ,连接BF .将直线l 绕点A 旋转的过程中,在什么情况下线段BF 的长取得最大值?若AC =22a ,试写出此时BF 的值. 5.如图1,矩形OACB 的顶点A 、B 分别在x 轴与y 轴上,且点()6,10C ,点()0,2D ,点P 为矩形AC 、CB 两边上的一个点.(1)当点P 与C 重合时,求直线DP 的函数解析式;(2)如图②,当P 在BC 边上,将矩形沿着OP 折叠,点B 对应点B '恰落在AC 边上,求此时点P 的坐标.(3)是否存P 在使BDP ∆为等腰三角形?若存在,直接写出点P 的坐标;若不存在,请说明理由. 6.(1)填空①把一张长方形的纸片按如图①所示的方式折叠,EM ,FM 为折痕,折叠后的C 点落在1B M 或1B M 的延长线上,那么EMF ∠的度数是________;②把一张长方形的纸片按如图②所示的方式折叠,B 点与M 点重合,EM ,FM 为折痕,折叠后的C 点落在1A M 或1A M 的延长线上,那么EMF ∠的度数是_______. (2)解答:①把一张长方形的纸片按如图③所示的方式折叠,EM ,FM 为折痕,折叠后的C 点落在1B M 或1B M 的延长线上左侧,且80EMF ∠=︒,求11C MB ∠的度数; ②把一张长方形的纸片按如图④所示的方式折叠,B 点与M 点重合,EM ,FM 为折痕,折叠后的C 点落在1A M 或1A M 的延长线右侧,且60EMF ∠=︒,求11C MA ∠的度数.(3)探究:把一张四边形的纸片按如图⑤所示的方式折叠,EB ,FB 为折痕,设ABC α∠=︒,EBF β∠=︒,11A BC γ∠=︒,求α,β,γ之间的数量关系.7.定义:在平面直角坐标系中,对于任意两点A (a ,b ),B (c ,d ),若点T (x ,y )满足x =3+a c ,y =3+b d,那么称点T 是点A 和B 的融合点.例如:M (﹣1,8),N (4,﹣2),则点T (1,2)是点M 和N 的融合点.如图,已知点D (3,0),点E 是直线y =x +2上任意一点,点T (x ,y )是点D 和E 的融合点.(1)若点E 的纵坐标是6,则点T 的坐标为 ; (2)求点T (x ,y )的纵坐标y 与横坐标x 的函数关系式:(3)若直线ET 交x 轴于点H ,当△DTH 为直角三角形时,求点E 的坐标.8.如图1,在等边△ABC 中,E 、D 两点分别在边AB 、BC 上,BE =CD ,AD 、CE 相交于点F .(1)求∠AFE 的度数;(2)过点A 作AH ⊥CE 于H ,求证:2FH +FD =CE ;(3)如图2,延长CE 至点P ,连接BP ,∠BPC =30°,且CF =29CP ,求PFAF的值. (提示:可以过点A 作∠KAF =60°,AK 交PC 于点K ,连接KB )9.如图,已知直线l 1:y 1=2x +1与坐标轴交于A 、C 两点,直线l 2:y 2=﹣x ﹣2与坐标轴交于B 、D 两点,两直线的交点为P 点. (1)求P 点的坐标; (2)求△APB 的面积;(3)x 轴上存在点T ,使得S △ATP =S △APB ,求出此时点T 的坐标.10.在ABC 中,AB AC =,D 是直线AB 上一点,E 在直线BC 上,且DE DC =. (1)如图1,当D 在AB 上,E 在CB 延长线上时,求证:EDB ACD ∠=∠; (2)如图2,当ABC 为等边三角形时,D 是BA 的延长线上一点,E 在BC 上时,作//EF AC ,求证:BE AD =;(3)在(2)的条件下,ABC ∠的平分线BF 交CD 于点F ,连AF ,过A 点作AH CD ⊥于点H ,当30EDC ∠=︒,6CF =时,求DH 的长度.11.在《经典几何图形的研究与变式》一课中,庞老师出示了一个问题:“如图1,等腰直角三角形的三个顶点分别落在三条等距的平行线1l ,2l ,3l 上,90BAC ∠=︒,且每两条平行线之间的距离为1,求AB 的长度”.在研究这道题的解法和变式的过程中,同学们提出了很多想法:(1)小明说:我只需要过B 、C 向1l 作垂线,就能利用全等三角形的知识求出AB 的长. (2)小林说:“我们可以改变ABC 的形状.如图2,AB AC =,120BAC ∠=︒,且每两条平行线之间的距离为1,求AB 的长.”(3)小谢说:“我们除了改变ABC 的形状,还能改变平行线之间的距离.如图3,等边三角形ABC 三个顶点分别落在三条平行线1l ,2l ,3l 上,且1l 与2l 之间的距离为1,2l 与3l 之间的距离为2,求AB 的长、”请你根据3位同学的提示,分别求出三种情况下AB 的长度.12.在Rt ABC 中,90ACB ∠=︒,30A ∠=︒,BD 是ABC 的角平分线,DE AB ⊥于点E .(1)如图1,连接EC ,求证:EBC 是等边三角形;(2)如图2,点M 是线段CD 上的一点(不与点,C D 重合),以BM 为一边,在BM 下方作60BMG ∠=︒,MG 交DE 延长线于点G .求证:AD DG MD =+;(3)如图3,点N 是线段AD 上的点,以BN 为一边,在BN 的下方作60BNG ∠=︒,NG 交DE 延长线于点G .直接写出ND ,DG 与AD 数量之间的关系.【参考答案】***试卷处理标记,请不要删除一、压轴题1.(1) (3,-2);(2) (n ,m );(3)图见解析, 点Q 到E 、F 点的距离之和最小值为10【解析】 【分析】(1)根据题意和图形可以写出C '的坐标;(2)根据图形可以直接写出点P 关于直线l 的对称点的坐标;(3)作点E 关于直线l 的对称点E ',连接E 'F ,根据最短路径问题解答. 【详解】(1)如图,C '的坐标为(3,-2), 故答案为(3,-2);(2)平面直角坐标系中点()P m n ,关于直线l 的对称点P '的坐标为(n ,m ), 故答案为(n ,m );(3)点E 关于直线l 的对称点为E '(-3,2),连接E 'F 角直线l 于一点即为点Q ,此时点Q 到E 、F 点的距离之和最小,即为线段E 'F ,∵E 'F ()[]221(3)2(4)210=---+--=⎡⎤⎣⎦, ∴点Q 到E 、F 点的距离之和最小值为210.【点睛】此题考查轴对称的知识,画关于直线的对称点,最短路径问题,勾股定理关键是找到点的对称点,由此解决问题.2.(1)(1,-4);(2)证明见解析;(3)()135,1,0APB P ︒∠=【解析】 【分析】(1)作CH ⊥y 轴于H ,证明△ABO ≌△BCH ,根据全等三角形的性质得到BH=OA=3,CH=OB=1,求出OH ,得到C 点坐标;(2)证明△PBA ≌△QBC ,根据全等三角形的性质得到PA=CQ ;(3)根据C 、P ,Q 三点共线,得到∠BQC=135°,根据全等三角形的性质得到∠BPA=∠BQC=135°,根据等腰三角形的性质求出OP ,得到P 点坐标. 【详解】解:(1)作CH ⊥y 轴于H , 则∠BCH+∠CBH=90°, 因为AB BC ⊥, 所以.∠ABO+∠CBH=90°, 所以∠ABO=∠BCH , 在△ABO 和△BCH 中,ABO BCH AOB BHC AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩ABO BCH ∴∆≅∆:BH=OA=3,CH=OB=1, :OH=OB+BH=4,所以C 点的坐标为(1,-4); (2)因为∠PBQ=∠ABC=90°,,PBQ ABQ ABC ABQ PBA QBC ∴∠-=∠-∠∴∠=∠在△PBA 和△QBC 中,BP BQ PBA QBC BA BC =⎧⎪∠=∠⎨⎪=⎩PBA QBC ∴∆≅∆:.PA=CQ ;(3) ()135,1,0APB P ︒∠=BPQ ∆是等腰直角三角形,:所以∠BQP=45°,当C 、P ,Q 三点共线时,∠BQC=135°,由(2)可知,PBA QBC∴∆≅∆;所以∠BPA=∠BQC=135°,所以∠OPB=45°,所以.OP=OB=1,所以P点坐标为(1,0) .【点睛】本题考查的是全等三角形的判定和性质、三角形的外角的性质,掌握全等三角形的判定定理和性质定理是解题的关键.3.(1)203;(2)①t=83;②a=185;(3)t=6.4或t=103【解析】【分析】(1)根据时间=路程÷速度即可求得答案;(2)①由题意得:BM=CN=3t,则只可以是△CMN≌△BAM,AB=CM,由此列出方程求解即可;②由题意得:CN≠BM,则只可以是△CMN≌△BMA,AB=CN=12,CM=BM,进而可得3t=10,求解即可;(3)分情况讨论,当△CMN≌△BPM时,BP=CM,若此时P由A向B运动,则12-2t=20-3t,但t=8不符合实际,舍去,若此时P由B向A运动,则2t-12=20-3t,求得t=6.4;当△CMN≌△BMP时,则BP=CN,CM=BM,可得3t=10,t=103,再将t=103代入分别求得AP,BP的长及a的值验证即可.【详解】解:(1)20÷3=203,故答案为:203;(2)∵CD∥AB,∴∠B=∠DCB,∵△CNM与△ABM全等,∴△CMN≌△BAM或△CMN≌△BMA,①由题意得:BM=CN=3t,∴△CMN≌△BAM∴AB=CM,∴12=20-3t,解得:t=83;②由题意得:CN≠BM,∴△CMN≌△BMA,∴AB=CN=12,CM=BM,∴CM=BM=12 BC,∴3t=10,解得:t=10 3∵CN=at,∴103a=12解得:a=185;(3)存在∵CD∥AB,∴∠B=∠DCB,∵△CNM与△PBM全等,∴△CMN≌△BPM或△CMN≌△BMP,当△CMN≌△BPM时,则BP=CM,若此时P由A向B运动,则BP=12-2t,CM=20-3t,∵BP=CM,∴12-2t=20-3t,解得:t=8 (舍去)若此时P由B向A运动,则BP=2t-12,CM=20-3t,∵BP=CM,∴2t-12=20-3t,解得:t=6.4,当△CMN≌△BMP时,则BP=CN,CM=BM,∴CM=BM=12 BC∴3t=10,解得:t=10 3当t=103时,点P的路程为AP=2t=203,此时BP=AB-AP=12-203=163,则CN=BP=16 3即at=163,∵t=103,∴a=1.6符合题意综上所述,满足条件的t的值有:t=6.4或t=10 3【点睛】本题考查了全等三角形的判定及性质的综合运用,解决本题的关键就是用方程思想及分类讨论思想解决问题,把实际问题转化为方程是常用的手段.4.(1)①详见解析;②12α;(2)详见解析;(3)当B、O、F三点共线时BF最长,a【解析】【分析】(1)①由线段垂直平分线的性质可得AD=AC=AB,即可证点B,C,D在以点A为圆心,AB为半径的圆上;②由等腰三角形的性质可得∠BAC=2∠BDC,可求∠BDC的度数;(2)连接CE,由题意可证△ABC,△DCE是等边三角形,可得AC=BC,∠DCE=60°=∠ACB,CD=CE,根据“SAS”可证△BCD≌△ACE,可得AE=BD;(3)取AC的中点O,连接OB,OF,BF,由三角形的三边关系可得,当点O,点B,点F三点共线时,BF最长,根据等腰直角三角形的性质和勾股定理可求BO=,OF OC==,即可求得BF【详解】(1)①连接AD,如图1.∵点C与点D关于直线l对称,∴AC = AD.∵AB= AC,∴AB= AC = AD.∴点B,C,D在以A为圆心,AB为半径的圆上.②∵AD=AB=AC,∴∠ADB=∠ABD,∠ADC=∠ACD,∵∠BAM=∠ADB+∠ABD,∠MAC=∠ADC+∠ACD,∴∠BAM=2∠ADB,∠MAC=2∠ADC,∴∠BAC=∠BAM+∠MAC=2∠ADB+2∠ADC=2∠BDC=α∴∠BDC=12α故答案为:12α.(2连接CE,如图2.∵∠BAC=60°,AB=AC,∴△ABC是等边三角形,∴BC=AC,∠ACB=60°,∵∠BDC=12α,∴∠BDC=30°,∵BD⊥DE,∴∠CDE=60°,∵点C关于直线l的对称点为点D,∴DE=CE,且∠CDE=60°∴△CDE是等边三角形,∴CD=CE=DE,∠DCE=60°=∠ACB,∴∠BCD=∠ACE,且AC=BC,CD=CE,∴△BCD≌△ACE(SAS)∴BD=AE ,(3)如图3,取AC 的中点O ,连接OB ,OF ,BF ,,F 是以AC 为直径的圆上一点,设AC 中点为O ,∵在△BOF 中,BO+OF≥BF ,当B 、O 、F 三点共线时BF 最长; 如图,过点O 作OH ⊥BC ,∵∠BAC=90°,2a ,∴24BC AC a ==,∠ACB=45°,且OH ⊥BC ,∴∠COH=∠HCO=45°,∴OH=HC , ∴2OC HC =, ∵点O 是AC 中点,AC 2a ,∴2OC a =, ∴OH HC a ==,∴BH=3a ,∴10BO a =,∵点C 关于直线l 的对称点为点D ,∴∠AFC=90°,∵点O 是AC 中点, ∴2OF OC a ==,∴102BF a =, ∴当B 、O 、F 三点共线时BF 最长;最大值为102)a .【点睛】本题是三角形综合题,考查了全等三角形的判定和性质,等腰三角形的性质,勾股定理,三角形的三边关系,灵活运用相关的性质定理、综合运用知识是解题的关键.5.(1)y=43x+2;(2)(103,10);(3)存在, P 坐标为(6,6)或(6,7+2)或(6,10-27).【解析】【分析】(1)设直线DP 解析式为y=kx+b ,将D 与C 坐标代入求出k 与b 的值,即可确定出解析式;(2)当点B 的对应点B′恰好落在AC 边上时,根据勾股定理列方程即可求出此时P 坐标; (3)存在,分别以BD ,DP ,BP 为底边三种情况考虑,利用勾股定理及图形与坐标性质求出P 坐标即可.【详解】解:(1)∵C (6,10),D (0,2),设此时直线DP 解析式为y=kx+b ,把D (0,2),C (6,10)分别代入,得2610b k b =⎧⎨+=⎩, 解得432k b ⎧=⎪⎨⎪=⎩ 则此时直线DP 解析式为y=43x+2; (2)设P (m ,10),则PB=PB′=m ,如图2,∵OB′=OB=10,OA=6,∴AB′=22OB OA '-=8,∴B′C=10-8=2,∵PC=6-m ,∴m 2=22+(6-m )2,解得m=103 则此时点P 的坐标是(103,10); (3)存在,理由为:若△BDP 为等腰三角形,分三种情况考虑:如图3,①当BD=BP 1=OB-OD=10-2=8,在Rt △BCP 1中,BP 1=8,BC=6,根据勾股定理得:CP1=∴AP 1P 1(6,);②当BP 2=DP 2时,此时P 2(6,6);③当DB=DP 3=8时,在Rt △DEP 3中,DE=6,根据勾股定理得:P3∴AP 3=AE+EP 3,即P 3(6,+2),综上,满足题意的P 坐标为(6,6)或(6,+2)或(6,).【点睛】此题属于一次函数综合题,待定系数法确定一次函数解析式,坐标与图形性质,等腰三角形的性质,勾股定理,熟练掌握待定系数法是解题的关键.6.90︒,45︒;20︒,30︒;2a γβ+=,2a γβ-=.【解析】【分析】(1)①如图①知1112EMC BMC ∠=∠,1112C MF C MC ∠=∠得 ()1112EMF BMC C MC ∠=∠+∠可求出解. ②由图②知111111,22EBA ABC C BF C BC ∠=∠∠=∠得()1112EBF ABC C BC ∠=∠+∠可求出解.(2)①由图③折叠知11,CMF FMC BME EMB ∠=∠∠=∠,可推出11()BMC EMF EMF C MB ∠-∠-∠=∠,即可求出解.②由图④中折叠知11,CMF C MF ABE A BE ∠=∠∠=∠,可推出()112906090A MC ︒︒︒-+∠=,即可求出解.(3)如图⑤-1、⑤-2中分别由折叠可知,a ββγ-=-、a ββγ-=+,即可求得 2a γβ+=、2a γβ-=.【详解】解:(1)①如图①中,1112EMC BMC ∠=∠,1112C MF C MC ∠=∠, ()1111111800229EMF EMC C MF BMC C MC ︒︒∴∠=∠+∠=∠⨯=+∠=, 故答案为90︒. ②如图②中,111111,22EBA ABC C BF C BC ∠=∠∠=∠,()111111904522EBF EBC C BF ABC C BC ︒︒∴∠=∠+∠=∠+∠=⨯=, 故答案为45︒.(2)①如图③中由折叠可知, 11,CMF FMC BME EMB ∠=∠∠=∠,1111C MF EMB EMF C MB ∠+∠-∠=∠,11CMF BME EMF C MB ∴∠+∠-∠=∠,11()BMC EMF EMF C MB ∴∠-∠-∠=∠,111808020C MB ︒︒︒∴-=∠=;②如图④中根据折叠可知,11,CMF C MF ABE A BE ∠=∠∠=∠,112290CMF ABE A MC ︒∠+∠+∠=,112()90CMF ABE A MC ︒∴∠+∠+∠=,()1129090EMF AMC ︒︒∴-∠+∠=,()112906090AMC ︒︒︒∴-+∠=, 1130A MC ︒∴∠=;(3)如图⑤-1中,由折叠可知,a ββγ-=-,2a γβ∴+=;如图⑤-2中,由折叠可知,a ββγ-=+,2a γβ∴-=.【点睛】本题考查了图形的变换中折叠属全等变换,图形的角度及边长不变及一些角度的计算问题,突出考查学生的观察能力、思维能力以及动手操作能力,本题是代数、几何知识的综合运用典型题目.7.(1)(73,2);(2)y =x ﹣13;(3)E 的坐标为(32,72)或(6,8) 【解析】【分析】(1)把点E 的纵坐标代入直线解析式,求出横坐标,得到点E 的坐标,根据融合点的定义求求解即可;(2)设点E 的坐标为(a ,a+2),根据融合点的定义用a 表示出x 、y ,整理得到答案;(3)分∠THD=90°、∠TDH=90°、∠DTH=90°三种情况,根据融合点的定义解答.【详解】解:(1)∵点E 是直线y =x +2上一点,点E 的纵坐标是6,∴x +2=6,解得,x =4,∴点E 的坐标是(4,6),∵点T (x ,y )是点D 和E 的融合点,∴x =343+=73,y =063+=2, ∴点T 的坐标为(73,2), 故答案为:(73,2); (2)设点E 的坐标为(a ,a +2),∵点T (x ,y )是点D 和E 的融合点,∴x =33a +,y =023a ++, 解得,a =3x ﹣3,a =3y ﹣2,∴3x ﹣3=3y ﹣2, 整理得,y =x ﹣13; (3)设点E 的坐标为(a ,a +2), 则点T 的坐标为(33a +,23a +), 当∠THD =90°时,点E 与点T 的横坐标相同, ∴33a +=a , 解得,a =32, 此时点E 的坐标为(32,72), 当∠TDH =90°时,点T 与点D 的横坐标相同, ∴33a +=3, 解得,a =6, 此时点E 的坐标为(6,8),当∠DTH =90°时,该情况不存在,综上所述,当△DTH 为直角三角形时,点E 的坐标为(32,72)或(6,8) 【点睛】 本题考查了一次函数图象上点的坐标特征、融合点的定义,解题关键是灵活运用分情况讨论思想.8.(1)∠AFE =60°;(2)见解析;(3)75【解析】【分析】(1)通过证明 BCE CAD ≌ 得到对应角相等,等量代换推导出60AFE ∠=︒;(2)由(1)得到60AFE ∠=︒,CE AD = 则在Rt AHF △ 中利用30°所对的直角边等于斜边的一半,等量代换可得;(3)通过在PF 上取一点K 使得KF =AF ,作辅助线证明ABK 和ACF 全等,利用对应边相等,等量代换得到比值.(通过将ACF 顺时针旋转60°也是一种思路.)【详解】(1)解:如图1中.∵ABC 为等边三角形,∴AC =BC ,∠BAC =∠ABC =∠ACB =60°,在BCE 和CAD 中,60BE CD CBE ACD BC CA =⎧⎪∠=∠=︒⎨⎪=⎩,∴ BCE CAD ≌(SAS ),∴∠BCE =∠DAC ,∵∠BCE +∠ACE =60°,∴∠DAC +∠ACE =60°,∴∠AFE =60°.(2)证明:如图1中,∵AH ⊥EC ,∴∠AHF =90°,在Rt △AFH 中,∵∠AFH =60°,∴∠FAH =30°,∴AF =2FH ,∵EBC DCA≌,∴EC=AD,∵AD=AF+DF=2FH+DF,∴2FH +DF=EC.(3)解:在PF上取一点K使得KF=AF,连接AK、BK,∵∠AFK =60°,AF=KF,∴△AFK为等边三角形,∴∠KAF=60°,∴∠KAB=∠FAC,在ABK和ACF中,AB ACKAB ACFAK AF=⎧⎪∠=∠⎨⎪=⎩,∴ABK ACF≌(SAS),BK CF=∴∠AKB=∠AFC=120°,∴∠BKE=120°﹣60°=60°,∵∠BPC=30°,∴∠PBK=30°,∴29BK CF PK CP===,∴79PF CP CF CP=-=,∵45()99AF KF CP CF PK CP CP CP==-+=-=∴779559CPPFAF CP== .【点睛】掌握等边三角形、直角三角形的性质,及三角形全等的判定通过一定等量代换为本题的关键.9.(1)P(﹣1,﹣1);(2)32;(3)T(1,0)或(﹣2,0).【解析】【分析】(1)解析式联立构成方程组,该方程组的解就是交点坐标;(2)利用三角形的面积公式解答;(3)求得C的坐标,因为S△ATP=S△APB,S△ATP=S△ATC+S△PTC=|x+12|,所以|x+12|=32,解得即可.【详解】解:(1)由212y xy x=+⎧⎨=--⎩,解得11xy=-⎧⎨=-⎩,所以P(﹣1,﹣1);(2)令x=0,得y1=1,y2=﹣2∴A(0,1),B(0,﹣2),则S△APB=12×(1+2)×1=32;(3)在直线l1:y1=2x+1中,令y=0,解得x=﹣12,∴C(﹣12,0),设T(x,0),∴CT=|x+12 |,∵S△ATP=S△APB,S△ATP=S△ATC+S△PTC=12•|x+12|•(1+1)=|x+12|,∴|x+12|=32,解得x=1或﹣2,∴T(1,0)或(﹣2,0).【点睛】本题考查一次函数与二元一次方程组,解题的关键是准确将条件转化为二元一次方程组,并求出各点的坐标.10.(1)见解析;(2)见解析;(3)3【解析】【分析】(1)根据等腰三角形的性质和外角的性质即可得到结论;(2)过E作EF∥AC交AB于F,根据已知条件得到△ABC是等边三角形,推出△BEF是等边三角形,得到BE=EF,∠BFE=60°,根据全等三角形的性质即可得到结论;(3)连接AF ,证明△ABF ≌△CBF ,得AF=CF ,再证明DH=AH=12CF=3. 【详解】解:(1)∵AB=AC ,∴∠ABC=∠ACB ,∵DE=DC ,∴∠E=∠DCE ,∴∠ABC-∠E=∠ACB-∠DCB ,即∠EDB=∠ACD ;(2)∵△ABC 是等边三角形,∴∠B=60°,∴△BEF 是等边三角形,∴BE=EF ,∠BFE=60°,∴∠DFE=120°,∴∠DFE=∠CAD ,在△DEF 与△CAD 中, EDF DCA DFE CAD DE CD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△DEF ≌△CAD (AAS ),∴EF=AD ,∴AD=BE ;(3)连接AF ,如图3所示:∵DE=DC ,∠EDC=30°,∴∠DEC=∠DCE=75°,∴∠ACF=75°-60°=15°,∵BF 平分∠ABC ,∴∠ABF=∠CBF ,在△ABF 和△CBF 中,AB BCABF CBFBF BF=⎧⎪∠=∠⎨⎪=⎩,△ABF≌△CBF(SAS),∴AF=CF,∴∠FAC=∠ACF=15°,∴∠AFH=15°+15°=30°,∵AH⊥CD,∴AH=12AF=12CF=3,∵∠DEC=∠ABC+∠BDE,∴∠BDE=75°-60°=15°,∴∠ADH=15°+30°=45°,∴∠DAH=∠ADH=45°,∴DH=AH=3.【点睛】本题考查了全等三角形的判定与性质,等腰三角形和直角三角形的性质,三角形的外角的性质,等边三角形的判定和性质,证明三角形全等是解决问题的关键.11.(1522213221【解析】【分析】(1)分别过点B,C向l1作垂线,交l1于M,N两点,证明△ABM≌△CAN,得到AM=CN,AN=BM,即可得出AB;(2)分别过点B,C向l1作垂线,交l1于点P,Q两点,在l1上取M,N使∠AMB=∠CNA=120°,证明△AMB≌△CAN,得到CN=AM,再通过△PBM和△QCN算出PM和NQ的值,得到AP,最后在△APB中,利用勾股定理算出AB的长;(3)在l3上找M和N,使得∠BNC=∠AMC=60°,过B作l3的垂线,交l3于点P,过A作l3的垂线,交l3于点Q,证明△BCN≌△CAM,得到CN=AM,在△BPN和△AQM中利用勾股定理算出NP和AM,从而得到PC,结合BP算出BC的长,即为AB.【详解】解:(1)如图,分别过点B,C向l1作垂线,交l1于M,N两点,由题意可得:∠BAC=90°,∵∠NAC+∠MAB=90°,∠NAC+∠NCA=90°,∴∠MAB=∠NCA,在△ABM和△CAN中,===AMB CNAMAB NCAAB AC∠∠⎧⎪∠∠⎨⎪⎩,∴△ABM≌△CAN(AAS),∴AM=CN=2,AN=BM=1,∴AB=22251=+;(2)分别过点B,C向l1作垂线,交l1于P,Q两点,在l1上取M,N使∠AMB=∠CNA=120°,∵∠BAC=120°,∴∠MAB+∠NAC=60°,∵∠ABM+∠MAB=60°,∴∠ABM=∠NAC,在△AMB和△CNA中,===AMB CNAABM NACAB AC∠∠⎧⎪∠∠⎨⎪⎩,∴△AMB≌△CNA(AAS),∴CN=AM,∵∠AMB=∠ANC=120°,∴∠PMB=∠QNC=60°,∴PM=12BM,NQ=12NC,∵PB=1,CQ=2,设PM=a,NQ=b,∴2221=4a a+,2222=4b b+,解得:3=3a ,23=3b , ∴CN=AM=222323⎛⎫+ ⎪ ⎪⎝⎭=43, ∴AB=22AP BP +=()22AM PM BP ++=221;(3)如图,在l 3上找M 和N ,使得∠BNC=∠AMC=60°,过B 作l 3的垂线,交于点P ,过A 作l 3的垂线,交于点Q ,∵△ABC 是等边三角形,∴BC=AC ,∠ACB=60°,∴∠BCN+∠ACM=120°,∵∠BCN+∠NBC=120°,∴∠NBC=∠ACM ,在△BCN 和△CAM 中,BNC CMA NBC MAC BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BCN ≌△CAM (AAS ),∴CN=AM ,BN=CM ,∵∠PBN=90°-60°=30°,BP=2,∴BN=2NP ,在△BPN 中,222BP NP BN +=,即22224NP NP +=,解得:NP=33, ∵∠AMC=60°,AQ=3,∴∠MAQ=30°,∴AM=2QM ,在△AQM 中,222AQ QM AM +=,即22234QM QM +=,解得:QM=3,∴AM=23=CN ,∴PC=CN-NP=AM-NP=43, 在△BPC 中,BP 2+CP 2=BC 2,即BC=22224322123BP CP ⎛⎫+=+= ⎪ ⎪⎝⎭, ∴AB=BC=2213.【点睛】本题考查了全等三角形的判定和性质,平行线之间的距离,等腰三角形的性质,等边三角形的性质以及勾股定理,解题的关键是利用平行线构造全等三角形,再利用全等三角形的性质以及勾股定理求解.12.(1)证明见解析;(2)证明见解析;(3)结论:AD DG ND =-,证明见解析.【解析】【分析】(1)先根据直角三角形的性质得出60ABC ∠=︒,再根据角平分线的性质可得CD ED =,然后根据三角形的判定定理与性质可得BC BE =,最后根据等边三角形的判定即可得证;(2)如图(见解析),延长ED 使得DF MD =,连接MF ,先根据直角三角形的性质、等边三角形的判定得出MDF ∆是等边三角形,再根据等边三角形的性质、角的和差得出,,F MDB MF MD FMG DMB ∠=∠=∠=∠,然后根据三角形全等的判定与性质、等量代换即可得证;(3)如图(见解析),参照题(2),先证HDN ∆是等边三角形,再根据等边三角形的性质、角的和差得出,,H NDG NH ND HNB DNG ∠=∠=∠=∠,然后根据三角形全等的判定与性质、等量代换即可得证.【详解】(1)3,090A ACB ∠=︒∠=︒9060ABC A ∴∠=︒-∠=︒BD是ABC∠的角平分线,DE AB⊥CD ED∴=在BCD∆和BED∆中,CD EDBD BD=⎧⎨=⎩()BCD BED HL∴∆≅∆BC BE∴=EBC∴∆是等边三角形;(2)如图,延长ED使得DF MD=,连接MF3,090AACB∠=︒∠=︒,BD是ABC∠的角平分线,DE AB⊥60,ADE BDE AD BD∴∠=∠=︒=60,18060 MDF ADE MDB ADE BDE∴∠=∠=︒∠=︒-∠-∠=︒MDF∴∆是等边三角形,60MF DM F DMF∴=∠=∠=︒60BMG∠=︒DMF DM B MGG DM G∴∠+∠=+∠∠,即FMG DMB∠=∠在FMG∆和DMB∆中,60F MDBMF MDFMG DMB∠=∠=︒⎧⎪=⎨⎪∠=∠⎩()FMG DMB ASA∴∆≅∆GF BD∴=,即DF DG BD+=AD DF DG MD DG∴=+=+即AD DG MD=+;(3)结论:AD DG ND=-,证明过程如下:如图,延长BD使得DH ND=,连接NH由(2)可知,60,18060,ADE HDN ADE BDE AD BD∠=︒∠=︒-∠-∠=︒= HDN∴∆是等边三角形,60NH ND H HND∴=∠=∠=︒60BNG∠=︒HND BND BNDBNG∠+∠=+∠∴∠,即NHNB D G∠=∠在HNB ∆和DNG ∆中,60H NDG NH ND HNB DNG ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩()HNB DNG ASA ∴∆≅∆HB DG ∴=,即DH BD DG +=ND AD DG ∴+=即AD DG ND =-.【点睛】本题考查了直角三角形的性质、等边三角形的判定与性质、三角形全等的判定定理与性质等知识点,较难的是题(2)和(3),通过作辅助线,构造一个等边三角形是解题关键.。
人教版八年级数学第一学期几何压轴题期末复习提高训练试题

人教版八年级数学第一学期几何压轴题期末复习提高训练试题1、如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.(1)求证:△ACD≌△CBE;(2)若AD=12,DE=7,求BE的长.2、已知,如图,△ABC和△BDE都是等边三角形,且点D在AC上.(1)求证:AE∥BC;(2)直接写出AE,AD和AB之间的关系;3、如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.(1)求证:AC∥DE;(2)若BF=13,EC=5,求BC的长.4、根据下列命题画出图形,写出已知、求证,并完成证明过程.命题:等腰三角形两底角的角平分线相等.已知:如图,_____________________________.求证:________________________.5、已知:如图,点A,B在∠MON的边OM,ON上,OA的垂直平分线CP与OB的垂直平分线DP相交于点P,连接P A,PO,PB,AB.(1)求证:①P A=PB;②∠APB=2∠CPD;(2)探究:∠MON满足什么条件时,△P AB是等边三角形,并说明理由;(3)若OA=OB,请在备用图中画出符合条件的图形,并探究∠CPO与∠APB之间的数量关系,并说明理由.6、如图,在△ABC中,AB=AC=18cm,BC=10cm,AD=2BD.(1)如果点P在线段BC上以2cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.①若点Q的运动速度与点P的运动速度相等,经过2s后,△BPD与△CQP是否全等,请说明理由;②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?7、已知:如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.(1)求证:AD=BE;(2)求∠AEB的度数;(3)拓展探究:如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.①∠AEB的度数为°;②探索线段CM、AE、BE之间的数量关系为.(直接写出答案,不需要说明理由)8、如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.(1)当∠BDA=110°时,∠EDC=°,∠DEC=°;点D从B向C的运动过程中,∠BDA逐渐变(填“大”或“小”);(2)当DC等于多少时,△ABD≌△DCE,请说明理由.(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数,若不可以,请说明理由.9、如图,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,BE=3cm,AD=9cm.求:(1)DE的长;(2)若CE在△ABC的外部(如图),其它条件不变,DE的长是多少?10、已知∠MAN=120°,点C是∠MAN的平分线AQ上的一个定点,点B,D分别在AN,AM上,连接BD.【发现】(1)如图1,若∠ABC=∠ADC=90°,则∠BCD=°,△CBD是三角形;【探索】(2)如图2,若∠ABC+∠ADC=180°,请判断△CBD的形状,并证明你的结论;【应用】(3)如图3,已知∠EOF=120°,OP平分∠EOF,且OP=1,若点G,H分别在射线OE,OF上,且△PGH 为等边三角形,则满足上述条件的△PGH的个数一共有.(只填序号)①2个②3个③4个④4个以上11、如图,△ACB和△DCE均为等腰三角形,点A,D,E在同一直线上,连接BE.(1)如图1,若∠CAB=∠CBA=∠CDE=∠CED=50°.①求证:AD=BE;②求∠AEB的度数.(2)如图2,若∠ACB=∠DCE=90°,CF为△DCE中DE边上的高,试猜想AE,CF,BE之间的关系,并证明你的结论.12、【问题原型】如图1,在等腰直角三角形ABC中,∠ACB=90°,BC=8.将边AB绕点B顺时针旋转90°得到线段BD,连结CD,过点D作△BCD的BC边上的高DE,易证△ABC≌△BDE,从而得到△BCD的面积为.【初步探究】如图2,在Rt△ABC中,∠ACB=90°,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD.用含a的代数式表示△BCD的面积并说明理由.【简单应用】如图3,在等腰三角形ABC中,AB=AC,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,求△BCD的面积(用含a的代数式表示).13、如图,△ABC是等边三角形,D、E为AC上两点,且AE=CD,延长BC至点F,使CF=CD,连接BD.(1)如图1,当D、E两点重合时,求证:BD=DF;(2)延长BD与EF交于点G.①如图2,求证:∠BGE=60°;②如图3,连接BE,CG.若∠EBD=30°,BG=4,则△BCG的面积为.14、在△ABC中,AB=AC,点D是直线BC上一点(不与B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=度;(2)如图2,如果∠BAC=60°,则∠BCE=度;(3)设∠BAC=α,∠BCE=β.①如图3,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;②当点D在直线BC上移动,请直接写出α,β之样的数量关系,不用证明.参考答案1、如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.(1)求证:△ACD≌△CBE;(2)若AD=12,DE=7,求BE的长.【解答】解:(1)∵∠ACB=90°,BE⊥CE,∴∠ECB+∠ACD=90°∠ECB+∠CBE=90°,∴∠ACD=∠CBE,∵AD⊥CE,BE⊥CE,∴∠ADC=∠CEB=90°,∵AC=BC,∴△ACD≌△CBE;(2)∵△ACD≌△CBE,∴AD=CE,CD=BE,∵AD=12,DE=7,∴BE=CD=CE﹣DE=12﹣7=5.2、已知,如图,△ABC和△BDE都是等边三角形,且点D在AC上.(1)求证:AE∥BC;(2)直接写出AE,AD和AB之间的关系;【解答】证明:(1)∵△ABC和△BDE都是等边三角形,∴AB=BC,BE=BD,∠ABC=∠DBE=∠C=60°,∴∠ABC﹣∠ABD=∠DBE﹣∠ABD,∴∠DBC=∠EBA,∴△DBC≌△EBA(SAS),∴∠C=∠EAB=∠ABC,∴EA∥BC(2)∵△DBC≌△EBA,∴AE=CD,∵AD+CD=AC=AB,∴AE+AD=AB.3、如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.(1)求证:AC∥DE;(2)若BF=13,EC=5,求BC的长.【解答】(1)证明:在△ABC和△DFE中,∴△ABC≌△DFE(SAS),∴∠ACE=∠DEF,∴AC∥DE;(2)解:∵△ABC≌△DFE,∴BC=EF,∴CB﹣EC=EF﹣EC,∴EB=CF,∵BF=13,EC=5,∴EB==4,∴CB=4+5=9.4、根据下列命题画出图形,写出已知、求证,并完成证明过程.命题:等腰三角形两底角的角平分线相等.已知:如图,△ABC中,AB=AC,BD,CE是△ABC的角平分线.求证:BD=CE.【解答】解:已知:如图,△ABC中,AB=AC,BD,CE是△ABC的角平分线.求证:BD=CE,证明:∵AB=AC,∴∠ABC=∠ACB,∵BD,CE是△ABC的角平分线,∴∠ABD=∠ABC,∠ACE=∠ACB,∴∠ABD=∠ACE,∵AB=AC,∠A=∠A,∴△ABD≌△ACE(ASA),∴BD=CE.故答案为:△ABC中,AB=AC,BD,CE是△ABC的角平分线,BD=CE.5、已知:如图,点A,B在∠MON的边OM,ON上,OA的垂直平分线CP与OB的垂直平分线DP相交于点P,连接P A,PO,PB,AB.(1)求证:①P A=PB;②∠APB=2∠CPD;(2)探究:∠MON满足什么条件时,△P AB是等边三角形,并说明理由;(3)若OA=OB,请在备用图中画出符合条件的图形,并探究∠CPO与∠APB之间的数量关系,并说明理由.【解答】(1)证明:①∵CP为OA的垂直平分线,∴P A=PO,同理:PB=PO,∴P A=PB;②∵P A=PO,PC⊥OA,∴∠APC=∠OPC=∠APO,同理,∠BPD=∠OPD=∠BPO,∠APB=∠APO+∠BPO=2∠CPO+2∠DPO=2(∠CPO+∠DPO)=2∠CPD;(2)∠MON=150°.理由:∵∠CPO+∠COP=90°,∠DPO+∠DOP=90°,∴∠MON+∠CPD=180°,∵∠MON=150°,∴∠CPD=180°﹣150°=30°,由(1)得∠APB=2∠CPD=60°,P A=PB,∴△P AB是等边三角形;(3)在备用图中画出符合条件的图形如备用图,∠CPO=∠APB.理由:∵OC=OA,OD=OB,OA=OB,∴OC=OD,在Rt△PCO和Rt△PDO中,,∴Rt△PCO≌Rt△PDO(HL),∴∠CPO=∠DPO,由(1)得∠APC=∠OPC,∠BPD=∠OPD,∴∠APC=∠CPO=∠OPD=∠BPD,∴∠CPO=∠APB.6、如图,在△ABC中,AB=AC=18cm,BC=10cm,AD=2BD.(1)如果点P在线段BC上以2cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.①若点Q的运动速度与点P的运动速度相等,经过2s后,△BPD与△CQP是否全等,请说明理由;②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?【解答】解:(1)①△BPD与△CQP全等,理由如下:∵AB=AC=18cm,AD=2BD,∴AD=12cm,BD=6cm,∠B=∠C,∵经过2s后,BP=4cm,CQ=4cm,∴BP=CQ,CP=6cm=BD,在△BPD和△CQP中,,∴△BPD≌△CQP(SAS),②∵点Q的运动速度与点P的运动速度不相等,∴BP≠CQ,∵△BPD与△CQP全等,∠B=∠C,∴BP=PC=BC=5cm,BD=CQ=6cm,∴t=,∴点Q的运动速度==cm/s,∴当点Q的运动速度为cm/s时,能够使△BPD与△CQP全等;(2)设经过x秒,点P与点Q第一次相遇,由题意可得:x﹣2x=36,解得:x=90,∴90﹣()×3=21(s),∴经过90s点P与点Q第一次相遇在线段AB上相遇.7、已知:如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.(1)求证:AD=BE;(2)求∠AEB的度数;(3)拓展探究:如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.①∠AEB的度数为90°;②探索线段CM、AE、BE之间的数量关系为AE=BE+2CM.(直接写出答案,不需要说明理由)【解答】解:(1)如图1,∵△ACB和△DCE均为等边三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=60°,∴∠ACD=∠BCE.在△ACD和△BCE中,,∴△ACD≌△BCE(SAS),∴AD=BE;(2)如图1,∵△ACD≌△BCE,∴∠ADC=∠BEC,∵△DCE为等边三角形,∴∠CDE=∠CED=60°,∵点A,D,E在同一直线上,∴∠ADC=120°,∴∠BEC=120°,∴∠AEB=∠BEC﹣∠CED=60°;(3)①如图2,∵△ACB和△DCE均为等腰直角三角形,∴AC=BC,CD=CE,∠ACB=∠DCE=90°,∠CDE=∠CED=45°,∴∠ACB﹣∠DCB=∠DCE﹣∠DCB,即∠ACD=∠BCE,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS),∴BE=AD,∠BEC=∠ADC,∵点A,D,E在同一直线上,∴∠ADC=180﹣45=135°,∴∠BEC=135°,∴∠AEB=∠BEC﹣∠CED=135°﹣45°=90°,故答案为:90;②如图2,∵∠DCE=90°,CD=CE,CM⊥DE,∴CM=DM=EM,∴DE=DM+EM=2CM,∵△ACD≌△BCE(已证),∴BE=AD,∴AE=AD+DE=BE+2CM,故答案为:AE=BE+2CM.8、如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.(1)当∠BDA=110°时,∠EDC=30°,∠DEC=110°;点D从B向C的运动过程中,∠BDA逐渐变小(填“大”或“小”);(2)当DC等于多少时,△ABD≌△DCE,请说明理由.(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数,若不可以,请说明理由.【解答】解:(1)∵∠ADB+∠ADE+∠EDC=180°,且∠ADE=40°,∠BDA=110°,∴∠EDC=30°,∵∠AED=∠EDC+∠ACB=30°+40°=70°∴∠EDC=180°﹣∠AED=110°,故答案为:30,110,∵∠BDA+∠B+∠BAD=180°,∴∠BDA=140°﹣∠BAD∵点D从B向C的运动过程中,∠BAD逐渐变大∴∠BDA逐渐变小,故答案为:小(2)当DC=2时,△ABD≌△DCE,理由如下:∵∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠CDE,∠B=∠ADE=40°,∴∠BAD=∠CDE,且AB=CD=2,∠B=∠C=40°,∴△ABD≌△DCE(ASA)(3)若AD=DE时,∵AD=DE,∠ADE=40°∴∠DEA=∠DAE=70°∵∠DEA=∠C+∠EDC∴∠EDC=30°∴∠BDA=180°﹣∠ADE﹣∠EDC=180°﹣40°﹣30°=110°若AE=DE时,∵AE=DE,∠ADE=40°∴∠ADE=∠DAE=40°,∴∠AED=100°∵∠DEA=∠C+∠EDC∴∠EDC=60°∴∠BDA=180°﹣∠ADE﹣∠EDC=180°﹣40°﹣60°=80°综上所述:当∠BDA=80°或110°时,△ADE的形状可以是等腰三角形9、如图,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,BE=3cm,AD=9cm.求:(1)DE的长;(2)若CE在△ABC的外部(如图),其它条件不变,DE的长是多少?【解答】解:(1)∵∠ACB=90°,BE⊥CE,∴∠BCE+∠CBE=90°,∠BCE+∠ECA=90°,∴∠CBE=∠ECA,∠BEC=∠CDA,∵在△BEC和△CDA中,,∴△BEC≌△CDA(AAS),∴BE=CD,CE=AD,∵BE=3cm,AD=9cm,∴CD=3cm,CE=9cm,∴DE=CE﹣CD=6cm.(2)∵∠ACB=90°,BE⊥CE于E,AD⊥CE于D,∴∠BCE+∠CBE=90°,∠BCE+∠DCA=90°,∠BEC=∠CDA=90°,∴∠CBE=∠ACD,∵在△CBE和△ACD中,,∴△CBE≌△ACD(AAS),∴BE=CD,CE=AD,∵BE=3cm,AD=9cm,∴DE=CD+CE=BE+AD=12cm.10、已知∠MAN=120°,点C是∠MAN的平分线AQ上的一个定点,点B,D分别在AN,AM上,连接BD.【发现】(1)如图1,若∠ABC=∠ADC=90°,则∠BCD=60°,△CBD是等边三角形;【探索】(2)如图2,若∠ABC+∠ADC=180°,请判断△CBD的形状,并证明你的结论;【应用】(3)如图3,已知∠EOF=120°,OP平分∠EOF,且OP=1,若点G,H分别在射线OE,OF上,且△PGH 为等边三角形,则满足上述条件的△PGH的个数一共有④.(只填序号)①2个②3个③4个④4个以上【解答】解:(1)如图1,连接BD,∵∠ABC=∠ADC=90°,∠MAN=120°,根据四边形的内角和得,∠BCD=360°﹣(∠ABC+∠ADC+∠MAN)=60°,∵AC是∠MAN的平分线,CD⊥AM.CB⊥AN,∴CD=CB,(角平分线的性质定理),∴△BCD是等边三角形;故答案为:60,等边;(2)如图2,同(1)得出,∠BCD=60°(根据三角形的内角和定理),过点C作CE⊥AM于E,CF⊥AN于F,∵AC是∠MAN的平分线,∴CE=CF,∵∠ABC+∠ADC=180°,∠ADC+∠CDE=180°,∴∠CDE=∠ABC,在△CDE和△CFB中,,∴△CDE≌△CFB(AAS),∴CD=CB,∵∠BCD=60°,∴△CBD是等边三角形;(3)如图3,∵OP平分∠EOF,∠EOF=120°,∴∠POE=∠POF=60°,在OE上截取OG'=OP=1,连接PG',∴△G'OP是等边三角形,此时点H'和点O重合,同理:△OPH是等边三角形,此时点G和点O重合,将等边△PHG绕点P逆时针旋转到等边△PG'H',在旋转的过程中,边PG,PH分别和OE,OF相交(如图中G'',H'')和点P围成的三角形全部是等边三角形,(旋转角的范围为(0°到60°包括0°和60°),所以有无数个;理由:同(2)的方法.故答案为④.11、如图,△ACB和△DCE均为等腰三角形,点A,D,E在同一直线上,连接BE.(1)如图1,若∠CAB=∠CBA=∠CDE=∠CED=50°.①求证:AD=BE;②求∠AEB的度数.(2)如图2,若∠ACB=∠DCE=90°,CF为△DCE中DE边上的高,试猜想AE,CF,BE之间的关系,并证明你的结论.【解答】(1)①证明:∵∠CAB=∠CBA=∠CDE=∠CED=50°,∴∠ACB=∠DCE=180°﹣2×50°=80°,∵∠ACB=∠ACD+∠DCB,∠DCE=∠DCB+∠BCE,∴∠ACD=∠BCE,∵△ACB,△DCE都是等腰三角形,∴AC=BC,DC=EC,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS),∴AD=BE.②解:∵△ACD≌△BCE,∴∠ADC=∠BEC,∵点A、D、E在同一直线上,且∠CDE=50°,∴∠ADC=180°﹣∠CDE=130°,∴∠BEC=130°,∵∠BEC=∠CED+∠AEB,∠CED=50°,∴∠AEB=∠BEC﹣∠CED=80°.(2)结论:AE=2CF+BE.理由:∵△ACB,△DCE都是等腰直角三角形,∴∠CDE=∠CED=45°,∵CF⊥DE,∴∠CFD=90°,DF=EF=CF,∵AD=BE,∴AE=AD+DE=BE+2CF.12、【问题原型】如图1,在等腰直角三角形ABC中,∠ACB=90°,BC=8.将边AB绕点B顺时针旋转90°得到线段BD,连结CD,过点D作△BCD的BC边上的高DE,易证△ABC≌△BDE,从而得到△BCD的面积为32.【初步探究】如图2,在Rt△ABC中,∠ACB=90°,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD.用含a的代数式表示△BCD的面积并说明理由.【简单应用】如图3,在等腰三角形ABC中,AB=AC,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,求△BCD的面积(用含a的代数式表示).【解答】解:问题原型:如图1中,如图2中,过点D作BC的垂线,与BC的延长线交于点E.∴∠BED=∠ACB=90°,∵线段AB绕点B顺时针旋转90°得到线段BD,∴AB=BD,∠ABD=90°.∴∠ABC+∠DBE=90°.∵∠A+∠ABC=90°.∴∠A=∠DBE.在△ABC和△BDE中,,∴△ABC≌△BDE(AAS)∴BC=DE=8.∵S△BCD=BC•DE∴S△BCD=32,故答案为32.初步探究:△BCD的面积为a2.理由:如图2中,过点D作BC的垂线,与BC的延长线交于点E.∴∠BED=∠ACB=90°∵线段AB绕点B顺时针旋转90°得到线段BE,∴AB=BD,∠ABD=90°.∴∠ABC+∠DBE=90°.∵∠A+∠ABC=90°.∴∠A=∠DBE.在△ABC和△BDE中,,∴△ABC≌△BDE(AAS)∴BC=DE=a.∵S△BCD=BC•DE∴S△BCD=a2;简单应用:如图3中,过点A作AF⊥BC与F,过点D作DE⊥BC的延长线于点E,∴∠AFB=∠E=90°,BF=BC=a.∴∠F AB+∠ABF=90°.∵∠ABD=90°,∴∠ABF+∠DBE=90°,∴∠F AB=∠EBD.∵线段BD是由线段AB旋转得到的,∴AB=BD.在△AFB和△BED中,,∴△AFB≌△BED(AAS),∴BF=DE=a.∵S△BCD=BC•DE,∴S△BCD=•a•a=a2.∴△BCD的面积为a2.13、如图,△ABC是等边三角形,D、E为AC上两点,且AE=CD,延长BC至点F,使CF=CD,连接BD.(1)如图1,当D、E两点重合时,求证:BD=DF;(2)延长BD与EF交于点G.①如图2,求证:∠BGE=60°;②如图3,连接BE,CG.若∠EBD=30°,BG=4,则△BCG的面积为2.【解答】(1)证明:如图1中,∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,BA=BC,∵AD=DC=CF,∴∠DBC=∠ABC=30°,∠F=∠CDF,∵∠ACB=∠F+∠CDF=60°,∴∠F=30°,∴∠DBC=∠F,∴BD=DF.(2)①证明:如图2中,作EH∥BC交AB于H,连接BE.∵EH∥BC,∴∠AHE=∠ABC=60°,∠AEH=∠ACB=60°,∵∠A=60°,∴△AEH是等边三角形,∴AE=EH=AH,∵AB=AC,∴BH=CE,∵AE=CF,∴EH=CF,∵∠BHE=∠ECF=120°,∴△BEH≌△EFC(SAS),∴∠EBH=∠CEF,∵AB=BC,∠A=∠BCD,AE=CD,∴△ABE≌△CBD(SAS),∴∠ABE=∠CBD,∴∠CBD=∠DEG,∵∠CDB=∠GDE,∴∠EGD=∠DCB=60°,即∠BGE=60°.②解:如图3中,在BC上取一点T,使得BT=TG,连接TG,设CG=x.由题意:∠ABE=∠CBD=15°,∵∠BCE=∠BGE=60°,∴B,C,G,E四点共圆,∴∠ECG=∠EBG=30°,∴∠BCG=90°,∵TB=TG,∴∠TBG=∠TGB=15°,∴∠GTC=∠TBG+∠BGT=30°,∴BT=GT=2GC=2c,TC=x,∵BG2=CG2+BC2,∴42=x2+(2x+x)2,∴x2=4(2﹣)∴S△BCG=•BC•CG=×(2+)x2=2,故答案为2.14、在△ABC中,AB=AC,点D是直线BC上一点(不与B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=90度;(2)如图2,如果∠BAC=60°,则∠BCE=120度;(3)设∠BAC=α,∠BCE=β.①如图3,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;②当点D在直线BC上移动,请直接写出α,β之样的数量关系,不用证明.【解答】解:(1)∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,∵∠DAE=∠BAC,∴∠BAD=∠CAE,且AB=AC,AD=AE,∴△BAD≌△CAE(SAS)∴∠ABC=∠ACE=45°,∴∠BCE=∠ACB+∠ACE=90°,故答案为:90;(2)∵∠BAC=60°,AB=AC,∴△ABC为等边三角形,∴∠ABD=∠ACB=60°,∵∠BAC=∠DAE,∴∠BAD=∠CAE,在△ABD和△ACE中,∵∠BAD=∠CAE,且AB=AC,AD=AE,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE=60°,∴∠BCE=∠ACE+∠ACB=60°+60°=120°,故答案为:120.(3)①α+β=180°,理由:∵∠BAC=∠DAE,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC.即∠BAD=∠CAE.在△ABD与△ACE中,,∴△ABD≌△ACE(SAS),∴∠B=∠ACE.∴∠B+∠ACB=∠ACE+∠ACB.∵∠ACE+∠ACB=β,∴∠B+∠ACB=β,∵α+∠B+∠ACB=180°,∴α+β=180°.②如图1:当点D在射线BC上时,α+β=180°,连接CE,∵∠BAC=∠DAE,∴∠BAD=∠CAE,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE,在△ABC中,∠BAC+∠B+∠ACB=180°,∴∠BAC+∠ACE+∠ACB=∠BAC+∠BCE=180°,即:∠BCE+∠BAC=180°,∴α+β=180°,如图2:当点D在射线BC的反向延长线上时,α=β.连接BE,∵∠BAC=∠DAE,∴∠BAD=∠CAE,且AB=AC,AD=AE,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE,∴∠ABD=∠ACE=∠ACB+∠BCE,∴∠ABD+∠ABC=∠ACE+∠ABC=∠ACB+∠BCE+∠ABC=180°,∵∠BAC=180°﹣∠ABC﹣∠ACB,∴∠BAC=∠BCE.∴α=β;综上所述:点D在直线BC上移动,α+β=180°或α=β.。
人教版八年级上册数学期末压轴题训练

八年级上学期数学期末压轴题训练1.已知,ABC AB AC =.(1)若90BAC ∠=︒,作BCE ,点A 在BCE 内.①如图1,延长CA 交BE 于点D ,若75,2EBC BD DE ∠=︒=,则DCE ∠的度数为 ; ①如图2,DF 垂直平分BE ,点A 在DF 上,3ADAF=ABD AFCS S 的值;(2)如图3,若120BAC ∠=︒,点E 在AC 边上,10EBC ∠=︒,点D 在BC 边上,连接,,40DE AD CAD ∠=︒,求BED ∠的度数. 2.如图,在ABCD 中,过点C 分别向AB ,AD 作垂线,垂足分别为E ,F ,ABC ∠的平分线分别交CE ,CF ,CD 于点M ,N ,P .(1)求证:CMN 为等腰三角形;(2)若11134AF FD CF === 求线段CM 的长;(3)若AD CF =,试探究线段CM ,FD ,AB 之间的数量关系,并说明理由.3.平面直角坐标系中,O 为坐标原点,点A 、B 分别为x 轴正半轴和y 轴正半轴上的点,点A (0,5),连接AB ,252AOB S =△.(1)如图1,求点B 的坐标;(2)如图2,点C 为AB 中点,点P 为线段BC 上一动点,点P 的纵坐标为m ,连接OC ,若①POC 的面积为S ,用含m 的式子表示S (不要求写出m 的取值范围);(3)如图3,在(2)条件下,点E 为y 轴点A 上方一点,点F 为y 轴负半轴上一点,AE =OF ,连接BE ,若射线OP ①BE4.在ABC 中,BD 平分ABC ∠,CE 平分ACB ∠,BD 和CE 交于点O ,其中令BAC x ∠=,BOC y ∠=.(1)【计算求值】如图1,①如果50x =︒,则y =______;①如果130y =︒,则x =______.(2)【猜想证明】如图2请你根据(1)中【计算求值】的心得猜想写出y 与x 的关系式为y =______,并请你说明你的猜想的正确性.(3)【解决问题】如图3,某校园内有一个如图2所示的三角形的小花园,花园中有两条小路,BD 和CE 为三角形的角平分线,交点为点O ,在O 处建有一个自动浇水器,需要在BC 边取一处接水口F ,经过测量得知120BAC ∠=︒,12000OD OE ⋅=米2,170BC BE CD --=米,请你求出水管OF 至少要多长?(结果取整数)5.在平面直角坐标系中,已知M (0,4),N (3,2),线段MN 平移得到线段PQ ,使点M 的对应点为P ,点N 的对应点为Q ,若点P 的坐标为()2,1--,点Q 的坐标为(),a b ,(1)=a ___________,b =___________;(2)若点E 为x 轴正半轴上的一个动点,探究MNE ∠、NEQ ∠和EQP ∠之间的数量关系并证明;(注:MNE ∠、NEQ ∠和EQP ∠均为大于0︒且小于180︒的角)(3)将线段MN 向下平移得到线段AB ,从使得点N 的对应点B 落在x 轴上,点M 的对应点A 落在y 轴上,动点C 从点B 出发,以每秒钟移动3个单位长度的速度沿x 轴向左运动,动点D 从点A 出发,以每秒钟移动2个单位长度的速度沿y 轴向下运动,直线BD 与直线AC 交于点F ,设点F 的坐标为(),m n .动点C 和动点D 同时出发且它们的运动时间为t 秒.①在01t <<时,试探究ADF △与BCF △的面积关系,并说明理由; ①若在点C 、D 的运动过程中,ABF △的面积为7,请直接写出m 的值.6.已知,在平面直角坐标系中,AB x ⊥轴于点B ,点(,)A a b |3|0b -=0,平移线段AB 使点A 与原点重合,点B 的对应点为点C .(1)=a ______,b =______,点C 坐标为__________; (2)图1,点(,)D m n 是线段CB 上一个动点.①连接OD ,利用,,OBC OBD OCD △△△的面积关系,可以得到m 、n 满足一个固定的关系式,请写出这个关系式:________;①过点A 作直线l x ∥轴,在l 上取点M ,使得2MA =,若CDM 的面积为4,请求出点D 的坐标.(3)如图2,以OB 为边作BOG AOB ∠=∠,交线段BC 于点G ,E 是线段OB 上一动点,连接CE 交OG 于点F ,当点E 在线段OB 上运动过程中,OFC FCGOEC∠+∠∠的值是否发生变化?若变化说明理由,若不变,求其值.7.已知:(,0)A a ,(0,)B b .(1)当a ,b 满足225010()++=+a b a b 时,连接AB ,如图1. ①求:AO BO +的值.①点M 为线段AB 上的一点(点M 不与A ,B 重合,其中BM >AM ),以点M 为直角顶点,OM 为腰作等腰直角①MON ,连接BN ,求证:∠=∠BNO BMO .(2)当3a =-,6b =,连接AB ,若点(9,0)D ,过点D 作DE AB ⊥于点E ,点B 与点C 关于x 轴对称,点F 是线段DE 上的一点(点F 不与点E ,D 重合)且满足DF AB =,连接AF ,试判断线段AC 与AF 之间的位置关系和数量关系,并证明你的结论.8.如图,在平面直角坐标系xOy 中,点A (a ,0),B (c ,c ),C (0,c ),且满足(a ﹣c +4)22c a -+0,P 点从A 点出发沿x 轴正方向以每秒2个单位长度的速度匀速移动,Q 点从O 点出发沿y 轴负方向以每秒1个单位长度的速度匀速移动.(1)求点B 的坐标及AO 和BC 位置关系;(2)当P 、Q 分别是线段AO ,OC 上时,连接PB ,QB ,使2PAB QBC S S △△=,求出点P 的坐标; (3)在P 、Q 的运动过程中,当①CBQ =30°时,请探究①OPQ 和①PQB 的数量关系,并说明理由.9.直线AB 、CD 相交于点O ,①AOC =α,点F 在直线AB 上且在点O 的右侧,点E 在直线CD 上(点E 与点O 不重合),连接EF ,直线EM 、FN 交于点G .(1)如图1,若点E 在射线OC 上,α=60°,EM 、FN 分别平分①CEF 和①AFE ,求①EGF 的度数;(2)如图2,点E 在射线OC 上,①MEF =m ①CEF ,①NFE =(1﹣2m )①AFE ,若①EGF 的度数与①AFE 的度数无关,求m 的值及①EGF 的度数(用含有α的代数式表示);(3)如图3,若将(2)中的“点E 在射线OC 上”改为“点E 在射线OD 上”,其他条件不变,直接写出①EGF 的度数(用含有a 的代数式表示)10.问题提出:(1)我们把两个面积相等但不全等的三角形叫做偏等积三角形,如图,ABC 中,7AC =9BC =,10AB =,P 为AC 上一点,当AP =______时,ABP 与CBP 是偏等积三角形;问题探究:(2)如图,ABD △与ACD 是偏等积三角形,2AB =,6AC =,且线段AD 的长度为正整数,过点C 作//CE AB 交AD 的延长线于点E ,求AE 的长度; 问题解决:(090)BCE <∠<︒.①ACD 与BCE 是偏等积三角形吗?请说明理由;①已知60m BE =,ACD 的面积为22100m .如图,计划修建一条经过点C 的笔直的小路CF ,F 在BE 边上,FC 的延长线经过AD 中点G .若小路每米造价600元,请计算修建小路的总造价.11.如图①,将长方形纸片沿对角线剪成两个全等的直角三角形ABC 、EDF ,其中8cm AB =,6cm BC ,10cm AC =.现将ABC ∆和EDF ∆按如图①的方式摆放(点A 与点D 、点B 与点E 分别重合).动点P 从点A 出发,沿AC 以2cm/s 的速度向点C 匀速移动;同时,动点Q 从点E 出发,沿射线ED 以a cm/s (0<<3a )的速度匀速移动,连接PQ 、CQ 、FQ ,设移动时间为t s (05t ≤≤).(1)当2t =时,2AQF BQC S S ∆∆=,求a 的值;(2)当以P 、C 、Q 为顶点的三角形与BQC ∆全等时,则=a ___________;(3)如图①,在动点P 、Q 出发的同时,ABC ∆也以3cm/s 的速度沿射线ED 匀速移动,当以A 、P 、Q 为顶点的三角形与EFQ ∆全等时,求a 与t 的值.12.如图1,在平面直角坐标系中,线段AB 与x 轴负半轴交于点A (0α,),与y 轴正半轴交于点B (0b ,),若a 、b 满足224a b b =-- (1)求A 、B 两点的坐标;(2)如图2,C 、D 在坐标轴上,且CD ①AB ,点F 在①ABO 的内部,连F A ,连FC 并延长至点G ,若①BAF =2①F AO ,①AFG =120°,求①DCG :①GCE 的值; (3)设P (m n ,),且0m n +=,若2ABPOBPSS≥,请直接写出m 的取值范围13.已知:如图四边形ABCD是正方形,①EAF=45°.(1)如图1,若点E,F分别在边BC、CD上,延长线段CB至G,使得BG=DF,若BE=4,BG=3,求EF的长;(2)如图2,若点E,F分别在边CB、DC延长线上时,求证:EF=DF﹣BE;(3)如图3,如果四边形ABCD不是正方形,但满足AB=AD,①BAD=①BCD=90°,①EAF=45°,且BC=8,DC =12,CF=6,请你直接写出BE的长.14.直线MN与直线PQ垂直相交于点O,点A在直线PQ上运动,点B在直线MN上运动.(1)如图1,已知AE BE 、分别是BAO ∠和ABO ∠角的平分线,点AB 、在运动的过程中,AEB ∠的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出AEB ∠的大小.(2)如图2,已知AB 不平行CD AD BC ,、分别是BAP ∠和ABM ∠的角平分线,又DE CE 、分别是ADC ∠和BCD∠的角平分线,点AB 、在运动的过程中,CED ∠的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出CED ∠的度数.(3)如图3,延长BA 至G ,已知BAO OAG ∠∠、的角平分线与BOQ ∠的角平分线及反向延长线相交于E F 、,在AEF △中,如果有一个角是另一个角的3倍,则ABO ∠的度数为____(直接写答案)15.在平面直角坐标系中,点A 的坐标()0,4,点C 的坐标()6,0, 点P 是x 轴上的一个动点,从点C 出发,沿x 轴的负半轴方向运动,速度为2个单位/秒,运动时间为秒,点B 在x 轴的负半轴上,且AOC 的面积:AOB 的面积3:1=.(1)求点B 的坐标;(2)若点D 在y 轴上,是否存在点P ,使以P D O 、、为顶点的三角形与AOB 全等?若存在,直接写出点D 坐标;若不存在,请说明理由;(3)点Q 是y 轴上的一个动点,从点A 出发,向y 轴的负半轴运动,速度为2个单位/秒.若P 、Q 分别从C 、A 两点同时出发,求:t 为何值时,以P Q O 、、三点构成的三角形与AOB 全等.16.已知,如图①,点D ,E ,F ,G 是ABC 三边上的点,且//FG AC , (1)若EDC FGC ∠=∠,试判断DE 与BC 是否平行,并说明理由.(2)如图①,点M 、N 分别在边AC 、BC 上,且//MN AB ,连结GM ,若60A ∠=,55C ∠=,4FGM MGC ∠=∠,求GMN ∠的度数.(3)点M 、N 分别在射线AC 、BC 上,且//MN AB ,连结GM .若A α∠=,ACB β∠=,FGM n MGC ∠=∠,直接写出GMN ∠的度数(用含α,β,n 的代数式表示)17.如图1,在ABC 中,ACB ∠为锐角,点D 为射线BC 上一点,连接AD ,以AD 为一边且在AD 的右侧作等腰直角ADF △,90DAF ∠=︒,AD AF =. (1)如果AB AC =,90BAC ∠=︒,①当点D 在线段BC 上时(与点B 不重合),如图2,线段CF ,BD 所在直线的位置关系为______,线段CF ,BD 的数量关系为______;①当点D 在线段BC 的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;(2)如果AB AC ≠,BAC ∠是锐角,点D 在线段BC 上,CF BC ⊥能成立吗?若不能,说明理由,若能,直接写出ACB ∠的度数.18.已知点C 是①MAN 平分线上一点,①BCD 的两边CB 、CD 分别与射线AM 、AN 相交于B ,D 两点,且①ABC +①ADC =180°.过点C 作CE ①AB ,垂足为E .(1)如图1,当点E 在线段AB 上时,求证:BC =DC ;(2)如图2,当点E 在线段AB 的延长线上时,探究线段AB 、AD 与BE 之间的等量关系;(3)如图3,在(2)的条件下,若①MAN =60°,连接BD ,作①ABD 的平分线BF 交AD 于点F ,交AC 于点O ,连接DO 并延长交AB 于点G .若BG =1,DF =2,求线段DB 的长.参考答案:1.(1)①15︒;①ABD AFCSS的值为13(2)30BED ∠=︒【分析】(1)①连接AE ,由已知易得30DBA ∠=︒,继而可知2BD AD =,则有AD AE =,30AED DAE ︒∠=∠=,所以AB AE AC ==,得ACE △是等腰三角形,再由三角形外角的性质即可求解.①过C 点作CH FD ⊥交延长线于H ,构造K 字形全等ABD CAH ≌,得CHAD ,AH BD =,再由AB AC AE ==可得45BEC ∠=︒,进而可得ED DF =,而BD DE =,即有BD AF AD =+,再由三角形面积公式可求比值.(2)以AB 为边作等边三角形,由ABC 是顶角为120︒的等腰三角形,易得BC 垂直平分,AN AD ND =,由40DAC ∠=︒可知20NAD DNA ︒∠=∠=,再在BE 上取M 点,使20MAB ABM ︒∠=∠=,由ASA 即可判定ABM AND △≌△,所以AM AD =,再由已有条件易得AM AE =,所以ADE 是等腰三角形,进而求出,AED BED ∠∠度数即可. 【解析】(1)解:①连接AE ,①,90AB AC BAC =∠=︒, ①=45ABC ∠︒, ①75EBC ∠=︒, ①30ABD ∠=︒,①在Rt △ABD 中,2,60BD AD BDA ︒=∠=, 又①2BD DE =, ①DE DA =,①30DEA DAE ︒∠=∠=, ①30ABD DEA ︒∠=∠=, ①AB AE =,①AE AC =, ①AEC ACE ∠=∠,又①30AEC ACE EAD ∠︒+∠=∠=, ①15DCE ∠=︒, 故答案为:15︒.①解:连接AE ,过C 点作CH FD ⊥交延长线于H ,①DF 垂直平分BE ,即90,ADE ADB DE DB ∠=∠=︒=, ①AB AE =,①90ABD BAD ∠+∠=︒, 又①90BAC ∠=︒, ①90CAH BAD ︒∠+∠=, ①ABD CAH ∠=∠, 在ABD △和CAH 中, ADB CHA ABD CAH AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩, ①(AAS)ABD CAH ≌, ①,CH AD AH BD ==, ①AB AC AE ==,又①BAC ABE AEB ACE AEC ∠=∠+∠+∠+∠, ①290BEC BAC ∠=∠=︒, ①45BEC ∠=︒,①Rt FDE △是等腰直角三角形, ①DF DE =, ①DB DF =,①3ADAF=3AD =, ①3BD AD AF AF =+=+, ①111,222ABDAFC S BD AD S AF CH AF AD ∆=⋅=⋅=⋅, ①313ABD AFCS BD AF AFS AF +== 故ABD AFCS S的值为13(2)解:以AB 为边作等边ABN ,连接DN ,①120,BAC AB AC ∠=︒=, ①30ABD ∠=︒, ①BD 垂直平分AN , ①AD ND =, ①40DAC ∠=︒, ①20NAD DNA ︒∠=∠=,在BE 上取M 点,使20MAB ∠=︒, ①10EBC ∠=︒, ①20EBA MAB ︒∠=∠=, 在ABM 和ADN △中,BAM NADABM AND AB AN ∠=∠⎧⎪∠=∠⎨⎪=⎩, ①(AAS)ABM AND ≌, ①AM AD =,①20,10,30EBA MAB EBC C ︒∠=∠=∠∠=︒︒=,①40,40AME AEM ︒︒∠=∠=,①AM AE =, ①AD AE =, ①40DAC ∠=︒, ①70AED ∠=︒,①704030BED AED AEB ∠=∠-∠=︒-︒=︒.【点评】此题是三角形综合题,主要考查了全等三角形的判定和性质,等腰三角形的性质,等腰直角三角形的性质,解本题的关键是作出辅助线构造K 字形全等和旋转全等,找出图形中等腰三角形.这也是本题的难点. 2.(1)见解析; (2)2;(3)CM FD AB +=,见解析【分析】()1由平行四边形的性质及角平分线的定义证出CMN CNM ∠=∠ ,则可得出结论;()2过点M 作MH BC ⊥于H ,由平行四边形的面积求出CE 的长,由勾股定理求出BE 的长,设CM x =,165MH ME x ==- 证明M BEM BH ∆∆≌,由全等三角形的性质求出125BH BE ==,由勾股定理可求出答案; ()3在射线FA 上截取FQ CM =,连接CQ ,证明N CFQ BC ∆∆≌,由全等三角形的性质证出,CQF CNB FCQ CBN ∠=∠∠=∠ ,由平行四边形的性质及角平分线的定义证出DQ DC =,则可得出结论.(1)证明:四边形ABCD 是平行四边形,AD //BC CF AD ⊥,CF BC ∴⊥90°BCF ∴∠= 90°CBN CNB ∴∠+∠=CE AB ⊥,°90EBC ∴∠=90°EBM EMB ∴∠+∠=BP 平分ABC ∠ABP CBP ∴∠=∠ EMB CNB ∴∠=∠ EMB CMN∠=∠CMN CNM ∴∠=∠ CMN ∴∆为等腰三角形;(2)过点M 作MH BC ⊥于H11134AF DF CF ===3,4FD CF ∴== ∴ 134AD AF FD =+=+= 90°CFD ∠= ,根据勾股定理5CD AB ∴==,CE AB CF AD ⊥⊥ 在ABCD 中,由面积相等,有:AB CE AD CF ⋅=⋅ 即544CE =⨯516CE = 165CE ∴=90°CEB ∠= 165CE =,4BC =22216121655BE BC CE ∴=-=-=() BP 平分ABC ∠,MH BC ⊥,ME AB ⊥MH ME ∴=设CM x =,165MH ME x ==-,,BEM BHM EBM HBM BM BM ∠=∠∠=∠= 125BH BE ==85CH ∴= 90°MHC ∠=22216855x x ∴-+=()() 2x ∴=2CM ∴=;(3)线段CM ,FD ,AB 之间的数量关系为CM FD AB +=理由如下:在射线FA 上截取FQ CM = 连接CQ ,,CM CN FQ CM==FQ CN ∴=AD CF =∵,AD BC =,①BC CF =90°CFQ BCN ∠=∠= ∴NCFQ BC ∆∆≌CQF CNB FCQ CBN ∴∠=∠∠=∠,四边形ABCD 是平行四边形,//AB CD∴ABP CPB ∴∠=∠BP 平分ABC ∠ ABP CBN ∴∠=∠CBN CPN ∴∠=∠FCQ CPN ∴∠=∠CPN PCN FCQ PCN ∴∠+∠=∠+∠ BNC PCQ ∴∠=∠ PCQ FQC ∴∠=∠ DQ DC ∴=CM FD CD ∴+= CD AB = CM FD AB ∴+=【点评】本题是四边形综合题,考查了平行四边形的判定与性质,全等三角形的判定与性质,角平分线的定义,等腰三角形的性质,熟练掌握全等三角形的判定与性质是解题的关键. 3.(1)B (5,0); (2)S △POC =254-52m ; (3)E (0,7).【分析】(1)根据三角形面积252AOB S =△,即可求出B (5,0); (2)证明①AOC ①①BOC (SSS ),根据S △AOC +S △BOC =S △AOB =252,可得S △BOC =254,过点P 作PH ①OB 于点H ,表示出yP =m ,PH =m .所以S △OPB =12OB ·PH =12×5m =52m ,进一步可求出S △POC =S △BOC -S △BOP =254-52m ; (3)延长OC 交BE 于点G ,过点C 作CK ①OA 于点K .证明①CAK ①①COK (AA S ),①BCG ①①OCP (A S A ),①P AF ①①GOE (S A S ),可得:BG :GE =OP :PF =5:7.过点G 分别作GM ①OA 于点M ,GN ①OB 于点N .证明GM =GN .根据S △EOG =12OE ·GM =12GE ·OD ,S △BOG =12OB ·GN =12BG ·OD ,可得OE :OB =GE :GB =7:5,进一步可求出OE =7,即E (0,7).【解析】(1)解:①A (0,5), ①OA =5.①S △AOB =12OA ·OB =52OB =252,①OB =5, ①B (5,0),(2)解:①点C 为AB 中点, ①AC =B C .在①AOC 和①BOC 中, OA OBAC BC OC OC =⎧⎪=⎨⎪=⎩①①AOC ①①BOC (SSS ), ①S △AOC =S △BOC ,又①S △AOC +S △BOC =S △AOB =252, ①S △BOC =254. 过点P 作PH ①OB 于点H ,如图2,①yP=m,①PH=m.①S△OPB=12OB·PH=12×5m=52m,①S△POC=S△BOC-S△BOP=254-52m.(3)解:如图3,延长OC交BE于点G,过点C作CK①OA于点K.①①AKC=①BKC=90°,①①AOC①①BOC,①①AOC=①BOC,又①①AOC+①BOC=90°,①①COK=45°.同理,①CAK=45°,①①CAK=①COK,在①CAK和①COK中,CK CKCKA CKO ⎪=⎨⎪∠=∠⎩①①CAK ①①COK (AA S ), ①CA =CO , 又①CA =CB , ①CO =C B . ①①AOC ①①BOC , ①①ACO =①BCO , 又①①ACO +①BCO =180°, ①①OCP =90°,①①BCG =180°-①OCP =180°-90°=90°. ①①BCG =①OCP . ①OP ①BE 于点D , ①①BDP =90°.在Rt ①OCP 中,①COP =90°-①OPC ; 在Rt ①BDP 中,①CBG =90°-①BPD , 又①①OPC =①BPD , ①①COP =①CBG . 在①BCG 和①OCP 中, CBG COP BCG OCP CB CO ∠=∠⎧⎪∠=∠⎨⎪=⎩①①BCG ①①OCP (A S A ), ①CG =CP ,BG =OP①AP =AC +CP =OC +CG =OG , ①AE =OF ,①AE +OA =OF +OA ,即OE =AF , 在①P AF 和①GOE 中,AF OEAP OG ⎪=⎨⎪=⎩①①P AF ①①GOE (S A S ), ①PF =GE .①BG :GE =OP :PF =5:7.过点G 分别作GM ①OA 于点M ,GN ①OB 于点N . ①①AOG =①BOG , ①OG 平分①AOB , 又①GM ①OE ,GN ①OB , ①GM =GN .①S △EOG =12OE ·GM =12GE ·OD ,S △BOG =12OB ·GN =12BG ·OD , ①OE :OB =GE :GB =7:5 又①OB =5, ①OE =7, ①E (0,7)【点评】本题考查直角坐标系与三角形的综合,难度较大,解题的关键是掌握全等三角形的判定及性质,角平分线的性质定理,并能够熟练运用. 4.(1)①115°;①80°; (2)y =90°+12x ;理由见解析;(3)OF 至少要71米.【分析】(1)如图1,根据三角形的内角和定理由①BAC =50°可求得①ABC +①ACB = 130°,再根据角平分线的定义得①DBC =12①ABC ,①ECB =12①ACB ,从而可求得∠DBC +①ECB = 1130=652⨯︒︒,于是可求得y 的值,①先由三角形的内角和定理求得①OBC +①OCB =50°,再由BD 平分①ABC , CE 平分①ACB ,求得①ABC +①ACB =2①OBC +2①OCB =100°,从而即可求得x ;(2)如图2,用三角形的内角和求得①ABC +①ACB = 180°-x ,再角平分线求得①DBC =12①ABC ,①ECB=12①ACB,于是可得①DBC+①ECB=12( 180°-x ) =90°-12x,最后利用三角形的内角和即可得y=90°+12x,(3)如图3,在BC_上取点M和N,使BM=BE,CN=DC,先证明①BEO①①BMO,①ODC①①ONC,得①BOM=①BOE,①NOC=①DOC,OM=OE,ON=OD,从而由①BAC= 120°,得①OBC+①OCB=180302A︒-∠=︒,于是有①BOM=①NOC=30°,计算①MON=90°,从而得S△OMN=6000(米2),于是即可利用面积求得OF的最小值.(1)解①如图1,①①x=50°即①BAC=50°,①BAC+①ABC+①ACB=180°,①①ABC+①ACB= 130°,①BD平分①ABC,CE平分①ACB,①①DBC=12①ABC,①ECB=1 2①ACB,∠∠DBC+①ECB= 12(①ABC+①ACB ) =1130=652⨯︒︒,①①BOC+∠DBC+①ECB=180°,①y=①BOC=180°-65°=115°,故答案为① 115°;①①y=130°即①BOC=130°,①BOC+①OBC+①OCB=180°,①①OBC+①OCB=50°,①BD平分①ABC,CE平分①ACB,①①ABC=2①OBC,①ACB=2①OCB,①①ABC+①ACB=2①OBC+2①OCB=100°,①①BAC+①ABC+①ACB=180°,①x=①BAC=180°- 100°=80°,故答案为① 80°;(2)解:如图2,y=90°+12x,理由如下:①①BAC=x,①BAC+①ABC+①ACB= 180°,①①ABC+①ACB= 180°-x,①BD平分①ABC,CE平分①ACB,①①DBC=12①ABC,①ECB=12①ACB,①①DBC+①ECB=12(①ABC+①ACB) =12( 180°-x ) =90°-1 2x,①①BOC+①DBC+①ECB=180°,①y=①BOC=180°- ( 90°-12x ) =90°+12x,故答案为①y =90°+12x ;(3)解:如图3,在BC _上取点M 和N ,使BM =BE , CN =DC ,①BD , CE 分别是①ABC 、①ACB 的角平分线,①①EBO =①MBO ,①DCO =①NCO ,①BO =BO , CO =CO ,BM =BE , CN =DC ,①①BEO ①①BMO ,①ODC ①①ONC ,①①BOM =①BOE ,①NOC =①DOC , OM =OE ,ON =OD , ①①BAC = 120°,①①OBC +①OCB =180302A︒-∠=︒,①①BOE =①OBC +①OCB =30°=①DOC ,①BOC =150°,①①BOM =①NOC =30°,①①MON =①BOC -①BOM -①NOC =150°-30°-30°=90°,①S △OMN =11200060002OM ON OE OD ==⨯=(米2),①BC - BE -CD = 170米, ①MN = BC -BM -CN = BC - BE -CD = 170米,①①OMN 的底边MN 上的高为:260001200017071MN ⨯÷=÷≈(米)①OF 至上要71米,答①出水管OF 至少要71米.【点评】本题考查全等三角形的判定和性质,角平分线的定义,三角形面积等知识,作辅助线,利用角平分线构造全等三角形是解题的关键. 5.(1)1,3a b ==- (2)NEQEQPMNE 或360MNENEQEQP 或PQFMNENEQ(3)①ADF BCF S S =△△;①m 的值为2-或5.【分析】(1)由由()0,4M 平移到()2,1P --确定平移的方式,从而可得答案;(2)分三种情况讨论:如图,当E 在NQ 的左边时,连接NQ ,如图,当E 在NQ 的右边,直线MN 的左边时,(包括E 在这两条直线上),如图,当E 在直线MN 的右边时,记直线MN 与EQ 的交点为F ,再根据平行线的性质,三角形的内角和定理与三角形的外角的性质可得答案;(3)①当01t <<时,如图,由题意可得:0,2,3,0,A B2,3,22,33,AD t BC t OD t OC t 记四边形OCFD 的面积为m ,再分别表示两个三角形的面积即可得到答案;①由7,ABFS可得,C D 都在负半轴上,再分两种情况讨论:交点F 在第三象限,如图,证明2,3nm 即2,,3F m m 作A ,F 作x 轴的平行线,过F ,B 作y轴的平行线,交点分别即为L ,P ,Q ,则四边形LFQP 为矩形,再利用面积列方程,如图,当交点F 在第一象限,同理利用面积列方程即可. (1)解:由()0,4M 平移到2,1,P 而()3,2N 平移到,,Q a b ①321,253,a b(2)如图,当E 在NQ 的左边时,连接NQ ,由平移可得:,MN PQ ∥180,MNQ PQN EQPMNEENQEQN180,NEQ ENQ EQN ,NEQEQPMNE如图,当E 在NQ 的右边,直线MN 的左边时,(包括E 在这两条直线上),MNQ PQN QNE NEQ NQE同理可得:180,180, MNE NEQ EQP360,如图,当E在直线MN的右边时,记直线MN与EQ的交点为F,PQF NFE同理:,NFE MNE NEQ,①PQF MNE NEQ(3)①当01t<<时,如图,由题意可得:0,2,3,0,A B 2,3,22,33,AD t BC t OD t OC t记四边形OCFD 的面积为m , 123333,2ADF AOC SS m t m t m 132233,2BCF BOD S S mt m t m ①.ADF BCF SS ①7,ABF S 则,C D 都在负半轴上,交点F 在第三象限,如图,同理可得:,ADF BCF S S 而,,F m n 1123,22t m t n解得:2,3n m即2,,3F m m7,ABFS作A,F作x轴的平行线,过F,B作y轴的平行线,交点分别即为L,P,Q,则四边形LFQP为矩形,2112123223237,322323m m m m m m解得:2,m=-如图,当交点F在第一象限,同理可得:21211222337, 323223m m m m m m解得:5,m=综上:m的值为2-或5.【点评】本题考查的是坐标与图形,坐标系内图形的平移,平行线的性质,三角形的内角和定理的应用,三角形的外角的性质,利用割补法求解图形的面积,一元一次方程的应用,整式的乘法运算,本题的综合程度高,清晰的分类讨论是解本题的关键.6.(1)6,3,(0,3)-(2)①26m n-=;①(2,2)-或(4,)1-(3)OFC FCGOEC∠+∠∠的值为2,证明见解析【分析】(1)利用非负数的性质求解即可;(2)①如图1,过点D 分别作DM x ⊥轴于点M ,DN y ⊥轴于点N ,连接OD ,利用面积法求解即可;①如图11-中,设直线AM 交y 轴于T ,连接DT ,CM ,CM '.分两种情形:当点M 在点A 的左侧时,设(,3)2m D m -,根据4CDM CTD DTM CTM S S S S ∆∆∆∆=+-=,构建方程求解,当点M '在点A 的右侧时,同法可得;(3)OFC FCG OEC∠+∠∠的值不变,值为2.利用平行线的性质,三角形的外角的性质证明即可.(1)解:|3|0b -=0,30b ≥-≥, 60a ∴-=,30b -=,6a ∴=,3b =,3AB OC ==,且C 在y 轴负半轴上,(0,3)C ∴-,故答案为:6,3,(0,3)-;(2)①过点D 分别作DM x ⊥轴于点M ,DN y ⊥轴于点N ,连接OD ,如图所示:AB x ⊥轴于点B ,且点A (6,3),D (,)m n ,C (0,3)-,6OB ∴=,3OC =,MD n =-,ND m =,Δ192BOC S OB OC ∴=⨯=, 又ΔΔΔBOC BOD COD S S S =+1122OB MD OC ND =⨯+⨯116()322n m =⨯⨯-+⨯⨯ 332m n =-, ∴3392m n -=,26m n ∴-=, m ∴、n 满足的关系式为26m n -=,故答案为:26m n -=;①设直线AM 交y 轴于T ,连接DT ,CM ,CM ',如图所示:当点M 在点A 的左侧时,设(,3)2m D m -, 4CDM CTD DTM CTM S S S S ∆∆∆∆=+-=, ∴11164(33)4642222m m ⨯⨯+⨯⨯-+-⨯⨯=, 解得2m =,(2,2)D ∴-,当点M '在点A 的右侧时,设(,3)2m D m -, 4CDM CTD DTM CTM S S S S '''∆∆∆∆=+-=,11168338642222m m ⎛⎫∴⨯⨯+⨯⨯-+-⨯⨯= ⎪⎝⎭, 解得4m =,∴(4,1)D -,综上所述,满足条件的点D 的坐标为(2,2)-或(4,)1-,故答案为:(2,2)-或(4,)1-;(3)OFC FCG OEC∠+∠∠的值不变,值为2. 理由如下:线段OC 是由线段AB 平移得到,//BC OA ∴,AOB OBC ∴∠=∠,又BOG AOB ∠=∠,BOG OBC ∴∠=∠,根据三角形外角性质,可得2OGC OBC ∠=∠,OFC FCG OGC ∠=∠+∠,22OFC FCG FCG OBC ∴∠+∠=∠+∠2()FCG OBC =∠+∠2OEC =∠, ∴22OFC FCG OEC OEC OEC∠+∠∠==∠∠. 【点评】本题属于几何变换综合题,主要考查了非负数,坐标与图形,平行线的性质以及平移的性质,解决问题的关键是作辅助线,运用面积法,角的和差关系以及平行线的性质进行求解.7.(1)10;证明见解析;(2)AC AF ⊥,AC AF =,理由见解析;【分析】(1)①利用225010()++=+a b a b 可求出5a =,5b =,即可求出=10+AO BO ;①作NC AB ⊥交AB 与点C ,OF AB ⊥交AB 与点F ,证明()△≌△CNM DMO AAS ,再证明45=∠=︒∠BNC ENM ,利用∠+∠=∠CNE ENM DMO ,∠+∠=∠CNE BNC DMO 即可证明∠=∠BNO BMO ;(2)证明()△≌△ABC FDA SAS ,得到AC AF =,=∠∠FDA BCA ,再利用等量代换证明AC AF ⊥;【解析】(1)解:①由图可知=++AO BO a b ,①225010()++=+a b a b①22010251025+-+-=+a b a b ,即()()2255=0-+-a b ,①5a =,5b =,①=10+AO BO ;①作NC AB ⊥交AB 与点C ,OF AB ⊥交AB 与点F ,如图,①90∠+∠=︒NMC BMO ,90∠+∠=︒DOM BMO ,①∠=∠NMC DOM ,在CNM 和DMO 中,NMC DOM NCM MDO MN OM ∠=∠⎧⎪∠=∠⎨⎪=⎩①()△≌△CNM DMO AAS ,①∠=∠CNM DMO ,CN DM =,CM DO =,①OA OB =90BOA ∠=︒,①==OD BD DA ,①CM BD =,①-=-CM CD BD CD ,即DM BC =,①DM CN =,①BC CN =,①45=∠=︒∠BNC ENM ,①∠+∠=∠CNE ENM DMO ,①∠+∠=∠CNE BNC DMO ,即∠=∠BNO BMO ,(2)解:AC AF ⊥,AC AF =,理由如下:假设DE 交BC 于点G ,有已知可知:()30A -,,()0,6B ,()0,6C -,()9,0D , ①AD BC =,①DE AB ⊥①90BED ∠=︒①90∠+∠=︒EBG EGB ,90∠+∠=︒GDO OGD 且∠=∠EGB OGD ,①=∠∠EBG GDO ,在ABC 和FDA △中,=DF AB EBG GDO AD BC =⎧⎪∠∠⎨⎪=⎩①()△≌△ABC FDA SAS ,①AC AF =,=∠∠FDA BCA ,①90∠+∠=︒OAC BCA ,①90∠+∠=︒OAC FDA ,①AC AF ⊥,【点评】本题考查三角形全等的判定,等量代换,绝对值非负性的应用,直角坐标系中的图形,(1)的关键是证明()△≌△CNM DMO AAS ,(2)的关键证明()△≌△ABC FDA SAS . 8.(1)B (﹣4,﹣4),BC //AO ;(2)P (﹣4,0);(3)①PQB =①OPQ +30°或①BQP +①OPQ =150°,见解析【分析】(1)根据非负数的性质分别求出a 、c ,得到点B 的坐标,根据坐标与图形性质判断AO 和BC 位置关系;(2)过B 点作BE AO ⊥于E ,根据三角形的面积公式求出AP ,得到点P 的坐标;(3)分点Q 在点C 的上方、点Q 在点C 的下方两种情况,根据平行线的性质解答即可.【解析】解:(1)2(4)20a c c a -++-+,又2(4)0a c -+20c a -+,40a c ∴-+=,20c a -+=,解得,8a =-,4c =-,则点B 的坐标为(4,4)--,点B 的坐标为(4,4)--,点C 的坐标为(0,4)-,//BC AO .(2)过B 点作BE AO ⊥于E ,设时间经过t 秒,2PAB QBC S S ∆∆=,则2AP t =,OQ t =,4CQ t ∴=-, 4BE =,4BC =,111244222APB S AP BE AP BE t t ∆∴=⋅⋅=⋅⋅=⨯⨯=, 11(4)48222BCQ S CQ BC t t ∆=⋅⋅=⨯-⨯=-, 2APB BCQ S S ∆∆=,42(82)t t ∴=-,解得:2t =,24AP t ∴==,4OP OA AP ∴=-=,∴点P 的坐标为(4,0)-.(3)30PQB OPQ ∠=∠+︒或150BQP OPQ ∠+∠=︒.理由如下:①当点Q 在点C 的上方时,过Q 点作//QH AO ,如图2所示,OPQ PQH ∴∠=∠,//BC AO ,//QH AO ,//QH BC ∴,30HQB CBQ ∴∠=∠=︒,OPQ CBQ PQH BQH ∴∠+∠=∠+∠,PQB OPQ CBQ ∴∠=∠+∠,即30PQB OPQ ∠=∠+︒;①当点Q 在点C 的下方时;过Q 点作//HJ AO 如图3所示,OPQ PQJ ∴∠=∠,//BC AO ,//QH AO ,//QH BC ∴,//QH BC ∴,30HQB CBQ ∴∠=∠=︒,180HQB BQP PQJ ∴∠+∠+∠=︒,30180BQP OPQ ∴︒+∠+∠=︒,即150BQP OPQ ∠+∠=︒,综上所述,30PQB OPQ ∠=∠+︒或150BQP OPQ ∠+∠=︒. 【点评】本题考查了三角形综合题,考查的是三角形的面积计算、坐标与图形性质、平行线的性质、三角形内角和定理,掌握非负数的性质、灵活运用分情况讨论思想是解题的关键.9.(1)①EGF=60°;(2)m=13,①EGF=60°﹣13α;(3)①EGF=120°+13α,见解析.【分析】(1)利用三角形外角的性质以及角平分线的性质求解;(2)(3)利用三角形外角的性质,得出①EGF与①AFE的关系式,进而求解.【解析】(1)①EM、FN分别平分①CEF和①AFE,①①MEF=12①CEF,①EFG=12①AFE,①①EGF=①MEF﹣①EFG,①①EGF=12①CEF﹣12①AFE=12(①CEF﹣①AFE)=12①COF,而①AOC=α=60°,①①COF=180°﹣60°=120°,①①EGF=60°;(2)①①CEF﹣①AFE=①COF=180°﹣α,①①CEF=180°﹣α+①AFE,①①MEF=m①CEF,①①MEF=m(180°﹣α+①AFE),①①EGF=①MEF﹣①NFE,①①EGF=m(180°﹣α+①AFE)﹣(1﹣2m)①AFE=m(180°﹣α)+(3m﹣1)①AFE,①①EGF的度数与①AFE的度数无关,①3m﹣1=0,即m=13,①①EGF=13(180°﹣α)=60°﹣13α;(3)①①BOC=①CEF+①AFE=180°﹣α,①①CEF=180°﹣α﹣①AFE,①①MEF=m①CEF=m(180°﹣α﹣①AFE),而①NFE=(1﹣2m)①AFE,①①EGF=180°﹣①MEF﹣①NFE=180°﹣m(180°﹣α﹣①AFE)﹣(1﹣2m)①AFE=180°﹣m(180°﹣α)+(3m﹣1)①AFE,①①EGF的度数与①AFE的度数无关,①3m ﹣1=0,即m =13,①①EGF =180°﹣13(180°﹣α)=120°+13α.【点评】本题重点考察三角形外角的性质,熟练掌握是解决问题的关键.10.(1)72;(2)6;(3)①是偏等积三角形,理由见解析;①42000元【分析】(1)当AP CP =时,则72AP =,证ABP CBP S S ∆∆=,再证ABP ∆与CBP ∆不全等,即可得出结论;(2)由偏等积三角形的定义得ABD ACD S S ∆∆=,则BD CD =,再证()CDE BDA AAS ∆≅∆,则2CE AB ==,ED AD =,得2AE ED AD AD =+=,然后由三角形的三边关系求解即可;(3)①过A 作AM DC ⊥于M ,过B 作BN CE ⊥于N ,证()ACM BCN AAS ∆≅∆,得AM BN =,则ACD BCE S S ∆∆=,再证ACD ∆与BCE ∆不全等,即可得出结论;①过点A 作//AN CD ,交CG 的延长线于N ,证得()AGN DGC AAS ∆≅∆,得到AN CD =,再证()ACN CBE SAS ∆≅∆,得ACN CBE ∠=∠,由余角的性质可证CF BE ⊥,然后由三角形面积和偏等积三角形的定义得12BCE S BE CF ∆=⋅,2100BCE ACD S S ∆∆==,求出70()CF m =,即可求解. 【解析】解:(1)当72AP CP ==时,ABP ∆与CBP ∆是偏等积三角形,理由如下: 设点B 到AC 的距离为h ,则12ABP S AP h ∆=⋅,12CBP S CP h ∆=⋅,ABP CBP S S ∆∆∴=,10AB =,7BC =,AB BC ∴≠,AP CP =,PB PB =, ABP ∴∆与CBP ∆不全等, ABP ∴∆与CBP ∆是偏等积三角形,故答案为:72;(2)设点A 到BC 的距离为n ,则12ABD S BD n ∆=⋅,12ACD S CD n ∆=⋅,ABD ∆与ACD ∆是偏等积三角形,ABD ACD S S ∆∆∴=,BD CD ∴=,//CE AB ,ECD B ∴∠=∠,E BAD ∠=∠,在CDE ∆和BDA ∆中,ECD B E BAD CD BD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()CDE BDA AAS ∴∆≅∆,2CE AB ∴==,ED AD =,2AE ED AD AD ∴=+=,线段AD 的长度为正整数,AE ∴的长度为偶数,在ACE ∆中,6AC =,2CE =,6262AE ∴-<<+,即:48AE <<,6AE ∴=;(3)①ACD ∆与BCE ∆是偏等积三角形,理由如下: 过A 作AM DC ⊥于M ,过B 作BN CE ⊥于N ,如图3所示:则90AMC BNC ∠=∠=︒,ACB ∆、DCE ∆是等腰直角三角形,90ACB DCE ∴∠=∠=︒,AC BC =,CD CE =,3603609090180BCN ACD ACB DCE ∴∠+∠=︒-∠-∠=︒-︒-︒=︒,180ACM ACD ∠+∠=︒, ACM BCN ∴∠=∠,在ACM ∆和BCN ∆中,AMC BNC ACM BCN AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()ACM BCN AAS ∴∆≅∆,AM BN ∴=,12ACD S CD AM ∆=⋅,12BCE S CE BN ∆=⋅,ACD BCE S S ∆∆∴=,180BCE ACD ∠+∠=︒,090BCE ︒<∠<︒, ACD BCE ∴∠≠∠,CD CE =,AC BC =,ACD ∴∆与BCE ∆不全等, ACD ∴∆与BCE ∆是偏等积三角形;①如图4,过点A 作//AN CD ,交CG 的延长线于N ,则N GCD ∠=∠,G 点为AD 的中点,AG GD ∴=,在AGN ∆和DGC ∆中,N GCDAGN DGC AG DG ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()AGN DGC AAS ∴∆≅∆,AN CD ∴=,CD CE =,AN CE ∴=, //AN CD ,180CAN ACD ∴∠+∠=︒,90ACB DCE ∠=∠=︒,3609090180ACD BCE ∴∠+∠=︒-︒-︒=︒, BCE CAN ∴∠=∠,在ACN ∆和CBE ∆中,AN CE CAN BCE AC CB =⎧⎪∠=∠⎨⎪=⎩, ()ACN CBE SAS ∴∆≅∆,ACN CBE ∴∠=∠,1809090ACN BCF ∠+∠=︒-︒=︒, 90CBE BCF ∴∠+∠=︒,90BFC ∴∠=︒,CF BE ∴⊥.由①得:ACD ∆与BCE ∆是偏等积三角形,12BCE S BE CF ∆∴=⋅,2100BCE ACD S S ∆∆==, 22210070()60BCE S CF m BE ∆⨯∴===, ∴修建小路CF 的总造价为:6007042000⨯=(元).【点评】本题考查了新定义“偏等积三角形”的定义、全等三角形的判定与性质、等腰直角三角形的性质、三角形面积等知识;本题综合性强,熟练掌握“偏等积三角形”的定义,证明①A CM①①BCN 和①ACN ①①CBE 是解题的关键,属于中考常考题型. 11.(1)83;(2)32;(3)2a =时,2t =或 2.3a =时,5t =.【分析】(1)由题意得①BAF =①ABC =90°,BQ =at =2a ,AF =BC ,由三角形面积得2AQ =BQ ,则AB =32BQ =8,,得BQ =163=2a ,即可求得a 的值;(2)由题意得点P 与B 为对应顶点,PQ =BQ =at ,PC =BC =6,①CPQ =①ABC =90°,则AP =AC -PC =4,PQ ①AC ,得t =2,则PQ =BQ -2a ,最后根据三角形面积关系即可解答; (3)分两种情况:①AP 与EQ 为对应边,AQ 与EF 为对应边,则AP =EQ ,AQ =EF =10,求出a =2,BQ =BE -EQ =t ,则AQ =AB +BQ =8+t =10,解得t =2;①AP 与EF 为对应边,AQ 与EQ 为对应边,则AP =EF =10,AQ =EQ ,求出t -5,则AQ =EQ =5a ,得BQ =15-5a 或BQ =5a -15,最后求出a的值即可.【解析】解:(1)由题意得①BAF=①ABC=90°,BQ=at=2a,AF=BC,①112,,,22 AQF BQC AQF BQCS S S AF AQ S BC BQ ∆∆∆∆==⨯=⨯①2AQ=BQ,AQ=12BQ①AB=AQ+BQ=32BQ=8,即BQ=163①BQ=163=2a,即a=83;(2)①以P、C、Q为顶点的三角形与①BQC全等,CQ是公共边,①点P与B为对应顶点,PQ=BQ=at,PC=BC=6,①CPQ=①ABC=90°①AP=AC-PC= 10-6=4,PQ①AC,①AP=2t=4,即t=2①PQ=BQ=2a①①ABC的面积=①ACQ的面积+①BCQ的面积①1118610226222a a⨯⨯=⨯⨯+⨯⨯,解得a=32;(3)由题意得:①A=①E,则①A与①E为对应角,分两种情况:①AP与EQ为对应边,AQ与EF为对应边,则AP=EQ,AQ=EF=10,①EQ=at①at=2t,即a=2①EQ=2t①BE=3t①BQ=BE-EQ=t,①AQ= AB+BO=8+t=10解得:t=2;①AP与EF为对应边,AQ与EQ为对应边,则AP=EF=10,AQ=EQ,①2t=10①t=5,①AQ=EQ=5a,①BE=3t= 15①BQ=15-5a或BQ=5a-15当BQ =15-5a 时,AQ =15-5a +8=23-5a 或AQ =8-(15-5a )=5a -7, ①5a =23-5a 或5a =5a -7(无意义),解得a =2.3;当BQ =5a -15时,AQ =5a -15+8=5a -7或AQ =8-(5a -15)=23-5a ①5a =5a -7(无意义)或5a =7-5a 解得:a =0.7,不合题意舍去; 综上所述,a =2时,t =2或a =2.3时,t =5.【点评】本题主要考查全等三角形的综合问题及动点问题,根据题意找到动点之间的联系以及掌握分类讨论思想成为解答本题的关键.12.(1)点(4,0)A -,点(0,2)B ;(2)2;(3)4m ≤-或405m -≤<或0m > 【分析】(1)由非负数的性质可求2b =,4a =-,即可求解;(2)设FAO α∠=,则2BAO α∠=,用α分别表示DCG ∠和GCE ∠,即可求解; (3)分三种情况讨论,利用面积的和差关系可求解. 【解析】解:(1)224a b b =--,20b ∴-≥,20b -≥,2b ∴=,4a ∴=-,∴点(4,0)A -,点(0,2)B ;(2)设FC 与AD 交于点T ,设FAO α∠=,则2BAO α∠=,//AB CD ,3ODC BAO α∴∠=∠=,18012060FTA αα∴∠=︒-︒-=︒-,60OTC FTA α∴∠=∠=︒-,90(60)30OCT αα∴∠=︒-︒-=︒+,30GCE OCT α∴∠=∠=︒+, 903DCE DOC ODC α∠=∠+∠=︒+, 602DCG DCE GCE α∴∠=∠-∠=︒+, :2DCG GCE ∴∠∠=;(3)如图21-,当点P 在AB 的上方时,0m n +=,m n ∴=-,点(4,0)A -,点(0,2)B ;4∴=OA ,2OB =,2ABP OBP S S ∆∆≥,∴11114()2()4222()2222m m m ⨯⨯-+⨯⨯--⨯⨯⨯⨯⨯-,4m ∴≤-,当点P '在AB 的下方,且在x 轴的上方时,即0m <,2ABP OBP S S ∆∆≥,∴1111424()2()22()2222m m m ⨯⨯-⨯⨯--⨯⨯-⨯⨯⨯-,45m ∴≥-,405m ∴-≤<, 当点P ''在x 轴的下方时,即0m >,2ABP OBP S S ∆∆≥,∴11114242222222m m m ⨯⨯+⨯⨯+⨯⨯≥⨯⨯⨯,4m ∴≥-, 0m ∴>,综上所述:4m ≤-或405m -≤<或0m >.【点评】本题是三角形综合题,考查了平行线的性质,非负性,三角形内角和定理,三角形的外角性质,利用分类讨论思想解决问题是解题的关键. 13.(1)EF =7;(2)见解析;(3)BE =5613【分析】(1)由“SAS ”可证①ABG ①①ADF ,可得AG =AF ,①DAF =①BAG ,由“SAS ”可证①GAE ①①F AE ,可得EF =GE =BE +BG =7;(2)在DF 上截取DM =BE ,由“SAS ”可证①ABE ①①ADM ,可得AE =AM ,①EAB =①DAM ,由“SAS ”可证①AEF ①①AMF ,可得EF =FM ,可得结论;(3)同(2)可证EF =DF ﹣BE ,可得BE +EF =18,由勾股定理可得EF 2=CF 2+CE 2,可求BE 的长.【解析】证明:(1)①四边形ABCD 是正方形, ①AB =AD =BC =CD ,①D =①ABC =90°, ①AB =AD ,①D =①ABG ,BG =DF , ①①ABG ①①ADF (SAS ), ①AG =AF ,①DAF =①BAG , ①①EAF =45°, ①①DAF +①BAE =45°, ①①BAG +①BAE =45°=①GAE , ①①GAE =①EAF , 又①AG =AF ,AE =AE , ①①GAE ①①F AE (SAS ), ①EF =GE ,①EF =GE =BE +BG =4+3=7; (2)如图2,在DF 上截取DM =BE ,①AD=AB,①ABE=①ADM=90°,DM=BE,①①ABE①①ADM(SAS),①AE=AM,①EAB=①DAM,①①EAF=45°,且①EAB=①DAM,①①BAF+①DAM=45°,①①MAF=45°=①EAF,又①AE=AM,AF=AF,①①AEF①①AMF(SAS),①EF=FM,①DF=DM+FM,①DF=BE+EF,①EF=DF﹣BE;(3)如图,在DF上截取DM=BE,同(2)可证EF=DF﹣BE,①DF=BE+EF=CF+DC=18,。
人教版八年级上册数学期末动点问题压轴题专题训练(含解析)

人教版八年级上册数学期末动点问题压轴题专题训练(1)当时,点C 的坐标为 .(2)动点A 在运动的过程中,试判断发生变化,请说明理由.(3)当时,在坐标平面内是否存在一点若存在,请直接写出点P 的坐标;若不存在,请说明理由.(1)如图1,当点在边上时.①求证:;②求证:;(2)如图2,当点在边的延长线上时,其他条件不变,请写出2a =3a =D BC ABD ACE ≌△△BC DC CE =+D BC(1)请直接写出点A 和点B 的坐标;(2)请判断的形状并说明理由;(3)下列结论:①四边形为定值.请选择一个正确的结论并说明理由.(1)求证:;(2)求的面积;(3)点M ,N 分别是线段,上的动点,连接,求的最小值.DEF OEDF OEF DFE ∠+∠CD CE =CDE BC BD MN 12MN DN +(1)求出点的坐标.(2)求证:.(3)数学活动小组进行深入探究后发现变,你同意这个说法吗?请说明理由B OD BC =(1)如图①,请找出图中与相等的角,并说明理由;(2)如图②,交轴于点,过点作轴于点,求证:平分;(3)如图③,若,点在轴正半轴移动,且,取,连交轴OAB ∠BC x M C CD x ⊥,2D AM CD =AD BAC ∠()3,0A B y OB OA >()0,3P CP x边三角形,使其与点在直线的两侧,与直线相交于点(点与点A 不重合),连接.(1)如图,当时,①求证:;②在点A 运动的过程中,的度数是否会发生改变?如果会请说明理由,如果不会请求出的度数;(2)在点A 运动的过程中,试探究线段,,之间的数量关系.11.在平面直角坐标系中,点在轴的正半轴上,点在第一象限,,.(1)如图1,求证:是等边三角形;(2)如图1,若点M 为y 轴正半轴上一动点,以为边作等边三角形,连接并延长交轴于点,求证:;(3)如图2,若,,点为的中点,连接、交于,请问、与之间有何数量关系,并证明你的结论.12.在平面直角坐标系中,点A 为y 轴正半轴上一点,点B 为x 轴上一动点,连接ABD C AB DC l E E EB 120BAC ∠<︒ABE ACE =∠∠DCB ∠DCB ∠EA EB ED A y B OB AB =150BOP ∠=︒OAB BM BMN NA x P 2AP AO =BC BO ⊥BC BO =D CO AC DB E AE BE CE,以为腰作等腰,.(1)如图1,点B 在x 轴负半轴上,点C 的坐标是,直接写出点A 和点B 的坐标;(2)如图2,点B 在x 轴负半轴上,交x 轴于点D ,若平分.且点C 的纵坐标是,求线段的长;(3)如图3,点B 在x 轴正半轴上,以为边在左侧作等边,连接,,若,且,求的面积.13.等腰直角中,,,,点、分别是轴,轴上两个动点,直角边交轴于点,斜边交轴于点.(1)如图1,已知点的横坐标为,直接写出点的坐标;(2)如图2,若点为轴上的固定点,且,当点在轴正半轴运动时,分别以、为直角边在第一、二象限作等腰直角和等腰直角,连接交轴于点,问当点在轴的正半轴上运动时,的长度是否变化?若变化请说明理由;若不变化,请求出的长度.14.在平面直角坐标系中,点为坐标原点,点、分别位于轴和轴AB AB Rt ABC △90BAC ∠=︒(2,2)-AC BD ABC ∠3-BD BC BC BCE EO CO 60COE ∠=︒8CO =AOC ABC 90BAC ∠=︒AB AC =ABC C ∠=∠B A x y AC x D BC y E C 2-A A x ()6,0A -B y OB AB BOD ABC CD y P B y BP BP O ()6,0B -()0,6A x y上,连接,交轴于点.(1)求点的坐标;(2)动点从出发以个单位/秒的速度沿轴向终点运动,连接,将线段绕着点逆时针旋转后得到线段,与为对应点.连接、,为的面积,用含的式子表示;(3)在()的条件下,连接,过点作于,交轴于,交于,若,求点的坐标.15.如图①,在中,,现有一动点,从点出发,沿着三角形的边运动,回到点停止,速度为,设运动时间为秒.(1)如图①,当的面积等于面积的一半时,求的值:(2)如图②,点在边上,点在边上,在的边上,若另外有一个动点与点同时从点出发,沿着边运动,回到点停止.在两点运动过程中的某一时刻,以为顶点的三角形恰好与全等,求点的运动速度.16.如图,在平面直角坐标系中,,点在轴正半轴上,.AB CA AB ⊥x C C P B 2x C AP AP A 90︒AQ P Q PQ CQ S PCQ △t S 2BQ A AH BQ ⊥G x H PQ AC M :2:1APM AQM S S = H Rt ABC △90,12cm,16cm,20cm B AB BC AC ∠=︒===P A AB BC CA →→A 2cm /s t ABP ABC t D BC 4cm CD =E AC 5cm,,3cm CE ED BC ED =⊥=ABC Q P A AC CB BA →→A ,,A P Q EDC △Q ()0,9A B x 45OAB ∠=︒(1)求出点坐标;(2)动点从点出发,以每秒个单位长度的速度沿轴正半轴运动,同时点从点出发,以相同速度沿轴向左运动,连接,过点作交直线于点,连接,设点的运动时间为,请用含的式子表示的面积;(3)在(2)的条件下,直线与直线交于点,当时,求点坐标.17.已知中,,过点的直线交轴于,其中是方程组的解,(1)求的值(2)动点从点出发,沿线段以每秒1个单位的速度运动,运动时间为秒;请用含的式子表示线段的长度;并直接写出此时的取值范围;(3)在(2)的条件下,当为何值时,直线与直线互相垂直.18.在平面直角坐标系中,O 为坐标原点,直线交x 轴的正半轴于点A ,交y 轴的B P O 1y Q B x PQ O OG PQ ⊥AB G PG P t t OPG PQ AB H 72OPG S =△H AOB OA OB a ==A AM x (),0M b ,a b 3830a b a b +=⎧⎨+=⎩,a b P A AO t t OP t t BP AM AB(1)如图1求的长;(2)如图2动点E 在第二象限,点E 的坐标为,连接,,请写出面积s 与t 的关系;(3)在(2)的条件下,如图3点F 在第一象限,连接、、,,连接,当,求的值.OD (,)t m DE OE ODE FE FD FA 30ADF ∠=FE FA =EB 12,4EBO ODA ODA EFA EOB ∠=∠∠+∠=∠t m +参考答案:1.(1)(2)动点A 在运动的过程中,的值不变,(3)或或【分析】本题考查全等三角形判定及性质.(1)根据题意过点C 作轴于点,证明出,利用全等性质即可得到本题答案;(2)由(1)得,利用全等性质及点坐标表示线段长即可得到本题答案;(3)根据题意分3种情况讨论P 点位置,利用全等三角形性质及判定即可得到本题答案.【详解】(1)解:如下图,过点C 作轴于点E ,则,,∵是等腰直角三角形,∴,∴,∴.在和中,∴(AAS ),∵,∴,∴,∴;(2)解:动点A 在运动的过程中,的值不变.理由如下:(2,3)-+c d (4,)1-(3,2)--(2,1)-CE y ⊥E ACE BAO ≌ACE BAO ≌CE y ⊥CEA AOB ∠=∠ABC ,90AC BA BAC =∠︒=90ACE CAE BAO CAE ∠+∠=︒=∠+∠ACE BAO ∠=∠ACE △BAO CEA AOB ACE BAOAC BA ∠=∠⎧⎪∠=∠⎨⎪=⎩ACE BAO ≌(0,1),(0,2)B A -12BO AE AO CE ====,123OE =+=2,3C -()+c d由(1)知,,∵,,∴,∴,∴,又∵点C 的坐标为,∴,即的值不变;(3)解:存在一点P ,使与全等,符合条件的点P 的坐标是或或,分为三种情况讨论:①如下图,过点P 作轴于点E ,则,∴,∴,在和中,,∴(AAS ),∴,∴,即点P 的坐标是,②如下图,过点C 作轴于点M ,过点P 作轴于点E ,ACE BAO ≌(0,1)B (0,)A a -1,BO AE AO CE a ====1OE a =+(,1)C a a --(,)c d 11c d a a +=--=-+c d PAB ABC (4,)1-(3,2)--(2,1)-PE x ⊥90PBA AOB PEB ∠=∠=∠=︒90,90EPB PBE PBE ABO ∠+∠=︒∠+∠=︒EPB ABO ∠=∠PEB △BOA △EPB OBA PEB BOA PB BA ∠=∠⎧⎪∠=∠⎨⎪=⎩PEB BOA △≌△1,3PE BO EB AO ====314OE =+=(4,)1-CM x ⊥PE x ⊥则.∵,∴,∴,∴,∴,在和中,,∴(AAS ),∴.∵,∴,即点P 的坐标是;③如下图,过点P 作轴于点E ,则.∵,∴,∴,90CMB PEB ∠=∠=︒CAB PAB △≌△45,PBA CBA BC BP ∠=∠=︒=90CBP ∠=︒90,90MCB CBM CBM PBE ∠+∠=︒∠+∠=︒MCB PBE ∠=∠CMB BEP △MCB EBP CMB BEP BC PB ∠=∠⎧⎪∠=∠⎨⎪=⎩CMB BEP △≌△,PE BM CM BE ==3,4),10C B -((,)2,413PE OE BE BO ==-=-=(3,2)--PE x ⊥90BEP BOA ∠=∠=︒CAB PBA △≌△,90AB BP CAB ABP =∠=∠=︒90,90ABO PBE PBE BPE ∠+∠=︒∠+∠=︒∴.在和中,,∴(AAS ),∴,∴,即点P 的坐标是,综上所述,符合条件的点P 的坐标是或或.2.(1)①见解析;②见解析;(2),见解析【分析】本题主要考查了等边三角形,全等三角形.(1)①根据等边三角形的性质得出,,,根据得出,从而说明三角形全等;②根据全等的性质得出,然后根据即得;(2)根据等边三角形的性质得出,,,根据得出,从而说明,根据全等的性质得出,然后根据即得.【详解】(1)证明:①∵和是等边三角形,∴,,.∴,∴.在和中,,∴;②∵,ABO BPE ∠=∠BOA △PEB △ABO BPE BOA PEB BA PB ∠=∠⎧⎪∠=∠⎨⎪=⎩BOA PEB △≌△1,3PE BO BE OA ====312OE BE BO =-=-=(2,1)-(4,)1-(3,2)--(2,1)-BC CD CE +=AB AC =AD AE =60BAC DAE ∠=∠=︒BAC DAC DAE DAC ∠-∠=∠-∠BAD EAC ∠=∠BD CE =BC BD CD =+AB AC =AD AE =60BAC DAE ∠=∠=︒BAC DAC DAE DAC ∠+∠=∠+∠BAD EAC ∠=∠ABD ACE ≌△△BD CE =+=BC CD BD ABC ADE V 60BAC DAE ∠=∠=︒AB BC AC ==AD DE AE ==BAC DAC DAE DAC ∠-∠=∠-∠BAD CAE ∠=∠ABD △ACE △AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩()SAS ABD ACE △≌△ABD ACE ≌△△∵,,∴,∴是等腰直角三角形,即∵点D 是线段中点,∴,,(0,6)A (6,0)B 6O A O B ==AOB ∠AB OD AB ⊥12OD AD AB ==∠∵,,∴在中,∵在(1)中已求出根据翻折可知:、∴N 点关于的对称点H 在根据对称性有:∴,∴是等边三角形,∵N 点关于的对称点是点H ,3BD =30CBD ∠=︒DG Rt BDG △12DG BD =CE CD =11BDC BKC △BE BK DBC KBC ∠=∠60BDK DBC KBC ∠=∠+∠=︒BDK BE NH如图,,即:,在中,PNC DNC∠=∠24PNC αβ∠==2αβ=MCN DCM DCN x β∠=∠+∠=+MCN △180MCN DCN NMC ∠+∠+∠=2180x βαα+++=︒3180x βα++=︒解得:,.II.当点在线段上时,如图,,,即:,在中,,,即:联立得:,解得:,此时:,不合题意舍去;III .当点在线段上时,如图,,52550x βα=︒⎧⎪=︒⎨⎪=︒⎩∴5DCM ∠=︒N PD 180PNC DNC ∠+∠=︒∴24180αβ+=︒290αβ+=︒∴MCN DCM DCN x β∠=∠+∠=+ CMN PCN MCN CMN x βα∠=∠+∠=++∴4180PCN NDC x βαβ∠+∠=+++=︒5180x βα++=︒2602905180x x ααββα+=︒⎧⎪+=︒⎨⎪++=︒⎩11.2526.2537.5x βα=︒⎧⎪=︒⎨⎪=︒⎩11.2526.5PCN DCN ∠=︒<∠=︒N DM PNC DNC ∠=∠【详解】(1)解:过点B 作轴于点D ,∵,∴,∵轴,∴,∵,∴,∴,在和中,,∴,∴,∵,∴;(2)解:∵,∴,∴,∵轴,∴,∴,∴,在和中,BD y ⊥()()6,0,0,3A C -6,3OA OC ==BD y ⊥90BCD CBD ∠+∠=︒90ACB ∠=︒90BCD ACO ∠+∠=︒ACO CBD ∠=∠ACO △CBD △90AOC CDB ACO CBDAC BC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩≌ACO CBD 6,3OA CD OC BD ====()0,3C ()3,3B -90ACB ∠=︒90BCF ∠=︒90CBF F ∠+∠=︒BE y ∥90AEF ∠=︒90CAD F ∠+∠=︒CAD CBF ∠=∠CAD CBF V∴,∴,∵,∴∴.【点睛】本题主要考查了三角形综合,折叠的性质,全等三角形的判定和性质,角平分线的性质,解题的关键是掌握全等三角形的判定方法,全等三角形对应边相等,对应角相等;折叠前后对应角相等;角平分线上的点到两边距离相等.7.(1)(2)见解析(3)的度数总是保持不变,理由见解析【分析】本题考查了全等三角形的性质与判定,等腰三角形的性质,坐标与图形;(1)根据等腰三角形的性质解答即可;(2)根据等式的性质得出,进而利用证明与全等,进而解答即可;(3)根据全等三角形的性质得出,进而利用平角的定义解答即可.【详解】(1)解:如图所示,过作轴于,()Rt Rt HL EFO EFN ≌FN FO =(),0F t FO t=-2FG HG t +=-()2,0-COD ∠BAC OAD ∠=∠SAS BAC OAD AOD ABO ∠=∠A AE x ⊥E),点C 是的中点,,D 作轴于点F ,,,4=AB 114222AB ==⨯=DF x ⊥90DFO =︒90FDO DOF +∠=︒),的坐标为,关于x 轴的对称点,则的坐标为,交x 轴于点,则为定值,此时的周长最小.作轴于点Q ,114222AB '==⨯=M '()0,2M '''M ''M AM ''P PAM C AM AP ''=+ AM 'PAM '△()4,4A -AQ y ⊥对于(3),作轴,先证明,可得,再得出,进而得出,根据等腰直角三角形的性质和判定即可得出答案.【详解】(1).理由:,;(2)证明:如图②中,延长交的延长线于点..∵,,,.,即.垂直平分,平分.(3)的长度不变,.理由:如图③中,过点作轴于点...CH y ⊥≌CHB BOA △△,3===CH BO BH OA 3==OA OP ==OB PH CH OAB OBC ∠=∠90,90OAB OBA OBC OBA ∠+∠=∠+∠=︒︒ OAB OBC ∴∠=∠AB CD T ,90,90,AD CD ADT T BAM BCT BAM ⊥∴∠=∴∠+∠=∴∠=∠︒︒ BC BA ===90CB T A B M ∠∠︒()CBT ABM ASA ∴≌△△CT AM ∴=2,2AM CD CT CD =∴= CD DT =,AD CT AD ⊥∴ CT ,AC AT AD ∴=∴BAC ∠OQ 3OQ =C CH y ⊥H 90,90CHB BOA HBC HCB ∴∠=∠=∴∠+∠=︒︒90,90,ABC OBA HBC HCB OBA ∠=∴∠+∠=︒︒∴∠=∠..,..,.【点睛】本题主要考查了全等三角形的性质和判定,同角的余角相等,线段垂直平分线的性质,等腰直角三角形的性质和判定等,构造辅助线是解题的关键.10.(1)①见解析;②不变,(2)或【分析】(1)①根据垂直平分线的性质得出,再由等边对等角及各角之间的数量关系求解即可;②设与交于点M ,根据等边三角形的性质及各角之间的关系得出,即可求解;(2)分两种情况进行分析:当时,当时,分别利用全等三角形的判定和性质及等边三角形的判定和性质分析求解即可.【详解】(1)证明:①点A 、E 在线段的垂直平分线l 上,∴,∴,∴,即;②在点A 运动的过程中,的度数不变,理由如下:如图,设与交于点M ,(),CB AB CHB BOA AAS =∴ ≌△△,3∴===CH BO BH OA ()()3,0,0,3,3A P OA OP ∴== ,BH OP OB PH CH ∴=∴==90,45CHP CPH OPQ ∠=∴∠=∠=︒︒ 90,45∠=∴∠=︒=︒∠ POQ OQP OPQ 3OQ OP ∴==30DCB ∠=︒ED EB EA =+EB ED EA=+AC AB EC EB ==,AB CD 260ECB ∠=︒120BAC ∠<︒120BAC ∠>︒BC ,AC AB EC EB ==,ABC ACB EBC ECB ∠∠∠∠==ABC EBC ACB EBC ∠∠∠∠-=-ABE ACE ∠∠=DCB ∠AB CD∵是等边三角形,∴ ,∴,∴,∴,∴,∴,∵,∴,即;(2)当时,在上截取,连接,∵,∴,由(1)得直线,,∴,∴是等边三角形,∴ ,∴,即,ABD ,60AB AD BAD ∠==︒AD AC =ADC ACE ∠∠=,ABE ADC EBC ECB ∠∠∠∠==,180,180AMD EMB BED ABE EMB BAD ADC AMD ∠∠∠∠∠∠∠∠==︒--=︒--60BED BAD ∠∠==︒,EBC ECB BED EBC ECB ∠∠∠∠∠+==260ECB ∠=︒30DCB ∠=︒120BAC ∠<︒ED EF EA =AF ED DF EF =+ED DF EA =+l BC ⊥30DCB ∠=︒903060AED ∠=︒-︒=︒AEF 60,EAF BAD AE AF ∠∠==︒=–EAF BAF BAD BAF ∠∠∠∠=-BAE DAF ∠∠=∴,∴,∵,∴;当时,如图所示在上截取,连接,∵,∴,由(1)得直线,,,∴,∴F 是等边三角形,∴,∴,∴,∴,∴,∵,∴;综上可得:或.【点睛】题目主要考查线段垂直平分线的性质,全等三角形的判定和性质,等边三角形的判定和性质等,理解题意,作出相应辅助线是解题关键,同时注意进行分类讨论.11.(1)见解析(2)见解析(3),证明见解析【分析】(1)根据有一个角是的等腰三角形是等边三角形可得结论;(SAS)BAE DAF ≌ EB DF =ED DF EA =+ED EB EA =+120BAC ∠>︒EB EF EA =AF EB BF EF =+EB BF EA =+l BC ⊥30DCB ∠=︒BE BC =903060AEB AEC ∠∠==︒-︒=︒AE 60,EAF BAD AE AF ∠∠==︒=–EAF DAF BAD DAF ∠∠∠∠-=EAD BAF ∠∠=(SAS)BAF DAE ≌ BF ED =EB BF EA =+EB ED EA =+ED EB EA =+EB ED EA =+AE BE CE =+60︒(2)根据证明,得,由8字形可得,最后由含角的直角三角形的性质可得结论;(3)如图2,在上截取,先证,方法是根据题意得到三角形为等边三角形,三角形为等腰直角三角形,确定出度数,根据,且,得到度数,进而确定出为,再由,得到,再由,且夹角,利用得到三角形与三角形全等,利用全等三角形的对应边相等得到,得到三角形为等边三角形,得到,由,等量代换即可得证.【详解】(1)解:证明:,,,,是等边三角形;(2)证明:由(1)知:是等边三角形,,是等边三角形,,,,,,,,,,,,SAS MBO NBA ≌OMB ANB ∠∠=60FAM FBN ∠∠==︒30︒AC AG CE =60AEB ∠=︒ABO BOC ABD ∠AB BC =150ABC ∠=︒BAE ∠AEB ∠60︒AG CE =AE CG =AB CB =BAC BCA ∠=∠SAS BCG BAE BG BE =BEG BE EG =AE EG AG =+150BOP ∠=︒ 90AOP ︒=∠60AOB ∴∠=︒OB AB = OAB ∴ OAB 60ABO ∴∠=︒BMN BM BN ∴=60MBN ∠=︒MBO NBA ∴∠=∠AB OB = (SAS)MBO NBA ∴△≌△OMB ANB ∴∠=∠AFM BFN ∠=∠ 60FAM FBN ∴∠=∠=︒60OAP FAM ∠=∠=︒ 90AOP ︒=∠30APO ∴∠=︒;(3),理由如下:如图2,在上截取,连接,,即,,,,为的中点,平分,即,,,,,,,在和中,,,,为等边三角形,,.【点睛】本题是三角形综合题,考查了等腰直角三角形的性质和判定,等边三角形的性质和判定,全等三角形的判定和性质,以及含角的直角三角形的性质,添加辅助线.12.(1),2AP AO ∴=AE BE CE =+AC AG EC =BG AG EG CE EG +=+AE CG =BC BO ⊥ BC BO =90OBC ∴∠=︒D CO BD ∴OBC ∠45CBD OBD ∠=∠=︒60ABO ∠=︒ 105ABD ∴∠=︒150ABC ∠=︒AB OB BC == 15BAC BCA ∴∠=∠=︒154560AEB ∴∠=︒+︒=︒ABE CBG AB CB BAE BCG AE CG =⎧⎪∠=∠⎨⎪=⎩(SAS)ABE CBG ∴△≌△BG BE ∴=BEG ∴△BE EG ∴=AE AG EG CE BE ∴=+=+30︒()02A ,()40B -,∴,∵∴,∵,∴,,90ADC BOA ∠=︒=∠90CAD BAO ABO ∠+∠=︒=∠CAD ABO ∠=∠(2,2)C -2CD =2OD =∴,,∴,;(2)解:如图2,作轴,交轴于,交的延长线于,∴,∵平分,∴,,,∴,∴,∵,∴,∵,∴,∴,∵,,∴,∴,∴的长为6;(3)解:∵为等边三角形,∴,,如图3,在上截取,使,连接,2AO CD ==4BO AD AO OD ==+=()02A ,()40B -,CM x ⊥x N BA M 90BNM BNC ∠=︒=∠BD ABC ∠MBN CBN ∠=∠BN BN =90BNM BNC ∠=︒=∠()ASA MBN CBN ≌3MN CN ==∥CM AO ACM CAO ∠=∠90CAO BAO ABD BAO ∠+∠=︒=∠+∠CAO ABD ∠=∠ACM ABD ∠=∠AC AB =90MAC DAB ∠=︒=∠()ASA ACM ABD ≌6BD CM CN MN ==+=BD BCE BE CE =60BEC EBC ECB ∠=∠=∠=︒OC OF OF OE =EF∴是等边三角形,∴,∴∵,∴,∴,OEF OE EF =60OEF ∠=︒=∠OEF BEF BEC ∠-∠=∠-∠OE EF =BEO CEF ∠=∠()SAS BEO CEF ≌OBE FCE ∠=∠13.(1)(2)【分析】(1)如图①,过作 轴于, 证明可得从而可得答案;(2)如图①,过点作 轴于点.证明 ,可得 ,再证明,从而可得: .【详解】(1)解: 如图①,过作 轴于,∴,∵,∴,∴,∵,∴.∴,,∴,∴,故答案为 : .(2)的长度不变,理由如下:如图②, 过点作 轴于点.()0,23BP =C CF y ⊥F ,ACF BAO ≌CF AO =C CE y ⊥E CBE BAO ≌,6CE BO BE AO ===CPE DPB ≌3BP EP ==C CF y ⊥F 90,90CFA AOB ACF CAF ∠=∠=︒∠+∠=︒90BAC ∠=︒90CAF OAB ∠+∠=︒ACF OAB ∠=∠AC AB =()AAS ACF BAO ≌CF AO =2c x =- 2CF AO ==()0,2A ()0,2BP C CE y ⊥E∵ ,∴∵∴ .∵90ABC ∠=︒90CBE ABO ∠+∠=︒90BAO ABO ∠+∠=︒CBE BAO ∠=∠90CEB AOB ∠=∠=∵,∴,在和中,90BAC PAQ ∠=∠=︒BAP CAQ ∠=∠BAP △CAQ AB AQ =⎧∴四边形为正方形,∴,过作于点,∵AOCN 6OA CN OC ===T TL CN ⊥L AH BQ⊥AOH TLQ ≌∴,解得;②当点在上,点∴,解得;3AP DE cm AQ EC ===,352x =103x =cm/s P AB 5AP EC cm AQ ==,532x =65x =cm/s∴点P 的路程为∴点P 的路程为3AP ED AQ EC ===,AB +1216205AQ =++-=4543x =5AP EC cm AQ ==,AB +1216203AQ =++-=4345x =从出发,以每小时从出发,以相同速度沿,①当在线段上时,P O Q B OQ ∴=AP =t P AO,等腰,,设,,为的一个外角,RO PO ∴=∴POR 45R BAO ∴∠=∠=︒QPO α∠=45RPQ α∴∠=︒-QON BOG α∠==∠ABO ∠ OBG,,,,90HTA ∴∠=︒45HAT OAB ∠=∠=︒45HAT AHT ∴∠=∠=︒HT AT ∴=由(1)知,,则,∵直线与直线互相垂直,∴,()1.0M -1OM =BP AM 90MNB ∠=︒。
八上数学代几综合压轴题

八上数学代几综合压轴题
八上数学代几综合压轴题指的是在八年级上学期数学中,结合代数和几何知识,难度较大、综合性较强的压轴题目。
这类题目通常涉及多个知识点,需要学生具备扎实的数学基础和较高的思维能力才能解决。
以下是3道八上数学代几综合压轴题的示例:
1.题目:在直角坐标系中,点A的坐标为(-3, 2),点B的坐标为(1, t)。
如果
线段AB的长度为5,求t的值。
2.题目:已知抛物线y = ax^2 + bx + c经过点(0, 1)和点(4, 7),且与x轴只
有一个交点,求该抛物线的解析式。
3.题目:在四边形ABCD中,已知AB平行于CD,且AB = 2,CD = 4,如
果四边形ABCD的面积是10,求BC和AD的长度。
总结:八上数学代几综合压轴题指的是在八年级上学期数学中,结合代数和几何知识,难度较大、综合性较强的压轴题目。
这些题目需要学生具备扎实的数学基础和较高的思维能力才能解决,通过解决这些题目,学生可以进一步提高自己的数学能力,拓展思维视野。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级上学期数学压轴题
复习学生
Newly compiled on November 23, 2020
八年级上学期数学几何复习
【图形的剪拼】
1.如图,有边长为1、3的两个连接的正方形纸片,用两刀裁剪成三
块,然后拼成一个正方形,如何拼
2.如图,有一张长为5 ,宽为3的矩形纸片ABCD,要通过适当的
剪拼,得到一个与之面积相等的正方形
(1)正方形的边长为____________.(结果保留根号)
(2)现要求只能用两条裁剪线,请你设计出一种裁剪的方法,在图中画出裁剪线,并简要说明剪拼过程_____________.
(天津市中考题)【三角形】
1.在△ABC中,∠ACB=90°,直线MN经过点C且AD⊥MN于D,BE⊥MN于E
(1)当直线MN绕点C旋转到图①的位置时,求证:DE=AD+BE
(2)当直线MN绕点C旋转到图②的位置时,求证:DE=AD-BE
(3)当直线MN绕点C旋转到图③的位置时,试问DE、AD、BE具有怎样的等量关系并证明。
3.如图,△ABC中AB=AC,∠ABC=36°,D、C为BC上的
点,且∠BAD=∠DAE=∠EAC,则图中的等腰三角形有
()个。
A. 2
B. 4
C. 6
D. 8
4.如图,在△ABC中,∠BAC=90°,AB=AC=6,D为BC的中点.
(1)若E、F分别是AB、AC上的点,且AE=CF,求证:△AED≌△CFD;
(2)当点F、E分别从C、A两点同时出发,以每秒1个单位长度的速度沿CA、AB运动,到
点A、B时停止;设△DEF的面积为y,F点运动的时间为x,
求y与x的函数关系式;
(3)在(2)的条件下,点F、E分别沿CA、AB的延长线继续
运动,求此时y与x的函数关系式
(4)当x的值为多少事,S△DEF能最大化
图一图二
5.M为△ABC中BC 中点,AN平分∠BAC,BN⊥AN,已知
AB=10,BC=15,MN=3
(1)求证:BN=DN
(2)求△ABC周长
6.在△ABC中,∠ACB=90°,AC=BC,DA=DB,CD为直角边作等腰直角三角形CDE,∠DCE=90°
(1)求证:△ACD≌△BCE
(2)若AC=3cm,则BE = ________ cm .
7.已知:△ABC为等边三角形,ED=EC,探究AE与DB的大小关系
8.如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上一点,且CE=CA
(1)求证:DE平分∠BDC;
(2)若点M在DE上,且DC=DM.,求证:ME=BD.
9.如图,DE=BF,将平行四边形沿EF折叠,求证:(1)∠1=∠2 (2)DG=B’G
10.已知,△ABC为等边三角形,D为AC中点,CE=CD
(1)用尺规作图,过D作DM⊥BE,垂足为M
(2)求证:BM=EM
11.(1)操作发现:如图①,D是等边△ABC边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF.你能发现线段
AF与BD之间的数量关系吗并证明你发现的结论.
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长
线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是
否仍然成立
(3)深入探究:
Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与点B不重合)连接DC,以DC 为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF、BF′,探究AF、BF′与AB 有何数量关系并证明你探究的结论.
Ⅱ.如图④,当动点D在等边△边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立若不成立,是否有新的结论并证明你得出的结论.
12.
操作:如图
①
,△ABC是正三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角两边分别交AB,AC边于M,N两点,连接MN.
(1)探究线段BM、MN、NC之间的关系,并加以证明
(2)若点M、N分别是射线AB、CA上的点,其它条件不变,请你再探线段BM,MN,NC 之间的关系,在图④中画出图形,并说明理由.
(3)求证:CN-BM=MN
13.如图,已知△ABC和△ADC是以AC为公共底边的等腰三角
形,E、F分别在AD和CD上,已知:∠ADC+∠ABC=180°,∠
ABC=2∠EBF
(1)求证:EF=AE+FC
(2)若点E、F在直线AD和BD上,则是否有类似的结论
图①图②图③图④。
