普通物理学教程力学课后答案高等教育出版社第五章 角动量
大学物理学第五章角动量角动量守恒定律习题
第5章角动量角动量守恒定律一、本章总结1.请总结角动量、角动量守恒定律一章的知识点。
2.请画出本章的知识脉络框图。
二、填空题1. 如图所示，圆盘绕着与盘面垂直且过圆心O 的轴旋转，轴固定且光滑，转动角速度为ω。
这时，一对力偶沿着盘面作用在圆盘上（每个力大小为F ），圆盘的角速度ω 。
（填增大、减小或不能确定）2. 一个立方体放在粗糙的水平地面上，其质量分布均匀，为50 kg ，边长为1m 。
现用一水平拉力F 作用于立方体的定边中点。
如果地面摩擦力足够大，立方体不会滑动，那么要使该立方体翻转90︒，拉力F 至少为 。
3.一长为L 、质量为M 的均匀细棒，放在水平面上。
通过棒的端点O 有一垂直于水平面的光滑固定转轴，如图所示。
一质量为m 、速率为v 的子弹在水平面内垂直射向细棒，随后以速率v 21穿出，这时细棒的角速度 。
4. 刚体角动量守恒的充分而必要的条件是 。
5. 气候变暖造成地球两极的冰山融化，海平面因此上升。
这种情况将使地球的转动惯量 ，自转角速度 ，角动量 ，自转动能 。
（填变大、变小或不变）三、推导题6.试推导质量为m ，半径为R 的实心球体的转动惯量？（答：252mR ）四、计算和证明题7.如图所示，一个质量均匀分布的梯子靠墙放置，和地面成θ角，下端A 处连接一个弹性系数为k 的弹簧。
已知梯子的长度为l ，重量为W ，靠墙竖直放置时弹簧处于自然伸长，所有接触面均光滑。
如果梯子处于平衡状态，求地面、墙面对梯子的作用力，以及W 、k 、l 和θ满足的关系。
（答：W ；kl cos θ；OF Fω O v 21v 俯视图θsin 2kl W =）8. 半径为r = 1.5 m 的飞轮，初角速度ω0= 10 rad ⋅s -1，角加速度α= -5 rad ⋅s -2。
试问经过多长时间飞轮的角位移再次回到初始位置？此时飞轮边缘上的线速度为多少？（答：4s ；-15m ⋅s -1）9.质量分别为m 和2m 的两物体(都可视为质点)，用一长为l 的刚性细杆（质量为M ）相连，系统绕通过杆且与杆垂直的竖直固定轴O 转动。
角动量守恒定理及其应用
角动量守恒定理及其应用摘要:角动量这一概念是经典物理学里面的重要组成部分，角动量的研究主要是对于物体的转动方面，并且可以延伸到量子力学以、原子物理及天体物理等方面。
角动量这一概念范畴系统的介绍的力矩、角速度、角加速度的概念，并且统筹的联系到质点系、质心系、对称性等概念。
关键词:角动量；力矩；角动量守恒；矢量；转动；应用Angular momentum conservation theorems and theirapplicationAbstract:Angular momentum to the concept of classical physics there is an important component of angular momentum of research mainly for the rotation, and may extend to the quantum mechanics and physical and in the astrophysical. angular momentum in the categorical system of the present moment, the angular velocity, the concepts of angular acceleration and co-ordination of the particle, the quality of heart, symmetry, and concepts.Key words:Angular momentum;Torque;Conservation of angular momentum; Vector; Turn; application.引言在研究物体运动时,人们经常可以遇到质点或质点系绕某一定点或轴线运动的情况。
例如太阳系中行星绕太阳的公转、月球绕地球的运转、物体绕某一定轴的转动等,在这类运动中,运动物体速度的大小和方向都在不断变化,因而其动量也在不断变化。
《大学物理》第5单元课后答案 高等教育出版社
2
ww
1 3
0－2＝2
1 2 2 m m l 3 ＝15.4 rad 2M r
t＝2 / r ＝11.4 s
Page28
杭州电子科技大学
co
题14. 图 题15. 图
《大学物理习题集》 （下册）
m
2 分∴ 2分 2分 2分 2分 2分
作业登记号
学号
题1. 图
态为静止悬挂．现有一个小球自左方水平打击细杆．设小球与细杆之间为非弹性碰 撞，则在碰撞过程中对细杆与小球这一系统 (A) 只有机械能守恒． (B) 只有动量守恒． (C) 只有对转轴 O 的角动量守恒． (D) 机械能、动量和角动量均守恒． 【 C 】
3.如图所示，一个小物体，位于光滑的水平桌面上，与一绳的一端相连结，绳
w.
杭州电子科技大学
(A) 角动量从小到大，角加速度从大到小． (B) 角动量从小到大，角加速度从小到大． (C) 角动量从大到小，角加速度从大到小． (D) 角动量从大到小，角加速度从小到大． 【 B 】
题4. 图
ww
5.刚体角动量守恒的充分而必要的条件是 (A) 刚体不受外力矩的作用． (B) 刚体所受合外力矩为零． (C) 刚体所受的合外力和合外力矩均为零． (D) 刚体的转动惯量和角速度均保持不变．
沿相对圆盘转动相反的方向走动时圆盘对地的绕轴角速度为则人对与地固联的转轴的角速度为人与盘视为系统所受对转轴合外力矩为零系统的角动量守恒设盘的质量为m则人的质量杭州电子科技大学page31大学物理习题集下册
课后答案网，用心为你服务！
大学答案 --- 中学答案 --- 考研答案 --- 考试答案 最全最多的课后习题参考答案，尽在课后答案网（）！ Khdaw团队一直秉承用心为大家服务的宗旨，以关注学生的学习生活为出发点， 旨在为广大学生朋友的自主学习提供一个分享和交流的平台。 爱校园（） 课后答案网（） 淘答案（）
第五章 角动量
v v 相对于参考点O 相对于参考点O的位置矢量 r 与力F 的矢积(叉积)： 的矢积(叉积)
定义：力 F对参考点O的力矩为力 F 的作用点A 对参考点O的力矩为力 的作用点A 定义：
v
v
v v v M = r ×F v v v 大小： 大小： M = Fr sin r , F ≥ 0
（ 3）
v转至 v的角 α 是 v v v 方向： 方向：r , F, M 构成右手螺旋系统。(注意:由 r 构成右手螺旋系统。 注意: 0 ≤α ≤ π ) F
P m α r
v 的正方向到动量 v 的正方向转动方向所经过的 角和Z 或者： 或者 ：从 r α角和Z p
轴正向构成右手螺旋法则。 轴正向构成右手螺旋法则。
二者之间的关系
v v v LZ = (L0 ) Z = (r0 × p) Z
即：质点对轴的角动量等于对轴上任一点的角动量在该轴上的投影。 质点对轴的角动量等于对轴上任一点的角动量在该轴上的投影。 3
Lz = xp
y
− yp x
方法2： 和 投影到任选的xy平面来计算 方法 ：把r和p 投影到任选的 平面来计算
第五章 角动量
14
二、 力矩 torque
1、力对轴的力矩 torque of the force exerted on the particle with respect
to the axis z 1．力和轴平行时，例如开门, MZ F Z = 0 力和轴平行时，例如开门, 2．力和轴垂直时： 力和轴垂直时： （ 1） MZ (F ⊥ Z) = F⊥ ⋅ d = F ⋅ r sinα v v 角的规定： α角的规定：从 r 的正方向到力 F的正方向的转动方向所经过的 α角 和Z轴正向成右手螺旋。 轴正向成右手螺旋。
大学物理第五章习题答案
L
o
y
x
22
在锥体上 z 坐标处任取半径为 r高为 dz 的小柱体，则
L z 2 dm dv r dz ( R ) dz L 根据质心定义得
2
z
1 zC M
L
0
1 zdm M
L
L
0
L z 2 z ( R ) dz L
r
dz
L
R ML2 0 L L R 2 L 2 2 3 x [ zL dz 2 Lz dz z dz ] 2 0 0 0 ML R 2 L4 2 L4 L4 R 2 2 3 M L [ ] L L 2 ML 2 3 4 12 M 12 M 4
11
如果一个长度已知的不规则物体的重量超过一个弹簧秤的最大 量度，问怎样用这弹簧秤称出该物体的重量？ F 上图，根据合力矩为零得
Gx Fl
N
下图，根据合力矩为零得
F l G(l x )
x
F
l
整理可得：
G F F
G
N
G
课后习题
12
5-3：静止的电动机皮带轮半径为 5 cm，接通电源后做匀变速 转动，30 s 后转速达到152 rad / s，求： 1）30 s 内电动机皮带轮转过的转数； 2）通电后 20 s 时皮带轮的角速度； 3）通电后 20 s 时皮带轮边缘上一点的速度、切向加速度和法 向加速度。 解：皮带轮的角加速度为 152 t 0 t t 5 (rad/s 2 )
8
来复线的作用是增加炮弹的射程和准确性。由于炮弹射出时 绕自身轴线高速转动，空气阻力产生的对质心的力矩使炮弹 围绕前进方向产生进动效应，弹头的轴线始终围绕着弹道切 线向前且做锥形运动，从而能克服空气阻气，保证弹头稳定 地向前飞行，避免大的偏离，提高射程与准确性。
普通物理学教程力学课后答案高等教育出版社刚体力学习题解答
第七章刚体力学习题解答7.1.2 汽车发动机的转速在12s 内由1200rev/min 增加到3000rev/min.⑴假设转动是匀加速转动，求角加速度。
⑵在此时间内，发动机转了多少转？解：⑴21260/2)12003000(/7.15s rad t===-∆∆πωβ⑵rad 27.152)60/2)(12003000(21039.26222202⨯===∆⨯--πβωωθ对应的转数=42010214.3239.262≈⨯=⨯∆πθ7.1.3 某发动机飞轮在时间间隔t 内的角位移为):,:(43s t rad ct bt at θθ-+=。
求t 时刻的角速度和角加速度。
解：23212643ct bt ct bt a dtd dtd -==-+==ωθβω7.1.4 半径为0.1m 的圆盘在铅直平面内转动，在圆盘平面内建立o-xy 坐标系，原点在轴上，x 和y 轴沿水平和铅直向上的方向。
边缘上一点A 当t=0时恰好在x 轴上，该点的角坐标满足θ=1.2t+t 2 (θ:rad,t:s)。
⑴t=0时，⑵自t=0开始转45º时，⑶转过90º时，A 点的速度和加速度在x 和y 轴上的投影。
解：0.222.1==+==dtd dtd t ωθβω⑴t=0时，s m R v v y x /12.01.02.10,2.1=⨯====ωω2222/2.01.00.2/144.01.0/12.0/sm R a a s m R v a a y y n x =⨯===-=-=-=-=βτ⑵θ=π/4时,由θ=1.2t+t 2,求得t=0.47s,∴ω=1.2+2t=2.14rad/ssm R v s m R v y x /15.02/21.014.245sin /15.02/21.014.245cos =⨯⨯=︒=-=⨯⨯-=︒-=ωω222222222222/182.0)14.20.2(1.0)(45sin 45sin 45sin /465.0)14.20.2(1.0)(45cos 45cos 45cos s m R R R a s m R R R a y x -=-⨯=-︒=︒-︒=-=+⨯-=+︒-=︒-︒-=ωβωβωβωβ⑶θ=π/2时,由θ=1.2t+t 2,求得t=0.7895s,ω=1.2+2t=2.78rad/s2222/77.01.078.2/2.01.00.20/278.01.078.2s m R a s m R a v s m R v y x y x -=⨯-=-=-=⨯-=-==-=⨯-=-=ωβω7.1.5 钢制炉门由两个各长1.5m 的平行臂AB 和CD 支承，以角速率ω=10rad/s 逆时针转动，求臂与铅直成45º时门中心G 的速度和加速度。
力学(漆安慎版)答案第05章 角动量
第五章 角动量 习题5.1.1 我国发射的第一颗人造地球卫星近地点高度d 439km =近，远地点d 2384km =远，地球半径R 6370km =地，求卫星在近地点和远地点的速度之比.[解 答]卫星所受的引力对O 点力矩为零，卫星对O 点角动量守恒。
r m =r m νν远远近近2384+63701.29439+6370d +R r r d +R νν====远近远地远近近地5.1.2 一个质量为m 的质点沿着一条由ˆˆr =acos ti bsin tj ωω+ 定义的空间曲线运动，其中a,b 及ω皆为常数，求此质点所受的对原点的力矩.[解 答] 2222ˆˆˆˆˆˆˆˆ()r =acos ti bsin tj a sin ti b cos tj a =-a cos tib sin tj acos ti bsin tj r ωωνωωωωωωωωωωωω+=-+-=-+=-2F m r ω=-，通过原点0τ= 。
5.1.3 一个具有单位质量的质点在力场ˆˆ2F =(3t -4t)i +(12t -6)j中运动，其中t 是时间.设该质点在t=0时位于原点，且速度为零，求t=2时该质点所受的对原点的力矩.[解 答] 已知，m=1kg有牛顿第二定律 F ma =1ˆˆa F m 2(3t -4t)i+(12t -6)j == 0d a ,t 0,0dt νν===tt 000322ˆˆd adt dt ˆˆ=(t 2t )(6t 6t)2(3t -4t)i+(12t -6)j i jννν∴==-+-⎰⎰⎰同理由,t 0,0dr r dt ν===t3220ˆˆd [(t 2t )(6t 6t)]dtrr i j =-+-⎰⎰ˆˆ423212r =(t -t )i+(2t -3t )j 43ˆˆˆˆ4t =2:r =i 4j,F =4i 18j 3-++0ˆˆˆˆM r F ()()4i 4j 4i18j 3=⨯=-+⨯+ x y y y x x x y y xx y ˆˆˆ i j kˆˆˆA B A A A (A B A B )i (A B A B )j (A B A B )k B B B z z z z z z⨯==-+-+-0ˆˆˆ i j k4ˆM 4 040k34 18 0=-=-5.1.4 地球质量为246.010kg ⨯，地球与太阳相距614910km ⨯，视地球为质点，它绕太阳作圆周运动.求地球对医圆轨道中心的角动量.[解 答]2L rm mr ,2(rar/s)365243600νωπω===⨯⨯将624r 14910km,m 6.010kg =⨯=⨯代入上式得402L 2.6510kg m /s =⨯⋅5.1.5 根据5.1.2题所给的条件，求该质点对原点的角动量.[解 答]ˆˆˆˆr =acos ti bsin tj a sin tib cos tj ωωνωωωω+∴=-+质点对原点的角动量： ˆˆˆˆL r m ()m()acos ti bsin tj a sin ti b cos tj νωωωωωω=⨯=+⨯-+ˆˆˆ i j kˆcos sin 0abm k m m 0a tb t a sin t b cos t ωωωωωωω==-5.1.6 根据5.1.3题所给的条件，求该质点在t=2时对原点的角动量.[解 答]由5.1.3，t=2s 时22ˆˆˆ,12j,m 1kg 4r =i 4j 3ν-+== ˆˆˆL r m ()12j4i 4j 3ν=⨯=-+⨯2ˆˆˆ i j k4ˆL 4 016k(kg m /s)30 12 0=-=-⋅5.1.7 水平光滑桌面中间有一光滑小孔，轻绳一端伸入孔中，另一端系一质量为10g 的小球，沿半径为40cm 的圆周做匀速圆周运动，这是从孔下拉绳的力为310N -.如果继续向下拉绳，而使小球沿半径为10cm 的圆周做匀速圆周运动，这时小球的速率是多少？拉力所做的功是多少？[解 答](1)小球角动量守恒：00m R m R νν= ①由牛顿第二定律：最初20002F T mR ν== ②又②解出0ν代入①得 00R0.8(m /s)R νν==（2）拉力所作的功223011A m m 3.010(J)22νν-=-=⨯5.1.8 一个质量为m 的质点在O-xy 平面内运动，其位置矢量为ˆˆr =acos ti bsin tj ωω+其中a,b 和ω是正常数，试以运动学及动力学观点证明该质点对于坐标原点角动量守恒.[解 答]（1）以运动学观点证明ˆˆr =acos ti bsin tj ωω+ˆˆdr a sin ti b cos tj dt νωωωω==-+质点对坐标原点的角动量为：ˆˆˆˆL r m ()m()acos ti bsin tj a sin ti b cos tj νωωωωωω=⨯=+⨯-+ˆˆˆ i j kˆcos sin 0abm k m m 0a tb t a sin t b cos t ωωωωωωω==-=常矢量（守恒）（2）以动力学观点证明222d ra ==-rdt ω由牛顿第二定律：2F =ma =-m r ω质点对坐标原点的力矩为： 20()0M r F r m r ω=⨯=⨯-=由dL M ,L=dt = 常矢量（守恒）5.1.9 质量为200g 的小球B 以弹性绳在光滑水平面上与固定点A 相连.弹性绳的劲度系数为8N/m ，其自由伸展长度为600mm.最初小球的位置及速度0ν如图所示.当小球的速度变为ν时，它与A 点的距离最大，且等于800mm ，求此时的速度ν及初速度0ν.[解 答] 由角动量守恒：00m d m d sin30νν=00d d sin30νν= （1）再由机械能守恒：2220111m m k(d 0.6)222νν=+- （2）联立求解：01.306(m/s),0.3266(m/s)νν==5.1.10 一条不可伸长的绳穿过铅直放置的、管口光滑的细管，一端系一个质量为0.5g 的小球，小球沿水平圆周运动.最初112m,30θ==，后来继续向下拉绳使小球以260θ=沿水平圆周运动.求小球最初的速度1ν、最后的速度2ν、以及绳对小球做的总功.[解 答]初时，112m,30,F T w,θ===+指向圆心。
物理学教程(第二版)上册第五章课后习题答案详解
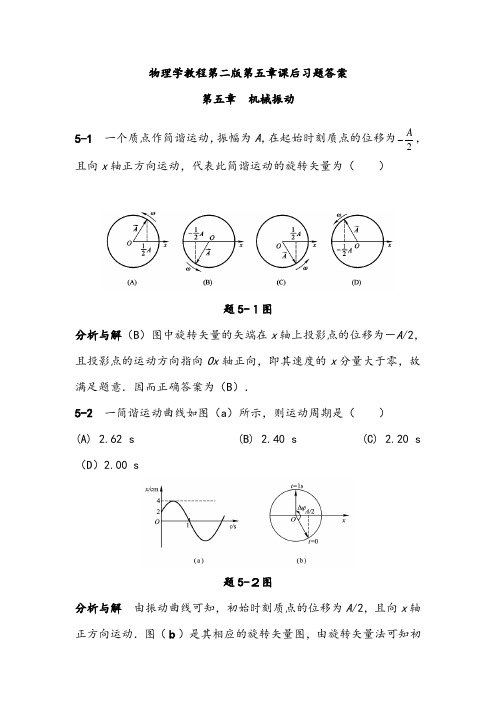
物理学教程第二版第五章课后习题答案第五章 机械振动5-1 一个质点作简谐运动，振幅为A ，在起始时刻质点的位移为2A，且向x 轴正方向运动，代表此简谐运动的旋转矢量为（ ）题5-１图分析与解（B ）图中旋转矢量的矢端在x 轴上投影点的位移为－A /2，且投影点的运动方向指向Ox 轴正向，即其速度的x 分量大于零，故满足题意．因而正确答案为（B ）．5-2 一简谐运动曲线如图（a ）所示，则运动周期是（ ）(A) 2.62 s (B) 2.40 s (C) 2.20 s（D ）2.00 s题5-２图分析与解 由振动曲线可知，初始时刻质点的位移为A /2，且向x 轴正方向运动．图（ｂ）是其相应的旋转矢量图，由旋转矢量法可知初相位为-3/π2．振动曲线上给出质点从A /2 处运动到x =0处所需时间为1 s ，由对应旋转矢量图可知相应的相位差65232πππϕ=+=∆，则角频率1s rad 65Δ/Δ-⋅==πϕωt ，周期s 40.22==ωπT .故选（B ）． 5-3 两个同周期简谐运动曲线如图（a ）所示， x 1的相位比x 2的相位（ ）（A ）落后2π（B ）超前2π（C ）落后π（D ）超前π分析与解 由振动曲线图作出相应的旋转矢量图（b ）即可得到答案为（B ）．题5 -３图5-4 两个同振动方向、同频率、振幅均为A 的简谐运动合成后，振幅仍为A ，则这两个简谐运动的相位差为（ ）（A ）60 （B ）90 （C ）120 （D ）180分析与解 由旋转矢量图可知两个简谐运动1和2的相位差为120 时，合成后的简谐运动3的振幅仍为A .正确答案为（C ）．题5-4图5-5 若简谐运动方程为⎪⎭⎫ ⎝⎛+=4ππ20cos 10.0t x ，式中x 的单位为m ，t 的单位为s.求：（1）振幅、频率、角频率、周期和初相；（2）s 2=t 时的位移、速度和加速度．分析 可采用比较法求解．将已知的简谐运动方程与简谐运动方程的一般形式()ϕω+=t A x cos 作比较，即可求得各特征量．运用与上题相同的处理方法，写出位移、速度、加速度的表达式，代入t 值后，即可求得结果．解 （1）将()()m π25.0π20cos 10.0+=t x 与()ϕω+=t A x cos 比较后可得：振幅A ＝0.10m ，角频率1s rad π20-⋅=ω，初相ϕ＝0.25π，则周期s 1.0/π2==ωT ，频率Hz /1T =v ．（２）s 2=t 时的位移、速度、加速度分别为()m 1007.7π25.0π40cos 10.02-⨯=+=t x()-1s m 44.4π25.0π40sin π2d /d ⋅-=+-==t x v()-22222s m 1079.2π25.0π40cos π40d /d ⋅⨯-=+-==t x a5-6 一远洋货轮，质量为m ，浮在水面时其水平截面积为S ．设在水面附近货轮的水平截面积近似相等，水的密度为ρ，且不计水的粘滞阻力，证明货轮在水中作振幅较小的竖直自由运动是简谐运动，并求振动周期．分析 要证明货轮作简谐运动，需要分析货轮在平衡位置附近上下运动时，它所受的合外力F 与位移x 间的关系，如果满足kx F -=，则货轮作简谐运动．通过kx F -=即可求得振动周期k m ωT /π2/π2==． 证 货轮处于平衡状态时［图（a ）］，浮力大小为F ＝mg ．当船上下作微小振动时，取货轮处于力平衡时的质心位置为坐标原点O ，竖直向下为x 轴正向，如图（b ）所示．则当货轮向下偏移x 位移时，受合外力为∑'+=F P F其中F '为此时货轮所受浮力，其方向向上，大小为gSx mg gSx F F ρρ+=+='题5-6图则货轮所受合外力为kx gSx F P F -=-='-=∑ρ式中gS k ρ=是一常数．这表明货轮在其平衡位置上下所作的微小振动是简谐运动．由∑=t x m F 22d d /可得货轮运动的微分方程为0d d 22=+m gSx t x //ρ令m gS /ρω=2，可得其振动周期为gS ρm πωT /2/π2==5-7 如图（a ）所示，两个轻弹簧的劲度系数分别为1k 、2k ．当物体在光滑斜面上振动时．（1）证明其运动仍是简谐运动；（2）求系统的振动频率．题5-7图分析 从上两题的求解知道，要证明一个系统作简谐运动，首先要分析受力情况，然后看是否满足简谐运动的受力特征（或简谐运动微分方程）．为此，建立如图（b ）所示的坐标．设系统平衡时物体所在位置为坐标原点O ，Ox 轴正向沿斜面向下，由受力分析可知，沿Ox 轴，物体受弹性力及重力分力的作用，其中弹性力是变力．利用串联时各弹簧受力相等，分析物体在任一位置时受力与位移的关系，即可证得物体作简谐运动，并可求出频率υ．证 设物体平衡时两弹簧伸长分别为1x 、2x ，则由物体受力平衡，有2211sin x k x k mg ==θ（1）按图（b ）所取坐标，物体沿x 轴移动位移x 时，两弹簧又分别被拉伸1x '和2x '，即21x x x '+'=．则物体受力为 ()()111222sin sin x x k mg x x k mg F '+-='+-=θθ（２） 将式（1）代入式（2）得1122x k x k F '-='-=（３） 由式（3）得11k F x /-='、22k F x /-='，而21x x x '+'=，则得到()[]kx x k k k k F -=+-=2121/式中()2121k k k k k +=/为常数，则物体作简谐运动，振动频率 ()m k k k k πm k ωv 2121/21/π21π2/+=== 讨论 （1）由本题的求证可知，斜面倾角θ对弹簧是否作简谐运动以及振动的频率均不产生影响．事实上，无论弹簧水平放置、斜置还是竖直悬挂，物体均作简谐运动．而且可以证明它们的频率相同，均由弹簧振子的固有性质决定，这就是称为固有频率的原因．（2）如果振动系统如图（c ）（弹簧并联）或如图（d ）所示，也可通过物体在某一位置的受力分析得出其作简谐运动，且振动频率均为()m k k v /π2121+=，读者可以一试．通过这些例子可以知道，证明物体是否作简谐运动的思路是相同的．5-8 一放置在水平桌面上的弹簧振子，振幅A ＝2.0 ×10-2 m ，周期T ＝0.50ｓ．当t ＝0 时，（1）物体在正方向端点；（2）物体在平衡位置、向负方向运动；（3）物体在x ＝-1.0×10-2m 处，向负方向运动；（4）物体在x ＝-1.0×10-2 m 处，向正方向运动．求以上各种情况的运动方程．分析 在振幅A 和周期T 已知的条件下，确定初相φ是求解简谐运动方程的关键．初相的确定通常有两种方法．（1）解析法：由振动方程出发，根据初始条件，即t ＝0 时，x ＝x 0和v ＝v 0来确定φ值．（2）旋转矢量法：如图（a ）所示，将质点P 在Ox 轴上振动的初始位置x 0和速度v 0的方向与旋转矢量图相对应来确定φ．旋转矢量法比较直观、方便，在分析中常采用．题5-8图解 由题给条件知A ＝2.0 ×10-2 m ，1s π4/2-==T ω，而初相φ可采用分析中的两种不同方法来求．解析法：根据简谐运动方程()ϕω+=t A x cos ，当0t =时有()ϕω+=t A x cos 0，sin 0ϕωA -=v ．当（1）A x =0时，1cos 1=ϕ，则01=ϕ；（2）00=x 时，0cos 2=ϕ，2π2±=ϕ，因00<v ，取2π2=ϕ；（3）m 100120-⨯=.x 时，50cos 3.=ϕ，3π3±=ϕ，由00<v ，取3π3=ϕ；（4）m 100120-⨯-=.x 时，50cos 4.-=ϕ，3ππ4±=ϕ，由00>v ，取3π44=ϕ． 旋转矢量法：分别画出四个不同初始状态的旋转矢量图，如图（b ）所示，它们所对应的初相分别为01=ϕ，2π2=ϕ，3π3=ϕ，3π44=ϕ． 振幅A 、角频率ω、初相φ均确定后，则各相应状态下的运动方程为（1）()m t πcos4100.22-⨯=x（2）()()m /2πt π4cos 100.22+⨯=-x（3）()()m /3πt π4cos 100.22+⨯=-x（4）()()m0.22+10=-xcos⨯/3π44tπ5-9有一弹簧，当其下端挂一质量为m的物体时，伸长量为9.8 ×10-2 m．若使物体上、下振动，且规定向下为正方向．（1）当t＝0 时，物体在平衡位置上方8.0 ×10-2ｍ处，由静止开始向下运动，求运动方程．（2）当t＝０时，物体在平衡位置并以0.6ｍ·s-1的速度向上运动，求运动方程．分析求运动方程，也就是要确定振动的三个特征物理量A、ω和φ．其中振动的角频率是由弹簧振子系统的固有性质（振子质量m及弹簧劲度系数k）决定的，即k mω=/，k可根据物体受力平衡时弹簧的伸长来计算；振幅A和初相φ需要根据初始条件确定．题5-9图解物体受力平衡时，弹性力F与重力P的大小相等，即F＝mg．而此时弹簧的伸长量Δl＝9.8 ×10-2m．则弹簧的劲度系数k＝F／Δl ＝mg／Δl．系统作简谐运动的角频率为1ωmk//g=s=l10-∆=（1）设系统平衡时，物体所在处为坐标原点，向下为x轴正向．由初始条件t ＝0 时，x10＝8.0 ×10-2m、v10＝0 可得振幅()m 10082210210-⨯=+=./ωv x A ；应用旋转矢量法可确定初相π1=ϕ［图（a ）］．则运动方程为()()m π10t cos 100.821+⨯=-x（2）t ＝０时，x 20＝0、v 20＝0.6 ｍ·s -1，同理可得()m 100622202202-⨯=+=./ωv x A ；2/π2=ϕ［图（b ）］．则运动方程为 ()()m π5.010t cos 100.622+⨯=-x5-10 某振动质点的x -t 曲线如图（a ）所示，试求：（1）运动方程；（2）点P 对应的相位；（3）到达点P 相应位置所需的时间．分析 由已知运动方程画振动曲线和由振动曲线求运动方程是振动中常见的两类问题．本题就是要通过x －t 图线确定振动的三个特征量A 、ω和0ϕ，从而写出运动方程．曲线最大幅值即为振幅A ；而ω、0ϕ通常可通过旋转矢量法或解析法解出，一般采用旋转矢量法比较方便．解 （1）质点振动振幅A ＝0.10 ｍ．而由振动曲线可画出t 0＝0 和t 1＝4 ｓ时旋转矢量，如图（b ）所示．由图可见初相3/π0-=ϕ（或3/π50=ϕ），而由()3201//ππω+=-t t 得1s 24/π5-=ω，则运动方程为()m 3/π24π5cos 10.0⎪⎭⎫ ⎝⎛-=t x题5-10图（2）图（a ）中点P 的位置是质点从A ／2 处运动到正向的端点处．对应的旋转矢量图如图（c ）所示．当初相取3/π0-=ϕ时，点P 的相位为()000=-+=p p t ωϕϕ（如果初相取成3/π50=ϕ，则点P 相应的相位应表示为()π200=-+=p p t ωϕϕ．（3）由旋转矢量图可得()3/π0=-p t ω，则s 61.=p t ．5-11 质量为10 g 的物体沿x 的轴作简谐运动，振幅A =10 cm ，周期T =4.0 s ，t =0 时物体的位移为，cm 0.50-=x 且物体朝x 轴负方向运动，求（1）t =1.0 s 时物体的位移；（2）t =1.0 s 时物体受的力；（3）t =0之后何时物体第一次到达x =5.0 cm 处；（4）第二次和第一次经过x =5.0 cm 处的时间间隔.分析根据题给条件可以先写出物体简谐运动方程)cos(ϕω+=t A x .其中振幅A ，角频率Tπ2=ω均已知，而初相ϕ可由题给初始条件利用旋转矢量法方便求出. 有了运动方程，t 时刻位移x 和t 时刻物体受力x m ma F 2ω-==也就可以求出. 对于（3）、（4）两问均可通过作旋转矢量图并根据公式t ∆=∆ωϕ很方便求解.解由题给条件画出t =0时该简谐运动的旋转矢量图如图（a ）所示，可知初相3π2=ϕ.而A =0.10 m ，1s 2ππ2-==T ω.则简谐运动方程为m )3π22πcos(10.0+=t x (1)t =1.0 s 时物体的位移m 1066.8m )3π22π0.1cos(10.02-⨯-=+⨯=x（2）t =1.0 s 时物体受力N1014.2N)1066.8()2π(101032232---⨯=⨯-⨯⨯⨯-=-=x m F ω （3）设t =0时刻后，物体第一次到达x =5.0 cm 处的时刻为t 1，画出t =0和t =t 1时刻的旋转矢量图，如图（b ）所示，由图可知，A 1与A 的相位差为π，由t ∆=∆ωϕ得s 2s 2/ππ1==∆=ωϕt （4）设t =0时刻后，物体第二次到达x =5.0 cm 处的时刻为t 2,画出t =t 1和t = t 2时刻的旋转矢量图，如图（c ）所示，由图可知，A 2与A 1的相位差为3π2，故有 s 34s 2/π3/π212==∆=-=∆ωϕt t t题 5-11 图5-12 图（a ）为一简谐运动质点的速度与时间的关系曲线，且振幅为2cm ，求（1）振动周期；（2）加速度的最大值；（3）运动方程． 分析 根据v -t 图可知速度的最大值v max ，由v max ＝Aω可求出角频率ω，进而可求出周期T 和加速度的最大值a max ＝Aω2．在要求的简谐运动方程x ＝A cos （ωt ＋φ）中，因为A 和ω已得出，故只要求初相位φ即可．由v －t 曲线图可以知道，当t ＝0 时，质点运动速度v 0＝v max /2 ＝Aω/2，之后速度越来越大，因此可以判断出质点沿x 轴正向向着平衡点运动．利用v 0＝－Aωsinφ就可求出φ． 解 （1）由ωA v =max 得1s 51-=.ω，则s 2.4/π2==ωT（2）222max s m 1054--⋅⨯==.ωA a（3）从分析中已知2/sin 0ωA ωA =-=v ，即21sin /-=ϕ6/π5,6/π--=ϕ因为质点沿x 轴正向向平衡位置运动，则取6/π5-=，其旋转矢量图如图（b ）所示．则运动方程为()cm 6π55.1cos 2⎪⎭⎫⎝⎛-=t x题5-12图5-13 有一单摆，长为1.0m ，最大摆角为5°，如图所示．（1）求摆的角频率和周期；（2）设开始时摆角最大，试写出此单摆的运动方程；（3）摆角为3°时的角速度和摆球的线速度各为多少？题5-13图分析 单摆在摆角较小时（θ＜5°）的摆动，其角量θ与时间的关系可表示为简谐运动方程()ϕωθθ+=t cos max ，其中角频率ω仍由该系统的性质（重力加速度g 和绳长l ）决定，即l g /=ω．初相φ与摆角θ，质点的角速度与旋转矢量的角速度（角频率）均是不同的物理概念，必须注意区分． 解 （1）单摆角频率及周期分别为s 01.2/π2;s 13.3/1====-ωT l g ω（2）由0=t 时o max 5==θθ可得振动初相0=ϕ，则以角量表示的简谐运动方程为t θ13.3cos 36π=（３）摆角为3°时，有()60cos max ./==+θθϕωt ，则这时质点的角速度为()()1max 2max max s2180800cos 1sin /d d --=-=+--=+-=..ωθϕωωθϕωωθθt t t线速度的大小为1s m 218.0/d d -⋅-==t l v θ讨论 质点的线速度和角速度也可通过机械能守恒定律求解，但结果会有极微小的差别．这是因为在导出简谐运动方程时曾取θθ≈sin ，所以，单摆的简谐运动方程仅在θ较小时成立．*5-14 一飞轮质量为12kg ，内缘半径r ＝0.6ｍ，如图所示．为了测定其对质心轴的转动惯量，现让其绕内缘刃口摆动，在摆角较小时，测得周期为2.0s ，试求其绕质心轴的转动惯量．题5-14图分析 飞轮的运动相当于一个以刃口为转轴的复摆运动，复摆振动周期为c /π2mgl J T =，因此，只要知道复摆振动的周期和转轴到质心的距离c l ，其以刃口为转轴的转动惯量即可求得．再根据平行轴定理，可求出其绕质心轴的转动惯量．解 由复摆振动周期c /π2mgl J T =，可得22π4/m g r T J =（这里r l C ≈）．则由平行轴定理得222220m kg 83.2π4⋅=-=-=mr mgrT mr J J 5-15 如图（a ）所示，质量为 1.0 ×10-2kg 的子弹，以500m·s -1的速度射入木块，并嵌在木块中，同时使弹簧压缩从而作简谐运动，设木块的质量为4.99 kg ，弹簧的劲度系数为8.0 ×103 N·m -1，若以弹簧原长时物体所在处为坐标原点，向左为x 轴正向，求简谐运动方程．题5-15图分析 可分为两个过程讨论．首先是子弹射入木块的过程，在此过程中，子弹和木块组成的系统满足动量守恒，因而可以确定它们共同运动的初速度v 0，即振动的初速度．随后的过程是以子弹和木块为弹簧振子作简谐运动．它的角频率由振子质量m 1＋m 2和弹簧的劲度系数k 确定，振幅和初相可根据初始条件（初速度v 0和初位移x 0）求得．初相位仍可用旋转矢量法求． 解 振动系统的角频率为()121s 40-=+=m m k /ω由动量守恒定律得振动的初始速度即子弹和木块的共同运动初速度v 0为12110s m 0.1-⋅=+=m m vm v又因初始位移x 0＝0，则振动系统的振幅为()m 105.2//202020-⨯==+=ωωx A v v图（b ）给出了弹簧振子的旋转矢量图，从图中可知初相位2/π0=ϕ，则简谐运动方程为()()m π0.540cos 105.22+⨯=-t x5-16 如图（a ）所示，一劲度系数为k 的轻弹簧，其下挂有一质量为m 1的空盘．现有一质量为m 2的物体从盘上方高为h 处自由落入盘中，并和盘粘在一起振动．问：（1）此时的振动周期与空盘作振动的周期有何不同？（2）此时的振幅为多大？题5-16图分析 原有空盘振动系统由于下落物体的加入，振子质量由m 1变为m 1 + m 2，因此新系统的角频率（或周期）要改变．由于()2020/ωx A v +=，因此，确定初始速度v 0和初始位移x 0是求解振幅A 的关键．物体落到盘中，与盘作完全非弹性碰撞，由动量守恒定律可确定盘与物体的共同初速度v 0，这也是该振动系统的初始速度．在确定初始时刻的位移x 0时，应注意新振动系统的平衡位置应是盘和物体悬挂在弹簧上的平衡位置．因此，本题中初始位移x 0，也就是空盘时的平衡位置相对新系统的平衡位置的位移．解 （1）空盘时和物体落入盘中后的振动周期分别为k m ωT /π2/π21== ()k m m ωT /π2/π221+='='可见T ′＞T ，即振动周期变大了．（2）如图（b ）所示，取新系统的平衡位置为坐标原点O ．则根据分析中所述，初始位移为空盘时的平衡位置相对粘上物体后新系统平衡位置的位移，即g kmg k m m k g m l l x 2211210-=+-=-= 式中k g m l 11=为空盘静止时弹簧的伸长量，l 2＝g km m 21+为物体粘在盘上后，静止时弹簧的伸长量．由动量守恒定律可得振动系统的初始速度，即盘与物体相碰后的速度gh m m m m m m 22122120+=+=v v 式中gh 2=v 是物体由h 高下落至盘时的速度．故系统振动的振幅为()gm m khk g m x A )(21/2122020++='+=ωv 本题也可用机械能守恒定律求振幅A ．5-17 质量为0.10kg 的物体，以振幅1.0×10-2 m 作简谐运动，其最大加速度为4.0 ｍ·s -1求：（1）振动的周期；（2）物体通过平衡位置时的总能量与动能；（3）物体在何处其动能和势能相等？（4）当物体的位移大小为振幅的一半时，动能、势能各占总能量的多少？分析 在简谐运动过程中，物体的最大加速度2max ωA a =，由此可确定振动的周期T ．另外，在简谐运动过程中机械能是守恒的，其中动能和势能互相交替转化，其总能量E ＝kA 2/2．当动能与势能相等时，E k ＝E P ＝kA 2/4．因而可求解本题． 解 （1）由分析可得振动周期s 314.0/π2/π2max ===a A ωT（2）当物体处于平衡位置时，系统的势能为零，由机械能守恒可得系统的动能等于总能量，即J 100221213max22k -⨯====.m Aa m A E E ω （3）设振子在位移x 0处动能与势能相等，则有42220//kA kx =得m 100772230-⨯±=±=./A x（４）物体位移的大小为振幅的一半（即2x A =/）时的势能为4221212P /E A k kx E =⎪⎭⎫⎝⎛==则动能为43P K /E E E E =-=5-18 一劲度系数k =312 1m N -⋅的轻弹簧，一端固定，另一端连接一质量kg 3.00=m 的物体，放在光滑的水平面上，上面放一质量为kg 2.0=m 的物体，两物体间的最大静摩擦系数5.0=μ.求两物体间无相对滑动时，系统振动的最大能量.分析简谐运动系统的振动能量为2p k 21kA E E E =+=.因此只要求出两物体间无相对滑动条件下，该系统的最大振幅max A 即可求出系统振动的最大能量.因为两物体间无相对滑动，故可将它们视为一个整体，则根据简谐运动频率公式可得其振动角频率为mm k+=0ω.然后以物体m 为研究对象，它和m 0一起作简谐运动所需的回复力是由两物体间静摩擦力来提供的.而其运动中所需最大静摩擦力应对应其运动中具有最大加速度时，即max 2max A m ma mg ωμ==，由此可求出max A . 解根据分析，振动的角频率mm k+=0ω 由max 2max A m ma mg ωμ==得kgm m g A μωμ)(02max +=则最大能量J1062.92)(])([212132220202max max -⨯=+=+==kg m m kg m m k kA E μμ5-19 已知两同方向、同频率的简谐运动的运动方程分别为()()m π75.010cos 05.01+=t x ；()()m π25.010cos 06.02+=t x ．求：（1）合振动的振幅及初相；（2）若有另一同方向、同频率的简谐运动()()m 10cos 07033ϕ+=t x .，则3ϕ为多少时，x 1＋x 3的振幅最大？又3ϕ为多少时，x 2＋x 3的振幅最小？题5-19图分析 可采用解析法或旋转矢量法求解.由旋转矢量合成可知，两个同方向、同频率简谐运动的合成仍为一简谐运动，其角频率不变；合振动的振幅()12212221cos 2ϕϕ-++=A A A A A ，其大小与两个分振动的初相差12ϕϕ-相关．而合振动的初相位()()[]22112211cos cos sin sin arctanϕϕϕϕϕA A A A ++=/ 解 （1）作两个简谐运动合成的旋转矢量图（如图）．因为2/πΔ12-=-=ϕϕϕ，故合振动振幅为()m 1087cos 2212212221-⨯=-++=.ϕϕA A A A A合振动初相位()()[]rad1.48arctan11cos cos sin sin arctan22112211==++=ϕϕϕϕϕA A A A /（2）要使x 1＋x 3振幅最大，即两振动同相，则由π2Δk =ϕ得,...2,1,0,π75.0π2π213±±=+=+=k k k ϕϕ要使x 1＋x 3的振幅最小，即两振动反相，则由()π12Δ+=k ϕ得(),...2,1,0,π25.1π2π1223±±=+=++=k k k ϕϕ5-20 两个同频率的简谐运动1 和2 的振动曲线如图（a ）所示，求（1）两简谐运动的运动方程x 1和x 2；（2）在同一图中画出两简谐运动的旋转矢量，并比较两振动的相位关系；（3）若两简谐运动叠加，求合振动的运动方程．分析 振动图已给出了两个简谐运动的振幅和周期，因此只要利用图中所给初始条件，由旋转矢量法或解析法求出初相位，便可得两个简谐运动的方程．解 （1）由振动曲线可知，A ＝0.1 ｍ，T ＝2ｓ，则ω＝2π／T ＝πｓ-1．曲线1表示质点初始时刻在x ＝0 处且向x 轴正向运动，因此φ1＝－π／2；曲线2 表示质点初始时刻在x ＝A /2 处且向x 轴负向运动，因此φ2＝π／3．它们的旋转矢量图如图（b ）所示．则两振动的运动方程分别为()()m 2/ππcos 1.01-=t x 和()()m 3/ππcos 1.02+=t x（2）由图（b ）可知振动2超前振动1 的相位为5π／6． （3）()ϕω+'=+=t A x x x cos 21其中()m 0520cos 212212221.=-++='ϕϕA A A A A()12π0.268arctan cos cos sin sin arctan22112211-=-=++=ϕϕϕϕϕA A A A则合振动的运动方程为 ()()m π/12πcos 052.0-=t x题5-20 图5-21 将频率为348 Hz 的标准音叉振动和一待测频率的音叉振动合成，测得拍频为3.0Hz ．若在待测频率音叉的一端加上一小块物体，则拍频数将减少，求待测音叉的固有频率．分析 这是利用拍现象来测定振动频率的一种方法．在频率υ1和拍频数Δυ＝|υ2－υ1|已知的情况下，待测频率υ2可取两个值，即υ2＝υ1 ±Δυ．式中Δυ前正、负号的选取应根据待测音叉系统质量改变时，拍频数变化的情况来决定．解 根据分析可知，待测频率的可能值为υ2＝υ1 ±Δυ＝（348 ±3） Hz因振动系统的固有频率mkπ21=v ，即质量m 增加时，频率υ减小．从题意知，当待测音叉质量增加时拍频减少，即｜υ2－υ1｜变小．因此，在满足υ2与Δυ均变小的情况下，式中只能取正号，故待测频率为υ2＝υ1＋Δυ＝351 Hz*5-22 图示为测量液体阻尼系数的装置简图，将一质量为m 的物体挂在轻弹簧上，在空气中测得振动的频率为υ1，置于液体中测得的频率为υ2，求此系统的阻尼系数．题5-22图分析 在阻尼不太大的情况下，阻尼振动的角频率ω与无阻尼时系统的固有角频率ω0及阻尼系数δ有关系式220δωω-=．因此根据题中测得的υ1和υ2（即已知ω0、ω），就可求出δ．解 物体在空气和液体中的角频率为10π2v =ω和2π2v =ω，得阻尼系数为2221220π2v v -=-=ωωδ。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第五章 角动量习题解答5.1.1 我国发射的第一颗人造地球卫星近地点高度d 近=439km,远地点高度d 远=2384km,地球半径R 地=6370km,求卫星在近地点和远地点的速度之比。
解：卫星在绕地球转动过程中，只受地球引力（有心力）的作用，力心即为地心，引力对地心的力矩为零，所以卫星对地心的角动量守恒m 月v 近（d 近+R 地）=m 月v 远（d 远+R 地）v 近/v 远=（d 远+R 地）/（d 近+R 地）=（2384+6370）/（439+6370）≈1.295.1.2 一个质量为m 的质点沿着j t b i t a r ˆsin ˆcos ωω+=的空间曲线运动，其中a 、b 及ω皆为常数。
求此质点所受的对原点的力矩。
解： 0)ˆsin ˆcos (ˆsin ˆcos /ˆcos ˆsin /222222=⨯-=⨯=-==-=+-=--==+-==r r m F r r m a m F r j t b i t a j t b i t a dt v d a j t b i t a dt r d v ωτωωωωωωωωωωωωω5.1.3 一个具有单位质量的质点在力场j t i t t F ˆ)612(ˆ)43(2-+-= 中运动，其中t 是时间。
该质点在t=0时位于原点，且速度为零。
求t=2时该质点所受的对原点的力矩。
解：据质点动量定理的微分形式，)1()(===m v d v m d dt Fdt j t i t t v d ]ˆ)612(ˆ)43[(2-+-=∴kk k k ij k j i j j i i j i j i F r j i j i F ji j i r j t t i t t r dt t t j dt t t i r d dtj t t i t t dt v r d j t t i t t v dt t j dt t t i v d r t t t t v ˆ40)ˆ(44ˆ18)2(ˆˆˆ,ˆˆˆ,0ˆˆˆˆ)ˆ18ˆ4()ˆ4ˆ()2()2()2(ˆ18ˆ4ˆ)6212(ˆ)2423()2(ˆ4ˆˆ)2322(ˆ)22()2(ˆ)32(ˆ)()(ˆ6)2(ˆ]ˆ)(6ˆ)2[(ˆ)(6ˆ)2()612(ˆ)43(ˆ343423423332441233324410002232232230020-=-⨯+⨯-=∴-=⨯=⨯=⨯=⨯+⨯+-=⨯=+=-⨯+⨯-⨯=+-=⨯-⨯+⨯-⨯=-+-=-+-=-+-==-+-=-+-=⎰⎰⎰⎰⎰⎰ττ5.1.4地球质量为6.0×1024kg ，地球与太阳相距149×106km ，视地球为质点，它绕太阳做圆周运动，求地球对于圆轨道中心的角动量。
解：606024365)10149(2100.629242⨯⨯⨯⨯⨯⨯===πωr m mvr L s kgm /1065.21060602436514920.6240422⨯=⨯⨯⨯⨯⨯⨯=π5.1.5根据5.1.2题所给的条件，求该质点对原点的角动量。
解：v r m p r L⨯=⨯= kmab k t ab k t ab m j t b i t a j t b i t a m ˆ)ˆsin ˆcos ()ˆcos ˆsin ()ˆsin ˆcos (22ωωωωωωωωωωω=+=+-⨯+=5.1.6根据5.1.3题所给的条件，求质点在t=2时对原点的角动量。
解：)2()2()2()2()2(v r m p r L⨯=⨯= kj j i ˆ16ˆ12)ˆ4ˆ(134-=⨯+-⨯=5.1.7 水平光滑桌面中间有一光滑小孔，轻绳一端伸入孔中，另一端系一质量为10g 小球，沿半径 为40cm 的圆周作匀速圆周运动，这时从孔下拉绳的力为10-3N 。
如果继续向下拉绳，而使小球沿半径为10cm 的圆周作匀速圆周运动，这时小球的速率是多少？拉力所做的功是多少？解：设小球的质量为m=10×10-3kg,原来的运动半径为R 1=40cm,运动速率为v 1;后来的运动半径为R 2=10cm,运动速率为v 2.i ˆj ˆk ˆ先求小球原来的速率v 1：据牛顿第二定律，F=mv 12/R 1，所以，s m m F R v /2.010/104.0/2311=⨯==--由于各力对过小孔的竖直轴的力矩为零，所以小球对该轴的角动量守恒，m v 1R 1=m v 2R 2，v 2=v 1R 1/R 2=0.2×0.4/0.1=0.8m/s在由R 1→R 2的过程中，只有拉力F 做功，据动能定理，有J v v v v m v v m mv mv A F 322112122121222121212221103)2.08.0)(2.08.0(10))(()(--⨯=-+⨯=-+=-=-=5.1.8 一个质量为m 的质点在o-xy 平面内运动，其位置矢量为j t b i t a r ˆsin ˆcos ωω+= ，其中a 、b 和ω是正常数，试以运动学和动力学观点证明该质点对于坐标原点角动量守恒。
证明：rj t b i t a dt v d a j t b i t a dt r d v 222ˆsin ˆcos /ˆcos ˆsin /ωωωωωωωωω-=--==+-== ⑴运动学观点：k mab k t mab kt mab L k i j j i j j i i j t b i t a m j t b i t a v m r L ˆˆsin ˆcos ˆ)ˆ(ˆˆˆ,0ˆˆˆˆ)ˆcos ˆsin ()ˆsin ˆcos (22ωωωωωωωωωωω=+=∴=-⨯=⨯=⨯=⨯+-⨯+=⨯= 显然与时间t 无关，是个守恒量。
⑵动力学观点： ∵0)(22=⨯-=-⨯=⨯=⨯=r r m r m r a m r F rωωτ,∴该质点角动量守恒。
5.1.9 质量为200g 的小球 B 以弹性绳在光滑水平面上与固定点A 相连。
弹性绳的劲度系数为8 N/m ，其自由伸展长度为600mm.最初小球的位置及速度v 0如图所示。
当小球的速率变为v 时，它与A 点的距离最大，且等于800mm ，求此时的速率v 及初速率v 0.解：设小球B 的质量m=0.2kg,原来与固定点A 的距离r 0=0.4m,当速率为v 时，与A 点距离r =0.8m,弹性绳自由伸展的长度为d =0.6m.小球B 的速率由v 0→v 的过程中，作用在小球B 上的力对过A 点轴的力矩之和始终为零，因而小球对A 点的角动量守恒，有r 0mv 0sin30º= rmv (最大距离时，)v r ⊥ （1）另外,在此过程中,只有保守内力（绳的弹力）做功,因而能量守恒，)2()(2212212021mv d r k mv +-=为求解方便，将⑴⑵化简，并代入已知数据可得：)'2(6.1)'1(42200v v v v +==解此方程组，求得：v 0 ≈1.3 m/s v ≈0.33 m/s5.1.10 一条不可伸长的细绳穿过铅直放置的、管口光滑的细管，一端系一质量为0.5g 的小球，小球沿水平圆周运动。
最初l 1=2m,θ1=30º，后来继续向下拉绳使小球以θ2=60º沿水平圆周运动。
求小球最初的速度v 1，最后的速度v 2以及绳对小球做的总功。
解：隔离小球，受力情况如图示，应用牛顿第二定律，有：)3(sin cos /)2/()1()2(cos )1(sin /sin sin cos sin 22θθθθθθθθgl v mg F l mv F gl v =∴===得 当θ=θ1时s m gl v /38.23/48.9sin cos /211111=⨯==θθ 当θ=θ2时,)4(322223cos sin 22222222g v gl l gl v =∴==θθ 由于作用质点上的力对管轴的力矩始终等于零,∴角动量守恒： 1sin sin 22221112211sin sin v v l mv l mv l l θθθθ=∴=，将（4）式和三角函数值代入，可求得： s m v v gl /43.338.228.93233323211=⨯⨯⨯==将v 2代入（4）中，可求得l 2=0.8m ，根据质点动能定理： Jl l mg v v m E E A p k F 0806.0)8.02(105.0)38.243.3(105.0)cos cos ()(21233223212211212221=⨯-⨯⨯+-⨯⨯⨯=-+-=∆+∆=--θθ5.2.2 理想滑轮悬挂两质量为m 的砝码盘。
用轻线拴住轻弹簧两端使它处于压缩状态，将此弹簧竖直放在一砝码盘上，弹簧上端放一质量为m 的砝码。
另一砝码盘上也放置质量为m 的砝码，使两盘静止。
燃断轻线，轻弹簧达到自由伸展状态即与砝码脱离。
求砝码升起的高度，已知弹簧劲度系数为k ，被压缩的长度为l 0.解：设滑轮半径为R ，弹簧释放后，弹簧上边的砝码获得的速度为v ，方向向上，左边砝码盘获得的速度为v '，方向向下，显然右边砝码盘及砝码获得的速度大小也是v ',但方向向上（如图示）。
把左盘、左盘上的砝码和右盘及盘中砝码视为一个质点系，作为研究对象。
在弹簧释放过程中，作用于质点系的外力对滑轮轴的力矩之和始终为零，故质点系对滑轮轴的角动量守恒，规定垂直纸面向外的角动量为正，则有：-mvR+mv ’R+2mv ’R = 0，即 v = 3 v ' (1)另外，在此过程中，只有弹簧的弹力和重力做功，因而质点系能量守恒，忽略重力势能的微小变化，则有：2212212021')3(v m mv kl +=，即 )2('32022kl mv mv =+左盘中的砝码脱离弹簧获得速度v 后做竖直上抛运动,达到最大高度h 时速度为零,据能量守恒,)3(2/2221g v h mgh mv =∴=由⑴⑵可求得v 2=3kl 02/4m ，代入⑶中得：h = 3 k l 02/8mg5.2.3 两个滑冰运动员的质量各为70kg ，以6.5m/s 的速率沿相反方向滑行，滑行路线间的垂直距离为10m ，当彼此交错时，各抓住10m 绳索的一端，然后相对旋转。
⑴在抓住绳索一端之前，各自对绳索中心的角动量是多少？抓住之后是多少？⑵它们各自收拢绳索，到绳长为5m 时，各自的速率如何？⑶绳长为5m 时，绳内张力多大？⑷二人在收拢绳索时，各自做了多少功〉⑸总动能如何变化？解：设每个运动员的质量为m=70kg ，收绳前相对绳中心o 的距离为d = d 1= 5m ，速率为v=v 1=6.5m/s ；当把绳收拢为d = d 2= 2.5m 时, 速率v=v 2.⑴对绳中心o 点的角动量各为L=mv 1d 1=70×6.5×5=2275kgm 2/s （抓住绳索前后角动量相同）⑵把两个运动员视为一个质点系,在收绳过程中，质点系对o 轴的角动量守恒有2m v 1d 1 = 2m v 2 d 2∴v 2 = v 1d 1/d 2 = 6.5×5/2.5 =13 m/s⑶把某一运动员视为质点，作为研究对象，由牛顿第二定律，绳中张力F = m v 22/d 2 = 70×132 /2.5 = 4732 N⑷由质点动能定理，每人所做的功均为：J v v v v m mv mv A 4436)5.613)(5.613(70))((2112122121212221=+-⨯=+-=-=⑸总动能增大了ΔE k = 2×4436 = 8872 J。