学习探究诊断必修二
学探诊(高中物理必修二)测试二

C . ω =D .v =ωr物理必修 2 测试二A 卷(满分 100 分)一、单项选择题(本题共 10 个小题,每小题 3 分,共 30 分。
在每小题给出的四个选项中,只有一个选项是符合题意的)1.关于物体的动能,下列说法正确的是( )A .质量大的物体,动能一定大B .速度大的物体,动能一定大C .速度方向变化,动能一定变化D .物体的质量不变,速度变为原来的两倍,动能将变为原来的四倍 2.关于功和能,下列说法正确的是( )A .功有正负,因此功是矢量B .功是能量转化的量度C .能量的单位是焦耳,功的单位是瓦特D .1N 的力作用在物体上,使物体发生 1m 的位移,力对物体做的功一定为 1J 3.关于万有引力和万有引力定律,下列说法正确的是( )A .只有天体间才存在相互作用的引力B .只有质量很大的物体间才存在相互作用的引力C .物体间的距离变大时,它们间的引力将变小D .物体对地球的引力小于地球对物体的引力4.一物体做匀速圆周运动的半径为 r ,线速度大小为 v ,角速度为ω,周期为 T 。
关于这些物理量的关系,下列说法正确的是( )A . v =ωrB . v =2π 2πRT T5.开普勒分别于 1609 年和 1619 年发表了他发现的行星运动规律,后人称之为开普勒行星运动定律。
关于开普勒行星运动定律,下列说法正确的是( ) A .所有行星绕太阳运动的轨道都是圆,太阳处在圆心上 B .对任何一颗行星来说,离太阳越近,运行速率就越大C .在牛顿发现万有引力定律后,开普勒才发现了行星的运行规律D .开普勒独立完成了观测行星的运行数据、整理观测数据、发现行星运动规律等全部工作6.关于经典力学,下列说法正确的是( )A .由于相对论、量子论的提出,经典力学已经失去了它的意义B .经典力学在今天广泛应用,它的正确性无可怀疑,仍是普遍适用的C .经典力学在宏观低速运动、引力不太大时适用D .经典力学对高速运动的电子、中子、质子等微观粒子是适用的7.一薄圆盘可绕通过圆盘中心且垂直于盘面的竖直轴 OO ′转动,如图所示。
人教版生物必修二同步导学精品检测:学业质量标准检测5含解析

个帅哥帅哥的 ffff第五章学业质量标准检测本试卷分第Ⅰ卷 (选择题 )和第Ⅱ卷 (非选择题 )两部分。
满分100 分,考试时间90 分钟。
第Ⅰ卷 (选择题共50分)一、选择题 (共 25 小题,每题 2 分,共 50 分,在每题给出的 4 个选项中,只有1项是切合题目要求的)1.控制正常蛋白的基因发生突变后惹起的氨基酸序列的改变以下图。
图中①、②两种基因突变分别属于( C )A .碱基对的替代碱基对的缺失B.碱基对的缺失碱基对的增加C.碱基对的替代碱基对的增加或缺失D.碱基对的增加或缺失碱基对的替代[分析 ]从题图中能够看出,突变①只惹起一个氨基酸的改变,所以应属于碱基对的替换。
突变②惹起突变位点此后的多种氨基酸的改变,所以可能属于碱基对的增加或缺失。
2.以下对于基因突变和基因重组的表达中,错误的选项是( D )A.基因突变和基因重组都对生物进化有重要意义B.基因突变能改变基因中的碱基序列,而基因重组只好改变基因型C.真核细胞分裂过程中的基因重组只好发生在减数分裂过程中D.基因突变和基因重组都能发生在受精过程中[分析 ]基因突变能够产生新基因,基因重组能够产生新的基因型,都对生物进化有重要意义, A 项正确;基因突变能够改变基因中的碱基序列,但基因重组只好改变生物个体的基因型, B 项正确;真核细胞的分裂包含有丝分裂、无丝分裂、减数分裂三种方式,而自然状态下基因重组发生在有性生殖过程中,即减数分裂过程中, C 项正确, D 项错误。
3.基因型为AaBb( 位于非同源染色体上) 的小麦,将其花粉培养成幼苗,用秋水仙素处理后的成体自交后辈的表现型及其比率为( C )A.1 种,所有B.2 种, 3∶1C.4 种, 1∶1∶ 1∶ 1D. 4 种, 9∶ 3∶ 3∶ 1[分析 ]基因型为AaBb( 位于非同源染色体上)的小麦,将其花粉培养成幼苗,用秋水仙素办理后的成体为纯合体,共四种:AABB 、 AAbb 、 aaBB、 aabb,纯合体自交后辈不发生性状分别,仍为纯合体,表现型及其比率为1∶ 1∶ 1∶ 1。
北京西城学习探究诊断高中数学选修2-1全本练习

北京西城区学习探究诊断高中数学选修2- 1第一章 常用逻辑用语 测试一 命题与量词Ⅰ 学习目标会判断命题的正误,理解全称量词与存在量词的意义.Ⅱ 基础性训练一、选择题1.下列语句中不是命题的是( )(A)(C)2(A)3>3(A)y =(C)4①∃x ③∃x (A)05(A)x >(C)6(A)b a ∀⊥(C)⊥∃b a 7.下列命题是假命题的是( )(A)对于非零向量a ,b ,若a ·b =0,则a ⊥b (B)若|a |=|b |,则a =b (C)若ab >0,a >b ,则ba 11< (D)a 2+b 2≥2ab8.若命题“ax 2-2ax +3>0对x ∈R 恒成立”是真命题,则实数a 的取值范围是( )(A)0≤a <3(B)0≤a ≤3(C)0<a <3(D)0≤a <3二、填空题9.在R 上定义运算⊗:x ⊗y =x (1-y ),若不等式(x -a )⊗(x +a )<1对于∀x ∈R 均成立,则实数a 的取值范围是______. 10.设A 、B 为两个集合,下列四个命题:①A ⊄B ⇔对任意x ∈A ,有x ∉B ②A ⊆/B ⇔A ∩B =∅③A ⊆/B ⇔A ⊇B④A ⊆/B ⇔存在x ∈A ,使得x ∉B其中真命题的序号是______.(把符合要求的命题序号都填上)三、解答题11.判断下列语句哪些是命题?如果是命题,是真命题还是假命题?(1)末位数字是0的整数能被5整除; (2)平行四边形的对角线相等且互相平分; (3)(4)△(5)12(1)(2)(3)13(1)(2)(3)∃x 1.D 29.21<-11.(1)(4)12.(1)∀(2)∃x (3)∃(13.测试二 基本逻逻辑联结词Ⅰ 学习目标1.了解逻辑联结词“或”、“且”、“非”的含义. 2.能正确地对含有一个量词的命题进行否定.Ⅱ 基础性训练一、选择题1.命题“菱形的对角线互相垂直平分”是( )(A)简单命题(B)“非p ”形式的命题(C)“p 且q ”形式的命题 (D)“p 或q ”形式的命题2.下列结论中正确的是( )(A)p是真命题时,“p且q”一定是真命题(B)p是假命题时,“p且q”不一定是假命题(C)“p且q”是假命题时,p一定是假命题(D)“p且q”是真命题时,p一定是真命题3.如果“p或q”与“非p”都是真命题,那么( )(A)q一定是真命题(B)q不一定是真命题(C)p不一定是假命题(D)p与q的真假相同4.“xy≠0”是指( )(A)x≠0且y≠0 (B)x≠0或y≠0(C)x,y至少一个不为零(D)x,y不都为零5.命题p(A)(C)6(A)∀x(C)∃x7(A)∃x(C)∀x8.已知U(A)2∈(C)29“非p(A)p:(B)p:{0}{(C)p(D)p10.命题(A)(B)不存在实数a,使方程x2+ax+1=0没有实数根(C)对任意实数a,使方程x2+ax+1=0没有实数根(D)至多有一个实数a,使方程x2+ax+1=0有实数根二、填空题11.命题“∀x∈A,x∈A∪B”的命题的否定是________________.12.“l⊥??”的定义是“若∀g⊂??,l⊥g,则称l⊥??”,那么“直线l不垂直于平面??”的定义是_____________________________.13.已知命题:“非空集合A的元素都是集合B的元素”是假命题.那么给出下列命题:①“A中的元素都不是集合B的元素”;②“A中有不属于B的元素”;③“A中有B的元素”;④“A中的元素不都是B的元素”.其中真命题的序号是______.(将正确命题的序号都填上)14.“A是B的子集”可以用下列数学语言表达:“若对任意的x∈A,都有x∈B,则称A⊆B”.那么“A不是B的子集”可用数学语言表达为________________.三、解答题15.写出下列命题的否定,并判断真假:(1)质数都是奇数;(2)∀x∈R,3x-5>2x;(3)∀A⊆U(U为全集),∅是集合A的真子集.16.命题p:正方形是菱形;q:正方形是梯形.写出其构成的“p或q”,“p且q”,“非p”形式的命题,并判断1.C 2.11.∃x∈12.∃g⊂13.②④14.若∃x15.解:16.答:pp121(A)(C)2.已知a(A)(C)充要条件(D)既不充分也不必要条件3.条件p:ac2>bc2是条件q:a>b(A)充分不必要条件(B)必要不充分条件(C)充要条件(D)既不充分又不必要条件4.若条件甲:“=”,条件乙:“ABCD是平行四边形”,则甲是乙的( )(A)充分不必要条件(B)必要不充分条件(C)充要条件(D)既不充分又不必要条件5.若命题p的逆命题是q,命题p的逆否命题是r,则q是r的( )(A)逆命题(B)否命题(C)逆否命题(D)非四种命题关系6.原命题的否命题为假,可判断( )(A)原命题为真(B)原命题的逆命题为假(C)原命题的逆否命题为假(D)都无法判断7.已知集合A={x|x2-5x-6≤0},B=x|x2-6x+8≤0,则x∈A是x∈B的( )(A)充分不必要条件(B)必要不充分条件(C)充要条件(D)既不充分也不必要条件8.在下列命题中,真命题是( )(A)命题“若ac>bc,则a>b”(B)命题“若a n是n的一次函数,则数列{a n}是等差数列”的逆命题(C)命题“若x=3,则x2-4x+3=0”的否命题(D)9.设x,y(A)x=(C)x≠10.下列(A)(B)(C)(D)111213141516其中正确的命题是______(请填入正确命题的序号).17.①“若xy=1,则x,y互为倒数”的逆命题;②“相似三角形的周长相等”的否命题;③“若a≤-1,则方程x2-2ax+a2⊆+a=0有实数根”的逆否命题;④“若A∩B=B,则A⊆B”的逆否命题.其中正确的命题是______.(填上你认为正确的命题序号)18.设全集为S,集合A,B⊆S,有下列四个命题:①A∩B=A;②s A⊇s B;③(s B)∩A=∅;④(s A)∩B=∅.其中是命题A⊆B的充要条件的命题序号是______.测试三充分条件、必要条件与四种命题1.C 2.B 3.A 4.B 5.B 6.B 7.B 8.D 9.C 10.D 11.若x ≥4,则x ≥3 12.充分不必要13.若x ≠0且y ≠0,则xy ≠0 14.b ≥-2 15.2,2-==b a 都是无理数,但a +b =0是有理数;也可举例2,21-=+=b a 等.16.①②④ 17.①③ 18.①②③121.在点A (A)1个2.方程x 2(A)(C)3(A)y =4.方程(A)y =(C)y =5.方程(2(A)(C)6.直线x 7.圆x 2+y 2+Dx +Ey +F =0(D 2+E 2-4F >0)经过坐标原点的充要条件是______. 8.到两平行线l 1:3x +2y -4=0,l 2:3x +2y -8=0距离相等的点的轨迹方程是______. 9.若动点P 到点(1,1)的距离等于它到y 轴的距离,则动点P 的轨迹方程是______. 10.已知两定点A (-1,0),B (3,0),动点P 满足21||||=PB PA ,则动点P 的轨迹方程是 ________________________. 三、解答题11.已知动点P 到两定点M (1,3),N (3,1)的距离平方之和为20,求动点P 的轨迹方程. 12.试画出方程|x +|y |=1的曲线,并研究其性质.13.如图,设D 为圆C :x 2+y 2-4x +4y +6=0的圆心,若P 为圆C 外一动点,过P 向圆C 作切线PM ,M 为切点,设2=PM ,求动点P 的轨迹方程.Ⅲ 拓展性训练14.如图,已知点P (-3,0),点Q 在x 轴上,点A 在y 轴上,且0=⋅AQ PA ,AQ QM 2=.当点A 在y 轴上移动时,求动点M 的轨迹方程.第二章 圆锥曲线与方程测试四 曲线与方程1.C 2.B 3.D 4.B 5.B6.(5,2),)25,4( 7.F =0 8.3x +2y -6=0 9.21(2)1(2-=-x y 10.3x 2+3y 2+14x -5=011.x 2+y 2-4x -4y =0. 12.方程的曲线如图.(1)曲线的组成:由四条线段首尾连接构成的正方形;13.14测试五 椭圆AⅠ 学习目标1.理解椭圆的定义,掌握椭圆的两种标准方程.2.掌握椭圆的几何性质,椭圆方程中的a ,b ,c ,e 的几何意义、相互关系、取值范围等对图形的影响.Ⅱ 基础性训练一、选择题1.长半轴长为4,短半轴长为1,目焦点在x 轴上的椭圆标准方程是( )(A)1422=+y x(B)1422=+y x(C)11622=+y x(D)11622=+y x2.椭圆1251622=+y x 的焦点坐标是( )(A)(0,3),(0,-3) (B)(3,0),(-3,0) (C)(0,5),(0,-5)(D)(4,0),(-4,0)3.若椭圆13610022=+y x 上一点P 到其焦点F 1的距离为6,则P 到另一焦点F 2的距离为( )(A)4(B)194(C)94(D)144.已知F 1,F 2是定点,821=F F ,动点M 满足|MF 1|+|MF 2|=8,则动点M 的轨迹是( )(A)椭圆 (B)直线 (C)圆 (D)线段5.如果方程x 2+ky 2=1表示焦点在x 轴上的椭圆,那么实数k 的取值范围是( )(A)k <6.经过点7.设a ,. 8.设P _______.9.过椭圆101134|1=,|2PF 12轴上.(1)(2)13求点1.C 2.6.151522=+y x 7.a >b >c 8.)1,215(±± 9.22 10.)0(1203622=/=+y y x 11.因为点P 在椭圆C 上,所以2a =|PF 1|+|PF 2|=6,所以a =3.在Rt △PF 1F 2中,52||||||212221=-=PF PF F F ,故椭圆的半焦距5=c ,从而b 2=a 2-c 2=4,所以,椭圆C 的方程为14922=+y x .12.(1)长半轴长10,短半轴长8,焦点坐标(6,0)、(-6,0),离心率53=e; (2)椭圆164100:222=+x y C ,性质:①范围:-8≤x ≤8,-10≤y ≤10;②对称性:关于x 轴,y 轴,原点对称;③顶点:长轴端点(0,10),(0,-10),短轴端点(-8,0),(8,0); ④离心率:53=e. 13.由题意,)0,5(),0,5(21F F -,设P (x ,y ),1212(A)3(A)4.已知F (c ,0)是椭圆)0(1:2222>>=+b a by a x C 的右焦点,设b >c ,则椭圆C 的离心率e 满足( )(A)20<<e (B)220<<e (C)210<<e (D)122<<e 5.已知两定点M (-1,0)、N (1,0),直线l :y =-2x +3,在l 上满足|PM |+|PN |=4的点P 有( )(A)0个 (B)1个(C)2个(D)3个二、填空题6.若方程1162522=++-my m x 表示焦点在y 轴上的椭圆,则实数m 的取值范围是______.7.若椭圆)8(19822->=++k y k x 的离心率21=e ,则k 的值为________.8.过椭圆)0(12222>>=+b a by a x 的中心的直线l 与椭圆相交于两点A 、B ,设F 2为该椭圆的右焦点,则△ABF 2面积的最大值是________.9.椭圆192522=+y x 上一点M 到左焦点F 1的距离为2,点N 是MF 1的中点,设O 为坐标原点,则ON =________.10.P 为椭圆16410022=+y x 上一点,左右焦点分别为F 1、F 2,若∠F 1PF 2=60°,则△PF 1F 2的面积为________.11121314=b 2+c 2,a>0,1A 2的中点. (1)(2)设B 1,B 2或A 1(3)若测试六 椭圆B1.C 2.A 3.B 4.B 5.C 6.2529<<m 7.4或45- 8.22b a b - 9.4 10.3364 提示:9.设F 2为椭圆的右焦点,由椭圆的定义|MF 2|+MF 1|=2a ,得|MF 2|=10-2=8,在△MF 1F 2中,∵|MN |=NF 1|,|OF 1|=|OF 2|, ∴4||21||2==MF ON. 10.设|PF 1|=r 1,|PF 2|=r 2,由椭圆定义,得r 1+r 2=20……①由①211.设A (x 把y 解得所以故AB (12.设P (x 则|13则有⎩⎨⎧-==.||,||1r R CC r CP 消去r ,得CC 1|+CP |=10,又C 1(-3,0),P (3,0),|C 1P |=6<10,所以,由椭圆的定义知圆心C 的轨迹是以C 1,P 为焦点的椭圆, 且半焦距c =3,2a =10,a =5,从而b =4,所以,所求的动圆的圆心C 的轨迹方程为1162522=+y x .14.(1)∵),0(),,0(),0,(2222210c b F c b F c F ---,∴1)(||32220==+-=b c c b F F ,12||2221=-=c b F F ,于是47,432222=+==c b a c, 所求“果圆”方程为)0(134),0(1742222≤=+≥=+x x y x y x .(2)∵M 是线段A 1A 2的中点,又A 1(-c ,0),A 2(a ,0),∴)0,2(ca M -,设P (x ,y ),则12222=+c x b y ,即22222x c b b y -=,又222c a -∵(3)x ≥0)上的当当|综上所述,若a ≤2c ,当|PM |取得最小值时,点P 的横坐标是22c ;若a >2c ,当|PM |取得最小值时,点P 的横坐标是a 或-c .测试七 双曲线Ⅰ 学习目标1.理解双曲线的定义,掌握椭圆的两种标准方程.2.掌握双曲线的几何性质,双曲线方程中的a ,b ,c ,e 的几何意义、相互关系、取值范围等对图形的影响. 3.能初步应用双曲线的定义、几何性质解决与双曲线有关的简单问题,并初步体会数形结合的思想.Ⅱ 基础性训练一、选择题1.双曲线117822=-x y 的焦点坐标为( )(A)(±5,0)(B)(±3,0)(C)(0,±3)(D)(0,±5)23456789.双曲线191622=-y x 上的一点P ,到点(5,0)的距离为15,则点P 到点(-5,0)的距离为_____________________.10.已知双曲线)2(12222>=-a y a x 两条渐近线的夹角为3π,则此双曲线的离心率为_________________. 三、解答题11.已知三点P (5,2),F 1(-6,0),F 2(6,0).(1)求以F 1,F 2为焦点,且过点P 的椭圆的标准方程;(2)设点P ,F 1,F 2关于直线y =x 的对称点分别为P ′,F 1′,F 2′,求以F 1′,F 2′为焦点且过点P ′的双曲线的标准方程.12.已知定圆O 1:x 2+y 2+10x +24=0,定圆O 2:x 2+y 2-10x +9=0,动圆M 与定圆O 1,O 2都外切,求动圆圆心M的轨迹方程.13.以双曲线)0,0(1:2222>>=-b a b y a x C 的虚轴为实轴,实轴为虚轴的双曲线叫做C 的共轭双曲线.(1)写出双曲线15422=-y x 的共轭双曲线的方程;(2)设双曲线C 与其共轭双曲线的离心率分别为e 1,e 2,求证1112221=+e e . 测试七 双曲线1.D 2.A 3.C 4.D 5.C6.(9.711.1242故双曲线的方程为)23(19149422>-≤=-x y x . 13.(1)双曲线15422=-y x 的共轭双曲线的方程为14522=-x y ;(2)在双曲线C 中,半焦距22b ac +=,所以离心率ab a ace 221+==;双曲线C 共轭双曲线方程为)0,0(12222>>=-b a x by α,其半焦距为22b a +,所以离心率bb a e 222+=. 所以,1112222222221=+++=+b a b b a a e e. 测试八 抛物线A121(A)y 2=2.抛物线(A)(-3(A)(18(C)(184.方程2(A)(C)5.点P (A)y 26.准线为7.过点A 8.抛物线910①焦点在y 轴上; ②焦点在x 轴上;③抛物线上横坐标为1的点到焦点的距离等于6; ④由原点向过焦点的某条直线作垂线,垂足坐标为(2,1).能使这抛物线方程为y 2=10x 的条件是_______.(要求填写合适条件的序号) 三、解答题11.抛物线的顶点在原点,焦点在直线x -2y -4=0上,求抛物线的标准方程.12.求以抛物线2y =8x 的顶点为中心,焦点为右焦点且渐近线为x y 3±=的双曲线方程.13.设P 是抛物线221x y =上任意一点,A (0,4),求|PA |的最小值. 测试八 抛物线A 1.B 2.D 3.C 4.A 5.C 6.x y 82-= 7.x y342=或y x 292= 8.161-=y 9.4 10.②,④ 11.由题意,焦点既在坐标轴上,又在直线x -2y -4=0上,令x =0,得焦点为(0,-2);令y =0,得焦点为(4,0) 当焦点为(0,-2)时,抛物线方程为x 2=-8y ; 当焦点为(4,0)时,抛物线方程为y 2=16x . 12.抛物线y 2=8x 的顶点为(0,0),焦点为(2,0),即2λx 13则|因为因为121.抛物线x 2=y 的准线方程是( )(A)4x +1=0(B)4y +1=0(C)2x +1=0(D)2y +1=02.抛物线的顶点在原点,焦点是椭圆4x 2+y 2=1的一个焦点,则此抛物线的焦点到准线的距离是( )(A)32(B)3(C)321 (D)341 3.连接抛物线x 2=4y 的焦点F 与点M (1,0)所得的线段与抛物线交于点A ,设点O 为坐标原点,则三角形OAM 的面积为( ) (A)21+-(B)223- (C)21+(D)223+ 4.抛物线y =-x 2上的点到直线4x +3y -8=0距离的最小值是( )(A)34 (B)57 (C)58 (D)35.设O 为坐标原点,F 为抛物线y 2=4x 的焦点,A 为抛物线上的一点,若4-=⋅,则点A 的坐标为( )(A))22,2(± (B)(1,2)(C)(1,±2)(D))22,2(二、填空题6.过抛物线y 2=6x 的焦点F ,作垂直于抛物线对称轴的直线l ,设l 交抛物线于A ,B 两点,则|AB |=_________. 7.抛物线y =-ax 2(a >0)的焦点坐标为_________.8.已知圆x 2+y 2-6x -7=0与抛物线y 2=2px (p >0)的准线相切,则p =_________. 9.过抛物线y 2=4x 的焦点作直线交抛物线于A 、B 两点,若线段AB 的中点横坐标为3,则|10.设F |MF 11 122=x 1+x 3,13点的坐标.14.设F l :x =-1(1)(2)设1.B 2.6.6 7.11所以(所以抛物线的标准方程为x 2=2y ,或x 2=18y . 12.由抛物线定义,知2||11p x PF +=,2||22p x F P +=,2||33px F P +=, 所以|FP 1|+|FP 3|=x 1+x 2+p ,2|FP 2|=2x 2+p , 又x 1+x 3=2x 2,所以2|FP 2|=|FP 1|+|FP 3|. 13.直线AB 的方程为30233--+=x y ,即3x -y -3=0, 102)33()20(||22=--+-=AB ,因为点P 在x 2=y 上,所以设P (x ,x 2),所以点P 到直线AB 的距离10|43)23(|91|33|22+-=+--=x x x d , 因为x ∈R ,所以当23=x 时,1043min =d , 故当49,23(P 时,△PAB 面积有最小值43104310221=⨯⨯=S . 14.(1)(2)设∴∵∴∵当121.过点P (A)1条2.一个正三角形的顶点都在抛物线y 2=4x 上,其中一个顶点在坐标原点,则这个三角形的面积是( )(A)348(B)324(C)3916(D)3463.过双曲线1222=-y x 的右焦点F 作直线l 交双曲线于A 、B 两点,若|AB |=4,则这样的直线有( )(A)1条(B)2条(C)3条(D)4条4.已知椭圆)0(12222>>=+b a by a x 上总存在点P ,使021=⋅PF PF ,其中F 1,F 2是椭圆的焦点,那么该椭圆的离心率的取值范围是( )(A)]21,12[-(B))12,0(- (C)]22,21[ (D))1,22[5.已知双曲线)0,0(12222>>=-b a by a x 的左焦点F 1,左、右顶点分别为A 1、A 2,P 为双曲线上任意一点,则分别以线段PF 1,A 1A 2为直径的两个圆的位置关系为( ) (A)相切 (B)相交(C)相离(D)以上情况都有可能二、填空题6.直线y =x +1与抛物线y 2=4x 的公共点坐标为____________.7228.设P |PF 191011C 的方程.12(1)若(2)1314.设点AB ,都有(1)判断椭圆的“左特征点”是否存在,若存在,求出该点坐标;若不存在,请说明理由;(2)参考椭圆的“左特征点”定义,给出双曲线)0,0(12222>>=-b a by a x 的“左特征点”定义,并指出该点坐标.测试十 圆锥曲线综合练习(选学)1.B 2.A 3.C 4.D 5.A6.(1,2) 7.m ≥1且m ≠5 8.x 2-y 2=4 9.179010.2>e 11.由题意,设椭圆150:2222=-+a x ay C ,把直线y =3x -2代入椭圆方程150222=-+a x ay , 得(a 2-50)(3x -2)2+a 2x 2=a 2(a 2-50),整理得(10a 2-450)x 2-12(a 2-50)x -a 4+54a 2-200=0, 设直线与椭圆的两个交点A (x 1,y 1),B (x 2,y 2),则有45010)50(122221--=-a a x x ,?=144(a 2-50)2-4(10a 2-450)(-a 4+54a 2-200)>0, 由题意,得1)50(622221=-=+a x x ,解得a 2=75, 12.(1)(2)由⎪⎩>-=∆04242k 解得:)3,6(--∈k ∪)6,3(.13.因为AB //CD ,所以设直线CD 方程为y =x +t ,把y =x +t 代入y 2=x ,消去y ,得x 2+(2t -1)x +t 2=0, 设C (x 1,y 1)、D (x 2,y 2),所以x 1+x 2=1-2t , x 1·x 2=t 2,?=(2t -1)2-4t 2>0, 所以)41(2]4)21[(2)()(||22221221t t t y y x x CD -=--=-+-=,又AB 与CD 间的距离为2|4|||-=t AD , 由正方形ABCD ,得|AD |=|CD |,即2|4|)41(2-=-t t , 解得t =-2,或t =-6, 从而,边长|AD|=23或25,所以正方形面积为18)23(21==S 或50)25(22==S . 14.(1)y ∴?∴=k [2x 1·x 2+c (x 1+x 2)-x 0(x 1+x 2)-2cx 0]∵M (x 0,0)是椭圆的“左特征点”,∴∠AMF =∠BMF . ∴k AM =-k BM ,即k AM +k BM =0, ∴分子0222220222222222222222222[cx ka b ck a x k a b c k a c ab b ac k a k k-+-⨯-+-⨯++-⨯=0, ∵上式要对任意非零实数k 都成立, ∴02222202222202222222222222=-+-⨯-+-⨯++-⨯cx ka b ck a x k a b c k a c ab b ac k a k∴2a 2k 2c 2-2a 2b 2-2a 2k 2c 2+2a 2k 2cx 0-2b 2cx 0-2a 2k 2cx 0=0,∴0220222=--cx b b a ∴ca x 20-=.故对过F 与两坐标轴都不垂直的任意弦AB ,点)0,(2c a M -都能使MF 为△AMB 的一条内角平分线, 所以,椭圆的“左特征点”存在,即为点)0,(2c a M -.方法2:先用特殊值法(可用一条特殊直线AB ,如斜率为1的直线)找出符合“左特征点”性质的一个点M (具体找的过程略,可找到点)0,(2c a M -,即为椭圆的左准线与x 轴的交点),再验证对任意一条与两坐标轴都F=M ,过A x 轴(2)AB ,且A ,B 在双曲线左支上,都有MF 为△AMB 的一条内角平分线,则称点M 为该双曲线的“左特征点”.点)0,(2c a M -是双曲线的左特征点.(其中22b a c +=).第三章 空间向量与立体几何 测试十一 空间向量及其运算AⅠ 学习目标1.会进行空间向量的加法、减法、数乘运算.2.会利用空间向量基本定理处理向量共线,共面问题以及向量的分解.3.会进行空间向量数量积的运算,并会求简单的向量夹角.Ⅱ 基础性训练一、选择题1.在长方体ABCD -A 1B 1C 1D 1中,1DD ++=( )(A)11B D (B)D 1 (C)1DB(D)1BD2.平行六面体ABCD -A 1B 1C 1D 1中,M 为AC 和BD 的交点,若c b a ===1,,AA AD AB ,则下列式子中与M B 1相(A)(C)3(A)(C)4b 共面,则实数(A)15(A)1 67. 8;异面直线AB 9.已知10.______. 11.如图,平行六面体ABCD -A 1B 1C 1D 1中,c b a ===1,,,E 为A 1D 1中点,用基底{a ,b ,c }表示下列向量(1)AF BE DB ,,1;(2)在图中画出DD ++1化简后的向量.12.已知向量a =2i +j +3k ,b =-i -j +2k ,c =5i +3j +4k ,求证向量a ,b ,c 共面. 13.正方体ABCD -A 1B 1C 1D 1中,棱长为1,E 为CC 1中点,(1)求⋅1;(2)求><⋅BE AB BE AB ,cos ,11.Ⅲ 拓展性训练14.如图,点A 是△BCD 所在平面外一点,G 是△BCD 的重心,求证:)(31++=. (注:重心是三角形三条中线的交点,且CG ∶GE =2∶1)第三章 空间向量与立体几何1234567891011111111112.解:设c =m a +n b ,则5i +3j +4k =m (2i +j +3k )+n (-i -j +2k ) =(2m -n )i +(m -n )j +(3m +2n )k ,⎪⎩⎪⎨⎧=+=-=-423352n m n m n m ,解得⎩⎨⎧-==12n m ,所以c =2a -b ,所以向量a ,b ,c 共面. 13.)()(1111CC BC BB AB BC AB +⋅+=⋅2121000=+++=. 1010||||,cos ,25||,2||1111=>=<==BE AB AB AB . 14.证明∵+= ∴)(31)2(31AD AC AB AD AB CA AC AG ++=+++=.测试十二 空间向量及其运算B1231.a =(2(A)(14(C)(142(A)a =(C)e =3(A)24(A)31((C)31(5(A)2 6.已知点A (3,2,1),向量=(2,-1,5),则点B 的坐标为______,||=______. 7.已知3(2,-3,1)-3x =(-1,2,3),则向量x =______. 8.若向量a =(2,1,-2),b =(6,-3,2),则cos<a ,b>=______.9.已知向量a =(1,1,0),b =(-1,0,2),且k a +b 与2a -b 互相垂直,则k 值是______. 10.若空间三点A (1,5,-2),B (2,4,1),C (p ,3,q +2)共线,则p =______,q =______. 三、解答题11.已知向量a =(1,-1,2),b =(-2,1,-1),c =(2,-2,1),求(1)(a +c )·a ; (2)|a -2b +c |;(3)cos 〈a +b ,c 〉.12.已知向量a =(2,-1,0),b =(1,2,-1),(1)求满足m ⊥a 且m ⊥b 的所有向量m . (2)若302||=m ,求向量m .13.已知向量a =(-2,1,-2),b =(1,2,-1),c =(x ,5,2),若c 与向量a ,b 共面,求实数x 的值.14.直三棱柱ABC -A 1B 1C 1的底面△ABC 中,CA =CB =1,∠BCA =90°,棱AA 1=2,M 、N 分别是A 1B 1,A 1A 的中点。
北京西城学习探究诊断高中数学必修二第二章平面解析几何初步练习

第二章平面解析几何初步测试十平面直角坐标系中的基本公式Ⅰ学习目标理解和掌握数轴上的基本公式,平面上两点间的距离公式,中点坐标公式.Ⅱ基础训练题一、选择题1.点A(-1,2)关于y轴的对称点坐标为( )(A)(-1,-2) (B)(1,2) (C)(1,-2) (D)(2,-1)2.点A(-1,2)关于原点的对称点坐标为( )(A)(-1,-2) (B)(1,2) (C)(1,-2) (D)(2,-1)3.已知数轴上A,B两点的坐标分别是x1,x2,且x1=1,d(A,B)=2,则x2等于( )(A)-1或3 (B)-3或3 (C)-1 (D)34.已知点M(-1,4),N(7,0),x轴上一点P满足|PM|=|PN|,那么P点的坐标为( )(A)(-2,0) (B)(-2,1) (C)(2,0) (D)(2,1)5.已知点P(x,5)关于点Q(1,y)的对称点是M(-1,-2),则x+y等于( )9(A)6 (B)12 (C)-6 (D)2二、填空题6.点A(-1,5),B(3,-3)的中点坐标为______.7.已知A(a,3),B(3,a),|AB|=2,则a=______.8.已知M(-1,-3),N(1,1),P(3,x)三点共线,则x=______.9.设点A(0,1),B(3,5),C(4,y),O为坐标原点.若OC∥AB,则y=______;若OC⊥AB,则y=______.10.设点P,Q分别是x轴和y轴上的点,且中点M(1,-2),则|PQ|等于______.三、解答题11.已知△ABC的顶点坐标为A(1,-1),B(-1,3),C(3,0).(1)求证:△ABC是直角三角形;(2)求AB边上的中线CM的长.12.已知矩形ABCD相邻两个顶点A(-1,3),B(-2,4),若矩形对角线交点在x轴上,求另两个顶点C和D的坐标.13.已知AD是△ABC底边的中线,用解析法证明:|AB|2+|AC|2=2(|AD|2+|DC|2).Ⅲ拓展训练题14.利用两点间距离公式求出满足下列条件的实数x的集合:(1)|x-1|+|x-2|=3;(2)|x-1|+|x-2|>3;(3)|x-1|+|x-2|≤3.测试十一 直线的方程Ⅰ 学习目标1.理解直线斜率和倾斜角的概念,掌握两点连线的斜率公式.2.掌握直线方程的点斜式、斜截式及一般式.Ⅱ 基础训练题一、选择题1.已知直线AB 的斜率为21,若点A (m ,-2),B (3,0),则m 的值为( ) (A )1 (B )-1 (C )-7(D )7 2.如图所示,直线l 1,l 2,l 3的斜率分别为k 1,k 2,k 3,则( )(A )k 1<k 2<k 3(B )k 3<k 1<k 2 (C )k 3<k 2<k 1 (D )k 1<k 3<k 23.直线l 经过二、三、四象限,l 的倾斜角为α,斜率为k ,则( )(A )k sin α>0 (B )k cos α>0 (C )k sin α=0 (D )k cos α符号不定4.一条光线从点M (5,3)射出,遇x 轴后反射,反射光线过点N (2,6),则反射光线所在直线方程是( )(A )3x -y -12=0 (B )3x +y +12=0(C )3x -y +12=0 (D )3x +y -12=05.直线x -2y +2k =0与两坐标轴围成的三角形面积不小于1,那么k 的取值范围是( )(A )k ≥-1 (B )k ≤1 (C )|k |≤1 (D )|k |≥1二、填空题6.斜率为-2且在x 轴上截距为-1的直线方程是______.7.y 轴上一点M 与点N (-3,1)所在直线的倾斜角为120°,则M 点坐标为______.8.已知直线3a x -2y -4a =0(a ≠0)在x 轴上的截距是它在y 轴上的截距的3倍,则a =______.9.已知直线l 过点A (-2,1)且与线段BC 相交,设B (-1,0),C (1,0),则直线l 的斜率k 的取值范围是______.10.如果直线l 沿x 轴负方向平移3个单位,接着再沿y 轴正方向平移1个单位后又回到原来的位置,则直线l 的斜率为______.三、解答题11.直线l 过原点且平分平行四边形ABCD 的面积.若平行四边形两个相对顶点为B (1,4),D (5,0),求直线l 的方程.12.直线l与直线y=1,x-y-7=0分别交于P、Q两点,线段PQ的中点为(1,-1).求直线l的方程.Ⅲ拓展训练题13.设A(0,3),B(3,3),C(2,0),直线x=a将△ABC分割成面积相等的两部分,求a 的值.14.一条直线l过点P(2,3),并且分别满足下列条件,求直线l的方程.(1)倾斜角是直线x-4y+3=0的倾斜角的两倍;(2)与x轴、y轴的正半轴交于A、B两点,且△AOB的面积最小;(3)|P A|²|PB|为最小(A、B分别为直线与x轴、y轴的正半轴的交点).测试十二 两条直线的位置关系(一)Ⅰ 学习目标掌握两条直线平行、垂直的条件,会利用两条直线平行、垂直的条件解决相关的问题.Ⅱ 基础训练题一、选择题1.如果直线ax +2y +2=0与直线3x -y -2=0平行,那么a 等于( )(A )-3 (B )-6 (C )-23 (D )32 2.如果直线ax +2y +2=0与直线3x -y -2=0垂直,那么a 等于( ) (A )-3 (B )-6 (C )-23 (D )32 3.若两条直线A 1x +B 1y +C 1=0,A 2x +B 2y +C 2=0垂直,则( )(A )A 1A 2+B 1B 2=0 (B )A 1A 2-B 1B 2=0(C )2121B B A A =-1 (D )2121A A B B =1 4.设A ,B 是x 轴上两点,点P 的横坐标为2,且|P A |=|PB |,若直线P A 的方程为x -y +1=0,则直线PB 的方程为( )(A )x +y -5=0 (B )2x -y -1=0(C )2y -x -4=0 (D )x +y -7=05.已知直线y =kx +2k +1与y =-21x +2的交点在第一象限,则k 的取值范围是( ). (A )-6<k <2(B )-21<k <21 (C )-61<k <21 (D )k <21 二、填空题6.以A (1,3)、B (-1,1)为端点的线段的垂直平分线方程是______.7.若三条直线l 1:2x -y =0,l 2:x +y -3=0,l 3:mx +ny +5=0交于一点,则实数m ,n 满足的关系式是______.8.直线y =2x +3关于点(2,3)对称的直线方程为______.9.直线2x -y +1=0绕着它与y 轴的交点逆时针旋转45°角,此时直线的方程为______.10.若三条直线x +y =2,x -y =0,x +ay =3构成三角形,则a 的取值范围是______.三、解答题11.求经过两条直线l 1:2x +3y +1=0和l 2:x -3y +4=0的交点,并且垂直于直线3x +4y -7=0的直线方程.12.平行四边形ABCD 的两边AB ,AD 所在的直线方程分别为x +y -1=0,3x -y +4=0,其对角线的交点坐标为(3,3),求另两边BC ,CD 所在的直线方程.13.已知三角形三条边AB,BC,AC中点分别为D(2,1)、E(5,3)、F(3,-4).求各边所在直线的方程.14.已知两条直线l1:mx+8y+n=0和l2:2x+my-1=0,试确定m,n的值,使l1,l2分别满足下列条件:(1)l1,l2相交于点P(m,-1);(2)l1∥l2;(3)l1与l2重合.测试十三 两条直线的位置关系(二)Ⅰ 学习目标会应用点到直线的距离公式解决相关的问题.Ⅱ 基础训练题一、选择题1.点P (0,2)到直线y =3x 的距离是( )(A )1 (B )510 (C )2 (D )55 2.平行线3x +4y +2=0与3x +4y -12=0之间的距离为( ) (A )2 (B )310 (C )514 (D )33.若直线(2+m )x -y +5-n =0与x 轴平行且与x 轴相距5时,则m +n 等于( )(A )-2或8 (B )-2 (C )8 (D )04.直线l 1:ax -y +b =0与l 2:bx -y +a =0(ab ≠0,a ≠b )在坐标系中的位置可能是( )5.A 、B 、C 为△ABC 的三个内角, 它们的对边分别为a 、b 、c .已知原点到直线x sin A +y sin B +sin C =0的距离大于1,则此三角形形状为( )(A )锐角三角形 (B )直角三角形 (C )钝角三角形 (D )不能确定二、填空题6.若直线ax +4y -2=0与直线2x -5y +c =0垂直相交于点(1,m ),则a =____,c =_____,m =______.7.已知定点A (0,1).点B 在直线x +y =0上运动,当线段AB 最短时,点B 的坐标是____.8.两平行直线分别过点(1,0)与(0,5),且距离为5,它们的方程为______.9.若点A (1,1)到直线l :x cos θ+y sin θ=2(θ为实数)的距离为f (θ),则f (θ)的最大值是___.10.若动点A (x 1,y 1),B (x 2,y 2)分别在直线l 1:x +y -7=0和l 2:x +y -5=0上移动,则AB 中点M 到原点距离的最小值是______.三、解答题11.过点P (1,2)的直线l 与两点A (2,3),B (4,-5)的距离相等,求直线l 的方程.12.已知直线l :x +2y -2=0,试求:(1)与直线l 的距离为5的直线的方程;(2)点P (-2,-1)关于直线l 的对称点的坐标.13.已知△ABC的垂心H(5,2),且A(-10,2)、B(6,4),求点C的坐标.Ⅲ拓展训练题14.在△ABC中,点B(1,2),BC边上的高所在的直线方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0,求|BC|.测试十四 圆的方程Ⅰ 学习目标掌握圆的标准方程及一般方程,能根据已知条件求圆的方程.Ⅱ 基础训练题一、选择题1.圆x 2+y 2+ax =0的圆心的横坐标为1,则a 等于( )(A )1 (B )2 (C )-1 (D )-22.与圆C :x 2+y 2-2x -35=0的圆心相同,且面积为圆C 的一半的圆的方程是( )(A )(x -1)2+y 2=3 (B )(x -1)2+y 2=6(C )(x -1)2+y 2=9 (D )(x -1)2+y 2=183.曲线x 2+y 2+22x -22=0关于( )(A )直线x =2轴对称(B )直线y =-x 轴对称 (C )点(-2,2)中心对称 (D )点(-2,0)中心对称4.如果圆x 2+y 2+Dx +Ey +F =0与y 轴相交,且两个交点分别在原点两侧,那么( )(A )D ≠0,F >0 (B )E =0,F >0(C )F <0 (D )D =0,E ≠05.方程x -1=()211--y 所表示的曲线是( ) (A )一个圆 (B )两个圆(C )半个圆 (D )四分之一个圆二、填空题6.过原点的直线将圆x 2+y 2-2x +4y =0的面积平分,则此直线的方程为______.7.已知圆的方程(x -a )2+(y -b )2=r 2(r >0),试根据下列条件,分别写出a ,b ,r 应满足的条件.(1)圆过原点且与y 轴相切:______;(2)原点在圆内:______;(3)圆与x 轴相交:______.8.圆(x -1)2+y 2=1的圆心到直线y =33x 的距离是______. 9.P (x ,y )是圆x 2+y 2-2x +4y +1=0上任意一点,则x 2+y 2的最大值是______;点P 到直线3x +4y -15=0的最大距离是______.10.设P (x ,y )是圆(x -3)2+y 2=4上的点,则xy 的最小值是______. 三、解答题11.方程x 2+y 2+ax +2ay +2a 2+a -1=0表示圆,求a 的取值范围.12.求过三个点A (0,0),B (4,0),C (2,2)的圆的方程.13.已知圆C的圆心在直线x+y-1=0上,且A(-1,4)、B(1,2)是圆C上的两点,求圆C的方程.Ⅲ拓展训练题14.已知曲线C:x2+y2-4ax+2ay+20a-20=0.(1)证明:不论a取何实数,曲线C必过定点;(2)当a≠2时,证明曲线C是一个圆,且圆心在一条直线上.测试十五 直线与圆的位置关系Ⅰ 学习目标1.会用解析法及几何的方法判定直线与圆的位置关系,并会求弦长和切线方程; 2.会用几何的方法判定圆和圆的位置关系.Ⅱ 基础训练题一、选择题1.圆x 2+y 2-2x =0和x 2+y 2+4y =0的位置关系是( ) (A )相离 (B )外切 (C )相交 (D )内切2.直线3x +4y +2=0与圆x 2+y 2+4y =0交于A 、B 两点,则线段AB 的垂直平分线的方程是( )(A )4x -3y -2=0 (B )4x -3y -6=0 (C )3x +4y +8=0 (D )3x -4y -8=0 3.直线3x +y -23=0截圆x 2+y 2=4得的劣弧所对的圆心角为( ) (A )6π(B )4π (C )3π (D )2π 4.若圆x 2+y 2=r 2(r >0)上恰有相异两点到直线4x -3y +25=0的距离等于1,则r 的取值范围是( ) (A )[4,6] (B )(4,6] (C )(4,6) (D )[4,6) 5.从直线y =3上的点向圆x 2+y 2=1作切线,则切线长的最小值是( ) (A )22(B )7(C )3(D )10二、填空题6.以点(-2,3)为圆心且与y 轴相切的圆的方程是______.7.已知直线x =a (a >0)和圆(x -1)2+y 2=4相切,那么a 的值是______.8.设圆x 2+y 2-4x -5=0的弦AB 的中点为P (3,1),则直线AB 的方程是______.9.过定点(1,2)可作两直线与圆x 2+y 2+kx +2y +k 2-15=0相切,则k 的取值范围是____. 10.直线x +3y -m =0与圆x 2+y 2=1在第一象限内有两个不同的交点,则m 的取值范围是______. 三、解答题11.圆x 2+y 2=8内有一点P (-1,2),AB 为过点P 且倾斜角为α的弦. (1)当α=4π3时,求AB 的长; (2)当弦AB 被点P 平分时,求直线AB 的方程.12.求经过点P (6,-4)且被圆x 2+y 2=20截得的弦长为62的直线的方程.13.求过点P (4,-1)且与圆x 2+y 2+2x -6y +5=0外切于点M (1,2)的圆的方程.Ⅱ 拓展训练题14.已知圆满足:①截y 轴所得弦长为2;②被x 轴分成两段圆弧,其弧长的比为3∶1;③圆心到直线l :x -2y =0的距离为55. 求该圆的方程.测试十六空间直角坐标系Ⅰ学习目标1.理解空间直角坐标系的概念,能写出满足某些条件的点的坐标.2.会用空间两点间距离公式进行相关的计算.Ⅱ基础训练题一、选择题1.点A(2,0,3)在空间直角坐标系的位置是( )(A)y轴上(B)xOy平面上(C)xOz平面上(D)yOz平面上2.在空间直角坐标系中,点P(-2,-1,3)到原点的距离为( )(A)14(B)5(C)14 (D)53.点A(-1,2,1)在xOy平面上的射影点的坐标是( )(A)(-1,2,0) (B)(-1,-2,0)(C)(-1,0,0) (D)(1,-2,0)4.在空间直角坐标系中,两个点A(2,3,1)、A′(2,-3,1)关于( )对称(A)平面xOy (B)平面yOz(C)平面xOz(D)y轴5.设a是任意实数,则点P(a,1,2)的集合在空间直角坐标系中所表示的图形是( )(A)垂直于平面xOy的一条直线(B)垂直于平面yOz的一条直线(C)垂直于平面xOz的一条直线(D)以上均不正确二、填空题6.点M(4,-3,5)到x轴的距离为______.7.若点P(x,2,1)与Q(1,1,2)、R(2,1,1)的距离相等,则x的值为______.8.已知点A(-2,3,4),在y轴上求一点B,使|AB|=6,则点B的坐标为______.9.已知两点A(2,0,0),B(0,3,0),那么线段AB的中点的坐标是______.10.在空间直角坐标系中,点A(1,2,a)到点B(0,a,1)的距离的最小值为______.三、解答题11.在空间直角坐标系中,设点M的坐标为(1,-2,3),写出点M关于各坐标面对称的点、关于各坐标轴对称的点的坐标.12.在空间直角坐标系中,设点M的坐标为(1,-2,3),写出点M到原点、各坐标轴及各坐标面的距离.13.如图,正方体OABC-A1B1C1D1的棱长为a,|AM|=2|MB|,|B1N|=|NC1|,分别写出点M与点N的坐标.-1)的距离的两倍,求点P的坐标.测试十七 平面解析几何初步全章综合练习Ⅰ 基础训练题一、选择题1.方程y =k (x -2)表示( ) (A )经过点(-2,0)的所有直线 (B )经过点(2,0)的所有直线(C )经过点(2,0)且不垂直于x 轴的所有直线 (D )经过点(2,0)且去掉x 轴的所有直线2.点P (x ,y )在直线x +y -4=0上,O 为坐标原点,则|OP |的最小值为( ) (A )10(B )22(C )6(D )23.若直线l :y =kx -3与直线2x +3y -6=0的交点位于第一象限,则直线l 的倾斜角的取值范围是( ) (A ))3π,6π[(B ))2π,6π((C ))2π,3π((D )]2π,6π[4.若直线(1+a )x +y +1=0与圆x 2+y 2-2x =0相切,则a 的值为( ) (A )1或-1 (B )2或-2 (C )1 (D )-15.如果直线l 将圆:x 2+y 2-2x -4y =0平分,且不通过第四象限,那么直线l 的斜率的取值范围是( ) (A )[0,2](B )[0,1](C )]21,0[(D ))21,0[二、填空题6.经过点P (-2,3)且在x 轴、y 轴上截距相等的直线方程为______.7.若直线mx +ny -3=0与圆x 2+y 2=3没有公共点,则m 、n 满足的关系式为______. 8.已知圆x 2+(y -1)2=1及圆外一点P (-2,0),过点P 作圆的切线,则两条切线夹角的正切值是______. 9.已知P 是直线3x +4y +8=0上的动点,P A ,PB 是圆x 2+y 2-2x -2y +1=0的两条切线.A 、B 是切点,C 是圆心,那么四边形P ACB 面积的最小值为______.10.已知两个圆x 2+y 2=1①与x 2+(y -3)2=1②,则由①式减去②式可得上述两圆的对称轴方程.将上述命题在曲线仍为圆的情况下加以推广,即要求得到一个更一般的命题,而已知命题应成为所推广命题的一个特例.推广的命题为______. 三、解答题11.已知直线l 1:2x -y +3=0与直线l 2关于直线y =-x 对称,求直线l 2的方程.12.圆心在直线x -2y -3=0上,且圆与两坐标轴都相切,求此圆的方程.13.求通过直线2x +y -4=0及圆x 2+y 2+2x -4y +1=0的交点,并且有最小面积的圆的方程.14.在△ABC中,顶点A(2,4)、B(-4,2),一条内角平分线所在直线方程为2x-y=0,求AC边所在的直线方程.Ⅱ拓展训练题15.已知过原点O的一条直线与函数y=log8x的图象交于A、B两点(A在B的右侧),分别过点A、B作y轴的平行线与函数y=log2x的图象交于C、D两点.(1)证明:点C、D和原点O在同一条直线上.(2)当BC平行于x轴时,求点A的坐标.16*.已知圆C:(x-1)2+(y-2)2=25,及直线l:(2m+1)x+(m+1)y=7m+4(m∈R).(1)证明:不论m取什么实数,直线l与圆C恒相交;(2)求直线l被圆C截得的弦长最短长度及此时的直线方程.参考答案第二章 平面解析几何初步 测试十 平面直角坐标系中的基本公式一、选择题1.B 2.C 3.A 4.C 5.D 提示:1.点(a ,b )关于x 轴、y 轴、坐标原点O 、直线y =x 的对称点坐标为(a ,-b ),(-a ,b ),(-a ,-b ),(b ,a ). 二、填空题6.(1,1); 7.2或4; 8.5; 9.3,316-; 10.52. 提示:9.若AB =(x 1,y 1),CD =(x 2,y 2),则∥⇔x 1y 2-x 2y 1=0(应注意向量平行与直线平行的关系); 则⊥⇔x 1x 2+y 1y 2=0(即⋅=0); 三、解答题11.(1)证明:由已知计算得5||,52)31()11(||22==--++=BC AB5||=AC ,所以,|AB |2+|AC |2=|BC |2,所以△ABC 是直角三角形.另解:由已知=(-2,4),=(2,1), 所以,AB ²AC =-2³2+4³1=0, 所以,AB ⊥AC ,△ABC 是直角三角形. (2)解:由已知,AB 的中点M 的坐标为)231,211(+--,即M (0,1), 所以,.1013||22=+=CM12.设矩形对角线交点为M (x ,0),因为|MA |=|MB |,则22224)2(3)1(++=++x x ,解得x =-5,所以M (-5,0).设C (x 1,y 1),因为M 为AC 中点,所以023,52111=+-=-y x , 解得x 1=-9,y 1=-3,所以,C (-9,-3),同理,D (-8,-4).注:本题也可以利用向量平行、垂直的有关知识来解. 13.提示:通过建立适当的坐标系,利用坐标法来证明.14.(1){x |x =0,x =3};(2){x |x <0或x >3};(3){x |0≤x ≤3}.测试十一 直线的方程一、选择题1 B2 B3 B4 D5 D 提示:3.由题意知,l 的倾斜角α为钝角,cos α<0,k <0,故k cos α>0.4.反射光线过点N (2,6),同时,还经过点M (5,3)关于x 轴的对称点M ′(5,-3),所以,反射光线的斜率为352)3(6-=---,直线方程为3x +y -12=0.要注意,“光线”问题常用对称点的思路去思考问题.5.直线x -2y +2k =0与两坐标轴交点为A (-2k ,0).B (0,k ), 所以,2|||2|21||||21k k k OB OA S AOB =⋅-=⋅=∆,由题意k 2≥1, 得|k |≥1为所求.二、填空题6.2x +y +2=0; 7.(0,-2); 8.a =-2; 9.311-≤≤-k ; 10.⋅-31提示:10.提示:设A (x 0,y 0)为直线l 上一点,根据题意,A 点沿x 轴负方向平移3个单位,接着再沿y 轴正方向平移1个单位后仍应在直线l 上,即点(x 0-3,y 0+1)在直线l 上.所以直线l 的斜率为⋅-=---+31310000x x y y三、解答题11.提示:平分平行四边形面积的直线必过平行四边形的对角线交点,即过BD 的中点(3,2).所以,所求直线方程为2x -3y =0.12.略解:设P (x 1,1),因为PQ 的中点为(1,-1),根据中点坐标公式,可得Q (2-x 1,-3),因为点Q 在直线x -y -7=0上, 所以,(2-x 1)-(-3)-7=0,解得x 1=-2,所以,P (-2,1),Q (4,-3),⋅-=----=3242)3(1/k所以,l :2x +3y +1=0.13.略解:由已知得AB ∥x 轴,作CD ⊥AB 于D ,∵C (2,0),A (0,3),B (3,3).∴S △ADC >S △BDC . ∵x =a 将△ABC 面积平分,∴x =a 在直线CD 左侧,即0<a <2.由题意得)3(2123321p ABC y a S -⋅=⋅⋅=∆,其中y p 表示AC 与x =a 的交点的纵坐标. ∵直线AC 的方程为132=+yx .即3x +2y -6=0.当x =a 时,236,236ay a y p -=∴-=,代入上式,得.3±=a∵a ∈(0,2).3=∴a 为所求.14.(1)设直线l 的倾斜角为α,则所求直线倾斜角为2α,由已知,41tan =α,所以,tan2α=158tan 1tan 22=-αα,所以,所求直线l 方程为)2(1583-=-x y ,即8x -15y +29=0.(2)依题意,设直线l 方程为y -3=k (x -2),k <0,则)0,32(kA -,B (0,3-2k ),S △AOB 1266)292(621=+≥-+-+==kk y x B A ,此时,kk 292-=-,即.23±=k ,因为k <0,所以23-=k ,所求直线l 方程为)2(233--=-x y ,即3x +2y -12=0. (3)依题意,设直线l 方程为y -3=k (x -2),k <0,则)23,0(),0,32(k B kA --,12)1(6||164499||||222≥-+-⨯=+⨯=+⨯+=⋅kk k k k k PB PA , 此时,kk -=-1,即k =±1,因为k <0,所以k =-1, 所求直线l 方程为y -3=-(x -2),即x +y -5=0.测试十二 两条直线的位置关系(一)一、选择题1.B 2.D 3.A 4.A 5.C 提示:5.提示:可以求出两条直线的交点坐标)1216,1242(+++-k k k k ,解不等式组⎪⎪⎩⎪⎪⎨⎧>++>+-0121601242k k k k,可得⋅<<-2161k 另外,注意到直线y =kx +2k +1可变形为y -1=k (x +2),即此直线过定点(-2,1),又,直线221+-=x y 与x 轴、y 轴的交点坐标为(4,0),(0,2).利用数形结合的思路可得结论. 二、填空题6.x +y -2=0; 7.m +2n +5=0; 8.2x -y -5=0; 9.3x +y -1=0; 10.a ∈R ,a ≠±1且a ≠2. 提示:9.设直线2x -y +1=0的倾斜角为α,由已知,所求直线的倾斜角为α+45°,因为tan α=2,所以,345tan tan 145tan tan )45tan(-=-+=+ααα,又直线2x -y +1=0与y 轴的交点为(0,1),所以,所求直线方程为3x +y -1=0.10.直线x +ay =3与另两条直线不平行也不重合,并且三条直线不过同一点. 三、解答题11.4x -3y +9=0.12.CD :x +y -11=0,BC :3x -y -16=0. 13.方法一:用中点.DE 中点)2,27(G ,又G 为BF 的中点,∴B (4,8). 同理,EF 中点).2,6(),21,4(-∴-C HDF 中点).6,0(),23,25(-∴-A M.01227,627:=---=∴y x x y AB BC :y +2=-5(x -6),5x +y -28=0..01832,632:=---=y x x y AC 方法二:用斜率. EF 斜率为)2(271:27-=-∴⋅x y AB ,得7x -2y -12=0. FD 斜率为-5.∴BC :y -3=-5(x -5),得5x +y -28=0. DE 斜率为)3(324:32-=+∴⋅x y AC ,得2x -3y -18=0, 14.解:(1)由⎩⎨⎧=--=+-,012,082m m n m 解得m =1,n =7.(2)易知m ≠0,所以,当182-=/=n m m 时, 即m =4,n ≠-2,或m =-4,n ≠2时l 1∥l 2.(3)结合(2)的结果,当m =4,n =-2,或m =-4,n =2时,l 1与l 2重合.测试十三 两条直线的位置关系(二)一、选择题1.B 2.C 3.A 4.D 5.C 提示: 5.由已知,1sin sin |sin |22>+BA C ,所以,sin 2C >sin 2A +sin 2B .又R CcB b A a 2sin sin sin ===,所以,c 2>a 2+b 2, 由余弦定理,得02cos 222<-+=abc b a C ,所以,C 为钝角,三角形为钝角三角形. 二、填空题6.10,-12,-2; 7.)21,21(-; 8.y =0,y =5或5x -12y -5=0,5x -12y +60=0; 9.22+; 10..23提示:7.当AB 与已知直线垂直时,线段AB 最短. 9.|2)cos 22sin 22(2||2cos sin |cos sin |2cos sin |)(22-+=-+=+-+=θθθθθθθθθf)4πsin(22|2)4πsin(2|+-=-+=θθ,所以,f (θ)的最大值为.22+10.由已知,点M 到两直线l 1,l 2的距离相等.即点M 在直线x +y -6=0上,于是,问题变成“点M 在直线x +y -6=0上运动,求原点到点M 的最小距离”,可利用第7题的思路加以解决. 三、解答题11.提示:满足题目条件的直线l 或者与直线AB 平行,或者经过线段AB 的中点.当直线l 与直线AB 平行时,l :4x +y -6=0;当直线l 经过线段AB 的中点时,l :3x +2y -7=0. 12.解:(1)设所求直线方程为x +2y +c =0,根据题意55|2|=+c ,解得c =3或c =-7, 所以,所求直线方程为x +2y +3=0或x +2y -7=0. (2)设P (-2,-1)关于直线l 的对称点为P ′(x 0,y 0). 则k pp 'k l =-1,且PP ′的中点在直线l 上,即点)21,22(00--y x 在直线l 上. 所以,⎪⎪⎩⎪⎪⎨⎧-=-⋅++=--⨯+-1)21(2102212220000x y y x ,即⎩⎨⎧=+-=-+0320820000y x y x ,解得⋅==519,5200y x 即)519,52('P .13.解:AB 斜率为81,设C 坐标(x 0,y 0). 所以,85200-=--x y ……………………①因为AH 斜率为0,∴BC 斜率不存在,即BC 直线方程为x =6, 所以,x 0=6.…………………………②②代入①,得y 0=-6.∴C 点坐标(6,-6). 14.略解:解⎩⎨⎧==+-,0,012y y x 得A (-1,0),所以AB :x -y +1=0.设C (x 0,y 0),因为BC 与BC 边上的高线垂直,并且C 关于直线y =0(∠A 的平分线)的对称点C ′在直线AB 上.所以,k BC =-2,C ′(x 0,-y 0)在直线AB 上.所以,⎪⎩⎪⎨⎧=++-=--012120000y x x y 解得x 0=5,y 0=-6,即C (5,-6),故|BC |=54.测试十四 圆的方程一、选择题1.D 2.D 3.D 4.C 5.C 提示:4.只需坐标原点在圆内,即原点与圆心的距离小于半径,已知圆圆心为)2,2(ED --,半径为)04(242222>-+-+F E D F E D ,结合44)02()02(2222FE D E D -+<-+-及D 2+E 2-4F >0,可得F <0.5.方程2)1(11--=-y x 可以等价变形为(x -1)2+(y -1)2=1,且x -1≥0,1-(y -1)2≥0.即(x -1)2+(y -1)2=1,且x ≥1,0≤y ≤2.所以,方程2)1(11--=-y x 所表示的曲线是半个圆.二、填空题 6.2x +y =0;7.(1)a 2+b 2=r 2且|a |=r 或b =0,|a |=r ;(2)a 2+b 2<r 2;(3)|b |<r ; 8.21; 9.6,549+; 10.⋅-552 提示:9.x 2+y 2的几何意义是点P (x ,y )到原点距离的平方.利用这个几何意义求解. 10.xy的几何意义是点P (x ,y )与原点连线的斜率.利用这个几何意义求解. 三、解答题11.提示:将方程配方为222431)()2(a a a y a x --=+++,则,04312>--a a 即3a 2+4a -4<0,(3a -2)(a +2)<0,解得,⋅<<-322a12.提示:方法一:设圆的方程为x 2+y 2+D x +Ey +F =0,由已知三个点在圆上,可得⎪⎩⎪⎨⎧=+++=++=082204160F E D F D F 解得D =-4,E =0,F =0,所以,所求圆方程为x 2+y 2-4x =0.方法二:注意到k AC =1,k BC =-1,k AC k BC =-1,所以,三角形ABC 是直角三角形,∠C =90°,所以,所求圆心为AB 边中点,即(2,0)点,可求半径r =2, 所以,所求圆的方程为(x -2)2+y 2=4.13.提示:因为A (-1,4),B (1,2)是圆C 上的两点,所以圆心在线段AB 的中垂线上,因为AB 中点坐标为(0,3),k AB =-1,所以线段AB 的中垂线方程为x -y +3=0,解⎩⎨⎧=-+=+-0103y x y x 得圆心坐标为(-1,2),半径,2)22()11(22=-+--=r所以,圆C 的方程为(x +1)2+(y -2)2=4.14.分析:(1)曲线C 方程可变形为(x 2+y 2-20)+a (-4x +2y +20)=0,由⎩⎨⎧=++-=-+020*******y x y x ,解得⎩⎨⎧-==24y x . 即点(4,-2)满足曲线C 的方程,故曲线C 过定点(4,-2).(2)曲线C 方程(x -2a )2+(y +a )2=5(a -2)2,因为a ≠2,所以曲线C 是圆心为(2a ,-a ),半径为|2|5-a 的圆. 设圆心坐标为(x ,y ),则有⎩⎨⎧-==ay a x 2,消去a 可得x y 21-=,故圆心必在直线x y 21-=. 测试十五 直线与圆的位置关系一、选择题1.C 2.B 3.C 4.C 5.A 提示:5.圆方程x 2+y 2=1,圆心(0,0),半径1,切线长的平方=圆心到直线y =3距离的最小值的平方.22813222==-=-r二、填空题6.(x +2)2+(y -3)2=4; 7.3; 8.x +y -4=0; 9.⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛--338,23,338 ; 10..23<<m提示:9.圆方程配方为,4316)1()2(222k y k x -=+++依题意,2224316)12()21(k k ->+++,且,043162>-k解得k <-3或k >2,且338338<<-k ,所以,⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛--338,23,338 . 10.结合图形,求出直线与圆在第一象限相切时的m 值为2,求出直线过(0,1)点时的m值为3.进而得出m 值范围. 三、解答题11.提示:(1)方法一:由已知,AB :x +y -1=0,与圆方程联立,解方程组得,2151±=x 则.304πcos||||12=-=x x AB 方法二:圆心到直线AB 的距离,222|1|=-=d 所以.3021822||22=-=-=dr AB(2)当弦AB 被点P 平分时,AB ⊥OP ,又k OP =-2, 所以,.052:,21=+-=y x AB k AB 12.提示:注意到,过点P (6,-4)倾斜角为90°的直线不满足题意,设所求直线为y +4=k (x -6),由弦长为26,圆半径为20,所以圆心O 到所求直线的距离为2, 即21|46|2=++k k ,解得k =-1或177-=k ,所以所求直线方程为x +y -2=0或7x +17y +26=0.13.略解:圆(x +1)2+(y -3)2=5的圆心为(-1,3),设圆心(a ,b ),得⎪⎩⎪⎨⎧---=--++-=-+-,112312)1()4()2()1(2222a b b a b a解得⎩⎨⎧==13b a ,圆心(3,1),半径为5,所以,所求圆方程为(x -3)2+(y -1)2=5.14.分析:设所求圆的圆心为P (a ,b ),半径为r ,则P 到x 轴、y 轴的距离分别为|b |,|a |.由题设圆P 截x 轴所得劣弧所对圆心角为90°,圆P 截x 轴所得弦长为r 2, 故r 2=2b 2.又圆P 截y 轴所得弦长为2,所以有r 2=a 2+1,从而有2b 2-a 2=1. 又点P (a ,b )到直线x -2y =0的距离555|2|=-=b a d ,所以|a -2b |=1, 解⎩⎨⎧=-=-121|2|22a b b a ,得⎩⎨⎧==11b a 或⎩⎨⎧-=-=11b a . 由于r 2=2b 2,知2=r ,于是所求圆的方程为(x -1)2+(y -1)2=2或(x +1)2+(y +1)2=2.测试十六 空间直角坐标系一、选择题1.C 2.A 3.A 4.C 5.B 二、填空题6.34; 7.1; 8.(0,-1,0),(0,7,0); 9.)0,23,1(; 10.26.三、解答题11.答:点M 关于平面xOy 的对称点为(1,-2,-3);点M 关于平面yOz 的对称点为(-1,-2,3); 点M 关于平面xOz 的对称点为(1,2,3); 点M 关于x 轴的对称点为(1,2,-3);点M 关于y 轴的对称点为(-1,-2,-3);点M 关于z 轴的对称点为(-1,2,3). 12.答:点M 到原点的距离为14;点M 到平面xOy 的距离为3;点M 到平面yOz 的距离为1;点M 到平面xOz 的距离为2; 点M 到x 轴的距离为13;点M 到y 轴的距离为10; 点M 到z 轴的距离为5. 13.答:).,,21(),0,32,(a a a N a a M 14.答:(1,0,0)或(-1,0,0).测试十七 平面解析几何初步全章综合练习一、选择题1.C 2.B 3.B 4.D 5.A 提示:3.直线3:-=kx y l 过定点)3,0(-,直线2x +3y -6=0与x 轴、y 轴交点坐标为(3,0)、(0,2),作图分析可得答案. 二、填空题6.x +y -1=0,3x +2y =0; 7.0<m 2+n 2<3; 8.34; 9.22; 10.两圆(x -a )2+(y -b )2=r 2与(x -c )2+(y -d )2=r 2的对称轴的方程为2(c -a )x +2(d -b )y +a 2+b 2-c 2-d 2=0. 提示: 9.r PA S PACB ||212⨯=(r 是圆的半径),由已知r =1,所以,即求|P A |的最小值,又|P A |=12-PC ,而|PC |的最小值为C 到直线3x +4y +8=0的距离,即343|843|22=+++,所以,所求最小值为.22||212=⨯=r PA S PACB 三、解答题11.提示:直线l 1与l 2的交点坐标为(-1,1),直线l 1与y 轴交点坐标为(0,3),且(0,3)点关于直线y =-x 对称点坐标为(-3,0),所以,直线l 2过点(-3,0)和(-1,1),l 2:x -2y +3=0.12.提示:设圆心为(a ,b ),由已知|a |=|b |=r ,又a -2b -3=0,解⎩⎨⎧==--b a b a 032及⎩⎨⎧-==--b a b a 032得⎩⎨⎧-=-=33b a 或⎩⎨⎧-==11b a ,所以,所求圆方程为(x +3)2+(y +3)2=9或(x -1)2+(y +1)2=1.13.提示:所求圆即为以已知直线和已知圆相交的弦为直径的圆.解⎩⎨⎧=-+=+-++,042014222y x y x y x 得⎩⎨⎧==21y x 或⎪⎪⎩⎪⎪⎨⎧==51851y x .即直线与圆的交点坐标为)518,51(),2,1(,弦长为554, 所以圆心为)514,53(,半径为552, 所求圆方程为54)514()53(22=-+-y x . 14.提示:注意到点A (2,4)在直线2x -y =0上,所以,已知直线为∠A 的平分线l ,过B作与l 垂直的直线m :x +2y =0,l 与m 的交点为(0,0),B (-4,2)关于(0,0)的对称点为B ′(4,-2),AB ′所在直线即为AC 边所在的直线,所以AC 边所在的直线方程为3x +y -10=0.15.(1)证明:设A 、B 的横坐标分别为x 1、x 2,由题设知x 1>1、x 2>1,点A (x 1,log 8x 1),B (x 2,log 8x 2). 因为A 、B 在过点O 的直线上,⋅=∴228118log log x x x x又点C 、D 的坐标分别为(x 1,log 2x 1)、(x 2,log 2x 2), 由于,log 32log log log ,log 32log log log 28828221881812x x x x x x ====所以OC 的斜率和OD 的斜率分别为:228222118112log 3log ,log 3log x x x xk x x x x k OD OC ====由此得k OC =k OD ,即点O 、C 、D 在同一条直线上.(2)解:由BC 平行于x 轴,有log 2x 1=log 8x 2,解得x 2=31x .将其代入228118log log x x x x =,得1811831log 3log x x x x =. 由x 1>1,知log 8x 1≠0,故31x =3x 1,即31=x ,于是点A 的坐标为).3log ,3(816.分析:(1)直线l 的方程可化为x +y -4+m (2x +y -7)=0,则l 是过定点(3,1)的直线束.又(3-1)2+(1-2)2=5<25,∴点(3,1)在圆内部,因此不论m 为何实数,直线l 与圆恒相交.(2)由(1)可知,直线l 过点M (3,1),则过此点的直线l 与圆O 的半径垂直且M 为AB 中点时,l 被圆所截得的弦长|AB |最短.)542|(|22=-=OM r AB .此时212311=---=-=OMl k k , 直线方程为y -1=2(x -3),即2x -y -5=0.。
高一地理人教版学探诊电子必修二

高一地理人教版学探诊电子必修二1、2、人类活动也呈现明显的差异。
下列叙述不正确的是()[单选题] *A.农业具有西牧东耕的分布特点B.人口、交通线表现为东密西疏的特点C.经济发展水平东部高、西部低D.农作物具有南麦北稻、南甘北甜的分布特点(正确答案)2、53.关于两极地区的叙述,正确的是()[单选题] *A.北极地区比南极地区冷B.北极地区的降水比南极地区少C.南极地区被称为地球上的“白色荒漠”和“风库”(正确答案)D.北极地区的风速比南极地区大3、印度水旱灾害频繁的主要原因是()[单选题] *A.濒临海洋B.西南季风不稳定(正确答案)C.受地形的影响D.受纬度位置的影响4、下列关于我国人口与民族的说法,正确的是()[单选题] *A.人口主要集中分布在中、西部地区B.以漠河---腾冲一线为界,人口东多西少C.人口最多的少数民族是藏族D.民族分布具有“大散居、小聚居、交错杂居”特点(正确答案)5、亚洲、非洲的分界线是[单选题] *苏伊士运河(正确答案)德雷克海峡白令海峡巴拿马运河6、中日文化交流渊远流长,日本文化、艺术深受中国的影响,最明显地表现在()*A、语言方面B、古代建筑(正确答案)C、文字方面(正确答案)D、农业技术7、临中南半岛,有“彩云之南”之誉的是:()[单选题] *A. ①(正确答案)B. ②C. ③D. ④8、1.我们到外地出差或者旅游,会经常提前通过网络查阅地图,通过输入“起点”和“终点”,可以查询行走路线和距离,还可以通过操作鼠标“放大”或“缩小”地图,查询到更多信息。
这类地图为[单选题] *A.交通地图B.旅游地图C.遥感地图D.电子地图(正确答案)9、俄罗斯地形以()为主[单选题] *A、山地B、平原(正确答案)C、高原D、丘陵10、亚洲与非洲的分界线是:()[单选题] *A、尼罗河B、乌拉尔河C、苏伊士运河(正确答案)D、红海11、俄罗斯大部分地区冬季十分寒冷的主要原因是()[单选题] *A、地形因素B、纬度因素(正确答案)C、洋流因素D、海陆因素12、下列对上述三江源所在地区的描述,正确的是( ) [单选题] * A.是世界上纬度最高的高原,所以气候严寒B.冬季寒冷、夏季凉爽、降水较少(正确答案)C.是世界上面积最大的高原D.空气稀薄、日照充足、全年高温13、东南亚地区主要气候类型是()[单选题] *A、热带雨林气候、热带季风气候(正确答案)B、热带雨林气候、热带沙漠气候C、亚热带季风气候、温带海洋气候D、温带大陆气候、温带沙漠气候14、56.据报道,第32届日本东京奥运会的奖牌所用金属是从淘汰的笔记本电脑、手机等小家电中提炼而成。
人教版高中物理必修二(理科)诊断性测试.docx

高中物理学习材料(灿若寒星**整理制作)山东省2007-2008学年度第二学期学分认定诊断性考试物理试题 (理科) 2008-4-2说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟.寄语:人生的加、减、乘、除需要每一位同学用心去感悟。
“加法”告诉我们:合抱之木,生于毫末,九层之台,起于垒土,人生需要不断积累。
“减法”告诫我们:行走人生间,有时要减掉一些风景,牺牲某些潇洒,才能达到“一览众山小”的顶点……命题人:杜士迎第Ⅰ卷 (选择题 共60分)一、本题共30小题,每小题2分,共60分.1.16世纪,哥白尼根据天文观测的大量资料,经过40多年的天文观测和潜心研究,提出“日心说”的如下四个基本论点,这四个论点目前看存在缺陷的是 ( ) A .宇宙的中心是太阳,所有行星都在绕太阳作匀速圆周运动 B .地球是绕太阳作匀速圆周运动的行星,月球是绕地球作匀速圆周运动的卫星,它绕地球运转的同时还跟地球一起绕太阳运动 C .天穹不转动,因为地球每天自西向东自转一周,造成天体每天东升西落的现象 D .与日地距离相比,恒星离地球都十分遥远,比日地间的距离大得多2.下列关于万有引力的说法,正确的有 ( ) A .物体落到地面上,说明地球对物体有引力,物体对地球没有引力 B .万有引力定律是牛顿在总结前人研究的基础上发现的 C .地面上自由下落的苹果和天空中运行的月亮,受到的都是地球的万有引力D .F =221rmm G 中的G 是一个比例常数,是没有单位的3.关于万有引力定律的适用范围,下列说法中正确的有 ( ) A .只适用于天体,不适用于地面的物体 B .只适用于球形物体,不适用于其他形状的物体 C .只适用于质点,不适用于实际物体 D .适用于自然界中任何两个物体之间4.从天文望远镜中观察到银河系中有两颗行星绕某恒星运行,两行星的轨道均为椭圆,观 察测量到它们的运转周期之比为8:1,则它们椭圆轨道的半长轴之比为 ( ) A .2:1 B .4:1 C .8:1 D .1:45.地球半径为R ,地球表面的重力加速度为g ,若高空中某处的重力加速度为g /2,则该处 距地面的高度为 ( )A .(2一1)RB .RC .2R D .2R6.在地球(看作质量均匀分布的球体)上空有许多同步卫星,下面说法中正确的是( )A .它们的质量可能不同B .它们的速度可能不同C .它们的向心加速度可能不同D .它们离地心的距离可能不同7.已知引力常数G 和下列各组数据,能计算出地球质量的是 ( ) A .地球绕太阳运行的周期及地球离太阳的距离 B .月球绕地球运行的周期及月球离地球的距离 C .人造地球卫星在地面附近绕行的速度及运行周期D .若不考虑地球自转,己知地球的半径及重力加速度8.若有一艘宇宙飞船在某一行星表面做匀速圆周运动,设其周期为T ,引力常量为G ,那么该行星的平均密度为 ( )A .π32GT B .23GT π C .π42GT D .24GT π9.关于第一宇宙速度,下列说法正确的是 ( ) A .它是人造地球卫星绕地球作匀速圆周运动的最大速度 B .它是人造地球卫星在圆形轨道上的最小运行速度 C .它是能使卫星绕地球运行的最小发射速度D .它是人造卫星绕地球作椭圆轨道运行时在近地点的速度10.下列关于地球同步卫星的说法正确的是 ( )A .它的周期与地球自转同步,但高度和速度可以选择,高度增大,速度减小B .它的周期、高度、速度都是一定的C .我们国家发射的同步通讯卫星定点在北京上空D .我国发射的同步通讯卫星也定点在赤道上空11.人造卫星绕地球做圆周运动时,卫星离地面的高度越高,( )A .速度越大B .角速度越大C .周期越大D .向心加速度越大12.人造卫星在太空绕地球运行中,若天线偶然折断,天线将( )A .继续和卫星一起沿轨道运行B .做平抛运动,落向地球C .由于惯性,沿轨道切线方向做匀速直线运动,远离地球D .做自由落体运动,落向地球13.人造卫星绕地球作匀速圆周运动,关于它运转的轨道平面,下列情况可能的有( )A .运转轨道平面与赤道平面是重合的B .轨道平面与某经线所在平面是重合的C .轨道平面与赤道以外的某纬线所在平面是重合的D .轨道平面通过地球球心,但平面与任一纬线和经线均不重合14.人造卫星离地面距离等于地球半径R ,卫星以速度v 沿圆轨道运动,设地面的重力加速度为g ,则有( )A .v =gR 4B .v =gR 2C .v =gRD .v =2/gR15.人造卫星绕地球做匀速圆周运动,其轨道半径为R ,线速度为v ,周期为T ,若要使它周期变为2T ,可能的方法是( )A .R 不变,使线速度变为v /2B .v 不变,使轨道半径变为2RC .轨道半径变为R 34D .无法实现16.科学家设想在太空设立太阳能卫星电站,先用硅太阳能电池将太阳能转化成电能,再利 用微波—电能转换装置,将电能转换成微波向地面发送。
人教版高二选择性必修2生物学习探究诊断电子版

人教版高二选择性必修2生物学习探究诊断电子版一、单项选择题1、有关糖的叙述,正确的是()A、葡萄糖在线粒体中合成B、葡萄糖遇碘变为蓝色C、纤维素由葡萄糖组成D、胰岛素促进糖原分解2、1953年Watson和Crick构建了DNA双螺旋结构模型,其重要意义在于()①证明DNA是主要的遗传物质②确定DNA是染色体的组成成分③发现DNA如何存储遗传信息④为DNA复制机构的阐明奠定基础A、①③B、②③C、②④D、③④3、从某海洋动物中获得一基因,其表达产物为一种抗菌体和溶血性均较强的多肽P1。
目前在P1的基础上研发抗菌性强但溶血性弱的多肽药物,首先要做的是()A、合成编码目的肽的DNA片段B、构建含目的肽DNA片段的表达载体C、依据P1氨基酸序列设计多条模拟肽D、筛选出具有优良火性的模拟肽作为目的肽4、果蝇红眼对白眼为显性,控制这对性状的基因位于X染色体。
果蝇缺失1条Ⅳ号染色体仍能正常生存和繁殖,确实2调则致死。
一对都缺失1条Ⅳ号染色体的红眼果蝇杂交(亲本雌果蝇为杂合子),F1中()A.白眼雄果蝇占1/4B、红眼磁果蝇占1/4C.染色体数正常的红眼果蝇占1/4D、缺失1条Ⅳ号染色体的白眼果蝇占1/45、下列关于生物体内各种有机物的叙述,正确的是()A.脂肪是生物体最重要的直接供能物质B.糖类是构成组织细胞的基本物质C.核酸是生物体储存遗传信息的物质D.蛋白质是重要的储备能源物质6、以下是利用幼小蝌蚪和甲状腺激素探究甲状腺激素作用的实验设计,不合理的是()A.实验组饵料中添加甲状腺激素,对照组不做任何处理B.实验组与对照组应饲喂等量的同种饲料,放在相同的环境中饲养C.实验组与对照组的饲养环境应适合蝌蚪的生长和发育D.实验组与对照组的蝌蚪数量应相同但大小和发育程度可不予考虑7、当遇到下列情况时,你的正确选择是()A.被农药污染的食品一定要充分煮熟再食用B.被毒蛇咬伤手臂后,应首先扎住伤口处的近心端C.进行人工呼吸过程中,吹气者应始终捏紧被救者的鼻孔D.处方药和非处方药都必须在医生的指导下购买和使用8、下列对作物栽培过程的叙述,科学合理的是()A.安丘蜜桃夏季修剪的目的主要是为了调节主侧枝的张开角度B.用种子繁殖能保持青州蜜桃的优良特性,加快繁殖速度C.诸城板栗的花为风媒花,异花传粉坐果率高D.增加温室内氧气的浓度可提高大棚银瓜的产量9、下列生殖方式与豌豆杂交实验原理相同的是()A.植物组织培养B.大棚黄瓜嫁接C、克隆羊多莉的培育D.“试管婴儿”的培育10、下列有关潍坊生物的描述,正确的是()A、临朐山蝎一生经受精卵、幼虫、成虫三个阶段,属不完全变态B、虹鳟鱼是我市成功引进的渔业资源,不属于外来物种C、通过嫁接技术可使昌乐西瓜抗病增产D、沂山银杏的“银杏果”是由子房发育而来11、下列对人类生殖和发育的叙述,正确的是()A、受精卵形成和胚胎发育的场所分别是卵巢和子宫B、胎儿通过胎盘与母体完成物质交换C、身高和体重迅速增长,是青春期发育最突出的特征D、怀孕又称着床,是指受精卵植入子宫内膜的过程12、下列关于生物与人类进化的叙述,错误的是()A.遗传和变异为生物进化提供了原材料B.山旺化石是研究生物进化的最直接证据C.从寿光大鸡的人工选择中可以观察到自然选择的效应D.人类进化的先后顺序是:南方古猿→直立人→能人→智人二、简答题13、(8分)根据以下材料,回答相关问题:据报道,英国科学家发现了一种叫“固氮醋杆菌”的特殊固氮菌,这种固氮菌的固氮基因可植入到某些农作物植株内,使这些作物的细胞具有固氮能力,从而“捕获”空气中的氮。
学年鲁人版高中语文必修二检测:第二单元 探索科学奥 学业分层测评6 论无性造人 Word版含解析

学业分层测评(六)[语言运用层]1.依次填入下列各句横线处的成语,最恰当的一组是()(1)小时候的中夜,我每回都是咽着口水焦急地等长辈拜完月神,接着就迫不及待地将粗黑的海碗填满芋头,敞开肚皮,在饭香芋酥中______。
(2)89式12.7毫米重机枪可发射穿爆燃曳弹、穿爆燃弹等,可以对付各种轻型装甲目标以及反武装直升机和近程反导,是战场上______的钢铁利器。
(3)随着《相爱穿梭千年》《栀子花开》《旋风少女》等接连几部新片的播出,新一波90后“小花旦”的发展______,冲击着我们的视野。
A.势如破竹风卷残云横扫千军B.风卷残云横扫千军势如破竹C.横扫千军风卷残云势如破竹D.风卷残云势如破竹横扫千军【解析】风卷残云:大风吹散残存的浮云,比喻一下子消灭干净。
横扫千军:形容气势迅猛,一举歼灭大量敌人。
势如破竹:形势像劈竹子一样,劈开上端之后,底下的都随着刀刃分开了,形容节节胜利,毫无阻碍。
【答案】 B2.(·全国甲卷)下列各句中,没有语病的一句是()A.自从我国第一颗人造地球卫星“东方红一号”成功发射,成为世界上第五个把卫星送上天的国家以来,我国的航天事业取得了巨大的突破。
B.国务院近日发布盐业体制改革方案,提出不再核准新增食盐定点生产批发企业,取消食盐批发企业只能在指定范围内销售,允许它们开展跨区域经营。
C.职业教育的意义不仅在于传授技能,更在于育人,因此有意识地把工匠精神渗透进日常的技能教学中是职业教育改革的重要课题。
D.面对突然发生的灾难,一个地方抗灾能力的强弱既取决于当地经济实力的雄厚,更取决于政府的应急机制和领导人的智慧。
【解析】本题从成分残缺或赘余、结构混乱等角度考查对病句的辨析。
A项,结构混乱,可将“成功发射”提到“自从我国”后。
B项,成分残缺,可在“提出不再核准新增食盐定点生产批发企业”后加“的要求”,在“取消食盐批发企业只能在指定范围内销售”后加“的规定”。
D项,结构混乱,一面对两面,可将“的雄厚”去掉,并在“当地”后加“的”。
(新教材)高中生物必修二全册教材“问题探讨、探究实践、思考讨论、练习与应用”汇总(附答案)

(新教材)高中生物必修二全册“问题探讨、探究实践、思考讨论、练习与应用”汇总(附答案)第1章遗传因子的发现第1节孟德尔的豌豆杂交实验(一)【问题探讨】人们曾经认为,两个亲本杂交后,双亲的遗传物质会在子代体内发生混合,使子代表现出介于双亲之间的性状。
就像把一瓶蓝墨水和一瓶红墨水倒在一起,混合液是另外一种颜色,再也无法分出蓝色和红色。
这科观点也称作融合遗传。
讨论1.按照上述观点,当红花豌豆与白花豌豆杂交后,子代的豌豆花会是什么颜色?答:粉色。
按照融合遗传的观点,双亲的遗传物质会在于代体内发生混合,子代表现出介于双亲之间的性状,即红色和白色的混合色一粉色。
2.你同意上述观点吗?你的证据有哪些?答:不同意。
因为自然界的遗传现象并不是融合遗传的结果。
例如,红花豌豆与白花豌豆杂交后,其后代仍出现红花或白花;再例如,人的性别遗传说明控制男女性别的遗传物质没有发生混合。
探究•实践:性状分离比的模拟实验讨论1.将每个小组的实验结果与全班慈的实验结果作比较,你有什么发现?如果孟德尔当时只对F₂中10株豌豆的性状进行统计,他还能正确地解释性状分离现象吗?答:与每个小组的实验结果相比,全班总的实验结果更接近预测的结果,即彩球组合类型数量比DD: Dd: dd=1:2:1,彩球代表的显性与隐性类型的数量比为3:1。
因为实验统计的样本数量越大,越接近统计规律。
如果孟德尔当时只对F₂中10株豌豆的性状进行统计,那么他很难正确地解释性状分离现象。
因为实验统计的样本数量足够大,是盂德尔能够正确分析实验结果的前提条件之一。
只对10株豌豆的性状进行统计,会出现较大的误差。
2.将模拟实验的结果与孟德尔的杂交实验结果相比较,你认为孟德尔的假说是否合理?答:合理。
因为甲、乙小桶内的彩球分别代表孟德尔杂交实验中的雌、雄配子,从两个桶内分别随机抓取-个彩球进行组合,实际上是模拟雌雄配子的随机结合,统计的样本数量也足够大,出现了3:1的结果。
但孟德尔提出的假说是否正确还需要实验来验证。
高一英语学探诊必修二电子版

高一英语学探诊必修二电子版1、We had ____ wonderful lunch last Saturday. [单选题] *A. /B. theC. oneD. a(正确答案)2、I couldn’t find Peter,_____did I know where he had gone. [单选题] *A.nor(正确答案)B.eitherC.neverD.as3、You can borrow my book, _____ you promise to give it back to me by the end of this month. [单选题] *A.even ifB. as long as(正确答案)C. in caseD. even though4、He didn't allow _____ in his room. Actually he didn't allow his family _____ at all. [单选题] *A. to smoke; to smokeB. smoking; to smoke(正确答案)C. to smoke; smokingD. smoking; smoking5、Our teacher suggested that each of us _____ a study plan for the tong summer vacation. [单选题] *A. make(正确答案)B. madeC. will makeD. would make6、Tomorrow is Ann’s birthday. Her mother is going to make a _______ meal for her. [单选题] *A. commonB. quickC. special(正确答案)D. simple7、The rain is very heavy _______ we have to stay at home. [单选题] *A. butB. becauseC. so(正确答案)D. and8、—When are you going to Hainan Island for a holiday? —______ the morning of 1st May.()[单选题] *A. InB. AtC. On(正确答案)D. For9、It took a long time to _______ Tom to go shopping with me. [单选题] *A. speakB. tellC. persuade(正确答案)D. talk10、The work will be finished _______ this month. [单选题] *A. at the endB. in the endC. by the endD. at the end of(正确答案)11、The reason why I didn't attend the lecture was simply()I got a bad cold that day. [单选题] *A. becauseB. asC. that(正确答案)D. for12、One effective()of learning a foreign language is to study the language in its cultural context. [单选题] *A. approach(正确答案)B. wayC. mannerD. road13、Jim, it’s dark now. Please _______ the light in the room. [单选题] *A. turn on(正确答案)B. turn upC. turn offD. turn down14、No writer will be considered()of the name until he writes a work. [单选题] *A. worthlessB. worthy(正确答案)C. worthwhileD. worth15、We are living in an age()many things are done by computer. [单选题] *A. thatB. whichC. whyD. when(正确答案)16、84.There is a big tree? ? ? ? ? ? ? ?the house and the river. [单选题] * A.between(正确答案)B.inC.overD.of17、Becky is having a great time ______ her aunt in Shanghai. ()[单选题] *A. to visitB. visitedC. visitsD. visiting(正确答案)18、Everyone here is _______ to me. [单选题] *A. happyB. wellC. kind(正确答案)D. glad19、They will hold the party if they _____ the project on time. [单选题] *A. will completeB. complete(正确答案)C.completedD. had completed20、The bookstore is far away. You’d better _______ the subway. [单选题] *A. sitB. take(正确答案)C. missD. get21、His mother’s _______ was a great blow to him. [单选题] *A. diedB. deadC. death(正确答案)D. die22、There _______ no water or milk in the fridge. [单选题] *A. is(正确答案)B. areC. hasD. have23、—How do you find()birthday party of the Blairs? —I should say it was __________ complete failure.[单选题] *A.a; aB. the ; a(正确答案)C.a; /D.the; /24、25.—I ______ Beijing for a holiday.—________. [单选题] *A.will go;GoodbyeB.will go;Have a good time(正确答案)C.will go to;Have a good timeD.am going to;Have a fun25、It seems slow for children to become _____ ,while adults often feel time flies. [单选题] *A. growns-upsB. growns-upC. grown upsD. grown-ups(正确答案)26、41.My father is a headmaster and he is _____ charge _____ a primary school. [单选题] * A./, ofB./, withC.in, of (正确答案)D.in, with27、I repeated my question several times. [单选题] *A. 到达B. 惊奇C. 重复(正确答案)D. 返回28、If we want to keep fit, we should try to _______ bad habits. [单选题] *A. keepB. haveC. getD. get rid of(正确答案)29、Alice is fond of playing ____ piano while Henry is interested in listening to ___ music. [单选题] *A. the, /(正确答案)B. the, theC. the, aD. /, the30、The notice put _______ on the wall says “No Smoking”. [单选题] *A. up(正确答案)B. offC. awayD. out。
必修二语文学习探究诊断在线阅读

必修二语文学习探究诊断在线阅读1、1“青出于蓝而胜于蓝”这句格言出自于荀子的《劝学》。
[判断题] *对(正确答案)错2、“秩序”的读音是“chìxù”。
[判断题] *对错(正确答案)3、46. 下列句子中加双引号的成语使用正确的一项是()[单选题] *A.北京冬奥会已经“销声匿迹”,人们便要潜心剖析它留下了什么精粹。
B.我们班阅读之星王晓明学习刻苦,数学作业做得“天衣无缝”。
C.中国的戏曲艺术,以它的神奇魅力,令人“叹为观止”。
(正确答案)D.在抗疫过程中,大多数公职人员依法行事,坚决执行上级命令,“阳奉阴违”,展现了人民公仆的风采。
4、1苏轼与辛弃疾合称为苏辛,同为豪放派代表。
[判断题] *对错(正确答案)5、1“不积跬步,无以至千里;不积小流,无以成江海。
”这一名言出自于《师说》。
[判断题] *对(正确答案)错6、泰山岩岩出自()[单选题] *孟子论语诗经(正确答案)荀子7、成语完形:语()词穷[单选题] *言空尽竭(正确答案)8、《雨中登泰山》作者是[单选题] *李建李健吾(正确答案)李白李康9、下列对有关名著的说明,不正确的一项是( ) [单选题] *A.《红楼梦》秦可卿死后,贾珍因尤氏犯了旧疾,不能料理事务,请王熙凤帮助丧事。
王熙凤安排妥当,恩威并施,威重令行,将两府的事情安排得停停当当。
B.《红楼梦》展现了贾府这一富贵之家从繁盛到衰败的过程,描写了以贾宝玉和一群红楼女子为中心的人物的悲剧命运,反映了具有一定觉醒意识的青年男女在封建体制下的历史宿命。
C.《红楼梦》中宝玉挨打后,林黛玉“早听人一句话,也不至今日。
别说老太太,太太心疼,就是我们看着,心里也疼”的一席话,表达了对宝玉的无比爱怜与关心。
(正确答案)D.“玫瑰花又红又香,无人不爱的,只是刺戳手,也是一位神道,可惜不是太太养的,”“老鸹窝里出凤凰”。
这是《红楼梦》中兴儿所言,“玫瑰花”指的是探春。
10、成语完形:繁()丛杂[单选题] *芜(正确答案)复多忙11、关联词选用:路一直是宽整的,()探出身子的时候,()指导自己站在深不可测的山沟边,明明有水流,却听不见水声。
北京西城区学习探究诊断高中数学必修二模块自我检测题

测试十八 数学必修2模块自我检测题一、选择题1.下列条件中哪一个能够推出直线a ∥b ( ) (A )a 、b 都平行于同一个平面 (B )a 、b 都垂直于同一个平面 (C )a 、b 分别在两个平行平面内(D )a 平行于b 所在的平面2.已知点A (1,2),B (3,1),则线段AB 的垂直平分线的方程是( ) (A )4x +2y -5=0 (B )4x -2y -5=0 (C )x +2y -5=0(D )x -2y -5=03.若正方体的一条对角线的长度为2,则正方体的表面积为( ) (A )4(B )22(C )43(D )124.设直线ax +by +c =0的倾斜角为α,且sin α+cos α=0,则a ,b 满足( ) (A )a +b =1(B )a -b =1(C )a +b =0(D )a -b =05.若l 、m 、n 是互不相同的空间直线,α、β是不重合的平面,则下列命题中为真命题的是( )(A )若α∥β,l ⊂α,n ⊂β,则l ∥n (B )若α⊥β,l ⊂α,则l ⊥β (C )若l ⊥n ,m ⊥n ,则l ∥m(D )若l ⊥α,l ∥β,则α⊥β6.若过点(3,1)总可作两条直线和圆(x -2k )2+(y -k )2=k (k >0)相切,则k 的取值范围是( ) (A )(0,2)(B )(1,2) (C )(0,1)∪(2,+∞)(D )(2,+∞)7.过原点的直线与圆x 2+y 2+4x +3=0相切,若切点在第二象限,则该直线的方程是( ) (A )x y 3=(B )x y 3-=(C )x y 33=(D )x y 33-= 8.在斜三棱柱A 1B 1C 1-ABC 中,∠BAC =90°,BC 1⊥AC ,则C 1在底面ABC 上的射影一定在( ) (A )直线AB 上 (B )直线BC 上 (C )直线AC 上(D )△ABC 内部二、填空题9.直线y =x +a 与连接两点A (0,1),B (1,0)的线段相交,则a 的取值范围是______.10.过点(1,3)且与原点距离为1的直线方程为______. 11.一个正方体的顶点都在一个球的球面上,若这个球的体积为π29,则这个正方体的表面积为______.12.已知直线l 1:x +2y +5=0和直线l 2:x +ny +p =0,且l 1,l 2关于y 轴对称,则n =______;p =______.13.集合A ={(x ,y )|x 2+y 2=4},B ={(x ,y )|(x -3)2+(y -4)2=r 2},其中r >0,若A ∩B 中有且仅有一个元素,则r 的值是______.14*.一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱,这个四棱锥的底面为正方形,且底面边长与各侧棱长相等,这个三棱锥的底面边长与各侧棱长也都相等.设四棱锥、三棱锥、三棱柱的高分别为h 1,h 2,h ,则h 1∶h 2∶h =______. 三、解答题15.已知圆x 2+y 2-8x -2y +12=0,求过圆内一点P (3,0)的最长弦和最短弦所在的直线方程.16.如图,直棱柱ABC -A 1B 1C 1中,AB =AC =4,∠BAC =90°,E 为BC 的中点.(1)求证:平面AB 1E ⊥平面BCC 1B 1;(2)若侧面ABB 1A 1为正方形,求证:BC 1⊥平面AB 1E .17.如图,已知三个平面两两垂直,求证:它们的三条交线也两两垂直.18.如图,A ,B ,C ,D 为空间四点.在△ABC 中,AB =2,2==BC AC .等边三角形ADB 以AB 为轴转动.(1)当平面ADB ⊥平面ABC 时,求CD ;(2)当△ADB 转动时,是否总有AB ⊥CD ?证明你的结论.19.设圆上的点A (2,3)关于直线x +2y =0的对称点仍在这个圆上,且圆截直线x -y +1=0所得的弦长为22,求圆的方程.20.关于x ,y 的方程为x 2+y 2-2x -4y +m =0.(1)若上述关于x ,y 的方程表示圆C ,求m 的取值范围;(2)*若圆C 与直线x +2y -4=0的两个交点为M 、N ,且满足⋅=0(其中O 为坐标原点),求此时m 的值.测试十八 数学必修2模块自我检测题参考答案一、选择题1.B 2.B 3.A 4.D 5.D 6.C 7.D 8.A 提示:6.圆心到点(3,1)的距离大于半径时,可做两条切线. 圆心(2k ,k ),(2k -3)2+(k -1)2>k . 4k 2-12k +9+k 2-2k +1>k . 5k 2-15k +10>0,k 2-3k +2>0. ∴k <1或k >2.又k >0,得C .8.由已知,AC ⊥BC 1,AC ⊥AB ,所以AC ⊥平面ABC 1,所以平面ABC ⊥平面ABC 1,所以,C 1在底面ABC 上的射影一定在直线AB 上. 二、填空题9.-1≤a ≤1; 10.4x -3y +5=0,x =1; 11.18; 12.n =-2或p =-5; 13.3或7; 14..2:2:3 提示:14.易知,棱柱与三棱锥是等高的,即h 2=h ,设所有棱长均为1,可求得三棱锥的高36=h ,四棱锥的高为221=h ,所以,2:3:1=h h ,所以,.2:2:3::21=h h h 三、解答题15.提示:最长弦为过圆心的弦,即直径.最短弦为过点P 且与过点P 的直径垂直的弦.已知圆圆心为(4,1),所以,最长弦所在的直线方程为x -y -3=0. 最短弦所在的直线方程为x +y -3=0. 16.证明:(1)直棱柱ABC -A 1B 1C 1中,BB 1⊥平面ABC ,所以,BB 1⊥AE ,由已知,△ABC 是等腰直角三角形,又E 为BC 的中点, 所以,AE ⊥BC ,BB 1∩BC =B , 所以,AE ⊥平面BCC 1B 1, 所以平面AB 1E ⊥平面BCC 1B 1. (2)设B 1E ∩BC 1=O ,因为△ABC 是等腰直角三角形,AB =AC =4,所以24=BC , 侧面ABB 1A 1为正方形,所以,四边形BCC 1B 1是边长为4,24的矩形,所以,2424,22241111====BB C B BE BB ,即1111BBC B BE BB =, 所以Rt △B 1BE ~Rt △C 1B 1B ,所以∠B 1EB =∠C 1BB 1, 所以∠BB 1E +∠B 1BC 1=∠BB 1E +∠B 1EB =90°, 所以∠B 1OB =90°,BC 1⊥B 1E ,又由AE ⊥平面BCC 1B 1, 可得AE ⊥BC 1,AE ∩B 1E =E ,所以BC 1⊥平面AB 1E .17.证明:如图,设α∩β=α,β∩γ=b ,γ∩α=c .在平面γ内任取一点O (O ∉b ,O ∉c ),过点O 作OM ⊥b ,点M 是垂足,ON ⊥c ,点N 是垂足. ∵β⊥γ,β∩γ=b ,γ⊥α,γ∩α=c , ∴OM ⊥β,ON ⊥α.∵a ⊂α,a ⊂β,∴a ⊥ON ,a ⊥OM . ∵OM ∩ON =O ,OM ⊂γ,ON ⊂γ,∴a ⊥γ. ∵b ⊂γ,c ⊂γ,∴a ⊥b ,a ⊥c .同理可证b ⊥a ,b ⊥c .∴a ,b ,c 三条直线两两垂直18.解:(1)取AB 的中点E ,连结DE ,CE ,因为ADB 是等边三角形,所以DE ⊥AB .当平面ADB ⊥平面ABC 时, 因为平面ADB ∩平面ABC =AB , 所以DE ⊥平面ABC , 可知DE ⊥CE由已知可得1,3==EC DE ,在Rt △DEC 中,.222=+=EC DE CD(2)证明:①当D 在平面ABC 内时,因为AC =BC ,AD =BD ,所以C ,D 都在线段AB 的垂直平分线上,即AB ⊥CD .②当D 不在平面ABC 内时,由(2)知AB ⊥DE .又因AC =BC ,所以AB ⊥CE . 又DE ,CE 为相交直线,所以AB ⊥平面CDE ,由CD ⊂平面CDE ,得AB ⊥CD .综上所述,总有AB ⊥CD .19.解:设圆心为(a ,b ),半径为r .因为点A (2,3)关于直线x +2y =0的对称点仍在这个圆上,所以圆心在直线x +2y =0上,所以,a +2b =0,r 2=(a -2)2+(b -3)2, 圆截直线x -y +1=0所得的弦长为22,所以,22|1|2-=+-r b a , 解⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧-+-==+-=+-2222)3()2(0222|1|b a r b a r b a 消去a 得⎪⎩⎪⎨⎧++=+-=132556922222b b r b b r , 解得,b =-3或b =-7,所以,a =6,b =-3,r 2=52或a =14,b =-7,r 2=244,圆的方程为(x -6)2+(y +3)2=52或(x -14)2+(y +7)2=244. 20.解:(1)由x 2+y 2-2x -4y +m =0配方得(x -1)2+(y -2)2=5-m .该方程表示圆C ,所以m <5.(2)设M (x 1,y 1),N (x 2,y 2),则=(x 1,y 1),=(x 2,y 2). 由ON OM ⋅=0,得x 1x 2+y 1y 2=0. 由⎩⎨⎧=+--+=-+04204222m y x y x y x 消x ,得(4-2y )2+y 2-2(4-2y )-4y +m =0.整理得5y 2-16y +8+m =0,① 根据韦达定理⋅+==+∴58,5162121m y y y y 由x 1=4-2y 1,x 2=4-2y 2,⋅++-=++-=∴5)8(45484)(816212121m y y y y x x由x 1x 2+y 1y 2=0,得0585)8(4548=++++-m m .解得58=m .由①知,当Δ=162-20(8+m )>0时,524<m ,故58=m 满足题意, 因此58=m 为所求.。
必修二学业水平检测题答案打印

必修二学业水平测试模拟题答案一、选择题1-5 DABBC 6-10 BCACC 11-15 DDBDB 16-20 BCADC21-25 DDBDD 26-30 ABBAC 31-35 DCBCC 36-40 DCCAC二、非选择题(每空1分)41.(5分)⑴①脱氧核苷酸②氢键③碱基对④一条脱氧核苷酸片段⑵②42. (5分)⑴Aa Aa ⑵1/4 ⑶AA或Aa 2/343. (7分)(1)A和B A (2)有丝分裂 4 4(3)初级精母细胞精细胞44.(11分)Ⅰ.(1)遗传信息(2)转录翻译(3)19 60Ⅱ.(1)杂交基因重组(2)花药离体培养单(3)秋水仙素幼苗细胞细胞处于有丝分裂过程中,能够被秋水仙素抑制其纺锤体的形成45.(5分)(1)转录细胞核(2)密码子(3)转移RN A(tRNA)识别密码子并运载氨基酸46.(7分)(1)雄蕊人工传粉(2)3/8 9 (3)绿色皱粒黄色圆粒 1:1:1:1必修二学业水平测试模拟题答案一、选择题1-5 DABBC 6-10 BCACC 11-15 DDBDB 16-20 BCADC21-25 DDBDD 26-30 ABBAC 31-35 DCBCC 36-40 DCCAC二、非选择题(每空1分)41.(5分)⑴①脱氧核苷酸②氢键③碱基对④一条脱氧核苷酸片段⑵②42. (5分)⑴Aa Aa ⑵1/4 ⑶AA或Aa 2/343. (7分)(1)A和B A (2)有丝分裂 4 4(3)初级精母细胞精细胞44.(11分)Ⅰ.(1)遗传信息(2)转录翻译(3)19 60Ⅱ.(1)杂交基因重组(2)花药离体培养单(3)秋水仙素幼苗细胞细胞处于有丝分裂过程中,能够被秋水仙素抑制其纺锤体的形成45.(5分)(1)转录细胞核(2)密码子(3)转移RN A(tRNA)识别密码子并运载氨基酸46.(7分)(1)雄蕊人工传粉(2)3/8 9 (3)绿色皱粒黄色圆粒 1:1:1:1必修二学业水平测试模拟题答案一、选择题1-5 DABBC 6-10 BCACC 11-15 DDBDB 16-20 BCADC21-25 DDBDD 26-30 ABBAC 31-35 DCBCC 36-40 DCCAC二、非选择题(每空1分)41.(5分)⑴①脱氧核苷酸②氢键③碱基对④一条脱氧核苷酸片段⑵②42. (5分)⑴Aa Aa ⑵1/4 ⑶AA或Aa 2/343. (7分)(1)A和B A (2)有丝分裂 4 4(3)初级精母细胞精细胞44.(11分)Ⅰ.(1)遗传信息(2)转录翻译(3)19 60Ⅱ.(1)杂交基因重组(2)花药离体培养单(3)秋水仙素幼苗细胞细胞处于有丝分裂过程中,能够被秋水仙素抑制其纺锤体的形成45.(5分)(1)转录细胞核(2)密码子(3)转移RN A(tRNA)识别密码子并运载氨基酸46.(7分)(1)雄蕊人工传粉(2)3/8 9 (3)绿色皱粒黄色圆粒 1:1:1:1。
学习探究诊断 化学 必修二

学习探究诊断化学必修二本课程旨在探究化学必修二的相关内容。
通过研究这门课程,你将深入了解化学领域的重要概念、原理和实践应用。
课程内容将帮助你建立起对化学知识的系统性理解,为将来在化学领域的研究和研究打下坚实基础。
本课程的概况如下:课程名称:研究探究诊断化学必修二课程类型:必修课程授课方式:在线研究课程学时:若干学时(具体学时根据实际课程安排而定)课程难度:适用于化学相关专业学生或对化学感兴趣的研究者研究目标:通过研究本课程,你将能够掌握化学必修二的基本概念、实验技能和分析方法。
你将能够深入了解化学反应、元素周期表、化学键以及酸碱中和等方面的知识。
此外,你还将培养科学实验的基本操作技能和数据分析能力。
适用对象:本课程适用于高中化学教师、化学学科学生、对化学感兴趣的研究者等。
在本课程中,我们将采用探究研究的教学方法,通过实验、案例研究和讨论等方式来帮助学生深入理解化学知识。
希望通过本课程的研究,你能对化学产生更浓厚的兴趣,并为更深入的研究和研究奠定坚实的基础。
课程目标本节介绍了《研究探究诊断化学必修二》课程的目标和预期研究成果。
课程内容本课程主要涵盖了化学必修二的核心内容和主题。
研究探究诊断化学是一门重要的学科,旨在帮助学生加深对化学知识的理解和应用能力。
课程内容包括以下几个方面:化学反应与方程式:介绍化学反应以及如何用方程式表示化学反应过程。
研究如何平衡化学方程式,并探究化学反应的速率和反应机制。
化学主题:深入探讨化学中的主题,如离子式和化学键的形成。
了解常见的化学键类型,并研究如何预测元素之间的化学反应。
物质的组成和结构:研究物质的组成方式,包括元素、化合物和混合物。
了解各种物质的结构特征,并探究它们的性质和变化。
化学反应的能量变化:研究化学反应中的能量变化,包括热力学和热化学反应。
研究如何计算化学反应的能量变化,并探讨能量转化与化学反应之间的关系。
酸碱中和反应:研究酸碱中和反应的原理和常见实例。
学习探究诊断 ( 化学必修2)

学习探究诊断·化学 (必修2)第一章物质结构元素周期律第一节元素周期表学习目标学习重点1.认识元素性质的递变规律与原子结构的关系。
2.通过对碱金属和卤族元素性质相似性和递变性的学习,感受元素周期表在化学学习、科学研究和生产实践中的重要作用。
课时ⅠⅠ探究训练一、选择题(每小题只有1个选项符合题意)1.下列说法中,正确的是( )A.元素周期表有9个横行,分为9个周期B.元素周期表有7个横行,分为7个周期C.元素周期表有18个纵行,分为16个族D.元素周期表有18个纵行,分为18个族2.同周期元素,其原子具有相同的( )A.核外电子数B.核电荷数C.电子层数D.质子数3.2007年3月21日,我国公布了111号元素Rg的中文名称。
该元素名称及所在周期( ) A.第七周期B.镭第七周期C.铼第六周期D.氡第六周期4.下列各表中的数字代表元素的原子序数,表中数字所表示的元素与它们在周期表中的相对位置相符的一组是( )5.下列各组中的元素用原子序数表示,其中都属于主族的一组元素是( ) A.2、4、6 B.19、20、21 C.1、3、5 D.8、16、186.在元素周期表的前4周期中,有如图排列的5种元素。
若B元素的核电荷数为Z,则这5种元素的核电荷数之和可能为( )A.5Z+12 B.5Z+8C.5Z+10 D.5Z+18二、填空题7.在周期表主族元素中,甲元素与乙、丙、丁3种元素上下或左右相邻。
甲、乙两元素的原子序数之和等于丙元素的原子序数。
这4种原子的最外层电子数之和为20。
据此判断:元素甲为_________,元素丙为_________,元素乙和丁所形成的化合物的化学式为_________或_________。
Ⅱ诊断提高一、选择题(每小题只有1个选项符合题意)1.某周期ⅡA族元素的原子序数为x,则同周期的ⅢA族元素的原子序数是( ) A.只有x+1 B.可能是x+8或x+18C.可能是x+2 D.可能是x+1或x+11或x+252.取2.4 g某元素的单质X,在一定条件下与氧气充分作用,得到8.8 g化合物XO,该元2素原子数-质子数=中子数,则该元素在周期表中的位置为( )A.第三周期第ⅣA族B.第二周期第ⅣA族C.第二周期第ⅤA族D.第三周期第ⅥA族二、填空题3.根据周期表推算:(1)第五周期第一种元素和最后一种元素的原子序数分别为______和______。
北京市高中化学必修二学习·探究·诊断第一章 第二节
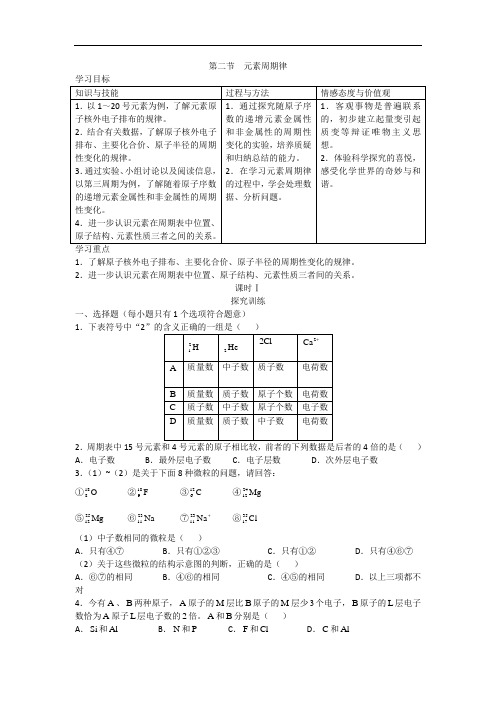
第二节元素周期律1.了解原子核外电子排布、主要化合价、原子半径的周期性变化的规律。
2.进一步认识元素在周期表中位置、原子结构、元素性质三者间的关系。
课时Ⅰ探究训练一、选择题(每小题只有1个选项符合题意)1.下表符号中“22.周期表中15号元素和4号元素的原子相比较,前者的下列数据是后者的4倍的是()A.电子数B.最外层电子数C.电子层数D.次外层电子数3.(1)~(2)是关于下面8种微粒的问题,请回答:①188O②189F③126C④2412Mg⑤2512Mg⑥2311Na⑦2311Na+⑧3517Cl(1)中子数相同的微粒是()A.只有④⑦B.只有①②③C.只有①②D.只有④⑥⑦(2)关于这些微粒的结构示意图的判断,正确的是()A.⑥⑦的相同B.④⑥的相同C.④⑤的相同D.以上三项都不对4.今有A、B两种原子,A原子的M层比B原子的M层少3个电子,B原子的L层电子数恰为A原子L层电子数的2倍。
A和B分别是()A.Si和A l B.N和P C.F和Cl D.C和A l5.核外电子层结构相同的一组微粒是( ) A .2Mg +、3Al +、Cl -、Ne B .Na +、F -、2S -、Ar C .K +、2Ca +、2S -、ArD .2Mg +、Na +、Cl -、2S -二、填空题6.画出下列元素的原子结构示意图。
(1)原子核外有2个电子层,核外有10个电子的原子__________。
(2)质量数为23,中子数为12的原子__________。
(3)最外层电子数是次外层电子数3倍的原子__________。
7.A 、B 、C 、D 、E(1)属于同一周期的元素是____________________。
(2)属于同一主族的元素是____________________。
(3)B 与水反应的化学反应方程式是____________________。
(4)E 与水反应的化学反应方程式是____________________。
北京市高中化学必修二学习·探究·诊断第三章 第一节

第一节 最简单的有机化合物——甲烷课时Ⅰ Ⅰ探究训练一、选择题(每小题有l ~2个选项符合题意) 1.下列关于烃的说法中,正确的是( ) A .含碳、氢元素的化合物 B .含有碳元素的化合物 C .完全燃烧只生成2CO 、2H O 的有机物 D .仅由碳、氢两种元素组成的化合物 2.下列关于甲烷的性质叙述不.正确的是( ) A .甲烷是一种无色、无味的气体 B .甲烷的密度比空气的密度小 C .甲烷极难溶于水 D .甲烷性质稳定,不和其他物质反应 3.下列叙述错误的是( )A .通常情况下,甲烷跟强酸、强碱、强氧化剂不起反应B .甲烷化学性质比较稳定,不能被任何氧化剂氧化C .甲烷跟氯气反应无论生成3CH Cl 、22CH Cl 、3CHCl 还是4CCl ,都属于取代反应D .甲烷的四种取代物都难溶于水4.下列物质常温下呈气态的是( ) A .3CH Cl B .22CH C1 C .3CHCl D .4CCl 5.若甲烷与氯气以物质的量之比11∶混合,在光照下得到的取代产物是( ) ①3CH Cl ②22CH C1 ③3CHCl ④4CCl A .只有① B .只有③C .①②③的混合物D .①②③④的混合物 6.下列分子具有正四面体结构的是( )A . H |H C H |H ----B .H|H C Cl |H ---- C . Br |H C Cl |H---- D .Cl |Cl C Cl |Cl ----7.在下列反应中,光照对反应几乎没有影响的是( ) A .氯气与氢气的反应 B .氯气与甲烷的反应 C .氧气与甲烷的反应 D .次氯酸的分解 二、填空题8.某元素的原子最外层电子数是次外层电子数的2倍,该元素的符号是__________,它和氢元素组成的最简单的化合物的化学式为__________,在这种化合物中氢元素的质量分数为__________。
9.如图是某同学利用日常用品注射器设计的简易实验装置。
英语必修二学探诊电子版

英语必修二学探诊电子版1、_____ the plan carefully,he rejected it. [单选题] *A. To have consideredB.To considerC. Having considered(正确答案)D. Considering2、35.Everyone in China ______ Mid-Autumn Day. [单选题] * A.likes(正确答案)B.likeC.is likingD.are like3、My brother is _______ actor. He works very hard. [单选题] *A. aB. an(正确答案)C. theD. one4、—Who came to your office today, Ms. Brown?—Sally came in. She hurt ______ in P. E. class. ()[单选题] *A. sheB. herC. hersD. herself(正确答案)5、Actually, we don't know whether this news comes from a reliable()or not. [单选题] *A. source(正确答案)B. originC. basisD. base6、If you had told me earlier, I _____ to meet you at the hotel. [单选题] *A. had comeB. will have comeC. would comeD. would have come(正确答案)7、--Do you know _______ girl with long curly hair?--Yes. She is Mary. She plays _______ piano very well. [单选题] *A. a; /B. the; /C. the; the(正确答案)D. a; the8、Amy and her best friend often ______ books together.()[单选题] *A. read(正确答案)B. readsC. is readingD. to read9、Obviously they didn’t see the significance of the plan. That is()the problem lies. [单选题] *A. where(正确答案)B. whyC. /D. how10、_______! Jack,the floor is wet. [单选题] *A. Be careful(正确答案)B. Be careful toC. Be careful forD. Be careful with11、You wouldn't have seen her if it _____ not been for him . [单选题] *A. hasB. had(正确答案)C. haveD.is having12、I saw the boy _______?the classroom. [单选题] *A. enter intoB. enter(正确答案)C. to enter intoD. to enter13、I don’t know how to improve my English. Can I ask you for some _______? [单选题] *A. answersB. advice(正确答案)C. questionsD. words14、The bookshop is far away. You’d better _______. [单选题] *A. by the busB. by busC. take busD. take?the bus(正确答案)15、( ) She keeps on learning English all the time. So far, she______three books of New Concept English. [单选题] *A. has learned(正确答案)B. have learnedC. had learnedD. learn16、Tony wants _______ a job as a language teacher in China. [单选题] *A. findB. findingC. to find(正确答案)D. to be found17、Could you please ______ why you can’t come to attend the meeting? [单选题] *A. explain(正确答案)B. understandC. giveD. reach18、_______ is on September the tenth. [单选题] *A. Children’s DayB. Teachers’Day(正确答案)C. Women’s DayD. Mother’s Day19、The huntsman caught only a()of the deer before it ran into the woods. [单选题] *A. gazeB. glareC. glimpse(正确答案)D. stare20、The Chinese team are working hard _______ honors in the Olympic Games. [单选题] *A. to win(正确答案)B. winC. winningD. won21、Experts are making an investigation on the spot. They want to find a way to()the tower. [单选题] *A. Restore(正确答案)B. resumeC. recoverD. reunite22、The market economy is quickly changing people’s idea on_____is accepted. [单选题] *A.what(正确答案)B.whichC.howD.that23、63.There will be? ? ? ? ??? water on the road after the heavy rain. [单选题] *A.too much(正确答案)B.much tooC.too manyD.many too24、—Is this Tony’s history book?—No, it isn’t ______.()[单选题] *A. himB. his(正确答案)C. heD. himself25、We are very hungry now. Can you _______ us something to eat? [单选题] *A. carryB. takeC. borrowD. bring(正确答案)26、Many volunteers _______ food and water to the local people in Japan after tsunami(海啸). [单选题] *A. gave out(正确答案)B. cut outC. put outD. found out27、The museum is _______ in the northeast of Changsha. [单选题] *A. sitB. located(正确答案)C. liesD. stand28、Alice hopes to _______ more friends at her new school. [单选题] *A. visitB. make(正确答案)C. missD. take29、We all wondered()Tom broke up with his girlfriend. [单选题] *A. thatB. whatC. whoD. why(正确答案)30、Tom didn’t _______ his exam again. It was a pity. [单选题] *A. winB. pass(正确答案)C. beatD. Fail。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章平面解析几何初步测试十平面直角坐标系中的基本公式Ⅰ学习目标理解和掌握数轴上的基本公式,平面上两点间的距离公式,中点坐标公式.Ⅱ基础训练题一、选择题1.点A(-1,2)关于y轴的对称点坐标为( )(A)(-1,-2) (B)(1,2) (C)(1,-2) (D)(2,-1)2.点A(-1,2)关于原点的对称点坐标为( )(A)(-1,-2) (B)(1,2) (C)(1,-2) (D)(2,-1)3.已知数轴上A,B两点的坐标分别是x1,x2,且x1=1,d(A,B)=2,则x2等于( )(A)-1或3 (B)-3或3 (C)-1 (D)34.已知点M(-1,4),N(7,0),x轴上一点P满足|PM|=|PN|,那么P点的坐标为( )(A)(-2,0) (B)(-2,1) (C)(2,0) (D)(2,1)5.已知点P(x,5)关于点Q(1,y)的对称点是M(-1,-2),则x+y等于( )9(A)6 (B)12 (C)-6 (D)2二、填空题6.点A(-1,5),B(3,-3)的中点坐标为______.7.已知A(a,3),B(3,a),|AB|=2,则a=______.8.已知M(-1,-3),N(1,1),P(3,x)三点共线,则x=______.9.设点A(0,1),B(3,5),C(4,y),O为坐标原点.若OC∥AB,则y=______;若OC⊥AB,则y=______.10.设点P,Q分别是x轴和y轴上的点,且中点M(1,-2),则|PQ|等于______.三、解答题11.已知△ABC的顶点坐标为A(1,-1),B(-1,3),C(3,0).(1)求证:△ABC是直角三角形;(2)求AB边上的中线CM的长.12.已知矩形ABCD相邻两个顶点A(-1,3),B(-2,4),若矩形对角线交点在x轴上,求另两个顶点C和D的坐标.13.已知AD是△ABC底边的中线,用解析法证明:|AB|2+|AC|2=2(|AD|2+|DC|2).Ⅲ拓展训练题14.利用两点间距离公式求出满足下列条件的实数x的集合:(1)|x-1|+|x-2|=3;(2)|x-1|+|x-2|>3;(3)|x-1|+|x-2|≤3.测试十一 直线的方程Ⅰ 学习目标1.理解直线斜率和倾斜角的概念,掌握两点连线的斜率公式. 2.掌握直线方程的点斜式、斜截式及一般式.Ⅱ 基础训练题一、选择题1.已知直线AB 的斜率为21,若点A (m ,-2),B (3,0),则m 的值为( ) (A )1 (B )-1 (C )-7(D )72.如图所示,直线l 1,l 2,l 3的斜率分别为k 1,k 2,k 3,则( )(A )k 1<k 2<k 3 (B )k 3<k 1<k 2 (C )k 3<k 2<k 1 (D )k 1<k 3<k 23.直线l 经过二、三、四象限,l 的倾斜角为α,斜率为k ,则( ) (A )k sin α>0 (B )k cos α>0 (C )k sin α=0 (D )k cos α符号不定 4.一条光线从点M (5,3)射出,遇x 轴后反射,反射光线过点N (2,6),则反射光线所在直线方程是( ) (A )3x -y -12=0 (B )3x +y +12=0 (C )3x -y +12=0 (D )3x +y -12=05.直线x -2y +2k =0与两坐标轴围成的三角形面积不小于1,那么k 的取值范围是( ) (A )k ≥-1 (B )k ≤1 (C )|k |≤1 (D )|k |≥1 二、填空题6.斜率为-2且在x 轴上截距为-1的直线方程是______.7.y 轴上一点M 与点N (-3,1)所在直线的倾斜角为120°,则M 点坐标为______. 8.已知直线3ax -2y -4a =0(a ≠0)在x 轴上的截距是它在y 轴上的截距的3倍,则a =______.9.已知直线l 过点A (-2,1)且与线段BC 相交,设B (-1,0),C (1,0),则直线l 的斜率k 的取值范围是______.10.如果直线l 沿x 轴负方向平移3个单位,接着再沿y 轴正方向平移1个单位后又回到原来的位置,则直线l 的斜率为______. 三、解答题 11.直线l 过原点且平分平行四边形ABCD 的面积.若平行四边形两个相对顶点为B (1,4),D (5,0),求直线l 的方程.12.直线l与直线y=1,x-y-7=0分别交于P、Q两点,线段PQ的中点为(1,-1).求直线l的方程.Ⅲ拓展训练题13.设A(0,3),B(3,3),C(2,0),直线x=a将△ABC分割成面积相等的两部分,求a 的值.14.一条直线l过点P(2,3),并且分别满足下列条件,求直线l的方程.(1)倾斜角是直线x-4y+3=0的倾斜角的两倍;(2)与x轴、y轴的正半轴交于A、B两点,且△AOB的面积最小;(3)|P A|·|PB|为最小(A、B分别为直线与x轴、y轴的正半轴的交点).测试十二 两条直线的位置关系(Ⅰ 学习目标掌握两条直线平行、垂直的条件,会利用两条直线平行、垂直的条件解决相关的问题.Ⅱ 基础训练题一、选择题1.如果直线ax +2y +2=0与直线3x -y -2=0平行,那么a 等于( ) (A )-3(B )-6(C )-23 (D )32 2.如果直线ax +2y +2=0与直线3x -y -2=0垂直,那么a 等于( ) (A )-3(B )-6(C )-23 (D )32 3.若两条直线A 1x +B 1y +C 1=0,A 2x +B 2y +C 2=0垂直,则( ) (A )A 1A 2+B 1B 2=0 (B )A 1A 2-B 1B 2=0 (C )2121B B A A =-1 (D )2121A A B B =1 4.设A ,B 是x 轴上两点,点P 的横坐标为2,且|P A |=|PB |,若直线P A 的方程为x -y +1=0,则直线PB 的方程为( ) (A )x +y -5=0 (B )2x -y -1=0 (C )2y -x -4=0 (D )x +y -7=0 5.已知直线y =kx +2k +1与y =-21x +2的交点在第一象限,则k 的取值范围是( ). (A )-6<k <2 (B )-21<k <21(C )-61<k <21(D )k <21二、填空题6.以A (1,3)、B (-1,1)为端点的线段的垂直平分线方程是______.7.若三条直线l 1:2x -y =0,l 2:x +y -3=0,l 3:mx +ny +5=0交于一点,则实数m ,n 满足的关系式是______.8.直线y =2x +3关于点(2,3)对称的直线方程为______.9.直线2x -y +1=0绕着它与y 轴的交点逆时针旋转45°角,此时直线的方程为______. 10.若三条直线x +y =2,x -y =0,x +ay =3构成三角形,则a 的取值范围是______. 三、解答题11.求经过两条直线l 1:2x +3y +1=0和l 2:x -3y +4=0的交点,并且垂直于直线3x +4y-7=0的直线方程.12.平行四边形ABCD 的两边AB ,AD 所在的直线方程分别为x +y -1=0,3x -y +4=0,其对角线的交点坐标为(3,3),求另两边BC ,CD 所在的直线方程.13.已知三角形三条边AB,BC,AC中点分别为D(2,1)、E(5,3)、F(3,-4).求各边所在直线的方程.14.已知两条直线l1:mx+8y+n=0和l2:2x+my-1=0,试确定m,n的值,使l1,l2分别满足下列条件:(1)l1,l2相交于点P(m,-1);(2)l1∥l2;(3)l1与l2重合.测试十三 两条直线的位置关系(二)Ⅰ 学习目标会应用点到直线的距离公式解决相关的问题.Ⅱ 基础训练题一、选择题1.点P (0,2)到直线y =3x 的距离是( ) (A )1(B )510 (C )2 (D )55 2.平行线3x +4y +2=0与3x +4y -12=0之间的距离为( ) (A )2(B )310 (C )514 (D )33.若直线(2+m )x -y +5-n =0与x 轴平行且与x 轴相距5时,则m +n 等于( ) (A )-2或8 (B )-2 (C )8 (D )04.直线l 1:ax -y +b =0与l 2:bx -y +a =0(ab ≠0,a ≠b )在坐标系中的位置可能是( )5.A 、B 、C 为△ABC 的三个内角, 它们的对边分别为a 、b 、c .已知原点到直线x sin A +y sin B +sin C =0的距离大于1,则此三角形形状为( ) (A )锐角三角形 (B )直角三角形 (C )钝角三角形 (D )不能确定 二、填空题 6.若直线ax +4y -2=0与直线2x -5y +c =0垂直相交于点(1,m ),则a =____,c =_____,m =______. 7.已知定点A (0,1).点B 在直线x +y =0上运动,当线段AB 最短时,点B 的坐标是____. 8.两平行直线分别过点(1,0)与(0,5),且距离为5,它们的方程为______. 9.若点A (1,1)到直线l :x cos θ+y sin θ=2(θ为实数)的距离为f (θ),则f (θ)的最大值是___. 10.若动点A (x 1,y 1),B (x 2,y 2)分别在直线l 1:x +y -7=0和l 2:x +y -5=0上移动,则AB 中点M 到原点距离的最小值是______. 三、解答题11.过点P (1,2)的直线l 与两点A (2,3),B (4,-5)的距离相等,求直线l 的方程.12.已知直线l :x +2y -2=0,试求:(1)与直线l 的距离为5的直线的方程; (2)点P (-2,-1)关于直线l 的对称点的坐标.13.已知△ABC的垂心H(5,2),且A(-10,2)、B(6,4),求点C的坐标.Ⅲ拓展训练题14.在△ABC中,点B(1,2),BC边上的高所在的直线方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0,求|BC|.测试十四 圆的方程Ⅰ 学习目标掌握圆的标准方程及一般方程,能根据已知条件求圆的方程.Ⅱ 基础训练题一、选择题1.圆x 2+y 2+ax =0的圆心的横坐标为1,则a 等于( ) (A )1 (B )2 (C )-1 (D )-22.与圆C :x 2+y 2-2x -35=0的圆心相同,且面积为圆C 的一半的圆的方程是( ) (A )(x -1)2+y 2=3 (B )(x -1)2+y 2=6 (C )(x -1)2+y 2=9 (D )(x -1)2+y 2=18 3.曲线x 2+y 2+22x -22=0关于( ) (A )直线x =2轴对称 (B )直线y =-x 轴对称 (C )点(-2,2)中心对称(D )点(-2,0)中心对称4.如果圆x 2+y 2+Dx +Ey +F =0与y 轴相交,且两个交点分别在原点两侧,那么( ) (A )D ≠0,F >0 (B )E =0,F >0 (C )F <0 (D )D =0,E ≠0 5.方程x -1=()211--y 所表示的曲线是( )(A )一个圆 (B )两个圆 (C )半个圆 (D )四分之一个圆 二、填空题6.过原点的直线将圆x 2+y 2-2x +4y =0的面积平分,则此直线的方程为______.7.已知圆的方程(x -a )2+(y -b )2=r 2(r >0),试根据下列条件,分别写出a ,b ,r 应满足的条件.(1)圆过原点且与y 轴相切:______; (2)原点在圆内:______; (3)圆与x 轴相交:______. 8.圆(x -1)2+y 2=1的圆心到直线y =33x 的距离是______. 9.P (x ,y )是圆x 2+y 2-2x +4y +1=0上任意一点,则x 2+y 2的最大值是______;点P 到直线3x +4y -15=0的最大距离是______. 10.设P (x ,y )是圆(x -3)2+y 2=4上的点,则xy的最小值是______. 三、解答题11.方程x 2+y 2+ax +2ay +2a 2+a -1=0表示圆,求a 的取值范围.12.求过三个点A (0,0),B (4,0),C (2,2)的圆的方程.13.已知圆C的圆心在直线x+y-1=0上,且A(-1,4)、B(1,2)是圆C上的两点,求圆C的方程.Ⅲ拓展训练题14.已知曲线C:x2+y2-4ax+2ay+20a-20=0.(1)证明:不论a取何实数,曲线C必过定点;(2)当a≠2时,证明曲线C是一个圆,且圆心在一条直线上.测试十五 直线与圆的位置关系Ⅰ 学习目标1.会用解析法及几何的方法判定直线与圆的位置关系,并会求弦长和切线方程; 2.会用几何的方法判定圆和圆的位置关系.Ⅱ 基础训练题一、选择题1.圆x 2+y 2-2x =0和x 2+y 2+4y =0的位置关系是( ) (A )相离 (B )外切 (C )相交 (D )内切2.直线3x +4y +2=0与圆x 2+y 2+4y =0交于A 、B 两点,则线段AB 的垂直平分线的方程是( )(A )4x -3y -2=0 (B )4x -3y -6=0 (C )3x +4y +8=0 (D )3x -4y -8=0 3.直线3x +y -23=0截圆x 2+y 2=4得的劣弧所对的圆心角为( ) (A )6π(B )4π (C )3π (D )2π 4.若圆x 2+y 2=r 2(r >0)上恰有相异两点到直线4x -3y +25=0的距离等于1,则r 的取值范围是( ) (A )[4,6] (B )(4,6] (C )(4,6) (D )[4,6) 5.从直线y =3上的点向圆x 2+y 2=1作切线,则切线长的最小值是( ) (A )22(B )7(C )3(D )10二、填空题6.以点(-2,3)为圆心且与y 轴相切的圆的方程是______.7.已知直线x =a (a >0)和圆(x -1)2+y 2=4相切,那么a 的值是______.8.设圆x 2+y 2-4x -5=0的弦AB 的中点为P (3,1),则直线AB 的方程是______.9.过定点(1,2)可作两直线与圆x 2+y 2+kx +2y +k 2-15=0相切,则k 的取值范围是____. 10.直线x +3y -m =0与圆x 2+y 2=1在第一象限内有两个不同的交点,则m 的取值范围是______. 三、解答题11.圆x 2+y 2=8内有一点P (-1,2),AB 为过点P 且倾斜角为α的弦. (1)当α=4π3时,求AB 的长; (2)当弦AB 被点P 平分时,求直线AB 的方程.12.求经过点P (6,-4)且被圆x 2+y 2=20截得的弦长为62的直线的方程.13.求过点P (4,-1)且与圆x 2+y 2+2x -6y +5=0外切于点M (1,2)的圆的方程.Ⅱ 拓展训练题14.已知圆满足:①截y 轴所得弦长为2;②被x 轴分成两段圆弧,其弧长的比为3∶1;③圆心到直线l :x -2y =0的距离为55. 求该圆的方程.测试十六空间直角坐标系Ⅰ学习目标1.理解空间直角坐标系的概念,能写出满足某些条件的点的坐标.2.会用空间两点间距离公式进行相关的计算.Ⅱ基础训练题一、选择题1.点A(2,0,3)在空间直角坐标系的位置是( )(A)y轴上(B)xOy平面上(C)xOz平面上(D)yOz平面上2.在空间直角坐标系中,点P(-2,-1,3)到原点的距离为( )(A)14(B)5(C)14 (D)53.点A(-1,2,1)在xOy平面上的射影点的坐标是( )(A)(-1,2,0) (B)(-1,-2,0)(C)(-1,0,0) (D)(1,-2,0)4.在空间直角坐标系中,两个点A(2,3,1)、A′(2,-3,1)关于( )对称(A)平面xOy (B)平面yOz(C)平面xOz(D)y轴5.设a是任意实数,则点P(a,1,2)的集合在空间直角坐标系中所表示的图形是( )(A)垂直于平面xOy的一条直线(B)垂直于平面yOz的一条直线(C)垂直于平面xOz的一条直线(D)以上均不正确二、填空题6.点M(4,-3,5)到x轴的距离为______.7.若点P(x,2,1)与Q(1,1,2)、R(2,1,1)的距离相等,则x的值为______.8.已知点A(-2,3,4),在y轴上求一点B,使|AB|=6,则点B的坐标为______.9.已知两点A(2,0,0),B(0,3,0),那么线段AB的中点的坐标是______.10.在空间直角坐标系中,点A(1,2,a)到点B(0,a,1)的距离的最小值为______.三、解答题11.在空间直角坐标系中,设点M的坐标为(1,-2,3),写出点M关于各坐标面对称的点、关于各坐标轴对称的点的坐标.12.在空间直角坐标系中,设点M的坐标为(1,-2,3),写出点M到原点、各坐标轴及各坐标面的距离.13.如图,正方体OABC-A1B1C1D1的棱长为a,|AM|=2|MB|,|B1N|=|NC1|,分别写出点M与点N的坐标.14.在空间直角坐标系中,设点P在x轴上,它到点P1(0,2,3)的距离为到点P2(0,1,-1)的距离的两倍,求点P的坐标.测试十七Ⅰ 基础训练题一、选择题1.方程y =k (x -2)表示( ) (A )经过点(-2,0)的所有直线 (B )经过点(2,0)的所有直线(C )经过点(2,0)且不垂直于x 轴的所有直线 (D )经过点(2,0)且去掉x 轴的所有直线2.点P (x ,y )在直线x +y -4=0上,O 为坐标原点,则|OP |的最小值为( ) (A )10(B )22(C )6(D )23.若直线l :y =kx -3与直线2x +3y -6=0的交点位于第一象限,则直线l 的倾斜角的取值范围是( ) (A ))3π,6π[(B ))2π,6π((C ))2π,3π((D )]2π,6π[4.若直线(1+a )x +y +1=0与圆x 2+y 2-2x =0相切,则a 的值为( ) (A )1或-1 (B )2或-2 (C )1 (D )-15.如果直线l 将圆:x 2+y 2-2x -4y =0平分,且不通过第四象限,那么直线l 的斜率的取值范围是( ) (A )[0,2](B )[0,1](C )]21,0[(D ))21,0[二、填空题6.经过点P (-2,3)且在x 轴、y 轴上截距相等的直线方程为______.7.若直线mx +ny -3=0与圆x 2+y 2=3没有公共点,则m 、n 满足的关系式为______. 8.已知圆x 2+(y -1)2=1及圆外一点P (-2,0),过点P 作圆的切线,则两条切线夹角的正切值是______. 9.已知P 是直线3x +4y +8=0上的动点,P A ,PB 是圆x 2+y 2-2x -2y +1=0的两条切线.A 、B 是切点,C 是圆心,那么四边形P ACB 面积的最小值为______.10.已知两个圆x 2+y 2=1①与x 2+(y -3)2=1②,则由①式减去②式可得上述两圆的对称轴方程.将上述命题在曲线仍为圆的情况下加以推广,即要求得到一个更一般的命题,而已知命题应成为所推广命题的一个特例.推广的命题为______. 三、解答题11.已知直线l 1:2x -y +3=0与直线l 2关于直线y =-x 对称,求直线l 2的方程.12.圆心在直线x -2y -3=0上,且圆与两坐标轴都相切,求此圆的方程.13.求通过直线2x +y -4=0及圆x 2+y 2+2x -4y +1=0的交点,并且有最小面积的圆的方程.14.在△ABC中,顶点A(2,4)、B(-4,2),一条内角平分线所在直线方程为2x-y=0,求AC边所在的直线方程.Ⅱ拓展训练题15.已知过原点O的一条直线与函数y=log8x的图象交于A、B两点(A在B的右侧),分别过点A、B作y轴的平行线与函数y=log2x的图象交于C、D两点.(1)证明:点C、D和原点O在同一条直线上.(2)当BC平行于x轴时,求点A的坐标.16*.已知圆C:(x-1)2+(y-2)2=25,及直线l:(2m+1)x+(m+1)y=7m+4(m∈R).(1)证明:不论m取什么实数,直线l与圆C恒相交;(2)求直线l被圆C截得的弦长最短长度及此时的直线方程.参考答案第二章 平面解析几何初步 测试十 平面直角坐标系中的基本公式一、选择题1.B 2.C 3.A 4.C 5.D 提示:1.点(a ,b )关于x 轴、y 轴、坐标原点O 、直线y =x 的对称点坐标为(a ,-b ),(-a ,b ),(-a ,-b ),(b ,a ). 二、填空题6.(1,1); 7.2或4; 8.5; 9.3,316-; 10.52. 提示:9.若=(x 1,y 1),=(x 2,y 2),则∥⇔x 1y 2-x 2y 1=0(应注意向量平行与直线平行的关系); 则⊥⇔x 1x 2+y 1y 2=0(即⋅=0); 三、解答题11.(1)证明:由已知计算得5||,52)31()11(||22==--++=BC AB5||=AC ,所以,|AB |2+|AC |2=|BC |2,所以△ABC 是直角三角形.另解:由已知=(-2,4),AC =(2,1), 所以,AB ·AC =-2×2+4×1=0, 所以,⊥,△ABC 是直角三角形. (2)解:由已知,AB 的中点M 的坐标为)231,211(+--,即M (0,1), 所以,.1013||22=+=CM12.设矩形对角线交点为M (x ,0),因为|MA |=|MB |,则22224)2(3)1(++=++x x ,解得x =-5,所以M (-5,0). 设C (x 1,y 1),因为M 为AC 中点,所以023,52111=+-=-y x , 解得x 1=-9,y 1=-3,所以,C (-9,-3),同理,D (-8,-4).注:本题也可以利用向量平行、垂直的有关知识来解. 13.提示:通过建立适当的坐标系,利用坐标法来证明.14.(1){x |x =0,x =3};(2){x |x <0或x >3};(3){x |0≤x ≤3}.测试十一 直线的方程一、选择题1 B2 B3 B4 D5 D 提示:3.由题意知,l 的倾斜角α为钝角,cos α<0,k <0,故k cos α>0.4.反射光线过点N (2,6),同时,还经过点M (5,3)关于x 轴的对称点M ′(5,-3),所以,反射光线的斜率为352)3(6-=---,直线方程为3x +y -12=0.要注意,“光线”问题常用对称点的思路去思考问题.5.直线x -2y +2k =0与两坐标轴交点为A (-2k ,0).B (0,k ), 所以,2|||2|21||||21k k k OB OA S AOB =⋅-=⋅=∆,由题意k 2≥1, 得|k |≥1为所求.二、填空题6.2x +y +2=0; 7.(0,-2); 8.a =-2; 9.311-≤≤-k ; 10.⋅-31提示:10.提示:设A (x 0,y 0)为直线l 上一点,根据题意,A 点沿x 轴负方向平移3个单位,接着再沿y 轴正方向平移1个单位后仍应在直线l 上,即点(x 0-3,y 0+1)在直线l 上.所以直线l 的斜率为⋅-=---+31310000x x y y三、解答题11.提示:平分平行四边形面积的直线必过平行四边形的对角线交点,即过BD 的中点(3,2).所以,所求直线方程为2x -3y =0.12.略解:设P (x 1,1),因为PQ 的中点为(1,-1),根据中点坐标公式,可得Q (2-x 1,-3),因为点Q 在直线x -y -7=0上, 所以,(2-x 1)-(-3)-7=0,解得x 1=-2,所以,P (-2,1),Q (4,-3),⋅-=----=3242)3(1/k所以,l :2x +3y +1=0.13.略解:由已知得AB ∥x 轴,作CD ⊥AB 于D ,∵C (2,0),A (0,3),B (3,3).∴S △ADC >S △BDC . ∵x =a 将△ABC 面积平分,∴x =a 在直线CD 左侧,即0<a <2.由题意得)3(2123321p ABC y a S -⋅=⋅⋅=∆,其中y p 表示AC 与x =a 的交点的纵坐标. ∵直线AC 的方程为132=+yx .即3x +2y -6=0.当x =a 时,236,236ay a y p -=∴-=,代入上式,得.3±=a∵a ∈(0,2).3=∴a 为所求.14.(1)设直线l 的倾斜角为α,则所求直线倾斜角为2α,由已知,41tan =α,所以,tan2α=158tan 1tan 22=-αα,所以,所求直线l 方程为)2(1583-=-x y ,即8x -15y +29=0.(2)依题意,设直线l 方程为y -3=k (x -2),k <0,则)0,32(kA -,B (0,3-2k ),S △AOB 1266)292(621=+≥-+-+==kk y x B A ,此时,kk 292-=-,即.23±=k ,因为k <0,所以23-=k ,所求直线l 方程为)2(233--=-x y ,即3x +2y -12=0. (3)依题意,设直线l 方程为y -3=k (x -2),k <0,则)23,0(),0,32(k B kA --,12)1(6||164499||||222≥-+-⨯=+⨯=+⨯+=⋅kk k k k k PB PA , 此时,kk -=-1,即k =±1,因为k <0,所以k =-1, 所求直线l 方程为y -3=-(x -2),即x +y -5=0.测试十二 两条直线的位置关系(一)一、选择题1.B 2.D 3.A 4.A 5.C 提示:5.提示:可以求出两条直线的交点坐标)1216,1242(+++-k k k k ,解不等式组⎪⎪⎩⎪⎪⎨⎧>++>+-0121601242k k k k, 可得⋅<<-2161k 另外,注意到直线y =kx +2k +1可变形为y -1=k (x +2),即此直线过定点(-2,1),又,直线221+-=x y 与x 轴、y 轴的交点坐标为(4,0),(0,2).利用数形结合的思路可得结论. 二、填空题6.x +y -2=0; 7.m +2n +5=0; 8.2x -y -5=0; 9.3x +y -1=0; 10.a ∈R ,a ≠±1且a ≠2. 提示:9.设直线2x -y +1=0的倾斜角为α,由已知,所求直线的倾斜角为α+45°,因为tan α=2,所以,345tan tan 145tan tan )45tan(-=-+=+οοοααα,又直线2x -y +1=0与y 轴的交点为(0,1),所以,所求直线方程为3x +y -1=0.10.直线x +ay =3与另两条直线不平行也不重合,并且三条直线不过同一点. 三、解答题11.4x -3y +9=0.12.CD :x +y -11=0,BC :3x -y -16=0. 13.方法一:用中点.DE 中点)2,27(G ,又G 为BF 的中点,∴B (4,8). 同理,EF 中点).2,6(),21,4(-∴-C HDF 中点).6,0(),23,25(-∴-A M.01227,627:=---=∴y x x y AB BC :y +2=-5(x -6),5x +y -28=0..01832,632:=---=y x x y AC 方法二:用斜率. EF 斜率为)2(271:27-=-∴⋅x y AB ,得7x -2y -12=0. FD 斜率为-5.∴BC :y -3=-5(x -5),得5x +y -28=0. DE 斜率为)3(324:32-=+∴⋅x y AC ,得2x -3y -18=0, 14.解:(1)由⎩⎨⎧=--=+-,012,082m m n m 解得m =1,n =7.(2)易知m ≠0,所以,当182-=/=n m m 时, 即m =4,n ≠-2,或m =-4,n ≠2时l 1∥l 2.(3)结合(2)的结果,当m =4,n =-2,或m =-4,n =2时,l 1与l 2重合.测试十三 两条直线的位置关系(二)一、选择题1.B 2.C 3.A 4.D 5.C 提示: 5.由已知,1sin sin |sin |22>+BA C ,所以,sin 2C >sin 2A +sin 2B .又R CcB b A a 2sin sin sin ===,所以,c 2>a 2+b 2, 由余弦定理,得02cos 222<-+=abc b a C ,所以,C 为钝角,三角形为钝角三角形.二、填空题6.10,-12,-2; 7.)21,21(-; 8.y =0,y =5或5x -12y -5=0,5x -12y +60=0; 9.22+; 10..23提示:7.当AB 与已知直线垂直时,线段AB 最短. 9.|2)cos 22sin 22(2||2cos sin |cos sin |2cos sin |)(22-+=-+=+-+=θθθθθθθθθf)4πsin(22|2)4πsin(2|+-=-+=θθ,所以,f (θ)的最大值为.22+10.由已知,点M 到两直线l 1,l 2的距离相等.即点M 在直线x +y -6=0上,于是,问题变成“点M 在直线x +y -6=0上运动,求原点到点M 的最小距离”,可利用第7题的思路加以解决. 三、解答题11.提示:满足题目条件的直线l 或者与直线AB 平行,或者经过线段AB 的中点.当直线l 与直线AB 平行时,l :4x +y -6=0;当直线l 经过线段AB 的中点时,l :3x +2y -7=0. 12.解:(1)设所求直线方程为x +2y +c =0,根据题意55|2|=+c ,解得c =3或c =-7, 所以,所求直线方程为x +2y +3=0或x +2y -7=0. (2)设P (-2,-1)关于直线l 的对称点为P ′(x 0,y 0). 则k pp 'k l =-1,且PP ′的中点在直线l 上,即点)21,22(00--y x 在直线l 上. 所以,⎪⎪⎩⎪⎪⎨⎧-=-⋅++=--⨯+-1)21(2102212220000x y y x ,即⎩⎨⎧=+-=-+0320820000y x y x ,解得⋅==519,5200y x 即)519,52('P .13.解:AB 斜率为81,设C 坐标(x 0,y 0). 所以,85200-=--x y ……………………①因为AH 斜率为0,∴BC 斜率不存在,即BC 直线方程为x =6, 所以,x 0=6.…………………………②②代入①,得y 0=-6.∴C 点坐标(6,-6). 14.略解:解⎩⎨⎧==+-,0,012y y x 得A (-1,0),所以AB :x -y +1=0.设C (x 0,y 0),因为BC 与BC 边上的高线垂直,并且C 关于直线y =0(∠A 的平分线)的对称点C ′在直线AB 上.所以,k BC =-2,C ′(x 0,-y 0)在直线AB 上.所以,⎪⎩⎪⎨⎧=++-=--012120000y x x y 解得x 0=5,y 0=-6,即C (5,-6),故|BC |=54.测试十四 圆的方程一、选择题1.D 2.D 3.D 4.C 5.C 提示:4.只需坐标原点在圆内,即原点与圆心的距离小于半径,已知圆圆心为)2,2(ED --,半径为)04(242222>-+-+F E D FE D ,结合 44)02()02(2222FE D E D -+<-+-及D 2+E 2-4F >0,可得F <0.5.方程2)1(11--=-y x 可以等价变形为(x -1)2+(y -1)2=1, 且x -1≥0,1-(y -1)2≥0.即(x -1)2+(y -1)2=1,且x ≥1,0≤y ≤2.所以,方程2)1(11--=-y x 所表示的曲线是半个圆.二、填空题 6.2x +y =0;7.(1)a 2+b 2=r 2且|a |=r 或b =0,|a |=r ;(2)a 2+b 2<r 2;(3)|b |<r ; 8.21; 9.6,549+; 10.⋅-552 提示:9.x 2+y 2的几何意义是点P (x ,y )到原点距离的平方.利用这个几何意义求解. 10.xy的几何意义是点P (x ,y )与原点连线的斜率.利用这个几何意义求解. 三、解答题11.提示:将方程配方为222431)()2(a a a y a x --=+++,则,04312>--a a 即3a 2+4a -4<0,(3a -2)(a +2)<0,解得,⋅<<-322a12.提示:方法一:设圆的方程为x 2+y 2+D x +Ey +F =0,由已知三个点在圆上,可得⎪⎩⎪⎨⎧=+++=++=082204160F E D F D F 解得D =-4,E =0,F =0,所以,所求圆方程为x 2+y 2-4x =0.方法二:注意到k AC =1,k BC =-1,k AC k BC =-1,所以,三角形ABC 是直角三角形,∠C =90°,所以,所求圆心为AB 边中点,即(2,0)点,可求半径r =2, 所以,所求圆的方程为(x -2)2+y 2=4.13.提示:因为A (-1,4),B (1,2)是圆C 上的两点,所以圆心在线段AB 的中垂线上,因为AB 中点坐标为(0,3),k AB =-1,所以线段AB 的中垂线方程为x -y +3=0,解⎩⎨⎧=-+=+-0103y x y x 得圆心坐标为(-1,2),半径,2)22()11(22=-+--=r所以,圆C 的方程为(x +1)2+(y -2)2=4.14.分析:(1)曲线C 方程可变形为(x 2+y 2-20)+a (-4x +2y +20)=0,由⎩⎨⎧=++-=-+0202402022y x y x ,解得⎩⎨⎧-==24y x .即点(4,-2)满足曲线C 的方程,故曲线C 过定点(4,-2).(2)曲线C 方程(x -2a )2+(y +a )2=5(a -2)2,因为a ≠2,所以曲线C 是圆心为(2a ,-a ),半径为|2|5-a 的圆. 设圆心坐标为(x ,y ),则有⎩⎨⎧-==ay a x 2,消去a 可得x y 21-=,故圆心必在直线x y 21-=. 测试十五 直线与圆的位置关系一、选择题1.C 2.B 3.C 4.C 5.A 提示:5.圆方程x 2+y 2=1,圆心(0,0),半径1,切线长的平方=圆心到直线y =3距离的最小值的平方.22813222==-=-r二、填空题6.(x +2)2+(y -3)2=4; 7.3; 8.x +y -4=0; 9.⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛--338,23,338Y ; 10..23<<m提示:9.圆方程配方为,4316)1()2(222k y k x -=+++依题意,2224316)12()21(k k ->+++,且,043162>-k解得k <-3或k >2,且338338<<-k ,所以,⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛--338,23,338Y . 10.结合图形,求出直线与圆在第一象限相切时的m 值为2,求出直线过(0,1)点时的m值为3.进而得出m 值范围. 三、解答题11.提示:(1)方法一:由已知,AB :x +y -1=0,与圆方程联立,解方程组得,2151±=x 则.304πcos||||12=-=x x AB 方法二:圆心到直线AB 的距离,222|1|=-=d 所以.3021822||22=-=-=dr AB(2)当弦AB 被点P 平分时,AB ⊥OP ,又k OP =-2, 所以,.052:,21=+-=y x AB k AB 12.提示:注意到,过点P (6,-4)倾斜角为90°的直线不满足题意,设所求直线为y +4=k (x -6),由弦长为26,圆半径为20,所以圆心O 到所求直线的距离为2, 即21|46|2=++k k ,解得k =-1或177-=k ,所以所求直线方程为x +y -2=0或7x +17y +26=0.13.略解:圆(x +1)2+(y -3)2=5的圆心为(-1,3),设圆心(a ,b ),得⎪⎩⎪⎨⎧---=--++-=-+-,112312)1()4()2()1(2222a b b a b a解得⎩⎨⎧==13b a ,圆心(3,1),半径为5,所以,所求圆方程为(x -3)2+(y -1)2=5.14.分析:设所求圆的圆心为P (a ,b ),半径为r ,则P 到x 轴、y 轴的距离分别为|b |,|a |.由题设圆P 截x 轴所得劣弧所对圆心角为90°,圆P 截x 轴所得弦长为r 2, 故r 2=2b 2.又圆P 截y 轴所得弦长为2,所以有r 2=a 2+1,从而有2b 2-a 2=1. 又点P (a ,b )到直线x -2y =0的距离555|2|=-=b a d ,所以|a -2b |=1, 解⎩⎨⎧=-=-121|2|22a b b a ,得⎩⎨⎧==11b a 或⎩⎨⎧-=-=11b a . 由于r 2=2b 2,知2=r ,于是所求圆的方程为(x -1)2+(y -1)2=2或(x +1)2+(y +1)2=2.测试十六 空间直角坐标系一、选择题1.C 2.A 3.A 4.C 5.B 二、填空题6.34; 7.1; 8.(0,-1,0),(0,7,0); 9.)0,23,1(; 10.26. 三、解答题11.答:点M 关于平面xOy 的对称点为(1,-2,-3);点M 关于平面yOz 的对称点为(-1,-2,3); 点M 关于平面xOz 的对称点为(1,2,3); 点M 关于x 轴的对称点为(1,2,-3);点M 关于y 轴的对称点为(-1,-2,-3);点M 关于z 轴的对称点为(-1,2,3). 12.答:点M 到原点的距离为14;点M 到平面xOy 的距离为3;点M 到平面yOz 的距离为1;点M 到平面xOz 的距离为2; 点M 到x 轴的距离为13;点M 到y 轴的距离为10; 点M 到z 轴的距离为5. 13.答:).,,21(),0,32,(a a a N a a M 14.答:(1,0,0)或(-1,0,0).测试十七 平面解析几何初步全章综合练习一、选择题1.C 2.B 3.B 4.D 5.A 提示:3.直线3:-=kx y l 过定点)3,0(-,直线2x +3y -6=0与x 轴、y 轴交点坐标为(3,0)、(0,2),作图分析可得答案. 二、填空题6.x +y -1=0,3x +2y =0; 7.0<m 2+n 2<3; 8.34; 9.22; 10.两圆(x -a )2+(y -b )2=r 2与(x -c )2+(y -d )2=r 2的对称轴的方程为2(c -a )x +2(d -b )y +a 2+b 2-c 2-d 2=0. 提示: 9.r PA S PACB ||212⨯=(r 是圆的半径),由已知r =1,所以,即求|P A |的最小值,又|P A |=12-PC ,而|PC |的最小值为C 到直线3x +4y +8=0的距离,即343|843|22=+++,所以,所求最小值为.22||212=⨯=r PA S PACB 三、解答题11.提示:直线l 1与l 2的交点坐标为(-1,1),直线l 1与y 轴交点坐标为(0,3),且(0,3)点关于直线y =-x 对称点坐标为(-3,0),所以,直线l 2过点(-3,0)和(-1,1),l 2:x -2y +3=0.12.提示:设圆心为(a ,b ),由已知|a |=|b |=r ,又a -2b -3=0,解⎩⎨⎧==--b a b a 032及⎩⎨⎧-==--b a b a 032得⎩⎨⎧-=-=33b a 或⎩⎨⎧-==11b a ,所以,所求圆方程为(x +3)2+(y +3)2=9或(x -1)2+(y +1)2=1.13.提示:所求圆即为以已知直线和已知圆相交的弦为直径的圆.解⎩⎨⎧=-+=+-++,042014222y x y x y x 得⎩⎨⎧==21y x 或⎪⎪⎩⎪⎪⎨⎧==51851y x .即直线与圆的交点坐标为)518,51(),2,1(,弦长为554, 所以圆心为)514,53(,半径为552, 所求圆方程为54)514()53(22=-+-y x . 14.提示:注意到点A (2,4)在直线2x -y =0上,所以,已知直线为∠A 的平分线l ,过B作与l 垂直的直线m :x +2y =0,l 与m 的交点为(0,0),B (-4,2)关于(0,0)的对称点为B ′(4,-2),AB ′所在直线即为AC 边所在的直线,所以AC 边所在的直线方程为3x +y -10=0.15.(1)证明:设A 、B 的横坐标分别为x 1、x 2,由题设知x 1>1、x 2>1,点A (x 1,log 8x 1),B (x 2,log 8x 2). 因为A 、B 在过点O 的直线上,⋅=∴228118log log x x x x又点C 、D 的坐标分别为(x 1,log 2x 1)、(x 2,log 2x 2), 由于,log 32log log log ,log 32log log log 28828221881812x x x x x x ====所以OC 的斜率和OD 的斜率分别为:228222118112log 3log ,log 3log x x x x k x x x x k OD OC ====由此得k OC =k OD ,即点O 、C 、D 在同一条直线上. (2)解:由BC 平行于x 轴,有log 2x 1=log 8x 2,解得x 2=31x . 将其代入228118log log x x x x =,得1811831log 3log x x x x =. 由x 1>1,知log 8x 1≠0,故31x =3x 1,即31=x ,于是点A 的坐标为).3log ,3(816.分析:(1)直线l 的方程可化为x +y -4+m (2x +y -7)=0,则l 是过定点(3,1)的直线束.又(3-1)2+(1-2)2=5<25,∴点(3,1)在圆内部,因此不论m 为何实数,直线l 与圆恒相交.(2)由(1)可知,直线l 过点M (3,1),则过此点的直线l 与圆O 的半径垂直且M 为AB 中点时,l 被圆所截得的弦长|AB |最短.)542|(|22=-=OM r AB .此时212311=---=-=OMl k k , 直线方程为y -1=2(x -3),即2x -y -5=0.。
