缓冲算子、函数变换
灰色系统理论及其应用

灰色系统理论及其应用第一章灰色系统的概念与基本原理1.1灰色系统理论的产生和发展动态1982年,北荷兰出版公司出版的《系统与控制通讯》杂志刊载了我国学者邓聚龙教授的第一篇灰色系统理论论文”灰色系统的控制问题”,同年,《华中工学院学报》发表邓聚龙教授的第一篇中文论文《灰色控制系统》,这两篇论文的发表标志着灰色系统这一学科诞生。
1985灰色系统研究会成立,灰色系统相关研究发展迅速。
1989海洋出版社出版英文版《灰色系统论文集》,同年,英文版国际刊物《灰色系统》杂志正式创刊。
目前,国际、国内300多种期刊发表灰色系统论文,许多国际会议把灰色系统列为讨论专题。
国际著名检索已检索我国学者的灰色系统论著3000多次。
灰色系统理论已应用范围已拓展到工业、农业、社会、经济、能源、地质、石油等众多科学领域,成功地解决了生产、生活和科学研究中的大量实际问题,取得了显著成果。
1.2几种不确定方法的比较(系统科学---系统理论)概率统计,模糊数学和灰色系统理论是三种最常用的不确定系统研究方法。
其研究对象都具有某种不确定性,是它们共同的特点。
也正是研究对象在不确定性上的区别,才派生了这三种各具特色的不确定学科。
模糊数学着重研究“认识不确定”问题,其研究对象具有“内涵明确,外延不明确”的特点。
比如“年轻人”内涵明确,但要你划定一个确定的范围,在这个范围内是年轻人,范围外不是年轻人,则很难办到了。
概率统计研究的是“随机不确定”现象,考察具有多种可能发生的结果之“随机不确定”现象中每一种结果发生的可能性大小。
要求大样本,并服从某种典型分布。
灰色系统理论着重研究概率统计,模糊数学难以解决的“小样本,贫信息”不确定性问题,着重研究“外延明确,内涵不明确”的对象。
如到2050年,中国要将总人口控制在15亿到16亿之间,这“15亿到16亿之间“是一个灰概念,其外延很清楚,但要知道具体数值,则不清楚。
三种不确定性系统研究方法的比较分析项目灰色系统概率统计模糊数学研究对象贫信息不确定随机不确定认知不确定基础集合灰色朦胧集康托集模糊集方法依据信息覆盖映射映射途径手段灰序列算子频率统计截集数据要求任意分布典型分隶属度可布知侧重点内涵内涵外延认知表达目标现实规律历史统计规律特色小样本大样本凭经验1.3灰色系统理论的基本概念定义1.3.1信息完全明确的系统称为白色系统。
季度性用电需求预测的移动平均GM(1,1)模型

季度变动的影响。先计算 4 个季度的移动平均值,在此基
统计与决策 2021 年第 9 期·总第 573 期 169
管理决策
础上继续计算相邻 2 个移动平均值的移动平均值,得到序 列的二次移动平均趋势值,计算过程根据定义 2 中的式 (4)、式(5)两式进行,对应的移动项数分别为 4 和 2。
步骤 2:将原始数据分别除以对应的二次移动平均趋 势值,得出修匀比率,从而使数据振荡的影响因素得以消 除;进一步将各年同季度的修匀比率进行平均,分别得到 4 个季度的季度性影响因素的权值,以表明各季度的季度 变动程度。
中图分类号:C81;N941.5
文献标识码:A
文章编号:1002-6487(2021)09-0168-04
0 引言
经济和社会的发展与电力消耗密切相关,而电力能源 作为一种特殊的商品,很难被存储,是实时消耗的,需要将 所发的电量迅速地通过电网输送到用户端消耗,实现发 电、用电的动态平衡。发电的不足与过量均会造成一定 的社会问题、经济问题和环境问题。因此,准确预测用电 需求后,再进行指导发电配电,维持电力市场供需平衡, 具有重要的现实意义。常用的用电需求预测的方法包 括:指数平滑[1]、线性模型的使用[2]、回归分析[3,4]、自回归综 合移动平均(ARIMA)模型[5]、支持向量机(SVM)模型[6]和 人工神经网络模型[7],上述方法都是基于大数据集的统计 建模方法。
Forecasting of Railway Container Shipping Volume Based on Deep Learning
Yan Yubo, Ren Shuang, Jin Xubo
(School of Computer and Information Technology, Beijing Jiaotong University, Beijing 100044, China)
几何变权缓冲算子及其作用强度研究

几何变权缓冲算子及其作用强度研究“几何变权缓冲”是一种新型数字图像处理技术,它可以提取出空间特征,并且可以局部调整几何特征的空间变换方程,实现快速局部处理和滤波。
相对于传统线性缓冲算子,几何变权缓冲算子可以更好地保持空间特征的清晰度,避免平滑造成的失真,从而提升图像处理的效果。
本文旨在评估几何变权缓冲算子的作用强度。
首先,我们介绍了几何变权缓冲算子的原理。
一般来说,几何变权缓冲算子的实现方法可以分为两种:空间变换算子和时间变换算子。
空间变换算子主要是通过改变局部几何特征的空间变换方程来实现几何变权缓冲,而时间变换算子主要是通过调整图像的时间变换方程来实现几何变权缓冲。
其次,本文基于模拟数据,以不同参数对几何变权缓冲算子的作用强度进行了评估。
实验中,我们采用基于椭圆拟合的几何变权缓冲算子,参数包括平均掩膜系数、掩膜角度、掩膜半径和角度差等。
通过比较不同参数设置下的图像处理效果,我们发现平均掩膜系数对几何变权缓冲算子作用强度有显著影响,而其他参数对作用强度影响较小。
综上所述,本文以“几何变权缓冲算子及其作用强度研究”为标题,首先介绍了几何变权缓冲算子的原理;接着介绍了基于模拟数据,对几何变权缓冲算子作用强度进行了评估;最后得出结论:平均掩膜系数对几何变权缓冲算子作用强度有显著影响,而其他参数对作用强度影响较小。
本文的研究结果有助于为当前图像处理技术提供重要参考。
几何变权缓冲算子作为数字图像处理技术中较新的算法,其用于处理空间特征的能力被广泛认可。
然而,随着计算机技术的发展,它们生成的数据量不断增加,从而对算法的复杂度、精确度和作用强度提出了更高的要求。
因此,有必要系统地研究几何变权缓冲算子,充分利用其优点,保持空间特征的清晰度,提高图像处理的效果。
在未来的研究中,我们可以采用多样化的数据来评估几何变权缓冲算子作用强度,尝试采用多种参数设置,以提高图像处理的效果。
综上所述,本文从理论介绍到实验评估,详细介绍了几何变权缓冲算子的原理和作用强度,为当前图像处理技术提供了重要参考。
灰色系统理论

灰模型特性
灰色模型既不是一般的函数模型,也不是完全(纯粹) 的差分方程模型,或者完全(纯粹)的微分方程模型,而是 具有部分差分、部分微分性质的模型。
灰色模型建模条件
结构条件、材料条件、品质条件
•贺利坚 Email: sxhelijian@
谢 谢 指 正!
•贺利坚 Email: sxhelijian@
灰色关联分析
基本原理:通过对统计序列几何关系的比较来分清系统中多
因素间的关联程度,序列曲线的几何形状越接近,则它们之 间的关联度越大 。
灰色关联分析方法要求样本容量可以少到4个,对数据无规
律同样适用,不会出现量化结果与定性分析结果不符的情况。
灰色关联度的应用涉及社会科学和自然科学的各个领域,尤
科学、医药卫生、矿业工程、教育科学、水 利水电、图像信息、生命科学、控制科学、 航空航天等众多领域中得到了广泛的应用, 解决了许多过去难以解决的实际问题,展示 了极为广泛的应用前景。
•贺利坚 Email: sxhelijian@
灰色预测
灰预测是灰色系统理论中的一个重要内容, 它是指基
其在社会经济领域,如国民经济各部门投资收益、区域经济 优势分析、产业结构调整等方面,都取得较好的应用效果。
基本功能:分析因子与行为的影响,判别主要和次要因子,
识别模式,确认同构,鉴别效果,灰色关联聚类,灰色关联 决策等。
•贺利坚 Email: sxhelijian@
灰色关联分析的具体计算步骤
灰色系统理论
贺利坚
灰色系统理论及起源
1982年,中国学者邓聚龙教授创立的灰色系统理论,
是一种研究少数据、贫信息不确定性问题的新方法。
matlab函数、命令最全地自己的总结

《数字图像处理》冈萨雷斯,Matlab函数汇总 .图像显示colorbar 显示彩条getimage 由坐标轴得到图像数据ice(DIPUM)交互彩色编辑image 创建和显示图像对象imagesc 缩放数据并显示为图像immovie 由多帧图像制作电影imshow 显示图像imview 在Image Viewer中显示图像montage 将多个图像帧显示为矩阵蒙太奇movie 播放录制的电影帧rgbcube 显示一个彩色RGB立方体subimage 在单个图形中显示多幅图像truesize 调整图像的显示尺寸warp 将图像显示为纹理映射的表面图像文件输入/输出Dicominfo 从一条DICOM消息中读取元数据Dicomread 读一幅DICOM图像Dicomwrite 写一幅DICOM图像Dicom-dict.txt 包含DICOM数据字典的文本文件Dicomuid 产生DICOM唯一的识别器Imfinfo 返回关于图像的文件的信息Imread 读图像文件Imwrite 写图像文件图像算术Imabsdiff 计算两幅图像的绝对差Imadd 两幅图像相加或把常数加到图像上Imcomplement 图像求补Imdivide 两幅图像相除,或用常数除图像Imlincomb 计算图像的线性组合Immultiply 两幅图像相乘或用常数乘图像Imsubtract 两幅图像相减,或从图像中减去常数几何变换Checkerboard 创建棋盘格图像Findbounds 求几何变换的输出范围Fliptform 颠倒TFORM结构的输入/输出Imcrop 修剪图像Imresize 调整图像大小Imrotate 旋转图像Imtransform 对图像应用几何变换Intline 整数坐标线绘制算法Makersampler 创建重取样器结构Maketform 创建几何变换结构(TFORM)Pixeldup(DIPUM)在两个方向上复制图像的像素Tformarray 对N-D数组应用几何变换Tformfwd 应用正向几何变换Tforminv 应用反向几何变换Vstformfwd(DIPUM)可视化正向几何变换图像匹配Cpstruct2pairs 将CPSTRUCT转换为有效的控制点对Cp2tform 由控制点对推断几何变换Cpcorr 使用互相关校准控制点位置Cpselect 控制点选择工具Normxcorr2 归一化二维互相关像素值及统计Corr2 计算二维相关系数Covmatrix(DIPUM)计算向量族的协方差矩阵Imcontour 创建图像数据的轮廓线Imhist 显示图像数据的直方图Impixel 确定像素的彩色点Improfile 计算沿着线段的像素值横截面Mean2 计算矩阵元素的均值Pixval 显示关于像素的信息Regionprops 测量图像区域的属性Statmoments(DIPUM)计算一幅图像直方图的统计中心距Std2 计算矩阵元素的标准偏差图像分析(包括分割、描述和识别)Bayesgauss(DIPUM)高斯模式的贝叶斯分类器Bound2eight(DIPUM)将4连接边界转换为8连接边界Bound2four(DIPUM)将8连接边界转换为4连接边界Bwboundaries 追踪区域边界Bwtraceboundary 追踪单个边界Bound2im(DIPUM)将边界转换为图像Boundaries(DIPUM)追踪区域边界Bsubsamp(DIPUM)对边界二次取样Colorgrad(DIPUM)计算一幅RGB图像的向量梯度Colorseq(DIPUM)分割一幅彩色图像Connectpoly(DIPUM)连接多边形的顶点Diameter(DIPUM)测量图像区域的直径Edge(DIPUM)在一幅亮度图像中寻找边缘Fchcode(DIPUM)计算边界的freeman链码Frdescp(DIPUM)计算傅里叶描绘子Graythresh 使用Ostu方法计算图像的全局阈值Hough(DIPUM) Hough变换Houghlines(DIPUM)基于Hough变换提取线段Houghpeaks(DIPUM)在Hough变换中检测峰值Houghpixels(DIPUM)计算属于Hough变换bin的图像像素Ifrdescp(DIPUM)计算逆傅里叶描绘子Imstack2vectors(DIPUM)从图像堆栈提取向量Invmoments(DIPUM)计算图像不变距Mahalanobis(DIPUM)计算Mahalanobis距离Minperpoly(DIPUM)计算最小周长多边形Polyangles(DIPUM)计算多边形内角Princomp(DIPUM)得到主分量向量和相关量Qtdecomp 执行四叉树分解Qtgetblk 得到四叉树分解中的块值Qtsetblk 在四叉树中设置块值Randvertex(DIPUM)随机置换多边形顶点Regiongrow(DIPUM)由区域生长来执行分割Signature(DIPUM)计算边界的标记Specxture(DIPUM)计算图像的谱纹理Splitmerge(DIPUM)使用分离-合并算法分割图像Statxture(DIPUM)计算图像中纹理的统计度量Strsimilarity(DIPUM)两个串间的相似性度量X2majoraxis(DIPUM)以区域的主轴排列坐标x图像压缩Compare(DIPUM)计算和显示两个矩阵间的误差Entropy(DIPUM)计算矩阵的熵的一阶估计Huff2mat(DIPUM)解码霍夫曼编码矩阵Huffman(DIPUM)为符号源建立一个变长霍夫曼码Im2jpeg(DIPUM)使用JPEG近似压缩一幅图像Im2jpeg2k(DIPUM)使用JPEG2000近似压缩一幅图像Imratio(DIPUM)计算两幅图像或变量中的比特率Jpeg2im(DIPUM)解码IM2JPEG压缩的图像Jpeg2k2im(DIPUM)解码IM2JPEG2K压缩的图像Lpc2mat(DIPUM)解压缩一维有损预测编码矩阵Mat2huff(DIPUM)霍夫曼编码矩阵Mat2lpc(DIPUM)使用一维有损预测编码矩阵Quantize(DIPUM)量化UINT8类矩阵的元素图像增强Adapthisteq 自适应直方图量化Decorrstretch 对多通道图像应用去相关拉伸Gscale(DIPUM)按比例调整输入图像的亮度Histeq 使用直方图均衡化来增强对比度Intrans(DIPUM)执行亮度变换Imadjust 调整图像亮度值或彩色映射Stretchlim 寻找对比度拉伸图像的限制图像噪声Imnoise 给一幅图像添加噪声Imnoise2(DIPUM)使用指定的PDF生成一个随机数数组Imnoise3(DIPUM)生成周期噪声线性和非线性空间滤波Adpmedian(DIPUM)执行自适应中值滤波Convmtx2 计算二维卷积矩阵Dftcorr(DIPUM)执行频率域相关Dftfilt(DIPUM)执行频率域滤波Fspecial 创建预定义滤波器Medfilt2 执行二维中值滤波Imfilter 滤波二维和N维图像Ordfilter2 执行二维顺序统计滤波Spfilt(DIPUM)执行线性和非线性空间滤波Wiener2 执行二维去噪滤波线性二维滤波器设计Freqspace 确定二维频率响应间隔Freqz2 计算二维频率响应Fsamp2 使用频率取样设计二维FIR滤波器Ftrans2 使用频率变换设计二维FIR滤波器Fwind1 使用一维窗法设计二维滤波器Fwind2 使用二维窗法设计二维滤波器Hpfilter(DIPUM)计算频率域高通滤波器Lpfilter(DIPUM)计算频率域低通滤波器图像去模糊(复原)Deconvblind 使用盲去卷积去模糊图像Deconvlucy 使用Lucy-Richardson方法去模糊Deconvreg 使用规则化滤波器去模糊Deconvwnr 使用维纳滤波器去模糊Edgetaper 使用点扩散函数锐化边缘Otf2psf 光传递函数到点扩散函数Pst2otf 点扩散函数到光传递函数图像变换Dct2 二维离散余弦变换Dctmtx 离散余弦变换矩阵Fan2para 将扇形束投影变换为并行射束Fanbeam 计算扇形射束变换Fft2 二维快速傅里叶变换Fftn N维快速傅里叶变换Fftshift 颠倒FFT输出的象限Idct2 二维逆离散余弦变换Ifanbeam 计算扇形射束逆变换Ifft2 二维快速傅里叶逆变换Ifftn N维快速傅里叶逆变换Iradon 计算逆Radon变换Para2fan 将并行射束投影变换为扇形射束Phantom 生成头部仿真模型的图像Radon 计算Radon变换小波Wave2gray(DIPUM)显示小波分解系数Waveback(DIPUM)执行多灰度级二维快速小波逆变换Wavecopy(DIPUM)存取小波分解结构的系数Wavecut(DIPUM)在小波分解结构中置零系数Wavefast(DIPUM)执行多灰度级二维快速小波变换Wavefilter(DIPUM)构造小波分解和重构滤波器Wavepaste(DIPUM)在小波分解结构中放置系数Wavework(DIPUM)编辑小波分解结构Wavezero(DIPUM)将小波细节系数设置为零领域和块处理Bestblk 为块处理选择块大小Blkproc 为图像实现不同的块处理Col2im 将矩阵列重排为块Colfilt 按列邻域操作Im2col 将图像块重排为列Nlfilter 执行一般的滑动邻域操作形态学操作(亮度和二值图像)Conndef 默认连通性Imbothat 执行底帽滤波Imclearborder 抑制与图像边框相连的亮结构Imclose 关闭图像Imdilate 膨胀图像Imerode 腐蚀图像Imextendedmax 最大扩展变换Imextendedmin 最小扩展变换Imfill 填充图像区域和孔洞Imhmax H最大变换Imhmin H最小变换Imimposemin 强制最小Imopen 打开图像Imreconstruct 形态学重构Imregionalmax 局部最大区域Imregionalmin 局部最小区域Imtophat 执行顶帽滤波Watershed 分水岭变换形态学操作(二值图像)Applylut 使用查表法执行邻域操作Bwarea 计算二值图像中的对象面积Bwareaopen 打开二值区域(删除小对象)Bwdist 计算二值图像的距离变换Bweuler 计算二值图像的欧拉数Bwhitmiss 二值击不中操作Bwlabel 在二维图像中标记连接分量Bwlabeln 在N维二值图像中标记连接分量Bwmorph 对二值图像执行形态学操作Bwpack 打包二值图像Bwperim 确定二值图像中的对象的周长Bwselect 选择二值图像中的对象Bwulterode 最终腐蚀Bwunpack 解包二值图像Endpoints(DIPUM)计算二值图像的端点Makelut 构建applylut使用的查找表结构元素(STREL)的创建和操作Getheight 得到strel的高度Getneighbors 得到strel邻域的偏移位置和高度Getnhood 得到strel邻域Getsequence 得到分解的strel序列Isflat 对平坦的strel返回值Reflect 以其中心反射strelStrel 创建形态学结构元素Translate 变换strel基于区域的处理Histroi(DIPUM)计算图像中的ROI的直方图Poly2mask 将ROI多边形转换为掩膜Roicolor 基于颜色选择ROIRoifill 在任意区域内平稳地内插Roifilt2 对ROI进行滤波Roipoly 选择多边形ROI彩色映射处理Brighten 加亮或加暗彩色映射Cmpermute 在彩色映射中重排颜色Cmunique 寻找唯一的彩色映射颜色和相应的图像Colormap 设置或得到彩色查找表Imapprox 以很少的颜色近似被索引的图像Rgbplot 绘制RGB彩色映射分量彩色空间转换Applyform 应用独立于设备的彩色空间变换Hsv2rgb 将HSV值转换为RGB彩色空间Iccread 读ICC彩色配置文件Lab2double 将L*a*b*彩色值转换为double类Lab2uint16 将L*a*b*彩色值转换为uint16类Lab2uint8 将L*a*b*彩色值转换为uint8类Makecform 创建独立于设备的彩色空间变换结构Ntsc2rgb 将NTSC值转换为RGB彩色空间Rgb2hsv 将RGB值转换为HSV彩色空间Rgb2ntsc 将RGB值转换为NTSC彩色空间Rgb2ycbcr 将RGB值转换为YCBCR彩色空间Ycbcr2rgb 将YCBCR值转换为RGB彩色空间Rgb2hsi(DIPUM)将RGB值转换为HSI彩色空间Hsi2rgb(DIPUM)将HSI值转换为RGB彩色空间Whitepoint 返回标准照明的XYZ值Xyz2double 将XYZ彩色值转换为double类Xyz2uint16 将XYZ彩色值转换为uint16类数组操作Circshift 循环地移位数组Dftuv(DIPUM)计算网格数组Padarray 填充数组Paddedsize(DIPUM)计算用于FFT的最小填充尺寸图像类型和类型转换Changeclass 改变一幅图像的类Dither 使用抖动转换图像Gray2ind 将亮度图像转换为索引图像Grayslice 通过阈值处理从亮度图像创建索引图像Im2bw 通过阈值处理将图像转换为二值图像Im2double 将图像数组转换为双精度Im2java 将图像转换为Java图像Im2java2d 将图像转换为Java缓存的图像对象Im2uint8 将图像数组转换为8比特无符号整数Im2uint16 将图像数组转换为16比特无符号整数Ind2gray 将索引图像转换为亮度图像Ind2rgb 将索引图像转换为RGB图像Label2rgb 将标记矩阵转换为RGB图像Mat2gray 将矩阵转换为亮度图像Rgb2gray 将RGB图像或彩色映射转换为灰度图像Rgb2ind 将RGB图像转换为索引图像其他函数Conwaylaws(DIPUM)对单个像素应用Conway的遗传定律Manualhist(DIPUM)交互地生成2模式直方图Twomodegauss(DIPUM)生成一个2模式高斯函数Uintlut 基于查找表计算新数组值工具箱参数Iptgetpref 获得图像处理工具箱参数的值Iptsetpref 设置图像处理工具箱参数的值matlab 标注连通域clear;clc;f=imread('c:\1.jpg');gray_level=graythresh(f);f=im2bw(f,gray_level);[l,n]=bwlabel(f,8)imshow(f)hold onfor k=1:n[r,c]=find(l==k);rbar=mean(r);cbar=mean(c);plot(cbar,rbar,'Marker','o','MarkerEdgeColor','k','MarkerFaceColor','k','MarkerSize',1 0);plot(cbar,rbar,'Marker','*','MarkerEdgecolor','w');end主要概念:1. 4连接 8连接0 1 01 p 1 ===> 4连接,p为当前像素点。
第四讲之变换域运算讲解

频域技术与空域技术
在频域中分析图像的频率成分与图像的视觉效果间 的对应关系比较直观。 空域滤波在具体实现上和硬件设计上有一定优点。
频域技术与空域技术
二者比较:
当滤波器尺寸相同时,借且快速傅里叶变换的频域滤波效 率更高。但空域常可使用较小的滤波器来达到相似的滤波 效果。
频域中分析图像频率成分与视觉效果直观对应。但空域滤 波在具体实现和设计上稍有优势。
二 同态滤波
原理:利用取对数的方法把影响图像 的两个卷积分量分开;然后使用滤波器 同时对它们进行滤波,并施加不同的影 响;最后再经指数运算还原出处理效果。
影响图像的两个分量经过FFT变换后 一个处在低频段,一个处在高频段。
二 同态滤波
同态滤波是一种在频域中同时将图像亮度范 围进行压缩和将图像对比度增强的方法。
频域技术与空域技术
空间滤波器的工作原理可借助频域进行分析
空间平滑滤波器 消除或减弱图象中灰度值具有较大较快变化部分的 影响,这些部分对应频域中的高频分量,所以可用 频域低通滤波来实现
空间锐化滤波器 消除或减弱图象中灰度值缓慢变化的部分,这些部 分对应频域中的低频分量,所以可用频域高通滤波 来实现
采用图像同态滤波方法,如果使用合适 的滤波特性函数,可以达到既压缩灰度 动态范围,又能让感兴趣的物体部分灰 度级扩展,从而使图像清晰。
二 同态滤波
同态滤波效果好坏取决于同态滤波传递函 数的选择
入射光分量一般反映灰度恒定分量,类似 于低频信息,减弱入射光可缩小图像的灰度范 围;
反射光与物体的边界特性密切相关,类似 于高频信息,增强反射光可提高对比度。
许多空域增强技术可借助频域概念来分析和帮助设计, 一方面,许多空域增强技术可转化到频域实现,另一 方面,许多频域增强技术可转化到空域实现。 频域里低通滤波器的转移(或传递)函数应该对应空 域里平滑滤波器的模板函数的傅里叶变换。频域里高 通滤波器的转移函数应该对应空域里锐化滤波器的模 板函数的傅里叶变换。即空域和频域的滤波器组成傅 里叶变换对。给定一个域内的滤波器,通过傅里叶变 换或反变换得到在另一个域内对应的滤波器。
【国家自然科学基金】_预测决策_基金支持热词逐年推荐_【万方软件创新助手】_20140801
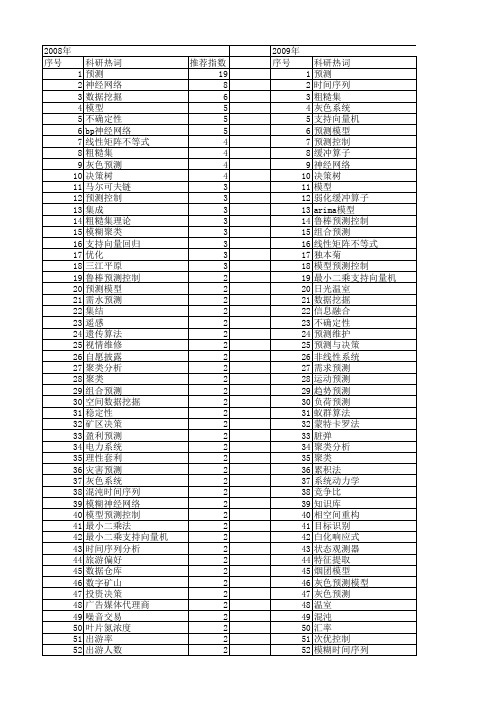
107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160
科研热词 预测 神经网络 数据挖掘 模型 不确定性 bp神经网络 线性矩阵不等式 粗糙集 灰色预测 决策树 马尔可夫链 预测控制 集成 粗糙集理论 模糊聚类 支持向量回归 优化 三江平原 鲁棒预测控制 预测模型 需水预测 集结 遥感 遗传算法 视情维修 自愿披露 聚类分析 聚类 组合预测 空间数据挖掘 稳定性 矿区决策 盈利预测 电力系统 理性套利 灾害预测 灰色系统 混沌时间序列 模糊神经网络 模型预测控制 最小二乘法 最小二乘支持向量机 时间序列分析 旅游偏好 数据仓库 数字矿山 投资决策 广告媒体代理商 噪音交管理 供应链 人工神经网络 产客量模型 交通工程 主成分分析 主成份 owa算子 h.264 黄河三角洲 鲁棒自适应控制器 鲁棒离散优化 鲁棒优化 马尔科夫链 香港 饮水安全 飞机发动机 风险评估 风险补偿模型 风险收益协调 风险值估计库存管理策略(var) 风格指数 领导行为 预测调度算法 预测误差 预测评价学 预测观测器 预测系统 预测精度 预测方法 面板数据 非集计模型 非线性预测控制 非线性赫布学习算法 非线性有限元 非线性动力学 非线性不确定系统 非参数的生产函数 需求预测模型 需求量 需求偏差 需求不确定 集散控制系统 随机需求 随机荷载 随机森林 随机分布概型 降水预报 防洪决策支持系统 问题权变模型 镇平县 销售量激励契约 链梯法 铁路客流预测
变权缓冲算子及其作用强度的研究

λ为可变权重 , 0 < λ < 1 ; k = 1 , 2 , …, n. 则当 其中 :
X 为单调增长序列 、 单调衰减序列或振荡序列时 , D2 皆为强化缓冲算子 .
证明 容易验证 , D2 满足缓冲算子三公理 , 因 而 D2 为缓冲算子 .
1) 当 X 为单调增长序列时 , 由于
x ( k) d2 = ( x ( k) ) 2 ≤ λ ) x ( k) x ( n) + ( 1 - λ
x ( 2) , …, x ( n) ) , 数据序列 X 中 x ( k) 到 x ( n) 的平均
证明 容易验证 , D1 满足缓冲算子三公理 , 因 而 D1 为缓冲算子 . 1 ) 当 X 为单调增长序列时 , 由于 ) x ( k) ≥ x ( k) d1 = λ x ( n) + ( 1 - λ λ ) x ( k) = x ( k) , x ( k) + ( 1 - λ 则有 x ( k) d1 ≥ x ( k) . 即当 X 为单调增长序列时 , D1 为弱化缓冲算子 . 2 ) 同理可证 , 当 X 为单调衰减序列时 , D1 为弱 化缓冲算子 . 3 ) 当 X 为振荡序列时 , 设 x ( l) = max{ x ( k) | k = 1 , 2 , …, n} , ( 2) x ( h) = min{ x ( k) | k = 1 , 2 , …, n} . 由于 ) x ( l) ≤ x ( l) d1 = λ x ( n) + ( 1 - λ λ ) x ( l) = x ( l) , x ( l) + ( 1 - λ 则有 x ( l) d1 ≤ x ( l) . 同理可证 x ( h) d1 ≥ x ( h) .
灰色预测与决策

灰色猜测与决策灰色系统中的猜测与决策部分主要包括序列算子生成;GM猜测模型即GM(1,1), GM(1, N)z GM(O, N),GM(2,1),Verhulst及GM(r,h)模型和离散灰色模型等;灰色系统猜测;灰色关联分析;灰色聚类评估;灰色决策模型等内容。
我们知道灰色系统理论是讨论少数据,贫信息不确定性问题的新方法,是通过对原始数据的挖掘、整理中寻求其变化规律。
而且传统的GM(1,1)模型采用的数据是近指数,低增长的数据,所以就需要我们对数据进行处理。
这里可以用缓冲算子、初值化生成算子、均值化生成算子、区间值化生成算子削减干扰或函数变换即对数变换、平移变换、开方变换、余弦函数变换、正切函数变换、负指数函数变换、累函数变换、中心位似函数变换等缩小级比偏差,使数据适于建模。
1、灰色猜测部分:1)、数据经过以上的处理后,基本适于建模,传统的猜测模型有GMQI)模型,其原始形式如下:x(°)(Q + o?)(Q = 〃,其基本形式如下:x(°)(Q + az”Q = b ,此方程是用均值Z⑴⑹代替X⑴⑹,使得数据更平滑,其中Z⑴优)=,(”(%—1)+”(%)),叫做方程的背景值,-〃是进展系数,人是灰作用量。
这里的a,b是采用最小二乘法求出来的。
白化方程为:竺+ α√D(Q = 8dt―)⑺=G ⑴⑴一4-"g)+2时间响应函数为:∖ a) ax(l)(⅛ + l) = f?0)(l)--V^ +-I a) a时间响应序列为:Λ(°)八⑴八⑴/ / h∖还原值是「(攵)=X 卜 + 1)-X 仕) =模型的求解是先用最小二乘法将a,b求出,再采用白化微分方程求出解。
而将白化方k程还原为基本模型的形式时,会消失误差,即用Z⑴(。
代替JX⑴力消失的误差,很多学者k—l 在此基础上提出了很多优化模型。
在实际应用与理论讨论过程中,人们对GMQl)模型进行了诸多改进。
新强化缓冲算子的构造及应用

统理 论 , 一种 研究 少数据 、 是 贫信 息不 确定 性 问题 的
新 方 法. 色系 统理论 以部 分信 息 已知 、 分信息 未 灰 部
知 的小样 本 、 信息 不确定 性系 统为 研究对 象 , 过 贫 通
1 缓 冲算 子 基本 概 念 及 其 公 理
定 义 1 设 系统行 为数 据序 列为 ¨
设 为系 统 行 为数 据 序 列 , D为 作
色生成 算 子或序 列算 子 的作 用生 成新 的数 据序列 .
刘 思峰等 提 出 了 冲击 扰 动 系 统 并 给 出缓 冲 算子 的概 念 , 造 了 实 用 的 缓 冲算 子 ; 耀 国等 构 党
用 于 的算子 , 经 过算 子 D作 用后 所 得 数据 序 列
滑度 . 对原 始数 据序 列 进 行 变换 的方 法 就是 通 过 灰
设 M =ma { k x ( )f k= I2 … , } ,, n , m =mi { k =1 2 … , } n ( )I ,, H ,
称 M —m 为振荡 序列 的振 幅. 定义 2
记 为 X = ( 1 d 2 d … ( ) ) D ( ) ,( ) , nd ,
灰 色 系 统 理 论 研究 的基 本 准则 . 对 现 有 强 化 缓 冲 算 子 深 入 分 析 的基 础 上 , 据 缓 冲算 子 公 理 以 及 新 信 息 优 在 根
先 利 用 原 理 , 建 了新 的强 化 缓 冲算 子 , 从 理 论 上 进 行 了 证 明 , 例 应 用 验 证 了 构 造 的 强 化 缓 冲 算 子 的 有 构 并 实
预 测效 果. 是在 对原始 数列 进行 建模 时 , 往 出现 但 往 定 量预 测和定 性 分析 不 相 符 的 情况 , 因此 在 提 高模
小波变换及分析原理知识

- 252 -小波分析原理1.1 小波变换及小波函数的多样性小波是函数空间2()L R 中满足下述条件的一个函数或者信号()x ψ:2ˆ().R C d ψψωωω+=<∞⎰式中,*{0}R R =-表示非零实数全体,ˆ()ψω是()x ψ的傅里叶变换,()x ψ成为小波母函数。
对于实数对(,)a b ,参数a 为非零实数,函数(,)()x b a b x a ψ-⎛⎫=⎪⎝⎭称为由小波母函数()x ψ生成的依赖于参数对(,)a b 的连续小波函数,简称小波。
其中:a 称为伸缩因子;b 称为平移因子。
对信号()f x 的连续小波变换则定义为,(,)()(),()f a b Rx b W a b f x dx f x x a ψψ-⎛⎫==〈〉 ⎪⎝⎭其逆变换(回复信号或重构信号)为*1()(,)fR R x b f x W a b dadb C a ψψ⨯-⎛⎫=⎪⎝⎭⎰⎰ 信号()f x 的离散小波变换定义为2(2,2)2()(2)j j j j f W k f x x k dx ψ+∞---∞=-⎰其逆变换(恢复信号或重构信号)为(2,2)()(2,2)()j j j j fk j k f t C Wk x ψ+∞+∞=-∞=-∞=∑∑其中,C 是一个与信号无关的常数。
显然小波函数具有多样性。
在MA TLAB 小波工具箱中提供了多种小波幻术,包括Harr 小波,Daubecheies (dbN )小波系,Symlets (symN )小波系,ReverseBior (rbio )小波系,Meyer (meyer )小波,Dmeyer (dmey )小波,Morlet(morl)小波,Complex Gaussian(cgau)小波系,Complex morlet(cmor)小波系,Lemarie (lem )小波系等。
实际应用中应根据支撑长度、对称性、正则性等标准选择合适的小波函数。
- 253 -1.2 小波的多尺度分解与重构1988年Mallat 在构造正交小波基时提出多尺度的概念,给出了离散正交二进小波变换的金字塔算法,其小波分析树形结构如图1所示,即任何函数2()()f x L R ∈都可以根据分辨率为2N-的()f x 的低频部分(近似部分)和分辨率为2(1)j j N -≤≤下()f x 的高频部分(细节部分)完全重构。
信号处理常用的函数

在信号处理领域,有许多常用的函数被广泛应用。
以下列举了一些常见的信号处理函数:
1. 傅里叶变换(Fourier Transform):将时域信号转换为频域表示,可以分析信号的频谱特性和频率成分。
2. 快速傅里叶变换(Fast Fourier Transform,FFT):是一种高效计算离散傅里叶变换的算法,常用于实时信号处理和频谱分析。
3. 滤波器函数:包括低通滤波器、高通滤波器、带通滤波器等,用于对信号进行去噪、频率选择或频带限制。
4. 卷积函数:用于信号的线性系统建模与分析,以及信号的卷积运算。
5. 采样函数:包括采样定理(Nyquist-Shannon采样定理)和重采样函数,用于将连续时间信号转换为离散时间信号,并进行采样率转换。
6. 自相关函数(Autocorrelation)和互相关函数
(Cross-correlation):用于分析信号的自相似性和信号之间的相似度。
7. 小波变换(Wavelet Transform):用于对非平稳信号进行局部频率分析,具有时频域分辨率可调的特点。
8. 包络检测函数:用于提取信号的包络轨迹,常用于振动信号分析和故障诊断。
9. 平滑函数:如移动平均、指数平滑等,用于对信号进行平滑处理,降低噪声或波动。
10. 调制函数:如调幅(AM)、调频(FM)、调相(PM)等,用于在调制与解调过程中改变信号的特性。
当然,这只是信号处理领域中的一小部分常用函数。
实际应用中,根据具体问题和需求,可能还会涉及其他更多的函数和算法。
数字图像处理-空间域处理-灰度变换-基本灰度变换函数(反转变换、对数变换、伽马变换和分段线性变换)
数字图像处理-空间域处理-灰度变换-基本灰度变换函数(反转变换、对数变换、伽马变换和分段线性变换)总结性的⼀篇博⽂,内容其实很简单,之所以写出来是为了对⾃⼰之前所学做⼀些总结。
参考⾃:《数字图像处理》--第三版--冈萨勒斯--中,以及师兄提供的参考资料,在此对师兄表⽰感谢。
空间域处理是直接对像素进⾏操作的⽅法,这是相对于频率域处理⽽⾔的。
空间域处理主要分为两⼤类:灰度变换和空间滤波。
灰度变换在图像单个像素上操作,主要以对⽐度和阈值处理为⽬的。
空间滤波涉及改善性能的操作,通过像元领域来处理。
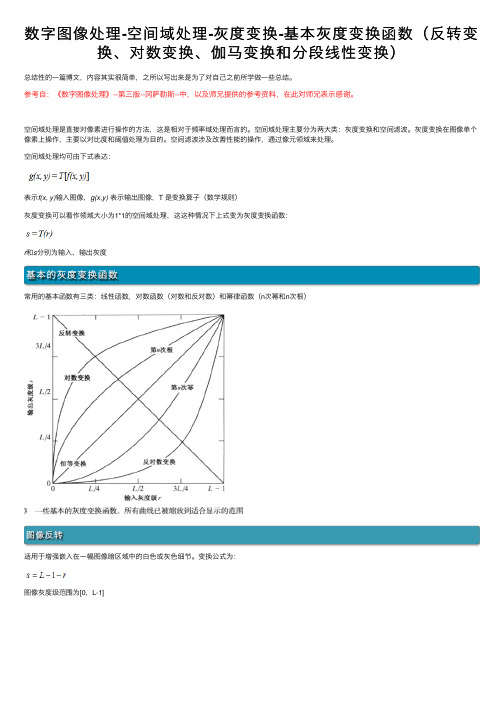
空间域处理均可由下式表达:表⽰f(x, y)输⼊图像,g(x,y)表⽰输出图像,T 是变换算⼦(数学规则)灰度变换可以看作领域⼤⼩为1*1的空间域处理,这这种情况下上式变为灰度变换函数:r和s分别为输⼊、输出灰度基本的灰度变换函数常⽤的基本函数有三类:线性函数,对数函数(对数和反对数)和幂律函数(n次幂和n次根)图像反转适⽤于增强嵌⼊在⼀幅图像暗区域中的⽩⾊或灰⾊细节。
变换公式为:图像灰度级范围为[0,L-1]"""反转变换"""import numpy as npimport cv2import matplotlib.pyplot as pltdef reverse(img):output = 255 - imgreturn outputimg1 = cv2.imread(r'F:\program_study\Python\data\breast.tif') # 前头加r是消除反斜杠转义cv2.imshow('input', img1)x = np.arange(0, 256, 0.01)y = 255 - xplt.plot(x, y, 'r', linewidth=1)plt.title('反转变换函数图')plt.xlim([0, 255]), plt.ylim([0, 255])plt.show()img_output = reverse(img1)dWindow('output', cv2.WINDOW_NORMAL) # 可改变窗⼝⼤⼩cv2.imshow('output', img_output)cv2.waitKey(0)cv2.destroyAllWindows()反转变换对数变换对数变换可以拉伸范围较窄的低灰度值,同时压缩范围较宽的⾼灰度值。
拉普拉斯变换的性质

1[esF(s)] f(t)u (t).
8
P222 例9.12
解 方法一 已知
[sint]
1 s2
, 1
方法一 先充零再平移
根据延迟性质有
[sin(t
π )] 2
1 s2
1
e
π 2
s
.
sint(π)u(tπ)
2
2
方法二 先平移再充零
1
F (s) .
0
s
19
四、积分性质
1. 积分的象函数
性质
[
t
f (t)dt ]
1
F (s);
0
s
一般地,有
20
解 已知
[sin2t]
s2
2 22
,
根据微分性质有
[tsi2nt]d dss2 222
再由积分性质得
t
[ tsin2tdt ] 0
1 s
4s (s2 4)2
线性性质 [af(t)bg(t) ]a F (s) b G (s); 1[aF(s)bG (s)] af(t) b g (t).
相似性质 延迟性质Biblioteka [ f(at)]1 a
F
s a
.
[f(t)]esF(s).
1[esF(s)] f(t)u (t).
sin t t
]
1 s 1 s2 ds
即 sitnestdsarcsc.ot
0t
在上式中,如果令 s = 0,则有
sint dsπ.
0t
2
启示 在 Laplace 变换及其性质中,如果取 s 为某些特定的值,
泛函分析第3章 连续线性算子与连续线性泛函

第3章 连续线性算子与连续线性泛函本章将介绍赋范线性空间上,特别是Banach 空间上的有界线性算子与有界线性泛函的基本理论,涉及到泛函分析的三大基本定理,即共鸣定理,逆算子定理及Hahn-Banach 定理。
他们是泛函分析早期最光辉的成果,有广泛的实际背景,尤其在各种物理系统研究中应用十分广泛。
3.1 连续线性算子与有界线性算子在线性代数中,我们曾遇到过把一个n 维向量空间n E 映射到另一个m 维向量空间m E 的运算,就是借助于m 行n 列的矩阵111212122212n n m m mn a a a a a a A a a a ⎛⎫⎪ ⎪= ⎪⎪⎝⎭对n E 中的向量起作用来达到的。
同样,在数学分析中,我们也遇到过一个函数变成另一个函数或者一个数的运算,即微分和积分的运算等。
把上述的所有运算抽象化后,我们就得到一般赋范线性空间中的算子概念。
撇开各类算子的具体属性,我们可以将它们分成两类:一类是线性算子;一类是非线性算子。
本章介绍有界线性算子的基本知识,非线性算子的有关知识留在第5章介绍。
[定义3.1] 由赋范线性空间X 中的某子集D 到赋范线性空间Y 中的映射T 称为算子,D 称为算子T 的定义域,记为()D T ,为称像集(){},y y Tx x D T =∈为算子的值域,记作()T D 或TD 。
若算子T 满足: (1)()()(),T x y Tx Ty x y D T +=+∀∈ (2)()()(),T x TxF x D T ααα=∀∈∈称T 为线性算子。
对线性算子,我们自然要求()T D 是X 的子空间。
特别地,如果T 是由X 到实数(复数)域F 的映射时,那么称算子T 为泛函。
例 3.1 设X 是赋范线性空间,α是一给定的数,映射:T x x α→是X 上的线性算子,称为相似算子;当1α=时,称T 为单位算子或者恒等算子,记作I 。
例3.2 [],x C a b ∀∈,定义()()ta Tx t x d ττ=⎰由积分的线性知,T 是[],C a b 到[],C a b 空间中的线性算子。
缓冲算子、函数变换

一增一减 i 1 i 1 也是统一形式 i 1 《The Jornal of Grey System》07年1、3期,08年1、4期。
|
1 1 x(k ) y (k ) 1 1 y (k ) / | | / / | k 1 k 1 k 1 k 1 k 1 k 1 k 1 k 1 x(i) x(i) y (i) y (i ) /
序列算子的作用可以进行多次,若D1,D2,D3 皆为序列算子,我们称D1D2为二阶算子,并称 XD1D2=(x(1)d1d2, x(2)d1d2 , …,x(n)d1d2) 为二阶算子作用序列.
定义3.2.4 称上述三个公理为缓冲算子三公理(three axioms of buffer operators),满足缓冲算子三公理 的序列算子,称为缓冲算子,一阶、二阶、 … … 缓冲算子作用后的序列称为一阶、二阶、 … … 缓冲序列(buffer sequences)。 定义3.2.5 设X为原始数据序列,D为缓冲算子,当X 分别为增长序列,衰减序列或振荡序列时: 1 若缓冲序列XD比原始序列X的增长速度(或衰减 速度)减缓或振幅减小,我们称缓冲算子D为弱化 算子;(是各瞬时速度还是仅平均速度?有歧义!) 2 若缓冲序列XD比原始序列X的增长速度(或衰减 速度)加快或振幅增大,则称缓冲算子D为强化算 子.
j 1 n
[ x(k ) x(i)] [ x( j ) x(i)]
i j ik n
n
yj
满足yk x(k )d
即缓冲算子除x(n)d=x(n)以外其余可以随 心所欲规定!仍然满足公理2)、3)
3.3.2 实用缓冲算子的构造举例
定理3.3.2 设原始数据序列X=(x(1),x(2), …,x(n)),令 XD=(x(1)d,x(2)d, …,x(n)d) 其中 1
算子和变换

算子和变换1. 算子的概念在计算机科学中,算子是指对数据进行处理和操作的一种函数或操作符。
它是一种数学上的抽象概念,用于描述对数据进行转换、过滤、合并等操作的方法。
算子可以应用于各种数据类型,包括数字、字符串、集合等。
算子通常用于函数式编程和数据流处理领域,它们可以作为函数的参数或返回值,以实现更加灵活和可组合的代码逻辑。
通过使用算子,我们可以将复杂的问题拆分为简单的操作,并通过组合这些操作来解决问题。
2. 常见的算子类型2.1 转换算子转换算子是指将一个数据流转换为另一个数据流的操作。
常见的转换算子包括映射(map)、过滤(filter)、扁平化(flatMap)等。
•映射算子(map):将输入流中的每个元素通过指定的函数进行映射,并返回一个新的流。
•过滤算子(filter):根据指定条件过滤输入流中的元素,并返回满足条件的元素组成的新流。
•扁平化算子(flatMap):将输入流中每个元素通过指定函数映射为一个或多个元素,并将所有元素组成的新流作为输出。
2.2 聚合算子聚合算子是指将多个元素合并为一个元素的操作。
常见的聚合算子包括求和(sum)、求平均值(average)、最大值(max)、最小值(min)等。
•求和算子(sum):将输入流中的所有元素进行求和,并返回结果。
•求平均值算子(average):将输入流中的所有元素进行求和,并计算平均值。
•最大值算子(max):返回输入流中的最大值。
•最小值算子(min):返回输入流中的最小值。
2.3 合并算子合并算子是指将多个数据流合并为一个数据流的操作。
常见的合并算子包括连接(concat)、合并(merge)、压缩(zip)等。
•连接算子(concat):将多个输入流按顺序连接起来,形成一个新的输出流。
•合并算子(merge):将多个输入流按顺序交错地合并起来,形成一个新的输出流。
•压缩算子(zip):将多个输入流中对应位置上的元素组合成一个元组,形成一个新的输出流。
硕士毕业论文

硕士毕业论文篇一:硕士毕业论文范本分类号: N941.5密级:学校代码: 10638 学号: 308070104013 硕士学位论文GM(1,1)模型的优化与一类强化缓冲算子的构造姓名******* 指导教师 *******教授培养单位数学与信息学院学科专业应用数学研究方向不确定信息系统的预测与决策申请学位类别理学硕士论文提交日期二○一一年四月论文答辩日期二○一一年六月西华师范大学学位评定委员会四川·南充二○一一年六月Optimization of GM (1, 1) and a Kind ofPractical Strengthening Buffer OperatorA DissertationSubmitted to the Graduate FacultyIn Partial Fulfillment of the RequirementFor the Degree of Master of Natural ScienceBySUN Yan-naSupervised byProfessor WEI YongMajor inApplied MathematicsInDepartment of Mathematics and InformationChina West Normal UniversityNanchong, Sichuan Province, ChinaJun, 20xx目录摘要................................................................... .. (II)ABSTRACT............................................................. . (IV)第1章前言................................................................... (1)1.1 本课题的目的、意义................................................................... .. (1)1.2 论文的主要内容................................................................... . (2)第2章灰建模及缓冲算子的基础理论 (3)2.1 灰建模的基本原理................................................................... (3)2.2 缓冲算子的基本理论................................................................... .. (4)第3章灰色GM(1,1)模型及缓冲算子的研究 (6)3.1 GM(1,1)模型的研究现状................................................................... (6)3.2 缓冲算子的研究现状................................................................... .. (8)第4章GM(1,1)模型建模方法的改进 (9)4.1 优化灰导数的等间距GM(1,1).............................................................. . (9)4.2 优化灰导数的非等间距GM(1,1).............................................................. . (13)第5章一类新的缓冲算子的构造及缓冲算子新定理 (19)5.1 一类新的实用强化缓冲算子的构造 (19)5.2 缓冲算子新定理................................................................... .. (22)第6章结论与展望 .................................................................. . (25)6.1 全文总结................................................................... .. (25)6.2 研究展望................................................................... .. (26)参考文献................................................................... ................................................... 27 致谢................................................................... ....................................................... ⅰ 关于学位论文使用授权的声明................................................................... ............... ⅱ 关于学位论文原创性的声明................................................................... ................... ⅲ 在学期间的科研情况................................................................... . (ⅳ)摘要GM(1,1)模型是灰色系统预测理论的基础与核心[1],它已被广泛应用于农业、工业、气象、电力、经济、社会等领域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一次累加(同理二次累加,...)
定义3.1.2 (传统定义)若序列X满足
1 2 3
(k 1) 1(即 ( k ) ) (k )
(k ) [0, ]
<0.5
则称X为准光滑序列(quasi-smooth sequence).
比较原则: 光滑序列小好,级比接近1好, 级比偏差接近0好
j 1 n
[ x(k ) x(i)] [ x( j ) x(i)]
i j ik n
n
yj
Байду номын сангаас
满足yk x(k )d
即缓冲算子除x(n)d=x(n)以外其余可以随 心所欲规定!仍然满足公理2)、3)
3.3.2 实用缓冲算子的构造举例
定理3.3.2 设原始数据序列X=(x(1),x(2), …,x(n)),令 XD=(x(1)d,x(2)d, …,x(n)d) 其中 1
x(k )d
2k 1
(分母刚好是分子系数和)
x(n)d=x(n) 则当X为单调增长序列或单调衰减序列时,D皆为强 化算子(strengthening operator).(缺点: x(n)d=x(n)不自然) 推论3.2.2 设D为定理3.2.3中定义的强化算子,令 XD2=(x(1)d2,x(2)d2, …,x(n)d2) 其中 x(n)d2=x(n)d=x(n)
公理3.2.3(解析化、规范化公理, Axiom of Analytic Representations) 任意的x(k)d,皆 可由一个统一的x(1), x(2), …,x(n)的初等 解析式表达。
定义3.2.3 设X为系统行为数据序列,D为作 用于X的算子,X经过算子D作用后所得序列记为 XD=(x(1)d,x(2)d, …,x(n)d) 称D为序列算子,称XD为一阶算子作用序列.
3.2.3 缓冲算子的性质(续)
对任意yk 存在缓冲算子:
( x(k ) x(2))( x(k ) x(3)) ( x(k ) x(n)) x(k )d y1 ( x(1) x(2))( x(1) x (3)) ( x(1) x(n)) ( x(k ) x(1))( x(k ) x(3)) ( x(k ) x(n)) y2 ( x(2) x(1))( x(2) x(3)) ( x(2) x( n)) ( x(k ) x(1))( x(k ) x(2)) ( x(k ) x( n 1)) + yn ( x(n) x(1))( x(n) x(2)) ( x(n) x(n 1)) =
1 x(k )d [ x(k )d x(k 1)d x(n)d ] n k 1
2
则D2对于单调增长、单调衰减或振荡序列,皆为二阶弱化 算子。
定理3.2.3 设原始序列和其缓冲序列分别为 X=(x(1),x(2), …,x(n)) XD=(x(1)d,x(2)d, …,x(n)d) 其中 x(1) x(2) x (k 1) kx (k )
3.2.3 缓冲算子的性质 定理3.2.1 设X为单调增长序列,XD为其缓冲序列, 则有 1 D为弱化算子x(k)≤x(k)d k=1,2,…n(缩小差别) 2 D为强化算子x(k) ≥x(k)d k=1,2,…n(扩大差别) 直观意义:最左、最高点没有变,其他点被抬高
问题: 抬得太高,改变了增减趋势,预测无效 弥补办法:王正新论文《系统工程理论与实践》
k 1
x(i )
i 1
k 1
y (i )
i 1
k 1
x(i )
i 1
k 1
k 1
y (i )
i 1
k 1
k 1
单减之间
y (k )
y (i )
i 1
k 1
x(k )
x(i )
i 1
k 1
1 k 1
y (k ) 1 x(k ) 1 即 k 1 / k 1 / 1 k 1 k 1 y (i) x(i)
i 1
x(k )
定理3.1.1 X为齐次指数序列的充分必要 条件是,对于k=1,2, …,n,恒有(k)=const成立. 定义3.1.2 设序列X=(x(1), x(2), …,x(n)),若 ] • k , (k ) (0,1 则称序列 X具有负(降)的灰指数规律 ] • k , (k ) (1, b 则称序列 X具有正(升)的灰指数规律 • k , (k ) (a, b],b a 则称序列 X具有绝对灰度 •为的灰指数规律(级比的绝对宽度) • <0.5时,称X具有准指数规律(the law of quasiexponent)
排除方法:用缓冲算子处理数据后建模
3.2.2 缓冲算子公理(the axioms of buffer operator)
公理3.2.1(不动点公理, Axiom of Fixed Points) 设X为系统行为数据序列,D为序列算子, 则D满足 x(n)d=x(n)(因新信息优先原理)
公理3.2.2(信息充分利用公理, Axiom on Sufficient Usage of Information)系统行为数 据序列X中的每一个数据 x(k),k=1,2, …,n,都应充分参与算子作用 .
自由摆动时振幅的大小决定了振动的剧烈程度, 但外力强制振动则不然,往返的频率则是一个重要指标。 用总变差或对应时刻的瞬时变差来刻划
( 0) ( 0) ( 0) ( 0) 定义3.2.2 设 X ( x (1), x (2), , x (n)) 为系统真实行为序列,而观测到的系统行为数据 序列为 X ( x(1), x(2), , x(n)) ( x(0) (1) 1, x(0) (2) 2 , , x(0) (n) n )
定理3.2.2 设X为单调衰减序列,XD为其缓冲序列, 则有 1 D为弱化算子x(k) ≥x(k)d (缩小差别) 2 D为强化算子x(k) ≤ x(k)d (扩大差别)
3.2.3 缓冲算子的性质 定理3.2.3 设X为振荡序列,XD为其缓冲序 列,则有 1 D为弱化算子(大变小, 小变大) max{x(k)}≥max{x(k)d} min {x(k)}≤min{x(k)d} (缩小差别) 2 D为强化算子(大变大,小变小) max{x(k)} ≤ max{x(k)d} min {x(k)} ≥ min{x(k)d} (扩大差别) 问题:以整体振幅变小为标志,可能出现局 部变化幅度增大的情形,注意《实变函数论》全 变差思想,并应用此思维方法改造缓冲算子定义
序列算子的作用可以进行多次,若D1,D2,D3 皆为序列算子,我们称D1D2为二阶算子,并称 XD1D2=(x(1)d1d2, x(2)d1d2 , …,x(n)d1d2) 为二阶算子作用序列.
定义3.2.4 称上述三个公理为缓冲算子三公理(three axioms of buffer operators),满足缓冲算子三公理 的序列算子,称为缓冲算子,一阶、二阶、 … … 缓冲算子作用后的序列称为一阶、二阶、 … … 缓冲序列(buffer sequences)。 定义3.2.5 设X为原始数据序列,D为缓冲算子,当X 分别为增长序列,衰减序列或振荡序列时: 1 若缓冲序列XD比原始序列X的增长速度(或衰减 速度)减缓或振幅减小,我们称缓冲算子D为弱化 算子;(是各瞬时速度还是仅平均速度?有歧义!) 2 若缓冲序列XD比原始序列X的增长速度(或衰减 速度)加快或振幅增大,则称缓冲算子D为强化算 子.
X (0)
这里 (1 , 2 ,..., n )
其中为冲击扰动项,则称X为冲击扰动序列. 要从冲击扰动序列X出发实现对真实行为序列 X(0)的系统之变化规律的正确把握和认识,必须 首先跨越障碍 .如果不事先排除干扰,而用失真 的数据X 直接建模、预测,则会因模型所描述 的并非由X(0) 所反映的系统真实变化规律而导 致预测的失败。
西华师范大学 灰色系统研究所
3.1 级比与光滑比(Stepwise and Smooth Ratios)
在建模过程中往往先通过看级比、级必偏差、 光滑比来判断能否建模,若不能再选择恰当算子或 变换处理后再看能否建模
定义3.1.1 设序列X=(x(1), x(2), …,x(n)),我们分别称 x(k ) x(k ) (k ) , ( k ) | 1 | x( k 1) x( k 1)
定义3.1.1 设序列X=(x(1), x(2), …,x(n)),我们称
(k )
x(k )
k 1 i 1
x(i)
(k ) (即 (1) ) x (k 1)
x
(0)
为序列的光滑比 (smooth ratio).
x (k 1) x (0) (i )称为
(1) i 1 k 1
新定义: 相对低增长序列的光滑性(系统工程理论与实践09年8期) (魏勇) 相对于齐次指数序列的光滑性(Kybernite09年8期) 相对于非齐次指数序列的光滑性(美国会议09年10月)
y 就相对于低增长序列的光滑性而言比较原则 :X比Y好分三种情况 1 x(k ) y (k ) x(k ) 1 y(k ) 1 单增之间 ,即 1 / /
i 1 i 1
一增一减 i 1 i 1 也是统一形式 i 1 《The Jornal of Grey System》07年1、3期,08年1、4期。
|
1 1 x(k ) y (k ) 1 1 y (k ) / | | / / | k 1 k 1 k 1 k 1 k 1 k 1 k 1 k 1 x(i) x(i) y (i) y (i ) /
(k ) |
x( k 1) x(k ) | x( k ) x( k 1)
