三线摆和扭摆
课题_三线摆和扭摆实验报告

实验报告专业班级计算机1042姓名学号长春工程学院电气与信息学院图3-2-1三线摆实验装置示意图图3-2-2 三线摆原理图实验题目 转动惯量的测定实验室实验时间2015 年 11 月 28 日转动惯量是刚体转动时惯性的量度,是表征转动物体惯性大小的物理量,其量值取决于物体的形状、质量分布及转轴的位置。
刚体的转动惯量有着重要的物理意义,是研究、设计、控制转动物体运动规律的重要工程技术参数。
在科学实验、工程技术、航天、电力、机械、仪表等工业领域也是一个重要参量。
如钟表摆轮、精密电表动圈的体形设计、枪炮的弹丸、电机的转子、机器零件、导弹和卫星的发射等,都不能忽视转动惯量的大小。
因此测定物体的转动惯量具有重要的实际意义。
刚体的转动惯量与刚体的质量分布、形状和转轴的位置都有关系。
对于形状较简单的刚体,可以通过计算求出它绕定轴的转动惯量,但形状较复杂的刚体计算起来非常困难,通常采用实验方法来测定。
转动惯量的测量,一般都是使刚体以一定的形式运动。
通过表征这种运动特征的物理量与转动惯量之间的关系,进行转换测量。
测量刚体转动惯量的方法有多种,三线摆法是具有较好物理思想的实验方法,它具有设备简单、直观、测试方便等优点。
一、实验目的:1、验证转动惯量平行轴定理。
2、了解转动惯量的平行轴定理,理解“对称法”验证平行轴定理的实验思想,学会验证平行轴定理的实验方法。
3、掌握定标测量思想方法。
4、掌握不确定度的估算方法。
5、学会正确测量长度、质量和时间。
6、 学习用三线摆测量圆盘和圆环绕对称轴的转动惯量。
二、实验要求:1、学会用累积放大法测量周期运动的周期。
2、验证转动惯量的平行轴定理。
三、实验原理:图3-2-1是三线摆实验装置示意图。
三线摆是由上、下两个匀质圆盘,用三条等长的摆线(摆线为不易拉伸的细线)连接而成。
上、下圆盘的系线点构成等边三角形,下盘处于悬挂状态,并可绕OO ‘轴线作扭转摆动,称为摆盘。
由于三线摆的摆动周期与摆盘的转动惯量有一定关系,所以把待测样品放在摆盘上后,三线摆系统的摆动周期就要相应的随之改变。
三线摆与扭摆实验报告

三线摆与扭摆实验报告三线摆与扭摆实验报告摆是物理学中常见的实验装置,通过对摆的研究可以深入了解力学和动力学的基本原理。
本次实验主要研究了三线摆和扭摆的运动规律及其相互关系。
一、实验目的本次实验的目的是通过观察和测量三线摆和扭摆的运动过程,探究摆的周期与摆长、重力加速度以及摆角等因素之间的关系。
二、实验装置与方法1. 实验装置本次实验使用的实验装置包括三线摆和扭摆,三线摆由一根细绳和一个小球组成,扭摆由一根细绳和一个重物组成。
2. 实验方法首先,我们将三线摆和扭摆分别固定在实验台上,保证它们能够自由摆动。
然后,通过改变摆长和摆角等参数,记录下摆的运动过程,并测量摆的周期。
三、实验结果与分析1. 三线摆的运动规律我们首先研究了三线摆的运动规律。
在实验过程中,我们固定了摆长,并改变了摆角。
通过观察和测量,我们发现三线摆的周期与摆角的正弦函数成正比,即周期T与摆角θ之间存在着如下关系:T = 2π√(L/g)。
2. 扭摆的运动规律接下来,我们研究了扭摆的运动规律。
在实验过程中,我们固定了摆角,并改变了摆长。
通过观察和测量,我们发现扭摆的周期与摆长的平方根成正比,即周期T与摆长L之间存在着如下关系:T = 2π√(I/k)。
3. 三线摆与扭摆的关系通过对三线摆和扭摆的运动规律的研究,我们发现它们之间存在着一定的关系。
具体来说,当摆长相等时,三线摆的周期比扭摆的周期要小。
这是因为三线摆的摆线长度比扭摆的摆线长度要长,所以摆线上的重力分量较大,从而加速了摆的运动。
四、实验结论通过本次实验,我们得出了以下结论:1. 三线摆的周期与摆角的正弦函数成正比,即周期T与摆角θ之间存在着如下关系:T = 2π√(L/g)。
2. 扭摆的周期与摆长的平方根成正比,即周期T与摆长L之间存在着如下关系:T = 2π√(I/k)。
3. 当摆长相等时,三线摆的周期比扭摆的周期要小。
五、实验总结通过本次实验,我们深入了解了摆的运动规律以及三线摆和扭摆之间的关系。
三线摆和扭摆 实验报告

三线摆和扭摆实验报告三线摆和扭摆实验报告摆是物理学中经常用来研究力学和振动的实验装置。
本次实验主要研究了三线摆和扭摆的运动特性和影响因素。
通过观察和分析实验数据,我们可以深入了解摆的运动规律和振动特性。
一、实验目的本次实验的主要目的是研究三线摆和扭摆的运动规律,探究摆的周期与摆长、质量、重力加速度等因素之间的关系,并通过实验验证理论模型的正确性。
二、实验装置和方法1. 三线摆实验装置:实验装置由一个固定在支架上的金属球和三根不同长度的线组成。
通过改变线的长度,可以调节摆的摆长。
实验过程中,我们固定一个线的长度,然后改变其他两根线的长度,观察摆的运动情况。
2. 扭摆实验装置:实验装置由一个金属球和一根可扭转的金属棒组成。
通过扭转金属棒,可以给金属球施加扭矩,使其发生摆动。
实验过程中,我们改变扭矩的大小和方向,观察摆的运动情况。
三、实验结果与分析1. 三线摆实验结果:我们固定了一根线的长度,然后改变其他两根线的长度,观察摆的运动情况。
实验结果表明,摆的周期与摆长成正比,即摆长越长,摆的周期越长。
这符合理论模型中的预测结果。
此外,我们还发现,摆的周期与重力加速度无关,而与摆的质量有关。
质量越大,周期越长。
2. 扭摆实验结果:我们改变了扭矩的大小和方向,观察摆的运动情况。
实验结果表明,扭摆的周期与扭矩成正比,即扭矩越大,周期越长。
这也符合理论模型中的预测结果。
此外,我们还发现,扭摆的周期与摆的质量无关,而与扭矩的方向有关。
扭矩方向相同时,周期较长;扭矩方向相反时,周期较短。
四、实验误差与改进在实验过程中,我们注意到了一些误差,并提出了一些改进的方法。
首先,在三线摆实验中,由于线的粗细和摆球的形状可能会对实验结果产生影响,我们可以使用更精确的测量工具来减小误差。
其次,在扭摆实验中,由于扭矩的施加方式可能不够均匀,我们可以改进扭矩装置,使其施加的扭矩更加均匀,减小误差。
五、实验结论通过本次实验,我们得出了以下结论:1. 三线摆的周期与摆长成正比,与质量和重力加速度无关。
三线摆和扭摆(DH4605AP)实验讲义

三线摆和扭摆(DH4605AP)实验讲义本次实验主要研究三线摆和扭摆的运动学和运动学模型,了解其动力学特性和建立数学模型。
实验设备使用的是DH4605AP型号的三线摆和扭摆模型。
一、实验原理和介绍1.1 三线摆三线摆是一种具有三个拖线的物理模型,其运动方程比较复杂,但是很适合研究复杂物体运动的模拟,常被用来研究非线性动力学中的混沌现象。
三线摆由一个高挂的圆盘和三条细绳组成,每条细绳的下端各系着质点,质点间相互接触或相互靠近会对系统的运动产生影响。
通过对三线摆的运动学和动力学研究,可以揭示非线性系统的混沌现象和稳定性特征。
扭摆也称扭力摆,是由一个重锤和一根刚性杆组成的物理模型,通过扭力和压力的作用使其产生回归运动,是一种常见的物理现象。
扭摆的运动学可以用简单的三角函数表示,其运动周期与长度、重力常数和摆角都有关系。
扭摆广泛应用于天文学、物理学和化学等领域,是研究旋转运动和动态稳定性的重要模型。
二、实验步骤2.1 设置实验装置将DH4605AP三线摆和扭摆装置放置在实验桌面上,并连接电源,打开电源开关。
2.2 安装实验工具安装实验所需的各种钳子、支架和传感器,保证三线摆和扭摆的稳定性,并确保传感器能够准确感知到振动。
2.3 实验数据采集开启数据采集软件,按照提示进行设备校准和数据采集操作,确保所采集到的数据准确无误。
2.4 实验参数调整根据实验要求,调整实验装置的参数,如三线摆的绳长、扭摆的长度、质量等,确保实验数据能够反映出不同情况下系统的运动学和动力学特性。
2.5 实验结果分析根据采集到的实验数据,进行分析和处理,建立系统的运动学和动力学模型,并对其进行分析和讨论,深入了解三线摆和扭摆的运动学和动力学特性。
三、实验注意事项1. 安全第一,实验过程中应注意电源和装置的安全,避免发生意外。
2. 实验操作过程应严格按照实验流程和步骤进行,不得随意更改。
3. 实验设备要保持干燥、清洁,定期检查维护。
4. 实验时间应控制在规定范围内,避免出现实验耗时过长的问题。
三线摆与扭摆实验报告

再求不确定度,先求 T2 的不确定度
∆T2B
=
10 × 10−3 35
= 2.857 × 10−4s
∆T2A
=
t√p(v) n
ST2
=
2√.57 6
×
1.191 × 10−3
=
1.250
× 10−3s
√
∆T2 = ∆2T2A + ∆2T2B = 1.282 × 10−3s
再求 J2 的不确定度
∆J2
=
(74.96
+ 110.78) × 10−3 × 9.80 × 34.22 × 4π2 × 39.410 × 10−2
10−3
× 14.66
×
10−3
×
0.95262
= 5.326 × 10−5kg/m2
再求不确定度,先求 T1 的不确定度
∆T1B
=
10 × 10−3 35
= 2.857 × 10−4s
T1 = 0.9526 s。
2.3.3 加三个小球
n0 = 35,H2 = 39.408 cm,m2 = 32.74 g。每个小球到三线摆中心轴的距离 R1 = 21.85 mm。
2
次数
1
2
3
4
5
6
n0T2/s 45.717 45.840 45.764 45.804 45.795 45.797
表 7: 加上三个小球的三线摆的周期
√(
=
∆m0 +3m2
)2 + ( ∆R )2 + ( ∆r )2 + ( 2∆T2 )2 + ( ∆H2 )2
J2
m0 + 3m2
三线摆和扭摆(预习报告)

三线摆和扭摆(预习报告)实验目的(1) 加深对转动惯量概念和平行轴定理的理解。
(2) 了解用三线摆和扭摆测转动惯量的原理和方法。
学习用电子天平、游标高度尺和多功能数字测量仪等仪器的使用, 掌握质量和周期等量的测量方法。
实验原理三线摆:三线摆的主要部分是两个水平同轴的圆盘(圆盘间距为H), 三根对称分布的等长线相连。
上盘(半径为r )在一固定的横梁上, 可以固定不动。
下盘(质量为m0半径为r )可以绕中心轴做周期为(T0)扭摆运动。
可计算出下盘绕中心轴转动惯量J0为:若将质量为m 的待测刚体放在下圆盘上, 并使它的质心位于中心轴上。
测出此时的摆动周期T 和上下圆盘间的垂直距离H1, 则待测刚体和下圆盘对中心轴的总转动惯量J1为:则待测刚体对中心轴的总转动惯量J=J 0- J 1利用三线摆可以验证平行轴定理。
平行轴定理指出: 如果一刚体(质量为m)对通过质心的某一轴的转动惯量为Jc, 则这刚体对平行于该轴、且相距为d 另一转轴的转动惯量Jx 为:J x =J c +md 2实验时将三个同样大小的钢球放置在均匀分布于半径为R 1圆周上的三个孔上进行测量。
扭摆:将一金属丝上端固定, 下端悬挂一刚体就构成扭摆。
本实验所用悬挂物为三爪盘。
在三抓盘上施加一外力矩, 使之扭转一角度θ。
由于悬线上端是固定的。
悬线因扭转而产生弹性恢复力矩M 。
外力撤去后, 在M 的作用下三爪盘做反复扭动, 其绕中心轴转动惯量为J0。
若再加上一转动惯量J1已知的刚体, 测出其周期T 经计算得到:12220J T T T J -=20141)(128T T d LJ G -=π式中G 为悬线的切变模量, L 为悬线长度, d 为悬线直径。
本实验附加物为一组直径不同的金属圆环, 转动惯量J1由右式计算: m1为圆环质量, D1和D2分别为圆环的内直径和外直径。
实验步骤1) 用三线摆测定下圆盘对中心轴OO ′转动惯量和大钢球对其质心轴的转动惯量。
清华大学物理实验A1三线摆和扭摆实验报告

清华大学物理实验A1三线摆和扭摆实验报告清华大学三线摆和扭摆试验物理实验完整报告班级姓名学号结稿日期:三线摆和扭摆实验一、实验目的1. 加深对转动惯量概念和平行轴定理等的理解;2. 了解用三线摆和扭摆测量转动惯量的原理和方法;3. 学习电子天平、游标高度尺和多功能数字测量仪等仪器的使用,掌握测量质量和周期等量的测量方法。
二、实验装置和原理1.三线摆:如图一,上、下圆盘均处于水平,悬挂在横梁上。
横梁由立柱和底座支承着,三根对称分布的等长悬线将两个圆盘相连。
上圆盘可以固定不动。
拧动旋钮就可以使得下圆盘绕中心轴OO ’作扭摆运动。
当下圆盘的摆角很小且忽略空气阻力和悬线扭力影响时,可推出下圆盘绕中心轴OO ’的转动惯量为:200024m gRr J T Hπ=其中,0m 是下圆盘质量,g 取29.80m s -g ,r 为上圆盘半径,R 为下圆盘半径,H 为平衡时上下圆盘的垂直距离,0T 为下圆盘摆动周期。
图1 三线摆示意图将质量为m 的待测刚体放在下圆盘上,并使它的质心位于中心轴OO ’上,测出此时的摆动周期T 和上下圆盘之间的垂直距离1H ,则待测刚体和下圆盘对于中心轴OO ’的总转动惯量1J 为:()021214m m gRr J T H π+= 且待测刚体对于中心轴OO ’的转动惯量1J JJ =-。
利用三线摆可以验证平行轴定理。
平行轴定理指出:如果一个刚体对于通过质心的某一转轴的转动惯量为cJ ,则这个刚体对平行于该轴且相距为d 的另一转轴的转动惯量为:2xcJ J md =+式中,m 为刚体的质量。
图2 三个孔均匀分布在本实验中,将三个等大的钢球对称分布在下圆盘的三个均匀分布的孔(如图2)上,测出三个球对于中心轴OO ’的转动惯量xJ 。
如果测得的xJ 的值与由2xc JJ md =+右式计算得到的结果比较相对误差在测量允许的范围内()005≤,则平行轴定理得到验证。
本实验中,用于测量基本物理量的仪器还有:电子天平,游标高度尺,配有光电接收装置的多功能数字测量仪。
三线摆和扭摆

• 水准泡(仪器调平)
三、实验任务及注意事项
三线摆—— • 测空摆J0;
加重物后需重测 摆高H; 为避免钢球不圆 需多测几次直径。
• 测大纲球的J并与理论值比较; • 用3个一致小球离轴摆放验证平行轴定理。
周期测量 合理选择摆动次数 n0,以减少分到每 个周期的仪器误差 6次测量以消除 随机误差
• ������ =
二、实验仪器
• 三线摆和扭摆主体仪器,了解各部件及旋钮功能
• 被测元件(小球、圆环) • 多功能计数器(测T),Δ仪=10ms • 天平(测m), Δ仪=0.05g • 50分度游标高度尺(测H、L), Δ仪=0.02mm
• 50分度游标尺(测直径), Δ仪=0.02mm
• 千分尺(用24组测悬丝直径), Δ仪=0.004mm
小角度摆动,且 水平面内无晃动!
三、实验任务及注意事项
扭摆—— • 按序测20T0、 20T1 、根据小环J1求K(得
G),再测大环的J并与理论值比较。
弯曲!
• 测钢丝直径用样品,防止把自己的扭摆丝农
小角度摆动,且水平 面内无晃动!
四、实验要求
无特殊说明的量或实验室给出的量为单
次测量,其不确定度取B类不确定度(即 只考虑Δ仪),特殊注意H的不确定度;
球体������ = 圆柱体������ 同心环������
+ ������������ ������
平行轴定理������������ = ������ + ������������������
一、实验原理——三线摆测J
横梁
• ������ =
������������������������ ������ ������ ������ ������������ ������
三线摆和扭摆实验报告

三线摆和扭摆实验报告三线摆和扭摆实验报告引言:三线摆和扭摆是物理学中经典的实验,通过对它们的研究可以深入理解振动和波动的基本原理。
本实验旨在通过观察和测量三线摆和扭摆的运动来探究它们的特性和规律。
实验一:三线摆三线摆是由一个重物通过三根不同长度的线组成,悬挂在固定支点上的一种装置。
在这个实验中,我们将研究三线摆的周期与摆长之间的关系。
实验装置:1. 三线摆装置2. 计时器3. 钢球实验步骤:1. 将三线摆装置固定在支架上,并调整线的长度为不同值。
2. 将钢球拉至一侧,释放并开始计时。
3. 记录钢球来回摆动的时间,并计算出周期。
4. 重复以上步骤,每次改变线的长度。
实验结果:通过多次实验得到的数据,我们可以绘制出三线摆周期与摆长之间的关系曲线。
实验结果表明,三线摆的周期与摆长的平方根成正比。
这一结果与理论预期相符,验证了摆动周期与摆长之间的关系。
实验二:扭摆扭摆是由一个悬挂在支点上的细线和一个重物组成的装置。
在这个实验中,我们将研究扭摆的周期与振幅之间的关系。
实验装置:1. 扭摆装置2. 计时器3. 钢球实验步骤:1. 将扭摆装置固定在支架上,并调整细线的长度。
2. 将钢球拉至一侧,释放并开始计时。
3. 记录钢球来回摆动的时间,并计算出周期。
4. 重复以上步骤,每次改变振幅。
实验结果:通过多次实验得到的数据,我们可以绘制出扭摆周期与振幅之间的关系曲线。
实验结果表明,扭摆的周期与振幅成正比。
这一结果与理论预期相符,验证了振动周期与振幅之间的关系。
实验讨论:通过对三线摆和扭摆的实验研究,我们发现它们的振动特性与摆长、振幅之间存在一定的关系。
这些关系可以通过数学模型进行描述和预测,为进一步研究振动和波动提供了理论基础。
结论:三线摆和扭摆实验结果验证了振动周期与摆长、振幅之间的关系。
这一研究对于理解振动和波动的基本原理具有重要意义,也为其他领域的应用提供了基础。
通过进一步深入研究,我们可以探索更多有关振动和波动的规律和特性。
大学物理实验三线摆和扭摆实验报告

另一方面 J
2 5
m1
(
d1) 2
2
2 111.75103 kg (3.018102 m)2
5
2
1.018105 kg m2
相对误差为 1.347 1.018 32.3% 偏大。实验中对周期的测量有问题。尽管去除了一 1.018
个数据,还是有很大误差。可能是三线摆振幅没有设好,光电门没有摆好所致。
r
T
100 T
-1-
三线摆和扭摆 2004 年 10 月 22 日 星期三
袁强 2003011737 工物 33 班
又 T t仪 t 1000ms 计算得 n≈100 故取 n 为 100。 T nt
-2-
三线摆和扭摆 2004 年 10 月 22 日 星期三
袁强 2003011737 工物 33 班
三线摆和扭摆
实验数据处理表格
测转动惯量 π =3.14 g=9.80m/s2 m0 =76.69g n=n1=100 m1=111.75g
H 上 /mm H 下 /mm H1 上 /mm H1 下 /mm
n 的取值计算:
由 J0
m0 gRr 4 2H
T2 0
得
J 0 J0
4 ( T )2 ( m0 )2 ( R )2 ( r )2 ( H )2
T
m0
R
r
H
由 m0 0.02g R r 0.02mm H 2 0.02mm 有 上 式 后 四 项 中 最 大 的 为
( r )2 1.769 106 要求 4 ( T )2 误差不得超过此值的 1 , T 0.0003
测 t1 时,带星号的数据明显偏离其它值,舍弃不用。
T0=t/n /s T1=t1/n1 /s H= H 上-H 下 /mm H1= H 上 1-H 下1 /mm
三线摆与扭摆实验报告(共10篇)

三线摆与扭摆实验报告(共10篇)三线摆实验报告课题用三线摆测物理的转动惯量教学目的1、了解三线摆原理,并会用它测定圆盘、圆环绕对称轴的转动惯量;2、学会秒表、游标卡尺等测量工具的正确使用方法,掌握测周期的方法;3、加深对转动惯量概念的理解。
重难点1、理解三线摆测转动惯量的原理;2、掌握正确测三线摆振动周期的方法。
教学方法讲授、讨论、实验演示相结合学时3个学时一、前言转动惯量是刚体转动惯性的量度,它的大小与物体的质量及其分布和转轴的位置有关对质量分布均匀、形状规则的物体,通过简单的外形尺寸和质量的测量,就可以测出其绕定轴的转动惯量。
但对质量分布不均匀、外形不规则的物体,通常要用实验的方法来测定其转动惯量。
三线扭摆法是测量转动惯量的优点是:仪器简单,操作方便、精度较高。
二、实验仪器三线摆仪,游标卡尺,钢直尺,秒表,水准仪三、实验原理1、原理简述:将三线摆绕其中心的竖直轴扭转一个小小的角度,在悬线张力的作用下,圆盘在一确定的平衡位置左右往复扭动,圆盘的振动周期与其转动惯量有关。
悬挂物体的转动惯量不同,测出的转动周期就不同。
测出与圆盘的振动周期及其它有关量,就能通过转动惯量的计算公式算出物体的转动惯量。
2、转动惯量实验公式推导如图,将盘转动一个小角,其位置升高为h,增加的势能为mgh;当盘反向转回平衡位置时,势能E?0,此时,角速度?最大,圆盘具有转动动能:E?J0?02/2则根据机械能守恒有:mgh?J0?02/2 (1)上式中的m0为圆盘的质量,?0为盘过平衡位置时的瞬时角速度,J0为盘绕中心轴的转动惯量。
当圆盘扭转的角位移?很小时,视圆盘运动为简谐振动,角位移与时间t的关系为:0sin(2?t/T0??)(2)经过平衡位置时最大角速度为将?0代入(1)式整理后得式中的h是下盘角位移最大时重心上升的高度。
由图可见,下盘在最大角位移?0时,上盘B点的投影点由C点变为D点,即h?CD?BCBC2AB2BD2A'B2A'B2(R2r考虑到AB?A'所以因为?0很小,用近似公式sin?0??0,有将h代入式,即得到圆盘绕OO'轴转动的实验公式设待测圆环对OO'轴的转动惯量为J。
三线摆和扭摆

转动惯量和切变模量的测量DH4601A 三线摆和扭摆实验仪实验讲义杭州大华科教仪器研究所杭州大华仪器制造有限公司转动惯量和切变模量的测量转动惯量是刚体转动惯性的量度,它与刚体的质量分布和转轴的位置有关。
对于形状简单的均匀刚体,测出其外形尺寸和质量,就可以计算其转动惯量。
对于形状复杂、质量分布不均匀的刚体,通常利用转动实验来测定其转动惯量。
三线摆法和扭转摆法是其中的两种办法。
为了便于与理论计算值比较,实验中的被测刚体均采用形状规则的刚体。
[实验目的]1. 加深对转动惯量概念和平行轴定理等的理解;2. 了解用三线摆和扭摆测转动惯量的原理和方法;3. 掌握周期等量的测量方法[实验装置和原理简介]一、三线摆图1是三线摆示意图。
上、下圆盘均处于水平,悬挂在横梁上。
横梁由立柱和底座(图中未画出)支承着。
三根对称分布的等长悬线将两圆盘相连。
拨动转动杆就可以使上圆盘小幅度转动,从而带动下圆盘绕中心轴OO '作扭摆运动。
当下圆盘的摆角θ很小,并且忽略空气摩擦阻力和悬线扭力的影响时,根据能量守恒定律或者刚体转动定律都可以推出下圆盘绕中心轴OO '的转动惯量0J 为(1) 式中,m 0为下圆盘的质量;r 和R 分别为上下悬点离各自圆盘中心的距离;H 0为平衡时上下圆盘间的垂直距离;T 0为下圆盘的摆动周期,g 为重力加速度。
北京地区的重力加速度为9.80ms -2。
将质量为m 的待测刚体放在下圆盘上,并使它的质心位于中心轴OO '上。
测出此时的摆动周期T 和上下圆盘间的垂直距离H ,则待测刚体和下圆盘对中心轴的总转动惯量J 1为图1 三线摆示意图 200200T H 4gRr m J π=2201T H4gRr )m m (J π+=(2) 待测刚体对中心轴的转动惯量J 与J 0和J 1的关系为 J= J 1-J 0 (3)利用三线摆可以验证平行轴定理。
平行轴定理指出:如果一刚体对通过质心的某一转轴的转动惯量为J c ,则这刚体对平行于该轴、且相距为d 的另一转轴的转动惯量J x 为J x =J c +md 2 (4)式中,m 为刚体的质量。
三线摆和扭摆20141013

一、实验原理
• 定义 :������ =
∆������������ ������������ ������ ������������ ������������
• 质量连续: ������ =
• 质量分布均匀的规则物
体J可以由公式求出。
������ ������������������ ������������ ������ = ������������������ ������ ������ = ������ ������������ ������ ������
旋钮 锁紧钮 r 上圆盘
• 条件:三线等长且很长,
上下摆盘水平,摆角很 小 • 空摆盘J0可测,加重物后 总J可测,则被测物转动 惯量为:J-J0
摆高H
悬线
下圆盘
R
O 挡光纸片
一、实验原理——扭摆法测J
• ������ =
• K未知、 J0未知、T0可测时需
������ ������ ������ ������������������
小角度摆动,且 水平面内无晃动!
三、实验任务及注意事项
扭摆—— • 按序测20T0、 20T1 、根据小环J1求K(得
G),再测大环的J并与理论值比较。
弯曲!
• 测钢丝直径用样品,防止把自己的扭摆丝农
小角度摆动,且水平 面内无晃动!
四、实验要求
无特殊说明的量或实验室给出的量为单
次测量,其不确定度取B类不确定度(即 只考虑Δ仪),特殊注意H的不确定度;
球体������ = 圆柱体������ 同心环������
+ ����������� ������
平行轴定理������������ = ������ + ������������������
三线摆和扭摆

转动惯量和切变模量的测量DH4601A 三线摆和扭摆实验仪实验讲义杭州大华科教仪器研究所杭州大华仪器制造有限公司转动惯量和切变模量的测量转动惯量是刚体转动惯性的量度,它与刚体的质量分布和转轴的位置有关。
对于形状简单的均匀刚体,测出其外形尺寸和质量,就可以计算其转动惯量。
对于形状复杂、质量分布不均匀的刚体,通常利用转动实验来测定其转动惯量。
三线摆法和扭转摆法是其中的两种办法。
为了便于与理论计算值比较,实验中的被测刚体均采用形状规则的刚体。
[实验目的]1. 加深对转动惯量概念和平行轴定理等的理解; 2. 了解用三线摆和扭摆测转动惯量的原理和方法; 3. 掌握周期等量的测量方法 [实验装置和原理简介] 一、三线摆图1是三线摆示意图。
上、下圆盘 均处于水平,悬挂在横梁上。
横梁由立 柱和底座(图中未画出)支承着。
三根 对称分布的等长悬线将两圆盘相连。
拨 动转动杆就可以使上圆盘小幅度转动, 从而带动下圆盘绕中心轴OO '作扭摆 运动。
当下圆盘的摆角θ很小,并且忽 略空气摩擦阻力和悬线扭力的影响时, 根据能量守恒定律或者刚体转动定律都 可以推出下圆盘绕中心轴OO '的转动惯量0J 为(1) 式中,m 0为下圆盘的质量;r 和R 分别为上下悬点离各自圆盘中心的距离;H 0为平衡时上下圆盘间的垂直距离;T 0为下圆盘的摆动周期,g 为重力加速度。
北京地区的重力加速度为9.80ms -2。
将质量为m 的待测刚体放在下圆盘上,并使它的质心位于中心轴OO '上。
测出此时的摆动周期T 和上下圆盘间的垂直距离H ,则待测刚体和下圆盘对中心轴的总转动惯量J 1为图1 三线摆示意图 200200T H 4gRr m J π=2201T H4gRr )m m (J π+=(2)待测刚体对中心轴的转动惯量J 与J 0和J 1的关系为J= J 1-J 0 (3)利用三线摆可以验证平行轴定理。
平行轴定理指出:如果一刚体对通过质心的某一转轴的转动惯量为J c ,则这刚体对平行于该轴、且相距为d 的另一转轴的转动惯量J x 为J x =J c +md 2 (4) 式中,m 为刚体的质量。
用三线摆 (2)
三线摆、扭摆、双线摆实验论文单摆扭摆双线摆姓名:杨联君学院:轻纺与食品学院学号:104309302用三线摆、扭摆、双线摆进行物体转动惯量、切变模量测定以及平行轴定理的验证摘要:对与形状规则,质量分布均匀的物体,利用三线摆、扭摆、双显摆法是对其进行转动惯量测定的基本方法。
关键词:三线摆 扭摆 双线摆 转动惯量转动惯量是刚体转动惯性的量度,它与刚体的质量分布和转轴的位置有关。
对于形状简单的均匀刚体,测出其外形尺寸和质量,就可以计算其转动惯量。
同时可验证平行轴定理及测定切变模量。
三线摆法和扭转摆法是其中的两种办法。
为了便于与理论计算值比较,本实验中的被测刚体均采用形状规则的刚体。
1. 三线摆1.1 实验装置及原理简介图1是三线摆示意图。
拨动转动杆就可以使上圆盘小幅度转动, 从而带动下圆盘绕中心轴OO '作扭摆运动。
当下圆盘的摆角θ很小,并忽略空气阻力和悬线扭力的影响时, 根据能量守恒定律或者刚体转动定律都可以推出下圆盘绕中心轴OO '的转动惯量0J 为(1)式中,m 0为下圆盘的质量;r 和R 分别为上下悬点离各自圆盘中心的距离;H 0为平衡时上下圆盘间的垂直距离;T 0为下圆盘的摆动周期,g 为重力加速度。
北京地区的重力加速度为9.80ms -2。
将质量为m 的待测刚体放在下圆盘上,并使它的质心位于中心轴OO '上。
测出此时的摆动周期T 和上下圆盘间的垂直距离H ,则待测刚体和下圆盘对中 心轴的总转动惯量J 1为2201T H4gRr )m m (J π+= (2) 待测刚体对中心轴的转动惯量J 与J 0和J 1的关系为J= J 1-J 0 (3)利用三线摆可以验证平行轴定理。
平行轴定理指出:如果一刚体对通过质心的某一转轴的转动惯量为J c ,则这刚体对平行于该轴、且相距为d 的另一转轴的转动惯量J x 为J x =J c +md 2 (4) 式中,m 为刚体的质量。
202004T H gRr m J π=实验时,将二个同样大小的圆柱体放置在对称分布于半径为R 1的圆周上的二个孔上,如图2所 示。
转动惯量的测量方法

转动惯量的测量方法一、转动惯量测量的重要性。
1.1转动惯量是描述刚体转动惯性大小的物理量。
这就好比在生活中,胖的人转身可能比瘦的人要费劲些,物体的转动惯量就类似这个道理。
它在很多实际工程和物理研究里都是个关键因素。
要是不了解转动惯量,就像盲人摸象,只能看到一部分情况。
比如说机械工程里设计旋转部件,不知道转动惯量,那这个部件可能就转得磕磕绊绊,甚至根本转不起来。
1.2在物理研究方面,转动惯量与角动量等概念息息相关。
这就像齿轮与链条,一环扣一环。
研究天体的自转,转动惯量也起着不可或缺的作用。
要是不重视转动惯量的测量,那很多物理现象就解释不通,就像丈二和尚摸不着头脑。
二、常见的测量方法。
2.1三线摆法。
这方法有点像玩跷跷板的感觉。
三线摆是由上、下两个圆盘,用三条等长的摆线连接而成。
把待测物体放在下圆盘上,让它摆动起来。
通过测量摆动的周期等数据,再利用相关公式就能算出转动惯量。
这个方法操作起来相对简单,就像搭积木一样,按照步骤来就好。
但是它也有局限性,精度可能不是特别高,就像一个业余画家的作品,能看但不够精细。
2.2扭摆法。
扭摆就像一个倔强的小弹簧,扭一下就会来回摆动。
把待测物体固定在扭摆上,给它一个初始扭转角,然后它就会做周期性的扭转振动。
根据振动的周期等参数,就能算出转动惯量。
这种方法精度比三线摆法可能高一点,就像一个熟练工做出来的东西,质量有一定保障。
不过呢,它对实验装置的要求相对高一些,就像娇贵的花朵需要精心照料。
2.3复摆法。
复摆就像一个大摆锤,在一个固定点附近摆动。
通过测量复摆的摆动周期和摆动中心等数据,利用相应公式算出转动惯量。
这个方法原理比较直观,就像一加一等于二那么容易理解。
但是它的计算过程可能会稍微复杂一点,就像走迷宫,虽然路是通的,但得费点心思。
三、测量中的注意事项。
3.1仪器的精度很关键。
这就像厨师做菜的刀具,刀具不好,切出来的菜就不整齐,测量仪器精度不够,那测出来的转动惯量肯定也不准确。
三线摆和扭摆
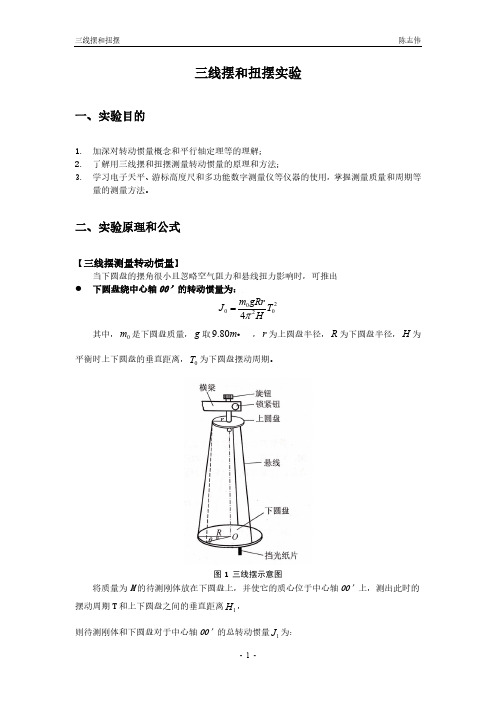
T0 = 1.457109375s
②加大球 n0 = 32 , H1 = 523.32mm − 85.78mm = 437.54mm , M1 = 110.69g
次数
n0T1 / s
1 32.840
2 32.829
3 32.828
4 32.562
5 33.045
6 33.045
平均 32.85816667
钢丝直径为 d = d − d0 = 0.508833333mm - (-0.005333333mm) = 0.514166666mm
-6-
三线摆和扭摆
陈志伟
②钢丝长度
钢丝上端高度: L1 = 519.02mm ;钢丝下端高度: L2 = 195.50mm ;钢丝长度为: L = L1 − L2 = 519.02mm −195.50mm = 323.52mm
J1
G
=
32L d4
4 2 T 2 − T02
J1
三、实验任务
三线摆实验
1. 调三线摆底座水平、高度尺调下圆盘水平 2. 测量三线摆基本参数和钢球参数 3. 粗测摆动周期,确定实际测量次数 4. 开始计时。先测空摆时的周期,后测加载球后的盘间距高度和周期 5. 加载 3 个球,测量各球参数,通过实验验证平行轴定理
陈志伟
T0
=
t仪 n
10 10−3 s =
32
= 3.12510−4 s
下圆盘对于中心轴 OO’的转动惯量
J0
=
m0 gRr 4 2H
T02
=
75.10 10-3
9.80 34.19 10-3 14.62 10-3 4 2 436.52 10-3
(1.457109375)2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
转动惯量和切变模量的测量DH4601A 三线摆和扭摆实验仪
实
验
讲
义
杭州大华科教仪器研究所杭州大华仪器制造有限公司
转动惯量和切变模量的测量
转动惯量是刚体转动惯性的量度,它与刚体的质量分布和转轴的位置有关。
对于形状简单的均匀刚体,测出其外形尺寸和质量,就可以计算其转动惯量。
对于形状复杂、质量分布不均匀的刚体,通常利用转动实验来测定其转动惯量。
三线摆法和扭转摆法是其中的两种办法。
为了便于与理论计算值比较,实验中的被测刚体均采用形状规则的刚体。
[实验目的]
1. 加深对转动惯量概念和平行轴定理等的理解; 2. 了解用三线摆和扭摆测转动惯量的原理和方法; 3. 掌握周期等量的测量方法 [实验装置和原理简介] 一、三线摆
图1是三线摆示意图。
上、下圆盘 均处于水平,悬挂在横梁上。
横梁由立 柱和底座(图中未画出)支承着。
三根 对称分布的等长悬线将两圆盘相连。
拨 动转动杆就可以使上圆盘小幅度转动, 从而带动下圆盘绕中心轴OO '作扭摆 运动。
当下圆盘的摆角θ很小,并且忽 略空气摩擦阻力和悬线扭力的影响时, 根据能量守恒定律或者刚体转动定律都 可以推出下圆盘绕中心轴OO '的转动
惯量0J 为
(1) 式中,m 0为下圆盘的质量;r 和R 分别为上下悬点离各自圆盘中心的距离;H 0为平衡时上下圆盘间的垂直距离;T 0为下圆盘的摆动周期,g 为重力加速度。
北京地区的重力加速度为9.80ms -2。
将质量为m 的待测刚体放在下圆盘上,并使它的质心位于中心轴OO '上。
测出此时的摆动周期T 和上下圆盘间的垂直距离H ,则待测刚体和下圆盘对中心轴的总转动惯量J 1为
图1 三线摆示意图 2
00
200T H 4gRr m J π=
2
201T H
4gRr )m m (J π+=
(2)
待测刚体对中心轴的转动惯量J 与J 0和J 1的关系为
J= J 1-J 0 (3)
利用三线摆可以验证平行轴定理。
平行轴定理指出:如果一刚体对通过质心的某一转轴的转动惯量为J c ,则这刚体对平行于该轴、且相距为d 的另一转轴的转动惯量J x 为
J x =J c +md 2 (4) 式中,m 为刚体的质量。
实验时,将二个同样大小的圆柱体放置在对称 分布于半径为R 1的圆周上的二个孔上,如图2所 示。
测出二个圆柱体对中心轴OO '的转动惯量J x 。
如果测得的J x 值与由(4)式右边计算得的结果比 较时的相对误差在测量误差允许的范围内(≤5%), 则平行轴定理得到验证。
二、扭摆
将一金属丝上端固定,下端悬挂一刚体就构成扭摆。
图3表示扭摆的悬挂物为圆盘。
在圆盘上施加一外力矩,使之扭转一角度θ。
由于悬线上端是固定的,悬线因扭转而产生弹性恢复力矩。
外力矩撤去后,在弹性恢复力矩M 作用下圆盘作往复扭动。
忽略空气阻尼力矩的作用,根据刚体转动定理有
(5) 式中,0J 为刚体对悬线轴的转动惯量,θ
为角加速度。
弹性恢复力矩M 转角θ的关系为
θ-=K M (6)
式中,K 称为扭转模量。
它与悬线长度L ,悬线直径d 及悬线材料的切变模量G 有如下关系
(7) 扭摆的运动微分方程为
(8) 可见,圆盘作简谐振动。
其周期0T 为
(9) 若悬线的扭摆模量K 已知,则测出圆盘的摆动周期T 0后,由(9)式就可
图1 二孔对称分布
θ
= 0
J M L
32G d K 4
π=
θ-=θ
J K K
J 2T 00π=
计算
出圆盘的转动惯量。
若K 未知,可利用一个对其质心轴的转动惯量J 1已知的物体将它附加到圆盘上,并使其质心位于扭摆悬线上,组成复合体。
此复合体对以悬线为轴的转动惯量为J 0+J 1复合体的摆动周期T 为
(10) 由(9)式和(10)式可得
(11)
(12) 测出0T 和T 后就可以计算圆盘的转动惯量0J 和悬线的切变模型G 。
图 3 扭摆 圆环对悬线轴的转动惯量J 1有以下计算
(13) 式中,m 1为圆环的质量;D 1和D 2分别为圆环的内直径和外直径。
[实验任务]
1、用三线摆测定下圆盘对中心轴OO '的转动惯量和圆柱体对其质心轴的
转动惯量。
要求测得的圆柱体的转动惯量值与理论计算值(21mr 2
1
J = ,r 1为圆
柱体半径)之间的相对误差不大于5%。
2、用三线摆验证平行轴定理。
3、用扭摆测定圆盘的转动惯量和切变模量。
[实验仪器]
三线摆及扭摆实验仪、水准仪、米尺、游标卡尺、物理天平及待测物体等。
()
22
2
111D D 8
m J +=K
J J 2T 1
0+π=12022
00J T T T J -=1
20
22
J T T 4K -π=
[仪器使用]
1、打开电源,程序预置周期为T=30(数显),即:挡光杆来回经过光电门的次数为T=2n+1次。
2、据具体要求,若要设置10次,先按“置数”开锁,再按下调(或上调)改变周期T ,再按“置数”锁定,此时,即可按执行键开始计时,信号灯不停闪烁,即为计时状态,这时显示的是计数的次数;当物体经过光电门的周期次数达到设定值,数显将显示具体时间,单位“秒”。
须再执行“10”周期时,无须重设置,只要按“返回”即可回到上次刚执行的周期数“10”,再按“执行”键,便可以第二次计时。
(当断电再开机时,程序从头预置30次周期,须重复上述步骤) [实验注意事项]
1、测量前,根据水准泡的指示,先调整三线摆底座台面的水平,再调整三线摆下圆盘的水平。
测量时,摆角θ尽可能小些,以满足小角度近似。
防止三线摆和扭摆在摆动时发生晃动,以免影响测量结果。
2、测量周期时应合理选取摆动次数。
对三线摆,测得R 、r 、m 0和H 0后,由(1)式推出J 0的相对误差公式,使误差公式中的2∆T 0/ T 0项对∆J 0/J 0的影响比其它误差项的影响小作为依据来确定摆动次数。
估算时,∆m 0取0.02g ,时间测量误差∆t 取0.03s ,∆R 、∆r 和∆H 0可根据实际情况确定。
对于扭摆,先由(13)式估算J 1的相对误差,然后由(11)式推出J 0的相对误差公式。
根据使T 0或(T )的相对误差项对∆J 0/J 0的贡献比J 1的相对误差贡献小的原则,确定摆动次数。
估算时,∆m 1取0.02g ,∆D 1和∆D 2均取0.04mm ,J 0取400g ·cm 2,∆t 取0.03s ,T 0和T 1可先大概测出。
[思考题]
1、三线摆在摆动过程中要受到空气的阻尼,振幅会越来越小,它的周期是否会随时间而变?
2、在三线摆下圆盘上加上待测物体后的摆动周期是否一定比不加时的周期大?试根据(1)式和(2)式分析说明之。
3、如果三线摆的三根悬线与悬点不在上、下圆盘的边缘上,而是在各圆盘内的某一同心圆周上,则(1)式和(2)式中的r 和R 各应为何值?
4、证明三线摆的机械能为2
020H
gRr m 21J 21θ+θ,并求出运动微分方程,从
而导出(1)式。
.。
