反比例函数重难点
反比例函数教案设计(篇)

反比例函数教案设计(优秀篇)一、教学目标:知识与技能:1. 理解反比例函数的定义及其性质;2. 学会如何求反比例函数的解析式;3. 能够运用反比例函数解决实际问题。
过程与方法:1. 通过观察实例,引导学生发现反比例函数的规律;2. 利用图形计算器,让学生直观地感受反比例函数的图像和性质;3. 培养学生运用数学知识解决实际问题的能力。
情感态度与价值观:1. 培养学生对数学的兴趣和好奇心;2. 培养学生勇于探索、积极思考的科学精神;3. 培养学生合作交流、解决问题的能力。
二、教学重点与难点:重点:1. 反比例函数的定义及其性质;2. 反比例函数的图像特征。
难点:1. 反比例函数解析式的求解;2. 反比例函数在实际问题中的应用。
三、教学过程:环节一:导入新课1. 利用实例引入反比例函数的概念;2. 引导学生发现反比例函数的规律;3. 提问:什么是反比例函数?它有哪些特点?环节二:自主探究1. 学生利用图形计算器,观察反比例函数的图像;2. 学生总结反比例函数的性质;3. 学生分组讨论,探讨反比例函数的解析式求解方法。
环节三:课堂讲解1. 教师讲解反比例函数的定义及其性质;2. 教师示范求解反比例函数解析式;3. 教师举例说明反比例函数在实际问题中的应用。
环节四:巩固练习1. 学生完成课后练习题;2. 学生互相讨论,解决练习题中的问题;3. 教师点评并讲解练习题。
环节五:课堂小结1. 学生总结本节课所学内容;2. 教师强调反比例函数的重要性和应用价值;3. 学生分享学习心得和感悟。
四、教学评价:1. 课后练习题的完成情况;2. 学生对反比例函数的理解程度;3. 学生在实际问题中运用反比例函数的能力。
五、教学资源:1. 反比例函数的PPT;2. 图形计算器;3. 课后练习题及答案。
六、教学策略:1. 采用问题驱动的教学方法,引导学生主动探索反比例函数的定义和性质;2. 利用信息技术工具,如图形计算器,直观展示反比例函数的图像,增强学生对函数概念的理解;3. 通过实际问题的引入,让学生体会反比例函数在生活中的应用,提高学生解决实际问题的能力;4. 注重学生合作交流,鼓励学生分组讨论,培养学生的团队协作精神;5. 及时反馈,针对学生的掌握情况,调整教学进度和方法。
反比例函数基础重难点复习

反比例函数基础重难点复习【学习目标】1.使学生理解并掌握反比例函数的概念,能根据实际问题中的条件确定反比例函数的解析式()0ky k x=≠,能判断一个给定函数是否为反比例函数; 2.能描点画出反比例函数的图象,会用待定系数法求反比例函数的解析式; 3.能根据图象数形结合地分析并掌握反比例函数()0ky k x=≠的性质,能利用这些性质分析和解决一些简单的实际问题. 【知识网络】【要点梳理】要点一、反比例函数的概念一般地,形如ky x=(k 为常数,0k ≠)的函数称为反比例函数,其中x 是自变量,y 是函数,自变量x 的取值范围是不等于0的一切实数.要点诠释:在ky x=中,自变量x 的取值范围是,k y x=()可以写成()的形式,也可以写成的形式.要点二、反比例函数解析式的确定反比例函数解析式的确定方法是待定系数法.由于反比例函数ky x=中,只有一个待定系数k ,因此只需要知道一对x y 、的对应值或图象上的一个点的坐标,即可求出k 的值,从而确定其解析式.要点三、反比例函数的图象和性质 1.反比例函数的图象反比例函数()0ky k x=≠的图象是双曲线,它有两个分支,这两个分支分别位于第一、三象限或第二、四象限.它们关于原点对称,反比例函数的图象与x 轴、y 轴都没有交点,即双曲线的两个分支无限接近坐标轴,但永远不与坐标轴相交. 要点诠释:观察反比例函数的图象可得:x 和y 的值都不能为0,并且图象既是轴对称图形,又是中心对称图形,它有两条对称轴,对称中心是坐标原点.①)0(≠=k x ky 的图象是轴对称图形,对称轴为x y x y -==和两条直线; ②)0(≠=k x ky 的图象是中心对称图形,对称中心为原点(0,0);③xky x k y -==和(k≠0)在同一坐标系中的图象关于x 轴对称,也关于y 轴对称.注:正比例函数x k y 1=与反比例函数xk y 2=, 当021<⋅k k 时,两图象没有交点;当021>⋅k k 时,两图象必有两个交点,且这两个交点关于原点成中心对称.2.反比例函数的性质(1)图象位置与反比例函数性质当0k >时,x y 、同号,图象在第一、三象限,且在每个象限内,y 随x 的增大而减小;当0k <时,x y 、异号,图象在第二、四象限,且在每个象限内,y 随x 的增大而增大.(2)若点(a b ,)在反比例函数ky x=的图象上,则点(a b --,)也在此图象上,故反比例函数的图象关于原点对称.(3)正比例函数与反比例函数的性质比较 正比例函数反比例函数解析式图 像 直线 有两个分支组成的曲线(双曲线)位 置 0k >,一、三象限; 0k <,二、四象限 0k >,一、三象限 0k <,二、四象限增减性0k >,y 随x 的增大而增大 0k <,y 随x 的增大而减小 0k >,在每个象限,y 随x 的增大而减小 0k <,在每个象限,y 随x 的增大而增大(4)反比例函数y =中k 的意义①过双曲线x ky =(k ≠0) 上任意一点作x 轴、y 轴的垂线,所得矩形的面积为k . ②过双曲线x ky =(k ≠0) 上任意一点作一坐标轴的垂线,连接该点和原点,所得三角形的面积为2k.要点四、应用反比例函数解决实际问题须注意以下几点1.反比例函数在现实世界中普遍存在,在应用反比例函数知识解决实际问题时,要注意将实际问题转化为数学问题.2.列出函数关系式后,要注意自变量的取值范围. 【典型例题】类型一、确定反比例函数的解析式1、已知函数()32k y k x -=+是反比例函数,则k 的值为 .【答案】2k =【解析】根据反比例函数概念,3k -=1-且20k +≠,可确定k 的值.【总结升华】反比例函数要满足以下两点:一个是自变量的次数是-1,另一个是自变量的系数不等于0. 举一反三:【变式】反比例函数5n y x+=图象经过点(2,3),则n 的值是( ). A. 2-B. 1-C. 0D. 1【答案】D ;反比例函数5n y x +=过点(2,3).53,12n n +==∴∴. 类型二、反比例函数的图象及性质2、已知,反比例函数42my x-=的图象在每个分支中y 随x 的增大而减小,试求21m -的取值范围.【思路点拨】由反比例函数性质知,当k >0时,在每个象限内y 随x 的增大而减小,由此可求出m 的取值范围,进一步可求出21m -的取值范围. 【答案与解析】解:由题意得:420m ->,解得2m <,所以24m <,则21m -<3.【总结升华】熟记并能灵活运用反比例函数的性质是解答本题的关键. 举一反三:【变式】已知反比例函数2k y x-=,其图象位于第一、第三象限内,则k 的值可为________(写出满足条件的一个k 的值即可). 【答案】3(满足k >2即可).3、在函数||k y x-=(0k ≠,k 为常数)的图象上有三点(-3,1y )、(-2,2y )、(4,3y ),则函数值的大小关系是( )A .123y y y <<B .321y y y <<C .231y y y <<D .312y y y << 【答案】D ; 【解析】∵ |k |>0,∴ -|k |<0,∴反比例函数的图象在第二、四象限,且在每一个象限里,y 随x 增大而增大,(-3,1y )、(-2,2y )在第二象限,(4,3y )在第四象限,∴ 它们的大小关系是:312y y y <<.【总结升华】根据反比例函数的性质,比较函数值的大小时,要注意相应点所在的象限,不能一概而论,本题的点(-3,1y )、(-2,2y )在双曲线的第二象限的分支上,因为-3<-2,所以12y y <,点(4,3y )在第四象限,其函数值小于其他两个函数值. 举一反三:【变式1】在同一坐标系中,函数y=和y=kx+3(k≠0)的图象大致是( ).A. B.C. D.【答案】C ;提示:分两种情况讨论:①当k >0时,y=kx+3与y 轴的交点在正半轴,过一、二、三象限,y=的图象在第一、三象限;②当k <0时,y=kx+3与y 轴的交点在正半轴,过一、二、四象限,y=的图象在第二、四象限.故选C .【变式2】已知>b a ,且,0,0,0≠+≠≠b a b a 则函数b ax y +=与xba y +=在同一坐标系中的图象不可能是( ) .【答案】B ;提示:因为从B 的图像上分析,对于直线来说是<0,0a b <,则0a b +<,对于反比例函数来说,0a b +>,所以相互之间是矛盾的,不可能存在这样的图形.4、如图所示,P 是反比例函数ky x=图象上一点,若图中阴影部分的面积是2,求此反比例函数的关系式.【思路点拨】要求函数关系式,必须先求出k 的值,P 点既在函数的图象上又是矩形的顶点,也就是说,P 点的横、纵坐标的绝对值是矩形的边长. 【答案与解析】解:设P 点的坐标为(x ,y ),由图可知,P 点在第二象限,∴ x <0,y >0. ∴ 图中阴影部分矩形的长、宽分别为-x 、y . ∵ 矩形的面积为2,∴ -xy =2,∴ xy =-2. ∵ xy =k ,∴ k =-2. ∴ 此反比例函数的关系式是2y x=-. 【总结升华】此类题目,要充分利用过双曲线上任意一点作x 轴、y 轴的垂线所得矩形面积为|k |这一条件,进行坐标、线段、面积间的转换.举一反三:【变式】如图,过反比例函数)(0x x2y >=的图象上任意两点A 、B ,分别作x 轴的垂线,垂足为''B A 、,连接OA ,OB ,'AA 与OB 的交点为P ,记△AOP 与梯形B B PA ''的面积分别为21S S 、,试比较21S S 与的大小.【答案】解:∵AOP AOA A OP S S S ''∆∆∆=-,OB A OP A PBB S B S S ''''∆∆=-梯形且AOA 112122A A S x y '∆==⨯=,OB 112122B B B S x y '∆==⨯= ∴21S S =.类型三、反比例函数与一次函数综合5、已知反比例函数ky x=和一次函数y mx n =+的图象的一个交点坐标是(-3,4),且一次函数的图象与x 轴的交点到原点的距离为5,分别确定反比例函数和一次函数的表达式.【思路点拨】因为点(-3,4)是反比例函数ky x=与一次函数y mx n =+的图象的一个交点,所以把(-3,4)代入ky x=中即可求出反比例函数的表达式.欲求一次函数y mx n =+的表达式,有两个待定未知数m n ,,已知一个点(-3,4),只需再求一个一次函数图象上的点即可.由已知一次函数图象与x 轴的交点到原点的距离是5,则这个交点坐标为(-5,0)或(5,0),分类讨论即可求得一次函数的解析式. 【答案与解析】 解:因为函数ky x=的图象经过点(-3,4), 所以43k=-,所以k =-12. 所以反比例函数的表达式是12y x=-. 由题意可知,一次函数y mx n =+的图象与x 轴的交点坐标为(5,0)或(-5,0),则分两种情况讨论:当直线y mx n =+经过点(-3,4)和(5,0)时,有43,05,m nm n=-+⎧⎨=+⎩解得1,25.2mn⎧=-⎪⎪⎨⎪=⎪⎩所以1522y x=-+.当直线y mx n=+经过点(-3,4)和(-5,0)时,有43,05,m nm n=-+⎧⎨=-+⎩解得2,10.mn=⎧⎨=⎩所以210y x=+.所以所求反比例函数的表达式为12yx=-,一次函数的表达式为1522y x=-+或210y x=+.【总结升华】本题考查待定系数法求函数解析式,解答本题时要注意分两种情况讨论,不能漏解.举一反三:【变式】如图所示,A、B两点在函数(0)my xx=>的图象上.(1)求m的值及直线AB的解析式;(2)如果一个点的横、纵坐标均为整数,那么我们称这个点是格点.请直接写出图中阴影部分(不包括边界)所含格点的个数.【答案】解:(1)由图象可知,函数(0)my xx=>的图象经过点A(1,6),可得m=6.设直线AB的解析式为y kx b=+.∵ A(1,6),B(6,1)两点在函数y kx b=+的图象上,∴6,61,k bk b+=⎧⎨+=⎩解得1,7.kb=-⎧⎨=⎩∴直线AB的解析式为7y x=-+.(2)题图中阴影部分(不包括边界)所含格点的个数是3.类型四、反比例函数应用6、一辆客车从甲地出发前往乙地,平均速度v(千米/小时)与所用时间t(小时)的函数关系如图所示,其中60≤v≤120.(1)直接写出v与t的函数关系式;(2)若一辆货车同时从乙地出发前往甲地,客车比货车平均每小时多行驶20千米,3小时后两车相遇.①求两车的平均速度;②甲、乙两地间有两个加油站A、B,它们相距200千米,当客车进入B加油站时,货车恰好进入A加油站(两车加油的时间忽略不计),求甲地与B加油站的距离.【答案与解析】解:(1)设函数关系式为v=,∵t=5,v=120,∴k=120×5=600,∴v与t的函数关系式为v=(5≤t≤10);(2)①依题意,得3(v+v﹣20)=600,解得v=110,经检验,v=110符合题意.当v=110时,v﹣20=90.答:客车和货车的平均速度分别为110千米/小时和90千米/小时;②当A加油站在甲地和B加油站之间时,110t﹣(600﹣90t)=200,解得t=4,此时110t=110×4=440;当B加油站在甲地和A加油站之间时,110t+200+90t=600,解得t=2,此时110t=110×2=220.答:甲地与B加油站的距离为220或440千米.【总结升华】解决反比例函数与实际问题相结合的问题,要理解问题的实际意义及与之相关的数学知识.反比例函数是解决现实世界反比例关系的有力工具.。
专题01 反比例函数重难点题型专训(5大题型)(解析版)

专题01反比例函数重难点题型专训(5大题型)【题型目录】题型一用反比例函数描述数量关系题型二根据定义判断是否是反比例函数题型三根据反比例函数的定义求参数题型四求反比例函数值题型五由反比例函数值求自变量【知识梳理】【知识点1反比例函数的定义】一般的,形如 0ky k k x为常数,的函数,叫做反比例函数。
其中x 是自变量,y 是函数。
自变量x 的取值范围是不等于0的一切实数。
【经典例题一用反比例函数描述数量关系】1.(2022上·云南文山·九年级统考期末)已知点 3,1是反比例函数ky x上一点,则下列各点中在该图像上的点是()A . 1,3B .11,3C .1,93D .16,2【答案】D【分析】先把点(3,1)代入双曲线ky x(k ≠0),求出k 的值,再对各选项进行判断即可.【详解】解:∵点(3,1)是双曲线ky x(k ≠0)上一点,∴k =3×1=3,A 、1×3=-3≠3,此点不在反比例函数的图像上,故本选项错误;B 、1×13=13≠3,此点不在反比例函数的图像上,故本选项错误;C 、13×(-9)=-3≠3,此点不在反比例函数的图像上,故本选项错误;D 、6×12=3,此点在反比例函数的图像上,故本选正确,故选:D .【点睛】本题考查了反比例函数,解题的关键是熟知反比例函数图像上各点的坐标一定适合此函数的解析式.2.(2022·湖北恩施·统考一模)如图的电路图中,用电器的电阻R 是可调节的,其范围为110~220 ,已知电压220V U ,下列描述中错误的是()A .P 与R 成反比例:220P RB .P 与R 成反比例:2220P RC .电阻R 越大,功率P 越小D .用电器的功率P 的范围为220~440W【答案】A【分析】根据功率2U P R 判断即可.【详解】∵220V U ,2U P R∴2220P R,∴A 选项错误故选:A .【点睛】本题考查物理的电功率公式,熟记物理公式2U P R是解题的关键.3.(2022上·江苏苏州·九年级星海实验中学校考阶段练习)若以方程 223410x k x k k -2---=的两个实数根作为横坐标、纵坐标的点恰在反比例函数y 11x的图象上,则满足条件的k 值为.【答案】-2【分析】设方程的两个根分别为11x x,,根据题意得到11x x =241k k ,结合判别式,即可求解.【详解】解:∵以方程 223410x k x k k -2---=的两个根为横坐标、纵坐标的点恰在反比例函数数y 11x的图象上,∴设方程的两个根分别为11x x,,∴11x x=241k k ,即21141k k =,∴24120k k 解得:1262k k ,∵ 2234410k k k-2---,∴5k ,∴2k .故答案为:-2.【点睛】本题考查了一元二次方程200ax bx c a ()的根的判别式24b ac =:当0 >,方程有两个不相等的实数根;当0 =,方程有两个相等的实数根;当0 <,方程没有实数根,也考查了反比例函数.4.(2020上·广东江门·九年级统考期末)验光师测得一组关于近视眼镜的度数y (度)与镜片焦距x (米)的对应数据如下表:近视眼镜的度数y (度)2002504005001000镜片焦距x (米)0.500.400.250.200.10根据表中数据,可得y 关于x 的函数表达式为.【答案】100y x【分析】由表中数据可得,100xy ,从而可得y 关于x 的函数表达式.【详解】由表中数据可得,100xy ,∴y 关于x 的函数表达式为100y x.故答案为:100y x【点睛】本题考查求反比例函数解析式,分析表中每一组值,从中得到变量间的关系是解题的关键.5.(2021上·福建三明·九年级统考阶段练习)水池内有污水360m ,设放净全池污水所需时间为 h y ,每小时放水量为 3m x .(1)试写出y 与x 之间的函数关系式;(2)求当15x 时,y 的值.【答案】(1)60y x(2)4y 【分析】(1)根据所需时间=池内污水量÷每小时放水量可得y 与x 之间的函数关系式;(2)把15x 代入(1)中函数关系式计算即可.【详解】(1)解:由题意得:60y x;(2)当15x 时,6060415y x.【点睛】本题考查了由实际问题抽象出反比例函数关系以及求反比例函数值,正确列出函数关系式是解题的关键.【经典例题二根据定义判断是否是反比例函数】1.(2023上·全国·九年级专题练习)下列函数中:①12xy ,②3y x ,③55y x ,④2ky x (k 为常数,且0k );属于反比例函数的个数为()A .1B .2C .3D .4【答案】C【分析】根据反比例函数的定义逐一分析判断即可,形如y =kx(0k )的函数是反比例函数.【详解】①∵12xy ,∴1122y x x,是反比例函数,符合题意;②3y x ,不是反比例函数,不合题意;③∵55y x,∴1y x,是反比例函数,符合题意;④2ky x(k 为常数,且0k ),是反比例函数,符合题意;是反比例函数的有①③④,共3个,故选:C .【点睛】本题考查了反比例函数的辨别,熟练掌握反比例函数的形式是解题的关键.y =kx(0k )的函数是反比例函数.2.(2021上·江西赣州·九年级统考期末)下列函数:①2y x ,②3y x,③2y x =,④234y x x ,y 是x 的反比例函数的个数有().A .1个B .2个C .3个D .4个【答案】A【分析】根据反比例函数、一次函数、二次函数的性质,对各个选项逐个分析,即可得到答案.【详解】2y x 是一次函数,故选项①不符合题意;3y x是反比例函数,故选项②符合题意;2y x =是二次函数,故选项③不符合题意;234y x x 是二次函数,故选项④不符合题意;∴y 是x 的反比例函数的个数有:1个故选:A .【点睛】本题考查了反比例函数、二次函数、一次函数的知识;解题的关键是熟练掌握反比例函数、二次函数、一次函数的定义,从而完成求解.3.(2022上·八年级课时练习)下列函数,①(2)1x y ②.11y x ③21y x④.12y x⑤2xy ⑥13y x;其中是y 关于x 的反比例函数的有:.【答案】④⑥.【分析】根据反比例函数的定义依次判断后即可解答.【详解】①x (y+2)=1,可化为y=12xx,不是反比例函数;②11y x ,y 与(x+1)成反比例关系;③21y x是y 关于x 2的反比例函数;④12y x符合反比例函数的定义,是反比例函数;⑤2xy 是正比例函数;⑥13y x符合反比例函数的定义,是反比例函数;故答案为④⑥.【点睛】本题考查了反比例函数的定义,熟知反比例函数的定义是解决问题的关键.4.(2022上·全国·九年级统考期末)下列关系式:①13y x ;②67y x ;③1xy ;④51y x ;⑤112y x ,其中y 是x 的反比例函数的为(只填序号)【答案】②③⑤【分析】根据反比例函数解析式的一般形式y =kx(k≠0),也可转化为y=kx -1(k≠0)的形式,即可作出判断.【详解】y 是x 的反比例函数的为②③⑤.故答案是:②③⑤.【点睛】本题考查了反比例函数的定义,解题的关键是熟练的掌握反比例函数的定义.5.(2023下·浙江·八年级专题练习)先列出下列问题中的函数表达式,再指出它们各属于什么函数.(1)电压为16V 时,电阻R 与电流I 的函数关系;(2)食堂每天用煤1.5t ,用煤总量W (t )与用煤天数t (天)的函数关系;(3)积为常数m 的两个因数y 与x 的函数关系;(4)杠杆平衡时,阻力为800N ,阻力臂长为5cm ,动力y (N )与动力臂x (cm )的函数关系(杠杆本身所受重力不计).【答案】(1)16I R,故是反比例函数关系(2) 1.5W t ,故是正比例函数关系(3)my x,故是反比例函数关系(4)4000y x,故是反比例函数关系【分析】(1)利用UI R,进而得出答案;(2)利用煤总量W (t )=用煤天数t (天) 1.5 ,进而得出答案;(3)利用 xy m ,进而得出答案;(4)动力大小×动力臂=阻力臂大小×阻力进而求出即可.【详解】(1)16I R,故是反比例函数关系;(2) 1.5W t ,故是正比例函数关系(3)my x,故是反比例函数关系(4)4000y x,故是反比例函数关系【点睛】此题主要考查了正比例和反比例函数的定义,正确得出函数关系式是解题关键.【经典例题三根据反比例函数的定义求参数】1.(2021·广东广州·统考三模)若关于x 的一元二次方程x 2﹣2x ﹣m =0无实数根,则反比例函数1m y x的图象可能经过点()A .(3,1)B .(0,3)C .(﹣3,﹣1)D .(﹣3,1)【答案】D【分析】由方程根的情况可求得m 的取值范围,则可求得反比例函数图象经过的象限,可求得答案.【详解】解:∵关于x 的一元二次方程x 2﹣2x ﹣m =0无实数根,∴Δ<0,即(﹣2)2+4m <0,解得m <﹣1,∴m +1<0,∴反比例函数1m y x的图象经过二、四象限,∴反比例函数1m y x的图象可能经过点(﹣3,1),故选:D .【点睛】本题主要考查反比例函数的性质和一元二次方程根的判别式,根据一元二次方程根的判别式求得m 的取值范围是解题的关键.2.(2022下·河南开封·八年级统考期中)若函数2m y x的图象在其每一个分支中y 的值随x 值的增大而增大,则m 的取值范围是()A .2mB .2m <C .2m D .2m <【答案】D【分析】根据k <0,反比例函数的函数值y 在每一个分支中随x 值的增大而增大列出不等式计算即可得解.【详解】解:∵2m y x在其每一个分支中y 的值随x 值的增大而增大,20m ,2m .故选:D .【点睛】此题考查反比例函数的性质.解题关键在于掌握反比例函数y=kx,当k >0时,在每一个象限内,函数值y 随自变量x 的增大而减小;当k <0时,在每一个象限内,函数值y 随自变量x 增大而增大.3.(2023下·山西长治·八年级长治市第五中学校校考阶段练习)若点 1A a ,, 3B b ,(其中0b )都在反比例函数 0ky k x的图象上,则一次函数 1y a b x 中的y 随着x 的增大而(填“增大”或“减小”).【答案】减小【分析】根据点 1A a ,, 3B b ,在反比例函数图象上,可得03ka kb k ,,,从而可得2033k ka b k,即可得到答案.【详解】解:∵点 1A a ,, 3B b ,(其中0b )都在反比例函数 0ky k x的图象上,31k ka b,,03ka kb k ,,,2033k k a b k, 一次函数 1y a b x 中的y 随着x 的增大而减小,故答案为:减小.【点睛】本题主要考查了反比例函数与一次函数的图象的特征,熟练掌握反比例函数与一次函数的图象的特征是解题的关键.4.(2023·陕西西安·西安高级中学校考模拟预测)如图,矩形ABCD 的边AB 与y 轴平行,顶点A 的坐标为 1,4,顶点C 的坐标为 3,1,若反比例函数ky x的图像与矩形ABCD 有公共点,则k 的值可以是.(写出一个即可)【答案】2(答案不唯一)【分析】根据矩形写出B ,D 两点坐标,然后利用双曲线ky x经过点B ,D 时对应的k 值,从而得到k 的取值范围.【详解】解:∵矩形ABCD 的顶点 1,4A , 3,1C ,∴ 1,1B , 3,4D ,当双曲线ky x经过点B 时,k 的值最小,此时111k ,当双曲线ky x经过点D 时,k 的值最大,此时3412k ,∴k 的取值范围为112k .∴k 可以取2故答案为:2(答案不唯一).【点睛】本题考查反比例函数图像上点的坐标特征,熟记点的横纵坐标的积是定值k 是解题的关键.5.(2023下·四川成都·七年级成都外国语学校校考期中)根据所学函数知识,解答下列问题:(1)已知函数 124m y m xn ,当m ,n 为何值时,此函数是一次函数?(2)当m 为何值时,函数 43m y m x 是反比例函数,并求当3y 时,x 的值为多少?【答案】(1)2m ,n 为任意实数(2)3m ,2x 【分析】(1)根据一次函数的定义列出关于m 的不等式组,求出m 的值即可;(2)根据反比例函数的定义列出关于m 的不等式组,求出m 的值,故可得出反比例函数的解析式,再把3y 代入解析式即可得出x 的值.【详解】(1)∵函数 124m y m xn 是一次函数,2011m m 且4n 为任意实数,解得2m ,2m ,n 为任意实数;(2)∵函数 43m y m x是反比例函数,3041m m,解得3m ,反比例函数的解析式为6y x,当3y 时,63x,2x .【点睛】本题考查的是反比例函数及一次函数的性质,反比例函数及一次函数的定义,熟知以上知识是解题的关键.【经典例题四求反比例函数值】1.(2022下·江苏泰州·八年级统考期末)函数132y x 的图像可以由1y x 的图像先向右平移2个单位,再向上平移3个单位得到.根据所获信息判断,下列直线中与函数121y x 的图像没有公共点的是()A .经过点 0,2且平行于x 轴的直线B .经过点 0,3 且平行于x 轴的直线C .经过点 1,0 且平行于y 轴的直线D .经过点 1,0且平行于y 轴的直线【答案】D【分析】分别计算对应的自变量的值或函数值即可判断.【详解】解:A 、当y =2时,1221x ,解得x =54,故直线y =2与函数121y x 的图像有公共点;B 、当y =-3时,121x =-3,解得x =0,故直线y =-3与函数121y x 的图像有公共点;C 、当x =-1时,15212y x,故直线x =-1与函数121y x 的图像有公共点;D 、分式有意义的条件是x ≠1,∴函数121y x 的图像与直线x =1没有公共点;故选:D .【点睛】此题考查了求函数值或求自变量的值,分式有意义的条件,正确计算是解题的关键.2.(2023下·江苏连云港·八年级统考期末)已知点 2,4A 在反比例函数ky x(k 为常数,0k )的图象上,下列各点中,一定在该函数图像上的是()A .4,2B .2,4 C .2,4 D .4,2【答案】A【分析】先把点 2,4A 代入反比例函数y kx,求出k 的值,再根据k xy 为定值对各选项进行逐一检验即可.【详解】解:∵点 2,4A 在反比例函数y kx的图象上,∴248k .A 、∵428 ,∴此点在函数图象上;B 、∵ 2488 ,∴此点不在函数图象上;C 、∵ 2488 ,此点不在函数图象上;D 、∵ 4288 ,此点不在函数图象上.故选:A .【点睛】本题考查了反比例函数图象上点的坐标特点,掌握反比例函数图象上各点的坐标一定适合此函数的解析式是解题的关键.3.(2022下·江苏宿迁·八年级沭阳县怀文中学校考阶段练习)已知反比例函数8y x,若2x ,则y 的取值范围是.【答案】4y 或0y 【分析】先求出x =-2时y 的值,根据反比例函数性质得出即可.【详解】解:把x =-2代入8y x得:y =-4,∵8>0,∴在每个象限内,y 随x 的增大而减小,图象在第一、三象限,∴当x ≥-2时,函数y 的取值范围是y ≤-4或y >0,故答案为:y ≤-4或y >0.【点睛】本题考查了反比例函数的图象和性质,能熟记反比例函数的性质是解此题的关键.4.(2021·北京石景山·统考二模)在平面直角坐标系xOy 中,点 ,A a b 在双曲线1y x上.若a<0,则点A 在第象限.【答案】二【分析】由点A (a ,b )在双曲线1y x上,可得ab =-1,由a<0可得到点0b 的坐标,进而得出答案.【详解】解:∵点 ,A a b 在双曲线1y x上,∴ab =-1,∵a<0∴0b ∴点A 在第二象限.故答案为:二.【点睛】考查反比例函数图象上的点坐标的特征,求出0b 是解答此题的关键.5.(2022上·广西桂林·九年级统考期中)已知反比例函数6y x的图像经过点(2,)A m .(1)求m 的值;(2)当1x 且0x 时,直接写出y 的取值范围.【答案】(1)3(2)当1x 且0x 时,0y 或6y 【分析】(1)将点(2,)A m 代入反比例函数6y x即可求解;(2)根据反比例函数的图像可知,反比函数图像在第二象限和第四象限,由1x 且0x 即可求出图像位置,由此即可求解.【详解】(1)解:∵反比例函数6y x的图像经过点(2,)A m ,∴632y,∴3m .(2)解:反比例函数6y x的图像如图所示,当1x 且0x 时,在第二象限:0y 或在第四象限:6y .【点睛】本题主要考查反比例函数图像的性质,掌握反比例函数图像的特点是解题的关键.【经典例题五由反比例函数值求自变量】1.(2021·山西·统考模拟预测)在平面直角坐标系xoy 中,将横纵坐标相等的点称为“好点”,下列函数图像中不存在“好点”的是()A .2y xB .2y xC .1y xD .22y x x【答案】B【分析】根据“好点”的概念:当x =y 时,对应的方程有解进行判断即可.【详解】解:A 、当x =y =0时,满足y =2x ,(0,0)为“好点”,该选项不符合题意;B 、不存在横纵坐标相等的“好点”,该选项符合题意;C 、当x =y =1或x =y =﹣1时,满足1y x,(1,1)和(﹣1,﹣1)是“好点”,该选项不符合题意;D 、当x =y =0或x =y =2时,满足22y x x ,(0,0)和(2,2)为“好点”,不符合题意,故选:B .【点睛】本题考查一次函数图象上点的坐标特征、二次函数图象上点的坐标特征、反比例函数图象上点的坐标特征,解答的关键是熟悉每个函数的图象与性质.2.(2020·四川·统考中考真题)已知函数1(2)2(2)x x y x x,当函数值为3时,自变量x 的值为()A .﹣2B .﹣23C .﹣2或﹣23D .﹣2或﹣32【答案】A【分析】根据分段函数的解析式分别计算,即可得出结论.【详解】解:若x <2,当y =3时,﹣x +1=3,解得:x =﹣2;若x ≥2,当y =3时,﹣2x=3,解得:x =﹣23,不合题意舍去;∴x =﹣2,故选:A .【点睛】本题考查了反比例函数的性质、一次函数的图象上点的坐标特征;根据分段函数进行分段求解是解题的关键3.(2021上·山西·九年级山西实验中学校考阶段练习)观查反比例函数2y x的图象,当2y 时,x 的取值范围是.【答案】x <﹣1或x >0/x >0或x <-1【分析】利用函数值找到分界点(-1,-2),根据反比例函数的图象和性质与直线y=-2的位置关系解答即可.【详解】解:∵k =2>0,反比例函数图像位于一三象限,在每个象限内y 随x 的增大而减小,∴y =-2时,22x,解得x =-1,∴当y >-2时x <﹣1或x >0,故答案为x <﹣1或x >0.【点睛】本题重点考查学生对反比例函数图像和性质的理解,掌握反比例函数的图象和性质,以及利用反比例函数与直线y=-2的交点求不等式解集是解题的关键.4.(2021上·九年级课时练习)考察函数2y x的图象,当2x 时,y ;当<2x 时,y 的取值范围是;当1y 时,x 的取值范围是.【答案】110y <2x 或0x 【分析】把2x 代入反比例函数解析式求解即可;根据2y x得到2x y ,再根据<2x 求解即可;(3)根据2y x得到2x y ,再根据1y 求解即可.【详解】解:∵2y x,∴把2x 代入反比例函数解析式得:212y ∵2y x,<2x ∴2x y,0y ∵<2x ,∴22y,解得y >-1∴10y ,∵2y x,1y ∴2x y ,x >-2,即21x,解得x ≤-2∵当x >0时,y >0∴当y >-1时,<2x 或0x .【点睛】本题主要考查了反比例函数图像的性质、求反比例函数函数值的范围等知识点,熟练掌握并运用相关知识成为解答本题的关键.5.(2020下·广东广州·九年级校考阶段练习)已知22211211a a Q a a a(1)化简Q .(2)若点 ,Aa a 在反比例函数4y x的图象上,求Q 的值.【答案】(1)2a 1(2)当2a 时,2Q ,当2a 时,23Q .【分析】(1)先计算括号内的分式的加法,再把除法化为乘法,再约分即可;(2)根据反比例函数的性质先求解a 的值,再代入2a 1进行计算即可.【详解】(1)解:22211211a a Q a a a2222211111aa a a a a212111a a aa a a2211aa aa21a;(2)∵点 ,A a a 在反比例函数4y x的图象上,∴24a ,解得:2a ,当2a 时,原式2221,当2a 时,原式22213.【点睛】本题考查的是分式的化简求值,反比例函数的性质,掌握分式的混合运算的运算顺序与反比例函数的性质是解本题的关键.【重难点训练】1.(2023上·山东东营·九年级校联考阶段练习)下列函数:①2y x ,②3y x,③1y x ,④21y x =+,⑤11xy ,⑥k y x ,⑦25y x ,⑧1yx.其中y 是x 的反比例函数的有()A .1个B .2个C .3个D .4个【答案】C【分析】根据反比例的三种形式判断即可.【详解】解:反比例的三种形式分别为:(0)ky k x,()0xy k k ,1(0)y kx k .①中x 的次数是1,是一次函数,不是反比例函数;②,③是反比例函数;④中分母是1x ,故不是反比例函数;⑤是反比例函数;⑥中没有0k ,故不是反比例函数;⑦分母是2x ,故不是反比例函数;⑧中x 的次数是1,是一次函数,不是反比例函数.故有三个是反比例函数.故选C .【点睛】本题主要考查反比例的定义,熟练掌握反比例函数的性质是解题的关键.2.(2022上·湖南娄底·九年级期中)现有A 、B 两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).用小莉掷A 立方体朝上的数字为x 、小明掷B 立方体朝上的数字为y 来确定点 ,P x y ,那么他们各掷一次所确定的点P 落在双曲线6y x上的概率为()A .19B .23C .118D .16【答案】A【分析】点P 若落在6y x上,则6xy ,可采用列表法确定所有可能情况及满足要求的情况,求得概率.【详解】解:表格列示所有投掷情况如下,小明小莉12345611,11,21,31,41,51,622,12,22,32,42,52,633,13,23,33,43,53,644,14,24,34,44,54,655,15,25,35,45,55,666,16,26,36,46,56,6点P 若落在6y x上,则6xy .如上表,两人掷的组合情况共有6636 种,其中满足要求的有4种:2,3;3,2;1,6;6,1,故概率为41369;故选:A【点睛】本题考查列举法求概率、反比例函数解析式;运用表格列示所有可能的情况是解题的关键.3.(2022上·广西贵港·九年级统考期中)如图,已知点 1,6A 在双曲线 0ky k x上,动点P 在y 轴正半轴上,将点A 绕点P 逆时针旋转90°,点A 的对应点为B ,若点B 恰好落在双曲线上,则点P 的坐标为()A . 0,3B . 3,0或 4,0C . 0,2或 0,6D . 0,3或0,4【答案】D【分析】先把 1,6A 代入反比例函数 0ky k x求出k 的值,分别过A 、B 两点作x 轴的垂线AC ,BD ,由旋转的性质证明APC PBD ≌,再设 0,P m ,即可得出B 的坐标,由双曲线上的点横坐标与纵坐标的积即相等,列方程求m 的值,确定P 点坐标.【详解】解:分别过A 、B 两点作AC y 轴,BD y 轴,垂足为C 、D ,∵ 1,6A 是双曲线 0ky k x上一点,6k ,反比例函数的解析式为6y x,90APB ∵,90APC BPD ,又90APC PAC ,PAC BPD ,在APC 和PBD 中,90PAC BPD ACP PDB AP PB, AAS APC PBD ≌,CP BD ,1AC PD ,设 0,P m ,OP m ,6PC m , 6,1B m m ,∵点B 在双曲线上,616m m,解得3m 或4m , 0,3P 或 0,4.故选:D .【点睛】本题考查的是反比例函数图象的性质,旋转的性质,全等三角形的性质与判定,熟练掌握反比例函数图象的性质是解答此题的关键.4.(2022上·江苏苏州·九年级校考阶段练习)如图,点P 在y 轴正半轴上,⊙P 交x 轴于A ,B 两点,连接BP 并延长交⊙P 于C ,且⊙P 的半径为5,AB =4.若函数 0ky x x的图像过C 点,则k 的值是()A .4B .4C .25D .4【答案】B【分析】连接AC ,由圆周角定理可知90CAB ,AC AB ,在Rt ACB 中由勾股定理可计算AC 的长;由垂径定理可知12OA AB,进而确定点C 的坐标,最后将点C 坐标代入 0ky x x 即可计算出k 的值.【详解】如图,连接AC∵CB 是直径,225CB BP 由圆周角定理可知90CAB 在Rt CAB △中,由勾股定理可得:22222542AC CB AB,y ∵轴是P 直径所在的直线,且AB y 轴, 由垂径定理可得:122OA ABAB AC∵ 点C 的横坐标2C x OA ,纵坐标2C y AC 2,2C 将 2,2C 代入 0ky x x,解得:4k 故选:B .【点睛】本题考查了在圆的背景下用待定系数法求反比例函数解析式,熟练掌握垂径定理和圆周角定理并能使用数形结合思想解题,是本题的解题关键.5.(2022下·湖北武汉·九年级校考阶段练习)在平面直角坐标系中,反比例函数3y x的图象经过 33a m b m ,,,两点,则代数式2227aba b ab的值是()A .23B .23C .2D .2【答案】C【分析】根据题意得到333m a,3m b ,从而得到113 a b ,进一步得到3a b ab ,代入变形后的代数式即可求得.【详解】解:∵反比例函数3y x的图象经过33a m b m ,,,两点,333m a,3m b ,∴3333a b ,113a b,3b aab,3a b ab ,22222767ab aba b ab ab ab,故选:C .【点睛】本题考查了反比例函数图象上点的坐标特征,反比例函数图象上的点的坐标适合解析式是解题的关键.6.(2023下·江苏连云港·八年级校考阶段练习)已知实数x 、y 满足338x y ,当1x 时,y 的取值范围是.【答案】20y 【分析】由338x y 可得出2xy ,结合x 的取值范围,即可求出y 的取值范围.【详解】解:333()8x y xy ∵,2xy ,2y x.又1x Q ,20y .故答案为:20y .【点睛】本题考查了反比例函数,立方根、幂的乘方与积的乘方以及实数大小比较,牢记()n n n ab a b 是解题的关键.7.(2023下·江苏·八年级期末)当m 时,函数 2212mm y m m x 是反比例函数.【答案】1【分析】根据反比例函数定义列出代数式求解即可得到答案.【详解】解:∵ 2212mm y m m x 是反比例函数,∴221120m m m m,解得1m ,故答案为:1.【点睛】本题考查反比例函数定义、解方程及不等式,熟练掌握反比例函数定义,掌握因式分解解方程及不等式是解决问题的关键.8.(2023下·江苏泰州·八年级统考期末)如图,点A 在反比例函数(0)ky k x的图象上,过点A 作y 轴的平行线l .已知点A 坐标为 2,1,结合函数图象可知,当2x 时,y 的取值范围是.【答案】0y 或1y 【分析】根据题意,求对应直线l 左侧图象函数值的取值范围.【详解】2x 时,对应函数图象在直线l 左侧,两部分,0y 或1y 故答案为:0y 或1y 【点睛】本题考查反比例函数的图象,确定自变量取值范围对应的函数图象部分是解题的关键.9.(2023·山东临沂·统考中考真题)小明利用学习函数获得的经验研究函数22y x x的性质,得到如下结论:①当1x 时,x 越小,函数值越小;②当10x 时,x 越大,函数值越小;③当01x 时,x 越小,函数值越大;④当1x 时,x 越大,函数值越大.其中正确的是(只填写序号).【答案】②③④【分析】列表,描点、连线,画出图象,根据图象回答即可.【详解】解:列表,x L 2.5 2 1 0.5 0.512L yL5.45313.754.2535L描点、连线,图象如下,根据图象知:①当1x 时,x 越小,函数值越大,错误;②当10x 时,x 越大,函数值越小,正确;③当01x 时,x 越小,函数值越大,正确;④当1x 时,x 越大,函数值越大,正确.故答案为:②③④.【点睛】本题考查二次函数、反比例函数与不等式等知识,解题的关键是理解题意,学会画出函数图象,利用图象解决问题,属于中考常考题型.10.(2023·四川乐山·统考中考真题)定义:若x ,y 满足224,4x y t y x t 且x y (t 为常数),则称点(,)M x y 为“和谐点”.(1)若(3,)P m 是“和谐点”,则m .(2)若双曲线(31)ky x x存在“和谐点”,则k 的取值范围为.【答案】734k 【分析】(1)根据“和谐点”的定义得到224,433m t m t ,整理得到24210m m ,解得2137,m m (不合题意,舍去),即可得到答案;(2)设点 ,a b 为双曲线(31)ky x x上的“和谐点”,根据“和谐点”的定义整理得到 40a b a b ,由a b ¹得到40a b ,则4b a ,由(31)k b a a进一步得到 224k a ,且31a ,根据二次函数的图象和性质即可得到k 的取值范围.【详解】解:(1)若(3,)P m 是“和谐点”,则224,433m t m t ,则22,3412m t m t ,∴223124m m ,即24210m m ,解得2137,m m (不合题意,舍去),∴7m ,故答案为:7(2)设点 ,a b 为双曲线(31)ky x x上的“和谐点”,∴224,4b t b a t a ,(31)kb a a,即2244a a b b ,∴ 40a b a b a b ,则 40a b a b ,∵a b ¹,∴40a b ,即4b a ,∵(31)kb a a,∴ 224424k ab a a a a a ,且31a ,对抛物线 224k a 来说,∵10 ,∴开口向下,当1a 时, 21243k ,当3a 时, 23243k ,∵对称轴为2a ,31a ,∴当2a 时,k 取最大值为4,∴k 的取值范围为34k ,故答案为:34k 【点睛】此题考查了反比例函数的性质、二次函数的图象和性质等知识,读懂题意,熟练掌握反比例函数和二次函数的性质是解题的关键.11.(2023上·上海青浦·八年级校考期中)已知:122y y y ,并且1y 与x 成正比例,2y 与(2)x 成反比例,且当2x 时,7y ,当3x 时,13y ,求y 与x 之间的函数解析式.【答案】432y x x【分析】本题考查了待定系数法求函数的解析式,注意在本题中的正比例系数和反比例系数是两个不同的值,用不同的字母区分.设11y k x ,222k y x则1222x x k k y ,然后利用待定系数法即可求得;【详解】∵1y 与x 成正比例,2y 与(2)x 成反比例,∴设11y k x ,222k y x,∴1212222k k y y x y x,∵当2x 时,7y ,当3x 时,13y ,∴212122722231332k k k k,解得1232k k ,∴y 与x 之间的函数解析式为432y x x.12.(2023上·安徽合肥·九年级阶段练习)在平面直角坐标系中,如果一个点的横坐标与纵坐标互为相反数,则称该点为“黎点”.例如 1,1 , 2023,2023 都是“黎点”.(1)求双曲线9y x上的“黎点”;(2)若抛物线27y ax x c (a 、c 为常数)上有且只有一个“黎点”,当1a 时,求c 的取值范围.【答案】(1) 3,3 或 3,3 ;(2)09c 【分析】(1)设双曲线9y x上的“黎点”为 ,m m ,构建方程求解即可;(2)抛物线27y ax x c (a 、c 为常数)上有且只有一个“黎点”,推出方程 270ax x c x a 有且只有一个解,3640ac ,可得结论.【详解】(1)解:设双曲线9y x上的“黎点”为 ,m m ,则有9m m,解得3m ,∴9y x上的“黎点”为 3,3 , 3,3 .(2)解:∵抛物线27y ax x c 上有且只有一个“黎点”,∴方程 270ax x c x a 有且只有一个解,即260ax x c ,3640ac ,9ac ,∴9a c.∵1a ,∴09c .【点睛】本题考查反比例函数图象上的点特征,二次函数的性质等知识,解题的关键是理解题意,学会用转化的思想思考问题.13.(2023上·安徽安庆·九年级校联考阶段练习)已知ABC 的三个顶点为 1,1A 、 1,3B 、 3,3C ,将ABC 向右平移m (0m )个单位后成111A B C △,此时111A B C △某一边的中点恰好落在反比例函数3y x的图像上,求m 的值.【答案】m 的值为4或0.5【分析】求出各边的中点坐标,将其纵坐标代入3y x,求出平移后的横坐标,进而可求出m 的值.【详解】解①∵点A 的坐标为 1,1 ,点B 的坐标为 1,3 ,∴AB 中点坐标为 1,1 .在3y x中,当1y 时,3x ,故 314m ;②∵点A 的坐标为 1,1 ,点C 的坐标为 3,3 ,∴AC 中点坐标为 2,2 ,在3y x 中,当=2y 时, 1.5x ,故 1.520.5m ;③∵点B 的坐标为 1,3 ,点C 的坐标为 3,3 ,∴BC 中点坐标为 2,0 ,。
反比例函数教案及教学反思

一、教案设计1.1 教学目标:(1) 知识与技能:使学生理解反比例函数的概念,掌握反比例函数的性质,能够运用反比例函数解决实际问题。
(2) 过程与方法:通过观察、分析、归纳等方法,引导学生发现反比例函数的规律,提高学生解决问题的能力。
(3) 情感态度价值观:培养学生对数学的兴趣,激发学生探索数学规律的欲望,培养学生的团队合作精神。
1.2 教学内容:(1) 反比例函数的概念:反比例函数是指形如y = k/x (k为常数,k≠0) 的函数。
(2) 反比例函数的性质:反比例函数的图像是一条通过原点的曲线,称为双曲线。
当k>0时,双曲线在第一、三象限;当k<0时,双曲线在第二、四象限。
(3) 反比例函数的应用:解决实际问题,如计算面积、速度、浓度等。
1.3 教学重点与难点:(1) 重点:反比例函数的概念和性质。
(2) 难点:反比例函数的应用。
1.4 教学方法:采用问题驱动法、案例分析法、小组合作法等,引导学生主动探究,提高学生解决问题的能力。
1.5 教学过程:(1) 导入:通过生活中的实例,引导学生思考反比例关系,激发学生的学习兴趣。
(2) 讲解:讲解反比例函数的概念,引导学生观察、分析反比例函数的性质。
(3) 实践:让学生通过实际问题,运用反比例函数解决问题,巩固所学知识。
(5) 作业:布置相关练习题,巩固所学知识。
二、教学反思2.1 教学效果:通过本节课的教学,学生能够理解反比例函数的概念,掌握反比例函数的性质,并能够运用反比例函数解决实际问题。
2.2 教学亮点:(1) 采用问题驱动法,引导学生主动探究,提高学生解决问题的能力。
(2) 结合生活中的实例,让学生感受到数学与生活的紧密联系,激发学生学习数学的兴趣。
2.3 改进措施:(1) 在实践环节,可以增加一些具有挑战性的问题,让学生在解决问题的过程中,进一步提高反比例函数的应用能力。
(2) 在教学过程中,要注意关注学生的学习情况,及时解答学生的疑问,提高教学效果。
反比例函数教案及教学反思

反比例函数教案及教学反思一、教学目标知识与技能:1. 理解反比例函数的定义及其性质;2. 学会如何求反比例函数的导数;3. 能够运用反比例函数解决实际问题。
过程与方法:1. 通过观察实例,引导学生发现反比例函数的规律;2. 利用导数研究反比例函数的单调性;3. 运用反比例函数解决实际问题,培养学生的数学建模能力。
情感态度价值观:1. 培养学生对数学的兴趣和好奇心;2. 培养学生勇于探索、积极思考的科学精神;3. 培养学生运用数学知识解决实际问题的能力。
二、教学重点与难点重点:1. 反比例函数的定义及其性质;2. 反比例函数的导数;3. 反比例函数在实际问题中的应用。
难点:1. 反比例函数的导数;2. 反比例函数在实际问题中的应用。
三、教学过程1. 导入:通过展示实际问题,引导学生思考反比例函数的概念。
2. 自主学习:学生通过教材或课外资料,了解反比例函数的定义及其性质。
3. 课堂讲解:讲解反比例函数的定义、性质及求导公式。
4. 课堂练习:学生分组讨论,练习求解反比例函数的导数。
5. 应用拓展:引导学生运用反比例函数解决实际问题。
四、教学方法1. 实例导入:通过展示实际问题,引发学生的兴趣和思考;2. 自主学习:培养学生的独立思考和自主学习能力;3. 课堂讲解:采用讲解、提问、讨论等方式,引导学生理解和掌握知识;4. 课堂练习:分组讨论、互动交流,提高学生的合作能力和解题能力;5. 应用拓展:培养学生运用数学知识解决实际问题的能力。
五、教学反思1. 反思教学内容:检查是否全面讲解了反比例函数的定义、性质和应用;2. 反思教学方法:观察学生的参与程度和理解程度,调整教学方法,提高教学效果;3. 反思教学效果:评估学生对反比例函数知识的掌握程度,发现存在的问题,及时改进教学策略。
六、教学评价1. 课堂提问:通过提问了解学生对反比例函数的理解程度;2. 课堂练习:检查学生求解反比例函数导数的正确性;3. 应用拓展:评估学生运用反比例函数解决实际问题的能力;4. 课后作业:布置有关反比例函数的题目,巩固所学知识。
反比例知识梳理

知识梳理知识点l. 反比例函数的概念重点:掌握反比例函数的概念 难点:理解反比例函数的概念一般地,如果两个变量x 、y 之间的关系可以表示成xk y =或y=kx -1(k 为常数,0k ≠)的形式,那么称y 是x 的反比例函数。
反比例函数的概念需注意以下几点:(1)k 是常数,且k 不为零;(2)x k中分母x 的指数为1,如22y x=不是反比例函数。
(3)自变量x 的取值范围是0x ≠一切实数.(4)自变量y 的取值范围是0y ≠一切实数。
知识点2. 反比例函数的图象及性质重点:掌握反比例函数的图象及性质 难点:反比例函数的图象及性质的运用反比例函数xky =的图象是双曲线,它有两个分支,这两个分支分别位于第一、三象限或第二、四象限。
它们关于原点对称、反比例函数的图象与x 轴、y 轴都没有交点,即双曲线的两个分支无限接近坐标轴,但永远不与坐标轴相交。
画反比例函数的图象时要注意的问题: (1)画反比例函数图象的方法是描点法;(2)画反比例函数图象要注意自变量的取值范围是0x ≠,因此不能把两个分支连接起来。
(3)由于在反比例函数中,x 和y 的值都不能为0,所以画出的双曲线的两个分支要分别体现出无限的接近坐标轴,但永远不能达到x 轴和y 轴的变化趋势。
反比例函数的性质xky =)0k (≠的变形形式为k xy =(常数)所以: (1)其图象的位置是:当0k >时,x 、y 同号,图象在第一、三象限; 当0k <时,x 、y 异号,图象在第二、四象限。
(2)若点(m,n)在反比例函数xky =的图象上,则点(-m,-n )也在此图象上,故反比例函数的图象关于原点对称。
(3)当0k >时,在每个象限内,y 随x 的增大而减小; 当0k <时,在每个象限内,y 随x 的增大而增大; 知识点3. 反比例函数解析式的确定。
重点:掌握反比例函数解析式的确定 难点:由条件来确定反比例函数解析式(1)反比例函数关系式的确定方法:待定系数法,由于在反比例函数关系式xky =中,只有一个待定系数k ,确定了k 的值,也就确定了反比例函数,因此只需给出一组x 、y 的对应值或图象上点的坐标,代入xky =中即可求出k 的值,从而确定反比例函数的关系式。
6.1反比例函数(教案)(3)

三、教学难点与重点
1.教学重点
(1)反比例函数的定义:y = k/x(k≠0),强调k不为零,这是反比例函数成立的前提条件。
举例:在实际问题中,如速度与时间的关系,当时间为零时,速度没有意义,因此k不能为零。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解反比例函数的基本概念。反比例函数是形如y = k/x(k≠0)的函数。它在描述现实生活中的反比关系方面具有重要应用。
2.案例分析:接下来,我们来看一个具体的案例。这个案例展示了反比例函数在描述物体在反比例力作用下运动的应用,以及它如何帮助我们解决问题。
针对这个问题,我计划在接下来的课程中,增加一些与生活紧密相关的反比例函数实例,让学生更加直观地感受反比例函数的作用。此外,我还将加强对学生的引导,鼓励他们在小组讨论中积极发表自己的观点,提高他们的参与度。
另外,我在课程中强调了反比例函数与一次函数图像的关系,但感觉学生们对此部分的掌握程度并不理想。在今后的教学中,我需要更加注重这方面的讲解和练习,让学生更好地理解两者之间的联系和区别。
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了反比例函数的基本概念、图像性质和实际应用。同时,我们也通过实践活动和小组讨论加深了对反比例函数的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
(2)反比例函数的图像与性质:双曲线、在每个象限内y随x的增大而减小(k>0)或增大(k<0)。
反比例函数重难点题型

反比例函数重难点题型1. 概述反比例函数是数学中的一种重要函数类型。
本文将讨论反比例函数的重点难点题型,并提供解题方法和技巧。
2. 难点一:变量的理解在解题过程中,理解变量的含义是至关重要的。
反比例函数的一般形式为 y = k/x,其中 k 是常数。
要理解变量的含义,我们需要注意以下几点:- k 的取值范围:在题目中,通常会给定 k 的取值范围,我们需要确保我们的解答在这个范围内。
- x 的取值范围:确定x 的取值范围有助于我们理解问题背景,并选择适当的解题方法。
3. 难点二:题目解读与转化在解决反比例函数的题目时,我们需要仔细解读题目要求,并将其转化为数学表达式。
以下是一些常见的解题技巧:- 明确问题:弄清楚题目要求我们求解的是什么,是x 还是y?这有助于确定我们的解题方向。
- 转化为反比例函数:如果题目描述了一种倒数关系,我们可以将其转化为反比例函数进行求解。
4. 难点三:解题方法解决反比例函数题目的方法有多种,我们需要选择最合适的方法。
以下是几种常用的解题方法:- 建立比例:可以通过建立比例,利用已知条件求解未知量。
例如,已知 x 和 y 满足 y = k/x,且已知 x = 5 时,求解 y 的值。
- 绘制图象法:通过绘制反比例函数的图象,可以更直观地理解函数的性质,并求解特定问题。
例如,通过绘制函数图象找到函数的零点或极值点。
5. 难点四:注意事项在解题过程中,我们需要注意以下事项,以避免常见错误:- 分母为零的情况:反比例函数中分母不能为零,因此我们需要排除这种情况,以免出现错误。
- 保留结果的合理性:在计算结果时,我们需要对结果进行合理性判断,确保结果符合题目要求和变量的取值范围。
6. 总结反比例函数是一种重要的数学概念,掌握解题方法和技巧可以帮助我们更好地解决相关题目。
通过理解变量的含义、准确解读题目、选择合适的解题方法,并注意一些细节问题,我们可以提高解题的准确性和效率。
以上就是反比例函数重难点题型的文档内容。
反比例函数高频考点重难点总结

反比例函数高频考点重难点总结一、反比例函数的概念:一般地,形如 y = k/x ( k是常数, k ≠ 0 ) 的函数叫做反比例函数。
二、反比例函数的图象和性质:1、形状:图象是双曲线。
2、位置:(1)当k>0时,双曲线分别位于第一、三象限内;(2)当k<0时,>3、增减性:(1)当k>0时,在每个象限内,y随x的增大而减小;(2)当k<>在每个象限内,y随x的增大而增大。
4、变化趋势:双曲线无限接近于x、y轴,但永远不会与坐标轴相交。
5、对称性:(1)对于双曲线本身来说,它的两个分支关于直角坐标系原点中心对称;(2)对于k取互为相反数的两个反比例函数(如:y = 6/x 和y = -6/x)来说,它们是关于x轴,y轴对称。
三、反比例函数中比例系数k的几何意义:1、反比例函数与矩形面积:若P(x,y)为反比例函数y=k/x(k≠0)图像上的任意一点如图1所示,过P作PM⊥x轴于M,作PN⊥y轴于N,求矩形PMON的面积.分析:S矩形PMON=PM·PN=│y│·│x│=│xy│∵y=k/x,∴ xy=k,∴S =│k│.2、反比例函数与三角形面积:若Q(x,y)为反比例函数y=k/x(k≠0)图像上的任意一点如图2所示,过Q作QA⊥x轴于A(或作QB⊥y轴于B),连结QO,则所得三角形的面积为:S△QOA=│k│/2(或S△QOB=│k│/2).说明:以上结论与点在反比例函数图像上的位置无关.四、反比例函数图像与一次函数图像的交点(难点)求两个函数图像的交点,往往把两个函数的表达式联立组成方程组,方程组的解就是交点的坐标。
(1)正比例函数y=k₁x(k₁≠0)与反比例函数y=k₂/x(k₂≠0),当k₁与k₂同号时,正比例函数图像与反比例函数图像有两个交点,即对应方程组的解,且两个交点关于原点对称;当k₁与k₂异号时,两个函数图像没有交点。
反比例函数的概念教案

反比例函数的概念教案一、教学目标1.知识与能力目标:理解反比例函数的概念,掌握反比例函数的特征和性质。
2.过程与方法目标:通过实例分析和图像观察,培养学生观察和总结问题的能力。
3.情感态度与价值观目标:培养学生协作学习的能力,提高对数学知识的兴趣和探索精神。
二、教学重难点1.教学重点:理解反比例函数的概念及其性质。
2.教学难点:掌握反比例函数的图像及其变化规律。
三、教学过程Step 1 引入新知1.通过提问的方式引入:当两个量成反比例关系时,我们如何表示它们之间的数学关系呢?请举一个简单的例子并分析。
2.鼓励学生思考:在这个例子中,两个量的变化有什么特点?如何用数学语言来描述它们之间的关系?Step 2 探究反比例函数的概念及性质1.寻找并分析反比例关系的实例:让学生观察和描述一些反比例关系的实例,并总结它们之间的特点。
2.引入反比例函数的概念:根据学生的描述,引导他们得出反比例关系可以用函数来表示的结论,并引入反比例函数的概念。
3.反比例函数的定义:引导学生理解反比例函数的定义,并让学生能够用数学语言来描述反比例函数。
4.反比例函数的性质:引导学生通过实例分析和图像观察,总结出反比例函数的特征和性质。
Step 3 反比例函数的图像和性质1.给出一个简单的反比例函数:y=k/x,其中k为常数,让学生观察并绘制函数的图像。
2.观察图像的变化:通过改变k的值,观察和总结图像的变化规律,并解释这种变化规律与反比例函数的性质有关。
3.解答问题:根据图像的变化规律,解答一些关于反比例函数的问题。
Step 4 拓展练习1.练习反比例函数的问题:布置一些练习题,让学生自主完成,加深对反比例函数的理解和应用能力。
2.小组合作练习:划分小组,让学生在小组内讨论并解答一些复杂应用的反比例函数问题,鼓励他们进行合作学习和思考。
四、教学反思通过本节课的学习,学生能够理解反比例函数的概念,掌握反比例函数的特征和性质。
通过实例分析和图像观察,培养了学生的观察和总结问题的能力。
初中数学反比例函数重难点汇总
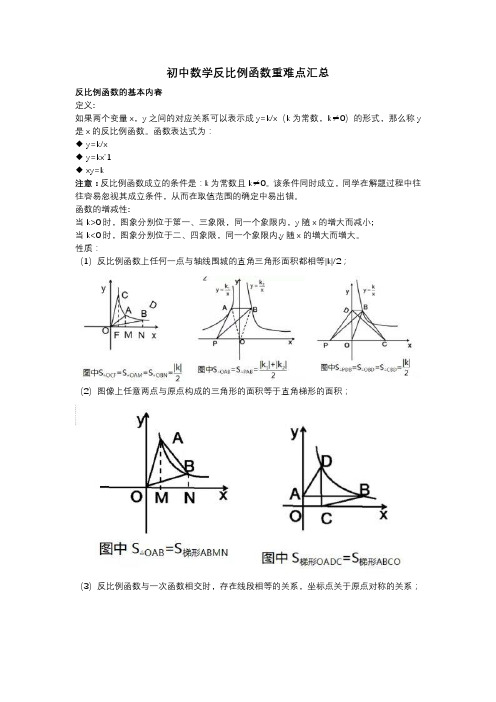
初中数学反比例函数重难点汇总反比例函数的基本内容定义:如果两个变量x,y之间的对应关系可以表示成y=k/x(k为常数,k≠0)的形式,那么称y 是x的反比例函数。
函数表达式为:◆ y=k/x◆y=kxˉ1◆ xy=k注意:反比例函数成立的条件是:k为常数且k≠0。
该条件同时成立,同学在解题过程中往往容易忽视其成立条件,从而在取值范围的确定中易出错。
函数的增减性:当k>0时,图象分别位于第一、三象限,同一个象限内,y随x的增大而减小;当k<0时,图象分别位于二、四象限,同一个象限内,y随x的增大而增大。
性质:(1)反比例函数上任何一点与轴线围城的直角三角形面积都相等|k|/2;(2)图像上任意两点与原点构成的三角形的面积等于直角梯形的面积;(3)反比例函数与一次函数相交时,存在线段相等的关系,坐标点关于原点对称的关系;(4)反比例与一次函数有交点时,可以联立求出交点坐标(二次联立可以求一元二次方程,反映方程根的个数问题)。
反比例函数常考题型结合近几年的考情分析,反比例函数往往出现在填空题和解答题中,其出题类型一般与一次函数、三角函数、相似、全等、圆等相结合,成为学生的“一大障碍”,但是其单独出题时,相对简单。
判断函数图像①看系数:一次函数只有一个未知数a;注意:若一次函数的一次项系数与反比例函数的反比例系数正负相同,直线与双曲的两支都有交点。
② 找矛盾:通常需要运用排除法,排除错误选项得到正确答案。
反比例函数只有一个未知数,因此常从反比例函数的图象入手进行判断。
如果a>0,反比例函数图像在第一、三象限,如果a<0,反比例函数图象在第二、四象限。
注意:当反比例函数与其他函数相结合出题时,需要再判断其他函数图象经过的象限就可确定其函数图像。
求解析式一般需要求出函数图象上的点的坐标,函数解析式上有几个未知数,就要找几个点。
函数图像绘制步骤:列表---描点---连线(1)列表取值时,x≠0,因为x=0函数无意义,为了使描出的点具有代表性,可以以“0”为中心,向两边对称式取值,即正、负数各一半,且互为相反数,这样也便于求y值。
专题01 反比例函数(重难点突破)(解析版)

专题01 反比例函数重点用待定系数法求反比例函数的解析式,反比例函数的图象和性质难点反比例函数中比例系数k 的几何意义易错反比例函数解析式的条件忽略k ≠0一、反比例函数的概念识别一个函数是不是反比例函数,可对照反比例函数的基本形式k y x=或变形形式xy =k (k 是常数,k ≠0),1y kx -=(k 是常数,k ≠0)进行筛选.【例1】下列函数中,y 是x 的反比例函数的有( )个.①1y x -=;②3y x =;③1xy -=;④3y x =;⑤21y x =-;⑥11y x -=.A .2B .3C .4D .5【答案】B【详解】根据反比例函数的定义可得:①1y x -=;②3y x=;③1xy -=;是反比例函数,④3y x =;⑤21y x =-;⑥11y x -=不是反比例函数,故选:B .二、用待定系数法求反比例函数的解析式确定反比例函数解析式的方法是待定系数法,由于在反比例函数(0)k y k x=¹中只有一个待定系数,因此只需要一对对应的x ,y 值或图象上一个点的坐标,即可求出k 的值,从而确定其解析式.【例2】已知y 与x 成反比例函数,且2x =时,3y =,则该函数表达式是( )A .6y x =B . 16y x =C . 6y x =D . 16y x -=-【答案】C【详解】解:∵y 与x 成反比例函数,∴设k y x=,把23x y ==,代入k y x=得6k =,所以该函数表达式是6y x =.故选:C .三、反比例函数的图象和性质(1)对于反比例函数(0)k y k x=¹,因为x ≠0,y ≠0,所以它的图象不经过原点.反比例函数的图象由两个分支组成,分别位于第一、第三象限或第二、第四象限.(2)反比例函数的增减性不是连续的,因此在谈反比例函数的增减性时,必须强调在“每一个象限内”,不能笼统地说,“当k >0时,y 随x 的增大而减小”,这样就会出现与事实不符的矛盾.(3)反比例函数图象的位置和函数的增减性都是由比例系数太的符号决定的;反过来,由双曲线所在位置和函数的增减性,也可以推断出k 的符号.【例3】函数k y x=与y =ax 2﹣bx +c 的图象如图所示,则函数y =kx +b 的大致图象为( )A .B .C .D .【答案】D 【详解】解:根据反比例函数的图象位于一、三象限知k >0,根据二次函数的图象可知a <0,-b <0,即b >0,∴函数y =kx +b 的大致图象经过一、二、三象限,故选:D .四、反比例函数ky x =中比例系数k 的几何意义在一个反比例函数图象上任取两点P ,Q ,过点P 分别作x 轴、y 轴的垂线,与坐标轴围成的矩形面积为S 1;过点Q 分别作x 轴、y 轴的垂线,与坐标轴围成的矩形面积为S 2,则S 1=S 2.【例4】如图,矩形的中心为直角坐标系的原点O ,各边分别与坐标轴平行,其中一边AB 交x 轴于点C ,交反比例函数图象于点P .当点P 是AC 的中点时,求得图中阴影部分的面积为8,则该反比例函数的表达式是( )A .2y x =B .4y x =C .8y x =D .16y x=【答案】B【详解】解:如下图所示,设矩形与y 轴交于点D ,∵矩形的中心为直角坐标系的原点O ,反比例函数的图象是关于原点对称的中心对称图形,且图中阴影部分的面积为8,∴矩形OCAD 的面积是8,设()A x y ,,则8xy =,∵点P 是AC 的中点,∴12P x y æöç÷èø,,设反比例函数的解析式为k y x =,∵反比例函数图象于点P ,∴11422k x y xy =´==,∴反比例函数的解析式为4y x =.故选:B .一、单选题1.下列函数中,y 是x 的反比例函数的是( )A .y x=-B .2y x =-C .21y x =D .221y x x =-+【答案】B【详解】A 、y x =-,不符合一般式()0k y k x =¹,故此选项错误.B 、2y x =-,符合一般式()0k y k x=¹,故此选项正确.C 、21y x =,不符合一般式()0k y k x =¹,故此选项错误.D 、221y x x =-+,不符合一般式()0k y k x =¹,故此选项错误.故选:B .2.如果反比例函数2k y x -=的图象位于第二、四象限,那么k 的取值范围是( )A . 2k <B .2k -<C .2k > D .2k ->【答案】A 【详解】解:∵反比例函数的图象位于第二、四象限,∴20k -<,∴2k <,故选:A .3.下列说法中不正确的是( )A .函数3y x =的图象经过原点B .函数1y x =的图象位于第一、三象限C .函数21y x =-的图象不经过第二象限D .函数3y x=-的值随x 的值的增大而增大【答案】D【详解】解:A 、函数3y x =的图象经过原点,故本选项正确,不符合题意;B 、函数1y x =的图象位于第一、三象限,故本选项正确,不符合题意;C 、函数21y x =-的图象不经过第二象限,故本选项正确,不符合题意;D 、在每一象限内,函数3y x=-的值随x 的值的增大而增大,故本选项错误,符合题意;故选:D4.已知正比例函数0y kx k =¹(),y 的值随x 的值的增大而减小,那么它和反比例函数()0k y k x=-¹在同一直角坐标平面内的大致图象是( )A .B .C .D .【答案】C 【详解】解:∵函数0y kx k =¹()中y 随x 的增大而减小,∴0k <,该函数图象经过第二,四象限;∴函数k y x=-的图象经过第一、三象限,故C 正确.故选:C .5.反比例函数1y x=-上图象上有三个点()()()112233,,,,,x y x y x y ,其中1230x x x <<<,则123,,y y y 的大小关系是( )A .123y y y <<B .231y y y <<C .132y y y <<D .321y y y <<【答案】B 【详解】解:∵反比例函数1y x=-的图象在二,四象限,在每一象限内y 随x 的增大而增大,而1230x x x <<<,∴123320,0,0,,y y y y y ><<>∴231,y y y <<故选B .6.如图,正比例函数1y k x =与反比例函数2k y x =的图像交于(1,)A m 、B 两点,当21k k x x£时,x 的取值范围是( )A .10x -£<或1x ³B .1x £-或01x <£C .1x £-或1x ³D .10x -£<或01x <£【答案】A 【详解】解析:Q 正比例函数1y k x =与反比例函数2k y x=的图像交于(1,)A m 、B 两点,(1,)B m \--,由图像可知,当21k k x x £时,x 的取值范围是10x -£<或1x ³,故选:A .二、填空题7.若点()1,1A x -,()2,2B x ,()3,3C x 都在反比例函数6y x =的图象上,则1x ,2x ,3x 的大小关系是______.【答案】132x x x <<##231x x x >>【详解】解:∵60>,∴反比例函数6y x =的图象在一三象限,在在每一象限内,y 随x 的增大而减小,∵1023-<<<,∴132x x x <<.故答案为:132x x x <<.8.反比例函数k y x=的图象如图所示,点A 在该函数图象上,AB 垂直于x 轴,垂足为点B ,如果2AOB S =△,那么k =________.【答案】4-【详解】设()00,A x y ,由2AOB S D =可知00.122x y = ,所以00.4x y =而点A 在第二象限,则00 . 4x y =-,因为点A 是函数图象上的一点,所以00k y x =,则004k x y =×=-故答案为:4-.三、解答题9.已知12y y y =+,1y 与x 成正比例,2y 与x 成反比例,且当=1x -时,4y =- ;当3x =时,4y =.(1)求y 关于x 的函数解析式;(2)当2x =-时,求y 的值.【答案】(1)3y x x=+(2)72-【详解】(1)解:(1)设12,n y mx y x==,则n y mx x =+,根据题意得4343m n n m --=-ìïí+=ïî,解得13m n =ìí=î.所以y 与x 的函数表达式为3y x x =+.(2)把2x =-代入得,37222y =-+=--.10.如图,一次函数()10y k x b k =+¹与反比例函数()20k y x x=>的图像交于()1,6A ,()3,B m 两点.(1)求反比例函数和一次函数的解析式:(2)根据图象直接写出21k k x b x +<时,x 的取值范围:(3)求AOB V 的面积.【答案】(1)28y x =-+,6y x =(2)01x <<或3x >(3)8【详解】(1)(1,6)A Q ,(3,)B m 在2k y x=的图象上,26k \=,\反比例函数的解析式是6y x=.2m \=.(1,6)A Q ,(3,2)B 在函数1y k x b =+的图象上,\11632k b k b +=ìí+=î,解得:128k b =-ìí=î.则一次函数的解析式是28y x =-+.所以一次函数的解析式是28y x =-+,反比例函数的解析式是6y x=;(2)由图象得:当01x <<或3x >时,21k k x b x +<;(3)Q 直线28y x =-+与y 轴相交于点C ,C \的坐标是(0,8).ΔΔΔ18(31)82AOB BOC AOC S S S \=-=´´-=.一、单选题1.已知反比例函数1a y x -=的图象位于第一、三象限,则a 的取值范围是( )A .1a =B .1a ¹C .1a >D .1a <【答案】C【详解】解:∵反比例函数1a y x -=的图象位于第一、三象限,∴10a ->,解得:1a >,故选:C .2.点()11,y ,()22,y ,()33,y ,()44,y 在反比例函数4y x =图象上,则1y ,2y ,3y ,4y 中最小的是( )A .1yB .2yC .3yD .4y 【答案】D【详解】解:∵ 40k =>,∴在第一象限内,y 随x 的增大而减小,∵()11,y ,()22,y ,()33,y ,()44,y 在反比例函数4y x =图象上,且1<2<3<4,∴4y 最小.故选:D .3.对于反比例函数5y x =-,下列说法正确的是( )A .图象经过点()2,3-B .图象位于第一、三象限C .当0x <时,y 随x 的增大而减小D .当0x >时,y 随x 的增大而增大【答案】D【详解】解:A 、()2365k ´-=-¹=-Q ,点()2,3-不满足关系式,因此A 选项不符合题意;B 、50k =-<Q ;\它的图象在第二、四象限,因此B 选项不符合题意;C 、50k =-<Q ;\它的图象在第二、四象限,当0x <时,y 随x 的增大而增大,因此C 选项不符合题意;D 、50k =-<Q ;\它的图象在第二、四象限,当0x >时,y 随x 的增大而增大,因此D 选项符合题意.故选:D .4.函数()0k y k x=¹与函数y kx k =-在同一坐标系中的图像可能是( )A .B .C .D .【答案】A 【详解】解:Q 函数y kx k =-的图像经过点(1,0),\选项B 、选项D 不符合题意;由A 、C 选项可知:0k >,\反比例函数()0k y k x=¹的图像在第一、三象限,故选项A 符合题意,选项C 不符合题意;故选:A .5.如图,在平面直角坐标系内,正方形OABC 的顶点A ,B 在第二象限内,且点A ,B 在反比例函数()0k y k x =¹的图象上,点C 在第三象限内.其中,点A 的纵坐标为3,则2k 的值为( )A .9-B .9-C .27-D .27-【答案】B【详解】解:过点A 作AE x ^轴于E ,过点B 作BF x P 轴,交AE 于F ,∵90OAE BAF OAE AOE Ð+Ð=°=Ð+Ð,∴BAF AOE Ð=Ð,在AOE △和BAF △中90AOE BAF AEO BFA OA AB Ð=ÐìïÐ=Ð=°íï=î∴()AAS AOE BAF ≌△△,∴OE AF AE BF ==,,∵点A ,B 在反比例函数()0k y k x=¹的图象上,点A 的纵坐标为3,∴33k A æöç÷èø,∴33k AE OE ==-,,∴3333k k B æö-+ç÷èø,,∴3333k k k æöæö=-+ç÷ç÷èøèø,∴29k -解得k =(正数舍去),∴29k =-故选B .6.定义:一次函数y ax b =+的特征数为[],a b .一次函数2y x m =+的图像向上平移3个单位长度后与反比例函数3y x=的图像交于点A ,B .若点A ,B 关于原点对称,则一次函数2y x m =+的特征数是( )A .[]2,0B .[]2,3C .[]2,3-D .[]2,6-【答案】C【详解】将一次函数2y x m =+向上平移3个单位长度后得到23y x m =++,设 ()()12,0, ,0,A x B x 联立233y x m y x =++ìïí=ïî22(3)30x m x \++-=,12,x x Q 是方程的两根,1232m x x +\+=-,又A Q ,B 两点关于原点对称,302m +\-=,3m \=-根据定义,一次函数2y x m =+的特征数是[]2,3-故选:C .7.如图,点A 是反比例函数4y x=图像上的一动点,连接AO 并延长交图像的另一支于点B .在点A 的运动过程中,若存在点(),C m n ,使得AC BC ^,AC BC =,则m ,n 满足( )A .mn 2=-B .4mn =-C .2n m =-D .4n m=-【答案】B 【详解】解:连接OC ,过点A 作AE x ^轴于点E ,过点C 作CF y ^轴于点F,如图所示:Q 由直线AB 与反比例函数4y x=的对称性可知A 、B 点关于O 点对称,AO BO \=,又AC BC ^Q ,AC BC =,CO AB \^,12CO AB OA ==,90AOE AOF Ð+Ð=°Q ,90AOF COF Ð+Ð=°,AOE COF \Ð=Ð,又90AEO Ð=°Q ,90CFO Ð=°,()AOE COF AAS \D @D ,OE OF \=,AE CF =,Q 点(,)C m n ,CF m \=-,OF n =,AE m \=-,OE n =,(),A n m \-,Q 点A 是反比例函数4y x=图像上,4mn \-=,即4mn =-,故选:B .8.如图,在平面直角坐标系中,正方形ABCD 的顶点A 的坐标为(﹣1,2),点B 在x 轴正半轴上,点D 在第三象限的双曲线15y x=上,过点C 作CE ∥x 轴交双曲线于点E ,则CE 的长为( )A .245B .236C .437D .214【答案】C 【详解】解:设点15,D m m æöç÷èø,如图所示,过点D 作x 轴的垂线交CE 于点G ,过点A 过x 轴的平行线交DG 于点H ,过点A 作AN ⊥x 轴于点N ,∵∠GDC +∠DCG =90°,∠GDC +∠HDA =90°,∴∠HDA =∠GCD ,在△DHA 和△CGD 中,90HDA GCDDHA CGD AD DCÐ=ÐìïÐ=Ð=°íï=î ,∴△DHA ≌△CGD (AAS),∴HA =GD ,DH =CG ,同理可证得△ANB ≌△DGC (AAS),∴AN =DG =2=AH ,则点15,2G m m æö-ç÷èøG ,CG =DH ,AH =−1−m =2,解得:m =−3,故点G (−3,−7),D (−3,−5),H (−3,2),则点15,77E æö--ç÷èø,156377GE =-=,DH=5+2=7,643777CE CG GE DH GE =-=-=-=,故选:C .二、填空题9.如图,点A 在反比例函数my x =的图象上,AB x ^轴于点B ,点C 在x 轴上,且CO OB =,ABC V 的面积为2,则m 的值为______.【答案】2-【详解】解:设||CO BO a ==,则||||m AB a =,∵ABC V 的面积为2,∴1||2||22||m a a ´´=,∵0m <解得:2m =- .故答案为:2-.10.在反比例函数4y x=中,已知四边形ABDC 与四边形BOFE 都是正方形,则点C 的坐标为_________.【答案】1)+【详解】解:设,OB a AB b ==,则点,E a a (),点(),C b a b +,∵反比例函数4y x=的图像过点C E 、,∴24()·4a a b b ì=í+=î,解得:1b ìïí=-ïî或1a b ìïí=-ïî(舍去)或1a b =ìïí=+ïî1a b =ìïí=ïî∴1AB AC b ===,21AO =,故点C 的坐标为1)+.故答案为:1)-.三、解答题11.已知反比例函数(0)k y k x=¹,当3x =-时,4y =.(1)求y 关于x 的函数表达式;(2)当43y £且0y ¹时,求自变量x 的取值范围.【答案】(1)12y x =-(2)9x £-或0x >【详解】(1)解:∵反比例函数(0)k y k x =¹,当3x =-时,4y =.∴3412k =-´=∴12y x=-,(2)当43y =时,9x =-,∵12y x=-的图象在第二、四象限,∴当43y £且0y ¹时,9x £-或0x >.12.如图,一次函数y kx b =+的图象与反比例函数m y x =的图象交于()()4,,2,4A n B -- 两点.(1)求反比例函数和一次函数的解析式;(2)设点()()1122,,,M x y N x y 是反比例函数m y x =图象上的两个点,若12x x <,试比较1y 与2y 的大小;(3)求AOB V 的面积.【答案】(1)8y x =-,2y x =--(2)见解析(3)6【详解】(1)解:(1)将点()2,4B -代入反比例函数m y x=,得2(4)8m =´-=-,∴反比例函数解析式:8y x =-,将点()4,A n -代入8y x=-,得48n -=-,解得2n =,∴()4,2A -,将A ,B 点坐标代入一次函数y kx b =+,得4224k b k b -+=ìí+=-î,解得12k b =-ìí=-î,∴一次函数解析式:2y x =--;(2)∵8y x=-,80k =-<,∴图象过二,四象限,在每一个象限内,y 随x 的增大而增大,若12x x <,分三种情况:①12120,x x y y <<<,②12120,x x y y <<>,③12120,x x y y <<<;(3)设一次函数与y 轴的交点为D ,则D 点坐标为(0,2)-,∴2OD =,∵(4,2),(2,4)A B --,∴112422622AOB AOD BDD S S S D D D =+=´´+´´=,∴AOB V 的面积为6.13.如图,直线6y ax =+经过点()30A -,,交反比例函数()0ky x x=>的图象于点()1,B m .(1)求k 的值;(2)点D 为第一象限内反比例函数图象上点B 下方的一个动点,过点D 作DC y ^轴交线段AB 于点C ,连接AD ,求ACD V 的面积的最大值.【答案】(1)8(2)254【详解】(1)解:把()30A -,代入6y ax =+,得360a -+=,解得2a =,∴直线的函数表达式为26y x =+,∴当1x =时,2168y =´+=,∴()1,8B ,把()1,8B 代入反比例函数k y x=,得188k =´=.(2)解:设点C 的坐标为(),26x x +,由于DC y ^轴,所以点D 的纵坐标为26x +,∴点8,2626D x x æö+ç÷+èø,∴()()22118325262634222624ACD S CD x x x x x x x æöæö=´+=-´+=--+=-++ç÷ç÷+èøèø△,∴当 1.5x =-时,254ACD S =△最大值,答:ACD S V 的最大值为254.14.如图,函数y =k x(x >0)的图像过点A (n ,2)和B (85,2n −3)两点.(1)求n 和k 的值;(2)将直线OA 沿x 轴向左移动得直线DE ,交x 轴于点D ,交y 轴于点E ,交y =k x (x >0)于点C ,若ACO S V =6,求直线DE 解析式;(3)在(2)的条件下,第二象限内是否存在点F ,使得△DEF 为等腰直角三角形,若存在,请直接写出点F 的坐标;若不存在,请说明理由.【答案】(1)4,8n k ==;(2)132y x =+;(3)(9,6)-或(3,9)-或99(,22-.【详解】(1)解:Q 函数=k y x (x >0)的图像过点A (n ,2)和B (85,2n −3)两点,2=8(23)=5n k n k \-ìïíïî,解得=4=8n k ìíî,故n 和k 的值分别为4,8.(2)解:4,8n k ==Q ,8(4,2),(,5)5A B \,直线OA 的解析式为:12y x =,过点C 作CG x ^轴于点G ,交直线OA 于点H ,设8(,0)C m m m>,1(,)2H m m \,162AOC A S CH x D \=×=,181()4622m m \-´=,2m \=或=8m(不符合题意舍去)(2,4)C \,DE OA ∥Q ,\设直线DE 的解析式为:12y x b =+,Q 点C 在直线DE 上,1422b \=´+即=3b ,\直线DE 的解析式为:132y x =+.(3)解:根据题意,分三种情况进行讨论:①以DE 为直角边,D 为直角顶点;如图,过F 做FK x ^轴于点K ,易知:90FKD DOE Ð=Ð=°,90FDE Ð=°Q ,90FDK EDO \Ð+Ð=°,又90DEO EDO Ð+Ð=°Q ,FDK DEO \Ð=Ð,又FD =DE ,FKD DOE \D D ≌,\FK =DO =6,KD =OE =3,故点D 到点F 的平移规律是:D 向左移3个单位,向上移6个单位得点1F 坐标,(6,0)D -Q ,且F 在第二象限,1(63,06)F \--+即1(9,6)F -;②以DE 为直角边,E 为直角顶点;同①理,将E 点向左移3个单位,向上移6个单位得点F 坐标,得2(3,9)F -;③以DE 为斜边边时.同理,将ED 中点3(3,2-向左移32个单位,向上移3个单位得点F 坐标,得399(,)22F -;综上所述,点F 的坐标为:(9,6)-或(3,9)-或99(,)22-.。
(完整版)反比例函数教案

第十七章 反比例函数17.1.1反比例函数的意义一、教学目标1.使学生理解并掌握反比例函数的概念2.能判断一个给定的函数是否为反比例函数,并会用待定系数法求函数解析式 3.能根据实际问题中的条件确定反比例函数的解析式,体会函数的模型思想 二、重、难点1.重点:理解反比例函数的概念,能根据已知条件写出函数解析式 2.难点:理解反比例函数的概念 3.难点的突破方法:(1)在引入反比例函数的概念时,可适当复习一下第11章的正比例函数、一次函数等相关知识,这样以旧带新,相互对比,能加深对反比例函数概念的理解(2)注意引导学生对反比例函数概念的理解,看形式xky =,等号左边是函数y ,等号右边是一个分式,自变量x 在分母上,且x 的指数是1,分子是不为0的常数k;看自变量x 的取值范围,由于x 在分母上,故取x ≠0的一切实数;看函数y 的取值范围,因为k ≠0,且x ≠0,所以函数值y 也不可能为0.讲解时可对照正比例函数y =kx (k ≠0),比较二者解析式的相同点和不同点。
(3)xky =(k ≠0)还可以写成1-=kx y (k ≠0)或xy =k(k ≠0)的形式三、例题的意图分析教材第46页的思考题是为引入反比例函数的概念而设置的,目的是让学生从实际问题出发,探索其中的数量关系和变化规律,通过观察、讨论、归纳,最后得出反比例函数的概念,体会函数的模型思想。
教材第47页的例1是一道用待定系数法求反比例函数解析式的题,此题的目的一是要加深学生对反比例函数概念的理解,掌握求函数解析式的方法;二是让学生进一步体会函数所蕴含的“变化与对应”的思想,特别是函数与自变量之间的单值对应关系。
补充例1、例2都是常见的题型,能帮助学生更好地理解反比例函数的概念.补充例3是一道综合题,此题是用待定系数法确定由两个函数组合而成的新的函数关系式,有一定难度,但能提高学生分析、解决问题的能力。
四、课堂引入1.回忆一下什么是正比例函数、一次函数?它们的一般形式是怎样的?2.体育课上,老师测试了百米赛跑,那么,时间与平均速度的关系是怎样的? 五、例习题分析例1.见教材P47分析:因为y 是x 的反比例函数,所以先设xky =,再把x =2和y =6代入上式求出常数k,即利用了待定系数法确定函数解析式。
九年级反比例函数重难点题型

反比例函数章末重难点题型一、反比例函数的概念一般地,可化为形如:(),0ky k kx=≠为常数且叫做反比例函数,即y是x的反比例函数。
(x为自变量,y为因变量,其中x、y不能为零)反比例函数的等价形式:y是x的反比例函数:①一般式()0ky kx=≠,②指数式(主要用于填空选择题)()10y kx k-=≠,③乘积式(变量积为定值是分析反比例函数应用的理论基础)()0xy k k=≠←→变量y与x成反比例,比例系数为k,k不为零是重要条件.二、反比例函数性质①当k>0时,双曲线的两支分别位于一、三象限;在每个象限内,y随x的增大而减小;②当k<0时,双曲线的两支分别位于二、四象限;在每个象限内,y随x的增大而增大;③双曲线的两支会无限接近坐标轴(x轴和y轴),但不会与坐标轴相交。
拓展:反比例函数的图像(双曲线)既是轴对称图形也是中心对称图形,两条对称轴分别为直线xy±=,对称中心为坐标原点。
三、反比例函数图象的几何特征:(如下图所示)点P(x,y)在双曲线上都有11||||||||22AOBOAPBS xy k S xy k∆====矩形PBAOP BA O反比例函数()0≠=k xky 图像是双曲线,我们会经常遇到与之有关的面积问题,现对这部分内容进行拓展。
【考点1反比例函数的定义】【方法点拨】一般地,形如xky =(k 为常数,o k ≠)的函数称为反比例函数。
(自变量x 的取值:o x ≠)反比例函数的等价形式:①xk y =(o k ≠)②kxy =1-(o k ≠)③xy=k(o k ≠)【例1】下列函数中,是反比例函数的是()A .3y x =+B .21y x =C .2y x=D .34y x=【变式1-1】若函数()21-+=m x m y 是反比例函数,则=m ()A .1±B .3±C .1-D .1【变式1-2】下列函数:①2y x =-,②3x y =,③1y x -=,④21y x =+,y 是x 的反比例函数的个数有()A .0个B .1个C .2个D .3个【变式1-3】下列函数中,y 是x 的反比例函数有()(1)3y x =;(2)2y x =-;(3)3xy =;(4)3xy -=;(5)21y x =+;(6)21y x =;(7)22y x -=;(8)ky x=.A .(2)(4)B .(2)(3)(5)(8)C .(2)(7)(8)D .(1)(3)(4)(6)【考点2反比例函数的性质】【方法点拨】反比例函数性质如下表:k 的取值图像所在象限函数的增减性0>k 一、三象限在每个象限内,y 值随x 的增大而减小0<k 二、四象限在每个象限内,y 值随x 的增大而增大【例2】在反比例函数3my x-=的图象在某象限内,y 随着x 的增大而减小,则m 的取值范围是()A .3m >-B .3m <-C .3m >D .3m <【变式2-1】若反比例函数2ky x-=的图象位于第一、第三象限,则k 的取值范围是()A .2k <B .2k >-C .2k <-D .2k >【变式2-2】从3、1、1-、2-、3-这五个数中,取一个数作为函数2k y x-=和关于x 的方程2(1)210k x kx +++=中k 的值,恰好使所得函数的图象经过第二、四象限,且方程有实根,满足要求的k 的值共有()个.A .1B .2C .3D .4【变式2-3】已知关于x 的方程2(1)10x m x --+=有两个相等的实数根,且反比例函数1m y x-=的图象在每个象限内y 随x 的增大而减小,那么m 的值为()A .3B .3或1-C .2-D .1-【考点3反比例函数值大小比较】【方法点拨】灵活运用反比例函数的图象和性质进行推理是解此类题的关键,反比例函数的增减性只指在同一象限内.【例3】反比例函数ky x=的图象经过点(1,2)-,1(A x ,1)y 、2(B x ,2)y 是图象上另两点,其中120x x <<,那么1y 、2y 的大小关系是()A .12y y >B .12y y <C .12y y =D .都有可能【变式3-1】已知反比例函数2y x=-的图象上有三个点1(x ,1)y 、2(x ,2)y 、3(x ,3)y ,若1230x x x >>>,则下列关系是正确的是()A .123y y y <<B .213y y y <<C .321y y y <<D .231y y y <<【变式3-2】设1(2,)A y -,2(1,)B y ,3(2,)C y 是双曲线3y x=-上的三点,则()A .123y y y >>B .132y y y >>C .321y y y >>D .312y y y >>【变式3-3】若反比例函数1(1,0)a y a x x-=><图象上有两个点1(x ,1)y ,2(x ,2)y ,设1212()()m x x y y =--,则y mx m =-不经过第()象限.A .一B .二C .三D .四【考点4与反比例函数有关的图象问题】【例4】反比例函数ky x=与1(0)y kx k =-+≠在同一坐标系的图象可能为()A .B .C .D .【考点5反比例函数K 的几何意义】【方法点拨】反比例函数x k y =(0≠k )中比例系数k 的几何意义是:过双曲线xk y =(0≠k )上任意引x 轴y 轴的垂线,所得矩形面积为k 。
人教版九年级数学下册:26.1.1《反比例函数》说课稿

人教版九年级数学下册:26.1.1《反比例函数》说课稿一. 教材分析《反比例函数》是人教版九年级数学下册第26章第一节的内容,本节课主要介绍了反比例函数的定义、性质及图象。
这部分内容是在学生已经掌握了函数的概念、正比例函数的知识基础上进行学习的,为后续学习二次函数打下基础。
反比例函数是实际应用中经常遇到的一种函数形式,对于学生来说,理解和掌握反比例函数的知识,能够提高他们解决实际问题的能力。
二. 学情分析九年级的学生已经具备了一定的函数知识,对于正比例函数的概念和图象已经有了一定的了解。
但是,反比例函数的概念和性质相对复杂,学生可能难以理解和接受。
因此,在教学过程中,需要关注学生的认知水平,通过合适的教学方法,帮助学生理解和掌握反比例函数的知识。
三. 说教学目标1.知识与技能目标:让学生理解反比例函数的定义,掌握反比例函数的性质,能够绘制反比例函数的图象。
2.过程与方法目标:通过观察、分析、归纳等方法,让学生学会如何从实际问题中抽象出反比例函数模型。
3.情感态度与价值观目标:培养学生对数学的兴趣,提高学生解决实际问题的能力。
四. 说教学重难点1.教学重点:反比例函数的定义,反比例函数的性质,反比例函数图象的特点。
2.教学难点:反比例函数概念的理解,反比例函数性质的证明,反比例函数图象的绘制。
五. 说教学方法与手段1.教学方法:采用问题驱动法、案例分析法、小组合作学习法等,引导学生主动探究,培养学生的动手操作能力和思维能力。
2.教学手段:利用多媒体课件、实物模型、反比例函数图象软件等,帮助学生直观地理解反比例函数的知识。
六. 说教学过程1.导入:通过展示实际问题,引导学生思考如何用数学模型来解决这些问题,从而引出反比例函数的概念。
2.新课讲解:讲解反比例函数的定义,通过示例让学生理解反比例函数的概念。
然后,引导学生通过观察、分析、归纳等方法,总结出反比例函数的性质。
3.实践操作:让学生利用反比例函数图象软件,绘制反比例函数的图象,观察图象的特点,进一步理解反比例函数的性质。
反比例函数教案设计(篇)

反比例函数教案设计(优秀篇)一、教学目标1. 知识与技能:(1)理解反比例函数的定义;(2)掌握反比例函数的性质;(3)能够运用反比例函数解决实际问题。
2. 过程与方法:(1)通过观察实例,引导学生发现反比例函数的规律;(2)利用图形演示反比例函数的特点;(3)运用数学建模的方法,解决生活中的反比例函数问题。
3. 情感态度与价值观:(1)培养学生对数学的兴趣和好奇心;(2)培养学生运用数学知识解决实际问题的能力;(3)培养学生的团队协作和交流能力。
二、教学重点与难点1. 教学重点:(1)反比例函数的定义;(2)反比例函数的性质;(3)反比例函数在实际问题中的应用。
2. 教学难点:(1)反比例函数图形的特点;(2)解决实际问题时,如何建立反比例函数模型。
三、教学过程1. 导入新课:(1)引导学生回顾正比例函数的知识;(2)通过提问,激发学生对反比例函数的好奇心。
2. 自主学习:(1)让学生阅读教材,理解反比例函数的定义;(2)学生相互讨论,总结反比例函数的性质。
3. 课堂讲解:(1)利用图形演示反比例函数的特点;(2)讲解反比例函数在实际问题中的应用。
4. 课堂练习:(1)布置一些反比例函数的题目,让学生独立完成;(2)挑选学生回答,总结解题思路。
5. 课后作业:(1)巩固反比例函数的知识;(2)培养学生运用反比例函数解决实际问题的能力。
四、教学评价1. 课堂讲解:评价学生对反比例函数的理解程度;2. 课堂练习:评价学生运用反比例函数解决问题的能力;3. 课后作业:评价学生对反比例函数知识的掌握情况。
五、教学资源1. 教材:提供反比例函数的相关知识;2. 图形演示软件:帮助学生直观地理解反比例函数的特点;3. 实际问题案例:培养学生运用反比例函数解决实际问题的能力。
六、教学策略1. 实例引导:通过展示实际生活中的反比例关系,如人口增长、radioactive decay等,让学生直观地感受反比例函数的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反比例函数
考点一、反比例函数的定义
例1、若点(3,6)在反比例函数x
k
y =
(k ≠0)的图象上,那么下列各点在此图象上的是 ( )
A. (3-,6)
B. (2,9)
C. (2,9-)
D. (3,6-)
练习题1、已知反比例函数的图象过(2,-2)和(-1,n ),则n 等于 ( ) A. 3 B. 4 C. 6 D. 12 2、 当_____=k 时,双曲线y=x
k
过点(3,23) 考点二:反比例函数的图象
例2、若()()()321,1,,2,,3y C y B y A ---三点都在函数x
y 1
-
=的图象上,则321,,y y y 的大小关系是( )
A. 321y y y <<
B. 321y y y ==
C. 231y y y <<
D. 321y y y >>
练习题1、若点 (x 1,y 1),(x 2,y 2),(x 3,y 3)都是反比例函数y = 3
x
的图象上的点,并且
x 1 < 0 < x 2 < x 3,则下列各式正确的是( ).
A. y 1 < y 2 < y 3
B. y 2 < y 3 < y 1
C. y 1 < y 3 < y 2
D. y 3 < y 2 < y 1
2、如图,是三个反比例函数x
k y x k
y x k y 321,,===
在x 轴上的图像,由此观察得到k 1、k 2、k 3的大小关系为 ( )
A. k 1>k 2>k 3
B. k 1>k 3>k 2
C. k 2>k 3>k 1
D. k 3>k 2>k 1
考点三:反比例函数的性质 例5、已知反比例函数x
k
y -=
4,分别根据以下条件求出k 的取值范围。
(1)函数图象位于第一、三象限内;
(2)在每一个象限内,y 随x 的增大而增大。
2. 如图,若反比例函数x
k
y =
的图象过点(-2,3),则该函数的解析式为__________; 考点四:反比例函数与坐标轴 例、如图,在函数)0(≠=
k x
k
y 的图象上有三点A ,B ,C 过这三个点分别向x 轴、y 轴引垂线,过每个点所引的两条垂线与x 轴,y 轴围成的矩形的面积分别是S 1、S 2、S 3,则( )
A S 1>S 2>S 3
B S 1<S 2<S 3
C S 1<S 3<S 2
D S 1=S 2=S 3
练习:如图,点P 是双曲线上的一点,过P 点分别向x 轴, y 轴引垂线,得到图中的阴影部分的矩形面积为3,则这个反比例函数的解析式为 。
考点五:反比例函数的实际应用
例7、小明将一篇24000字的社会调查报告录入电脑,打印成文.
(1)如果小明以每分钟120字的速度录入,他需要多长时间才能完成录入任务? (2)录入文字的速度v (字/min )与完成录入的时间t (min )有怎样的函数关系. (3)小明希望能在3h 内完成录入任务,那么他每分钟至少应录入多少个字?
练习:蓄电池的电压为定值,使用此电源时,电流I (A )与电阻R (Ω)之间的函数关系如图所示。
(1)蓄电池的电压是多少?你能写出这一函数的表达式吗? (2)完成下表,并回答问题:如果以此蓄电池为电源的用电器限制电流不得超过10A ,那么用电器的可变电阻应控制在什么范围内?
Ω/R 3 4 5 6 7 8 9 10 A /I
4
考点六:反比例函数与一次函数的应用
例10、如图,一次函数b kx y +=的图象与反比例函数x
m
y =的图象相交于A 、B 两点。
(1)根据图象,写出B 点的坐标; (2)求出两函数的解析式;
(3)根据图象回答:当x 为何值时,一次函数的函数值大于反比例函数的值。
练习题:如图,平行于直线x y =的直线l 不经过第四象限,且与函数()03
>=
x x
y 的图象交于点A ,过点A 作AB⊥y 轴于点B ,AC⊥x 轴于点C ,四边形ABOC 的周长是8,求直线l 的解析式。
考点七:课外拓展
1、如图,反比例函数x
k
=
y (k >0)与一次函数b x 21y +=的图象相交于两点A (1x ,
1y ),B (2x ,2y ),线段AB 交y 轴与C ,当|1x -2x |=2且AC = 2BC 时,k 、b 的值分别为
( ) A.k =
21,b =2 B.k =94,b =1 C.k =13,b =13 D.k =9
4
,b =13
2、如图,直线l是经过点(1,0)且与y 轴平行的直线.Rt△ABC 中直角边AC=4,BC=3.将BC 边在直线l上滑动,使A ,B 在函数x
k
y =的图象上.那么k 的值是( ) A .3 B .6 C.12 D .4
15
3、定义新运算: a ⊕b =⎪⎩⎪
⎨⎧≠>-≤-)0()(1b b a b
a b a a 且,则函数y=3⊕x 的图象大致是( )
4、方程x 2
+2x -1=0的根可看成函数y =x +2与函数1
y x
=
的图象交点的横坐标,用此方法可推断方程x 3
+x -1=0的实根x 所在范围为( ) A . 102x -<< B .102x << C .112x << D .312
x <<。
