2018学年上海市各区一模考第25题
闵行区九年级一模数学附解析

闵行区2018学年第一学期九年级质量调研考试数 学 试 卷测试时间:100分钟,满分:150分1.本试卷含三个大题,共25题.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤. 3.本次考试可使用科学计算器.一、选择题:本大题共6题,每题4分,满分24分1.在Rt△ABC 中,∠C = 90°,∠A 、∠B 、∠C 所对的边分别为a 、b 、c ,下列等式中不成立的是 A tan b B a=;B cos a B c=; C sin a A c=;D cot a A b=.2.如果从甲船看乙船,乙船在甲船的南偏东30°方向,那么从乙船看甲船,甲船在 乙船的A 北偏东30°;B 北偏西30°;C 北偏东60°;D 北偏西60°.3.将二次函数22(2)y x =-的图像向左平移1个单位,再向下平移3个单位后所得图像的函数解析式为 A 22(2)4y x =--; B 22(1)3y x =-+; C 22(1)3y x =--; D 223y x =-.4.已知二次函数2y a x b x c =++的图像如图所示,下列判断中不正确的是 A a < 0; B b > 0; C c > 0;D abc > 0.5.已知:点C 在线段AB 上,且AC = 2BC ,那么下列等式一定正确的是 A 423AC BC AB +=;B 20AC BC -=; C AC BC BC +=;D AC BC BC -=. 6.已知在△ABC 中,点D 、E 、F 分别在边AB 、AC 和BC 上,且DE // BC ,DF // AC ,那么下列比例式中,正确的是 AFBCFEC AE =; B BCDEEC AE =; C BCDEAC DF =; DBCFCAC EC =. 二、填空题:本大题共12题,每题4分,满分48分 7.已知:x ︰y = 2︰5,那么x +y ︰y = .第4题图8.化简:313()222a b a b -++-= .9.抛物线232y x x =++与y 轴的公共点的坐标是 .10.已知二次函数2132y x =--,如果x > 0,那么函数值y 随着自变量x 的增大而.填“增大”或“减小”.11.已知线段AB = 4厘米,点P 是线段AB 的黄金分割点AP > BP ,那么线段 AP = 厘米.结果保留根号12.在△ABC 中,点D 、E 分别在边AB 、AC 上,且DE // BC .如果35AD AB =,DE = 6,那么BC = .13.已知两个相似三角形的相似比为2︰3,那么这两个相似三角形的面积比为 .14.在Rt △ABC 中,∠C= 90°,AB =1tan 3A =,那么BC = . 15.某超市自动扶梯的坡比为1︰.一位顾客从地面沿扶梯上行了米,那么这位顾客此时离地面的高度为米.16.在△ABC 和△DEF 中,AB BCDE EF=.要使△ABC ∽△DEF ,还需要添加一个条件,那么这个条件可以是 只需填写一个正确的答案.17.如图,在Rt △ABC 中,∠ACB = 90°,AC BC ==,点D 、E分别在边AB 上,且AD = 2,∠DCE = 45°,那么DE =.18.如图,在Rt △ABC 中,∠ACB = 90°,BC = 3,AC = 4,点D为边AB上一点.将△BCD 沿直线CD 翻折,点B 落在点E 处,联结AE .如果AE // CD ,那么BE = . 三、解答题:本大题共7题,满分78分 19.本题满分10分已知在平面直角坐标系xOy 中,二次函数2y a x bx c =++的图像经过点A 1,0、B 0,-5、C 2,3.求这个二次函数的解析式,并求出其图像的顶点坐标和对称轴.20.本题共2小题,第1小题4分,第2小题6分,满分10分如图,在平行四边形ABCD 中,对角线AC 、BD 相交于点O .E 为边AB 上一点,且BE = 2AE .设AB a =,AD b =.1填空:向量DE = _ ;2如果点F 是线段OC 的中点,那么向量EF = _ ,并在图中画出向量EF 在向量AB 和AD方向第20题图ABCDEOABC第18题图A BCDE第17题图上的分向量.注:本题结果用向量a b 、的式子表示.画图不要求写作法,但要指出所作图中表示结论的向量.21.本题共2小题,每小题5分,满分10分如图,在Rt △ABC 中,∠ACB = 90°,BC = 6,AC =8.点D 是AB 边上一点,过点D 作DE // BC ,交边AC 于E .过点C 作CF // AB ,交DE 的延长线于点F . 1如果13AD AB =,求线段EF 的长; 2求∠CFE 的正弦值. 22.本题满分10分如图,某公园内有一座古塔AB ,在塔的北面有一栋建筑物,某日上午9时太阳光线与水平面的夹角为32°,此时塔在建筑物的墙上留下了高3米的影子CD .中午12时太阳光线与地面的夹角为45°,此时塔尖A 在地面上的影子E 与墙角C 的距离为15米B 、E 、C 在一条直线上,求塔AB 的高度.结果精确到米参考数据:sin 32°≈,cos 32°≈,tan 32°≈,1.4142≈.23.本题共2小题,每小题6分,满分12分如图,在△ABC 中,点D 为边BC 上一点,且AD = AB ,AE ⊥BC ,垂足为点E .过点D 作DF // AB ,交边AC 于点F ,联结EF ,212EF BD EC =⋅. 1求证:△EDF ∽△EFC ; 2如果14EDF ADCS S=,求证:AB = BD . 24.本题共3小题,每小题4分,满分12分已知:在平面直角坐标系xOy 中,抛物线2y a x b x =+经过点A 5,0、B -3,4,抛物线的对称轴与x 轴相交于点D . 1求抛物线的表达式;2联结OB 、BD .求∠BDO 的余切值; 3如果点P 在线段BO 的延长线上,且∠PAO =∠BAO ,求点P 的坐标.25.本题满分14分,其中第1小题4分、第2、3小题各5分xyO第24题图ABCDEF第21题图第22题图A BCDEF第23题图如图,在梯形ABCD 中,AD // BC ,AB = CD ,AD = 5,BC = 15,5cos 13ABC ∠=.E 为射线CD 上任意一点,过点A 作AF // BE ,与射线CD 相交于点F .联结BF ,与直线AD 相交于点G .设CE = x ,AGy DG=. 1求AB 的长;2当点G 在线段AD 上时,求y 关于x 的函数解析式,并写出函数的定义域; 3如果23ABEF ABCDS S =四边形四边形,求线段CE 的长.ABC DEF G第25题图A BCD备用图闵行区2018学年第一学期九年级质量调研考试数学试卷参考答案及评分标准一、选择题:1.D ; 2.B ; 3.C ; 4.B ; 5.C ; 6.A . 二、填空题:7.7︰5或75; 8.14a b -+; 9.0,2; 10.减小; 11.2; 12.10; 13.4︰9或49; 14.2; 15.2; 16.∠B =∠E 或AB AC DE DF =或BC ACEF DF=; 17.103; 18.245或. 三、解答题:19.解:由这个函数的图像经过点A 1,0、B 0,-5、C 2,3,得0,5,42 3.a b c c a b c ++=⎧⎪=-⎨⎪++=⎩…………………………………………………………3分 解得 1,6,5.a b c =-⎧⎪=⎨⎪=-⎩……………………………………………………………3分所以,所求函数的解析式为265y x x =-+-.…………………………1分2265(3)4y x x x =-+-=--+.所以,这个函数图像的顶点坐标为3,4,…………………………2分 对称轴为直线x = 3.……………………………………………………1分20.解:113a b -.4分 253124a b +.4分画图及结论正确.2分 21.解:1∵ DE // BC ,∴13AD DE AB BC ==.………………………………1分 又∵ BC = 6,∴ DE = 2.………………………………………1分 ∵ DF // BC ,CF // AB ,∴ 四边形BCFD 是平行四边形.…1分 ∴ DF = BC = 6.∴ EF = DF – DE = 4.………………………2分 2∵ 四边形BCFD 是平行四边形, ∴ ∠B =∠F .……………1分在Rt△ABC 中,∠ACB = 90°,BC = 6,AC = 8,利用勾股定理,得10AB =.………1分 ∴ 84sin 105AC B AB ===.∴ 4sin 5CFE ∠=.…………………2分 22.解:过点D 作DH ⊥AB ,垂足为点H .由题意,得 HB = CD = 3,EC = 15,HD = BC ,∠ABC =∠AHD = 90°, ∠ADH = 32°.设AB = x ,则 AH = x – 3.………………………………………………1分在Rt△ABE 中,由 ∠AEB = 45°,得 tan tan 451ABAEB EB∠=︒==.2分 ∴ EB = AB = x .∴ HD = BC = BE + EC = x + 15.………………2分 在Rt△AHD 中,由 ∠AHD = 90°,得 tan AHADH HD∠=. 即得 3tan3215x x -︒=+.…………………………………………………2分 解得 15tan32332.99331tan32x ⋅︒+=≈≈-︒.…………………………………2分∴ 塔高AB 约为33米. ………………………………………………1分23.证明:1∵ AB = AD ,AE ⊥BC ,∴ 12ED BE BD ==.……………2分∵ 212EF BD EC =⋅,∴ 2EF ED EC =⋅.即得EF EDEC EF=.2分 又∵ ∠FED =∠CEF ,∴ △EDF ∽△EFC .………………2分 2∵ AB = AD ,∴ ∠B =∠ADB .………………………………1分又∵ DF // AB ,∴ ∠FDC =∠B . ∴ ∠ADB =∠FDC .∴ ∠ADB +∠ADF =∠FDC +∠ADF ,即得 ∠EDF =∠ADC .2分 ∵ △EDF ∽△EFC ,∴ ∠EFD =∠C .∴ △EDF ∽△ADC .……………………………………………1分∴2214EDF ADCS ED SAD ==. ∴12ED AD =,即 12ED AD =.………………………………1分 又∵ 12ED BE BD ==,∴ BD = AD .∴ AB = BD .……………………………………………………1分24.解:1∵ 抛物线2y a x b x =+经过点A 5,0、B -3,4,∴ 2550,93 4.a b a b +=⎧⎨-=⎩…………………………………………………2分解得 1,65.6a b ⎧=⎪⎪⎨⎪=-⎪⎩……………………………………………………1分∴ 所求抛物线的表达式为21566y x x =-.………………………1分 2由21566y x x =-,得抛物线的对称轴为直线52x =.∴ 点D 52,0.………………………………………………1分 过点B 作BC ⊥x 轴,垂足为点C .由A 5,0、B -3,4,得 BC = 4,OC = 3,511322CD =+=.1分 ∴ 11cot 8CD BDO CB ∠==. ………………………………………2分 3设点Pm ,n .过点P 作PQ ⊥x 轴,垂足为点Q .则 PQ = -n ,OQ = m ,AQ = 5 – m . 在Rt△ABC 中,∠ACB = 90°,∴ 8cot 24AC BAC BC ∠===. ∵ ∠PAO =∠BAO ,∴ 5cot 2AQ mPAO PQ n-∠===-. 即得 25m n -=. ①…………………………………………1分 由 BC ⊥x 轴,PQ ⊥x 轴,得 ∠BCO =∠PQA = 90°. ∴ BC // PQ . ∴BC OC PQ OQ =,即得 43n m=-.∴ 4 m = - 3 n . ②………1分 由 ①、②解得 1511m =,2011n =-.……………………………1分 ∴ 点P 的坐标为1511,2011-.………………………………1分 25.解:1分别过点A 、D 作AM ⊥BC 、DN ⊥BC ,垂足为点M 、N .∵ AD // BC ,AB = CD ,AD = 5,BC = 15,∴ 11()(155)522BM BC AD =-=-=.…………………………2分 在Rt△ABM 中,∠AMB = 90°, ∴ 55cos 13BM ABM AB AB ∠===. ∴ AB = 13.………………………………………………………2分 2∵AG y DG =,∴ 1AG DGy DG+=+.即得 51DG y =+.……1分 ∵ ∠AFD =∠BEC ,∠ADF =∠C .∴ △ADF ∽△BCE . ∴51153FD AD EC BC ===.…………………………………………1分 又∵ CE = x ,13FD x =,AB = CD = 13.即得 1133FC x =+.∵ AD // BC ,∴ FD DG FC BC =.∴ 5113115133x y x +=+.………1分 ∴ 3923xy x-=. ∴ 所求函数的解析式为3923x y x -=,函数定义域为3902x <<.2分 3在Rt△ABM 中,利用勾股定理,得12AM =.∴ 11()(515)1212022ABCD S AD BC AM =+⋅=+⨯=梯形. ∵ 23ABEF ABCDS S =四边形四边形,∴ 80ABEF S =四边形. ………………………1分 设ADFSS =.由 △ADF ∽△BCE ,13FD EC =,得 9BECS S =.过点E 作EH ⊥BC ,垂足为点H . 由题意,本题有两种情况:ⅰ如果点G 在边AD 上,则 840ABCD ABEF S S S -==四边形四边形.∴ S = 5. ∴ 945BECS S ==.∴ 11154522BEC SBC EH EH =⋅=⨯⋅=. ∴ 6EH =.由 DN ⊥BC ,EH ⊥BC ,易得 EH // DN . ∴61122CE EH CD DN ===. 又 CD = AB = 13,∴ 132CE =.………………………………2分 ⅱ如果点G 在边DA 的延长线上,则 9ADFABCD ABEF S S SS ++=四边形四边形.∴ 8200S =.解得 25S =. ∴ 9225BECS S ==.∴ 111522522BEC S BC EH EH =⋅=⨯⋅=.解得 30EH =. ∴305122CE EH CD DN ===.∴ 652CE =.………………………2分 ∴ 136522CE =或.。
(11套)2018年上海市 含所有区 高考数学一模试卷 汇总 (2)(打包下载)

(11套)2018年上海市含所有区高考数学一模试卷汇总2018年上海市崇明区高考数学一模试卷一、填空题(本大题共有12题,满分54分,其中1-6题每题4分,7-12题每题5分)1.(4分)已知集合A={1,2,5},B={2,a},若A∪B={1,2,3,5},则a=.2.(4分)抛物线y2=4x的焦点坐标为.3.(4分)不等式<0的解是.4.(4分)若复数z满足iz=1+i(i为虚数单位),则z=.5.(4分)在代数式(x﹣)7的展开式中,一次项的系数是.(用数字作答)6.(4分)若函数y=2sin(ωx﹣)+1(ω>0)的最小正周期是π,则ω=.7.(5分)若函数f(x)=x a的反函数的图象经过点(,),则a=.8.(5分)将一个正方形绕着它的一边所在的直线旋转一周,所得几何体的体积为27πcm3,则该几何体的侧面积为cm2.9.(5分)已知函数y=f(x)是奇函数,当x<0 时,f(x)=2x﹣ax,且f(2)=2,则a=.10.(5分)若无穷等比数列{a n}的各项和为S n,首项a1=1,公比为a﹣,且S n=a,则a=.11.(5分)从5男3女共8名学生中选出队长1人,副队长1人,普通队员2人组成4人志愿者服务队,要求服务队中至少有 1 名女生,共有种不同的选法.(用数字作答)12.(5分)在ABC中,BC边上的中垂线分别交BC,AC于点D,E.若•=6,||=2,则AC=.二、选择题(本大题共有4题,满分20分)13.(5分)展开式为ad﹣bc的行列式是()A.B.C.D.14.(5分)设a,b∈R,若a>b,则()A.<B.lga>lgb C.sin a>sin b D.2a>2b15.(5分)已知等差数列{a n}的公差为d,前n项和为S n,则“d>0”是“S4+S6>2S5”的()A.充分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分也不必要条件16.(5分)直线x=2与双曲线﹣y2=1的渐近线交于A,B两点,设P为双曲线上任一点,若=a+b(a,b∈R,O为坐标原点),则下列不等式恒成立的是()A.a2+b2≥1 B.|ab|≥1 C.|a+b|≥1 D.|a﹣b|≥2三、解答题(本大题共有5题,满分76分)17.(14分)如图,长方体ABCD﹣A1B1C1D1中,AB=BC=2,A1C与底面ABCD所成的角为60°,(1)求四棱锥A1﹣ABCD的体积;(2)求异面直线A1B与B1D1所成角的大小.18.(14分)已知f(x)=2sinxcosx+2cos2x﹣1.(1)求f(x)的最大值及该函数取得最大值时x的值;(2)在△ABC 中,a,b,c分别是角A,B,C所对的边,若a=,b=,且f()=,求边c的值.19.(14分)2016 年崇明区政府投资8 千万元启动休闲体育新乡村旅游项目.规划从2017 年起,在今后的若干年内,每年继续投资 2 千万元用于此项目.2016 年该项目的净收入为 5 百万元,并预测在相当长的年份里,每年的净收入均为上一年的基础上增长50%.记2016 年为第 1 年,f (n)为第 1 年至此后第n (n∈N*)年的累计利润(注:含第n 年,累计利润=累计净收入﹣累计投入,单位:千万元),且当 f (n)为正值时,认为该项目赢利.(1)试求 f (n)的表达式;(2)根据预测,该项目将从哪一年开始并持续赢利?请说明理由.20.(16分)在平面直角坐标系中,已知椭圆C:+y2=1 (a>0,a≠1)的两个焦点分别是F1,F2,直线l:y=kx+m(k,m∈R)与椭圆交于A,B两点.(1)若M为椭圆短轴上的一个顶点,且△MF1F2是直角三角形,求a的值;(2)若k=1,且△OAB是以O为直角顶点的直角三角形,求a与m满足的关系;(3)若a=2,且k OA•k OB=﹣,求证:△OAB的面积为定值.21.(18分)若存在常数k(k>0),使得对定义域D内的任意x1,x2(x1≠x2),都有|f(x1)﹣f(x2)|≤k|x1﹣x2|成立,则称函数f(x)在其定义域D上是“k﹣利普希兹条件函数”.(1)若函数f(x)=,(1≤x≤4)是“k﹣利普希兹条件函数”,求常数k的最小值;(2)判断函数f(x)=log2x 是否是“2﹣利普希兹条件函数”,若是,请证明,若不是,请说明理由;(3)若y=f(x)(x∈R )是周期为2的“1﹣利普希兹条件函数”,证明:对任意的实数x1,x2,都有|f(x1)﹣f(x2)|≤1.2018年上海市崇明区高考数学一模试卷参考答案与试题解析一、填空题(本大题共有12题,满分54分,其中1-6题每题4分,7-12题每题5分)1.(4分)已知集合A={1,2,5},B={2,a},若A∪B={1,2,3,5},则a=3.【解答】解:∵集合A={1,2,5},B={2,a},A∪B={1,2,3,5},∴a=3.故答案为:3.2.(4分)抛物线y2=4x的焦点坐标为(1,0).【解答】解:∵抛物线y2=4x是焦点在x轴正半轴的标准方程,p=2∴焦点坐标为:(1,0)故答案为:(1,0)3.(4分)不等式<0的解是(﹣1,0).【解答】解:不等式<0,即x(x+1)<0,求得﹣1<x<0,故答案为:(﹣1,0).4.(4分)若复数z满足iz=1+i(i为虚数单位),则z=1﹣i.【解答】解:由iz=1+i,得z==1﹣i故答案为:1﹣i.5.(4分)在代数式(x﹣)7的展开式中,一次项的系数是21.(用数字作答)【解答】解:(x﹣)7的展开式的通项为=,由7﹣3r=1,得r=2,∴一次项的系数是.故答案为:21.6.(4分)若函数y=2sin(ωx﹣)+1(ω>0)的最小正周期是π,则ω=2.【解答】解:根据正弦函数的图象与性质,知函数y=2sin(ωx﹣)+1(ω>0)的最小正周期是T==π,解得ω=2.故答案为:2.7.(5分)若函数f(x)=x a的反函数的图象经过点(,),则a=.【解答】解:若函数f(x)=x a的反函数的图象经过点(,),则:(,)满足f(x)=xα,所以:,解得:,故答案为:.8.(5分)将一个正方形绕着它的一边所在的直线旋转一周,所得几何体的体积为27πcm3,则该几何体的侧面积为18πcm2.【解答】解:将一个正方形绕着它的一边所在的直线旋转一周,所得几何体是圆柱体,设正方形的边长为acm,则圆柱体的体积为V=πa2•a=27π,解得a=3cm;∴该圆柱的侧面积为S=2π×3×3=18πcm2.故答案为:18π.9.(5分)已知函数y=f(x)是奇函数,当x<0 时,f(x)=2x﹣ax,且f(2)=2,则a=﹣.【解答】解:∵函数y=f(x)是奇函数,当x<0 时,f(x)=2x﹣ax,∴x>0时,﹣f(x)=2﹣x﹣a(﹣x),∴f(x)=﹣2﹣x﹣ax,∵f(2)=2,∴f(2)=﹣2﹣2﹣2a=2,解得a=﹣.故答案为:﹣.10.(5分)若无穷等比数列{a n}的各项和为S n,首项a1=1,公比为a﹣,且S n=a,则a=2.【解答】解:无穷等比数列{a n}的各项和为S n,首项a1=1,公比为a﹣,且S n=a,可得=a,即有=a,即为2a2﹣5a+2=0,解得a=2或,由题意可得0<|q|<1,即有0<|a﹣|<1,检验a=2成立;a=不成立.故答案为:2.11.(5分)从5男3女共8名学生中选出队长1人,副队长1人,普通队员2人组成4人志愿者服务队,要求服务队中至少有 1 名女生,共有780种不同的选法.(用数字作答)【解答】解:根据题意,要求服务队中至少有 1 名女生,则分3种情况讨论:①、选出志愿者服务队的4人中有1名女生,有C53C31=30种选法,这4人选2人作为队长和副队有A42=12种,其余2人为普通队员,有1种情况,此时有30×12=360种不同的选法,②、选出志愿者服务队的4人中有2名女生,有C52C32=30种选法,这4人选2人作为队长和副队有A42=12种,其余2人为普通队员,有1种情况,此时有30×12=360种不同的选法,③、选出志愿者服务队的4人中有3名女生,有C51C33=5种选法,这4人选2人作为队长和副队有A42=12种,其余2人为普通队员,有1种情况,此时有5×12=60种不同的选法,则一共有360+360+60=780;故答案为:780.12.(5分)在ABC中,BC边上的中垂线分别交BC,AC于点D,E.若•=6,||=2,则AC=4.【解答】解:建立平面直角坐标系如图所示,设B(﹣a,0),C(a,0),E(0,b),∠ABC=α,由||=2,知A(﹣a+2cosα,2sinα),∴=(a﹣2cosα,b﹣2sinα),=(2a,0),∴•=2a(a﹣2cosα)+0=2a2﹣4acosα=6,∴a2﹣2acosα=3;又=(2a﹣2cosα,﹣2sinα),∴=(2a﹣2cosα)2+(﹣2sinα)2=4a2﹣8acosα+4=4(a2﹣2acosα)+4=4×3+4=16,∴||=4,即AC=4.故答案为:4.二、选择题(本大题共有4题,满分20分)13.(5分)展开式为ad﹣bc的行列式是()A.B.C.D.【解答】解:根据叫做二阶行列式,它的算法是:ad﹣bc,由题意得,=ad﹣bc.故选B.14.(5分)设a,b∈R,若a>b,则()A.<B.lga>lgb C.sin a>sin b D.2a>2b【解答】解:由a>b,利用指数函数的单调性可得:2a>2b.再利用不等式的性质、对数函数的定义域与单调性、三角函数的单调性即可判断出A,B,C不正确.故选:D.15.(5分)已知等差数列{a n}的公差为d,前n项和为S n,则“d>0”是“S4+S6>2S5”的()A.充分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【解答】解:∵S4+S6>2S5,∴4a1+6d+6a1+15d>2(5a1+10d),∴21d>20d,∴d>0,故“d>0”是“S4+S6>2S5”充分必要条件,故选:C16.(5分)直线x=2与双曲线﹣y2=1的渐近线交于A,B两点,设P为双曲线上任一点,若=a+b(a,b∈R,O为坐标原点),则下列不等式恒成立的是()A.a2+b2≥1 B.|ab|≥1 C.|a+b|≥1 D.|a﹣b|≥2【解答】解:双曲线﹣y2=1的渐近线为:y=±x.把x=2代入上述方程可得:y=±1.不妨取A(2,1),B(2,﹣1).=a+b=(2a+2b,a﹣b).代入双曲线方程可得:﹣(a﹣b)2=1,化为ab=.∴=ab,化为:|a+b|≥1.故选:C.三、解答题(本大题共有5题,满分76分)17.(14分)如图,长方体ABCD﹣A1B1C1D1中,AB=BC=2,A1C与底面ABCD所成的角为60°,(1)求四棱锥A1﹣ABCD的体积;(2)求异面直线A1B与B1D1所成角的大小.【解答】解:(1)∵长方体ABCD﹣A1B1C1D1中,AB=BC=2,∴AA1⊥平面ABCD,AC==2,∴∠A1CA是A1C与底面ABCD所成的角,∵A1C与底面ABCD所成的角为60°,∴∠A1CA=60°,∴AA1=AC•tan60°=2•=2,=AB×BC=2×2=4,∵S正方形ABCD∴四棱锥A1﹣ABCD的体积:V===.(2)∵BD∥B1D1,∴∠A1BD是异面直线A1B与B1D1所成角(或所成角的补角).∵BD=,A1D=A1B==2,∴cos∠A1BD===.∴∠A1BD=arccos.∴异面直线A1B与B1D1所成角是arccos.18.(14分)已知f(x)=2sinxcosx+2cos2x﹣1.(1)求f(x)的最大值及该函数取得最大值时x的值;(2)在△ABC 中,a,b,c分别是角A,B,C所对的边,若a=,b=,且f()=,求边c的值.【解答】解:f(x)=2sinxcosx+2cos2x﹣1=sin2x+cos2x=2sin(2x+)(1)当2x+=时,即x=(k∈Z),f(x)取得最大值为2;(2)由f()=,即2sin(A+)=可得sin(A+)=∵0<A<π∴<A<∴A=或∴A=或当A=时,cosA==∵a=,b=,解得:c=4当A=时,cosA==0∵a=,b=,解得:c=2.19.(14分)2016 年崇明区政府投资8 千万元启动休闲体育新乡村旅游项目.规划从2017 年起,在今后的若干年内,每年继续投资 2 千万元用于此项目.2016 年该项目的净收入为 5 百万元,并预测在相当长的年份里,每年的净收入均为上一年的基础上增长50%.记2016 年为第 1 年,f (n)为第 1 年至此后第n (n∈N*)年的累计利润(注:含第n 年,累计利润=累计净收入﹣累计投入,单位:千万元),且当 f (n)为正值时,认为该项目赢利.(1)试求 f (n)的表达式;(2)根据预测,该项目将从哪一年开始并持续赢利?请说明理由.【解答】解:(1)由题意知,第1年至此后第n(n∈N*)年的累计投入为8+2(n﹣1)=2n+6(千万元),第1年至此后第n(n∈N*)年的累计净收入为+×+×+…+×=(千万元).∴f(n)=﹣(2n+6)=﹣2n﹣7(千万元).(2)方法一:∵f(n+1)﹣f(n)=[﹣2(n+1)﹣7]﹣[﹣2n﹣7]=[﹣4],∴当n≤3时,f(n+1)﹣f(n)<0,故当n≤4时,f(n)递减;当n≥4时,f(n+1)﹣f(n)>0,故当n≥4时,f(n)递增.又f(1)=﹣<0,f(7)=≈5×﹣21=﹣<0,f(8)=﹣23≈25﹣23=2>0.∴该项目将从第8年开始并持续赢利.答:该项目将从2023年开始并持续赢利;方法二:设f(x)=﹣2x﹣7(x≥1),则f′(x)=,令f'(x)=0,得=≈=5,∴x≈4.从而当x∈[1,4)时,f'(x)<0,f(x)递减;当x∈(4,+∞)时,f'(x)>0,f(x)递增.又f(1)=﹣<0,f(7)=≈5×﹣21=﹣<0,f(8)=﹣23≈25﹣23=2>0.∴该项目将从第8年开始并持续赢利.答:该项目将从2023年开始并持续赢利.20.(16分)在平面直角坐标系中,已知椭圆C:+y2=1 (a>0,a≠1)的两个焦点分别是F1,F2,直线l:y=kx+m(k,m∈R)与椭圆交于A,B两点.(1)若M为椭圆短轴上的一个顶点,且△MF1F2是直角三角形,求a的值;(2)若k=1,且△OAB是以O为直角顶点的直角三角形,求a与m满足的关系;(3)若a=2,且k OA•k OB=﹣,求证:△OAB的面积为定值.【解答】解:(1)∵M为椭圆短轴上的一个顶点,且△MF1F2是直角三角形,∴△MF1F2为等腰直角三角形,∴OF1=OM,当a>1时,=1,解得a=,当0<a<1时,=a,解得a=,(2)当k=1时,y=x+m,设A(x1,y1),(x2,y2),由,即(1+a2)x2+2a2mx+a2m2﹣a2=0,∴x1+x2=﹣,x1x2=,∴y1y2=(x1+m)(x2+m)=x1x2+m(x1+x2)+m2=,∵△OAB是以O为直角顶点的直角三角形,∴•=0,∴x1x2+y1y2=0,∴+=0,∴a2m2﹣a2+m2﹣a2=0∴m2(a2+1)=2a2,(3)证明:当a=2时,x2+4y2=4,设A(x1,y1),(x2,y2),∵k OA•k OB=﹣,∴•=﹣,∴x1x2=﹣4y1y2,由,整理得,(1+4k2)x2+8kmx+4m2﹣4=0.∴x1+x2=,x1x2=,∴y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=++m2=,∴=﹣4×,∴2m2﹣4k2=1,∴|AB|=•=•=2•=∵O到直线y=kx+m的距离d==,=|AB|d==•==1∴S△OAB21.(18分)若存在常数k(k>0),使得对定义域D内的任意x1,x2(x1≠x2),都有|f(x1)﹣f(x2)|≤k|x1﹣x2|成立,则称函数f(x)在其定义域D上是“k﹣利普希兹条件函数”.(1)若函数f(x)=,(1≤x≤4)是“k﹣利普希兹条件函数”,求常数k的最小值;(2)判断函数f(x)=log2x 是否是“2﹣利普希兹条件函数”,若是,请证明,若不是,请说明理由;(3)若y=f(x)(x∈R )是周期为2的“1﹣利普希兹条件函数”,证明:对任意的实数x1,x2,都有|f(x1)﹣f(x2)|≤1.【解答】解:(1)若函数f(x)=,(1≤x≤4)是“k﹣利普希兹条件函数”,则对于定义域[1,4]上任意两个x1,x2(x1≠x2),均有|f(x1)﹣f(x2)|≤k|x1﹣x2|成立,不妨设x1>x2,则k≥=恒成立.∵1≤x2<x1≤4,∴<<,∴k的最小值为.(2)f(x)=log2x的定义域为(0,+∞),令x1=,x2=,则f()﹣f()=log2﹣log2=﹣1﹣(﹣2)=1,而2|x1﹣x2|=,∴f(x1)﹣f(x2)>2|x1﹣x2|,∴函数f(x)=log2x 不是“2﹣利普希兹条件函数”.证明:(3)设f(x)的最大值为M,最小值为m,在一个周期[0,2]内f(a)=M,f(b)=m,则|f(x1)﹣f(x2)|≤M﹣m=f(a)﹣f(b)≤|a﹣b|.若|a﹣b|≤1,显然有|f(x1)﹣f(x2)|≤|a﹣b|≤1.若|a﹣b|>1,不妨设a>b,则0<b+2﹣a<1,∴|f(x1)﹣f(x2)|≤M﹣m=f(a)﹣f(b+2)≤|a﹣b﹣2|<1.综上,|f(x1)﹣f(x2)|≤1.2018年上海市虹口区高考数学一模试卷一.填空题(本大题共12题,1-6每题4分,7-12每题5分,共54分)1.(4分)函数f(x)=lg(2﹣x)定义域为.2.(4分)已知f(x)是定义在R上的奇函数,则f(﹣1)+f(0)+f(1)=.3.(4分)首项和公比均为的等比数列{a n},S n是它的前n项和,则=.4.(4分)在△ABC中,∠A,∠B,∠C所对的边分别是a,b,c,如果a:b:c=2:3:4,那么cosC=.5.(4分)已知复数z=a+bi(a,b∈R)满足|z|=1,则a•b的范围是.6.(4分)某学生要从物理、化学、生物、政治、历史、地理这六门学科中选三门参加等级考,要求是物理、化学、生物这三门至少要选一门,政治、历史、地理这三门也至少要选一门,则该生的可能选法总数是.7.(5分)已知M、N是三棱锥P﹣ABC的棱AB、PC的中点,记三棱锥P﹣ABC 的体积为V1,三棱锥N﹣MBC的体积为V2,则等于.8.(5分)在平面直角坐标系中,双曲线的一个顶点与抛物线y2=12x的焦点重合,则双曲线的两条渐近线的方程为.9.(5分)已知y=sinx和y=cosx的图象的连续的三个交点A、B、C构成三角形△ABC,则△ABC的面积等于.10.(5分)设椭圆的左、右焦点分别为F1、F2,过焦点F1的直线交椭圆于M、N两点,若△MNF2的内切圆的面积为π,则=.11.(5分)在△ABC中,D是BC的中点,点列P n(n∈N*)在线段AC上,且满足,若a1=1,则数列{a n}的通项公式a n=.12.(5分)设f(x)=x2+2a•x+b•2x,其中a,b∈N,x∈R,如果函数y=f(x)与函数y=f(f(x))都有零点且它们的零点完全相同,则(a,b)为.二.选择题(本大题共4题,每题5分,共20分)13.(5分)异面直线a和b所成的角为θ,则θ的范围是()A.B.(0,π) C.D.(0,π]14.(5分)命题:“若x2=1,则x=1”的逆否命题为()A.若x≠1,则x≠1或x≠﹣1 B.若x=1,则x=1或x=﹣1C.若x≠1,则x≠1且x≠﹣1 D.若x=1,则x=1且x=﹣115.(5分)已知函数,则f(1)+f(2)+f(3)+…+f(2017)=()A.2017 B.1513 C.D.16.(5分)已知Rt△ABC中,∠A=90°,AB=4,AC=6,在三角形所在的平面内有两个动点M和N,满足,,则的取值范围是()A.B.[4,6]C.D.三.解答题(本大题共5题,共14+14+14+16+18=76分)17.(14分)如图,在三棱锥P﹣ABC中,PA=AC=PC=AB=a,PA⊥AB,AC⊥AB,M为AC的中点.(1)求证:PM⊥平面ABC;(2)求直线PB和平面ABC所成的角的大小.18.(14分)已知函数,其中x∈R,ω>0,且此函数的最小正周期等于π.(1)求ω的值,并写出此函数的单调递增区间;(2)求此函数在的最大值和最小值.19.(14分)如图,阴影部分为古建筑群所在地,其形状是一个长为2km,宽为1km的矩形,矩形两边AB、AD紧靠两条互相垂直的路上,现要过点C修一条直线的路l,这条路不能穿过古建筑群,且与另两条路交于点P和Q.(1)设AQ=x(km),将△APQ的面积S表示为x的函数;(2)求△APQ的面积S(km)的最小值.20.(16分)已知平面内的定点F到定直线l的距离等于p(p>0),动圆M过点F且与直线l相切,记圆心M的轨迹为曲线C,在曲线C上任取一点A,过A 作l的垂线,垂足为E.(1)求曲线C的轨迹方程;(2)记点A到直线l的距离为d,且,求∠EAF的取值范围;(3)判断∠EAF的平分线所在的直线与曲线的交点个数,并说明理由.21.(18分)已知无穷数列{a n}的各项均为正数,其前n项和为S n,a1=4.(1)如果a2=2,且对于一切正整数n,均有,求S n;(2)如果对于一切正整数n,均有a n•a n+1=S n,求S n;(3)如果对于一切正整数n,均有a n+a n+1=3S n,证明:a3n﹣1能被8整除.2018年上海市虹口区高考数学一模试卷参考答案与试题解析一.填空题(本大题共12题,1-6每题4分,7-12每题5分,共54分)1.(4分)函数f(x)=lg(2﹣x)定义域为(﹣∞,2).【解答】解:要使函数有意义,可得2﹣x>0,即x<2.函数f(x)=lg(2﹣x)定义域为:(﹣∞,2).故答案为:(﹣∞,2).2.(4分)已知f(x)是定义在R上的奇函数,则f(﹣1)+f(0)+f(1)=0.【解答】解:∵f(x)是定义在R上的奇函数,∴f(﹣1)=﹣f(1),f(0)=0,即f(﹣1)+f(0)+f(1)=0,故答案为:0.3.(4分)首项和公比均为的等比数列{a n},S n是它的前n项和,则= 1.【解答】解:根据题意,等比数列{a n}的首项和公比均为,则其前n项和S n==1﹣()n,则=1;故答案为:1.4.(4分)在△ABC中,∠A,∠B,∠C所对的边分别是a,b,c,如果a:b:c=2:3:4,那么cosC=﹣.【解答】解:因为a:b:c=2:3:4,所以设a=2k,b=3k,c=4k,则根据余弦定理得:cosC===﹣.故答案为:﹣5.(4分)已知复数z=a+bi(a,b∈R)满足|z|=1,则a•b的范围是[,] .【解答】解:∵z=a+bi(a,b∈R),且|z|=1,∴,即a2+b2=1,令a=cosθ,b=sinθ,则ab=cosθ•sinθ=,∴ab∈[,].故答案为:.6.(4分)某学生要从物理、化学、生物、政治、历史、地理这六门学科中选三门参加等级考,要求是物理、化学、生物这三门至少要选一门,政治、历史、地理这三门也至少要选一门,则该生的可能选法总数是18.【解答】解:根据题意,要求是物理、化学、生物这三门至少要选一门,政治、历史、地理这三门也至少要选一门,分2种情况讨论:①、从物理、化学、生物这三门中选1门,政治、历史、地理这三门选2门,有C31C32=9种选法,②、从物理、化学、生物这三门中选2门,政治、历史、地理这三门选1门,有C31C32=9种选法,则一共有9+9=18种选法;故答案为:187.(5分)已知M、N是三棱锥P﹣ABC的棱AB、PC的中点,记三棱锥P﹣ABC 的体积为V1,三棱锥N﹣MBC的体积为V2,则等于.【解答】解:如图,设三棱锥P﹣ABC的底面积为S,高为h,∵M是AB的中点,∴,∵N是PC的中点,∴三棱锥N﹣MBC的高为,则,,∴=.故答案为:.8.(5分)在平面直角坐标系中,双曲线的一个顶点与抛物线y2=12x 的焦点重合,则双曲线的两条渐近线的方程为.【解答】解:根据题意,抛物线y2=12x的焦点为(3,0),若双曲线的一个顶点与抛物线y2=12x的焦点重合,则双曲线的顶点坐标为(±3,0),则有a2=9,则双曲线的方程为:﹣y2=1,双曲线的焦点在x轴上,则其渐近线方程为故答案为:9.(5分)已知y=sinx和y=cosx的图象的连续的三个交点A、B、C构成三角形△ABC,则△ABC的面积等于.【解答】解:由题意正余弦函数的图象可得:y=sinx和y=cosx的图象的连续的三个交点A、B、C构成三角形△ABC是等腰三角形,∵底边长为一个周期T=2π,高为,∴△ABC的面积=2=,故答案为:.10.(5分)设椭圆的左、右焦点分别为F1、F2,过焦点F1的直线交椭圆于M、N两点,若△MNF2的内切圆的面积为π,则=4.【解答】解:∵椭圆+的左右焦点分别为F1,F2,a=2,过焦点F1的直线交椭圆于M(x1,y1),N(x2,y2)两点,△MNF2的内切圆的面积为π,∴△MNF2内切圆半径r=1.∴△MNF2面积S=×1×(MN+MF2+MF2)=2a=4,故答案为:411.(5分)在△ABC中,D是BC的中点,点列P n(n∈N*)在线段AC上,且满足,若a1=1,则数列{a n}的通项公式a n=.【解答】解:如图所示,∵D是BC的中点,∴=+=+,又=+,,∴+=+a n(+),化为:=(1﹣a n﹣a n+1)+,∵点列P n(n∈N*)在线段AC上,∴1﹣a n﹣a n+1+=1,化为:a n=﹣,又a1=1,+1则数列{a n}是等比数列,首项为1,公比为﹣.∴a n=.故答案为:.12.(5分)设f(x)=x2+2a•x+b•2x,其中a,b∈N,x∈R,如果函数y=f(x)与函数y=f(f(x))都有零点且它们的零点完全相同,则(a,b)为(0,0)或(1,0).【解答】解:根据题意,函数y=f(x)的零点为方程x2+2a•x+b•2x=0的根,如果函数y=f(x)与函数y=f(f(x))的零点完全相同,则有f(x)=x,即x2+2a•x+b•2x=x,方程x2+2a•x+b•2x=x的根就是函数y=f(x)与函数y=f(f(x))的零点,则有,解可得x=0,即x2+2a•x+b•2x=0的1个根为x=0,分析可得b=0,则f(x)=x2+2a•x,解可得x1=0或x2=﹣2a,f(f(x))=(x2+2a•x)2+2a(x2+2a•x),若函数y=f(x)与函数y=f(f(x))的零点完全相同,分析可得a=0或a=1,则(a,b)为(0,0)或(1,0);故答案为(0,0)或(1,0).二.选择题(本大题共4题,每题5分,共20分)13.(5分)异面直线a和b所成的角为θ,则θ的范围是()A.B.(0,π) C.D.(0,π]【解答】解:∵异面直线a和b所成的角为θ,∴θ的范围是(0,].故选:C.14.(5分)命题:“若x2=1,则x=1”的逆否命题为()A.若x≠1,则x≠1或x≠﹣1 B.若x=1,则x=1或x=﹣1C.若x≠1,则x≠1且x≠﹣1 D.若x=1,则x=1且x=﹣1【解答】解:命题:“若x2=1,则x=1”的逆否命题为“若x≠1,则x2≠1”;即“若x≠1,则x≠1且x≠﹣1”.故选:C.15.(5分)已知函数,则f(1)+f(2)+f(3)+…+f(2017)=()A.2017 B.1513 C.D.【解答】解:∵函数,∴f(1)+f(2)+f(3)+…+f(2017)=1009×f(﹣1)+1008×f(0)=1009×2﹣1+1008×20=.故选:D.16.(5分)已知Rt△ABC中,∠A=90°,AB=4,AC=6,在三角形所在的平面内有两个动点M和N,满足,,则的取值范围是()A.B.[4,6]C.D.【解答】解:以AB,AC为坐标轴建立坐标系,则B(4,0),C(0,6),∵||=2,∴M的轨迹是以A为圆心,以2为半径的圆.∵,∴N是MC的中点.设M(2cosα,2sinα),则N(cosα,sinα+3),∴=(cosα﹣4,sinα+3),∴||2=(cosα﹣4)2+(sinα+3)2=6sinα﹣8cosα+26=10sin(α﹣φ)+26,∴当sin(α﹣φ)=﹣1时,||取得最小值=4,当sin(α﹣φ)=1时,||取得最大值=6.故选B.三.解答题(本大题共5题,共14+14+14+16+18=76分)17.(14分)如图,在三棱锥P﹣ABC中,PA=AC=PC=AB=a,PA⊥AB,AC⊥AB,M为AC的中点.(1)求证:PM⊥平面ABC;(2)求直线PB和平面ABC所成的角的大小.【解答】证明:(1)在三棱锥P﹣ABC中,∵PA=AC=PC=AB=a,PA⊥AB,AC⊥AB,M为AC的中点.∴PM⊥AC,AB⊥平面PAC,∴PM⊥AB,∵AB∩AC=A,∴PM⊥平面ABC.解:(2)连结BM,∵PM⊥平面ABC,∴∠PBM是直线PB和平面ABC所成的角,∵PA=AC=PC=AB=a,PA⊥AB,AC⊥AB,M为AC的中点,∴PM==,BM===,∴tan∠PBM===,∴.∴直线PB和平面ABC所成的角为arctan.18.(14分)已知函数,其中x∈R,ω>0,且此函数的最小正周期等于π.(1)求ω的值,并写出此函数的单调递增区间;(2)求此函数在的最大值和最小值.【解答】解:函数=sinωx+cosωx=2sin (ωx),(1)∵函数的最小正周期等于π.即∴ω=2.可得f(x)=2sin(2x),由2x,k∈Z得:≤x≤故得函数的单调递增区间为[,],k∈Z(2)∵f(x)=2sin(2x),当,(2x)∈[]∴当2x=时,函数f(x)取得最大值为2.当2x=时,函数f(x)取得最小值为﹣1.19.(14分)如图,阴影部分为古建筑群所在地,其形状是一个长为2km,宽为1km的矩形,矩形两边AB、AD紧靠两条互相垂直的路上,现要过点C修一条直线的路l,这条路不能穿过古建筑群,且与另两条路交于点P和Q.(1)设AQ=x(km),将△APQ的面积S表示为x的函数;(2)求△APQ的面积S(km)的最小值.【解答】解:(1)设AQ=x,则由得:即AP=故S==(x>1);(2)由(1)得:S′=(x>1);当x∈(1,2)时,S′<0,当x∈(2,+∞)时,S′>0,故x=2时,S min=4.20.(16分)已知平面内的定点F到定直线l的距离等于p(p>0),动圆M过点F且与直线l相切,记圆心M的轨迹为曲线C,在曲线C上任取一点A,过A 作l的垂线,垂足为E.(1)求曲线C的轨迹方程;(2)记点A到直线l的距离为d,且,求∠EAF的取值范围;(3)判断∠EAF的平分线所在的直线与曲线的交点个数,并说明理由.【解答】解:(1)如图,以FK的中点为坐标原点O,FK所在的直线为x轴,过O的垂线为y轴建立直角坐标系,即有F(,0),直线l:x=﹣,动圆M过点F且与直线l相切,可得|AE|=|AF|,由抛物线的定义可得曲线C的轨迹为F为焦点、直线l为准线的抛物线,可得方程为y2=2px;(2)点A到直线l的距离为d,可得|AE|=|AF|=d,且,设A(x0,y0),可得y02=2px0,即有d=x0+,则x0=d﹣,即有|EF|2=p2+y02=p2+2p(d﹣)=2pd,在△EAF中,cos∠EAF==1﹣,可得﹣≤cos∠EAF≤,可得arccos≤π﹣arccos,则∠EAF的取值范围是[arccos];(3)∠EAF的平分线所在的直线与曲线的交点个数为1.设A(x0,y0),可得y02=2px0,当A与O重合时,显然一个交点;当A不与O重合,由∠EAF的平分线交x轴于M,连接EM,可得∠AMF=∠MAF,即有|MF|=|AF|=d,四边形AEMF为菱形,EF垂直平分AM,可得∠AMF+∠EFM=90°,tan∠AMF=cot∠EFM==,可设y0>0,则直线AM的方程为y﹣y0=(x﹣x0),则y0y﹣y02=px﹣px0,化为y0y=px+px0,代入抛物线的方程y2=2px,消去x可得,y2﹣2y0y+2px0=0,即为(y﹣y0)2=0,可得y=y0,x=x0,即∠EAF的平分线所在的直线与曲线的交点个数为1.21.(18分)已知无穷数列{a n}的各项均为正数,其前n项和为S n,a1=4.(1)如果a2=2,且对于一切正整数n,均有,求S n;(2)如果对于一切正整数n,均有a n•a n+1=S n,求S n;(3)如果对于一切正整数n,均有a n+a n+1=3S n,证明:a3n﹣1能被8整除.【解答】解:(1)∵无穷数列{a n}的各项均为正数,其前n项和为S n,a1=4.a2=2,且对于一切正整数n,均有,∴==1,=,由此猜想=23﹣n.再利用数学归纳法证明:①当n=1时,=4,成立.②假设n=k时,成立,即,====2(6﹣2k)﹣(4﹣k)=22﹣k=23﹣(k+1).则a k+1由①②得,∴{a n}是首项为4,公比为的等比数列,∴S n==8(1﹣).(2)∵对于一切正整数n,均有a n•a n+1=S n,∴S n=a n a n+1,S n﹣1=a n﹣1a n,∴a n=a n(a n+1﹣a n﹣1),∴a n+1﹣a n﹣1=1.a1=4,由a n•a n+1=S n,得a2=1,a3=5,a4=3,…∴当n为偶数时,+===.当n为奇数时,S n=++==.证明:(3)∵对于一切正整数n,均有a n+a n+1=3S n,∴a n+a n+1=3S n,a n﹣1+a n=3S n﹣1,﹣a n﹣1=3a n,∴a n+1a1+a2=3a1,a2=2a1=8,能被8整除,a3﹣a1=3a2,a3=28,假设a3k﹣1=8m,m∈N*.=3a2k+1+a3k=3(3a3k+a3k﹣1)+a3k则a3k+2=10a3k+a3k﹣1=40p+24q,p,q∈N*能被8整除,综上,a3n能被8整除.﹣12018年上海市黄浦区高考数学一模试卷一、填空题(本大题共有12题,满分36分.其中第1~6题每题满分36分,第7~12题每题满分36分)1.(3分)已知全集U=R,集合,则(∁U B)∩A=.2.(3分)函数的定义域是.3.(3分)若复数z满足(i为虚数单位),则z=.4.(3分)已知sin(α+)=,α∈(﹣,0),则tanα=.5.(3分)若无穷等比数列中任意一项均等于其之后所有项的和,则其公比为.6.(3分)若函数y=a+sinx在区间[π,2π]上有且只有一个零点,则a=.7.(3分)已知向量=(x,y)(x,y∈R),=(1,2),若x2+y2=1,则|﹣|的最小值为.8.(3分)已知函数y=f(x)是奇函数,且当x≥0时,f(x)=log2(x+1).若函数y=g(x)是y=f(x)的反函数,则g(﹣3)=.9.(3分)已知m,n,α,β∈R,m<n,α<β,若α,β是函数f(x)=2(x﹣m)(x﹣n)﹣7的零点,则m,n,α,β四个数按从小到大的顺序是(用符号“<“连接起来).10.(3分)已知点O,A,B,F分别为椭圆的中心、左顶点、上顶点、右焦点,过点F作OB的平行线,它与椭圆C在第一象限部分交于点P,若,则实数λ的值为.11.(3分)已知x∈R,定义:A(x)表示不小于x的最小整数.如,A(﹣1.1)=﹣1.若A(2x•A(x))=5,则正实数x的取值范围是.12.(3分)已知点M(m,0),m>0和抛物线C:y2=4x.过C的焦点F的直线与C交于A,B两点,若=2,且||=||,则m=.二、选择题(本大题共有4题,满分12分.)13.(3分)若x∈R,则“x>1”是“”的()A.充分非必要条件 B.必要非充分条件C.充要条件D.既非充分也非必要条件14.(3分)已知向量,则下列能使成立的一组向量是()A.B.C.D.15.(3分)一个算法的程序框图如图所示,则该程序运行后输出的值是()A.4 B.5 C.6 D.716.(3分)已知a1,a2,a3,a4是各项均为正数的等差数列,其公差d大于零,若线段l1,l2,l3,l4的长分别为a1,a2,a3,a4,则()A.对任意的d,均存在以l1,l2,l3为三边的三角形B.对任意的d,均不存在以为l1,l2,l3三边的三角形C.对任意的d,均存在以l2,l3,l4为三边的三角形D.对任意的d,均不存在以l2,l3,l4为三边的三角形三、解答题(本大题共有5题,满分74分.)17.(12分)在长方体ABCD﹣A1B1C1D1中,AB=AA1=4,BC=3,E,F分别是所在棱AB,BC的中点,点P是棱A1B1上的动点,联结EF,AC1.如图所示.(1)求异面直线EF,AC1所成角的大小(用反三角函数值表示);(2)求以E,F,A,P为顶点的三棱锥的体积.18.(12分)如图,已知点A是单位圆上一点,且位于第一象限,以x轴的正半轴为始边,OA为终边的角设为α,将OA绕坐标原点逆时针旋转至OB.(1)用α表示A,B两点的坐标;(2)M为x轴上异于O的点,若MA⊥MB,求点M横坐标的取值范围.19.(14分)已知函数g(x)=,x∈R,函数y=f(x)是函数y=g(x)的反函数.(1)求函数y=f(x)的解析式,并写出定义域D;(2)设h(x)=,若函数y=h(x)在区间(0,1)内的图象是不间断的光滑曲线,求证:函数y=h(x)在区间(﹣1,0)内必有唯一的零点(假设为t),且﹣1.20.(18分)(理科)定义:若各项为正实数的数列{a n}满足,则称数列{a n}为“算术平方根递推数列”.已知数列{x n}满足,且,点(x n+1,x n)在二次函数f(x)=2x2+2x 的图象上.(1)试判断数列{2x n+1}(n∈N*)是否为算术平方根递推数列?若是,请说明你的理由;(2)记y n=lg(2x n+1)(n∈N*),求证:数列{y n}是等比数列,并求出通项公式y n;(3)从数列{y n}中依据某种顺序自左至右取出其中的项,把这些项重新组成一个新数列{z n}:.若数列{z n}是首项为、公比为的无穷等比数列,且数列{z n}各项的和为,求正整数k、m的值.21.(18分)已知椭圆Γ:+=1(a>b>0),过原点的两条直线l1和l2分别与Γ交于点A、B和C、D,得到平行四边形ACBD.(1)当ACBD为正方形时,求该正方形的面积S;(2)若直线l1和l2关于y轴对称,Γ上任意一点P到l1和l2的距离分别为d1和d2,当d12+d22为定值时,求此时直线l1和l2的斜率及该定值.(3)当ACBD为菱形,且圆x2+y2=1内切于菱形ACBD时,求a,b满足的关系式.2018年上海市黄浦区高考数学一模试卷参考答案与试题解析一、填空题(本大题共有12题,满分36分.其中第1~6题每题满分36分,第7~12题每题满分36分)1.(3分)已知全集U=R,集合,则(∁U B)∩A= {x|﹣1<x≤} .【解答】解:A={x|﹣1<x<1},∁U B={x|x≤},则(∁U B)∩A={x|﹣1<x≤},故答案为:{x|﹣1<x≤},2.(3分)函数的定义域是(1,+∞).【解答】解:要使函数有意义,需满足解得x>1故答案为:(1,+∞)3.(3分)若复数z满足(i为虚数单位),则z=1+2i.【解答】解:由,得z=1+2i.故答案为:1+2i.4.(3分)已知sin(α+)=,α∈(﹣,0),则tanα=﹣2.【解答】解:∵sin(α+)=cosα,sin(α+)=,∴cosα=,又α∈(﹣,0),∴sinα=﹣,∴tanα==﹣2.故答案为:﹣2.5.(3分)若无穷等比数列中任意一项均等于其之后所有项的和,则其公比为.【解答】解:设数列中的任意一项为a,由无穷等比数列中的每一项都等于它后面所有各项的和,得a=,即1﹣q=q∴q=.故答案为:.6.(3分)若函数y=a+sinx在区间[π,2π]上有且只有一个零点,则a=1.【解答】解:作函数y=sinx在区间[π,2π]上的图象如下,,结合图象可知,若函数y=a+sinx在区间[π,2π]上有且只有一个零点,则a﹣1=0,故a=1;故答案为:1.7.(3分)已知向量=(x,y)(x,y∈R),=(1,2),若x2+y2=1,则|﹣|的最小值为﹣1.【解答】解:设O(0,0),P(1,2),∴|﹣|=≥||﹣1=﹣1=﹣1,∴|﹣|的最小值为﹣18.(3分)已知函数y=f(x)是奇函数,且当x≥0时,f(x)=log2(x+1).若函数y=g(x)是y=f(x)的反函数,则g(﹣3)=﹣7.【解答】解:∵反函数与原函数具有相同的奇偶性.∴g(﹣3)=﹣g(3),∵反函数的定义域是原函数的值域,∴log2(x+1)=3,解得:x=7,即g(3)=7,故得g(﹣3)=﹣7.故答案为:﹣7.9.(3分)已知m,n,α,β∈R,m<n,α<β,若α,β是函数f(x)=2(x﹣m)(x﹣n)﹣7的零点,则m,n,α,β四个数按从小到大的顺序是α<m<n <β(用符号“<“连接起来).【解答】解:∵α、β是函数f(x)=2(x﹣m)(x﹣n)﹣7的零点,∴α、β是函数y=2(x﹣m)(x﹣n)与函数y=7的交点的横坐标,且m、n是函数y=2(x﹣m)(x﹣n)与x轴的交点的横坐标,故由二次函数的图象可知,α<m<n<β;故答案为:α<m<n<β.10.(3分)已知点O,A,B,F分别为椭圆的中心、左顶点、上顶点、右焦点,过点F作OB的平行线,它与椭圆C在第一象限部分交于点P,若,则实数λ的值为.【解答】解:如图,A(﹣a,0),B(0,b),F(c,0),则P(c,),∴,,由,得,即b=c,∴a2=b2+c2=2b2,.则.故答案为:.11.(3分)已知x∈R,定义:A(x)表示不小于x的最小整数.如,A(﹣1.1)=﹣1.若A(2x•A(x))=5,则正实数x的取值范围是(1,] .【解答】解:当A(x)=1时,0<x≤1,可得4<2x≤5,得2<x≤,矛盾,故A(x)≠1,当A(x)=2时,1<x≤2,可得4<4x≤5,得1<x≤,符合题意,故A(x)=2,当A(x)=3时,2<x≤3,可得4<6x≤5,得<x≤,矛盾,故A(x)≠3,由此可知,当A(x)≥4时也不合题意,故A(x)=2∴正实数x的取值范围是(1,]故答案为:(1,]12.(3分)已知点M(m,0),m>0和抛物线C:y2=4x.过C的焦点F的直线与C交于A,B两点,若=2,且||=||,则m=.【解答】解:由题意可知:F(1,0),由抛物线定义可知A(x1,y1),可知B(x2,y2),∵=2,可得:2(x2﹣1,y2)=(1﹣x1,﹣y1),可得y2=﹣,x2=,,解得x1=2,y1=±2.||=||,。
2018年上海市各区中考一模压轴题图文解析15.88

所以 QC=5-3m,QE=5m-x.
由 FC DE 5 ,得 x 3m 5 . QC QE 6 5 3m 5m x 6
解得 x 175 .此时 BF=6-x= 527 .
117
117
图6
图7
Hale Waihona Puke 图86例2018 年上海市奉贤区中考一模第 24 题
如图 1,在平面直角坐标系中,已知抛物线 y 3 x2 bx c 与 x 轴交于点 A(-2,0)和点 8
QF QD 2m 5 x
在 Rt△DFM 中,由勾股定理,得 (4m)2 42 (3 x)2 .
联立 x 3m 和 (4m)2 42 (3 x)2 ,消去 m,整理,得11x2 58x 75 0 . 2m 5 x
解得 x= 25 .此时 BF=6-x= 41 .
11
11
③如图 8,当 FQ=FC=x 时,DE=DQ=3m.
图2
(3)因为△APM 是直角三角形,如果△BPN 与△APM 相似,那么△BPN 也是直角三
角形.
由于∠BPN=∠APM=∠ABO 为定值,所以存在两种情况:
①如图 3,当∠BNP=90°时,BN//x 轴.所以 yN=yB=2.
解方程 4 m2 10 m 2 2 ,得 m 5 ,或 m 0 (舍去).此时 M (5 , 0) .
33
2
2
②如图 4,当∠NBP=90°时,作 NH⊥y 轴于 H,那么△NHB∽△BOA.
所以 NH BO 2 .所以 NH 2 BH .
BH AO 3
3
解方程 m 2 ( 4 m2 10 m) ,得 m 11 ,或 m 0 (舍去).此时 M (11, 0) ..
33 3
2018年初三一模 伏安法测电阻专题汇编

上海市各区县2018届初三物理试题伏安法测电阻专题分类精编1.(2018年宝山第25题).根据“用电流表、电压表测电阻”的实验,完成下列要求。
⑴ 实验原理_________。
⑵ 请依照图13电路图,用笔画线替代导线将图13所示的实物连接完整,________。
(用2B 铅笔在答题纸的相应位置连线)⑶ 闭合电键前,需将滑动变阻器的滑片P 移到_____端(选填“A ”或“B ”)。
⑷小顾同学在本实验中,将最后一根导线连接完毕后闭合电键,发现电流表和电压表的示数都超出它们所能测的最大值,其原因可能是:_________________________。
⑸ 解决上述问题后,小顾重新进行实验,前两次测得的电阻分别是51.9欧和51.8欧,第三次测量时,电流表和电压表的示数如图14所示,则该待测电阻的阻值为_____欧。
2.(2018年奉献第25题)某小组同学做“用电流表、电压表测电阻”实验,实验器材齐全且完好,电源电压保持不变。
(1)他们正确串联实验器材,并将变阻器的滑片放置于一端,然后将电压表并联在电路中。
闭合电键后,观察到电压表示数为6伏,电流表示数为0.58安。
接着移动变阻器的滑片,将滑片移动某一位置时,观察到电流表的示数如图15(a )所示,电压表的示数始终不变。
请根据上述现象判断实验过程中电压表示数不变的原因_____(9)_________。
(2)经思考分析检查,他们重新正确连接电路,操作步骤正确。
闭合电键后,发现电压表指针所指的刻度与原先一致,电流表示数如图15(b )所示。
接着移动变阻器的滑片,观察到当电流表的示数如图15(a )所示,电压表的示数如图15(c )所示。
(3)请你根据上述实验过程中得到的数据将下表填写完整(电阻精确到0.1欧)。
图13B图14⑾ ⑿3.(2018年虹口第26题) 小李同学做“用电流表、电压表测电阻”实验,现有电源(电压为2伏的整数倍且保持不变)、一个待测电阻Rx 、电流表、电压表、滑动变阻器、电键及导线若干。
2018-2019年上海中考数学各区一模汇编-03提升题(18、23、24、25题)(无答案)

2019届一模提升题汇编目录2019届一模提升题汇编目录 (1)Ⅰ第18题(填空小压轴) (3)【2019届一模徐汇】 (3)【2019届一模浦东】 (3)【2019届一模杨浦】 (3)【2019届一模普陀】 (4)【2019届一模奉贤】 (4)【2019届一模松江】 (4)【2019届一模嘉定】 (5)【2019届一模青浦】 (5)【2019届一模青浦】 (5)【2019届一模静安】 (6)【2019届一模宝山】 (6)【2019届一模长宁】 (6)【2019届一模金山】 (7)【2019届一模闵行】 (7)【2019届一模虹口】 (7)Ⅱ第23题(几何证明题) (8)【2019届一模徐汇】 (8)【2019届一模浦东】 (8)【2019届一模杨浦】 (9)【2019届一模普陀】 (9)【2019届一模奉贤】 (10)【2019届一模松江】 (10)【2019届一模嘉定】 (11)【2019届一模青浦】 (11)【2019届一模静安】 (12)【2019届一模宝山】 (12)【2019届一模长宁】 (13)【2019届一模金山】 (13)【2019届一模闵行】 (14)【2019届一模虹口】 (14)Ⅲ第24题(二次函数综合) (15)【2019届一模徐汇】 (15)【2019届一模浦东】 (16)【2019届一模普陀】 (18)【2019届一模奉贤】 (19)【2019届一模松江】 (20)【2019届一模嘉定】 (21)【2019届一模青浦】 (22)【2019届一模静安】 (23)【2019届一模宝山】 (24)【2019届一模长宁】 (25)【2019届一模金山】 (26)【2019届一模闵行】 (27)【2019届一模虹口】 (28)Ⅳ第25题(压轴题) (29)【2019届一模徐汇】 (29)【2019届一模浦东】 (30)【2019届一模杨浦】 (31)【2019届一模普陀】 (32)【2019届一模奉贤】 (33)【2019届一模松江】 (34)【2019届一模嘉定】 (35)【2019届一模青浦】 (36)【2019届一模静安】 (37)【2019届一模宝山】 (38)【2019届一模长宁】 (39)【2019届一模金山】 (40)【2019届一模闵行】 (41)【2019届一模虹口】 (42)Ⅰ第18题(填空小压轴)【2019届一模徐汇】18.在梯形ABCD 中,AB ∥DC ,∠B =90°,BC=6,CD =2,3tan 4A =.点E 为BC 上一点,过点E 作EF ∥AD 交边AB 于点F .将△BEF 沿直线EF 翻折得到△GEF ,当EG 过点D 时,BE 的长为 ▲ .【2019届一模浦东】18. 将矩形纸片ABCD 沿直线AP 折叠,使点D 落在原矩形ABCD 的边BC 上的点E 处,如果∠AED 的余弦值为35,那么ABBC =__________.【2019届一模杨浦】18.Rt △ABC 中,∠C =90°,AC =3,BC =2,将此三角形绕点A 旋转,当点B 落在直线BC 上的点D 处时,点C 落在点E 处,此时点E 到直线BC 的距离为 ▲ .GEABC DF (第18题图)ACB(第18题图)18.如图5,△ABC 中,8AB AC ==,3cos 4B =,点D 在边BC 上,将△ABD 沿直线AD 翻折得到△AED ,点B 的对应点为点E ,AE 与边BC 相交于点F ,如果2BD =,那么EF = ▲ .【2019届一模奉贤】18.如图5,在△ABC 中,AB =AC =5,3sin =5C ,将△ABC 绕点A 逆时针旋转得到△ADE ,点B 、C 分别与点D 、E 对应,AD 与边BC 交于点F .如果AE //BC ,那么BF 的长是 ▲ .【2019届一模松江】18.如图,在直角坐标平面xoy 中,点A 坐标为(3,2),∠AOB =90°,∠OAB =30°,AB 与x 轴交于点C ,那么AC :BC 的值为______.图5ABCD图5AB C(第18题图)xyC BOA18.在△ABC 中,︒=∠90ACB ,点D 、E 分别在边BC 、AC 上,AE AC 3=,︒=∠45CDE (如图3),△DCE 沿直线DE 翻折,翻折后的点C 落在△ABC 内部的点F ,直线AF 与边BC 相交于点G ,如果AE BG =,那么=B tan ▲ .【2019届一模青浦】17.如图,在Rt △ABC 中,∠ACB=90°,AC=1,tan ∠CAB=2,将△ABC 绕点A 旋转后,点B 落在AC 的延长线上的点D ,点C 落在点E ,DE 与直线BC 相交于点F ,那么CF= ▲ .【2019届一模青浦】18.对于封闭的平面图形,如果图形上或图形内的点S 到图形上的任意一点P 之间的线段都在图形内或图形上,那么这样的 点S 称为“亮点”. 如图,对于封闭图形ABCDE ,S 1是 “亮点”,S 2不是“亮点”,如果AB ∥DE ,AE ∥DC , AB=2,AE=1,∠B=∠C= 60°,那么该图形中所有“亮点” 组成的图形的面积为 ▲ .EDCBAS 2S 1(第18题图)18.如图6,将矩形ABCD 沿对角线BD 所在直线翻折后,点A 与点E 重合,且ED 交BC 于点F ,联结AE .如果2tan 3DFC ∠=,那么BDAE的值是 ▲ .【2019届一模宝山】18.如图4,Rt △ABC 中,∠ACB =90°,AC =4,BC =5,点P 为AC 上一点,将△BCP 沿直线BP 翻折,点C落在C ’处,连接AC ’,若AC ’∥BC ,则CP 的长为 ▲ .【2019届一模长宁】18.如图,点P 在平行四边形ABCD 的边BC 上,将ABP ∆沿直线AP 翻折,点B 恰好落在边AD 的垂直平分线上,如果5=AB ,8=AD ,34tan =B ,那么BP 的长为 ▲ .AC(图4)B图6F BACDEBACD第18题图18.如图,在ABC Rt ∆中,o90=∠C ,8=AC ,6=BC .在边AB 上取一点O ,使BC BO =,以点O 为旋转中心,把ABC ∆逆时针旋转90,得到C B A '''∆(点A 、B 、C 的对应点分别是点A '、B '、C '),那么ABC ∆与C B A '''∆的重叠部分的面积是 ▲ .【2019届一模闵行】18.如图,在Rt △ABC 中,∠ACB = 90°,BC = 3,AC = 4,点D 为边AB 上一点.将△BCD 沿直线CD 翻折,点B 落在点E 处,联结AE .如果AE // CD ,那么BE = ▲ .【2019届一模虹口】18.如图,正方形ABCD 的边长为4,点O 为对角线AC 、BD 的交点,点E 为边AB 的中点,△BED 绕着点B 旋转至△BD 1E 1,如果点D 、E 、D 1在同一直线上,那么EE 1的长为 ▲ .ABC第18题OABC (第18题图)C第18题图A BDE OⅡ第23题(几何证明题)【2019届一模徐汇】23.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分)如图,已知菱形ABCD ,点E 是AB 的中点,AF BC ⊥于点F ,联结EF 、ED 、DF ,DE 交AF 于点G ,且2AE EG ED =⋅.(1) 求证:DE EF ⊥; (2) 求证:22BC DF BF =⋅.【2019届一模浦东】23. (本题满分12分,其中每小题各6分)已知:如图8,在平行四边形ABCD 中,M 是边BC 的中点,E 是边BA 延长线上的一点,联结EM ,分别交线段AD 于点F 、AC 于点G .(1)求证:GF EFGM EM=; (2)当22BC BA BE =⋅时,求证:∠EMB =∠ACD .G DEF BCA(第23题图)(图8)DCM BAF GE23.(本题满分12分,每小题各6分)已知:如图,在△ABC 中,点D 在边AB 上,点E 在线段CD 上,且∠ACD =∠B =∠BAE. (1)求证:AD DEBC AC=; (2)当点E 为CD 中点时,求证:22AE ABCE AD=.【2019届一模普陀】23.(本题满分12分)已知:如图9,△ADE 的顶点E 在△ABC 的边BC 上,DE 与AB 相交于点F ,AE AF AB =⋅2,DAF EAC ∠=∠.(1)求证:△ADE ∽△ACB ;(2)求证:DF CE DE CB=.(第23题图)EABCDF图9ABCDE23.(本题满分12分,第(1)小题满分5分,第(2)小题满分7分)已知:如图9,在△ABC 中,点D 在边AC 上,BD 的垂直平分线交CA 的延长线于点E , 交BD 于点F ,联结BE ,EC EA ED •=2. (1)求证:∠EBA =∠C ;(2)如果BD =CD ,求证:AC AD AB •=2.【2019届一模松江】23.(本题满分12分,第(1)小题5分,第(2)小题7分)已知:如图,在梯形ABCD 中,AD ∥BC ,AB=DC ,E 是对角线AC 上一点,且AC ·CE=AD ·BC . (1)求证:∠DCA=∠EBC ;(2)延长BE 交AD 于F ,求证:AB 2=AF ·AD .ABCDEF 图9 (第23题图)EDCBAF(第23题图)EDCBA23.(本题满分12分,每小题6分)如图6,已知点D 在△ABC 的外部,AD //BC ,点E 在边AB 上,AE BC AD AB ⋅=⋅. (1)求证:AED BAC ∠=∠;(2)在边AC 取一点F ,如果D AFE ∠=∠, 求证:ACAFBC AD =.【2019届一模青浦】23.(本题满分12分,第(1)小题7分,第(2)小题5分)已知:如图,在△ABC 中,点D 、E 分别在边BC 、AC 上,点F 在DE 的延长线上,AD=AF ,AE CE DE EF ⋅=⋅.(1)求证:△ADE ∽△ACD ;(2)如果AE BD EF AF ⋅=⋅,求证:AB=AC .图6BCDAE FABCDEF(第23题图)23.(本题满分12分,其中第(1)小题6分,第(2)小题6分)已知:如图9,在ABC ∆中,点D 、E 分别在边BC 和AB 上,且AD AC =,EB ED =,分别延长ED 、AC 交于点F .(1)求证:ABD ∆∽FDC ∆; (2)求证:2AE BE EF =⋅.【2019届一模宝山】23.(本题满分12分)地铁10号线某站点出口横截面平面图如图8所示,电梯AB 的两端分别距顶部9.9米和2.4米,在距电梯起点A 端6米的P 处,用1.5米的测角仪测得电梯终端B 处的仰角为14°,求电梯AB 的坡度与长度. 参考数据:24.014sin ≈︒,25.014tan ≈︒,97.014cos ≈︒.Q 9.9米B出口顶部1.5米(图8)AP6米2.4米︒14图9 AC BDEF23.(本题满分12分,第(1)小题5分,第(2)小题7分)如图,点D 、E 分别在ABC ∆的边AC 、AB 上,延长DE 、CB 交 于点F ,且AC AD AB AE ⋅=⋅. (1)求证:C FEB ∠=∠;(2)联结AF ,若FD CD AB FB =,求证:FB AC AB EF ⋅=⋅.【2019届一模金山】23.如图,M 是平行四边形ABCD 的对角线上的一点,射线AM 与BC 交于点F ,与DC 的延长线交于点H .(1)求证:MH MF AM ⋅=2.(2)若DM BD BC ⋅=2,求证:ADC AMB ∠=∠.第23题图CEDABF ABCD HF M第23题23.(本题共2小题,每小题6分,满分12分)如图,在△ABC 中,点D 为边BC 上一点,且AD = AB ,AE ⊥BC ,垂足为点E .过点D 作DF // AB ,交边AC 于点F ,联结EF ,212EF BD EC =⋅.(1)求证:△EDF ∽△EFC ; (2)如果14EDF ADC S S =V V ,求证:AB = BD .【2019届一模虹口】23.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分)如图,在△ABC 中,AB=AC ,D 是边BC 的中点,DE ⊥AC ,垂足为点E . (1)求证:DE CD AD CE ⋅=⋅;(2)设F 为DE 的中点,联结AF 、BE ,求证:=AF BC AD BE ⋅⋅.ABCDE F(第23题图)D 第23题图AECBⅢ第24题(二次函数综合)【2019届一模徐汇】24.(本题满分12分,第(1)小题4分,第(2)小题4分,第(3)小题4分)如图,在平面直角坐标系xoy 中,顶点为M 的抛物线C 1:2(0)y ax bx a =+<经过点A 和x 轴上的点B ,AO =OB =2,120AOB ∠=o . (1)求该抛物线的表达式; (2)联结AM ,求AOM S V ;(3)将抛物线C 1向上平移得到抛物线C 2,抛物线C 2与x 轴分别交于点E 、F (点E 在点F 的左侧),如果△MBF 与△AOM 相似,求所有符合条件的抛物线C 2的表达式.(第24题图)【2019届一模浦东】24.(本题满分12分,其中每小题各4分)已知:如图9,在平面直角坐标系xOy中,直线12y x b=-+与x轴相交于点A,与y轴相交于点B. 抛物线244y ax ax=-+经过点A和点B,并与x轴相交于另一点C,对称轴与x轴相交于点D.(1)求抛物线的表达式;(2)求证: △BOD∽△AOB;(3)如果点P在线段AB上,且∠BCP=∠DBO,求点P的坐标.(图9)xBO Ay【2019届一模杨浦】24.(本题满分12分,每小题各4分)在平面直角坐标系xOy 中,抛物线2(0)y ax bx c a =++?与y 轴交于点C (0,2),它的顶点为D (1,m ),且1tan 3COD ?. (1)求m 的值及抛物线的表达式;(2)将此抛物线向上平移后与x 轴正半轴交于点A ,与y 轴交于点B ,且OA =OB .若点A 是由原抛物线上的点E 平移所得,求点E 的坐标;(3)在(2)的条件下,点P 是抛物线对称轴上的一点(位于x 轴上方),且∠APB =45°.求P 点的坐标.O xy 1 2 3 4 1 2 3 45-1-2 -3 -1 -2 -3 (第24题图)24.(本题满分12分)如图10,在平面直角坐标系xOy 中,抛物线23y ax bx =+-(0)a ≠与x 轴交于点A ()1,0-和点B ,且3OB OA =,与y 轴交于点C ,此抛物线顶点为点D .(1)求抛物线的表达式及点D 的坐标;(2)如果点E 是y 轴上的一点(点E 与点C 不重合),当BE DE ⊥时,求点E 的坐标; (3)如果点F 是抛物线上的一点,且135FBD ∠=,求点F 的坐标.图10C BAOyx24.(本题满分12分,每小题满分6分)如图10,在平面直角坐标系xOy 中,直线AB 与抛物线2y ax bx =+交于点A (6,0)和点B (1,-5). (1)求这条抛物线的表达式和直线AB 的表达式; (2)如果点C 在直线AB 上,且∠BOC 的正切值是32, 求点C 的坐标.图10 ABxyo24.(本题满分12分,第(1)小题3分,第(2)小题4分,第(3)小题5分)如图,抛物线c bx x y ++-=221经过点A (﹣2,0),点B (0,4). (1)求这条抛物线的表达式;(2)P 是抛物线对称轴上的点,联结AB 、PB ,如果∠PBO=∠BAO ,求点P 的坐标;(3)将抛物线沿y 轴向下平移m 个单位,所得新抛物线与y 轴交于点D ,过点D 作DE ∥x 轴交新抛物线于点E ,射线EO 交新抛物线于点F ,如果EO =2OF ,求m 的值.(第24题图)y xOBA【2019届一模嘉定】24.(本题满分12分,每小题4分)在平面直角坐标系xOy (如图7)中,抛物线22++=bx ax y 经过点)0,4(A 、)2,2(B , 与y 轴的交点为C .(1)试求这个抛物线的表达式;(2)如果这个抛物线的顶点为M ,求△AMC 的面积; (3)如果这个抛物线的对称轴与直线BC 交于点D ,点E 在线段AB 上,且︒=∠45DOE ,求点E 的坐标.图7 O 11 xy--【2019届一模青浦】24.(本题满分12分, 其中第(1)小题3分,第(2)小题5分,第(3)小题4分)在平面直角坐标系xOy 中,将抛物线2y x =-平移后经过点A (-1,0)、B (4,0),且平移后的抛物线与y 轴交于点C (如图).(1)求平移后的抛物线的表达式;(2)如果点D 在线段CB 上,且CD =2,求∠CAD 的正弦值;(3)点E 在y 轴上且位于点C 的上方,点P 在直线BC 上,点Q 在平移后的抛物线上,如果四边形ECPQ 是菱形,求点Q 的坐标.CB A xyOCB A xyO(第24题图)(备用图)24.(本题满分12分,其中第(1)小题4分,第(2)小题3分,第(3)小题5分)在平面直角坐标系xOy 中(如图10),已知抛物线2(0)y ax bx c a =++≠的图像经过点(40)B ,、(53)D ,,设它与x 轴的另一个交点为A (点A 在点B 的左侧),且ABD ∆的面积是3. (1)求该抛物线的表达式; (2)求ADB ∠的正切值;(3)若抛物线与y 轴交于点C ,直线CD 交x 轴于点E ,点P 在射线AD 上,当APE ∆与 ABD ∆相似时,求点P 的坐标.BD O图10xy﹒﹒24.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分)如图9,已知:二次函数2y x bx =+的图像交x 轴正半轴于点A ,顶点为P ,一次函数132y x =-的图像交x 轴于点B ,交y 轴于点C , ∠OCA 的正切值为23. (1)求二次函数的解析式与顶点P 坐标;(2)将二次函数图像向下平移m 个单位,设平移后抛物线顶点为P ’,若,求m 的值.A B C O yx(图9)24.(本题满分12分,每小题4分)如图,在直角坐标平面内,抛物线经过原点O 、点)3,1(B ,又与x 轴正半轴相交于点A ,︒=∠45BAO ,点P 是线段AB 上的一点,过点P 作OB PM //,与抛物线交于点M ,且点M 在第一象限内.(1)求抛物线的表达式;(2)若AOB BMP ∠=∠,求点P 的坐标;(3)过点M 作x MC ⊥轴,分别交直线AB 、x 轴于点N 、C ,若ANC ∆的面积等于PMN ∆的面积的2倍,求NC MN 的值.第24题图 xO A By备用图xO A By24.已知抛物线c bx x y ++=2经过点()6,0A ,点()3,1B ,直线1l :()0≠=k kx y ,直线2l :2--=x y ,直线1l 经过抛物线c bx x y ++=2的顶点P ,且1l 与2l 相交于点C ,直线2l 与x 轴、y 轴分别交于点D 、E .若把抛物线上下平移,使抛物线的顶点在直线2l 上(此时抛物线的顶点记为M ),再把抛物线左右平移,使抛物线的顶点在直线1l 上(此时抛物线的顶点记为N ). (1)求抛物线c bx x y ++=2的解析式.(2)判断以点N 为圆心,半径长为4的圆与直线2l 的位置关系,并说明理由.(3)设点F 、H 在直线1l 上(点H 在点F 的下方),当MHF ∆与OAB ∆相似时,求点F 、H 的坐标(直接写出结果).第24题yxO24.(本题共3小题,每小题4分,满分12分)已知:在平面直角坐标系xOy 中,抛物线2y a x b x =+经过点A (5,0)、B (-3,4),抛物线的对称轴与x 轴相交于点D .(1)求抛物线的表达式;(2)联结OB 、BD .求∠BDO 的余切值;(3)如果点P 在线段BO 的延长线上,且∠P AO =∠BAO ,求点P 的坐标.xy O (第24题图)24.(本题满分12分,第(1)小题满分4分,第(2)小题满分4分,第(3)小题满分4分)如图,在平面直角坐标系xOy 中,抛物线2y x bx c =-++与x 轴相交于原点O 和点B (4,0),点A(3,m )在抛物线上.(1)求抛物线的表达式,并写出它的对称轴; (2)求tan ∠OAB 的值;(3)点D 在抛物线的对称轴上,如果∠BAD =45°,求点D 的坐标.OAy 第24题图xBF EA CB DF E A CB DⅣ第25题(压轴题)【2019届一模徐汇】25. (本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分)已知:在梯形ABCD 中,AD //BC ,AC =BC =10,54cos =∠ACB ,点E 在对角线AC 上(不与点A 、C 重合),EDC ACB ∠=∠,DE 的延长线与射线CB 交于点F ,设AD 的长为x . (1)如图1,当DF BC ⊥时,求AD 的长; (2)设EC 的长为y ,求y 关于x 的函数解析式,并直接写出定义域; (3)当△DFC 是等腰三角形时,求AD 的长.(第25题图1) (第25题图)【2019届一模浦东】25. (本题满分14分,其中第(1)小题3分,第(2)小题5分,第(3)小题6分)将大小两把含30°角的直角三角尺按如图10-1位置摆放,即大小直角三角尺的直角顶点C 重合,小三角尺的顶点D 、E 分别在大三角尺的直角边AC 、BC 上, 此时小三角尺的斜边DE 恰好经过大三角尺的重心G . 已知∠A =∠CDE =30°,AB =12. (1)求小三角尺的直角边CD 的长;(2)将小三角尺绕点C 逆时针旋转,当点D 第一次落在大三角尺的边AB 上时(如图10-2),求点B 、E 之间的距离;(3)在小三角尺绕点C 旋转的过程中,当直线DE 经过点A 时,求∠BAE 的正弦值.G(图10-1)(图10-2)E DCABDCBAE25.(本题满分14分,第(1)小题4分,第(2)、(3)小题各5分)已知:梯形ABCD 中,AD //BC ,AB ⊥BC ,AD =3,AB =6,DF ⊥DC 分别交射线AB 、射线CB 于点E 、F .(1)当点E 为边AB 的中点时(如图1),求BC 的长; (2)当点E 在边AB 上时(如图2),联结CE ,试问:∠DCE 的大小是否确定?若确定,请求出∠DCE 的正切值;若不确定,则设AE =x ,∠DCE 的正切值为y ,请求出y 关于x 的函数解析式,并写出定义域; (3)当△AEF 的面积为3时,求△DCE 的面积.A BC D EF (图1) (第25题图) A B C D E F (图2)25.(本题满分14分)如图11,点O 在线段AB 上,22AO OB a ==,60BOP ∠=︒,点C 是射线OP 上的一个动点. (1)如图11①,当90ACB ∠=︒,2OC =,求a 的值;(2)如图11②,当AC =AB 时,求OC 的长(用含a 的代数式表示);(3)在第(2)题的条件下,过点A 作AQ ∥BC ,并使∠QOC=∠B ,求:AQ OQ 的值.A BCPOABCPO图11①图11②25.(本题满分14分,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分5分) 如图11,已知梯形ABCD 中,AB ∥CD ,∠DAB =90°,AD =4,26AB CD ==,E 是边BC 上一点,过点D 、E 分别作BC 、CD 的平行线交于点F ,联结AF 并延长,与射线DC 交于点G . (1)当点G 与点C 重合时,求:CE BE 的值;(2)当点G 在边CD 上时,设CE m =,求△DFG 的面积;(用含m 的代数式表示) (3)当AFD ∆∽ADG ∆时,求∠DAG 的余弦值.图11ABC D F E G 备用图ABC D25.(本题满分14分,第(1)小题4分,第(2)、(3)小题各5分)如图,已知△ABC 中,∠ACB =90°,D 是边AB 的中点,P 是边AC 上一动点,BP 与CD 相交于点E . (1)如果BC =6,AC =8,且P 为AC 的中点,求线段BE 的长; (2)联结PD ,如果PD ⊥AB ,且CE =2,ED =3,求cosA 的值; (3)联结PD ,如果222BP CD ,且CE =2,ED =3,求线段PD 的长.(备用图2)ABCD(备用图1)ABCD(第25题图)ABPCD E25.(满分14分,第(1)小题4分,第(2)、(3)小题各5分)在矩形ABCD 中,6=AB ,8=AD ,点E 是边AD 上一点,EC EM ⊥交AB 于点M ,点N 在射线MB 上,且AE 是AM 和AN 的比例中项. (1)如图8,求证:DCE ANE ∠=∠;(2)如图9,当点N 在线段MB 之间,联结AC ,且AC 与NE 互相垂直,求MN 的长; (3)联结AC ,如果△AEC 与以点E 、M 、N 为顶点所组成的三角形相似,求DE 的长.A备用图BD CA 图8B M E DC N A 备用图 BD C ME N A 图9 B D C25.(本题满分14分,其中第(1)小题4分,第(2)小题6分,第(3)小题4分)如图,在梯形ABCD 中,AD//BC ,BC =18,DB =DC =15,点E 、F 分别在线段BD 、CD 上,DE =DF =5. AE 的延长线交边BC 于点G , AF 交BD 于点N 、其延长线交BC 的延长线于点H . (1)求证:BG =CH ;(2)设AD =x ,△ADN 的面积为y ,求y 关于x 的函数解析式,并写出它的定义域; (3)联结FG ,当△HFG 与△ADN 相似时,求AD 的长.NHGFEDC AB (第25题图)图11ABCPQM25.(本题满分14分,其中第(1)小题4分,第(2)小题5分,第(3)小题5分)已知:如图11,在ABC ∆中,6AB =,9AC =,tan 22ABC ∠=.过点B 作BM //AC ,动点P 在射线BM 上(点P 不与点B 重合),联结PA 并延长到点Q ,使AQC ABP ∠=∠. (1)求ABC ∆的面积;(2)设BP x =,AQ y =,求y 关于x 的函数解析式,并写出x 的取值范围; (3)联结PC ,如果PQC ∆是直角三角形,求BP 的长.25.(本题满分14分,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分)如图10,已知:梯形ABCD 中,∠ABC =90°,∠A =45°,AB ∥DC ,DC =3,AB =5,点 P 在AB 边上,以点A 为圆心AP 为半径作弧交边DC 于点E ,射线EP 与射线CB 交于点F .(1)若13AP ,求DE 的长; (2)联结CP ,若CP=EP ,求AP 的长;(3)线段CF 上是否存在点G ,使得△ADE 与△FGE 相似,若相似,求FG 的值;若不相似,请说明理由.备用图A BCD PEABCDF(图10)25.(本题满分14分,第(1)小题4分,第(2)小题6分,第(3)小题4分)已知锐角MBN ∠的余弦值为53,点C 在射线BN 上,25=BC ,点A 在MBN ∠的内部, 且︒=∠90BAC ,MBN BCA ∠=∠.过点A 的直线DE 分别交射线BM 、射线BN 于点D 、E . 点F 在线段BE 上(点F 不与点B 重合),且MBN EAF ∠=∠. (1)如图1,当BN AF ⊥时,求EF 的长;(2)如图2,当点E 在线段BC 上时,设x BF =,y BD =,求y 关于x 的函数解析式并写出函数定义域;(3)联结DF ,当ADF ∆与ACE ∆相似时,请直接写出BD 的长.第25题图如图2BF EC N DA MB FC E N AD M如图1备用图BC NAM25.已知多边形ABCDEF 是⊙O 的内接正六边形,联结AC 、FD ,点H 是射线AF 上的一个动点,联结CH ,直线CH 交射线DF 于点G ,作CH MH ⊥交CD 的延长线于点M ,设⊙O 的半径为()0>r r . (1)求证:四边形ACDF 是矩形.(2)当CH 经过点E 时,⊙M 与⊙O 外切,求⊙M 的半径(用r 的代数式表示).(3)设()900<<=∠ααHCD ,求点C 、M 、H 、F 构成的四边形的面积(用r 及含α的三角比的式子表示).A B C D EF G O HM第25题图第25题备用图 ABCD E FO25.(本题满分14分,其中第(1)小题4分、第(2)、(3)小题各5分)如图,在梯形ABCD 中,AD // BC ,AB = CD ,AD = 5,BC = 15,5cos 13ABC ∠=.E 为射线CD 上任意一点,过点A 作AF // BE ,与射线CD 相交于点F .联结BF ,与直线AD 相交于点G .设CE = x ,AG y DG=. (1)求AB 的长; (2)当点G 在线段AD 上时,求y 关于x 的函数解析式,并写出函数的定义域;(3)如果23ABEF ABCD S S =四边形四边形,求线段CE 的长.AB CDEFG (第25题图)A B C D (备用图)25.(本题满分14分,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分)如图,在四边形ABCD 中,AD ∥BC ,∠A =90°,AB =6,BC =10,点E 为边AD 上一点,将△ABE 沿BE 翻折,点A 落在对角线BD 上的点G 处,联结EG 并延长交射线BC 于点F .(1)如果cos ∠DBC =23,求EF 的长; (2)当点F 在边BC 上时,联结AG ,设AD=x ,ABG BEFS y S ∆∆= ,求y 关于x 的函数关系式,并写出x 的取值范围;(3)联结CG ,如果△FCG 是等腰三角形,求AD 的长.第25题备用图 A B C 第25题图 E A B C F D G。
上海市各区2018届中考物理一模试卷按考点分类汇编压强计算-附答案

压强计算宝山:21.如图9所示,高为1米、底面积为0.5米2的轻质薄壁圆柱形容器置于水平地面上,且容器内盛满水。
⑴求水对容器底部的压强p 。
⑵若将一个体积为0.05米3的实心小球慢慢地放入该容器中,当小球静止不动时,发现容器对水平地面的压强没有发生变化。
求小球质量的最大值m 球最大。
答案:奉贤:21.如图11所示,两个均匀的实心正方体甲和乙放置在水平地面上,甲的质量为6千克,边长为0.1米。
求:(1)甲的密度 (2)甲对地面的压强P 甲(3)a.若甲乙对水平地面的压强相等,且密度之比为3:2,现分别在两物体上沿竖直方向切去质量相等的部分并分别放在对方剩余部分上,则甲乙切去部分和地面的接触面积之比b.若叠放后甲乙对地面的压强的增加量分别为ΔP 甲、ΔP 乙,且当ΔP 甲:ΔP乙=5:1时,甲物体小题无需写出计算过程) 答案:图9虹口:22. 如图10所示,轻质薄壁圆柱形容器置于水平地面,容器盛有质量为4千克的水. ①求水的体积V 水;②求0.1米深处水的压强P 水;③现有质量为4千克的物体,其底面积是容器的一半。
若通过两种方法增大地面受到的压强,并测出压强的变化量,如下表所示.根据表中的信息,通过计算判断将物体放入容器时是否有水溢出,若有水溢出请求出溢出水的重力G 溢水,若无水溢出请说明理由. 答案:金山:23.如图14所示,底面积为10米2、高为0.4米长方体甲(ρ甲=2×103千克/米3)和底面积为米2的薄壁柱形容器乙放在水平地面上。
乙容器足够高,内盛有0.1米深的水。
(1)求甲的质量m 甲。
(2)求水对乙容器底部的压强p 水。
(3)现沿水平方向将长方体甲截取一定的厚度,并将截取部分竖直放入乙容器中,使得水对容器底部的压强最大,且长方体甲对地面的压强减少量最小,请求出甲对地面的压强减少量。
答案:静安:22.盛有水的薄壁圆柱形容器置于水平地面,其底面积为2×10-2米2,甲和乙是由同种金属制成、体积不同的圆柱体。
2018年上海市各区中考一模压轴题图文解析.Removed-Output

图1
图
图
动感体验
请打开几何画板文件名“18 崇明一模 25”,拖动点 E 运动,可以体验到,△CQF 有三
次机会成为等腰三角形.
图文解析
( )在 Rt△ABC 中,AC=8,os A= 4 ,所以 AB=10,BC=6. 5
当 DE⊥AC 时,四边形 DECF 是矩形.此时 DE BC,DF AC.
C△BAF
AF 2
2x . 2 x2 4
22
9
整理,得 y 2 2 .定义域是 <x< . 2 x
( )如图 ,在 Rt△ABE 中,由 tan∠ABE= AE = 3 ,得 AB= 5 AE = 5 (2 x) .
AB 5
3
3
由△BAF∽△CAE,根据相似三角形的周长比等于相似比,得 y= C△CAE = AC .
边上一点,联结 DE,过点 D 作 DF⊥DE 交 BC 边于点 F,联结 EF.
( )如图 ,当 DE⊥AC 时,求 EF 的长;
( )如图 ,当点 E 在 AC 边上移动时,∠DFE 的正切值是否会发生变化,如果变化
请说出变化情况;如果保持不变,请求出∠DFE 的正切值;
( )如图 ,联结 CD 交 EF 于点 Q,当△CQF 是等腰三角形时,请直接写出 BF 的长.
C△BAF
AB
所以
22 2 x
5
2 (2
2 x)
.解得
x=
1 2
.所以
AB=
5 3
(2
x)
=
5 2
.
3
图4
图
第( )题的过程很繁,结果为什么很简单?
由△CEF∽△BAF(如图 ),可得△AEF∽△BCF(如图6).
对上海市宝山区2018年一模第25题的看法
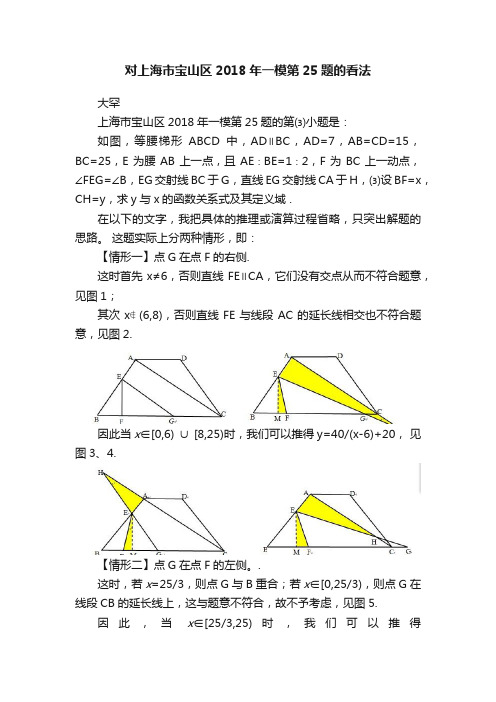
对上海市宝山区2018年一模第25题的看法大罕上海市宝山区2018年一模第25题的第⑶小题是:如图,等腰梯形ABCD中,AD∥BC,AD=7,AB=CD=15,BC=25,E为腰AB上一点,且AE∶BE=1∶2,F为BC上一动点,∠FEG=∠B,EG交射线BC于G,直线EG交射线CA于H,⑶设BF=x,CH=y,求y与x的函数关系式及其定义域 .在以下的文字,我把具体的推理或演算过程省略,只突出解题的思路。
这题实际上分两种情形,即:【情形一】点G在点F的右侧.这时首先x≠6,否则直线FE∥CA,它们没有交点从而不符合题意,见图1;其次x∉(6,8),否则直线FE与线段AC的延长线相交也不符合题意,见图2.因此当x∈[0,6) ∪ [8,25)时,我们可以推得y=40/(x-6)+20,见图3、4.【情形二】点G在点F的左侧。
.这时,若x=25/3,则点G与B重合;若x∈[0,25/3),则点G在线段CB的延长线上,这与题意不符合,故不予考虑,见图5.因此,当x∈[25/3,25)时,我们可以推得y=(260+2000]/(7x+150),见图6.【我的看法】这道压轴题出得好不好?从难度上来说够了,几种情形下的讨论够呛了,即便是在某种情形下,找出一组两个直角三角形证明其相似也是件困难的事情。
从思路上讲,两种情形,主要是要考虑点F与点G一左一右而产生的,可是在两种情形下的计算途径迥然不同,这样的安排无疑是增加了难度。
但是,在难度已经足够的情况下,再“节外生枝”,无非是想“考倒”学生,其实是不必要的。
同时,可惜的是,就是在第一种情形下(即点G在点F的右侧),有一个绝妙的设问因题目的设计而被遗弃了,即当BF=x∈(6,8)时,直线FE与线段AC的延长线相交.这时的结果与另两种情况的结果仅一个符号之差别,即y=40/(x-6)-20。
本来妙笔可生花,却失之交臂,岂能不可惜乎?鉴于此,笔者建议把此题略加修改,成为:如图,等腰梯形ABCD中,AD∥BC,AD=7,AB=CD=15,BC=25,E为腰AB上一点,且AE∶BE=1∶2,F为BC上一动点,∠FEG=∠B,EG交射线BC于G,并且点G在点F的右侧,直线EG交直线AC于H,⑶设BF=x,CH=y,求y与x的函数关系式及其定义域.2018-1-17。
2018上海初三数学一模压轴题汇总(各区23~25题)
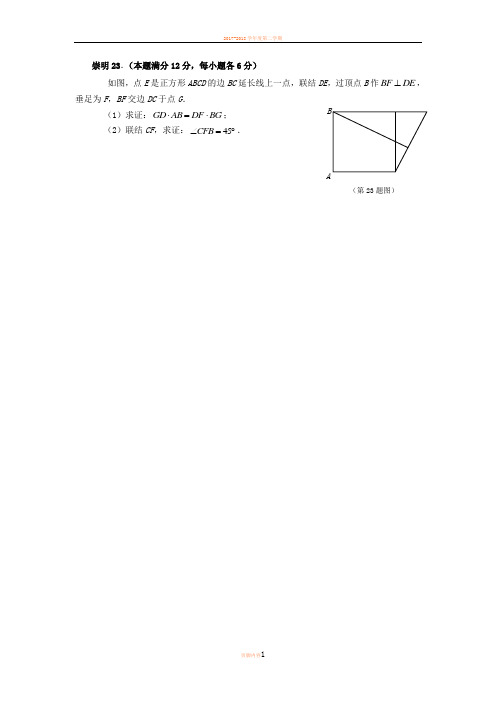
崇明23.(本题满分12分,每小题各6分)如图,点E 是正方形ABCD 的边BC 延长线上一点,联结DE ,过顶点B 作BF DE ⊥,垂足为F ,BF 交边DC 于点G .(1)求证:GD AB DF BG ⋅=⋅; (2)联结CF ,求证:45CFB ∠=︒.(第23题图)ABDECGF崇明24.(本题满分12分,每小题各4分)如图,抛物线24yx bx c =-++过点(3,0)A ,(0,2)B .(,0)M m 为线段OA 上一个x P 、N .((第24题图)xx(备用图)崇明25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)如图,已知ABC △中,90ACB ∠=︒,8AC =,4cos 5A =,D 是AB 边的中点,E 是AC 边上一点,联结DE ,过点D 作DF DE ⊥交BC 边于点F ,联结EF .(1)如图1,当DE AC ⊥时,求EF 的长;(2)如图2,当点E 在AC 边上移动时,DFE ∠的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出DFE ∠的正切值;(3)如图3,联结CD 交EF 于点Q ,当CQF △是等腰三角形时,请直接写出....BF 的长.(第25题图1)ABCDFEBDFECA(第25题图2)BDFECA(第25题图3)金山23. (本题满分12分,每小题6分)如图,已知在Rt△ABC中,∠ACB=90°,AC>BC,CD是Rt△ABC的高,E是AC的中点,ED的延长线与CB的延长线相交于点F.(1)求证:DF是BF和CF的比例中项;(2)在AB上取一点G,如果AE:AC=AG:AD,求证:EG:CF=ED:DF.金山24. (本题满分12分,每小题4分)y ax bx与y轴相交于点C,与平面直角坐标系xOy中(如图),已知抛物线23x轴正半轴相交于点A,OA OC,与x轴的另一个交点为B,对称轴是直线1x,顶点为P.(1)求这条抛物线的表达式和顶点P的坐标;(2)抛物线的对称轴与x轴相交于点M,求∠PMC的正切值;(3)点Q在y轴上,且△BCQ与△CMP相似,求点Q的坐标.金山25. (本题满分14分,第(1)小题3分,第(2)小题5分,第(3)小题6分)如图,已知在△ABC中,4 5,cos5AB AC B,P是边AB一点,以P为圆心,PB 为半径的P与边BC的另一个交点为D,联结PD、AD.(1)求△ABC的面积;(2)设PB =x,△APD的面积为y,求y关于x的函数关系式,并写出定义域;(3)如果△APD是直角三角形,求PB的长.青浦23.(本题满分12分,第(1)小题4分,第(2)小题8分)如图8,已知点D、E分别在△ABC的边AC、BC上,线段BD与AE交于点F,且CD CA CE CB⋅=⋅.(1)求证:∠CAE=∠CBD;(2)若BE ABEC AC=,求证:AB AD AF AE⋅=⋅.AB CDEF图青浦24.(本题满分12分,第(1)小题3分,第(2)小题4分,第(3)小题5分) 如图9,在平面直角坐标系xOy 中,抛物线()20y axbx c a =++>与x 轴相交于点A (-1,0)和点B ,与y 轴交于点C ,对称轴为直线1x =.(1)求点C 的坐标(用含a 的代数式表示);(2)联结AC 、BC ,若△ABC 的面积为6,求此抛物线的表达式;(3)在第(2)小题的条件下,点Q 为x 轴正半轴上一点,点G 与点C ,点F 与点A 关于点Q 成中心对称,当△CGF 为直角三角形时,求点Q 的坐标.图青浦25.(本题满分14分,第(1)小题5分,第(2)小题5分,第(3)小题4分) 如图10,在边长为2的正方形ABCD 中,点P 是边AD 上的动点(点P 不与点A 、点 D 重合),点Q 是边CD 上一点,联结PB 、PQ ,且∠PBC =∠BPQ . (1)当QD =QC 时,求∠ABP 的正切值;(2)设AP =x ,CQ =y ,求y 关于x 的函数解析式;(3)联结BQ ,在△PBQ 中是否存在度数不变的角,若存在,指出这个角,并求出它的度数;若不存在,请说明理由.图QP D C BA 备用图A B CD黄浦23、(本题满分12分)如图,BD 是ABC △的角平分线,点E 位于边BC 上,已知BD 是BA 与BE 的比例中项.(1)求证:12CDE ABC ∠=∠(2)求证:AD CD AB CE ⋅=⋅ED CBA黄浦24、(本题满分12分)在平面直角坐标系xOy 中,对称轴为直线1x =的抛物线28y ax bx =++过点()2,0-. (1)求抛物线的表达式,并写出其顶点坐标;(2)现将此抛物线沿y 方向平移若干个单位,所得抛物线的顶点为D ,与y 轴的交点为B ,与x 轴负半轴交于点A ,过点B 作x 轴的平行线交所得抛物线于点C ,若AC BD ∥,试求平移后所得抛物线的表达式.黄浦25、(本题满分14分)如图,线段5AB =,4AD =,90A ∠=︒,DP AB ∥,点C 为射线DP 上一点,BE 平分ABC ∠交线段AD 于点E (不与端点A 、D 重合).(1)当ABC ∠为锐角,且tan 2ABC ∠=时,求四边形ABCD 的面积;(2)当ABE △与BCE △相似时,求线段CD 的长;(3)设DC x =,DE y =,求y 关于x 的函数关系式,并写出定义域.PDBA P EDC BA松江23.(本题满分12分,每小题6分)已知四边形ABCD中,∠BAD=∠BDC=90°,2=⋅.BD AD BC(1)求证:AD∥BC;(2)过点A作AE∥CD交BC于点E.请完善图形并求证:2=⋅.CD BE BC松江24.(本题满分12分,每小题4分)如图,在平面直角坐标系xOy 中,抛物线2y x bx c =++的对称轴为直线x =1,抛物线与x 轴交于A 、B 两点(点A 在点B 的左侧),且AB =4,又P 是抛物线上位于第一象限的点,直线AP 与y 轴交于点D ,与对称轴交于点E ,设点P 的横坐标为t .(1)求点A 的坐标和抛物线的表达式; (2)当AE :EP =1:2时,求点E 的坐标;(3)记抛物线的顶点为M ,与y 轴的交点为C ,当四边形CDEM 是等腰梯形时,求t 的值.松江25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)如图,已知△ABC中,∠ACB=90°,AC=1,BC=2,CD平分∠ACB交边AB与点D,P是射线CD上一点,联结AP.(1)求线段CD的长;(2)当点P在CD的延长线上,且∠PAB=45°时,求CP的长;(3)记点M为边AB的中点,联结CM、PM,若△CMP是等腰三角形,求CP的长.闵行23.(本题共2小题,每小题6分,满分12分)如图,已知在△ABC 中,∠BAC =2∠B ,AD 平分∠BAC ,DF //BE ,点E 在线段BA 的延长线上,联结DE ,交AC 于点G ,且∠E =∠C .(1)求证:2AD AF AB =⋅; (2)求证:AD BE DE AB ⋅=⋅.(第23题ABDCEFG闵行24.(本题共3题,每小题4分,满分12分)抛物线23(0)y ax bx a=++≠经过点A(1-,0),B(3 2且与y轴相交于点C.(1)求这条抛物线的表达式;(2)求∠ACB的度数;(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.(第24题x闵行25.(共3小题,第(1)小题4分,第(2)小题6分,第(3)小题4分,满分14分)如图,在Rt △ABC 中,∠ACB =90°,AC =4,BC =3,CD 是斜边上中线,点E 在边AC 上,点F 在边BC 上,且∠EDA =∠FDB ,联结EF 、DC 交于点G .(1)当∠EDF =90°时,求AE 的长;(2)CE = x ,CF = y ,求y 关于x 的函数关系式,并指出x 的取值范围; (3)如果△CFG 是等腰三角形,求CF 与CE 的比值.(备用图)ABDC(第25题ABEFG浦东23.(本题满分12分,其中第(1)小题6分,第(2)小题6分) 如图,已知,在锐角△ABC 中,CE ⊥AB 于点E ,点D 在边AC 上, 联结BD 交CE 于点F ,且DF FB FC EF ⋅=⋅. (1)求证:BD ⊥AC ;(2)联结AF ,求证:AF BE BC EF ⋅=⋅.A (第23题DEFBC浦东24.(本题满分12分,每小题4分)已知抛物线y=ax2+bx+5与x轴交于点A(1,0)和点B(5,0),顶点为M.点C在x轴的负半轴上,且AC=AB,点D的坐标为(0,3),直线l经过点C、D.(1)求抛物线的表达式;(2)点P是直线l在第三象限上的点,联结AP,且线段CP是线段CA、CB的比例中项,求tan∠CPA的值;(3)在(2)的条件下,联结AM、BM,在直线PM上是否存在点E,使得∠AEM=∠AMB.若存在,求出点Ex(第24题图)浦东25.(本题满分14分,其中第(1)小题4分,第(2)小题5分,第(3)小题5分)如图,已知在△ABC中,∠ACB=90°,BC=2,AC=4,点D在射线BC上,以点D为圆心,BD为半径画弧交边AB于点E,过点E作EF⊥AB交边AC于点F,射线ED交射线AC于点G.(1)求证:△EFG∽△AEG;(2)设FG=x,△EFG的面积为y,求y关于x的函数解析式并写出定义域;(3)联结DF,当△EFD是等腰三角形时,请直接..写出FG的长度.(第25题备用图)AB C(第25题备用图)AB C虹口23.(本题满分12分,第(1)题满分6分,第(2)题满分6分)如图,在△ABC 中,点D 、E 分别在边AB 、AC 上,DE 、BC 的延长线相交于点F ,且EF DF BF CF ⋅=⋅.(1)求证AD AB AE AC ⋅=⋅;(2)当AB =12,AC =9,AE =8时,求BD 的长与△△ADEECFS S 的值.虹口24.(本题满分12分,第(1)小题满分4分,第(2)小题满分4分,第(3)小题满分4分)如图,在平面直角坐标系xOy中,抛物线与x轴相交于点A(-2,0)、B(4,0),与y轴交于点C(0,-4),BC与抛物线的对称轴相交于点D.(1)求该抛物线的表达式,并直接写出点D的坐标;(2)过点A作AE⊥AC交抛物线于点E,求点E的坐标;(3)在(2)的条件下,点F在射线AE上,若△ADF∽△ABC,求点F的坐标.虹口25.(本题满分14分,第(1)小题满分5分,第(2)小题满分5分,第(3)小题满分4分)已知AB=5,AD=4,AD∥BM,3cos5B=(如图),点C、E分别为射线BM上的动点(点C、E都不与点B重合),联结AC、AE,使得∠DAE=∠BAC,射线EA交射线CD于点F.设BC=x,AFyAC=.(1)如图1,当x=4时,求AF的长;(2)当点E在点C的右侧时,求y关于x的函数关系式,并写出函数的定义域;(3)联结BD交AE于点P,若△ADP是等腰三角形,直接写出x的值.普陀23. (本题满分12分)已知:如图9,四边形ABCD 的对角线AC 和BD 相交于点E ,2,AD DC DC DE DB ==⋅.求证:(1)BCE ADE ∽; (2)··AB BC BD BE =.图9A Bx普陀24.(本题满分12分,每小题满分各4分)如图10,在平面直角坐标系中,已知抛物线22y ax ax c +=+(其中a c 、为常数,且0a <)与x 轴交于点A ,它的坐标是()3, 0-,与y 轴交于点B ,此抛物线顶点C 到x 轴的距离为4.(1)求该抛物线的表达式; (2)求CAB ∠的正切值;(3)如果点P 是抛物线上的一点,且ABP CAO ∠=∠,试直接写出点P 的坐标.普陀25.(本题满分14分,第(1)小题满分3分,第(1)小题满分5分,第(1)小题满分6分)如图11,BAC ∠的余切值为2,AB =D 是线段AB 上的一动点(点D 不与点A B 、重合),以点D 为顶点的正方形DEFG 的另两个顶点E F 、都在射线AC 上,且点F 在点E 的右侧.联结BG ,并延长BG ,交射线EC 于点P .(1)点D 在运动时,下列的线段和角中,______是始终保持不变的量(填序号); ①AF ; ②FP ; ③BP ; ④BDG ∠; ⑤GAC ∠; ⑥BPA ∠; (2)设正方形的边长为x ,线段AP 的长为y ,求y 与x 之间的函数关系式,并写出定义域;(3)如果PFG 与AFG 相似,但面积不相等,求此时正方形的边长.备用图图11BPACCE F嘉定23.(本题满分12分,每小题6分)如图6,已知梯形ABCD 中,AD ∥BC ,CD AB =,点E 在对角线AC 上,且满足BAC ADE ∠=∠.(1)求证:BC DE AE CD ⋅=⋅;(2)以点A 为圆心,AB 长为半径画弧交边BC 于点F ,联结求证:CA CE AF ⋅=2.C图嘉定24.(本题满分12分,每小题4分)已知在平面直角坐标系xOy (如图7)中,已知抛物线c bx x y ++=232点经过)0,1(A 、)2,0(B .(1)求该抛物线的表达式;(2)设该抛物线的对称轴与x 轴的交点为C , 第四象限内的点D 在该抛物线的对称轴上,如果 以点A 、C 、D 所组成的三角形与△AOB 相似, 求点D 的坐标;(3)设点E 在该抛物线的对称轴上,它的纵坐标是1, 联结AE 、BE ,求ABE ∠sin .嘉定25.(满分14分,第(1)小题4分,第(2)、(3)小题各5分) 在正方形ABCD 中,8=AB ,点P 在边CD 上,43tan =∠PBC ,点Q 是在射线BP 上的一个动点,过点Q 作AB 的平行线交射线AD 于点M ,点R 在射线AD 上,使RQ 始终与直线BP 垂直.(1)如图8,当点R 与点D 重合时,求PQ 的长; (2)如图9,试探索:MQRM的比值是否随点Q 的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;(3)如图10,若点Q 在线段BP 上,设x PQ =,y RM =,求y 关于x 的函数关系式,并写出它的定义域.QM 图8M 图9图10静安23. (本题满分12分,其中第1小题6分,第2小题6分)已知:如图,梯形ABCD 中,//,,DC AB AD BD AD DB =⊥,点E 是腰AD 上一点,作45EBC ∠=,联结CE ,交DB 于点F . (1)求证:ABE ∽DBC ;(2)如果56BC BD =,求BCE BDAS S 的值.静安24. (本题满分12分,第1小题4分,第2小题8分)在平面直角坐标系xOy中(如图),已知抛物线25 3y ax bx=+-经过点(1,0)A-、(5,0)B.(1)求此抛物线顶点C的坐标;(2)联结AC交y轴于点D,联结BD、BC,过点C作CH BD⊥,垂足为点H,抛物线对称轴交x轴于点G,联结HG,求HG的长.静安25. (本题满分14分,第1小题4分,第2小题6分,第3小题4分) 已知:如图,四边形ABCD 中,090,,,BAD AD DC AB BC AC <∠≤==平分BAD ∠.(1)求证:四边形ABCD 是菱形;(2)如果点E 在对角线AC 上,联结BE 并延长,交边DC 于点G ,交线段AD 的延长线于点F (点F 可与点D 重合),AFB ACB ∠=∠,设AB 长度是a (a 实常数,且0a >),,AC x AF y ==,求y 关于x 的函数解析式,并写出定义域;(3)在第(2)小题的条件下,当CGE 是等腰三角形时,求AC 的长.(计算结果用含a 的代数式表示)长宁23.(本题满分12分,第(1)小题6分,第(2)小题6分) 如图,在∆ABC 中,点D 在边BC 上,联结AD ,∠ADB=∠CDE ,DE 交边AC 于点E ,DE 交BA 延长线于点F ,且DF DE AD ⋅=2.(1)求证:BFD ∆∽CAD ∆; (2)求证:AD AB DE BF ⋅=⋅.F EDA第23题长宁24.(本题满分12分,每小题4分) 在直角坐标平面内,直线221+=x y 分别与x 轴、y 轴交于点A 、C . 抛物线c bx x y ++-=221经过点A 与点C ,且与x 轴的另一个交点为点B . 点D 在该抛物线上,且位于直线AC 的上方.(1)求上述抛物线的表达式;(2)联结BC 、BD ,且BD 交AC 于点E ,如果∆ABE 的面积与∆ABC 的面积之比为4:5, 求∠DBA 的余切值;(3)过点D 作DF ⊥AC ,垂足为点F ,联结CD . 若∆CFD 与∆AOC 相似,求点D 的坐标.备用图 第24题长宁25.(本题满分14分,第(1)小题3分,第(2)小题6分,第(3)小题5分) 已知在矩形ABCD 中,AB =2,AD =4. P 是对角线BD 上的一个动点(点P 不与点B 、D 重合),过点P 作PF ⊥BD ,交射线BC 于点F . 联结AP ,画∠FPE =∠BAP ,PE 交BF 于点E .设PD=x ,EF =y .(1)当点A 、P 、F 在一条直线上时,求 ABF 的面积;(2)如图1,当点F 在边BC 上时,求y 关于x 的函数解析式,并写出函数定义域; (3)联结PC ,若∠FPC =∠BPE ,请直接写出PD 的长.备用图 备用图图1DCBA DCBA F EP D CB A 第25题图徐汇23.(本题满分12分,第(1)小题满分5分,第(2)小题满分7分)如图在△ABC中,AB=AC,点D、E、F分别在边BC、AB、AC上,且∠ADE=∠B,∠ADF=∠C,线段EF交线段AD于点G.(1)求证:AE=AF;(2)若DF CFDE AE,求证:四边形EBDF是平行四边形.徐汇24.(本题满分12分,第(1)小题满分3分,第(2)小题满分4分,第(3)小题满分5分)如图,在平面直角坐标系xOy 中,直线y =kx (k ≠0)沿着y 轴向上平移3个单位长度后,与x 轴交于点B (3,0),与y 轴交于点C ,抛物线2y x bx c =++过点B 、C 且与x 轴的另一个交点为A .(1)求直线BC 及该抛物线的表达式; (2)设该抛物线的顶点为D ,求△DBC 的面积;(3)如果点F 在y 轴上,且∠CDF =45°,求点F 的坐标.徐汇25.(本题满分14分,第(1)小题3分,第(2)小题7分,第(3)小题4分)已知,在梯形ABCD中,AD∥BC,∠A=90°,AD=2,AB=4,BC=5,在射线BC任取一点M,联结DM,作∠MDN=∠BDC,∠MDN的另一边DN交直线BC于点N(点N在点M的左侧).(1)当BM的长为10时,求证:BD⊥DM;(2)如图(1),当点N在线段BC上时,设BN=x,BM=y,求y关于x的函数关系式,并写出它的定义域;(3)如果△DMN是等腰三角形,求BN的长.杨浦23.(本题满分12分,第(1)小题5分,第(2)小题7分)已知:梯形ABCD 中,AD //BC ,AD =AB ,对角线AC 、BD 交于点E ,点F 在边BC 上,且∠BEF =∠BAC .(1)求证:△AED ∽△CFE ;(2)当EF //DC 时,求证:AE =DE .(第23题C杨浦24.(本题满分12分,第(1)小题3分,第(2)小题5分,第(3)小题4分)在平面直角坐标系xOy 中,抛物线2221y x mx m m =-+--+交 y 轴于点为A ,顶点为D ,对称轴与x 轴交于点H .(1)求顶点D 的坐标(用含m 的代数式表示);(2)当抛物线过点(1,-2),且不经过第一象限时,平移此抛物线到抛物线22y x x =-+的位置,求平移的方向和距离;(3)当抛物线顶点D 在第二象限时,如果∠ADH =∠AHO ,求m 的值.x(第24题图)杨浦25.(本题满分14分,第(1)、(2)小题各6分,第(3)小题2分)已知:矩形ABCD 中,AB =4,BC =3,点M 、N 分别在边AB 、CD 上,直线MN 交矩形对角线AC 于点E ,将△AME 沿直线MN 翻折,点A 落在点P 处,且点P 在射线CB 上.(1)如图1,当EP ⊥BC 时,求CN 的长; (2)如图2,当EP ⊥AC 时,求AM 的长;(3)请写出线段CP 的长的取值范围,及当CP 的长最大时MN 的长.(备用(图1)A B C D NP ME(图2) A B C D N P M E (第25题A B CD奉贤23.(本题满分 12 分,每小题满分各 6 分)已知:如图 8,四边形90ABCD DCB ∠=︒,,对角线 BD ⊥AD ,点 E 是边 AB 的中点,CE 与 BD 相交于点 F ,2·BD AB BC =.(1) 求证:BD 平分∠ABC ;(2) 求证:··BE CF BC EF =.奉贤24. (本题满分 12 分,每小题满分各 4 分)如图9,在平面直角坐标系xOy 中,抛物线238y x bx c =++与x 轴相交于点(2,0)A -和点B ,与y 轴相交于点(0,3)C -,经过点A 的射线AM 与y 轴相交于点E ,与抛物线的另一个交点为点F ,且13AE EF =. (1)求这条抛物线的表达式,并写出它的对称轴; (2)求FAB ∠的余切值;(3)点D 是点C 关于抛物线对称轴的对称点,点 P 是 y 轴上一点,且AFP DAB ∠=∠,求点 P 的坐标.奉贤25.(本题满分 14 分,第(1)小题满分 3 分,第(1)小题满分 5 分,第(1)小题满分 6 分)已知:如图10,在梯形ABCD 中,//,90,2AB CD D AD CD ∠===,点E 在边AD 上(不与点A 、D 重合),45,CEB EB ∠=与对角线AC 相交于点F ,设DE x =.(1)用含x 的代数式表示线段CF 的长; (2)如果把CAE 的周长记作CAE C,BAF 的周长记作BAF C,设CAE BAFCy C=,求y关于x 的函数关系式,并写出它的定义域;(3)当ABE ∠的正切值是35时,求AB 的长.宝山23、(满分12分,每小题各6分)如图,ABC 中,AB AC =,过点C 作//CF AB 交ABC 的中位线DE 的延长线于F ,联结BF ,交AC 于点G .(1)求证:AE EGAC CG=; (2)若AH 平分BAC ∠,交BF 于H ,求证:BH 是HG 和HF 的比例中项.宝山24、(满分12分,每小题各4分)设,a b 是任意两个不等实数,我们规定:满足不等式a x b ≤≤的实数x 的所有取值的全体叫做闭区间,表示为[],a b ,对于一个函数,如果它的自变量x 与函数值y 满足:当m x n ≤≤时,有m y n ≤≤,我们就此称此函数是闭区间[],m n 上的“闭函数”。
2018年上海市初三数学一模试卷18题汇总解析

2018年上海市初三一模数学考试18题解析2018.01一. 普陀区18. 如图,ABC 中,5AB ,6AC ,将ABC 翻折,使得点A 落到边BC 上的点A 处,折痕分别交边AB 、AC 于点E 、点F ,如果A F ∥AB ,那么BE【解析】设BE x ,由题意可知:5A E AE xA F ∥AB 13 又∵12 ∴23 A E ∥AC ∴AE BE AC AB 即565x x 解得2511x 即2511BE 二. 奉贤区18. 已知ABC ,AB AC ,8BC ,点D 、E 分别在边BC 、AB 上,将ABC 沿着直线DE 翻折,点B 落在边AC 上的点M 处,且4AC AM ,设BD m ,那么ACB 的正切值是 (用含m 的代数式表示)【解析】作MN BC 于N ,AH BC 于H ,MD BD mAB AC ,8BC ,AH BC 4BH CHMN BC ,AH BC MN ∥AH CN CM CH AC3CN ∴835DN BC BD CN m m在Rt MND 中,222MN DN MD 3MN∴tan 9MN ACB CN三. 杨浦区18. 如图,在ABC 中,AB AC ,将ABC 绕点A 旋转,当点B 与点C 重合时,点C 落 在点D 处,如果2sin 3B ,6BC ,那么BC 的中点M 和CD 的中点N 的距离是【解析】12 ,M 为BC 的中点,N 为CD 的中点 1MAN ,AM AN 又∵AB AC ∴AB AM AC AN ,1MAN AMN ∽ABC AM MN AB BC ∵2sin 3AM B AB,6BC ∴4MN 四. 黄浦区18. 如图,平面上七个点A 、B 、C 、D 、E 、F 、G ,图中所有的连线长均相等,则cos BAF【解析】联结AC 、AD 、BF ,作CH AD 于H∵ABG 、BCG 、AEF 、DEF 为等边三角形 120ABC AED 又∵AB BC AE DE ∴ABC ≌AED AC AD四边形ABCG 和四边形AEDF 为菱形 12 BAF CAD又AB AF ,AC AD ∴ABF ∽ACD设2AB 那么AC ADCH CH,解得3AH ,5cos 6AH BAF AC解法二:根据上面分析,问题可以简化为,已知边长比为2CD ,∴AC AD ,取CD 中点K ,∴1CK KD ,易得△ADK ∽△CDH ,∴3KD HD HD AD CD,即3AH 5cos 6AH CAH AC .五. 松江区18. 如图,在ABC 中,90C ,4AC BC ,将ABC 翻折,使得点A 落在边BC 的中点A 处,折痕分别交边AB 、AC 于点D 、点E ,那么:AD AE 的值为【解析】作AF AB 于F在Rt ECA 中,222CE A C A E 即222()AC A E A C A E∵4AC ,2A C ∴52A E 即52AEAF AB ,2A B ,45B A F BF在Rt A DF 中,222A F DF A D 即222()A F AB BF A D A D∵AB ,A F BF∴3A D AD ∴5::323AD AE 六. 徐汇区18. 在ABC 中,90C ,3AC ,4BC (如图),将ACB 绕点A 顺时针方向旋转得ADE (点C 、B 的对应点分别为点D 、E ),点D 恰好落在直线BE 上,直线BE 与直线AC 交于点F ,则线段AF 的长为【解析】如图所示,点D 恰好落在直线BE 上AD BE ,AB AE 4BD DE在Rt BCF ,222BC CF BF 即BFADF ∽BCF AD AFBC BF ,即34 ,解得757AF七. 闵行区18. 如图,在等腰ABC 中,AB AC ,30B ,以点B 为旋转中心,旋转30°,点A 、 C 分别落在点A 、C 处,直线AC 、A C 交于点D ,那么AD AC的值为【解析】设2AB AC ,那么BC(1)顺时针旋转,如图1,303060C BA ,30C AB C D在Rt BC E 中,30C ,BC BC BE 2AE60BAD ABC AD ∥BC 1sin 42AE ADE AD AD∴ 422AD AC (2)逆时针旋转,如图2,303060CBA ,30C A B CD在Rt BCE 中,30C ,BC BE 2A E 1AE60BA D A BC tan 33A E A DE DE DE∴ 2AD ,1AD AC综上所述:AD AC 的值为21 八. 虹口区18. 在Rt ABC 中,90C ,6AC ,8BC (如图),点D 是边AB 上一点,把ABC 绕着点D 旋转90°,得到A B C ,边B C 与边AB 相交于点E ,如果AD BE ,那么AD 长为【解析】当点D 位于图1位置时,边B C 与边AB 不相交当点D 位于图2位置时,设AD x ,BE x ,10B D BD x ,① 当ABC 是顺时针旋转时,AD BE AB DE 210DE xB DE ∽BC A DE BD A C B C 即2101068x x 解得7011x ② 当ABC 是逆时针旋转时,AD BE DE AB 102DE xB DE ∽BC ADE B D A C B C 即1021068x x 解得2x , 当2x 时,即图1的情况,不符,舍去,综上,7011AD九. 静安区18. 如图,矩形纸片ABCD ,4AD ,3AB ,如果点E 在边BC 上,将纸片沿AE 折叠,使点B 落在点F 处,联结FC ,当EFC 是直角三角形时,那么BE 的长为【解析】① 当EFC 是直角时(如图1),设BE x ,4CE x∵190B ∴1180EFC 即A 、F 、C 在同一条直线上∴532CF AC AF在Rt EFC 中,222EF CF CE 即2222(4)x x 解得32x② 当CEF 是直角时(如图2)那么1245 ,点B 正好落在边AD 上∵90B ,245 ,∴3BE AB ,综上:BE 的长为32或3.十. 浦东新区18. 如图,已知在Rt ABC 中,90ACB ,4cos 5B ,8BC ,点D 在边BC 上, 将ABC 沿着过点D 的一条直线翻折,使点B 落在AB 边上的点E 处,联结CE 、DE , 当BDE AEC 时,则BE 的长是【解析】作CF AB 于F ,DH AB 于H设3DH x ,那么4BH EH x ,5BD x 90ACB ,4cos 5B,8BC 245AC BC CF AB DH BH CF BF 325BF ∴3285EF BE BF x 在Rt CEF 中,222222432((8)55CE CF EF x ∵BDE AEC ,∴CEB CDE 又∵ECB DCE , ∴BCE ∽ECD 2CE BC CD ∴222432((8)8(85)55x x 解得3940x ∴3985BE x 十一. 长宁18. 如图,在边长为2的菱形ABCD 中,60D ,点E 、F 分别在边AB 、BC 上,将BEF 沿着直线EF 翻折,点B 恰好与边AD 的中点G 重合,则BE 的长等于【解析】如右图所示,在Rt △GFC 中,设GF BF x ,2FC x ,GC ,∴22(2)3x x ,74x ,即74BF ,∵2IO ,1BI ,∴34IF ,设BH m ,∴EH ,74HF m ,EH OI HF IF ,解得710m ,∴725BE m18. 如图,点M 是正方形ABCD 的边BC 的中点,联结AM ,将BM 沿某一过M 的直线翻折,使B 落在AM 上的E 处,将线段AE 绕A 顺时针旋转一定角度,使E 落在F 处,如果E 在旋转过程中曾经交AB 于G ,当EF BG 时,旋转角EAF 的度数是【解析】作FE FH ,设2AB ,AM ,1MB ME ,1AE AF AG ,∴3GB EF FH AFE ∽△FEH ,∴24EF AE HE HE ,∴3AH ,∴AH HF FE ,∴5180EAF AFE FEA EAF , 即36EAF .十三. 崇明县18. 如图,在ABC 中,90ACB ,点D 、E 分别在AC 、BC 上,且CDE B ,将CDE 沿DE 折叠,点C 恰好落在AB 边上的点F 处,如果8AC ,10AB ,那么CD 的长为【解析】CF DE ,CDE B 190CDE∵CDE B ,90A B ∴1A∴ABC ∽CDOAC AB OC CD45OC CD ∴85CF CD 12A ACF ∽CFD AC CF CFDF即2CF AC CD ∴28()85CD CD 解得258CD18. 如图,在直角梯形ABCD 中,AD ∥BC ,90B ,3AD ,4AB ,8BC ,点E 、F 分别在边CD 、BC 上,联结EF ,如果CEF 沿直线EF 翻折,点C 与点A 恰好重合,那么DE EC的值是【解析】作DG ∥EF 交AC 于G在Rt ABC 中,8BC ,4AB AC ∴12CH AC DG ∥EF ,EF AC DG AC 又AD ∥BC 12∴ADG ∽CAB AD AG AC BC AG HG AC AG CH DG ∥EF 25DE HG EC CH十五. 青浦区18. 如图,在ABC 中,7AB ,6AC ,45A ,点D 、E 分别在边AB 、BC 上,将BDE 沿着DE 所在直线翻折,点B 落在点P 处,PD 、PE 分别交边AC 于点M 、N ,如果2AD ,PD AB ,垂足为点D ,那么MN 的长是【解析】7AB ,2AD 5BD DPPD AB ,45A ,2AD 2DM ∴3MPPD AB 1245又45A DE ∥ACDE BD AC AB 307DE ,MN MP DE DP 187MN18. 如图,在矩形ABCD 中,E 是AD 上一点,把ABE 沿直线BE 翻折,点A 正好落在BC 边上的点F 处,如果四边形CDEF 和矩形ABCD 相似,那么四边形CDEF 和矩形ABCD 面积比是【解析】四边形CDEF 和矩形ABCD 相似DE CD CD AD 即2CD DE AD ∵()CD EF AE AD DE∴2()AD DE DE AD 即2230AD AD DE DE解得32DE AD3=2CDEFABCD S CD DE DE S CD AD AD 四边形矩形。
2018上海各区一模分类整理(第25题压轴题)

2018年初三一模知识点分类整理——压轴题第25题压轴题1. 如图,等腰梯形ABCD中,AD//BC,AD=7,AB=CD=15,BC=25,E为腰AB上一点且AE:BE=1:2,F为BC一动点,∠FEG=∠B,EG交射线BC于G,直线EG交射线CA于H.(1)求sin∠ABC;(2)求∠BAC的度数;(3)设BF=x,CH=y,求y与x的函数关系式及其定义域.B2. (崇明) 如图,已知△ABC 中,∠ACB =90°,AC =8,cos A =45,D 是AB 边的中点, E 是AC 边上一点,联结DE ,过点D 作DF ⊥DE 交BC 边于点F ,联结EF . (1)如图1,当DE ⊥AC 时,求EF 的长;(2)如图2,当点E 在AC 边上移动时,∠DFE 的正切值是否会发生变化,如果变化请说出变化 情况;如果保持不变,请求出∠DFE 的正切值;(3)如图3,联结CD 交EF 于点Q ,当△CQF 是等腰三角形时,请直接写出BF 的长.F EA(第25题图1)FC(第25题图2)FC(第25题图3)3. (奉贤)已知:如图,在梯形ABCD 中,//,90,2AB CD D AD CD ∠===,点E 在边AD 上(不与点A 、D 重合),45,CEB EB ∠=与对角线AC 相交于点F ,设DE x =. (1)用含x 的代数式表示线段CF 的长; (2)如果把CAE 的周长记作CAE C,BAF 的周长记作BAFC,设CAE BAFCy C=,求y 关于x 的函数关系式,并写出它的定义域; (3)当ABE ∠的正切值是35时,求AB 的长.4. (虹口)已知AB=5,AD=4,AD∥BM,3cos5B=(如图),点C、E分别为射线BM上的动点(点C、E都不与点B重合),联结AC、AE,使得∠DAE=∠BAC,射线EA交射线CD于点F.设BC=x,AFy AC=.(1)如图1,当x=4时,求AF的长;(2)当点E在点C的右侧时,求y关于x的函数关系式,并写出函数的定义域;(3)联结BD交AE于点P,若△ADP是等腰三角形,直接写出x的值.5. (黄浦)如图,线段5AB =,4AD =,90A ∠=︒,DP AB ∥,点C 为射线DP 上一点,BE 平分ABC ∠交线段AD 于点E (不与端点A 、D 重合).(1)当ABC ∠为锐角,且tan 2ABC ∠=时,求四边形ABCD 的面积; (2)当ABE △与BCE △相似时,求线段CD 的长;(3)设DC x =,DE y =,求y 关于x 的函数关系式,并写出定义域. PDBA P EDC BA6. (嘉定)在正方形ABCD 中,8=AB ,点P 在边CD 上,43tan =∠PBC ,点Q 是在射线BP 上 的一个动点,过点Q 作AB 的平行线交射线AD 于点M ,点R 在射线AD 上,使RQ 始终与直线BP 垂直.(1)如图8,当点R 与点D 重合时,求PQ 的长;(2)如图9,试探索:MQRM的比值是否随点Q 的运动而发生变化?若有变化,请说明你的理由; 若没有变化,请求出它的比值;(3)如图10,若点Q 在线段BP 上,设x PQ =,y RM =,求y 关于x 的函数关系式, 并写出它的定义域.图8图9图107. (闵行) 如图,在Rt △ABC 中,∠ACB =90°,AC =4,BC =3,CD 是斜边上中线,点E 在边AC 上,点F 在边BC 上,且∠EDA =∠FDB ,联结EF 、DC 交于点G . (1)当∠EDF =90°时,求AE 的长;(2)CE = x ,CF = y ,求y 关于x 的函数关系式,并指出x 的取值范围; (3)如果△CFG 是等腰三角形,求CF 与CE 的比值.(备用图)ABDC(第25题图)ABCEFG8. (浦东)如图,已知在△ABC 中,∠ACB=90°,BC =2,AC =4,点D 在射线BC 上,以点D 为圆心,BD 为半径画弧交边AB 于点E ,过点E 作EF ⊥AB 交边AC 于点F ,射线ED 交射线AC 于点G . (1)求证:△EFG ∽△AEG ;(2)设FG =x ,△EFG 的面积为y ,求y 关于x 的函数解析式并写出定义域; (3)联结DF ,当△EFD 是等腰三角形时,请直接..写出FG 的长度.C ABGF D E(备用图)AB C(备用图)AB C9. (普陀)如图,∠BAC的余切值为2,AB=D是线段AB上的一动点(点D不与点A、B重合),以点D为顶点的正方形DEFG的另两个顶点E、F都在射线AC上,且点F在点E的右侧.联结BG,并延长BG,交射线EC于点P.(1)点D在运动时,下列的线段和角中,______是始终保持不变的量(填序号);①AF;②FP;③BP;④∠BDG;⑤∠GAC;⑥∠BP A;(2)设正方形的边长为x,线段AP的长为y,求y与x之间的函数关系式,并写出定义域;(3)如果△PFG与△AFG相似,但面积不相等,求此时正方形的边长.图11 备用图10. (静安)已知:如图,四边形ABCD 中,090,,,BAD AD DC AB BC AC <∠≤==平分BAD ∠.(1)求证:四边形ABCD 是菱形;(2)如果点E 在对角线AC 上,联结BE 并延长,交边DC 于点G ,交线段AD 的延长线于 点F (点F 可与点D 重合),AFB ACB ∠=∠,设AB 长度是a (a 实常数,且0a >),,A C xA F y ==,求y 关于x 的函数解析式,并写出定义域;(3)在第(2)小题的条件下,当CGE 是等腰三角形时,求AC 的长. (计算结果用含a 的代数式表示)11. (松江)如图,已知△ABC中,∠ACB=90°,AC=1,BC=2,CD平分∠ACB交边AB与点D,P是射线CD上一点,联结AP.(1)求线段CD的长;(2)当点P在CD的延长线上,且∠P AB=45°时,求CP的长;(3)记点M为边AB的中点,联结CM、PM,若△CMP是等腰三角形,求CP的长.12. (徐汇)已知,在梯形ABCD中,AD∥BC,∠A=90°,AD=2,AB=4,BC=5,在射线BC任取一点M,联结DM,作∠MDN=∠BDC,∠MDN的另一边DN交直线BC于点N(点N在点M的左侧).(1)当BM的长为10时,求证:BD⊥DM;(2)如图(1),当点N在线段BC上时,设BN=x,BM=y,求y关于x的函数关系式,并写出它的定义域;(3)如果△DMN是等腰三角形,求BN的长.13. (杨浦)已知:矩形ABCD 中,AB =4,BC =3,点M 、N 分别在边AB 、CD 上,直线MN 交矩形对角线AC 于点E ,将△AME 沿直线MN 翻折,点A 落在点P 处,且点P 在射线CB 上. (1)如图1,当EP ⊥BC 时,求CN 的长; (2)如图2,当EP ⊥AC 时,求AM 的长;(3)请写出线段CP 的长的取值范围,及当CP 的长最大时MN 的长.(备用图)(图1)ABC D NPME(图2) A BCD N P ME(第25题图)AB CD14. (金山)如图,已知在△ABC中,AB=AC=5,cos B=45,P是边AB上一点,以P为圆心,PB为半径的⊙P与边BC的另一个交点为D,联结PD、AD.(1)求△ABC的面积;(2)设PB=x,△APD的面积为y,求y关于x的函数关系式,并写出定义域;(3)如果△APD是直角三角形,求PB的长.15. (长宁)已知在矩形ABCD 中,AB =2,AD =4. P 是对角线BD 上的一个动点(点P 不与点B 、D重合),过点P 作PF ⊥BD ,交射线BC 于点F . 联结AP ,画∠FPE =∠BAP ,PE 交BF 于点E . 设PD=x ,EF =y .(1)当点A 、P 、F 在一条直线上时,求 ABF 的面积;(2)如图1,当点F 在边BC 上时,求y 关于x 的函数解析式,并写出函数定义域; (3)联结PC ,若∠FPC =∠BPE ,请直接写出PD 的长.备用图备用图图1DCBA DCBA F EP DCB A第25题图16. (青浦)如图10,在边长为2的正方形ABCD 中,点P 是边AD 上的动点(点P 不与点A 、点D重合),点Q 是边CD 上一点,联结PB 、PQ ,且PBC BPQ ∠=∠. (1)当QD QC =时,求ABP ∠的正切值;(2)设AP x =,CQ y =,求y 关于x 的函数解析式;(3)联结BQ ,在PBQ △中是否存在度数不变的角,若存在,指出这个角,并求出它的度数; 若不存在,请说明理由.图10QP D C BA 备用图A BCD。
2015-2018年上海初三数学一模第25题汇编-答案版

2015 年初三一模25 题汇编题型一:等腰三角形分类议论(黄浦 2015 年初三一模)25.(此题满分 14 分,此中第 (1) 小题 4 分,第 (2) 小题 5 分,第 (3) 小题 5 分)如图 12,在矩形ABCD中,AB8, BC 6 对角线 AC、 BD 交于点 O ,点E在AB延伸线上,联结 CE ,AF CE ,AF分别交线段 CE 、边 BC 、对角线BD于点 F、 G、 H (点F不与点 C、 E 重合)。
( 1)当点F是线段CE的中点时,求GF 的长;( 2)设BE x, OH y ,求y对于x的函数分析式,并写出它的定义域;( 3)当BHG 是等腰三角形时,求BE 的长。
【答案】 25.(此题满分14 分,此中第( 1)小题 4 分,第( 2)小题 5 分,第( 3)小题 5 分)(1)矩形 ABCD 中, ABC 90 ,AB 8, BC 6, AC 10A F C E CE,且点 F 是线段的中点,A E AC10, BE 2RtCBE 中, tan ECBBE 1BC3CEBC 2 BE 22 10, CF 10 Rt CBE ,GFCF tanECB103( 2)ABC CBE 90 , AGBCGF ,BAG BCEBG AB BG 4BE, x.BC3矩形 ABCD 中, AD / /BC,BGBH4 x5 y, 3 AD DH 6 y 5y45 10 x (0 x 9).2 x 92(3)1 当BHBG 时, DHAD ,5 y6 ,即4510y 1 ,解得 x 32x 92 当GH BG 时, AD AH过点 A 作AMDH ,垂足为 H 。
5 yRt CBE 中, cos ADB3 .2 3( 1)5 6.5将 y45 10x代入( 1) 解得 x72x943 当GH BH 时, DH AH ,点 H 在 AD 垂直均分线上,此时 F 点与点 C 重合,x9(舍)2综上所述 BE 的长是 3或7.4(普陀 2015 初三一模)25、如图 12、等边ABC , AB 4 ,点 P 是射线 AC 上的一个动点。
上海市徐汇区2018年初三一模语文试卷(含答案)

徐汇区2018届九年级上学期期末(一模)语文试卷(满分150分,考试时间100分钟)考生注意:1.本试卷共26题。
2.请将所有答案做在答题纸的指定位置上,做在试卷上一律不计分。
一、文言文(39分)(一)默写(15分)1.必先苦其心志,,饿其体肤。
(孟子《生于忧患,死于安乐》)2.东边日出西边雨,。
(刘禹锡《竹枝词》)3.,此日中流自在行。
(朱熹《观书有感》(其二))4.,匹马戍梁州。
(陆游《诉衷情》)5.草枯鹰眼疾,。
(王维《观猎》)(二)阅读下面这首曲,完成第6—7题(4分)天净沙•秋思枯藤老树昏鸦,小桥流水人家,古道西风瘦马。
夕阳西下,断肠人在天涯。
6.这首元曲的作者是。
(2分)7.对这首元曲的理解不正确...一项是()(2分)A. “枯藤老树昏鸦”呈现出萧索枯败的冬日景象。
B. “小桥流水人家”的画面勾起旅人的向往之情。
C. “古道西风瘦马”写出游子漂泊无依的状态。
D. “断肠人在天涯”以游子思乡之苦收束全篇。
(三)阅读下文,完成第8—10题(8分)黔之驴柳宗元黔无驴,有好事者船载以入。
至则无可用,放之山下。
虎见之,庞然大物也,以为神。
蔽林间窥之,稍出近之,慭慭然,莫相知。
他日,驴一鸣,虎大骇,远遁;以为且噬己也,甚恐。
然往来视之,觉无异能者,益习其声,又近出前后,终不敢搏。
稍近益狎,荡倚冲冒,驴不胜怒,蹄之。
虎因喜,计之曰:“技止此耳!”因跳踉大㘎,断其喉,尽其肉,乃去。
8.请写出一个出自本文的成语(2分)9.用现代汉语翻译下面的句子。
(3分)蔽林间窥之,稍出近之10.下列选项中与本文主旨最接近的语句是()(3分)A.苛政猛于虎也。
B.出淤泥而不染。
C.天时不如地利,地利不如人和。
D.金玉其外,败絮其中。
(四)阅读下面语段,完成第11—13题(12分)宋孝宗时,张子韶在讲筵。
上尝问曰:“何以见教?”张曰:“臣安敢当.见教之语?抑不知陛下临朝对群臣时,如何存心?”上曰:“以至诚。
”又曰:“入而对宦官、嫔御如何?”曰:“亦至诚。
2018上海初三年级数学一模压轴题汇总(各区23~25题)
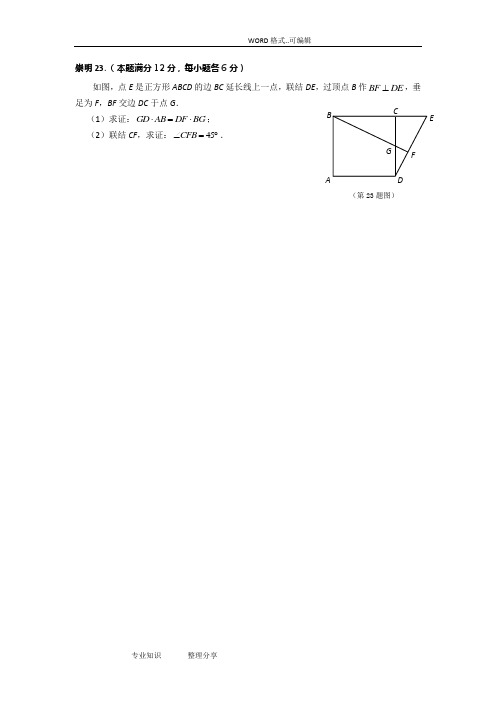
崇明23.(本题满分12分,每小题各6分)如图,点E 是正方形ABCD 的边BC 延长线上一点,联结DE ,过顶点B 作BF DE ⊥,垂足为F ,BF 交边DC 于点G . (1)求证:GD AB DF BG ⋅=⋅; (2)联结CF ,求证:45CFB ∠=︒.(第23题图)ABDECGF崇明24.(本题满分12分,每小题各4分)如图,抛物线24yx bx c =-++过点(3,0)A ,(0,2)B .(,0)M m 为线段OA 上一个动点(点N .(((△(第24题图) (备用图)崇明25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)如图,已知ABC △中,90ACB ∠=︒,8AC =,4cos 5A =,D 是AB 边的中点,E 是AC 边上一点,联结DE ,过点D 作DF DE ⊥交BC 边于点F ,联结EF .(1)如图1,当DE AC ⊥时,求EF 的长;(2)如图2,当点E 在AC 边上移动时,DFE ∠的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出DFE ∠的正切值;(3)如图3,联结CD 交EF 于点Q ,当CQF △是等腰三角形时,请直接写出....BF 的长.(第25题图1) ABCD FE BD FE CA(第25题图2)BDFECA(第25题图3)如图,已知在Rt△ABC中,∠ACB=90°,AC>BC,CD是Rt△ABC的高,E是AC 的中点,ED的延长线与CB的延长线相交于点F.(1)求证:DF是BF和CF的比例中项;(2)在AB上取一点G,如果AE:AC=AG:AD,求证:EG:CF=ED:DF.平面直角坐标系xOy 中(如图),已知抛物线23y ax bx =++与y 轴相交于点C ,与x 轴正半轴相交于点A ,OA OC =,与x 轴的另一个交点为B ,对称轴是直线1x =,顶点为P .(1)求这条抛物线的表达式和顶点P 的坐标;(2)抛物线的对称轴与x 轴相交于点M ,求∠PMC 的正切值; (3)点Q 在y 轴上,且△BCQ 与△CMP 相似,求点Q 的坐标.金山25. (本题满分14分,第(1)小题3分,第(2)小题5分,第(3)小题6分)如图,已知在△ABC中,45,cos5AB AC B===,P是边AB一点,以P为圆心,PB为半径的Pe与边BC的另一个交点为D,联结PD、AD.(1)求△ABC的面积;(2)设PB =x,△APD的面积为y,求y关于x的函数关系式,并写出定义域;(3)如果△APD是直角三角形,求PB的长.青浦23.(本题满分12分,第(1)小题4分,第(2)小题8分)如图8,已知点D、E分别在△ABC的边AC、BC上,线段BD与AE交于点F,且CD CA CE CB⋅=⋅.(1)求证:∠CAE=∠CBD;(2)若BE ABEC AC=,求证:AB AD AF AE⋅=⋅.ADEF图8如图9,在平面直角坐标系xOy 中,抛物线()20y axbx c a =++>与x 轴相交于点A (-1,0)和点B ,与y 轴交于点C ,对称轴为直线1x =.(1)求点C 的坐标(用含a 的代数式表示);(2)联结AC 、BC ,若△ABC 的面积为6,求此抛物线的表达式;(3)在第(2)小题的条件下,点Q 为x 轴正半轴上一点,点G 与点C ,点F 与点A 关于点Q 成中心对称,当△CGF 为直角三角形时,求点Q 的坐标.图9如图10,在边长为2的正方形ABCD 中,点P 是边AD 上的动点(点P 不与点A 、点 D 重合),点Q 是边CD 上一点,联结PB 、PQ ,且∠PBC =∠BPQ . (1)当QD =QC 时,求∠ABP 的正切值; (2)设AP =x ,CQ =y ,求y 关于x 的函数解析式;(3)联结BQ ,在△PBQ 中是否存在度数不变的角,若存在,指出这个角,并求出它的度数;若不存在,请说明理由.图10QP D C BA备用图A BCD黄浦23、(本题满分12分)如图,BD 是ABC △的角平分线,点E 位于边BC 上,已知BD 是BA 与BE 的比例中项. (1)求证:12CDE ABC ∠=∠(2)求证:AD CD AB CE ⋅=⋅ED CBA在平面直角坐标系xOy 中,对称轴为直线1x =的抛物线28y ax bx =++过点()2,0-. (1)求抛物线的表达式,并写出其顶点坐标;(2)现将此抛物线沿y 方向平移若干个单位,所得抛物线的顶点为D ,与y 轴的交点为B ,与x 轴负半轴交于点A ,过点B 作x 轴的平行线交所得抛物线于点C ,若A C B D ∥,试求平移后所得抛物线的表达式.如图,线段5AB =,4AD =,90A ∠=︒,DP AB ∥,点C 为射线DP 上一点,BE 平分ABC ∠交线段AD 于点E (不与端点A 、D 重合).(1)当ABC ∠为锐角,且tan 2ABC ∠=时,求四边形ABCD 的面积; (2)当ABE △与BCE △相似时,求线段CD 的长;(3)设DC x =,DE y =,求y 关于x 的函数关系式,并写出定义域.PDBA P EDC BA已知四边形ABCD中,∠BAD=∠BDC=90°,2=⋅.BD AD BC(1)求证:AD∥BC;(2)过点A作AE∥CD交BC于点E.请完善图形并求证:2=⋅.CD BE BC如图,在平面直角坐标系xOy 中,抛物线2y x bx c =++的对称轴为直线x =1,抛物线与x 轴交于A 、B 两点(点A 在点B 的左侧),且AB =4,又P 是抛物线上位于第一象限的点,直线AP 与y 轴交于点D ,与对称轴交于点E ,设点P 的横坐标为t . (1)求点A 的坐标和抛物线的表达式; (2)当AE :EP =1:2时,求点E 的坐标;(3)记抛物线的顶点为M ,与y 轴的交点为C ,当四边形CDEM是等腰梯形时,求t 的值.松江25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)如图,已知△ABC中,∠ACB=90°,AC=1,BC=2,CD平分∠ACB交边AB与点D,P是射线CD上一点,联结AP.(1)求线段CD的长;(2)当点P在CD的延长线上,且∠P AB=45°时,求CP的长;(3)记点M为边AB的中点,联结CM、PM,若△CMP是等腰三角形,求CP的长.如图,已知在△ABC 中,∠BAC =2∠B ,AD 平分∠BAC , DF //BE ,点E 在线段BA 的延长线上,联结DE ,交AC 于点G ,且∠E =∠C .(1)求证:2AD AF AB =⋅; (2)求证:AD BE D E AB ⋅=⋅.(第23题图)ABDCEFG抛物线23(0)y ax bx a=++≠经过点A(1-,0),B(3 2且与y轴相交于点C.(1)求这条抛物线的表达式;(2)求∠ACB的度数;(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.(第24题图)闵行25.(共3小题,第(1)小题4分,第(2)小题6分,第(3)小题4分,满分14分)如图,在Rt △ABC 中,∠ACB =90°,AC =4,BC =3,CD 是斜边上中线,点E 在边AC 上,点F 在边BC 上,且∠EDA =∠FDB ,联结EF 、DC 交于点G . (1)当∠EDF =90°时,求AE 的长;(2)CE = x ,CF = y ,求y 关于x 的函数关系式,并指出x 的取值范围; (3)如果△CFG 是等腰三角形,求CF 与CE 的比值.(备用图)ABDC(第25题图)AB DCEFG浦东23.(本题满分12分,其中第(1)小题6分,第(2)小题6分)如图,已知,在锐角△ABC 中,CE ⊥AB 于点E ,点D 在边AC 上, 联结BD 交CE 于点F ,且DF FB FC EF ⋅=⋅. (1)求证:BD ⊥AC ;(2)联结AF ,求证:AF BE BC EF ⋅=⋅.A (第23题图)DEFBC浦东24.(本题满分12分,每小题4分)已知抛物线y=ax2+bx+5与x轴交于点A(1,0)和点B(5,0),顶点为M.点C在x轴的负半轴上,且AC=AB,点D的坐标为(0,3),直线l经过点C、D.(1)求抛物线的表达式;(2)点P是直线l在第三象限上的点,联结AP,且线段CP是线段CA、CB的比例中项,求tan∠CPA的值;(3)在(2)的条件下,联结AM、BM,在直线PM上是否存在点E,使得∠AEM=∠AMB.若存在,求出点E(第24题图)浦东25.(本题满分14分,其中第(1)小题4分,第(2)小题5分,第(3)小题5分)如图,已知在△ABC 中,∠ACB=90°,BC =2,AC =4,点D 在射线BC 上,以点D 为圆心,BD 为半径画弧交边AB 于点E ,过点E 作EF ⊥AB 交边AC 于点F ,射线ED 交射线AC 于点G . (1)求证:△EFG ∽△AEG ;(2)设FG =x ,△EFG 的面积为y ,求y 关于x 的函数解析式并写出定义域; (3)联结DF ,当△EFD 是等腰三角形时,请直接..写出FG 的长度.(第25题备用图)ABC(第25题备用图)ABC虹口23.(本题满分12分,第(1)题满分6分,第(2)题满分6分)如图,在△ABC中,点D、E分别在边AB、AC上,DE、BC的延长线相交于点F,且EF DF BF CF⋅=⋅.(1)求证AD AB AE AC⋅=⋅;(2)当AB=12,AC=9,AE=8时,求BD的长与△△ADE ECFSS的值.分4分)如图,在平面直角坐标系xOy中,抛物线与x轴相交于点A(-2,0)、B(4,0),与y轴交于点C(0,-4),BC与抛物线的对称轴相交于点D.(1)求该抛物线的表达式,并直接写出点D的坐标;(2)过点A作AE⊥AC交抛物线于点E,求点E的坐标;(3)在(2)的条件下,点F在射线AE上,若△ADF∽△ABC,求点F的坐标.分4分)已知AB=5,AD=4,AD∥BM,3cos5B=(如图),点C、E分别为射线BM上的动点(点C、E都不与点B重合),联结AC、AE,使得∠DAE=∠BAC,射线EA交射线CD于点F.设BC=x,AFy AC=.(1)如图1,当x=4时,求AF的长;(2)当点E在点C的右侧时,求y关于x的函数关系式,并写出函数的定义域;(3)联结BD交AE于点P,若△ADP是等腰三角形,直接写出x的值.普陀23. (本题满分12分)已知:如图9,四边形ABCD 的对角线AC 和BD 相交于点E ,2,AD DC DC DE DB ==⋅.求证:(1)BCE ADE ∽;(2)··AB BC BD BE =.图9Bx普陀24.(本题满分12分,每小题满分各4分)如图10,在平面直角坐标系中,已知抛物线22y ax ax c +=+(其中a c 、为常数,且0a <)与x 轴交于点A ,它的坐标是()3, 0-,与y 轴交于点B ,此抛物线顶点C 到x 轴的距离为4.(1)求该抛物线的表达式; (2)求CAB ∠的正切值;(3)如果点P 是抛物线上的一点,且ABP CAO ∠=∠,试直接写出点P 的坐标.普陀25.(本题满分14分,第(1)小题满分3分,第(1)小题满分5分,第(1)小题满分6分)如图11,BAC ∠的余切值为2,AB =D 是线段AB 上的一动点(点D 不与点A B 、重合),以点D 为顶点的正方形DEFG 的另两个顶点E F 、都在射线AC 上,且点F 在点E 的右侧.联结BG ,并延长BG ,交射线EC 于点P .(1)点D 在运动时,下列的线段和角中,______是始终保持不变的量(填序号);①AF ; ②FP ; ③BP ; ④BDG ∠; ⑤GAC ∠; ⑥BPA ∠; (2)设正方形的边长为x ,线段AP 的长为y ,求y 与x 之间的函数关系式,并写出定义域;(3)如果PFG 与AFG 相似,但面积不相等,求此时正方形的边长.备用图图11P ACC E F嘉定23.(本题满分12分,每小题6分)如图6,已知梯形ABCD 中,AD ∥BC ,CD AB =,点E 在对角线AC 上,且满足BAC ADE ∠=∠.(1)求证:BC DE AE CD ⋅=⋅;(2)以点A 为圆心,AB 长为半径画弧交边BC 于点F ,联结AF .求证:CA CE AF ⋅=2.图6嘉定24.(本题满分12分,每小题4分)已知在平面直角坐标系xOy (如图7)中,已知抛物线c bx x y ++=232点经过)0,1(A 、)2,0(B .(1)求该抛物线的表达式;(2)设该抛物线的对称轴与x 轴的交点为C , 第四象限内的点D 在该抛物线的对称轴上,如果 以点A 、C 、D 所组成的三角形与△AOB 相似, 求点D 的坐标;(3)设点E 在该抛物线的对称轴上,它的纵坐标是1, 联结AE 、BE ,求ABE ∠sin .嘉定25.(满分14分,第(1)小题4分,第(2)、(3)小题各5分)在正方形ABCD 中,8=AB ,点P 在边CD 上,43tan =∠PBC ,点Q 是在射线BP 上的一个动点,过点Q 作AB 的平行线交射线AD 于点M ,点R 在射线AD 上,使RQ 始终与直线BP 垂直.(1)如图8,当点R 与点D 重合时,求PQ 的长; (2)如图9,试探索:MQRM的比值是否随点Q 的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;(3)如图10,若点Q 在线段BP 上,设x PQ =,y RM =,求y 关于x 的函数关系式,并写出它的定义域.图8图9图10静安23. (本题满分12分,其中第1小题6分,第2小题6分)已知:如图,梯形ABCD 中,//,,DC AB AD BD AD DB =⊥,点E 是腰AD 上一点,作45EBC ∠=,联结CE ,交DB 于点F . (1)求证:ABE ∽DBC ; (2)如果56BC BD =,求BCE BDAS S的值.静安24. (本题满分12分,第1小题4分,第2小题8分)在平面直角坐标系xOy中(如图),已知抛物线25 3y ax bx=+-经过点(1,0)A-、(5,0)B.(1)求此抛物线顶点C的坐标;(2)联结AC交y轴于点D,联结BD、BC,过点C作CH BD⊥,垂足为点H,抛物线对称轴交x轴于点G,联结HG,求HG的长.静安25. (本题满分14分,第1小题4分,第2小题6分,第3小题4分)已知:如图,四边形ABCD 中,090,,,BAD AD DC AB BC AC <∠≤==平分BAD ∠.(1)求证:四边形ABCD 是菱形;(2)如果点E 在对角线AC 上,联结BE 并延长,交边DC 于点G ,交线段AD 的延长线于点F (点F 可与点D 重合),A F B A C B ∠=∠,设AB 长度是a (a 实常数,且0a >),,A C xA F y ==,求y 关于x 的函数解析式,并写出定义域;(3)在第(2)小题的条件下,当CGE 是等腰三角形时,求AC 的长.(计算结果用含a 的代数式表示)长宁23.(本题满分12分,第(1)小题6分,第(2)小题6分)如图,在∆ABC 中,点D 在边BC 上,联结AD ,∠ADB=∠CDE , DE 交边AC 于点E ,DE 交BA 延长线于点F ,且DF DE AD ⋅=2. (1)求证:BFD ∆∽CAD ∆; (2)求证:AD AB DE BF ⋅=⋅.F EDA第23题图长宁24.(本题满分12分,每小题4分)在直角坐标平面内,直线221+=x y 分别与x 轴、y 轴交于点A 、C . 抛物线c bx x y ++-=221经过点A 与点C ,且与x 轴的另一个交点为点B . 点D 在该抛物线上,且位于直线AC 的上方.(1)求上述抛物线的表达式;(2)联结BC 、BD ,且BD 交AC 于点E ,如果∆ABE 的面积与∆ABC 的面积之比为4:5,求∠DBA 的余切值;(3)过点D 作DF ⊥AC ,垂足为点F ,联结CD . 若∆CFD 与∆AOC 相似,求点D 的坐标.备用图第24题图长宁25.(本题满分14分,第(1)小题3分,第(2)小题6分,第(3)小题5分) 已知在矩形ABCD 中,AB =2,AD =4. P 是对角线BD 上的一个动点(点P 不与点B 、D 重合),过点P 作PF ⊥BD ,交射线BC 于点F . 联结AP ,画∠FPE =∠BAP ,PE 交BF 于点E .设PD=x ,EF =y .(1)当点A 、P 、F 在一条直线上时,求 ABF 的面积;(2)如图1,当点F 在边BC 上时,求y 关于x 的函数解析式,并写出函数定义域; (3)联结PC ,若∠FPC =∠BPE ,请直接写出PD 的长.备用图 备用图图1DCBA DCBA F EP D CB A 第25题图徐汇23.(本题满分12分,第(1)小题满分5分,第(2)小题满分7分) 如图在△ABC 中,AB =AC ,点D 、E 、F 分别在边BC 、AB 、AC 上,且∠ADE =∠B , ∠ADF =∠C ,线段EF 交线段AD 于点G . (1)求证:AE =AF ;(2)若DF CFDE AE,求证:四边形EBDF 是平行四边形.徐汇24.(本题满分12分,第(1)小题满分3分,第(2)小题满分4分,第(3)小题满分5分)如图,在平面直角坐标系xOy中,直线y=kx(k≠0)沿着y轴向上平移3个单位长度后,与x轴交于点B(3,0),与y轴交于点C,抛物线2=++过点B、C且与x轴的另一个交y x bx c点为A.(1)求直线BC及该抛物线的表达式;(2)设该抛物线的顶点为D,求△DBC的面积;(3)如果点F在y轴上,且∠CDF=45°,求点F的坐标.徐汇25.(本题满分14分,第(1)小题3分,第(2)小题7分,第(3)小题4分)已知,在梯形ABCD中,AD∥BC,∠A=90°,AD=2,AB=4,BC=5,在射线BC任取一点M,联结DM,作∠MDN=∠BDC,∠MDN的另一边DN交直线BC于点N(点N在点M 的左侧).(1)当BM的长为10时,求证:BD⊥DM;(2)如图(1),当点N在线段BC上时,设BN=x,BM=y,求y关于x的函数关系式,并写出它的定义域;(3)如果△DMN是等腰三角形,求BN的长.杨浦23.(本题满分12分,第(1)小题5分,第(2)小题7分)已知:梯形ABCD中,AD//BC,AD=AB,对角线AC、BD交于点E,点F在边BC上,且∠BEF=∠BAC.(2)当EF//DC时,求证:AE=DE.(第23题图)杨浦24.(本题满分12分,第(1)小题3分,第(2)小题5分,第(3)小题4分)在平面直角坐标系xOy 中,抛物线2221y x mx m m =-+--+交 y 轴于点为A ,顶点为D ,对称轴与x 轴交于点H .(1)求顶点D 的坐标(用含m 的代数式表示);(2)当抛物线过点(1,-2),且不经过第一象限时,平移此抛物线到抛物线22y x x =-+的位置,求平移的方向和距离;(3)当抛物线顶点D 在第二象限时,如果∠ADH =∠AHO ,求m 的值.(第24题图)杨浦25.(本题满分14分,第(1)、(2)小题各6分,第(3)小题2分)已知:矩形ABCD 中,AB =4,BC =3,点M 、N 分别在边AB 、CD 上,直线MN 交矩形对角线AC 于点E ,将△AME 沿直线MN 翻折,点A 落在点P 处,且点P 在射线CB 上. (1)如图1,当EP ⊥BC 时,求CN 的长; (2)如图2,当EP ⊥AC 时,求AM 的长;(3)请写出线段CP 的长的取值范围,及当CP 的长最大时MN 的长.(备用图)(图1) A B D NME(图2) A B C D N P M E (第25题图)A B C D奉贤23.(本题满分 12 分,每小题满分各 6 分)已知:如图 8,四边形90ABCD DCB ∠=︒,,对角线 BD ⊥AD ,点 E 是边 AB 的中点,CE 与 BD 相交于点 F ,2·BD AB BC =.(1) 求证:BD 平分∠ABC ;(2) 求证:··BE CF BC EF =.奉贤24. (本题满分 12 分,每小题满分各 4 分)如图9,在平面直角坐标系xOy 中,抛物线238y x bx c =++与x 轴相交于点(2,0)A -和点B ,与y 轴相交于点(0,3)C -,经过点A 的射线AM 与y 轴相交于点E ,与抛物线的另一个交点为点F ,且13AE EF =. (1)求这条抛物线的表达式,并写出它的对称轴; (2)求FAB ∠的余切值;(3)点D 是点C 关于抛物线对称轴的对称点,点 P 是 y 轴上一点,且AFP DAB ∠=∠,求点 P 的坐标.奉贤25.(本题满分 14 分,第(1)小题满分 3 分,第(1)小题满分 5 分,第(1)小题满分 6 分)已知:如图10,在梯形ABCD 中,//,90,2AB CD D AD CD ∠===,点E 在边AD上(不与点A 、D 重合),45,C E B E B ∠=与对角线AC 相交于点F ,设DE x =.(1)用含x 的代数式表示线段CF 的长; (2)如果把CAE 的周长记作CAE C,BAF 的周长记作BAF C ,设CAE BAFCy C=,求y 关于x 的函数关系式,并写出它的定义域; (3)当ABE ∠的正切值是35时,求AB 的长.如图,ABC 中,AB AC =,过点C 作//CF AB 交ABC 的中位线DE 的延长线于F ,联结BF ,交AC 于点G . (1)求证:AE EGAC CG=; (2)若AH 平分BAC ∠,交BF 于H ,求证:BH 是HG 和HF 的比例中项.设,a b 是任意两个不等实数,我们规定:满足不等式a x b ≤≤的实数x 的所有取值的全体叫做闭区间,表示为[],a b ,对于一个函数,如果它的自变量x 与函数值y 满足:当m x n ≤≤时,有m y n ≤≤,我们就此称此函数是闭区间[],m n 上的“闭函数”。
2018年上海市各区县中考数学一模压轴题图文解析第24、25题

2018年上海市各区县中考数学一模压轴题图文解析 目录例 2018年上海市崇明县中考一模第24题如图1,在直角坐标系中,一条抛物线与x 轴交于A 、B 两点,与y 轴交于点C ,其中B (3, 0),C (0, 4),点A 在x 轴的负半轴上,OC =4OA .(1)求这条抛物线的解析式,并求出它的顶点坐标;(2)联结AC 、BC ,点P 是x 轴正半轴上的一个动点,过点P 作PM //BC 交射线AC 于M ,联结CP ,若△CPM 的面积为2,则请求出点P 的坐标.动感体验请打开几何画板文件名“16崇明一模24”,拖动点P 在x 轴的正半轴上运动,可以体验到,有两个时刻,△CPM 的面积为2. 满分解答(1)由C (0, 4),OC =4OA ,得OA =1,A (-1, 0).设抛物线的解析式为y =a (x +1)(x -3),代入点C (0, 4),得4=-3a . 解得43a =-.所以244(1)(3)(23)33y x x x x =-+-=---2416(1)33x =--+.顶点坐标为16(1)3,.(2)如图2,设P (m , 0),那么AP =m +1. 所以S △CPA =12AP CO ⋅=1(1)42m +⨯=2m +2.由PM //BC ,得CMBPCABA=.又因为CPMCPAS CM S CA=△△,所以S △CPM =(22)BP m BA+.①如图2,当点P 在AB 上时,BP =3-m . 解方程3(22)4m m -+=2,得m =1.此时P (1, 0).②如图3,当点P 在AB 的延长线上时,BP =m -3.图2 图3例2018年上海市崇明县中考一模第25题如图1,已知矩形ABCD中,AB=6,BC=8,点E是BC边上一点(不与B、C重合),过点E作EF⊥AE交AC、CD于点M、F,过点B作BG⊥AC,垂足为G,BG交AE于点H.(1)求证:△ABH∽△ECM;=y,求y关于x的函数解析式,并写出定义域;(2)设BE=x,EHEM(3)当△BHE为等腰三角形时,求BE的长.图1 备用图动感体验请打开几何画板文件名“16崇明一模25”,拖动点E在BC上运动,可以体验到,有三个时刻,△BHE可以成为为等腰三角形.满分解答(1)如图2,因为∠1和∠2都是∠BAC的余角,所以∠1=∠2.又因为∠BAH和∠CEM都是∠AEB的余角,所以∠BAH=∠CEM.所以△ABH ∽△ECM .图2 图3(2)如图3,延长BG 交AD 于N .在Rt △ABC 中,AB =6,BC =8,所以AC =10.在Rt △ABN 中,AB =6,所以AN =AB tan ∠1=34AB =92,BN =152.如图2,由AD //BC ,得92AHAN EH BE x==. 由△ABH ∽△ECM ,得68AH AB EM EC x==-.所以y =EH EM=AH AH EM EH ÷=6982x x ÷-=12729xx -.定义域是0<x <8.(3)如图2,由AD //BC ,得92NHAN BHBE x ==.所以292BN x BH x+=. 所以215292x BH x =⨯+=1529xx +. 在△BHE 中,BE =x ,cos ∠HBE =35,1529xBH x =+. 分三种情况讨论等腰三角形BHE : ①如图4,当BE =BH 时,解方程1529xx x =+,得x =3. ②如图5,当HB =HE 时,1cos 2BE BH B =⋅∠.解方程11532295x x x =⨯+,得92x =.③如图6,当EB =EH 时,1cos 2BH BE B =⋅∠.解方程11532295x x x ⨯=+,得74x =.图4 图5 图6例2018年上海市奉贤区中考一模第24题如图1,二次函数y=x2+bx+c的图像经过原点和点A(2, 0),直线AB与抛物线交于点B,且∠BAO=45°.(1)求二次函数的解析式及顶点C的坐标;(2)在直线AB上是否存在点D,使得△BCD为直角三角形,若存在,求出点D的坐标;若不存在,请说明理由.图1动感体验请打开几何画板文件名“16奉贤一模24”,可以体验到,以BC为直径的圆恰好经过点A,直角三角形BCD存在两种情况.满分解答(1)因为抛物线y=x2+bx+c与x轴交于O、A(2, 0)两点,所以y=x(x-2)=(x-1)2-1.顶点C的坐标为(1,-1).(2)如图2,作BH⊥x轴于H.设B(x, x2-2x).由于∠BAH=45°,所以BH=AH.解方程x2-2x=2-x,得x=-1,或x=2.所以点B的坐标为(-1, 3).图2①∠BDC=90°.如图3,由A (2, 0)、C (1,-1),可得∠CAO =45°.因此∠BAC =90°. 所以当点D 与点A (2, 0)重合时,△BCD 是直角三角形.②∠BCD =90°.由A (2, 0)、B (-1, 3),可得直线AB 的解析式为y =-x +2. 【解法一】如图4,过点C 作BC 的垂线与直线AB 交于点D .设D (m ,-m +2 ).由BD 2=BC 2+CD 2,得(m +1)2+(-m -1)2=22+42+(m -1)2+(-m +3)2.解得73m =.此时点D 的坐标为71(,)33-.【解法二】构造△BMC ∽△CND ,由BMCNMCND=,得4123m m -=-+.解得73m =.图2 图3 图4例 2018年上海市奉贤区中考一模第25题如图1,在Rt △ABC 中,∠ACB =90°,AB =5,BC =3,点D 是斜边AB 上任意一点,联结DC ,过点C 作CE ⊥CD ,联结DE ,使得∠EDC =∠A ,联结BE .(1)求证:AC ·BE =BC ·AD ;(2)设AD =x ,四边形BDCE 的面积为S ,求S 与x 之间的函数关系式,并写出定义域;(3)当S △BDE =14S △ABC 时,求tan ∠BCE 的值.图1 备用图动感体验请打开几何画板文件名“16奉贤一模25”,拖动点E在AD边上运动,可以体验到,△ABC与△DEC保持相似,△ACD与△BCE保持相似,△BDE是直角三角形.满分解答(1)如图2,在Rt△BAC和Rt△EDC中,由tan∠A=tan∠EDC,得B C E CA C D C=.如图3,已知∠ACB=∠DCE=90°,所以∠1=∠2.所以△ACD∽△BCE.所以AC BCAD BE=.因此AC·BE=BC·AD.图2 图3(2)在Rt△ABC中,AB=5,BC=3,所以AC=4.所以S△ABC=6.如图3,由于△ABC与△ADC是同高三角形,所以S△ADC∶S△ABC=AD∶AB=x∶5.所以S△ADC=65x.所以S△BDC=665x-.由△ADC∽△BEC,得S△ADC∶S△BEC=AC2∶BC2=16∶9.所以S△BEC=916S△ADC=96165x⨯=2740x.所以S =S 四边形BDCE =S △BDC +S △BEC =6276540x x -+=21640x -+.定义域是0<x <5.(3)如图3,由△ACD ∽△BCE ,得AC BC ADBE=,∠A =∠CBE .由43x BE=,得BE =34x .由∠A =∠CBE ,∠A 与∠ABC 互余,得∠ABE =90°(如图4). 所以S △BDE =1133(5)(5)2248BD BE x x x x ⋅=-⨯=--.当S △BDE =14S △ABC =13642⨯=时,解方程33(5)82x x --=,得x =1,或x =4.图4 图5 图6作DH ⊥AC 于H .①如图5,当x =AD =1时,在Rt △ADH 中,DH =35AD =35,AH =45AD=45.在Rt △CDH 中,CH =AC -AH =416455-=,所以tan ∠HCD =DH CH=316.②如图6,当x =AD =4时,在Rt △ADH 中,DH =35AD =125,AH =45AD=165.在Rt △CDH 中,CH =AC -AH =164455-=,所以tan ∠HCD =DH CH=3.综合①、②,当S △BDE =14S △ABC 时, tan ∠BCE 的值为316或3.例 2018年上海市虹口区中考一模第24题如图1,在平面直角坐标系中,抛物线y =ax 2+bx +3与x 轴分别交于点A (2, 0)、点B (点B 在点A 的右侧),与y 轴交于点C ,tan ∠CBA =12.(1)求该抛物线的表达式;(2)设该抛物线的顶点为D ,求四边形ACBD 的面积;(3)设抛物线上的点E 在第一象限,△BCE 是以BC 为一条直角边的直角三角形,请直接写出点E 的坐标.图1动感体验请打开几何画板文件名“16虹口一模24”,可以体验到,以BC 为直角边的直角三角形BCE 有2个. 满分解答(1)由y =ax 2+bx +3,得C (0, 3),OC =3. 由tan ∠CBA =OC OB=12,得OB =6,B (6, 0).将A (2, 0)、B (6, 0)分别代入y =ax 2+bx +3,得4230,36630.a b a b ++=⎧⎨++=⎩ 解得14a =,b =-2.所以221123(4)144y x x x =-+=--.(2)如图2,顶点D 的坐标为(4,-1).S 四边形ACBD =S △ABC +S △ABD =1123+2122⨯⨯⨯⨯=4.(3)如图3,点E 的坐标为(10, 8)或(16, 35).思路如下:设E 21(,23)4x x x -+.当∠CBE =90°时,过点E 作EF ⊥x 轴于F ,那么2EFBOBFCO==.所以EF =2BF .解方程21232(4)4x x x -+=-,得x =10,或x =4.此时E (10, 8).当∠BCE =90°时,EF =2CF .解方程21224x x x -=,得x =16,或x =0.此时E (16, 35).图2 图3例 2018年上海市虹口区中考一模第25题如图1,在平行四边形ABCD 中,E 为BC 的中点,F 为线段AE 上一点,联结BF 并延长交边AD 于点G ,过点G 作AE 的平行线,交射线DC 于点H .设AD EFx AB AF==. (1)当x =1时,求AG ∶AB 的值;(2)设GDH EBAS S △△=y ,求y 关于x 的函数关系式,并写出x 的取值范围;(3)当DH =3HC 时,求x 的值.图1 备用图动感体验请打开几何画板文件名“16虹口一模25”,拖动点B 可以改变平行四边形的邻边比,可以体验到,当菱形ABCD 时,G 是AD 的中点,△GDH 与△EBA 保持相似.还可以体验到,DH =3HC 存在两种情况.满分解答(1)如图2,当x =1时,AD =AB ,F 是AE 的中点. 因为AD //CB ,所以AG =BE =12BC =12AD =12AB .所以AG ∶AB =1∶2. (2)如图3,已知AD EF x AB AF ==,设AB =m ,那么AD =xm ,BE =12xm .由AD //BC ,得BE EFx AG AF==. 所以12BE AG m x==.所以DG =12xm m -.图2 图3 图4如图4,延长AE 交DC 的延长线于M . 因为GH //AE ,所以△GDH ∽△ADM . 因为DM //AB ,所以△EBA ∽△ADM . 所以△GDH ∽△EBA . 所以y =GDHEBAS S △△=2()DG BE =2211()()22xm m xm -÷=22(21)x x -.(3)如图5,因为GH //AM ,所以11()2122DHDG xm m m x HMGA ==-÷=-. 因为DM //AB ,E 是BC 的中点,所以MC =AB =DC .DH =3HC 存在两种情况:如图5,当H 在DC 上时,35DH HM =.解方程3215x -=,得45x =. 如图6,当H 在DC的延长线上时,3DH HM =.解方程213x -=,得45x =.图5 图6例 2018年上海市黄浦区中考一模第24题如图1,在平面直角坐标系中,抛物线y =ax 2-3ax +c 与x 轴交于A (-1, 0)、B 两点(点A 在点B 左侧),与y 轴交于点C (0, 2).(1)求抛物线的对称轴及点B 的坐标; (2)求证:∠CAO =∠BCO ;(3)点D 是射线BC 上一点(不与B 、C 重合),联结OD ,过点B 作BE ⊥OD ,垂足为△BOD 外一点E ,若△BDE 与△ABC 相似,求点D 的坐标.图1动感体验请打开几何画板文件名“16黄浦一模24”,拖动点D 在射线BC 上运动,可以体验到,当点E 在△BOD 外时,有两个时刻,Rt △BDE 的两条直角边的比为1∶2. 满分解答(1)由y =ax 2-3ax +c ,得抛物线的对称轴为直线32x =.因此点A (-1, 0)关于直线32x =的对称点B 的坐标为(4, 0).(2)如图2,因为tan ∠CAO =2CO AO=,tan ∠BCO =2BO CO=,所以∠CAO =∠BCO .(3)由B (4, 0)、C (0, 2),得直线BC 的解析式为122y x =-+.设D 1(,2)2x x -+.以∠ABC (∠OBC )为分类标准,分两种情况讨论:①如图3,当∠OBC =∠DBE 时,由于∠OBC 与∠OCB 互余,∠DBE 与∠ODC 互余,所以∠OCB =∠ODC .此时OD =OC =2.根据OD 2=4,列方程221+(2)42x x -+=.解得x =0,或85x =.此时D 86(,)55.②如图4,当∠OBC =∠EDB 时,OD =OB =4.根据OD 2=16,列方程221+(2)162x x -+=.解得x =4,或125x =-.此时D 1216(,)55-.图2图3 图4例 2018年上海市黄浦区中考一模第25题如图1,已知直线l 1//l 2,点A 是l 1上的点,B 、C 是l 2上的点,AC ⊥BC ,∠ABC =60°,AB =4,O 是AB 的中点,D 是CB 的延长线上的点,将△DOC 沿直线CO 翻折,点D 与点D ′重合.(1)如图1,当点D 落在直线l 1上时,求DB 的长;(2)延长DO 交直线l 1于点E ,直线OD ′分别交直线l 1、l 2于点M 、N . ①如图2,当点E 在线段AM 上时,设AE =x ,DN =y ,求y 关于x 的解析式及定义域;②若△DONAE 的长.图1 图2动感体验请打开几何画板文件名“16黄浦一模25”,拖动点D 在CB 的延长线上运动,可以体验到,CD ′与AB 保持平行,△BON 与△BDO 保持相似.还可以体验到,有两个时刻DN =3. 满分解答(1)如图3,在Rt △ABC 中,∠ABC =60°,AB =4,O 是AB 的中点,所以△OBC 是边长为2的等边三角形.又因为△DOC 与△D ′OC 关于CO 对称,所以∠BCD ′=120°,CD ′=CD .所以AB //D ′C .当点D ′ 落在直线l 1上时, AD ′//BC . 所以四边形ABCD ′是平行四边形. 所以CD ′=BA =4.此时BD =CD -CB =CD ′-CB =4-2=2. 图3(2)①如图4,由于AE //BD ,O 是AB 的中点,所以AE =BD =x . 因为AB //D ′C ,所以∠AOM =∠2.又因为∠AOM =∠BON ,∠2=∠1,所以∠BON =∠1. 又因为∠OBN =∠DBO ,所以△BON ∽△BDO .所以BO BD BN BO =.因此22x x y =+.于是得到24x y x -=.定义域是0<x ≤2.②在△DON 中,DN当S△DON DN =3.有两种情形:情形1,如图4,当D 在BN 上时,DN =24x y x-==3,解得x =1,或x =-4.此时AE =1.情形2,如图5,当D 在BN 的延长线上时,由BO BD BNBO=,得22xx y =-. 于是得到24x y x -=.当DN =24x y x-==3时,解得x =4,或x =-1.此时AE =4.图4 图5例 2018年上海市嘉定区中考一模第24题如图1,在平面直角坐标系中,抛物线212y x bx c =++经过点A (4, 0)、点C (0,-4),点B 与点A 关于这条抛物线的对称轴对称.(1)用配方法求这条抛物线的顶点坐标; (2)联结AC 、BC ,求∠ACB 的正弦值;(3)点P 是这条抛物线上的一个动点,设点P 的横坐标为m (m >0),过点P 作y 轴的垂线PQ ,垂足为Q ,如果∠QPO =∠BCO ,求m 的值.图1动感体验请打开几何画板文件名“16嘉定一模24”,可以体验到,QO ∶QP =OB ∶OC .满分解答(1)将A (4, 0)、C (0,-4)分别代入212y x bx c =++,得840,4.b c c ++=⎧⎨=-⎩ 解得b =-1,c =-4.所以2142y x x =--=1(2)(4)2x x +-=219(1)22x --.点B 的坐标是(-2, 0),顶点坐标是9(1,)2-.(2)由A (4, 0)、B (-2, 0)、C (0,-4),得AC =BC =AB =6,CO =4.作BH ⊥AC 于H .由S△ABC =12AB CO ⋅=12AC BH ⋅.得AB CO BH AC⋅=因此sin ∠ACB =BH BC.(3)点P 的坐标可以表示为21(,4)2m m m --. 由tan ∠QPO =tan ∠BCO ,得12QO OB QPOC==.所以QP =2QO .解方程212(4)2m m m =--,得m = 图2所以点P 的横坐标m =32+.例 2018年上海市嘉定区中考一模第25题如图1,已知△ABC 中,∠ABC =90°,tan ∠BAC =12.点D 在AC 边的延长线上,且DB 2=DC ·DA .(1)求DC CA的值;(2)如果点E 在线段BC 的延长线上,联结AE ,过点B 作AC 的垂线,交AC 于点F ,交AE 于点G .①如图2,当CE =3BC 时,求BF FG的值;②如图3,当CE =BC 时,求BCD BEGS S △△的值.图1动感体验请打开几何画板文件名“16嘉定一模25”,拖动点E 运动,可以体验到,当CE =3BC 时,BD //AE ,BG 是直角三角形ABE 斜边上的中线.当CE =BC 时,△ABF ≌△BEH ,AF =2EH =4CF . 满分解答(1)如图1,由DB 2=DC ·DA ,得DB DA DCDB=.又因为∠D 是公共角,所以△DBC ∽△DAB .所以DB BC CD DA AB BD ==.又因为tan ∠BAC =BC AB =12,所以12CD BD =,12BD DA =.所以14CD DA =.所以13DC CA =.(2)①如图4,由△DBC ∽△DAB ,得∠1=∠2. 当BF ⊥CA 时,∠1=∠3,所以∠2=∠3.因为13DC CA =,当CE =3BC 时,得DC BC CA CE=.所以BD //AE .所以13BD EA =,∠2=∠E .所以∠3=∠E .所以GB =GE .于是可得G B 是Rt △ABE 斜边上的中线.所以23BD GA=.所以23BF BD FGGA ==. ②如图5,作EH ⊥BG ,垂足为H .当CE =BC 时,CF 是△BEH 的中位线,BF =FH .设CF =m .由tan ∠1=tan ∠3=12,得BF =2m ,AF =4m .所以FH =2m ,EH =2m ,DC =1533CA m =.因此422FG AF m HG EH m ===.所以2433FG FH m ==.所以103BG m =.于是5121321102323BCDBEGm m DC BFS S BG EH m m ⨯⋅===⋅⨯△△.图4 图5例 2018年上海市静安区青浦区中考一模第24题如图1,直线121+=x y 与x 轴、y 轴分别相交于点A 、B ,二次函数的图像与y轴相交于点C ,与直线121+=x y 相交于点A 、D ,CD //x 轴,∠CDA =∠OCA .(1)求点C 的坐标;(2)求这个二次函数的解析式.图1动感体验请打开几何画板文件名“16静安青浦一模24”,可以体验到,△AOB 与△COA 相似. 满分解答(1)由121+=x y ,得A (-2, 0),B (0, 1).所以OA =2,OB =1.由于CD //x 轴,所以∠CDA =∠1. 又已知∠CDA =∠OCA ,所以∠1=∠OCA . 由tan ∠1=tan ∠OCA ,得OB OAOA OC=. 所以122OC=.解得OC =4.所以C (0, 4).(2)因为CD //x 轴,所以y D =y C =4. 图2 解方程1142x +=,得x =6.所以D (6, 4). 所以抛物线的对称轴为直线x =3.因此点A (-2, 0)关于直线x =3的对称点为(8, 0).设抛物线的解析式为y =a (x +2)(x -8).代入点C (0, 4),得4=-16a . 解得14a =-.所以2113(2)(8)4442y x x x x =-+-=-++.例 2018年上海市静安区青浦区中考一模第25题如图1,在梯形ABCD 中,AD //BC ,AC =BC =10,cos ∠ACB =45,点E在对角线AC 上,且CE =AD ,BE 的延长线与射线AD 、射线CD 分别相交于点F 、G .设AD =x ,△AEF 的面积为y .(1)求证:∠DCA =∠EBC ;(2)当点G 在线段CD 上时,求y 关于x 的函数解析式,并写出它的定义域;(3)如果△DFG 是直角三角形,求△AEF 的面积.图1动感体验请打开几何画板文件名“16静安青浦一模25”,拖动点D 运动,可以体验到,直角三角形DFG 存在两种情况. 满分解答(1)如图2,因为AD //BC ,所以∠DAC =∠ECB .又因为AC =CB ,AD =CE ,所以△ADC ≌△CEB .所以∠DCA =∠EBC . (2)如图3,作EH ⊥BC 于H .在Rt △EHC 中,CE =x ,cos ∠ECB =45,所以CH =45x ,EH =35x .所以S △CEB =12BC EH ⋅=131025x ⨯⨯=3x .因为AD //BC ,所以△AEF ∽△CEB .所以2()AEF CEBS AE S CE=△△. 所以22103(10)()3AEFx x y S x x x--==⨯=△.定义域是0<x≤5.定义域中x=5的几何意义如图4,D 、F 重合,根据AD AECBCE=,列方程1010x x x-=.图2 图3 图4(3)①如图5,如果∠FGD =90°,那么在Rt △BCG 和Rt △BEH 中,tan ∠GBC =335104504xGC HE x GB HB x x===--. 由(1)得∠ACD =∠CBE .由cos ∠ACD =cos ∠CBE ,得GC GB CEBC=.所以10GC CExGB BC==. 因此350410x x x =-.解得x =5.此时S △AEF =23(10)15x y x-==.②如图6,如果∠FDG =90°,那么在Rt △ADC 中,AD =AC cos ∠CAD =4105⨯=8.此时S △AEF =23(10)32x y x -==.图5 图6例2018年上海市闵行区中考一模第24题如图1,在平面直角坐标系中,二次函数y=x2+bx+c的图像与x轴交于A、B两点,点B的坐标为(3, 0),与y轴交于点C(0,-3),点P是直线BC下方的抛物线上的任意一点.(1)求这个二次函数的解析式;(2)联结PO,PC,并将△POC沿y轴对折,得到四边形POP′C,如果四边形POP′C为菱形,求点P的坐标;(3)如果点P在运动过程中,使得以P、C、B为顶点的三角形与△AOC相似,请求出此时点P的坐标.图1动感体验请打开几何画板文件名“16闵行一模24”,拖动点P在直线BC下方的抛物线上运动,可以体验到,当四边形POP′C为菱形时,PP′垂直平分OC.还可以体验到,当点P 与抛物线的顶点重合时,或者点P 落在以BC 为直径的圆上时,△PCB 是直角三角形. 满分解答(1)将B (3, 0)、C (0,-3)分别代入y =x 2+bx +c ,得930,3.b c c ++=⎧⎨=-⎩. 解得b =-2,c =-3.所以二次函数的解析式为y =x 2-2x -3.(2)如图2,如果四边形POP ′C 为菱形,那么PP ′垂直平分OC ,所以y P=32-.解方程23232x x --=-,得x =P 的坐标为3)2-.图2 图3 图4(3)由y =x 2-2x -3=(x +1)(x -3)=(x -1)2-4,得A (-1, 0),顶点M (1,-4).在Rt △AOC 中,OA ∶OC =1∶3.分两种情况讨论△PCB 与△AOC 相似: ①如图3,作MN ⊥y 轴于N .由B (3, 0)、C (0,-3),M (1,-4),可得∠BOC =∠MCN =45°,所以∠BCM =90°.又因为CM ∶CB =1∶3,所以当点P 与点M (1,-4)重合时,△PCB ∽△AOC . ②如图4,当∠BPC =90°时,构造△AEP ∽△PFB ,那么CE PF EPFB=.设P (x , x 2-2x -3),那么22(3)(23)3(23)x x xx x x -----=---.化简,得1(2)1x x --=+.解得x =.此时点P 的横坐标为x =.而2(23)32CB NB x x x CP MP x x---===-++是个无理数,所以当∠BPC =90°时,△PCB 与△AOC 不相似.例 2018年上海市闵行区中考一模第25题如图1,在直角梯形ABCD 中,AB //CD ,∠ABC =90°,对角线AC 、BD 交于点G ,已知AB =BC =3,tan ∠BDC =12,点E 是射线BC 上任意一点,过点B作BF ⊥DE ,垂足为F ,交射线AC 于点M ,交射线DC 于点H .(1)当点F 是线段BH 的中点时,求线段CH 的长;(2)当点E 在线段BC 上时(点E 不与B 、C 重合),设BE =x ,CM =y ,求y 关于x 的函数解析式,并指出x 的取值范围;(3)联结GF ,如果线段GF 与直角梯形ABCD 中的一条边(AD 除外)垂直时,求x 的值.图1 备用图动感体验请打开几何画板文件名“16闵行一模25”,拖动点E 在射线BC 上运动,可以体验到,点G 是BD 的一个三等分点,CH 始终都有CE 的一半.还可以体验到,GF 可以与BC 垂直,也可以与DC 垂直. 满分解答(1)在Rt △BCD 中,BC =3,tan ∠BDC =BCDC=12,所以DC =6,DB = 如图2,当点F 是线段BH 的中点时,DF 垂直平分BH ,所以DH =DB =此时CH =DB -DC =6.图2 图3(2)如图3,因为∠CBH 与∠CDE 都是∠BHD 的余角,所以∠CBH =∠CDE . 由tan ∠CBH =tan ∠CDE ,得CH CECBCD =,即336CH x -=. 又因为CH //AB ,所以CH MCABMA =,即3CH =.因此36x -=)3x y x-=+.x 的取值范围是0<x <3.(3)如图4,不论点E 在BC 上,还是在BC 的延长线上,都有12BG AB GDDC ==,12CH CE =. ①如图5,如果GF ⊥BC 于P ,那么AB //GF //DH . 所以13BP PF BG BC CH BD ===.所以BP =1,111(3)366PF CH CE x ===-.由PF //DC ,得PF PE DC CE =,即12(3)(3)363x x x---=-.整理,得242450x x -+=.解得21x =±21BE =-②如图6,如果GF ⊥DC 于Q ,那么GF //BE . 所以23QFDQ DG CEDC DB ===.所以DQ =4,2(3)3QF x =-.由QF //BC ,得QFQH BCCH=,即21(3)2(3)3213(3)2x x x ---=-. 整理,得223450x x --=.解得34x ±=.此时34BE +=.图4 图5 图6例 2018年上海市浦东新区中考一模第24题如图1,抛物线y =ax 2+2ax +c (a >0)与x 轴交于A (-3,0)、B 两点(A 在B 的左侧),与y 轴交于点C (0,-3),抛物线的顶点为M .(1)求a 、c 的值; (2)求tan ∠MAC 的值;(3)若点P 是线段AC 上的一个动点,联结OP .问:是否存在点P ,使得以点O 、C 、P 为顶点的三角形与△ABC 相似?若存在,求出点P 的坐标;若不存在,请说明理由.图1动感体验请打开几何画板文件名“16浦东一模24”,拖动点P 在线段AC 上运动,可以体验到,△COP 与△ABC 相似存在两种情况. 满分解答(1)将A (-3,0)、C (0,-3)分别代入y =ax 2+2ax +c ,得960,3.a a c c -+=⎧⎨=-⎩ 解得a =1,c =-3.(2)由y =x 2+2x -3=(x +1)2-4,得顶点M 的坐标为(-1,-4). 如图2,作MN ⊥y 轴于N .由A (-3,0)、C (0,-3)、M (-1,-4),可得OA =OC =3,NC =NM =1. 所以∠ACO =∠MCN =45°,AC =MC所以∠ACM =90°.因此tan ∠MAC =MC AC=13.(3)由y =x 2+2x -3=(x +3)(x -1),得B (1, 0).所以AB =4. 如图3,在△COP 与△ABC 中,∠OCP =∠BAC =45°,分两种情况讨论它们相似:当CP ABCOAC =时,3CP =CP =P 的坐标为(-2,-1).当CPACCOAB =时,3CP =.解得CP =.此时点P 的坐标为93(,)44--.图2 图3例2018年上海市浦东新区中考一模第25题如图1,在边长为6的正方形ABCD中,点E为AD边上的一个动点(与A、D不重合),∠EBM=45°,BE交对角线AC于点F,BM交对角线于点G,交CD 于点M.的值;(1)如图1,联结BD,求证:△DEB∽△CGB,并写出DECG(2)如图2,联结EG,设AE=x,EG=y,求y关于x的函数解析式,并写出函数的定义域;(3)当M为边DC的三等分点时,求S△EGF的面积.图1 图2动感体验请打开几何画板文件名“16浦东一模25”,拖动点E在AD边上运动,可以体验到,△EBD与△GBC保持相似,△EBG保持等腰直角三角形.满分解答(1)如图3,因为∠EBM=∠DBC=45°,所以∠1=∠2.又因为∠EDB=∠GCB=45°,所以△DEB∽△CGB.因此DE DB==CG CB图3 图4(2)如图3,由△DEB ∽△CGB ,得EB DB GBCB=.又因为∠EBM =∠DBC =45°,所以△EBG ∽△DBC (如图4). 所以△EBG 是等腰直角三角形.如图4,在Rt △ABE 中,AB =6,AE =x ,所以BE所以y =EG.定义域是0<x <6. (3)如图5,由于S △EGB =12EG 2=2364x +,EGFEGBS EFS EB=△△,所以2364EGFEF x S EB +=⨯△. 由(1)知,DE,所以 x =AE =AD -DE=6.①如图6,当13CMCD =时,13CG CM AG AB ==.所以1144CG CA ==⨯=.此时x =AE=6=3.所以3162EF AE BF CB ===.所以13EF EB =.所以2364EGF EF x S EB +=⨯△=2133634+⨯=154.②如图7,当23CM CD =时,23CG CM AG AB ==.所以2255CG CA ==⨯=此时x =AE=6=65.所以61655EF AE BF CB ==÷=.所以16EF EB =.所以2364EGF EF x S EB +=⨯△=26()361564+⨯=3925.图5 图6图7第(2)题也可以这样证明等腰直角三角形EBG : 如图8,作GH ⊥EB 于H ,那么△GBH 是等腰直角三角形.一方面GB CB EBDB=,另一方面cos 45HB GB =︒=GB HB EB GB =.于是可得△EBG ∽△GBH .所以△EBG 是等腰直角三角形. 如图9,第(2)题也可以构造Rt △EGN 来求斜边EG =y :在Rt △AEN 中,AE =x ,所以AN =EN =2x .又因为CGDE )x -,所以GN =AC -AN -CG =所以y =EG.如图10,第(2)题如果构造Rt △EGQ 和Rt △CGP ,也可以求斜边EG =y :由于CG )x -,所以CP =GP =1(6)2x -=132x -.所以GQ =PD =16(3)2x --=132x +,EQ =16(3)2x x ---=132x -.所以y =EG.图8 图9 图10例 2018年上海市普陀区中考一模第24题如图1,已知二次函数273y ax x c =-+的图像经过A (0, 8)、B (6, 2)、C (9, m )三点,延长AC 交x 轴于点D .(1)求这个二次函数的解析式及m 的值; (2)求∠ADO 的余切值;(3)过点B 的直线分别与y 轴的正半轴、x 轴、线段AD 交于点P (点A 的上方)、M 、Q ,使以点P 、A 、Q 为顶点的三角形与△MDQ 相似,求此时点P 的坐标. 图1 动感体验请打开几何画板文件名“16普陀一模24”,拖动点Q 在线段AD 上运动,可以体验到,△APQ 与△MDQ 相似只存在一种情况. 满分解答(1)将A (0, 8)、B (6, 2)分别代入273y ax x c =-+,得8,3614 2.c a c =⎧⎨-+=⎩解得29a =,c =8.所以二次函数的解析式为227893y x x =-+.所以227(9)818218593m f x x ==-+=-+=. (2)由A (0, 8)、C (9, 5),可得直线AC 的解析式为183y x =-+.所以D (24, 0). 因此cot ∠ADO =OD OA=248=3.(3)如图2,如果△APQ 与△MDQ 相似,由于∠AQP =∠MQD ,∠PAQ 与∠DMQ 是钝角,因此只存在一种情况,△APQ ∽△MDQ .因此∠APQ =∠D .作BN ⊥y 轴于N ,那么∠BPN =∠D .因此cot ∠BPN =cot ∠D =3.所以PN =3BN =18.此时点P 的坐标为(0, 20).图2例 2018年上海市普陀区中考一模第25题如图1,已知锐角∠MBN 的正切值等于3,△PBD 中,∠BDP =90°,点D 在∠MBN 的边BN 上,点P 在∠MBN 内,PD =3,BD =9.直线l 经过点P ,并绕点P 旋转,交射线BM 于点A ,交射线DN 于点C ,设CA x CP=.(1)求x =2时,点A 到BN 的距离;(2)设△ABC 的面积为y ,求y 关于x 的函数解析式,并写出函数的定义域; (3)当△ABC 因l 的旋转成为等腰三角形时,求x 的值.图1 备用图动感体验请打开几何画板文件名“16普陀一模25”,拖动点C 运动,可以体验到,AH 与BH 的比值=tan ∠B =3为定值,AH 与PD 的比值=CA ∶CP =x .满分解答(1)如图2,作AH ⊥BC 于H ,那么PD //AH . 因此2AHCAx PDCP===. 所以AH =2PD =6,即点A 到BN 的距离为6.图2 图3(2)如图3,由AHCAx PDCP==,得AH =xPD =3x .又因为tan ∠MBN =AH BH=3,所以BH =x .设BC =m .由CH CA x CD CP ==,得9m x x m -=-.整理,得81x m x =-.所以y =S △ABC =12BC AH ⋅=18321x x x ⨯⨯-=2121x x -. 定义域是0<x ≤9.x =9的几何意义是点C 与点H 重合,此时CA =27,CP =3.(3)在△ABC 中,BA ,cos ∠ABCBC =81x x -.①如图4,当BA =BC 81xx =-,得1x = ②如图5,当AB =AC时,BC =2BH .解方程821x x x =-,得x =5.③如图6,当CA =CB 时,由cos ∠ABC 12AB BC .解方程1821xx =-,得135x =.图4 图5 图6例 2018年上海市松江区中考一模第24题如图1,已知抛物线y =ax 2+bx -3与x 轴交于A 、B 两点,与y 轴交于点C ,O 是坐标原点,已知点B 的坐标是(3, 0),tan ∠OAC =3.(1)求该抛物线的函数表达式;(2)点P 在x 轴上方的抛物线上,且∠PAB =∠CAB ,求点P 的坐标; (3)点D 是y 轴上的一动点,若以D 、C 、B 为顶点的三角形与△ABC 相似,求出符合条件的点D 的坐标.图1动感体验请打开几何画板文件名“16松江一模24”,拖动点D 在y 轴正半轴上运动,可以体验到,△BCD 与△ABC 相似存在两种情况. 满分解答(1)由y =ax 2+bx -3,得C (0,-3),OC =3. 由tan ∠OAC =3,得OA =1,A (-1, 0).因为抛物线与x 轴交于A (-1, 0)、B (3, 0)两点,设y =a (x +1)(x -3). 代入点C (0,-3),得a =1.所以y =(x +1)(x -3)=x 2-2x -3. (2)如图2,作PH ⊥x 轴于H .设P (x , (x +1)(x -3)). 由tan ∠PAB =tan ∠CAB ,得3PHCO AHAO ==.所以(1)(3)31x x x +-=+. 解得x =6.所以点P 的坐标为(6, 21).(3)由A (-1, 0)、B (3, 0)、C (0,-3),得BA =4,BC =∠ABC =∠BCO=45°.当点D 在点C 上方时,∠ABC =∠BCD =45°.分两种情况讨论△BCD 与△ABC相似:如图3,当CD BA CBBC=时,CD =BA =4.此时D (0, 1).如图4,当CD BCCBBA=4=92CD =.此时D 3(0,)2.图2 图3 图4例 2018年上海市松江区中考一模第25题已知等腰梯形ABCD 中,AD //BC ,∠B =∠BCD =45°,AD =3,BC =9,点P 是对角线AC 上的一个动点,且∠APE =∠B ,PE 分别交射线AD 和射线CD 于点E 和点G .(1)如图1,当点E 、D 重合时,求AP 的长;(2)如图2,当点E 在AD 的延长线上时,设AP =x ,DE =y ,求y 关于x 的函数解析式,并写出它的定义域;(3)当线段DG AE 的长.图1 图2动感体验请打开几何画板文件名“16松江一模25”,拖动点P 在AC 上运动,可以体验到,DG DE 也存在两种情况.满分解答(1)如图3,作AM ⊥BC ,DN ⊥BC ,垂足分别为M 、N ,那么MN =AD =3.在Rt △ABM 中,BM =3,∠B =45°,所以AM =3,AB =在Rt △AMC 中,AM =3,MC =6,所以CA =如图4,由AD //BC ,得∠1=∠2.又因为∠APE =∠B ,当E 、D 重合时,△APD ∽△CBA .所以AP CBADCA=.因此3AP =AP .(2)如图5,设(1)中E 、D 重合时点P 的对应点为F . 因为∠AFD =∠APE =45°,所以FD //PE .所以AFADAPAE =33y=+.因此3y x =-<x ≤图3 图4 图5(3)如图6,因为CA =AF =,所以FC .由DF //PE ,得13FP DG FCDC===.所以FP =.由DF //PE ,92AD AF DEFP===.所以2293DE AD ==.①如图6,当P 在AF 的延长线上时,233AE AD DE =+=.②如图7,当P 在AF 上时,123AE AD DE =-=.图6 图7例 2018年上海市徐汇区中考一模第24题如图1,在Rt △AOB 中,∠AOB =90°,已知点A (-1,-1),点B 在第二象限,OB=235y x bx c =++经过点A 和B .(1)求点B 的坐标;(2)求抛物线235y x bx c =++的对称轴;(3)如果该抛物线的对称轴分别和边AO 、BO 的延长线交于点C 、D ,设点E 在直线AB 上,当△BOE 和△BCD 相似时,直接写出点E 的坐标.图1动感体验请打开几何画板文件名“16徐汇一模24”,拖动点E 在射线BA 上运动,可以体验到,△BOE 和△BCD 相似存在两种情况. 满分解答(1)由A (-1,-1),得OA 与x 轴负半轴的夹角为45°. 又因为∠AOB =90°,所以OB 与x 轴负半轴的夹角也为45°. 当OB=B 到x 轴、y 轴的距离都为2.所以点B 的坐标为(-2,2).(2)将A (-1,-1)、B (-2,2)分别代入235y x bx c =++,得31,5122 2.5b c b c ⎧-+=-⎪⎪⎨⎪-+=⎪⎩解得65b =-,145c =-.所以23614555y x x =--.抛物线的对称轴是直线x =1.(3)如图2,由A (-1,-1)、B (-2,2)、C (1, 1)、D (1,-1),以及∠AOB =90°,可得BO 垂直平分AC ,BO =BA =BC BD =如图3,过点A 、E 作y 轴的平行线,过点B 作y 轴的垂线,构造Rt △ABM 和Rt △EBN ,那么BA BMMABEBNNE==.设点E 的坐标为(x , y )1322x y==+-.图2图3当点E 在射线BA 上时,∠EBO =∠DBC .分两种情况讨论相似:①当BE BCBOBD ==BE =1322x y==+-.解得x =43-,y =0.所以E 4(,0)3-(如图4).②当BE BDBOBC ==BE =1322x y==+-.解得x =45-,y =85-.所以E 48(,)55--(如图5).图4 图5例2018年上海市徐汇区中考一模第25题如图1,四边形ABCD中,∠C=60°,AB=AD=5,CB=CD=8,点P、Q分别是边AD、BC上的动点,AQ与BP交于点E,且∠BEQ∠BAD.设A、P两点间的距离为x.=90°-12(1)求∠BEQ的正切值;=y,求y关于x的函数解析式及定义域;(2)设AEPE(3)当△AEP是等腰三角形时,求B、Q两点间的距离.图1动感体验请打开几何画板文件名“16徐汇一模25”,拖动点P在AD边上运动,可以体验到,∠AEP=∠BEQ=∠ABH=∠ADH,△ABF∽△BEF∽△BDP,△AEP∽△ADF.满分解答(1)如图2,联结BD、AC交于点H.因为AB=AD,CB=CD,所以A、C在BD的垂直平分线上.所以AC垂直平分BD.因此∠BAH=1∠BAD.2∠BAD,因为∠BEQ=90°-12所以∠BEQ=90°-∠BAH=∠ABH.在Rt △ABH 中,AB =5,BH =4,所以AH =3. 所以tan ∠BEQ =tan ∠ABH =34. 图2(2)如图3,由于∠BEQ =∠ABH ,∠BEQ =∠AEP ,∠ABH =∠ADH , 所以∠AEP =∠BEQ =∠ABH =∠ADH .图3 图4 图5如图3,因为∠BFA 是公共角,所以△BEF ∽△ABF . 如图4,因为∠DBP 是公共角,所以△BEF ∽△BDP . 所以△ABF ∽△BDP .所以AB BD BF DP =.因此585BF x=-. 所以5(5)8BF x =-.所以518(5)(539)88FD BD BF x x =-=--=+.如图5,因为∠DAF 是公共角,所以△AEP ∽△ADF . 所以5401539(539)8AE AD y PEFDx x ====++.定义域是0≤x ≤5.(3)分三种情况讨论等腰△AEP :①当EP =EA 时,由于△AEP ∽△ADF ,所以DF =DA =5(如图6). 此时BF =3,HF =1. 作QM ⊥BD 于M .在Rt △BMQ 中,∠QBM =60°,设BQ =m ,那么12BMm =,QM =. 在Rt △FMQ 中,132FM m =-,tan ∠MFQ =tan ∠HFA =3,所以QM =3FM .13(3)2m =-,得BQ =m =9- ②如图7,当AE =AP 时,E 与B 重合,P 与D 重合,此时Q 与B 重合,BQ =0. ③不存在PE =PA 的情况,因为∠PAE >∠PAH >∠AEP .图6图7例 2018年上海市杨浦区中考一模第24题如图1,在平面直角坐标系中,抛物线212y x bx c =-++与x 轴交于A 、B 两点,与y 轴交于点C ,直线y =x +4经过A 、C 两点.(1)求抛物线的表达式;(2)如果点P 、Q 在抛物线上(点P 在对称轴左边),且PQ //AO ,PQ =2AO ,求点P 、Q 的坐标;(3)动点M 在直线y =x +4上,且△ABC 与△COM 相似,求点M 的坐标. 图1 动感体验请打开几何画板文件名“16杨浦一模24”,拖动点M 在射线CA 上运动,可以体验到,△ABC 与△COM 相似存在两种情况. 满分解答(1)由y =x +4,得A (-4, 0),C (0, 4).将A (-4, 0)、C (0, 4)分别代入212y x bx c =-++,得840,4.b c c --+=⎧⎨=⎩ 解得b =-1,c =4.所以抛物线的表达式为2142y x x =--+.(2)如图2,因为PQ //AO ,所以P 、Q 关于抛物线的对称轴对称. 因为抛物线的对称轴是直线x =-1,PQ =2AO =8,所以x P =-5,x Q =3. 当x =3时,2142y x x =--+=72-.所以P 7(5,)2--,Q 7(3,)2-.(3)由2114(4)(2)22y x x x x =--+=-+-,得B (2, 0).由A (-4, 0)、B (2, 0)、C (0, 4),得AB =6,AC =CO =4.当点M 在射线CA 上时,由于∠MCO =∠BAC =45°,所以分两种情况讨论相似:①当CM ABCOAC =时,4CM=CM =M (-3, 1)(如图3).②当CMACCOAB=时,4CM=CM =M 84(,)33-(如图4).图2图3图4例 2018年上海市杨浦区中考一模第25题如图1,已知菱形ABCD 的边长为5,对角线AC 的长为6,点E 为边AB 上的动点,点F 在射线AD 上,且∠ECF =∠B ,直线CF 交直线AB 于点M .(1)求∠B 的余弦值;(2)当点E 与点A 重合时,试画出符合题意的图,并求BM 的长; (3)当点M 在AB 的延长线上时,设BE =x ,BM =y ,求y 关于x 的函数解析式,并写出定义域.图1 备用图动感体验请打开几何画板文件名“16杨浦一模25”,拖动点E 在AB 上慢慢运动,可以体验到,∠1=∠2=∠3,△MCE 与△MBC 保持相似. 满分解答(1)如图2,作AN ⊥BC 于N ,联结BD 交AC 于O ,那么BO 垂直平分AC .在Rt △ABO 中,AB =5,AO =3,所以BO =4.因为S 菱形ABCD =12AC BD ⋅=BC AN ⋅,所以64=5AN ⨯⨯.解得AN =245.在Rt △ABN 中,AB =5,AN =245,所以BN =75.因此cos ∠B =BN AB =725. (2)如图3,当点E 与点A 重合时,由于∠ECF =∠B ,∠FEC =∠1, 所以△ECF ∽△ABC .所以EFACECAB =,即665EF =.解得365EF =.由BC //AF ,得AMAF BMBC=,即53625BMBM+=.解得12511BM =.图2图3(3)如图4,因为∠ECF =∠ABC ,根据等角的邻补角相等,得∠MCE =∠MBC .如图5,因为∠M 是公共角,所以△MCE ∽△MBC . 所以MC MB MEMC=.因此22()MC MB ME y x y xy y =⋅=+=+.作MH ⊥BC ,垂足为H .在Rt △MBH 中,MB =y ,cos ∠MBH =725,所以BH =725y ,MH =2425y .在Rt △MCH 中,根据勾股定理,得MC 2=MH 2+CH 2. 因此222247()(5)2525xy y y y +=++.整理,得125514y x =-.定义域是145<x ≤5.定义域中x =145的几何意义如图6所示,此时D 、F 重合,AB //CF .由CF =CE ,CF =CB ,得CE =CB . 所以1cos 2BE BC B =⋅.解得BE =72525⨯⨯=145.图4 图5 图6。
2018年上海各区高考语文一模分类汇编(文言文二)

【浦东卷】(五) 阅读下文,完成第21-25题。
(13分)《梅谱》序(明)王思任摘看一世之心,卑者逐无涯,高者命不朽。
至百年之外,其人与心,俱血俱土也。
有荧然一点如火之传薪者,无几也。
②山阴刘雪湖,少时见王元章①画梅而悦之,至忘寝食。
学之成,遂负笈买履,走名山幽壑,不知老之将至。
始焉以元章画,继焉以梅画,迄于今从心所欲。
腕脱神飞,墨停三日,而淋漓之气不止。
曾有严某泛舟,展视其图,值花蝶翩来,依依数里许。
又曾画倪中丞之壁,越半载,蜂食其华殆尽。
化则还天,诚能动物,一之至也。
③雪湖尝告人曰:“画梅以韵格胜。
”夫韵在声后,格在局先。
善歌善弈者可知而不可解,即可解而又不可知。
雪湖直以梅知之,而以画解之,此其心之独至,千载而下有必传者也。
著《梅谱》凡四刻,俱为好事者携去。
性既孤高,而家贫不能再刻,无以应问奇者。
④予偶还里中,访雪湖山房,出旧稿示余,余为刻之于姑孰官邸。
人共谓雪湖得梅之趣,而吾独谓雪湖得梅之苦。
人徒欲传雪湖之画,而吾独欲传雪湖之心。
倘从此有如其歌弈之悟....以至心而心传焉,则是《梅谱》乃导师也。
(选自《刘雪湖梅谱》,有删节)【注】①王元章:即元代著名画家王冕。
21.可填入第①段方框处的虚词是()。
(1分)A.焉B.与C.也D.矣22.赏析第②段画线句的表达效果。
(3分)23.对第④段加点短语“歌弈之悟”理解正确的一项是()。
(3分)A.善歌善弈者可知而不可解。
B.善歌善弈者可解而不可知。
C.雪湖以梅知之,以画解之。
D.韵在声后,格在局先。
24.下列对第④段画线句的理解正确的一项是( )。
(2分)A. 人们普遍认为刘雪湖悟出了梅的志趣。
B. 人们普遍认为刘雪湖获得了画梅乐趣。
C. 作者认为刘雪湖悟出了梅的孤寒本色。
D. 作者认为刘雪湖从画梅中体悟到甘苦。
25.概括这篇序言的行文思路。
(4分)【宝山卷】(五)阅读下文,完成第21-25题。
(13分)彭州圆觉禅院记北宋苏洵①人之居乎此也,其必有乐乎此也。
2018年上海市各区数学中考一模压轴题解析

图文解析
(1)由 A(3, 0)、B(0, 2),得直线 AB 的解析式为 y
2 x2. 3
4 由 A(3, 0)设抛物线的解析式为 y ( x 3)( x x2 ) ,代入点 B(0, 2),得 4 x2 2 . 3 1 4 1 4 10 所以 x2 .所以 y ( x 3)( x ) x 2 x 2 . 2 3 2 3 3
图1
图2
图3
动感体验
请打开几何画板文件名“18 崇明一模 25” ,拖动点 E 运动,可以体验到,△CQF 有三 次机会成为等腰三角形.
2018 年上海市各区中考数学一模压轴题图文解析 目录
第 24、25 题图文解析 例 2018 年上海市崇明县中考一模第 24、25 题 / 例 2018 年上海市奉贤区中考一模第 24、25 题 / 例 2018 年上海市黄浦区中考一模第 24、25 题 / 例 2018 年上海市嘉定区中考一模第 24、25 题 / 例 2018 年上海市金山区中考一模第 24、25 题 / 例 2018 年上海市闵行区中考一模第 24、25 题 / 例 2018 年上海市浦东新区中考一模第 24、25 题 例 2018 年上海市普陀区中考一模第 24、25 题 / 例 2018 年上海市青浦区中考一模第 24、25 题 / 例 2018 年上海市松江区中考一模第 24、25 题 / 例 2018 年上海市徐汇区中考一模第 24、25 题 / 例 2018 年上海市杨浦区中考一模第 24、25 题 / 例 2018 年上海市宝山区中考一模第 24、25 题 / 第 18 题图文解析 例 2018 年上海市崇明县中考一模第 18 题 / 65 例 2018 年上海市奉贤区中考一模第 18 题 / 66 例 2018 年上海市虹口区中考一模第 18 题 / 67 例 2018 年上海市黄浦区中考一模第 18 题 / 68 例 2018 年上海市嘉定区中考一模第 18 题 / 69 例 2018 年上海市金山区中考一模第 18 题 / 70 例 2018 年上海市静安区中考一模第 18 题 / 71 例 2018 年上海市闵行区中考一模第 18 题 / 72 例 2018 年上海市浦东新区中考一模第 18 题 / 73 例 2018 年上海市普陀区中考一模第 18 题 / 74 例 2018 年上海市青浦区中考一模第 18 题 / 75 例 2018 年上海市松江区中考一模第 18 题 / 76 例 2018 年上海市徐汇区中考一模第 18 题 / 77 例 2018 年上海市杨浦区中考一模第 18 题 / 78 例 2018 年上海市长宁区中考一模第 18 题 / 79 例 2018 年上海市宝山区中考一模第 18 题 / 80 3 7 16 19 23 30 / 34 38 42 45 49 52 60
2018-2019学年上海中考数学各区一模汇编提升题(18、23、24、25题

目录Ⅰ第18题(填空小压轴) (3)【2019届一模徐汇】 (3)【2019届一模浦东】 (3)【2019届一模杨浦】 (3)【2019届一模普陀】 (4)【2019届一模奉贤】 (4)【2019届一模松江】 (4)【2019届一模嘉定】 (5)【2019届一模青浦】 (5)【2019届一模青浦】 (5)【2019届一模静安】 (6)【2019届一模宝山】 (6)【2019届一模长宁】 (6)【2019届一模金山】 (7)【2019届一模闵行】 (7)【2019届一模虹口】 (7)Ⅱ第23题(几何证明题) (8)【2019届一模徐汇】 (8)【2019届一模浦东】 (8)【2019届一模杨浦】 (9)【2019届一模普陀】 (9)【2019届一模奉贤】 (10)【2019届一模松江】 (10)【2019届一模嘉定】 (11)【2019届一模青浦】 (11)【2019届一模静安】 (12)【2019届一模宝山】 (12)【2019届一模长宁】 (13)【2019届一模金山】 (13)【2019届一模闵行】 (14)【2019届一模虹口】 (14)Ⅲ第24题(二次函数综合) (15)【2019届一模徐汇】 (15)【2019届一模浦东】 (16)【2019届一模普陀】 (18)【2019届一模奉贤】 (19)【2019届一模松江】 (20)【2019届一模嘉定】 (21)【2019届一模青浦】 (22)【2019届一模静安】 (23)【2019届一模宝山】 (24)【2019届一模长宁】 (25)【2019届一模金山】 (26)【2019届一模闵行】 (27)【2019届一模虹口】 (28)Ⅳ第25题(压轴题) (29)【2019届一模徐汇】 (29)【2019届一模浦东】 (30)【2019届一模杨浦】 (31)【2019届一模普陀】 (32)【2019届一模奉贤】 (33)【2019届一模松江】 (34)【2019届一模嘉定】 (35)【2019届一模青浦】 (36)【2019届一模静安】 (37)【2019届一模宝山】 (38)【2019届一模长宁】 (39)【2019届一模金山】 (40)【2019届一模闵行】 (41)【2019届一模虹口】 (42)Ⅰ第18题(填空小压轴)【2019届一模徐汇】18.在梯形ABCD 中,AB ∥DC ,∠B =90°,BC=6,CD =2,3tan 4A =.点E 为BC 上一点,过点E 作EF ∥AD 交边AB 于点F .将△BEF 沿直线EF 翻折得到△GEF ,当EG 过点D 时,BE 的长为 ▲ .【2019届一模浦东】18. 将矩形纸片ABCD 沿直线AP 折叠,使点D 落在原矩形ABCD 的边BC 上的点E 处,如果∠AED 的余弦值为35,那么ABBC =__________.【2019届一模杨浦】18.Rt △ABC 中,∠C =90°,AC =3,BC =2,将此三角形绕点A 旋转,当点B 落在直线BC 上的点D 处时,点C 落在点E 处,此时点E 到直线BC 的距离为 ▲ .GEABC DF (第18题图)ACB(第18题图)18.如图5,△ABC 中,8AB AC ==,3cos 4B =,点D 在边BC 上,将△ABD 沿直线AD 翻折得到△AED ,点B 的对应点为点E ,AE 与边BC 相交于点F ,如果2BD =,那么EF = ▲ .【2019届一模奉贤】18.如图5,在△ABC 中,AB =AC =5,3sin =5C ,将△ABC 绕点A 逆时针旋转得到△ADE ,点B 、C 分别与点D 、E 对应,AD 与边BC 交于点F .如果AE //BC ,那么BF 的长是 ▲ .【2019届一模松江】18.如图,在直角坐标平面xoy 中,点A 坐标为(3,2),∠AOB =90°,∠OAB =30°,AB 与x 轴交于点C ,那么AC :BC 的值为______.图5ABCD图5AB C(第18题图)xyC BOA18.在△ABC 中,︒=∠90ACB ,点D 、E 分别在边BC 、AC 上,AE AC 3=,︒=∠45CDE (如图3),△DCE 沿直线DE 翻折,翻折后的点C 落在△ABC 内部的点F ,直线AF 与边BC 相交于点G ,如果AE BG =,那么=B tan ▲ .【2019届一模青浦】17.如图,在Rt △ABC 中,∠ACB=90°,AC=1,tan ∠CAB=2,将△ABC 绕点A 旋转后,点B 落在AC 的延长线上的点D ,点C 落在点E ,DE 与直线BC 相交于点F ,那么CF= ▲ .【2019届一模青浦】18.对于封闭的平面图形,如果图形上或图形内的点S 到图形上的任意一点P 之间的线段都在图形内或图形上,那么这样的 点S 称为“亮点”. 如图,对于封闭图形ABCDE ,S 1是 “亮点”,S 2不是“亮点”,如果AB ∥DE ,AE ∥DC , AB=2,AE=1,∠B=∠C= 60°,那么该图形中所有“亮点” 组成的图形的面积为 ▲ .EDCBAS 2S 1(第18题图)18.如图6,将矩形ABCD 沿对角线BD 所在直线翻折后,点A 与点E 重合,且ED 交BC 于点F ,联结AE .如果2tan 3DFC ∠=,那么BDAE的值是 ▲ .【2019届一模宝山】18.如图4,Rt △ABC 中,∠ACB =90°,AC =4,BC =5,点P 为AC 上一点,将△BCP 沿直线BP 翻折,点C落在C ’处,连接AC ’,若AC ’∥BC ,则CP 的长为 ▲ .【2019届一模长宁】18.如图,点P 在平行四边形ABCD 的边BC 上,将ABP ∆沿直线AP 翻折,点B 恰好落在边AD 的垂直平分线上,如果5=AB ,8=AD ,34tan =B ,那么BP 的长为 ▲ .AC(图4)B图6F BACDEBACD第18题图18.如图,在ABC Rt ∆中,o90=∠C ,8=AC ,6=BC .在边AB 上取一点O ,使BC BO =,以点O 为旋转中心,把ABC ∆逆时针旋转90,得到C B A '''∆(点A 、B 、C 的对应点分别是点A '、B '、C '),那么ABC ∆与C B A '''∆的重叠部分的面积是 ▲ .【2019届一模闵行】18.如图,在Rt △ABC 中,∠ACB = 90°,BC = 3,AC = 4,点D 为边AB 上一点.将△BCD 沿直线CD 翻折,点B 落在点E 处,联结AE .如果AE // CD ,那么BE = ▲ .【2019届一模虹口】18.如图,正方形ABCD 的边长为4,点O 为对角线AC 、BD 的交点,点E 为边AB 的中点,△BED 绕着点B 旋转至△BD 1E 1,如果点D 、E 、D 1在同一直线上,那么EE 1的长为 ▲ .ABC第18题OABC (第18题图)C第18题图A BDE OⅡ第23题(几何证明题)【2019届一模徐汇】23.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分)如图,已知菱形ABCD ,点E 是AB 的中点,AF BC ⊥于点F ,联结EF 、ED 、DF ,DE 交AF 于点G ,且2AE EG ED =⋅.(1) 求证:DE EF ⊥; (2) 求证:22BC DF BF =⋅.【2019届一模浦东】23. (本题满分12分,其中每小题各6分)已知:如图8,在平行四边形ABCD 中,M 是边BC 的中点,E 是边BA 延长线上的一点,联结EM ,分别交线段AD 于点F 、AC 于点G .(1)求证:GF EFGM EM=; (2)当22BC BA BE =⋅时,求证:∠EMB =∠ACD .G DEF BCA(第23题图)(图8)DCM BAF GE23.(本题满分12分,每小题各6分)已知:如图,在△ABC 中,点D 在边AB 上,点E 在线段CD 上,且∠ACD =∠B =∠BAE. (1)求证:AD DEBC AC=; (2)当点E 为CD 中点时,求证:22AE ABCE AD=.【2019届一模普陀】23.(本题满分12分)已知:如图9,△ADE 的顶点E 在△ABC 的边BC 上,DE 与AB 相交于点F ,AE AF AB =⋅2,DAF EAC ∠=∠.(1)求证:△ADE ∽△ACB ;(2)求证:DF CE DE CB=.(第23题图)EABCDF图9ABCDE23.(本题满分12分,第(1)小题满分5分,第(2)小题满分7分)已知:如图9,在△ABC 中,点D 在边AC 上,BD 的垂直平分线交CA 的延长线于点E , 交BD 于点F ,联结BE ,EC EA ED •=2. (1)求证:∠EBA =∠C ;(2)如果BD =CD ,求证:AC AD AB •=2.【2019届一模松江】23.(本题满分12分,第(1)小题5分,第(2)小题7分)已知:如图,在梯形ABCD 中,AD ∥BC ,AB=DC ,E 是对角线AC 上一点,且AC ·CE=AD ·BC . (1)求证:∠DCA=∠EBC ;(2)延长BE 交AD 于F ,求证:AB 2=AF ·AD .ABCDEF图9(第23题图)EDCBAF(第23题图)EDCBA23.(本题满分12分,每小题6分)如图6,已知点D 在△ABC 的外部,AD //BC ,点E 在边AB 上,AE BC AD AB ⋅=⋅. (1)求证:AED BAC ∠=∠;(2)在边AC 取一点F ,如果D AFE ∠=∠, 求证:ACAFBC AD =.【2019届一模青浦】23.(本题满分12分,第(1)小题7分,第(2)小题5分)已知:如图,在△ABC 中,点D 、E 分别在边BC 、AC 上,点F 在DE 的延长线上,AD=AF ,AE CE DE EF ⋅=⋅.(1)求证:△ADE ∽△ACD ;(2)如果AE BD EF AF ⋅=⋅,求证:AB=AC .图6BCDAE FABCDEF(第23题图)23.(本题满分12分,其中第(1)小题6分,第(2)小题6分)已知:如图9,在ABC ∆中,点D 、E 分别在边BC 和AB 上,且AD AC =,EB ED =,分别延长ED 、AC 交于点F .(1)求证:ABD ∆∽FDC ∆; (2)求证:2AE BE EF =⋅.【2019届一模宝山】23.(本题满分12分)地铁10号线某站点出口横截面平面图如图8所示,电梯AB 的两端分别距顶部9.9米和2.4米,在距电梯起点A 端6米的P 处,用1.5米的测角仪测得电梯终端B 处的仰角为14°,求电梯AB 的坡度与长度. 参考数据:24.014sin ≈︒,25.014tan ≈︒,97.014cos ≈︒.Q 9.9米B出口顶部1.5米(图8)AP6米2.4米︒14图9 AC BDEF23.(本题满分12分,第(1)小题5分,第(2)小题7分)如图,点D 、E 分别在ABC ∆的边AC 、AB 上,延长DE 、CB 交 于点F ,且AC AD AB AE ⋅=⋅. (1)求证:C FEB ∠=∠;(2)联结AF ,若FD CD AB FB =,求证:FB AC AB EF ⋅=⋅.【2019届一模金山】23.如图,M 是平行四边形ABCD 的对角线上的一点,射线AM 与BC 交于点F ,与DC 的延长线交于点H .(1)求证:MH MF AM ⋅=2.(2)若DM BD BC ⋅=2,求证:ADC AMB ∠=∠.第23题图CEDABF ABCD HF M第23题23.(本题共2小题,每小题6分,满分12分)如图,在△ABC 中,点D 为边BC 上一点,且AD = AB ,AE ⊥BC ,垂足为点E .过点D 作DF // AB ,交边AC 于点F ,联结EF ,212EF BD EC =⋅.(1)求证:△EDF ∽△EFC ; (2)如果14EDF ADC S S =V V ,求证:AB = BD .【2019届一模虹口】23.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分)如图,在△ABC 中,AB=AC ,D 是边BC 的中点,DE ⊥AC ,垂足为点E . (1)求证:DE CD AD CE ⋅=⋅;(2)设F 为DE 的中点,联结AF 、BE ,求证:=AF BC AD BE ⋅⋅.ABCDE F(第23题图)D 第23题图AECBⅢ第24题(二次函数综合)【2019届一模徐汇】24.(本题满分12分,第(1)小题4分,第(2)小题4分,第(3)小题4分)如图,在平面直角坐标系xoy 中,顶点为M 的抛物线C 1:2(0)y ax bx a =+<经过点A 和x 轴上的点B ,AO =OB =2,120AOB ∠=o . (1)求该抛物线的表达式; (2)联结AM ,求AOM S V ;(3)将抛物线C 1向上平移得到抛物线C 2,抛物线C 2与x 轴分别交于点E 、F (点E 在点F 的左侧),如果△MBF 与△AOM 相似,求所有符合条件的抛物线C 2的表达式.(第24题图)【2019届一模浦东】24.(本题满分12分,其中每小题各4分)已知:如图9,在平面直角坐标系xOy中,直线12y x b=-+与x轴相交于点A,与y轴相交于点B. 抛物线244y ax ax=-+经过点A和点B,并与x轴相交于另一点C,对称轴与x轴相交于点D.(1)求抛物线的表达式;(2)求证: △BOD∽△AOB;(3)如果点P在线段AB上,且∠BCP=∠DBO,求点P的坐标.(图9)xBO Ay【2019届一模杨浦】24.(本题满分12分,每小题各4分)在平面直角坐标系xOy 中,抛物线2(0)y ax bx c a =++?与y 轴交于点C (0,2),它的顶点为D (1,m ),且1tan 3COD ?. (1)求m 的值及抛物线的表达式;(2)将此抛物线向上平移后与x 轴正半轴交于点A ,与y 轴交于点B ,且OA =OB .若点A 是由原抛物线上的点E 平移所得,求点E 的坐标;(3)在(2)的条件下,点P 是抛物线对称轴上的一点(位于x 轴上方),且∠APB =45°.求P 点的坐标.O xy 1 2 3 4 1 2 3 45-1-2 -3 -1 -2 -3 (第24题图)24.(本题满分12分)如图10,在平面直角坐标系xOy 中,抛物线23y ax bx =+-(0)a ≠与x 轴交于点A ()1,0-和点B ,且3OB OA =,与y 轴交于点C ,此抛物线顶点为点D .(1)求抛物线的表达式及点D 的坐标;(2)如果点E 是y 轴上的一点(点E 与点C 不重合),当BE DE ⊥时,求点E 的坐标; (3)如果点F 是抛物线上的一点,且135FBD ∠=,求点F 的坐标.图10C BAOyx24.(本题满分12分,每小题满分6分)如图10,在平面直角坐标系xOy 中,直线AB 与抛物线2y ax bx =+交于点A (6,0)和点B (1,-5). (1)求这条抛物线的表达式和直线AB 的表达式; (2)如果点C 在直线AB 上,且∠BOC 的正切值是32, 求点C 的坐标.图10 ABxyo24.(本题满分12分,第(1)小题3分,第(2)小题4分,第(3)小题5分)如图,抛物线c bx x y ++-=221经过点A (﹣2,0),点B (0,4). (1)求这条抛物线的表达式;(2)P 是抛物线对称轴上的点,联结AB 、PB ,如果∠PBO=∠BAO ,求点P 的坐标;(3)将抛物线沿y 轴向下平移m 个单位,所得新抛物线与y 轴交于点D ,过点D 作DE ∥x 轴交新抛物线于点E ,射线EO 交新抛物线于点F ,如果EO =2OF ,求m 的值.(第24题图)y xOBA24.(本题满分12分,每小题4分)在平面直角坐标系xOy (如图7)中,抛物线22++=bx ax y 经过点)0,4(A 、)2,2(B , 与y 轴的交点为C .(1)试求这个抛物线的表达式;(2)如果这个抛物线的顶点为M ,求△AMC 的面积; (3)如果这个抛物线的对称轴与直线BC 交于点D ,点E 在线段AB 上,且︒=∠45DOE ,求点E 的坐标.图7O 11 xy--24.(本题满分12分, 其中第(1)小题3分,第(2)小题5分,第(3)小题4分)在平面直角坐标系xOy 中,将抛物线2y x =-平移后经过点A (-1,0)、B (4,0),且平移后的抛物线与y 轴交于点C (如图).(1)求平移后的抛物线的表达式;(2)如果点D 在线段CB 上,且CD =2,求∠CAD 的正弦值;(3)点E 在y 轴上且位于点C 的上方,点P 在直线BC 上,点Q 在平移后的抛物线上,如果四边形ECPQ 是菱形,求点Q 的坐标.CB A xyOCB A xyO(第24题图)(备用图)24.(本题满分12分,其中第(1)小题4分,第(2)小题3分,第(3)小题5分)在平面直角坐标系xOy 中(如图10),已知抛物线2(0)y ax bx c a =++≠的图像经过点(40)B ,、(53)D ,,设它与x 轴的另一个交点为A (点A 在点B 的左侧),且ABD ∆的面积是3. (1)求该抛物线的表达式; (2)求ADB ∠的正切值;(3)若抛物线与y 轴交于点C ,直线CD 交x 轴于点E ,点P 在射线AD 上,当APE ∆与 ABD ∆相似时,求点P 的坐标.BD O图10xy﹒﹒24.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分)如图9,已知:二次函数2y x bx =+的图像交x 轴正半轴于点A ,顶点为P ,一次函数132y x =-的图像交x 轴于点B ,交y 轴于点C , ∠OCA 的正切值为23. (1)求二次函数的解析式与顶点P 坐标;(2)将二次函数图像向下平移m 个单位,设平移后抛物线顶点为P ’,若,求m 的值.A B C O yx(图9)24.(本题满分12分,每小题4分)如图,在直角坐标平面内,抛物线经过原点O 、点)3,1(B ,又与x 轴正半轴相交于点A ,︒=∠45BAO ,点P 是线段AB 上的一点,过点P 作OB PM //,与抛物线交于点M ,且点M 在第一象限内.(1)求抛物线的表达式;(2)若AOB BMP ∠=∠,求点P 的坐标;(3)过点M 作x MC ⊥轴,分别交直线AB 、x 轴于点N 、C ,若ANC ∆的面积等于PMN ∆的面积的2倍,求NC MN 的值.第24题图 xO A By备用图xO A By24.已知抛物线c bx x y ++=2经过点()6,0A ,点()3,1B ,直线1l :()0≠=k kx y ,直线2l :2--=x y ,直线1l 经过抛物线c bx x y ++=2的顶点P ,且1l 与2l 相交于点C ,直线2l 与x 轴、y 轴分别交于点D 、E .若把抛物线上下平移,使抛物线的顶点在直线2l 上(此时抛物线的顶点记为M ),再把抛物线左右平移,使抛物线的顶点在直线1l 上(此时抛物线的顶点记为N ). (1)求抛物线c bx x y ++=2的解析式.(2)判断以点N 为圆心,半径长为4的圆与直线2l 的位置关系,并说明理由.(3)设点F 、H 在直线1l 上(点H 在点F 的下方),当MHF ∆与OAB ∆相似时,求点F 、H 的坐标(直接写出结果).第24题yxO24.(本题共3小题,每小题4分,满分12分)已知:在平面直角坐标系xOy 中,抛物线2y a x b x =+经过点A (5,0)、B (-3,4),抛物线的对称轴与x 轴相交于点D .(1)求抛物线的表达式;(2)联结OB 、BD .求∠BDO 的余切值;(3)如果点P 在线段BO 的延长线上,且∠P AO =∠BAO ,求点P 的坐标.xy O (第24题图)24.(本题满分12分,第(1)小题满分4分,第(2)小题满分4分,第(3)小题满分4分)如图,在平面直角坐标系xOy 中,抛物线2y x bx c =-++与x 轴相交于原点O 和点B (4,0),点A (3,m )在抛物线上.(1)求抛物线的表达式,并写出它的对称轴; (2)求tan ∠OAB 的值;(3)点D 在抛物线的对称轴上,如果∠BAD =45°,求点D 的坐标.OAy 第24题图xBF EA CB DF E A CB DⅣ第25题(压轴题)【2019届一模徐汇】25. (本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分)已知:在梯形ABCD 中,AD //BC ,AC =BC =10,54cos =∠ACB ,点E 在对角线AC 上(不与点A 、C 重合),EDC ACB ∠=∠,DE 的延长线与射线CB 交于点F ,设AD 的长为x . (1)如图1,当DF BC ⊥时,求AD 的长; (2)设EC 的长为y ,求y 关于x 的函数解析式,并直接写出定义域; (3)当△DFC 是等腰三角形时,求AD 的长.(第25题图1) (第25题图)【2019届一模浦东】25. (本题满分14分,其中第(1)小题3分,第(2)小题5分,第(3)小题6分)将大小两把含30°角的直角三角尺按如图10-1位置摆放,即大小直角三角尺的直角顶点C 重合,小三角尺的顶点D 、E 分别在大三角尺的直角边AC 、BC 上, 此时小三角尺的斜边DE 恰好经过大三角尺的重心G . 已知∠A =∠CDE =30°,AB =12. (1)求小三角尺的直角边CD 的长;(2)将小三角尺绕点C 逆时针旋转,当点D 第一次落在大三角尺的边AB 上时(如图10-2),求点B 、E 之间的距离;(3)在小三角尺绕点C 旋转的过程中,当直线DE 经过点A 时,求∠BAE 的正弦值.G(图10-1)(图10-2)E DCABDCBAE25.(本题满分14分,第(1)小题4分,第(2)、(3)小题各5分)已知:梯形ABCD 中,AD //BC ,AB ⊥BC ,AD =3,AB =6,DF ⊥DC 分别交射线AB 、射线CB 于点E 、F .(1)当点E 为边AB 的中点时(如图1),求BC 的长; (2)当点E 在边AB 上时(如图2),联结CE ,试问:∠DCE 的大小是否确定?若确定,请求出∠DCE 的正切值;若不确定,则设AE =x ,∠DCE 的正切值为y ,请求出y 关于x 的函数解析式,并写出定义域; (3)当△AEF 的面积为3时,求△DCE 的面积.A BC D EF (图1) (第25题图) A B C D E F (图2)25.(本题满分14分)如图11,点O 在线段AB 上,22AO OB a ==,60BOP ∠=︒,点C 是射线OP 上的一个动点. (1)如图11①,当90ACB ∠=︒,2OC =,求a 的值;(2)如图11②,当AC =AB 时,求OC 的长(用含a 的代数式表示);(3)在第(2)题的条件下,过点A 作AQ ∥BC ,并使∠QOC=∠B ,求:AQ OQ 的值.A BCPOABCPO图11①图11②25.(本题满分14分,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分5分)如图11,已知梯形ABCD 中,AB ∥CD ,∠DAB =90°,AD =4,26AB CD ==,E 是边BC 上一点,过点D 、E 分别作BC 、CD 的平行线交于点F ,联结AF 并延长,与射线DC 交于点G . (1)当点G 与点C 重合时,求:CE BE 的值;(2)当点G 在边CD 上时,设CE m =,求△DFG 的面积;(用含m 的代数式表示) (3)当AFD ∆∽ADG ∆时,求∠DAG 的余弦值.图11ABC D F E G 备用图ABC D25.(本题满分14分,第(1)小题4分,第(2)、(3)小题各5分)如图,已知△ABC 中,∠ACB =90°,D 是边AB 的中点,P 是边AC 上一动点,BP 与CD 相交于点E . (1)如果BC =6,AC =8,且P 为AC 的中点,求线段BE 的长; (2)联结PD ,如果PD ⊥AB ,且CE =2,ED =3,求cosA 的值; (3)联结PD ,如果222BP CD ,且CE =2,ED =3,求线段PD 的长.(备用图2)ABCD(备用图1)ABCD(第25题图)ABPC D E25.(满分14分,第(1)小题4分,第(2)、(3)小题各5分)在矩形ABCD 中,6=AB ,8=AD ,点E 是边AD 上一点,EC EM ⊥交AB 于点M ,点N 在射线MB 上,且AE 是AM 和AN 的比例中项. (1)如图8,求证:DCE ANE ∠=∠;(2)如图9,当点N 在线段MB 之间,联结AC ,且AC 与NE 互相垂直,求MN 的长; (3)联结AC ,如果△AEC 与以点E 、M 、N 为顶点所组成的三角形相似,求DE 的长.A备用图BD CA 图8B M E DC N A 备用图 BD C ME N A 图9 B D C25.(本题满分14分,其中第(1)小题4分,第(2)小题6分,第(3)小题4分)如图,在梯形ABCD 中,AD//BC ,BC =18,DB =DC =15,点E 、F 分别在线段BD 、CD 上,DE =DF =5. AE 的延长线交边BC 于点G , AF 交BD 于点N 、其延长线交BC 的延长线于点H . (1)求证:BG =CH ;(2)设AD =x ,△ADN 的面积为y ,求y 关于x 的函数解析式,并写出它的定义域; (3)联结FG ,当△HFG 与△ADN 相似时,求AD 的长.NHGFEDC AB (第25题图)图11ABCPQM25.(本题满分14分,其中第(1)小题4分,第(2)小题5分,第(3)小题5分)已知:如图11,在ABC ∆中,6AB =,9AC =,tan 22ABC ∠=.过点B 作BM //AC ,动点P 在射线BM 上(点P 不与点B 重合),联结PA 并延长到点Q ,使AQC ABP ∠=∠. (1)求ABC ∆的面积;(2)设BP x =,AQ y =,求y 关于x 的函数解析式,并写出x 的取值范围; (3)联结PC ,如果PQC ∆是直角三角形,求BP 的长.25.(本题满分14分,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分)如图10,已知:梯形ABCD 中,∠ABC =90°,∠A =45°,AB ∥DC ,DC =3,AB =5,点 P 在AB 边上,以点A 为圆心AP 为半径作弧交边DC 于点E ,射线EP 与射线CB 交于点F .(1)若13AP ,求DE 的长; (2)联结CP ,若CP=EP ,求AP 的长;(3)线段CF 上是否存在点G ,使得△ADE 与△FGE 相似,若相似,求FG 的值;若不相似,请说明理由.备用图A BCD PEABCDF(图10)25.(本题满分14分,第(1)小题4分,第(2)小题6分,第(3)小题4分)已知锐角MBN ∠的余弦值为53,点C 在射线BN 上,25=BC ,点A 在MBN ∠的内部, 且︒=∠90BAC ,MBN BCA ∠=∠.过点A 的直线DE 分别交射线BM 、射线BN 于点D 、E . 点F 在线段BE 上(点F 不与点B 重合),且MBN EAF ∠=∠. (1)如图1,当BN AF ⊥时,求EF 的长;(2)如图2,当点E 在线段BC 上时,设x BF =,y BD =,求y 关于x 的函数解析式并写出函数定义域;(3)联结DF ,当ADF ∆与ACE ∆相似时,请直接写出BD 的长.第25题图图2 BFE C N DA MB FC E N AD M图1备用图BC NAM25.已知多边形ABCDEF 是⊙O 的内接正六边形,联结AC 、FD ,点H 是射线AF 上的一个动点,联结CH ,直线CH 交射线DF 于点G ,作CH MH ⊥交CD 的延长线于点M ,设⊙O 的半径为()0>r r . (1)求证:四边形ACDF 是矩形.(2)当CH 经过点E 时,⊙M 与⊙O 外切,求⊙M 的半径(用r 的代数式表示).(3)设()900<<=∠ααHCD ,求点C 、M 、H 、F 构成的四边形的面积(用r 及含α的三角比的式子表示).A B C D EF G O HM第25题图第25题备用图 ABCD E FO25.(本题满分14分,其中第(1)小题4分、第(2)、(3)小题各5分)如图,在梯形ABCD 中,AD // BC ,AB = CD ,AD = 5,BC = 15,5cos 13ABC ∠=.E 为射线CD 上任意一点,过点A 作AF // BE ,与射线CD 相交于点F .联结BF ,与直线AD 相交于点G .设CE = x ,AG y DG=. (1)求AB 的长; (2)当点G 在线段AD 上时,求y 关于x 的函数解析式,并写出函数的定义域;(3)如果23ABEFABCDS S =四边形四边形,求线段CE 的长.AB CDEFG (第25题图)A B C D (备用图)25.(本题满分14分,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分)如图,在四边形ABCD 中,AD ∥BC ,∠A =90°,AB =6,BC =10,点E 为边AD 上一点,将△ABE 沿BE 翻折,点A 落在对角线BD 上的点G 处,联结EG 并延长交射线BC 于点F .(1)如果cos ∠DBC =23,求EF 的长; (2)当点F 在边BC 上时,联结AG ,设AD=x ,ABG BEFS y S ∆∆= ,求y 关于x 的函数关系式,并写出x 的取值范围;(3)联结CG ,如果△FCG 是等腰三角形,求AD 的长.第25题备用图 A B C 第25题图 E A B C F D G。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
已知:梯形 ABCD 中,AD//BC,AB⊥BC,AD=3,AB=6,DF⊥DC 分别交射线 AB、射
线 CB 于点 E、F.
(1)当点 E 为边 AB 的中点时(如图 1),求 BC 的长;
(2)当点 E 在边 AB 上时(如图 2),联结 CE,试问:∠DCE 的大小是否确定?若确定,
请求出∠DCE 的正切值;若不确定,则设 AE=x,∠DCE 的正切值为 y,请求出 y 关于 x 的
(1)求 ABC 的面积; (2)设 BP x , AQ y ,求 y 关于 x 的函数解析式,并写出 x 的取值范围; (3)联结 PC ,如果 PQC 是直角三角形,求 BP 的长.
7
2018 学年上海市各区一模考第 25 题
(闵行)25.(本题满分 14 分,其中第(1)小题 4 分、第(2)、(3)小题各 5 分) 如图,在梯形 ABCD 中,AD // BC,AB = CD,AD = 5,BC = 15, cos ABC 5 .E 13
且 BAC 90 , BCA MBN .过点 A 的直线 DE 分别交射线 BM 、射线 BN 于点
D、E. 点 F 在线段 BE 上(点 F 不与点 B 重合),且 EAF MBN .
(1)如图 1,当 AF BN 时,求 EF 的长; (2)如图 2,当点 E 在线段 BC 上时,设 BF x , BD y ,求 y 关于 x 的函数解析式
并写出函数定义域;
(3)联结 DF ,当 ADF 与 ACE 相似时,请直接写出 BD 的长.
M
M
M
D
D A
A
A
B
F C ENB F
E C NB
CN
如图 1
如图 2
备用图
第 25 题图
14
长.
A
E
D
A
E
D
A
D
M
B
图8
C
N
M
N
B 图9
C
B
备用图 C
A
D
B
备用图 C
9
2018 学年上海市各区一模考第 25 题
(金山)25.已知多边形 ABCDEF 是⊙ O 的内接正六边形,联结 AC 、 FD ,点 H 是射
线 AF 上的一个动点,联结 CH ,直线 CH 交射线 DF 于点 G ,作 MH CH 交 CD 的延
EG AB ,垂足为点 G , EG 分别交 BD 、 DF 、 DC 于点 M 、 N 、 H .
(1)求证: DE NE ;
A
DB OB
(2)设 CD x , NE y ,求 y 关于 x 的函数关系式及其定义域;
(3)当 DEF 是以 DE 为腰的等腰三角形时,求线段 CD 的长.
为射线 CD 上任意一点,过点 A 作 AF // BE,与射线 CD 相交于点 F.联结 BF,与直线 AD 相交于点 G.设 CE = x, AG y .
DG (1)求 AB 的长; (2)当点 G 在线段 AD 上时,求 y 关于 x 的函数解析式,并写出函数的定义域; (3)如果 S 四边形ABEF 2 ,求线段 CE 的长.
的一个动点,过点 P 作 PF ∥ AC 交线段 BD 于点 F,作 PG⊥AB 交 AD 于点 E,交线段 CD
于点 G,设 BP x .
(1)用含 x 的代数式表示线段 DG 的长;
(2)设 △DEF 的面积为 y,求 y 与 x 之间的函数关系式,并写出定义域;
(3) △PEF 能否为直角三角形?
D
GC
D
C
F
E
A 图 11
B
A
B
备用图
6
2018 学年上海市各区一模考第 25 题
(静安)25.(本题满分 14 分,其中第(1)小题 4 分,第(2)小题 5 分,第(3)小题 5 分)已知:如图 11,在 ABC 中,AB 6 ,AC 9 ,tan ABC 2 2 .过点 B 作 BM // AC , 动点 P 在射线 BM 上(点 P 不与点 B 重合),联结 PA 并延长到点 Q ,使 AQC ABP .
(1)若 AP 13,求 DE 的长;
(2)联结 CP,若 CP=EP,求 AP 的长; (3)线段 CF 上是否存在点 G,使得△ADE 与△FGE 相似,若相似,求 FG 的值;若 不相似,请说明理由.
D
C
A
B
(图 10)
备用图
3
2018 学年上海市各区一模考第 25 题
(虹口)25.(本题满分 14 分,第(1)小题满分 4 分,第(2)小题满分 6 分,第(3)小 题满分 4 分)
O
G
D
M
NH
B
FC E
(第 25 题图)
2
2018 学年上海市各区一模考第 25 题
(宝山)如图 10,已知:梯形 ABCD 中,∠ABC=90°,∠A=45°,AB∥DC,DC=3,AB=5, 点 P 在 AB 边上,以点 A 为圆心 AP 为半径作弧交边 DC 于点 E,射线 EP 与射线 CB 交于点 F.
BC 上一点,过点 D、E 分别作 BC、CD 的平行线交于点 F,联结 AF 并延长,与射线 DC 交
于点 G.
(1)当点 G 与点 C 重合时,求 CE : BE 的值; (2)当点 G 在边 CD 上时,设 CE m ,求△DFG 的面积;(用含 m 的代数式表示) (3)当 AFD ∽ ADG 时,求∠DAG 的余弦值.
S 四边形ABCD 3
F
A
D
G
A
D
E
B
C
B
(第 25 题图)
C
(备用图)
8
2018 学年上海市各区一模考第 25 题
(嘉定)25.(满分 14 分,第(1)小题 4 分,第(2)、(3)小题各 5 分)
在矩形 ABCD 中, AB 6 , AD 8 ,点 E 是边 AD 上一点, EM EC 交 AB 于点 M ,点 N 在射线 MB 上,且 AE 是 AM 和 AN 的比例中项. (1)如图 8,求证: ANE DCE ; (2)如图 9,当点 N 在线段 MB 之间,联结 AC ,且 AC 与 NE 互相垂直,求 MN 的长; (3)联结 AC ,如果△ AEC 与以点 E 、 M 、 N 为顶点所组成的三角形相似,求 DE 的
长线于点 M ,设⊙ O 的半径为 rr 0 .
(1)求证:四边形 ACDF 是矩形. (2)当 CH 经过点 E 时,⊙ M 与⊙ O 外切,求⊙ M 的半径(用 r 的代数式表示).
(3)设 HCD 0 90 ,求点 C 、 M 、 H 、 F 构成的四边形的面积(用 r 及含
(1)求证:BG=CH; (2)设 AD=x,△ADN 的面积为 y,求 y 关于 x 的函数解析式,并写出它的定义域; (3)联结 FG,当△HFG 与△ADN 相似时,求 AD 的长.
12
2018 学年上海市各区一模考第 25 题
(杨浦)25.(本题满分 14 分,第(1)小题 4 分,第(2)、(3)小题各 5 分)
函数解析式,并写出定义域;
(3)当△AEF 的面积为 3 时,求△DCE 的面积.
A
D
A
D
E
E
FB
(图 1)
C
F
(第 25 题图)
B
C
(图 2)
13
2018 学年上海市各区一模考第 25 题
(长宁)25.(本题满分 14 分,第(1)小题 4 分,第(2)小题 6 分,第(3)小题 4 分)
已知锐角 MBN 的余弦值为 3 ,点 C 在射线 BN 上, BC 25 ,点 A 在 MBN 的内部, 5
如果能,求出 BP 的长;如果不能,请说明理由.
A
P E
B
FD G
C
(第 25 题图)
5
2018 学年上海市各区一模考第 25 题
(奉贤)25.(本题满分 14 分,第(1)小题满分 4 分,第(2)小题满分 5 分,第(3)小题满分 5
分)
如图 11,已知梯形 ABCD 中,AB∥CD,∠DAB=90°,AD=4, AB 2CD 6 ,E 是边
(第 25 题图 1)
(第 25 题图)
1
2018 学年上海市各区一模考第 25 题
(黄浦)在 ABC 中,ACB 90 ,BC 3 , AC 4 ,点 O 是 AB 的中点,点 D 是边 AC
上一点, DE BD ,交 BC 的延长线于点 E , OD DF ,交 BC 边于点 F ,过点 E 作
2018 学年上海市各区一模考第 25 题
(徐汇)已知:在梯形 ABCD 中,AD//BC,AC=BC=10, cosACB 4 ,点 E 在对角线 5
AC 上(不与点 A、C 重合), EDC ACB ,DE 的延长线与射线 CB 交于点 F,设 AD 的 长为 x.
(1)如图 1,当 DF BC 时,求 AD 的长; (2)设 EC 的长为 y,求 y 关于 x 的函数解析式,并直接写出定义域; (3)当△DFC 是等腰三角形时,求 AD 的长.
的三角比的式子表示).
A
F
H
A
F
O
B
G
C
D
第 25 题图
B
O
E
M
C
D
第 25 题备用图
10
2018 学年上海市各区一模考第 25 题
(普陀)25.(本题满分 14 分) 如图 11,点 O 在线段 AB 上, AO 2OB 2a ,BOP 60 ,点 C 是射线 OP 上的一个动 点. (1)如图 11①,当 ACB 90 , OC 2 ,求 a 的值; (2)如图 11②,当 AC=AB 时,求 OC 的长(用含 a 的代数式表示); (3)在第(2)题的条件下,过点 A 作 AQ∥BC,并使∠QOC=∠B,求 AQ : OQ 的值.
