统计学(第四版)考试题贾俊平高等教育出版社
统计学(贾俊平,第四版)第五章习题答案

《统计原理》第五章练习题答案5.1 (1)平均分数是范围在0-100之间的连续变量,Ω=[0,100](2)已经遇到的绿灯次数是从0开始的任意自然数,Ω=N(3)之前生产的产品中可能无次品也可能有任意多个次品,Ω=[10,11,12,13…….]5.2 设订日报的集合为A ,订晚报的集合为B ,至少订一种报的集合为A ∪B ,同时订两种报的集合为A ∩B 。
P(A ∩B)=P(A)+ P(B)-P(A ∪B)=0.5+0.65-0.85=0.35.3 P(A ∪B)=1/3,P(A ∩B )=1/9, P(B)= P(A ∪B)- P(A ∩B )=2/95.4 P(AB)= P(B)P(A ∣B)=1/3*1/6=1/18 P(A ∪B )=P(B A )=1- P(AB)=17/18 P(B )=1- P(B)=2/3 P(A B )=P(A )+ P(B )- P(A ∪B )=7/18 P(A ∣B )= P(B A )/P(B )=7/125.5 设甲发芽为事件A ,乙发芽为事件B 。
(1)由于是两批种子,所以两个事件相互独立,所以有:P(AB)= P(B)P(B)=0.56(2)P(A ∪B)=P(A)+P(B)-P(A ∩B)=0.94(3)P(A B )+ P(B A )= P(A)P(B )+P(B)P(A )=0.385.6 设合格为事件A ,合格品中一级品为事件BP(AB)= P(A)P(B ∣A)=0.96*0.75=0.725.7 设前5000小时未坏为事件A ,后5000小时未坏为事件B 。
P(A)=1/3,P(AB)=1/2, P(B ∣A)= P(AB)/ P(A)=2/35.8 设职工文化程度小学为事件A ,职工文化程度初中为事件B ,职工文化程度高中为事件C ,职工年龄25岁以下为事件D 。
P(A)=0.1 P(B)=0.5, P(C)=0.4P(D ∣A)=0.2, P(D ∣B)=0.5, P(D ∣C)=0.7P(A ∣D)=2/55)C P(C)P(D )B P(B)P(D )A P(A)P(D )A P(A)P(D =++同理P(B ∣D)=5/11, P(C ∣D)=28/555.9 设次品为D ,由贝叶斯公式有:P(A ∣D)=)C P(C)P(D )B P(B)P(D )A P(A)P(D )A P(A)P(D ++=0.249同理P(B ∣D)=0.1125.10 由二项式分布可得:P (x=0)=0.25, P (x=1)=0.5, P (x=2)=0.255.11 (1) P (x=100)=0.001, P (x=10)=0.01, P (x=1)=0.2, P (x=0)=0.789(2)E(X)=100*0.001+10*0.01+1*0.2=0.45.13 答对至少四道题包含两种情况,对四道错一道,对五道。
统计学第四版答案(贾俊平)知识分享

统计学第四版答案(贾俊平)请举出统计应用的几个例子:1、用统计识别作者:对于存在争议的论文,通过统计量推出作者2、用统计量得到一个重要发现:在不同海域鳗鱼脊椎骨数量变化不大,推断所有各个不同海域内的鳗鱼是由海洋中某公共场所繁殖的3、挑战者航天飞机失事预测请举出应用统计的几个领域:1、在企业发展战略中的应用2、在产品质量管理中的应用3、在市场研究中的应用④在财务分析中的应用⑤在经济预测中的应用你怎么理解统计的研究内容:1、统计学研究的基本内容包括统计对象、统计方法和统计规律。
2、统计对象就是统计研究的课题,称谓统计总体。
3、统计研究方法主要有大量观察法、数量分析法、抽样推断法、实验法等。
④统计规律就是通过大量观察和综合分析所揭示的用数量指标反映的客观现象的本质特征和发展规律。
举例说明分类变量、顺序变量和数值变量:分类变量:表现为不同类别的变量称为分类变量,如“性别”表现为“男”或“女”,“企业所属的行业”表现为“制造业”、“零售业”、“旅游业”等,“学生所在的学院”可能是“商学院”、“法学院”等顺序变量:如果类别有一定的顺序,这样的分类变量称为顺序变量,如考试成绩按等级分为优、良、中、及格、不及格,一个人对事物的态度分为赞成、中立、反对。
这里的“考试成绩等级”、“态度”等就是顺序变量。
数值变量:可以用数字记录其观察结果,这样的变量称为数值变量,如“企业销售额”、“生活费支出”、“掷一枚骰子出现的点数”。
定性数据和定量数据的图示方法各有哪些:1、定性数据的图示:条形图、帕累托图、饼图、环形图2、定量数据的图示:a、分组数据看分布:直方图b、未分组数据看分布:茎叶图、箱线图、垂线图、误差图c、两个变量间的关系:散点图d、比较多个样本的相似性:雷达图和轮廓图直方图与条形图有何区别:1、条形图中的每一个矩形表示一个类别,其宽度没有意义,而直方图的宽度则表示各组的组距。
2、由于分组数据具有连续性,直方图的各矩形通常是连续排列,而条形图则是分开排列。
统计学第四版贾俊平人大-回归与时间序列stata

回归分析与时间序列一、一元线性回归11。
1 (1)编辑数据集,命名为linehuigui1.dat输入命令scatter cost product,xlabel(#10,grid) ylabel(#10,grid),得到如下散点图,可以看到,产量和生产费用是正线性相关的关系。
(2)输入命令regcost product,得到如下图:可得线性函数(product为自变量,cost为因变量):y=0。
4206832x+124。
15,即β0=124。
15,β1=0。
4206832(3)对相关系数的显著性进行检验,可输入命令pwcorr cost product,sig star (.05) print(。
05),得到下图:可见,在α=0。
05的显著性水平下,P=0。
0000<α=0。
05,故拒绝原假设,即产量和生产费用之间存在显著的正相关性。
11。
2 (1)编辑数据集,命名为linehuigui2。
dat输入命令scatterfenshu time,xlabel(#4, grid) ylabel(#4,grid),得到如下散点图,可以看到,分数和复习时间是正线性相关的关系。
2)输入命令cor fenshu time计算相关系数,得下图:可见,r=0.8621,可见分数和复习时间之间存在高度的正相关性。
11.3 (1)(2)对于线性回归方程y=10-0。
5x,其中β0=10,表示回归直线的截距为10;β1=—0.5,表示x变化一单位引起y的变化为—0.5。
(3)x=6时,E(y)=10-0.5*6=7.11.4(1)R2=SSRSST =SSRSSR+SSE=3636+4=0.9,判定系数R2测度了回归直线对观测数据的拟合程度,即在分数的变差中,有90%可以由分数与复习时间之间的线性关系解释,或者说,在分数取值的变动中,有90%由复习时间决定。
可见,两者之间有很强的线性关系.(2)估计标准误差S e=√SSEn−2=√418−2=0.25分,即根据复习时间来估计分数时,平均的估计误差为0.25分.11.5 (1)编辑数据集,命名为linehuigui3。
贾俊平第四版统计学-第四章-习题

第四章习题一、选择题1. 一组数据中出现频数最多的变量值称为()。
A.众数B.中位数C.四分位数D.均值2.一组数据排序后处于中间位置上的变量值称为()。
A.众数B.中位数C.四分位数D.均值3. n个变量值乘积的n次方根称为()。
A.众数B.中位数C.四分位数D.几何平均数4. 非众数组的频数占总频数的比率称为()。
A.异众比率B.离散系数C.平均差D.标准差5. 一组数据的最大值与最小值之差称为()。
A.平均差B.标准差C.极差D.四分位差6. 如果一个数据的标准分数是-2,表明该数据()。
A.比平均数高出2个标准差B.比平均数低2个标准差C.等于2倍的平均数D.等于2倍的标准差7. 一组数据的标准分数,其()。
A.均值为1,方差为0 B.均值为0,方差为1C.均值为0,方差为0 D.均值为1,方差为18. 经验法则表明,当一组数据对称分布式,在均值加减1个标准差的范围内大约有()。
A.68%的数据B.95%的数据C.99%的数据D.100%的数据9. 离散系数的主要用途是()。
A.反映一组数据的离散程度B.反映一组数据的平均水平C.比较多组数据的离散程度D.比较多组数据的平均水平10. 两组数据相比较()。
A.标准差大的离散程度也大B.标准差大的离散程度也小C.离散系数大的离散程度也大D.离散系数大的离散程度也小11. 某大学经济管理学院有1200名学生,法学院有800名学生,医学院有320名学生,理学院有200名学生。
在上面的描述中,众数是()。
A.1200 B.经济管理学院C.200 D.理学院12. 对于分类数据,测度其离散程度使用的统计量主要是()。
A.众数B.异众比率C.标准差D.均值13. 对于右偏分布,均值、中位数和众数之间的关系是()。
A.均值>中位数>众数B.中位数>均值>众数C.众数>中位数>均值D.众数>均值>中位数14. 在某行业中随即抽取10家企业,第一季度的利润额(单位:万元)分别为72,63.1,54.7,54.3,29,26.9,25,23.9,23,20。
统计学第四版答案(贾俊平)

统计学第四版答案(贾俊平)第1章统计和统计数据1.1 指出下⾯的变量类型。
(1)年龄。
(2)性别。
(3)汽车产量。
(4)员⼯对企业某项改⾰措施的态度(赞成、中⽴、反对)。
(5)购买商品时的⽀付⽅式(现⾦、信⽤卡、⽀票)。
详细答案:(1)数值变量。
(2)分类变量。
(3)数值变量。
(4)顺序变量。
(5)分类变量。
1.2 ⼀家研究机构从IT从业者中随机抽取1000⼈作为样本进⾏调查,其中60%回答他们的⽉收⼊在5000元以上,50%的⼈回答他们的消费⽀付⽅式是⽤信⽤卡。
(1)这⼀研究的总体是什么?样本是什么?样本量是多少?(2)“⽉收⼊”是分类变量、顺序变量还是数值变量?(3)“消费⽀付⽅式”是分类变量、顺序变量还是数值变量?详细答案:(1)总体是“所有IT从业者”,样本是“所抽取的1000名IT从业者”,样本量是1000。
(2)数值变量。
(3)分类变量。
1.3 ⼀项调查表明,消费者每⽉在⽹上购物的平均花费是200元,他们选择在⽹上购物的主要原因是“价格便宜”。
(1)这⼀研究的总体是什么?(2)“消费者在⽹上购物的原因”是分类变量、顺序变量还是数值变量?详细答案:(1)总体是“所有的⽹上购物者”。
(2)分类变量。
1.4 某⼤学的商学院为了解毕业⽣的就业倾向,分别在会计专业抽取50⼈、市场营销专业抽取30、企业管理20⼈进⾏调查。
(1)这种抽样⽅式是分层抽样、系统抽样还是整群抽样?(2)样本量是多少?详细答案:(1)分层抽样。
(2)100。
第3章⽤统计量描述数据为7.2分钟,标准差为1.97分钟,第⼆种排队⽅式的等待时间(单位:分钟)如下:5.56.6 6.7 6.87.1 7.3 7.4 7.8 7.8(1)计算第⼆种排队时间的平均数和标准差。
(2)⽐两种排队⽅式等待时间的离散程度。
(3)如果让你选择⼀种排队⽅式,你会选择哪⼀种?试说明理由。
详细答案:(1)(岁);(岁)。
(2);。
第⼀中排队⽅式的离散程度⼤。
统计学贾俊平-第四版课后习题答案

3.3 某百货公司连续40天的商品销售额如下:单位:万元41 25 29 47 38 34 30 38 43 40 46 36 45 37 37 36 45 43 33 44 35 28 46 34 30 37 44 26 38 44 42363737493942323635要求:根据上面的数据进行适当的分组,编制频数分布表,并绘制直方图. 1、确定组数:()lg 40lg() 1.60206111 6.32lg(2)lg 20.30103n K =+=+=+=,取k=62、确定组距:组距=< 最大值 - 最小值>÷ 组数=〔49-25〕÷6=4,取5(1) 对这个年龄分布作直方图;(2) 从直方图分析成人自学考试人员年龄分布的特点. 解:〔1〕制作直方图:将上表复制到Excel 表中,点击:图表向导→柱形图→选择子图表类型→完成.即得到如下的直方图:<见Excel 练习题2.6>〔2〕年龄分布的特点:自学考试人员年龄的分布为右偏. 解:3.12 甲乙两个班各有40名学生,期末统计学考试成绩的分布如下:要求:<1>根据上面的数据,画出两个班考试成绩的对比条形图和环形图.3.14 已知1995—20##我国的国内生产总值数据如下<按当年价格计算>:<2>绘制第一、二、三产业国内生产总值的线图.4.1 一家汽车零售店的10名销售人员5月份销售的汽车数量<单位:台>排序后如下:2 4 7 10 10 10 12 12 14 15要求:〔1〕计算汽车销售量的众数、中位数和平均数.<2>根据定义公式计算四分位数.<3>计算销售量的标准差.<4>说明汽车销售量分布的特征.解:Statistics汽车销售数量N Valid 10Missing 0Mean 9.60Median 10.00Mode 10Std. Deviation 4.169Percentiles 25 6.2550 10.0075 12.504.3 某银行为缩短顾客到银行办理业务等待的时间.准备采用两种排队方式进行试验:一种是所有颐客都进入一个等待队列:另—种是顾客在三千业务窗口处列队3排等待.为比较哪种排队方式使顾客等待的时间更短.两种排队方式各随机抽取9名顾客.得到第一种排队方式的平均等待时间为7.2分钟,标准差为1.97分钟.第二种排队方式的等待时间<单位:分钟>如下:5.5 6.6 6.7 6.8 7.1 7.3 7.4 7.8 7.8要求:<1>画出第二种排队方式等待时间的茎叶图.第二种排队方式的等待时间<单位:分钟> Stem-and-Leaf PlotFrequency Stem & Leaf1.00 Extremes <=<5.5>3.00 6 . 6783.00 7 . 1342.00 7 . 88Stem width: 1.00Each leaf: 1 case<s><2>计算第二种排队时间的平均数和标准差.Mean7Std. Deviation0.714143Variance0.51<3>比较两种排队方式等待时间的离散程度.第二种排队方式的离散程度小.<4>如果让你选择一种排队方式,你会选择哪—种?试说明理由.选择第二种,均值小,离散程度小.要求:<1>计算120家企业利润额的平均数和标准差.<2>计算分布的偏态系数和峰态系数.解:Statistics企业利润组中值Mi〔万元〕N Valid 120Missing 0Mean 426.6667Std. Deviation 116.48445Skewness 0.208Std. Error of Skewness 0.221Kurtosis -0.625Std. Error of Kurtosis 0.4384.7 为研究少年儿童的成长发育状况,某研究所的一位调查人员在某城市抽取100名7~17岁的少年儿童作为样本,另一位调查人员则抽取了1 000名7~17岁的少年儿童作为样本.请回答下面的问题,并解释其原因.<1>两位调查人员所得到的样本的平均身高是否相同?如果不同,哪组样本的平均身高较大?<2>两位调查人员所得到的样本的标准差是否相同?如果不同,哪组样本的标准差较大?<3>两位调查人员得到这l 100名少年儿童身高的最高者或最低者的机会是否相同?如果不同,哪位调查研究人员的机会较大?解:〔1〕不一定相同,无法判断哪一个更高,但可以判断,样本量大的更接近于总体平均身高.〔2〕不一定相同,样本量少的标准差大的可能性大.〔3〕机会不相同,样本量大的得到最高者和最低者的身高的机会大.4.8 一项关于大学生体重状况的研究发现.男生的平均体重为60kg,标准差为5kg;女生的平均体重为50kg,标准差为5kg.请回答下面的问题:<1>是男生的体重差异大还是女生的体重差异大?为什么?女生,因为标准差一样,而均值男生大,所以,离散系数是男生的小,离散程度是男生的小.<2>以磅为单位<1ks=2.2lb>,求体重的平均数和标准差.都是各乘以2.21,男生的平均体重为60kg×2.21=132.6磅,标准差为5kg×2.21=11.05磅;女生的平均体重为50kg×2.21=110.5磅,标准差为5kg×2.21=11.05磅.<3>粗略地估计一下,男生中有百分之几的人体重在55kg一65kg之间?计算标准分数:Z1=x xs-=55605-=-1;Z2=x xs-=65605-=1,根据经验规则,男生大约有68%的人体重在55kg一65kg之间.<4>粗略地估计一下,女生中有百分之几的人体重在40kg~60kg之间?计算标准分数:Z1=x xs-=40505-=-2;Z2=x xs-=60505-=2,根据经验规则,女生大约有95%的人体重在40kg一60kg之间.4.9 一家公司在招收职员时,首先要通过两项能力测试.在A项测试中,其平均分数是100分,标准差是15分;在B项测试中,其平均分数是400分,标准差是50分.一位应试者在A项测试中得了115分,在B项测试中得了425分.与平均分数相比,该应试者哪一项测试更为理想?解:应用标准分数来考虑问题,该应试者标准分数高的测试理想.Z A=x xs-=11510015-=1;Z B=x xs-=42540050-=0.5因此,A项测试结果理想.4.10 一条产品生产线平均每天的产量为3 700件,标准差为50件.如果某一天的产量低于或高于平均产量,并落人士2个标准差的X围之外,就认为该生产线"失去控制〞.下面是4.13 在金融证券领域,一项投资的预期收益率的变化通常用该项投资的风险来衡量.预期收益率的变化越小,投资风险越低;预期收益率的变化越大,投资风险就越高.下面的两个直方图,分别反映了200种商业类股票和200种高科技类股票的收益率分布.在股票市场上,高收益率往往伴随着高风险.但投资于哪类股票,往往与投资者的类型有一定关系.<1>你认为该用什么样的统计量来反映投资的风险? 标准差或者离散系数.<2>如果选择风险小的股票进行投资,应该选择商业类股票还是高科技类股票? 选择离散系数小的股票,则选择商业股票.<3>如果进行股票投资,你会选择商业类股票还是高科技类股票? 考虑高收益,则选择高科技股票;考虑风险,则选择商业股票. 解:〔1〕方差或标准差;〔2〕商业类股票;〔3〕〔略〕.7.1 从一个标准差为5的总体中抽出一个容量为40的样本,样本均值为25.(1) 样本均值的抽样标准差x σ等于多少?(2) 在95%的置信水平下,允许误差是多少?解:已知总体标准差σ=5,样本容量n =40,为大样本,样本均值x =25, 〔1〕样本均值的抽样标准差x σσ5=0.7906 〔2〕已知置信水平1-α=95%,得 α/2Z =1.96,于是,允许误差是E =α/2σZ =1.96×0.7906=1.5496. 7.2 某快餐店想要估计每位顾客午餐的平均花费金额.在为期3周的时间里选取49名顾客组成了一个简单随机样本.<1>假定总体标准差为15元,求样本均值的抽样标准误差.x σ===2.143 <2>在95%的置信水平下,求边际误差.x x t σ∆=⋅,由于是大样本抽样,因此样本均值服从正态分布,因此概率度t=2z α因此,x x t σ∆=⋅2x z ασ=⋅0.025x z σ=⋅=1.96×2.143=4.2 <3>如果样本均值为120元,求总体均值 的95%的置信区间. 置信区间为:(),x x x x -∆+∆=()120 4.2,120 4.2-+=〔115.8,124.2〕7.107.11 某企业生产的袋装食品采用自动打包机包装,每袋标准重量为l00g.现从某天生产的一每包重量〔g 〕 包数 96~98 98~100 100~102 102~104 104~106 2 3 34 7 4 合计50<1>确定该种食品平均重量的95%的置信区间. 解:大样本,总体方差未知,用z 统计量样本均值=101.4,样本标准差s=1.829 置信区间:1α-=0.95,z α=0.025z =1.96=101.4 1.96 1.965050⎛-+ ⎝=〔100.89,101.91〕 <2>如果规定食品重量低于l00g 属于不合格,确定该批食品合格率的95%的置信区间.解:总体比率的估计大样本,总体方差未知,用z 统计量 样本比率=〔50-5〕/50=0.9 置信区间:1α-=0.95,z α=0.025z =1.96=()()0.910.90.910.90.9 1.96,0.9 1.965050⎛-- -+ ⎝=〔0.8168,0.9832〕 7.13 一家研究机构想估计在网络公司工作的员工每周加班的平均时间,为此随机抽取了18个员工.得到他们每周加班的时间数据如下<单位:小时>: 6 321 817 1220 117 90 218 2516 1529 16置信区间.解:小样本,总体方差未知,用t 统计量均值=13.56,样本标准差s=7.801 置信区间:1α-=0.90,n=18,()21t n α-=()0.0517t =1.7369=13.56 1.7369 1.7369⎛-+ ⎝=〔10.36,16.75〕 7.15 在一项家电市场调查中.随机抽取了200个居民户,调查他们是否拥有某一品牌的电视机.其中拥有该品牌电视机的家庭占23%.求总体比例的置信区间,置信水平分别为90%和95%.解:总体比率的估计大样本,总体方差未知,用z 统计量 样本比率=0.23 置信区间:1α-=0.90,z α=0.025z =1.645=0.23 1.645 1.645⎛ -+ ⎝ =〔0.1811,0.2789〕1α-=0.95,z α=0.025z =1.96=0.23 1.96 1.96⎛ -+ ⎝=〔0.1717,0.2883〕7.28 某超市想要估计每个顾客平均每次购物花费的金额.根据过去的经验,标准差大约为120元,现要求以95%的置信水平估计每个顾客平均购物金额的置信区间,并要求边际误差不超过20元,应抽取多少个顾客作为样本? 解:2222xz n ασ⋅=∆,1α-=0.95,2z α=0.025z =1.96,2222xz n ασ⋅=∆2221.9612020⨯==138.3,取n=139或者140,或者150.8. 18.2 一种元件,要求其使用寿命不得低于700小时.现从一批这种元件中随机抽取36件,测得其平均寿命为680小时.已知该元件寿命服从正态分布,σ=60小时,试在显著性水平0.05下确定这批元件是否合格. 解:H 0:μ≥700;H 1:μ<700已知:x =680 σ=60由于n=36>30,大样本,因此检验统计量:x z==-2 当α=0.05,查表得z α=1.645.因为z <-z α,故拒绝原假设,接受备择假设,说明这批产品不合格.8.4 糖厂用自动打包机打包,每包标准重量是100千克.每天开工后需要检验一次打包机工作是否正常.某日开工后测得9包重量<单位:千克>如下:99.3 98.7 100.5 101.2 98.3 99.7 99.5 102.1 100.5已知包重服从正态分布,试检验该日打包机工作是否正常<a =0.05>? 解:H 0:μ=100;H 1:μ≠100经计算得:x =99.9778 S =1.21221 检验统计量:x t =-0.055 当α=0.05,自由度n -1=9时,查表得()9t α=2.262.因为t <2t α,样本统计量落在接受区域,故接受原假设,拒绝备择假设,说明打包机工作正常.8.5 某种大量生产的袋装食品,按规定不得少于250克.今从一批该食品中任意抽取50袋,发现有6袋低于250克.若规定不符合标准的比例超过5%就不得出厂,问该批食品能否出厂<a =0.05>?解:解:H 0:π≤0.05;H 1:π>0.05已知: p =6/50=0.12 检验统计量:Z ==2.271当α=0.05,查表得z α=1.645.因为z >z α,样本统计量落在拒绝区域,故拒绝原假设,接受备择假设,说明该批食品不能出厂.8.7 某种电子元件的寿命x<单位:小时>服从正态分布.现测得16只元件的寿命如下: 159 280 101 212 224 379 179 264 222 362 168 250 149 260 485 170问是否有理由认为元件的平均寿命显著地大于225小时<a =0.05>? 解:H 0:μ≤225;H 1:μ>225经计算知:x =241.5 s =98.726 检验统计量:x t=0.669 当α=0.05,自由度n -1=15时,查表得()15t α=1.753.因为t <t α,样本统计量落在接受区域,故接受原假设,拒绝备择假设,说明元件寿命没有显著大于225小时. 9.19.2 9.3 9.410.210.410.7 某企业准备用三种方法组装一种新的产品,为确定哪种方法每小时生产的产品数量最多,随机抽取了30名工人,并指定每个人使用其中的一种方法.通过对每个工人生产的产品数进行方差分析得到下面的结果;<1>完成上面的方差分析表.<2>若显著性水平a=0.05,检验三种方法组装的产品数量之间是否有显著差异?解:〔2〕P=0.025>a=0.05,没有显著差异.11.311.411.9 某汽车生产商欲了解广告费用<x>对销售量<y>的影响,收集了过去12年的有关数据.通过计算得到下面的有关结果:方差分析表要求:<1>完成上面的方差分析表.<2>汽车销售量的变差中有多少是由于广告费用的变动引起的?<3>销售量与广告费用之间的相关系数是多少?<4>写出估计的回归方程并解释回归系数的实际意义.<5>检验线性关系的显著性<a=0.05>.解:〔2〕R2=0.9756,汽车销售量的变差中有97.56%是由于广告费用的变动引起的.〔3〕r=0.9877.〔4〕回归系数的意义:广告费用每增加一个单位,汽车销量就增加1.42个单位.〔5〕回归系数的检验:p=2.17E—09<α,回归系数不等于0,显著.回归直线的检验:p=2.17E—09<α,回归直线显著.11.1013.1 下表是1981年—1999年国家财政用于农业的支出额数据年份支出额〔亿元〕年份支出额〔亿元〕1981 110.21 1991 347.571982 120.49 1992 376.021983 132.87 1993 440.451984 141.29 1994 532.981985 153.62 1995 574.931986 184.2 1996 700.431987 195.72 1997 766.391988 214.07 1998 1154.761989 265.94 1999 1085.761990 307.84〔1〕绘制时间序列图描述其形态.〔2〕计算年平均增长率.〔3〕根据年平均增长率预测20##的支出额.详细答案:〔1〕时间序列图如下:从时间序列图可以看出,国家财政用于农业的支出额大体上呈指数上升趋势.〔2〕年平均增长率为:.〔3〕.13.2 下表是1981年—20##我国油彩油菜籽单位面积产量数据〔单位:kg / hm2〕年份单位面积产量年份单位面积产量1981 1451 1991 12151982 1372 1992 12811983 1168 1993 13091984 1232 1994 12961985 1245 1995 14161986 1200 1996 13671987 1260 1997 14791988 1020 1998 12721989 1095 1999 14691990 1260 2000 1519〔1〕绘制时间序列图描述其形态.〔2〕用5期移动平均法预测20##的单位面积产量.〔3〕采用指数平滑法,分别用平滑系数a=0.3和a=0.5预测20##的单位面积产量,分析预测误差,说明用哪一个平滑系数预测更合适?详细答案:〔1〕时间序列图如下:〔2〕20##的预测值为:| 〔3〕由Excel输出的指数平滑预测值如下表:年份单位面积产量指数平滑预测a=0.3 误差平方指数平滑预测a=0.5误差平方1981 14511982 1372 1451.0 6241.0 1451.0 6241.0 1983 1168 1427.3 67236.5 1411.5 59292.3 1984 1232 1349.5 13808.6 1289.8 3335.1 1985 1245 1314.3 4796.5 1260.9 252.0 1986 1200 1293.5 8738.5 1252.9 2802.4 1987 1260 1265.4 29.5 1226.5 1124.3 1988 1020 1263.8 59441.0 1243.2 49833.6 1989 1095 1190.7 9151.5 1131.6 1340.8 1990 1260 1162.0 9611.0 1113.3 21518.4 1991 1215 1191.4 558.1 1186.7 803.51992 1281 1198.5 6812.4 1200.8 6427.7 1993 1309 1223.2 7357.6 1240.9 4635.8 1994 1296 1249.0 2213.1 1275.0 442.8 1995 1416 1263.1 23387.7 1285.5 17035.9 1996 1367 1308.9 3369.9 1350.7 264.4 1997 1479 1326.4 23297.7 1358.9 14431.3 1998 1272 1372.2 10031.0 1418.9 21589.8 1999 1469 1342.1 16101.5 1345.5 15260.3 2000 1519 1380.2 19272.1 1407.2 12491.7 合计——291455.2 —239123.0 20##a=0.3时的预测值为:a=0.5时的预测值为:比较误差平方可知,a=0.5更合适.13.3 下面是一家旅馆过去18个月的营业额数据月份营业额〔万元〕月份营业额〔万元〕1 295 10 4732 283 11 4703 322 12 4814 355 13 4495 286 14 5446 379 15 6017 381 16 5878 431 17 6449 424 18 660〔1〕用3期移动平均法预测第19个月的营业额.〔2〕采用指数平滑法,分别用平滑系数a=0.3、a=0.4和a=0.5预测各月的营业额,分析预测误差,说明用哪一个平滑系数预测更合适?〔3〕建立一个趋势方程预测各月的营业额,计算出估计标准误差.详细答案:〔1〕第19个月的3期移动平均预测值为:〔2〕月份营业额预测a=0.3误差平方预测a=0.4误差平方预测a=0.5误差平方1 2952 283 295.0 144.0 295.0 144.0 295.0 144.03 322 291.4 936.4 290.2 1011.2 289.0 1089.04 355 300.6 2961.5 302.9 2712.3 305.5 2450.35 286 316.9 955.2 323.8 1425.2 330.3 1958.16 379 307.6 5093.1 308.7 4949.0 308.1 5023.37 381 329.0 2699.4 336.8 1954.5 343.6 1401.68 431 344.6 7459.6 354.5 5856.2 362.3 4722.39 424 370.5 2857.8 385.1 1514.4 396.6 748.510 473 386.6 7468.6 400.7 5234.4 410.3 3928.711 470 412.5 3305.6 429.6 1632.9 441.7 803.112 481 429.8 2626.2 445.8 1242.3 455.8 633.513 449 445.1 15.0 459.9 117.8 468.4 376.914 544 446.3 9547.4 455.5 7830.2 458.7 7274.815 601 475.6 15724.5 490.9 12120.5 501.4 9929.416 587 513.2 5443.2 534.9 2709.8 551.2 1283.317 644 535.4 11803.7 555.8 7785.2 569.1 5611.718 660 567.9 8473.4 591.1 4752.7 606.5 2857.5 合计——87514.7—62992.5—50236由Excel输出的指数平滑预测值如下表:a=0.3时的预测值:,误差均方=87514.7.a=0.4时的预测值:,误差均方=62992.5..a=0.5时的预测值:,误差均方=50236.比较各误差平方可知,a=0.5更合适.〔3〕根据最小二乘法,利用Excel输出的回归结果如下:回归统计Multiple R 0.9673R Square 0.9356Adjusted R Square 0.9316标准误差31.6628观测值18方差分析df SS MS F Significance F回归分析 1 232982.5 232982.5 232.3944 5.99E-11残差16 16040.49 1002.53总计17 249022.9Coefficients 标准误差t Stat P-value Lower 95% Upper 95% Intercept 239.73203 15.57055 15.3965 5.16E-11 206.7239 272.7401 X Variable 1 21.928793 1.438474 15.24449 5.99E-11 18.87936 24.97822.估计标准误差.14.114.2。
统计学第四版答案(贾俊平)

请举出统计应用的几个例子:1、用统计识别作者:对于存在争议的论文,通过统计量推出作者2、用统计量得到一个重要发现:在不同海域鳗鱼脊椎骨数量变化不大,推断所有各个不同海域内的鳗鱼是由海洋中某公共场所繁殖的3、挑战者航天飞机失事预测请举出应用统计的几个领域:1、在企业发展战略中的应用2、在产品质量管理中的应用3、在市场研究中的应用④在财务分析中的应用⑤在经济预测中的应用你怎么理解统计的研究内容:1、统计学研究的基本内容包括统计对象、统计方法和统计规律。
2、统计对象就是统计研究的课题,称谓统计总体。
3、统计研究方法主要有大量观察法、数量分析法、抽样推断法、实验法等。
④统计规律就是通过大量观察和综合分析所揭示的用数量指标反映的客观现象的本质特征和发展规律。
举例说明分类变量、顺序变量和数值变量:分类变量:表现为不同类别的变量称为分类变量,如“性别”表现为“男”或“女”,“企业所属的行业”表现为“制造业”、“零售业”、“旅游业”等,“学生所在的学院”可能是“商学院”、“法学院”等顺序变量:如果类别有一定的顺序,这样的分类变量称为顺序变量,如考试成绩按等级分为优、良、中、及格、不及格,一个人对事物的态度分为赞成、中立、反对。
这里的“考试成绩等级”、“态度”等就是顺序变量。
数值变量:可以用数字记录其观察结果,这样的变量称为数值变量,如“企业销售额”、“生活费支出”、“掷一枚骰子出现的点数”。
定性数据和定量数据的图示方法各有哪些:1、定性数据的图示:条形图、帕累托图、饼图、环形图2、定量数据的图示:a、分组数据看分布:直方图b、未分组数据看分布:茎叶图、箱线图、垂线图、误差图c、两个变量间的关系:散点图d、比较多个样本的相似性:雷达图和轮廓图直方图与条形图有何区别:1、条形图中的每一个矩形表示一个类别,其宽度没有意义,而直方图的宽度则表示各组的组距。
2、由于分组数据具有连续性,直方图的各矩形通常是连续排列,而条形图则是分开排列。
贾俊平第四版统计学-第十一章一元线性回归练习答案

第十一章一元线性回归练习题答案二.填空题 1. 不能;因为该相关系数为样本计算出的相关系数,它的大小受样本数据波动的影响,它是否显著尚需检验;t 检验;2.图1;不能;因为图1反映的是线性相关关系,图2反映的是非线性性相关关系,相关系数只能反映线性相关变量间的相关性的强弱,不能反映非线性相关性的强弱。
三.计算题1.(1) SSR 的自由度是1,SSE 的自由度是18。
(2)2418/6080220/1/==-=SSE SSR F(3)判定系数%14.57140802===SST SSR R 在y 的总变差中,由57.14%的变差是由于x 的变动说引起的。
(4)7559.05714.02-=-=-=R r相关系数为-0.7559。
(5)线性关系显著和:线性关系不显著和y x y x H 10H :因为414.424=>=αF F,所以拒绝原假设,x 与y 之间的线性关系显著。
2.(1)方差分析表df SS MS F Significance F回归分析 1 425 425 85 0.017 残差 15 75 5 - - 总计16500---(2)判定系数%8585.05004252====SST SSR R表明在维护费用的变差中,有85%的变差可由使用年限来解释。
(3)9220.085.02===R r二者相关系数为0.9220,属于高度相关(4)x y248.1388.6ˆ+= 分布;显著。
的自由度为t n r n r t 2);12||2---=回归系数为1.248,表示每增加一个单位的产量,该行业的生产费用将平均增长1.248个单位。
(5)线性关系显著性检验:线性关系显著:生产费用和产量之间性关系不显著生产费用和产量之间线10:H H因为Significance F=0.017<05.0=α,所以线性关系显著。
(6)348.3120248.1388.6248.1388.6ˆ==⨯++=x y当产量为10时,生产费用为31.348万元。
2019年贾俊平_统计学_第四版_习题答案.doc

第1章绪论1.什么是统计学?怎样理解统计学与统计数据的关系?2.试举出日常生活或工作中统计数据及其规律性的例子。
3..一家大型油漆零售商收到了客户关于油漆罐分量不足的许多抱怨。
因此,他们开始检查供货商的集装箱,有问题的将其退回。
最近的一个集装箱装的是2 440加仑的油漆罐。
这家零售商抽查了50罐油漆,每一罐的质量精确到4位小数。
装满的油漆罐应为4.536 kg。
要求:(1)描述总体;(2)描述研究变量;(3)描述样本;(4)描述推断。
答:(1)总体:最近的一个集装箱内的全部油漆;(2)研究变量:装满的油漆罐的质量;(3)样本:最近的一个集装箱内的50罐油漆;(4)推断:50罐油漆的质量应为4.536×50=226.8 kg。
4.“可乐战”是描述市场上“可口可乐”与“百事可乐”激烈竞争的一个流行术语。
这场战役因影视明星、运动员的参与以及消费者对品尝试验优先权的抱怨而颇具特色。
假定作为百事可乐营销战役的一部分,选择了1000名消费者进行匿名性质的品尝试验(即在品尝试验中,两个品牌不做外观标记),请每一名被测试者说出A品牌或B品牌中哪个口味更好。
要求:(1)描述总体;(2)描述研究变量;(3)描述样本;(4)一描述推断。
答:(1)总体:市场上的“可口可乐”与“百事可乐”(2)研究变量:更好口味的品牌名称;(3)样本:1000名消费者品尝的两个品牌(4)推断:两个品牌中哪个口味更好。
第2章统计数据的描述——练习题●1.为评价家电行业售后服务的质量,随机抽取了由100家庭构成的一个样本。
服务质量的等级分别表示为:A.好;B.较好;C.一般;D.差;E.较差。
调查结果如下:B EC C AD C B A ED A C B C DE C E EA DBC C A ED C BB ACDE A B D D CC B C ED B C C B CD A C B C DE C E BB EC C AD C B A EB ACDE A B D D CA DBC C A ED C BC B C ED B C C B C(1) 指出上面的数据属于什么类型;(2)用Excel制作一张频数分布表;(3) 绘制一张条形图,反映评价等级的分布。
统计学(第四版)贾俊平 第八章 方差分析与实验设计 练习题答案
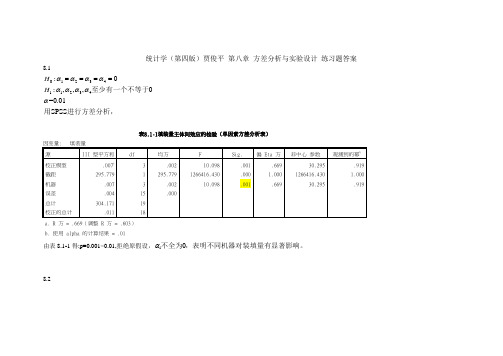
统计学(第四版)贾俊平 第八章 方差分析与实验设计 练习题答案8.10123411234:0:,,,0=0.01SPSS H H ααααααααα====至少有一个不等于用进行方差分析,表8.1-1填装量主体间效应的检验(单因素方差分析表)因变量: 填装量 源 III 型平方和df均方F Sig.偏 Eta 方非中心 参数观测到的幂b校正模型 .007a3 .002 10.098 .001 .669 30.295 .919 截距 295.7791 295.7791266416.430.000 1.000 1266416.4301.000 机器 .007 3 .002 10.098.001.66930.295.919误差 .004 15 .000总计 304.17119 校正的总计.01118a. R 方 = .669(调整 R 方 = .603)b. 使用 alpha 的计算结果 = .01由表8.1-1得:p=0.001<0.01,拒绝原假设,i 0α不全为,表明不同机器对装填量有显著影响。
8.201231123:0:,,0=0.05SPSS H H ααααααα===至少有一个不等于用进行方差分析,表8.2-1满意度评分主体间效应的检验(单因素方差分析表)因变量: 评分 源III 型平方和df 均方 F Sig.校正模型 29.610a2 14.805 11.756 .001 截距 975.156 1 975.156 774.324 .000 管理者 29.610 2 14.805 11.756.001误差 18.890 15 1.259总计 1061.000 18 校正的总计48.50017a. R 方 = .611(调整 R 方 = .559)由表8.2-1得:p=0.001<0.05,拒绝原假设,i 0α不全为,表明管理者水平不同会导致评分的显著差异。
8.301231123:0:,,0=0.05SPSS H H ααααααα===至少有一个不等于用进行方差分析,表8.3-1电池寿命主体间效应的检验(单因素方差分析表)因变量: 电池寿命 源III 型平方和df 均方 F Sig. 偏 Eta 方 非中心 参数 观测到的幂b校正模型 615.600a2 307.800 17.068 .000 .740 34.137 .997 截距 22815.000 1 22815.000 1265.157 .000 .991 1265.157 1.000 企业 615.600 2 307.800 17.068.000.74034.137.997误差 216.400 12 18.033总计 23647.000 15 校正的总计832.00014a. R 方 = .740(调整 R 方 = .697)b. 使用 alpha 的计算结果 = .05由表8.2-1得:p=0.001<0.05,拒绝原假设,i 0α不全为,表明3个企业生产的电池平均寿命之间存在显著差异。
统计学(第四版)贾俊平 第二章 部分练习题答案

统计学(第四版)贾俊平第二章部分练习题答案2.1 1表1 家电售后等级评价频数分布表评价等级频率百分比有效百分比累积百分比有效 A 14 14.0 14.0 14.0B 21 21.0 21.0 35.0C 32 32.0 32.0 67.0D 18 18.0 18.0 85.0E 15 15.0 15.0 100.0合计100 100.0 100.02.1.2图1 家电售后等级评价条形图等级分布较集中与C级,整体呈左偏正态分布。
2.1.3图2 家电售后等级评价帕累托图2.1.4图3 家电售后等级评价饼图评价等级中C级占大多数,BD级较少,AE级更少。
2.2.1表2 灯泡使用寿命频数分布表接收频率650 0660 2670 5680 6690 16700 26710 18720 12730 9740 3750 3其他02.2.2图4 灯泡使用寿命直方图灯泡使用寿命呈正态分布,大多集中于680—720。
2.2.3使用寿命 Stem-and-Leaf PlotFrequency Stem & Leaf1.00 Extremes (=<651)1.00 65 . 82.00 66 . 143.00 66 . 5683.00 67 . 1343.00 67 . 6797.00 68 . 11233347.00 68 . 555889913.00 69 . 001111222334413.00 69 . 55666778888998.00 70 . 0011223410.00 70 . 56667788896.00 71 . 0022337.00 71 . 56778894.00 72 . 01226.00 72 . 5678991.00 73 . 32.00 73 . 561.00 74 . 11.00 74 . 71.00 Extremes (>=749)Stem width: 10Each leaf: 1 case(s)图5 灯泡使用寿命茎叶图直方图和茎叶图都可以直观的看出灯泡使用寿命呈正态分布,大多集中于680—720.但是茎叶图保留了灯泡使用寿命的原始数据。
统计学第四版答案(贾俊平)

40 30 20 10 0
25
30
35
40
●4. 为了确定灯泡的使用寿命(小时) ,在一批灯泡中随机抽取 100 只进行测试,所得结果 如下: 700 706 708 668 706 694 688 701 716 715 729 710 692 690 689 671 728 712 694 693 691 736 683 718 719 722 681 697 747 689 685 707 685 691 695 674 699 696 702 683 709 708 685 658 682 651 741 717 691 690 706 698 698 673 698 733 684 692 661 666 700 749 713 712 705 707 735 696 710 708 676 683 718 701 665 698 722 727 702 692
● 2. 某行业管理局所属 40 个企业 2002 年的产品销售收入数据如下(单位:万元) : 152 124 129 116 100 103 92 95 127 104
105 119 114 115 87 103 118 142 135 125 117 108 105 110 107 137 120 136 117 108 97 88 123 115 119 138 112 146 113 126 (1)根据上面的数据进行适当的分组,编制频数分布表,并计算出累积频数和累积频率; (2)如果按规定:销售收入在 125 万元以上为先进企业,115 万~125 万元为良好企业, 105 万~115 万元为一般企业,105 万元以下为落后企业,按先进企业、良好企业、一般 企业、落后企业进行分组。 解 :(1)要求对销售收入的数据进行分组, 全部数据中,最大的为 152,最小的为 87,知数据全距为 152-87=65; 为便于计算和分析,确定将数据分为 6 组,各组组距为 10,组限以整 10 划分; 为使数据的分布满足穷尽和互斥的要求,注意到,按上面的分组方式,最小值 87 可能落在最小组之下,最大值 152 可能落在最大组之上,将最小组和最大组设计成开口形
统计学第四版(贾俊平)课后所有题答案很全期末考试必备

统计课后思考题答案第一章思考题1.1什么是统计学统计学是关于数据的一门学科,它收集,处理,分析,解释来自各个领域的数据并从中得出结论。
1.2解释描述统计和推断统计描述统计;它研究的是数据收集,处理,汇总,图表描述,概括与分析等统计方法。
推断统计;它是研究如何利用样本数据来推断总体特征的统计方法。
1.3统计学的类型和不同类型的特点统计数据;按所采用的计量尺度不同分;(定性数据)分类数据:只能归于某一类别姆鞘中褪荩嵌允挛锝蟹掷嗟慕峁荼硐治啾穑梦淖掷幢硎觯唬ǘㄐ允荩┧承蚴荩褐荒芄橛谀骋挥行蚶啾鸬姆鞘中褪荨K彩怯欣啾鸬模庑├啾鹗怯行虻摹#渴荩┦敌褪荩喊词殖叨炔饬康墓鄄熘担浣峁硐治咛宓氖怠?统计数据;按统计数据都收集方法分;观测数据:是通过调查或观测而收集到的数据,这类数据是在没有对事物人为控制的条件下得到的。
实验数据:在实验中控制实验对象而收集到的数据。
统计数据;按被描述的现象与实践的关系分;截面数据:在相同或相似的时间点收集到的数据,也叫静态数据。
时间序列数据:按时间顺序收集到的,用于描述现象随时间变化的情况,也叫动态数据。
1.4解释分类数据,顺序数据和数值型数据答案同 1.31.5举例说明总体,样本,参数,统计量,变量这几个概念对一千灯泡进行寿命测试,那么这千个灯泡就是总体,从中抽取一百个进行检测,这一百个灯泡的集合就是样本,这一千个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是参数,这一百个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是统计量,变量就是说明现象某种特征的概念,比如说灯泡的寿命。
1.6变量的分类变量可以分为分类变量,顺序变量,数值型变量。
变量也可以分为随机变量和非随机变量。
经验变量和理论变量。
1.7举例说明离散型变量和连续性变量离散型变量,只能取有限个值,取值以整数位断开,比如“企业数”连续型变量,取之连续不断,不能一一列举,比如“温度”。
1.8 统计应用实例人口普查,商场的名意调查等。
统计学课后习题答案第四版贾俊平

统计学课后习题答案-(第四版)-贾俊平《统计学》第四版 第四章练习题答案4.1 (1)众数:M 0=10; 中位数:中位数位置=n+1/2=5.5,M e =10;平均数:6.91096===∑n x x i(2)Q L 位置=n/4=2.5, Q L =4+7/2=5.5;Q U 位置=3n/4=7.5,Q U =12(3)2.494.1561)(2==-=∑-n i s x x(4)由于平均数小于中位数和众数,所以汽车销售量为左偏分布。
4.2 (1)从表中数据可以看出,年龄出现频数最多的是19和23,故有个众数,即M 0=19和M 0=23。
将原始数据排序后,计算中位数的位置为:中位数位置= n+1/2=13,第13个位置上的数值为23,所以中位数为M e =23(2)Q L 位置=n/4=6.25, Q L ==19;Q U 位置=3n/4=18.75,Q U =26.5(3)平均数==∑nx x i600/25=24,标准差65.612510621)(2=-=-=∑-n i s x x(4)偏态系数SK=1.08,峰态系数K=0.77 (5)分析:从众数、中位数和平均数来看,网民年龄在23-24岁的人数占多数。
由于标准差较大,说明网民年龄之间有较大差异。
从偏态系数来看,年龄分布为右偏,由于偏态系数大于1,所以,偏斜程度很大。
由于峰态系数为正值,所以为尖峰分布。
4.3 (1)茎叶图如下:(2)==∑n x x i63/9=7,714.0808.41)(2==-=∑-n i s x x(3)由于两种排队方式的平均数不同,所以用离散系数进行比较。
第一种排队方式:v 1=1.97/7.2=0.274;v 21>v 2,表明第一种排队方式的离散程度大于第二种排队方式。
(4)选方法二,因为第二种排队方式的平均等待时间较短,且离散程度小于第一种排队方式。
4.4 (1)==∑n x x i8223/30=274.1中位数位置=n+1/2=15.5,M e =272+273/2=272.5 (2)Q L 位置=n/4=7.5, Q L ==(258+261)/2=259.5;Q U 位置=3n/4=22.5,Q U =(284+291)/2=287.5 (3)17.211307.130021)(2=-=-=∑-n i s x x4.5 (1)甲企业的平均成本=总成本/总产量=41.193406600301500203000152100150030002100==++++乙企业的平均成本=总成本/总产量=29.183426255301500201500153255150015003255==++++原因:尽管两个企业的单位成本相同,但单位成本较低的产品在乙企业的产量中所占比重较大,因此拉低了总平均成本。
统计学(贾俊平 第四版)课后习题答案
频数
2 3 9 12 7 4 2 1 40
频率%
5.0 7.5 22.5 30.0 17.5 10.0 5.0 2.5 100.0
要求:根据上面的数据进行适当的分组,编制频数分布表,并绘制直方图。
K 1
l g 4 0 l gn ( ) 1.60206 ,取 1 1 6.3 2 k=6 lg(2) lg 2 0.30103
2、确定组距: 组距=( 最大值 - 最小值)÷ 组数=(49-25)÷6=4,取 5 3、分组频数表
要求: (1)根据上面的数据进行适当的分组,编制频数分布表,并计算出累积频数和累积频率。 1、确定组数:
K 1
l g 4 0 l gn ( ) 1.60206 ,取 1 1 6.3 2 k=6 lg(2) lg 2 0.30103
2、确定组距: 组距=( 最大值 - 最小值)÷ 组数=(152-87)÷6=10.83,取 10 3、分组频数表 销售收入
直方图:
组距4,小于等于
40
30
Frequency
20
10
Mean =4.06 Std. Dev. =1.221 N =100 0 0 2 4 6 8
组距4,小于等于
组距 5,上限为小于等于 频数 有效 <= 45.00 46.00 - 50.00 51.00 - 55.00 56.00 - 60.00 61.00+ 合计 12 37 34 16 1 100 百分比 12.0 37.0 34.0 16.0 1.0 100.0 累计频数 12.0 49.0 83.0 99.0 100.0 累积百分比 12.0 49.0 83.0 99.0 100.0
统计学第四版问题详解(贾俊平)
第1章统计和统计数据1.1 指出下面的变量类型。
(1)年龄。
(2)性别。
(3)汽车产量。
(4)员工对企业某项改革措施的态度(赞成、中立、反对)。
(5)购买商品时的支付方式(现金、信用卡、支票)。
详细答案:(1)数值变量。
(2)分类变量。
(3)数值变量。
(4)顺序变量。
(5)分类变量。
1.2 一家研究机构从IT从业者中随机抽取1000人作为样本进行调查,其中60%回答他们的月收入在5000元以上,50%的人回答他们的消费支付方式是用信用卡。
(1)这一研究的总体是什么?样本是什么?样本量是多少?(2)“月收入”是分类变量、顺序变量还是数值变量?(3)“消费支付方式”是分类变量、顺序变量还是数值变量?详细答案:(1)总体是“所有IT从业者”,样本是“所抽取的1000名IT从业者”,样本量是1000。
(2)数值变量。
(3)分类变量。
1.3 一项调查表明,消费者每月在网上购物的平均花费是200元,他们选择在网上购物的主要原因是“价格便宜”。
(1)这一研究的总体是什么?(2)“消费者在网上购物的原因”是分类变量、顺序变量还是数值变量?详细答案:(1)总体是“所有的网上购物者”。
(2)分类变量。
1.4 某大学的商学院为了解毕业生的就业倾向,分别在会计专业抽取50人、市场营销专业抽取30、企业管理20人进行调查。
(1)这种抽样方式是分层抽样、系统抽样还是整群抽样?(2)样本量是多少?详细答案:(1)分层抽样。
(2)100。
第3章用统计量描述数据););=426.67;,,第五章1.23.4.5.6.7.5.8 (1)(3.02%,16.98%)。
(2)(1.68%,18.32%)。
5.9 详细答案:(4.06,24.35)。
5.10详细答案: 139。
5.11 详细答案: 57。
5.12 769。
第6章假设检验平看电,绝平,,绝,,绝在,,=100 =50=14.8 =10.4=0.8 =0.6对,,绝。
对设,。
统计学贾俊平_第四版课后习题答案

统计学贾俊平_第四版课后习题答案3.3 某百货公司连续40天的商品销售额如下:单位:万元41 25 29 47 38 34 30 38 43 40 46 36 45 37 37 36 45 43 33 44 35 28 46 34 30 37 44 26 38 44 42 36 37 37 49 39 42 32 36 35 要求:根据上面的数据进行适当的分组,编制频数分布表,并绘制直方图。
1、确定组数:()lg 40lg() 1.60206111 6.32lg(2)lg 20.30103n K =+=+=+=,取k=6 2、确定组距:组距=( 最大值 - 最小值)÷ 组数=(49-25)÷6=4,取54.8 一项关于大学生体重状况的研究发现.男生的平均体重为60kg,标准差为5kg;女生的平均体重为50kg,标准差为5kg。
请回答下面的问题:(1)是男生的体重差异大还是女生的体重差异大?为什么?女生,因为标准差一样,而均值男生大,所以,离散系数是男生的小,离散程度是男生的小。
(2)以磅为单位(1ks=2.2lb),求体重的平均数和标准差。
都是各乘以2.21,男生的平均体重为60kg×2.21=132.6磅,标准差为5kg ×2.21=11.05磅;女生的平均体重为50kg×2.21=110.5磅,标准差为5kg×2.21=11.05磅。
(3)粗略地估计一下,男生中有百分之几的人体重在55kg一65kg之间?计算标准分数:Z1=x xs-=55605-=-1;Z2=x xs-=65605-=1,根据经验规则,男生大约有68%的人体重在55kg一65kg之间。
(4)粗略地估计一下,女生中有百分之几的人体重在40kg~60kg之间?计算标准分数:Z1=x xs-=40505-=-2;Z2=x xs-=60505-=2,根据经验规则,女生大约有95%的人体重在40kg一60kg之间。
统计学(第四版)贾俊平 第八章 方差分析与实验设计 练习题答案

统计学(第四版)贾俊平 第八章 方差分析与实验设计 练习题答案8.10123411234:0:,,,0=0.01SPSS H H ααααααααα====至少有一个不等于用进行方差分析,表8.1-1填装量主体间效应的检验(单因素方差分析表)因变量: 填装量 源 III 型平方和df均方F Sig.偏 Eta 方非中心 参数观测到的幂b校正模型 .007a3 .002 10.098 .001 .669 30.295 .919 截距 295.7791 295.7791266416.430.000 1.000 1266416.4301.000 机器 .007 3 .002 10.098.001.66930.295.919误差 .004 15 .000总计 304.17119 校正的总计.01118a. R 方 = .669(调整 R 方 = .603)b. 使用 alpha 的计算结果 = .01由表8.1-1得:p=0.001<0.01,拒绝原假设,i 0α不全为,表明不同机器对装填量有显著影响。
8.201231123:0:,,0=0.05SPSS H H ααααααα===至少有一个不等于用进行方差分析,表8.2-1满意度评分主体间效应的检验(单因素方差分析表)因变量: 评分 源III 型平方和df 均方 F Sig.校正模型 29.610a2 14.805 11.756 .001 截距 975.156 1 975.156 774.324 .000 管理者 29.610 2 14.805 11.756.001误差 18.890 15 1.259总计 1061.000 18 校正的总计48.50017a. R 方 = .611(调整 R 方 = .559)由表8.2-1得:p=0.001<0.05,拒绝原假设,i 0α不全为,表明管理者水平不同会导致评分的显著差异。
8.301231123:0:,,0=0.05SPSS H H ααααααα===至少有一个不等于用进行方差分析,表8.3-1电池寿命主体间效应的检验(单因素方差分析表)因变量: 电池寿命 源III 型平方和df 均方 F Sig. 偏 Eta 方 非中心 参数 观测到的幂b校正模型 615.600a2 307.800 17.068 .000 .740 34.137 .997 截距 22815.000 1 22815.000 1265.157 .000 .991 1265.157 1.000 企业 615.600 2 307.800 17.068.000.74034.137.997误差 216.400 12 18.033总计 23647.000 15 校正的总计832.00014a. R 方 = .740(调整 R 方 = .697)b. 使用 alpha 的计算结果 = .05由表8.2-1得:p=0.001<0.05,拒绝原假设,i 0α不全为,表明3个企业生产的电池平均寿命之间存在显著差异。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模拟试题一单项选择题(每小题2分,共20分)1.一项调查表明,在所抽取的1000个消费者中,他们每月在网上购物的平均花费是200元,他们选择在网上购物的主要原因是“价格便宜”。
这里的参数是( A )A. 1000个消费者B. 所有在网上购物的消费者C. 所有在网上购物的消费者的平均花费额D. 1000个消费者的平均花费金额2.为了调查某校学生的购书费用支出,从男生中抽取60名学生调查,从女生中抽取40名学生调查,这种抽样方法属于( D )A. 简单随机抽样B. 整群抽样C. 系统抽样D. 分层抽样3.某班学生的平均成绩是80分,标准差是10分。
如果已知该班学生的考试分数为对称分布,可以判断考试分数在70到90分之间的学生大约占( C )A. 95%B. 89%C. 68%D. 99%4.已知总体的均值为50,标准差为8,从该总体中随机抽取容量为64的样本,则样本均值的数学期望和抽样分布的标准误差分别为( )A. 50,8B. 50,1C. 50,4D. 8,85.根据某班学生考试成绩的一个样本,用95%的置信水平构造的该班学生平均考试分数的置信区间为75分~85分。
全班学生的平均分数( D )A .肯定在这一区间内B .有95%的可能性在这一区间内C .有5%的可能性在这一区间内D .要么在这一区间内,要么不在这一区间内6.一项研究发现,2000年新购买小汽车的人中有40%是女性,在2005年所作的一项调查中,随机抽取120个新车主中有57人为女性,在05.0=α的显着性水平下,检验2005年新车主中女性的比例是否有显着增加,建立的原假设和备择假设为( C ) A .%40:,%40:10≠=ππH H B .%40:,%40:10<≥ππH H C .%40:,%40:10>≤ππH H D .%40:,%40:10≥<ππH H7.在回归分析中,因变量的预测区间估计是指( B )A. 对于自变量x 的一个给定值0x ,求出因变量y 的平均值的区间B. 对于自变量x 的一个给定值0x ,求出因变量y 的个别值的区间C. 对于因变量y 的一个给定值0y ,求出自变量x 的平均值的区间D. 对于因变量y 的一个给定值0y,求出自变量x 的平均值的区间8.在多元线性回归分析中,如果F 检验表明线性关系显着,则意味着( A ) A. 在多个自变量中至少有一个自变量与因变量之间的线性相关系着 B. 所有的自变量与因变量之间的线性关系都显着C. 在多个自变量中至少有一个自变量与因变量之间的线性关系不显着D. 所有的自变量与因变量之间的线性关系都不显着9.如果时间序列的逐期观察值按一定的增长率增长或衰减,则适合的预测模型是( D ) A. 移动平均模型 B. 指数平滑模型 C. 线性模型 D. 指数模型10.设p 为商品价格,q 销售量,则指数∑∑010qp q p 的实际意义是综合反映( B )A. 商品销售额的变动程度B. 商品价格变动对销售额影响程度C. 商品销售量变动对销售额影响程度D. 商品价格和销售量变动对销售额影响程度 二、简要回答下列问题(每小题5分,共15分) 1、简述直方图和茎叶图的区别。
2、简述假设检验中P 值的含义。
3、解释指数平滑法。
4、(15分)甲、乙两个班参加同一学科考试,甲班的平均考试成绩为86分,标准差为12分。
乙班考试成绩的分布如下:(1) 画出乙班考试成绩的直方图。
(2)计算乙班考试成绩的平均数及标准差。
(3)比较甲乙两个班哪个班考试成绩的离散程度大?5/(25分) 某企业生产的袋装食品采用自动打包机包装,每袋标准重量为100克。
现从某天生产的一批产品中按(1)假定食品包重服从正态分布,要求:(2)确定该种食品平均重量95%的置信区间。
(3)如果规定食品重量低于100克属于不合格,确定该批食品合格率95%的置信区间。
(4)采用假设检验方法检验该批食品的重量是否符合.(5)标准要求?(05.0=α,写出检验的具体步骤)。
7、(25分)一家产品销售公司在30个地区设有销售分公司。
为研究产品销售量(y)与该公司的销售价格(x1)、各地区的年人均收入(x2)、广告费用(x3)之间的关系,搜集到30个地区的有关数据。
利用Excel 得到下面的回归结果(05.0=α):(1)将方差分析表中的所缺数值补齐。
(2)写出销售量与销售价格、年人均收入、广告费用的多元线性回归方程,并解释各回归系数的意义。
(3)检验回归方程的线性关系是否显着? (4)计算判定系数2R ,并解释它的实际意义。
(5)计算估计标准误差ys ,并解释它的实际意义。
模拟试题一解答一、单项选择题1. A ;2. D ;3. C ;4. B ;5. D ;6. C ;7. B ;8. A ;9. D ;10. B 。
二、简要回答下列问题1. (1)直方图虽然能很好地显示数据的分布,但不能保留原始的数值;茎叶图类似于横置的直方图,与直方图相比,茎叶图既能给出数据的分布状况,又能给出每一个原始数值,即保留了原始数据的信息。
(2)在应用方面,直方图通常适用于大批量数据,茎叶图通常适用于小批量数据。
2. 如果原假设H 是正确的,所得到的样本结果会像实际观测结果那么极端或更极端的概率,称为P 值P 值是假设检验中的另一个决策工具,对于给定的显着性水平α,若α<P ,则拒绝原假设。
3. 指数平滑法是对过去的观察值加权平均进行预测的一种方法,该方法使得第t +1期的预测值等于t 期的实际观察值与第t 期预测值的加权平均值。
一次指数平滑法是适合于平稳序列的一种预测方法,其模型为tt t F Y F )1(1αα-+=+。
三、(1)乙班考试成绩的直方图如下:(2)77302310305957859757652551==⨯+⨯+⨯+⨯+⨯==∑=nf Mx ki ii分分86.112940801305)7795(7)7785(9)7775(7)7765(2)7755(1)(2222212==-⨯-+⨯-+⨯-+⨯-+⨯-=--=∑=n f x Ms ki ii(3)甲班考试分数的离散系数为:1395.08612===x s v 甲。
乙班考试分数的离散系数为:5401.07768.11===x s v 乙。
由于乙甲v v <,所以甲班考试成绩的离散程度小于乙班。
四、(1)已知:50=n ,96.1205.0=z 。
样本均值为:32.1015050661===∑=nf Mx ki ii克,样本标准差为:634.14988.1301)(12==--=∑=n f x Ms ki ii克。
由于是大样本,所以食品平均重量95%的置信区间为:453.032.10150634.196.132.1012±=⨯±=±ns z x α即(,)。
(2)提出假设:100:0=μH ,100:1≠μH计算检验的统计量:712.550634.110032.1010=-=-=nsx z μ由于96.1712.5205.0=>=z z ,所以拒绝原假设,该批食品的重量不符合标准要求。
五、(1) 方差分析表(2)多元线性回归方程为:321。
8861.117ˆ1-=β表示:在年人均收入和广告费用不变的情况下,销售价格每增加一个单位,销售量平均下降个单位;6107.80ˆ2=β表示:在销售价格和广告费用不变的情况下,年人均收入每增加一个单位,销售量平均增加个单位;5012.0ˆ3=β表示:在年销售价格和人均收入不变的情况下,广告费用每增加一个单位,销售量平均增加个单位。
(3)由于Significance F=<05.0=α,表明回归方程的线性关系显着。
(4)%36.897.134585861.120267742===SST SSR R ,表明在销售量的总变差中,被估计的多元线性回归方程所解释的比例为%,说明回归方程的拟合程度较高。
(5)67.2347.550691===--=MSE k n SSEs e 。
表明用销售价格、年人均收入和广告费用来预测销售量时,平均的预测误差为。
模拟试题二单项选择题(每小题2分,共20分)1.根据所使用的计量尺度不同,统计数据可以分为( )A. 分类数据、顺序数据和数值型数据B. 观测数据和试验数据C. 截面数据和时间序列数据D. 数值型数据和试验数据 2.饼图的主要用途是( )A. 反映一个样本或总体的结构B. 比较多个总体的构成C. 反映一组数据的分布D. 比较多个样本的相似性3.如果一组数据是对称分布的,则在平均数加减2个标准差之内的数据大约有( ) A. 68% B. 90% C. 95% D. 99%4.从均值为200、标准差为50的总体中,抽出100=n 的简单随机样本,用样本均值x 估计总体均值μ,则x 的数学期望和标准差分别为( )A. 200,5B. 200,20C. 200,D. 200,25 %的置信水平是指( )A .总体参数落在一个特定的样本所构造的区间内的概率为95%B .总体参数落在一个特定的样本所构造的区间内的概率为5%C .在用同样方法构造的总体参数的多个区间中,包含总体参数的区间比率为95%D .在用同样方法构造的总体参数的多个区间中,包含总体参数的区间比率为5% 6.在假设检验中,如果所计算出的P 值越小,说明检验的结果( ) A .越显着 B .越不显着 C .越真实 D .越不真实7.在下面的假定中,哪一个不属于方差分析中的假定( ) A .每个总体都服从正态分布 B. 各总体的方差相等 C. 观测值是独立的 D. 各总体的方差等于08.在方差分析中,数据的误差是用平方和来表示的,其中组间平方和反映的是( ) A. 一个样本观测值之间误差的大小 B. 全部观测值误差的大小C. 各个样本均值之间误差的大小D. 各个样本方差之间误差的大小 9.在多元线性回归分析中,t 检验是用来检验( )A. 总体线性关系的显着性B. 各回归系数的显着性C. 样本线性关系的显着性D. 0:210====k H βββΛ10.下面的哪种方法不适合对平稳序列的预测( )简单平均法 B. 移动平均法 C. 指数平滑法 D. 线性模型法简要回答下列问题(每小题5分,共20分) 1.简述直方图和条形图的区别。
2.简述中心极限定理。
3.回归分析主要解决以下几个方面的问题?4.解释拉氏价格指数和帕氏价格指数。
(20分)一家物业公司需要购买大一批灯泡,你接受了采购灯泡的任务。
假如市场上有两种比较知名品牌的灯泡,你希望从中选择一种。
为此,你从两个供应商处各随机抽取了60个灯泡的随机样本,进行“破坏性”试验,请用直方图直观地比较这两个样本,你能得到什么结论?你认为应当采用哪一种统计量来分别描述供应商甲和供应商乙灯泡寿命的一般水平?请简要说明理由。
