多元统计分析实验报告计算协方差矩阵相关矩阵SAS

合集下载

SAS简单的矩阵运算和变量的协方差矩阵

SAS/IML矩阵功能简介SAS/IML是SAS提供的一个可以进行矩阵运算编程的工具，详细使用请参见有关资料或系统帮助（Help | Extended Help | SAS System Help: Main Menu | Help for SAS Products | SAS/IML）。

下面给出SAS/IML常用命令：●proc iml 调用SAS/IML矩阵运算编程的工具；●用＋、－、*符号表示矩阵的加减乘；●用||表示矩阵左右连接，用//表示矩阵上下连接；●用＃表示用某个常数分别乘以矩阵中的每个元素3＃x；●用/表示用某个常数分别去除矩阵中的每个元素x/3；●用＃＃矩阵中的每个元素进行乘方运算x＃＃2；●用g=inv(x)表示g是x的逆;●用e=eigval(x) 表示e是x特征值;●用d=eigvec(x) 表示d是x特征向量;●用h=det(x) 表示h是x行列式;●用t=trace(x) 表示t是x的迹;●用rank=round(trace(ginv(x)*x)) 表示rank是x的秩;G = GINV(A) 表示求A的广义逆矩阵，如果G = GINV(A)，那么AGA = A，GAG =G，(AG)' = AG和(GA)' = GA；●用下面的程序表示求矩阵x的某个子矩阵proc iml;x={123,456,789};m=x[2:3,1:3]; （矩阵m是x的第2行到第3行和第1列到第3列构成的子矩阵）print m;●用下面的程序求由几个子矩阵构成一个矩阵⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦ABC。

proc iml; a={2 2, 4 4} ;b={6 6,8 8} ;c=block(a,b);print c;2 2 0 04 4 0 00 0 6 60 0 8 8⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦c● 用a=I(k)求k 阶单位矩阵a=I(k) 111k ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦I = ● 用b=j(k)求每个元素均为“1”的k 阶矩阵111111111k⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦J 。

SAS学习系列32. 协方差分析资料报告

32. 协方差分析（一）原理一、基本思想在实际问题中，有些随机因素是很难人为控制的，但它们又会对结果产生显著影响。

如果忽略这些因素的影响，则有可能得到不正确的结论。

这种影响的变量称为协变量（一般是连续变量）。

例如，研究3种不同的教学方法的教学效果的好坏。

检查教学效果是通过学生的考试成绩来反映的，而学生现在考试成绩是受到他们自身知识基础的影响，在考察的时候必须排除这种影响。

协方差分析回归分析与方差分析的结合，在做两组和多组均值之间的比较前，用直线回归的方法找出各组因变量Y与协变量X之间的数量关系，求得在假定X相等时的修正均均值，然后用方差分析比较修正均值之间的差别。

简单来说，协方差分析就是扣除协变量的影响，或者将这些协变量处理成相等，再对修正的Y的均值作方差分析。

根据协变量的个数的不同，协方差分析分为一元协方差分析和多元协方差分析。

二、协方差分析需要满足的条件（1）自变量是分类变量，协变量是定距变量，因变量是连续变量；对连续变量或定距变量的协变量的测量不能有误差；（2）协变量与因变量之间的关系是线性关系，可以用协变量和因变量的散点图来检验是否违背这一假设；协变量的回归系数（即各回归线的斜率）是相同的，且不等于0，即各组的回归线是非水平的平行线。

否则，就有可能犯第一类错误，即错误地接受虚无假设；（3）自变量与协变量相互独立，若协方差受自变量的影响，那么协方差分析在检验自变量的效应之前对因变量所作的控制调整将是偏倚的，自变量对因变量的间接效应就会被排除；（4）各样本来自具有相同方差σ2的正态分布总体，即要求各组方差齐性。

三、基本理论1. 观测值=均值+分组变量影响+协变量影响+随机误差. 即()ij i ij ij y u t x x βε=++-+ （1）其中，X 为所有协变量的平均值。

注：在方差分析中，协变量影响是包含在随机误差中的，在协方差分析中需要分离出来。

用协变量进行修正，得到修正后的y ij (adj)为(adj)()ij ij ij i ij y y x x u t βε=--=++就可以对y ij (adj)做方差分析了。

多元统计分析实验指导书——实验一均值向量和协方差阵检验

实验一SPSS软件的基本操作与均值向量和协方差阵的检验【实验目的】通过本次实验，了解SPSS的基本特征、结构、运行模式、主要窗口等，了解如何录入数据和建立数据文件，掌握基本的数据文件编辑与修改方法,对SPSS有一个浅层次的综合认识。

同时能够掌握对均值向量和协方差阵进行检验。

【实验性质】必修，基础层次【实验仪器及软件】计算机及SPSS软件【实验内容】1.操作SPSS的基本方法(打开、保存、编辑数据文件)2.问卷编码3.录入数据并练习数据相关操作4.对均值向量和协方差阵进行检验，并给出分析结论。

【实验学时】4学时【实验方法与步骤】1.开机2.找到SPSS的快捷按纽或在程序中找到SPSS，打开SPSS3.认识SPSS数据编辑窗、结果输出窗、帮助窗口、图表编辑窗、语句编辑窗4.对一份给出的问卷进行编码和变量定义5.按要求录入数据6.练习基本的数据修改编辑方法7.检验多元总体的均值向量和协方差阵8.保存数据文件9.关闭SPSS，关机。

【实验注意事项】1.实验中不轻易改动SPSS的参数设置，以免引起系统运行问题。

2.遇到各种难以处理的问题，请询问指导教师。

3.为保证计算机的安全，上机过程中非经指导教师和实验室管理人员同意，禁止使用移动存储器。

4.每次上机，个人应按规定要求使用同一计算机，如因故障需更换，应报指导教师或实验室管理人员同意。

5.上机时间，禁止使用计算机从事与课程无关的工作。

【上机作业】1.定义变量：试录入以下数据文件，并按要求进行变量定义。

表1学号姓名性别生日身高（cm）体重（kg）英语（总分100分）数学（总分100分）生活费（$代表人民币）200201 刘一迪男1982.01.12 156.42 47.54 75 79 345.00 200202 许兆辉男1982.06.05 155.73 37.83 78 76 435.00 200203 王鸿屿男1982.05.17 144.6 38.66 65 88 643.50 200204 江飞男1982.08.31 161.5 41.68 79 82 235.50 200205 袁翼鹏男1982.09.17 161.3 43.36 82 77 867.00 200206 段燕女1982.12.21 158 47.35 81 74200207 安剑萍女1982.10.18 161.5 47.44 77 69 1233.00 200208 赵冬莉女1982.07.06 162.76 47.87 67 73 767.80 200209 叶敏女1982.06.01 164.3 33.85 64 77 553.90 200210 毛云华女1982.09.12 144 33.84 70 80 343.00200211 孙世伟男1981.10.13 157.9 49.23 84 85 453.80200212 杨维清男1981.12.6 176.1 54.54 85 80 843.00男1981.11.21 168.55 50.67 79 79 657.40 200213 欧阳已祥200214 贺以礼男1981.09.28 164.5 44.56 75 80 1863.90200215 张放男1981.12.08 153 58.87 76 69 462.20200216 陆晓蓝女1981.10.07 164.7 44.14 80 83 476.80200217 吴挽君女1981.09.09 160.5 53.34 79 82200218 李利女1981.09.14 147 36.46 75 97 452.80200219 韩琴女1981.10.15 153.2 30.17 90 75 244.70200220 黄捷蕾女1981.12.02 157.9 40.45 71 80 253.00要求：1）变量名同表格名，以“（）”内的内容作为变量标签。

多元统计公式大揭秘协方差矩阵与多元正态分布的计算公式

多元统计公式大揭秘协方差矩阵与多元正态分布的计算公式多元统计公式大揭秘——协方差矩阵与多元正态分布的计算公式统计学中的多元统计分析是一门研究多个变量之间相互关系的学科。

在多元统计分析中，协方差矩阵和多元正态分布是两个重要的概念和计算工具。

本文将为大家揭秘协方差矩阵和多元正态分布的计算公式。

让我们一起进入多元统计的世界，掌握这些重要的概念和工具。

一、协方差矩阵协方差矩阵是用于度量多个变量之间线性关系的工具。

它描述了各个变量之间的相关程度，以及每个变量本身的方差。

协方差矩阵是一个方阵，其行和列对应于各个变量。

协方差矩阵的计算公式如下：假设我们有n个变量(x1, x2, ..., xn)，每个变量有m个观测值。

计算协方差矩阵的步骤如下：1. 计算每个变量的平均值：x1̄= (x1₁ + x1₂ + ... + x1m) / mx2̄= (x2₁ + x2₂ + ... + x2m) / m...x n = (xn₁ + xn₂ + ... + xnm) / m2. 计算协方差：cov(x1, x1) = (x11 - x1̄) * (x11 - x1̄) + (x12 - x1̄) * (x12 - x1̄) + ... + (x1m - x1̄) * (x1m - x1̄)cov(x1, x2) = (x11 - x1̄) * (x21 - x2̄) + (x12 - x1̄) * (x22 - x2̄) + ... + (x1m - x1̄) * (x2m - x2̄)...cov(xn, xn) = (xn1 - x n) * (xn1 - x n) + (xn2 - x n) * (xn2 - x n) + ... + (xnm - x n) * (xnm - x n)3. 构建协方差矩阵：Cov = [ cov(x1, x1) cov(x1, x2) ... cov(x1, xn) ][ cov(x2, x1) cov(x2, x2) ... cov(x2, xn) ][ ... ... ... ... ][ cov(xn, x1) cov(xn, x2) ... cov(xn, xn) ]协方差矩阵的主对角线上的元素是各个变量的方差，非对角线上的元素是各个变量之间的协方差。

《多元统计分析》实验四

实验四上市公司财务报表数据的因子分析（王学民编写）一、实验目的1.掌握如何使用SAS 软件来进行因子分析；2.看懂和理解SAS 输出的结果，并学会以此来作出分析；3.掌握对实际数据如何来进行因子分析；4.了解异常值对数据分析的影响二、实验内容数据集sasuser.case4中含有2001年沪市611家上市公司年财务报表的十个主要财务指标。

对这些数据进行因子分析，可将这十个指标成功地归结于三个公共因子，达到较好的降维目的，并给出符合实际背景和意义的解释。

在作因子分析之前需先进行预分析，找出影响因子分析的不合理数据和异常数据。

通过因子分析，对各因子的得分大小进行排序分析，同时结合各上市公司的三个因子得分用SAS 软件建立旋转图，通过三维图形的旋转进行分析和描述。

由于图中有600多个散点，故需巧妙地运用SAS 软件不断地对图形作出调节使之能更清楚地用来进行观测。

实验1剔除不合理数据和异常数据。

实验2进行因子分析。

实验3利用SAS 软件观测和调节含600多个散点的旋转图。

三、实验要求1.用SAS 软件完成因子分析的计算；2.根据SAS 输出结果完成因子分析；3.学会利用软件观测含有众多散点的旋转图。

四、实验指导1.剔除不合理数据和异常数据（1）注意到，如每股净资产（6x ）值接近于零或为负，通常将使净资产收益率（7x ）没有意义或数值特大。

为发现这些值，在inshigt环境下打开数据集sasuser.case4，见图1。

选菜单过程如下：在图1中，选x6⇒在数据区域点击右键，出现上托菜单⇒选排序…图1随即得到图1中按每股净资产值从小到大的排序。

每股净资产最小的三只股票：“PT郑百”（66.166x=-元），“ST同达”（60.488x=-元）和“PT红光”（60.006x=元）必须被删去。

其原因有两个：(i)这三只股票的每股净资产为负或非常接近于零，它们的净资产收益率没有意义。

(ii) “PT红光”和“ST同达”的净资产收益率（7x）分别是621.15和82.34，在数值上比排名第三的40.20要大许多，特别是前者为一个非常大的异常值，会对因子分析的结果产生明显的不良影响。

第3章统计实验(多元正态总体检验)

实验零多元正态总体检验（均值向量检验）1．实验目的：本实验讨论利用多元正态总体检验中的均值向量检验方法去判断满足多元正态分布的总体的均值是否等于预先判断的向量（单正态总体检验）或判断两个独立的、满足多元正态分布的总体的均值是否相等（双正态总体检验）。

通过该实验，能够起到如下的效果：(1) 理解多元正态总体检验中的均值向量检验方法的作用、思想、数学基础、方法和步骤；(2) 熟悉如何利用多元正态总体检验中的均值向量检验方法，提出问题、分析问题、解决问题、得出结论；（3）会调用SAS软件实现多元正态总体检验中的均值向量检验方法的各个步骤，根据计算的结果进行分析，得出正确的结论，解决实际的问题。

2．知识准备：多元正态总体检验中的均值向量检验是从判断满足多元正态分布的总体的均值是否等于预先判断的向量（单正态总体检验）或判断两个独立的、满足多元正态分布的总体的均值是否相等（双正态总体检验）。

其思想和步骤是：1.假设“需判断的总体均值等于预先判断的向量（单正态总体检验）”或“需判断的两个总体的均值相等（双正态总体检验）”；2.在该假设下，构造适当的统计量并给出其分布；3.根据观测数据算出其统计量的值；4.根据预先确定的检验水平查阅相应的分布表确定临界值和拒绝域；5.根据结果判断接受或拒绝原假设，得出结论。

（具体见书【1】第三章）3．实验内容：一、单正态总体检验：人出汗多少与人体内钠、钾含量有一定关系。

今测20名健康成年女性出汗多少(X1)、钠含量(X2)、钾含量(X3)，其数据如下表１：表1 健康成年女性出汗情况的基本数据序号X1 X2 X3 序号X1 X2 X31 3.7 48.5 9.3 11 3.9 36.9 12.72 5.7 65.1 8 12 4.5 58.8 12.33 3.8 47.2 10.9 13 3.5 27.8 9.84 3.2 53.2 12 14 4.5 40.2 8.45 3.1 55.5 9.7 15 1.5 13.5 10.16 4.6 36.1 7.9 16 8.5 56.4 7.17 2.4 24.8 14 17 4.5 71.6 8.28 7.2 33.1 7.6 18 6.5 52.8 10.99 6.7 47.4 8.5 19 4.1 44.1 11.210 5.4 54.1 11.3 20 5.5 40.9 9.4利用多元正态总体检验中的单正态均值向量检验方法判断“（X1,X2,X3）的均值是否等于（4，50，10）”【1】(假设总体服从正态分布，分别取检验水平为0.05、0.01)。

应用多元统计分析实验报告

多元统计分析实验报告学院名称理学院专业班级应用统计学14-2学生姓名张艳雪学号201411081051工资、受教育年限、初始工资和工作经验资料如下表所示：设职工总体的以上变量服从多元正态分布，根据样本资料利用 SPSS 软件求出均注 1：最大似然估计公式为： μˆ = X = ∑ ∑ (X i - X )(X i - X )' ； ˆ第一章多元正态分布1.1 从某企业全部职工中随机抽取一容量为 6 的样本，该样本中个职工的目前值向量和协方差矩阵的最大似然估计。

1 n n i =1 X i ， Σ = 1 nn i =1一．SPSS 操作步骤：第一步：利用 spss 建立数据集第二步：分析--描述统计--描述计算样本均值向量第三步：分析--相关--双变量计算样本协方差阵与样本相关系数二．输出结果：⎪ μ= 37125 ⎪ 152.50⎪ ⎛ 352068000 12500 -110677500 102000 ⎫= -110677500 - 86250 2192793750 691125 ⎪16695.1⎪⎭ ∑ X i，∑ (X i - X )(X i - X )'ˆ三．实验结果分析：样本均值为样本的协方差∑⎪⎪如此就可以按照极大似然估计方程：1 nΣ =n i =1得出均值向量与协方差向量的最大似然估计结果。

μ=X=1nn i=1ˆ第三章聚类分析3.1下表是15个上市公司2001年的一些主要财务指标，使用系统聚类法和K－均值法利用SPSS软件分别对这些公司进行聚类，并对结果进行比较分析。

公司编号净资产收益率每股净利润总资产周转率资产负债率流动负债比率每股净资产净利润增长率总资产增长率111.090.210.0596.9870.53 1.86-44.0481.99211.960.590.7451.7890.73 4.957.0216.11300.030.03181.99100-2.98103.3321.18411.580.130.1746.0792.18 1.14 6.55-56.325-6.19-0.090.0343.382.24 1.52-1713.5-3.366100.470.4868.486 4.7-11.560.85710.490.110.3582.9899.87 1.02100.2330.32811.12-1.690.12132.14100-0.66-4454.39-62.759 3.410.040.267.8698.51 1.25-11.25-11.4310 1.160.010.5443.7100 1.03-87.18-7.411130.220.160.487.3694.880.53729.41-9.97128.190.220.3830.31100 2.73-12.31-2.771395.79-5.20.5252.3499.34-5.42-9816.52-46.821416.550.350.9372.3184.05 2.14115.95123.4115-24.18-1.160.7956.2697.8 4.81-533.89-27.74一、实验原理:1.系统聚类的基本思想是：首先，每个样品（或变量）先聚成一类，然后，选择距离公式计算类与类之间的距离，把距离相近的样品（或变量）先聚成类，距离相远的后聚成类，该过程一直进行下去，每个样品（或变量）总能聚到合适的类中，最后，所有的样品（或变量）聚成一类。

多元统计分析——典型相关分析实验报告

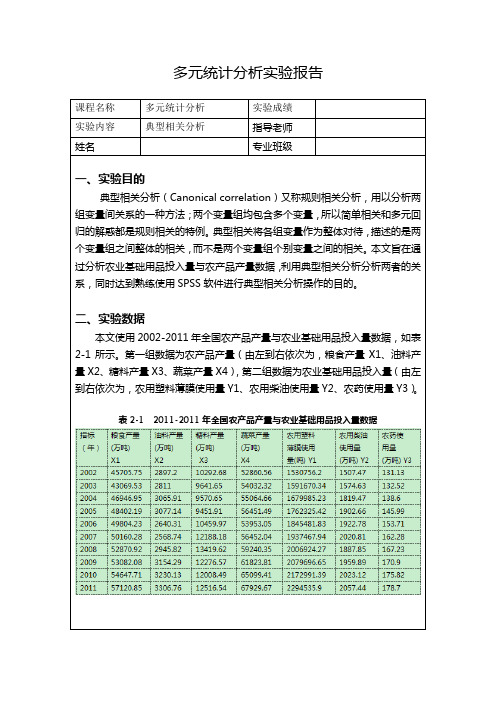
多元统计分析实验报告课程名称多元统计分析实验成绩实验内容典型相关分析指导老师姓名专业班级一、实验目的典型相关分析（Canonical correlation）又称规则相关分析，用以分析两组变量间关系的一种方法；两个变量组均包含多个变量，所以简单相关和多元回归的解惑都是规则相关的特例。

典型相关将各组变量作为整体对待，描述的是两个变量组之间整体的相关，而不是两个变量组个别变量之间的相关。

本文旨在通过分析农业基础用品投入量与农产品产量数据，利用典型相关分析分析两者的关系，同时达到熟练使用SPSS软件进行典型相关分析操作的目的。

二、实验数据本文使用2002-2011年全国农产品产量与农业基础用品投入量数据，如表2-1所示。

第一组数据为农产品产量（由左到右依次为，粮食产量X1、油料产量X2、糖料产量X3、蔬菜产量X4），第二组数据为农业基础用品投入量（由左到右依次为，农用塑料薄膜使用量Y1、农用柴油使用量Y2、农药使用量Y3）。

表2-1 2011-2011年全国农产品产量与农业基础用品投入量数据由于cancorr不能读取中文名称，所以变量名均需为英文名。

将表2-1数据转换为能够进行典型相关分析形式的数据，如表2-2所示。

表2-2 典型相关分析数据（农产品产量与农业基础用品投入量数据）三、实验过程SPSS 16.0并未提供典型相关分析的交互窗口，只能直接在syntax editor 窗口呼叫SPSS的CANCORR程序来执行分析。

选择【File】—【New】—【Syntax】，弹出Syntax对话框，在对话框中写入调用Cancorr程序，如图3-1所示。

图3-1 Syntax窗口调用CONCORR函数四、实验结果表4-1为第一组数据，即农产品产量之间的相关关系表。

从表中可以看出，粮食产量（X1）与蔬菜产量（X4）有较高的相关关系，相关系数高达0.9035；粮食产量（X1）与糖料产量（X3）相关关系也较大，相关系数为0.8081；油料产量（X2）与蔬菜产量（X4）的相关关系较大，为0.7442。

多元统计实验SAS软件应用基础

5 100 91 72 96 78
6 90 78 82 75 97
7 75 73 88 97 89
8 93 84 83 68 88
9 87 73 60 76 84
10 95 82 90 62 39
11 76 72 43 67 78
12 85 75 50 34 37
请计算各门成绩的均值、方差、标准差、变异系数、偏度、峰度。
二，实验原理
对于样本容量为n的一个样本：
有如下概念：
均值(Mean)：
方差（)：
偏度(SKEWNESS)：
峰度(KURTOSIS)：
中位数(MEDIUM)：
分位数：
上四分位数：
下四分位数：
三均值：
极差（RANGE）
Proc步具有大致相同的程序结构：
PROC过程名<option(s)> <statistic-keyword(s)>;
2.学生管理数据库中数据集如下：
姓名
出生日期
年龄
学号
数学
英语
王红
1977-06-02
22
9810012
90
73
李明
1978-03-23
21
9810004
88
68
徐凯歌
1978-11-14
21
9810034
92
78
吴青云
1978-04-12
21
9810023
89
84
李清华
1978-10-24
21
9810024
②plot：要求对所分析的各变量的观测值产生一个茎叶图（或水平直方图）、一个箱线图和一个正态QQ图。若某区间的观测值超过48，则不绘制茎叶图，而改绘制直方图。在正态QQ图中，以“*”表示正态QQ图上的点，以“+”表示相应的参考直线。

多元统计分析多元统计分析15

)
1
W1 ( n, 2 )就是 2 2 ( n).
一般地,设X(α)～Np(μ,Σ) (α＝1,…,n) 相互独立,记
p
1

M
1n ,

n p
1

p

则称W＝X'X服从非中心参数为Δ的非中心Wishart分布,记为
W～Wp(n,Σ,Δ). 其中
M M (1n )(1n ) 1n1n n
Np(μ,Σ/n).S~?.
1、威沙特(Wishart)分布的定义
定义3.1.4 设X(α) ～Np(0,Σ) (α＝1,…,n)相互独立，则称随机矩阵
n
W X ( ) X ( ) X X
1
的分布为Wishart分布(威沙特分布)，记为W～Wp(n,Σ).
显然p=1时
n
W X (2 ) ~ 2 2 (,n即
一元统计中，用样本方差
n
1
2
S2
(
X

X
)
(i )
n 1 i 1
作为σ2的估计，而且知道
1
2
n
2
2
(
X

X
)
~

( n 1)
(i )
i 1
ഥ 作为μ的估计，样本
多元正态总体Np(μ,Σ)中,常用样本均值向量
ഥ～
协方差阵S＝A/(n-1)作为Σ的估计.由第二章的定理2.5.2已给出了
11 12 r
1,…,n)相互独立，其中

21 22 p r
又已知随机矩阵
W11 W12 r

实验报告-判别分析(多元统计)

实验报告5判别分析（设计性实验）(Discriminant analysis)实验原理：判别分析是判别样品所属类型的一种统计方法。

判别分析是在已知研究对象分成若干类型（或组别）并已取得各种类型的一批已知样品的观测数目，在此基础上根据某些准则建立判别式，然后对未知类型的样品进行判别分类。

本实验要求学生应用距离判别准则（即，对任给的一次观测，若它与第i类的重心距离最近，就认为它来自第i类），对两总体和多总体情形下分别进行判别分析。

实验中需注意协方差矩阵相等时，选取线性判别函数；协方差矩阵不相等时，应选取二次判别函数。

实验题目一：为了检测潜在的血友病A携带者，下表中给出了两组数据：(t11a8)其中x1＝log10（AHF activity），x2＝log10（AHF antigen）。

下表给出了五个新的观测，试对这些观测判别归类；(t11b8)实验要求：（1）分别检验两组数据是否大致满足二元正态性；（2）分别计算两组数据的协方差矩阵，是否可以认为两者近似相等？（3）对训练样本和新观测合并作散点图，不同的类用不同颜色标识；（4）用lda函数做判别分析，即在协方差矩阵相等的情形下作判别分析；（5）用qda函数做判别分析，即在协方差矩阵不相等的情形下作判别分析；（6）比较方法（4）和方法（5）的误判率。

实验题目二：某商学研究生院的招生官员利用指标――大学期间平均成绩GPA和研究生管理能力考试GMAT的成绩，将申请者分为三类：接受，不接受，待定。

下表中给出了三类申请者的GPA与GMAT成绩：(t11a6)GPA （x1）GMAT（x2）接受GPA（x1）GMAT（x2）不接受GPA（x1）GMAT（x2）待定2.96 596 1 2.54 446 2 2.86 494 33.14 473 1 2.43 425 2 2.85 496 3 3.22 482 1 2.2 474 2 3.14 419 3 3.29 527 1 2.36 531 2 3.28 371 3 3.69 505 1 2.57 542 2 2.89 447 3 3.46 693 1 2.35 406 2 3.15 313 3 3.03 626 1 2.51 412 2 3.5 402 3 3.19 663 1 2.51 458 2 2.89 485 3 3.63 447 1 2.36 399 2 2.8 444 3 3.59 588 1 2.36 482 2 3.13 416 33.3 563 1 2.66 420 2 3.01 471 33.4 553 1 2.68 414 2 2.79 490 33.5 572 1 2.48 533 2 2.89 431 33.78 591 1 2.46 509 2 2.91 446 33.44 692 1 2.63 504 2 2.75 546 33.48 528 1 2.44 336 2 2.73 467 33.47 552 1 2.13 408 2 3.12 463 33.35 520 1 2.41 469 2 3.08 440 33.39 543 1 2.55 538 2 3.03 419 33.28 523 1 2.31 505 2 3 509 33.21 530 1 2.41 489 2 3.03 438 33.58 564 1 2.19 411 2 3.05 399 33.33 565 1 2.35 321 2 2.85 483 33.4 431 1 2.6 394 2 3.01 453 33.38 605 1 2.55 528 2 3.03 414 33.26 664 1 2.72 399 2 3.04 446 33.6 609 1 2.85 381 23.37 559 1 2.9 384 23.8 521 13.76 646 13.24 467 1实验要求：（1）对上表中的数据作散点图，不同的类用不同的颜色标识；（2）用lda函数做判别分析，即在协方差矩阵相等的情形下作判别分析；（3）用qda函数做判别分析，即在协方差矩阵不相等的情形下作判别分析；（4）比较方法（2）和方法（3）的误判率；（5）现有一新申请者的GPA为3.21，GMAT成绩为497。

多元统计分析实验报告（精选多篇）

多元统计分析实验报告（精选多篇）第一篇：多元统计分析实验报告多元统计分析得实验报告院系:数学系班级:1３级 B 班姓名:陈翔学号:2013１611233 实验目得:比较三大行业得优劣性实验过程有如下得内容:(１)正态性检验;(2)主体间因子,多变量检验a;(３)主体间效应得检验;(4)对比结果(K 矩阵);(5)多变量检验结果;(６)单变量检验结果;(7)协方差矩阵等同性得Box 检验ａ,误差方差等同性得Ｌevene 检验 a;(8)估计;(9)成对比较,多变量检验;(10)单变量检验。

实验结果:综上所述,我们对三个行业得运营能力进行了具体得比较分析,所得数据表明,从总体来瞧,信息技术业要稍好于电力、煤气及水得生产与供应业以及房地产业。

１。

正态性检验Kｏlmogorｏv－SｍirnovaShapiｒ o—Wilk 统计量 dｆ Sig.统计量ｄｆ Sig、净资产收益率。

１１３ 35、2００＊。

97８ 35。

6７7 总资产报酬率。

121 35、２00＊。

964 3５、298 资产负债率。

08６ 35。

2００*.9６2 35、265 总资产周转率.1８0 3５、006。

864 ３5。

00０流动资产周转率、164 3５、０18.88５35、002 已获利息倍数、２8１35.０00。

55１３5、0０0 销售增长率.1０3 ３５、2０0＊。

９4９ 35、104 资本积累率。

251 35。

０00、655 35。

0０0 *。

这就是真实显著水平得下限。

ａ。

Lillｉeforｓ显著水平修正此表给出了对每一个变量进行正态性检验得结果,因为该例中样本中ｎ＝35<2000,所以此处选用 Shapiro—W ｉｌk 统计量。

由 Sig。

值可以瞧到,总资产周转率、流动资产周转率、已获利息倍数及资本积累率均明显不遵从正态分布,因此,在下面得分析中,我们只对净资产收益率、总资产报酬率、资产负债率及销售增长率这四个指标进行比较,并认为这四个变量组成得向量遵从正态分布(尽管事实上并非如此)。

多元统计分析判别分析(方法+步骤+分析总结)

判别分析：实验步骤：1.在SPSS窗口中选择：分析-分类-判别，将变量导入自变量框中，group导入分组变量中，选择定义范围，最小为1最大为3，并选择一起输入自变量，点击继续2.点击统计量，描述性中选择“均值”，“单变量”和”Box”，选择函数系数中的“Fisher”“未标准化”，矩阵中选择“组内相关”，点击继续3.点击分类点击继续4.点击“保存”，三个框均选中，点击继续5.点击确定实验结果分析：1.表1 组统计量看各个总体在均值等指标上的值是否接近，若接近说明各类之间在该指标差异不大表2表3 汇聚的组内矩阵若自变量之间存在高度相关，则判别分析价值不大，但并不严格，允许出现一定的相关表4 协方差矩阵的均等性的箱式检验检验结果p值>0.05时，说明协方差矩阵相等，可以进行bayes检验表7由表7可知，两个Fisher 判别函数分别为1123456212345674.99 1.861 1.6560.8770.7980.098 1.57929.4820.867 1.1550.3560.0890.0540.69y XX X X X X y X X X XX X =--+-+++=--+--++表8 结构矩阵该表是原始变量与典型变量（标准化的典型判别函数）的相关系数，相关系数的绝对值越大，说明原始变量与这个判别函数的相关性越强由表9可知各类别重心的位置，通过计算观测值与各重心的距离，距离最小的即为该观测值的分类。

表10 给出贝叶斯判别函数系数第一类：11234565317.2143.9153.190.153.011.0189.3F X X X X X X =--+-+++2. 将各样品的自变量值代入上述三个Bayes 判别函数，得到函数值。

比较函数值，哪个函数值比较大就可以判断该样品判入哪一类。

多元统计实验三方差分析

桂林电子科技大学数学与计算科学学院实验报告145.29m ，中殿的平均高度为22.69m.n=16个哥特式教堂的样本数据如下：序号长度/m 中殿高度/m 序号长度/m 中殿高度/m1 158.19 30.49 9 124.05 21.952 68.58 22.8610 89.92 26.82 3 91.44 15.85 11 83.21 16.764 127.41 18.90 12 126.49 20.425 124.66 20.73 13 55.47 13.726 129.54 26.21 14 161.54 31.397 112.78 17.37 15 186.23 31.398 154.28 24.99 16 144.17 25.6试检验'00:(145.29,22.69)H μμ==, 10:H μμ≠ (0.05)α=.四，实验过程原始记录（数据，图表，计算等）data shiyan3;input no x1 x2 @@;long=x1-145.29;haigh=x2-22.69;cards ;1 158.19 30.49 9 124.05 21.952 68.58 22.86 10 89.92 26.823 91.44 15.85 11 83.21 16.764 127.41 18.90 12 126.49 20.425 124.66 20.73 13 55.47 13.726 129.54 26.21 14 161.54 31.397 112.78 17.37 15 186.23 31.398 154.28 24.99 16 144.17 25.6;proc means data =shiyan3 probt ; /* probt 用于检验正态总体均值是否为零*/ var long haigh ;run ;proc univariate data =shiyan3 normal ;var long haigh;run ;方法1.图2.2.2 位置检验由于样本量<2000,因此，采用Shapiro-Wilk检验。

spss主成分分析报告

spss主成分分析报告目录spss主成分分析报告 (1)引言 (2)研究背景 (2)研究目的 (2)研究意义 (3)主成分分析的基本概念 (4)主成分分析的定义 (4)主成分分析的原理 (5)主成分分析的应用领域 (6)数据收集与准备 (7)数据收集方法 (7)数据预处理 (8)数据清洗 (9)主成分分析的步骤 (9)因子提取 (9)因子旋转 (10)因子解释 (11)SPSS软件在主成分分析中的应用 (12)SPSS软件的介绍 (12)数据导入与处理 (13)主成分分析的操作步骤 (14)主成分分析结果的解读 (15)因子载荷矩阵的解读 (15)方差解释率的解读 (16)因子得分的解读 (17)主成分分析的结果验证与评价 (18)因子可靠性分析 (18)因子有效性分析 (19)结果的稳定性分析 (19)主成分分析的局限性与改进 (20)主成分分析的局限性 (20)主成分分析的改进方法 (21)结论 (22)研究总结 (22)研究展望 (23)引言研究背景主成分分析（Principal Component Analysis，简称PCA）是一种常用的多元统计分析方法，广泛应用于各个领域的研究中。

它通过将原始数据转换为一组新的无关变量，即主成分，来揭示数据中的潜在结构和模式。

主成分分析不仅可以帮助我们降低数据的维度，减少冗余信息，还可以提取出数据中的主要特征，帮助我们更好地理解和解释数据。

在当今信息爆炸的时代，数据的获取和处理变得越来越重要。

各个领域的研究者和决策者需要从大量的数据中提取有用的信息，以支持决策和研究。

然而，原始数据往往包含大量的冗余信息和噪声，使得数据分析变得困难和复杂。

主成分分析作为一种有效的数据降维方法，可以帮助我们从复杂的数据中提取出关键信息，简化数据分析的过程。

主成分分析最早由卡尔·皮尔逊（Karl Pearson）于1901年提出，并在之后的几十年中得到了广泛的研究和应用。

多元统计实验报告

多元统计实验报告关于某校导师研究生指标的分配问题班级：***姓名：***学号：***目录一．问题背景 (4)二．实验要求 (4)三．数据预处理 (4)3.1 数据分离3.2 数量化3.3 归一化四．建模及求解 (6)4.1多元线性回归填补模型 (6)4.1.1 多元线性回归模型简介4.1.1.1 向前选择法4,1.1.2 向后消去法4.1.1.3 逐步删选法4.1.2 多元线性回归填补模型4.1.2.1 建模4.1.2.1 求解A. 向前选择法B. 向后消去发C. 逐步删选法4.2判别分析填补模型 (9)4.2.1 判别分析模型简介4.2.1.1 概论4.2.1.2 分类4.2.1.3 常用判别方法A. 距离判别法B. Fisher判别法C. Bayes判别法4.2.2 判别分析填补模型4.2.2.1 建模4.2.2.2 求解4.3主成分分析验证模型 (12)4.3.1 主成分分析简介4.3.1.1 概论4.3.1.2 数学模型4.3.1.3 主成分分析步骤4.3.2 主成分分析验证模型4.3.2.1 建模4.3.2.2 求解4.4典型相关分析验证模型 (15)4.4.1 典型相关性分析简介4.4.1.1 概论4.4.1.2 数学模型4.4.2 典型相关性分析验证模型4.4.2.1 建模4.4.2.2 求解A. 典型相关结果B. 多种多元统计结果比较C. 典型变量的标准线性方程D. 原始变量与典型变量的相关度4.5聚类分析 (18)4.5.1 聚类分析简介4.5.1.1 概论4.5.1.2 常用方法A.最短距离法B.平均距离法C.Ward法4.5.1 聚类分析4.5.1.1 建模4.5.1.2 求解A.聚类图形表示B.Ward聚类详解C.基于Ward分类的预测五．体会及建议 (24)六．SAS程序 (25)七．附录 (28)一．问题背景高等学校研究生招生指标分配问题，对研究生的培养质量、教育资源利用率、学科建设和科研成果的取得有直接影响。

多元统计分析方法

<多元统计分析方法> Ch1 基本概念1.多元总体：该总体有多个属性，可表示为X=x 1…x p ，考察一个P 元总体即是考察这个总体中每个对象的P 个属性。

2.多元样本数据：X=[x 1,x 2…x n ]=x 11,x 12,…,x 1n…x p1,x p2,…,x pn3.多元总体的样本统计参数： 3.1 单总体3.1.1 分属性行样本统计参数样本平均值向量：中心化数据：原始数据-平均数标准化数据=中心化数据/该行样本标准差样本离差矩阵Q ：Q=XX ’,即两两中心化属性行乘积和，q αβ=∑(x αi −x α̅̅̅)(x βi −x β̅̅̅)(1≤n 1α,β≤p)样本协方差矩阵S ：S=Q/n=XX ’/n(n 为样本数)样本相关矩阵R ：用X 中的两行计算两属性间的相关，r αβ=√s s =√q q3.1.2 样本间统计参数各种距离：欧氏距离，马氏距离，B 模距离，绝对距离，切比雪夫距离相似系数：定量：用X 中的两列算出的相关系数；夹角余弦c αβ=i ′j|x ||x |αi αjp 1√∑x αi 21∑x αj21定性：首先转化为0,1型定性数据；对于p 元总体的变量α，两样本单元i,j 配对情况有四种(1,1),(1,0),(0,1),(0,0)，分别用a,b,c,d 表示所有变量中这四种情况出现的次数。

显然a,d 出现的次数越多，两样本越接近。

由此定义匹配系数：f ij =a+d p=1−绝对距离p；修正的夹角余弦f ij =√(a+b )(a+c )(b+d )(c+d)3.2 两总体(样本数均为n)两组样本的协方差矩阵：Y p×n ,X q×n ,Y 与X 的协方差矩阵cov ̂(y,x )=c 11,c 12,…,c 1q…c p1,c p2,…,c pq =YX ′(Y,X 分别表示Y,X 中心化数据)，其中c αβ=1n ∑(y αi −y α̅̅̅)(x βi −x β̅̅̅)(α≤p,β≤q)n 1,注意两个样本的协方差一般不对称，即c αβ≠c βα。

多元统计分析课程设计题目

多元统计分析课程设计题⽬课程设计题⽬1. 下表给出了1991年我国30个省、区、市城镇居民的⽉平均消费数据，所考察的⼋个指标如下（单位均为元/⼈）X1 ：⼈均粮⾷⽀出；X2 ：⼈均副⾷⽀出；X3 ：⼈均烟酒茶⽀出；X4 ：⼈均其他副⾷⽀出；X5 ：⼈均⾐着商品⽀出；X6 ：⼈均⽇⽤品⽀出；X7 ：⼈均燃料⽀出；X8 ：⼈均⾮商品⽀出；问题：（1）求样品相关系数矩阵R;（2）从R 出发做主成分分析，求各主成分的贡献率，及前两个主成分的累积贡献率；（3）求出前两个主成分并解释其意义.按第⼀主成分将30个省、区、市排序，结果如何？2. 下表是49位⼥性在空腹情况下三个不同时刻的⾎糖含量（⽤X1 ,X2 ,X3表⽰）和摄⼊等量⾷糖⼀⼩时后的三个时刻的⾎糖含量（⽤⼩X4 ,X5 ,X6表⽰）的观测值（单位：mg/100ml）.问题：分别从样本协⽅差阵S和样本相关系数矩阵R出发做主成分分析，求主成分的贡献率和各个主成分. 在两种情况下，你认为应保留⼏个主成分？其意义如何解释？就此⽽⾔，你认为基于S和R的分析那个结果更为合理？3. 考察1985年⾄2000年全国如下各价格指数：X1 ：商品零售价格指数；X2 ：居民消费价格指数；X3 ：城市居民消费价格指数；X4 ：农村居民消费价格指数；X5 ：农产品收购价格指数；X6 ：农村⼯业品零售价格指数；观测数据见下表.问题：按年份⽤下列⽅法进⾏系统聚类分析，画出谱系聚类图，并给出聚为3类的结果.（a）最短距离法；（b）最长距离法；（c）类平均距离法；4. 考察1985年⾄2000年全国如下各价格指数：X1 ：商品零售价格指数；X2 ：居民消费价格指数；X3 ：城市居民消费价格指数；X4 ：农村居民消费价格指数；X5 ：农产品收购价格指数；X6 ：农村⼯业品零售价格指数；观测数据见下表.问题：先将数据标准化，再按年份⽤下列⽅法进⾏系统聚类分析，画出谱系聚类图，并给出聚为3类的结果.（a）最短距离法；（b）最长距离法；（c）重⼼距离法.5. 研究货运总量y（万吨）与⼯业总产值x1（亿元）、农业总产值x2（亿元）。