四年级奥数题相遇问题习题及答案三篇
四年级奥数题相遇问题习题及答案三篇

四年级奥数题相遇问题习题及答案三篇篇一:四年级奥数题:相遇问题习题(A)年级班姓名得分一、填空题1.小张从甲地到乙地步行需要36分钟,小王骑自行车从乙地到甲地需要12分钟.他们同时出发,______分钟后两人相遇?2.甲、乙二人同时从学校出发到少年宫去,已知学校到少年宫的距离是2400米,甲到少年宫后立即返回学校,在距离少年宫300米处遇到乙,此时他们离开学校已30分钟.甲每分钟走_______米,乙每分钟走_______米.3.甲、乙两车同时从A、B两地相向而行,它们相遇时距A、B两地中心处8千米,已知甲车速度是乙车的1.2倍,求A、B两地的距离是_______千米.4.一列火车长152米,它的速度是每小时63.36公里.一个人与火车相向而行,全列火车从他身边开过用8秒钟.这个人的步行速度是每秒_______米.5.如图,A 、B 是圆直径的两端,小张在A 点,小王在B 点同时出发反向行走,他们在C 点第一次相遇,C 离A 点80米;在D 点第二次相遇,D 点离B 点60米.求这个圆的周长.6.甲、乙两地间的路程是600千米,上午8点客车以平均每小时60千米的速度从甲地开往乙地.货车以平均每小时50千米的速度从乙地开往甲地.要使两车在全程的中点相遇,货车必须在上午_______点出发.7.两列对开的火车途中相遇,甲车上的乘客从看到乙车到乙车从旁边开过去,共用6秒钟.已知甲车每小时行45千米,乙车每小时行36千米,乙车全长______米.8.小张与小王分别从甲、乙两村同时出发,在两村之间往返行走(到达另一村后就马上返回),他们在离甲村3.5千米处第一次相遇,在离乙村2千米处第二次相遇,问他们两人第四次相遇的地点离乙村______千米.(相遇指迎面相遇)9.甲村、乙村相距6千米,小张与小王分别从甲、乙两村同时出B发,在两村之间往返行走(到达另一村后马上返回).在出发后40分钟两人第一次相遇.小王到达甲村后返回,在离甲村2千米的地方两人第二次相遇.小张每小时走______千米,小王每小时走______千米.10.小张从甲地到乙地,每小时步行5千米,小王从乙地到甲地,每小时步行4千米.两人同时出发,然后在离甲、乙两地的中点1千米的地方相遇,求甲、乙两地间的距离是______千米.二、解答题11.甲乙两站相距360千米.客车和货车同时从甲站出发驶向乙站,客车每小时行60千米,货车每小时行40千米,客车到达乙站后停留0.5小时,又以原速返回甲站,两车对面相遇的地点离乙站多少千米?12.甲每分钟走50米,乙每分钟走60米,丙每分钟70米,甲乙两人从A地,丙一人从B地同时相向出发,丙遇到乙后2分钟又遇到甲,A、B两地相距多少米?13.A、B两地相距21千米,甲从A地出发,每小时行4千米,同时乙从B地出发相向而行,每小时行3千米.在途中相遇以后,两人又相背而行.各自到达目的的地后立即返回,在途中二次相遇.两次相遇点间相距多少千米?14.一列客车和一列货车同时从两地相向开出,经过18小时两车在某处相遇,已知两地相距1488千米,货车每小时比客车少行8千米,货车每行驶3小时要停驶1小时,客车每小时行多少千米?———————————————答案——————————————————————一、填空题1. 9分钟.36:12=3:136÷(3+1)=9(分)2. 甲90米/分;乙70米/分.速度差=300×2÷30=20(米/分)速度和=2400×2÷30=160(米/分)甲:(160+20)÷2=90(米/分)乙:(160-20)÷2=70(米/分)3. 176千米乙速:8×2÷(1.2-1)=80(千米/小时)甲速:80×1.2=96(千米/小时)相遇时间:1)8096(28=-÷⨯(小时)AB 间距离:1761)8096(=⨯+(千米)4. 1.4米/秒152÷8-63360÷3600=1.4(米/秒)5. 360米第二次相遇时两人合起来所走的行程是第一次相遇时合起来所走行程的3倍.则(80×3-60)×2=360(米)6. 上午7点7602160050216008=⎪⎭⎫ ⎝⎛÷⨯-÷⨯-(点)7. 135米.(45000+36000)÷(60×60)×6=135(米)8. 1千米(3.5×3-2)-[3.5×7-(3.5×3-2)×2]=1(千米)9. 小张:5千米/小时;小王:4千米/小时.小张:[6×(40×3÷60)-2]÷2=5(千米/小时)小王:(6+40×3÷60)÷2=4(千米/小时)10. 18千米(5+4)×[2÷(5-4)]=18(千米)二、解答题11. 客车从甲站行至乙站需要360÷60=60(小时)客车在乙站停留0.5小时后开始返回甲站时,货车行了40×(6+0.5)=260(千米)货车此时距乙站还有360-260=100(千米)货车继续前行,客车返回甲站(化为相遇问题)“相遇时间”为 100÷(60+40)=1(小时)所以,相遇点离乙站60×1=60(千米)12. 甲、丙相遇时,甲、乙两人相距的路程就是乙、丙相背运动的路程和,即(60+70)×2=260(米)甲、乙是同时出发的,到甲、丙相遇时,甲、乙相距260米,所以,从出发到甲、丙相遇需260÷(60-50)=26(分)所以,A 、B 两地相距(50+70)×26=3120(米)13. 画线段图如下:设第一次相遇点为M,第二次相遇点为N,AM=4×[21÷(4+3)]=12(千米)AN+AM=3×[21÷(4+3)]×2=18(千米)两次相遇点相距:12-(18-12)=6(千米)14. ①因为18小时=(3小时+1小时)×4+2小时,所以,货车实际行驶时间为3×4+2=14(小时)②设客车每小时行x千米,则货车每小时行(x -8)千米,列方程得18 x +14×(x -8)=1488,x =50篇二:四年级奥数题相遇问题习题及答案(B)年级班姓名得分一、填空题1.某列车通过250米长的隧道用25秒,通过210米长的隧道用23秒.问:该列车与另一列长320米、时速64.8千米的列车错车而过需要______秒?2.甲、乙二人骑车同时从环形公路的某点出发,背向而行,已知甲骑一圈需48分钟,出发后30分钟两人相遇.问:乙骑一圈需______分钟.3.甲、乙二人从相距36千米的两地相向而行.若甲先出发2小时,则在乙动身2.5小时后两人相遇;若乙先出发2小时,则甲动身3小时后两人相遇.甲每小时走______千米.乙每小时走_______千米.4.两列火车相向而行,甲车每小时行48千米,乙车每小时行60千米,两车错车时,甲车上一乘客从乙车车头经过他的车窗时开始计时,到车尾经过他的车窗共用13秒钟,求乙车全长_______米.5.李华从学校出发,以每小时4千米的速度步行到20.4千米外的冬令营报到.半小时后,营地老师闻讯前往迎接,每小时比李华多走1.2千米.又过了1.5小时,张明从学校骑车去营地报到,结果三人在途中某地相遇.问骑车人每小时行________千米.6.甲、乙、丙三辆车同时从A地出发到B地去,甲、乙两车的速度分别为每小时60千米和48千米.有一辆迎面开来的卡车分别在他们出发后6小时、7小时、8小时先后与甲、乙、丙三辆车相遇.求丙车的速度是_______千米/小时.7.已知甲、乙两车站相距470千米,一列火车于中午1时从甲站出发,每小时行52千米,另一列火车于下午2时30分从乙站开出,下午6时两车相遇.问:从乙站开出的火车的速度是_______千米/小时.8.一列快车和一列慢车相向而行,快车的车长是280米,慢车的车长是385米.坐在快车上的人看见慢车驶过的时间是11秒,那么坐在慢车上的人看见快车驶过的时间是______秒?9.操场正中央有一旗竿,小明开始站在旗竿正东离旗竿10米远的地方.然后向正北走了10米,再左转弯向正西走了20米,再左转弯向正南走了30米,再左转弯向正东走了40米,再左转弯向正北走了20米.这时小明离旗竿______米.10.甲乙两地相距258千米.一辆汽车和一辆拖拉机同时分别从两地相对开出,经过4小时两车相遇.已知汽车的速度是拖拉机速度的2倍.相遇时,汽车比拖拉机多行_______千米.二、解答题11.甲、乙二人分别从A 、B 两地同时出发,在A 、B 之间往返跑步.甲每秒跑3米,乙每秒跑7米,如果他们第四次迎面相遇点与第五次迎面相遇点之间相距150米,求A 、B 间相距多少米?12.如下图,A 、C 两地相距2千米,CB 两地相距5千米.甲、乙两人同时从C 地出发,甲向B 地走,到达B 地后立即返回;乙向A 地走, 到达A 地后立即返回;如果甲速度是乙速度的1.5倍,那么在乙到达D 地时,还未能与甲相遇,他们还相距0.5千米,这时甲距C 地多少千米?13.一只小船从A 地到B 地往返一次共用2小时.回来时顺水,比去时的速度每小时多行驶8千米,因此第二小时比第一小时多行驶6千米.求A 至B 两地距离.14.甲、乙两地之间有一条公路,李明从甲地出发步行往乙地;同时张平从乙地出发骑摩托车往甲地.80分后两人在途中相遇.张平到达甲地后马上折回往乙地,在第一次相遇后又经过20分张平在途中追上李明.张平到达乙地后又马上折回往甲地,这样一直下去,当李明到达乙地时,张平追上李明的次数是多少?5———————————————答 案——————————————————————一、填空题1. 15秒该车速:(250-210)÷ (25-23)=20(米/秒)车长:25×20-250=250(米)(64.8千米/小时=18米/秒)错车时间:(250+320)÷(20+18)=15(秒)2. 80分钟804813011=⎪⎭⎫ ⎝⎛-÷(分)3. 甲:6千米/时;乙:3.6千米/小时.36×2÷(2+3+2.5)=9.6(千米/小时)甲速:(36-9.6×2.5)÷2=6(千米/小时)乙速:(36-9.6×3)÷2=3.6(千米/小时)4. 390米甲速:48千米/小时=3113米/秒乙速:60千米/小时=3216米/秒 乙车长:3901331133216=⨯⎪⎭⎫ ⎝⎛+(米)5. 20千米/小时()205.12.1442144.202124=⎥⎦⎤⎢⎣⎡-++÷⎪⎭⎫ ⎝⎛⨯-÷⎪⎭⎫ ⎝⎛+⨯(千米/小时)6. 39千米/小时卡车速度:(60-48)×6÷(7-6)-48=24(千米/小时)丙车速度:48-(48+24)÷8=39(千米/小时)7. 60千米/时()60213552470=÷⨯-(千米/小时)8. 8秒11×280÷385=8(秒)9. 30米.10. 86千米.258÷4×(2-1)÷(2+1)×4=86(千米)11. 设甲、乙两人第i 次迎面相遇点为Ci(i=1,2,3,4,5).由甲、乙速度之比为3:7,令AB=1,则7:3:11=B C AC ,1031=AC .如下图:同理可得: 210321⨯=C C ,故1012=BC ; 5332=+BC B C ,故213=BC ; A B C 1 C 3 C 5 C 2 C 45343=+AC A C ,故53;101544==C C AC ;所以25053150=÷=AB (米).答:A 、B 相距250米.12. 由甲速是乙速的1.5倍的条件,可知甲路程是乙路程的1.5倍.设CD 距离为x 千米,则乙走的路程是(4+x)千米,甲路程为(4+x)×1.5千米或(5×2- x –0.5)千米.列方程得(4+ x)×1.5=5×2- x-0.5x =1.4这时甲距C 地:1.4+0.5=1.9(千米).13. 顺水速度:逆水速度=5:3由于两者速度差是8千米.立即可得出逆水速度123358=-÷=(千米/小时). A 至B 距离是12+3=15(千米)答:A 至B 两地距离是15千米.14. 画线段图如下:设从第一次相遇后到张平第一次追上李明时李明走了x 千米,则相同时间内张平走了: x(80÷20)×2+ x=9 x(千米),即在相同时间内,张平速度是李明速度的:9x ÷x=9(倍).这就是说,李明从甲地步行到乙地时,张平骑摩托车行走了9个全程.很明显,其中有5个全程是从乙地到甲地,有4个全程是从甲地到乙地.从甲地到乙地张平每走一个全程,必然追上李明一次.因此,张平共追上李明4次.张平 乙篇三:四年级奥数练习题相遇问题1、甲乙两列火车同时从相距700千米的两地相向而行,甲列车每小时行85千米,乙列车每小时行90千米,几小时两列火车相遇?2、甲乙两车从两地同时出发相向而行,甲车每小时行40千米,乙车每小时行60千米,经过3小时相遇。
含答案】四年级奥数行程问题精选练习(相遇、追及)

含答案】四年级奥数行程问题精选练习(相遇、追及)小牛老师工作室精华讲义:小学奥数行程问题知识点一:相遇问题1.两辆汽车同时从相距325千米的两地相对开出。
甲车速度为35千米/时,乙车速度为30千米/时。
当甲、乙两车相遇时,它们各行驶了多少千米?解答:两车相对速度为35+30=65千米/时。
根据相遇问题,它们行驶的总时间相等,所以它们各行驶了325/2=162.5千米。
2.高小帅家距离学校3000米。
小帅妈妈从家出发接小帅放学,小帅也要从学校回家。
他们同时出发。
小帅妈妈每分钟比小帅多走24米。
30分钟后两人相遇。
那么小帅的速度是多少?解答:设小帅速度为v,则小帅妈妈速度为v+24.根据相遇问题,它们行驶的总时间相等,所以小帅行驶了30v米,小帅妈妈行驶了30(v+24)米。
因为两人相遇,所以它们行驶的总路程为3000米,即30v+30(v+24)=3000,解得v=48米/分钟,即小帅的速度为48/60=0.8米/秒。
3.甲、乙两辆汽车分别从A、B两地相对而行。
已知甲车的速度为38千米/时,乙车的速度为40千米/时。
甲车先行2小时后,乙车才开始出发,乙车行驶5小时后两车相遇。
求A、B两地的距离。
解答:设A、B两地的距离为d。
则甲车行驶了d+2×38千米,乙车行驶了5×40千米。
因为它们相遇,所以它们行驶的总路程相等,即d+2×38+5×40=2×38+5×40+d,解得d=342千米。
4.两列城际列车从两城同时相对开出,其中一列车的速度为40千米/时,另一列车的速度为45千米/时。
在行驶途中,两列车先后各停车4次,每次停车15分钟。
这样经过7小时后两车相遇。
求两城的距离。
解答:设两城的距离为d。
则两车相对速度为40+45=85千米/时。
因为两车在行驶途中各停车4次,所以它们行驶的总时间为7小时-4×4×15分钟=6.4小时。
四年级数学相遇问题练习题及答案

四年级数学相遇问题练习题及答案知识目标:解答此类题应作一条线段图来全面考虑运动物体的个数、运动的方向、出发的地点以及运动的路线形式等。
下面的关系式必须牢记:(1)速度和×相遇时间=相遇路程(2)相遇路程÷速度和=相遇时间(3)相遇路程÷相遇时间=速度和速度和:两人或两车速度的和;相遇时间:两人或两车同时开出到相遇所用的时间。
【经典习题1】:两列火车同时从两地相对开出,甲列火车每小时行86千米,乙列火车每小时行102千米,经过5小时两车在途中相遇,求两地相距多少千米?【经典习题2】:甲、乙两人分别从相距20千米的两地同时出发相向而行,甲每小时走6千米,经过2小时后两人相遇,问乙每小时行多少千米?【经典习题3】:王明和妹妹两人从相距2000米的两地相向而行,王明每分钟行110米,妹妹每分钟行90米,如果一只狗与王明同时同向而行,每分钟行500米,遇到妹妹后,立即回头向王明跑去,遇到王明再向妹妹跑去,这样不断来回,直到王明和妹妹相遇为止。
狗共行了多少米?【经典习题4】:甲每小时行7千米,乙每小时行5千米,两人由相隔18千米的两地相背而行,几小时后两人相隔54千米?【经典习题5】:甲乙两艘舰由相距418千米的两个港口同时相对开出,甲舰每小时行36千米,乙舰每小时行34千米,开出1小时候,甲舰因有紧急任务返回原港,又立即起航与乙舰继续相对开出,经过多少小时两舰相遇?【经典习题6】:甲地到乙地快车每小时行32千米,慢车每小时行18千米,如果两车同时从甲乙两地相对开出,可在距中点35千米的地方相遇,甲乙两地相距是多少千米?经典习题解析【经典习题1】:两列火车同时从两地相对开出,甲列火车每小时行86千米,乙列火车每小时行102千米,经过5小时两车在途中相遇,求两地相距多少千米?(86+102)×5=940千米或者86×5+102×5=940千米【经典习题2】:甲、乙两人分别从相距20千米的两地同时出发相向而行,甲每小时走6千米,经过2小时后两人相遇,问乙每小时行多少千米?20÷2-6=4千米或者(20-6×2)÷2=4千米【经典习题3】:王明和妹妹两人从相距2000米的两地相向而行,王明每分钟行110米,妹妹每分钟行90米,如果一只狗与王明同时同向而行,每分钟行500米,遇到妹妹后,立即回头向王明跑去,遇到王明再向妹妹跑去,这样不断来回,直到王明和妹妹相遇为止。
小学四年级奥数-相遇问题

添加标题
每小时行的路程=快车每小时的路程+慢车每小时的路程
05
添加标题
450KM
06
每小时行的路程: 85+65=150(千米)
时间:450÷150=3(小时)
例3: 甲乙两站相距450千米,一列快车从甲站开出,每小时行驶85千米,一列慢车从乙站开出,每小时行驶65千米。 若两车同时相向而行,快车行驶多少小时与慢车相遇?
甲乙两地相距1500米,两人分别从甲乙两地相向出发,10分钟后相遇。如果两人每分钟各自提速15米,仍从甲乙两地相向出发,则出发后多少秒两人相遇?
24
500
甲乙两车同时从东西两地相对开出,6小时相遇。如果甲车每小时少行9千米,乙车每小时多行6千米,那么经过6小时后,两车已行路程是剩下路程的19倍。东西两地相距多少千米?
360
:
例8:甲乙两人同时从A到B地,甲每分钟行250米,乙每分钟行90米,甲到达B地后立即返回A地,在离B地1200米处与乙相遇,A、B两地相距多少千米?
2×1200÷(250-90)=15(分钟) 250×15-1200=2550(米) 答:A、B两地相距2550千米。 分析及详解】画图,从图中我们可以知道,甲比乙多走了2个1200,甲每分钟比乙多走250-90=160米,我们就可以求出总共走了多少时间:2×1200÷160=15分钟,那么A、B两地相距:250×15-1200=2550米
54×5+52×5
=270+260
=530(米)
(54+52)×5
=106×5
=530(米)
答:两地相距530米。
志明和小花同时从两地对面走去。经过5分钟相遇,两地相距多少米?(用两种方法解答)
1、
志明每分54米
四年级奥数培优《相遇问题》含答案

相遇问题例1.一辆客车与一辆货车同时从甲、乙两个城市相对开出,客车每小时行46 千米,货车每小时行48 千米。
3.5 小时两车相遇。
甲、乙两个城市的路程是多少千米?例2.大头儿子的家距离学校3000 米,小头爸爸从家去学校接大头儿子放学,大头儿子从学校回家,他们同时出发,小头爸爸每分钟比大头儿子多走24 米,50 分钟后两人相遇,那么大头儿子的速度是每分钟走多少米?例3.甲、乙两辆汽车分别从A、B 两地出发相向而行,甲车先行3小时后乙车从B地出发,乙车出发5小时后两车还相距15 千米.甲车每小时行48 千米,乙车每小时行50 千米.求A、B 两地间相距多少千米?例4.甲、乙二人分别从东、西两镇同时出发相向而行.出发2小时后,两人相距54 千米;出发5小时后,两人还相距27 千米.问出发多少小时后两人相遇?例5.两列城铁从两城同时相对开出,一列城铁每小时走40 千米,另一列城铁每小时走45 千米,在途中每列车先后各停车4次,每次停车15 分钟,经过7小时两车相遇,求两城的距离?例6.两地相距3300 米,甲、乙二人同时从两地相对而行,甲每分钟行82 米,乙每分钟行83 米,已经行了15 分钟,还要行多少分钟两人可以相遇?例7.甲、乙两辆汽车同时从A地出发去B地,甲车每小时行50 千米,乙车每小时行40 千米.途中甲车出故障停车修理了3小时,结果甲车比乙车迟到1小时到达B地.A、B两地间的路程是多少?例8.甲、乙两列火车同时从A地开往B地,甲车8小时可以到达,乙车每小时比甲车多行20 千米,比甲车提前2小时到达.求A、B 两地间的距离.例9.军事演习中,“我”海军英雄舰追及“敌”军舰,追到A岛时,“敌”舰已在10 分钟前逃离,“敌”舰每分钟行驶1000 米,“我”海军英雄舰每分钟行驶1470 米,在距离“敌”舰600 米处可开炮射击,问“我”海军英雄舰从A 岛出发经过多少分钟可射击敌舰?例10.甲乙两车分别从A、B 两地同时相向开出,4 小时后两车相遇,然后各自继续行驶3小时,此时甲车距B 地10 千米,乙车距A地80 千米.问:A,B 两地的距离是多少千米?例11.甲乙两车分别从A、B 两地同时相向开出,4 小时后两车相遇,然后各自继续行驶3小时,此时甲车距B 地10 千米,乙车距A地80 千米.问:甲车到达B地时,乙车还要经过多少时间才能到达A地?相遇问题例1.一辆客车与一辆货车同时从甲、乙两个城市相对开出,客车每小时行46 千米,货车每小时行48 千米。
小学奥数四年级--相遇问题及答案

小学奥数四年级参考资料第五讲:相遇问题【知识与方法】:相遇问题是两个物体,从不同的地点做面对面的运动,即相向运动,相向运动会使两个物体在途中相遇。
其路程、速度和、相遇时间之间的关系为:路程=速度和×相遇时间速度和=路程÷时间时间=路程÷速度和【例题精讲】例1:两列火车同时从两地相对开出,快车每小时行80千米,慢车每小时行60千米,4小时相遇,两地相距多少千米?思维点拨:速度和×时间=路程模仿练习:两汽车同时从两个车站对开,甲车每小时行40千米,乙车每小时行38千米,经过6小时两车相遇。
这两个车站相距多少千米?例2、甲乙两人同时从相距1080米的两地相对而行,8分钟相遇。
已知甲每分钟走65米,乙每分钟走多少米?思维点拨:乙的速度=路程÷相遇时间-甲的速度模仿练习:北京到沈阳的铁路长830千米,两火车同时相对开出,10小时相遇。
已知甲车每小时行41千米,乙车每小时行多少千米?例3:两辆汽车同时从甲乙两地相对开出,A车每小时行50千米,B车每小时行40千米,两车在距中点20千米处相遇。
则甲乙两地相距多少千米?思维点拨:相遇时,A车比B车多行40千米,A车的速度比B车的速度快10千米,即得出相遇时间为4小时。
再根据:速度和×相遇时间=路程模仿练习:甲、乙两汽车同时从A、B两地相对开出,已知A车每小时行40千米,经过4小时,A车已经驶过中点25千米,这时与B车还相距6千米,B车每小时行多少千米?例4:甲乙两地相距300千米,客车和货车同时从甲地出发驶向乙地。
货车的速度为每小时60千米,客车的速度为每小时40千米,货车到达乙地后立即以原速返回甲地,从甲地出发后几小时两车相遇?思维点拨:用线段图分析行程问题,直观明了。
模仿练习:甲、乙两人同时从学校出发到少年宫去,已知学校到少年宫的距离是2400米,甲到少年宫后立即返回学校,在距离少年宫300米的地方遇到乙,此时他们已经离开学校30分钟了。
四年级奥数-相遇问题

相遇问题(一)例1:A、B两地相距138千米,甲、乙两人骑自行车分别从两地同时出发,相向而行。
甲每小时行13千米,乙每小时行12千米,乙在行进中因修车耽误了1小时,然后继续行进,与甲相遇。
求出发到相遇经过几小时例2:甲、乙两车分别从相距480千米的两地同时相向而行,5小时后相遇。
已知甲车每小时比乙车快8千米,相遇时乙车行了多少路程例3:A、B两地相距520千米,甲车从A地开出2小时后,乙车从B地相对开出,乙车开出后5小时后与甲车相遇,已知甲车比乙车每小时少行8千米。
问甲、乙两车每小时各行多少千米例4:某县举行长跑比赛,运动员跑到离起点5千米处要向起跑点返回,领先的运动员每分跑320米,最后的运动员每分跑305米。
起跑后多少分这两个运动员相遇相遇时离返回点有多少米练一练1.甲、乙两地相距450千米,客车10小时行完全程,货车15小时行完全程,客车和货车同时从两地出发,相向而行,几小时后相遇相遇时两车各行了多少千米2.甲、乙两人从同一地点出发,背向而行,甲以每分钟60米的速度先行,12分钟后乙才出发,乙行了20分钟后与甲相距3220米,乙每分钟行多少米3.甲、乙两地相距180千米,一人骑自行车从甲地出发每小时走15千米,另一人骑摩托车从乙地同时出发,两人相向而行,已知摩托车车速是自行车的3倍,问多少小时后两人相遇4.两地相距320千米,甲车从一地开出1小时后,乙车从另一地相对开出,又经过4小时与甲车相遇,已知甲车每小时比乙车多行10千米,问一车每小时行多少千米5.甲、乙二人从相距116千米的A、B两地出发相向而行,甲先出发1小时。
他们二人在乙出后的4小时相遇,又已知甲比乙每小时慢2千米,求甲、乙二人的速度。
6.A、B两地相距496千米,甲车从A地出发开往B地,每小时行32千米,甲车开出半小时后,乙车从B地出发开往A地,它的速度是甲车的2倍,问乙车开出几小时后,两车相遇7.甲、乙两人骑自行车,分别从相距75千米处同时相向而行,3小时后两人相遇,已知甲骑车比一骑车每小时快5千米。
小学四年级奥数相遇问题练习题5篇

小学四年级奥数相遇问题练习题5篇1.小学四年级奥数相遇问题练习题1、甲乙两列火车分别从A、B两地同时出发相向而行,甲车每小时行驶75千米,乙车每小时行驶69千米,经过18小时两车途中相遇,两地间的铁路长多少千米?2、甲乙两车分别从相距480千米的A、B两城同时出发相向而行,已知甲车从A城到B城需要6小时,乙车从B城到A城需要12小时,两车出发后几小时相遇?3、甲乙两列火车同时从相距700千米的两地开出,甲车每小时行75千米,经过5小时相遇,乙车每小时行多少千米?4、甲乙两队学生从相隔18千米的两地同时出发相向而行。
一个同学骑自行车以每小时14千米的速度在两队之间不停地往返联络。
甲队每小时行5千米,乙队每小时行4千米,两队相遇时,骑自行车的同学共行多少千米?5、东西两镇相距20千米,甲乙两人分别从两镇同时出发相背而行,甲每小时行的路程是乙的2倍,3小时后两人相距56千米,两人的速度各是多少?2.小学四年级奥数相遇问题练习题1、甲乙两人同时从相距90千米的两地相向而行。
甲每小时行8千米,乙每小时比甲多行2千米。
几小时后他们在途中相遇?2、甲乙两人从相距99千米的两地相对开出,3小时后相遇,已知甲每小时行15千米,乙每小时行多少千米?3、甲乙两人同时从两地骑车相向而行,甲的速度是每小时20千米,乙每小时行18千米,两人在距离中点3千米的地方相遇。
问两地相距多少千米?4、两列火车同时从甲乙两城相对开出,甲车每小时行76千米,乙车每小时行82千米,两车开出3小时后,还相距156千米。
甲乙两城相距多少千米?5、甲乙两地相距384千米,两辆汽车从两地相对开出,甲车每小时行38千米,乙车每小时行42千米。
甲车开出64千米后,两车才出发,再经过几小时两车相遇?3.小学四年级奥数相遇问题练习题1、一列货车早晨8时从甲地开往乙地,平均每小时行40千米,一列客车从乙地开往甲地,平均每小时行60千米。
已知客车在货车开出后2小时才出发,下午2时两车同时经过途中某站,然后仍继续前进。
四年级奥数-相遇问题

相遇问题(一)例1:A、B两地相距138 千米,甲、乙两人骑自行车分别从两地同时出发,相向而行。
甲每小时行13 千米,乙每小时行12 千米,乙在行进中因修车耽误了 1 小时,然后继续行进,与甲相遇。
求出发到相遇经过几小时例2:甲、乙两车分别从相距480 千米的两地同时相向而行, 5 小时后相遇。
已知甲车每小时比乙车快8 千米,相遇时乙车行了多少路程例3:A、B两地相距520千米,甲车从A地开出2小时后,乙车从B地相对开出,乙车开出后 5 小时后与甲车相遇,已知甲车比乙车每小时少行8千米。
问甲、乙两车每小时各行多少千米例 4 :某县举行长跑比赛,运动员跑到离起点 5 千米处要向起跑点返回,领先的运动员每分跑320 米,最后的运动员每分跑305 米。
起跑后多少分这两个运动员相遇相遇时离返回点有多少米练一练1.甲、乙两地相距450 千米,客车10 小时行完全程,货车15 小时行完全程,客车和货车同时从两地出发,相向而行,几小时后相遇相遇时两车各行了多少千米2.甲、乙两人从同一地点出发,背向而行,甲以每分钟60 米的速度先行,12分钟后乙才出发,乙行了20 分钟后与甲相距3220米,乙每分钟行多少米3.甲、乙两地相距180 千米,一人骑自行车从甲地出发每小时走15千米,另一人骑摩托车从乙地同时出发,两人相向而行,已知摩托车车速是自行车的3 倍,问多少小时后两人相遇4.两地相距320千米,甲车从一地开出 1 小时后,乙车从另一地相对开出,又经过 4 小时与甲车相遇,已知甲车每小时比乙车多行10 千米,问一车每小时行多少千米5.甲、乙二人从相距116千米的A、B两地出发相向而行,甲先出发 1 小时。
他们二人在乙出后的 4 小时相遇,又已知甲比乙每小时慢2千米,求甲、乙二人的速度。
6.A、B两地相距496千米,甲车从 A 地出发开往B地,每小时行32 千米,甲车开出半小时后,乙车从B地出发开往A地,它的速度是甲车的 2 倍,问乙车开出几小时后,两车相遇7.甲、乙两人骑自行车,分别从相距75 千米处同时相向而行,3 小时后两人相遇,已知甲骑车比一骑车每小时快 5 千米。
四年级奥数多次相遇问题试题及答案

四年级奥数多次相遇问题试题及答案【篇一】有人沿公路前进,对面来了一辆汽车,他问司机:“后面有自行车吗?”司机回答:“十分钟前我超过一辆自行车”,这人继续走了十分钟,遇到自行车,已知自行车速度是人步行速度的三倍,问汽车的速度是步行速度的()倍.考点:多次相遇问题.分析:人遇见汽车的时候,离自行车的路程是:(汽车速度-自行车速度)×10,这么长的路程要自行车和人合走了10分钟,即:(自行车+步行)×10,等式:(汽车速度-自行车速度)×10=(自行车+步行)×10,即:汽车速度-自行车速度=自行车速度+步行速度.汽车速度=2×自行车速度+步行速度,又自行车的速度是步行的3倍,所以汽车速度是步行的7倍.解答:(汽车速度-自行车速度)×10=(自行车+步行)×10,即:汽车速度-自行车速度=自行车速度+步行速度.汽车速度=2×自行车速度+步行,又自行车的速度是步行的3倍,所以汽车速度=(2×3+1)×步行速度=步行速度×7.故答案为:7.点评:解答此题的关键是要推出:汽车与自行车的速度差等于人与自行车的速度和. 【篇二】1.前进钢铁厂用两辆汽车从距工厂90千米的矿山运矿石,现有甲、乙两辆汽车,甲车自矿山,乙车自钢铁厂同时出发相向而行,速度分别为每小时40千米和50千米,到达目的地后立即返回,如此反复运行多次,如果不计装卸时间,且两车不作任何停留,则两车在第三次相遇时,距矿山多少千米?解析请看下一页分析:在往返来回相遇问题中,第一次相遇两人合走完一个全程,以后每次再相遇,都合走完两个全程.即:两人相遇时是在他们合走完1,3,5个全程时.然后根据路程÷速度和=相遇时间解答即可.解答:解答:①第三次相遇时两车的路程和为:90+90×2+90×2,=90+180+180,=450(千米);②第三次相遇时,两车所用的时间:450÷(40+50)=5(小时);③距矿山的距离为:40×5-2×90=20(千米);答:两车在第三次相遇时,距矿山20千米.点评:在多次相遇问题中,相遇次数n与全程之间的关系为:1+(n-1)×2个全程=一共行驶的路程.【篇三】求两地之间的距离1.给出两人的速度以及某次相遇的时间,求两地距离。
四年级数学相遇问题经典例题和练习(有答案)

四年级数学相遇问题知识目标:解答此类题应作一条线段图来全面考虑运动物体的个数、运动的方向、出发的地点以及运动的路线形式等。
下面的关系式必须牢记:(1)速度和×相遇时间=相遇路程(2)相遇路程÷速度和=相遇时间(3)相遇路程÷相遇时间=速度和速度和:两人或两车速度的和;相遇时间:两人或两车同时开出到相遇所用的时间。
【经典习题1】:两列火车同时从两地相对开出,甲列火车每小时行86千米,乙列火车每小时行102千米,经过5小时两车在途中相遇,求两地相距多少千米?【经典习题2】:甲、乙两人分别从相距20千米的两地同时出发相向而行,甲每小时走6千米,经过2小时后两人相遇,问乙每小时行多少千米?【经典习题3】:王明和妹妹两人从相距2000米的两地相向而行,王明每分钟行110米,妹妹每分钟行90米,如果一只狗与王明同时同向而行,每分钟行500米,遇到妹妹后,立即回头向王明跑去,遇到王明再向妹妹跑去,这样不断来回,直到王明和妹妹相遇为止。
狗共行了多少米?【经典习题4】:甲每小时行7千米,乙每小时行5千米,两人由相隔18千米的两地相背而行,几小时后两人相隔54千米?【经典习题5】:甲乙两艘舰由相距418千米的两个港口同时相对开出,甲舰每小时行36千米,乙舰每小时行34千米,开出1小时候,甲舰因有紧急任务返回原港,又立即起航与乙舰继续相对开出,经过多少小时两舰相遇?【经典习题6】:甲地到乙地快车每小时行32千米,慢车每小时行18千米,如果两车同时从甲乙两地相对开出,可在距中点35千米的地方相遇,甲乙两地相距是多少千米??『经典习题解析』【经典习题1】:两列火车同时从两地相对开出,甲列火车每小时行86千米,乙列火车每小时行102千米,经过5小时两车在途中相遇,求两地相距多少千米?(86+102)×5=940千米或者86×5+102×5=940千米【经典习题2】:甲、乙两人分别从相距20千米的两地同时出发相向而行,甲每小时走6千米,经过2小时后两人相遇,问乙每小时行多少千米?20÷2-6=4千米或者(20-6×2)÷2=4千米【经典习题3】:王明和妹妹两人从相距2000米的两地相向而行,王明每分钟行110米,妹妹每分钟行90米,如果一只狗与王明同时同向而行,每分钟行500米,遇到妹妹后,立即回头向王明跑去,遇到王明再向妹妹跑去,这样不断来回,直到王明和妹妹相遇为止。
四年级奥数题相遇问题习题及答案

十五、相遇问题(B卷)年级班姓名得分一、填空题1.某列车通过250米长的隧道用25秒,通过210米长的隧道用23秒.问:该列车与另一列长320米、时速64.8千米的列车错车而过需要秒?2.甲、乙二人骑车同时从环形公路的某点出发,背向而行,已知甲骑一圈需48分钟,出发后30分钟两人相遇.问:乙骑一圈需分钟.3.甲、乙二人从相距36千米的两地相向而行.若甲先出发2小时,则在乙动身2.5小时后两人相遇;若乙先出发2小时,则甲动身3小时后两人相遇.甲每小时走千米.乙每小时走千米.4.两列火车相向而行,甲车每小时行48千米,乙车每小时行60千米,两车错车时,甲车上一乘客从乙车车头经过他的车窗时开始计时,到车尾经过他的车窗共用13秒钟,求乙车全长米.5.李华从学校出发,以每小时4千米的速度步行到20.4千米外的冬令营报到.半小时后,营地老师闻讯前往迎接,每小时比李华多走1.2千米.又过了1.5小时,张明从学校骑车去营地报到,结果三人在途中某地相遇.问骑车人每小时行千米.6.甲、乙、丙三辆车同时从4地出发到8地去,甲、乙两车的速度分别为每小时60千米和48千米.有一辆迎面开来的卡车分别在他们出发后6小时、7小时、8小时先后与甲、乙、丙三辆车相遇.求丙车的速度是千米/小时.7.已知甲、乙两车站相距470千米,一列火车于中午1时从甲站出发,每小时行52千米,另一列火车于下午2时30分从乙站开出,下午6时两车相遇.问:从乙站开出的火车的速度是千米/小时.8.一列快车和一列慢车相向而行,快车的车长是280米,慢车的车长是385米.坐在快车上的人看见慢车驶过的时间是11秒,那么坐在慢车上的人看见快车驶过的时间是秒?9.操场正中央有一旗竿,小明开始站在旗竿正东离旗竿10米远的地方.然后向正北走了10米,再左转弯向正西走了20米,再左转弯向正南走了30米,再左转弯向正东走了40米,再左转弯向正北走了20米.这时小明离旗竿米.10.甲乙两地相距258千米.一辆汽车和一辆拖拉机同时分别从两地相对开此经过4小时两车相遇.已知汽车的速度是拖拉机速度的2倍.相遇时,汽车比拖拉机多行千米.二、解答题11甲、乙二人分别从A、8两地同时出发,在A、3之间往返跑步.甲每秒跑3米,乙每秒跑7米,如果他们第四次迎面相遇点与第五次迎面相遇点之间相距150米,求A、B间相距多少米?12.如下图,A、C两地相距2千米,CB两地相距5千米.甲、乙两人同时从C 地出发,甲向8地走,到达B地后立即返回;乙向4地走,到达A地后立即返回;如果甲速度是乙速度的 1.5倍,那么在乙到达。
奥数相遇问题(含答案)

相遇问题相遇问题一般是指两个物体从两地出发,相向而行,共同行一段路程,直至相遇,这类应用题的基本数量关系是:总路程=速度和×相遇时间这里的“速度和”是指两个物体在单位时间内共同行的路程。
例题与方法例1.甲、乙两辆汽车同时从东村、西村之间公路的中点向相反方向行驶,6小时后,甲车到达东村,乙车离西村还有42千米。
已知甲车的速度是乙车的2倍。
东、西两村之间的公路长多少千米?42×2×2=168例2.一支1800米长的队伍以每分90米的速度行进,队伍前端的联系员用9分的时间跑到队伍末尾传达命令。
联络员每分跑多少米?1800÷9-90=110例3.甲、乙两车相距516千米,两车同时从两地出发相向而行,乙车行驶6小时后停下修理车子,这时两车相距72千米。
甲车保持原速继续前进,经过2小时与乙车相遇。
求乙车的速度。
72÷2=36【 516-36×(6+2)】÷6=38例4.甲、乙两列车同时从A、B两地相对开出,第一次在离A地75千米处相遇。
相遇后两列车继续前进,到达目的地后又立刻返回,第二次相遇在离B地55千米处。
求A、B两会间的路程。
75×3-55=170练习与思考1.甲、乙两人分别从东、西两地同时相向而行。
2小时后两人相距96千米,5小时后两人相距36千米。
东、西两地相距多少千米?(96-36)÷(5-2)=20 20×2+96=1362.甲、乙两人骑车从同一地点向相反方向出发,甲车每小时行13千米,乙车每小时行12千米。
如果甲先行2小时,那么,乙行几小时后两人相距99千米?(99-13×2)÷(13+12)=2.923.甲、乙两地相距49千米,汽车行完全程要0.7小时,步行要14小时。
一个人从甲地出发,步行1.5小时后改乘汽车,他到达乙地共要几小时?(49-49÷14×1.5)÷(49÷0.7)+1.5=2.1254.甲、乙两车分别从A、B两地同时相向而行。
应用题板块-行程问题之相遇追及(小学四年级奥数题)
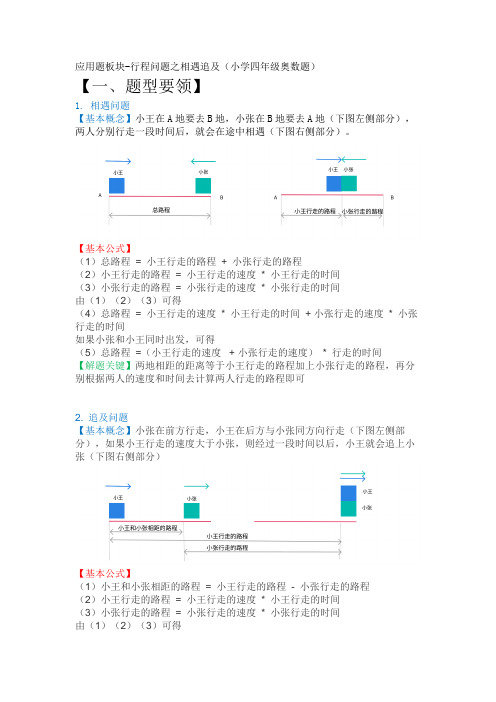
应用题板块-行程问题之相遇追及(小学四年级奥数题)【一、题型要领】1. 相遇问题【基本概念】小王在A地要去B地,小张在B地要去A地(下图左侧部分),两人分别行走一段时间后,就会在途中相遇(下图右侧部分)。
【基本公式】(1)总路程= 小王行走的路程+ 小张行走的路程(2)小王行走的路程= 小王行走的速度* 小王行走的时间(3)小张行走的路程= 小张行走的速度* 小张行走的时间由(1)(2)(3)可得(4)总路程= 小王行走的速度* 小王行走的时间+ 小张行走的速度* 小张行走的时间如果小张和小王同时出发,可得(5)总路程=(小王行走的速度 + 小张行走的速度)* 行走的时间【解题关键】两地相距的距离等于小王行走的路程加上小张行走的路程,再分别根据两人的速度和时间去计算两人行走的路程即可2. 追及问题【基本概念】小张在前方行走,小王在后方与小张同方向行走(下图左侧部分),如果小王行走的速度大于小张,则经过一段时间以后,小王就会追上小张(下图右侧部分)【基本公式】(1)小王和小张相距的路程= 小王行走的路程- 小张行走的路程(2)小王行走的路程= 小王行走的速度* 小王行走的时间(3)小张行走的路程= 小张行走的速度* 小张行走的时间由(1)(2)(3)可得(4)小王和小张相距的路程 = 小王行走的速度* 小王行走的时间- 小张行走的速度* 小张行走的时间如果小张和小王同时出发,可得(5)小王和小张相距的路程 =(小王行走的速度 - 小张行走的速度)* 行走的时间【解题关键】小王和小张相距的距离等于小王行走的路程减去小张行走的路程,再分别根据两人的速度和时间去计算两人行走的路程即可【举一反三】有一类题目是为赶时间,题目描述“为了节省XX时间从原本的速度x变成了之后的速度y”,解题时可以假象成另一个人以原速度提前走了XX 时间,而自身以修改后的速度从原地出发,最终两人同时到达终点,即可用“追及”问题解答【二、重点例题】例题1【题目】小张从甲地到乙地步行需要36分钟,小王骑自行车从乙地到甲地需要12分钟,他们同时出发,几分钟后两人相遇?【分析】走同样长的距离,小张花费的时间是小王花费时间的36 ÷ 12 = 3(倍),因此自行车的速度是步行速度的3倍。
小学四年级二次相遇问题奥数练习题及答案

小学四年级二次相遇问题奥数练习题及答案小学四年级二次相遇问题奥数练习题及答案1. 甲乙二人分别从A、B两地同时出发,并在两地间往返行走。
第一次二人在距离B点400米处相遇,第二次二人又在距离B点100米处相遇,问两地相距多少米?答案:(1)第一次二人在距离B点400米处相遇.说明第一次相遇时乙行400米.(2)甲、乙从出发到第二次相遇共行3个全程。
从第一次相遇后时到第二次相遇他们共行2个全程。
在这2个全程中甲行400+100=500米。
说明甲在每个全程中行500/2=250米。
(3)因此在第一次相遇时(一个全程)250+400=650米答:两地相距650米。
2. 甲每分钟走50米,乙每分钟走60米,丙每分钟走70米,甲乙两人从A地,丙一人从B地同时相向出发,丙遇到乙后2分钟又遇到甲,A、B 两地相距多少米?解答:丙遇到乙后此时与甲相距(50+70)×2=240米,也是甲乙的路程差,所以240÷(60-50)=24分,即乙丙相遇用了24分钟,A、B相距(70+60)×24=3120米.3. 甲、乙两车同时从A、B两地出发相向而行,两车在离B地64千米处第一次相遇.相遇后两车仍以原速继续行驶,并且在到达对方出发点后,立即沿原路返回,途中两车在距A地48千米处第二次相遇,A、B之间的距离是多少?解题思路:解答:【分析】甲、乙两车共同走完一个AB全程时,乙车走了64千米,从上图可以看出:它们到第二次相遇时共走了3个AB全程,因此,我们可以理解为乙车共走了3个64千米,再由上图可知:减去一个48千米后,正好等于一个AB全程.AB间的距离是64×3-48=144(千米)4. 甲乙二人分别从A、B两地同时出发,并在两地间往返行走。
第一次二人在距离B点400米处相遇,第二次二人又在距离B点100米处相遇,问两地相距多少米?答案:(1)第一次二人在距离B点400米处相遇.说明第一次相遇时乙行400米.(2)甲、乙从出发到第二次相遇共行3个全程。
高斯小学奥数四年级上册含答案第06讲_相遇问题

第六讲相遇问题院子里两棵槐树之间的距离是10米,一只小猫从一棵槐树跑到10米外的另一棵槐树需要5秒,那么小猫每秒跑10÷5=2米.行程问题是研究路程、时间和速度之间的关系.速度是衡量运动快慢的量.一般我们选用1个单位的时间,如用1小时或1分钟或1秒,用1个单位的时间内经过的路程的多少来表示速度的大小.因此,我们有了速度的定义:速度就是单位时间内所经过的路程.速度、时间和路程是行程问题中最重要的三个量,它们之间的关系如下:路程=速度⨯时间速度=路程÷时间时间=路程÷速度那么本文一开始提到的小猫跑过的距离10米就为路程,行程问题中常用的「分析」要计算速度,找清楚对应的路程和时间即可.路程单位是米和千米.而小猫跑了 5 秒就是时间,时间的常用单位有秒、分钟和小时.那么小猫的速度就是 2 米/秒,行程问题中常用的速度单位有米/秒、米/分和千米/时.练一练1.汽车以每小时 15 千米的速度行驶,那么 5 小时内,它行驶了_______千米.2.长跑运动员每秒跑 4 米,如果按照这个速度跑完 10000 米,需要________秒.3.一颗子弹射出后 2 秒钟,恰好击中 1800 米处的目标,那么它的速度是每秒_________米.4.一名长跑运动员以每秒 4 米的速度奔跑,那么 2 分钟内,他跑了_______米. 5.小高每分钟骑 100 米,如果要骑完 6000 米的路程,需要________小时.例题 1甲、乙两地相距 360 千米,一辆汽车原计划用 8 小时从甲地到乙地,那么汽车每小时应该行驶多少千米?实际上汽车行驶了一半路程后 发生了故障,在途中停留了 1 小时.如果按照原定的时间到达乙地, 汽车在后一半路程上每小时应该行驶多少千米?..练习 1兔子和乌龟赛跑,从 A 地跑到 B 地,全程共 6000 米.兔子计划 5 分钟跑完全程,结果比赛时兔子实际每分钟跑的路程要比计划的要少 200 米.那么兔子实际跑完全程用了多长时间?例题 2A、B两地相距4800米,甲、乙两人分别从A、B两地同时出发,相向而行,如果甲每分钟走60米,乙每分钟走100米,请问:(1)甲从A走到B需要多长时间?(2)两个人从出发到相遇需要多长时间?「分析」从出发到相遇,两人一共走了多远?他俩每分钟一共走多远呢?练习2阿呆和阿瓜从相距5000米的A、B两地同时出发,相向而行.阿呆每分钟走150米,阿瓜每分钟走350米,那么两人从出发到相遇需要多长时间?在两个运动物体在一条直线上运动,行进的方向可能相同,也可能相反.当它们行进方向相反时,如果它们面对面地接近,我们就称为“相向而行”;如果它们背对背地远离,我们就称为“相背而行”.两人之间的“相遇问题”既可以是“相向而行”也可以是“相背而行”,其中“相向而行”的相遇问题更常见一些.相遇问题关心的是两个人的“速度和”以及“路程和”.根据行程问题基本公式,我们可以类似得到相遇问题的三个基本公式:路程和=速度和⨯相遇时间相遇时间=路程和÷速度和速度和=路程和÷相遇时间在使用上述公式的时侯一定要注意,两个运动物体必须同时行进.如果整个相遇过程中并不是同时行进的,这个公式就不能直接应用了,需要分段考虑.例题3一辆公共汽车和一辆小轿车同时从相距350千米的两地相向而行,公共汽车每小时行40千米,小轿车每小时行60千米,问:(1)2小时后两车相距多少千米?(2)出发几小时后两车第一次相距50千米?(3)出发几小时后两车第二次相距50千米?「分析」两辆车从两地出发相向而行,为什么会有两次相距50千米呢?画出线段图,试着找找相同时间内两辆车的路程和吧!练习3A、B两地相距400千米,甲、乙两车分别从A、B同时出发,相向而行.甲车的速度为每小时60千米,乙车的速度为每小时40千米,请问:出发几小时后甲、乙两车第一次相距100千米?再过多长时间两车第二次相距100千米?对一些复杂的行程问题,单靠凭空想象已经无能为力了,这时就需要用一种形象的语言,把运动过程直观地表现出来,这就是我们解行程问题最得力的助手——线段图.画线段图时要特别注意:(1)专人专线:如果我们考虑的是两个或多个对象的运动,可以把它们的运动路线并排摆放,要注意不同人的运动路线不同;(2)同时性:如果运动时间分为几个阶段,那么应该在运动路线上表示相应的时刻.甲地乙地汽车A①③②②③①汽车B比如上图表示汽车A与汽车B分别从甲地、乙地同时出发,从开始①时刻到②时刻两车相遇,从②时刻到③时刻表示两车相遇后各自的运动情况.这样一来,我们就可以借助线段图把整个行程过程看得更清楚.画线段图是解行程问题最基本的方法.通过作图,可以将题目中的条件梳理清楚,还可以通过对图形的观察,挖掘出很多字面上看不出来的隐藏条件,进而找到解题的的突破口.例题4甲、乙两地相距350千米,一辆汽车在早上8点从甲地出发,以每小时40千米的速度开往乙地.2小时后另一辆汽车以每小时50千米的速度从乙地开往甲地.问:什么时候两车在途中相遇?「分析」两辆车不同时出发,可是不能直接用公式计算时间的.还是画出线段图,寻找相同时间内的路程和进行分析计算吧!练习4小王和小许从相距5000米的各自的家里出发,相向而行.小王每分钟走300米,小许每分钟走200米.小王出发10分钟后小许才从家出发,那么小王走了多长时间两人才相遇?例题5(1)小高跑400米用50秒,旗鱼每小时能游120千米.请问:谁的速度更快?(2)一般情况下,成年人跑100米要用14秒,河马奔跑的速度是40千米/时,河马跑的比人快吗?「分析」单位相同时,比较速度的大小即得谁快谁慢,这两小问中速度单位都没办法统一,该怎么去比较快慢呢?例题6甲、乙两人分别从A、B两地同时出发相向而行,已知甲每分钟走50米,乙走完全程要18分钟,出发3分钟后,甲、乙仍相距450米.请问:还要过多少分钟,甲、乙两人才能相遇?「分析」乙已经走了3分钟,那么走完剩下的路程就还需要多长时间?你能找到这段时间的路程吗?画出线段图分析吧!课堂内外作业1.一名长跑运动员以每秒4米的速度奔跑,那么5分钟后,他跑了多少米?2.甲、乙两车从相距700千米的两地同时出发,相向而行.甲车每小时行40千米,乙车每小时行60千米,出发几小时后两车相遇?3.甲、乙两车从两地同时出发,相向而行.甲车每小时行60千米,乙车每小时行75千米,出发2小时后两车相遇.请问两地相距多少千米?4.一只大老鼠和一只小老鼠分别从一根长1000厘米的直面条的两端开始吃.大老鼠每秒钟吃3厘米,小老鼠每秒钟吃1厘米,请问多长时间后,大老鼠和小老鼠第一次相距40厘米?5.甲、乙两城相距580千米,从甲城开往乙城的客车每小时行驶60千米.客车出发1小时后,货车从乙城开往甲城,每小时行70千米.货车开出多少小时后两车相遇?( ( ( (( “ ( 1 (第六讲 相遇问题1.例题 1答案:45 千米/小时;60 千米/小时. 详解: 1)行驶路程是 360 千米,行驶时间是 8 小时,所以行驶速度是 360 ÷ 8 = 45 千米/小时; (2)后一半路程是 360 ÷ 2 = 180 千米,行驶总时间仍然是 8 小时,前半程花了 4 + 1 = 5 小时, 所以后半程行驶时间是 3 小时,后半程的速度是 180 ÷ 3 = 60 千米/小时.2.例题 2答案:80 分钟;30 分钟详解: 1)甲行驶的路程是 4800 米,行驶的速度是 60 米/分钟,所以行驶的时间是 4800 ÷ 60 = 80分钟; 2)两人从出发到相遇行驶的路程和是 4800 米,行驶的速度和是 60 + 100 = 160 米/分钟, 所以相遇时间是 4800 ÷160 = 30 分钟.3. 例题 3答案:150 千米;3 小时;4 小时详解: 1)两车的速度和是 40 + 60 = 100 千米/小时,行驶时间是 2 小时,所以两车的路程和是100 ⨯ 2 = 200 千米,两车相距350 - 200 = 150 千米; 2)两车第一次相距 50 千米,两车还没有相遇,两车行驶的路程和是 350 - 50 = 300 千米,两车的速度和是 40 + 60 = 100 千米/小时,行驶时间是 300 ÷100 = 3 小时;(3)两车相遇后继续行驶,第二次相距 50 千米时,两车行驶的路程和 是 350 + 50 = 400 千米,两车的速度和是 40 + 60 = 100 千米/小时,行驶时间是 400 ÷100 = 4 小时.4. 例题 4 答案:13 点详解:画行程图,如下图所示,“车 1”提前出发 2 小时所行驶的路程是 40 ⨯ 2 = 80 千米,剩下 的路程是两辆汽车在相同时间内行驶的路程和,路程和是 350 - 80 = 270 千米,速度和是40 + 50 = 90 千米/小时,所以相遇时间是 270 ÷ 90 = 3 小时, 车 2”从 10 点出发,行驶了 3 小时, 所以 13 点两车在途中相遇.甲 350km乙车 1 2h40km /h车 250km /h5. 例题 5答案:旗鱼快;河马比人快详解: 1)小高的速度是 400 ÷ 50 = 8 米/秒,单位不一样,无法比较,所以把小高的速度变成米 /小时, 小时小高跑 8 ⨯ 3600 = 28800 米,速度即 28800 米/小时;旗鱼的速度是 120000 米/小时, 所以旗鱼的速度更快; 2)成年人 14 秒跑 100 米,所以 1 秒跑 7 米多;河马 1 小时跑 40 千米,(所以 1 秒跑 11 米多,所以河马跑的比人快;或者可以统一路程比速度:河马跑 40000 米用 1 小 时即 3600 秒,而成人跑 40000 米需要 14 ⨯ 400 = 5600 秒,路程相同,河马用时短,所以更快.6. 例题 6 答案:5 分钟详解:甲 3 分钟所行驶的路程是 50 ⨯ 3 = 150 米,乙距离 A 地还有 150 + 450 = 600 米.乙行驶全 程要 18 分钟,已经行驶了 3 分钟,还需要行驶 15 分钟才能走完 600 米,所以乙的速度是600 ÷15 = 40 米/分, 450 米是两人之后的路程和,速度和是50 + 40 = 90 米/分,所以还需要450 ÷ 90 = 5 分钟,甲、乙两人才能相遇.A甲3 分钟50 米/分450 米3 分钟B乙7.练习 1答案:6 分钟详解: 原计划 5 分钟跑完 6000 米,所以原计划速度为 6000 ÷ 5 = 1200 米/分,实际每分钟跑1200 - 200 = 1000 米,所以实际时间为 6000 ÷1000 = 6 分钟.8. 练习 2答案:10 分钟详 解 : 从出发到相遇,路程和为 5000 米,速度和为 150 + 350 = 500 米 / 分,所以时间为5000 ÷ 500 = 10 分钟.9. 练习 3答案:3 小时;5 小时简答: 1)两车第一次相距 100 千米,两车还没有相遇,两车行驶的路程和是400 -100 = 300 千 米,两车的速度和是 40 + 60 = 100 千米/小时,行驶时间是 300 ÷100 = 3 小时;(2)两车相遇后继 续行驶,第二次相距 100 千米时,两车行驶的路程和是 400 + 100 = 500 千米,两车的速度和是40 + 60 = 100 千米/小时,行驶时间是 500 ÷100 = 5 小时.10. 练习 4答案:14 分钟简答:画行程图,如下图所示,小王提前出发 10 分钟所行驶的路程是 300 ⨯10 = 3000 米,剩下 的 路 程 是 两 人 在 相 同 时 间 内 行 驶 的 路 程 和 , 路 程 和 是 5000 - 3000 = 2000 米 , 速 度 和 是300 + 200 = 500 米/分,相遇时间是 2000 ÷ 500 = 4 分钟,所以小王一共走了 10 + 4 = 14 分钟两人 才相遇.5000王10 分30011. 作业 1许200答案:1200米简答:4⨯5⨯60=1200米.注意单位换算.12.作业2答案:7小时简答:相遇时间为700÷(40+60)=7小时.13.作业3答案:270千米简答:两地距离即为两车路程和,为(60+75)⨯2=270千米.14.作业4答案:240秒简答:第一次相距40厘米,两只老鼠共同吃的面条长度和为1000-40=960厘米,用时960÷(3+1)=240秒.15.作业5答案:4小时简答:客车1小时行60千米,货车出发时两车相距580-60=520千米,相遇时间为520÷(60+70)=4小时.所以货车出发后4小时两车相遇了.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四年级奥数题相遇问题习题及答案三篇篇一:四年级奥数题:相遇问题习题(A)年级班姓名得分一、填空题1.小张从甲地到乙地步行需要36分钟,小王骑自行车从乙地到甲地需要12分钟.他们同时出发,______分钟后两人相遇?2.甲、乙二人同时从学校出发到少年宫去,已知学校到少年宫的距离是2400米,甲到少年宫后立即返回学校,在距离少年宫300米处遇到乙,此时他们离开学校已30分钟.甲每分钟走_______米,乙每分钟走_______米.3.甲、乙两车同时从A、B两地相向而行,它们相遇时距A、B两地中心处8千米,已知甲车速度是乙车的1.2倍,求A、B两地的距离是_______千米.4.一列火车长152米,它的速度是每小时63.36公里.一个人与火车相向而行,全列火车从他身边开过用8秒钟.这个人的步行速度是每秒_______米.5.如图,A 、B 是圆直径的两端,小张在A 点,小王在B 点同时出发反向行走,他们在C 点第一次相遇,C 离A 点80米;在D 点第二次相遇,D 点离B 点60米.求这个圆的周长.6.甲、乙两地间的路程是600千米,上午8点客车以平均每小时60千米的速度从甲地开往乙地.货车以平均每小时50千米的速度从乙地开往甲地.要使两车在全程的中点相遇,货车必须在上午_______点出发.7.两列对开的火车途中相遇,甲车上的乘客从看到乙车到乙车从旁边开过去,共用6秒钟.已知甲车每小时行45千米,乙车每小时行36千米,乙车全长______米.8.小张与小王分别从甲、乙两村同时出发,在两村之间往返行走(到达另一村后就马上返回),他们在离甲村3.5千米处第一次相遇,在离乙村2千米处第二次相遇,问他们两人第四次相遇的地点离乙村______千米.(相遇指迎面相遇)9.甲村、乙村相距6千米,小张与小王分别从甲、乙两村同时出B发,在两村之间往返行走(到达另一村后马上返回).在出发后40分钟两人第一次相遇.小王到达甲村后返回,在离甲村2千米的地方两人第二次相遇.小张每小时走______千米,小王每小时走______千米.10.小张从甲地到乙地,每小时步行5千米,小王从乙地到甲地,每小时步行4千米.两人同时出发,然后在离甲、乙两地的中点1千米的地方相遇,求甲、乙两地间的距离是______千米.二、解答题11.甲乙两站相距360千米.客车和货车同时从甲站出发驶向乙站,客车每小时行60千米,货车每小时行40千米,客车到达乙站后停留0.5小时,又以原速返回甲站,两车对面相遇的地点离乙站多少千米?12.甲每分钟走50米,乙每分钟走60米,丙每分钟70米,甲乙两人从A地,丙一人从B地同时相向出发,丙遇到乙后2分钟又遇到甲,A、B两地相距多少米?13.A、B两地相距21千米,甲从A地出发,每小时行4千米,同时乙从B地出发相向而行,每小时行3千米.在途中相遇以后,两人又相背而行.各自到达目的的地后立即返回,在途中二次相遇.两次相遇点间相距多少千米?14.一列客车和一列货车同时从两地相向开出,经过18小时两车在某处相遇,已知两地相距1488千米,货车每小时比客车少行8千米,货车每行驶3小时要停驶1小时,客车每小时行多少千米?———————————————答案——————————————————————一、填空题1. 9分钟.36:12=3:136÷(3+1)=9(分)2. 甲90米/分;乙70米/分.速度差=300×2÷30=20(米/分)速度和=2400×2÷30=160(米/分)甲:(160+20)÷2=90(米/分)乙:(160-20)÷2=70(米/分)3. 176千米乙速:8×2÷(1.2-1)=80(千米/小时)甲速:80×1.2=96(千米/小时)相遇时间:1)8096(28=-÷⨯(小时)AB 间距离:1761)8096(=⨯+(千米)4. 1.4米/秒152÷8-63360÷3600=1.4(米/秒)5. 360米第二次相遇时两人合起来所走的行程是第一次相遇时合起来所走行程的3倍.则(80×3-60)×2=360(米)6. 上午7点7602160050216008=⎪⎭⎫ ⎝⎛÷⨯-÷⨯-(点)7. 135米.(45000+36000)÷(60×60)×6=135(米)8. 1千米(3.5×3-2)-[3.5×7-(3.5×3-2)×2]=1(千米)9. 小张:5千米/小时;小王:4千米/小时.小张:[6×(40×3÷60)-2]÷2=5(千米/小时)小王:(6+40×3÷60)÷2=4(千米/小时)10. 18千米(5+4)×[2÷(5-4)]=18(千米)二、解答题11. 客车从甲站行至乙站需要360÷60=60(小时)客车在乙站停留0.5小时后开始返回甲站时,货车行了40×(6+0.5)=260(千米)货车此时距乙站还有360-260=100(千米)货车继续前行,客车返回甲站(化为相遇问题)“相遇时间”为 100÷(60+40)=1(小时)所以,相遇点离乙站60×1=60(千米)12. 甲、丙相遇时,甲、乙两人相距的路程就是乙、丙相背运动的路程和,即(60+70)×2=260(米)甲、乙是同时出发的,到甲、丙相遇时,甲、乙相距260米,所以,从出发到甲、丙相遇需260÷(60-50)=26(分)所以,A 、B 两地相距(50+70)×26=3120(米)13. 画线段图如下:设第一次相遇点为M,第二次相遇点为N,AM=4×[21÷(4+3)]=12(千米)AN+AM=3×[21÷(4+3)]×2=18(千米)两次相遇点相距:12-(18-12)=6(千米)14. ①因为18小时=(3小时+1小时)×4+2小时,所以,货车实际行驶时间为3×4+2=14(小时)②设客车每小时行x千米,则货车每小时行(x -8)千米,列方程得18 x +14×(x -8)=1488,x =50篇二:四年级奥数题相遇问题习题及答案(B)年级班姓名得分一、填空题1.某列车通过250米长的隧道用25秒,通过210米长的隧道用23秒.问:该列车与另一列长320米、时速64.8千米的列车错车而过需要______秒?2.甲、乙二人骑车同时从环形公路的某点出发,背向而行,已知甲骑一圈需48分钟,出发后30分钟两人相遇.问:乙骑一圈需______分钟.3.甲、乙二人从相距36千米的两地相向而行.若甲先出发2小时,则在乙动身2.5小时后两人相遇;若乙先出发2小时,则甲动身3小时后两人相遇.甲每小时走______千米.乙每小时走_______千米.4.两列火车相向而行,甲车每小时行48千米,乙车每小时行60千米,两车错车时,甲车上一乘客从乙车车头经过他的车窗时开始计时,到车尾经过他的车窗共用13秒钟,求乙车全长_______米.5.李华从学校出发,以每小时4千米的速度步行到20.4千米外的冬令营报到.半小时后,营地老师闻讯前往迎接,每小时比李华多走1.2千米.又过了1.5小时,张明从学校骑车去营地报到,结果三人在途中某地相遇.问骑车人每小时行________千米.6.甲、乙、丙三辆车同时从A地出发到B地去,甲、乙两车的速度分别为每小时60千米和48千米.有一辆迎面开来的卡车分别在他们出发后6小时、7小时、8小时先后与甲、乙、丙三辆车相遇.求丙车的速度是_______千米/小时.7.已知甲、乙两车站相距470千米,一列火车于中午1时从甲站出发,每小时行52千米,另一列火车于下午2时30分从乙站开出,下午6时两车相遇.问:从乙站开出的火车的速度是_______千米/小时.8.一列快车和一列慢车相向而行,快车的车长是280米,慢车的车长是385米.坐在快车上的人看见慢车驶过的时间是11秒,那么坐在慢车上的人看见快车驶过的时间是______秒?9.操场正中央有一旗竿,小明开始站在旗竿正东离旗竿10米远的地方.然后向正北走了10米,再左转弯向正西走了20米,再左转弯向正南走了30米,再左转弯向正东走了40米,再左转弯向正北走了20米.这时小明离旗竿______米.10.甲乙两地相距258千米.一辆汽车和一辆拖拉机同时分别从两地相对开出,经过4小时两车相遇.已知汽车的速度是拖拉机速度的2倍.相遇时,汽车比拖拉机多行_______千米.二、解答题11.甲、乙二人分别从A 、B 两地同时出发,在A 、B 之间往返跑步.甲每秒跑3米,乙每秒跑7米,如果他们第四次迎面相遇点与第五次迎面相遇点之间相距150米,求A 、B 间相距多少米?12.如下图,A 、C 两地相距2千米,CB 两地相距5千米.甲、乙两人同时从C 地出发,甲向B 地走,到达B 地后立即返回;乙向A 地走, 到达A 地后立即返回;如果甲速度是乙速度的1.5倍,那么在乙到达D 地时,还未能与甲相遇,他们还相距0.5千米,这时甲距C 地多少千米?13.一只小船从A 地到B 地往返一次共用2小时.回来时顺水,比去时的速度每小时多行驶8千米,因此第二小时比第一小时多行驶6千米.求A 至B 两地距离.14.甲、乙两地之间有一条公路,李明从甲地出发步行往乙地;同时张平从乙地出发骑摩托车往甲地.80分后两人在途中相遇.张平到达甲地后马上折回往乙地,在第一次相遇后又经过20分张平在途中追上李明.张平到达乙地后又马上折回往甲地,这样一直下去,当李明到达乙地时,张平追上李明的次数是多少?5———————————————答 案——————————————————————一、填空题1. 15秒该车速:(250-210)÷ (25-23)=20(米/秒)车长:25×20-250=250(米)(64.8千米/小时=18米/秒)错车时间:(250+320)÷(20+18)=15(秒)2. 80分钟804813011=⎪⎭⎫ ⎝⎛-÷(分)3. 甲:6千米/时;乙:3.6千米/小时.36×2÷(2+3+2.5)=9.6(千米/小时)甲速:(36-9.6×2.5)÷2=6(千米/小时)乙速:(36-9.6×3)÷2=3.6(千米/小时)4. 390米甲速:48千米/小时=3113米/秒乙速:60千米/小时=3216米/秒 乙车长:3901331133216=⨯⎪⎭⎫ ⎝⎛+(米)5. 20千米/小时()205.12.1442144.202124=⎥⎦⎤⎢⎣⎡-++÷⎪⎭⎫ ⎝⎛⨯-÷⎪⎭⎫ ⎝⎛+⨯(千米/小时)6. 39千米/小时卡车速度:(60-48)×6÷(7-6)-48=24(千米/小时)丙车速度:48-(48+24)÷8=39(千米/小时)7. 60千米/时()60213552470=÷⨯-(千米/小时)8. 8秒11×280÷385=8(秒)9. 30米.10. 86千米.258÷4×(2-1)÷(2+1)×4=86(千米)11. 设甲、乙两人第i 次迎面相遇点为Ci(i=1,2,3,4,5).由甲、乙速度之比为3:7,令AB=1,则7:3:11=B C AC ,1031=AC .如下图:同理可得: 210321⨯=C C ,故1012=BC ; 5332=+BC B C ,故213=BC ; A B C 1 C 3 C 5 C 2 C 45343=+AC A C ,故53;101544==C C AC ;所以25053150=÷=AB (米).答:A 、B 相距250米.12. 由甲速是乙速的1.5倍的条件,可知甲路程是乙路程的1.5倍.设CD 距离为x 千米,则乙走的路程是(4+x)千米,甲路程为(4+x)×1.5千米或(5×2- x –0.5)千米.列方程得(4+ x)×1.5=5×2- x-0.5x =1.4这时甲距C 地:1.4+0.5=1.9(千米).13. 顺水速度:逆水速度=5:3由于两者速度差是8千米.立即可得出逆水速度123358=-÷=(千米/小时). A 至B 距离是12+3=15(千米)答:A 至B 两地距离是15千米.14. 画线段图如下:设从第一次相遇后到张平第一次追上李明时李明走了x 千米,则相同时间内张平走了: x(80÷20)×2+ x=9 x(千米),即在相同时间内,张平速度是李明速度的:9x ÷x=9(倍).这就是说,李明从甲地步行到乙地时,张平骑摩托车行走了9个全程.很明显,其中有5个全程是从乙地到甲地,有4个全程是从甲地到乙地.从甲地到乙地张平每走一个全程,必然追上李明一次.因此,张平共追上李明4次.张平 乙篇三:四年级奥数练习题相遇问题1、甲乙两列火车同时从相距700千米的两地相向而行,甲列车每小时行85千米,乙列车每小时行90千米,几小时两列火车相遇?2、甲乙两车从两地同时出发相向而行,甲车每小时行40千米,乙车每小时行60千米,经过3小时相遇。
