极限平衡法介绍
基坑支护结构的稳定性分析方法

基坑支护结构的稳定性分析方法引言:在城市建设中,基坑开挖是常见且必不可少的过程。
然而,基坑的开挖会导致周围土体失去支撑,从而导致基坑失稳的危险。
为了确保基坑工程的安全与稳定,我们需要对基坑的支护结构进行稳定性分析。
一、基坑支护结构的分类:基坑支护结构按材料分类可分为刚性支护和柔性支护。
刚性支护主要包括钢板桩、混凝土连续墙等,其特点是刚度大、稳定性强;而柔性支护则包括了土钉墙、搪瓷土工袋墙等,其特点是弯曲变形能力较好。
二、常见的基坑支护结构的稳定性分析方法:1. 极限平衡法:极限平衡法是基坑支护结构常用的稳定性分析方法之一。
该方法基于支护结构达到平衡时的刚恢复力和土体的抗力之间的平衡关系。
通过平衡方向的判断,可以确定支护结构是否稳定。
2. 有限元法:有限元法是一种通过将结构或土体划分为单元,并对各个单元进行计算和分析来确定稳定性的方法。
该方法能够考虑到不同材料的刚度和力学性质,较为准确地分析基坑支护结构的稳定性。
3. 解析法:解析法是通过解析解方程来求解支护结构的稳定性问题的方法。
该方法适用于解决几何形状简单、边界条件明确的基坑支护结构。
4. 数值模拟法:数值模拟法是一种通过数值计算来模拟基坑工程中各种复杂情况的方法。
通过建立适当的物理模型和假设,可以使用数值方法对基坑的支护结构进行稳定性分析和计算。
三、基坑支护结构的稳定性分析方法的适用范围:不同的稳定性分析方法适用于不同类型的基坑支护结构。
极限平衡法适用于简单的基坑支护结构,能够直观地判断结构的稳定性;有限元法适用于复杂的基坑支护结构,可以更准确地分析结构的受力和位移情况;解析法适用于几何形状简单、边界条件明确的基坑支护结构;数值模拟法适用于模拟复杂的基坑工程过程,可以较为真实地反映实际工程中的情况。
结论:基坑支护结构的稳定性分析是确保基坑工程安全与稳定的重要环节。
不同的稳定性分析方法适用于不同类型的基坑支护结构。
在实际工程中,可以根据基坑工程的具体情况选择适合的分析方法,以确保基坑支护结构的稳定性,并采取相应的措施确保工程的顺利进行。
滑坡计算方法(极限平衡法)

6.3 极限平衡法•6.3.1 概述•6.3.2 简单(瑞典)条分法•6.3.3 简化毕肖甫法•6.3.4 Janbu法•6.3.5 Spencer方法•6.3.6 Morgenstern-Price方法•6.3.7 陈祖煜的通用条分法•6.3.8 总结•6.3.9 孔隙水压力的考虑•6.3.10 最小滑裂面的搜索6.3.1 概述•极限平衡法是建立在(刚体)极限状态时的静力平衡基础上;•不考虑变形协调条件与变形过程;•假设滑裂面(圆形或者任意);•由于求解条件不足,需要一些假设;R M =∫()n n l σσ=其中是未知函数syxE 方程数:静力平衡+力矩平衡=3n滑动面上极限平衡条件=n 未知数:条块间力+水平力作用点位置=2(n -1)+(n -1) =3n -3滑动面上的力=2n 安全系数F=14n5n -2未知数-方程数=n-2q图6-64忽略土条体底部力N i 的作用点位置yE i i安全系数定义:条块底部:F c c =e ee e ef tg sec tg ϕαϕτi i i i i i N x c N l c l T +∆=+=⋅=Fϕϕtg tg e =en e f tg ϕστ+=c 极限平衡条件图6-65几种极限平衡法iq方程数:未知数:(5n -2)-3(n -1)=2n +14n图6-66h瑞典条分法0方程数:未知数:(5n-2)-(n -1)=4n -14nE iq图6-69毕肖普法(cos sin )(sin cos tg )(eee e =−∆−∆+∆−+∆+∆+∆∑∑∑R h Q x q W tg x c x q W i i i i i i i ααϕααϕFcc =e Fϕϕtg tg e =一个方程,一个未知数F ,可解,需试算。
6.3.4Janbu 法假定:假定各土条间推力作用点连线为光滑连续曲线↔“推力作用线”方程数:未知数:(5n -2)-(n -1)=4n -14ni qh i 即假定了条块间力的作用点位置Janbu 法)}tg()()]tg(tg 1[{eee=−∆−∆+∆+−+∆−∆∑ϕαϕααiiiiiiX x q W x c Q 此式可用于迭代求解安全系数F s ,但尚须先得到∆X i6.3.5 Spencer 法假定:假定土条间的切向力与法向力之比为常数,即方程数:未知数:(5n -2)-(n -1)+1=4n 4niqX i / E i = tg β= λSpencer 法补充一个方程:根据力矩平衡条件得到两个未知数:F 、β]cos sec )cos()sin()[sec(eeeee=∆−−∆+−∆−−∑ϕαϕαϕαϕβαiiiiiix c QW 1)(,0)()()(tan 1010==+=x f x f x f x f λβV 6.3.6 Morgenstern-Price 方法yxMorgenstern & Price 待求,f 1(x )为人为假定函数其中k 、m 为常数f 1(x )=1 Spencer 方法f 1(x )=0 Bishop 方法6-81Morgenstern-Price方法两个未知数F λ、两个方程,于是可以求解6.3.7yx假定:陈祖煜在Morgenstern & Price 方法的基础上,提出了更具一般性的方法其中λ待求,f 0(x )、f (x ) 为人为假定函数6.3.8 总结图6-97 几种计算方法小结极限平衡法边坡稳定分析的一些结论Duncan 关于边坡稳定分析方法的结论(1980、1996):(1)瑞典条分法所得安全系数较小,在圆弧中心角较大和孔隙水压力较大时,安全系数的误差较大。
边坡稳定的极限平衡法

极限平衡法在边坡工程设计中应用广泛,可以帮助工程师确定边坡的安 全系数和稳定性。
极限平衡法基本原理:通过计算土体的抗剪强度和滑动面的抗剪强度,判断边坡的稳 定性
计算参数:包括土体的内聚力、内摩擦角、黏聚力、黏聚力等
计算方法:采用极限平衡法计算公式,如瑞典圆弧法、毕肖普法等
边界元法:适用于非 连续介质问题,求解 速度快,但需要大量 的计算
极限平衡法与边界元法 的比较:极限平衡法适 用于连续介质问题,而 边界元法适用于非连续 介质问题,两者在求解 速度上都有优势,但都 需要大量的计算。
边坡稳定的极限平 衡法的发展趋势和 未来展望
极限平衡法在 边坡稳定分析 中的应用越来
性的弹性体
计算原理:通 过求解土体的 应力、应变和 位移方程,得 到边坡的稳定
安全系数
应用范围:适 用于各种土质 边坡,特别是 那些受水、温 度等因素影响
的边坡
Байду номын сангаас
基本假设:土体为连续、均匀、各向同性的弹性体
计算方法:通过求解土体的静力平衡方程,得到土体的应力状态和变形状态
适用范围:适用于土体变形较小、应力状态较简单的情况 优点:计算简单、易于理解,能够快速得到土体的应力状态和变形状态
越广泛
极限平衡法的 计算方法和软 件不断改进和
完善
极限平衡法与 其他分析方法 相结合,提高 边坡稳定分析 的准确性和可
靠性
极限平衡法在 边坡稳定预警 和防治中的应
用前景广阔
技术进步:随着科技 的发展,极限平衡法 的计算方法和技术将 不断完善和改进。
应用领域拓展:极限平 衡法将在更多领域得到 应用,如地质灾害防治、 土木工程、环境工程等。
强度折减法和极限平衡法

强度折减法和极限平衡法强度折减法和极限平衡法是土木工程设计中常用的两种结构分析方法。
本文将分步骤阐述这两种方法的基本原理和应用。
一、强度折减法强度折减法是基于材料强度折减原理的一种结构分析方法。
常见的材料强度折减因素有冲切、弯曲、拉伸、压缩等,这些因素使得材料的承载能力会降低。
在进行强度折减法分析时,需要按照结构受力状态对材料进行分类,然后对不同材料种类进行强度折减计算,最后进行整体承载能力计算。
具体步骤如下:1. 确定受力状态:根据实际情况确定结构所受的荷载类型和大小、支撑方式、连接方式等,从而确定结构的受力状态。
2. 材料分类:将材料按照受到的荷载类型和强度折减因素进行分类。
3. 强度折减计算:按照不同的强度折减因素对不同材料种类进行强度折减计算。
4. 整体承载能力计算:将强度折减后的各种材料的承载能力加起来,得到结构的整体承载能力。
二、极限平衡法极限平衡法是基于结构极限状态的一种结构分析方法。
这种方法的基本思想是先假设结构处于破坏的边缘状态,然后根据物理平衡原理进行分析,在保证结构不发生破坏的前提下确定荷载的大小和分布情况。
具体步骤如下:1. 假设结构破坏:假设结构处于破坏的边缘状态,根据实际情况选择不同的破坏模式。
2. 平衡方程:根据物理平衡原理列出平衡方程,包括受力平衡、几何平衡和位移平衡方程。
3. 荷载确定:在保证结构不发生破坏的前提下,根据平衡方程确定荷载的大小和分布情况。
4. 校核:对计算结果进行校核,判断结构是否符合设计要求。
总的来说,强度折减法和极限平衡法都是基于结构力学原理的分析方法。
具体采用哪种方法视情况而定,但需要注意的是,分析方法的准确性和有效性直接关系到结构的安全性和经济性,因此需要结合实际情况进行灵活运用。
极限平衡法介绍

si i si i bi i i Q e ϕδϕαϕsec )[cos(-+-=)cos(i ei i a i W Q P αϕ-•=)tan (si i i si i PW d C S ϕ•-•=)(11111+++++•-•=si i i si i tn PW d C S ϕ)tan sec (bi i i i bi i u b C R ϕα•-•=11cos )sec(+++-=si si i bi i Q ϕϕαϕbi ϕ——条块底面摩擦角bic ——条块底面粘聚力si ϕ——条块侧面摩擦角sic ——条块侧面粘聚力式(12—1)分成n 块滑体达到静力平衡的条件。
该式物理意义是:使滑体达到极限平衡状态,必须在滑体上施加一个临界水平加速度Kc 。
Kc 为正时,方向向坡外,Kc 为负时,方向向坡内,Kc 的大小由式(12—1)确定。
在对该方法应用中,对其进行了进一步完善,充分考虑了分层作用,并使不同层位赋予不同的强度参数,同时它还要求对解的合理性进行校核,使分析计算更趋合理,从而显示了该方法很强的适用性。
Bishop 法概述:目前,在工程上常用的两种土坡稳定分析方法仍为瑞典圆弧法(Fellenius 法)和简化毕肖普法,它们均属于极限平衡法。
瑞典圆弧法的土条间作用力的假设不太合理,得出的安全系数明显偏低,而简化毕肖普法的假设较为合理,计算也不复杂,因而在工程中得到了十分广泛的应用。
当土坡处于稳定状态时,任一土条内滑弧面上的抗剪强度只发挥了一部分, 并与切向力T i 相平衡,见图 1(a),其算式为T i =c i l i F s+N i tanφiF s(1)如图 1(b)所示,将所有的力投影到弧面的法线方向上,则得N i =[W i +(H i+1−H i )]cos αi −(P i+1−P i )sin αi (2)当整个滑动体处于平衡时(图 1(c)),各土条对圆心的力矩之和应为零,此时,条间推力为内力,将相互抵消,因此得∑W i x i −∑T i R =0 (3)图1 毕肖普法计算图将式(2)代入式(3),且x i=R sinαi,最后得到土坡的安全系数为F s=∑{c i l i+[(W i+H i−H i+1)cosαi−(P i+1−P i)sinαi]tanφi}∑W i sinαi(4)实用上,毕肖普建议不计分条间的摩擦力之差,即H i+1−H i=0,式(4)将简化为F s=∑{c i l i+[W i cosαi−(P i+1−P i)sinαi]tanφi}∑W i sinαi(5)所有作用力在竖直向和水平向的总和都应为零,即∑F x=0,∑F y=0,并结合摩擦力之差为零,得出P i+1−P i=1F sW i cosαi tanφi+c i l iF s−W i sinαitanφiF ssinαi+cosαi(6)代入式(5),简化后得F s=∑(c i l i cosαi+W i tanφi)1tanφi sinαi F s+cosαi⁄∑W i sinαi(7)当采用有效应力法分析时,重力项W i将减去孔隙水压力u i l i,并采用有效应力强度指标c i′,φi′有F s=∑(c i′l i cosαi+W i tanφi′)1tanφi′sinαi F s+cosαi⁄∑W i sinαi(8)在计算时,一般可先给F s假定一值,采用迭代法即可求出。
滑坡计算方法(极限平衡法)

6.3 极限平衡法•6.3.1 概述•6.3.2 简单(瑞典)条分法•6.3.3 简化毕肖甫法•6.3.4 Janbu法•6.3.5 Spencer方法•6.3.6 Morgenstern-Price方法•6.3.7 陈祖煜的通用条分法•6.3.8 总结•6.3.9 孔隙水压力的考虑•6.3.10 最小滑裂面的搜索6.3.1 概述•极限平衡法是建立在(刚体)极限状态时的静力平衡基础上;•不考虑变形协调条件与变形过程;•假设滑裂面(圆形或者任意);•由于求解条件不足,需要一些假设;R M =∫()n n l σσ=其中是未知函数syxE 方程数:静力平衡+力矩平衡=3n滑动面上极限平衡条件=n 未知数:条块间力+水平力作用点位置=2(n -1)+(n -1) =3n -3滑动面上的力=2n 安全系数F=14n5n -2未知数-方程数=n-2q图6-64忽略土条体底部力N i 的作用点位置yE i i安全系数定义:条块底部:F c c =e ee e ef tg sec tg ϕαϕτi i i i i i N x c N l c l T +∆=+=⋅=Fϕϕtg tg e =en e f tg ϕστ+=c 极限平衡条件图6-65几种极限平衡法iq方程数:未知数:(5n -2)-3(n -1)=2n +14n图6-66h瑞典条分法0方程数:未知数:(5n-2)-(n -1)=4n -14nE iq图6-69毕肖普法(cos sin )(sin cos tg )(eee e =−∆−∆+∆−+∆+∆+∆∑∑∑R h Q x q W tg x c x q W i i i i i i i ααϕααϕFcc =e Fϕϕtg tg e =一个方程,一个未知数F ,可解,需试算。
6.3.4Janbu 法假定:假定各土条间推力作用点连线为光滑连续曲线↔“推力作用线”方程数:未知数:(5n -2)-(n -1)=4n -14ni qh i 即假定了条块间力的作用点位置Janbu 法)}tg()()]tg(tg 1[{eee=−∆−∆+∆+−+∆−∆∑ϕαϕααiiiiiiX x q W x c Q 此式可用于迭代求解安全系数F s ,但尚须先得到∆X i6.3.5 Spencer 法假定:假定土条间的切向力与法向力之比为常数,即方程数:未知数:(5n -2)-(n -1)+1=4n 4niqX i / E i = tg β= λSpencer 法补充一个方程:根据力矩平衡条件得到两个未知数:F 、β]cos sec )cos()sin()[sec(eeeee=∆−−∆+−∆−−∑ϕαϕαϕαϕβαiiiiiix c QW 1)(,0)()()(tan 1010==+=x f x f x f x f λβV 6.3.6 Morgenstern-Price 方法yxMorgenstern & Price 待求,f 1(x )为人为假定函数其中k 、m 为常数f 1(x )=1 Spencer 方法f 1(x )=0 Bishop 方法6-81Morgenstern-Price方法两个未知数F λ、两个方程,于是可以求解6.3.7yx假定:陈祖煜在Morgenstern & Price 方法的基础上,提出了更具一般性的方法其中λ待求,f 0(x )、f (x ) 为人为假定函数6.3.8 总结图6-97 几种计算方法小结极限平衡法边坡稳定分析的一些结论Duncan 关于边坡稳定分析方法的结论(1980、1996):(1)瑞典条分法所得安全系数较小,在圆弧中心角较大和孔隙水压力较大时,安全系数的误差较大。
极限平衡法介绍

基于极限平衡法原理的边坡稳定计算有多种方法,根据不同的适用条件,主要有摩根斯坦-普瑞斯(Morgenstern-Price)法、毕肖普(Bishop)法、简布(Janbu)法、推力法、萨尔玛(Sarma)法等。
摩根斯坦-普瑞斯(Morgenstern-Price)法该方法考虑了全部平衡条件与边界条件,消除了计算方法上的误差,并对Janbu推导,滑ϕ——条块侧面摩擦角sic——条块侧面粘聚力si式(12—1)分成n块滑体达到静力平衡的条件。
该式物理意义是:使滑体达到极限平衡状态,必须在滑体上施加一个临界水平加速度Kc。
Kc为正时,方向向坡外,Kc为负时,方向向坡内,Kc 的大小由式(12—1)确定。
在对该方法应用中,对其进行了进一步完善,充分考虑了分层作用,并使不同层位赋予不同的强度参数,同时它还要求对解的合理性进行校核,使分析计算更趋合理,从而显示了该方法很强的适用性。
Bishop法概述:(1)(2)推力为内力,将相互抵消,因此得∑T T T T−∑T T T=0(3)图1 毕肖普法计算图将式(2)代入式(3),且T T=T TTT T T,最后得到土坡的安全系数为T T=∑{T T T T+[(T T+T T−T T+1)cos T T−(T T+1−T T)sin T T]tan T T}(4)∑T T sin T T实用上,毕肖普建议不计分条间的摩擦力之差,即T T+1−T T=0,式(4)将简化为T T=∑{T T T T+[T T cos T T−(T T+1−T T)sin T T]tan T T}(5)∑T T sin T T所有作用力在竖直向和水平向的总和都应为零,即∑T T=0,∑T T=0,并结合摩擦简布(janbu)法简布(janbu)法是假定条块间的水平作用力的位置,每个条块都满足全部的静力平衡条件和极限平衡条件,滑动土体的整体力矩平衡条件也满足,而且它适用于任何滑动面而不必规定滑动面是一个圆弧面,所以又称为普遍条分法。
刚体极限平衡法的原理定义

刚体极限平衡法的原理定义
刚体极限平衡法(Method of Virtual Work)是一种基于平衡条件的经典力学方法,用于分析刚体系统的平衡状态。
其基本原理可以概括为:“在达到平衡的刚体系统中,刚体及外力所做的虚功和等于零”。
具体而言,刚体极限平衡法基于以下两个关键假设:
1. 刚体假设:假设刚体是一个刚硬而不可形变的物体,即不考虑刚体内部的应变和变形。
2. 平衡假设:假设刚体系统在平衡状态下,即不受外力的影响而处于静止或匀速直线运动。
基于上述假设,刚体极限平衡法主要应用虚功原理进行分析。
虚功原理认为,刚体在平衡状态下,任意微小的虚位移所做的虚功等于零。
具体而言,刚体极限平衡法的步骤如下:
1. 选择适当的广义坐标系统来描述刚体的位移情况。
2. 通过平衡条件和几何约束关系得出刚体系统的限制方程式。
3. 对于每个位移坐标,引入一个虚位移(非零),并通过虚功原理计算虚功。
4. 通过对所有虚功求和并使其等于零,可以得到未知约束力的方程组。
5. 解方程组得到未知约束力的值,从而确定刚体系统的平衡状态。
总而言之,刚体极限平衡法通过应用虚功原理,结合平衡条件和几何约束关系,
可以解析地确定刚体系统在平衡状态下的未知约束力的值。
极限平衡法
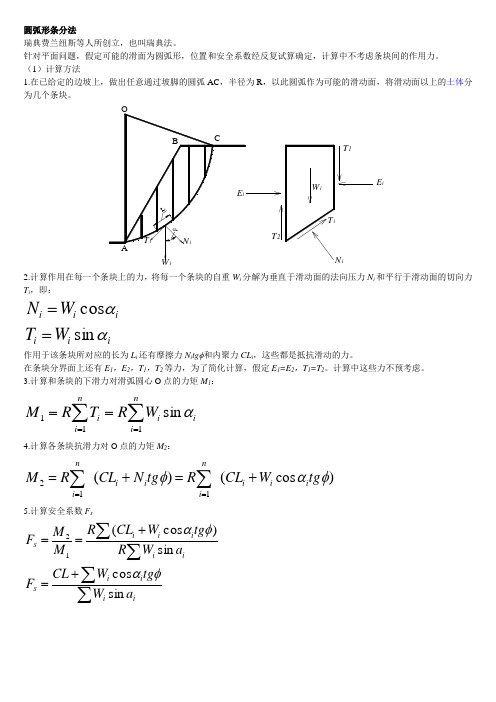
圆弧形条分法
瑞典费兰纽斯等人所创立,也叫瑞典法。
针对平面问题,假定可能的滑面为圆弧形,位置和安全系数经反复试算确定,计算中不考虑条块间的作用力。
(1)计算方法
1.在已给定的边坡上,做出任意通过坡脚的圆弧AC ,半径为R ,以此圆弧作为可能的滑动面,将滑动面以上的土体分为几个条块。
A B
C
O
L i T i
W i N i αi
N i T i
T 2T 1E i
E i
W i
2.计算作用在每一个条块上的力,将每一个条块的自重W i 分解为垂直于滑动面的法向压力N i 和平行于滑动面的切向力T i ,即:
i i i i
i i W T W N ααsin cos ==
作用于该条块所对应的长为L i 还有摩擦力N i tg φ和内聚力CL i ,这些都是抵抗滑动的力。
在条块分界面上还有E 1,E 2,T 1,T 2等力,为了简化计算,假定E 1=E 2,T 1=T 2。
计算中这些力不预考虑。
3.计算和条块的下滑力对滑弧圆心O 点的力矩M 1:
i n
i i n i i W R T R M αsin 1
11∑∑==== 4.计算各条块抗滑力对O 点的力矩M 2: )cos ()(1
12φαφtg W CL R tg N CL R M i i i n
i i i n i +=+=∑∑== 5.计算安全系数F s ∑∑∑∑+=+==i i i i s i
i i i i s a W tg W CL F a W R tg W CL R M M F sin cos sin )cos (12φαφα。
硕士高等土力学极限平衡法

硕士高等土力学极限平衡法简介硕士高等土力学极限平衡法是土力学中的一种分析方法,用于研究土体在极限状态下的力学行为。
该方法是以学界著名学者Alfreds R. Jaeger和John N. Huddleston提出的边坡稳定分析理论为基础,根据边坡的工程实例对理论进行了验证和修正,形成了一套较为完整的分析方法。
原理该分析方法基于以下几个假设:1.边坡的稳定取决于其剪切强度;2.边坡的结构可以视为一个由土体和水组成的复合体系;3.边坡的力学行为是由多个因素的相互作用所决定的。
根据以上假设,极限平衡法首先将复合边坡体系分解为若干简单的力学元件,然后分别对每个元件进行力学分析,从而得到边坡的稳定状态。
具体来说,该方法可以被描述为以下几个步骤:1.确定边坡的几何形状和土体性质;2.将边坡分解为若干较小的力学元件;3.对每个元件进行平衡分析,确定其相应的稳定因素;4.整合所有力学元件的稳定因素,得出边坡的稳定状态;5.比较边坡的稳定状态和其实际状态,分析边坡是否具有稳定性。
应用硕士高等土力学极限平衡法被广泛应用于边坡工程、挖掘工程、隧道工程等土力学领域。
在实践中,该方法常被用于评估边坡的稳定性、确定边坡的最大可支撑高度、计算边坡的稳定系数等。
此外,该方法还可以进行隧道围岩的稳定分析、基坑支撑设计等。
优缺点作为土力学领域的一种分析方法,硕士高等土力学极限平衡法具有以下优点:1.该方法适用于各种类型的土体和边坡;2.该方法分析较为简便,可快速得出稳定性;3.该方法还可以考虑多种因素对边坡稳定性的影响。
但是,该方法也存在一些缺点:1.该方法忽略了土体内部的应力分布信息;2.该方法对随机因素的处理较为困难;3.该方法对土石块、软土等具有一定局限性。
硕士高等土力学极限平衡法是一种土力学分析方法,主要用于研究土体在极限状态下的力学行为。
该方法基于边坡稳定分析理论和工程实践,制定了较为完整的分析流程,并在土力学的多个领域得到了广泛应用。
刚体极限平衡法的基本假定

刚体极限平衡法是一种力学方法,用于分析处于平衡状态下的刚体系统。
在使用刚体极限平衡法时,通常需要基于以下基本假定:
刚体假设:假设所研究的物体是一个刚体,即假定物体的形状和结构保持不变,不存在形变或变形。
平衡假设:假设系统处于平衡状态,即物体不会发生线性或角度上的加速度,所有受力和力矩之和为零。
重力假设:假设系统中的重力受力可以近似为作用在刚体的质心上,且具有恒定的大小和方向。
摩擦假设:在分析刚体的平衡时,通常假设刚体表面之间不存在摩擦力。
这些基本假设在刚体极限平衡法中起着重要的作用,它们使得分析过程更加简化和可行。
然而,这些假设并不一定适用于所有情况,特别是当考虑非常大的变形或非理想的接触情况时,可能需要考虑更为复杂的因素。
因此,在实际应用中,需要根据具体情况和问题的复杂程度来评估和使用这些假设。
岩土中的边坡稳定性分析方法

岩土中的边坡稳定性分析方法边坡稳定性是岩土工程中重要的研究内容,对于保障工程安全具有重要意义。
岩土中的边坡稳定性分析方法多种多样,以下将介绍几种常用的分析方法。
一、平衡法平衡法是边坡稳定性分析中最基本的方法之一。
该方法基于稳定条件,即在不考虑边坡变形情况下,边坡上的重力和抗滑力之间达到平衡。
通过计算边坡上各力的合力和合力矩,判断边坡的稳定性。
二、极限平衡法极限平衡法是在平衡法基础上进一步发展的,主要用于对边坡的最不利失稳形态进行分析。
该方法通过建立边坡失稳条件的公式,求解失稳时的平衡边坡剪切力和抗剪强度之间的关系,从而判断边坡的稳定性。
三、变形法变形法是一种考虑了边坡变形的分析方法。
在边坡失稳时,通过考虑边坡的变形和土体内部的力学性质,确定边坡的稳定性。
该方法需要进行较为复杂的数值计算和模拟,但能更加真实地反映边坡的变形和稳定情况。
四、综合分析法综合分析法是将以上几种方法综合应用的一种边坡稳定性分析方法。
该方法通过综合考虑边坡的不同特点和条件,选用适当的分析方法进行边坡稳定性评估。
综合分析法可以有效地避免单一方法的局限性,提高分析的准确性。
需要注意的是,在进行边坡稳定性分析方法选择时,应根据具体的工程情况和数据条件进行合理选择。
同时,在进行分析时也需要充分考虑边坡土体的力学性质、水文条件、地质背景等因素,以获得更加准确的分析结果。
总结起来,岩土中的边坡稳定性分析方法包括平衡法、极限平衡法、变形法和综合分析法。
这些方法的选择应根据具体情况进行合理使用,以确保工程的安全性。
通过科学准确的边坡稳定性分析,可以有效地提高岩土工程的可靠性和安全性。
岩土工程中边坡稳定性分析方法

岩土工程中边坡稳定性分析方法岩土工程中边坡稳定性分析是一个重要且复杂的课题,它涉及到土体的力学性质、地质条件以及边坡的几何形状等因素。
正确的边坡稳定性分析方法能够为工程设计提供合理的基础参数,从而确保工程的安全可靠性。
本文将探讨岩土工程中常用的边坡稳定性分析方法。
1. 传统切片法传统切片法是岩土工程中最早使用的边坡稳定性分析方法之一。
它基于土体的切割面,将边坡划分为多个切片,然后根据力学平衡条件计算每个切片的受力和力矩,进而得到边坡的稳定性。
传统切片法适用于边坡稳定性分析的初步估算,但它忽略了土体内的应力分布、渗流和变形等因素,导致结果存在一定的误差。
2. 极限平衡法极限平衡法是岩土工程中常用的边坡稳定性分析方法之一,它基于土体达到稳定状态的条件,通过假设边坡表面的滑动类型,建立边坡的平衡方程,进而确定边坡的临界平衡状态。
极限平衡法考虑了土体内的应力分布和边坡的几何形状等因素,具有较高的精度和可靠性,适用于各种类型的边坡稳定性分析。
3. 桩土共同作用法桩土共同作用法是一种综合考虑桩与土体相互作用的边坡稳定性分析方法。
在边坡设计中,桩的设置可以有效地提高边坡的整体稳定性,减小滑坡的发生概率。
桩土共同作用法将桩与土体看作一个整体系统,通过数值模拟和实验测试等方法,研究桩土间的相互作用力,从而得到边坡的稳定状态。
这种方法适用于需要增加边坡整体稳定性的工程项目。
4. 数值模拟方法随着计算机技术的发展,数值模拟方法在岩土工程中的应用越来越广泛。
数值模拟方法通过对土体力学性质和边坡几何形状的数学描述,采用有限元或边界元等计算方法,模拟土体的力学行为和边坡的稳定性。
数值模拟方法具有较高的灵活性和准确性,能够考虑复杂的工程情况,但对计算机资源和模型设置要求较高。
综上所述,岩土工程中的边坡稳定性分析方法多种多样,每种方法都有其适用范围和局限性。
工程设计人员应根据具体工程情况选择合适的分析方法,综合考虑土体力学性质、地质条件和工程要求等因素,以确保边坡的安全稳定。
极限平衡法介绍

基于极限平衡法原理的边坡稳定计算有多种方法,根据不同的适用条件,主要有摩根斯坦-普瑞斯(Morgenstern-Price )法、毕肖普(Bishop )法、简布(Janbu )法、推力法、萨尔玛(Sarma )法等。
摩根斯坦-普瑞斯(Morgenstern-Price )法该方法考虑了全部平衡条件与边界条件,消除了计算方法上的误差,并对Janbu 推导出来的近似解法提供了更加精确的解答;对方程式的求解采用数值解法(即微增量法),滑面形状任意,通过力平衡法所计算出的稳定系数值可靠程度较高。
图12—1 力学模型示意图根据其力学模型和几何条件以及静力平衡方程 可解得平衡条件:23111212311121e e e e P e e P e P P e e e e e e e K n n n n n n n n n n n n n n n n c ∙∙∙++∙∙+∙+∙∙∙++∙∙+∙+=-------- αααα (12—1)式中:biϕ——条块底面摩擦角 bic ——条块底面粘聚力 siϕ——条块侧面摩擦角 sic ——条块侧面粘聚力式(12—1)分成n 块滑体达到静力平衡的条件。
该式物理意义是:使滑体达到极限平衡状态,必须在滑体上施加一个临界水平加速度Kc 。
Kc 为正时,方向向坡外,Kc 为负时,方向向坡内,Kc 的大小由式(12—1)确定。
在对该方法应用中,对其进行了进一步完善,充分考虑了分层作用,并使不同层位赋予不同的强度参数,同时它还要求对解的合理性进行校核,使分析计算更趋合理,从而显示了该方法很强的适用性。
Bishop法概述:目前,在工程上常用的两种土坡稳定分析方法仍为瑞典圆弧法(Fellenius法)和简化毕肖普法,它们均属于极限平衡法。
瑞典圆弧法的土条间作用力的假设不太合理,得出的安全系数明显偏低,而简化毕肖普法的假设较为合理,计算也不复杂,因而在工程中得到了十分广泛的应用。
当土坡处于稳定状态时,任一土条内滑弧面上的抗剪强度只发挥了一部分,并与切向力相平衡,见图1(a),其算式为(1)如图1(b)所示,将所有的力投影到弧面的法线方向上,则得(2)当整个滑动体处于平衡时(图1(c)),各土条对圆心的力矩之和应为零,此时,条间推力为内力,将相互抵消,因此得(3)图1 毕肖普法计算图将式(2)代入式(3),且,最后得到土坡的安全系数为(4)实用上,毕肖普建议不计分条间的摩擦力之差,即,式(4)将简化为(5)所有作用力在竖直向和水平向的总和都应为零,即并结合摩擦力之差为零,得出(6)代入式(5),简化后得(7)当采用有效应力法分析时, 重力项 将减去孔隙水压力 ,并采用有效应力强度指标有(8)在计算时,一般可先给 假定一值,采用迭代法即可求出。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
极限平衡法介绍————————————————————————————————作者:————————————————————————————————日期:基于极限平衡法原理的边坡稳定计算有多种方法,根据不同的适用条件,主要有摩根斯坦-普瑞斯(Mor gens tern-P rice )法、毕肖普(B ishop )法、简布(Janbu )法、推力法、萨尔玛(Sarma )法等。
摩根斯坦-普瑞斯(Mor gens tern-Pri ce)法该方法考虑了全部平衡条件与边界条件,消除了计算方法上的误差,并对Janb u推导出来的近似解法提供了更加精确的解答;对方程式的求解采用数值解法(即微增量法),滑面形状任意,通过力平衡法所计算出的稳定系数值可靠程度较高。
Z i +1Z il i b iKWi WiNi EiXiXi +1 δ i α i Ei+1Tiyx图12—1 力学模型示意图根据其力学模型和几何条件以及静力平衡方程⎪⎩⎪⎨⎧==∑∑00Y X可解得平衡条件:(12—1)式中:sii si i bi i i Q e ϕδϕαϕsec )[cos(-+-=23111212311121e e e e P e e P e P P e e e e e e e K n n n n n n n n n n n n n n n n c •••++••+•+•••++••+•+=-------- αααα)cos(i ei i a i W Q P αϕ-•=)tan (si i i si i PW d C S ϕ•-•=)(11111+++++•-•=si i i si i tn PW d C S ϕ)tan sec (bi i i i bi i u b C R ϕα•-•= 11cos )sec(+++-=si si i bi i Q ϕϕαϕbi ϕ——条块底面摩擦角bic ——条块底面粘聚力si ϕ——条块侧面摩擦角sic ——条块侧面粘聚力式(12—1)分成n 块滑体达到静力平衡的条件。
该式物理意义是:使滑体达到极限平衡状态,必须在滑体上施加一个临界水平加速度Kc 。
Kc为正时,方向向坡外,Kc 为负时,方向向坡内,Kc 的大小由式(12—1)确定。
在对该方法应用中,对其进行了进一步完善,充分考虑了分层作用,并使不同层位赋予不同的强度参数,同时它还要求对解的合理性进行校核,使分析计算更趋合理,从而显示了该方法很强的适用性。
Bi shop 法概述:目前,在工程上常用的两种土坡稳定分析方法仍为瑞典圆弧法(Fel len ius 法)和简化毕肖普法,它们均属于极限平衡法。
瑞典圆弧法的土条间作用力的假设不太合理,得出的安全系数明显偏低,而简化毕肖普法的假设较为合理,计算也不复杂,因而在工程中得到了十分广泛的应用。
当土坡处于稳定状态时,任一土条内滑弧面上的抗剪强度只发挥了一部分,并与切向力T i相平衡,见图1(a),其算式为T i=c i l iF s +N i tanφiF sﻩﻩﻩﻩ(1)如图1(b)所示,将所有的力投影到弧面的法线方向上,则得N i=[W i+(H i+1−H i)]cosαi−(P i+1−P i)sinαi(2)当整个滑动体处于平衡时(图1(c)),各土条对圆心的力矩之和应为零,此时,条间推力为内力,将相互抵消,因此得∑W i x i−∑T i R=0 (3)图1 毕肖普法计算图将式(2)代入式(3),且x i=R sinαi,最后得到土坡的安全系数为F s=∑{c i l i+[(W i+H i−H i+1)cosαi−(P i+1−P i)sinαi]tanφi}∑W i sinαi(4)实用上,毕肖普建议不计分条间的摩擦力之差,即H i+1−H i=0,式(4)将简化为F s=∑{c i l i+[W i cosαi−(P i+1−P i)sinαi]tanφi}∑W i sinαi(5)所有作用力在竖直向和水平向的总和都应为零,即∑F x=0,∑F y=0,并结合摩擦力之差为零,得出P i+1−P i =1F s W i cos αi tan φi +c i l i F s−W i sin αi tan φiF ssin αi +cos αi (6)代入式(5),简化后得F s =∑(c i l i cos αi +W i tan φi )1tan φi sin αi F s +cos αi⁄∑W i sin αi(7)当采用有效应力法分析时, 重力项W i 将减去孔隙水压力u i l i ,并采用有效应力强度指标c i ′,φi ′有F s =∑(c i ′l i cos αi +W i tan φi′)1tan φi ′sin αi F s +cos αi⁄∑W i sin αi(8)在计算时,一般可先给F s 假定一值,采用迭代法即可求出。
根据经验,通常只要迭代3~4次就可满足精度要求,而且迭代通常总是收敛的。
简布(jan bu)法简布(ja nbu)法是假定条块间的水平作用力的位置,每个条块都满足全部的静力平衡条件和极限平衡条件,滑动土体的整体力矩平衡条件也满足,而且它适用于任何滑动面而不必规定滑动面是一个圆弧面,所以又称为普遍条分法。
简布(jan bu)法条块作用力分析。
oB CAW N T iiii iX iiH N T iii+1o i P i+1h i+1H iP h i iW ih iW iT iN iP iii(a ) (b)(c )其中:i 1(tg )i i i i sT c l N F φ=+(8-1)1i i iP P P +∆=-(8-2)1i i iH H H +∆=-(8-3)第i 条块力平衡条件:ZF=∑ 得cos sin i i i i i i W H N T θθ+=+(8-4)XF=∑ 得cos sin i i i i i P T N θθ=-(8-5)将8-1式、 8-2式、8-3式和8-5式代入到8-41式中,得[]2i i isec 1cos ()tg ()tg 0tg tg 1i i i i i i i ii i s a P c l W H W H F F θθθθθϕ=++-+=+ (8-6)条块侧面的法向力P ,显然有11P P =,21212P P P P P =+=+, 依次类推,有ii i j i P P ==∑若全部条块的总数为n ,则有10nn i i P P ===∑(8-7)将8-6式代入8-7,得[]2i sec ()tg 1tg tg /()tg ii i i i i i ss i i ic l W H FF W H θθθφθ+++=+∑∑(8-8)由以上公式,利用迭代法可以求得普遍条分法的边坡稳定性安全系数。
其步骤如下:(1)假定0i H ∆=,利用8-8公式求得第一次近似的安全系数F s1 。
(2)将F s1和0i H ∆=代入8-6式,求相应得i P ∆(对每一条块,从1到n)。
(3)用公式8-7,求条块的法向力(对每一条块,从1到n )。
(4)将i P 和i P ∆代入公式8-2和8-3种,求得条块间的切向作用力i H (对每一条块,从1到n)和i H ∆。
(5)将i H ∆重新代入到8-8公式中,迭代求新的稳定安全系数F s 2。
如果21s s F F ->,为规定的安全系数计算精度,重新按照上述步骤进行新的一轮计算。
如是反复进行,直到()(1)s k s k F F --≤为止。
此时()s k F 就是假定滑面的安全系数。
Sarm a法Sa rma 法属于刚体极限平衡分析法,其基于以下的6条假设: (1)将边坡稳定性问题视为平面应变问题;(2)滑动力以平行于滑动面的剪应力和垂直于滑动面的正应力集中作用于滑动面上;(3)视边坡为理想刚塑性材料,认为整个加荷过程中,滑体不会发生任何变形,一旦沿滑动面剪应力达到其剪切强度,则滑体即开始沿滑动面产生剪切变形;(4)滑动面的破坏服从Mohr -C oulo mb 破坏准则,即滑动面强度主要受粘聚力和摩擦力控制;(5)条块间的作用力合力(剩余下滑力)方向与滑动面倾角一致,剩余下滑力为负值时则传递的剩余下滑力为零;(6)沿着滑动面满足静力的平衡条件,但不满足力矩平衡条件。
i+1ii-1i+1ii-1nii E i-1W iR i图7-1 S arma 法岩体破坏形式 图7-2 S arma 法力学破坏模型将上一条块剩余下滑力向下一条块滑动面逐块投影法计算边坡的稳定性及滑坡推力,滑坡的稳定性及推力计算同时满足当剩余下滑力小于零时令其等于零的条件。
即条块间不出现拉应力的条件。
单元极限平衡公式为:(7.1)第i 条块剩余下滑力:(7.2)当小于零时,令,此时(7.3)公式8-9也可表达为(7.4)则稳定系数F st 计算公式如下:(7.5)当所有1至n 条块的剩余下滑力均大于等于零时,利用数学归纳法可以证明:(7.6)cos sin st W tg CLI F W αβα+=111sin()cos()i i i i st i st i st i i i i st tg E F E F T F E R F ααααα---⎡⎤-=⨯=⨯+⨯---⎢⎥⎣⎦i E 0i E =11i st i i E F T R ++=⨯-11111111sin()sin()cos()cos()i n n n n i n n n nst n n n st n n n n st nE tg R E tg R IF E F T E F T ααφααφαααα---------+-+==-+-+1111sin()cos()i n n n nst n n n nE tg RF E T ααφαα-----+=-+11111111()()n n ijni j st n n ijni j R R F T T ψψ--==--==+=+∑∏∑∏。
