四年级下册鸡兔同笼问题练习题(附答案及解析)

合集下载

小学鸡兔同笼问题练习题及答案解析

小学鸡兔同笼问题练习题及答案解析1.题目：鸡比兔多13只，鸡腿比兔腿多16条，鸡和兔各有多少只？答案：鸡有25只，兔有12只。

解析：设兔有x只，则鸡有x+13只。

根据题意，鸡腿比兔腿多16条，即2(x+13) - 4x = 16，解得x=12，所以兔有12只，鸡有25只。

2.题目：笼子里有若干只鸡和兔。

从上面数，有35个头，从下面数，有94只脚，鸡和兔各有多少只？答案：鸡有23只，兔有12只。

解析：设兔有x只，则鸡有35-x只。

根据题意，4x + 2(35-x) = 94，解得x=12，所以兔有12只，鸡有23只。

3.题目：鸡比兔多3只，鸡腿比兔腿多2条，鸡和兔各有多少只？答案：鸡有7只，兔有4只。

解析：设兔有x只，则鸡有x+3只。

根据题意，2(x+3) - 4x = 2，解得x=4，所以兔有4只，鸡有7只。

4.题目：鸡和兔共有100只，腿共248只，鸡和兔各有多少只？答案：鸡有34只，兔有66只。

解析：设兔有x只，则鸡有100-x只。

根据题意，4x + 2(100-x) = 248，解得x=66，所以兔有66只，鸡有34只。

5.题目：鸡比兔少5只，鸡腿比兔腿少6条，鸡和兔各有多少只？答案：鸡有19只，兔有24只。

解析：设兔有x只，则鸡有x-5只。

根据题意，2(x-5) - 4x = -6，解得x=24，所以兔有24只，鸡有19只。

6.题目：鸡和兔共有15只，腿共40条，鸡和兔各有多少只？答案：鸡有10只，兔有5只。

解析：设兔有x只，则鸡有15-x只。

根据题意，4x + 2(15-x) = 40，解得x=5，所以兔有5只，鸡有10只。

7.题目：鸡比兔多8只，鸡腿比兔腿多12条，鸡和兔各有多少只？答案：鸡有20只，兔有12只。

解析：设兔有x只，则鸡有x+8只。

根据题意，2(x+8) - 4x = 12，解得x=12，所以兔有12只，鸡有20只。

8.题目：笼子里有若干只鸡和兔。

从上面数，有28个头，从下面数，有76只脚，鸡和兔各有多少只？答案：鸡有10只，兔有18只。

人教版数学四年级下册：鸡兔同笼问题练习题(附答案及解析)

人教版数学四年级下册：鸡兔同笼问题练习题(附答案及解析)1.在一次数学竞赛中，共有20道题目，每做对一题得5分，每做错或不做一题扣1分。

XXX得了64分，问他做对了几道题？假设全做对，总分为20×5=100分。

而XXX得了64分，所以错了36分。

每错一题扣1分，所以错了36÷（5+1）=6道题。

因此，XXX做对的题目数为20-6=14道。

2.一共有鸡和兔两种动物，它们的脚的总数为100只。

如果将鸡换成兔，兔换成鸡，则脚的总数为86只。

问：鸡和兔各有几只？假设全是兔子，那么脚的总数为7×4=28只。

因此，还剩下100-28=72只是鸡的脚。

每组鸡和兔子的脚的总数为2+4=6只，所以共有12组鸡和兔子。

因此，兔子的总数为7+12=19只，而鸡的总数为12只。

3.一次自行车越野赛全程为220千米，分为20个路段。

其中一部分路段长14千米，其余路段长9千米。

问：有多少个长度为9千米的路段？假设所有路段长度都是9千米，那么总长度为20×9=180千米。

因此，剩下的路段长度为220-180=40千米。

每段14千米的路段可以替换成一个9千米和一个5千米的路段，因此共有8段14千米的路段。

因此，长度为9千米的路段总数为20-8=12段。

4.有一群鸡和兔子，它们的腿的总数比头的总数多18只。

问：有多少只兔子？如果所有动物都是鸡，那么腿的总数应该是头的总数的2倍。

因此，多出来的18条腿需要分配给兔子。

因为每只兔子有4条腿，所以共有18÷2=9只兔子。

5.在一次数学测验中，共有20道题目，做对一题得5分，做错一题扣1分，不做得分。

XXX得了76分，问他做对了几道题？如果假设所有题目都做对，那么总分为5×20=100分。

因此，XXX得了多出来的24分。

因为每道错题会扣1分，所以XXX答错了24÷（5+1）=4道题。

因此，他做对的题目数为20-4=16道。

四年级下册鸡兔同笼问题练习题(附答案及解析)

四年级下册鸡兔同笼问题练习题(附答案及解析).doc1、鸡兔同笼, 共100个头, 320只脚, 鸡有 ( ) 只, 兔 ( ) 只。

2、小明计算20道竞赛题，做对一道得5分，做错一道倒扣3分，结果小明考得60分，小明做对了( )道题。

3、松鼠妈妈采松子。

晴天每天可以采20个，雨天每天可以采12个。

它一连几天采了112个松子，平均每天采14个。

这几天中有 ( )天下雨。

4、个体户王小二承接了建筑公司一项运输1200块玻璃的业务，并签了合同。

合同上规定：每块玻璃运费2元；如果运输过程中有损坏，每损坏一块，除了扣除一块的运费外，还要赔偿25元。

王小二把这1200块玻璃运送到指定地点后，建筑公司按合同付给他2076元。

运输过程中损坏了 ( ) 块。

5、100名师生绿化校园，老师每人栽3棵树，学生每2人栽1棵，总共栽树100棵。

老师栽树( )棵，学生栽树( )棵。

6、 30枚硬币由2分和5分组成，共值9角9分， 2分硬币 ( ) 枚， 5分硬币( )枚。

7、某校数学竞赛，共有20道填空题，评分标准是每做对一题得5分，做错一题倒扣3分，某题没做该题得0分。

小英结果得了69分，那小英有()题没做。

8、蜘蛛有8只脚，蜻蜓有6只脚和2对翅膀，蝉有6只脚和1对翅膀，现在这三种昆虫18只，共有118只脚和20对翅膀。

蜘蛛有()只，蜻蜓有( )只,蝉有( )只。

9、甲、乙两人进行射击比赛，约定每中一发记20分，脱靶一发扣12分，两人各打10发，共得208分，其中甲比乙多64分，甲中了 ( ) 发，乙中了( )发。

10、鸡、兔共有脚96只，若将鸡、兔互换，则有脚84只，鸡有()只，兔有( )只。

附答案：1、40 602、 153、 64、 125、60 406、17 137、3.(100-69)/(5+3)=31/8 31-8*2=15 15/5=3所以有3道题没答8. 5 7 69、 8 610、 12 18。

数学下册四年级数学鸡兔同笼题含答案解析

精选20道题攻克鸡兔同笼问题1．小兔和小鸡共12只排成一列，每只小兔都发现，站在自己前面和后面的全是小鸡，而每只小鸡发现与自己相邻的动物中恰好有一只小兔，那么这12只小动物共有条腿（每只小兔4条腿，每只小鸡2条腿）．2．数学花园里盛开着三瓣花、四瓣花和六瓣花，其中三瓣花和六瓣花共有99片花瓣，四瓣花比六瓣花少3朵，花园里共有朵花．3．AMC是美国数学竞赛的简称，在过去的近10年中，有越来越多的中国学生参加了该项赛事．AMC的试卷共有25个选择题，规定每道题答对得6分，不答得1.5分，答错得0分．思敏在这项赛事中拿到了129分．则她答错了题．4．艾迪在IPS上做题目时发现，直接做对1道题目可以拿到10个积分，做错再订正的题目也可以拿到2个积分，今天他一共做了15道题目，拿到了126个积分，请问：艾迪直接做对了道题目．5．赵强有1元、5元、10元三种人民币共50张，共计260元，其中1元与10元的张数一样多，那么5元的人民币有多少张？6．若干只三脚猫组成一队，若干只四脚蛇组成一队，两支队伍进行比赛，已知两队成员数量相等，且两队所有成员共有28只脚，那么，三脚猫有只．7．小华参加数学竞赛，共有10道赛题．规定答对1题给10分，答错1题扣5分．小华10题全部答完得了85分．小华答对了道题．8．某校有学生1200人，每个学生一天要上5节课．假如一个教师一天教4节课，按每班30人计算，这所学校共需配备教师多少名？9．鸡、兔共有脚100只，若将鸡换成兔，兔换成鸡，则共有脚92只．问：鸡、兔各几只？10．乙两人进行射击比赛，约定每中一发得20分，脱靶一发扣12分，两人各打10发，共得208分，最后甲比乙多得64分，乙打中多少发？11．和尚分馒头：100个和尚分100个馒头，大和尚每人分3个，小和尚每3个人分1个，刚好分完，大、小和尚各有多少人？12．3名同学去参加数学竞赛，共10道题，答对一道题得10分，答错一道题扣3分．这3个同学都回答了所有的问题，小笨得了87分，小聪得了74分，香香得了9分，问，他们一共答对了几道题？13．一个养殖园内，鸡比兔多36只，共有脚792只，鸡兔各几只？14．小明参加有奖竞猜，共有30道选择题，评分标准是：自己答对一题得4分；现场求助答对得2分；不答不得分；答错一题倒扣3分（现场求助的题答错也扣3分），小明最后得分为50分，而且他自己答对的和不答的题是一样多；现场求助答对的题比不答的多1题，那么他现场求助答对的题有（）道题．A．7 B．8 C．9 D．1015．古怪星球上有一些稀奇古怪的动物，它们分别是单腿怪（1个头、1条腿）、双头虎（2个头、4条腿）、三脚猫（1个头、3条腿）和四爪蛇（1个头、4条腿），如果草坪上这四种动物共有58个头、160只脚，且四爪蛇的数量恰好是双头虎的2倍，那么“单腿怪”有只．某银行发行“十二生肖”邮票，每套12张，售价如下：（1）如果整套购买，每套售价100元；（2）如果单张购买，“猴”属相邮票每张16元，其它属相邮票每张10元；销售结束后，银行总共收入2016元，而且发现整套交易的套数与单张交易的张数相等，被交易走的“猴”属相邮票共有2424张．16．1千克大豆可以制成3千克豆腐，制成1千克豆油则需要6千克大豆，豆腐3元1千克，豆油15元1千克，一批大豆共460千克，制成豆腐或豆油销售后得到1800元，这批大豆中有千克被制成了豆油．校运动会有200个同学参加“3人4足”和“8人9足”项目，每人都参加其中一个项目，所有队伍同时进行比赛，一共240"足”，那么一共有个参赛队伍．17．动物园里有鸵鸟和梅花鹿若干，共有腿122条．如果将鸵鸟与梅花鹿的数目互换，则应有腿106条，那么鸵鸟有只，梅花鹿有只．19.60人参加脑筋急转弯答题游戏，共有10道题，每道题每人都答1次，共答对452次，已知每人都至少答对了6道题，且只答对6道题的有21人，只答对8道题的有12人，只答对7道题和只答对9道题的人数一样多，那么10道题全答对的有人．20.一张数学试卷，只有25道选择题．做对一题得4分，做错一题倒扣1分；如不做，不得分也不扣分．若小明得了78分，那么他做对多少题，做错多少题，没做多少题？精选20道题攻克鸡兔同笼问题18．小兔和小鸡共12只排成一列，每只小兔都发现，站在自己前面和后面的全是小鸡，而每只小鸡发现与自己相邻的动物中恰好有一只小兔，那么这12只小动物共有条腿（每只小兔4条腿，每只小鸡2条腿）．鸡兔鸡鸡兔鸡鸡兔鸡鸡兔鸡鸡：8只，兔4只8×2+4×4=32条19．数学花园里盛开着三瓣花、四瓣花和六瓣花，其中三瓣花和六瓣花共有99片花瓣，四瓣花比六瓣花少3朵，花园里共有朵花．设三瓣花有a朵，六瓣花有b朵，则3a+6b=99a+2b=33（朵）即a+b+b=33（朵），即a+b+b-3=30（朵），答：花园里共有30朵花．20．AMC是美国数学竞赛的简称，在过去的近10年中，有越来越多的中国学生参加了该项赛事．AMC的试卷共有25个选择题，规定每道题答对得6分，不答得1.5分，答错得0分．思敏在这项赛事中拿到了129分．则她答错了题．假设全部答对，则25×6=150分150-129=21分不答损失6-1.5=4.5分答错损失6分，我们分析下损失的21分是由多少道不答的题和多少道错题组成即可21．5是小数，如果要变整数，只能乘偶数，所以21=4.5×2+6×222．艾迪在IPS上做题目时发现，直接做对1道题目可以拿到10个积分，做错再订正的题目也可以拿到2个积分，今天他一共做了15道题目，拿到了126个积分，请问：艾迪直接做对了道题目．假设艾迪全部是直接做对，则15×10=150个150-126=24个做错再订正的：24÷（10－2）=3道直接做对的：15-3=12道23．赵强有1元、5元、10元三种人民币共50张，共计260元，其中1元与10元的张数一样多，那么5元的人民币有多少张？假设全部是5元人民币，1元和10元人民币加起来当成一张11元的人民币，则5×50=250元260-250=10元1元人民币或10元人民币：10÷（11-10）=10张5元人民币：50-10×2=30张答：5元人民币30张24．若干只三脚猫组成一队，若干只四脚蛇组成一队，两支队伍进行比赛，已知两队成员数量相等，且两队所有成员共有28只脚，那么，三脚猫有只．28÷(3+4)=425．小华参加数学竞赛，共有10道赛题．规定答对1题给10分，答错1题扣5分．小华10题全部答完得了85分．小华答对了道题．假设10道题全部答对，则10×10=100分100-85=15分答错的题：15÷（10+5）=1道答对的题：10-1=9道26．某校有学生1200人，每个学生一天要上5节课．假如一个教师一天教4节课，按每班30人计算，这所学校共需配备教师多少名？1200÷30=40个40×5=200节200÷4=50名答：这所学校共需配备教师50名。

四年级下册鸡兔同笼问题练习题附答案及解析

四年级下册鸡兔同笼问题练习题附答案及解析【题目】四年级下册鸡兔同笼问题练习题附答案及解析鸡兔同笼问题是一个数学中经典的问题，针对这个问题，本文将提供一些四年级下册鸡兔同笼的练习题，并附上答案及解析，帮助孩子们提高解决问题的能力和思维逻辑。

一、选择题1. 一共有10只兔子和30只鸡，他们共有多少只脚？A. 400只B. 500只C. 600只D. 700只答案及解析：B. 500只。

根据题目可知，每只兔子有4只脚，每只鸡有2只脚。

所以，10只兔子共有40只脚，30只鸡共有60只脚。

将两者相加得到总脚数：40 + 60 = 100。

故共有500只脚。

2. 一共有12只兔子和36只鸡，他们共有多少只脚？A. 512只B. 608只C. 704只D. 800只答案及解析：C. 704只。

同样地，根据题目可知，每只兔子有4只脚，每只鸡有2只脚。

所以，12只兔子共有48只脚，36只鸡共有72只脚。

将两者相加得到总脚数：48 + 72 = 120。

故共有704只脚。

二、填空题1. 有8只兔子和22只鸡，他们共有个_________。

答案及解析：240。

同样地，每只兔子有4只脚，每只鸡有2只脚。

所以，8只兔子共有32只脚，22只鸡共有44只脚。

将两者相加得到总脚数：32 + 44 = 76。

每只动物共有2只耳朵，所以8只兔子共有16只耳朵。

将脚和耳朵的数量相加：76 + 16 = 92。

每只动物还有一个头，所以总数再加1：92 + 1 = 93。

最后，将93乘以8只兔子：93 × 8 = 744。

故共有744个。

三、解答题1. 有18只动物，共有52只脚和106只耳朵，请问其中有多少只兔子和鸡分别是多少？答案及解析：假设兔子的数量为x，鸡的数量为18 - x（18只动物减去兔子的数量）。

根据题目可知，每只兔子有4只脚，每只鸡有2只脚。

所以，总脚数可以表示为：4x + 2(18 - x) = 52。

化简得到2x +36 - 2x = 52，解得x = 8。

小学四年级下学期数学鸡兔同笼练习题及答案

小学四年级下学期数学鸡兔同笼练习题及答案1.鸡兔同笼，共有30个头和86只脚，求鸡兔各有多少只？2.有20张5元和10元的人民币，一共是175元，求5元和10元的人民币各有多少张？3.XXX买了圆珠笔和钢笔共15枝，圆珠笔每枝1.5元，钢笔每枝4.5元，共花了49.5元，求圆珠笔和钢笔各买了多少枝？4.鸡兔同笼，共有35个头和94条腿，求鸡兔各有多少只？5.在一个停车场内，汽车和摩托车共停了48辆，其中每辆汽车有4个轮子，每辆摩托车有3个轮子，这些车共有172个轮子，求汽车和摩托车各有多少辆？6.XXX买了8分邮票和4分邮票共100张，共付出6.8元，求XXX买了这两种邮票各多少张？7.在知识竞赛中，有10道判断题，每答对一道题得两分，答错一道题要倒扣一分。

XXX答了全部题目，但最后只得了14分，求他答错了几道题？8.某运输队为超市运送暖瓶500箱，每箱装有6个暖瓶。

已知每10个暖瓶的运费为5元，损坏一个暖瓶不但不给运费还要赔10元，运后结算时，运输队共得1350元的运费。

求损坏了多少暖瓶？9.鸡兔同笼，共有20个头和62只脚，求鸡兔各有几只？10.XXX买了2元和5元邮票一共34张，用去98元钱。

求XXX买了2元和5元的邮票各多少张？11.全班46人去划船，共乘12只船，其中大船每只坐5人，小船每只坐3人，求大船和小船各有多少只？12.在一个停车场上，停了汽车和摩托车一共32辆。

其中汽车有4个轮子，摩托车有3个轮子，总共有108个轮子，求汽车和摩托车各有多少辆？13.XXX举行数学竞赛，共10题，做对一题得10分，做错一题倒扣两分。

XXX得了52分，求他做错了几道题？14.100名师生绿化校园，老师每人栽3棵树，学生每两人栽1棵树，共栽树100棵。

求老师和同学各栽树多少棵？15.XXX有3名同学去参加数学竞赛，一份试卷共10道题，答对一题得10分，答错一题扣3分。

这三名同学都答了全部题目，XXX得74分，XXX得22分，XXX得87分，他们三人共答对多少题？5.鸡兔同笼，设鸡有x只，兔有y只。

四年级下册数学鸡兔共笼题

四年级下册数学鸡兔共笼题一、鸡兔同笼题目。

1. 鸡兔同笼，共有头30个，脚86只，求鸡兔各有多少只？- 解析：假设全是鸡，那么脚的总数应该是2×30 = 60只，而实际有86只脚，多出来的脚是因为把兔子当成鸡了。

每只兔子比鸡多4 - 2=2只脚，总共多了86 - 60 = 26只脚，所以兔子的数量是26÷2 = 13只，鸡的数量就是30 - 13 = 17只。

2. 鸡兔同笼，有头25个，脚70只，鸡兔各多少只？- 解析：假设全是鸡，脚的总数为2×25 = 50只。

实际有70只脚，多了70 - 50 = 20只脚。

每只兔比鸡多2只脚，所以兔的数量为20÷2 = 10只，鸡的数量为25 - 10 = 15只。

3. 笼子里有鸡和兔共18只，脚共56只，鸡和兔各有几只？- 解析：假设全是鸡，脚有2×18 = 36只。

实际56只脚，多了56 - 36 = 20只脚。

每只兔比鸡多2只脚，兔的数量为20÷2 = 10只，鸡的数量为18 - 10 = 8只。

4. 鸡兔同笼，头共20个，脚共62只，鸡兔各几只？- 解析：假设全是鸡，脚数为2×20 = 40只。

实际62只脚，多了62 - 40 = 22只脚。

每只兔比鸡多2只脚，兔的数量为22÷2 = 11只，鸡的数量为20 - 11 = 9只。

5. 有鸡兔同笼，共有头16个，脚44只，鸡兔各多少只？- 解析：假设全是鸡，脚有2×16 = 32只。

实际44只脚，多了44 - 32 = 12只脚。

每只兔比鸡多2只脚，兔的数量为12÷2 = 6只，鸡的数量为16 - 6 = 10只。

6. 鸡兔同笼，头共15个，脚共40只，鸡兔各几只？- 解析：假设全是鸡，脚数为2×15 = 30只。

实际40只脚，多了40 - 30 = 10只脚。

每只兔比鸡多2只脚，兔的数量为10÷2 = 5只，鸡的数量为15 - 5 = 10只。

四年级数学下册《第九单元鸡兔同笼》练习题及答案解析

四年级数学下册《第九单元鸡兔同笼》练习题及答案解析学校:___________姓名：___________班级：_________________一、填空题1．选择正确的余数填在括号里。

÷=……( )（3，30）(1)7104017÷=……( )（5，50，500）(2)35006005÷=……( )（1，10，100）(3)190030062．幸福路小学六年级同学利用暑假进行拓展活动，晴天每日行17.5千米，雨天每日行11千米，13天共行201.5千米。

这期间雨天有( )天，晴天有( )天。

3．在投球比赛中，李明2分球和3分球一共进了8个，共得18分，他投进2分球( )个，3分球( )个。

4．6辆小轿车的轮子与( )辆三轮车的轮子相等。

5．张叔叔用90个轮子装配自行车和三轮车，一共装配了33辆。

张叔叔装配的三轮车和自行车各有多少辆？（先假设自行车和三轮车的辆数如下表，再调整）张叔叔装配的自行车有( )辆，三轮车有( )辆。

6．六年级进行计算比赛，共20题，规定算对一题得5分，错一题扣2分。

晓华得了79分，他做对( )题。

二、选择题7．有5元和10元的人民币共20张，一共是145元，5元的人民币有（）张。

A．11B．9C．138．鸡和兔的腿共有60条，鸡最多有（）只。

A．28B．56C．29D．309．一场篮球比赛中，3分线外投中一球得3分，3分线内投中一球得2分，李勇总共投中8个球，得21分，他投中了（）个3分球。

A．5B．4C．2三、脱式计算10．观察下面式子的特点并用简便方法计算。

25×125×4×8128－37－238×19×125173＋428＋27138＋25＋62＋175（41×4）×25四、解答题11．小明买5元的钢笔和3元的铅笔共8支，共花了34元。

这两种笔各买多少支？（用列表法完成）12．一头非洲狮有多重？从下面方框中选出两个条件。

四年级下册数学鸡兔同笼习题及答案-数学题鸡兔同笼解答

四年级下册数学鸡兔同笼习题及答案-数
学题鸡兔同笼解答
1、两辆汽车共运216吨货物，小汽车运了7小时，大汽车运了8小时。

已知小汽车5小时的运量等于大汽车2小时的运量，求大汽车每小时运多少吨？
假设全是小汽车，需要运的时间为（8÷2）×5＝20小时，加上大汽车的8小时，总共需要27小时。

因此，小汽车每小时运量为216÷27＝8吨。

又因为小汽车5小时运的数量等于大汽车2小时运的数量，所以大汽车每小时运量为8×5÷2＝20吨。

2、笼子里有鸡兔共27只，兔脚比鸡脚多18只，问有多少只鸡和兔？
假设全是兔子，它们的脚数为4×27＝108只，而实际上兔脚比鸡脚多了18只，所以有90只脚是属于兔子的。

如果将一只兔子的脚换成一只鸡的脚，就会多出6只脚。

因此，有90÷6＝15只鸡，剩下的就是27－15＝12只兔子。

3、有182只兔子，分别装在甲乙两种笼子里，甲种笼子每笼装6只，乙种笼子每笼装4只，两种笼子正好用36个。

问两种笼子各有多少个？
假设全部用甲种笼子，需要的笼子数为182÷6＝30.33，但是题目中说需要用36个笼子，因此需要换成乙种笼子。

每换一只乙种笼子就少2只兔子，所以需要换的次数为（30.33－36）÷2＝－2.83，即需要换3次。

因此，乙种笼子为36－3＝33个，甲种笼子为36－33＝3个。

四年级下册鸡兔同笼问题练习题(附答案及解析)

四年级下册鸡兔同笼问题练习题(附答案及解析)四年级下册鸡兔同笼问题练习题(附答案及解析)一、问题描述：在一个笼子里，鸡和兔子一共有35个头，94只脚。

问鸡和兔子各有多少只？二、问题分析：这是一个经典的鸡兔同笼问题，我们可以运用代数解法或者穷举法来求解。

本文将介绍两种解法，并提供相应的答案和解析。

三、代数解法：设鸡的数量为x，兔子的数量为y。

根据题目中的条件，可以列出以下两个方程：1. x + y = 35 （总头数为35个）2. 2x + 4y = 94 （总脚数为94只）利用这两个方程，我们可以解出鸡和兔子的数量。

下面是求解的步骤：1. 将方程1乘以2，得到2x + 2y = 70。

2. 将得到的等式与方程2相减，消去x的项，得到2y = 24，进一步化简得到y = 12。

3. 将y的值代入方程1，得到x = 23。

因此，根据代数解法，鸡的数量为23只，兔子的数量为12只。

四、穷举法：穷举法是通过尝试所有可能的情况来求解问题。

在这个问题中，我们可以从鸡和兔子的总数量开始尝试，逐渐减少其中一个种类的数量，直到满足题目中的头数和脚数条件。

具体的步骤如下：1. 假设鸡的数量为0，兔子的数量为35。

通过计算可得，鸡和兔子的总脚数为140，与题目中的脚数条件不符，因此排除此种情况。

2. 假设鸡的数量为1，兔子的数量为34。

通过计算可得，鸡和兔子的总脚数为138，与题目中的脚数条件不符，因此排除此种情况。

3. ...继续逐渐减少鸡的数量，直到满足题目中的脚数条件。

通过不断尝试，最终可以得出鸡的数量为23只，兔子的数量为12只，与代数解法的结果一致。

五、答案及解析：根据两种解法的计算，鸡的数量为23只，兔子的数量为12只。

代数解法通过建立方程组，通过代数方法求解得出结果。

它的优点是计算准确、简便快捷，适用于各种复杂的问题。

但对于一些年级较低的学生来说，可能会比较难理解和掌握。

穷举法则是通过尝试所有可能的情况，直到找到符合条件的解。

四年级数学奥数鸡兔同笼含答案

鸡兔同笼问题（一）1：（4×总只数－总脚数）÷（兔的脚数－鸡的脚数）=鸡的只数总只数－鸡的只数=兔的只数总只数－兔的只数=鸡的只数2：（总脚数－2×总只数）÷（4－2）=兔的只数1、鸡兔同笼，共30个头，88只脚。

笼中鸡兔各有多少只？2 某次数学竞赛共20道题，评分标准是：每做对一题得5分，每做错或不做一题扣1分．小华参加了这次竞赛，得了64分．问：小华做对几道题？2、小邮迷郑渊用10元钱正好买了20分和50分的邮票共35枚，这两种邮票各买了多少枚？3、小华买了2元和5元的纪念邮票一共34枚，用去98元钱。

小华买了2元和5元的纪念邮票各多少枚？4、小明的储蓄罐里共有1角和5角的硬币54枚，小明算了一下，一共有15元。

问：两种硬币各多少枚？6、45人去划船，一共乘坐7只船，其中每只大船坐7人，每只小船坐5人。

求大船和小船的只数。

7、46名同学去公园划船，共乘坐9只船，其中大船坐6人，小船坐4人。

大船和小船各有几只？8、六（1）班42个同学向2008年北京奥运会捐款。

其中12人每人捐2元，其余同学每人捐5元或10元，一共捐了229元。

求捐5元和10元的同学各有多少人？鸡兔同笼问题（一）1：（4×总只数－总脚数）÷（兔的脚数－鸡的脚数）=鸡的只数总只数－鸡的只数=兔的只数总只数－兔的只数=鸡的只数2：（总脚数－2×总只数）÷（4－2）=兔的只数1鸡兔同笼，共30个头，88只脚。

笼中鸡兔各有多少只？22 某次数学竞赛共20道题，评分标准是：每做对一题得5分，每做错或不做一题扣1分．小华参加了这次竞赛，得了64分．问：小华做对几道题？3小邮迷郑渊用10元钱正好买了20分和50分的邮票共35枚，这两种邮票各买了多少枚？4小华买了2元和5元的纪念邮票一共34枚，用去98元钱。

小华买了2元和5元的纪念邮票各多少枚？5小明的储蓄罐里共有1角和5角的硬币54枚，小明算了一下，一共有15元。

四年级下册数学鸡兔共笼题目

四年级下册数学鸡兔共笼题目一、鸡兔同笼题目。

1. 鸡兔同笼，共有头30个，足86只，求鸡兔各有多少只？解析：假设全是鸡，那么足的数量是2×30 = 60只，比实际的86只少了8660=26只。

每把一只兔当成鸡就少算4 2 = 2只足，所以兔的数量是26÷2 = 13只，鸡的数量就是30 13 = 17只。

2. 笼子里有鸡和兔共25只，鸡脚和兔脚共70只，问鸡、兔各有多少只？解析：假设全是鸡，脚的总数为2×25 = 50只，比实际少70 50 = 20只。

每把一只兔当成鸡少算4 2 = 2只脚，所以兔的数量为20÷2 = 10只，鸡的数量为25 10 = 15只。

3. 鸡兔同笼，头共46，足共128，鸡兔各几只？解析：假设全是鸡，足的数量是2×46 = 92只，比实际少128 92 = 36只。

每把一只兔当成鸡少算4 2 = 2只足，兔的数量为36÷2 = 18只，鸡的数量为46 18 = 28只。

4. 有鸡兔同笼，共有35个头，94只脚，问鸡兔各多少只？解析：假设全是鸡，脚数为2×35 = 70只，比实际少94 70 = 24只。

每把一只兔当成鸡少算4 2 = 2只脚，兔的数量为24÷2 = 12只，鸡的数量为35 12 = 23只。

5. 鸡兔同笼，鸡比兔多15只，鸡兔共有脚132只，问鸡兔各多少只？解析：设兔有x只，则鸡有x + 15只。

根据脚的总数可列方程4x+2(x +15)=132，展开得4x + 2x+30 = 132，6x=102，解得x = 17只，鸡的数量为17 + 15 = 32只。

6. 鸡兔同笼，兔比鸡少10只，共有脚100只，问鸡兔各多少只？解析：设鸡有x只，则兔有x 10只。

根据脚的总数可列方程2x+4(x 10)=100，展开得2x+4x 40 = 100，6x = 140，解得x=(70)/(3)（这种情况不符合实际，说明假设错误）。

人教版数学四年级下册9鸡兔同笼练习卷(含答案解析)

（3）列表假设假设
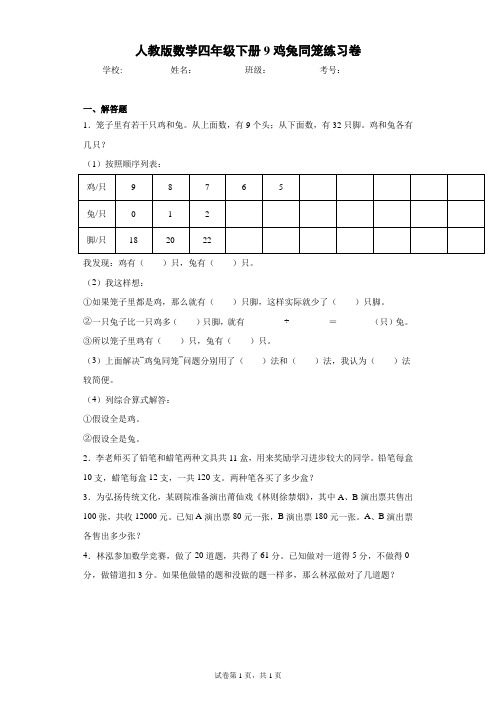
（4）鸡有2只，兔有7只。
【分析】
第一种是列表法，列表法是把所有可能的情况一一列出来，并从中找到符合条件的；第二种是假设法，假设法是解决此类问题的较为普遍的种解法。比如假设笼子里全是鸡，然后通过计算实际与假设情况下总脚数之差，进而推理出鸡、兔的只数。
【详解】
（1）
鸡/只
9
8
7
6
5
4
＝4÷2
＝2（只）
兔：（只）
答：鸡有2只，兔有7只。
【点睛】
本题考查的是解决鸡兔同笼的两种方法，从实际问题中感受两种方法的区别。
2．铅笔买了6盒，蜡笔买了5盒。
【分析】
本题可以用假设法来解答。方法一：假设11盒全是铅笔，先求出的盒数就是蜡笔的盒数，进而求出铅笔的盒数。方法二：假设11盒全是蜡笔，先求出的盒数就是铅笔的盒数，进而求出蜡笔的盒数。
3．A演出票售出60张，B演出票售出40张。
【分析】
方法一：假设100张全是A演出票，先求出的张数就是B演出票的张数，进而求出A演出票的张数。方法二：假设100张全是B演出票，先求出的张数就是A演出票的张数，进而求出B演出票的张数。
【详解】
方法一：假设全是A演出票。
＝40（张）
（张）
方法二：假设全是B演出票。
【详解】
方法一：假设全是铅笔。
蜡笔：
（120－11×10）÷（12－10）
＝（120－ห้องสมุดไป่ตู้10）÷2
＝10÷2
＝5（盒）
铅笔：（盒）
方法二：假设全是蜡笔。
铅笔：
（12×11－120）÷（12－10）
＝（132－120）÷2
＝12÷2
＝6（盒）

小学数学四年级下册《鸡兔同笼》应用题专项练习(附答案)

四年级数学下册应用题专项练习班级考号姓名总分（鸡兔同笼）附：参考答案1、鸡兔同笼共80个头，208只脚，鸡和兔各有几只？兔：(208－2×80)÷(4－2) 鸡：80－24＝56(只)＝48÷2＝24(只)鸡：(4×80－208)÷(4－2) 兔：80－56＝24(只)＝112÷2＝56(只)2、鸡兔同笼，共有30个头，88只脚。

求笼中鸡兔各有多少只？兔：（88-30×2）÷（4-2）鸡：30-14=16（只）=24÷2=14（只）鸡：（30×4-88）÷（4-2）兔：30-16=14（只）=32÷2=16（只）3、鸡兔同笼，共有头48个，脚132只，求鸡和兔各有多少只？兔：（132-48×2）÷（4-2）鸡：48-18=30（只）=36÷2=18（只）鸡:(48×4-132)÷（4-2）兔:48-30=18(只)=60÷2=30（只）4、鸡兔同笼共80个头，208只脚，鸡和兔各有几只？兔：（208-80×2）÷（4-2）鸡：80-24=56（只）=48÷2=24（只）鸡：（80×4-208）÷（4-2）兔：80 -56=24（只）=112÷2=56（只）5、鸡兔同笼共78头，共有200只脚，鸡和兔各有几只？兔：（200-78×2）÷（4-2）鸡：78-22=56（只）=44÷2=22（只）鸡：（78×4-200）÷（4-2）兔：78 -56=22（只）=112÷2=56（只）6、在一个停车场上，停了小轿车和摩托车一共32辆，这些车一共108个轮子。

求小轿车和摩托车各有多少辆？小轿车：（108-32×2）÷（4-2）摩托车：32-22=10（辆）=44÷2=22（辆）摩托车：（32×4-108）÷（4-2）小轿车：32-10=22（辆）=20÷2=10（辆）7、小明爱好收集邮票，他用20元买了8角和1.2元的两种邮票，共20张，求这两种邮票各买了多少张？20元=200角 1.2元=12角1.2元：（200-8×20）÷（12-8） 8角：20-10=10（张）=40÷4=10（张）8角：（12×20-200）÷（12-8） 1.2元：20-10=10（张）=40÷4=10（张）8、小明用10元钱正好买了20分和50分的邮票共35张，求这两种邮票各买了多少张？20分=2角50分=5角10元=100角50分：（100-2×35）÷（5-2） 20分：35-10=25（张）=30÷3=10（张）9、小刚的储蓄罐里共2分和5分硬币70枚，小刚数了一下，一共有194分，求两种硬币各有多少枚？5分：（194-2×70）÷（5-2） 2分：70-18=52（枚）=54÷3=18（枚）10、松鼠妈妈采松籽，晴天每天可以采20个，雨天每天只能采12个。

思维拓展训练：鸡兔同笼-数学2024四年级下册含答案

思维拓展训练：鸡兔同笼-数学2024四年级下册一、选择题1．鸡兔同笼，共有12个头，有36只脚，兔有（）只，鸡有（）只。

A．5；4 B．6；6 C．4；62．自行车和三轮车共10辆，共23个轮子，其中自行车有（）辆。

A．3 B．5 C．73．张华用130元买了2元和5元的邮票共50张，那么张华买了2元邮票（）张。

A．20 B．30 C．404．有5元和10元的人民币共10张，一共是80元，5元的人民币有（）张。

A．4 B．5 C．65．一块湿地上，有龟、鹤共30只，龟的腿和鹤的腿共100条，龟有（）只。

A．20 B．22 C．106．一场篮球比赛中，3分线外投中一球得3分，3分线内投中一球得2分，李勇总共投中8个球，得21分，他投中了（）个3分球。

A．5 B．4 C．27．一队猎手一队狗，二队并作一队走，数头一共三十三，数脚一共九十整。

猎手有（）人。

A．18 B．21 C．128．天童画室组织48名学员去南海公园划船。

大船每只坐6人，小船每只坐4人，他们共租了10只船，每只船上都坐满了人，大船、小船各租了（）只。

A．大船6只，小船4只B．大船5只，小船5只C．大船4只，小船6只二、填空题9．一款VR射击电玩游戏，要求击中屏幕里漂浮的气球。

击中1个气球记10分，未击中扣4分，明明一局射击15次，共得80分，他有( )次未击中。

10．自行车越野赛全程共260千米，全程被分为20个路段，其中一部分路段长15千米，其余的路段长10千米。

长15千米的路段有( )个，长10千米的路段有( )个。

11．迎亚运会，某校四年级举行乒乓球赛，有10张乒乓球桌正在进行单打、双打比赛，一共有28名同学正在比赛。

进行双打比赛的球桌有( )张。

12．为更好地开展垃圾分类工作，幸福小区规定：每次正确投放垃圾可获得8个积分，错误投放垃圾倒扣4个积分，小明家6月份一共投放垃圾30次，共获得192分，小明家这个月正确投放垃圾( )次。

小学四年级数学下册鸡兔同笼的习题及答案

小学鸡兔同笼的习题及答案1、某个笼子里有10只鸡和兔，一共有22只脚，请问这个笼子里有几只兔子？2、有一个笼子里面装有鸡和兔子，头数共35个，脚的数目共94只，请问笼子里有多少只鸡？多少只兔子？3、在一个笼子里，鸡和兔的总数为40只，它们的脚一共有100只，请问这个笼子里有几只兔子？4、有一个笼子，里面有若干只鸡和兔子，在数它们的头和脚时，得到了这样的结果：头数比脚数少5，问笼子里有多少只鸡和兔子？5、有一个笼子里关着鸡和兔，它们的头数为50，脚数为140，请问笼子里分别有多少只鸡和兔？6、一个笼子里有36个头，100只脚，问里面共有多少只鸡和多少只兔？7、在一个笼子里有十几只鸡和兔子，把它们全部赶出笼子，数了一下它们的头，数到45个。

请问这个笼子里原来有几只兔子？8、有一个笼子里面装着鸡和兔子，一共有50个头，130只脚，请问笼子里各有多少只鸡和兔子？9、一只鸟笼里关着若干只鸡和兔子，共有54只脚。

如果兔子的数量比鸡的数量多4只，那么这只鸟笼里一共关着多少只动物？10、一个农夫买了一批鸡和兔共80只，花费了240元；后来他又另外买了一批鸡和兔共60只，花费了180元。

他买第一批时，每只鸡和兔的价格都是3元，第二批则为4元。

请问他买来多少只鸡和兔？答案1.答案：笼子里有6只兔子。

2.答案：笼子里有23只鸡和12只兔子。

3.答案：笼子里有20只兔子。

4.答案：笼子里有8只鸡和3只兔子。

5.答案：笼子里有30只鸡和20只兔子。

6.答案：笼子里有22只鸡和14只兔子。

7.答案：笼子里原来有10只兔子。

8.答案：笼子里有40只鸡和10只兔子。

9.答案：笼子里一共有16只动物，其中有6只兔子和10只鸡。

10.答案：农夫买了40只鸡和40只兔（共80只），以及20只鸡和40只兔（共60只）。

四年级下册的鸡兔同笼问题及答案

四年级下册的鸡兔同笼问题及答案一、例题精讲若干只鸡和兔子关在同一个笼子里，从上边数，有35个头，从下边数，有94只脚，问，鸡和兔子各有几只。

【解析】题目中告诉我们鸡和兔子共有35个头，94只脚，而常识告诉我们，一只鸡有一个头两只脚，一只兔子有一个头4只脚，所以，我们可以假设鸡和兔子分别有x,y只，则有： x+y=35,2x+4y=94,由此可以解得x=23,y=12。

按照我们的方程法，其实就是可以解出的，但是在实际操作过程中，方程可能将比较耗时，所以我们须要给大家传授另外一种快速的方法，假设法。

在这道题中，我们可以假设全部的动物都就是鸡，则35个动物就可以存有70只脚，但实际上，存有94只脚，所以我们算是的70可以和实际差距24只脚，再去思索一下，为啥可以差距呢?是因为我们把所有的兔子都当作了鸡，每把一直兔子当作鸡的时候就可以太少两只脚，所以共少24只脚，就须要12只兔子。

因此就可以存有23只鸡。

对比上述两种方法，我们会发现假设法比较简单一些。

二、典型例题例1.某餐厅设有可坐12人和10人两种规格的餐桌共28张，最多可容纳人同时就餐，问餐厅有多少10人桌?a.2b.4c.6d.8【答案】a。

中公解析：假设全部都是10人桌，则共可以容纳人，但实际上容纳人，相差52人，而每一张12人桌和10人桌会相差2人，所以会有26张12人桌，因此我们可以得到10人桌有2张。

三、题目稳固例. 有一辆货车运输只玻璃瓶，运费按到达时完好的瓶子数目计算，每只2角钱，如有破损，破损一只还要倒赔2角，结果共得到运费.2元，破损的只数是：a.17b. 24c.34d.36【答案】a。

解析：假设所有的瓶子都是完好无损的，则可以得到运费元，但实际上只有.2，相差6.8元，因为当瓶子破损时，与好的瓶子相比，除了2角钱运费得不到还需要倒赔2角，所以每有一个坏瓶子会与好瓶子相差4角，因此共有17个坏的瓶子。

选择a。

四年级下册鸡兔同笼问题练习题(附答案及解析)

小学鸡兔同笼问题练习题及答案解析

人教版数学四年级下册：鸡兔同笼问题 练习题(附答案及解析)

四年级下册鸡兔同笼问题练习题(附答案及解析)

数学下册四年级数学鸡兔同笼题 含答案解析

四年级下册鸡兔同笼问题练习题 附答案及解析

小学四年级下学期数学鸡兔同笼练习题及答案

四年级下册数学鸡兔共笼题

四年级数学下册《第九单元 鸡兔同笼》练习题及答案解析

四年级下册数学鸡兔同笼习题及答案-数学题鸡兔同笼解答

四年级下册鸡兔同笼问题练习题(附答案及解析)

四年级数学奥数鸡兔同笼含答案

四年级下册数学鸡兔共笼题目

人教版数学四年级下册9鸡兔同笼练习卷(含答案解析)

小学数学四年级下册《鸡兔同笼》应用题专项练习(附答案)

思维拓展训练：鸡兔同笼-数学2024四年级下册含答案

小学四年级数学下册鸡兔同笼的习题及答案

四年级下册的鸡兔同笼问题及答案

人教版数学四年级下册：鸡兔同笼问题练习题(附答案及解析)

数学下册四年级数学鸡兔同笼题含答案解析

四年级下册鸡兔同笼问题练习题附答案及解析

四年级数学下册《第九单元鸡兔同笼》练习题及答案解析