力法习题课举例11
力的合成与分解经典例题

力的合成与分解练习一、计算题1. 如图所示,一轻质三角形框架B处悬挂一定滑轮(质量可忽略不计)。
一体重为500N的人通过跨定滑轮的轻绳匀速提起一重为300N的物体。
(1)此时人对地面的压力是多大?(2)轻绳BD所受的力是多大?(3)斜杆BC所受的力是多大?2. 如图所示,倾角θ=37°、斜面长为1m的斜面体放在水平面上.将一质量为2kg的小物块从斜面顶部由静止释放,1s后到达底端,斜面体始终保持静止.重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求:(1)小物块沿斜面下滑的加速度和到达底端时速度的大小;(2)小物块与斜面之间的动摩擦因数;(3)小物块运动过程中,水平面对斜面体的摩擦力大小和方向.3. 右图所示,ABC为一直角劈形物体,将其卡于孔中,劈的斜面AB=10cm,直角边AC=2cm.当用F=100N 的力沿水平方向推劈时,求劈的上侧面和下侧面产生的推力.4. 用细绳AC和BC吊一重物,绳与竖直方向夹角分别为30°和60°,如图,已知:物体重力为100N,求:(1)绳AC的弹力;(2)绳BC的弹力.5. 如图所示,在倾角α为37o的斜面上,一质量为m=10kg的光滑小球被竖直的木板挡住,处于静止状态,求:(1)斜面对小球的支持力为多大?(2)挡板对小球的支持力为多大?6. (12分)两物体M、m用跨过光滑定滑轮的轻绳相连,如图放置,M与水平面的滑动摩擦因数为μ.OA、OB与水平面的夹角分别为30°、60°,m重20N.M、m均处于静止状态.求:(1)OA、OB对O点的拉力的大小;(2)M受到的静摩擦力.(可以用分式表示)7. 如图,水平细杆上套一环A,环A与球B间用一不可伸长轻质绳相连,质量分别为M A=0.4kg和M B=0.3kg,由于B球受到水平风力作用,使环A与球B相对静止一起向右匀速运动。
结构力学力法习题及答案

力法 作业 01〔0601-0610 为课后练习,答案已给出〕0601 图示结构,若取梁 B 截面弯矩为力法的基本未知量1X ,当2I 增大时,则1X 绝对值:A .增大;B .减小;C .不变;D .增大或减小,取决于21/I I 比值。
〔 C 〕q0602 图示桁架取杆 AC 轴力(拉为正)为力法的基本未知量1X ,则有:A .X 10=;B .X 10>;C .X 10<;D .1X 不定,取决于12A A 值与α值。
〔 A 〕 a D0603图 b 示图a 结构的力法基本体系,则力法方程中的系数和自由项为:A .∆11200P ><,; δ B .∆11200P <<,;δ C .∆11200P>>,;δ D .∆11200P <>,δ。
〔 B 〕X X0604 图 a 结构取力法基本体系如图 b ,1X 是基本未知量,其力法方程可写为11111c X δ+∆=∆,其中:A .∆∆1100c >=,;B .∆∆1100c <=,;C.∆∆1100c =>,; D .∆∆1100c =<,。
〔 A 〕(a)(b)X 10605 图 a 结构的最后弯矩图为:A .图 b ;B .图 c ;C .图 d ;D .都不对。
〔 A 〕l 3M /4M /4(a)(b)M /43M /4M /8M /43M /4M/2(c)(d)0606图示结构 f (柔度) 从小到大时,固定端弯矩 m 为:A .从小到大;B .从大到小;C .不变化;D . m 反向。
〔 B 〕0607 图示对称结构,其半结构计算简图为图:B.原 图A 〕0608 图示结构( f 为柔度):A .MM A C >; B .M M A C =; C .M M A C <; D .M M A C =-。
〔 C 〕 A M C0609图 a 所示结构,取图 b 为力法基本体系,则基本体系中沿1X 方向的位移1∆等于:A .0;B .k ;C .-X k 1/;D .X k 1/。
力法 位移法

一般杆件
M M
AB BA
? ?
4i? A 2i? A
? ?
2i? B 4i? B
? ?
6i 6i
? l ? l
? ???? ? ??
?
(1)
FQAB
?
FQBA
?
?
6i l
?A
?
6i l
?
B
?
12i l2
?
?
(2)
? ? FQAB
?
FQBA ?
?1 l
M AB ?
M BA
几种不同远端支座的刚度方程
M BA ? ? i? A
由荷载求固端弯矩
载常数表 7-1,称为固端弯矩和固端剪力
M
F AB
,
FQFAB
一般杆件叠加公式 :
M ? 4i? ? 2i? ? 6i ?
AB
A
B
l
?
M
F AB
M ? 2i? ? 4i? ? 6i ?
BA
A
B
l
?
M
F BA
FQAB
?
?
6i l
?
A
?
6i l
?
B
?
12 i l2
?
?
FF QAB
FQBA
?
?
6i l
?
A
?
6i l
?
B
பைடு நூலகம்
?
12 i l2
?
?
FF QBA
小结
1、有几个未知结点位移就应建立几个平衡方程;
2、单元分析、建立单元刚度方程是基础;
初中物理力学经典例题15道题

初中物理力学经典例题15道题1. 一个质量为2kg的物体,在水平地面上受到10N的水平拉力,求物体的加速度。
解答:根据牛顿第二定律,物体的加速度等于合外力除以物体的质量。
所以物体的加速度为a = F/m = 10N / 2kg = 5m/s^2。
2. 一个质量为0.5kg的物体受到一个5N的竖直向下的重力,求物体的重力加速度。
解答:重力加速度是指物体在自由下落时垂直于地面的加速度。
根据牛顿第二定律,物体的重力加速度等于重力除以物体的质量。
所以物体的重力加速度为g = F/m = 5N / 0.5kg = 10m/s^2。
3. 一个质量为4kg的物体,向右运动时受到一个10N的水平拉力和一个8N的水平推力,求物体的加速度。
解答:物体的加速度等于合外力除以物体的质量。
合外力等于水平拉力减去水平推力,即F = 10N - 8N = 2N。
所以物体的加速度为a = F/m = 2N / 4kg = 0.5m/s^2。
4. 一个质量为2kg的物体,在斜面上受到一个与斜面垂直的力为10N的重力和一个沿斜面方向的力为4N,斜面的倾角为30度,求物体的加速度。
解答:首先将斜面上的力分解为与斜面垂直方向的力和沿斜面方向的力,即重力沿斜面方向的分力为F1 = mg * sinθ,沿斜面方向的合力为F2 = mg * cosθ。
其中,m = 2kg,g = 9.8m/s^2,θ = 30°。
所以沿斜面方向的合力为F2 = 2kg * 9.8m/s^2 * cos(30°) ≈ 16.96N。
物体的加速度等于沿斜面方向的合力除以物体的质量,即a = F2/m = 16.96N / 2kg ≈ 8.48m/s^2。
5. 一个质量为3kg的物体,向左运动时受到一个3N的水平拉力和一个5N的水平推力,求物体的加速度。
解答:物体的加速度等于合外力除以物体的质量。
合外力等于水平推力减去水平拉力,即F = 5N - 3N = 2N。
习题课力法(一)

24EI k= 3 l
28
四.求解下图a)所示的两次超静定结构,取一次超 静定结构作为基本体系。
q EI EI l l q X1
l a) 原结构
l b) 基本体系
29
解 1:
1) 先求解下图所示的一次超静定结构在荷载 作用下的弯矩图,取基本体系如下图示。
q EI EI l q X2 l
l
结构
l
基本体系
B
AB杆内力与右图单跨梁 相同。
q
EI1
1 2 ql 16
A
1 2 ql 8
15
(4) 设α = I1 / I 2 ,讨论 α = 0、 、 ∞ 的情况。 1
FP l FP A EI1 B A EI1 MP图 EI2 l A l C EI2 D l 0.5l l EI1 FP B X1 E D l
1 l2 2 5 1 3 δ 11 = ⋅ [ ⋅ l − ⋅ l] EI 2 3 8 3 8 1 l 2 7l 7l 3 = ⋅ ⋅ = EI 2 24 48 EI
M 1图
1)作 M 1图和MP图
EI h C
9
2)列出力法方程并求解
δ 11 X 1 + Δ1P = 0
l3 h3 δ11 = + 3EI 3EI
Δ1 P
1 1 1 2 3 − ql 4 =− ⋅ ⋅ l ⋅ ql ⋅ l = EI 3 2 4 8 EI
3)讨论
ql 4 3EI 3ql 1 X 1 = −Δ1P / δ 11 = (←→ ) ⋅ 3 = 3 8 EI (l + h ) 8 1 + ( h )3 l
10
h 1 = 0.5 l
h =1 2 l
力的正交分解法经典试题(内附答案)

力的正交分解法经典试题(内附答案)1.如图1,一架梯子斜靠在光滑竖直墙和粗糙水平面间静止,梯子和竖直墙的夹角为α。
当α再增大一些后,梯子仍然能保持静止。
那么α增大后和增大前比较,下列说法中正确的是 CA .地面对梯子的支持力增大B .墙对梯子的压力减小C .水平面对梯子的摩擦力增大D .梯子受到的合外力增大2.一个质量可以不计的细线,能够承受的最大拉力为F 。
现在把重力G =F 的重物通过光滑的轻质小钩挂在这根细线上,两手握住细线的两端,开始两手并拢,然后沿水平方向慢慢地分开,为了不使细线被拉断,细线的两端之间的夹角不能大于(C )A .60°B .90°C .120°D .150°3.放在斜面上的物体,所受重力G 可以分解使物体沿斜面向下滑的分力G 1和使物体压紧斜面的分力G 2,当斜面倾角增大时(C )A . G 1和G 2都增大B . G 1和G 2都减小C . G 1增大,G 2减小D . G 1减小,G 2增大4.如图所示,细绳MO 与NO 所能承受的最大拉力相同,长度MO>NO,则在不断增加重物G 的重力过程中(绳OC 不会断)( A )A .ON 绳先被拉断B .OM 绳先被拉断C .ON 绳和OM 绳同时被拉断D .条件不足,无法判断 5.如图所示,光滑的粗铁丝折成一直角三角形,BC 边水平,AC 边竖直,∠ABC=β,AB 、AC 边上分别套有细线系着的铜环,细线长度小于BC ,当它们静止时,细线与AB 边成θ角,则 ( D )A .θ=βB .θ<βC .θ>2πD .β<θ<2π6.质量为m 的木块沿倾角为θ的斜面匀速下滑,如图1所示,那么斜面对物体的作用力方向是 [D ]A .沿斜面向上B .垂直于斜面向上图C.沿斜面向下D.竖直向上7.物体在水平推力F的作用下静止于斜面上,如图3所示,若稍稍增大推力,物体仍保持静止,则 [BC ]A.物体所受合力增大B.物体所受合力不变C.物体对斜面的压力增大D.斜面对物体的摩擦力增大8.如图4-9所示,位于斜面的物块M在沿斜面向上的力F作用下,处于静止状态,则斜面作用于物块的静摩擦力的(ABCD )A.方向可能沿斜面向上B.方向可能沿斜面向下C.大小可能等于零D.大小可能等于F9.一个运动员双手对称地握住杠杆,使身体悬空.设每只手臂所受的拉力都是T,它们的合力是F,当两手臂之间的夹角增大时( C )A.T和F都增大B.T和F都增大C.T增大,F不变D.T不变,F增大10.如图2所示,人站在岸上通过定滑轮用绳牵引小船,若水的阻力恒定不变,则在船匀速靠岸的过程中 [AD]A.绳的拉力不断增大B.绳的拉力保持不变C.船受到的浮力不变D.船受到的浮力减小11.如图5-8所示,在一根绳子的中间吊着一个重物G,将绳的两端点往里移动,使θ角减小,则绳上拉力的大小将(A)A.拉力减小B.拉力增大C.拉力不变D .无法确定12.静止在斜面上的重物的重力可以分解为沿斜面方向向下的分力1F ,和垂直于斜面方向的分力2F ,关于这两个分力,下列的说明正确的是( D ) A .1F 作用在物体上,2F 作用在斜面上 B .2F 的性质是弹力C .2F 就是物体对斜面的正压力D .1F 和2F 是物体重力的等效代替的力,实际存在的就是重力13.如图6-17所示,OA 、OB 、OC 三细绳能承受的最大拉力完全一样.如果物体重力超过某一程度时,则绳子( A )A .OA 段先断B .OB 段先断C .OC 段先断D .一起断14.如图1—6—1所示,光滑斜面上物体重力分解为F 1、F 2两个力,下列说法正确的是CDA .F 1是斜面作用在物体上使物体下滑的力,F 2是物体对斜面的压力B .物体受到重力mg 、F N 、F 1、F 2四个力的作用C .物体只受到重力mg 和斜面支持力F N 的作用D .力F N 、F 1、F 2三力的作用效果与力mg 、F N 两个力的作用效果相同15.质量为m 的木块在推力F 作用下,在水平地面上做匀速运动(如图1—6—4).已知木块与地面间的动摩擦因数为μ,那么木块受到的滑动摩擦力为下列各值的哪一个B 、DA .μmgB .μ(mg +Fsin θ)C .μ(mg -Fsin θ)D .Fcos θ16.如图1—6—12所示,在倾角为α的斜面上,放一质量为m 的光滑小球,小球被竖直的木板挡住,则球对斜面的压力为CA.mgcosαB.mgtanαC.mg/cosαD.mg17.如图1—6—13长直木板的上表面的一端放有一铁块,木板由水平位置缓慢向上转动,(即木板与水平面的夹角α增大),另一端不动,则铁块受到的摩擦力F f随时间变化的图象可能正确的是图1—6—14中的哪一个(设最大静摩擦力与滑动摩擦力相等) C18.质量为m的物体A置于斜面体上,并被挡板B挡住,如图所示,下列判断正确的是(A )A.若斜面体光滑,则A、B之间一定存在弹力。
力法习题课及对称性的利用

P
C P
等代结构
P
P
P 等代结构
21
b)奇数跨对称结构的等代结构是将对称轴上的截面设置成支杆。 2、对称结构在反对称荷载作用下,内力、变形及位移是反对称的。 a)位于对称轴上的截面的位移 vc=0 , 内力 NC=0,MC=0
C EI P EI EI P P
QC NC MC NC
计算单位荷载下的内力图 计算支座反力:
1 4 1 3
1
1
代入位移计算公式得:
N s
5 12
Mds R k ck 0
1
5 1 1 1 1 0.001 1 2 3 1 0.002 0.003 4 12 200 2 3
1 2 0.005 m
9m
4m »
20o C
5o C
解: (1)选择基本体系 (2)列典型方程
5o C
q 15 kN m
X2
X1
151.875 4m
5o C 20o C
2 1
5o C
11 X 1 12 X 2 1P 1t 1c 0 21 X 1 22 X 2 2 P 2t 2c 0
»
. 5.05 X 1 0.03 X 2 5119 0 . 0.03 X 1 5.7 X 2 11143 0
X 1 10.02 kN X 2 19.5 kN
(3)绘制弯矩图
M X1 M 1 X 2 M 2 M P
10.02 A B 34.98 4m
19.5 C 4m 35.25 3m 3m
5o C
材料力学力法典型例题解

l
q
RB
B
l q
X1
B Δ1F
B δ11
1
Example 2 .画图示钢架旳弯矩图,EI=const .
P
a
B
A
CP B
A
a
CP
a
B
C
B
C
X1
M
1
M
A
A
Pa
a
解 : 1)选图示相当系统(:一次超静定)
2)力法方程:
X 0
11 1
1P
3)利用图乘法求系数:
a
P
a
B
A
a
C
P
a
B
C
B
C
M
1
M
A
A
PPal
X1
2)力法方程
F
X 0
11 1
1P
3)图乘法求系数
11
2 EI
(1 2
aa
2 3
a)
2a3 3EI
1P
2 EI
(1 2
a
Fa
2 3
a)
a a
2Fa3
M
3EI
4)解得:
1
C
X1
1P
11
F
1
C
Fa
X1=1 Fa
F
1
M
F
F1 C
F
Example 1 . 求RB (EI=const.).
解: 1)选图示相当系统 (一次超静定)
B
CP
P
P
a
a
X1
a a
X1 1
A
Pa
解:1)选图示静定基及相当系统
力的分解-力的分解典型例题

本文格式为 Word 版,下载可任意编辑,页眉双击删除即可。
题目 关于“杆的受力分解〞与“绳的受力分解〞商量 由于日常生活中,我们劳动、学习的工具一般以杆和绳子为主,其他 的工具也可以根据其进行分析,商量“杆的受力分解〞与“绳的受力分解〞 具有实践意义。有关内容可以参见备课资料中的“扩展资料〞。让同学观 看四周的力学工具,对比杆与绳子,分析说明各个物体的受力特点,与其 有关的题目可以参见如下: 1、晾晒衣服的绳子,为什么晾衣绳不易过紧? 2、为什么软纸经过折叠后,抗压性能提高?对比拱桥的设计,有什 么感想?
一、关于力的分解的教材分析和教法建议 力的分解是力的合成的逆预算,是求一个已知力的两个分力.在对已 知力进行分解时对两个分力的方向的确定,是根据力的作用效果进行 的.在前一节力的合成学习的基础上,学生对于运算规律的把握会比较快 速,而难在是对于如何根据力的效果去分解力,课本上列举两种状况进行 分析,一个是水平面上物体受到斜向拉力的分解,一个是斜面上物体所收 到的重力的分解,具有典型范例作用,教师在讲解时留意从以下方面具体 分析: 1、对合力特征的描述,如例题 1 中的几个关键性描述语句:水平面、
向上提物体,,因此力 可以分解为沿水平方向的分力 、和沿着竖直方向
教师总结并分析:图中重物拉铅笔的力 常被分解成 和 , 压缩铅笔,
的分力 ,力 和力 的大小为:
拉伸橡皮筋.
〔2〕学生试验 2,观看图示,分析 力的作用效果,用橡皮筋和铅笔
重复试验,对比结论是否正确.
例题 2:放在斜面上的物体,常把它所受的重力分解为平行于斜面的
手边的工具〔橡皮筋、铅笔、细绳、橡皮、三角板〕按图组装仪器、分组 按力的作用效果来分解.
商议 力产生的效果,并作出 力〔细绳对铅笔的拉力〕的分解示意图.
高一物理第三章力相互作用第5节力的分解课堂练习

高一物理第三章力相互作用第5节力的分解课堂练实例分析:1、斜而上物体重力的分解【例题11把一个物体静止在倾角为&的斜而上,物体受到竖直向下的重力,但它并不能 竖直下落。
那么,物体所受的重力会产生功能什么样的作用成效呢?【摸索与讨论】(l).Fx> F :是不是物体的真实受力?(2) •能不能讲F,是物体对斜而的圧力? 2、放在水平面上物体所受斜向上拉力的分解1.物体沿斜而下滑时,常把物体所受的重力分解为() A.使物体下滑的力和斜面的支持力.B.平行于斜而的分力和垂直于斜而的分力C.斜而的支持力和水平方向的分力D.对斜而的压力和水平方向的分力 2.把一个力分解为两个分力时,以下讲法中正确的选项是() A. 一个分力变大时,另一个分力一定变小 B.两个分力不能同时变大C.两个分力不能同时小于那个力的一半D.两个分力不能同时大于那个力的两倍 3・将一个力F 分解为两个分力,以下分解方法中不可能的是() A. —个分力的大小与F 的大小相同B. —个分力与力F 相同C. 一个分力垂直于FD.两个分力与F 都在一直线上 4.关于合力和分力的关系,以下讲法中正确的选项是( ) A.合力一定比分力大 B.合力能够同时垂直于两个分力C.合力的方向能够与一个分力的方向相反D.两个分力的夹角越大,它们的合力也越大 5•体育运动中包含着丰富的力学知识,如下图,铁柱举起质虽:80kg 的杠铃,双臂夹角为 120°, g 取10m/s 2,那么铁柱两臂对杠铃的作用力各为()A ・ 400NB ・ I600NC ・ 1 空D ・ 800N 33、三角支架悬物拉力的分解训练:F16.拖拉机和农具之间的牵引杆如不水平.拖拉机使农具前进的力就不等于牵引杆对农具的拉力F,而等于F在水平方向的分力.假如F=3・0X12N, F跟水平方向的夹角& = 15° ,那么使农具前进的力为多大?(cosl5° =0.966)7.如下图,物体重G=100N,并保持静止.绳子AC与BC分不与竖直方向成30°角和60c角,那么绳子AC和BC的拉力分不为多大?8•如下图,一个重为G的小球用两根细绳OA、OB拴住处于静止状态,绳OA是水平的, 求两根绳对小球的拉力.9.如下图,在倾角为&的斜而上有一块竖直放宜的挡板,在挡板和斜而间搁有一个重为G的光滑圆球,试求该球对斜而的压力和对挡板的压力.10.如下图,光滑小球放在夹角为45°的墙壁和斜面之间,处于静止状态,那么斜而对球的弹力与球的重力的大小之比为多少?墙对球的弹力与球的重力的大小之比又为多少?11・如下图,轻杆的一端A用狡链与竖直墙壁连接,它的另一端B用绳子连接至墙的C点,使轻杆保持水平,绳与轻杆的夹角为30°・在B端悬挂重10N 的物体,求轻杆和绳子各悠闲B端受到的作用力.12.如下图,绿妹将重1ON的气球用细绳拴在水平地而上,空气对英的浮力为16N.由于受到水平方向的风力的阻碍,系气球的绳子与水平方向成&=60°角.由此可知,绳子的拉力和水平方向的风力分不为多大?答案:1、B 2、C 3. B 4、C 5. D 6、2898N 7、AC 绳拉力为50^3 N,G BC绳的拉力为50N 8、OA绳对小球的拉力为Gtan 0, OB绳对小球的拉力为 ---------COS& 9、该球对斜而的压力为Gtan^,对挡板的压力为丄10.斜而对球的弹力与球的COS&重力的大小之比为血,墙对球的弹力与重力的大小之比为、二11、轻杆和绳子各悠闲2B端受到的作用力分不为10JJN和20N 12、绳子的拉力为4&N,水平方向的风力为2®。
力法计算举例
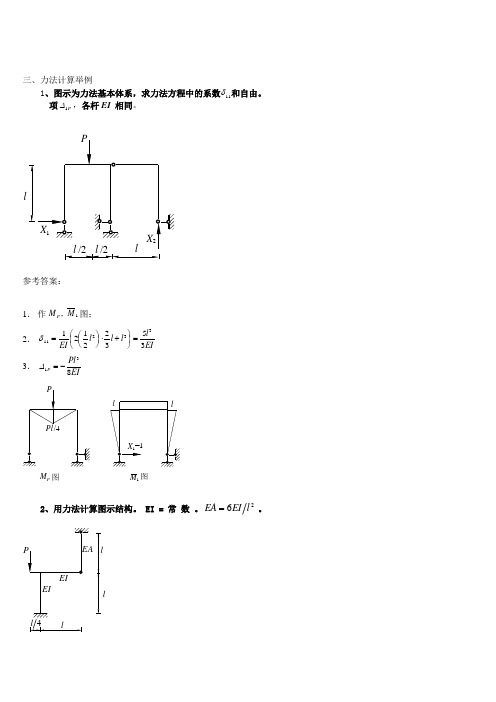
三、力法计算举例1、图示为力法基本体系,求力法方程中的系数δ11和自由。
项∆1P ,各杆EI 相同。
l参考答案:1. 作M M P , 1图; 2. δ1123312122353=⎛⎝ ⎫⎭⎪⋅+⎛⎝ ⎫⎭⎪=EIl l l l EI3. ∆138PPl EI=-M P 图M 图12、用力法计算图示结构。
EI = 常 数 。
26l EI EA =。
参考答案:1.取基本体系。
X15、作M图3、用力法计算图示结构。
ql l参考答案:这是一个对称结构。
1.利用对称性,选取基本体系。
()←-==∙∙∙∙=∆=∙∙∙∙+∙∙∙=∆=∆+ql X EI ql L L ql EI EI L L L L EI L L L EI X ,、、、M M 、X 、,、P P P 、P 12118213131323221131430211421311111111111δδδ并求求图作列力法方程基本体系数如图一次超静定结构取半结构如图所示解5、作M 图CBPP P P 、P M ,M M 、ql X EI ql L L ql EI EI L L L L EI L L EI X ,、、、M M 、X 、,、::+=-==∙∙∙∙=∆=∙∙∙∙+∙∙=∆=∆+114213211111111111586213113413221143021图作并求求图作列力法方程基本图形如图一次超静定解δδδ1.用力法计算图示结构,EI=常数。
解:1、二次超静定,基本结构如图:2、列力法方程⎪⎩⎪⎨⎧=∆++=∆++22221211212111ppχδχδχδχδ3、图作p,MM,M214、求11δ、12δ、22δ、21δ、p 1∆、p 2∆ EIEI 366323621111=⨯⨯⨯⨯∙=δ EIEI 1086662112112=⨯⨯⨯∙==δδEIEI 28866646621122=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯⨯=δ EI EI P 45023602133602111-=⎪⎭⎫⎝⎛⨯⨯⨯+⨯⨯⨯-=∆ EI EI P 54063602112-=⎪⎭⎫⎝⎛⨯⨯⨯-=∆ 5、求得144572521-=-=χχ6、作M 图p M x M x M M ++=22112.建立图示结构的力法方程。
龙驭球《结构力学Ⅰ》笔记和课后习题(含考研真题)详解(力 法)【圣才出品】

第6章力法6.1 复习笔记一、超静定次数的确定——力法的前期工作1.超静定结构的静力平衡特征和几何构造特征(1)静力平衡特征一个结构,如果它的支座反力和各截面的内力不能完全由静力平衡条件唯一地加以确定,就称为超静定结构。
(2)几何构造特征超静定结构是有多余约束的几何不变体系。
2.超静定次数的确定(1)从几何构造看,超静定次数=多余约束的个数。
(2)从静力分析看,超静定次数=未知力个数-平衡方程的个数。
(3)求超静定次数时,应注意以下事项:①撤去一根支杆或切断一根链杆,等于拆掉一个约束;②撤去一个铰支座或撤去一个单铰,等于拆掉两个约束;③撤去一个固定端或切断一个梁式杆,等于拆掉三个约束;④在连续杆中加入一个单铰,等于拆掉一个约束;⑤不要把必要约束拆掉;⑥要把全部多余约束都拆除。
二、力法的基本概念1.力法的基本未知量、基本体系和基本方程 (1)力法的基本未知量把多余未知力的计算问题当作超静定问题的关键问题,把多余未知力当作处于关键地位的未知力——称为力法的基本未知量。
(2)力法的基本体系和基本结构①含有多余未知力的静定结构,称为力法的“基本体系”; ②去掉多余约束力和荷载后的静定结构,称为力法的“基本结构”。
(3)力法的基本方程11δ——基本结构在单位未知力单独作用下沿1X 方向的位移;1X ——未知力;1P ∆——基本结构在荷载单独作用下沿1X 方向的位移。
2.多次超静定结构的计算 (1)二次超静定结构①图6-1-1(a )为二次超静定结构,取B 点两个支杆为多余约束,用X 1、X 2作为基本未知量代替,则基本体系如图6-1-1(b )所示。
图6-1-1②二次超静定结构的力法基本方程(2)多次超静定——力法典型方程——由荷载产生的沿方向的位移;——由单位力产生的沿方向的位移,常称为柔度系数。
在得到多余未知力的数值之后,超静定结构的内力可根据平衡条件求出,或者根据叠加原理用下式计算三、力法解超静定刚架和排架1.刚架的解法步骤(1)选取基本体系;(2)列出力法方程;(3)求系数和自由项;(4)求多余未知力;(5)作内力图。
(物理)初中物理运动和力的基本方法技巧及练习题及练习题(含答案)及解析

(物理)初中物理运动和力的基本方法技巧及练习题及练习题(含答案)及解析一、运动和力1.2018年1月30日,景驰在广州生物岛进行无人驾驶常态化试运营.如图所示,若汽车在平直的公路上做匀速直线运动,则下列各对力中,属于平衡力的是()A.汽车的牵引力和地面对汽车的摩擦力B.汽车对地面的压力和地面对汽车的支持力C.汽车所受的重力和汽车对地面的压力D.汽车对地面的摩擦力和汽车所受摩擦力【答案】A【解析】【详解】A.汽车的牵引力和地面对汽车的摩擦力符合作用在同一物体上、作用在一条直线上、大小相等、方向相反四个条件,是一对平衡力,符合题意;B.汽车所受的重力和地面对汽车的支持力,两个力不作用在同一物体上,因此不是一对平衡力,不合题意;C.汽车所受的重力和汽车对地面的压力方向相同不符合平衡力的条件;D.汽车对地面的摩擦力和汽车所受摩擦力,两个力不作用在同一物体上,因此不是一对平衡力,不合题意。
故选A。
【点睛】平衡力必须符合四个条件,即作用在同一物体上、作用在一条直线上、大小相等、方向相反.对照选项中的描述,看是否同时符合以上四个条件,即可做出判断。
2.有一个弹簧测力计,弹簧及其构件完好无损,某同学用其测量一物体的重力时,错将物体挂在了拉环上,当物体静止时,弹簧测力计的示数为10.0N,则物体的重力()A.一定等于10.0N B.一定小于10.0NC.一定大于10.0N D.以上判断都不正确【答案】B【解析】【详解】当将弹簧测力计倒置过来后,把物体挂在提环上,因为弹簧测力计本身有重力,挂钩显示的示数等于弹簧测力计自身的重力和物体的重力之和,所以此时物体的重力要小于测力计示数10N。
故ACD错误,B正确。
3.如图中,重为5N的木块A,在水中处于静止状态,此时绳子的拉力为3N,若绳子突然断了,木块A在没有露出水面之前,所受合力的大小和方向是()A.5N,竖直向下B.3N,竖直向上C.2N,竖直向上D.8N,竖直向下【答案】B【解析】【详解】绳子没断之前,受重力、浮力、绳子的拉力且三力平衡,故重力等于浮力、绳子拉力之和,则可求得浮力为5N-3N=2N;木块A在没有露出水面之前只受浮力和重力,因排开水的体积不变,所受浮力不变,而木块的质量不变,其重力不变,因浮力大于重力,则木块所受合力等于浮力减重力,即5N-2N=3N,合力方向与较大的浮力方向一致,竖直向上.故选B.4.如图所示的装置,重100 N的物体A在水平面做匀速直线运动,作用在绳自由端的拉力F 是20 N,则下列判断正确的是(不计滑轮重和滑轮间摩擦)A.作用在物体A上水平拉力是100 NB.作用在物体A上水平拉力是20 NC.物体A受到的滑动摩擦力是80 ND.物体A受到的滑动摩擦力是40 N【答案】D【解析】【详解】AB.根据二力平衡的条件进行分析,因为有两条绳子作用在动滑轮上,所以作用在物体A上的水平拉力F=2×20 N=40 N;故AB错误;CD.因为物体匀速运动,所以摩擦力等于作用在A上的水平拉力,大小为40 N,故C错误,D正确。
课时作业11:3.5 力的分解

5 力的分解一、选择题(1、2题为单选题,3、4题为多选题)1.如图所示,吊床用绳子拴在两棵树上等高位置。
某人先坐在吊床上,后躺在吊床上,均处于静止状态。
设吊床两端系绳的拉力为F 1、吊床对该人的作用力为F 2,则 ( )A .躺着比坐着时F 1大B .坐着比躺着时F 1大C .坐着比躺着时F 2大D .躺着比坐着时F 2大2.如图所示,置于水平地面的三脚架上固定着一质量为m 的照相机。
三脚架的三根轻质支架等长,与竖直方向均成30°角,则每根支架中承受的压力大小为 ( )A.13mg B .23mgC.36mg D.239mg3.自卸式运输车是车厢配有自动倾卸装置的汽车,又称为翻斗车、工程车,由汽车底盘、液压举升机构、取力装置和货厢组成。
如图所示,在车厢由水平位置逐渐抬起的过程中,有关货物所受车厢的支持力F N 和摩擦力F f ,下列说法中正确的是 ( )A .摩擦力F f 逐渐减小B .摩擦力F f 先增大后减小C .支持力F N 逐渐减小D .支持力F N 先增大后减小4.如图所示,用绳跨过定滑轮牵引小船,设水的阻力不变,则在小船匀速靠岸的过程中 ( )A.绳子的拉力不断增大B.绳子的拉力不变C.船所受浮力增大D.船所受浮力变小二、非选择题5.如图所示,长为10m的细绳的两端分别系于竖直立在地面上相距8m的两杆的顶端A、B,绳上挂一个光滑的轻质挂钩,其下连着一个重为18N的物体,平衡时,问:(1)绳中的张力T=_____N。
(已知cos53°=0.6,sin53°=0.8)(2)A点向下移动少许(重物未与地面接触),重新平衡后,绳中张力_____(变大,不变,变小)。
6.如图所示,楔形物体倾角为θ=30°,放在水平地面上,轻质硬杆下端带有滑轮,上端顶有重1000N的物体,硬杆只能沿滑槽上下滑动。
不计一切摩擦,求作用于楔形物体上的水平推力至少多大才能将重物顶起?7.如图所示,为拔桩装置,当用力大小为F且方向垂直向下的作用力拉图中E点时,绳CE被水平拉直,绳CA被拉为竖直,绳DE与水平方向夹角为α,绳BC与竖直方向的夹角为β,求绳CA拔桩的作用力的大小。
10力法--习题ppt课件

单位力可以加在任一基本结构上。可取原结构中已知位
移条件进行校核。
结构力学电子教程
10 力法
静定结构与超静定结构特性比较
组成
反 力 和 内 力 计 荷载作用 非 荷 载 因 素
算
作用
静定结构 无多余约 平 衡 条 件 能 完 内力与刚 无内力
束几何不 全 确 定 反 力 和 度无关
变体系 内力
超静定结 有多余约 平 衡 条 件 不 能 内力与刚 内 力 与 刚 度
结构力学电子教程
10 力法
【10.2】 用力法解下列结构,并作M、Q图。
(a) P A
EI
B
【解】 一、取力法基本体系
标准解题格式
l/2
l/2
二、列力法基本方程
P
A
力法基本体系
l
M1
Pl/2
3Pl/16
MP
(Pl/4)
5Pl/32 M
11X1+1P=0
B 三、计算系数11和自由项1P
X1
1P
M1MP dx
QBA
ql 2
ql 8(1
k)
QBC
QCB
ql 8(1
k)
① k=10
② k=0.1
43ql
17ql
88
ql
44
5ql
A
88
A
44
C
C
B
Q
45ql
B
Q
27ql
88
44
结构力学电子教程
10 力法
10.4 用力法计算下列刚架,作M图,EI=常数。
(a) D C E
【解】
60kN
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
试求图示两端固定单跨梁在下述情况 下的M图。 (a) A端逆时针转动单位转角。 (b) A端竖向向上移动了单位位移。 (c) A、B两端均逆时针转动单位转角。 (d) A、B两端相对转动单位转角。 P (e) A端竖向向上、BF 端竖向向下移动了单 位位移。
A
EI
B
例 3. 求图示刚架由于温度变
化引起的内力与K点的 Ky 。 内侧t2
解:取基本体系如图 (a) (b) t =250C 典型方程为: 1 t2=350C 11 X 1 1t 0 温度变化引起的结构位移与内力的计算公式 为:
外侧t1 EI 常 数
这时结构中的位移以及位移条件的校核公式如何? M k Mds M k Mds k k FRi ci EI EI
h l 11 22 EI 3 EI l 12 6 EI 3 2 2h hl 33 3 EI EI
基本结构在荷载作用下的弯矩图,是原超静定结构的弯矩 图
例 1. 求解图示加劲梁。 横梁 I 1 104 m4 解:取基本体系如图(b) 典型方程:
11 X 1 1 P 0
M 1 , M P , FN 1 , FNP 如图示:
FN1 1 FNP 0
FN
FNP
10.67 12.2 11 , EI EA 533.3 1 P EI
单位基本未知力引起的弯矩图和反力
b b b b 1 ( Δ) , 2Δ ( ) , 3 0 δ 、Δ 2Δ 3 1Δ 、 Δ等于多少? l l l l
最后内力(M图): M M 1 X 1 M 2 X 2 M 3 X 3
支座移动引起的内力与各杆的绝对刚度 EI 有关 吗?
FN 44.9
FN (kN )
当 A 1 10 3 m 2 , X 1 44.9 kN 内力 M M 1 X 1 M P , FN FN1 X 1 FN P 有无下部链杆时梁内 最大弯矩之比:
15.4 0.1925 19.3% 80
令梁内正、负弯矩 值相等可得:
求下图B的水平位移
1 2 ql 8
1 2 ql 8
l
l
3 2 ql 8
X
l
1
1
1 1 1 2 3 1 1 2 1 1 ql l l ql l l EI 3 2 4 EI 8 2
1 1 4 1 1 4 ql 4 ql ql EI 8 EI 16 16 EI
11 X 1 12 X 2 13 X 3 1 0 21 X 1 22 X 2 23 X 3 2 X X X a 31 1 32 2 33 3 3
其中 1 , 2 , 3 为由于支座移动所产生的位移, 即 i FRi ci
1 11 l EI
t1 t2 0 所以温度不产生轴向伸长,可证 由于 t0 2
t 2t 2tl 1t AM1 1 l h h h
2 EI t X1 h
M X1M1 M P
2 EI t h
§5-5对称性的应用
对称结构: 对超静定结构来说,如果杆件, 支座,和刚度分布均对称某一直线,则称 此轴线为对称轴,此结构为对称结构。
对称结构
对称结构
非对称结构
非对称结构
• 对称结构在对称荷载或反对称荷载作用 下,可利用对称性使结构得到简化。 • 对称结构受对称荷载或反对称荷载作用 下可取半边结构进行计算
对称结构按跨数可分为
超静定结构的位移计算
• 在满足位移协调条件下,基本体系的位 移与原结构的位移相同,基本体系的位 移即是原超静定结构的位移,因此求原 超静定结构位移问题转化为求解基本结 构位移问题; • 超静定结构可转换为多种基本结构,所 以基本结构可以不是原基本结构。
如何求 A ?
梁受力有利
FN 44.9
A 1.7 10 m
3
2
533.3 5 49.98 ql 当 A , X1 10.67 4
FN 50
FN (kN )
梁的受力与两跨 连续梁相同。
k
例 2. 求解图示刚架由 EI 常 于支座移动所产生的 数 内力。 解:取图示基本结构 力法典型方程为: 方程的物理意义是否明确?
2 h hl 13 23 2 EI 2 EI
问题:如何建立如下基本结构的典型方程?
X3
X1
基本体系2
X3
X1
X2
基本体系3
X2
X3
X1
基本体系2
X2
11 X 1 12 X 2 13 X 3 1 b 21 X 1 22 X 2 23 X 3 2 a X X X 31 1 32 2 33 3 3
X3
X1
X2
b a
1 l b 2 a 3
用几 何法 与公 式法 相对 比。
基本体系3
11 X 1 12 X 2 13 X 3 1 0 21 X 1 22 X 2 23 X 3 2 0 X X X 0 31 1 32 2 33 3 3
对于超静定结构温度变化时将引起结构内力,这一内力也 与杆件的绝对刚度有关,温度低的一侧受拉,此结论适用于温 度改变引起的其他情况。
例5 作单跨梁由于图示温度改变引起的弯矩图。材料线膨胀系数 为
EI
l
t
t
b
h
t
t
X1
明轴向力为零,在不计轴向变形时此梁超静定次 数为1 11 X1 1t 0 1 X1 1
