常见的全等三角形图形
全等三角形ppt课件

三、概念剖析
为了方便书写,我们可以用符号表示两个三角形的全等.
例如△ABC与△DEF是全等的,
A
D
可以记作:“△ABC ≌△DEF”,
读作:“△ABC 全等于△DEF”. B
CE
F
注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应位置上.
例如,△ABC与△DEF全等,点A 与点D、点B 与点E、点C 与点F为对应
三、概念剖析
猜想:全等三角形对应边和对应角有什么关系呢? 全等三角形的性质:全等三角形的对应边相等,对应角相等.
应用格式 ∵△ABC≌△DEF,
A
D
∴AB=DE,BC=EF,AC=DF
∠A=∠D,∠B=∠E,∠C=∠F B
CE
F
四、典型例题
例1.如图△OCA≌△OBD,点C和点B,点A和点D是对应点.
在我们的周围,经常可以看到形状、大小完全相同的图形, 这样的图形叫做全等形.研究全等形的性质和判定两个图形全等 的方法,是几何学的一个重要内容,本章将以三角形为例,对这 些问题进行研究.
同一种剪纸
风扇的叶片
上一章我们通过推理论证得到了三角形内角和定理等重要结 论.本章中,推理论证将发挥更大的作用.我们将通过证明三角 形全等来证明线段或角相等,利用全等三角形证明角的平分线的 性质.通过本章学习,你对三角形的认识会更加深入,推理论证 能力会进一步提高.
新知一览
全等三角形
“边边边”
全
等
三角形全等
“边角边”
三
的判定
“角边角”“角角边”
角
“斜边、直角边”
形 角平分线的性质
角平分线的性质
角平分线的判定
第十二章 全等三角形
全等三角形的基本模型复习(正式经典)PPT课件

2021
10
模型四 一线三垂直型 模型解读:基本图形如下:此类图形 通常告诉 BD⊥DE,AB⊥AC, CE⊥DE,那么一定有∠B=∠CAE.(常用到同(等)角的余角相等)
2021
11
4.如图,AD⊥AB于A,BE⊥AB于B,点C在AB上,且CD⊥CE,CD=CE. 求证:AB=AD+BE.
2021
2021
3
1.如图,AB∥DE,AC∥DF,BE=CF,求证:AB=DE.
2021
4
解:∵BE=CF,∴BE+EC=CF+EC,即 BC=EF, ∵AB∥DE,AC∥DF,∴∠B=∠DEF,∠ACB=∠F, 在△ABC 与△DEF 中 ∠B=∠DEF, BC=EF, ∠ACB=∠F, ∴△ABC≌△DEF(ASA) ∴AB=DE
2021
8
3.如图,AB⊥CD于B,CF交AB于E,CE=AD,BE=BD.求证:CF⊥AD.
2021
9
解:∵AB⊥CD,∴∠EBC=∠DBA=90°.在 Rt△CEB 与 Rt△ADB 中 CBEE= =ABDD,,∴Rt△CEB≌Rt△ADB(HL),∴∠C=∠A,又∵∠C+∠CEB= 90°,∠CEB=∠AEF,∴∠A+∠AEF=90°,∴CF⊥AD
12
解:∵AD⊥AB,BE⊥AB,CD⊥CE,∴∠DAC=∠CBE=∠DCE=90 °,又∵∠DCB=∠D+∠DAC=∠DCE+∠ECB,∴∠D=∠ECB.在△ACD
与△BEC 中,∠∠AD==∠∠BEC,B,∴△ACD≌△BEC(AAS),∴AC=BE,CB= DC=CE,
AD,∴AB=AC+CB=AD+BE
2021
5
模型二 翻折型 模型解读:将原图形沿着某一条直线折叠后,直线两边的部分能够完全重 合,这两个三角形称之为翻折型全等三角形.此类图形中要注意其隐含条件, 即公共边或公共角相等.
全等三角形几种类型总结(供参考)

全等三角形与角平分线全等图形:能够完全重合的两个图形就是全等图形.全等多边形:能够完全重合的多边形就是全等多边形.相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角•全等多边形的对应边、对应角分别相等•如下图,两个全等的五边形,记作:五边形ABCQE里五边形A'B'C'D'E' .这里符号徑"表示全等,读作"全等于"•全等三角形:能够完全重合的三角形就是全等三角形•全等三角形的对应边相等,对应角分别相等;反之,如果两个三角形的边和角分别对应相等,那么这两个三角形全等•全等三角形对应的中线、高线、角平分线及周长面积均相等.全等三角形的概念与表示:能够完全重合的两个三角形叫作全等三角形•能够相互重合的顶点、边、角分别叫作对应顶点、对应边、对应角•全等符号为“空‘ •全尊三角形的性质:对应角相等,对应边相等,对应边上的中线相等,对应边上的高相等,对应角的角平分线相等,面积相等•寻找对应边和对应角,常用到以下方法:(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边.(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角.(3)有公共边的,公共边常是对应边.(4)有公共角的,公共角常是对应角•(5)有对顶角的,对顶角常是对应角•全等三角形的判定方法:(1)边角边走理(SAS):两边和它们的夹角对应相等的两个三角形全等•⑵角边角走理(ASA):两角和它们的夹边对应相等的两个三角形全等•(3)边边边走理(SSS):三边对应相等的两个三角形全等•(4)角角边走理(MS):两个角和其中一个角的对边对应相等的两个三角形全等•(5)斜边、直角边定理(HD :斜边和一条直角边对应相等的两个直角三角形全等.判定三角形全等的基本思路:找夹角TSAS已知两边找直角THL找另一边TSSS边为角的对边一找任意一角一A4S找这条边上的另一角一ASA 找这条边上的对角一AAS 找该角的另一边一SAS全等三角形的图形归纳起来有以下几种典型形式:已知一边一角《边就是角的一条边已知两角<找两角的夹边T ASA 找任意一边T AAS(1)平移全等型⑴角的平分线上的点到这个角的两边的距离相等•⑵到一个角的两边的距离相同的点,在这个角的平分线上•⑶等腰三角形的性质走理:等腰三角形的两个底角相等(即等边对等角)•⑷等腰三角形的顶角平分线、底边上的中线底边上的高互相重合•⑸等腰三角形的判走走理如果一个三角形有两个角相等,那么这两个角所对的边也相等⑹线段垂直平分线上的点和这条线段两个端点的距离相等•(7)和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.与角平分线相关的问题角平分线的两个性质:⑴角平分线上的点到角的两边的距离相等;⑵到角的两边距离相等的点在角的平分线上•它们具有互逆性•角平分线是天然的、涉及对称的模型,一般情况下,有下列三种作辅助线的方式:1 •由角平分线上的一点向角的两边作垂线,2・过角平分线上的一点作角平分线的垂线,从而形成等腰三角形,3 . OA = OB ,这种对称的图形应用得也较为普遍,三角形中线的定义:三角形顶点和对边中点的连线三角形中线的相关定理:直角三角形斜边的中线等于斜边的一半等腰三角形底边的中线三线合一(底边的中线、顶角的角平分线、底边的高重合)三角形中位线定义:彫吉三角形两边中点的线段叫做三角形的中位线•三角形中位线定理:三角形的中位线平行于第三边并且等于它的一半•中位线判定定理:经过三角形一边中点且平行于另一边的直线必平分第三边•中线中位线相关问题(涉及中点的问题)见到中线(中点),我们可以联想的内容无^是倍长中线以及中位线走理(以后还要学习中线长公式),尤其是在涉及线段的等臺关系时,倍长中线的应用更是较为常见•【例1】在初、AC 上各取一点E. D, ^AE = AD 9连接3D 、CE 相交于O 再连结AO . BC 9若Z1 = Z2,则图中全等三角形共有哪几对?并简单说明理由・【巩固】如图所示,AB = AD 9 BC = DC, E 、尸在AC 上,AC 与BQ 相交于P.图中有几对全等三 角形?请一一找出来,并简述全等的理由.【例2】(2008年巴中市髙中阶段教育学校招生考试)如图,AC//DE 9 BC 〃 EF , AC = DE.求证: AF=BD ・【例3】(2008年宜宾市)已知:如图,AD = BC, AC = BD,求证:ZC = ZD ・【巩固】如图,AC. 3D 相交于O 点,RAC = BD 9 AB = CD 9求证:OA = OD.板块二、三角形全等的判定与应用【例4】(哈尔滨市2008年初中升学考试)已知:如图,B.E.F.C 四点在同一条直线上,AB = DC 9 BE = CF ■ = 求证:OA= OD.A I)【例5】 已知,如图,AB = AC 9 CE 丄AB 9 BF 丄AC 9求证:BF = CE.【例6】E 、F 分别是正方形ABCQ 的CQ 边上的点,且BE = CF •求证:AE 丄BF ・【巩固】E. F. G 分别是正方形ABCD 的BC 、CD 、AB 边上的点,GE 丄EF, GE = EF.求证:BG + CF = BC ・【例7】 在凸五边形中,Zfi = ZE, ZC = ZD, BC = DE , M 为CD 中点.求证:AM 丄CD.I) C板块三、截长补短类【例1】如图,点M为正三角形的边加所在直线上的任意一点(点3除外),作ZDMV = 60。
常见图形(全等三角形)

常见图形一、轴对称型:二、相交线型三、旋转型【典型例题】一、和差倍分——轴对称型 1、如图①,OP 是∠MON 的平分线,请你利用该图形画一对以OP 所在直线为对称轴的全等三角形。
请你参考这个作全等三角形的方法,解答下列问题:(1)如图②,在△ABC 中,∠ACB 是直角,∠B =60°,AD 、CE 分别是∠BAC 、∠BCA 的平分线,AD 、CE 相交于点F 。
请你判断并写出FE 与FD 之间的数量关系;(2)如图③,在△ABC 中,如果∠ACB 不是直角,而(1)中的其它条件不变,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由。
2、(第19届“希望杯”)如图1,矩形ABCD 的长AD=9cm ,宽AB=3cm ,将它折叠,使点D 与点B 重合,求折叠后DE 的长和折痕EF 的长A BCD A B C DE AB C D E AB C D E FAB CDE P A M N E B C DF A E F B图① 图②图③ O (第20题图) C D A B CD E F分别是( )A 、cm cm 10,5B 、cm cm3,5 C 、cm cm 10,6 D 、cm cm 4,5 3、如图,△ABC 中,∠A =90°,AB =AC ,BD 平分∠ABC 交AC 于D ,CE ⊥BD 的延长线于E ,求证:BD =2CE 。
4、如图所示,已知△ABC 中,∠B=60°,∠BAC 和∠BCA 的平分线AD 与CE 相交于点O 。
求证:AE+CD=AC 。
二、利用旋转,构造全等三角形 1、(2008年泰安市)两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E 在同一条直线上,连结DC .(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);(2)证明:.2、已知:如图△ABC 是边长为1的等边三角形,△BDC 是顶角∠BDC =120°的等腰三角形,点M 、N 分别在AB 、AC 上,且∠MDN =60°求证:△AMN 的周长l =2A EB D CO三、中点或中线问题 1、已知:如图2,AD 为△ABC 的中线,BE 交AC 于E ,交AD 于F ,且AE=EF ,求证:AC=B F.2、如图,已知ΔABC 中,A B=5,A C=3,连BC 上的中线AD=2,求BC 的长。
全等三角形的常见基本图
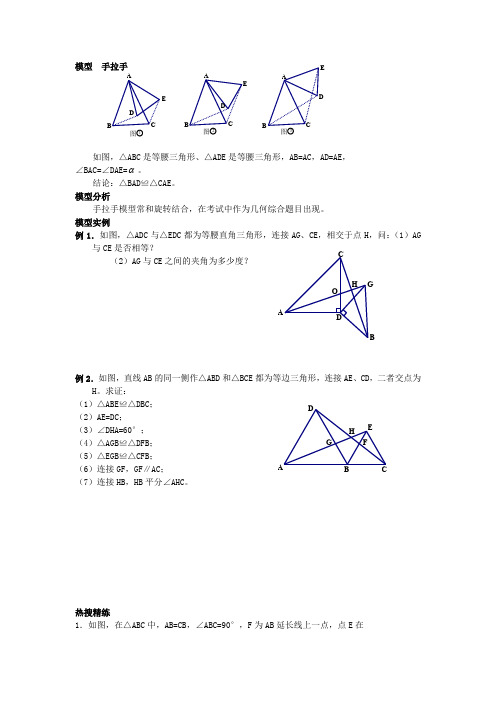
EAD B CE A DB C E DC B A 图3图21图OH G A B CDF G HD E C BA 模型 手拉手如图,△ABC 是等腰三角形、△ADE 是等腰三角形,AB=AC ,AD=AE , ∠BAC=∠DAE= 。
结论:△BAD ≌△CAE 。
模型分析手拉手模型常和旋转结合,在考试中作为几何综合题目出现。
模型实例例1.如图,△ADC 与△EDC 都为等腰直角三角形,连接AG 、CE ,相交于点H ,问:(1)AG与CE 是否相等?(2)AG 与CE 之间的夹角为多少度?例2.如图,直线AB 的同一侧作△ABD 和△BCE 都为等边三角形,连接AE 、CD ,二者交点为H 。
求证:(1)△ABE ≌△DBC ; (2)AE=DC ;(3)∠DHA=60°; (4)△AGB ≌△DFB ;(5)△EGB ≌△CFB ;(6)连接GF ,GF ∥AC ; (7)连接HB ,HB 平分∠AHC 。
热搜精练1.如图,在△ABC 中,AB=CB ,∠ABC=90°,F 为AB 延长线上一点,点E 在F E CB A HD E C B A M PD E C B A B A DCPE 3图B DAEC图21图PD ECB A BC 上,且AE=CF 。
(1)求证:BE=BF ;(2)若∠CAE=30°,求∠ACF 度数。
2.如图,△ABD 与△BCE 都为等边三角形,连接AE 与CD ,延长AE 交CD 于点H .证明:(1)AE=DC ; (2)∠AHD=60°; (3)连接HB ,HB 平分∠AHC 。
3.在线段AE 同侧作等边△CDE (∠ACE<120°),点P 与点M 分别是线段BE 和AD 的中点。
求证:△CPM 是等边三角形。
4.将等腰Rt △ABC 和等腰Rt △ADE 按图①方式放置,∠A=90°,AD 边与AB 边重合,AB=2AD=4。
人教版八年级数学全等三角形的常见模型总结(精选

人教版八年级数学全等三角形的常见模型总结(精选.)人教版八年级数学全等三角形常见模型总结要点梳理:全等三角形的判定与性质:一般三角形:边角边(SAS)、判角边角(ASA)、定角角边(AAS)、边边边(SSS)。
直角三角形:斜边、直角边定理(HL)。
性质:对应边相等,对应角相等(其他对应元素也相等,如对应边上的垂高相等)。
备判定:三角形全等必须有一组对应边相等。
注类型一:角平分线模型应用1.角平分性质模型:利用角平分线的性质。
例题解析:例1:如图1,在△ABC中,∠C=90°,AD平分∠CAB,BC=6cm,BD=4cm,那么点D到直线AB的距离是多少?答案】作DE⊥XXX于点E,DE=3cm。
例2:如图2,已知,∠1=∠2,∠3=∠4,求证:AP平分∠BAC。
答案】如图2,由角平分线的性质可知,PM=PN,PN=PQ,故PM=PQ,又因为PA是角BAC的平分线,所以XXX平分∠BAC。
类型二:角平分线模型应用2.角平分线,分两边,对称全等(截长补短构造全等)。
例题解析:例1:在△ABC中,∠BAC=60°,∠C=40°,AP平分∠XXX于P,BQ平分∠XXX于Q,求证:AB+BP=BQ+AQ。
答案】如图1,过O作OD∥BC交AB于D,∠ADO=∠ABC=180°-60°-40°=80°,又∵∠AQO=∠C+∠QBC=80°,∴∠ADO=∠AQO,又∵∠DAO=∠QAO,OA=AO,∴△ADO≌△AQO,∴OD=OQ,AD=AQ,又因为OD∥BP,所以∠PBO=∠DOB,又∠PBO=∠DBO,∴∠DBO=∠DOB,∴BD=OD,又∵∠XXX∠C+∠PAC=70°,∠BOP=∠OBA+∠BAO=70°,∴∠BOP=∠BPO,∴BP=OB,∴AB+BP=AD+DB+BP=AQ+OQ+BO=AQ+BQ。
如图,将△ADE逆时针旋转60°,使△ADE≌△ABC,从而得到△MDE≌△MAC,因为M为BD的中点,所以ME=MC,因此△EMC为等腰三角形,且∠MDE=∠MAC=30°,所以△EMC为等腰直角三角形。
全等三角形考点汇总

全等三角形全等三角形的概念:经过翻转、平移、旋转后,能够完全重合的两个三角形叫做全等三角形 全等三角形的性质:1. 对应边和对应角完全相等2. 能完全重合的顶点叫做对应顶点3. 全等三角形的周长和面积相等(反之不成立)4. 对应边上的高对应相等,对应边上的中线相等,对应角的角平分线相等 三角形全等判定定理1. 三边对应相等的三角形是全等三角形(SSS 边边边)2. 两边及其夹角对应相等的三角形是全等三角形(SAS 边角边)3. 两角及其夹边对应相等的三角形是全等三角形(ASA 角边角)4. 两角及其一角的对边对应相等的三角形是全等三角形(AAS 角角边)5. 在一对直角三角形中,斜边及一条直角边对应相等是全等三角形(HL) 备注:1)判定三角形全等必须有一组对应边相等2)三角形全等中,两边对应相等,一角,必须是夹角才全等 全等三角形的证明思路SAS HL SSS AAS SAS ASAAAS ASA AAS ⎧→⎧⎪⎪→⎨⎪⎪⎪→⎩⎪⎪→→⎧⎪⎪→⎧⎪⎪⎨⎨⎪→⎨⎪⎪⎪⎪⎪→⎩⎩⎪⎪→⎧⎪⎨→⎪⎩⎪⎩找夹角已知两边找直角找另一边边为角的对边找任一角找夹角的另一边已知一边一角边为角的邻边找夹边的另一角找边的对角找夹边已知两角找任一边专题一考点一 全等图形识别略定义:经过翻转 平移可以完全重合的图形才是全等图形考点二 利用全等图形求正方形网格中角度之和例题1:(2021·全国·八年级专题练习)如图为6个边长相等的正方形的组合图形,则∠1+∠3-∠2=( )A.30°B.45°C.60°D.135°+= 2.(2022·山东·济南市槐荫区教育教学研究中心二模)如图,在44⨯的正方形网格中,求αβ______度.3.(2020·江苏省灌云高级中学城西分校八年级阶段练习)如图,由4个相同的小正方形组成的格点图中,∠1+∠2+∠3=________度.考点三全等三角形的概念略考点四全等三角形的性质1.(2022·四川省南充市白塔中学八年级阶段练习)如图,在平面直角坐标系中,点A坐标为(-12,5),过点A作AB∠x轴于B,C是x轴负半轴上一动点,D是y轴正半轴上一动点,若始终保持CD=OA,且使∠ABO与∠OCD全等,则点D坐标为__________________.2.(2022·云南昭通·八年级期末)如图,把∠ABC沿线段DE折叠,使点B落在点F处;若∥,∠A=70°,AB=AC,则∠CEF的度数为()AC DEA.55°B.60°C.65°D.70°3.(2022·广西·西林县民族初中八年级期末)如图,△ABC∠∠ADE,若∠BAE=135°,∠DAC=55°,那么∠CFE的度数是_________.4.(2022·辽宁·东北育才学校七年级期中)如图,△ABC中,∠ACB=90°,AC=12,BC=16.点P从A点出发沿A—C—B路径向终点运动,终点为B点;点Q从B点出发沿B—C—A路径向终点运动,终点为A点.点P和Q分别以2和6的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE∠l于E,QF∠l于F.若要△PEC 与△QFC全等,则点P的运动时间为_______.专题二 全等三角形的判定(证明) 考点一 用SAS 证明三角形全等1.(2022·四川省南充市白塔中学八年级阶段练习)如图,点B 、C 、E 、F 共线,AB =DC ,∠B =∠C ,BF =CE .求证:∠ABE ∠∠DCF .考点二 用ASA 证明三角形全等1.(2022·广西百色·二模)如图,在△ABC 和△DCB 中,∠A =∠D ,AC 和DB 相交于点O ,OA =OD .(1)AB =DC ; (2)△ABC ∠∠DCB .2.(2022·贵州遵义·八年级期末)如图,已知AB DE ∥,ACB D ∠=∠,AC DE =.(1)求证:ABC EAD ≅.(2)若60BCE ∠=︒,求BAD ∠的度数.考点三 用AAS 证明三角形全等1.(2022·福建省福州第一中学模拟预测)如图,已知A ,F ,E ,C 在同一直线上,AB ∠CD ,∠ABE =∠CDF ,AF =CE .求证:AB =CD .考点四 用SSS 证明三角形全等1.(2021·河南省实验中学七年级期中)如图,在线段BC 上有两点E ,F ,在线段CB 的异侧有两点A ,D ,且满足AB CD =,AE DF =,CE BF =,连接AF ;(1)B 与C ∠相等吗?请说明理由.(2)若40B ∠=︒,20∠=DFC °,AF 平分BAE ∠时,求BAF ∠的度数.2.(2022·山东济宁·八年级期末)如图,在四边形ABCD 中,CB AB ⊥于点B ,CD AD ⊥于点D ,点E ,F 分别在AB ,AD 上,AE AF =,CE CF =.(1)若8AE =,6CD =,求四边形AECF 的面积;(2)猜想∠DAB ,∠ECF ,∠DFC 三者之间的数量关系,并证明你的猜想.考点五 用HL 证明三角形全等1.(2022·四川省南充市白塔中学八年级阶段练习)如图,AB =CD ,AE ∠BC 于E ,DF ∠BC 于F ,且BF =CE .(1)求证AE=DF;(2)判定AB和CD的位置关系,并说明理由.2.(2022·安徽安庆·八年级期末)如图,AD,BC相交于点O,AD=BC,∠C=∠D=90°.(1)求证:∠ACB∠∠BDA;(2)若∠CAB=54°,求∠CAO的度数.2.(2022·江西·永丰县恩江中学八年级阶段练习)如图,在∠ABC中,BC=AB,∠ABC=90°,F 为AB延长线上一点,点E在BC上,且AE=CF.(1)求证:Rt∠ABE∠Rt∠CBF;(2)若∠CAE=30°,求∠ACF的度数.全等三角形综合和常见全等模型汇总1.全等三角形中的平移模型几种常见全等三角形基本图形(平移)1.如图所示,AB∥DE,AC∥DF,BE=CF,求证AB=DE.2.如图,点O是线段AB的中点,OD∥BC且OD=BC,已知∠ADO=34°,∠B=67°,求∠A的度数.2.全等三角形中的轴对称模型1.如图,过等边△ABC的顶点A作线段AD,若∠DAB=20°,则∠COD的度数是()A,100°B,80°C,60°D,40°2.在等边△ABC,点E是AB上的动点,点E与点A,B不重合,点D在CB的延长线上,且EC=ED。
全等三角形证明方法总结

敷学培fit 方法*»1-2価明三廊形全箸(舍倦段相著、角相等)的几种方法一、三角形全等的判定:① 三组对应边分别相等的两个三角形全等(SSSJo 【最简单,考得也最少,考试过程中没有注意点】② 有两边及其夹角对应相等的两个三角形全等(SAS)。
【最常考,而且考试就考“角是不是两边夹角”】 r 当题目中得出“2对边及1对角相等”时,一定要检査“角是不是两边夹角“。
i ③ E鬲爲反養美另另航蒔京满不三浦花荃,新忑「① 有两角及一角的对边对应相等的两个三角形全等(AAS)o⑤直角三角形全等条件有:斜边及一直角边对应相等的两个直角三角形全等(HL)o F ............................ } j 直角三角形全等的特殊证法。
但当该方法不行时,前面的4种方法也能用来证明直角三角形全等。
: !如何找斜边:斜边是直角所对的边,只要找90。
的角所对的边就能找到斜边: ................................................................................................. J 二、全等三角形的性质: ① 全等三角形的对应边相等;全等三角形的对应角相等。
② 全等三角形的周长、面积相等。
③全等三角形的对应边上的高对应相等。
①全等三角形的对应角的角平分线相等。
⑤全等三角形的对应边上的中线相等。
几种常见全等三箱形的基本图形: 【平移】i 题目中只要得出“1对边及2对角相等",那就能证明三角\ ;形全等,唯一要做的就是区分好是ASA 还是AAS三、找全等三痢形的方法:①可以从结论出发,看要证明相等的两条线段(或角)分别在哪两个可能全等的三角形中:②可以从己知条件出发,看己知条件可以确定哪两个三角形相等;③从条件和结论综合考虑,看它们能一同确定哪两个三角形全等;①若上述方法均不行,可考虑添加辅助线,构造全等三角形。
人教版《全等三角形》优秀课件

全等三角形的性质的运用
边AB 与DE、边BC 与EF、
∠ABC=∠DBC,
已知:如图,△ABC ≌△DEF. ∴相等的边为:OC=OB,OA=OD,
3 cm,求MN和HG的长度.
请观察下面两组图形,它们是不是全等图形?为什么?与同伴进行交流。
(1)若DF =10 cm,则AC 的长为 (1)写出相等的线段与角.
∴相等的边为:AB=DB,BC=BC,
∠A 与∠D、∠B 与∠E、
∠AOC=∠DOB. (3)有对顶角的,对顶角是对应角.
AC=DC.
解:∵△ABC≌△DBF.
∴相等的角为:∠BAC=∠BDC, ∠C 与∠F 重合,称为对应角.
活动一:请同学们和同桌一起将两本数学课本叠放在一起,观察它们能重合吗?
∠ACB=∠DCB.
的度数为
能够完全重合 的两个图形叫做全等形.
___5_0_°________. C.58° D.50°
如图,△ABC≌△DEF,BE=3,AE=2,则DE的长是( )
如图,已知△EFG≌△NMH,∠F与∠M
点A 与点D、点B 与点E、 解:∵△ABC≌△DBC.
A
D
∵ △ABC ≌△DEF,
注意:书写全等式时要求把对应顶点字母放在对应的位置上。
全等三角形的定义: 能够完全重合的两个三角形叫做全等三角形.
点A 与点D、点B 与点E、
A
点C 与点F 重合,称为对应顶点;
边AB 与DE、边BC 与EF、
B
C
边AC 与DF 重合,称为对应边;
∠A 与∠D、∠B 与∠E、
∠C 与∠F 重合,称为对应角.
D
你能用符号表示出这两个全等三角形吗?
12.1全等三角形课件

从以上你能总结出找全等三角 形的对应边,对应角的规律吗?
B
C
Байду номын сангаас
找一找:请指出下列全等三角形的对应边和对应角 A
1、 △ ABE ≌ △ ACF
对应角是: ∠A和 ∠A、 ∠B和 ∠C、 ∠AEB和 ∠AFC ; 对应边是AB和 AC、 AE和 AF、 BE和 CF 。
F B
O
E C
2、 △ BCE ≌ △ CBF
例题讲解,掌握新知
例3 如图△ABC≌△DCB, 指出所有的对应边和对应角。
A D
B
C
解: ∵△ABC≌△DCB ∴AB与DC,BC与CB,AC与BD是对应边 ∠A与∠ D,∠ABC与∠DCB, ∠ACB与∠DBC是对应角
1.△ABO≌△DCO,试 写出这两个三角形中相等 的边和相等的角。
A
O
D
1、判断题 1)全等三角形的对应边相等,对应角相等(√ ) 2)全等三角形的周长相等,面积也相等(√ ) 3)面积相等的三角形是全等三角形。 ( X ) 4)周长相等的三角形是全等三角形。 ( X )
3. 若B、E、F、C在同一条直线上AB∥CD, AE∥FD, 若△ABE与△CDF全等, 指出图中相等的线段和相 等的角. 4. 已知△ABE≌△ACD, 指出它们的对应边和对应角. C A B E
对应角是: ∠BCE和 ∠CBF、 ∠BEC 和 ∠CFB、 ∠CBE和 ∠BCF。对应边是: BC和 、 BF、 BE。 CB和 CE CF和
3、 △ BOF ≌ △ COE
对应角是: ∠BOF和 ∠EOC、 ∠BFO和 ∠CEO、 ∠FBO和∠ECO、对应边是:FB和 EC、 BO和 CO、 OF和 OE.
全等三角形ppt课件

∴ △ABD≌△ACD(全__等__三__角__形__的__定__义__)_________
解:∵∠A=50°,∠B=48°, ∴∠C=180°-50°-48°=82°. 又∵△ABC≌△DEF, ∴∠C=∠F,∴∠F=82°. ∵DE的对应边为AB,所以DE=AB, ∴AB=10 cm.
【点悟】利用全等三角形的对应角相等、对应边相等解决问 题时,应注意不要将对应边(对应角)弄错,也就是要求在表 示两个三角形全等时书写规范.
寻找对应边、角的规律:
(1)有公共边的,公共边是对应边; (2)有公共角的,公共角是对应角; (3)有对顶角的,对顶角是对应角; (4)两个全等三角形最大的边是对应边,最小的边是对应边; (5)两个全等三角形最大的角是对应角,最小的角是对应角;
例2 如图,AD平分∠BAC,AB=AC.△ABD与△ACD全等吗?
起可以重合
能够完全重合的 两个图形叫做全
等图形
A
B′
A′
B
C
C′
1.它们重合时,能互相重合的顶点叫做全等三角形的对应顶点:如A和A′、B和 B′、C和C′; 2.互相重合的边叫做全等三角形的对应边:如AB和A′B′、BC和B′C′、CA和C′A′; 3.互相重合的角叫做全等三角形的对应角:如∠A和∠A′、 ∠B和∠B′、 ∠C和 ∠C′.
怎样判断两个图形是不是全等图形?
确定两个图形全等要符合两个条件: ①形状相同,②大小相同; 是否是全等图形与位置无关. 判断两个图形是否全等还可以通过平移、旋转、翻折等方法把两 个图形叠合在一起,看它们能否完全重合,即用叠合法判断.
全等三角形的经典模型(一)

全等三角形的经典模型(一)全等三角形的经典模型(一)在研究三角形的时候,全等三角形是一个非常重要的概念。
这里介绍一些经典的模型,帮助大家更好地理解和应用全等三角形。
三角形7级:倍长中线与截长补短倍长中线与截长补短是一个非常经典的全等三角形模型。
当三角形的中线等于另一条边的一半时,可以证明三角形全等。
此外,如果一条边被截成两段,其中一段的长度等于另一条边的长度减去另一段的长度,那么这两个三角形也是全等的。
三角形8级:全等三角形的经典模型(一)这是一个非常基础的全等三角形模型,利用的是三边对应相等的原理。
如果两个三角形的三条边分别相等,那么这两个三角形是全等的。
三角形9级:全等三角形的经典模型(二)这个模型利用的是两边一角相等的原理。
如果两个三角形的两条边和夹角分别相等,那么这两个三角形是全等的。
题型一:等腰直角三角形模型等腰直角三角形是一个非常特殊的三角形,可以利用其特殊的性质来解决问题。
常见的辅助线包括作高和补全为正方形等。
思路导航如果要解决一个等腰直角三角形的问题,可以尝试以下思路:1.利用特殊边特殊角证题,如AC=BC或90°,45,45。
2.常见辅助线为作高,利用三线合一的性质解决问题。
3.补全为正方形。
等腰直角三角形数学模型思路:⑴利用特殊边特殊角证题(AC=BC或90°,45,45).如图1;⑵常见辅助线为作高,利用三线合一的性质解决问题.如图2;⑶补全为正方形.如图3,4.典题精练例1】已知:如图所示,Rt△ABC中,AB=AC,BAC90°,O为BC的中点。
B⑴写出点O到△ABC的三个顶点A、B、C的距离的关系(不要求证明)⑵如果点M、N分别在线段AC、AB上移动,且在移动中保持AN=CM.试判断△XXX的形状,并证明你的结论.⑶如果点M、N分别在线段CA、AB的延长线上移动,且在移动中保持AN=CM,试判断⑵中结论是否依然成立,如果是请给出证明.解析】⑴OA=OB=OC⑴连接OA。
