定积分习题
定积分练习题(打印版)

定积分练习题(打印版)一、基础计算题1. 计算定积分 \(\int_{0}^{1} x^2 dx\)。
2. 计算定积分 \(\int_{1}^{2} \frac{1}{x} dx\)。
3. 计算定积分 \(\int_{0}^{2} (3x - 2) dx\)。
二、换元积分题1. 计算定积分 \(\int e^{2x} dx\),其中上下限为 \(0\) 到 \(\ln 2\)。
2. 计算定积分 \(\int \frac{1}{\sqrt{1 + x^2}} dx\),其中上下限为 \(0\) 到 \(1\)。
三、分部积分题1. 计算定积分 \(\int x e^x dx\),上下限为 \(0\) 到 \(1\)。
2. 计算定积分 \(\int \sin x \cos x dx\),上下限为 \(0\) 到\(\pi\)。
四、几何应用题1. 利用定积分计算圆 \(x^2 + y^2 = 1\) 在第一象限内围成的面积。
2. 利用定积分计算抛物线 \(y = x^2\) 与直线 \(y = 4\) 所围成的面积。
五、物理应用题1. 假设一物体的加速度 \(a(t) = 2t\),计算从 \(0\) 到 \(1\) 秒内物体的位移。
2. 假设一物体的力 \(F(x) = 3x + 1\),计算从 \(0\) 到 \(2\) 米内物体所做的功。
六、综合题1. 利用定积分计算函数 \(y = \sqrt{x}\) 与 \(x\) 轴,以及直线\(x = 1\) 所围成的面积。
2. 利用定积分计算函数 \(y = \ln x\) 与 \(x\) 轴,以及直线 \(x = e\) 所围成的面积。
七、挑战题1. 计算定积分 \(\int_{0}^{\pi/2} \sin^3 x \cos x dx\)。
2. 计算定积分 \(\int_{0}^{1} \frac{\ln x}{x} dx\)。
答案提示:- 对于基础计算题,可以直接应用定积分的基本公式进行计算。
常用积分练习题

常用积分练习题积分是微积分中重要的概念,它在求取函数面积、曲线长度、物理量等方面有广泛的应用。
为了帮助大家更好地理解和掌握积分运算,以下是一些常见的积分练习题,希望对大家的学习能有所帮助。
【题目一】计算下列定积分:(1) $\int_0^1 (2x^2+3x+1)dx$(2) $\int_1^2 \frac{1}{x}dx$【解答一】(1)$$\int_0^1 (2x^2+3x+1)dx =\left.\frac{2}{3}x^3+\frac{3}{2}x^2+x\right|_0^1 =\frac{2}{3}+\frac{3}{2}+1 - (0) = \frac{13}{6}$$(2)$$\int_1^2 \frac{1}{x}dx = \left.\ln|x|\right |_1^2 = \ln|2| - \ln|1| = \ln 2$$【题目二】计算下列定积分:(1) $\int_0^{\pi} \sin xdx$(2) $\int_0^{\pi} \cos^2 xdx$【解答二】(1)$$\int_0^{\pi} \sin xdx = \left. -\cos x\right |_0^{\pi} = -\cos(\pi) - (-\cos(0)) = -(-1) - (-1) = 2$$(2)$$\int_0^{\pi} \cos^2 xdx = \left. \frac{1}{2}(x+\sin x\cos x)\right|_0^{\pi} = \frac{1}{2}(\pi+\sin(\pi)\cos(\pi)) - (0+\sin(0)\cos(0)) =\frac{\pi}{2}$$【题目三】利用积分计算长度,计算曲线$y=x^3$在区间$[0, 1]$上的长度。
【解答三】曲线$y=x^3$在区间$[0, 1]$上的长度可以用积分来表示:$$\text{长度} = \int_0^1 \sqrt{1+(f'(x))^2}dx$$其中$f'(x)$表示曲线对应的导数。
定积分练习题

定积分 练习题一、填空题1.由定积分的几何意义可知,定积分⎰-102d 1x x 的值是 .2.由定积分的几何意义知a x -=⎰_ _______.3.由定积分的几何意义知21d x x -=⎰__ ______. 4.由定积分的几何意义知sin d x x ππ-=⎰__ ______.5.一物体以速度23()v t t m s =+做直线运动,则物体在0t =到3t =这段时间内行进的路程为__ ______.6.比较大小,120d x x ⎰ _______130d x x ⎰.(用“≤”、“≥”或“=” 填空)7.比较大小,1x ⎰ ______1x ⎰.(用“≤”、“≥”或“=” 填空) 8.比较大小,20sin d x x π⎰____320sin d x x π⎰.(用“≤”、“≥”或“=” 填空) 9.比较大小,53ln d x x ⎰ _____523(ln )d x x ⎰.(用“≤”、“≥”或“=” 填空)10.120d sin d d x x x =⎰ .11.2dsin d d x x x =⎰ .12.20d sin d d xt t x =⎰ .13.02d sin d d x x x x =⎰ .14.220d sin d d x t t x =⎰ .15.()2de d x t t -=⎰________________________.16.1sin d d x t t t ⎛⎫= ⎪⎝⎭⎰_________________________.17.20d d t t ⎛⎫= ⎪⎝⎭⎰_________________________.18.求极限211e d limln x t x tx→=⎰____________________.19.求极限203sin d limx x t t x→=⎰____________________.20.求极限203arctan d limxx t t x→=⎰.21.若11(2+)d 3ln 2a x x x=+⎰,则a 的值等于____________________.22.若(21)d 4a ax x --=⎰,则a =___________________.23.已知20()d 3f x x =⎰,则2[()+3]d f x x =⎰______________.24.由不等式222x y a +≤所确定区域的面积A = .25.由椭圆22221x y a b+=所围成图形的面积A = .26.由圆y =与直线0y =所围成图形的面积A = . 27.由圆x =0x =所围成图形的面积A = . 28.由曲线y x =,0x =,与直线2y =所围成图形的面积A = . 29.由曲线sin y x =与直线0y =,0,x x π==所围成图形的面积A = . 30.由曲线cos y x =与直线0y =,0,2x x π==所围成图形的面积A = .31.由不等式2214x y ≤+≤所确定区域的面积A = .二、单项选择题1.定积分1212ln d x x x ⎰值的符号为( ).(A )大于零; (B )小于零; (C )等于零; (D )不能确定.2.下列等于1的积分是( ).(A )10d x x ⎰; (B )10(1)d x x +⎰; (C )11d x ⎰; (D )101d 2x ⎰.3.1(+)d x x e e x -=⎰( ).(A )1e e +; (B )2e ; (C )2e ; (D )1e e -.4.220(sin +cos )d 22x xx π=⎰( ).(A )2π; (B )12π+; (C )2π-; (D )0,5.1(2+)d 2x k x =⎰,则k =( ).(A )0; (B )-1; (C )1; (D )2.6.10d x m e x =⎰与11d en x x=⎰的大小关系是( ). (A )m n >; (B )m n <; (C )m n =; (D )无法确定.7.下列式子中,正确的是( ).(A )11230d d x x x x ≤⎰⎰; (B )22211ln d ln d x x x x ≤⎰⎰;(C )22211d d x x x x ≤⎰⎰; (D )11d d xx e x e x -≤⎰⎰.8.已知自由落体运动的速度v gt =,则落体运动从0t =到0t t =所走的路成为( ).(A )203gt ; (B )20gt ; (C )202gt ; (D )206gt .9.积分中值定理()d ()()ba f x x fb a ξ=-⎰,其中( ).(A )ξ是[,]a b 内任一点; (B )ξ是[,]a b 内必定存在的某一点; (C )ξ是[,]a b 内唯一的某一点; (D )ξ是[,]a b 的中点. 10.设()f x 在[,]a b 连续,()()d xa x f t t ϕ=⎰,则( ).(A )()x ϕ是()f x 在[,]a b 上的一个原函数;(B )()f x 是()x ϕ的一个原函数;(C )()x ϕ是()f x 在[,]a b 上唯一的原函数; (D )()f x 是()x ϕ在[,]a b 上唯一的原函数. 11.设()d 0ba f x x =⎰且()f x 在[,]ab 连续,则( ).(A )()0f x ≡;(B )必存在x 使()0f x =; (C )存在唯一的一点x 使()0f x =; (D )不一定存在点x 使()0f x =.12.函数()f x 在[,]a b 上连续是()f x 在[,]a b 上可积的( ).(A )必要条件; (B )充分条件; (C )充要条件; (D )无关条件.13.下列各积分中能够直接应用牛顿—莱布尼茨公式的是( ).(A )311d 2x x-⎰; (B )30ln d x x ⎰;(C )04tan d x x π⎰; (D )22cot d x x ππ-⎰.14.极限0sin d limd xx x t tt t→=⎰⎰( ).(A )-1; (B )0; (C )1; (D )2.15.02sin xd t dt dx =⎰( ).(A )2sin x ; (B )2sin x -; (C )22sin x x -; (D )2sin t -. 16.定积分()()d ba x a xb x --=⎰( ).(A )3()6b a -; (B )3()6a b -;(C )3()3b a -; (D )336b a -.17.设函数()f x 在[,]a a -上的连续,则()d aa f x x -=⎰ ( ).(A )02()d af x x ⎰; (B )0;(C )0[()()]d a f x f x x +-⎰; (D )0[()()]d af x f x x --⎰.18.已知()f x 为偶函数且60()d 8f x x =⎰,则66()d f x x -=⎰ ( ).(A )0; (B )4; (C )8; (D )16. 19.222d x e x --=⎰( ).(A )4222d u eu --⎰; (B )22d te t --⎰;(C )222d x e x -⎰; (D )222d x e x --⎰. 20.由椭圆22194x y +=所围成图形的面积A =( ). (A) 6π; (B) 9π; (C) 12π; (D) 36π.21.由圆y =与直线0y =所围成图形的面积A =( ).(A) π; (B) 2π; (C) 3π; (D) 4π.22.由圆x =与直线0x =所围成图形的面积A =( ).(A)212a π; (B) 213a π; (C) 214a π; (D) 2a π. 23.由曲线sin y x =与x 轴,直线0x =,2x π=所围成图形的面积A =( ).(A)12; (B) 1; (C) 2; (D) 3. 24.由不等式22224a x y a ≤+≤所确定区域的面积A =( ).(A) 2a π; (B) 22a π; (C) 23a π; (D) 24a π. 25.设ln 1()()xx F x f t dt =⎰,其中()f x 为连续函数,则()F x '=( ).(A )2111(ln )()f x f x x x +; (B )1(ln )()f x f x +; (C )2111(ln )()f x f x x x -; (D )1(ln )()f x f x -.26.下面命题中错误的是( ).(A )若()f x 在(,)a b 上连续,则()d ba f x x ⎰存在;(B )若()f x 在[,]a b 上可积,则()f x 在[,]a b 上必有界; (C )若()f x 在[,]a b 上可积,则()f x 在[,]a b 上必可积; (D )若()f x 在[,]a b 上有界,且只有有限个间断点,则()f x 在[,]a b 上必可积.27.下列积分值为零的是( ).(A )222cos d x x x ππ-⎰; (B )220cos d x x x π⎰;.(C )222sin d x x x ππ-⎰; (D )022cos d x x x π-⎰.28.下列反常积分收敛的是( ).(A )1x +∞⎰; (B )211d x x +∞⎰; (C )11d x x+∞⎰; (D )1d x e x +∞⎰.29.下列反常积分收敛的是( ).(A )ln d e x x x +∞⎰; (B )1d lne x x x+∞⎰;(C )21d (ln )ex x x +∞⎰; (D )e x +∞⎰. 30.1211dx x -=⎰( ). (A )2; (B )-1; (C ); (D )不存在.三、判断题1.定积分的定义()()01lim nbi i a i f x dx f x λξ→==∆∑⎰中要求[,]a b 是任意分割,但i ξ必须是1[,]i i x x -的中点. ( )2.定积分的几何意义是相对应的各曲边梯形面积之和. ( )3.220sin 22sin 2xxdx x xdx πππ-=⎰⎰. ( )4.定积分的值是一个确定的常数. ( )5.若函数(),()f x g x 在区间[,]a b 上可积,且()()f x g x <,则()()bbaaf x dxg x dx <⎰⎰.( )6.若[,][,]c d a b ⊂,则()()d bcaf x dx f x dx <⎰⎰. ( )7.若函数()f x 在区间[,]a b 上可积,则函数()f x 在区间[,]a b 上有界.( )8. 11211112dx x x --=-=-⎰. ( )9.2200xdx ππ==⎰⎰. ( )10.若被积函数是连续的奇函数,积分区间关于原点对称,则定积分必等于零.( )四、计算题1.10(23)d x x +⎰. 2.2211()d x x x x-+⎰. 3.0(cos )d x x e x π-+⎰.4.x x x d )123(1024⎰-+.5.x a x a x a d ))((0⎰+-.6.x xx d )11(94+⎰.7.x x d 1123⎰--+. 8.3sin()d 3x x πππ+⎰. 9.(sin cos )d x x x π-⎰.10.3(sin sin 2)d x x x π-⎰. 11.x x d )sin 21(0⎰-π. 12.222cos d x x ππ-⎰.13.2(1cos )d πθθ-⎰. 14.π220cosd 2θθ⎰. 15.40sec tan d x x x π⎰.16.⎰+33/121d x x . 17.⎰-21021d x x .18.10⎰.19.221d 4x x +⎰. 20.2120d 1x x x +⎰.21.322d x ⎰. 22.x x x d 12134⎰-. 23.4120d 1x x x +⎰.24.212212d (1)x x x x ++. 25.11d (21)ex x x +⎰.26.221d (1)xx x + 27.251(1)d x x -⎰. 28.⎰-324)28(d x x. 29.x x x d 1sin /3/22⎰ππ.30.41x ⎰. 31.120arctan d 1xx x +⎰. 32.1d e x x⎰. 33.ln30 d 1xx e x e +⎰.34.2d x xe x . 35.⎰+302d 1x x x . 36.20sin cos d t t t π⎰.37.x x x d sin cos 04⎰π.38.20x π⎰. 39.102d x x e x ⎰.40.51x ⎰.41.41x ⎰. 42.x x xd 191⎰+.43.x xx d 4511⎰--. 44.x x d tan 302⎰π. 45.224cot d x x ππ⎰.五、证明题1.证明下列不等式:x x x x d cos d sin 4040⎰⎰≤ππ. 2.证明下列不等式:x x x x d )1(d e 11⎰⎰+≥.3.证明:当0=x 时,函数t t x I xt d e )(02⎰-=取得最小值.4.求证:1212141≤+≤⎰dx x. 5.证明不等式4/1022e 2d e e 22---≤≤-⎰x xx.6.设()f x 是以l 为周期的连续函数,证明:()d a l af x x +⎰的值与a 无关.7.设n 4 0()tan f n xdx π=⎰(n 为正整数),证明:1(3)(5)4f f +=. 8.若函数)(x f 连续,证明⎰⎰-=aa x x a f x x f 0d )(d )(.9.若函数)(x f 连续,证明⎰⎰=2020d )(cos d )(sin ππx x f x x f10.若函数)(x f 连续,证明⎰⎰+=+x x x x x x/112121d 1d )0(>x .11.若函数)(x f 连续,证明⎰⎰-=-110d )1(d )1(x x x x x x m n n m .12.证明等式0()d [()()]d a aaf x x f x f x x -=-+⎰⎰13.⎰⎰=πππd )(sin 2d )(sin x x f x x xf .14.设函数)(x f 在闭区间]10[,连续,且1)(<x f ,证明方程-x 21d )(0=⎰x t t f 在开区间)10(,有且仅有一个实根. 15.设函数()f x 在[,]a b 上连续,在(,)a b 内可导,且()0f x '≤,1()()d xa F x f t t x a=-⎰,证明在(,)a b 内()0F x '≤. 16.已知()f x 是连续函数,证明:20()d [()(2)]d a af x x f x f a x x =+-⎰⎰.17.设连续函数()f x 是奇函数,证明: 0() d x f t t ⎰是偶函数.18.若()x f ''在[]π,0连续,()20=f ,()1=πf ,证明:()()0sin d 3f x f x x x π''+=⎡⎤⎣⎦⎰.19.设01()0()0xt f t dtx F x xx ⎧>⎪=⎨⎪=⎩⎰,其中()f x 在[)0,+∞上连续,单调递增,且(0)0f ≥,证明:()F x 在[)0,+∞上连续且单调递增。
高中数学定积分计算习题

定积分的计算班级 姓名一、利用几何意义求下列定积分 (1)dx x ⎰11-2-1 (2)dx x ⎰22-4(3)dx x ⎰22-2x (4)()dx x x ⎰-24二、定积分计算 (1)()dx ⎰107-2x (2)()d x ⎰+21x2x 32(3)dx ⎰31x 3(4)dx x ⎰ππ-sin (5)dx x ⎰e 1ln (6)dx ⎰+1x 112(7)()d x x x⎰+-10232 (8)()dx 2311-x ⎰ (9)dx ⎰+11-2x x 2)((10)()d x x ⎰+212x1x (11)()d x x x ⎰-+11-352x (12)()d xe e x x ⎰+ln2x -e(13)dx x ⎰+ππ--cosx sin )( (14)dx ⎰e1x 2(15)dx x ⎰21-x sin -2e )((16)dx ⎰++21-3x1x x 2 (17)dx ⎰21x13 (18)()dx 22-1x ⎰+三、定积分求面积、体积1求由抛物线y 2=2x 与直线y =4-x 围成的平面图形的面积。
2.求曲线y =x ,y =2-x ,y =-13x 所围成图形的面积.3.求由曲线y =cos x (0≤x ≤2π)与直线y =1所围成的图形面积4.如图求由两条曲线y =-x 2,y =-14x 2及直线y =-1所围成的图形的面积.5、求函数f(x)=⎩⎪⎨⎪⎧x +1 (-1≤x<0)cosx (0≤x ≤π2)的图象与x 轴所围成的封闭图形的面积。
6.将由曲线y =x 2,y =x 3所围成平面图形绕x 周旋转一周,求所得旋转体的体积。
7.将由三条直线x =0、x =2、y =0和曲线y =x 3所围成的图形绕x 周旋转一周,求所得旋转体的体积。
8.由曲线y =x 与直线x =1,x =4及x 轴所围成的封闭图形绕x 周旋转一周,求所得旋转体的体积。
(完整版)定积分练习题

一、选择题1. 设连续函数f (x )>0,则当a <b 时,定积分⎠⎛a bf (x )d x 的符号( ) A .一定是正的 B .一定是负的C .当0<a <b 时是正的,当a <b <0时是负的D .以上结论都不对解析: 由⎠⎛a bf (x )d x 的几何意义及f (x )>0,可知⎠⎛a b f (x )d x 表示x =a ,x =b ,y =0与y =f (x )围成的曲边梯形的面积.∴⎠⎛ab f (x )d x >0.答案:A 2. 若22223,,sin a x dx b x dx c xdx ===⎰⎰⎰,则a ,b ,c 的大小关系是( )A .a <c <bB .a <b <cC .c <b <aD .c <a <b解析:a =13x 3 |20=83,b =14x 4 |20=4,c =-cos x |20=1-cos2,∴c <a <b . 答案:D3. 求曲线y =x 2与y =x 所围成图形的面积,其中正确的是( )A .S =⎠⎛01(x 2-x )d xB .S =⎠⎛01(x -x 2)d xC .S =⎠⎛01(y 2-y )d yD .S =⎠⎛01(y -y )d y[答案] B[解析] 两函数图象的交点坐标是(0,0),(1,1),故积分上限是1,下限是0,由于在[0,1]上,x ≥x 2,故函数y =x 2与y =x 所围成图形的面积S =⎠⎛01(x -x 2)d x .4.11(sin 1)x dx -+⎰的值为( )A. 2B.0C.22cos1+D. 22cos1- 【答案】A 【解析】[][]1111(sin 1)cos (cos11)cos(1)12x dx x x --+=-+=-+----=⎰5. 由曲线22y x x =+与直线y x =所围成的封闭图形的面积为 ( )A .16B .13C .56D .23【答案】 A由22,x x x +=解得两个交点坐标为(-1,0)和(0,0), 利用微积分的几何含义可得封闭图形的面积为:23201111111((2)()|().32326S x x x dx x x --=-+=--=--=⎰ 二、填空题6. 已知f (x )=⎠⎛0x(2t -4)d t ,则当x ∈[-1,3]时,f (x )的最小值为________.解析: f (x )=⎠⎛0x(2t -4)d t =(t 2-4t )| x 0=x 2-4x =(x -2)2-4(-1≤x ≤3),∴当x =2时,f (x )min =-4.答案: -47. 一物体以v (t )=t 2-3t +8(m/s)的速度运动,在前30 s 内的平均速度为________. 解析:由定积分的物理意义有:s =3020(38)t t dt -+⎰=(13t 3-32t 2+8t )|300=7890(m).∴v =s t =789030=263(m/s).答案:263 m/s 三、解答题8.求下列定积分:(1)⎠⎛12⎝⎛⎭⎫x -x 2+1x d x ;(2)(cos e )d x x x π-⎰+;(3)⎠⎛49x (1+x )d x ;(4)⎠⎛0πcos 2x 2d x .解析: (1)⎠⎛12⎝⎛⎭⎫x -x 2+1x d x =⎠⎛12x d x -⎠⎛12x 2d x +⎠⎛121x d x =x 22| 21-x 33| 21+ln x |21=32-73+ln 2=ln 2-56. (2)(cos e )d x x x π-⎰+=00cosxd e d x x x ππ--+⎰⎰=sin x ||0-π+e x 0-π=1-1eπ. (3)⎠⎛49x (1+x )d x =⎠⎛49(x 12+x )d x =⎪⎪⎝⎛⎭⎫23x 32+12x 249=23×932-23×432+12×92-12×42=4516. (4)⎠⎛πcos 2x 2d x =⎠⎛0π1+cos x 2d x =12x |0π+12sin x |0π=π2.9. 已知函数f (x )=x 3+ax 2+bx +c 的图象如图:直线y =0在原点处与函数图象相切,且此切线与函数图象所围成的区域(阴影)面积为274,求f (x ).解:由f (0)=0得c =0, f ′(x )=3x 2+2ax +b . 由f ′(0)=0得b =0, ∴f (x )=x 3+ax 2=x 2(x +a ),由∫-a 0[-f (x )]d x =274得a =-3. ∴f (x )=x 3-3x 2.10.已知f (x )为二次函数,且f (-1)=2,f ′(0)=0,⎠⎛01f (x )d x =-2. (1)求f (x )的解析式;(2)求f (x )在[-1,1]上的最大值与最小值. 解析: (1)设f (x )=ax 2+bx +c (a ≠0), 则f ′(x )=2ax +b .由f (-1)=2,f ′(0)=0,得⎩⎪⎨⎪⎧ a -b +c =2b =0,即⎩⎪⎨⎪⎧c =2-ab =0.∴f (x )=ax 2+(2-a ).又⎠⎛01f (x )d x =⎠⎛01[ax 2+(2-a )]d x=⎣⎡⎦⎤13ax 3+(2-a )x | 10=2-23a =-2, ∴a =6,∴c =-4. 从而f (x )=6x 2-4.(2)∵f (x )=6x 2-4,x ∈[-1,1], 所以当x =0时,f (x )min =-4; 当x =±1时,f (x )max =2.B 卷:5+2+2一、选择题1. 已知f (x )为偶函数且61(),2f x dx =⎰则66()f x dx -⎰等于( )A .2B .4C .1D .-1解析:∵f (x )为偶函数,∴661()(),2f x dx f x dx -==⎰⎰∴6660()2() 1.f x dx f x dx -==⎰⎰答案:C2. (改编题)A . 3 B. 4 C. 3.5 D. 4.5 【答案】C【解析】2220202101102,0()2,()(2)(2)(2)|(2)|2,02232 3.5.2x x x x f x x f x dx x dx x dx x x x x ----≥⎧=-=∴=++-=++-⎨+<⎩=+=⎰⎰⎰3. 已知函数y =x 2与y =kx (k >0)的图象所围成的阴影部分的面积为92,则k 等于( )A .2B .1C .3D .4答案:C解析:由⎩⎪⎨⎪⎧y =x2y =kx 消去y 得x 2-kx =0,所以x =0或x =k ,则阴影部分的面积为 ∫k 0(kx -x 2)d x =(12kx 2-13x 3) |k 0=92. 即12k 3-13k 3=92,解得k =3. 4. 一物体在力F (x )=⎩⎪⎨⎪⎧10 (0≤x ≤2)3x +4 (x >2)(单位:N)的作用下沿与力F 相同的方向,从x=0处运动到x =4(单位:m)处,则力F (x )作的功为( )A .44B .46C .48D .50解析: W =⎠⎛04F (x )d x =⎠⎛0210d x +⎠⎛24(3x +4)d x =10x | 20+⎝⎛⎭⎫32x 2+4x | 42=46.答案:B5. 函数()x f 满足()00=f ,其导函数()x f '的图象如下图,则()x f 的图象与x 轴所围成的A .31 B .34 C .2 D .38 【答案】B【解析】由导函数()x f '的图像可知,函数()x f 为二次函数,且对称轴为1,x =-开口方向向上,设函数2()(0),(0)0,0.()2,f x ax bx c a f c f x ax b '=++>=∴==+因过点(-1,0)与(0,2),则有2(1)0,202,1, 2.a b a b a b ⨯-+=⨯+=∴==2()2f x x x ∴=+, 则()x f 的图象与x 轴所围成的封闭图形的面积为232032-22114(2)()|=2)(2).333S x x dx x x -=--=--⨯+-=⎰(- 二、填空题6.(改编题)设20lg ,0(),3,0ax x f x x t dt x >⎧⎪=⎨+≤⎪⎩⎰若((1))1,f f =则a 为 。
定积分练习题

定积分练习题1基础题:一.选择题、填空题 1.下列等于1的积分是( )A .dx x ⎰1B .dx x ⎰+10)1(C .dx ⎰101D .dx ⎰10212.dx x |4|12⎰-=( )A .321B .322C .323D .325 3.曲线]23,0[,cos π∈=x x y 与坐标周围成的面积( )A .4B .2C .25D .3 4.dx e ex x⎰-+1)(=( )A .ee 1+ B .2e C .e 2 D .e e 1-5.若1xm e dx =⎰,11e n dx x =⎰,则m 与n 的大小关系是( )A .m n >B .m n <C .m n =D .无法确定6.由曲线21y x =-和x 轴围成图形的面积等于S .给出下列结果: ①121(1)x dx --⎰;②121(1)x dx --⎰;③1202(1)x dx -⎰;④0212(1)x dx --⎰.则S 等于( )A .①③B .③④C .②③D .②④7.0(sin cos sin )xy t t t dt =+⎰,则y 的最大值是( )A .1B .2C .72-D .08. 若()f x 是一次函数,且1()5f x dx =⎰,117()6xf x dx =⎰,那么21()f x dx x⎰的值是 .9.⎪⎪⎩⎪⎪⎨⎧=≠⎰=0,0,)()(2x cx x dt t tf x F x,其中)(x f 在0=x 处连续,且0)0(=f 若)(x F 在 0=x 处连续,则=c ( )。
(A).0=c ; (B).1=c ; (C).c 不存在; (D).1-=c .10.设⎪⎩⎪⎨⎧π<≤π=其余0x 3x sin )x (f ,则=⎰π02cos )(xdx x f ( ) (A )43 (B )43-(C )1 (D )-111.⎰202sin πdx x dxd =________ 12. 定积分 dx x x ⎰-π3sin sin 等于_______13. 定积分dx x x ⎰-π3cos cos 等于( )(A ) 0 (B )23(C ) 34(D ) 34-14. 定积分⎰-2|cos sin |πdx x x 等于( )(A ) 0 (B ) 1 (C ) 12+ (D ) )12(2- 15.定积分dx x x ⎰-2223}1,,max{等于( )(A ) 0 (B ) 4 (C )316(D )129716.设,2arcsin )(,)1ln()(202dt tx g dt t x f xx ⎰⎰=+=则当0→x 时,)(x f 是)(x g 的( ) (A) 同阶无穷小,但不等价 (B) 等价无穷小 (C) 低价无穷小 (D) 高价无穷小17. ⎰-=xttdt ex F 0,cos )(则)(x F 在],0[π上有( )(A) )2(πF 为极大值,)0(F 为最小值(B) )2(πF 为极大值,但无最小值(C) )2(πF 为极小值,但无极大值 (D) )2(πF 为最小值,)0(F 为最大值 综合题:11222520022(1)(2)ln(1)(3)(4cos )2x dx x dxx x x x dx x x -+--+--⎰⎰⎰212(8)()[0,2](2)1'(2)0()4''(2)f x f f f x dx x f x dx===⎰⎰已知函数在上二阶可导,且:,及,求:221sin (13)lim()xxx t dt tdt xx→++⎰⎰求极限2330(15)()ln 40:xt dy y y x x e dt y dx-=-++=⎰设隐函数由方程所确定,求2202(1)0(16)(),()00'(0).x t e dt x f x A f x x x A x f ⎧-⎪≠==⎨⎪=⎩⎰设问当为何值时,在点处可导,并求出定积分练习题2一.计算下列定积分的值 (1)⎰--312)4(dx x x ;(2)⎰-215)1(dx x ; (3)dx x x ⎰+20)sin (π;(4)dx x ⎰-222cos ππ;(5)π220cos 2d θθ⎰(6)⎰+10)32(dx x ; (7)⎰+-102211dx x x ; (8)⎰2ln e e x x dx ;(9)⎰--102dx e e x x ; (10)⎰302t a n πx d x (11)⎰+94;)1(dx x x (12)⎰+40;1xdx(13)⎰eedx x x 12)(ln 1 (14)⎰205;2s i n c o s πx d x x (15)⎰20;s i n πx d x e x (16)⎰+202;s i n 1c o s πdx x x (17)⎰-+10;x x e e dx二.求下列极限:(1)⎰→x x dt t x 02;cos 1lim(2).)(02222lim dte dt e x t xt x ⎰⎰∞→三.证明题1'()(,)(()'())()()xadf x x t f t d t f x f a dx-∞+∞-=-⎰()设在上连续,证明:。
定积分习题及讲解

第四部分 定积分[选择题]容易题1—36,中等题37—86,难题87—117。
1.积分中值定理⎰-=ba ab f dx x f ))(()(ξ,其中( )。
(A) ξ是],[b a 内任一点;(B). ξ是],[b a 内必定存在的某一点; (C). ξ是],[b a 内唯一的某一点; (D). ξ是],[b a 的中点。
答B2.⎪⎪⎩⎪⎪⎨⎧=≠⎰=0,0,)()(2x cx x dt t tf x F x,其中)(x f 在0=x 处连续,且0)0(=f 若)(x F 在 0=x 处连续,则=c ( )。
(A).0=c ; (B).1=c ; (C).c 不存在; (D).1-=c . 答A3.a dx xx I an n n (,1sin lim ⎰=+∞→为常数)由积分中值定理得⎰=+a n na dx x x ξξ1sin 1sin ,则 =I ( )。
(A)aa a a an 1sin1sinlim 1sinlim 2==→∞→ξξξξξ; (B).01sinlim 0=→ξξa ; (C).a a =∞→ξξξ1sinlim ;(D).∞=∞→ξξξ1sinlim a .答C4.设)(x f 在],[b a 连续,⎰=xa dt t f x )()(ϕ,则( )。
(A).)(x ϕ是)(x f 在],[b a 上的一个原函数; (B). )(x f 是)(x ϕ的一个原函数;(C). )(x ϕ是)(x f 在],[b a 上唯一的原函数; (D).)(x f 是)(x ϕ在],[b a 上唯一的原函数.答A5.设0)(=⎰b a dx x f 且)(x f 在],[b a 连续,则( )。
(A).0)(≡x f ;(B).必存在x 使0)(=x f ;(C).存在唯一的一点x 使0)(=x f ; (D).不一定存在点x 使 0)(=x f 。
答B6.设⎰=a dx x f x I 023)( (0.>a ), 则( )。
定积分练习题

定积分练习题一、基本概念题1. 计算定积分 $\int_{0}^{1} (3x^2 + 4) \, dx$。
2. 计算定积分 $\int_{1}^{2} (x^3 2x) \, dx$。
3. 设函数 $f(x) = x^2 3x + 2$,求 $\int_{1}^{3} f(x) \,dx$。
4. 已知函数 $g(x) = \sqrt{1 x^2}$,求 $\int_{1}^{1} g(x) \, dx$。
5. 计算 $\int_{0}^{\pi} \sin x \, dx$。
二、定积分的性质题6. 利用定积分的性质,计算 $\int_{0}^{2} (3x^2 + 4x) \,dx$。
7. 已知 $\int_{0}^{1} f(x) \, dx = 2$,求 $\int_{1}^{2}f(x) \, dx$。
8. 设 $f(x)$ 是奇函数,证明 $\int_{a}^{a} f(x) \, dx = 0$。
9. 已知 $\int_{0}^{1} (f(x) + g(x)) \, dx = 5$,$\int_{0}^{1} (f(x) g(x)) \, dx = 3$,求 $\int_{0}^{1} f(x) \, dx$ 和 $\int_{0}^{1} g(x) \, dx$。
三、定积分的计算题10. 计算 $\int_{0}^{\pi} x \cos x \, dx$。
11. 计算 $\int_{0}^{\frac{\pi}{2}} \ln(\sin x) \, dx$。
12. 计算 $\int_{1}^{e} \frac{1}{x} \, dx$。
13. 计算 $\int_{0}^{1} \frac{1}{\sqrt{1 x^2}} \, dx$。
14. 计算 $\int_{0}^{2} |x 1| \, dx$。
四、定积分的应用题15. 计算由曲线 $y = x^2$,直线 $x = 2$ 和 $y = 0$ 所围成的图形的面积。
定积分专项习题

第五章 定积分(A)1.利用定积分定义计算由抛物线12+=x y ,两直线)(,a b b x a x >==及横轴所围成的图形的面积。
2.利用定积分的几何意义,证明下列等式: ⎰=112)1x d x 41)212π=-⎰dx x⎰-=ππ0s i n )3x d x ⎰⎰-=2220cos 2cos )4πππxdx xdx3.估计下列各积分的值 ⎰331a r c t a n )1x d x x dx exx ⎰-022)24.根据定积分的性质比较下列各对积分值的大小 ⎰21ln )1xdx 与dx x ⎰212)(ln dx e x ⎰10)2与⎰+1)1(dx x5.计算下列各导数dt t dx d x ⎰+2021)1 ⎰+3241)2x x t dt dx d⎰xxdt t dx d cos sin 2)cos()3π6.计算下列极限xdt t xx ⎰→020cos lim)1 xdt t xx cos 1)sin 1ln(lim)20-+⎰→2220)1(lim)3x xt x xedt e t ⎰+→7.当x 为何值时,函数⎰-=xt dt tex I 02)(有极值?8.计算下列各积分 dx xx )1()12142⎰+dx x x )1()294+⎰⎰--21212)1()3x dx ⎰+ax a dx3022)4⎰---+211)5e x dx⎰π20sin )6dx xdx x x ⎰-π3sin sin )7⎰2)()8dx x f ,其中⎪⎩⎪⎨⎧+=2211)(x x x f11>≤x x9.设k ,l 为正整数,且l k ≠,试证下列各题:⎰-=ππ0c o s )1k x d x πππ=⎰-kxdx 2cos )2⎰-=⋅ππ0s i n c o s )3l x d x kx ⎰-=ππ0sin sin )4lxdx kx10.计算下列定积分 ⎰-πθθ03)s i n 1()1d ⎰262cos )2ππududx xx ⎰-121221)3 dx x a x a 2202)4-⎰ ⎰+31221)5xxdx dx x ⎰-2132)1(1)6⎰-2221)7x x dx ⎰--1145)8xxdx⎰-axa x d x 20223)9 dt tet ⎰-1022)10⎰-++02222)11x x dx⎰-222cos cos )12ππxdx x⎰--223c o s c o s )13ππdx x x ⎰-++2221)(cos )14xdxx x x ⎰+π2c o s 1)15dx x11.利用函数的奇偶性计算下列积分⎰-224c o s 4)1ππθθd dx xx ⎰--2121221)(arcsin )2dx x x xx ⎰-++55242312sin )312.设f (x )在[]b a ,上连续,证明:⎰⎰-+=babadx x b a f dx x f )()(13.证明:)0(1111212>+=+⎰⎰x x dx x dx xx14.计算下列定积分⎰-10)1dx xe x⎰342sin )2ππdx x xdx xx⎰41ln )3 ⎰10arctan )4xdx x⎰202c o s )5πx d x e x dx x x ⎰π2)sin ()6⎰edx x 1)sin(ln )7 dx x ee⎰1ln )815.判定下列反常积分的收敛性,如果收敛,计算反常积分的值。
(完整版)定积分习题及答案

第五章定积分(A 层次)1.203cos sin xdx x ;2.a dx x ax222;3.31221xxdx ;4.1145x xdx ;5.411xdx ;6.14311xdx ;7.21ln 1e xx dx ;8.02222xxdx ;9.dx x 02cos 1;10.dx x x sin 4;11.dx x 224cos 4;12.55242312sin dx xxx x ;13.342sin dx xx ;14.41ln dx xx ;15.1xarctgxdx ;16.202cosxdx e x ;17.dx x x 02sin ;18.dx x e 1ln sin ;19.243cos cos dx x x ;20.40sin 1sin dx x x ;21.dx xxx 02cos 1sin ;22.2111lndx xx x ;23.dx xx 4211;24.20sin ln xdx ;25.211dx xxdx0。
(B 层次)1.求由0cos 0x y ttdtdte 所决定的隐函数y 对x 的导数dxdy 。
2.当x 为何值时,函数x tdt tex I 02有极值?3.x xdt t dxd cos sin 2cos 。
4.设1,211,12xx x x xf ,求20dx x f 。
5.1lim22xdtarctgt xx 。
6.设其它,00,sin 21xx xf ,求x dt t f x。
7.设时当时当0,110,11xex xxf x,求201dx xf 。
8.2221limnn nnn。
9.求nk nknknnen e 12lim 。
10.设x f 是连续函数,且12dt t f x x f ,求x f 。
11.若2ln 261xtedt ,求x 。
12.证明:212121222dxeex。
13.已知axxx dx ex axa x 224lim,求常数a 。
定积分习题及答案

(A层次)1. 4.7. 兀f 。
2 s in x cos3 xdx ; r xdx -1✓5-4x ,e 2dx f 1 x ✓l +I n x ;10. f 一冗九x 4s in 汕; 冗13. f f-�dx; 4 Sill X 冗16. f 。
2产co sx dx ;冗第五章定积分2. f 。
a x 2✓a 2—x 2dx; 5.「I✓x dx +l ;8. f -o 2 x 2 + d 2xx + 2 ; 冗11. f� 冗4c os 4xdx ;14. 17. 2f14 Jn X`dx ;f 。
兀(xsinx)2dx ;冗19. f� ✓cosx-cos 3 xdx;20. f 。
4 smx dx · 1 + S lll . X , 22. 4If 0 2 xln l +x dx ; l -x25. f +00dx0 (1 + x 2 XI + xa \ (B层次)23. f +oo l +x 2 dx · -oo 1 +X 4' 心(a�o )。
3. 6.9. 厂dx1 X 飞l +x2 r dx`3 斤言-1;f。
冗✓1+ c os2xdx;3· 212 fs x sm xdx · ·-5 x 4 + 2x 2 + 1' 15. f 。
1 xa rct gxdx ; 18. {es in(lnx 雇21. 24. f 。
冗xs mx dx .1 +C OS 2X 冗f 。
2 ln sin x dx ;d y 1. 求由f 。
:e r dt+f x costd t=O所确定的隐函数对x 的导数odx 2. 当x 为何值时,函数I(x)= f x t e -t 2dt有极值?。
3.d厂cos矿t。
dx si n x(}Ix+l, x�14. 设八x )�{归,X > 1'求l。
勹(x )dx 。
2f x(a rc tg t) 2d t5. lirn 。
定积分习题
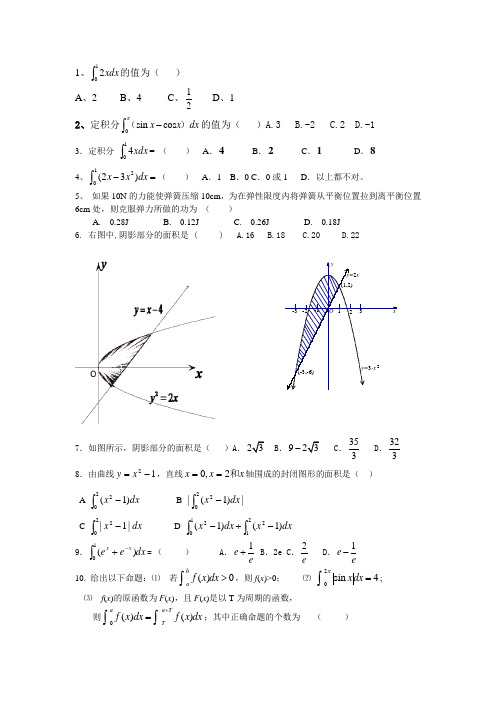
1、dx x ⎰12的值为( )A 、2B 、4C 、21 D 、12、定积分0sin cos x x dx π-⎰()的值为( )A.3 B.-2 C.2 D.-13.定积分⎰14xdx = ( ) A .4 B .2 C .1 D .84、120(23)x x dx -=⎰ ( ) A .1 B .0 C .0或1 D .以上都不对。
5、 如果10N 的力能使弹簧压缩10cm ,为在弹性限度内将弹簧从平衡位置拉到离平衡位置6cm 处,则克服弹力所做的功为 ( )A. 0.28JB. 0.12JC. 0.26JD. 0.18J 6. 右图中,阴影部分的面积是 ( ) A.16 B.18 C.20 D.227.如图所示,阴影部分的面积是( )A..9-.353D .3238.由曲线12-=x y ,直线x x x 和2,0==轴围成的封闭图形的面积是( ) A ⎰-202)1(dx x B |)1(|22⎰-dx xC⎰-22|1|dx x D⎰⎰-+-102122)1()1(dx x dx x9.dx ee xx⎰-+1)(= ( ) A .ee 1+B .2eC .e2 D .ee 1-10. 给出以下命题:⑴ 若()0b af x dx >⎰,则f (x )>0; ⑵ 20sin 4x dx =⎰π;⑶ f (x )的原函数为F (x ),且F (x )是以T 为周期的函数, 则0()()a a T Tf x dx f x dx +=⎰⎰;其中正确命题的个数为 ( )A .0B . 1C .2D .311.计算20sin xdx π⎰的值是 。
12.定积分3221(2)x dx x-⎰的值是13.1(2ln 2)1xe dx x+=⎰14.44cos 2___________xdx ππ-=⎰15、计算:0=⎰。
16. 一物体在力()34F x x =+(单位:N )的作用下,沿着与力相同的方向从0x =处运动到4x =处(单位:m ), 则力()F x 所作的功为 . 17.若0)13(02=-⎰dx x a()0>a ,则实数=a18.由3x y =与x y =所围成的图形(阴影部分)的面积为19.求下列曲线所围成的图形的面积: 32,2+==x y x y20. 求2y x =-+1与1y x =+围成图形的面积。
积分问题练习题

积分问题练习题一、基础练习1. 求下列定积分的值:a) ∫(2x - 3)dxb) ∫(3x^2 + 2x - 1)dxc) ∫(4sinx + 5cosx)dx2. 求下列不定积分:a) ∫(3x^2 + 2x - 1)dxb) ∫(6x^3 + cosx)dxc) ∫(e^x + ln x)dx3. 求下列定积分:a) ∫[a, b] (x^3 - 2x^2 + 3x - 4)dxb) ∫[0, 2π] sin2xdxc) ∫[-1, 1] |x|dx二、进阶练习1. 求下列带参数的积分:a) ∫[m, n] (mx^2 - 1)dx (其中m和n为常数)b) ∫[a, b] (ax^2 + bx + c)dx (其中a、b、c为常数)c) ∫[0, π/2] sin^kxdx (其中k为正整数)2. 求下列定积分:a) ∫[0, 1] x^ndx (其中n为正整数)b) ∫[0, π/4] tanxdxc) ∫[-∞, ∞] e^(-x^2)dx3. 已知函数f(x)在区间[0, π]上连续且单调递增,且f(0) = 0,f(π) = 1。
证明函数g(x) = ∫[0, x] f(t)dt在[0, π]上为单调递增函数。
三、挑战练习1. 计算下列积分:a) ∫[0, 1] e^x(x - 1)dxb) ∫[0, π/2] sin^3xdxc) ∫[1, e] lnxdx2. 设函数f(x)在区间[a, b]上连续,且单调递增。
证明在该区间上存在唯一的实数c,使得∫[a, b] f(x)dx = f(c)(b - a)。
3. 求函数f(x) = ∫[0, x] (x - t)f(t)dt的表达式。
结束语:以上就是一些关于积分的问题练习,通过这些练习,相信您对积分的求解有了更深入的理解。
希望您能够灵活运用所学知识,解决更加复杂的积分问题。
如果有任何疑问,请随时向我提问。
祝您学业进步!。
定积分练习题

定积分练习题1. 计算定积分 $\int_{0}^{1} x^2 dx$。
解:首先,我们可以使用不定积分的方式计算该定积分。
对函数$f(x) = x^2$ 进行不定积分,得到原函数 $F(x) = \frac{1}{3}x^3 + C$,其中 $C$ 为常数。
然后,我们可以应用定积分的性质,即 $\int_{a}^{b} f(x) dx = F(b) - F(a)$。
将 $F(x)$ 代入上述公式,我们得到:$\int_{0}^{1} x^2 dx = F(1) - F(0) = \frac{1}{3} \cdot 1^3 + C -\frac{1}{3} \cdot 0^3 - C$可简化为:$\int_{0}^{1} x^2 dx = \frac{1}{3}$因此,定积分 $\int_{0}^{1} x^2 dx$ 的结果为 $\frac{1}{3}$。
2. 计算定积分 $\int_{1}^{4} (2x+1) dx$。
解:我们可以先将被积函数 $2x+1$ 展开,并应用定积分的性质进行计算:$\int_{1}^{4} (2x+1) dx = \int_{1}^{4} 2x dx + \int_{1}^{4} 1 dx$对于第一项,我们可以使用不定积分的方式进行计算。
对函数 $f(x) = 2x$ 进行不定积分,得到原函数 $F(x) = x^2 + C$,其中 $C$ 为常数。
因此,第一项可以表示为:$\int_{1}^{4} 2x dx = [x^2]_{1}^{4} = 4^2 - 1^2 = 15$对于第二项,我们可以应用定积分的性质,即 $\int_{a}^{b} 1 dx =x \Big|_{a}^{b} = b - a$。
因此,第二项可以表示为:$\int_{1}^{4} 1 dx = 4 - 1 = 3$将两项结果相加,我们得到:$\int_{1}^{4} (2x+1) dx = 15 + 3 = 18$因此,定积分 $\int_{1}^{4} (2x+1) dx$ 的结果为 18。
定积分(辅导班、习题课)

例 32.(07.4)设函数 f(x)具有连续的一阶导 数, 且满足
f ( x) x ( x 2 t 2 ) f (t)dt x 2 0
求 f(x)的表达公式.
15
例
33.(07.2)设
f(x)是区间[0,
4
] 上的单调、
可导函数,且满足
f (x) f 1(t)dt x t cos t sin tdt
1内至少
2
一点 ζ ,使 f (ζ ) f (ζ ) .
10
例 21.
求函数
f
(x)
x2
0
(2
t )e t dt
的最大值和最
小值。(95.3)
x t2
例 22. 已知函数 f ( x) 0 e 2 dt, x ,
求 f (x) ,并讨论 f ( x) 的单调性,奇偶性及函
数图形的凹凸性,并求 f (x) 的图形的拐点和 水平渐近线。(88.4.5)
得
7.积分中值问题
解法思路: 通常是积分中值定理、介值定理和微分中值定理的联合使用。
23
例 41. 设在[a, b]上 f (x)连续.且满足
f (a) f ( x) f (b).证明:c [a, b]使
ab f ( x)dx f (a)(c a) f (b)(b c)
证:令 F( x) f (a)(x a) f (b)(b x)
解法思路:
一. 变量代换公式和分部积分公式 本身就是高度普遍性的积分等 式,亦可用来推出其它积分等 式;
二. 视为变限积分函数问题,转化 为导数的应用问题。
三. 用中值定理
17
例 34.设 f ( x) 处处连续,证明:
a x3 f ( x2 )dx 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九章 定 积 分练 习 题§1定积分概念习 题1. 按定积分定义证明:⎰-=ba ab k kdx ).(2. 通过对积分区间作等分分割,并取适当的点集{}i ξ,把定积分看作是对应的积分和的极限,来计算下列定积分: (1)⎰∑=+=112233)1(41:;ni n n i dx x 提示 (2)⎰10;dx e x(3)⎰ba x dx e ; (4)2(0).(:bi adxa b xξ<<=⎰提示取§2 牛顿一菜布尼茨公式1.计算下列定积分:(1)⎰+10)32(dx x ; (2)⎰+-102211dx x x ; (3)⎰2ln e e x x dx ;(4)⎰--102dx e e x x ; (5)⎰302tan πxdx (6)⎰+94;)1(dx xx (7)⎰+40;1x dx(8)⎰eedx x x 12)(ln 1 2.利用定积分求极限:(1));21(1334lim n nn +++∞→Λ (2);)(1)2(1)1(1222lim ⎥⎦⎤⎢⎣⎡++++++∞→n n n n n n Λ (3));21)2(111(222lim nn n n n +++++∞→Λ (4))1sin 2sin (sin 1lim n n n n nn -+++∞→Λππ3.证明:若f 在[a,b]上可积,F 在[a,b]上连续,且除有限个点外有F '(x )=f (x),则有()()().ba f x dx Fb F a =-⎰§3 可积条件1. 证明:若T ˊ是T 增加若干个分点后所得的分割,则∑∑∆≤∆'.''T Ti i i i χωχω2. 证明:若f 在[a,b]上可积,[][][]上也可积在则ββ,,,,a f b a a ⊂.3.设f ﹑g 均为定义在[a,b]上的有界函数。
证明:若仅在[a,b]中有限个点处()(),χχg f ≠则当f 在[a,b]上可积时,g 在[a,b]上也可积,且()().χχχχd g a bd f a b ⎰⎰=3. 设f 在[a,b]上有界,{}[],,b a a n ⊂.lim c ann =∞→证明:在[a,b]上只有()Λ,2,1=n a n 为其间断点,则f 在[a,b]上可积。
4. 证明:若f 在区间∆上有界,则()()()()"','".sup sup inf f f f f χχχχχχχχ∈∆∈∆∈∆-=-。
§4 定积分的性质1.证明:若f 与g 都在[a,b]上可积,则∑⎰=→=∆ni bai i i T dx x g x f x g f 10,)()()()(lim ηξ其中i i ηξ,是T 所属小区间△i 中的任意两点,i=1,2…,n.2.不求出定积分的值,比较下列各对定积分的大小: (1)⎰⎰11;2dx x xdx 与(2)⎰⎰2020.sin ππxdx xdx 与3.证明下列不等式:(1)20;22πππ<<⎰(2)1201x e dx e <<⎰;(3)20sin 12;xdx dx x ππ<<⎰(4)4 6.e e <⎰4.设f 在[a,b]上连续,且f(x)不恒等于零,证明()()20.baf x dx >⎰5.设f 与g 都在[a,b]上可积,证明[]{}[]{})(),()(,)(),()(min max ,,x g x f x m x g x f x M b a x b a x ∈∈==在[a,b]上也都可积.6.试求心形线πθθ20),cos 1(≤≤+=a r 上各点极径的平均值.7.设f 在[a,b]上可积,且在[a,b]上满足.0)(φm x f ≥证明f1在[a,b]上也可积. 8.进一步证明积分第一中值定理(包括定理和定理中的中值点ξ∈(a,b).9.证明:若f 与g 都在[a,b]上可积,且g(x)在[a,b]上不变号,M 、m 分别为 f(x)在[a,b]上的上、下确界,则必存在某实数μ(m ≤μ≤M),使得⎰⎰=babadx x g dx x g x f .)()()(μ10.证明:若f 在[a,b]上连续,且⎰⎰==b abadx x xf dx x f ,0)()(则在(a,b)内至少存在两点x 1,x 2,使f(x 1)= f(x 2)=0.又若⎰=badx x f x ,0)(2这时f 在(a,b)内是否至少有三个零点11.设f 在[a,b]上二阶可导,且"f (x)>0.证明:(1)⎰-≤⎪⎭⎫ ⎝⎛+b adx x f ab b a f ;)(12 (2)又若[],,,0)(b a x x f ∈≤则又有[].,,)(2)(b a x dx x f a b x f ba ∈-≥⎰12.证明:(1)11ln(1)11ln ;2n n n +<+++<+L (2).1ln 1211lim=+++∞→nn n Λ§5 微积分学基本定理·定积分计算(续)习 题1. 设f 为连续函数,u 、v 均为可导函数,且可实行复合f °u 与f °v 证明:⎰-=)()().('))(()('))(()(x v x u x u x u f x v x v f dt t f dx d2.设f 在[a,b]上连续,⎰-=xa dt t x t f x F .))(()(证明F ”b].[a,),()(∈=x x f x3.求下列极限: (1)⎰→x x dt t x 02;cos 1lim(2).)(02222lim dtedt e x t xt x ⎰⎰∞→4.计算下列定积分:(1)⎰205;2sin cos πxdx x (2)⎰-12;4dx x (3)⎰-aa dx x a x 0222);0(φ(4)⎰+-102/32;)1(x x dx (5)⎰-+10;x x e e dx(6)⎰+22;sin 1cos πdx xx(7)⎰1;arcsin xdx (8)⎰20;sin πxdx e x (9);ln 1dx x ee⎰(10)⎰10;dx e x (11)⎰+-aa dx xa xa x 02);0(φ (12)⎰+20.cos sin cos πθθνθd5.设f 在[-a,a]上可积。
证明: (1)若f 为奇函数,则⎰-=aa dx x f ;0)((2)若f 为偶函数,则⎰⎰-=aaadx x f dx x f 0.)(2)(6.设f 为(-∞,+∞)上以p 为周期的连续周期函数。
证明对任何实数a ,恒有⎰⎰+=pa padx x f dx x f a .)()(7.设f 为连续函数。
证明:(1)⎰⎰=2020;)(cos )(sin ππdx x f dx x f (2)⎰⎰=πππ.)(sin 2)(sin dx x f dx x xf8.设J (m,n )⎰=20,(cos sin πn m xdx x n m 为正整数)。
证明:),,2(1)2,(1),(n m J nm m n m J n m n n m J -+-=-+-=并求J(2m,2n).9.证明:若在(0,∞)上f 为连续函数,且对任何a >0有⎰==axx dt t f x g 常数)()(, ),,0(+∞∈x则c x xcx f ),,0(,)(+∞∈=为常数。
10.设f 为连续可微函数,试求⎰-xa dt t f t x dx d ,)(')(并用此结果求⎰-xtdt t x dx d 0.sin )(11.设)(x f y =为[a,b]上严格增的连续曲线(图 9-12)。
试证存在ξ∈(a,b ),使图中两阴影部分面积 相等。
12.设f 为[0,2π]上的单调递减函数。
证明:对任何正整数n 恒有 ⎰≥π20.0sin )(nxdx x f13.证明:当x >时有不等式 ).0(1sin 2φπc xdt t c x x⎰+ 14.证明:若f 在[a,b]上可积,[],)(,)(,,b a ==βϕαϕβαϕ上单调且连续可微在则有⎰⎰'=ba dt t t f dx x f βαϕϕ.)())(()(※15.证明:若在[a,b]上f 为连续可微的单调函数,则存在[],,b a ∈ξ使得⎰⎰⎰+=baabdx x f b g dx x f a g dx x g x f ξξ.)()()()()()((提示:与定理及其推论相比较,这里的条件要强得多, 因此可望有一个比较简单的,不同于的证明.)※§6 可积性理论补叙1. 证明性质2中关于下和的不等式(3).2. 证明性质6中关于下和的极限式S T s t =→)(lim 0.3. 设 ⎩⎨⎧=.,0.,)(为无理数为有理数x x x x f试求f 在[0,1]上的上积分和下积分;并由此判断f 在[0,1]上是否可积.4. 设f 在[a,b]上可积,且[]],[.,,0)(b a f b a x x f 在试问=上是否可积为什么5. 证明:定理中的可积第二充要条件等价于“任给T T 的对于一切满足存在δδε<>>,0,0都有εω''<-=∆∑)()(T s t s x i Ti .6.据理回答:(1) 何种函数具有“任意下和等于任意上和”的性质(2) 何种连续函数具有“所有下和(或上和)都相等”的性质 (3) 对于可积函数,若“所有下和(或上和)都相等”,是否仍有(2)的结论 7.本题的最终目的是要证明:若f 在[a,b]上可积,则f 在[a,b]内必定有无限多个处处稠密的连续点,这可用区间套方法按以下顺序逐一证明:(1)若T 是[a,b]的一个分割,使得S (T )s(T)<b —a ,则在T 中存存在某个小区间.1,<∆f i i ω使(2)存在区间),,(],[111b a b a I ⊂=使得.1)(inf )(sup )(111<-=∈∈x f x f I I x I x f ω(3)存在区间),,(],[11222b a b a I ⊂=使得.21)(inf )(sup )(222<-=∈∈x f x f I I x I x f ω(4)继续以上方法,求出一区间序列),,(],[11--⊂=n n n n n b a b a I .1)(inf )(sup )(nx f x f I nnI x I x n f <-=∈∈ω说明{}n I 为一区间套,从而存在;,2,1,0Λ=∈n I x n 而且f 在点x 0连续。
