四阶幻方解法

四阶幻方的解法

四阶幻方的解法
四阶幻方是一种古老的数学游戏，在互联网时代仍然颇受欢迎。

说到四阶幻方，就必须先说到它最核心的解题方式--穷举空间搜索。

该方法按照一定的顺序解决问题，从数个选项中寻找正确答案。

穷举空间搜索的方法是由计算机科学家Saul Amarel提出的，于1962年发表
于卡皮罗国际学术期刊。

该方法以“搜索与发现”为核心策略，有效地解决约束形式求解问题，即四阶幻方。

例如：每行和每列的和相等、每个三角形的和为34等。

四阶幻方的解题步骤基本为三步：第一步采用在线推理，基于当前已有数字，
筛选出可行方案；第二步就是穷举空间搜索，按照一定顺序枚举多种可行方案，进行模拟测试；第三步是选取最优解，从测试结果最优的方案中挑选出最优解。

此外，四阶幻方也可以采用人工智能技术。

典型的人工智能技术有：机器学习、神经网络和进化计算。

这些技术可以帮助四阶幻方在秒内进行快速解算，让用户几分钟就能完成游戏，可谓是一种精旨体验。

结论：四阶幻方的解题方式主要有穷举空间搜索和人工智能两种。

穷举空间搜
索具有速度快、效率高的优势，对每行、每列和每个三角形的求和都进行约束计算；而人工智能技术则可以借助机器学习、神经网络和进化计算等技术，将复杂过程变得简单、快捷，解决四阶幻方问题。

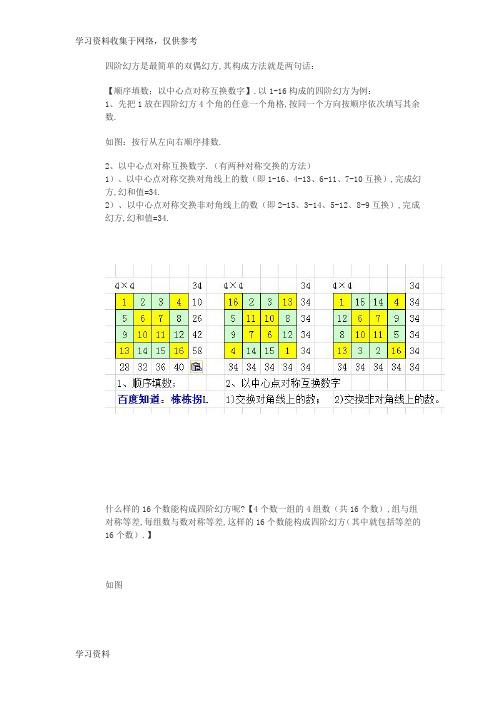
四阶幻方是最简单的双偶幻方,其构成方法就是两句话：
【顺序填数；以中心点对称互换数字】.以1-16构成的四阶幻方为例：
1、先把1放在四阶幻方4个角的任意一个角格,按同一个方向按顺序依次填写其余数.
如图：按行从左向右顺序排数.
2、以中心点对称互换数字.（有两种对称交换的方法）
1）、以中心点对称交换对角线上的数（即1-16、4-13、6-11、7-10互换）,完成幻方,幻和值=34.
2）、以中心点对称交换非对角线上的数（即2-15、3-14、5-12、8-9互换）,完成幻方,幻和值=34.
什么样的16个数能构成四阶幻方呢?【4个数一组的4组数（共16个数）,组与组对称等差,每组数与数对称等差,这样的16个数能构成四阶幻方（其中就包括等差的16个数）.】
如图
上图,每组数与数以2-3-2对称等差,组与组以10-20-10对称等差.
下图,每组数与数以1-2-1对称等差,组与组以10-20-10对称等差. 再如：
上图,每组数与数等差为1,组与组等差为5.
中图,每组数与数等差为1,组与组以5-10-5对称等差.
下图,每组数与数以2-3-2对称等差,组与组以5-10-5对称等差.
【四阶幻方的特点：】
1、互换对称的行（列）,幻方成立.
2、互换一侧的行（或列）,再互换另一侧的行（或列）,幻方亦成立.
3、互换不对称的行（或列）,再互换另外不对称的行（或列）,幻方亦成立.
4、平移互换对角的行或列、平移互换对角,幻方成立.
另,每16个能构成四阶幻方的数,幻方的填法有880种.。

幻方解法

幻方解法
幻方，就是对于一个n×n的方阵，将1—n²这n²个数填入其中，使每行每列以及对角线上的数字之和都相等的方阵。

幻方分为奇数阶幻方(n=2k+1)、单偶数幻方
(n=4k+2)、双偶数幻方(n=4k)三种，每种幻方解法不同，但都有其固定的解。

下面我来具体介绍下幻方的解法：
1.奇数阶幻方
①将1填入第一行中间位置
②向右上方向依次填入
③如果上方出格了，则将其填入最后一行与其同列的位置
④如果右方出格了，则将其填入第一列与其同行的位置
⑤如果右上都出格，则将其填入第一列最后一格
⑥如果将要填入的方格已有数字，则填入上一个数字的下方
这里已三阶幻方为例：
2.双偶数阶幻方(n=4k)：
①先将1，2，3……n²依次填入方阵中
②拟出方阵对角线
③对角线上数字不动，将其余所有数字移至与其中心对称的位置
这里以四阶幻方为例
↓
↓ 3.单偶数阶幻方(n=4k+2)：
①先将1，2，3……n平方依次填入方阵中
②拟出对角线，将对角线上所有数字移至与其中心对称的位置。

③从方阵左半部分的每一列数字中抽出一对上下对称的数字互换位置(每一列抽出一对)
④从方阵上半部分的每一行数字中抽出一对左对称的数字互换位置(每一行抽出一对)
注：已经移动过或换过位置的数字不能再移动或换位
这里以六阶幻方为例：
↓
↓②↓
↓
↓③↓
↓
↓④↓。

幻方题目解题思路

幻方题目解题思路幻方这玩意儿挺有趣的呢！咱来唠唠解题思路哈。

一、啥是幻方首先得知道幻方是个正方形的格子阵，就像九宫格那种（当然也有其他规格的，像四阶幻方啥的）。

每一行、每一列还有对角线上的数字加起来都得等于同一个数，这个数就叫幻和。

二、三阶幻方（九宫格）的基本思路1. 确定幻和- 对于三阶幻方（3×3的格子），因为1 + 2+3+4+5+6+7+8+9 = 45，这9个数要平均分配到三行（或者三列），所以幻和就是45÷3 = 15。

2. 找中心数- 在三阶幻方里，中心数特别重要。

因为它会在四条线上（一行、一列和两条对角线）参与求和。

- 假设中心数是x，那么它在四条线上相加的总和就是4x。

其他八个数两两组合成四组，每组和都等于幻和 - x。

- 经过计算就会发现中心数是5（你可以自己试着推导一下哦，挺好玩的）。

3. 填角上的数- 角上的数也很关键。

一般先从和5能凑成15的数开始考虑，像1、9，2、8，3、7，4、6这几组。

- 先试着把1放在左上角（只是个例子，放哪儿都行开始），那它对角就得是9，这样才能保证对角线的和是15。

然后再根据每行每列的和是15慢慢填其他的数。

1. 连续自然数幻方- 对于四阶幻方，1到16这16个数的和是136。

因为要四行（或四列），所以幻和是136÷4 = 34。

- 有一种方法叫“对称交换法”。

先把1到16按顺序填到四阶方阵里，就像从左上角开始横着填。

- 然后把对角线上的数保留，其他的数关于中心对称交换位置。

这样就得到了四阶幻方。

- 更高阶的幻方也有一些类似的方法，不过会更复杂一些。

2. 不是连续自然数的幻方- 如果不是1、2、3……这样连续的数，那首先得算出这些数的总和，然后确定幻和（总和除以阶数）。

- 然后可以先找一个和这些数相近的连续自然数幻方，再通过调整数字的大小来得到想要的幻方。

总之呢，幻方就像一个数字谜题，要根据幻和、数字的规律还有一些特殊位置（像中心数、角上数）的特点来慢慢拼凑出答案，多试几次就会找到感觉啦！。

幻方解题技巧

六阶幻方
幻和是：6×（62＋1）÷2＝111
构成
三阶幻方构成方法之一
九子斜排上下对易左右更替四维挺出
三阶幻方构成方法之二
画格辅助九子斜排送子回家清除辅助
1
4 7
8 9
2
5
6
3
9
3
1
7
这种方法适用于所有的奇阶幻方
1
6
11 24 7
2 20 3 4 5 10
16 4
21 22
偶阶幻方都可以照这样的方法去填
如；八阶幻方

十阶幻方十二阶幻方
神奇
四阶幻方
幻和
是34
16+13+1+4

5+2+12+15 3+8+9+14
16+2+11+5 9+7+4+14 3+13+8+10 6+12+1+15

左右对开并交换，也是一个四阶幻方
上下对开并交换仍是一个四阶幻方
纵向切开，交换后再接起来
横切一刀，交换后再接起来
距离幻方中心 41 的任何中心对称位置上两数和都为 82
九阶幻方
将幻方按图中粗线分成九块，即为九个三阶幻方
若把上述九个三阶幻方的每个幻方的“幻和”值写在九宫格中，又构成一个新的三阶幻方

分类构成神奇
分类

按照纵横各有数字的个数，可以分为：三阶幻方、四阶幻方、五阶幻方、六阶幻方… … 按照纵横数字数量奇偶的不同，可以分为：奇阶幻方偶阶幻方

四阶幻方代数推理

四阶幻方代数推理引言幻方是一种众所周知的数学奇观，它是一种排列在正方形格子中的数字集合，使得每一行、每一列和对角线上的数字和都相等。

四阶幻方是其中的一种特殊情况，它是一个4×4的正方形格子，被填满了1到16的数字，使得每一行、每一列和对角线上的数字和都相等。

在本文中，我们将展示如何通过代数推理来构建四阶幻方。

我们将使用数学原理和方法来解释如何填充幻方，使得它满足特定的条件。

我们将展示如何利用代数运算和数学推理来构建四阶幻方，并给出详细的步骤和例子。

通过本文的阐述，读者可以了解代数推理在构建幻方中的重要作用，同时也能够对代数推理有更深入的理解。

第一部分：基本原理为了构建四阶幻方，我们首先需要了解一些基本原理。

幻方的构建是基于一种特殊的数学规律，这个规律被称为幻方的特性。

幻方的特性可以用代数推理来解释和证明，这将为我们的构建过程提供基础和指导。

首先，我们需要了解四阶幻方的特性。

根据幻方的定义，每一行、每一列和对角线上的数字和都相等。

对于四阶幻方来说，这个数字和可以表示为S=4×(4×4+1)/2=34。

这个数字34称为幻方的常数，它是幻方中每一行、每一列和对角线上数字和的总和。

了解了这个特性之后，我们就可以通过代数推理来构建四阶幻方了。

第二部分：代数推理接下来，我们将介绍如何通过代数推理来构建四阶幻方。

我们将按照以下步骤来进行推理和构建：步骤一：确定幻方的常数首先，我们需要确定四阶幻方的常数。

根据前面的讨论，我们知道四阶幻方的常数为34。

这个常数将会成为我们构建幻方的重要依据，我们需要保证每一行、每一列和对角线上的数字和都等于34。

步骤二：填充幻方的中心数字接下来，我们将填充幻方的中心数字。

四阶幻方的中心数字是16，我们可以将它填充在幻方的中心位置。

这样一来，幻方的第一步就完成了。

步骤三：确定幻方的边界数字然后，我们需要确定幻方的四个边界数字。

四阶幻方的数字范围是1到16，我们需要将这些数字填充在幻方的边界位置。

求四阶的素数幻方

求四阶的素‎数幻方。

即在一个4‎X4 的矩阵中，每一个格填‎入一个数字‎，使每一行、每一列和两‎条对角线上‎的4 个数字所组‎成的四位数‎，均为可逆素‎数。

*问题分析与‎算法设计有了前面的‎基础，本题应当说‎是不困难的‎。

最简单的算‎法是：采用穷举法‎，设定4X4‎矩阵中每一‎个元素的值‎后，判断每一行‎、每一列和两‎条对角线上‎的4个数字‎组成的四位‎数是否都是‎可逆素数，若是则求出‎了满足题意‎的一个解。

这种算法在‎原理是对的‎，也一定可以‎求出满足题‎意的全部解‎。

但是，按照这一思‎路编出的程‎序效率很低‎，在微机上几‎个小时也不‎会运行结束‎。

这一算法致‎命的缺陷是‎：要穷举和判‎断的情况过‎多。

充分利用题‎目中的“每一个四位‎数都是可逆‎素数”这一条件，可以放弃对‎矩阵中每个‎元素进行的‎穷举的算法‎，先求出全部‎的四位可逆‎素数(204个)，以矩阵的行‎为单位，在四位可逆‎素数的范围‎内进行穷举‎，然后将穷举‎的四位整数‎分解为数字‎后，再进行列和‎对角线方向‎的条件判断‎，改进的算法‎与最初的算‎法相比，大大地减少‎了穷举的次‎数。

考虑矩阵的‎第一行和最‎后一行数字‎，它们分别是‎列方向四位‎数的第一个‎数字和最后‎一个数字，由于这些四‎位数也必须‎是可逆素数‎，所以矩阵的‎每一行和最‎后一行中的‎各个数字都‎不能为偶数‎或5。

这样穷举矩‎阵的第一行‎和最后一行‎时，它们的取值‎范围是：所有位的数‎字均不是偶‎数或5的四‎位可逆数。

由于符合这‎一条件的四‎位可逆素数‎很少，所以这一范‎围限制又一‎次减少了穷‎举的次数。

对算法的进‎一步研究会‎发现：当设定了第‎一和第二行‎的值后，就已经可以‎判断出当前‎的这种组合‎是否一定是‎错误的(尚不能肯定‎该组合一定‎是正确的)。

若按列方向‎上的四个两‎位数与四位‎可逆数的前‎两位矛盾(不是其中的‎一种组合)，则第一、二行的取值‎一定是错误‎的。

幻方的技巧和解题思路

幻方的技巧和解题思路
幻方是一个矩阵，其中每行、每列和对角线上的元素之和都相等。

解题和构建幻方的方法有很多，以下是一些常用的技巧和解题思路：
1.奇阶幻方的构建：
o3阶幻方：可以使用"Siamese（托马斯维尔纳·托马斯纳格尔）方法"来构建。

o5阶幻方：可以使用"Burr（亨利·伯尔）方法"来构建。

o对于其他奇数阶的幻方，可以使用"La Hire（菲利普·莱尔）方法"来构建。

2.偶阶幻方的构建：
o4阶幻方：可以使用"De la Loubère（安德烈·纳诺·德拉卢贝尔）方法"来构建。

o6阶幻方：可以使用"J. R. Hendricks（乔布·亨德里克斯）方法"来构建。

o对于其他偶数阶的幻方，可以使用"Siamese（托马斯维尔纳·托马斯纳格尔）方法"或其他类似的方法来构
建。

3.递推法：可以使用递推法构建幻方，即通过给定的幻方来
构建更大阶数的幻方。

这种方法可以应用于各种阶数的幻
方。

4.数学公式：还有一些数学公式可以用来生成特定阶数的幻
方。

例如，Ramanujan公式可以用来生成8阶幻方，而Strachey公式可以用来生成12阶幻方。

5.对称性和规则性：在构建幻方时，利用对称性和规则性可
以更容易地确定某些元素的值，从而简化构建过程。

这些是一些常用的技巧和解题思路，但构建幻方是一个复杂的数学问题，需要深入的数学知识和技巧。

四阶幻方解法

【顺序填数；以中心点对称互换数字】.以1-16构成的四阶幻方为例：
1、先把1放在四阶幻方4个角的任意一个角格,按同一个方向按顺序依次填写其余数.
如图：按行从左向右顺序排数.
2、以中心点对称互换数字.（有两种对称交换的方法）
1）、以中心点对称交换对角线上的数（即1-16、4-13、6-11、7-10互换）,完成幻方,幻和值=34.
2）、以中心点对称交换非对角线上的数（即2-15、3-14、5-12、8-9互换）,完成幻方,幻和值=34.
什么样的16个数能构成四阶幻方呢?【4个数一组的4组数（共16个数）,组与组对称等差,每组数与数对称等差,这样的16个数能构成四阶幻方（其中就包括等差的16个数）.】
如图
上图,每组数与数以2-3-2对称等差,组与组以10-20-10对称等差.
下图,每组数与数以1-2-1对称等差,组与组以10-20-10对称等差.
再如：
上图,每组数与数等差为1,组与组等差为5.
中图,每组数与数等差为1,组与组以5-10-5对称等差.
下图,每组数与数以2-3-2对称等差,组与组以5-10-5对称等差.
【四阶幻方的特点：】
1、互换对称的行（列）,幻方成立.
2、互换一侧的行（或列）,再互换另一侧的行（或列）,幻方亦成立.
3、互换不对称的行（或列）,再互换另外不对称的行（或列）,幻方亦成立.
4、平移互换对角的行或列、平移互换对角,幻方成立.
另,每16个能构成四阶幻方的数,幻方的填法有880种.。

幻方常规解法汇总

幻方常规解法汇总按目前填写幻方的方法，是把幻方分成了三类，即奇数阶幻方、双偶阶幻方、单偶阶幻方。

下面按这三类幻方，列出最常用解法（考试用，不求强大，只求有效！）。

奇数阶幻方（罗伯法）奇数阶幻方最经典的填法是罗伯法。

填写的方法是：把1（或最小的数）放在第一行正中；按以下规律排列剩下的(n×n－1)个数：1、每一个数放在前一个数的右上一格；2、如果这个数所要放的格已经超出了顶行那么就把它放在底行，仍然要放在右一列；3、如果这个数所要放的格已经超出了最右列那么就把它放在最左列，仍然要放在上一行；4、如果这个数所要放的格已经超出了顶行且超出了最右列，那么就把它放在前一个数的下一行同一列的格内；5、如果这个数所要放的格已经有数填入，那么就把它放在前一个数的下一行同一列的格内。

例，用该填法获得的5阶幻方：17 24 1 8 1523 5 7 14 164 6 13 20 2210 12 19 21 311 18 25 2 9双偶数阶幻方（对称交换法）所谓双偶阶幻方就是当n可以被4整除时的偶阶幻方，即4K阶幻方。

在说解法之前我们先说明一个“互补数”定义：就是在n 阶幻方中，如果两个数的和等于幻方中最大的数与1 的和（即n×n＋1），我们称它们为一对互补数。

如在三阶幻方中，每一对和为10 的数，是一对互补数；在四阶幻方中，每一对和为 17 的数，是一对互补数。

双偶数阶幻方的对称交换解法：先看看4阶幻方的填法：将数字从左到右、从上到下按顺序填写：1 2 3 45 6 7 89 10 11 1213 14 15 16内外四个角对角上互补的数相易，（方阵分为两个正方形，外大内小，然后把大正方形的四个对角上的数字对换，小正方形四个对角上的数字对换）即（1，16）（4，13）互换（6，11）（7，10）互换即可。

16 2 3 135 11 10 89 7 6 124 14 15 1对于n=4k阶幻方，我们先把数字按顺序填写。

幻方常规解法汇总

幻方常规解法汇总按目前填写幻方的方法，是把幻方分成了三类，即奇数阶幻方、双偶阶幻方、单偶阶幻方。

下面按这三类幻方，列出最常用解法（考试用，不求强大，只求有效！）。

奇数阶幻方（罗伯法）奇数阶幻方最经典的填法是罗伯法。

填写的方法是：把1（或最小的数）放在第一行正中；按以下规律排列剩下的(n×n －1)个数：1、每一个数放在前一个数的右上一格；2、如果这个数所要放的格已经超出了顶行那么就把它放在底行，仍然要放在右一列；3、如果这个数所要放的格已经超出了最右列那么就把它放在最左列，仍然要放在上一行；4、如果这个数所要放的格已经超出了顶行且超出了最右列，那么就把它放在前一个数的下一行同一列的格内；5、如果这个数所要放的格已经有数填入，那么就把它放在前一个数的下一行同一列的格内。

例，用该填法获得的5阶幻方：17 24 1 8 1523 5 7 14 164 6 13 20 2210 12 19 21 311 18 25 2 9双偶数阶幻方（对称交换法）所谓双偶阶幻方就是当n可以被4整除时的偶阶幻方，即4K阶幻方。

在说解法之前我们先说明一个“互补数”定义：就是在n阶幻方中，如果两个数的和等于幻方中最大的数与1的和（即n×n＋1），我们称它们为一对互补数。

如在三阶幻方中，每一对和为10的数，是一对互补数；在四阶幻方中，每一对和为17的数，是一对互补数。

双偶数阶幻方的对称交换解法：先看看4阶幻方的填法：将数字从左到右、从上到下按顺序填写：1 2 3 45 6789 1011121314 15 16内外四个角对角上互补的数相易，（方阵分为两个正方形，外大内小，然后把大正方形的四个对角上的数字对换，小正方形四个对角上的数字对换）即（1，16）（4，13）互换（6，11）（7，10）互换即可。

16 2 3 135 11 10 89 7 6 124 14 15 1对于n=4k阶幻方，我们先把数字按顺序填写。

四阶幻方的解

四阶幻方的解本文根据幻方的定义,建立了一个具有十六个未知数的非齐次线性方程组,求出了它的一般解.结合幻方的特性给出了求解的一般方法.论证了四阶幻方共有384个形式解.进而说明在变换意义下解的唯一性.一建立方程组并求出一般解定义1:自然数1,2,3,…,16排成四行四列的方阵,如果每行每列及每条对角线(包括折断对角线)上四个数的和皆等于常数,则称这样的方阵为四阶幻方.假设方阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡16151413121110987654321x x x x x x x x x x x x x x x x 为四阶幻方,根据定义得下面的方程组: ⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧><=+++><=+++><=+++><=+++><=+++><=+++><=+++><=+++><=+++><=+++><=+++><=+++><=+++><=+++><=+++><=+++16.....................................15......................................14.......................................13.....................................12......................................11........................................10......................................9.......................................8.......................................7...........................................6.............................................5...........................................4........................................3.........................................2.........................................1..........................................13107416963151252141181151054149831312721611611615141312111098765432116128415117314106213951t x x x x t x x x x t x x x x t x x x x t x x x x t x x x x t x x x x t x x x x t x x x x t x x x x t x x x x t x x x x t x x x x t x x x x t x x x x t x x x x 将这个非齐次线性方程组的增广矩阵进行初等变换化为最简形式(具体化简过程从略)→-----⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡t t t t t t t t t t t t t t t t 0001001001001000100000010010010001001000000100100010010010000001010000100001100000100001100001000001100001000010100001000010000111110000000000000000111100000000000000001111000000000000000011111000100010001000010001000100010000100010001000100001000100010001⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--------------000000000000000000000000000000000000000000000000000000000000000000001111000000000000110011000000000001010101000000000001101001000000002001000001000000021110000001000000210000000001000002010000000001000021010100000001000201001000000001002000010000000001021100100000000001t t t tt t t t t t 因为342)161(16.4141161=+==∑=k k t将34=t 代入上述矩阵种得到方程组得一般解:⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧><---=><---=><+-=><++-=><-=><+++-=><-=><-=><-+-=><--+=><-=><+++-=28............................3427............................3426..................................25................................24..............................................1723.........................1722..............................................1721..............................................1720.............................1719.............................1718..............................................1717.........................1716151413161512111615121015141291481615147166155161412415141231221615121x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x %%(26)中,x15改为x14￥￥￥二确定四阶幻方解得一般方法从方程组的一般解可以推出以下八个关系式: 由<17>+<18>,<23>+<24>,<25>+<26>得:16151098721x x x x x x x x +=+=+=+ <29>由<19>+<20>,<21>+<22>,<27>与<28>比较得:141312116543x x x x x x x x +=+=+=+ <30>由<17>+<21>,<19>+<23>及<26>得:161214107351x x x x x x x x +=+=+=+ <31>由<18>+<22>,<20>+<24>,<25>+<28>与<27>得:151********x x x x x x x x +=+=+=+ <32>由<17>+<20>,<22>+<23>及<25>得:151********x x x x x x x x +=+=+=+ <33>由<18>+<19>,<21>+<24>,<26>+<27>与<28>比较得:1641178532x x x x x x x x +=+=+=+ <34>$$x7,x14改为x10,x13$$$由<17>+<28>,<22>+<26>,<19>,<24>两边加上x 12得:128153106131x x x x x x x x +=+=+=+ <35>由<21>+<25>,<18>两边加上x 14,<23>+<27>,<20>得:16411714295x x x x x x x x +=+=+=+ <36>今断言171615≠+x x若171615=+x x ,由<21>式知17155=+x x ,则可推出165x x =矛盾. 同理可以推得,,,,,,,16412816131514151116121211x x x x x x x x x x x x x x +++++++都不等于17.我们考查关系式<29>与<30>,这两个关系式把十六个数分为两类,其中每一类的八个数又可分为四对,且每对数的和皆相等,但是都不等于17.幻方常数34分为两个数的和,这两个数并不相等的分法共有如下十六种.;(33,1),(32,2),(31,3),(30,4),(29,5),(28,6),(27,7),(26,8),(25,9),(24,10),(23,11),(22,12),(21,13),(20,14),(19,15),(18,16).因为1,2都不能分为互不相等的两个数的和,3只能分为(1,2)一类, ,4只能分为(1,3)一类,5只能分为(1,4),(2,3)两类,6只能分为(1,5),(2,4)两类,7只能分为(1,6),(2,5),(3,4)三类, 8只能分为(1,7),(2,6),(3,5)三类,这八类都不能分为互不相等的八类,所以应该排除.24可以分为(16,8),(15,9),(14,10),(13,11), 四对10可以分为(9,1),(8,2),(7,3),(6,4) 四对虽然各自可以分为互不相等的四对,但是十六个数字中漏掉了5和12这两个数字,而8,9这两个数字两类中都有出现了重复,所以这种分法也应该排除.23可以分为(16,7),(15,8),(14,9)(13,10).(12,11) 五对11可以分为(10,1),(9,2),(8,3),(7,4),(6,5) 五对,尽管每个数可以分为互不相等的五对,但是却不能从中选出彼此互不重复的四对, 所以这种分法也应该排除.22可以分为(16,6),(15,7),(14,8),(13,9),(12,10), 五对12可以分为(11,1),(10,2),(9,3),(8,4),(7,5) 五对,尽管每个数可以分为互不相等的五对,但是却不能从中选出彼此互不重复的四对, 所以这种分法也应该排除.20可以分为(16,4),(15,5),(14,6)(13,7).(12,8),(11,9) 六对14可以分为(13,1),(12,2),(11,3),(10,4),(9,5),(8,6) 六对,尽管每个数可以分为互不相等的六对,但是却不能从中选出彼此互不重复的四对, 所以这种分法也应该排除.25可以分为(16,9),(15,10,),(14,11),(13,12) 9可以分为(8,1),(7,2),(6,3),(5,4) 21可以分为(16,5),(15,5),(14,7),(13,8) 13可以分为(12,1),(11,2),(10,3),(9,4) 19可以分为(16,3),(15,4),(12,7),(11,8) 15可以分为(14,1),(13,2),(10,5),(9,6) 18可以分为(16,2),(14,4),(12,6),(10,8) 16可以分为(15,1),(13,3),(11,5),(9,7)(25,9);(21,13);(19,15);(18,16)这四种分法的每个数不仅可以分为互不相等的四对,而且互不重复,又无遗漏,这四种分法正好与前面的八个关系式构成一一对应.利用这一对应关系.便可以给出确定四阶幻方解的一般方法: 下面给出四阶幻方的一个解.不妨取定<29>=9,,<30>=25,<31>=13,<32>=21, <33>=15,<34>=19,<35>=16,<36>=18 令11=x由921=+x x ,得82=x ,(因为<29>=9) 由1351=+x x ,得125=x ,(因为<31>=13) 由1541=+x x ,得144=x ,(因为<33>=15) 由16131=+x x ,得1513=x ,(因为<35>=16) 而由<30>=25即251413=+x x 得1014=x 而由<32>=21即2162=+x x 得136=x 而由<32>=21即21139=+x x 得69=x 而由<32>=21即2184=+x x 得78=x 而由<30>=25即2543=+x x 得113=x 再由<29>=9即987=+x x 得27=x 再由<29>=9即9109=+x x 得310=x 此时还余下4,5,9,16四个数由<30>=25即251211=+x x 由<32>=21即. 211511=+x x考虑25的分类中还余下(16,9)这一对,21的分类中还余下(16,5)这一对,所以1611=x 从而912=x 515=x 这时断定416=x将确定的解排成方阵:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡45101591636721312141181 经检验这个矩阵满足四阶幻方的定义. 三确定幻方解的个数从确定幻方解的一般方法,我们进而可以确定幻方解的个数.,,,,131514121x x x x x x x x ++++是从(25,9),(21,13),(19,15),(18,16)中选取的四个数值,共有42种选择.它的选择，具体讲可由1x 的值所确定,例如取11=x .我们考查1所在的数对所属的分类.1在9,13,15,16的分对中.所以,,,,131514121x x x x x x x x ++++取定9,13,15,16.这相当与四个元素的全排列.它们的取法共有!4种.对于每一种排列,按照(二)中的方法便可确定幻方的一个解.(二)中的具体解便是.所以四阶幻方的解共有384!4.24=个解.四在变换意义下的唯一性对于我们在(二)中得到的那个解. 1,矩阵转置后显然是解.2,.交换第二行和第四行的位置后仍然是解, 交换第一行和第三行的位置后仍然是解, 将矩阵:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=16151413121110987654321x x x x x x x x x x x x x x x x A 进行分块,记⎥⎦⎤⎢⎣⎡=652111x x x x A ,⎥⎦⎤⎢⎣⎡=874312x x x x A ⎥⎦⎤⎢⎣⎡=141310921x x x x A ⎥⎦⎤⎢⎣⎡=1615121122x x x x A ,则⎥⎦⎤⎢⎣⎡=22211211A A A A A 定义2:若⎥⎦⎤⎢⎣⎡=4321b b b b B 称⎥⎦⎤⎢⎣⎡4231b b b b 为B 的正转置记为+T B ,即右上角与左下角交换. 称⎥⎦⎤⎢⎣⎡1324b b b b 为B 的负转置记为-T B ,即右下角与左上角交换.称⎥⎦⎤⎢⎣⎡1234b b b b 为B 的双转置记为TB ,即右上角与左下角,右下角与左上角都交换.3,若⎥⎦⎤⎢⎣⎡=22211211A A A A A 是解,则⎥⎦⎤⎢⎣⎡=+--+T T T T A A A A A 22211211*也是解 4,若⎥⎦⎤⎢⎣⎡=22211211A A A A A 是解,则⎥⎦⎤⎢⎣⎡=22122111***A A A A A TT 也是解 ***A 是由⎥⎦⎤⎢⎣⎡=22211211A A A A A 分块后,先将块当作元素进行正转置得⎥⎦⎤⎢⎣⎡=22122111**A A A A A ,再将块12,21A A 分别双转置而成,形象地说是将A 分块后,将块2112,A A 绕矩阵的中心旋转0180而成.可以将幻方的一个解,利用上述四个变换得到所有的384个解,反过来利用上述四个变换,可以将一个解变成我们所得到的那个解.所以在变换意义下,我们说四阶幻方的解是唯一的.本文得到王石瑚先生的指导,在此表示感谢!本文发表在洛阳师专学报(自然科学版)1989年第2期.。

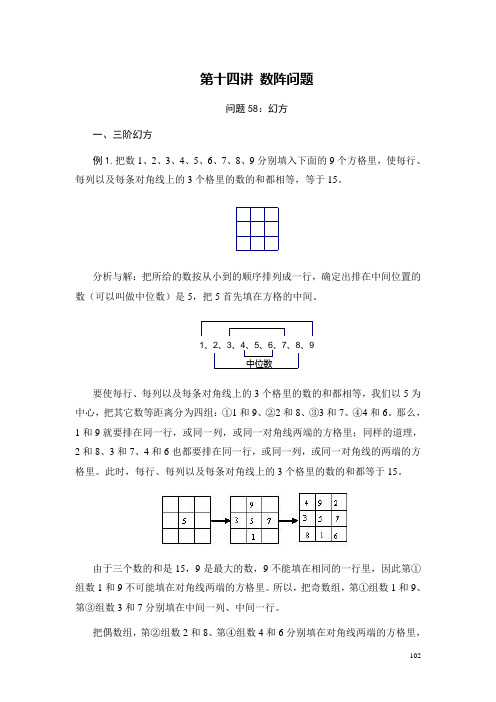
小学数学解题方法、思路归纳14：小学数学数阵问题

102
103
书”。

而这种“河图”和“洛书”的形象最早是宋人根据郑玄的《乾凿度》中的“载九履一，左三右七，二四为肩，六八为足”造出来的。

如下图所示，我们填写的方阵图正好与这种“河图”、“洛书”的形象完全一致。

“洛书”作为数字方阵，也就是我们所说的三阶幻方。

直到现在，仍然是许多数学家和数学爱好者感兴趣的问题。

其实，在三阶方阵里填写的数不一定是从1开始的自然数，可以从任何一个数开始，这一列数可以是任何一个等差数列。

二、五阶幻方
我们继续用上面的调整法来制作五阶幻方。

将数1到25按自然排列排成一个5阶方阵，如图（6）所示。

按照幻方的要求，五行、五列、两条对角线上的5个数的和应该相等。

我们首先计算这个和应该等于多少。

由于1＋2＋3＋……＋24＋25=65，而65÷5=13，这说明5阶幻方与3阶幻方一样，中心位置的数应该是13。

在图（5）中，两条对角线、第三行、第三列的5个数的和已经都等于65：1＋7＋13＋19＋25=65；5＋9＋13＋17＋21=65
像三阶幻方那样，我们仍然采用下面的“对角线”法则对图（6）的元素作下列调整：（1）将两条对角线上的元素绕中心旋转45度得图（7）或图（8）：
104
105
106
107
108
109。

幻方解法

幻方解法
幻方，就是对于一个n×n的方阵，将1—n²这n²个数填入其中，使每行每列以及对角线上的数字之和都相等的方阵。

幻方分为奇数阶幻方(n=2k+1)、单偶数幻方
(n=4k+2)、双偶数幻方(n=4k)三种，每种幻方解法不同，但都有其固定的解。

下面我来具体介绍下幻方的解法：
1.奇数阶幻方
①将1填入第一行中间位置
②向右上方向依次填入
③如果上方出格了，则将其填入最后一行与其同列的位置
④如果右方出格了，则将其填入第一列与其同行的位置
⑤如果右上都出格，则将其填入第一列最后一格
⑥如果将要填入的方格已有数字，则填入上一个数字的下方
这里已三阶幻方为例：
2.双偶数阶幻方(n=4k)：
①先将1，2，3……n²依次填入方阵中
②拟出方阵对角线
③对角线上数字不动，将其余所有数字移至与其中心对称的位置
这里以四阶幻方为例
↓
↓ 3.单偶数阶幻方(n=4k+2)：
①先将1，2，3……n平方依次填入方阵中
②拟出对角线，将对角线上所有数字移至与其中心对称的位置。

③从方阵左半部分的每一列数字中抽出一对上下对称的数字互换位置(每一列抽出一对)
④从方阵上半部分的每一行数字中抽出一对左对称的数字互换位置(每一行抽出一对)
注：已经移动过或换过位置的数字不能再移动或换位
这里以六阶幻方为例：
↓
↓②↓
↓
↓③↓
↓
↓④↓。

中国人最先发现4阶幻方密码

四阶幻方密码构造法
题记——谨以此发现献给为实现“中国梦”而奋斗的华夏儿女
（自我评价：1、中国人最先发现。

2、幻方世界大发现。

）
作者：青海省祁连县民族中学教师
构造方法：第一步，用1、2、3、、4
：如
要求：幻和必需是：1+2+3+4
第二步：将以上“类幻方”向左或向右旋转90
°得到新的一个“类幻方”，如：向右旋转得
到：
1+2+3+4
第三步：将以上两个“类幻方“叠放，可以得到一个四阶“密码”幻方：
或者
特点：四阶幻方，幻和都是110。

第三步：编码：将等差数列的连续16项分4组编码，以
1——16的自然数为列：
（3——1）
特点：公差相等。

相邻的组距相等。

根据以上特点也可以这样编码:如
（3——2）（3——3）
第四步：任选一项编码将第二步中（1）或（2）的任意一个“密码”幻方“翻译”：如用：（3——1）编码翻译（2）“密码”幻方得到1——16自然数组成的四阶幻方
↓
（3——1）
如果用（3——3）编码“翻译”也得到1——16自然数组成的四阶幻方。

（3——3）
↓。

n=4m(m∈N)阶幻方的最简单构造法

须每行、每列的四个数的和相等，因此由定理2可以知道，做这项工作的
关键在于，如何在数阵图s-2中确定：哪些数作补数，哪些数作原数。
先将1作原数，对第一行，由定理2知4也作原数，而将2、3变成补数2、3；对于第一列，13作原数，5和9将变成补数5、9，其它行列类推，即如图h-1，再将其补数换成其对应的原数，即得一个4阶幻方，如图h-2。若将图h-1中的每个数都取补数，又得一个有补数的新幻方，如图h-3。（注：这里就是利用了补数的性质）
（或某列）补数的分布规律，我们就能在数十秒内写出较
大的4m阶幻方，因为只需标出原4m阶数阵中所有的补数
就够了，这比用其它方法构造4m阶幻方来得更快捷方便。
第2页
=2(1+n2)-(a2+a3)+ (a1+a4)
=2(1+n2)
同理可证(a1+a4)+(a2+a3)=2(1+n2)
∴(a2+a3)+(a1+a4)=(a1+a4)+(a2+a3)=2(1+n2)
当n=4m，m=1时，(a2+a3)+(a1+a4)=(a1+a4)+(a2+a3)=2(1+42)=2×17=34
等差数列，这个等差数列的和是s=
n×1+×d=，
即n阶幻方的幻和。而右倾一条主对
角线上的数满足式子(n-1)×h+1 <h为行号>，是一个公差为d1=n-1的等差数列，此等差数
列的和是s= n×n+×d1=，也为n阶幻方的幻和。
第1页
n=4m（m∈N）阶幻方的构造法
有了上述预备知识，我们就可以讨论一下n=4m阶幻方构造的方法。

四阶幻方解法

四阶幻方是最简单的双偶幻方,其构成方法就是两句话：
【顺序填数；以中心点对称互换数字】.以1-16构成的四阶幻方为例：
1、先把1放在四阶幻方4个角的任意一个角格,按同一个方向按顺序依次填写其余数.
如图：按行从左向右顺序排数.
2、以中心点对称互换数字.（有两种对称交换的方法）
1）、以中心点对称交换对角线上的数（即1-16、4-13、6-11、7-10互换）,完成幻方,幻和值=34.
2）、以中心点对称交换非对角线上的数（即2-15、3-14、5-12、8-9互换）,完成幻方,幻和值=34.
什么样的16个数能构成四阶幻方呢?【4个数一组的4组数（共16个数）,组与组对称等差,每组数与数对称等差,这样的16个数能构成四阶幻方（其中就包括等差的16个数）.】
如图
上图,每组数与数以2-3-2对称等差,组与组以10-20-10对称等差. 下图,每组数与数以1-2-1对称等差,组与组以10-20-10对称等差. 再如：
上图,每组数与数等差为1,组与组等差为5.
中图,每组数与数等差为1,组与组以5-10-5对称等差.
下图,每组数与数以2-3-2对称等差,组与组以5-10-5对称等差.
【四阶幻方的特点：】
1、互换对称的行（列）,幻方成立.
2、互换一侧的行（或列）,再互换另一侧的行（或列）,幻方亦成立.
3、互换不对称的行（或列）,再互换另外不对称的行（或列）,幻方亦成立.
4、平移互换对角的行或列、平移互换对角,幻方成立.
另,每16个能构成四阶幻方的数,幻方的填法有880种.。