第(11)章如何选取样本.
第11章回归分析习题解答

B. 是随机变量,且有 y0 N (β0 + β1x0 ,σ 2 ) .
C. 当 β0 , β1 确知时等于 β0 + β1x0 .
D. 等于 βˆ0 + βˆ1x0 .
6. 在回归分析中,检验线性相关显著性常用的三种检验方法,不包含(
A. 相关系数显著性检验法.
B. t 检验法.
; 若 新 保 单 数 x0 = 1000 , 给 出 Y 的 估 计 值 为
yˆ0 = 0.118129 + 0.003585×1000 = 3.703129 .
16. 下表是 16 只公益股票某年的每股帐面价值 x 和当年红利 y ,利用 Excel 的数据分
析功能得到的统计分析结果如下:
方差分析
过 10 周时间,收集了每周加班工作时间的数据和签发的新保单数目, x 为每周签发的新保
单数目,Y 为每周加班工作时间(小时).利用 Excel 的数据分析功能得到统计分析如下表.
Coefficients
标准误差
Intercept X Variable 1
0.118129 0.003585
0.355148 0.000421
15.1
15.1
228.01
228.01
18
15.1
14.5
228.01
210.25
列和
270.1
265
计算可得:
4149.39
3996.14
∑ Syy =
y2 i
−
ny 2
=94.75
∑ Sxx =
x2 i
−
nx 2
=96.39
∑ Sxy = xi yi − nxy = 95.24
抽样技术-课件全-抽样技术-第11章全文

CPS的样本轮换具有如下主要特征
1.在任何一个月内,都有八分之一的住户单位第一次接受 调查,八分之一的住户单位第二次接受调查,如此下去
2.每个月都有新的样本组代替从样本中永久退出的老样本 组
3.每个月都有一个样本组在8个月的闲置后重新接受调查。 重新接受调查的样本组代替了刚刚退出,进入闲置期的 样本组
4.设计保证了每个样本单元在两个年份的4个相同月份中 接受调查
5.在连续的两个月内,有四分之三的样本是相同的;在连 续的两年中,有二分之一的样本是相同的。
劳动力特征
3. 抽样时以州为总体,因而设计也是以州为总体的设 计
4. 样本量由变异系数CV及可靠性要求所决定 5. 在失业率为6%的自定义下,各州对变异系数的要求 在8%—9%之间。这样就能保证进行全国估计的变异系 数控制在1.8%之内
11.2.2第一阶段的抽样
第一阶段的抽样涉及三个方面的工作。这些工 作是:初级抽样单元(PSU)的界定;将初级抽 样单元PSU分层;PSU的抽选
11.4.5 广义方差(Generalized Variance)
广义方差函数GVF用于产生人口总量x估计值的估计方差。 函数形式为
Var( Xˆ ) aX 2 bX 式中,a和b是用最小二乘法得到的估计参数。该模型的原理是假定x的方差可以表示为简 单随机样本的方差与设计效应(deff)的乘积。设计效应deff是指某一复杂抽样设计相对于
第11章 设计与方法-美国CPS案例
美国人口现状调查(Current Population Survey,简称CPS)被认为是全国性大规模居 民住户抽样调查的典范。
第十一章 t 检验

H0: μ=μ0, 即该山区成年男子的平均脉搏数与一般成年男
子脉搏 数相等 H1: μ>μ0, 即该山区成年男子的平均脉搏数高于一般成年 男子脉 搏数 单侧 α=0.05
(2) 选定检验方法,计算检验统计量t值
X 0 74.2 72 t 1.833 S 6 n 25
v n 1 25 1 24 t0.05 24 1.7109
单位:千克
94.5
101
110
103.5
97
88.5
96.5
101
104
116.5
85
89.5
101.5
96
86
80.5
87
93.5
93
102
首先进行假设:H0 :μ1 - μ2 ≤ 8.5
H1 :μ1 - μ2 > 8.5
即平均体重减少不足 8.5千克
即平均体重减少超过 8.5千克
然后计算参加前后体重变化差值,见下表:
(3) 判断结果 t=1.833 > t0.05(24)=1.7109, 拒绝H0,接受H1,差异有统计学意义。 可认为该山区健康成年男子脉搏数高于 一般成年男子脉搏数。
两配对样本 t 检验
配对样本:是指一个样本中的数据与另一个样本中的数据相对应的两 个样本。 例如,医生对药物治疗效果进行检验时,将病情相似的病人分为两组, 其中一组按时服用药物,另一组则不服用药物;我们将一个班级的同 学(同质性较强)随机分为两组,一组采用新教案授课,另一组按原 教案上课,最后通过比较分析新教案是否有利于提高学生成绩。
取 α= 0.05 。
首先进行假设:H0 :μ1 = μ2
H1 : μ 1 ≠ μ 2
14第十一章修匀法概述

n
n
ar[c0 c1r c2r 2 c3r3 ] x ar[c1 2rc2 3r 2c3 ]
n
n
n
n
x2 ar[c2 3rc3] x3c3 ar
19
n
n
误差分析
如无果偏待估估计参(U数E),tx 则的在估再计生量性U条x ,件是下,txV的x
也估是计量t x
的UE,如何比较估计量
第二步:修匀。我们着手初始数据的系统修订 工作,其目标是产生关于那个未知的,基死亡 模型的一个代表。它与已给的初始估计相比要
好一些。应该注意到,经过一次修匀,死亡数 据将被改变,这可适当地反映我们模型的这种 期望改进。在我们的精算方向中,把修匀看作 一种尝试,去得到通用的有效的死亡率的最佳 代表。
如Whittaker修匀。修匀表达式显含初始
估计值
的u函x 数。
,u而x 不是x,修匀算子是{
}
第二种:参数修匀。
取参数的“最佳”估计值来获得
修匀值。修匀算子是x的函数。
11
作业:p.276 7
12
第12章 表格数据修匀
本章内容:介绍几种常见的表格 数据修匀方法
0.30.2 0.70.5 0.41
3
修匀的定义
定义:一种利用初始估计,结合先验观 点修正初始估计值的数学方法。
在精算实务中的重要应用:编制生命表 (生存模型),根据这个模型计算保费 值。
4
建模工作的第一项任务:通过试验研究产生一 个关于某些特定年龄的死亡率(或概率)序列。 这些死亡率是基于某个观察群休的试验而得到 的,所以常被称为观察数据。
16
对称M-W-A公式中系数的确定
在§11.1中我们提到修匀的目的是减小误差,
第11章卡方检验(0429修改)
第十一章2χ检验2χ检验(chi-square test)是英国统计学家K. Pearson于1900年提出的,以2χ分布(chi-square distribution)和拟合优度检验(goodness-of-fit test)为理论依据,是一种应用范围很广的统计方法。
本章主要介绍率或构成比比较的2χ检验,频数分布的拟合优度2χ检验,线χ检验,以及四格表的Fisher确切概率法。
性趋势2第一节2χ检验的基本思想2χ检验是在2χ分布的基础上,利用样本信息考察样本频数分布与假设成立条件下的理论频数分布之间差异的假设检验方法。
下面以例11.1为例,说明2χ检验的基本思想。
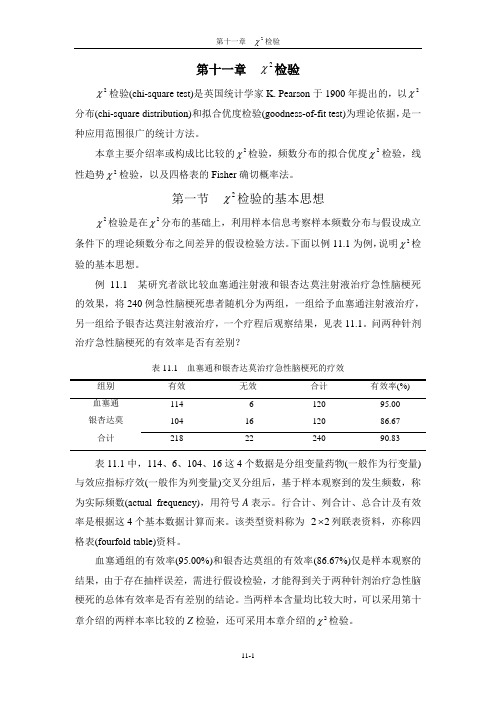
例11.1 某研究者欲比较血塞通注射液和银杏达莫注射液治疗急性脑梗死的效果,将240例急性脑梗死患者随机分为两组,一组给予血塞通注射液治疗,另一组给予银杏达莫注射液治疗,一个疗程后观察结果,见表11.1。
问两种针剂治疗急性脑梗死的有效率是否有差别?表11.1 血塞通和银杏达莫治疗急性脑梗死的疗效血塞通114 6 120 95.00银杏达莫104 16 120 86.67合计218 22 240 90.83表11.1中,114、6、104、16这4个数据是分组变量药物(一般作为行变量)与效应指标疗效(一般作为列变量)交叉分组后,基于样本观察到的发生频数,称为实际频数(actual frequency),用符号A表示。
行合计、列合计、总合计及有效率是根据这4个基本数据计算而来。
该类型资料称为22⨯列联表资料,亦称四格表(fourfold table)资料。
血塞通组的有效率(95.00%)和银杏达莫组的有效率(86.67%)仅是样本观察的结果,由于存在抽样误差,需进行假设检验,才能得到关于两种针剂治疗急性脑梗死的总体有效率是否有差别的结论。
当两样本含量均比较大时,可以采用第十章介绍的两样本率比较的Z检验,还可采用本章介绍的2χ检验。
一、对总体建立假设例11.1的无效假设为012:H ππ=,即两种针剂治疗急性脑梗死的有效率相同。
如何进行有效的调查研究与样本选择

如何进行有效的调查研究与样本选择调查研究是社会科学中广泛使用的一种研究方法,通过收集、分析和解释数据,来获取对特定问题的深入理解。
而一个有效的调查研究必须依赖于合适的样本选择和严谨的调查方法。
本文将介绍如何进行有效的调查研究与样本选择。
首先,样本选择是调查研究设计中至关重要的一步。
一个好的样本应当具有代表性,即能够准确反映目标群体的特征和态度。
为了实现代表性,我们可以采用随机抽样的方法。
随机抽样是指每个人都有相等机会被选中的抽样方法,可以减小样本的偏倚性。
常用的随机抽样方法有简单随机抽样、系统抽样、分层抽样等。
选择适当的抽样方法取决于研究的具体目的和资源预算。
其次,调查研究中收集数据的方法也需慎重选择。
调查方法可以是面对面访谈、电话访谈、邮寄调查或在线调查等。
不同的调查方法适用于不同的研究对象和研究目的。
面对面访谈有利于获取详细和全面的信息,但成本较高且可能引起被访者不真实回答的问题。
电话访谈则成本相对较低,但可能受到抽样偏差和拒绝参与的限制。
邮寄调查对于大规模样本的研究有优势,但需要注意回收率较低的问题。
在线调查则成本较低且方便参与者,但仍面临抽样偏差和样本不够代表性的问题。
根据研究的具体需求和资源条件,我们需要综合考虑选择合适的调查方法。
在实施调查过程中,确保数据的准确性和可靠性是至关重要的。
一些常见的数据收集问题包括问卷设计、访谈技巧和数据录入。
问卷设计时应注意问题的准确性、明确性和序列性,避免提问歧义或导致主观性答案的问题。
访谈人员应接受专业训练以获得高质量的数据。
数据录入过程中应注意对数据进行验证和清理,以确保数据的准确性和一致性。
最后,数据分析是一个关键的环节。
根据研究问题的性质和调查方法的特点,我们可以采用不同的数据分析方法。
对于定性分析,可以通过编码和归纳的方式对数据进行分析。
对于定量分析,我们可以使用统计软件进行描述性统计和推论统计分析。
需要注意的是,数据分析的结果需要客观、准确地反映研究问题,避免主观偏见和不恰当的解释。
卫生统计学第十一章统计设计

做答人数:0
做对人数:0
所占比例: 0
题号: 3 本题分数: 1.7
下列说法正确的是
A. 因抽样误差随抽样样本含量的增大而减小,所以在抽样研究中总是考虑样本含量越大越好
做答人数:0
做对人数:0
所占比例: 0
题号: 2 本题分数: 1.7
实验设计的四原则是
A. 收集、整理、分析、结论
B. 齐同、对照、重复、随机
C. 设计、操作、计算、推断
D. 对照、随机、操作、归纳
E. 对照、随机、操作、汇总
正确答案: B
D. 分组原则、随机原则、重复原则、均衡原则
E. 对照原则、随机原则、分组原则、均衡原则
正确答案: A
做答人数:0
做对人数:0
所占比例: 0
题号: 12 本题分数: 1.7
将实验和对照在同一受试对象身上进行的对照称为
A. 空白对照
B. 实验对照
做答人数:0
做对人数:0
所占比例: 0
题号: 14 本题分数: 1.7
将受试对象完全随机分配到各个处理组中进行实验观察或分别从不同总体中随机抽样进行对比观察,此种设计为
A. 随机区间设计
B. 完全随机设计
C. 配对设计
D. 配伍组设计
E. 以上均不对
做答人数:0
做对人数:0
所占比例: 0
题号: 7 本题分数: 1.7
抽样调查必须遵循
工作总结医学研究中的样本收集与处理

工作总结医学研究中的样本收集与处理在医学研究中,样本的收集与处理是非常重要的环节。
它涉及到研究结果的准确性和可靠性。
本文将从样本收集的主要步骤、样本处理的方法以及注意事项等方面进行总结。
一、样本收集1. 研究对象的选择在进行医学研究时,首先需要明确研究对象。
根据研究的目的和假设,选择合适的研究对象,如人体组织、血液、尿液、细胞等。
同时,要确定样本的数量和质量要求。
2. 规范化的操作步骤在样本收集过程中,需要严格按照规范化的操作步骤进行。
这包括消毒、穿戴无菌手套和口罩,避免污染样本。
3. 采集合适的样本量样本的数量要根据研究的需求和统计学原理进行确定。
过少的样本容易导致研究结果不够准确,而过多的样本则会增加工作量。
在样本采集过程中,要确保获得足够的样本量。
4. 样本记录和标识在收集样本的同时,要记录详细的信息,如样本编号、采集时间、采集者等。
同时,每个样本都需要进行标识,以便后续的处理与分析。
二、样本处理1. 样本保存与储存在医学研究中,样本的保存非常重要。
不同的样本要采用不同的保存方式,如低温冷冻、冷藏、干燥等。
在进行样本储存时,要确保样本的完整性和稳定性。
2. 样本预处理有时,样本需要经过预处理才能进行进一步的分析。
例如,血液样本可能需要离心来分离血清或血细胞。
在进行样本预处理时,要确保操作准确,避免对样本造成不必要的损伤。
3. 数据采集与分析样本处理后,需要进行数据采集与分析。
这包括对样本的性质、成分、浓度等进行测量和统计。
根据需要,可以采用各种各样的实验技术和仪器来获取所需数据。
三、注意事项1. 符合伦理要求在进行医学研究时,样本的收集和处理要符合伦理要求,尊重研究对象的权益。
研究项目需经过伦理委员会的审核和批准。
2. 严格控制实验条件样本的收集与处理过程中,实验条件的严密控制是确保结果准确的关键。
如操作环境的清洁、温度的控制、时间的准确记录等。
3. 重复实验与验证结果为了确保结果的可靠性,对于重要的实验结果,需进行重复实验与验证。
PPT-第11章-二值选择模型-计量经济学及Stata应用

© 陈强,2015年,《计量经济学及Stata应用》,高等教育出版社。
第11章二值选择模型11.1 二值选择模型如果被解释变量y离散,称为“离散选择模型”(discrete choice model)或“定性反应模型”(qualitative response model)。
最常见的离散选择模型是二值选择行为(binary choices)。
比如:考研或不考研;就业或待业;买房或不买房;买保险或不买保险;贷款申请被批准或拒绝;出国或不出国;回国或不回12国;战争或和平;生或死。
假设个体只有两种选择,比如1y =(考研)或0y =(不考研)。
最简单的建模方法为“线性概率模型”(Linear Probability Model ,LPM):1122(1,,)i i i K iK i i i y x x x i n βββεε'=+=+= +++x β (11.1)其中,解释变量12()i i i iK x x x '≡ x ,而参数12()K βββ'≡ β。
LPM 的优点是,计算方便,容易得到边际效应(即回归系数)。
3LPM 的缺点是,虽然y 的取值非0即1,但根据线性概率模型所作的预测值却可能出现ˆ1y>或ˆ0y <的不现实情形。
图11.1 线性概率模型4为使y 的预测值介于[0,1]之间,在给定x 的情况下,考虑y 的两点分布概率:P(1|)(,)P(0|)1(,)y F y F ==⎧⎨==-⎩x x x x ββ (11.2)函数(,)F x β称为“连接函数”(link function) ,因为它将x 与y 连接起来。
y 的取值要么为0,要么为1,故y 肯定服从两点分布。
连接函数的选择具有一定灵活性。
通过选择合适的连接函数(,)F x β(比如,某随机变量的累积分布函数),可保证ˆ01y≤≤,并将ˆy 理解为“1y =”发生的概率,因为5E(|)1P(1|)0P(0|)P(1|)y y y y =⋅=+⋅===x x x x (11.3)如果(,)F x β为标准正态的累积分布函数,则P(1|)(,)()()y F t dt φ'-∞'===Φ≡⎰x x x x βββ (11.4)()φ⋅与()Φ⋅分别为标准正态的密度与累积分布函数;此模型称为“Probit ”。
SPSS第11章聚类分析

• ③在图11.2中单击“Plots”按钮,进入对话框,如图11.2示。
• 选择“Variable Importance Plot”中“Rank Variable”的“by variable”,以便显示在两步聚类中各个变量重要性的图形, 再选择“Continue”按钮,回到原来菜单。
学习目标
解释聚类分析的基本概念
熟悉系统聚类分析方法 分析“Classify”菜单,阐述聚类分析与判别分析的基本原理和基本操作。用 实例说明5种方法的具体实现过程,解释其主要功能、背景知识及其主要选择 项。
第11章 聚类分析和判别分析
• 11.1 聚类分析和判别分析过程综述 • 11.2 两步聚类
11.4 分层聚类分析 11.6 判别分析
• ⑤单击“OK”按钮,在Output窗口和“Data View”中显示计算 结果。
2)基本输出结果与解释
•①首先,给出了最终的聚类结果(3类),并且给出了各类的 每个变量的均值与标准差(图略)。
•②其次,给出了3个分类中男女性、经济收入、教育水平变量 的分布状况图11.4。 •③给出了变量均值的95%置信区间在3类中的对比图图11.5。 •④图11.6所示,给出了一系列图形(本例中有6张图)表示给 个变量在聚类中的重要性。
预先并不知道类的特征,甚至不知道类的数目,因此要选择聚类的基 础变量、距离测量标准以及聚类标准。
11.1.3 Classify的功能
•SPSS的“Classify”菜单中提供了5种分类分析。 •① 两步聚类(TwoStep Cluster)提供了可以同时 根据连续变量和分类变量进行聚类的功能。
第11章 统计分析—双变量

10- 13 10-
社会 统计学
2、方差齐性检验和t检验结果 、方差齐性检验和t
F值>F 0.025 (n 1-1,n 2-1), 说明方差不齐。
10- 14 10-
P值小于给定的显著性水平α, 说明方差不齐。
P值小于给定的显著性水平α, 拒绝原假设。
社会 统计学
社会 统计学
10- 44 10-
社会 统计学
10- 45 10-
社会 统计学
【例2】“年龄段”与“忙碌程度”
10- 46 10-
社会 统计学
10- 47 10-
社会 统计学
10- 48 10-
社会 统计学
10- 49 10-
社会 统计学
斯皮尔曼等级相关系数(spearman)在这: 斯皮尔曼等级相关系数(spearman)在这: Analyze Correlate Bivariate
2、 比较重要 3、 一般 5、 很不重要 6 、说不清楚
10- 40 10-
社会 统计学
1、将被访者学历与“读书的地位”都看成 定类变量,作列联相关的检验。 2、被访者学历与“读书的地位”均为定序 量,作等级相关检验。
10- 41 10-
社会 统计学
10- 42 10-
社会 统计学
10- 43 10-
社会 统计学
二、独立样本T 检验 独立样本T
Analyze Compare Means
IndependentIndependent-Samples检验变量栏 T Test,
打开Independent-Samples T Test对 IndependentTest对
分组变量栏, 话框 只能有一个分 组变量
北京理工大学《概率论与数理统计》课件-第11章

区间估计的基本概念前面介绍了参数的点估计,讨论了估计量的优良性准则,给出了寻求估计量最常用的矩估计法和最大似然估计法.参数的点估计是用一个确定的值去估计未知参数,看似精确,实际上把握不大,没有给出误差范围,为了使估计的结论更可信,需要引入区间估计.Neyman(1894–1981)引例在估计湖中鱼数的问题中,若根据一个实际样本,得到鱼数N的最大似然估计为1000条.实际上,N的真值可能大于1000,也可能小于1000.为此,希望确定一个区间来估计参数真值并且满足:1.能以比较高的可靠程度相信它包含参数真值.“可靠程度”是用概率来度量的.2.区间估计的精度要高.可靠度:越大越好估计你的年龄八成在21-28岁之间区间:越小越好被估参数可靠度范围、区间一、置信区间的定义(Confidence Interval )对于任意θ∈Θ,满足设总体X 的分布函数F (x ,θ)含有一个未知参数θ,θ∈Θ,对于给定常数α(0<α<1),若由抽自X 的样本X 1,X 2,…,X n 确定两个统计量112212ˆˆ{(,,,)(,,,)}1n n P X X X X X X θθθα<<≥-112ˆ(,,,)nX X X θ212ˆ(,,,)nX X X θ和则称随机区间是θ的置信水平为1−α的置信区间.12ˆˆ(,)θθ和分别称为置信下限和置信上限.1ˆθ2ˆθ(1)当X 连续时,对于给定的α,可以求出置信区间满足此时,找区间使得至少为1−α,且尽可能接近1−α.12ˆˆ(,)θθ112212ˆˆ{(,,,)(,,,)}1nnP X X X X X X θθθα<<=-12ˆˆ(,)θθ112212ˆˆ{(,,,)(,,,)}1n n P X X X X X X θθθα<<=-12ˆˆ()P θθθ<<(2)当X 离散时,对于给定的α,常常找不到区间满足12ˆˆ(,)θθ说明:(2)估计的精度要尽可能高. 如要求区间长度尽可能短,或者能体现该要求的其他准则.(1)要求θ以很大的可能被包含在区间内,即概率尽可能的大.可靠度与精度是一对矛盾,一般是在保证可靠度的条件下尽可能提高精度.12ˆˆ()P θθθ<<12ˆˆ(,)θθ21ˆˆθθ-(3)对于样本(X 1,X 2,…,X n )112212ˆˆ((,,,),(,,,))n n X X X X X X θθ以1−α的概率保证其包含未知参数的真值.随机区间112212ˆˆ{(,,,)(,,,)}1n n P X X X X X X θθθα<<=-即有:(4)对于样本观测值(x 1,x 2,…,x n )可以理解为:该常数区间包含未知参数真值的可信程度为1−α.112212ˆˆ((,,,),(,,,))n n x x x x x x θθ常数区间只有两个结果,包含θ和不包含θ.此时,不能说:112212ˆˆ{(,,,)(,,,)}1n n P x x x x x x θθθα<<=-没有随机变量,自然不能谈概率如:取1−α=0.95.若反复抽样100次,样本观测值为112212ˆˆ{(,,,)(,,,)}1n n P X X X X X X θθθα<<=-1121ˆˆ((,,),(,,))i i i in n x x x x θθ于是在100个常数区间中,包含参数真值的区间大约为95个,不包含真值的区间大约为5个.12,,,ii i nx x x1,2,,100i =对应的常数区间为1,2,,100i =对一个具体的区间而言,它可能包含θ,也可能不包含θ,包含θ的可信度为95%.1121ˆˆ((,,),(,,))i i i i nnx x x x θθ二、构造置信区间的方法枢轴量法1.寻求一个样本X 1,X 2,…,X n 和θ的函数W =W (X 1,X 2,…,X n ;θ),使得W 的分布不依赖于θ和其他未知参数,称具有这种性质的函数W 为枢轴量(Pivotal quantity ).3.若由不等式a <W (X 1,X 2,…,X n ;θ)<b 得到与之等价的θ的不等式2.对于给定的置信水平1−α,定出两个常数a 和b ,使得P {a <W (X 1,X 2,…,X n ;θ)<b }=1−α112212ˆˆ(,,,)(,,,)n n X X X X X X θθθ<<即有P {a <W (X 1, X 2,…, X n ;θ)<b }关键:1.枢轴量W (X 1, X 2,…, X n ;θ)的构造2.两个常数a ,b 的确定一般从θ的一个良好的点估计出发构造,比如MLE因此,是θ的一个置信水平为1−α的置信区间.112212ˆˆ{(,,,)(,,,)}1n n P X X X X X X θθθα=<<=-12ˆˆ(,)θθf (w )ababab1−α1−α1−α希望置信区间长度尽可能短.对于任意两个数a 和b ,只要使得f (w )下方的面积为1−α,就能确定一个1−α的置信区间.f(w)abab ab1−α1−α1−α当W 的密度函数单峰且对称时,如:N (0,1),t 分布等,当a =−b 时求得的置信区间的长度最短.如:b =z α/2或t α/2(n )当W 的密度函数不对称时,如χ2分布,F 分布,习惯上仍取对称的分位点来计算未知参数的置信区间.χ21−αα/2α/222()n αχ21-2()n αχ单个正态总体参数的区间估计一、单个正态总体的情形X 1, X 2,…, X n 为来自正态总体N (μ,σ2)的样本,置信水平1−α.样本均值样本方差11nii X X n ==∑2211()1nii S X X n ==--∑0-4-3-2-1012340.050.10.150.20.250.30.350.4是枢轴量W 是样本和待估参数的函数,其分布为N (0,1),完全已知由于是μ的MLE ,且是无偏估计,由抽样分布定理知X ~(0,1)X W N nμσ-=1.均值μ的置信区间(方差σ2已知情形)单峰对称-4-3-2-1012340.050.10.150.20.250.30.350.4即等价变形为选择两个常数b =−a =z α/222{}1X P z z nααμασ--<<=-22{}1P X z X z nnαασσμα-<<+=-1−αα/2α/2z α/2−z α/2简记为因此,参数μ的一个置信水平为1−α的置信区间为22(,)X z X z nnαασσ-+2()X z nασ±置信区间的长度为22n l z nασ=说明:2.置信区间的中心是样本均值;4.样本容量n 越大,置信区间越短,精度越高;1.l n 越小,置信区间提供的信息越精确;5.σ越大,则l n 越大,精度越低.因为方差越大,随机影响越大,精度越低.3.置信水平1−α越大,则z α/2越大.因此,置信区间长度越长,精度越低;22n l z nασ=22(,)X z X z nnαασσ-+2.均值μ的置信区间(方差σ2未知情形)想法:用样本标准差S 代替总体标准差σ.是枢轴量包含了未知未知参数σ,~(0,1)X W N nμσ-=此时,因此不能作为枢轴量.~(1)X T t n Snμ-=-由抽样分布理论知:使即枢轴量~(1)X T t n Snμ-=-22((1)(1))1X P t n t n Snααμα---<<-=-22{(1)(1)}1P t n T t n ααα--<<-=-选择两个常数b =−a =t α/2 (n -1)等价于因此,方差σ2未知情形下均值μ的一个置信水平为1−α的置信区间为22{(1)(1)}1S S P X t n X t n nnααμα--<<+-=-22((1),(1))X t n X t n nnαα--+-例1.现从中一大批糖果中随机取16袋,称得重量(以克记)如下:506508 499 503 504 510 497 512 514 505 493 496 506 502 509 496设每袋糖果的重量近似服从正态分布. 试求总体均值μ的置信水平为0.95的置信区间.解:这是单总体方差未知,总体均值的区间估计问题.均值μ的置信水平1−α的置信区间为22((1),(1))x t n x t n nnαα--+-根据给出的数据,算得这里10.95,16n α-==/20.025(1)(15) 2.1315t n t α-==503.75, 6.2022x s ==因此,μ的一个置信水平为0.95的置信区间为6.20226.2022(503.75 2.1315,503.75 2.1315)1616(500.4,507.1)-⨯+⨯=此区间包含μ的真值的可信度为95%.22((1),(1))x t n x t n nnαα--+-3.方差σ2的置信区间(均值μ未知)σ2的常用点估计为S 2,且是无偏估计。
第十一章非参数检验

第十一章 非参数检验前面有关章节讨论的参数检验都要求总体服从一定的分布,对总体参数的检验是建立在这种分布基础上的。
例如,两样本平均数比较的t 检验和多个样本平均数比较的F 检验,都要求总体服从正态分布,推断两个或多个总体平均数是否相等。
本章引入另一类检验——非参数检验(non-parametric test )。
非参数检验是一种与总体分布状况无关的检验方法,它不依赖于总体分布的形式,应用时可以不考虑被研究的对象为何种分布以及分布是否已知。
非参数检验主要是利用样本数据之间的大小比较及大小顺序,对两个或多个样本所属总体是否相同进行检验,而不对总体分布的参数如平均数、标准差等进行统计推断。
当样本观测值的总体分布类型未知或知之甚少,无法肯定其性质,特别是观测值明显偏离正态分布,不具备参数检验的应用条件时,常用非参数检验。
非参数检验具有计算简便、直观,易于掌握,检验速度较快等优点。
非参数检验法从实质上讲,只是检验总体分布的位置(中位数)是否相同,所以对于总体分布已知的样本也可以采用非参数检验法,但是由于它不能充分利用样本内所有的数量信息,检验的效率一般要低于参数检验方法。
例如,非配对资料的秩和检验,其效率为t 检验的86.4%,就是说以相同概率判断出差异显著,t 检验所需的样本个数要少13.6%。
非参数检验内容很多,本章只介绍常用的符号检验(sign test ),秩和检验(rank-sum test )和等级相关分析(rank correlation analysis )三种。
第一节 符号检验一、配对资料的符号检验(一)配对资料符号检验的意义 配对资料符号检验是根据样本各对数据之差的正负符号多少来检验两个总体分布位置的异同,而不去考虑差值的大小。
每对数据之差为正值用“+”表示,负值用“-”表示。
可以设想如果两个总体分布位置相同,则正或负出现的次数应该相等。
若不完全相等,至少不应相差过大,否则超过一定的临界值就认为两个样本所来自的两个总体差异显著,分布的位置不同。
第11章__审计抽样

对特定的账户而言,当抽样风险一定时,如果注册会计师确 定的可容忍错报降低,所需的样本规模就增加。
使用统计抽样方法时,注册会计师必须对影响样本规模的因素进 行量化,并利用根据统计公式开发的专门的计算机程序或专门的 样本量表来确定样本规模。
在非统计抽样中,注册会计师可以只对影响样本规模的因素进行 定性的估计,并运用职业判断确定样本规模。
2019/9/9
审计
12
影响样本规模的因素:
1. 可接受的抽样风险
细节测试旨在对各类交易、账户余额、列报的相关认定进行测 试, 尤其是对存在或发生、计价认定的测试。注册会计师实 施审计程序的目标就是确定相关认定是否存在重大错报。例如, 通过在账户余额中选取项目进行测试,注册会计师可以检查出 那些虚构项目、余额中不应包含的项目(分类错误的项目)以 及估价错误的项目。
1. 风险评估程序通常不涉及使用审计抽样
2. 当控制的运行留下轨迹时,可以考虑使用审计抽样实施控 制测试。
3. 在实质性程序中,实施细节测试时,注册会计师可以使用 审计抽样获取审计证据,以验证有关财务报表金额的一项或 多项认定,或对某些金额作出独立估计。在实施实质性分析 程序时,注册会计师不宜使用审计抽样。
分层可以降低每一层中项目的变异性,从而在抽样风险没有 成比例增加的前提下减小样本规模。
注册会计师可以考虑将总体分为若干个离散的具有识别特征 的子总体(层),以提高审计效率。界定子总体时,应当使 每一抽样单元只能属于一个层。
第十一章 抽样

总体参数和样本统计量
总体参数:反映总体数量特征的指标。其数值是唯一的、确定的。 样本统计量:根据样本分布计算的指标。是随机变量。
总体
样本
参数
统计量 平均数 标准差、方差
X
、2
p
S、 S2
( x x )2 s2 n 1 ( x x )2 f s2 f 1
小故事:一次失败的二战士兵调查
二战期间,美国军方委托社会学家对军队士兵进行一项抽样调查。 在进行抽样之前,研究者对军方提供的总体名单未作认真考察, 他们在不知道该单位名册是按照十个士兵组成的一个班内的军队 军衔级别进行排序的(如上士、中士和下士)的情况下,就确定 将名单混在一起作为抽样框。 具体调查过程中,研究者按照等距抽样的规则计算出抽样间距是 10,于是在每十个士兵选择出一个作为样本,这个抽样间距正好 与班内的军衔级别重合,结果导致样本中的士兵全部是上士,中 士和下士一个都没有。 显然,这个抽样没有实现具有代表性的样本,而是一个上士士兵 调查的样本,最后的调查结果不是说明所有士兵的情况,最多只 能说明军衔是上士的那些士兵的情况。调查宣告失败。
63 32 79 72 43 93
74 50 07 45 51 25
71 37 78 93 09 23
47 71 44 09 03 93
62 32 53 15 90 78
67 75 38 62 74 47
要从94家上市公司中抽取12家作为调查样本,可 先将94空公司由1至94编号N=94,然后在乱数表上 任意上一点一行(或一列)中一个数字作为起点 数,从这个数字按上下或左右顺序读起,每出现 两个数字,即为被抽中的单位码号。假定本例是 从第四行左边第五个数字向右顺序读起,则所抽 取单位是:68 27 31 05 03 72 93 15 55 59 56 35 ,此过程中的96因大于94,舍 去不用是因为在顺序抽取的过程中,遇到比编号 大的数字,应该舍去。
《审计学教程》第十一章 生产与费用循环审计

引导 案例
振隆特产IPO造假
(接上)振隆特产IPO造假
证监会认为,瑞华所应保证所有存货都有被检查的机会,从而为注册会计师针对整个 总体得出结论提供合理基础。振隆特产存货密集堆放的方式不能成为注册会计师不对垛中 心存货进行检查的理由;相反,注册会计师应避免任何有意识的偏向或可预见性,如回避 难以找到的项目。
实物流转程序控制
成本费用管理控制
在生产循环中,产品的品种和数 量一般是由生产控制部门根据顾客订 单、销货合同、市场预测等来确定, 并下达生产计划和通知单。依据实物 流转程序控制的要求,各个生产环节 的相关部门必须制定严格的责任制度。
成本费用会计控制
成本费用管理控制对成本费用支出业 务进行计划、控制,对内部控制进行考核, 其具体内容包括:① 确定成本控制目标 和成本计划;② 制定各项消耗定额,包 括直接材料、直接人工和制造费用定额; ③ 编制成本、费用预算;④ 对各项成本 费用指标进行分解,建立成本费用归口、 分级管理责任制;⑤ 定期进行成本费用 考核与评价。
(一)生产循环的内部控制
第二节 生产与费用循环的内部控制及其测试 一、生产与费用循环的内部控制
费用作为会计要素或财务报表要素的构成内容之一,是企业经营活动垫支的现金流出,涉 及企业经营管理的各个环节,关系到企业产品成本的高低和企业盈利能力的大小。一个财 务管理较好的企业必然重视费用内部责任控制与监督。
第二节 生产与费用循环的内部控制及其测试 三、生产与费用循环的控制测试
测试生产与费用循环内部控制是在了解与描述的基础上,对其在实际业务上的执行与实施 情况和过程进行检查和观察,以确定制定的内部控制与实际执行的是否相符与一致,即控 制测试。生产与费用循环进行控制测试的程序主要包括以下几个方面:
样本量的确定范文

样本量的确定范文1.研究目的和研究问题:确定样本量前,首先要明确研究目的和研究问题。
不同的研究目的和问题需要不同样本量的支持。
例如,如果是进行描述性研究,样本量可以较小;如果是进行推断性研究,样本量则需要更大。
2.效应大小:效应大小是指研究中所关注的变量之间的差异或相关性的大小。
一般来说,效应越大,需要的样本量就越小。
3.α水平和β水平:α水平是指犯第一类错误的概率,即在实际上无差异的情况下,错误地拒绝了零假设。
β水平是指犯第二类错误的概率,即在实际上存在差异的情况下,错误地接受了零假设。
一般来说,α水平设定为0.05,β水平设定为0.2、样本量的确定需要考虑α水平和β水平的要求。
4.效应检验的统计方法:样本量的确定还与所采用的统计方法有关。
不同的统计方法要求不同的样本量。
例如,如果采用参数检验方法,需要的样本量一般较多;如果采用非参数检验方法,需要的样本量可以相对较少。
在确定样本量时,通常可以通过统计学中的样本量计算方法来进行估算。
常用的样本量计算方法包括:1.Z检验的样本量计算方法:用于比较两个独立样本的平均值差异。
2.t检验的样本量计算方法:用于比较两个相关样本或配对样本的平均值差异。
3.方差分析的样本量计算方法:用于比较多个样本的平均值差异。
4.相关分析的样本量计算方法:用于评估两个变量之间的相关性。
以上提到的方法都可以在各种统计软件中找到相应的样本量计算工具,根据研究设计和数据分析方法进行计算。
最后,还需要注意的是,样本量的确定是一种平衡考虑。
过小的样本量可能导致统计检验结果不可靠,过大的样本量则会浪费资源和时间。
因此,在确定样本量时,需要综合考虑以上多个因素,并在可行的范围内选择一个合适的样本量。
抽样调查-第11章 调查中的非抽样误差

r
Y
Y
1 n
n i 1
yi
此时估计量的偏倚为:E(Y)YW0(Y1Y0)
Y 的相对偏倚可以写为:
W0(Y1 Y0) W0(1r)
Y
精选r完整W p0pt课件(1W0)
9
由上式可以看出,如果丢失单元的均值与
抽样单元的均值相同,即
r
1
,则估计量
Y
是目标变量 Y 的无偏估计。
r 反之,如果 r 1,偏倚状况则随着
精选完整ppt课件
18
三、降低无回答的措施
主要措施是预防,预防措施有: ●问卷设计得具有吸引力; ●注意适当的长度; ●充分利用调查组织单位的权威性和影响力; ●注意调查员的挑选; ●做好调查员的培训; ●注意调查过程的监控; ●奖励措施; ●再次调查。
精选完整ppt课件
19
四、对存在无回答数据的调整
6
N1
(3)抽样框误差的影响
设目标总体单元:N
抽样框中单元:N1 抽样框中丢失的单元:N0
N=N1+N0 ■ 总体总量的估计 总体总量的真值是:
N1
N1
N0
Y Yi Yi Y1Y0
i1
i1
现从抽样框中的N1个单元中采用简单随机
抽样抽出容量为n的一个样本,由于n取自于N1
对总体总量的估计为:
精选完整ppt课件
7
Y
N1 n
n i1
yi
显然此时的估计是有偏的,偏倚为:
E(Y)YY1YY0
这表明估计量低估了总体总量,令
r
Y0 Y1
,W0
N0 N
Y的相对偏倚可以写为
Y0
W0r
Y
高考数学一轮复习第十一章统计与统计案例2用样本估计总体课件新人教A版2

;b.决定组距与
组数;c. 将数据分组
;d.列频率分布表;e.画频率分布直方
图.
-3知识梳理
双基自测
(3)总体密度曲线
①频率分布折线图:连接频率分布直方图中各小长方形上端的中
点,就得到频率分布折线图.
②总体密度曲线:随着样本容量的增加,作图时所分的组数增加,
底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方
24
图如图所示,则在抽测的60株树木中,有
株树木的底部
周长小于100 cm.
解析 由题意知,在抽测的60株树木中,底部周长小于100 cm的株
数为(0.015+0.025)×10×60=24.
-11考点1
考点2
考点3
考点 1
组距减小,相应的频率分布折线图会越来越接近于一条光滑曲线,
统计中称这条光滑曲线为总体密度曲线.总体密度曲线反映了总体
在各个范围内取值的百分比,它能提供更加精细的信息.
(4)茎叶图:茎叶图中茎是指 中间 的一列数,叶是从茎的 旁边
生长出来的数.当样本数据较少时,用茎叶图表示数据的效果较好,
它不但可以保留所有信息,而且可以随时记录,给数据的记录和表
月平均用电量在[260,280)的用户有0.005×20×100=10(户),
月平均用电量在[280,300]的用户有0.002 5×20×100=5(户),抽
11
1
= ,
取比例为
25+15+10+5
5
所以月平均用电量在[220,240)的用户中应抽取25×
1
5 =5(户).
-14考点1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(二) 《文学摘要》的厄运
在1936年美国总统选举中,由《文学摘要 》杂志组织了一项民意调查,这项民意调查动 用了大量的人力物力进行调查。 在调查的基础上,该杂志预测共和党候选 人阿尔夫•伦敦将击败在任总统富兰克林•罗斯 福,这个预测准不准呢?
阿尔夫•伦敦 预测结果 55%
富兰克林•罗斯福 41%
沃尔德告诉大家,从数学家的眼光来看,这 张图明显不符合概率分布的规律,而明显违反规 律的地方往往就是问题的关键。 飞行员最终明白了数学家沃尔德这套做法的 意义。如果飞行员座舱中弹,飞行员就完了;如 果飞机尾翼中弹,飞机失去平衡就会坠落—这两 处中弹,轰炸机多半就会掉下来了,难怪顺利返 航的轰炸机只有这两处几乎没有弹孔。 结论很简单,只需给这两个部位焊上防弹钢 板就可以了,一个两难的难题就这样解决了。
2、判断抽样
判断抽样:是按照调研设计者的主观判断选取调 查单位组成样本的一种抽样方法。应用前提是, 调研设计的必须以对调查总体的有关特征相当了 解,或者可以依靠专家判断来决定样本。 在判断抽样中,样本单位的选取通常分为两种情 况: 第一种情况是,选择最能代表普遍情况的调查对 象,即选取“多数型”、或“平均型”的样本作 为调查对象。 第二种情况是,选择那些异乎寻常的个案,目的 是调查造成异常的原因。
分层抽样和整群抽样的不同之处
操作的群体不同,分层抽样操作的是分层群体 ,而整群抽样操作的是子群体; 适用的总体不同,分层抽样适用于容易按属性 差异进行群体划分的总体,而整群抽样适用于 不容易按属性差异但容易按可见标志进行群体 划分的总体。
非概率抽样
1、便利抽样 2、判断抽样 3、推荐抽样 4、配额抽样
第11章
如何选取样本
兔年春晚调查
1、您今年收看了中央电视台春节联欢晚会了吗? A、看了 B、没看 2、如果你收看了,请问您对兔年春晚的评价如何 ? A、满意 B、一般 C、不满意
春晚满意度调查数据
央视市场研究股份有限公司的调查结果是:在全国 收看电视的家庭中,有93.88%的家庭收看了中央电视台 春节联欢晚会,有 81.92%的受访者认为今年中央电视 台春节联欢晚会办得好。 腾讯网对春晚满意度调查结果显示:有38.47%的网 友给春晚打出了60-80分,而有43%的人认为今年春晚表 现不及格。 在1万多人参与的微博小秘书发起的调查中,对兔年 春晚表示“满意”的只有6%,认为“一般”的有25%, 还有59%的人表示“失望”,10%的人“没看”。
上面两个案例都涉及同一个重要问题—抽 样问题。 但是,处理方式不同,导致两种完全不同 的结果—一个有效地解决了问题,另一个则被 问题所拖累,破产倒闭了。
样本和抽样的基本概念
1、总体 2、普查 3、样本和样本单位 4、抽样框和抽样框误差 5、抽样误差
什么是抽样?
抽样:是根据一定的规则和程序,从研究总体中抽取其 中的一部分样本来代表总体的过程。
1、便利抽样
便利抽样:就是依据方便原则抽取样本,对抽 样单位的选择主要是由调查人员完成,通常被 访者由于碰巧在适当的时间出现在适当的地点 而被选中。 例如: “街头拦人法”是在街上或路口任意找某个行 人,将其作为被调查者进行调查。 利用客户的名单进行调查 将问卷登在宣传媒体上,被调查者自填后寄回
概率抽样
1、简单随机抽样 2、系统抽样 3、整群抽样 4、分层抽样
1、简单随机抽样
简单随机抽样:在简单随机抽样中,总体中所 有的成员被选为样本的概率是相等的。 简单随机抽样即完全按照随机的原则来抽取样 本。 最常见的有抽签法和随机数表法。
简单随机抽样的优点: 最简单、最典型的概率抽样技术,易于理解; 抽样框不需要其他(辅助)信息就能进行抽样; 样本结果可以推论到目标总体上,大多数统计 推论方法都假定数据是由简单随机抽样方法收 集的。
排列调查总体单位时所依的标准有两种: 一种是按与调查项目无关的标志排队。例如: 在住户调查时,选择住户可以按住户所在街区 的门牌号码排队,然后每隔若干个号码抽选一 户进行调查; 另一种是按与调查项目有关标志排队。例如: 住户调查时,可按住户平均月收入排队,再进 行抽选。
总体单位的排序决定着系统抽样的代表性,并 决定系统抽样调查结果的统计效率,分三种情 况说明: 如果排序与要研究的特征无关,则结果与简单 随机抽样相似; 当排序与要研究的特征有关时,系统抽样能增 加样本的代表性。 若排序呈现循环形式,抽样间距又与循环周期 相同时,系统抽样会降低样本的代表性。
ቤተ መጻሕፍቲ ባይዱ
分层抽样的必要性
设计抽样方法时,最核心的问题是考虑如何使 抽取的具有代表性,为此在设计抽样方法时, 我们应考虑如何利用已有的总体。 例如:调查高一学生平均身高 由经验知,男同学一般要比女同学高,这时就 要采用分层抽样,因为简单随机抽样或系统抽 样都有可能产生部分是男生(或女生)或全部 是男生(或女生)的样本,这样的样本是不能 代表总体的。
为何抽样
首先,从成本的角度看,抽样比普查更优越; 其次,专业调研公司或调研人员不可能分析处 理由普查产生的大量数据。
两种基本的抽样方法
概率抽样:样本设计采取随机的办法,排除研 究人员主观因素的干扰,使样本总体中的每一 个成员都有一个事先确定好抽中概率。 非概率抽样:样本设计依赖于研究人员的个人 判断而非随机原则选择样本个体,事先并不确 定每个样本单位被抽中的概率。
美国空军请来数学家亚伯拉罕· 沃尔德。 数学家沃尔德的方法十分简单。他把统计表 发给地勤技师,让他们把飞机上中弹弹孔的位置 报上来。他自己铺开一张大纸,画出轰炸机的轮 廓,再把那些小窟窿一个个地填上去。 画完后大家一看,飞机浑身上下都是窟窿, 只有飞行员座舱和尾翼两个地方几乎是空白。 为什么是这样? 防弹钢板应该焊在哪里呢?
分层抽样的适用条件: 分层抽样比较适用于总体由差异明显的几 个层次组成且层内差异较小进行的抽样。
分层抽样和整群抽样的相同之处
都是先对总体中的群体再对个体进行操作; 都不是完全随机地抽取样本,都涉及一定的规则 :分层随机抽样涉及的规则是分层群体之间属性 的差异,而整群随机抽样涉及的规则是子群体之 间的相似; 都能提高随机抽样的效率和改善随机抽样的结果 。
整群抽样以群体为单位进行抽选,抽选单位 比较集中,明显得影响了样本分布的均衡性。 因此,整群抽样与其他抽样比较,在抽样单 位数目相同的条件下抽差误差较大,代表性较低 ,在抽样调查实践中,采用整群抽样技术一般都 要比其他抽样技术抽选更多的单位,以降低抽样 误差,提高抽样结果的准确程度。 当然,整群抽样的可靠程度主要还是取决于 群与群之间的差异的大小,当各群间差异较小时 ,整群抽样的调查结果就越准确。 因此,在大规模的市场调查中,当群体内各 单位间的误差较大,而各群之间的差异较小时, 最适宜采用整群抽样方式。
等比例分层抽样
等比例分层抽样是按各层中的个体数量占 总体数量的比例分配各层的样本数量。 这种方法简单易行,分配合理,计算方便 ,适用于各类型之间的个数差异不大的分类抽 样调查。
不等比例分层抽样
不等比例分层抽样不提按照各层中个体数 占总体数的比例分配样本个体,而是根据其他 因素,调整各层的样本数。 不等比例分层抽样适用于各类总体的个数 相差很大的情况。
简单随机抽样的局限性: (1)采用简单随机抽样,一般必须对总体各单 位加以编号,而实际所需调查总体往往是十分 庞大的,单位非常多,逐一编号几乎是不可能 的; (2)在总体单位数不清楚的情况下,无法采用 简单随机抽样;
(3)当总体各单位差异较大时,采用简单随 机抽样抽出的样本可能会集中于某类单位,不 能做到在各种类型的单位中较为均匀分布,其 样本的代表性就比较差; (4)采用简单随机抽样抽出的样本分布较为 分散,实地调查消耗的人力、物力、费用较大 ;
【教学目标】
熟悉抽样设计的术语 了解概率抽样与非概率抽样方法的区别 了解如何使用四种概率抽样 了解如何使用四种非概率抽样 掌握不同类型抽样技能 能够制定一份抽样计划
开篇案例:两种抽样两种命运
(一)防弹钢板应焊在哪里? 第二次世界大战后期,美军对德国和日本 展开了大规模战略轰炸,每天都有成千架轰炸 机呼啸而去,返回时则往往伤亡惨重。 美国空军对此十分头痛:如果要降低损失 ,就要往飞机上焊防弹钢板;但是飞机焊上防 弹钢板后,速度、航程、载弹量都会受影响, 同样也会影响轰炸机安全返航。 这是一个两难选择,怎么办呢?
整群抽样的适用条件: 整群抽样比较适用于适用群体内各单位间 的误差较大,而各群之间的差异较小的情况。 另一种适用情况:工业抽样 例如:对工业产品进行质量调查时,每隔五个 小时,抽取一个小时的产品进行检查。
4、分层抽样
分层抽样:指将调查总体中的所有单位按照一 定的属性或特征分成不相重叠的若干层次(或 类),然后在每一个层次(或类)中进行简单随 机抽样或等距抽样。 抽样程序: 1)确定分层变量 2)分层 3)确定各层的样本量 4)在各层内部进行抽样
有人会问,81.92%的受访者满意和43%的 人认为不及格,我们相信谁? 应该说,我们都没有绝对相信的理由,因 为我们不能确知调查的科学性。例如,由央视 自己调查自己的成绩,本身就缺乏公信力;其 次,调查方法我们也不知道,包括样本如何选 择、问题如何设置都会直接影响到调查结果。 因此,我们与其相信调查数据,还如靠自 己的判断。
实际结果
37%
61%
这项全国瞩目的民意调查得出了完全错误 的结论,《文学摘要》也因此关门倒闭。 为什么会出现这样严重的错误?
一个原因是抽样框架主要是根据电话号码 簿和汽车登记册建立的。 在1936年,拥有汽车或电话的这些人显然 是富裕的美国人,这些人大多是共和党的坚定 支持者,而大多数投票选民既不拥有电话,也 不拥有汽车。 另一个问题可能是由于无回答引起的偏倚 ——总共寄出了一千多万份的问卷,但是返回 的问卷不足25%。
