第六章例题
第六章例题

[例 6.1]某高层建筑基坑开挖深度m H 5.5=。
土层重度为19.2kN/m 3,内摩擦角 18=ϕ,粘聚力kPa c 12=,地面超载kPa q 150=。
采用悬臂式排桩支护,试确定排桩的最小长度和最大弯矩。
解:沿支护墙长度方向上取1延米进行计算,则有:主动土压力系数)21845(tan )245(tan 22-=-=φa K =0.53被动土压力系数)21845(tan )245(tan 22+=+=φp K =1.89因土体为粘性土,按朗肯土压力理论,墙顶部压力为零的临界高度为m K K q K c z a a a a 94.053.02.1953.01553.01222=⨯⨯-⨯=-=γ基坑开挖底面处土压力强度20/46.4653.012253.0)5.52.1915(2)(m kN K c K H q a a aH =⨯⨯-⨯⨯+=-+=γσ土压力零点距开挖面的距离m K K K K c K H q x a p a p a a 52.0)()(2)(=-+-+=γγ土压力分布示意图如例图6-14所示。
图6-14 例6-1图墙后土压力 E a 1=21×46.46×(5.5-0.94)=105.9kN/mE a 2=21×46.46×0.52=12.1 kN/m 墙后土压力合力 21a a a E E E +==105.9+12.1=118.0 kN/m合力作用点距地表的距离为[]mE h E h E h aa a a a a 15.40.118)3/52.05.5(1.123/2)94.05.5(94.09.1052211=+⨯+⨯-+⨯=+=将a E 和h a 代人式0)()(6)(63=--+---a p aa a p a K K E h x H t K K E t γγ得0)53.089.1(2.190.118)15.452.05.5(6)53.089.1(2.190.11863=-⨯⨯-+⨯--⨯⨯-t t即 07.501.273=--t t 解得 m t 97.5=,取增大系数2.1'=t K ,则得 桩最小长度m t x h l 2.1397.52.152.05.52.1min =⨯++=++=最大弯矩点距土压力零点距离m K K E x a p a m 0.32.19)53.089.1(0.1182)(2=⨯-⨯=-=γ最大弯矩mm kN x K K E h x x H M ma p a a m /.6.49260.3)53.089.1(2.19)15.40.352.05.5(0.1186)()(33max =⨯-⨯--++⨯=---++=γ[例6-2]某基坑工程开挖深度h=7.0m ,采用单支点桩墙支护结构,支点离地面距离 h T =1.2m ,支点水平间距为m S h 5.1=。
第六章例题

1.精馏塔中恒摩尔流假设,主要依据是各组分的________ ,但精馏段与提馏的摩尔流量由于________影响而不一定相等。
2.溶液的相对挥发度等于两组份________ ,а>1则表示组分A和B________ ,а=1则表示组分A和B________ 。
3.当某塔板上_______________时,该塔板称为理论塔板。
4.精馏过程的回流比是指________ ,最小回流比是指________。
5.在设计连续操作的精馏塔时,如保持x F,D/F,x D,R一定,进料热状态和选用的操作气速也一定,则增大进料量将使塔径________ ,而所需的理论板数________。
6.塔设计中求取精馏理论板时,以过两操作线交点的那块板作为最佳加料板位置时,所需理论数量最少,其原因是________ 。
7.精馏塔操作时,若加料板由最佳位置上移两板,则x D ________,x W ________ 。
(1)变小(2 )变大(3)不变(4)不确定8.某操作中的精馏塔,维持F、q 、X D、、V′不变,但XF增大,则D________ ,R ________ 。
(1)变小(2 )变大(3)不变(4)不确定9.填料塔设计时,空塔气速一般取________气速的60%-80%,理由________ 。
若填料层高度较高,为了有效地湿润填料,塔内应设置________装置。
一般而言,填料塔的压降________板式塔压降。
(>,=,<=)15.未饱和湿空气与同温度水接触,则传质方向为________。
若未饱和空气中的水汽分压与水表面的饱和蒸汽压相同,则传热方向为________ 。
例6-1每小时将15000kg含苯40%(质量%,下同)和甲苯60%的溶液,在连续精馏塔中进行分离,要求釜残液中含苯不高于2%,塔顶馏出液中苯的回收率为%。
试求馏出液和釜残液的流量及组成,以摩尔流量和摩尔分率表示。
解:苯的分子量为78;甲苯的分子量为92。
第六章 分层总和法和规范法计算的例子
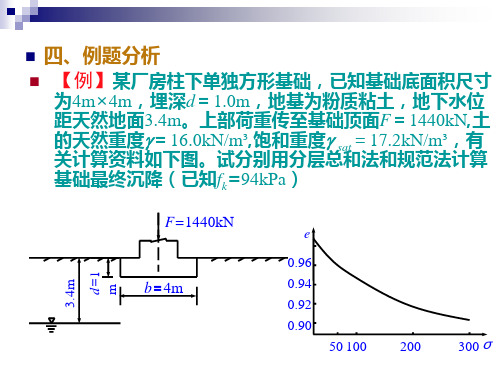
2.4 1.2 0.1516 57.0 54.4
4.0 2.0 0.0840 31.6 65.9
5.6 2.8 0.0502 18.9 77.4 0.24
7.2 3.6 0.0326 12.3 89.0 0.14 7.2
6.确定沉降计算深度zn
根据σz = 0.2σc的确定原则,由计算结果,取zn=7.2m
• 由公式得:S sS
•式中
S
p0 Es1
(z11)
p0 Es 2
( z2 2
z11 )
94( 2.4 0.8596 5.5
7.8 0.4544 2.4 0.8596) 6.5
56.68mm
经计算得7.2米处,沉降量为55.7
根据计算表所示△z=0.6m, △sn =1mm <0.025Σ si =1.39mm
基底附加压力:p0 D 110 16 94kPa
(3)求平均附加应力系数
采用角点法,分成四小块(每小块面积为l×b = 2×2 m2)进行计算。基础底
面至计算深度zn处分两层(以地下水位面为分界面)。
由z1=2.4m,z2 = zn = 7.8m ,
l
b =1.0 ,
z1 b
四、例题分析
【例】某厂房柱下单独方形基础,已知基础底面积尺寸
为4m×4m,埋深d=1.0m,地基为粉质粘土,地下水位 距天然地面3.4m。上部荷重传至基础顶面F=1440kN,土
的关天计然算重资料度如=下16图.0。kN试/m分³,别饱用和分重层度总 sa和t=法17和.2规kN范/m法³,计有算
ቤተ መጻሕፍቲ ባይዱ
按分层总和法求得基础最终沉降量为s=Σsi =54.7mm
电力系统第六章例题

B点折算到高压侧电压: 按调压要求10kV母线电压在最大负荷时不低于9.5kV和最小负运
行不高于10.5kV,则可得分接头: 取平均值: 选择变压器最接近的分接头 所以选-2.5%分接头,即 按所选分接头校验10kV母线的实际电压 电压偏移= 电压偏移= 可见,10kV母线上的电压在最小负荷与最大负荷时电压偏差不超过
解:
(1) 计算线路和变压器等值阻抗。 总阻抗Z
(2) 计算补偿前变电所二次侧母线归算到高压侧的电压。 因为首端电压已知,宜用首端功率计算网络的电压损耗。为此,先按额定电压计算输电系统的 功率损耗: 于是 利用首端功率可以算出:
(3) 选择静电电容器的容量 按最小负荷时无补偿确定变压器的分接头电压 最接近的抽头电压为110kV,可得降压变压器的变比为 求补偿容量 取补偿容量,且检验变电所二次侧母线电压 故 变电所二次侧母线电压满足调压要求。
因此 于是可选用110+5%的分接头,分接头电压为115.5kV。 (4) 校验低压母线电压。 最大负荷时: 最小负荷时: 低压母线电压偏移: 最大负荷时: 最小负荷时: 虽然最大负荷时的电压偏移要求较要求的低0.833%,但由于分接头
之间的电压差为2.5%, 求得的电压偏移较要求不超过1.25%是允许的,
-7 一条阻抗为21+j34Ω的110kV单回线路,将降压变电所与负荷中心连接,最大负荷为 22+j20MVA。线路允许的电压损耗为6%,为满足此要求在线路上串联标准为单相、 0.66kV、40kVA的电容器。试确定所需电容器数量和容量。
解: 未加串联电容时线路的电压损耗 允许电压损耗 由此可求所需电容器的容抗 得 线路的最大负荷电流 单个电容器的额定电流及额定容抗分别为 电容器组并联的组数应大于 取m=3 每串串联个数应大于 取n=6 则电容器组总数量 3mn=54个 电容器组总容量 验算电压损耗:实际电容器组的容抗 这时线路的电压损耗
第六章例题

[例6-1]设有三相对称电流θcos I i a =,)120cos( -=θI i b ,)120cos(+=θI i c ,t 'ωθθ+= 。
若d ,q 轴的旋转速度为ω,即t ωαα+= 。
试求三相电流的d ,q ,0轴分量。
解:利用变换式(6-30),可得])'()cos[()cos(t I I i d ωωθαθα-+-=-= ])'()sin[()sin(t I I i q ωωθαθα-+--=--=00=i现就'''0,,2ωωωωω===三种情况,将a ,b ,c 系统和d ,q ,0系统的电流列于表6-2。
[例6-2]已知同步发电机的参数为:X d =1.0,X q =0.6,85.0cos =ϕ。
试求在额定满载运行时的电势E q 和E Q 。
解:用标幺值计算,额定满载时V=1.0,I=1.0。
(1) 先计算E Q 。
由图6-15的向量图可得22)cos ()sin (ϕϕI X I X V E q q Q ++==41.1)85.06.0()53.06.01(22=⨯+⨯+(2) 确定QE •的相位。
向量QE •和V •间的相角差2153.06.0185.06.0arctansin cos arctan=⨯+⨯=+=ϕϕδI X V I X q q也可以直接计算QE •同I •的相位差)(ϕδ+ϕδ+= 5385.06.053.0arctancos sin arctan=+=+ϕϕV I X V q(3) 计算电流和电压的两个轴向分量8.053sin )sin(==+=I I I d ϕδ6.053cos )cos(==+= I I I q ϕδ36.021sin sin === V V V d δ93.021cos cos === V V V q δ(4) 计算空载电势q E 。
qE =QE +(dX -q X ) dI =1.41+(1-0.6)⨯0.8=1.73[例6-3] 就例6-2的同步发电机及所给运行条件,在给出'd X =0.3,试计算电势'q E 和'E 。
第六章 时序逻辑电路的分析与设计典型例题
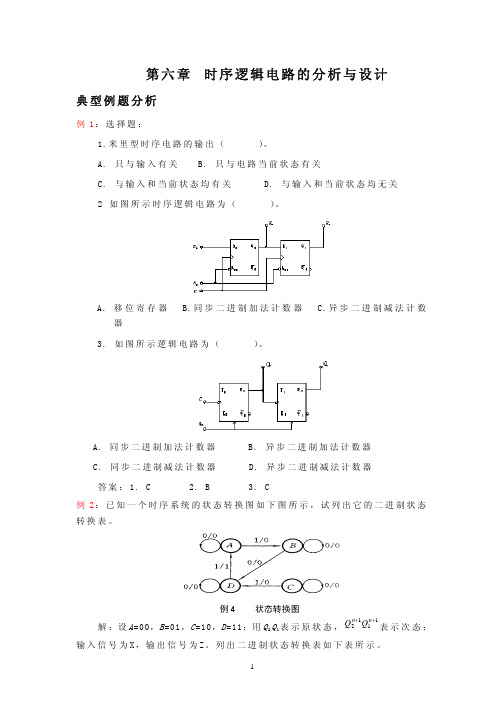
解:解题步骤如下: ( 1) 求 激 励 输 入 议 程 :
⎧ J 3 = Q2 , ⎨ ⎩K 3 = Q2 ⎧ J 2 = Q1 , ⎨ ⎩ K 2 = Q1 ⎧ J 1 = Q3 ⊕Q1 ⎨ ⎩K1 = J 1
因 为 将 J 3 = Q 2 , K 3 = Q2 代 入 J - K 触 发 器 次 态 方 程 , 有
3
n +1 励 方 程 D3、 D2、 D1中 , 然 后 根 据 D触 发 器 次 态 方 程 Q = D , 可 知 所 有 的 非 工
作 状 态 都 能 进 入 工 作 状 态 , 即 101→ 001; 110→ 101→ 001; 111→ 001。 因 此 电路可以自启动。 ( 6) 画 完 整 状 态 转 换 图 如 下 图 所 示 。
J 1 = Q3 Q1 + Q3 Q1 + Q2 Q1 = Q3 ⊕ Q1 + Q2 Q1
修改后,具有自启动功能的电路如下图所示。
修改后的可自启动电路
5
Q1n +1 0 0 1 1 0
D3
0 1 0 0 0
D2
1 0 0 1 0
D1
0 0 1 1 0
0 1 0 0 0
1 0 0 1 0
( 3) 求 激 励 输 入 方 程 组 。 首 先 要 根 据 状 态 转 换 真 值 表 , 画 D3、 D2、 D1的 卡 诺 图 , 然 后 通 过 卡 诺 图 化 简 得 到 激 励 输 入 方 程 。 D3、 D2、 D1的 卡 诺 图 如 下 图所示。
S0— — 为 初 始 状 态 以 及 不 属 于 以 下 定 义 的 状 态 ; S1— — 收 到 首 个 1; S2— — 收 1 后 再 收 1; S3— — 收 11 后 再 收 0; S4— — 收 110 后 再 收 1。
第六章例题

(c
'
'
)
180
90
tg
1 c
'
'
90
77
.2
12
.8
'' m (c '') 12.8 36.9
49.7 45符合要求
共175页第4页
确定开环增益K
6-3 串联校正
稳态误差的要求
画出未校正系统的伯德图,并求
L''(c '') L'(c '') Lc (m ) 查图 Lc (m ) 10 lg a ,计算 a
作用而不能正常工作
• 当()在c附近变化很大,由于校 正后
3、不宜
c提高,则 必须很大。
•
当c不允许提高时
6-3 串联校正
共175页第15页
6-3 串联校正
4.4
a 4
共175页第3页
6-3 串联校正
T 1 0.114 s
c '' a
1 0.456s 4Gc (s) 1 0.114s 校正后系统传递函数
G(s) 10(0.456 s 1) s(0.114 s 1)(s 1)
3)校验:
m
arcsin a 1 36.9 a 1
解:1)根据 ,确e定ss 开环增益,系统为I 型系统,r(t) t ,
ess 1/ K 0.1, K 10 , 这里取 K 10。
2)利用已确定的开环增益,计算未校正系统的相角裕度
L(
)
20 20
lg(10 lg(10
/ /
), 2 ),
1 1
共175页第10页
机械原理典型例题第六章齿轮

(6)当渐开线圆柱齿轮的齿数少于 时,可采用___A_的办法来避免根切。 A. 正变位 B. 负变位 C. 减少切削深度
(7)一对渐开线直齿圆柱标准齿轮的实际中心距大于无侧隙啮合中心距时, 啮合角___A_分度圆上的压力角,实际啮合线____B_。 A. 大于 B. 小于 C. 等于 A. 变长 B.变短 C.不变
角为20°,其余参数(包括齿数、模数、压力角、齿制、齿宽等)
均相等,则该两对齿轮传动时的重合度相等。 X
(13)渐开线直齿圆锥齿轮的标准参数取在齿宽中点处。X (14)直齿圆锥齿轮背锥上的齿廓曲线是球面渐开线. X
17
3.填空题:
1)渐开线直齿圆柱齿轮传动的主要优点为 定传动比、可,和分性 。
2)渐开对线于齿在廓恒上定K转点矩的的压传力动角中应,是轮齿间正压力的大所小夹和的方锐向角始,终齿不廓变上各点
15
2.判断题:
(1)一对能正确啮合传动的渐开线直齿圆柱齿轮,其啮合角一定为20°。X (2)渐开线标准齿轮的齿根圆恒大于基圆。 X (3)影响渐开线齿廓形状的参数有Z、α等,但同模数无关。 X (4) m,α,ha*,c*都是标准值的渐开线直齿圆柱齿轮,一定是标准直齿圆
柱齿轮。 X (5)渐开线直齿圆柱外齿轮,不管是标准的,还是变位的,其齿顶压力角
(1)轮坯由滚齿机传动机构带动,以w=1/22.5rad/s的角 速度转动。在切制标准齿轮时,滚刀轴向截面的齿条 中线相对于轮坯中心的距离L应等于多少?这时滚刀轴 向截面齿条移动速度V刀等于多少?
(2)如滚刀位置和齿条移动速度不变,而轮坯的角速 度w=1/23.5rad/s,则此时被切齿数为多少?它相当于 哪种变位齿轮?变位系数x为多少?
财务管理学---第6章-例题答案

第6章资本结构决策【例1·单选题】以下各种资本结构理论中,认为筹资决策无关紧要的是( B )。
A.代理理论B.无税MM理论C.融资优序理论D.权衡理论【解析】按照MM理论(无税),不存在最佳资本结构,筹资决策也就无关紧要。
【例2·计算分析题】某企业取得5年期长期借款200万元,年利率为10%,每年付息一次,到期一次还本,借款费用率0.2%,企业所得税税率20%,要求计算该借款的资本成本率。
【按照一般模式计算】银行借款资本成本率=[10%×(1-20%)]/(1-0.2%)=8.02%【按照折现模式计算】现金流入现值=200×(1-0.2%)=199.6(万元)现金流出现值=200×10%×(1-20%)×(P/A,K b,5)+200×(P/F,K b,5)=16×(P/A,K b,5)+200×(P/F,K b,5)16×(P/A,K b,5)+200×(P/F,K b,5)=199.6用8%进行第一次测试:16×(P/A,8%,5)+200×(P/F,8%,5)=16×3.9927+200×0.6806=200>199.6用9%进行第二次测试:16×(P/A,9%,5)+200×(P/F,9%,5)=16×3.8897+200×0.6499=192.22<199.6采用内插法:解之得K b=8.05%【例3·单选题】甲公司某长期借款的筹资净额为95万元,筹资费率为筹资总额的5%,年利率为4%,所得税税率为25%。
假设用一般模式计算,则该长期借款的筹资成本为(B)。
A.3%长期借款筹资总额=长期借款筹资净额/(1-长期借款筹资费率)=95/(1-5%)=100(万元)长期借款筹资成本=[筹资总额×利率×(1-所得税率)]/筹资净额=[100×4%×(1-25%)]/95=3.16% 【例4·计算分析题】某企业以1100元的价格,溢价发行面值为1000元、期限为5年、票面利率为7%的公司债券一批。
第六章成本逼近法

第六章成本逼近法例题分析1.成本逼近法的基本公式为:土地价格一土地取得费+土地开发费+利息+利润十土地增值收益。
( )答案:×解析:成本逼近法的基本公式为:土地价格=土地取得费+土地开发费+利息+利润+税费+土地增值收益。
2.采用成本逼近法评估地价时,土地取得费及其税费利息是以整个取得费为基数,计息期为整个开发期的一半。
( )答案:×解析:采用成本逼近法评估地价时,土地取得费及其税费利息是以整个取得费为基数,计息期为整个开发期。
3.若土地取得费10万元/亩,开发费用10万元/亩,开发周期为一年,开发费用均匀投入,当地一年期贷款利息率为10%,则用成本逼近法计算地价时,两次费用的利息之和为2万元/亩。
( )答案:×解析:土地取得费的利息应当是整个开发周期,计息期为一年,10×(1+10%)1;开发费用均匀投入,以整个开发费为基数,计息期为开发期(或资金投入期)的一半,10×(1+10%)0.5,答案为×。
练习题一、判断题1.采用成本逼近法进行地价评估,其中的土地取得费是指因土地所有权由农民集体所有转为国家所有而发生的费用。
( )2.成本逼近法一般适用于有收益的商业物业的评估。
( )3.成本逼近法以成本累加为途径,而成本高并不一定表明效用和价值高。
( )4.成本逼近法一般适用于新开发土地估价,也适用建成区域已开发土地估价。
( )5.土地取得费按该地块被征用前3年平均产值的6~10倍计算。
( )6.在成本逼近法中计算利润时,以土地取得费、土地开发费、税费、利息为计算利润的基数。
( )7.征地是土地买卖活动,征地费用也就是土地购买价格。
( )8.土地开发费用分摊的基本原理为:应分摊费用=受益程度×设施总费用。
( )9.采用成本逼近法进行评估时,土地取得费和土地开发费应以实际取得和开发利用土地时实际投入来计算。
( )10.土地增值是待估宗地因改变用途或进行土地开发,达到建设用地的某种利用条件而发生的价值增加。
第六章:挡土墙及土压力计算

2. 当墙后填土为粘性土时——为了得到确切的解析解,库仑理论假设墙后填土为无粘性土,当用粘性土回填时,在
BC 面上各力合成时,将出现粘聚力之和 C = c.BC 弧长,由于 BC 弧长度是变量,故无法得其确切解析解;C 参与合成
后,C、N 和 f 三者之和设为 RD,由图知:RD 一定位于 R 的下方,即 RD 与 N 之间的夹角φD 一定大于 R 与 N 之 间的夹角φ ,鉴于此,实用中,可考虑将粘性土的φ值适当增大,用增大后的Δφ来近似考虑 c 值对土压力的影响。
pp3 (1 h1 2 h2 q) / m22 2c2 / m2 (19 4.0 18 3.5 20) 0.577 2 212 0.577 518.57(kPa)
E p1
1 4.0 (69.39 224.49) 2
587.76(kN /
m)
Ep2
1 2
(329.57 518.57) 3.5
例题 1:某土样进行剪切试验,测得破坏时剪切破坏面上的应力如表 1,试根据测试结果计算土的抗剪强度指标;若 已知土中某点的大主应力σ1 =410kPa 、小主应力σ3 = 200kPa,试判断该点处于何种应力状态? 表 1 土样破坏时剪切破坏面上的应力值
解:根据τf= σ .tanφ +c 得:22.466= 50.0*tanφ+c <1>
的土压力称为主动土压力,记为 Ea 。
2.被动土压力 Ep——在外力作用下,挡土墙发生挤向土体方向的位移,墙后填土达到极限平衡状态,此时墙背上的
土压力称为被动土压力,记为 Ep 。
3.静止土压力 Eo——墙土间无位移,墙后填土处于弹性平衡状态,此时墙背上的土压力称为静止土压力,记为 Eo 。
第六章例题

第六章 电力系统的无功功率和电压调整6-3 如图6-3所示,某降压变电所装设一台容量为20MV A 、电压为110/11kV 的变压器,要求变压器低压侧的偏移在大小负荷时分别不超过额定值的2.5%和7.5%,最大负荷为18MV A ,最小负荷为7MV A ,8.0cos =ϕ,变压器高压侧的电压在任何运行情况下均维持107.5kV ,变压器参数为:U k %=10.5, P k =163kW ,激磁影响不计。
试选择变压器的分接头。
6-3 解:变压器参数为2222163110 4.93()1000100020k NT N PU R S ⨯===Ω⨯ 22%10.511063.5()10010020k N T N U U X S ⨯===Ω⨯末端负荷为:max min 18cos 18sin 180.8180.614.410.8()7cos 7sin 70.870.6 5.6 4.2()S j j j MVA S j j j MVA ϕϕϕϕ⎧=+=⨯+⨯=+⎨=+=⨯+⨯=+⎩按调压要求,变压器低压侧实际电压应为max min10(1 2.5%)10.2510(17.5%)10.75i i U U '=+=⎧⎨'=+=⎩在变压器上的电压损耗为PR QXU U+∆=,于是有 maxIm max max min Im minmin 14.4 4.9310.863.5107.5 5.6 4.93 4.263.5107.5i ax i i in i U U U U U U U U ⨯+⨯⎧=-∆=-⎪⎪⎨⨯+⨯⎪'=-∆=-⎪⎩107.5kV P 2+j Q 2图50 习题解图6-320MV A 110/11kVP i +Q i习题图6-3解得: max i U =99.9,min i U =104.6然而 maxmax maxIm minmin 1199.9107.2()10.2511104.6107()10.75iN TI i i iN T in i i U U U KV U U U U KV U ⎧==⨯=⎪'⎪⎨⎪==⨯=⎪'⎩max Im 107.2107107.1()22TI T in TI U U U KV ++===故选分接头电压为110(1-2.5%)=107.25kV 的分接头。
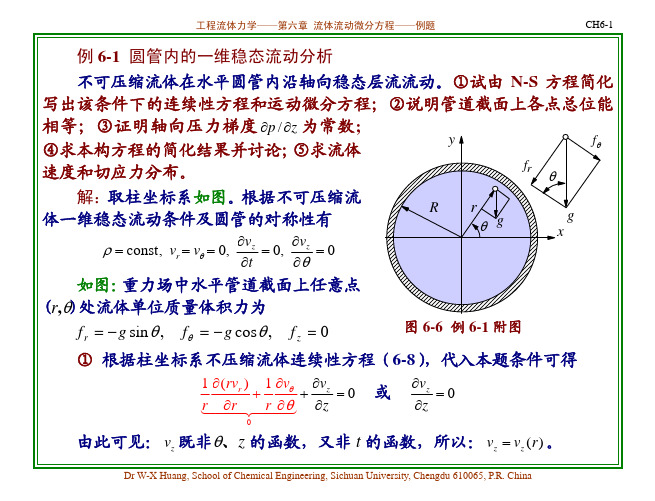
第6章-流体流动微分方程-例题
0 0 0
θ:
2 v ∂v v v ∂vθ ∂v ⎡ ∂ ⎛1 ∂ 1 1 ∂p ⎞ 1 ∂ vθ 2 ∂vr ⎤ + ν ⎢ ⎜ (rvθ) + + vr θ + θ θ + r θ = fθ − + ⎟ 2 ρ r ∂θ r r ∂θ r
∂r ⎝ r ∂r ∂t ∂r ∂θ 2 r 2 ∂θ ⎥ ⎠ ⎣ ⎦
工程流体力学——第六章 流体流动微分方程——例题
CH6-5
r:
2 ⎡ ∂ ⎛1 ∂ ∂vr ∂v v ∂v v 2 1 ∂p ⎞ 1 ∂ vr 2 ∂vθ ⎤ + vr r + θ r − θ = f r − + − 2 + ν ⎢ ⎜ (rvr) ⎥ ⎟ 2 2 r r ∂ r ∂θ ⎦ θ r N ρ ∂r ∂t ∂ ∂r ⎝ r ∂r ⎠ r ∂θ ⎣
∂vz dv =μ z ∂r dr
由此可知:(a)不可压缩一维稳态层流每点各方向正应力=-p,因此分析 相应问题时微元体表面正应力可直接以压力标注;(b)管内流体既有沿 z 方向 的切应力,同时也伴随有 r 方向的切应力。 ⑤ 因 ∂p*/ ∂z = ∂p / ∂z =const 且 vz =vz (r ) ,故 z 方向运动方程为常微分方程, 其边界条件为 vz r = R = 0 、 (dvz /dr ) r =0 = 0 ;积分运动方程并以 −Δp /L 替代 ∂p / ∂z 可得 速度分布,进而得到切应力分布,其结果为:
CH6-7
对于内筒转动外筒固定的情况, 由于离心 力与压差力均指向外壁, 两者都促使流体向外 层运动, 故流体沿切向的层流流动难以保持稳 定。该条件下,雷诺数定义及过渡雷诺数分别 为:
第六章例题

解: (1)定位基准与工序基准重合, ∆。
(2)定位基准相对于限位基准单向 移动,定位基准移动方向与加工尺寸 间的夹角为 ° ‘,则有
∆
.
.
°
(3)∆
.( )
∆
.
例4:铣轴零件外圆上的键槽,以圆柱面 在
°的V型
块上定位,不考虑V型块α角的制造误差,求加工尺寸分别为
, , 时的定位误差。
解: (1)加工尺寸 的定位误差:
1)垂直度的工序基准是Φ25H7孔轴线,定位基准也是Φ25H7
孔轴线,基准重合。 ∆
。
2) Φ25H7孔与长圆柱销 存在配合间隙,定位基准 相对限位基准可以两个方 向转动。
/ ∆
.
.
.
此处槽深为8mm,所以基准位移误差为
∆
∆
.
.
3)定位误差∆
.
,由于定位误差只有垂直度要
求(0.08mm)的1/8,故此装夹方案的定位精度足够。
① 的工序基准是圆柱轴线,定位基准也是圆柱轴线。两
者重合,∆
② 定位基准与限位基准不重合,两者的相对位移量为:
与加工尺寸方向一致,故∆ ③∆ ∆
(2)加工尺寸 的定位误差: ① 的工序基准是圆柱下母线,定位基准是圆柱轴线。两
者不重合,定位尺寸 ( ) ,故∆
。
② 定位基准与限位基准不重合:∆
③ 工序基准在定位基面上:当定位基面直径有大变小时,定 位基准朝下变动;当定位基面直径由大变小时,假定定位 基准不动,工序基准朝上变动,两者变动方向相反,取 “-”号。
∆ ∆ ∆=
=(
)
(3)加工尺寸 的定位误差: ① 的工序基准是圆柱上母线,定位基准是圆柱轴线。两
第六章-个人所得税例题答案

第六章个人所得税【例题-判断题6-1】如果一个外籍技术人员从2007年l0月起到中国境内的公司任职,在2008纳税年度内,曾于3月7~l2日离境回国,向其总公司述职,l2月23日又离境回国欢度圣诞节和元旦。
请问,该外籍技术人员,是否我国的居民纳税义务人?【答案】因为这两次离境时间相加,没有超过90日的标准,应视作临时离境,不扣减其在华居住天数。
因此,该纳税义务人应为居民纳税人。
【例题-多选题6-2】下列各项中,属于个人所得税居民纳税人的有()。
A.在中国境内无住所,但一个纳税年度中在中国境内居住满1年的个人B.在中国境内无住所且不居住的个人C.在中国境内无住所,而在境内居住超过6个月不满1年的个人D.在中国境内有住所的个人【答案】A.D[解析]本题考核个人所得税居民纳税人的判断。
税法规定,居民纳税人是在中国境内有住所的个人,或者在中国境内无住所,但居住时间满1年的。
因此本题的正确选项为A.D。
【例题-多选题6-3】我国个人所得税采用了()税率。
A比例税率B超额累进税率C定额税率D全额累进税率【答案】AB【例题-多选题6-4】下列各项中,适用5%~35%的五级超额累进税率征收个人所得税的有()。
A.个体工商户的生产经营所得B.合伙企业的生产经营所得C.个人独资企业的生产经营所得D.对企事业单位的承包经营、承租经营所得【答案】ABCD 个体工商户的生产、经营所得和对企事业单位的承包经营、承租经营所得,适用5%~35%的超额累进税率;个人独资企业和合伙企业的个人投资者取得的生产经营所得,也适用5%~35%的五级超额累进税率。
【例题-单选题6-5】下列所得中应计入工资薪金所得纳税的是()。
A.职工的加班补贴B.独生子女补贴C.托儿补贴D.误餐补贴【答案】A【例题-计算题6-6】赵先生为中国国籍,居住在中国,2011年10月1日领取工资为7000元,其中“三险一金”为500元,请计算赵先生每月需要缴纳多少个人所得税?【答案】首先确定应纳税所得额:7000-500-3500=3000其次确定税率和扣除数:3000应适用10%的税率和105的速算扣除数最后确定应纳税额为:3000×10%-105=195元【例题-计算题6-7】沈先生2011年11月工资为4500元,缴纳的“三险一金”为250元,请问,沈先生每月工资薪金所得应当缴纳多少税款?【答案】4500-250-3500=750;确定税率及速算扣除数:3%,0;应纳税款为:750×3%=22.5【例题-计算题6-8】某外商投资企业中工作的美国专家(假设为非居民纳税人),2011年11月份取得由该企业发放的工资收入l0000元人民币。
《工程造价案例分析》第六章例题

1.三个概念(三条 S 曲线)(已完工程实际投资、已完工程计划投资、拟完工程计划投 资)
2.三个公式 投资偏差=已完工程实际投资-已完工程计划投资 进度偏差=拟完工程计划投资-已完工程计划投资(用投资表示) 进度偏差=已完工程实际时间-已完工程计划时间(用时间表示) 3.三条线的来源(横道图、时标网络图) 4.实际进度前锋线
(0.5 分)
按合同多退少补,即应在第 3 个月末扣回多支付的 O.39 万元的措施费。 (0.5 分)
评分说明:以上计算式合并计算时,合并给分。
问题 6. 施工单位第 1 个月应得进度款为: (42.34+10.25)×(1+4.89%)(1+3.47%)×(1-3%)-16.89/2 =46.92(万元)
施费用以分部分项工程量清单计价合价为基数进行结算。剩余的 4 项措施费用共计 16 万元,
一次性包死,不得调价。全部措施项目费在开工后的第 1 个月末和第 2 月末按措施项目清单
中的数额分两次平均支付,环境保护措施等 3 项费用调整部分在最后一个月结清,多退少补。
(3)其他项目清单中只包括招标人预留金 5 万元,实际施工中用于处理变更洽商,最
表 3.2
工程量 月份 分项工程名称
850
1、2、3 月份实际完成的工程量表
950
300
单位:m3
1
2
3
4
5
6
A
560
550
B
680
1050
C
450
D
问题: 1.该工程预付款为多少万元?应扣留的保留金为多少万元? 2.各月应抵扣的预付款各是多少万元? 3.根据表 3.2 提供数据,计算 1、2、3 月份造价工程师应确认的工程进度款各为多少万
高中数学第六章平面向量及其应用经典大题例题(带答案)

高中数学第六章平面向量及其应用经典大题例题单选题1、在△ABC 中,点D 在边AB 上,BD =2DA .记CA ⃗⃗⃗⃗⃗ =m →,CD⃗⃗⃗⃗⃗ =n →,则CB ⃗⃗⃗⃗⃗ =( ) A .3m →−2n →B .−2m →+3n →C .3m →+2n →D .2m →+3n →答案:B分析:根据几何条件以及平面向量的线性运算即可解出.因为点D 在边AB 上,BD =2DA ,所以BD ⃗⃗⃗⃗⃗⃗ =2DA ⃗⃗⃗⃗⃗ ,即CD ⃗⃗⃗⃗⃗ −CB ⃗⃗⃗⃗⃗ =2(CA ⃗⃗⃗⃗⃗ −CD⃗⃗⃗⃗⃗ ), 所以CB ⃗⃗⃗⃗⃗ =3CD ⃗⃗⃗⃗⃗ −2CA ⃗⃗⃗⃗⃗ =3n ⃗ −2m ⃗⃗ =−2m →+3n →.故选:B .2、已知单位向量a →,b →,则下列说法正确的是( )A .a →=b →B .a →+b →=0→C .|a →|=|b →|D .a →//b →答案:C分析:利用向量的有关概念及单位向量的定义依次判断即得.对于A ,向量a →,b →为单位向量,向量a →,b →的方向不一定相同,A 错误;对于B ,向量a →,b →为单位向量,但向量a →, b →不一定为相反向量,B 错误;对于C ,向量a →,b →为单位向量,则|a →|=|b →|=1,C 正确;对于D ,向量a →,b →为单位向量,向量a →,b →的方向不一定相同或相反,即a →与b →不一定平行,D 错误. 故选:C.3、向量PA ⃗⃗⃗⃗⃗ =(k,12),PB ⃗⃗⃗⃗⃗ =(4,5),PC⃗⃗⃗⃗⃗ =(10,k).若A,B,C 三点共线,则k 的值为( ) A .−2B .1C .−2或11D .2或−11答案:C分析:求得BA ⃗⃗⃗⃗⃗ ,,利用向量共线的充要条件,可得关于k 的方程,求解即可. 解:由题可得:BA⃗⃗⃗⃗⃗ =PA ⃗⃗⃗⃗⃗ −PB ⃗⃗⃗⃗⃗ =(k,12)−(4,5)=(k −4,7), CA u u u rCA⃗⃗⃗⃗⃗ =PA ⃗⃗⃗⃗⃗ −PC ⃗⃗⃗⃗⃗ =(k,12)−(10,k )=(k −10,12−k ). 因为A,B,C 三点共线,所以BA⃗⃗⃗⃗⃗ ∥CA ⃗⃗⃗⃗⃗ ,所以(k −4)(12−k )−7(k −10)=0,整理得k 2−9k −22=0,解得k =−2或k =11.故选:C.4、如图,在梯形ABCD 中,AB ∥DC 且AB =2DC ,点E 为线段BC 的靠近点C 的一个四等分点,点F 为线段AD的中点,与BF 交于点O ,且AO ⃗⃗⃗⃗⃗ =xAB⃗⃗⃗⃗⃗ +yBC ⃗⃗⃗⃗⃗ ,则x +y 的值为( )A .1B .57C .1417D .56答案:C分析:由向量的线性运算法则化简得到AO ⃗⃗⃗⃗⃗ ==(x −y 2)AB ⃗⃗⃗⃗⃗ +2yAF ⃗⃗⃗⃗⃗ 和BO ⃗⃗⃗⃗⃗ =(1−x)BA ⃗⃗⃗⃗⃗ +4y 3BE ⃗⃗⃗⃗⃗ ,结合B,O,F 三点共线和A,O,E 三点共线,得出2x +3y −2=0和3x −4y =0,联立方程组,即可求解.根据向量的线性运算法则,可得AO⃗⃗⃗⃗⃗ =xAB ⃗⃗⃗⃗⃗ +yBC ⃗⃗⃗⃗⃗ =xAB ⃗⃗⃗⃗⃗ +y(BA ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ ) =xAB ⃗⃗⃗⃗⃗ −yAB ⃗⃗⃗⃗⃗ +yAC ⃗⃗⃗⃗⃗ =(x −y)AB ⃗⃗⃗⃗⃗ +y ⋅(AD ⃗⃗⃗⃗⃗ +DC⃗⃗⃗⃗⃗ ) =(x −y)AB ⃗⃗⃗⃗⃗ +y ⋅(2AF ⃗⃗⃗⃗⃗ +12AB ⃗⃗⃗⃗⃗ )=(x −y)AB ⃗⃗⃗⃗⃗ +2yAF ⃗⃗⃗⃗⃗ +12yAB ⃗⃗⃗⃗⃗ =(x −y 2)AB ⃗⃗⃗⃗⃗ +2yAF ⃗⃗⃗⃗⃗ , 因为B,O,F 三点共线,可得x −y 2+2y =1,即2x +3y −2=0;又由BO ⃗⃗⃗⃗⃗ =BA ⃗⃗⃗⃗⃗ +AO ⃗⃗⃗⃗⃗ =BA ⃗⃗⃗⃗⃗ +xAB ⃗⃗⃗⃗⃗ +yBC ⃗⃗⃗⃗⃗ =BA ⃗⃗⃗⃗⃗ −xBA ⃗⃗⃗⃗⃗ +y ⋅43BE ⃗⃗⃗⃗⃗ =(1−x)BA ⃗⃗⃗⃗⃗ +4y 3BE ⃗⃗⃗⃗⃗ , 因为A,O,E 三点共线,可得1−x +4y 3=1,即3x −4y =0,联立方程组{2x +3y −2=03x −4y =0,解得x =817,y =617,所以x +y =1417. 故选:C.5、若|AB⃗⃗⃗⃗⃗ |=5,|AC ⃗⃗⃗⃗⃗ |=8,则|BC ⃗⃗⃗⃗⃗ |的取值范围是( ) A .[3,8]B .(3,8)C .[3,13]D .(3,13) AE答案:C分析:利用向量模的三角不等式可求得|BC⃗⃗⃗⃗⃗ |的取值范围. 因为|BC⃗⃗⃗⃗⃗ |=|AC ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ |,所以,||AC ⃗⃗⃗⃗⃗ |−|AB ⃗⃗⃗⃗⃗ ||≤|BC ⃗⃗⃗⃗⃗ |≤|AC ⃗⃗⃗⃗⃗ |+|AB ⃗⃗⃗⃗⃗ |,即3≤|BC ⃗⃗⃗⃗⃗ |≤13. 故选:C.6、已知正三角形ABC 的边长为4,点P 在边BC 上,则AP⃗⃗⃗⃗⃗ ⋅BP ⃗⃗⃗⃗⃗ 的最小值为( ) A .2B .1C .−2D .−1答案:D分析:选基底,用基向量表示出所求,由二次函数知识可得.记|BP⃗⃗⃗⃗⃗ |=x ,x ∈[0,4] 因为AP⃗⃗⃗⃗⃗ =BP ⃗⃗⃗⃗⃗ −BA ⃗⃗⃗⃗⃗ , 所以AP⃗⃗⃗⃗⃗ ⋅BP ⃗⃗⃗⃗⃗ =BP ⃗⃗⃗⃗⃗ 2−BA ⃗⃗⃗⃗⃗ ⋅BP ⃗⃗⃗⃗⃗ =|BP ⃗⃗⃗⃗⃗ |2−2|BP ⃗⃗⃗⃗⃗ |=x 2−2x =(x −1)2−1≥−1. 故选:D7、若点M 是△ABC 所在平面内的一点,且满足3AM ⃗⃗⃗⃗⃗⃗ -AB⃗⃗⃗⃗⃗ -AC ⃗⃗⃗⃗⃗ =0→,则△ABM 与△ABC 的面积之比为( ) A .1∶2B .1∶3C .1∶4D .2∶5答案:B分析:由平面向量的加法结合已知可得M 为AD 的三等分点,然后由等高的三角形面积之比等于底边之比可得. 如图,D 为BC 边的中点,则AD ⃗⃗⃗⃗⃗ =12(AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ ) 因为3AM⃗⃗⃗⃗⃗⃗ -AB ⃗⃗⃗⃗⃗ -AC ⃗⃗⃗⃗⃗ =0→ 所以3AM⃗⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ =2AD ⃗⃗⃗⃗⃗ , 所以AM ⃗⃗⃗⃗⃗⃗ =23AD⃗⃗⃗⃗⃗ 所以S △ABM =23S △ABD =13S △ABC .故选:B8、如图,等腰梯形ABCD 中,AB =BC =CD =3AD ,点E 为线段CD 上靠近D 的三等分点,点F 为线段BC 的中点,则FE ⃗⃗⃗⃗⃗ =( )A .−1318AB ⃗⃗⃗⃗⃗ +518AC ⃗⃗⃗⃗⃗ B .−1318AB ⃗⃗⃗⃗⃗ +118AC ⃗⃗⃗⃗⃗ C .−1118AB ⃗⃗⃗⃗⃗ +49AC ⃗⃗⃗⃗⃗ D .−1118AB ⃗⃗⃗⃗⃗ +119AC⃗⃗⃗⃗⃗ 答案:B 分析:以AB⃗⃗⃗⃗⃗ ,AC ⃗⃗⃗⃗⃗ 为基底,利用平面向量线性运算的相关运算化简即可. FE⃗⃗⃗⃗⃗ =FC ⃗⃗⃗⃗⃗ +CE ⃗⃗⃗⃗⃗ =12BC ⃗⃗⃗⃗⃗ +23CD ⃗⃗⃗⃗⃗ =12(AC ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ )+23(BA ⃗⃗⃗⃗⃗ +23CB ⃗⃗⃗⃗⃗ ) =12AC ⃗⃗⃗⃗⃗ −12AB ⃗⃗⃗⃗⃗ −29AB ⃗⃗⃗⃗⃗ −49AC ⃗⃗⃗⃗⃗ =−1318AB ⃗⃗⃗⃗⃗ +118AC⃗⃗⃗⃗⃗ 故选:B多选题9、在△ABC 中,若(a 2+c 2−b 2)tanB =√3ac ,则角B 的值可以为( )A .π6B .π3C .2π3D .5π6答案:BC分析:利用余弦定理边化角可整理得到sinB ,结合B ∈(0,π)可得结果.∵(a 2+c 2−b 2)tanB =√3ac ,∴a 2+c 2−b 22ac ⋅tanB =cosB ⋅sinB cosB =sinB =√32, 又B ∈(0,π),∴B =π3或2π3.故选:BC.10、下列说法中正确的是( )A .平面向量的一个基底{e 1⃗⃗⃗ ,e 2⃗⃗⃗ }中,e 1⃗⃗⃗ ,e 2⃗⃗⃗ 一定都是非零向量.B .在平面向量基本定理中,若a =0⃗ ,则λ1=λ2=0.C .若单位向量e 1⃗⃗⃗ 、e 2⃗⃗⃗ 的夹角为2π3,则e 1⃗⃗⃗ 在e 2⃗⃗⃗ 方向上的投影向量是−12e 2⃗⃗⃗ .D .表示同一平面内所有向量的基底是唯一的.答案:ABC分析:由平面向量基本定理,依次判定即可选项A :作为基底的两个向量一定不共线,零向量与任意向量共线,因此e 1⃗⃗⃗ ,e 2⃗⃗⃗ 一定都是非零向量,故A 正确; 选项B :a =0⃗ =0⋅e 1⃗⃗⃗ +0⋅e 2⃗⃗⃗ ,由在同一基底下向量分解的唯一性,有λ1=λ2=0,故B 正确;选项C :e 1⃗⃗⃗ 在e 2⃗⃗⃗ 方向上的投影向量为:e 1⃗⃗⃗⃗ ⋅e 2⃗⃗⃗⃗ |e 2⃗⃗⃗⃗ |e 2⃗⃗⃗ =−12e 2⃗⃗⃗ ,故C 正确; 选项D :平面内任何两个不共线的向量都可作为基底,因此基底不是唯一的,故D 错误故选:ABC11、如图,B 是AC 的中点,BE⃗⃗⃗⃗⃗ =2OB ⃗⃗⃗⃗⃗ ,P 是平行四边形BCDE 内(含边界)的一点,且OP ⃗⃗⃗⃗⃗ =xOA ⃗⃗⃗⃗⃗ +yOB⃗⃗⃗⃗⃗ (x,y ∈R ),则下列结论正确的为( )A .当x =0时,y ∈[2,3]B .当P 是线段CE 的中点时,x =−12,y =52C .若x +y 为定值1,则在平面直角坐标系中,点P 的轨迹是一条线段D .x −y 的最大值为−1答案:BCD解析:利用向量共线的充要条件判断出A 错,C 对;利用向量的运算法则求出OP⃗⃗⃗⃗⃗ ,求出x ,y 判断出B 对,过P 作PM//AO ,交OE 于M ,作PN//OE ,交AO 的延长线于N ,则OP⃗⃗⃗⃗⃗ =ON ⃗⃗⃗⃗⃗⃗ +OM ⃗⃗⃗⃗⃗⃗ ,然后可判断出D 正确. 当x =0时,OP⃗⃗⃗⃗⃗ =yOB ⃗⃗⃗⃗⃗ ,则P 在线段BE 上,故1≤y ≤3,故A 错 当P 是线段CE 的中点时,OP ⃗⃗⃗⃗⃗ =OE ⃗⃗⃗⃗⃗ +EP ⃗⃗⃗⃗⃗ =3OB ⃗⃗⃗⃗⃗ +12(EB ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ ) =3OB ⃗⃗⃗⃗⃗ +12(−2OB ⃗⃗⃗⃗⃗ +AB ⃗⃗⃗⃗⃗ )=−12OA ⃗⃗⃗⃗⃗ +52OB ⃗⃗⃗⃗⃗ ,故B 对 x +y 为定值1时,A ,B ,P 三点共线,又P 是平行四边形BCDE 内(含边界)的一点,故P 的轨迹是线段,故C 对如图,过P 作PM//AO ,交OE 于M ,作PN//OE ,交AO 的延长线于N ,则:OP⃗⃗⃗⃗⃗ =ON ⃗⃗⃗⃗⃗⃗ +OM ⃗⃗⃗⃗⃗⃗ ;又OP⃗⃗⃗⃗⃗ =xOA ⃗⃗⃗⃗⃗ +yOB ⃗⃗⃗⃗⃗ ;∴x ⩽0,y ⩾1; 由图形看出,当P 与B 重合时:OP ⃗⃗⃗⃗⃗ =0⋅OA ⃗⃗⃗⃗⃗ +1⋅OB⃗⃗⃗⃗⃗ ; 此时x 取最大值0,y 取最小值1;所以x −y 取最大值−1,故D 正确故选:BCD小提示:名师点评若OC⃗⃗⃗⃗⃗ =xOA ⃗⃗⃗⃗⃗ +yOB ⃗⃗⃗⃗⃗ ,则A,B,C 三点共线⇔x +y =1. 12、下列说法正确的有( )A .若|a →+b →|=|b →|且b →≠0,则a →=0→B .设a →,b →是非零向量,若|a →+b →|=|a →−b →|,则a →⊥b →C .若a →b →=a →c →且a →≠0,则b →=c →D .设a →,b →是非零向量,若|a →+b →|=|a →|−|b →|,则存在实数λ,使得a →=λb → 答案:BD分析:A. 举反例说明该命题错误;B.若|a →+b →|=|a →−b →|,所以a →⋅b →=0,则a →⊥b →,所以该命题正确;C. 若a →b →=a →c →=0且a →≠0,则a →⊥b →,a →⊥c →,所以b →,c →不一定相等,所以该命题错误;D. 分析得a →与b →反向,因此存在实数λ,使得b →=λa →,所以该命题正确.A. 若a →=−2b →≠0→也满足已知,但是a →≠0→,所以该命题错误;B.若|a →+b →|=|a →−b →|,所以a →2+b →2+2a →⋅b →=a →2+b →2−2a →⋅b →,∴a →⋅b →=0,则a →⊥b →,所以该命题正确;C. 若a →b →=a →c →=0且a →≠0,则a →⊥b →,a →⊥c →,所以b →,c →不一定相等,所以该命题错误;D. 若|a →+b →|=|a →|−|b →|,则|a →|2+|b →|2+2a →b →=|a →|2+|b →|2−2|a →||b →|,得a →b →=−|a →||b →|,则a →,b →的夹角的余弦cosθ=−1,则a →与b →反向,因此存在实数λ,使得b →=λa →,所以该命题正确.故选:BD13、已知a ,b ,c 分别为△ABC 的三个内角A ,B ,C 的对边,∠C =45°,c =√2,a =x ,若满足条件的三角形有两个,则x 的值可能为( )A .1B .1.5C .1.8D .2答案:BC分析:利用正弦定理求得sinA =12x ,再根据三角形有两解的条件可得A ∈(45∘,135∘),且A ≠90∘,由此求出x 的范围即可得解.在△ABC 中,由正弦定理得,sinA =asinC c =∘√2=12x , 因满足条件的三角形有两个,则必有A ∈(45∘,135∘),且A ≠90∘,即√22<sinA <1, 于是得√22<12x <1,解得√2<x <2,显然x 可取1.5,1.8. 故选:BC填空题14、给出下列命题:①零向量没有确定的方向;②在正方体ABCD -A 1B 1C 1D 1中,AC ⃗⃗⃗⃗⃗ =A 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ;③若向量a 与向量b ⃗ 的模相等,则a ,b⃗ 的方向相同或相反; ④在四边形ABCD 中,必有AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ =AC⃗⃗⃗⃗⃗ . 其中正确命题的序号是________.答案:①②分析:根据零向量、相等向量、向量和及向量模等概念逐一判断.①正确;②正确,因为AC ⃗⃗⃗⃗⃗ 与A 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ 的大小和方向均相同;③|a|=|b ⃗ |,不能确定其方向,所以a 与b ⃗ 的方向不能确定;④只有当四边形ABCD 是平行四边形时,才有AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ =AC⃗⃗⃗⃗⃗ .综上可知,正确命题为①②. 故答案为:①②15、如图所示,在矩形ABCD 中,AB =√2,BC =2,点E 在边CD 上,且DE ⃗⃗⃗⃗⃗ =2EC ⃗⃗⃗⃗⃗ ,则AE ⃗⃗⃗⃗⃗ BE⃗⃗⃗⃗⃗ 的值是________. 答案:329 sin sin a c A C分析:由于向量的数量积可以进行坐标运算,所以将几何问题转化为代数问题,建立以A 为原点, AB 所在直线为x 轴的平面直角坐标系,分别写出A 、B 、E 的坐标,再通过向量的坐标运算即可求出向量的数量积.解析 以A 为原点,AB 所在直线为x 轴、AD 所在直线为y 轴建立如图所示平面直角坐标系.∵AB =√2,BC =2,∴A (0,0),B (√2,0),C (√2,2),D (0,2),∵点E 在边CD 上,且DE⃗⃗⃗⃗⃗ =2EC ⃗⃗⃗⃗⃗ , ∴E (2√23,2).∴AE ⃗⃗⃗⃗⃗ =(2√23,2),BE ⃗⃗⃗⃗⃗ =(−√23,2), ∴AE ⃗⃗⃗⃗⃗ BE ⃗⃗⃗⃗⃗ =−49+4=329. 16、设a →,b →为单位向量,且|a →+b →|=1,则|a →−b →|=______________.答案:√3分析:整理已知可得:|a +b ⃗ |=√(a +b ⃗ )2,再利用a ,b ⃗ 为单位向量即可求得2a ⋅b ⃗ =−1,对|a −b⃗ |变形可得:|a −b ⃗ |=√|a |2−2a ⋅b⃗ +|b ⃗ |2,问题得解. 因为a ,b ⃗ 为单位向量,所以|a |=|b⃗ |=1 所以|a +b ⃗ |=√(a +b ⃗ )2=√|a |2+2a ⋅b ⃗ +|b ⃗ |2=√2+2a ⋅b⃗ =1 解得:2a ⋅b⃗ =−1 所以|a −b ⃗ |=√(a −b ⃗ )2=√|a |2−2a ⋅b⃗ +|b ⃗ |2=√3 所以答案是:√3小提示:本题主要考查了向量模的计算公式及转化能力,属于中档题.解答题17、康平滕龙阁,位于康平县中央公园中心,建在有“敖包朝霞”之称的敖包山旧址上,是老百姓心中的祥瑞之地.如图,小明同学为测量滕龙阁的高度,在滕龙阁的正东方向找到一座建筑物AB,高为8米,在地面上的点M(B,M,D三点共线)测得楼顶A,滕龙阁顶部C的仰角分别为15°和60°,在楼顶A处测得阁顶部C的仰角为30°,试替小明求滕龙阁的高度?(精确到0.01米)答案:37.86米分析:在△ACM中,利用正弦定理求得CM,然后在Rt△CDM中,由CD=CMsin60°求解.解:由题意得,在Rt△ABM中,AM=ABsin15°,在△ACM中,∠CAM=30°+15°=45°,∠AMC=180°−15°−60°=105°,所以∠ACM=30°,由正弦定理AMsin∠ACM =CMsin∠CAM,得CM=sin∠CAMsin∠ACM ⋅AM=√2ABsin15°,又sin15°=sin(45°−30°)=√22×√32−√22×12=√6−√24,在Rt△CDM中,CD=CMsin60°=√6AB2sin15°=√62×√6−√24=24+8√3≈37.86.答:滕龙阁的高度约为37.86米.18、如图,在直角梯形OABC中,OA//CB,OA⊥OC,OA=2BC=2OC,M为AB上靠近B的三等分点,OM交AC于D,P为线段BC上的一个动点.(1)用OA ⃗⃗⃗⃗⃗ 和OC⃗⃗⃗⃗⃗ 表示OM ⃗⃗⃗⃗⃗⃗ ; (2)求OD DM ;(3)设OB⃗⃗⃗⃗⃗ =λCA ⃗⃗⃗⃗⃗ +μOP ⃗⃗⃗⃗⃗ ,求λ⋅μ的取值范围. 答案:(1)OM ⃗⃗⃗⃗⃗⃗ =23OA ⃗⃗⃗⃗⃗ +23OC ⃗⃗⃗⃗⃗ ;(2)3;(3)[0,34]. 分析:(1)根据给定条件及几何图形,利用平面向量的线性运算求解而得;(2)选定一组基向量,OD⃗⃗⃗⃗⃗⃗ 将由这一组基向量的唯一表示出而得解; (3)由动点P 设出CP ⃗⃗⃗⃗⃗ =xOA ⃗⃗⃗⃗⃗ (0≤x ≤12),结合平面向量基本定理,λ⋅μ建立为x 的函数求解. (1)依题意CB ⃗⃗⃗⃗⃗ =12OA ⃗⃗⃗⃗⃗ ,AM ⃗⃗⃗⃗⃗⃗ =23AB ⃗⃗⃗⃗⃗ , ∴AM ⃗⃗⃗⃗⃗⃗ =23(OB ⃗⃗⃗⃗⃗ −OA ⃗⃗⃗⃗⃗ )=23(OC ⃗⃗⃗⃗⃗ +CB ⃗⃗⃗⃗⃗ )−23OA ⃗⃗⃗⃗⃗ =23OC ⃗⃗⃗⃗⃗ +13OA ⃗⃗⃗⃗⃗ −23OA ⃗⃗⃗⃗⃗ =23OC ⃗⃗⃗⃗⃗ −13OA ⃗⃗⃗⃗⃗ , ∴OM ⃗⃗⃗⃗⃗⃗ =OA ⃗⃗⃗⃗⃗ +AM ⃗⃗⃗⃗⃗⃗ =OA ⃗⃗⃗⃗⃗ +(23OC ⃗⃗⃗⃗⃗ −13OA ⃗⃗⃗⃗⃗ )=23OA ⃗⃗⃗⃗⃗ +23OC ⃗⃗⃗⃗⃗ ; (2)因OM 交AC 于D ,由(1)知OD ⃗⃗⃗⃗⃗⃗ =tOM ⃗⃗⃗⃗⃗⃗ =t(23OA ⃗⃗⃗⃗⃗ +23OC ⃗⃗⃗⃗⃗ )=OD ⃗⃗⃗⃗⃗⃗ =2t 3OA ⃗⃗⃗⃗⃗ +2t 3OC ⃗⃗⃗⃗⃗ , 由共起点的三向量终点共线的充要条件知,2t 3+2t 3=1,则t =34,OD ⃗⃗⃗⃗⃗⃗ =3DM ⃗⃗⃗⃗⃗⃗ ,|OD ⃗⃗⃗⃗⃗⃗||DM ⃗⃗⃗⃗⃗⃗⃗ |=3; (3)由已知OB ⃗⃗⃗⃗⃗ =OC ⃗⃗⃗⃗⃗ +CB ⃗⃗⃗⃗⃗ =OC ⃗⃗⃗⃗⃗ +12OA ⃗⃗⃗⃗⃗ , 因P 是线段BC 上动点,则令CP ⃗⃗⃗⃗⃗ =xOA ⃗⃗⃗⃗⃗ (0≤x ≤12), OB⃗⃗⃗⃗⃗ =λCA ⃗⃗⃗⃗⃗ +μOP ⃗⃗⃗⃗⃗ =λ(OA ⃗⃗⃗⃗⃗ −OC ⃗⃗⃗⃗⃗ )+μ(OC ⃗⃗⃗⃗⃗ +CP ⃗⃗⃗⃗⃗ )=(λ+μx)OA ⃗⃗⃗⃗⃗ +(μ−λ)OC ⃗⃗⃗⃗⃗ , 又OC ⃗⃗⃗⃗⃗ ,OA ⃗⃗⃗⃗⃗ 不共线,则有{μ−λ=1λ+μx =12⇒{λ=μ−1μ=32+2x, 0≤x ≤12⇒1≤x +1≤32⇒1≤μ≤32, λ⋅μ=μ(μ−1)=(μ−12)2−14在μ∈[1,32]上递增,所以μ=1,(λ⋅μ)min =0,μ=32,(λ⋅μ)max =34,故λ⋅μ的取值范围是[0,34].小提示:由不共线的两个向量为一组基底,用该基底把相关条件和结论表示成向量的形式,再通过向量的运算来解决.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例6-
例6-
例6-
例6-
plot(t,u,'-.')
hold off
test(1,3,0.8,'输入\rightarrow')
text(5.4,0.8,'\leftarrow 输出')
例6-8
P124 离散时间系统重新采样函数d2d()
sys=d2d(model,Ts)
dstep(num,den) 离散系统单位阶跃响应
dimpulse(num,den) 离散系统单位脉冲响应
dsim(num,den) 离散系统任意函数的激励响应
G1=tf([1 1],[1 1 10]);
G0=c2d(G1,0.02,'zoh');
Gc=tf([1 -0.5],[0.1 0],0.02);
Wz=G0*Gc/(1+G0*Gc);
(1)建立一阶微分方程组
(2)建立描述系统微分方程的m-函数文件ehpcs.m
采用了带参数的ODE函数的调用
function dx=ehpcs(t,x,flag,ps)
kv=3.4e-8;Ap=0.006;ct=7e-12;bv=7e-12;m=25;
dx=zeros(3,1);
up=200*(2*sin(6*pi*t)-10*x(1));
plotyy(T1,X1(:,2),T1,X1(:,3))
text(0.4,2.5,'\leftarrow负载速度')
text(0.3,-1.8,'负载压力'\rightarrow')
xlabel('t(s)')
例6-4求单位阶跃响应
sys=tf([1,-1],[1,1,5]);
subplot(1,2,1),step(sys,20)
sys1=ss(A,B,C,D);
X0=[1 2]';
initial(sys1,X0)
例6-7 方波信号作用下的响应
sys=ft([3,100],[1,10,40,100]);
[u,t]=gensig('square',5,10);
lsim(sys,'r',u,t)
hold on
连续系统离散化函数c2d,调用格式为:
sysd=ced(sysc,Ts,method) %method为模型转换方法,零阶保持器为'zoh'
例6-1 已知某系统运动方程及初始条件,求时间区间t的微分方程的解。
(1)建立描述系统微分方程的m-函数文件rigit.m
function dy=rigit(t,y)
[num,den]=tfdata(Wz,'v');
subplot(2,1,1),dstep(num,den) %用step求系统单位阶跃响应
xlabel('time(samples)')
text(80,0.65,'dstep()')
subplot(2,1,2),step(Wz)
xlabel('time(samples)')
sys2=tf(num,den);
setp(sys1,'r',sys2,'b-.')
legend('状态空间模型','传递函数模型')
impulse(sys)用来计算单位脉冲响应
例6-6
A=[-0.5572 -0.7814;0.7814 0];
B=[1 0]';C=[1.6287 3.5609];D=0;
dy=zeros(2,1);
dy(1)=y(2);
dy(2)=(1-y(1)^2)*y(2)-y(1)
(3)主程序:
[T,Y]=ode45('vdp',[0 20],[0,1]);
plot(T,Y(:,1),'r-',Y,Y(:,2),'b:')
legend('y1','y2')
例6-3
subplot(1,2,2),step(sys)
例6-5 多系统
A=[-0.55=[1 0]';C=[1.6287 3.5609];D=0;
sys1=ss(A,B,C,D);
num=[3000];den=[1 40 440 300 584];
ps=5e6;[T2,X2]=ode45('ehpcs',tspan,x0,odeset,ps);
plot(T1,X1(:,1),'r',T2,X2(:,1),'b-.')
legend('Ps=2MPa','Ps=5MPa')
xlabel('t(s)'),ylabel('x(m)')
负载速度和压力曲线:
dy=zeros(3,1);
dy(1)=y(2)*y(3);
dy(2)=-y(1)*y(3);
dy(3)=-2*y(1)*y(2);
(2)编写调用函数rigit()的M文件,并执行
[T,y]=odc45('rigit',[0,20],[0,0.5,-0.5]); %调用odc45产生离散点时间向量和解向量
dx(1)=x(2);
dx(2)=Ap/m*x(3);
dx(3)=-Ap/bv*x(2)-ct/bv*x(3)+up*kv/bv*sqrt(ps-sign(up)*x(3));
主程序:
tspan=[0,0.7];x0=[0,0,0];
ps=2e6;[T1,X1]=ode45('ehpcs',tspan,x0,odeset,ps);
plot(T,y(:,1),'r',T,y(:,2),'b*',T,y(:,3),'k_.')
legend('y1','y2','y3')
例6-2已知二阶微分方程,求时间区间t的微分方程的解
(1)将微分方程表示为一阶微分方程组
(2)建立描述系统微分方程的m-函数文件vdp.m
function dy=vdp(t,y)
